Projection and Uncertainty Analysis of Future Temperature Change over the Yarlung Tsangpo-Brahmaputra River Basin Based on CMIP6
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Materials
2.3. BMA Estimation
2.4. Evaluation Metrics of Ensemble Mean
2.5. Uncertainty Estimation
2.6. Determine the Optimal Training Period
3. Results and Discussion
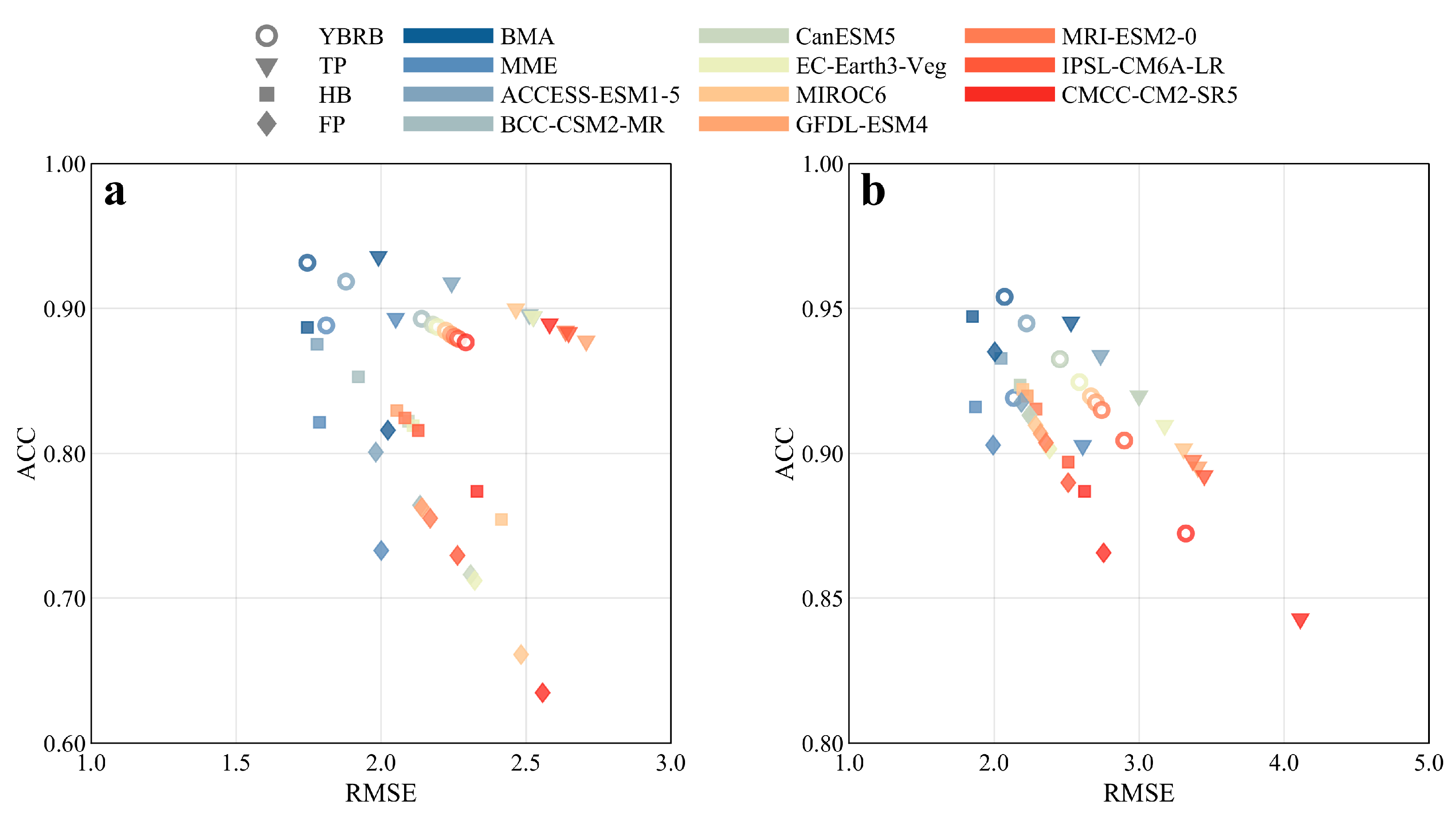
3.1. Evaluation of BMA Simulation
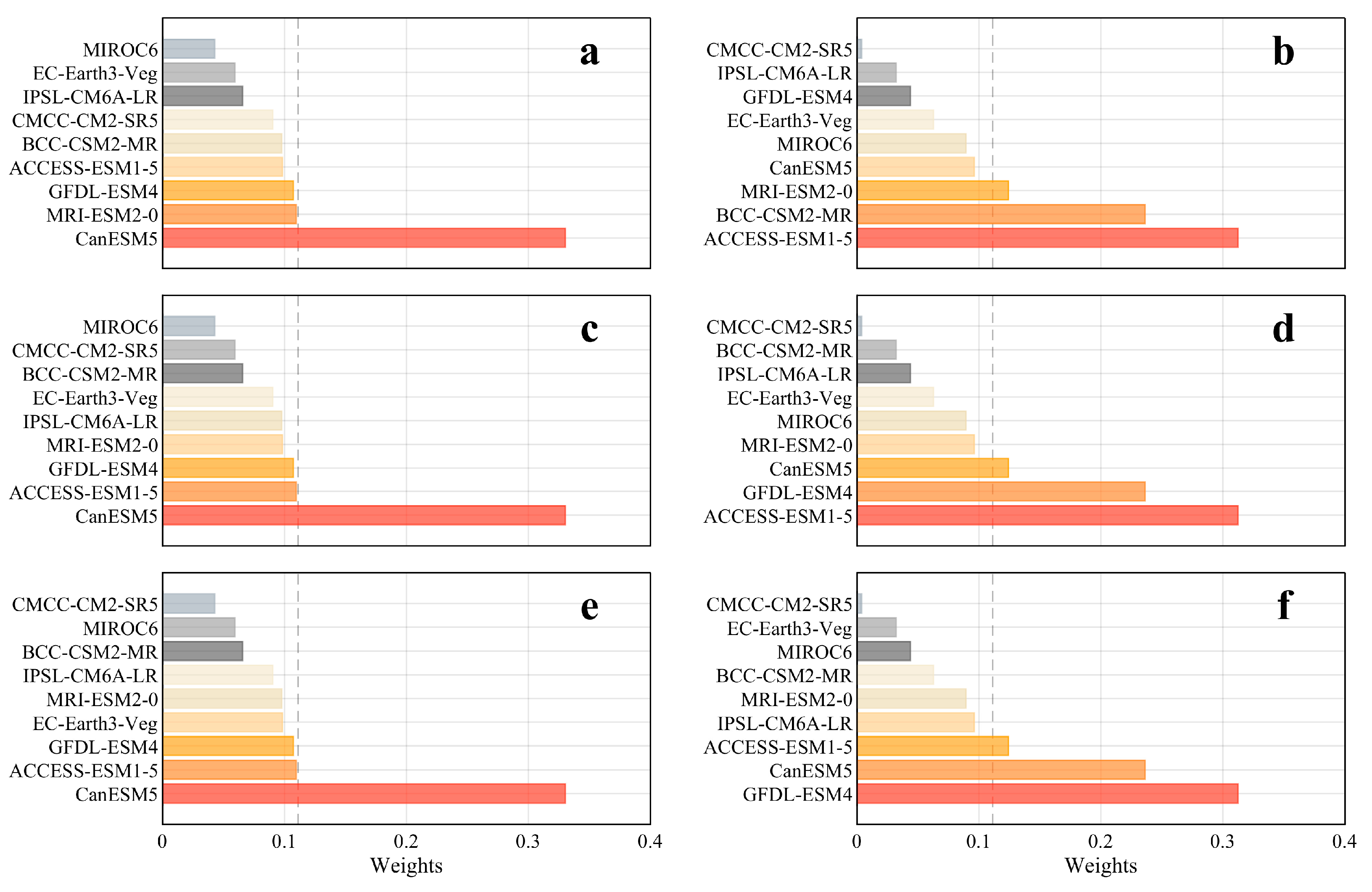
3.2. Evaluation of Weighted Model Performance
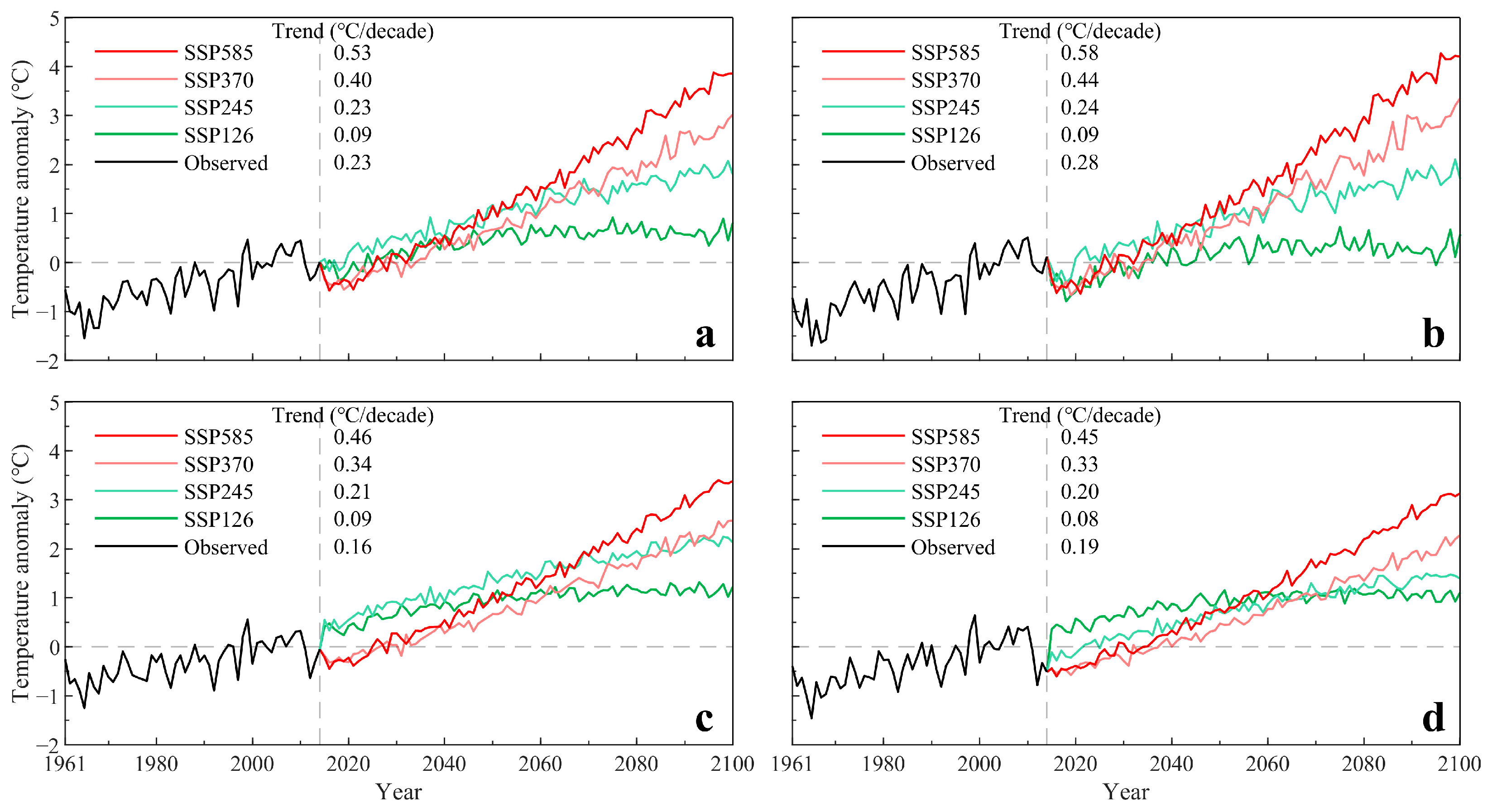
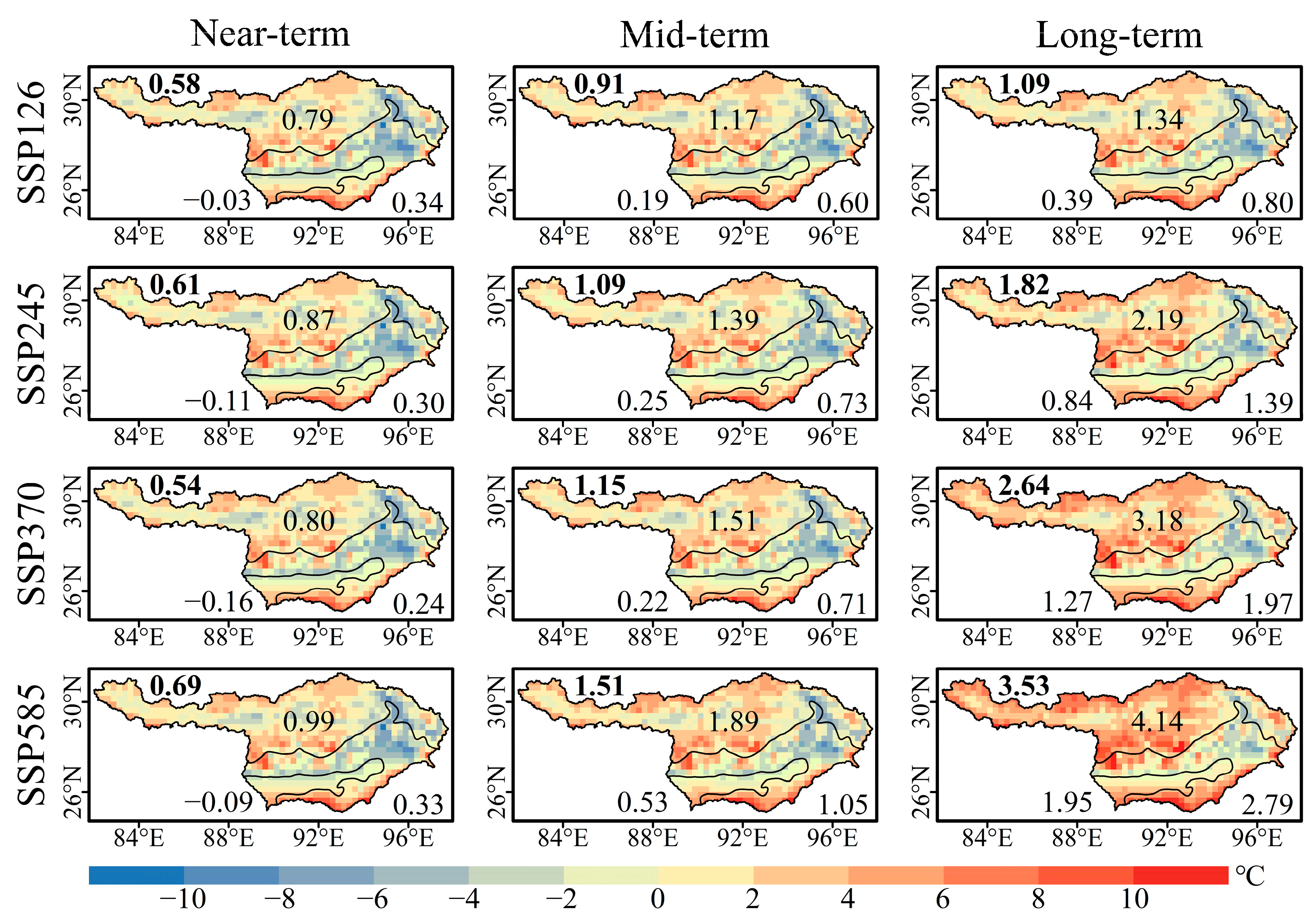
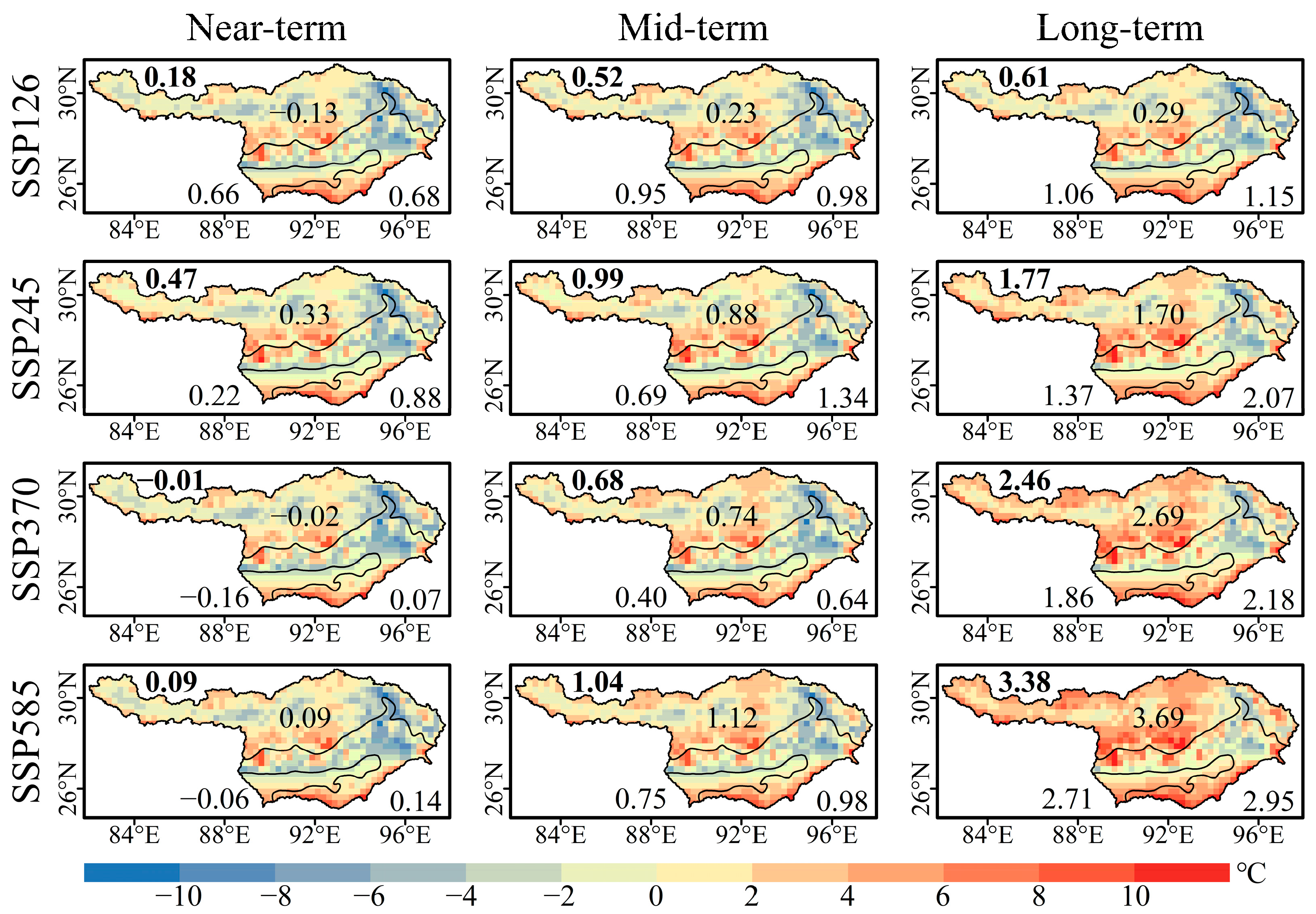
3.3. Spatiotemporal Distribution of Future YBRB Temperature Changes
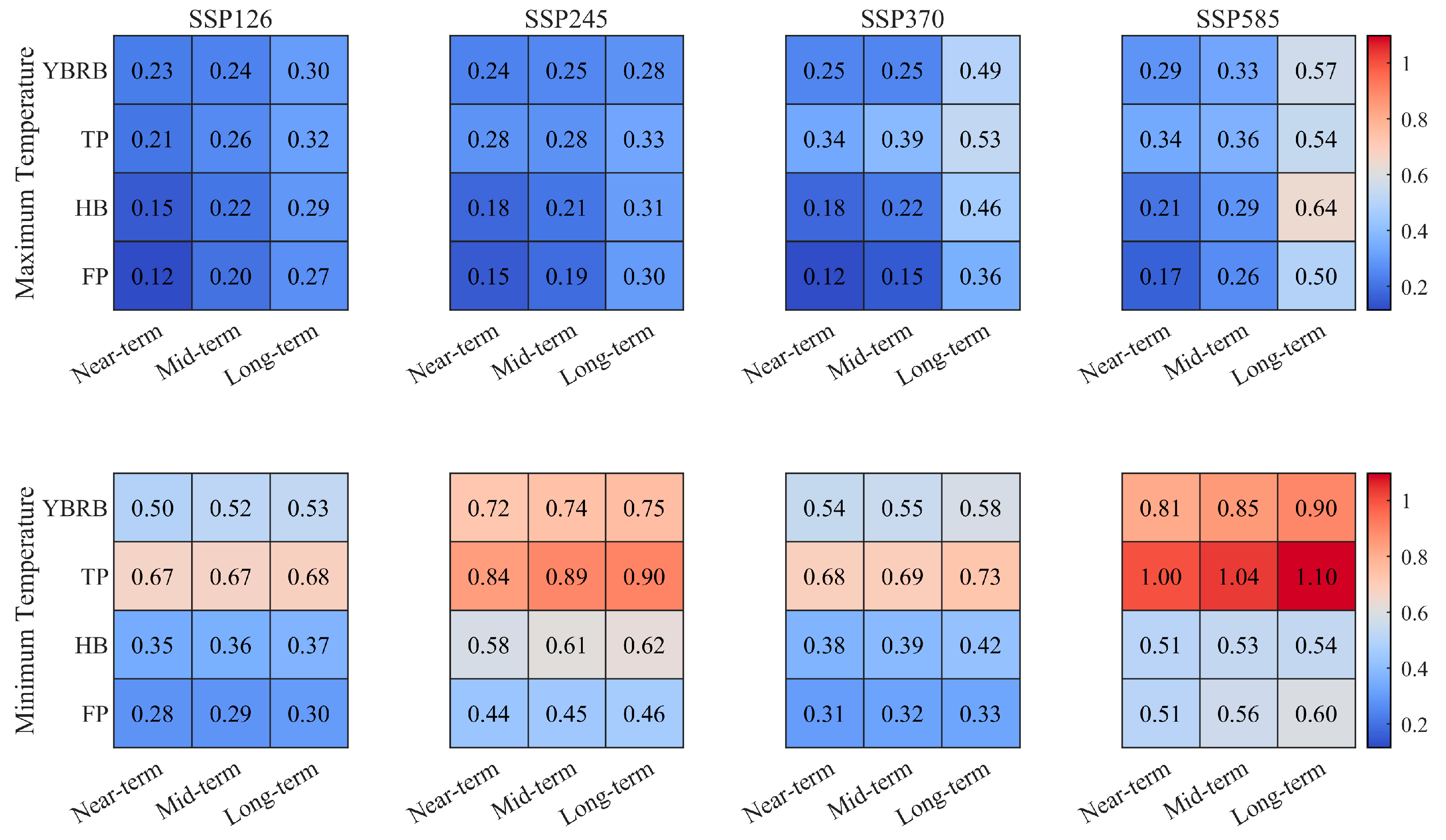
3.4. Uncertainty in Future Temperature Projections
4. Conclusions
- (1)
- By comparing the performances of the Tmax and Tmin via the RMSE and ACC, the BMA-simulation effect on the Tmax and Tmin was deemed superior to that of the MME or individual models. Regional comparisons further revealed that the BMA could better simulate the Tmax and Tmin over the HB versus the TP or FP. By comparing the model weights, it was found that CanESM5 and ACCESS-ESM1-5 were the top performers for the Tmax and Tmin, respectively.
- (2)
- According to the BMA prediction results, the Tmax and Tmin over the YBRB during 2015–2100 fluctuated upwards under each of the four scenarios, with their respective warming rates increasing with scenario intensity. Under the most ideal sustainable development scenario (SSP126), the increase in the Tmax over the near-, mid-, and long-terms will reach 0.58, 0.91, and 1.09 °C across the YBRB; whereas the increases of the Tmin will reach 0.18, 0.52, and 0.61 °C, respectively. Under the high emissions scenario (SSP585), the increases in the Tmax (Tmin) over the near-, mid-, and long-terms are 0.69 (0.09), 1.51 (1.04), and 3.53 (3.38) °C, respectively. Although the overall future increases in the Tmax and Tmin are predicted to fall below global averages, the spatial differentiation of temperature in the upper and lower reaches of the basin will be more obvious.
- (3)
- The uncertainty of the future Tmax was smaller than that of the Tmin according to the BMA-derived results. In general, uncertainty increased with the prediction time, while spatially, the regions with the uncertainty were the TP > HB > FP.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- IPCC. Climate Change 2021: The Physical Science Basis: Working Group I Contribution to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V.P., Zhaij, A., Pirani, S.L., Connors, C., Pean, S., Berger, N., Caud, Y., Chen, L., Goldfarb, M.l., Gomis, M., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; p. 2391. ISBN 978-1-00-915789-6. [Google Scholar]
- Vousdoukas, M.I.; Mentaschi, L.; Voukouvalas, E.; Verlaan, M.; Jevrejeva, S.; Jackson, L.P.; Feyen, L. Global probabilistic projections of extreme sea levels show intensification of coastal flood hazard. Nat. Commun. 2018, 9, 2360. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Miao, C.; AghaKouchak, A.; Mallakpour, I.; Ji, D.; Duan, Q. Possible Increased Frequency of ENSO-Related Dry and Wet Conditions over Some Major Watersheds in a Warming Climate. Bull. Am. Meteorol. Soc. 2020, 101, E409–E426. [Google Scholar] [CrossRef]
- Kharin, V.V.; Flato, G.M.; Zhang, X.; Gillett, N.P.; Zwiers, F.; Anderson, K.J. Risks from Climate Extremes Change Differently from 1.5 °C to 2.0 °C Depending on Rarity. Earth’s Future 2018, 6, 704–715. [Google Scholar] [CrossRef]
- Lipczynska-Kochany, E. Effect of climate change on humic substances and associated impacts on the quality of surface water and groundwater: A review. Sci. Total Environ. 2018, 640–641, 1548–1565. [Google Scholar] [CrossRef]
- Zheng, H.; Miao, C.; Wu, J.; Lei, X.; Liao, W.; Li, H. Temporal and spatial variations in water discharge and sediment load on the Loess Plateau, China: A high-density study. Sci. Total Environ. 2019, 666, 875–886. [Google Scholar] [CrossRef] [PubMed]
- Jiang, T.; Su, B.; Huang, J.; Zhai, J.; Xia, J.; Tao, H.; Wang, Y.; Sun, H.; Luo, Y.; Zhang, L.; et al. Each 0. 5 °C of Warming Increases Annual Flood Losses in China by More than US$60 Billion. Bull. Am. Meteorol. Soc. 2020, 101, E1464–E1474. [Google Scholar] [CrossRef]
- Gou, J.; Miao, C.; Duan, Q.; Tang, Q.; Di, Z.; Liao, W.; Wu, J.; Zhou, R. Sensitivity Analysis-Based Automatic Parameter Calibration of the VIC Model for Streamflow Simulations Over China. Water Resour. Res. 2020, 56, e2019WR025968. [Google Scholar] [CrossRef]
- Schleussner, C.-F.; Donges, J.F.; Donner, R.V.; Schellnhuber, H.J. Armed-conflict risks enhanced by climate-related disasters in ethnically fractionalized countries. Proc. Natl. Acad. Sci. USA 2016, 113, 9216–9221. [Google Scholar] [CrossRef]
- Harari, M.; Ferrara, E.L. Conflict, Climate, and Cells: A Disaggregated Analysis. Rev. Econ. Stat. 2018, 100, 594–608. [Google Scholar] [CrossRef]
- Gao, J.; Yao, T.; Masson-Delmotte, V.; Steen-Larsen, H.C.; Wang, W. Collapsing glaciers threaten Asia’s water supplies. Nature 2019, 565, 19–21. [Google Scholar] [CrossRef]
- Kraaijenbrink, P.D.A.; Stigter, E.E.; Yao, T.; Immerzeel, W.W. Climate change decisive for Asia’s snow meltwater supply. Nat. Clim. Chang. 2021, 11, 591–597. [Google Scholar] [CrossRef]
- Yang, T.; Tao, Y.; Li, J.; Zhu, Q.; Su, L.; He, X.; Zhang, X. Multi-criterion model ensemble of CMIP5 surface air temperature over China. Theor. Appl. Climatol. 2018, 132, 1057–1072. [Google Scholar] [CrossRef]
- Zhu, H.; Jiang, Z.; Li, J.; Li, W.; Sun, C.; Li, L. Does CMIP6 Inspire More Confidence in Simulating Climate Extremes over China? Adv. Atmos. Sci. 2020, 37, 1119–1132. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, W.; Ohn, I.; Kim, Y.-O. Leave-one-out Bayesian model averaging for probabilistic ensemble forecasting. Commun. Stat. Appl. Methods 2017, 24, 67–80. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2001: The Scientific Basis. Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change; Houghton, J.T., Ding, Y., Griggs, D.J., Noguer, M., van der Linden, P.J., Dai, X., Maskell, K., Johnson, C.A., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2001; p. 881. ISBN 0-521-80767-0. [Google Scholar]
- IPCC. Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S.D., Qin, M., Manning, Z., Chen, M., Marquis, K.B., Averyt, M., Tignor, M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007; p. 996. ISBN 978-0-521-88009-1. [Google Scholar]
- IPCC. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; p. 1535. ISBN 978-1-107-05799-1. [Google Scholar]
- Feng, S.; Hu, Q.; Huang, W.; Ho, C.-H.; Li, R.; Tang, Z. Projected climate regime shift under future global warming from multi-model, multi-scenario CMIP5 simulations. Glob. Planet. Chang. 2014, 112, 41–52. [Google Scholar] [CrossRef]
- Zhao, T.; Chen, L.; Ma, Z. Simulation of historical and projected climate change in arid and semiarid areas by CMIP5 models. Chin. Sci. Bull. 2014, 59, 412–429. [Google Scholar] [CrossRef]
- Murphy, J.M.; Sexton, D.M.H.; Barnett, D.N.; Jones, G.S.; Webb, M.J.; Collins, M.; Stainforth, D.A. Quantification of modelling uncertainties in a large ensemble of climate change simulations. Nature 2004, 430, 768–772. [Google Scholar] [CrossRef]
- Schmittner, A.; Latif, M.; Schneider, B. Model projections of the North Atlantic thermohaline circulation for the 21st century assessed by observations. Geophys. Res. Lett. 2005, 32, L23710. [Google Scholar] [CrossRef]
- Tebaldi, C.; Smith, R.L.; Nychka, D.; Mearns, L.O. Quantifying Uncertainty in Projections of Regional Climate Change: A Bayesian Approach to the Analysis of Multimodel Ensembles. J. Clim. 2005, 18, 1524–1540. [Google Scholar] [CrossRef]
- Räisänen, J.; Ylhäisi, J.S. How Much Should Climate Model Output Be Smoothed in Space? J. Clim. 2011, 24, 867–880. [Google Scholar] [CrossRef]
- Wenzel, S.; Eyring, V.; Gerber, E.P.; Karpechko, A.Y. Constraining Future Summer Austral Jet Stream Positions in the CMIP5 Ensemble by Process-Oriented Multiple Diagnostic Regression. J. Clim. 2016, 29, 673–687. [Google Scholar] [CrossRef]
- Knutti, R.; Sedláček, J.; Sanderson, B.M.; Lorenz, R.; Fischer, E.M.; Eyring, V. A climate model projection weighting scheme accounting for performance and interdependence. Geophys. Res. Lett. 2017, 44, 1909–1918. [Google Scholar] [CrossRef]
- Sanderson, B.M.; Wehner, M.; Knutti, R. Skill and independence weighting for multi-model assessments. Geosci. Model Dev. 2017, 10, 2379–2395. [Google Scholar] [CrossRef]
- Raftery, A.E.; Gneiting, T.; Balabdaoui, F.; Polakowski, M. Using Bayesian Model Averaging to Calibrate Forecast Ensembles. Mon. Weather. Rev. 2005, 133, 1155–1174. [Google Scholar] [CrossRef]
- Sloughter, J.M.L.; Raftery, A.E.; Gneiting, T.; Fraley, C. Probabilistic Quantitative Precipitation Forecasting Using Bayesian Model Averaging. Mon. Weather. Rev. 2007, 135, 3209–3220. [Google Scholar] [CrossRef]
- Yang, T.; Wang, X.; Zhao, C.; Chen, X.; Yu, Z.; Shao, Q.; Xu, C.-Y.; Xia, J.; Wang, W. Changes of climate extremes in a typical arid zone: Observations and multimodel ensemble projections. J. Geophys. Res. Atmos. 2011, 116, D19106. [Google Scholar] [CrossRef]
- He, Y. Current and future transboundary water cooperation over the YarlungZangbo/Brahmaputra River basin: From an interdisciplinary perspective. Water Policy 2021, 23, 1107–1128. [Google Scholar] [CrossRef]
- Shi, Y.; Gao, X.; Zhang, D.; Giorgi, F. Climate change over the Yarlung Zangbo–Brahmaputra River Basin in the 21st century as simulated by a high resolution regional climate model. Quat. Int. 2011, 244, 159–168. [Google Scholar] [CrossRef]
- Immerzeel, W. Historical trends and future predictions of climate variability in the Brahmaputra basin. Int. J. Climatol. 2008, 28, 243–254. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An Overview of CMIP5 and the Experiment Design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Eyring, V.; Cox, P.M.; Flato, G.M.; Gleckler, P.J.; Abramowitz, G.; Caldwell, P.; Collins, W.D.; Gier, B.K.; Hall, A.D.; Hoffman, F.M.; et al. Taking climate model evaluation to the next level. Nat. Clim. Chang. 2019, 9, 102–110. [Google Scholar] [CrossRef]
- Masood, M.; Yeh, P.J.-F.; Hanasaki, N.; Takeuchi, K. Model study of the impacts of future climate change on the hydrology of Ganges-Brahmaputra-Meghna basin. Hydrol. Earth Syst. Sci. 2015, 19, 747–770. [Google Scholar] [CrossRef]
- Xu, R.; Hu, H.; Tian, F.; Li, C.; Khan, M.Y.A. Projected climate change impacts on future streamflow of the Yarlung Tsangpo-Brahmaputra River. Glob. Planet. Chang. 2019, 175, 144–159. [Google Scholar] [CrossRef]
- Gain, A.K.; Immerzeel, W.W.; Sperna Weiland, F.C.; Bierkens, M.F.P. Impact of climate change on the stream flow of the lower Brahmaputra: Trends in high and low flows based on discharge-weighted ensemble modelling. Hydrol. Earth Syst. Sci. 2011, 15, 1537–1545. [Google Scholar] [CrossRef]
- Jiang, W.; Ji, X.; Li, Y.; Luo, X.; Yang, L.; Ming, W.; Liu, C.; Yan, S.; Yang, C.; Sun, C. Modified flood potential index (MFPI) for flood monitoring in terrestrial water storage depletion basin using GRACE estimates. J. Hydrol. 2023, 616, 128765. [Google Scholar] [CrossRef]
- Pervez, M.S.; Henebry, G.M. Assessing the impacts of climate and land use and land cover change on the freshwater availability in the Brahmaputra River basin. J. Hydrol. Reg. Stud. 2015, 3, 285–311. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Köppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef] [PubMed]
- Guo, R.-Y.; Ji, X.; Liu, C.-Y.; Liu, C.; Jiang, W.; Yang, L.-Y. Spatiotemporal variation of snow cover and its relationship with temperature and precipitation in the Yarlung Tsangpo-Brahmaputra River Basin. J. Mt. Sci. 2022, 19, 1901–1918. [Google Scholar] [CrossRef]
- O’Neill, B.C.; Tebaldi, C.; van Vuuren, D.P.; Eyring, V.; Friedlingstein, P.; Hurtt, G.; Knutti, R.; Kriegler, E.; Lamarque, J.-F.; Lowe, J.; et al. The Scenario Model Intercomparison Project (ScenarioMIP) for CMIP6. Geosci. Model Dev. 2016, 9, 3461–3482. [Google Scholar] [CrossRef]
- Allabakash, S.; Lim, S. Anthropogenic influence of temperature changes across East Asia using CMIP6 simulations. Sci. Rep. 2022, 12, 11896. [Google Scholar] [CrossRef]
- Xie, A.; Zhu, J.; Kang, S.; Qin, X.; Xu, B.; Wang, Y. Polar amplification comparison among Earth’s three poles under different socioeconomic scenarios from CMIP6 surface air temperature. Sci. Rep. 2022, 12, 16548. [Google Scholar] [CrossRef] [PubMed]
- Ji, X.; Li, Y.; Luo, X.; He, D.; Guo, R.; Wang, J.; Bai, Y.; Yue, C.; Liu, C. Evaluation of bias correction methods for APHRODITE data to improve hydrologic simulation in a large Himalayan basin. Atmos. Res. 2020, 242, 104964. [Google Scholar] [CrossRef]
- Glahn, H.R.; Lowry, D.A. The Use of Model Output Statistics (MOS) in Objective Weather Forecasting. J. Appl. Meteorol. Climatol. 1972, 11, 1203–1211. [Google Scholar] [CrossRef]
- Carter, G.M.; Dallavalle, J.P.; Glahn, H.R. Statistical Forecasts Based on the National Meteorological Center’s Numerical Weather Prediction System. Weather Forecast. 1989, 4, 401–412. [Google Scholar] [CrossRef]
- Fisher, R.A. On the Mathematical Foundations of Theoretical Statistics. In Breakthroughs in Statistics: Foundations and Basic Theory; Kotz, S., Johnson, N.L., Eds.; Springer: New York, NY, USA, 1992; pp. 309–368. [Google Scholar]
- Mclachlan, G.J.; Krishnan, T. The EM Algorithm and Extensions; John Wiley & Sons, Ltd: Hoboken, NJ, USA, 2008. [Google Scholar]
- Pennell, C.; Reichler, T. On the Effective Number of Climate Models. J. Clim. 2011, 24, 2358–2367. [Google Scholar] [CrossRef]
- Lun, Y.; Liu, L.; Cheng, L.; Li, X.; Li, H.; Xu, Z. Assessment of GCMs simulation performance for precipitation and temperature from CMIP5 to CMIP6 over the Tibetan Plateau. Int. J. Climatol. 2021, 41, 3994–4018. [Google Scholar] [CrossRef]
- Zhu, Y.-Y.; Yang, S. Evaluation of CMIP6 for historical temperature and precipitation over the Tibetan Plateau and its comparison with CMIP5. Adv. Clim. Chang. Res. 2020, 11, 239–251. [Google Scholar] [CrossRef]
- Veh, G.; Korup, O.; Walz, A. Hazard from Himalayan glacier lake outburst floods. Proc. Natl. Acad. Sci. USA 2019, 117, 907–912. [Google Scholar] [CrossRef]
- Islam, A.K.M.S.; Paul, S.; Mohammed, K.; Billah, M.; Fahad, M.G.R.; Hasan, M.A.; Islam, G.M.T.; Bala, S.K. Hydrological response to climate change of the Brahmaputra basin using CMIP5 general circulation model ensemble. J. Water Clim. Chang. 2018, 9, 434–448. [Google Scholar] [CrossRef]
- Uhe, P.F.; Mitchell, D.M.; Bates, P.D.; Sampson, C.C.; Smith, A.M.; Islam, A.S. Enhanced flood risk with 1.5 °C global warming in the Ganges–Brahmaputra–Meghna basin. Environ. Res. Lett. 2019, 14, 074031. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; van Beek, L.P.H.; Bierkens, M.F.P. Climate Change Will Affect the Asian Water Towers. Science 2010, 328, 1382–1385. [Google Scholar] [CrossRef]
- Allen, M.R.; Stott, P.A.; Mitchell, J.F.B.; Schnur, R.; Delworth, T.L. Quantifying the uncertainty in forecasts of anthropogenic climate change. Nature 2000, 407, 617–620. [Google Scholar] [CrossRef] [PubMed]
- Stott, P.A.; Kettleborough, J.A. Origins and estimates of uncertainty in predictions of twenty-first century temperature rise. Nature 2002, 416, 723–726. [Google Scholar] [CrossRef] [PubMed]
- Allen, M.; Raper, S.; Mitchell, J. Uncertainty in the IPCC’s Third Assessment Report. Science 2001, 293, 430–433. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Yu, R. Twentieth-Century Surface Air Temperature over China and the Globe Simulated by Coupled Climate Models. J. Clim. 2006, 19, 5843–5858. [Google Scholar] [CrossRef]
- Dessai, S.; Hulme, M.; Lempert, R.; Pielke Jr., R. Do We Need Better Predictions to Adapt to a Changing Climate? Eos Trans. Am. Geophys. Union 2009, 90, 111–112. [Google Scholar] [CrossRef]
- Chen, H.; Sun, J.; Lin, W.; Xu, H. Comparison of CMIP6 and CMIP5 models in simulating climate extremes. Sci. Bull. 2020, 65, 1415–1418. [Google Scholar] [CrossRef]
- Xin, X.; Wu, T.; Zhang, J.; Yao, J.; Fang, Y. Comparison of CMIP6 and CMIP5 simulations of precipitation in China and the East Asian summer monsoon. International. Int. J. Clim. 2020, 40, 6423–6440. [Google Scholar] [CrossRef]
- Zamani, Y.; Hashemi Monfared, S.A.; Azhdari moghaddam, M.; Hamidianpour, M. A comparison of CMIP6 and CMIP5 projections for precipitation to observational data: The case of Northeastern Iran. Theor. Appl. Climatol. 2020, 142, 1613–1623. [Google Scholar] [CrossRef]
- Almazroui, M.; Saeed, S.; Saeed, F.; Islam, M.N.; Ismail, M. Projections of Precipitation and Temperature over the South Asian Countries in CMIP6. Earth Syst. Environ. 2020, 4, 297–320. [Google Scholar] [CrossRef]
- Rivera, J.A.; Arnould, G. Evaluation of the ability of CMIP6 models to simulate precipitation over Southwestern South America: Climatic features and long-term trends (1901–2014). Atmos. Res. 2020, 241, 104953. [Google Scholar] [CrossRef]
- Jiang, J.; Zhou, T.; Chen, X.; Zhang, L. Future changes in precipitation over Central Asia based on CMIP6 projections. Environ. Res. Lett. 2020, 15, 054009. [Google Scholar] [CrossRef]
- Jiang, D.; Hu, D.; Tian, Z.; Lang, X. Differences between CMIP6 and CMIP5 Models in Simulating Climate over China and the East Asian Monsoon. Adv. Atmospheric Sci. 2020, 37, 1102–1118. [Google Scholar] [CrossRef]
- Qian, H.; Zhang, R. Future changes in wind energy resource over the Northwest Passage based on the CMIP6 climate projections. Int. J. Energy Res. 2021, 45, 920–937. [Google Scholar] [CrossRef]
- Wei, T.; Yan, Q.; Qi, W.; Ding, M.; Wang, C. Projections of Arctic sea ice conditions and shipping routes in the twenty-first century using CMIP6 forcing scenarios. Environ. Res. Lett. 2020, 15, 104079. [Google Scholar] [CrossRef]
- Burke, E.J.; Zhang, Y.; Krinner, G. Evaluating permafrost physics in the Coupled Model Intercomparison Project 6 (CMIP6) models and their sensitivity to climate change. Cryosphere 2020, 14, 3155–3174. [Google Scholar] [CrossRef]
- Akinsanola, A.A.; Kooperman, G.J.; Reed, K.A.; Pendergrass, A.G.; Hannah, W.M. Projected changes in seasonal precipitation extremes over the United States in CMIP6 simulations. Environ. Res. Lett. 2020, 15, 104078. [Google Scholar] [CrossRef]
- Cook, B.I.; Mankin, J.S.; Marvel, K.; Williams, A.P.; Smerdon, J.E.; Anchukaitis, K.J. Twenty-First Century Drought Projections in the CMIP6 Forcing Scenarios. Earth’s Futur. 2020, 8, e2019EF001461. [Google Scholar] [CrossRef]
- LI, J.; SU, J. Comparison of Indian Ocean warming simulated by CMIP5 and CMIP6 models. Atmospheric Ocean. Sci. Lett. 2020, 13, 604–611. [Google Scholar] [CrossRef]
- Guo, H.; Bao, A.; Chen, T.; Zheng, G.; Wang, Y.; Jiang, L.; De Maeyer, P. Assessment of CMIP6 in simulating precipitation over arid Central Asia. Atmospheric Res. 2021, 252, 105451. [Google Scholar] [CrossRef]
- Wild, M. The global energy balance as represented in CMIP6 climate models. Clim. Dyn. 2020, 55, 553–577. [Google Scholar] [CrossRef] [PubMed]
- Tokarska, K.B.; Stolpe, M.B.; Sippel, S.; Fischer, E.M.; Smith, C.J.; Lehner, F.; Knutti, R. Past warming trend constrains future warming in CMIP6 models. Sci. Adv. 2020, 6, eaaz9549. [Google Scholar] [CrossRef]
- Moseid, K.O.; Schulz, M.; Storelvmo, T.; Julsrud, I.R.; Olivie, D.; Nabat, P.; Wild, M.; Cole, J.N.S.; Takemura, T.; Oshima, N.; et al. Bias in CMIP6 models as compared to observed regional dimming and brightening. Atmospheric Meas. Tech. 2020, 20, 16023–16040. [Google Scholar] [CrossRef]
- Schlund, M.; Lauer, A.; Gentine, P.; Sherwood, S.C.; Eyring, V. Emergent constraints on equilibrium climate sensitivity in CMIP5: Do they hold for CMIP6? Earth Syst. Dyn. 2020, 11, 1233–1258. [Google Scholar] [CrossRef]
- Zhai, J.; Mondal, S.K.; Fischer, T.; Wang, Y.; Su, B.; Huang, J.; Tao, H.; Wang, G.; Ullah, W.; Uddin, M.J. Future drought characteristics through a multi-model ensemble from CMIP6 over South Asia. Atmospheric Res. 2020, 246, 105111. [Google Scholar] [CrossRef]
- Nooni, I.K.; Ogou, F.K.; Chaibou, A.A.S.; Nakoty, F.M.; Gnitou, G.T.; Lu, J. Evaluating CMIP6 Historical Mean Precipitation over Africa and the Arabian Peninsula against Satellite-Based Observation. Atmosphere 2023, 14, 607. [Google Scholar] [CrossRef]
- Zhang, C.; Qi, W.; Dong, J.; Deng, Y. How the CMIP6 climate models project the historical terrestrial GPP in China. Int. J. Clim. 2022, 42, 9449–9461. [Google Scholar] [CrossRef]
- Agyekum, J.; Annor, T.; Quansah, E.; Lamptey, B.; Okafor, G. Extreme precipitation indices over the Volta Basin: CMIP6 model evaluation. Sci. Afr. 2022, 16, e01181. [Google Scholar] [CrossRef]
- Makula, E.K.; Zhou, B. Coupled Model Intercomparison Project phase 6 evaluation and projection of East African precipitation. Int. J. Clim. 2022, 42, 2398–2412. [Google Scholar] [CrossRef]
- Deepthi, B.; Sivakumar, B. Shortest path length for evaluating general circulation models for rainfall simulation. Clim. Dyn. 2023, 61, 3009–3028. [Google Scholar] [CrossRef]
- Lin, X.; Massonnet, F.; Fichefet, T.; Vancoppenolle, M. Impact of atmospheric forcing uncertainties on Arctic and Antarctic sea ice simulations in CMIP6 OMIP models. Cryosphere 2023, 17, 1935–1965. [Google Scholar] [CrossRef]
- Allende, S.; Fichefet, T.; Goosse, H.; Treguier, A.M. On the ability of OMIP models to simulate the ocean mixed layer depth and its seasonal cycle in the Arctic Ocean. Ocean Model. 2023, 184, 102226. [Google Scholar] [CrossRef]
- Shiru, M.S.; Chung, E.-S. Performance evaluation of CMIP6 global climate models for selecting models for climate projection over Nigeria. Theor. Appl. Clim. 2021, 146, 599–615. [Google Scholar] [CrossRef]
- Deepthi, B.; Sivakumar, B. General circulation models for rainfall simulations: Performance assessment using complex networks. Atmospheric Res. 2022, 278, 106333. [Google Scholar] [CrossRef]

| No. | Model | Country/Region | Resolution |
|---|---|---|---|
| 1 | ACCESS-ESM1-5 | Australia | 1.88° × 1.24° |
| 2 | BCC-CSM2-MR | China | 1.13° × 1.13° |
| 3 | CanESM5 | Canada | 2.81° × 2.81° |
| 4 | CMCC-CM2-SR5 | Italy | 1.25° × 0.94° |
| 5 | EC-Earth3-Veg | Europe | 0.70° × 7.20° |
| 6 | GFDL-ESM4 | America | 1.00° × 1.00° |
| 7 | IPSL-CM6A-LR | France | 2.50° × 1.26° |
| 8 | MIROC6 | Japan | 1.41° × 1.41° |
| 9 | MRI-ESM2-0 | Japan | 1.13° × 1.13° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Chen, L.; Qin, P.; Ji, X. Projection and Uncertainty Analysis of Future Temperature Change over the Yarlung Tsangpo-Brahmaputra River Basin Based on CMIP6. Water 2023, 15, 3595. https://doi.org/10.3390/w15203595
Xu Z, Chen L, Qin P, Ji X. Projection and Uncertainty Analysis of Future Temperature Change over the Yarlung Tsangpo-Brahmaputra River Basin Based on CMIP6. Water. 2023; 15(20):3595. https://doi.org/10.3390/w15203595
Chicago/Turabian StyleXu, Zhangchao, Linyan Chen, Peng Qin, and Xuan Ji. 2023. "Projection and Uncertainty Analysis of Future Temperature Change over the Yarlung Tsangpo-Brahmaputra River Basin Based on CMIP6" Water 15, no. 20: 3595. https://doi.org/10.3390/w15203595






