Numerical Simulation Study on the Distribution Characteristics of Precipitation Seepage Field in Water-Rich Ultra-Thick Sand and Gravel Layer
Abstract
:1. Introduction
2. Methods of Analysis
2.1. Universal Model
2.2. Calculation Model
3. Distribution Characteristics of Seepage Field in Foundation Pits
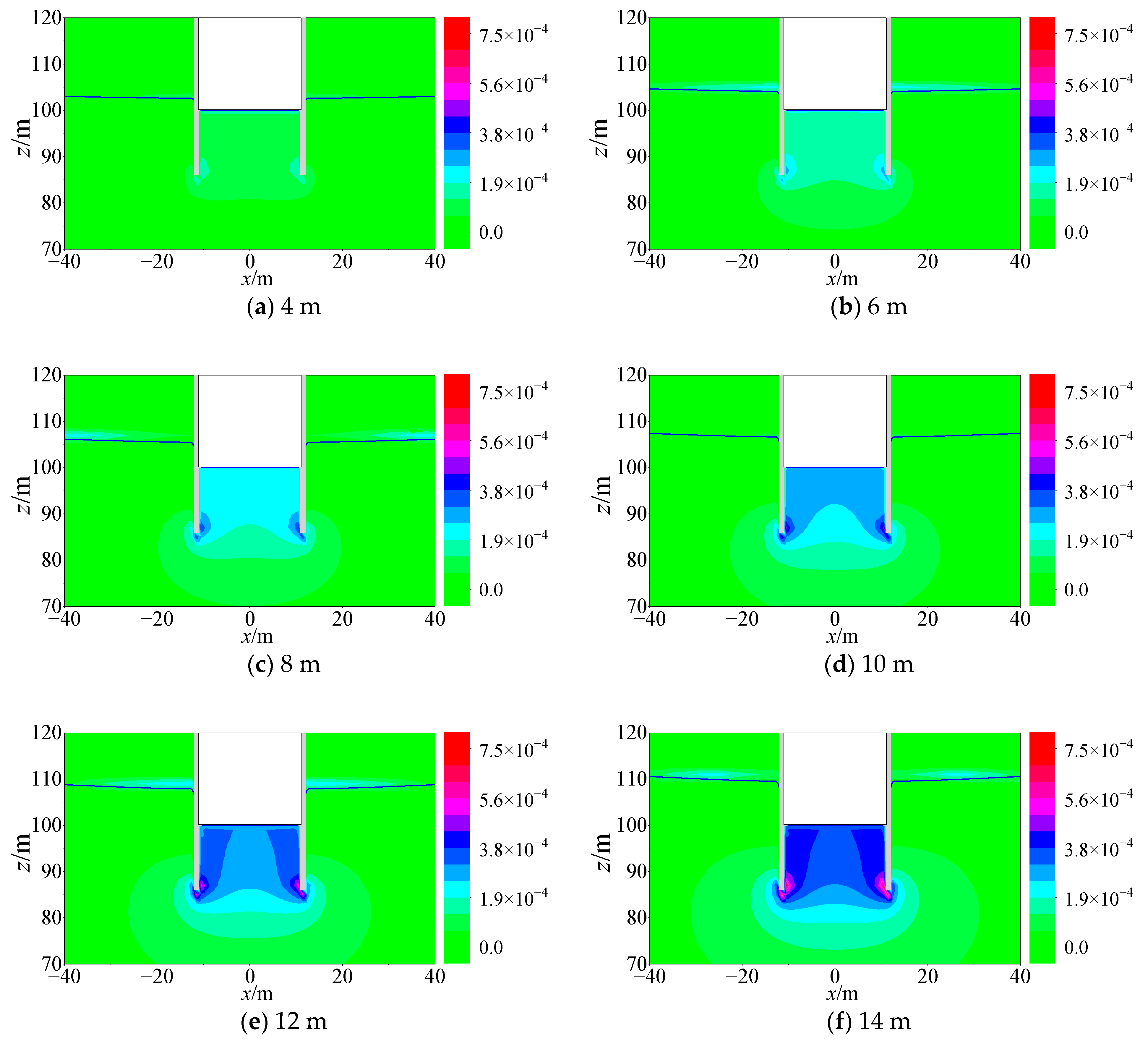
3.1. Distribution Characteristics of Seepage Field under the Influence of Precipitation Depth
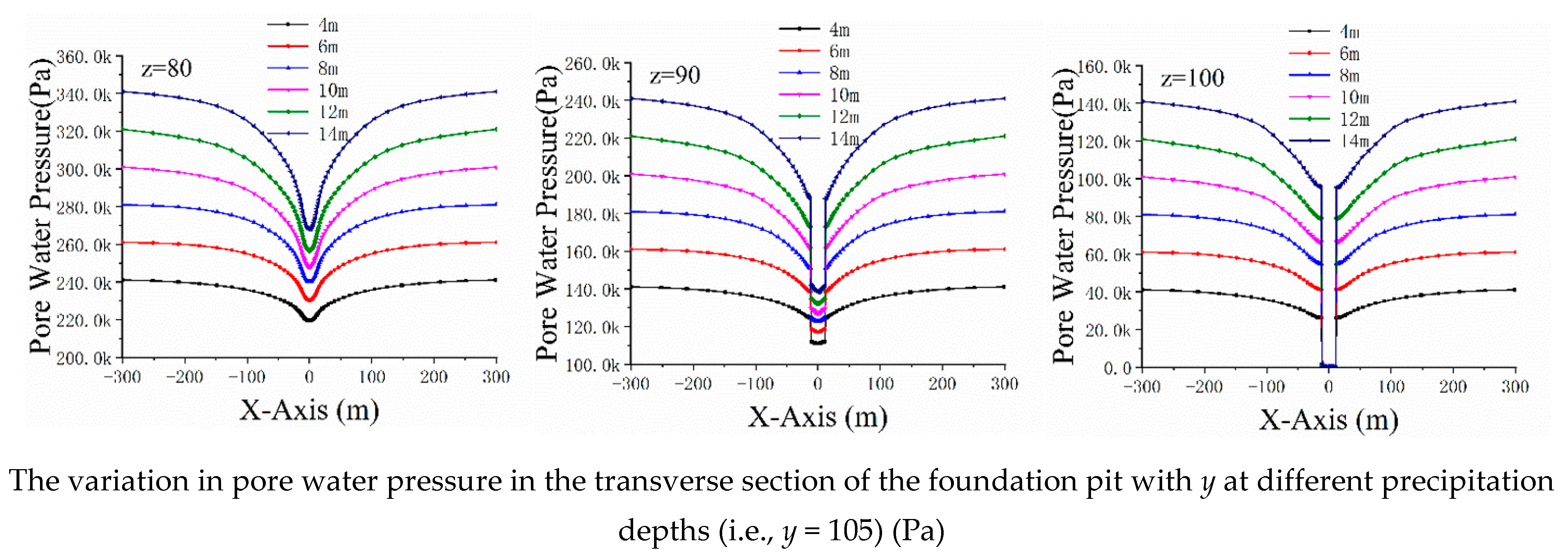
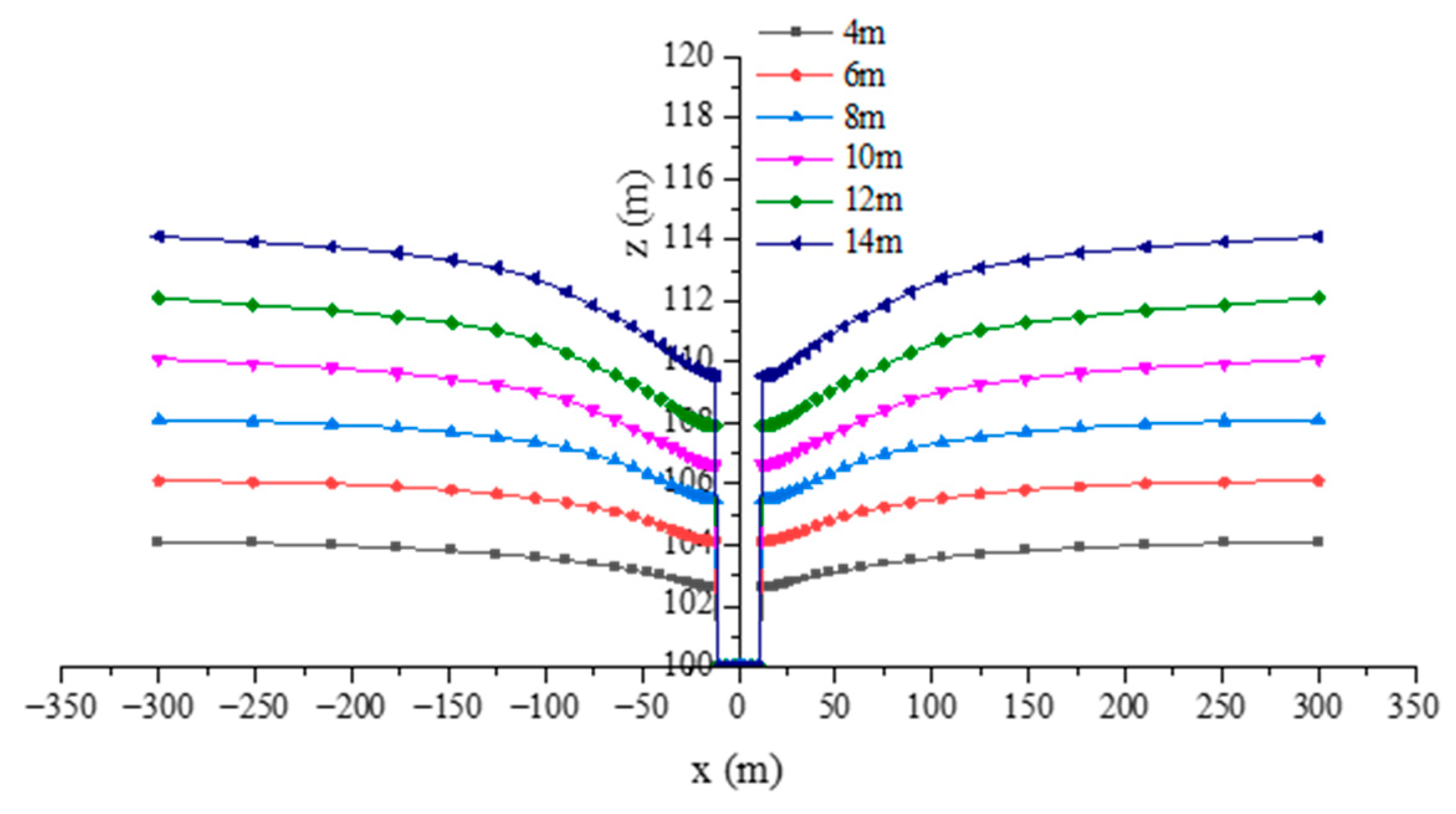
3.1.1. Effect on Pore Water Pressure
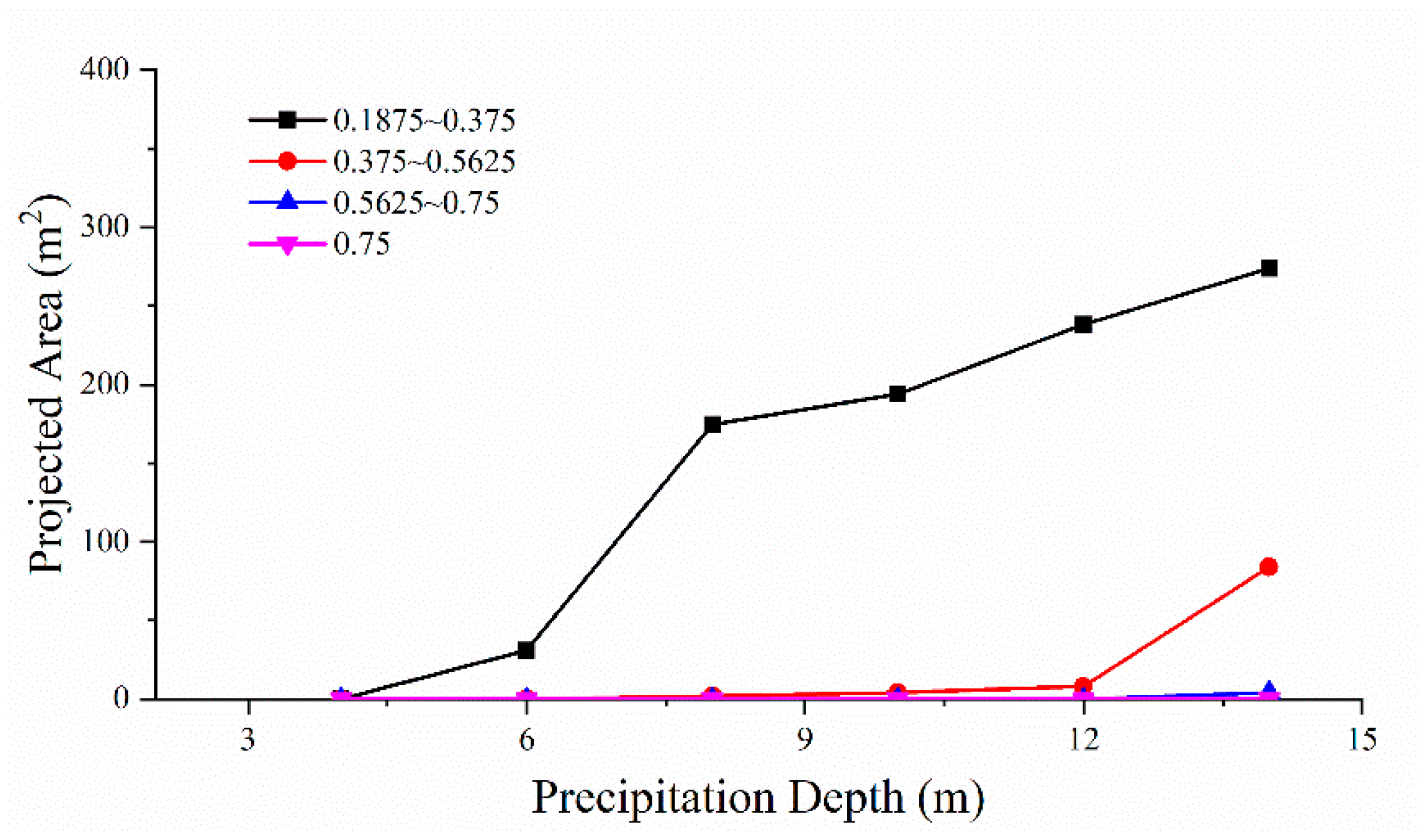
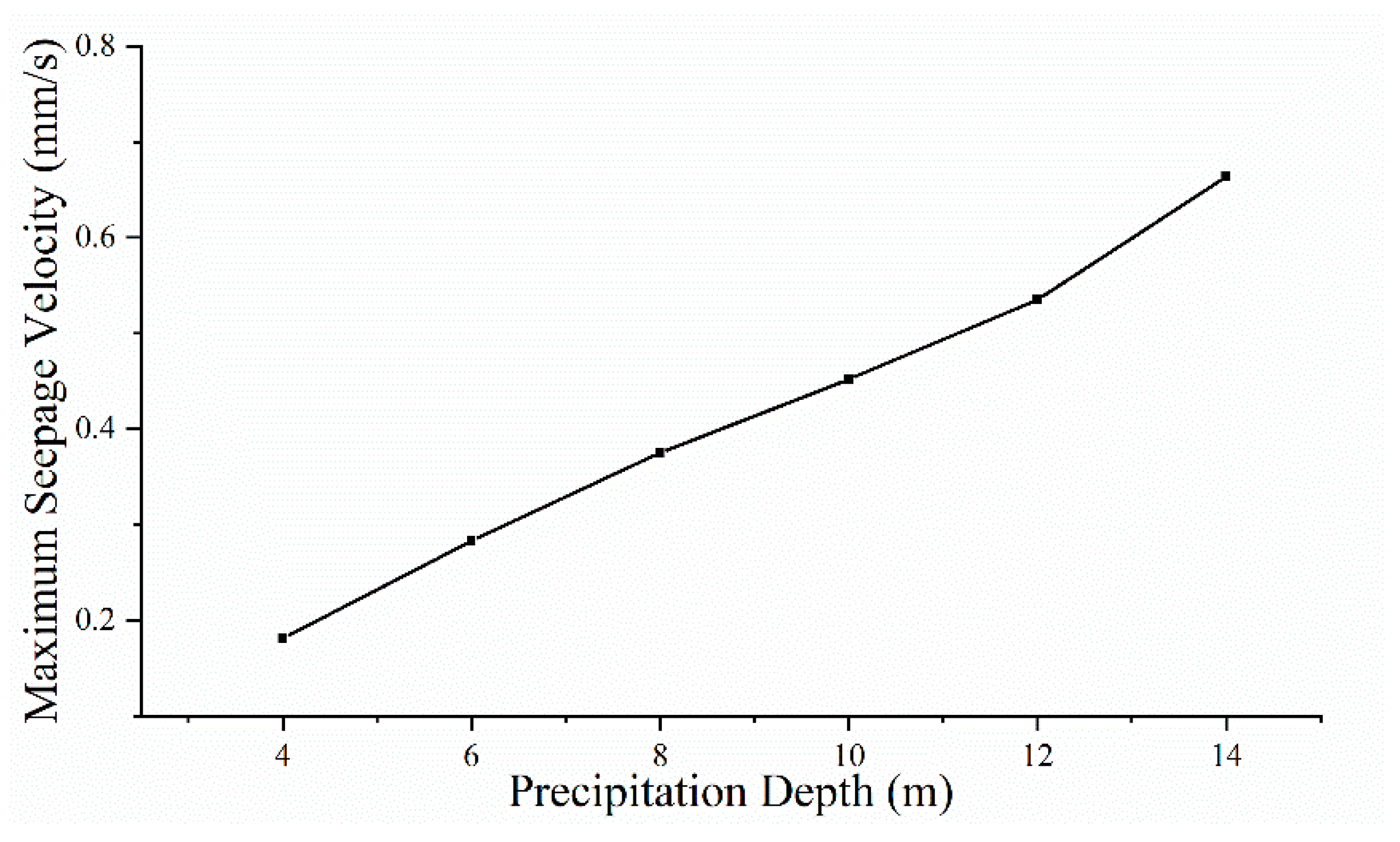
3.1.2. Effect on Flow Velocity
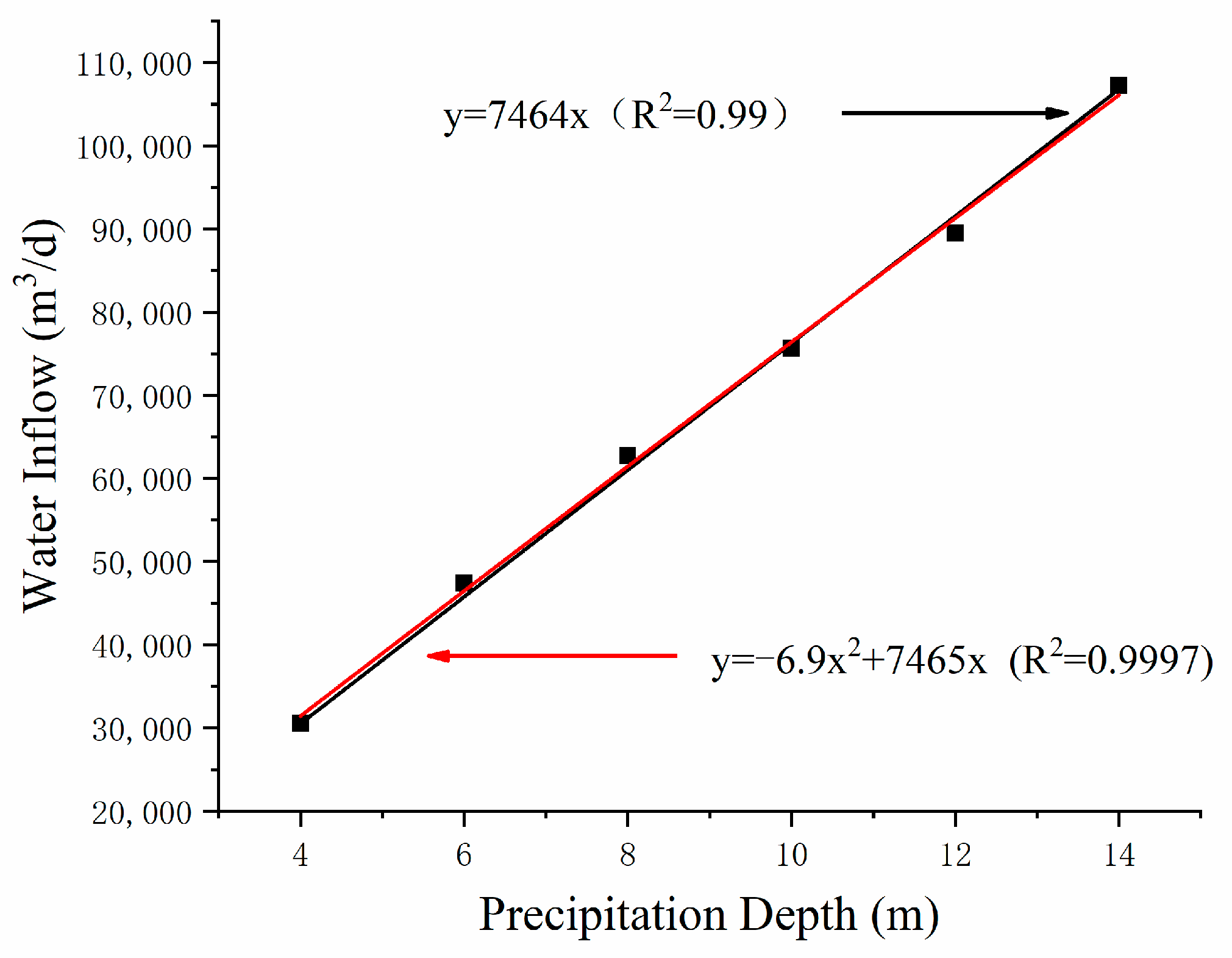
3.1.3. Effect on Water Inflow
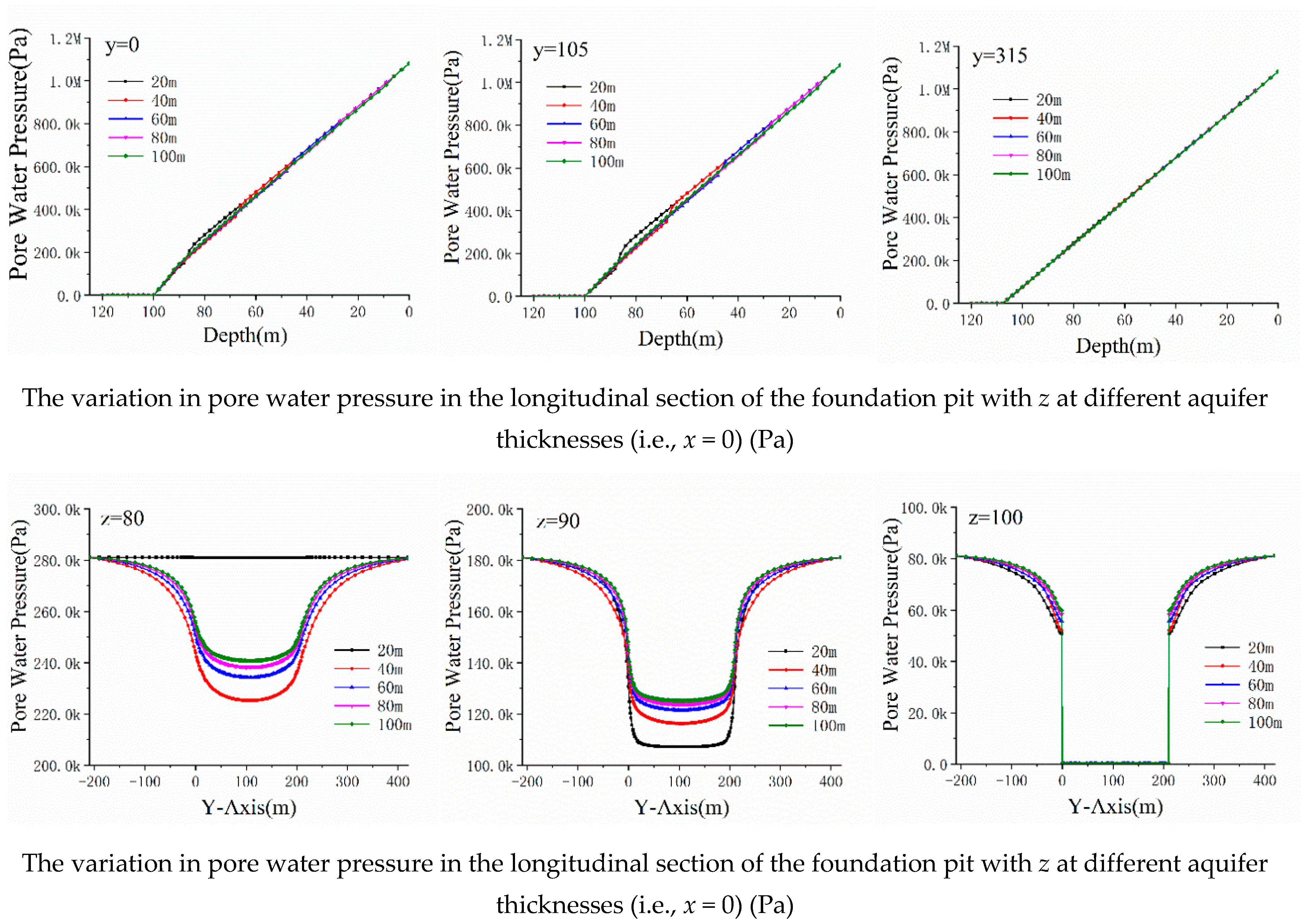
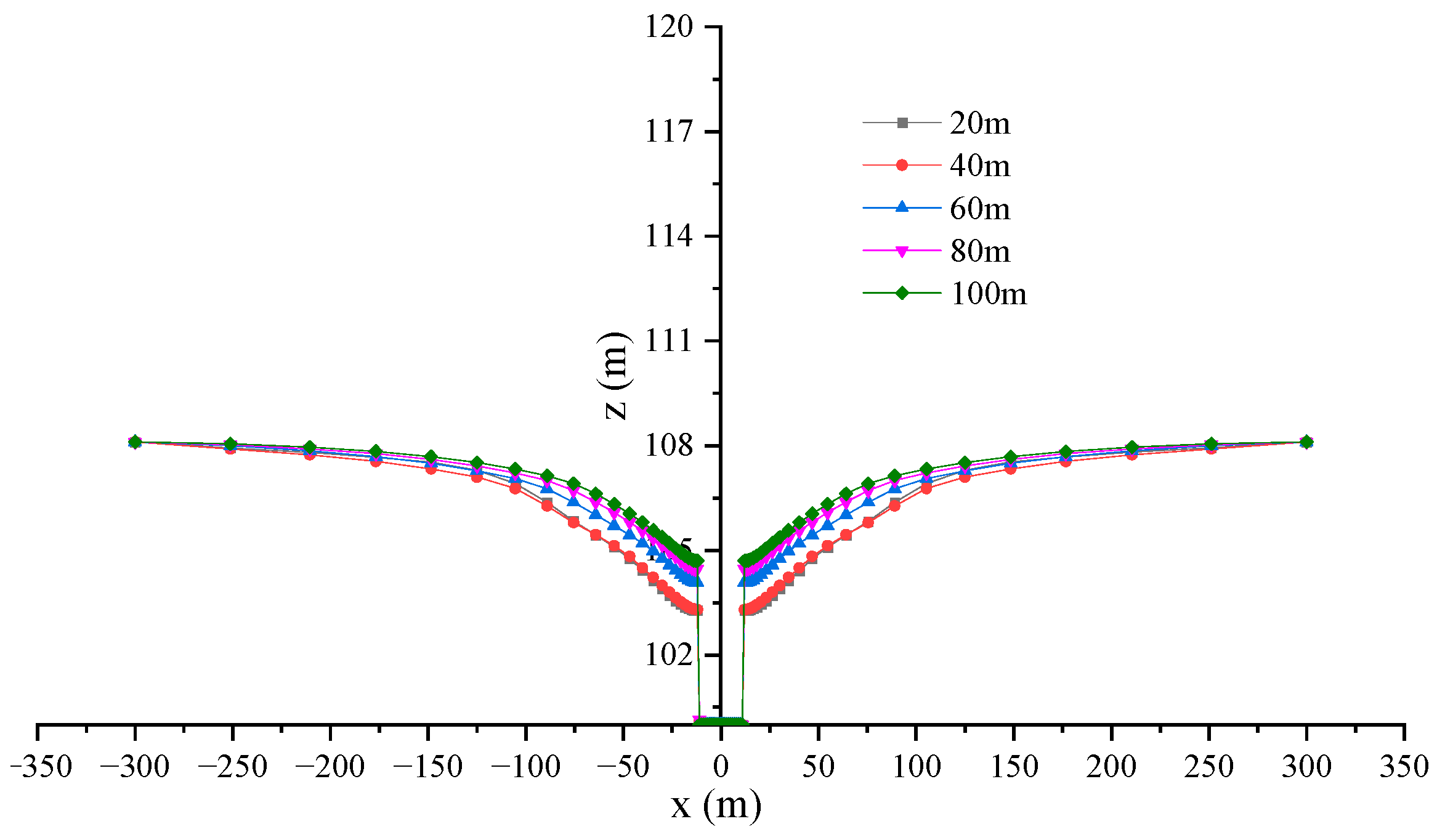
3.2. Distribution Characteristics of Seepage Field under the Influence of Aquifer Thickness
3.2.1. Effect on Pore Water Pressure
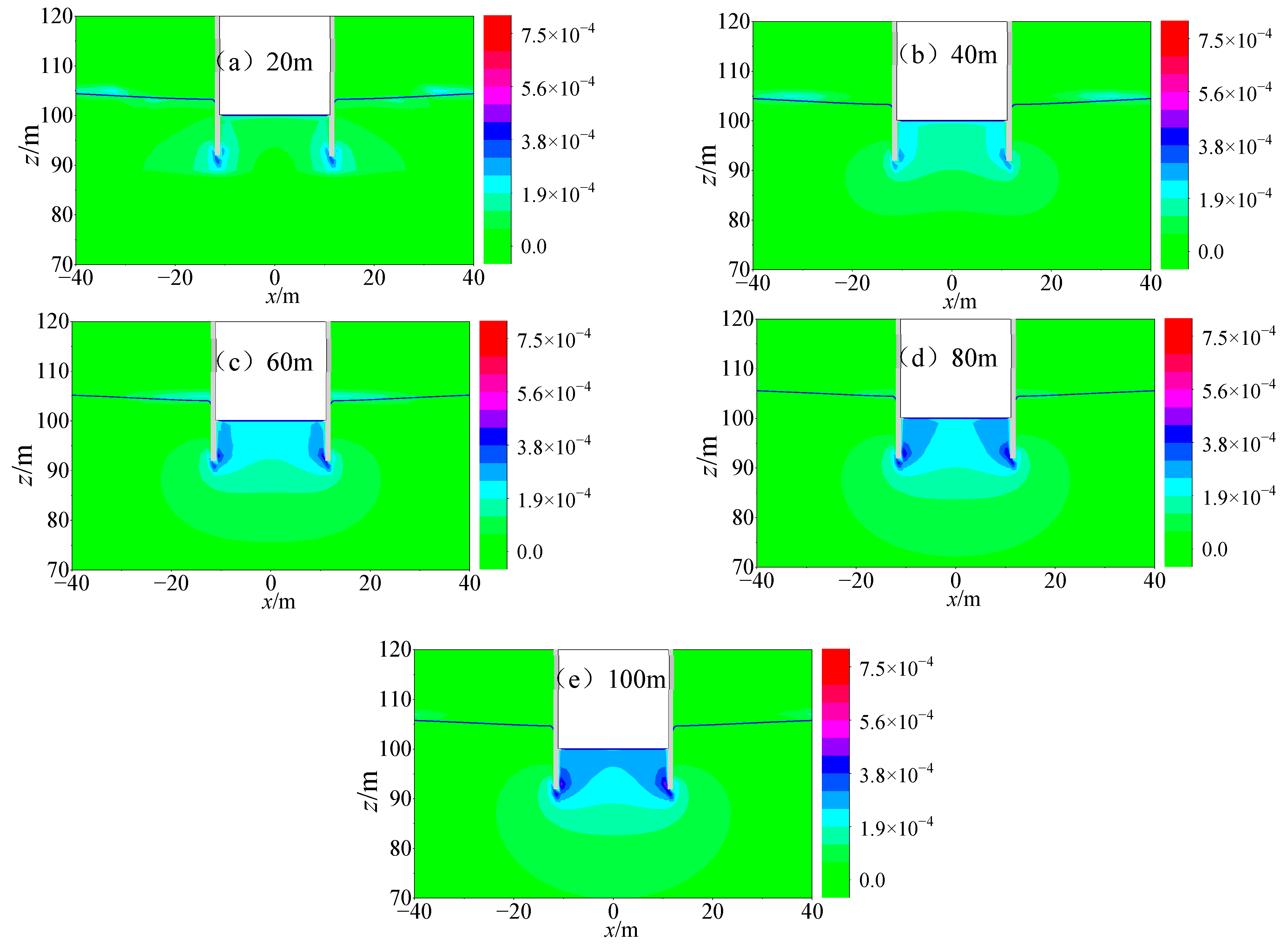
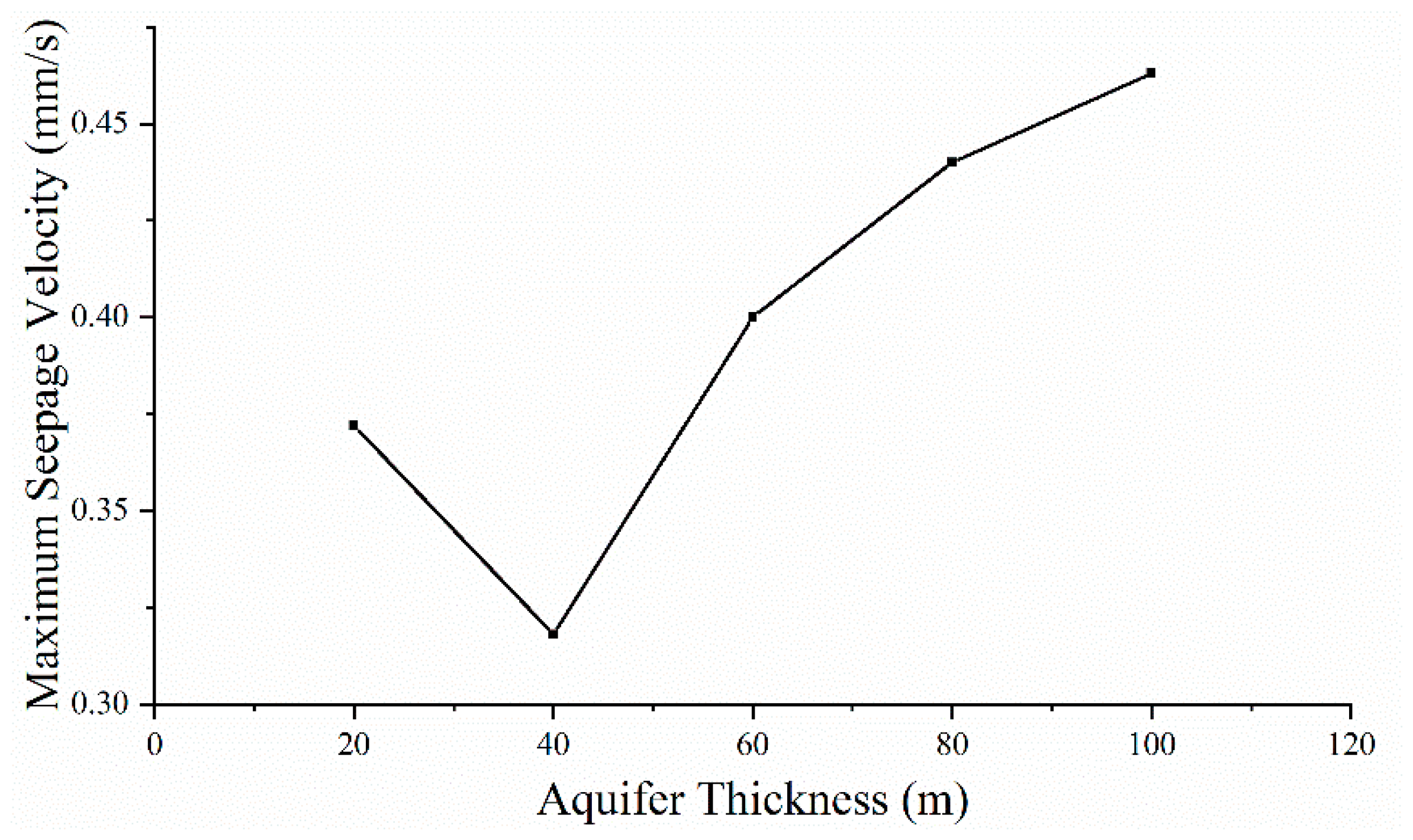
3.2.2. Effect on Flow Velocity
3.2.3. Effect on Water Inflow
4. Model Validation
5. Conclusions
- (1)
- Under the condition of the suspended water-stop curtain, the pore water pressure on the outer side of the water-stop curtain is greater than that on the inner side of the foundation pit. It increases linearly with an increase in the precipitation depth. As the aquifer thickness increases, it increases. The pore water pressure distribution characteristics deeply influence the dynamic water level curve.
- (2)
- Under the condition of the suspended water-stop curtain, the maximum seepage flow velocity occurs at the position where the curtain’s bottom leans towards the inner side of the foundation pit. The maximum seepage flow velocity increases linearly with an increase in the precipitation depth, and there is a threshold value for the aquifer thickness, which is five times the precipitation depth.
- (3)
- Under the condition of the suspended water-stop curtain, the relationship between the precipitation depth and water inflow can be described by a linear or parabolic function; the relationship between the aquifer thickness and water inflow can be described by a logistic function.
- (4)
- The calculation results are compared with the measured water level measurements. The average error of the water level drop in the pit and precipitation well under the suspended water-stop curtain condition is 11.7%, indicating that the established numerical model can meet the calculation requirements.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vaziri, H.H.; Xiao, Y.; Islam, R.; Nouri, A. Numerical modeling of seepage-induced sand production in oil and gas reservoirs. J. Pet. Sci. Eng. 2002, 36, 71–86. [Google Scholar] [CrossRef]
- Bai, H.; Ma, D.; Chen, Z. Mechanical behavior of groundwater seepage in karst collapse pillars. Eng. Geol. 2013, 164, 101–106. [Google Scholar] [CrossRef]
- Jafarian, Y.; Haddad, A.; Mehrzad, B. Load-Settlement Mechanism of Shallow Foundations Rested on Saturated Sand with Upward Seepage. Int. J. Geomech. 2017, 17, 1–14. [Google Scholar] [CrossRef]
- Yao, Y.; Ni, J.; Jue, L. Stress-dependent water retention of granite residual soil and its implications for ground settlement. Comput. Geotech. 2020, 129, 103835. [Google Scholar] [CrossRef]
- Xu, Y.; Yan, Y.Y. Optimal Design of Foundation Pit Dewatering Based on Objective Functions and Numerical Analysis. Adv. Mater. Res. 2012, 368–373, 2495–2499. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, J.; Zhan, H.; Wang, J.; Dou, Z.; Zhang, C.; Chen, C.; Fu, Y. Optimization schemes for deep foundation pit dewatering under complicated hydrogeological conditions using MODFLOW-USG. Eng. Geol. 2022, 303, 106653. [Google Scholar] [CrossRef]
- Wang, J.; Deng, Y.; Ma, R.; Liu, X.; Guo, Q.; Shao, Y.; Wu, L.; Zhou, J.; Yang, T. Model test on partial expansion in stratified subsidence during foundation pit dewatering. J. Hydrol. 2018, 557, 489–508. [Google Scholar] [CrossRef]
- Yong, Z.; YunYun, Z. Real time prediction of land subsidence caused by foundation pit dewatering. Rock Soil Mech. 2008, 29, 1593–1596. [Google Scholar] [CrossRef]
- Zeng, C.F.; Zheng, G.; Zhou, X.F.; Xue, X.L.; Zhou, H.Z. Behaviours of wall and soil during pre-excavation dewatering under different foundation pit widths. Comput. Geotech. 2019, 115, 103169. [Google Scholar] [CrossRef]
- Shi, J.; Wu, B.; Liu, Y.; Xu, S. Analysis of the influence of groundwater seepage on the deformation of deep foundation pit with suspended impervious curtain. Adv. Mech. Eng. 2022, 14, 117–121. [Google Scholar] [CrossRef]
- Banerjee, S. Design charts for double-walled cofferdams. J. Geotech. Eng. 1993, 119, 214–222. [Google Scholar] [CrossRef]
- Banerjee, S.; Muleshkov, A. Analytical Solution of Steady Seepage Into Double-Walled Cofferdams. J. Eng. Mech. 1992, 118, 525–539. [Google Scholar] [CrossRef]
- Bereslavskii, E.N. The flow of ground waters around a Zhukovskii sheet pile. J. Appl. Math. Mech. 2011, 75, 210–217. [Google Scholar] [CrossRef]
- Shen, S.L.; Wu, Y.X.; Misra, A. Calculation of head difference at two sides of a cut-off barrier during excavation dewatering. Comput. Geotech. 2017, 91, 192–202. [Google Scholar] [CrossRef]
- Wu, Y.X.; Shen, J.S.; Cheng, W.C.; Hino, T. Semi-analytical solution to pumping test data with barrier, wellbore storage, and partial penetration effects. Eng. Geol. 2017, 226, 44–51. [Google Scholar] [CrossRef]
- Zheng, C.; Xudong, W.; Jie, Z. Solution to one-dimensional nonlinear consolidation of foundation soil with variable pore pressure boundary. J. Nanjing Univ. Technol. Nat. Sci. Ed. 2014, 36, 90–94. [Google Scholar] [CrossRef]
- Schultz, D. Characterization of suspended substances in water. I. Analytical methods. Acta Hydrochim. Hydrobiol. 1980, 8, 175–180. [Google Scholar] [CrossRef]
- Kitajima, S.; Hatakeyama, M.; Tsuchiya, T.; Yasutaka, T. Development of an Analytical Method for Radioactive Cesium in Water Containing Suspended Solids Using Gellant. Bunseki Kagaku 2013, 62, 513–519. [Google Scholar] [CrossRef]
- Giraldez, H.; Segarra, C.D.P.; Rodriguez, I.; Oliva, A. Improved semi-analytical method for air curtains prediction. Energy Build. 2013, 66, 258–266. [Google Scholar] [CrossRef]
- Liu, X. Analytical solutions for steady two-dimensional suspended sediment transport in channels with arbitrary advection velocity and eddy diffusivity distributions. J. Hydraul. Res. 2016, 54, 389–398. [Google Scholar] [CrossRef]
- Zhao, N.; Shao, Z.; Yuan, B.; Chen, X.; Wu, K. Analytical Approach to the Coupled Effects of Slope Angle and Seepage on Shallow Lined Tunnel Response. Int. J. Appl. Mech. 2022, 14, 2250003. [Google Scholar] [CrossRef]
- Li, Z.; He, C.; Chen, Z.; Yang, S.; Ding, J.; Pen, Y. Study of seepage field distribution and its influence on urban tunnels in water-rich regions. Bull. Eng. Geol. Environ. 2019, 78, 4035–4045. [Google Scholar] [CrossRef]
- Madanayaka, T.A.; Sivakugan, N. Simple solutions for square and rectangular cofferdam seepage problems. Can. Geotech. J. 2018, 56, 730–745. [Google Scholar] [CrossRef]
- Miyake, N.; Kohsaka, N.; Ishikawa, A. Multi-aquifer pumping test to determine cutoff wall length for groundwater flow control during site excavation in Tokyo, Japan. Hydrogeol. J. 2008, 16, 995–1001. [Google Scholar] [CrossRef]
- Pujades, E.; López, A.; Carrera, J.; Vázquez-Suñé, E.; Jurado, A. Barrier effect of underground structures on aquifer. Eng. Geol. 2012, 145–146, 41–49. [Google Scholar] [CrossRef]
- Xu, Y.S.; Shen, S.L.; Du, Y.J.; Chai, J.-C. Modelling the cutoff behavior of underground structure in multi-aquifer-aquitard groundwater system. Nat. Hazards 2013, 66, 731–748. [Google Scholar] [CrossRef]
- ShuiLong, S.; ZhenYu, Y.; YeShuang, X.; YongXia, W. Characteristics of groundwater seepage with cut-off wall in gravel aquifer. I: Field observations. Can. Geotech. J. 2015, 52, 1526–1538. [Google Scholar] [CrossRef]
- Wu, Y.X.; Shen, S.L.; Yin, Z.Y.; Xu, Y.S. Characteristics of groundwater seepage with cut-off wall in gravel aquifer. II: Numerical analysis. Can. Geotech. J. 2015, 52, 1539–1549. [Google Scholar] [CrossRef]
- Wu, Y.X.; Shen, S.L.; Yuan, D.J. Characteristics of dewatering induced drawdown curve under blocking effect of retaining wall in aquifer. J. Hydrol. 2016, 539, 554–566. [Google Scholar] [CrossRef]
- Feng, B.; Liu, Y.; Wu, L.; Zhu, Y.; Zhang, X.; Tang, Y.; Yang, P. Controlling subsidence caused by de-watering in a deep foundation pit. Bull. Eng. Geol. Environ. 2012, 71, 545–555. [Google Scholar] [CrossRef]
- Wang, J.; Hu, L.; Tang, L.W.Y.; Zhu, Y.; Yang, P. Hydraulic barrier function of the underground continuous concrete wall in the pit of subway station and its optimization. Environ. Geol. 2009, 57, 447–453. [Google Scholar] [CrossRef]
- Luo, Z.J.; Zhang, Y.Y.; Wu, Y.X. Finite Element Numerical Simulation of Three-Dimensional Seepage Control for Deep Foundation Pit Dewatering. J. Hydrodyn. 2008, 20, 596–602. [Google Scholar] [CrossRef]
- Liu, S.; Jiang, S.; Cao, C. Comparison and optimization of alternatives to groundwater control for a deep excavation in highly permeable sand and gravel. J. Railw. Sci. Eng. 2018, 15, 3189–3197. [Google Scholar] [CrossRef]
- You, Y.; Yan, C.; Liu, S.; Xu, B.; Che, C.; Liu, J. Optimization Design for Dewatering of Large Deep Foundation Pit under Complex Geological Conditions. J. Eng. Geol. 2017, 25, 715–722. [Google Scholar] [CrossRef]
- Ma, C.; Mao, Y.; Huang, W.; Cai, H. Effects of dewatering methods on seepage and deformation of foundation pits. Chin. J. Geotech. Eng. 2014, 36, 294–298. [Google Scholar] [CrossRef]
- Jiang, X.; Zong, J. Three-dimensional finite element analysis of seepage fields in foundation pit. Chin. J. Geotech. Eng. 2006, 28, 564–568. [Google Scholar] [CrossRef]
- Bin, W.; Chang, Y.-H.; Zhi, L.-J. High yield production of graphene and its improved property in detecting heavy metal ions. J. Refrig. 2011, 26, 31–35. [Google Scholar] [CrossRef]
- Li, W.-Y.; Li, F.; Zhu, Z.-F. Numerical simulation and land subsidence control for deep foundation pit dewatering of Longyang Road Station on Shanghai Metro Line 18. J. Groundw. Sci. Eng. 2019, 7, 133–144. [Google Scholar] [CrossRef]
- Zhou, N.; Vermeer, P.A.; Lou, R.; Tang, Y.; Jiang, S. Numerical simulation of deep foundation pit dewatering and optimization of controlling land subsidence. Eng. Geol. 2010, 114, 251–260. [Google Scholar] [CrossRef]
- Li, J.; Ma, J.; Sun, X.; Shen, X.; Liu, Q. Numerical simulation of soil nitrogen transformation for water storage single pit irrigation. Trans. Chin. Soc. Agric. Eng. 2012, 28, 111–117. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Z.Q.; He, C.; Ma, C.C.; Duan, C.R. Seepage field distribution and water inflow laws of tunnels in water-rich regions. J. Mt. Sci. Engl. Ed. 2022, 19, 591–605. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, H.; Mao, J.; Guan, C. Numerical simulation of the bubbling phenomenon ahead of the dam using a two-phase seepage free surface model. Comput. Geotech. 2023, 155, 105239. [Google Scholar] [CrossRef]
- Zhang, Y.T. Analysis of Seepage Field of Highway Tunnel Excavation by Finite Difference Method. Appl. Mech. Mater. 2014, 638–640, 798–803. [Google Scholar] [CrossRef]
- Lin, Z.; Zhang, B.; Guo, J. Analysis of a Water-Inrush Disaster Caused by Coal Seam Subsidence Karst Collapse Column under the Action of Multi-Field Coupling in Taoyuan Coal Mine. Comput. Model. Eng. Sci. (Engl.) 2021, 126, 311–330. [Google Scholar] [CrossRef]
- Wang, X.; Tan, Z.; Wang, M.; Zhang, M.; Ming, H. Theoretical and experimental study of external water pressure on tunnel lining in controlled drainage under high water level. Tunn. Undergr. Space Technol. 2008, 23, 552–560. [Google Scholar] [CrossRef]
- Wang, W.; Han, Z.; Deng, J.; Zhang, X.; Zhang, Y. Study on soil reinforcement param in deep foundation pit of marshland metro station. Heliyon 2019, 5, e02836. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Liu, M.; Deng, S.; Li, Y.; Zhang, X.; Liu, T. Study on the law of influence of seepage field anomalies on displacement field induced by leakage of enclosure structure. Appl. Sci. 2022, 12, 3809. [Google Scholar] [CrossRef]
- Nikvar Hassani, A.; Katibeh, H.; Farhadian, H. Numerical analysis of steady-state groundwater inflow into Tabriz line 2 metro tunnel, northwestern Iran, with special consideration of model dimensions. Bull. Eng. Geol. Environ. 2016, 75, 1617–1627. [Google Scholar] [CrossRef]
- Yuan, C.; Hu, Z.; Zhu, Z.; Yuan, Z.; Fan, Y.; Guan, H.; Li, L. Numerical simulation of seepage and deformation in excavation of a deep foundation pit under water-rich fractured intrusive rock. Geofluids 2021, 2021, 6628882. [Google Scholar] [CrossRef]
- Tan, Y.; Smith, J.V.; Li, C.Q.; Currell, M.; Wu, Y. Predicting external water pressure and cracking of a tunnel lining by measuring water inflow rate. Tunn. Undergr. Space Technol. 2018, 71, 115–125. [Google Scholar] [CrossRef]
- Zhang, Q.; Wei, M.; Wang, C. Numerical Simulation of Groundwater Seepage from Suspended Water Stop Curtains. Geotech. Eng. Tech. 2021, 35, 146–150. [Google Scholar] [CrossRef]
- Hwang, J.-H.; Lu, C.-C. A semi-analytical method for analyzing the tunnel water inflow. Tunn. Undergr. Space Technol. 2007, 22, 39–46. [Google Scholar] [CrossRef]



| Soil Layer Number | Soil Layer | Thickness | Physical and Mechanical Parameters | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Poisson’s Ratio | Density (kg/m3) | Elastic Modulus (MPa) | Permeability Coefficient (m/d) | Internal Friction Angle (°) | Cohesive Force (MPa) | Void Ratio | |||
| 1 | Miscellaneous fill, loess- shaped silty clay | 2 | 0.35 | 1750 | 15.4 | 6 | 20 | 0.022 | 0.9 |
| 2 | Fine sand | 6 | 0.30 | 1850 | 24 | 15 | 20 | 0 | 0.46 |
| 3 | Loose to slightly dense sandy and gravel | 6 | 0.25 | 2100 | 46 | 60 | 30 | 0 | 0.42 |
| 4 | Medium-dense to dense sand and gravel | 16 | 0.25 | 2200 | 120 | 80 | 35 | 0 | 0.39 |
| 5 | Dense sand and gravel | 70 | 0.22 | 2200 | 120 | 60 | 42 | 0.36 | |
| 6 | Impermeable bedrock | 20 | 0.20 | 2500 | 1500 | - | - | - | 0.2 |
| 7 | Enclosure structure | - | 0.20 | 2500 | 3100 | 80 | - | - | 0.2 |
| Calculation Conditions | Parameter Setting Values | |||||
|---|---|---|---|---|---|---|
| Precipitation depth (m) | 4 | 6 | 8 | 10 | 12 | 14 |
| Groundwater level (m) | 104 | 106 | 108 | 110 | 112 | 114 |
| Silty clay bottom (m) | 114 | |||||
| Medium-dense to dense pebble bottom (m) | 24 | 26 | 28 | 30 | 32 | 34 |
| Impermeable bedrock (m) | 0~24 | 0~26 | 0~28 | 0~30 | 0~32 | 0~34 |
| The bottom of the suspended water-stop curtain (m) | 86 | |||||
| Precipitation Depth (m) | Projected Area (m2) | Maximum Seepage Flow Velocity (mm/s) | |||
|---|---|---|---|---|---|
| >0.1875 mm/s | >0.375 mm/s | >0.5625 mm/s | >0.75 mm/s | ||
| 4 | 0 | 0 | 0 | 0 | 0.18 |
| 6 | 31.1 | 0 | 0 | 0 | 0.28 |
| 8 | 174.66 | 2 | 0 | 0 | 0.38 |
| 10 | 194 | 4 | 0 | 0 | 0.45 |
| 12 | 238.39 | 8 | 0 | 0 | 0.54 |
| 14 | 273.928 | 84 | 4 | 0 | 0.66 |
| Calculation Conditions | Parameter Setting Values | ||||
|---|---|---|---|---|---|
| Precipitation depth (m) | 8 | ||||
| Groundwater level (m) | 108 | ||||
| Silty clay bottom (m) | 114 | ||||
| Medium-dense to dense gravel bottom (m) | 88 | 68 | 48 | 28 | 8 |
| Impermeable bedrock (m) | 0~88 | 0~68 | 0~48 | 0~28 | 0~8 |
| The bottom of the suspend water-stop curtain (m) | 92 | ||||
| Aquifer Thickness (m) | Projected Area (m2) | Maximum Seepage Flow Velocity (mm/s) | |||
|---|---|---|---|---|---|
| >0.1875 mm/s | >0.375 mm/s | >0.5625 mm/s | >0.75 mm/s | ||
| 20 | 24.33 | 0 | 0 | 0 | 0.37 |
| 40 | 50.66 | 0 | 0 | 0 | 0.32 |
| 60 | 115.05 | 2 | 0 | 0 | 0.40 |
| 80 | 128.00 | 4 | 0 | 0 | 0.44 |
| 100 | 136.00 | 4 | 0 | 0 | 0.46 |
| Position | Measurement Value | Calculated Value of Water Level Drop (m) | |
|---|---|---|---|
| Elevation (m) | Water Level Drop Value (m) | ||
| B8 | 112.50 | 1.78 | 1.53 |
| J6 | 101.78 | 12.50 | 13.9 |
| J9 | 112.38 | 1.90 | 2.01 |
| J70 | 112.39 | 1.88 | 1.98 |
| J72 | 109.45 | 4.83 | 5.08 |
| West End Head | 105.9 | 8.38 | 9.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Cheng, S.; Liu, N.; Liu, Z.; Sun, Y. Numerical Simulation Study on the Distribution Characteristics of Precipitation Seepage Field in Water-Rich Ultra-Thick Sand and Gravel Layer. Water 2023, 15, 3720. https://doi.org/10.3390/w15213720
Li D, Cheng S, Liu N, Liu Z, Sun Y. Numerical Simulation Study on the Distribution Characteristics of Precipitation Seepage Field in Water-Rich Ultra-Thick Sand and Gravel Layer. Water. 2023; 15(21):3720. https://doi.org/10.3390/w15213720
Chicago/Turabian StyleLi, Da, Shukai Cheng, Ningyi Liu, Zhongxin Liu, and Yinghao Sun. 2023. "Numerical Simulation Study on the Distribution Characteristics of Precipitation Seepage Field in Water-Rich Ultra-Thick Sand and Gravel Layer" Water 15, no. 21: 3720. https://doi.org/10.3390/w15213720
APA StyleLi, D., Cheng, S., Liu, N., Liu, Z., & Sun, Y. (2023). Numerical Simulation Study on the Distribution Characteristics of Precipitation Seepage Field in Water-Rich Ultra-Thick Sand and Gravel Layer. Water, 15(21), 3720. https://doi.org/10.3390/w15213720








