Spatial Effects of NAO on Temperature and Precipitation Anomalies in Italy

Abstract

The NAO teleconnective pattern has a great influence on the European climate; however, the exact quantification of NAO pattern in the different areas is sometimes lacking, and at other times, highlights even large differences between the various studies. This motivation led to the identification of the aim of this research in the study of the relationship between the NAO index and temperature and precipitation anomalies over the period 1991–2020, through the analysis of 87 rain gauges and 86 thermometric stations distributed as homogeneously as possible over the Italian territory. The results were sometimes at odds with the scientific literature on the subject, as significance was also found outside the winter season, e.g., in the spring for temperatures and in the autumn for precipitation, and in some cases, correlations were found, especially in August, even in southern Italy, which is usually considered a poorly correlated area. In addition, the linear relationship between the NAO index and temperature and precipitation anomalies was verified, with many weather stations obtaining significant coefficients of determinations as high as 0.5–0.6 in December, with 29 degrees of freedom, and a p-value set at 95%. Finally, for both climatic parameters, the presence of clusters and outliers at seasonal and monthly levels was assessed, obtaining a spatial distribution using the local Moran index, and summarising them in maps. This analysis highlighted important clusters in Northern and Central Italy, while clusters in the summer months occur in the South. These results provide information that may further elucidate local atmospheric dynamics in relation to NAO phases, as well as encourage future studies that may link other teleconnective indices aimed at better explaining the variance of climate parameters.

1. Introduction

1.1. Aim of the Study and State of the Art

The North Atlantic Oscillation (NAO) Index, is one of the most important teleconnective indices as it is capable of generating seasonal variations in atmospheric circulation, which produce appreciable changes in the climatic pattern of the areas affected by it [1]. The NAO is one of the world’s oldest known weather patterns and has very ancient roots; in fact, the first evidence of its presence dates to the 18th century by Scandinavian sailors [2]. Over the past 20–30 years, the scientific literature has been very actively concerned with the NAO index, looking for, and in some cases finding, correlations in various related scientific fields. One of the topics that most studies have focused on in recent years is hydrology, with the NAO index showing a strong relationship with rainfall patterns, which is reflected in river dynamics. In fact, spatial differences have been observed in the hydrological regime of some European rivers that, depending on the geographical area, show direct or inverse relationships with the NAO index [3]. Relationships with the NAO have been found in the time series of the hydrological regimes of many large rivers [4,5] and more generally with the hydrological resources of large geographical areas [6,7,8], in some cases even far from the presumed area of influence of this index. For example, the impacts of this index in ecology were analysed, assessing its impact on certain ecosystems in terms of plant phenology, always depending on its influence on climatic parameters [9]. Similarly, a correlation between NAO and forest decline in Spain has been observed [10]; furthermore, in some cases, forest species, such as Scots Pine, were used to reconstruct the historical trend of the NAO index [11]. Similarly, relationships between fauna and the NAO index have been studied and discovered. In particular, the advancement of the spring arrival of migratory birds were also investigated, which, however, allowed the explanation of about 6% of the variance, an interesting but not crucial result in terms of understanding the phenomenon [12]. With regard to biodiversity, it has been observed that NAO phases are characterised by important variations in the number of zooplankton [13] or jellyfish populations in the North Sea [14]. Oceanic circulation is also a topic of interest in relation to the NAO index. In 2013, a crucial paper stimulated much further research on the subject, and sea level dependencies of particularly intense NAO values, especially in the Mediterranean, have been found to explain much of the variance [15]. NAO also seems to be able to influence SST in addition to wind speed as observed in the Greenland Sea, where correlation coefficients were positive and unusually high [16]. Turning instead to more strictly meteorological-climatic topics, the NAO is held in high regard for the evaluation of both climatic parameters and the dynamics of the atmosphere. In particular, the impact that the NAO can exert on the generation of extra-tropical storms was investigated, as Seierstad and Bader demonstrate by highlighting the decrease in storminess correlated with a negative NAO phase [17]. In other research, a very good correlation was observed between storminess conditions and the NAO index in the North-East Atlantic region, in all seasons except autumn, analysing a very large time interval from 1874 to 2007 [18]. Furthermore, in the same vein, the relationship between the NAO and the number of tropical cyclones during the season has been assessed by numerous scholars. In particular, a positive relationship between the month of June and the generation of tropical cyclones in July and August in the North Pacific has been shown, although it may be influenced by other teleconnective indices that are out of phase with the NAO [19]. In addition, the NAO also seems to play a role with regard to extreme precipitation events, especially in the Euro-Mediterranean area it is recognised as having an impact that tends to increase potential vorticity and air humidity [20]. As far as precipitation and temperature are concerned, it is a key issue to assess the relationship with the NAO index, mainly in Europe, where, according to the scientific literature on the subject, there is the greatest variation in the climate parameters in question [21,22]. However, although there are many studies that testify to strong correlations, there are others that suggest that there seems to have been a non-stationary influence of the NAO index on precipitation throughout history [23]. On the one hand, this would explain why no strong correlations are found with European climate parameters, although it is acknowledged that there has been a strengthening of the relationship between the NAO index and precipitation in recent times [24]. Similarly in the case of temperature, the relationships with the NAO index in terms of intensity and phase appear to be non-linear, as well as spatially variable [25]. In particular, a study on the effects of the NAO on temperatures and precipitation in some mountainous regions of the Mediterranean area, highlighted that the same NAO values, depending on the geographical area, can show different but correlated temperature and precipitation patterns within the same weather station [26]. In this context, there is a lack of detailed studies in the international scientific literature for individual countries with a congruent number of weather stations, aimed at identifying correlations and linear relationships between the NAO index and precipitation or temperatures, as well as differentiating influences at an areal level. On the basis of this need, in-depth studies for not too large portions of the European territory would be desirable, in order to provide a defined overview of the influence of the NAO index on climate for different regions. The aim of this research is to analyse the relationship between the NAO index and the precipitation and temperature anomalies with respect to their 30-year average (1991–2020) for the entire Italian territory, subdivided into similar geographical areas. In this way it would be possible to understand both the strength of the linear relationship between the NAO index and the climate parameters studied, as well as the differential influence on them generated by the atmospheric dynamics gravitating over the Italian peninsula, modified by the pressure anomalies over the North Atlantic area.

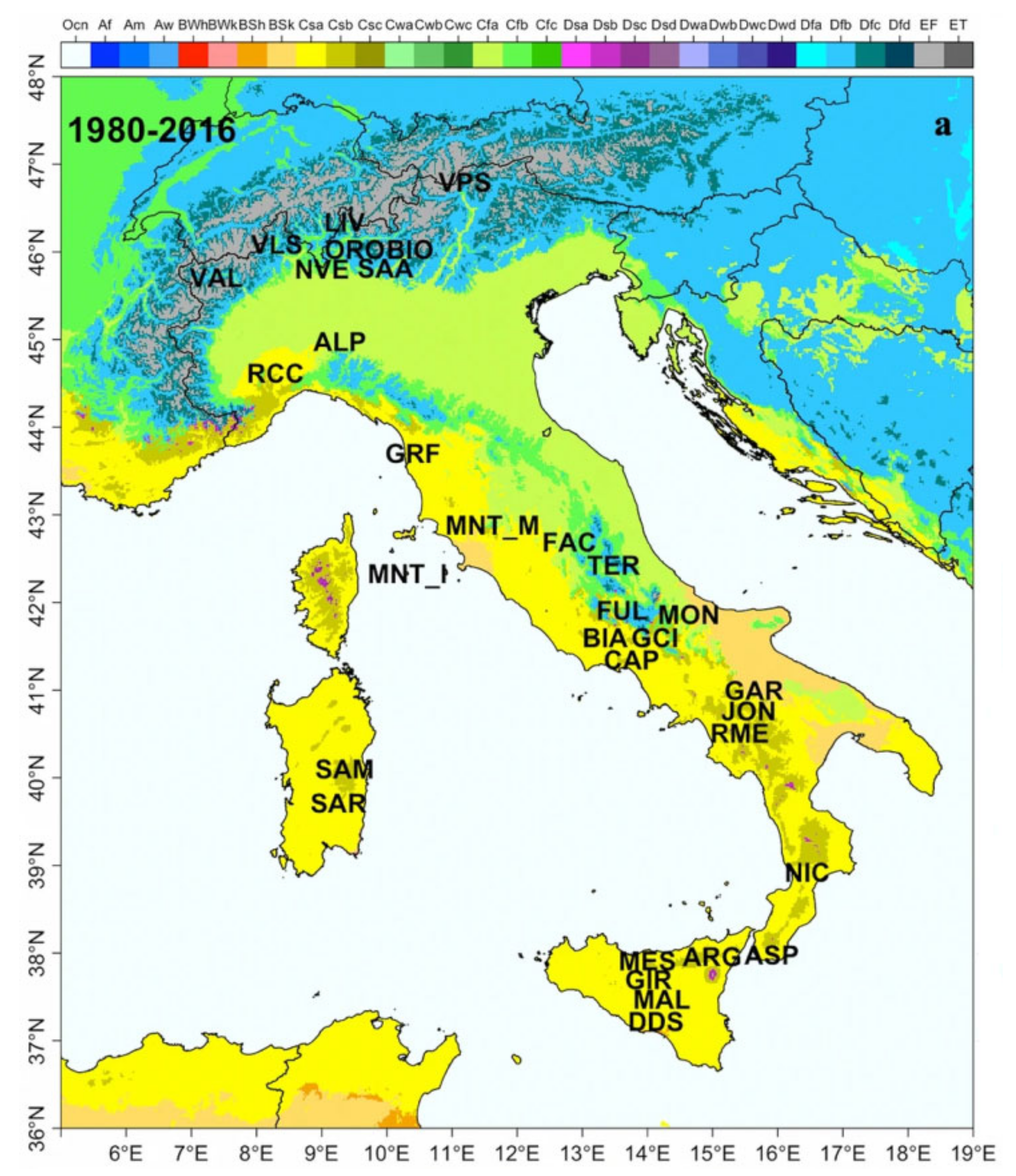
1.2. Study Area

Climatically speaking, Italy is a very heterogeneous country that stretches from about 47 to 35 degrees latitude. The Italian peninsula is also extremely heterogeneous in terms of altitude, with peaks of over 4000 m in the Alpine zone, over 2000 m in the Apennine zone that cuts the peninsula longitudinally, a large flat area in the north, and is bordered by the Mediterranean Sea with approximately 8300 km of coastline (Figure 1). The presence of the mountain ranges that cut the peninsula in a north–south and west–east direction introduces variations in the climatic dynamics that lead, on the upwind side, to more precipitation, while shielding it on the downwind side to. This extremely orographically complex situation results in a great variety of climates, and in relation to the variability linked to the NAO index, could lead to appreciable differences, as yet unknown.

Therefore, the geomorphological variety and the extension in terms of latitude of the Italian territory leads to very different climates. Following the Köppen–Geiger classification, up to 10 different climatic types can be distinguished, with a Mediterranean climate Csa present over a large part of the islands’ surface area, the entire coastal and pericoastal zone of the Tyrrhenian side, the Ionian side and the southernmost part of the Adriatic side (Figure 2). Cs-type climates then decline with the various thirds showing a decrease in temperature as the altitude in the continental area increases. A warm temperate climate of type Cfa in the Po Valley and in the areas surrounding the Adriatic coast in the centre-north modifies the third letter as altitude increases. Typical boreal forest climates (type D) on the Alpine and Apennine peaks with nival climate zones on the highest Alpine peaks (ET) [27,28].

2. Materials and Methods

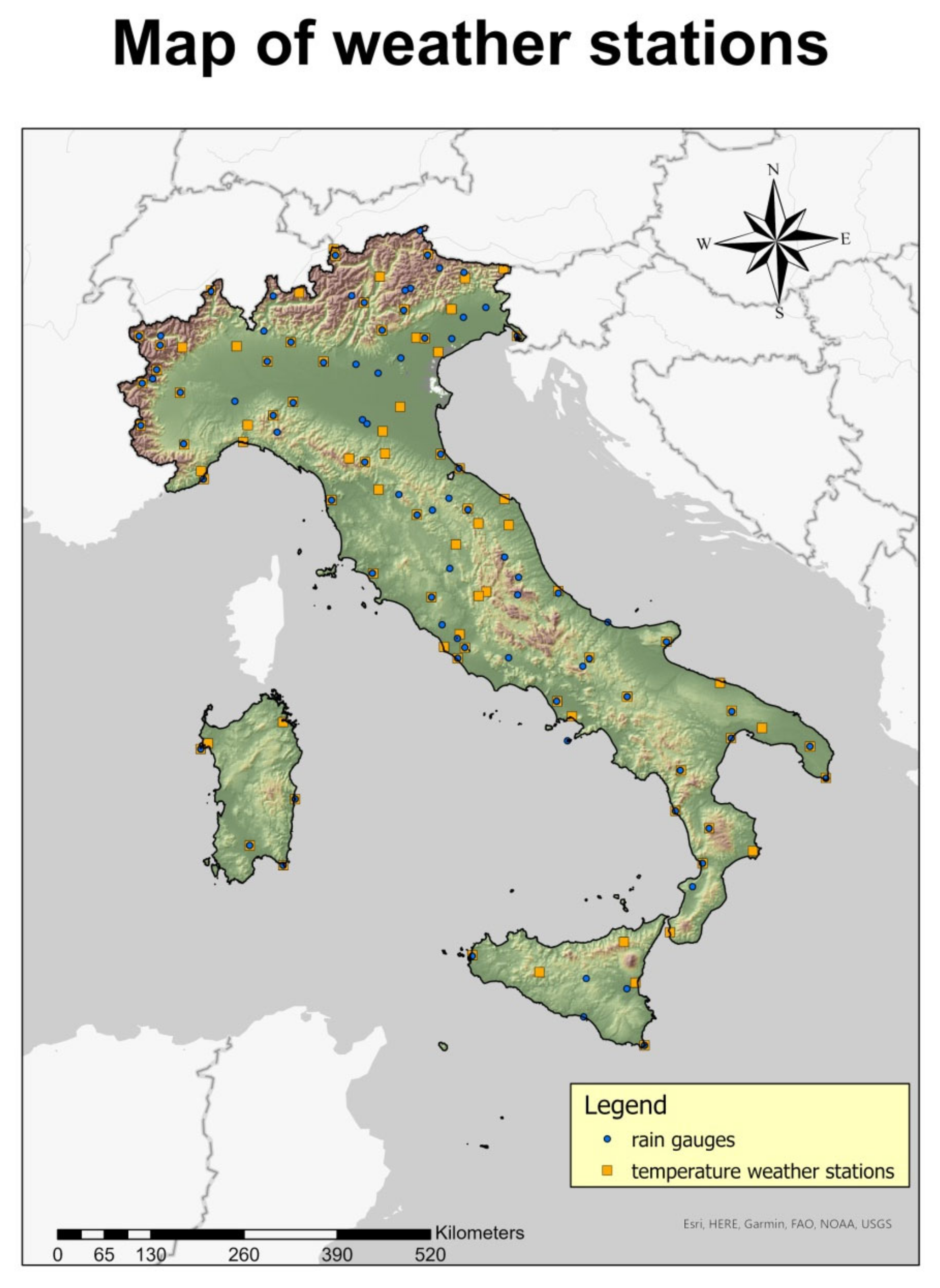
2.1. Weather Stations

Data were collected from some weather stations, 87 equipped with rain gauges and 86 with thermometers uniformly distributed over the Italian peninsula. The last reference period was chosen as the period of existence 1991–2020, in order to have a sufficiently complete historical time series, with a lack of data over the period always less than 20% (Figure 3). The data were collected through the SCIA system (National System for the Collection, Processing and Dissemination of Climatological Data of Environmental Interest) implemented by ISPRA (Istituto Superiore per la Protezione Ambientale) and with data from the National System for Environmental Protection and other observation networks throughout the country. These institutions transmit data and information on climate in Italy to the World Meteorological Organisation (WMO) and contribute to the knowledge framework on climate evolution on a global scale. The weather stations chosen for the analysis were further validated and homogenised following the guidelines dictated by the WMO [29,30], although they were already subject to data quality control processes, each of which was specific to the institution managing the weather stations under investigation. In particular, a validation was performed consisting of the following tests, gross error checking, internal consistency check, tolerance test, temporal consistency, spatial consistency, while Alexanderson’s standard normal homogeneity test (SNHT) was used for homogenization [30,31]. The choice of weather stations was made on the basis of a grid of Italy, prepared from the European reference grid with a side length of 100 km [32], looking for at least one weather station or more weather stations that could be representative of the area and that could have a sufficiently long time-series. In cases where the data showed a significant trend using the Mann–Kendall test, they were detrended by calculating the least squares and estimating the growth rate, then subtracting the deviations from the least squares line. Only the temperature data were detrended, while precipitation, as well as the NAO index, showed no significant trend. In order to analyse the area from the point of view of the NAO index, a canonical geographical subdivision was chosen (North-East, North-West, Centre, South and Islands), as the atmospheric dynamics also turn out to be predominantly homogeneous between these areas from previous research. This is the reason why a division on a climatic basis was avoided, which would have grouped together weather stations that respond very differently to the stimuli of the NAO index, even though they may have similar values on average.

2.2. NAO Index

The pressure anomaly between the Azores anticyclone and the Icelandic cyclone is called the North Atlantic Oscillation (NAO) and the NAO index is the value that expresses this pressure difference; it is the most influential teleconnective index for the climate of the North Atlantic area [33]. The NAO can have two phases; the positive, in which the pressure of the Azores anticyclone is above normal, while the pressure of the Icelandic cyclone is below normal. In the negative phase, the pressure of the Azores anticyclone is below normal and the pressure of the Icelandic cyclone is above normal.

A strongly positive phase is associated with above-normal temperatures and precipitation in the United States and Northern Europe, and below-normal in Greenland, Southern Europe and the Middle East, while in strongly negative phases the situation is the opposite (Figure 4). The NAO is able to influence the climate at a regional level precisely because it influences the jet stream, which may or may not be diverted, and as we know the jet stream can be responsible for generating cyclonic events on the ground with the mechanism of divergence and convergence at high altitudes. The NAO can show great interannual variability, but also continuous periods as long as many months of a single phase.

The NAO is also used for short- to medium-term climate forecasts, based on past observations and performing an ensemble mean forecast, not unlike weather forecasting (Figure 5) [35]. There are different methods to calculate the NAO index by referring to the different areas of the area affected by this anomaly, some refer to the difference between the atmospheric pressure measured in two different geographical locations, one representing the Azores anticyclone, the other the Icelandic cyclone. The locations that can be chosen or that have been chosen in the literature are many, it follows that the NAO index does not have an unambiguous value but depends on the method of calculation, in this context a advantage of these location-based methods is that it is possible to go back a long way in time with these measurements (as far as the mid-nineteenth century), while a shortcoming is that the data are not representative of the entire pressure anomaly, because they cannot precisely capture it throughout the year. Currently, the international scientific literature seems to be mainly oriented towards a calculation of the NAO index through the method called principal component analysis (PCA) or empirical orthogonal function (EOF), a multivariate statistical technique that allows for the synthesis of a dataset composed of many data into a few factors, called principal components, minimising the loss of information. In this research, the NAO index was calculated on the basis of the Rotated Principal Component Analysis (RPCA) [36] applied to standardised monthly anomalies at 500-mb height obtained from the Climate Data Assimilation System (CDAS) in the 20 °N 90 °N region between January 1950 and December 2000. The CDAS was produced by the joint effort within the “reanalysis” project of The National Centers for Environmental Prediction (NCEP) and National Center for Atmospheric Research (NCAR) to produce a retroactive record of more than 50 years of global atmospheric field analysis on a gridded file [37]. Thus, the NCEP and part of NOAA, and the monthly NAO index data were downloaded from the official NCEP website. As mentioned above, positive NAO phases tend to generate above-average precipitation and temperatures in the east coast of the United States and in Scandinavia, with a decrease of both in Greenland and the Mediterranean area in winter, while during negative NAO phases the situation is the opposite [38,39]. What is not clear in the scientific literature is a precise spatial definition of the influence of the NAO index on climate, which is why it is interesting to start differentiating the Italian territory based on the response of precipitation and temperature anomalies to this index.

2.3. Statistical Analysis

The correlation and the linear relationship between the NAO index and the two investigated variables, temperature and precipitation, was statistically tested. Data were collected on a monthly scale; however, the calculation was also performed on a seasonal scale. Kendall’s tau uses a formula that is based on the agreement or disagreement between pairs of observations and is especially suitable in the case of small samples. In particular, the Kendall tau-b has been used, which is always calculated as the proportion of agreeing pairs minus the proportion of disagreeing pairs, but also takes into account coincident pairs on a variable by adding them to the denominator of the proportions [40]. The closer the index is to zero, the weaker the concordance, while the closer it is to 1 the stronger the positive concordance, and if it is closer to −1 the negative concordance will be strong. The significance was tested at an alpha value of 95%, for all the months and for all the seasons; furthermore, the values of NAO index above 0.8 were isolated in order to find if there could be an increase in the correlation value. No emphasis was placed on significance as the reduction in the sample size could lead to poorly comparable results [24]. In particular, despite the increase in correlation for the NAO values above 0.8, the decrease in sample size would lead to fewer stations having a significant correlation. It follows that the lack of significance in the case of the partial analysis, with values above 0.8 and below −0.8, allows us to use this result as a rough indication of the correlation trend if the NAO were to take values above or below a certain threshold. A longer time series could bring even this small part of the study, which is only exploratory in purpose, to gain significance. This was done because other research on the subject has shown that a deeper anomaly can change climate variables by influencing them more than a shallower anomaly [41]. In the same way, the cause–effect relation with the linear regression was also tested, after some attempts with non-linear regressions that have not produced better results in terms of coefficient of determination (or pseudo R squared in the case of non-linear regressions). In this case, simple linear regression was used, since the only explanatory variable is the NAO index and the deterministic equation describing it is as follows:

$$y_i={\beta }_0+{\beta }_1*x_i+{\epsilon }_i$$

(1)

• $y_i$ = dependent variable;
• $x_i$ = independent variable;
• ${\beta }_0$ = intercept value;
• ${\beta }_1$ = slope value;
• ${\epsilon }_i$ = error term, consists of omitted factors, other than variable $x_i$, that influence $y_i$, the regression error (error term) also includes the error in the measurement of $y_i$.

The method used to verify the statistical significance of the linear regression was the F-test, which is based on the decomposition of deviances, the significance level was set to 95%.

2.4. Clusters and Outliers Analysis

Clusters analysis aims to verify the concentration of weather stations that show particularly high or particularly low values in the relationship between the NAO index and temperature and precipitation anomalies. There is also a great interest in the analysis of outliers because they can indicate, in clustered or otherwise homogeneous areas, weather stations that differ significantly from neighbouring weather stations, indicating local atmospheric dynamics that differ from neighbouring areas. This analysis was performed using the Local Moran Index [42,43,44,45] through GIS software (ArcGis 10.8) and the significance of both clusters and outliers was set at 95%.

$$I_i=\frac{z_i-\overline{z}}{{\sigma }^2}{{\displaystyle \sum }}_{j=1, j\ne i}^n\left[w_{ij}\left(z_j-\overline{z}\right)\right]$$

(2)

• $z_i$ = value of the variable z at location i;
• $\overline{z}$ = average value of z;
• $z_j$ = value of variable z in all other locations other than i;
• ${\sigma }^2$ = variance of z;
• $w_{ij}$ = weight, inverse distance among locations i and j.

3. Results

3.1. Correlation Analysis between NAO Index and Climate Variables

Correlation is a statistical measure that expresses the linear relationship between two variables; it is suitable for measuring the direction of the relationship, i.e., whether the correlation is positive or negative between the two variables, and the intensity of the relationship. The correlations between the NAO index, precipitation and temperatures anomalies were assessed for both seasons and months, and the results are shown in tabular form, by dividing the Italian territory into 4 similar geographical macro-areas (North-East, North-West, Centre, South and Islands), in order to assess the presence of homogeneous correlations within them (

Table 1. Kendall’s tau correlation index referring to the NAO values of the period 1991–2020 with temperature anomalies, with the significant values in bold, and a p-value less than 0.05.

NORTH-WEST	WIN	SPR	SUM	AUT	JAN	FEB	MAR	APR	MAY	JUN	JUL	AUG	SEP	OCT	NOV	DEC
ALA DI STURA	0.30	0.29	0.01	0.21	0.22	0.20	0.41	0.21	0.29	0.01	0.09	−0.08	0.41	0.03	0.21	0.36
ALBENGA	0.31	0.26	0.15	0.19	0.11	0.27	0.44	0.18	0.20	0.07	0.11	0.27	0.29	0.01	0.24	0.45
ALPE DEVERO	0.31	0.22	−0.02	0.23	0.26	0.15	0.32	0.14	0.16	−0.09	0.04	−0.03	0.35	0.02	0.30	0.50
BERGAMO	0.18	0.23	0.04	0.13	0.07	0.21	0.30	0.06	0.28	0.02	−0.01	0.09	0.48	−0.04	0.01	0.26
BRESCIA/GHE	0.14	0.23	−0.11	0.11	0.03	0.21	0.34	0.12	0.29	−0.04	−0.15	−0.11	0.33	−0.03	−0.03	0.16
COGNE	0.28	0.27	0.04	0.25	0.26	0.16	0.30	0.22	0.30	0.08	0.04	0.02	0.35	−0.02	0.46	0.43
DONNAS	0.23	0.27	0.01	0.16	0.14	0.16	0.29	0.20	0.42	0.08	−0.03	−0.07	0.40	−0.05	0.10	0.43
FUNIVIA BERNINA-CHIESA VALMA	0.25	0.23	0.07	0.22	0.15	0.12	0.34	0.18	0.28	−0.01	0.09	0.12	0.30	0.01	0.42	0.43
GENOVA/SESTRI	0.37	0.23	0.09	0.15	0.31	0.27	0.34	0.02	0.27	0.01	0.12	0.11	0.39	−0.12	0.14	0.55
LA THUILE	0.31	0.26	0.05	0.23	0.34	0.17	0.35	0.17	0.25	0.11	0.05	0.06	0.35	−0.04	0.38	0.46
MILANO/LINATE	0.15	0.22	0.05	0.09	0.07	0.18	0.25	0.09	0.34	0.01	0.09	0.03	0.33	−0.03	−0.07	0.18
MILANO/MALPENSA	0.19	0.21	−0.04	0.18	0.11	0.26	0.27	0.13	0.23	−0.26	0.07	0.07	0.36	0.06	0.09	0.24
MONDOVI	0.31	0.19	0.05	0.18	0.32	0.14	0.37	0.01	0.13	0.08	0.11	−0.03	0.36	−0.05	0.20	0.52
PASSO DEI GIOVI	0.37	0.26	0.00	0.14	0.41	0.23	0.34	0.21	0.28	−0.12	0.07	0.07	0.35	−0.05	0.15	0.51
PIETRASTRETTA	0.33	0.24	0.03	0.21	0.39	0.17	0.40	0.06	0.30	0.03	0.09	0.00	0.31	−0.01	0.29	0.47
PONTECHIANALE	0.35	0.27	−0.02	0.17	0.43	0.23	0.36	0.13	0.36	−0.07	0.03	−0.03	0.30	−0.09	0.28	0.52
TORINO/BRIC	0.31	0.17	0.05	0.25	0.35	0.20	0.38	0.06	0.13	0.06	0.05	0.12	0.46	0.00	0.29	0.46
NORTH-EAST	WIN	SPR	SUM	AUT	JAN	FEB	MAR	APR	MAY	JUN	JUL	AUG	SEP	OCT	NOV	DEC
AVIANO	0.18	0.25	0.07	0.12	0.06	0.26	0.36	0.16	0.28	−0.05	0.08	0.16	0.35	−0.01	−0.05	0.24
BOBBIO	0.30	0.20	−0.03	0.13	0.20	0.24	0.21	0.11	0.27	−0.06	−0.01	−0.05	0.34	−0.05	0.10	0.46
BOLOGNA/BORGO	0.22	0.27	0.00	0.04	0.11	0.27	0.31	0.06	0.44	−0.02	−0.03	0.02	0.22	0.00	−0.14	0.27
BOLZANO	0.12	0.22	−0.04	0.08	−0.01	0.20	0.37	0.17	0.19	−0.04	−0.01	−0.06	0.41	−0.13	−0.05	0.17
BRUSTOLE’ VELO D’ASTICO	0.19	0.26	0.01	0.16	0.05	0.25	0.35	0.14	0.36	−0.10	0.08	0.00	0.34	0.08	0.04	0.25
CASTELFRANCO VENETO	0.11	0.26	−0.03	0.11	−0.02	0.20	0.30	0.15	0.35	−0.13	0.00	−0.03	0.27	0.04	−0.02	0.17
CERVIA	0.18	0.21	−0.08	0.00	0.11	0.20	0.19	0.21	0.33	−0.26	−0.08	0.00	0.22	−0.21	−0.12	0.24
DOBBIACO	0.23	0.17	−0.03	0.16	0.08	0.30	0.23	0.11	0.24	−0.12	0.02	0.01	0.35	0.10	0.09	0.31
ENEMONZO	0.19	0.26	0.01	0.12	−0.01	0.13	0.33	0.18	0.30	−0.01	0.03	0.02	0.32	−0.04	0.08	0.32
FERRARA	0.17	0.19	0.01	0.02	0.15	0.18	0.28	0.15	0.21	−0.02	0.08	−0.02	0.26	−0.17	−0.12	0.17
LAMON	0.25	0.24	0.04	0.18	0.08	0.25	0.36	0.12	0.32	0.03	0.01	0.09	0.33	0.01	0.20	0.34
LOIANO	0.35	0.26	0.01	0.09	0.21	0.32	0.29	0.17	0.35	0.01	0.04	−0.01	0.24	−0.11	0.07	0.48
MONTE CIMONE	0.21	0.17	−0.09	0.15	0.03	0.19	0.14	0.19	0.25	−0.13	−0.14	−0.09	0.28	−0.07	0.24	0.42
PAGANELLA	0.24	0.19	0.05	0.20	0.05	0.19	0.27	0.08	0.35	−0.02	0.07	0.10	0.32	−0.01	0.32	0.44
PIACENZA	0.21	0.21	0.06	0.13	0.19	0.18	0.24	0.03	0.35	−0.09	0.13	0.10	0.42	−0.03	−0.01	0.27
PORRETTA TERME	0.25	0.29	0.05	0.00	0.11	0.28	0.29	0.33	0.37	−0.13	0.10	0.14	0.10	−0.10	−0.04	0.40
RESIA	0.24	0.22	0.07	0.20	0.12	0.12	0.38	0.10	0.18	−0.03	0.09	0.13	0.37	−0.01	0.22	0.39
RIMINI	0.18	0.24	−0.03	0.01	0.08	0.20	0.22	0.29	0.30	−0.09	0.05	−0.07	0.20	−0.16	−0.09	0.28
S. VALENTINO	0.28	0.20	0.04	0.25	0.12	0.14	0.36	0.07	0.15	−0.02	0.06	0.10	0.47	0.03	0.26	0.45
TARVISIO	0.29	0.24	0.08	0.05	0.15	0.28	0.40	0.10	0.27	−0.02	0.05	0.18	0.21	−0.11	−0.03	0.47
TREVISO/ISTRANA	0.12	0.22	−0.03	0.09	−0.02	0.12	0.29	0.08	0.31	−0.12	0.01	0.01	0.35	−0.04	−0.06	0.26
VENEZIA/TESSERA	0.12	0.32	0.02	0.04	−0.02	0.21	0.38	0.21	0.40	−0.08	0.04	0.03	0.24	−0.03	−0.12	0.17
CENTRO	WIN	SPR	SUM	AUT	JAN	FEB	MAR	APR	MAY	JUN	JUL	AUG	SEP	OCT	NOV	DEC
AREZZO	0.13	0.23	−0.07	0.07	−0.05	0.29	0.24	0.18	0.36	−0.22	−0.05	−0.01	0.23	−0.02	0.04	0.15
FABRIANO	0.12	0.21	−0.12	−0.07	−0.03	0.39	0.18	0.27	0.33	−0.25	−0.17	0.04	0.08	−0.27	−0.07	0.13
FALCONARA	0.11	0.25	−0.08	−0.06	0.00	0.15	0.20	0.18	0.43	−0.19	−0.09	0.00	0.10	−0.23	−0.13	0.18
FIRENZE	0.13	0.22	−0.05	0.10	0.02	0.23	0.23	0.15	0.33	−0.09	−0.07	−0.03	0.33	0.03	0.00	0.17
FRONTONE	0.21	0.18	−0.06	0.01	0.09	0.23	0.21	0.20	0.24	−0.14	−0.04	−0.04	0.24	−0.18	−0.11	0.36
GROSSETO	0.09	0.17	0.01	0.13	−0.07	0.19	0.20	0.15	0.29	−0.04	0.09	0.00	0.26	0.03	0.06	0.20
MACERATA/ MONTALBANO	0.34	0.19	−0.06	0.08	0.35	0.26	0.24	0.10	0.23	−0.03	−0.17	−0.02	0.15	−0.11	0.11	0.43
MONTE TERMINILLO	0.21	0.13	0.03	0.07	−0.04	0.36	0.19	0.01	0.29	0.03	−0.01	0.09	0.15	−0.13	0.17	0.27
PERUGIA	0.04	0.21	−0.02	0.07	−0.13	0.18	0.11	0.19	0.38	−0.05	−0.04	−0.04	0.34	−0.03	−0.09	0.04
PISA SAN GIUSTO	0.18	0.23	0.05	0.10	−0.08	0.26	0.25	0.22	0.32	−0.13	0.09	0.17	0.30	−0.05	0.08	0.32
PRATICA DI MARE	0.12	0.15	−0.02	0.07	−0.15	0.25	0.04	0.22	0.28	−0.11	0.07	−0.02	0.26	0.01	−0.06	0.23
RIETI	0.08	0.12	−0.20	0.03	−0.08	0.25	0.13	0.23	0.06	−0.16	−0.12	−0.29	0.23	−0.11	−0.08	0.05
ROMA CIAMPINO	0.11	0.16	−0.08	0.06	−0.10	0.24	0.13	0.19	0.24	−0.17	−0.03	−0.09	0.25	−0.10	−0.02	0.20
ROMA FIUMICINO	0.14	0.22	0.02	0.06	−0.06	0.31	0.16	0.21	0.37	−0.07	0.06	0.07	0.25	−0.03	−0.01	0.16
ROMA/URBE	0.12	0.20	0.02	0.06	−0.11	0.32	0.15	0.20	0.25	−0.02	0.01	0.08	0.28	−0.13	0.03	0.13
VITERBO	0.20	0.23	−0.06	0.08	0.01	0.29	0.28	0.18	0.26	−0.18	0.02	−0.04	0.18	−0.14	0.14	0.36
SUD	WIN	SPR	SUM	AUT	JAN	FEB	MAR	APR	MAY	JUN	JUL	AUG	SEP	OCT	NOV	DEC
ALGHERO	0.05	0.05	0.07	0.07	−0.10	0.18	−0.10	0.10	0.16	−0.04	0.14	0.11	0.35	−0.21	0.01	0.01
BARI/PALESE MACCHIE	0.07	0.14	−0.05	−0.02	−0.09	0.19	0.02	0.10	0.35	−0.13	−0.17	0.08	0.01	−0.06	−0.05	0.08
BONIFATI	0.08	0.09	−0.06	−0.05	−0.19	0.21	−0.01	0.20	0.10	−0.14	−0.08	0.03	0.02	−0.22	−0.02	0.16
CAMPOBASSO	0.16	0.15	−0.17	−0.01	−0.02	0.20	0.13	0.17	0.28	−0.29	−0.16	−0.13	0.06	−0.16	0.00	0.31
CAPO BELLAVISTA	0.08	0.09	−0.10	0.06	−0.16	0.18	−0.03	0.21	0.19	−0.08	−0.04	−0.19	0.25	−0.10	0.05	0.14
CAPODOCHINO	0.04	0.13	0.02	0.11	−0.16	0.19	0.10	0.10	0.25	−0.06	0.12	0.02	0.30	0.06	−0.12	0.13
CATANIA	−0.13	−0.03	0.05	−0.02	−0.29	0.07	−0.24	0.03	0.14	−0.05	0.13	0.01	0.12	−0.13	−0.10	−0.24
COZZO SPADARO	0.00	0.01	−0.07	0.05	−0.22	0.23	−0.11	0.16	0.16	−0.09	−0.11	−0.02	0.20	−0.10	0.07	−0.02
CROTONE	0.06	0.11	−0.10	0.01	−0.04	0.16	−0.03	0.11	0.29	−0.09	−0.19	−0.07	0.03	0.02	−0.06	0.10
DECIMOMANNU	0.04	0.06	−0.08	0.09	−0.08	0.14	−0.03	0.16	0.11	−0.16	−0.03	−0.09	0.24	−0.11	0.14	0.01
DIGA PLATANI	0.04	−0.01	−0.14	−0.03	−0.23	0.17	−0.10	0.18	−0.05	−0.16	−0.15	−0.12	0.05	−0.16	0.08	0.10
FLORESTA	0.07	0.06	−0.17	−0.02	−0.10	0.16	−0.14	0.39	0.01	−0.20	−0.22	−0.15	0.10	−0.15	0.15	0.07
GIOIA DEL COLLE	−0.03	0.11	−0.17	0.01	−0.16	0.16	−0.03	0.22	0.21	−0.26	−0.15	−0.06	0.11	0.00	−0.03	−0.07
GRAZZANISE	0.08	0.17	−0.01	0.10	−0.15	0.28	0.12	0.22	0.31	−0.10	0.07	0.01	0.33	−0.07	0.06	0.11
GROTTAGLIE	−0.01	0.18	−0.14	−0.07	−0.19	0.14	0.09	0.25	0.30	−0.17	−0.06	−0.21	−0.01	0.02	−0.22	−0.01
LAMEZIA TERME	−0.02	0.11	−0.08	0.01	−0.22	0.21	0.00	0.16	0.33	−0.14	−0.10	0.06	0.13	−0.11	0.05	−0.05
LATRONICO	0.11	0.06	−0.13	0.02	−0.03	0.25	−0.07	0.17	0.12	−0.25	−0.09	−0.15	0.16	−0.08	0.04	0.14
LECCE	−0.03	0.11	−0.07	0.02	−0.16	0.13	−0.13	0.26	0.29	−0.20	−0.02	0.10	0.10	0.01	−0.10	−0.03
MARINA DI GINOSA	0.02	0.16	−0.03	0.08	−0.15	0.08	0.01	0.26	0.21	0.01	−0.04	−0.06	0.15	−0.01	0.15	0.09
MONTE S. ANGELO	0.17	0.15	−0.10	0.02	−0.04	0.21	0.11	0.13	0.22	−0.22	−0.11	0.02	0.03	−0.15	0.08	0.30
MONTE SCURO	0.15	0.08	−0.18	0.05	−0.04	0.28	−0.08	0.22	0.12	−0.22	−0.22	−0.11	0.10	−0.09	0.10	0.16
OLBIA/COSTA SMERALDA	0.10	0.06	−0.01	0.07	−0.03	0.16	0.08	0.08	0.12	−0.09	0.02	0.05	0.29	−0.16	0.07	0.10
PESCARA	0.01	0.18	−0.14	−0.04	−0.11	0.10	0.09	0.07	0.39	−0.22	−0.14	−0.05	0.01	−0.05	−0.15	0.03
REGGIO CALABRIA	0.02	0.10	−0.07	0.00	−0.06	0.18	−0.02	0.28	0.19	−0.18	0.02	0.00	0.24	−0.20	0.02	−0.03
S. MARIA DI LEUCA	0.03	0.12	−0.09	−0.01	−0.12	0.10	0.00	0.20	0.27	−0.08	−0.07	−0.09	0.08	−0.05	−0.10	0.10
TRAPANI	−0.06	−0.03	−0.06	0.05	−0.25	0.13	−0.11	0.08	0.04	−0.19	−0.05	0.09	0.33	−0.19	−0.04	−0.18
TREVICO	0.11	0.16	−0.11	0.02	−0.11	0.24	0.00	0.26	0.24	−0.24	−0.04	−0.10	0.04	−0.05	0.02	0.20

and

Table 2. Kendall’s tau correlation index referring to the NAO values of the period 1991–2020 with precipitation anomalies, with the significant values in bold, and a p-value less than 0.05.

NORTH-WEST	WIN	SPR	SUM	AUT	JAN	FEB	MAR	APR	MAY	JUN	JUL	AUG	SEP	OCT	NOV	DEC
ALA DI STURA	−0.06	0.02	0.02	−0.02	−0.10	0.04	−0.15	−0.03	0.04	−0.12	0.03	0.22	−0.06	0.03	−0.06	−0.15
ALESSADRIA	−0.16	−0.16	0.04	−0.17	−0.16	0.03	−0.22	−0.04	−0.27	−0.14	0.02	0.16	−0.27	0.03	−0.23	−0.28
ALPE DEVERO	0.01	−0.06	−0.06	−0.15	0.05	0.00	−0.12	−0.06	−0.10	−0.10	−0.08	−0.01	−0.25	−0.03	−0.17	−0.07
BERGAMO ORIO	−0.02	−0.14	−0.10	−0.13	−0.01	0.03	−0.20	−0.07	−0.21	−0.16	−0.10	−0.09	−0.09	0.08	−0.27	−0.10
BRESCIA GHEDI	−0.30	−0.11	0.08	−0.19	−0.39	−0.16	−0.28	0.03	−0.06	−0.09	0.25	0.15	−0.40	−0.02	−0.24	−0.34
COGNE	−0.02	0.09	0.01	0.01	−0.17	0.07	−0.14	0.16	0.12	−0.09	0.05	0.18	−0.10	0.14	−0.12	−0.07
ERBA	−0.17	−0.11	−0.01	−0.19	−0.17	−0.09	−0.62	0.02	0.03	−0.09	0.00	0.02	−0.41	0.05	−0.21	−0.26
ETROUBLES	−0.02	−0.04	0.03	−0.11	−0.12	0.15	−0.24	−0.04	0.04	−0.09	0.02	0.10	−0.28	0.02	−0.19	−0.08
LA THUILE	−0.09	−0.12	−0.15	−0.08	−0.22	0.12	−0.29	−0.12	−0.04	−0.34	0.01	−0.20	−0.21	0.01	−0.20	−0.18
MILANO LINATE	−0.04	−0.04	0.07	−0.17	0.10	0.11	−0.19	0.12	−0.02	−0.02	0.05	0.15	−0.36	0.05	−0.22	−0.20
MONDOVì	−0.09	−0.08	−0.01	−0.09	−0.07	0.04	−0.26	−0.18	0.09	−0.11	−0.11	0.18	−0.33	0.17	−0.11	−0.19
PIETRASTRETTA	−0.14	−0.07	0.07	−0.07	−0.23	−0.02	−0.30	0.01	−0.08	−0.01	0.09	0.28	−0.17	0.02	−0.12	−0.25
PONTECHIANALE	−0.19	−0.01	0.10	−0.11	−0.29	−0.05	−0.19	−0.10	0.02	−0.10	0.11	0.28	−0.17	0.13	−0.22	−0.24
SAINT CHRISTOPHE	−0.01	0.00	−0.02	0.00	−0.05	0.07	−0.33	0.16	0.01	−0.24	0.15	0.11	−0.16	0.15	−0.10	−0.08
SALOMACO	−0.11	−0.07	−0.19	−0.19	−0.30	0.03	−0.31	0.00	−0.01	−0.43	−0.06	−0.10	−0.21	−0.09	−0.26	−0.15
SANTO STEFANO D’AVETO	−0.23	−0.19	0.06	−0.18	−0.25	−0.14	−0.29	−0.09	−0.17	−0.12	0.18	0.12	−0.38	0.07	−0.30	−0.27
TORINO BRIC DELLA C	−0.09	−0.08	0.04	−0.10	−0.05	0.00	−0.33	−0.12	0.06	−0.22	0.13	0.23	−0.21	0.03	−0.07	−0.21
NORTH-EAST	WIN	SPR	SUM	AUT	JAN	FEB	MAR	APR	MAY	JUN	JUL	AUG	SEP	OCT	NOV	DEC
AURONZO	−0.11	−0.04	−0.23	−0.16	−0.07	−0.08	−0.19	0.24	−0.12	−0.35	−0.17	−0.15	−0.30	0.10	−0.30	−0.21
BOBBIO	−0.24	−0.08	−0.05	−0.16	−0.23	−0.20	−0.14	−0.18	0.03	−0.11	−0.16	0.10	−0.41	0.15	−0.24	−0.29
BRUSTOLè	−0.18	−0.09	−0.05	−0.14	−0.20	−0.08	−0.22	0.07	−0.14	−0.21	0.02	0.04	−0.24	0.11	−0.27	−0.29
CASTELFRANCO EMILIA	−0.26	−0.10	0.07	−0.13	−0.44	−0.14	−0.17	0.00	−0.12	0.12	0.03	0.02	−0.40	0.13	−0.14	−0.29
CERVIA	−0.16	−0.09	0.03	−0.14	−0.26	0.00	−0.04	−0.01	−0.23	−0.07	0.06	0.07	−0.26	0.08	−0.33	−0.28
DOBBIACO	−0.08	0.01	−0.21	−0.14	0.02	−0.06	−0.10	0.13	0.08	−0.30	−0.26	−0.09	−0.32	0.06	−0.24	−0.19
ENEMONZO	−0.12	−0.01	−0.08	−0.14	−0.18	−0.12	−0.16	0.12	0.02	−0.15	−0.12	0.08	−0.28	0.12	−0.26	−0.14
GARES	−0.14	−0.04	−0.13	−0.15	−0.08	−0.07	−0.16	0.11	−0.05	−0.16	−0.15	−0.07	−0.33	0.03	−0.26	−0.25
LAMON	−0.15	−0.11	−0.01	−0.15	−0.15	−0.11	−0.22	0.03	−0.19	−0.13	−0.02	0.07	−0.28	0.13	−0.26	−0.22
MONTE GALDA	−0.26	−0.14	0.08	−0.15	−0.35	−0.05	−0.17	−0.11	−0.17	0.01	0.09	0.17	−0.34	0.11	−0.30	−0.39
NOVENTA DI PIAVE	−0.24	−0.12	0.03	−0.16	−0.33	−0.05	−0.10	−0.05	−0.16	−0.19	0.27	0.00	−0.24	0.09	−0.27	−0.40
PAGANELLA	0.03	−0.04	−0.16	−0.10	0.22	−0.05	−0.37	0.01	−0.06	−0.21	−0.12	−0.19	−0.29	0.19	−0.24	−0.13
PASSO ROLLE	−0.13	−0.02	−0.16	−0.12	−0.22	−0.12	−0.17	0.29	−0.06	−0.19	−0.20	−0.14	−0.23	0.16	−0.35	−0.20
PIACENZA	−0.29	−0.09	0.02	−0.23	−0.40	−0.11	−0.10	−0.13	−0.01	−0.13	0.05	0.18	−0.50	−0.04	−0.25	−0.34
PORRETTA TERME	−0.19	−0.11	0.16	−0.23	−0.35	−0.04	−0.21	0.04	−0.13	0.04	0.24	0.17	−0.38	0.05	−0.38	−0.21
PRADALAGO	−0.18	−0.07	−0.09	−0.17	−0.27	−0.10	−0.11	−0.04	0.04	−0.05	−0.14	−0.02	−0.37	0.12	−0.33	−0.20
PREDOI	−0.04	−0.07	−0.26	−0.13	0.06	0.04	−0.08	−0.09	0.00	−0.25	−0.41	−0.16	−0.23	−0.01	−0.26	−0.21
RIMINI	−0.14	−0.08	0.12	−0.06	−0.27	0.03	−0.11	0.03	−0.15	0.14	0.06	0.21	−0.21	0.08	−0.16	−0.16
ROVERCHIARA	−0.28	−0.19	0.04	−0.17	−0.46	−0.06	−0.19	−0.18	−0.25	−0.08	0.16	0.09	−0.25	−0.02	−0.21	−0.31
SAN VALENTINO	0.11	−0.09	−0.01	−0.11	0.25	0.19	−0.08	−0.02	−0.08	0.09	−0.06	−0.02	−0.09	−0.07	−0.29	−0.06
SAN VITO AL TAGLIAMENTO	−0.23	−0.11	−0.06	−0.18	−0.35	−0.10	−0.17	−0.04	−0.15	−0.06	−0.07	0.02	−0.32	0.05	−0.30	−0.27
TREVISO ISTRANA	−0.21	−0.13	0.06	−0.11	−0.27	−0.06	−0.16	−0.09	−0.08	0.06	0.04	0.18	−0.18	0.11	−0.26	−0.32
UDINE	−0.22	−0.11	−0.03	−0.13	−0.37	−0.13	−0.22	−0.01	−0.08	0.05	−0.08	0.06	−0.17	0.14	−0.37	−0.25
VERONA	−0.28	−0.11	−0.03	−0.17	−0.39	−0.06	−0.26	0.03	−0.14	−0.18	0.02	0.03	−0.33	0.00	−0.30	−0.34
CENTRO	WIN	SPR	SUM	AUT	JAN	FEB	MAR	APR	MAY	JUN	JUL	AUG	SEP	OCT	NOV	DEC
AREZZO	−0.18	−0.09	0.04	−0.23	−0.26	0.05	−0.17	−0.03	0.02	0.08	0.11	−0.05	−0.20	−0.20	−0.36	−0.28
CASSIODORO	−0.22	−0.22	0.27	−0.04	−0.29	−0.16	−0.25	−0.26	−0.25	0.12	0.19	0.47	−0.13	0.23	−0.21	−0.16
FRONTONE	−0.13	−0.03	0.05	−0.19	−0.13	0.06	−0.07	−0.01	0.01	−0.04	0.02	0.12	−0.31	−0.07	−0.31	−0.24
FROSINONE	−0.19	−0.12	0.19	−0.16	−0.16	−0.17	−0.17	−0.18	−0.07	0.01	0.19	0.37	−0.38	0.05	−0.23	−0.25
GROSSETO	−0.26	−0.14	0.08	−0.13	−0.25	−0.26	−0.35	−0.28	0.09	0.08	0.11	0.13	−0.32	−0.05	−0.06	−0.31
MONTEMONACO	−0.03	−0.03	0.16	−0.07	0.11	0.03	−0.15	−0.13	0.06	0.21	−0.04	0.32	0.00	0.10	−0.18	−0.13
PISA	−0.16	−0.12	0.06	−0.19	−0.21	−0.04	−0.26	0.01	−0.09	−0.05	0.18	0.09	−0.27	−0.08	−0.28	−0.25
PRATICA DI MARE	−0.22	−0.07	0.08	−0.10	−0.24	−0.20	−0.13	−0.01	−0.15	0.10	0.09	0.11	−0.15	−0.01	−0.13	−0.18
ROMA CIAMPINO	−0.24	−0.03	0.25	−0.11	−0.20	−0.27	−0.04	0.00	−0.05	0.14	0.26	0.40	−0.23	0.00	−0.18	−0.25
S. ANGELO IN VADO	−0.17	−0.10	0.05	−0.18	−0.20	0.09	−0.12	−0.05	−0.10	0.12	0.09	0.02	−0.48	0.00	−0.21	−0.33
SANTA FISTA	−0.26	−0.05	0.08	−0.21	−0.38	−0.07	−0.13	0.08	0.00	0.05	0.18	0.00	−0.17	−0.26	−0.29	−0.30
TODI	−0.21	−0.15	−0.01	−0.21	−0.29	−0.41	−0.28	−0.02	−0.11	−0.17	0.02	0.09	−0.36	0.04	−0.35	−0.05
VALLOMBROSA	−0.20	−0.12	0.08	−0.15	−0.28	0.05	−0.06	−0.10	−0.18	0.04	0.16	0.12	−0.24	−0.11	−0.25	−0.32
VIGNA DI VALLE	−0.28	−0.23	0.09	−0.08	−0.33	−0.20	−0.32	−0.23	−0.10	−0.03	0.17	0.18	−0.20	0.10	−0.18	−0.31
VITERBO	−0.26	−0.10	0.03	−0.09	−0.27	−0.23	−0.17	−0.18	0.03	−0.07	−0.02	0.18	−0.03	0.14	−0.26	−0.23
SUD	WIN	SPR	SUM	AUT	JAN	FEB	MAR	APR	MAY	JUN	JUL	AUG	SEP	OCT	NOV	DEC
ASSERGI	−0.19	−0.16	0.10	−0.13	−0.25	−0.31	−0.32	−0.26	0.03	0.20	−0.07	0.26	−0.18	0.02	−0.14	−0.08
BONIFATI	−0.15	−0.06	0.09	−0.12	0.01	−0.32	−0.10	−0.02	0.05	0.01	0.14	0.07	−0.17	−0.03	−0.23	−0.04
CAMPOBASSO	−0.21	−0.03	0.12	−0.03	−0.17	−0.41	−0.22	0.01	−0.01	0.14	0.16	0.11	−0.05	0.06	−0.10	−0.22
CAMPOCHIARO	−0.19	−0.16	0.26	−0.20	−0.19	−0.32	−0.21	−0.33	0.02	0.15	0.36	0.28	−0.19	−0.06	−0.30	−0.16
CAPO BELLAVISTA	−0.19	−0.09	0.14	0.10	−0.25	−0.10	−0.15	−0.05	0.03	0.14	0.11	0.32	0.00	0.03	0.23	−0.19
CAPRI	−0.14	−0.15	0.16	−0.01	−0.19	−0.16	−0.23	−0.19	0.10	0.05	0.18	0.33	−0.16	0.14	−0.07	−0.07
CATANIA SIGONELLA	−0.11	0.00	0.28	0.09	−0.11	−0.12	0.06	−0.05	0.08	0.35	0.17	0.39	0.09	0.00	0.17	−0.12
COZZO SPADARO	−0.03	0.03	0.08	0.15	0.00	−0.18	0.27	−0.19	0.03	0.02	0.29	0.28	0.06	0.07	0.33	−0.04
DECIMOMANNU	−0.18	−0.04	0.15	−0.03	−0.29	−0.24	−0.04	−0.06	0.01	0.21	0.04	0.20	0.03	0.08	−0.20	−0.09
ENNA	−0.14	0.07	0.27	−0.01	−0.30	−0.04	0.10	−0.04	0.21	0.22	0.31	0.37	−0.13	0.02	0.04	−0.09
GELA	−0.21	0.02	0.16	−0.01	−0.30	−0.23	0.07	0.00	0.07	0.18	0.17	0.29	−0.03	−0.14	0.11	−0.14
GIOIA DEL COLLE	−0.15	−0.02	0.07	0.04	−0.11	−0.14	−0.02	−0.03	0.02	0.08	0.02	0.10	0.05	0.05	0.05	−0.23
GRAZZANISE	−0.23	−0.14	0.21	−0.16	−0.30	−0.27	−0.27	−0.22	0.08	0.27	0.00	0.38	−0.28	0.06	−0.24	−0.20
LAMEZIA TERME	−0.26	−0.09	0.14	−0.09	−0.14	−0.26	−0.05	0.02	−0.18	0.07	0.22	0.19	−0.27	−0.02	−0.13	−0.23
LATRONICO	−0.10	−0.16	0.15	−0.08	0.11	−0.07	−0.18	−0.34	0.08	−0.01	0.27	0.11	−0.03	−0.10	−0.14	−0.25
LECCE	−0.11	−0.14	0.13	0.02	0.02	−0.13	−0.19	−0.03	−0.22	0.03	0.12	0.19	0.03	0.06	−0.01	−0.16
MARINA DI GINOSA	−0.10	−0.06	0.11	−0.02	−0.09	−0.21	−0.07	−0.01	−0.09	0.02	0.09	0.15	0.18	−0.01	−0.01	−0.04
MILETO	−0.16	−0.03	0.13	−0.02	−0.08	−0.28	−0.03	0.09	−0.09	−0.01	0.15	0.20	0.30	−0.14	−0.08	−0.16
MONTE SANT ANGELO	−0.17	0.01	0.14	0.00	−0.08	−0.09	−0.03	0.08	0.07	0.13	0.08	0.26	−0.04	0.12	0.00	−0.34
MONTE SCURO	−0.07	−0.01	0.07	−0.04	−0.03	−0.13	−0.21	0.25	−0.04	−0.09	0.10	0.27	−0.08	−0.02	0.02	−0.03
PAGLIAROLI	−0.04	−0.06	0.24	−0.08	0.16	−0.21	−0.22	0.01	−0.08	0.20	0.28	0.22	−0.08	0.11	−0.26	−0.13
PESCARA	−0.16	−0.05	0.08	0.04	−0.10	−0.11	−0.06	−0.34	0.18	0.01	−0.12	0.34	0.06	0.26	−0.13	−0.24
SANTA MARIA DI LEUCA	−0.19	0.05	0.11	−0.03	−0.18	−0.17	0.10	0.14	−0.02	0.07	0.23	0.01	−0.03	−0.01	0.02	−0.23
TRAPANI	−0.19	−0.02	0.19	−0.06	−0.11	−0.24	−0.09	−0.04	0.09	0.15	0.19	0.29	−0.16	−0.01	0.00	−0.22
TREVICO	0.04	0.00	0.18	−0.09	0.05	−0.10	−0.24	0.04	0.11	0.25	0.13	0.16	−0.25	−0.03	0.09	0.09

, Figure 4).

The correlation between the NAO index and temperature shows seasonally good and predominantly significant correlations for the Northwest in winter, spring and autumn, as well as monthly mainly in March, May, September and December. In the North-East, the situation is similar, although the correlation in autumn is weaker and with fewer significant weather stations. In central Italy, the significance and strength of the correlation is lower on average; however, it is acceptable in winter and spring, as well as monthly in February where it reaches a higher average than in the other geographical areas, May, September and December. In southern Italy, the correlation is even weaker, so much so that the month with the most significant weather stations is in May and there are essentially no other periods with high numbers of significant weather stations (Table 1).

For better clarity, seasonal maps of the correlation between the NAO index and temperature anomalies are shown. The seasons that show the most significantly correlated weather stations are winter and spring, especially in northern and central Italy, while in the south, there are not many significant weather stations (Figure 6). Significant weather stations are also present in autumn, but they are concentrated especially in the north-west and parts of the north-east (Figure 6). In summer, on the other hand, the few correlated weather stations are in southern and central Italy and have a negative correlation (Figure 6).

In addition, for a better spatial understanding of the magnitude of the correlation coefficient, the seasons showing the best results, namely, winter and spring, were interpolated (Figure 7). The result is a clear division between north-central and southern Italy, with the North having higher values and having a positive correlation between temperature anomalies and the NAO index, while the South shows low values and having a negative correlation.

Precipitation anomalies are, on average, less correlated with the NAO index than temperature anomalies. Furthermore, the influence on the geographical areas of the peninsula is also rather surprising: in the North-West, there are much fewer significant stations. In fact, there are, at most, 7 significant weather stations out of 16, in autumn, in March and in September, where, in particular, the latter month reaches rather remarkable values of inverse correlation. In the North-East, on the other hand, the correlation between the NAO index and precipitation anomalies is much stronger than in the North-West. In fact, numerous significant weather stations can be observed in the winter season, in autumn, in January, in September, in November and in December, with the latter three months approaching values close to −0.3. In the central part of the peninsula, it is surprising to see that almost all weather stations display a significant correlation between the NAO index and precipitation anomalies in winter; meanwhile, the rest are very similar to the situation in the North-East, with lower correlation values. Finally, Southern Italy has a good number of significant weather stations in winter and summer, as well as in August (Table 2).

The maps of the correlation between the NAO index and precipitation anomalies show significant correlations especially in winter and autumn; however, in this case, a low overall seasonal significance is highlighted in the north-western part of Italy, in contrast to what is shown by the temperatures (Figure 8).

In Figure 9, correlation coefficients were analysed over the Italian land area in order to identify areas that show a linear, direct or inverse relationship between the NAO index and temperature and precipitation anomalies.

Subsequently, in order to obtain a better overview of the dependence of the strength of the correlation on the intensity of the NAO index, it was decided to isolate the extremely high or extremely low values of the NAO index, i.e., those above 0.8 and −0.8. These values were correlated with precipitation and temperature anomalies and were compared with the complete data, evaluating the variation in the mean for each geographical area (

Table 3. Average correlation coefficient for the different geographical zones (NW—North-West, NE—North-East, C—Centre, S—South and Islands) with temperature, both for full NAO index values and for values outside the thresholds indicated in the table.

GEO. ZONE	WIN	SPR	SUM	AUT	JAN	FEB	MAR	APR	MAY	JUN	JUL	AUG	SEP	OCT	NOV	DEC
NW	0.28	0.24	0.03	0.18	0.23	0.20	0.34	0.13	0.27	0.00	0.05	0.04	0.36	−0.02	0.20	0.41
NW > ±0.8	0.35	0.31	0.12	0.11	0.41	0.40	0.40	0.28	0.40	−0.02	0.07	0.31	0.33	−0.13	0.35	0.48
NE	0.21	0.23	0.01	0.11	0.09	0.21	0.29	0.14	0.29	−0.07	0.03	0.04	0.30	−0.05	0.04	0.32
NE > ±0.8	0.27	0.30	0.07	0.03	0.23	0.28	0.36	0.28	0.43	−0.19	0.07	0.31	0.23	−0.11	0.02	0.37
C	0.15	0.19	−0.04	0.05	−0.03	0.26	0.18	0.18	0.29	−0.11	−0.03	−0.01	0.23	−0.09	0.01	0.21
C > ±0.8	0.20	0.26	−0.01	−0.01	0.09	0.23	0.21	0.34	0.34	−0.30	0.04	0.19	0.19	−0.15	−0.02	0.26
S	0.04	0.09	−0.08	0.02	−0.13	0.18	−0.02	0.18	0.20	−0.15	−0.06	−0.04	0.14	−0.09	0.00	0.06
S > ±0.8	0.08	0.13	−0.10	0.01	−0.03	0.13	−0.01	0.30	0.20	−0.35	−0.03	0.07	0.16	−0.09	−0.04	0.09

and

Table 4. Average correlation coefficient for the different geographical zones (NW—North-West, NE—North-East, C—Centre, S—South and Islands) with precipitation, both for full NAO index values and for values outside the thresholds indicated in the table.

GEO. ZONE	WIN	SPR	SUM	AUT	JAN	FEB	MAR	APR	MAY	JUN	JUL	AUG	SEP	OCT	NOV	DEC
NW	−0.11	−0.07	0.00	−0.11	−0.16	0.01	−0.27	−0.03	−0.03	−0.15	0.04	0.10	−0.23	0.05	−0.18	−0.18
NW > ±0.8	−0.20	−0.13	−0.05	−0.16	−0.12	−0.22	−0.32	−0.02	−0.11	−0.19	0.00	0.06	−0.47	0.27	−0.37	−0.29
NE	−0.17	−0.08	−0.04	−0.15	−0.21	−0.06	−0.16	0.01	−0.09	−0.10	−0.04	0.03	−0.29	0.08	−0.27	−0.25
NE > ±0.8	−0.24	−0.16	−0.08	−0.15	−0.30	−0.16	−0.23	0.00	−0.27	−0.15	−0.02	−0.08	−0.35	0.22	−0.47	−0.36
C	−0.20	−0.11	0.10	−0.14	−0.23	−0.12	−0.18	−0.09	−0.06	0.04	0.11	0.17	−0.23	−0.01	−0.23	−0.24
C > ±0.8	−0.20	−0.18	0.08	−0.13	−0.19	0.02	−0.24	−0.16	−0.21	0.06	0.06	0.12	−0.32	0.06	−0.35	−0.32
S	−0.15	−0.05	0.15	−0.03	−0.12	−0.19	−0.09	−0.06	0.02	0.11	0.14	0.23	−0.05	0.02	−0.04	−0.14
S > ±0.8	−0.11	−0.02	0.17	0.02	−0.04	−0.03	−0.09	−0.03	0.04	0.28	0.18	0.13	−0.13	0.23	−0.05	−0.16

).

With regard to the comparison in the various geographical areas between the correlations of temperature anomalies and the NAO index at full or those with the NAO index greater than 0.8 or less than −0.8, a certain increase in the intensity of the correlation is noted for the latter case. In particular, in the case of the months and seasons that have the most significant correlations with the NAO index complete of all values, increases between 20 and 30% are observed for those with the most intense NAO index (Table 3).

In the case of precipitation anomalies, the comparison of the NAO index with all values and the NAO index with only the most intense ones leads to increases ranging from 20 to 40 per cent (Table 4), so the increases are slightly more noticeable than in the case of temperature anomalies, observed in Table 3.

3.2. Regression Analysis between NAO Index and Climate Variables

Linear regression analysis, after correlation evaluation, is necessary to understand information that cannot be deduced from correlation analysis, i.e., whether there is a linear relationship between the NAO index and temperature and precipitation anomalies on the Italian peninsula. Linear regression provided the coefficient of determination R², which represents how much of the variance of a dependent variable, in our case, precipitation or temperature anomaly, is explained by the independent variable, the NAO index (

Table 5. Coefficient of determination R² derived from linear regression with NAO period as independent variable and temperature anomaly as dependent variable, period 1991–2020, in bold are the significant values, with a p-value less than 0.05.

NORTH-WEST	WIN	SPR	SUM	AUT	JAN	FEB	MAR	APR	MAY	JUN	JUL	AUG	SEP	OCT	NOV	DEC
ALA DI STURA	0.18	0.20	0.01	0.07	0.12	0.17	0.24	0.10	0.09	0.00	0.03	0.05	0.25	0.00	0.07	0.49
ALBENGA	0.22	0.18	0.05	0.11	0.01	0.22	0.36	0.07	0.12	0.05	0.00	0.10	0.08	0.00	0.09	0.56
ALPE DEVERO	0.17	0.12	0.00	0.10	0.12	0.12	0.14	0.04	0.00	0.00	0.00	0.04	0.20	0.01	0.13	0.62
BERGAMO	0.09	0.15	0.00	0.05	0.03	0.05	0.13	0.00	0.08	0.00	0.00	0.00	0.21	0.01	0.00	0.30
BRESCIA/GHEDI	0.04	0.16	0.03	0.03	0.00	0.04	0.15	0.02	0.08	0.02	0.01	0.03	0.11	0.01	0.00	0.16
COGNE	0.17	0.17	0.00	0.20	0.16	0.08	0.11	0.13	0.20	0.05	0.03	0.05	0.21	0.00	0.30	0.52
DONNAS	0.09	0.23	0.00	0.07	0.06	0.06	0.11	0.13	0.26	0.03	0.06	0.03	0.40	0.00	0.00	0.45
FUNIVIA BERNINA-CHIESA VALMA	0.34	0.19	0.01	0.09	0.11	0.05	0.12	0.03	0.16	0.00	0.00	0.08	0.25	0.01	0.25	0.55
GENOVA/SESTRI	0.60	0.17	0.02	0.01	0.24	0.19	0.29	0.00	0.23	0.00	0.01	0.11	0.30	0.01	0.02	0.62
LA THUILE	0.52	0.23	0.00	0.11	0.05	0.06	0.17	0.10	0.18	0.00	0.04	0.02	0.41	0.01	0.55	0.56
MILANO/LINATE	0.05	0.18	0.00	0.01	0.01	0.06	0.07	0.02	0.35	0.00	0.00	0.01	0.25	0.01	0.00	0.15
MILANO/MALPENSA	0.05	0.16	0.01	0.05	0.01	0.09	0.10	0.04	0.12	0.09	0.00	0.01	0.27	0.03	0.03	0.17
MONDOVI	0.17	0.13	0.00	0.03	0.18	0.02	0.24	0.04	0.09	0.01	0.01	0.00	0.24	0.02	0.05	0.63
PASSO DEI GIOVI	0.21	0.12	0.00	0.02	0.34	0.14	0.29	0.13	0.06	0.00	0.01	0.01	0.20	0.00	0.00	0.52
PIETRASTRETTA	0.19	0.14	0.00	0.04	0.22	0.08	0.30	0.03	0.13	0.00	0.00	0.00	0.31	0.01	0.03	0.55
PONTECHIANALE	0.19	0.13	0.00	0.05	0.12	0.11	0.22	0.07	0.18	0.00	0.05	0.00	0.28	0.00	0.09	0.56
TORINO/BRIC	0.19	0.10	0.02	0.08	0.27	0.09	0.21	0.06	0.05	0.01	0.00	0.03	0.41	0.04	0.04	0.45
NORTH-EAST	WIN	SPR	SUM	AUT	JAN	FEB	MAR	APR	MAY	JUN	JUL	AUG	SEP	OCT	NOV	DEC
AVIANO	0.07	0.19	0.00	0.03	0.00	0.08	0.12	0.01	0.09	0.01	0.00	0.01	0.08	0.00	0.00	0.22
BOBBIO	0.16	0.10	0.02	0.02	0.08	0.06	0.14	0.07	0.01	0.02	0.01	0.11	0.10	0.01	0.00	0.65
BOLOGNA/BORGO	0.11	0.19	0.01	0.00	0.01	0.10	0.13	0.02	0.36	0.02	0.01	0.02	0.00	0.00	0.05	0.32
BOLZANO	0.03	0.13	0.01	0.01	0.02	0.08	0.25	0.01	0.04	0.01	0.06	0.04	0.16	0.09	0.01	0.15
BRUSTOLE’ VELO D’ASTICO	0.08	0.18	0.00	0.04	0.00	0.09	0.14	0.00	0.16	0.01	0.00	0.03	0.13	0.02	0.00	0.24
CASTELFRANCO VENETO	0.03	0.13	0.00	0.03	0.01	0.05	0.07	0.00	0.17	0.02	0.00	0.02	0.08	0.00	0.00	0.15
CERVIA	0.06	0.13	0.00	0.00	0.01	0.04	0.01	0.06	0.26	0.08	0.03	0.01	0.02	0.11	0.02	0.16
DOBBIACO	0.08	0.07	0.00	0.07	0.00	0.17	0.01	0.00	0.26	0.10	0.00	0.03	0.20	0.01	0.00	0.40
ENEMONZO	0.08	0.16	0.01	0.07	0.00	0.06	0.09	0.02	0.22	0.00	0.00	0.01	0.31	0.02	0.01	0.36
FERRARA	0.04	0.10	0.00	0.00	0.02	0.06	0.12	0.03	0.18	0.03	0.01	0.02	0.31	0.07	0.06	0.16
LAMON	0.25	0.19	0.01	0.05	0.01	0.06	0.18	0.04	0.24	0.03	0.01	0.02	0.25	0.01	0.25	0.45
LOIANO	0.51	0.21	0.01	0.01	0.08	0.24	0.13	0.08	0.35	0.00	0.01	0.00	0.16	0.00	0.11	0.64
MONTE CIMONE	0.08	0.08	0.03	0.03	0.00	0.08	0.02	0.03	0.14	0.01	0.12	0.01	0.24	0.00	0.02	0.30
PAGANELLA	0.12	0.07	0.00	0.06	0.01	0.06	0.07	0.00	0.13	0.00	0.00	0.05	0.25	0.02	0.04	0.47
PIACENZA	0.05	0.10	0.00	0.01	0.02	0.07	0.07	0.01	0.18	0.01	0.00	0.04	0.31	0.00	0.02	0.24
PORRETTA TERME	0.10	0.14	0.00	0.00	0.07	0.11	0.06	0.16	0.24	0.00	0.00	0.12	0.11	0.01	0.03	0.39
RESIA	0.09	0.09	0.01	0.06	0.12	0.04	0.20	0.05	0.08	0.01	0.01	0.07	0.36	0.03	0.05	0.31
RIMINI	0.04	0.08	0.02	0.00	0.00	0.05	0.00	0.15	0.03	0.00	0.05	0.00	0.09	0.00	0.01	0.20
S. VALENTINO	0.15	0.08	0.00	0.13	0.19	0.07	0.13	0.03	0.10	0.00	0.00	0.01	0.36	0.04	0.07	0.37
TARVISIO	0.13	0.12	0.02	0.00	0.02	0.10	0.25	0.02	0.11	0.02	0.00	0.13	0.19	0.01	0.02	0.28
TREVISO/ISTRANA	0.03	0.13	0.00	0.01	0.00	0.00	0.07	0.03	0.12	0.03	0.00	0.03	0.27	0.00	0.04	0.17
VENEZIA/TESSERA	0.04	0.27	0.00	0.00	0.01	0.07	0.18	0.05	0.20	0.03	0.00	0.01	0.06	0.01	0.02	0.14
CENTRO	WIN	SPR	SUM	AUT	JAN	FEB	MAR	APR	MAY	JUN	JUL	AUG	SEP	OCT	NOV	DEC
AREZZO	0.04	0.11	0.03	0.01	0.01	0.11	0.00	0.01	0.08	0.05	0.03	0.02	0.02	0.06	0.01	0.19
FABRIANO	0.00	0.09	0.02	0.02	0.04	0.01	0.15	0.11	0.26	0.08	0.26	0.05	0.02	0.19	0.00	0.04
FALCONARA	0.02	0.13	0.01	0.01	0.00	0.02	0.00	0.01	0.38	0.12	0.05	0.02	0.08	0.08	0.03	0.18
FIRENZE	0.02	0.08	0.01	0.02	0.00	0.08	0.00	0.00	0.29	0.02	0.00	0.03	0.21	0.01	0.00	0.18
FRONTONE	0.25	0.08	0.02	0.00	0.01	0.05	0.00	0.00	0.12	0.07	0.07	0.00	0.17	0.05	0.01	0.41
GROSSETO	0.00	0.07	0.00	0.01	0.04	0.05	0.00	0.01	0.11	0.02	0.01	0.00	0.22	0.00	0.00	0.19
MACERATA/ MONTALBANO	0.48	0.13	0.01	0.01	0.18	0.12	0.14	0.00	0.19	0.00	0.04	0.00	0.09	0.01	0.05	0.50
MONTE TERMINILLO	0.08	0.03	0.00	0.01	0.00	0.14	0.01	0.00	0.08	0.00	0.00	0.03	0.20	0.01	0.00	0.20
PERUGIA	0.00	0.09	0.02	0.01	0.05	0.04	0.01	0.00	0.08	0.01	0.05	0.04	0.08	0.06	0.02	0.03
PISA SAN GIUSTO	0.05	0.10	0.01	0.01	0.00	0.08	0.02	0.09	0.21	0.02	0.00	0.05	0.19	0.05	0.01	0.20
PRATICA DI MARE	0.02	0.06	0.00	0.00	0.03	0.09	0.02	0.07	0.13	0.00	0.02	0.00	0.11	0.01	0.03	0.08
RIETI	0.00	0.04	0.10	0.00	0.09	0.04	0.02	0.10	0.00	0.03	0.03	0.24	0.19	0.00	0.03	0.01
ROMA CIAMPINO	0.01	0.06	0.02	0.00	0.00	0.12	0.01	0.04	0.08	0.03	0.03	0.04	0.15	0.00	0.03	0.02
ROMA FIUMICINO	0.02	0.09	0.00	0.01	0.00	0.14	0.00	0.10	0.27	0.00	0.04	0.00	0.10	0.00	0.00	0.06
ROMA/URBE	0.01	0.08	0.00	0.02	0.02	0.11	0.03	0.03	0.16	0.01	0.07	0.01	0.11	0.01	0.00	0.01
VITERBO	0.08	0.12	0.03	0.00	0.00	0.10	0.08	0.06	0.13	0.00	0.04	0.03	0.15	0.01	0.00	0.14
SUD	WIN	SPR	SUM	AUT	JAN	FEB	MAR	APR	MAY	JUN	JUL	AUG	SEP	OCT	NOV	DEC
ALGHERO	0.01	0.00	0.00	0.00	0.06	0.04	0.05	0.03	0.00	0.00	0.01	0.00	0.09	0.16	0.02	0.05
BARI/PALESE MACCHIE	0.02	0.05	0.01	0.00	0.03	0.07	0.03	0.04	0.11	0.10	0.10	0.00	0.02	0.08	0.03	0.06
BONIFATI	0.02	0.01	0.02	0.01	0.15	0.09	0.07	0.00	0.01	0.11	0.04	0.00	0.02	0.23	0.01	0.13
CAMPOBASSO	0.04	0.08	0.12	0.00	0.01	0.06	0.02	0.00	0.06	0.23	0.15	0.10	0.00	0.07	0.00	0.24
CAPO BELLAVISTA	0.00	0.00	0.04	0.01	0.09	0.06	0.17	0.04	0.00	0.04	0.01	0.12	0.13	0.03	0.03	0.10
CAPODOCHINO	0.00	0.04	0.00	0.03	0.12	0.05	0.00	0.01	0.12	0.12	0.10	0.00	0.08	0.03	0.02	0.06
CATANIA	0.04	0.01	0.00	0.00	0.29	0.00	0.17	0.00	0.01	0.02	0.00	0.00	0.00	0.08	0.05	0.16
COZZO SPADARO	0.00	0.00	0.00	0.01	0.21	0.05	0.09	0.00	0.01	0.10	0.00	0.00	0.04	0.07	0.01	0.00
CROTONE	0.01	0.02	0.05	0.00	0.03	0.03	0.07	0.02	0.14	0.17	0.15	0.02	0.00	0.01	0.10	0.00
DECIMOMANNU	0.00	0.00	0.01	0.01	0.05	0.03	0.02	0.00	0.05	0.09	0.01	0.04	0.17	0.13	0.05	0.02
DIGA PLATANI	0.00	0.00	0.05	0.00	0.20	0.03	0.09	0.00	0.01	0.11	0.03	0.07	0.00	0.14	0.00	0.19
FLORESTA	0.03	0.00	0.06	0.00	0.02	0.01	0.15	0.08	0.01	0.11	0.16	0.11	0.03	0.15	0.00	0.09
GIOIA DEL COLLE	0.02	0.03	0.04	0.00	0.07	0.01	0.11	0.00	0.11	0.20	0.11	0.10	0.06	0.04	0.02	0.00
GRAZZANISE	0.00	0.06	0.00	0.01	0.08	0.05	0.00	0.00	0.12	0.04	0.01	0.00	0.18	0.17	0.00	0.09
GROTTAGLIE	0.03	0.06	0.01	0.01	0.07	0.03	0.08	0.05	0.24	0.00	0.06	0.17	0.00	0.01	0.08	0.06
LAMEZIA TERME	0.01	0.02	0.01	0.00	0.07	0.02	0.02	0.02	0.08	0.00	0.02	0.00	0.01	0.09	0.02	0.04
LATRONICO	0.07	0.01	0.02	0.00	0.04	0.06	0.06	0.03	0.03	0.04	0.09	0.12	0.07	0.08	0.00	0.02
LECCE	0.06	0.01	0.02	0.00	0.09	0.00	0.11	0.13	0.10	0.00	0.10	0.01	0.03	0.07	0.13	0.01
MARINA DI GINOSA	0.00	0.05	0.00	0.02	0.04	0.00	0.03	0.11	0.12	0.01	0.04	0.02	0.04	0.03	0.01	0.00
MONTE S. ANGELO	0.03	0.07	0.04	0.00	0.00	0.11	0.02	0.02	0.27	0.03	0.04	0.01	0.04	0.03	0.00	0.14
MONTE SCURO	0.03	0.01	0.08	0.01	0.01	0.12	0.08	0.06	0.07	0.01	0.14	0.02	0.05	0.01	0.00	0.07
OLBIA/COSTA SMERALDA	0.03	0.00	0.00	0.00	0.01	0.06	0.01	0.08	0.00	0.10	0.00	0.00	0.07	0.20	0.00	0.17
PESCARA	0.00	0.05	0.04	0.02	0.07	0.00	0.01	0.01	0.32	0.01	0.02	0.02	0.00	0.06	0.10	0.00
REGGIO CALABRIA	0.00	0.00	0.01	0.00	0.04	0.04	0.08	0.16	0.06	0.00	0.02	0.02	0.04	0.05	0.03	0.00
S. MARIA DI LEUCA	0.00	0.02	0.03	0.00	0.02	0.00	0.11	0.08	0.10	0.00	0.01	0.05	0.05	0.02	0.03	0.03
TRAPANI	0.02	0.00	0.02	0.00	0.11	0.00	0.05	0.00	0.01	0.11	0.07	0.02	0.15	0.07	0.00	0.06
TREVICO	0.02	0.07	0.02	0.00	0.01	0.08	0.06	0.09	0.14	0.05	0.02	0.03	0.01	0.01	0.01	0.10

and

Table 6. Coefficient of determination R² derived from linear regression with NAO period as independent variable and precipitation anomaly as dependent variable, in the period 1991–2020, in bold are the significant values, with a p-value less than 0.05.

NORTH-WEST	WIN	SPR	SUM	AUT	JAN	FEB	MAR	APR	MAY	JUN	JUL	AUG	SEP	OCT	NOV	DEC
ALA DI STURA	0.00	0.00	0.00	0.01	0.04	0.01	0.06	0.00	0.05	0.02	0.02	0.03	0.18	0.12	0.00	0.04
ALESSADRIA	0.06	0.05	0.00	0.02	0.01	0.02	0.23	0.02	0.09	0.00	0.05	0.07	0.21	0.00	0.06	0.23
ALPE DEVERO	0.01	0.01	0.01	0.02	0.09	0.01	0.13	0.01	0.00	0.01	0.01	0.02	0.15	0.01	0.05	0.01
BERGAMO ORIO	0.01	0.06	0.05	0.01	0.03	0.01	0.29	0.02	0.06	0.04	0.01	0.06	0.08	0.04	0.14	0.27
BRESCIA GHEDI	0.17	0.02	0.00	0.07	0.21	0.11	0.37	0.01	0.00	0.00	0.22	0.01	0.28	0.03	0.19	0.49
COGNE	0.00	0.01	0.00	0.01	0.00	0.03	0.00	0.03	0.04	0.02	0.01	0.01	0.09	0.16	0.00	0.02
ERBA	0.08	0.05	0.00	0.04	0.08	0.02	0.52	0.00	0.00	0.01	0.00	0.00	0.24	0.05	0.01	0.21
ETROUBLES	0.00	0.04	0.00	0.01	0.00	0.14	0.16	0.00	0.00	0.01	0.02	0.00	0.13	0.10	0.11	0.04
LA THUILE	0.00	0.05	0.05	0.00	0.00	0.01	0.49	0.06	0.00	0.10	0.00	0.18	0.09	0.06	0.06	0.09
MILANO LINATE	0.01	0.01	0.02	0.05	0.00	0.11	0.17	0.01	0.00	0.01	0.00	0.03	0.39	0.02	0.23	0.17
MONDOVì	0.00	0.00	0.00	0.01	0.02	0.12	0.00	0.17	0.07	0.01	0.02	0.06	0.32	0.08	0.06	0.03
PIETRASTRETTA	0.01	0.02	0.01	0.02	0.01	0.09	0.19	0.03	0.02	0.02	0.05	0.36	0.16	0.01	0.03	0.04
PONTECHIANALE	0.08	0.00	0.01	0.03	0.08	0.02	0.16	0.07	0.06	0.02	0.11	0.28	0.15	0.04	0.07	0.11
SAINT CHRISTOPHE	0.00	0.00	0.01	0.00	0.00	0.09	0.29	0.01	0.02	0.09	0.01	0.02	0.11	0.15	0.04	0.03
SALOMACO	0.06	0.03	0.04	0.07	0.13	0.00	0.23	0.02	0.00	0.30	0.06	0.01	0.18	0.00	0.14	0.05
SANTO STEFANO D’AVETO	0.09	0.07	0.01	0.08	0.17	0.00	0.34	0.01	0.08	0.00	0.05	0.01	0.36	0.05	0.16	0.26
TORINO BRIC DELLA C	0.02	0.00	0.00	0.02	0.00	0.07	0.07	0.00	0.05	0.05	0.04	0.08	0.13	0.00	0.00	0.11
NORTH-EAST	WIN	SPR	SUM	AUT	JAN	FEB	MAR	APR	MAY	JUN	JUL	AUG	SEP	OCT	NOV	DEC
AURONZO	0.01	0.00	0.12	0.01	0.00	0.00	0.15	0.04	0.03	0.19	0.02	0.03	0.09	0.00	0.08	0.18
BOBBIO	0.11	0.01	0.01	0.02	0.13	0.02	0.22	0.02	0.00	0.02	0.02	0.02	0.25	0.00	0.09	0.28
BRUSTOLè	0.04	0.02	0.00	0.02	0.03	0.00	0.22	0.00	0.01	0.05	0.04	0.00	0.12	0.01	0.14	0.25
CASTELFRANCO EMILIA	0.09	0.04	0.01	0.01	0.38	0.09	0.10	0.00	0.14	0.04	0.02	0.00	0.26	0.00	0.03	0.26
CERVIA	0.05	0.02	0.02	0.05	0.04	0.00	0.01	0.00	0.09	0.00	0.02	0.02	0.35	0.00	0.11	0.17
DOBBIACO	0.03	0.00	0.08	0.03	0.02	0.02	0.01	0.04	0.01	0.09	0.09	0.00	0.18	0.03	0.08	0.12
ENEMONZO	0.01	0.00	0.02	0.04	0.01	0.00	0.00	0.00	0.01	0.02	0.09	0.00	0.19	0.07	0.07	0.06
GARES	0.03	0.01	0.04	0.05	0.00	0.02	0.07	0.00	0.08	0.04	0.03	0.04	0.42	0.01	0.11	0.15
LAMON	0.04	0.04	0.00	0.03	0.01	0.02	0.17	0.00	0.10	0.07	0.03	0.03	0.43	0.00	0.10	0.15
MONTE GALDA	0.12	0.08	0.02	0.06	0.13	0.01	0.19	0.17	0.06	0.01	0.02	0.01	0.34	0.03	0.24	0.43
NOVENTA DI PIAVE	0.09	0.07	0.00	0.07	0.11	0.01	0.08	0.09	0.10	0.01	0.15	0.02	0.26	0.00	0.23	0.49
PAGANELLA	0.00	0.00	0.06	0.03	0.09	0.02	0.09	0.01	0.00	0.11	0.01	0.09	0.16	0.06	0.17	0.02
PASSO ROLLE	0.04	0.01	0.06	0.03	0.04	0.01	0.36	0.03	0.02	0.02	0.03	0.01	0.09	0.02	0.25	0.11
PIACENZA	0.12	0.03	0.00	0.13	0.33	0.05	0.23	0.09	0.00	0.01	0.05	0.03	0.46	0.00	0.25	0.26
PORRETTA TERME	0.07	0.08	0.08	0.14	0.13	0.01	0.37	0.01	0.13	0.17	0.05	0.04	0.18	0.00	0.25	0.22
PRADALAGO	0.06	0.01	0.04	0.06	0.07	0.12	0.02	0.02	0.03	0.01	0.17	0.00	0.23	0.00	0.29	0.09
PREDOI	0.00	0.02	0.16	0.04	0.03	0.00	0.02	0.04	0.01	0.18	0.41	0.14	0.06	0.00	0.17	0.11
RIMINI	0.02	0.01	0.02	0.02	0.13	0.07	0.06	0.00	0.02	0.13	0.02	0.06	0.15	0.00	0.12	0.07
ROVERCHIARA	0.17	0.11	0.00	0.06	0.31	0.01	0.21	0.03	0.15	0.00	0.01	0.00	0.06	0.00	0.15	0.31
SAN VALENTINO	0.02	0.01	0.00	0.02	0.13	0.11	0.07	0.01	0.01	0.03	0.05	0.01	0.01	0.00	0.11	0.00
SAN VITO AL TAGLIAMENTO	0.05	0.08	0.01	0.09	0.15	0.02	0.21	0.08	0.05	0.00	0.03	0.02	0.24	0.00	0.19	0.38
TREVISO ISTRANA	0.07	0.03	0.00	0.02	0.05	0.04	0.17	0.01	0.00	0.01	0.01	0.01	0.01	0.00	0.12	0.40
UDINE	0.05	0.04	0.00	0.03	0.06	0.08	0.18	0.00	0.00	0.00	0.02	0.00	0.10	0.00	0.21	0.35
VERONA	0.16	0.02	0.01	0.06	0.36	0.10	0.17	0.00	0.00	0.01	0.02	0.00	0.21	0.00	0.16	0.46
CENTRO	WIN	SPR	SUM	AUT	JAN	FEB	MAR	APR	MAY	JUN	JUL	AUG	SEP	OCT	NOV	DEC
AREZZO	0.09	0.02	0.01	0.08	0.05	0.00	0.31	0.00	0.00	0.06	0.00	0.01	0.17	0.20	0.16	0.28
CASSIODORO	0.14	0.11	0.13	0.00	0.06	0.20	0.16	0.20	0.12	0.00	0.09	0.31	0.11	0.01	0.11	0.25
FRONTONE	0.08	0.00	0.00	0.06	0.00	0.07	0.03	0.02	0.01	0.00	0.00	0.02	0.05	0.00	0.09	0.14
FROSINONE	0.07	0.03	0.03	0.06	0.02	0.03	0.13	0.05	0.02	0.00	0.00	0.19	0.19	0.01	0.03	0.07
GROSSETO	0.10	0.06	0.00	0.04	0.17	0.06	0.24	0.12	0.02	0.01	0.00	0.00	0.04	0.00	0.05	0.06
MONTEMONACO	0.01	0.00	0.06	0.01	0.06	0.01	0.00	0.10	0.01	0.23	0.00	0.22	0.00	0.00	0.00	0.04
PISA	0.04	0.05	0.00	0.07	0.09	0.01	0.40	0.01	0.00	0.00	0.01	0.01	0.03	0.01	0.18	0.19
PRATICA DI MARE	0.08	0.02	0.00	0.01	0.13	0.00	0.11	0.00	0.03	0.12	0.00	0.03	0.09	0.00	0.07	0.14
ROMA CIAMPINO	0.07	0.02	0.05	0.05	0.15	0.09	0.04	0.04	0.00	0.11	0.10	0.27	0.12	0.00	0.15	0.19
S. ANGELO IN VADO	0.07	0.06	0.01	0.06	0.01	0.02	0.15	0.01	0.06	0.00	0.02	0.00	0.32	0.00	0.12	0.35
SANTA FISTA	0.13	0.04	0.04	0.13	0.38	0.02	0.12	0.06	0.01	0.01	0.01	0.01	0.01	0.17	0.21	0.37
TODI	0.04	0.04	0.00	0.09	0.25	0.06	0.21	0.00	0.02	0.02	0.00	0.04	0.30	0.00	0.33	0.06
VALLOMBROSA	0.11	0.02	0.01	0.07	0.38	0.08	0.11	0.04	0.01	0.01	0.04	0.04	0.10	0.09	0.08	0.25
VIGNA DI VALLE	0.11	0.07	0.02	0.02	0.27	0.00	0.29	0.06	0.02	0.01	0.00	0.03	0.12	0.01	0.12	0.29
VITERBO	0.06	0.01	0.01	0.02	0.24	0.01	0.17	0.05	0.07	0.00	0.01	0.08	0.02	0.00	0.14	0.20
SUD	WIN	SPR	SUM	AUT	JAN	FEB	MAR	APR	MAY	JUN	JUL	AUG	SEP	OCT	NOV	DEC
ASSERGI	0.04	0.05	0.00	0.03	0.02	0.22	0.08	0.24	0.00	0.05	0.07	0.13	0.02	0.05	0.01	0.00
BONIFATI	0.04	0.00	0.03	0.02	0.00	0.46	0.03	0.04	0.01	0.00	0.06	0.01	0.02	0.05	0.01	0.01
CAMPOBASSO	0.08	0.01	0.03	0.01	0.00	0.33	0.07	0.01	0.06	0.05	0.04	0.00	0.02	0.00	0.00	0.08
CAMPOCHIARO	0.07	0.03	0.14	0.09	0.01	0.18	0.07	0.01	0.01	0.02	0.17	0.06	0.00	0.07	0.44	0.12
CAPO BELLAVISTA	0.07	0.02	0.06	0.05	0.16	0.04	0.04	0.03	0.00	0.05	0.06	0.31	0.04	0.01	0.36	0.13
CAPRI	0.08	0.02	0.08	0.00	0.03	0.27	0.06	0.10	0.06	0.01	0.04	0.12	0.07	0.00	0.00	0.04
CATANIA SIGONELLA	0.04	0.02	0.17	0.04	0.03	0.04	0.00	0.01	0.18	0.38	0.00	0.40	0.05	0.00	0.30	0.06
COZZO SPADARO	0.01	0.03	0.10	0.05	0.00	0.04	0.03	0.02	0.09	0.17	0.15	0.04	0.00	0.01	0.38	0.00
DECIMOMANNU	0.07	0.00	0.07	0.00	0.07	0.00	0.01	0.02	0.02	0.07	0.01	0.26	0.03	0.04	0.00	0.14
ENNA	0.03	0.02	0.15	0.00	0.07	0.02	0.02	0.00	0.14	0.16	0.13	0.28	0.02	0.02	0.04	0.01
GELA	0.05	0.02	0.04	0.00	0.07	0.00	0.02	0.00	0.01	0.17	0.01	0.06	0.05	0.02	0.01	0.04
GIOIA DEL COLLE	0.05	0.00	0.02	0.00	0.03	0.00	0.00	0.00	0.06	0.06	0.00	0.02	0.16	0.01	0.01	0.04
GRAZZANISE	0.14	0.06	0.07	0.02	0.11	0.08	0.23	0.11	0.03	0.04	0.00	0.35	0.05	0.02	0.01	0.09
LAMEZIA TERME	0.14	0.00	0.04	0.00	0.07	0.13	0.00	0.02	0.08	0.04	0.16	0.00	0.12	0.01	0.01	0.18
LATRONICO	0.03	0.05	0.05	0.03	0.02	0.01	0.15	0.16	0.03	0.02	0.09	0.13	0.01	0.00	0.00	0.17
LECCE	0.01	0.02	0.05	0.01	0.01	0.04	0.14	0.03	0.20	0.01	0.08	0.15	0.02	0.14	0.03	0.03
MARINA DI GINOSA	0.03	0.00	0.03	0.00	0.01	0.04	0.01	0.02	0.05	0.01	0.00	0.08	0.13	0.00	0.00	0.00
MILETO	0.07	0.00	0.04	0.01	0.05	0.17	0.00	0.09	0.06	0.00	0.06	0.03	0.21	0.10	0.10	0.08
MONTE SANT ANGELO	0.05	0.00	0.01	0.02	0.00	0.01	0.01	0.00	0.00	0.12	0.06	0.12	0.02	0.00	0.02	0.11
MONTE SCURO	0.01	0.00	0.00	0.00	0.00	0.00	0.04	0.09	0.04	0.00	0.04	0.09	0.02	0.01	0.00	0.00
PAGLIAROLI	0.00	0.00	0.10	0.00	0.08	0.13	0.00	0.01	0.03	0.13	0.09	0.13	0.02	0.03	0.00	0.00
PESCARA	0.04	0.02	0.01	0.02	0.00	0.01	0.01	0.23	0.10	0.06	0.01	0.05	0.03	0.14	0.00	0.01
SANTA MARIA DI LEUCA	0.05	0.00	0.04	0.00	0.04	0.00	0.00	0.07	0.00	0.11	0.12	0.01	0.01	0.00	0.00	0.09
TRAPANI	0.04	0.00	0.10	0.00	0.03	0.03	0.00	0.01	0.13	0.08	0.00	0.13	0.02	0.01	0.00	0.16
TREVICO	0.01	0.01	0.10	0.05	0.01	0.01	0.10	0.00	0.10	0.14	0.02	0.10	0.19	0.00	0.00	0.01

).

The linear regression showed very variable coefficients of determination between the different areas; particularly in Northern Italy, there is a significance of the linear regression between the NAO index and the temperature anomalies for the winter and spring seasons, with rather high values in December and less high but still good values in September and May. The central areas in spring, May and December have the highest R² values and a greater number of significant weather stations, while in the south, there are rather low and generally non-significant values, highlighting that the NAO teleconnective index is not the most suitable for assessing the linear relationship with temperature anomalies (Table 5).

The investigation of the linear relationship between the NAO index and precipitation anomalies led to results that were certainly less good than those found with temperatures, especially in terms of the coefficient of determination (Table 6). In particular, at the seasonal level, although there are numerous significant weather stations, the coefficient of determination is very low so that it does not guarantee a good explanation of the variance, while the best results are obtained at the monthly level. The R² values are good, in relation to the expected results for this teleconnective index, for the months of September, December and especially in March, for North-Western Italy. In the North-East, on the other hand, the months that show better values of variance explanation in December, followed by September, November and March. In contrast, in Central Italy, the best R² values are recorded in December, March and January. Finally, Southern Italy also shows low values of the coefficient of determination, where the best results are achieved in August. The linear relationship between the NAO index and precipitation and temperature anomalies is established for some seasons and months in most of Italy, although much less so in the south. In this context, it is interesting to evaluate the variation in R² over the peninsula in the month that shows the greatest variance explanation for both temperature and precipitation anomalies (Figure 10).

The relationship between the NAO index and the temperature anomalies in December have very high coefficients of determination, for a relationship between a climate parameter and a teleconnective index, particularly in north-western Italy, although it remains acceptable up to central Italy (Figure 10). The R² of temperature anomalies varies more gradually than that of precipitation anomalies, which nevertheless show good but slightly lower values than those in Figure 10a. The precipitation anomalies have a very good coefficient of determination in December, especially in the North-East, part of the North-West and part of central Italy, with very low values in southern Italy, with the exception of Sardinia (Figure 10).

The trend in the coefficient of determination (Figure 10) mirrors that of the significance of the linear regression shown in Figure 11. However, it is interesting to know which weather stations are significant and how they describe geographical areas that are subject to a common atmospheric dynamic.

3.3. Analysis of Clusters and Outliers

Cluster and outlier analysis using the local Moran index allows to identify clusters of high or low values and spatial outliers where a high value is surrounded by low values and a low value by high values. This type of analysis helps to highlight the areas that are most affected in terms of precipitation and temperature anomalies, by the NAO index, as well as the weather stations that may represent outliers perhaps due to complex and varied atmospheric dynamics. The result of the analysis can be clearly displayed graphically; in fact, all the maps obtained monthly and seasonally have been summarised by the merging framework in Figure 12.

High-high clusters are found almost exclusively in northern Italy, predominantly in north-western Italy, while during spring a high-high cluster is found throughout northern Italy, with the exception of a few non-significant weather stations. Instead, low-low clusters are found in central and southern Italy and there are only a few exceptions such as in July where low-low clusters are in north-eastern Italy, while in October, the low-low cluster also affects north-western Italy. Outliers are not very present and vary from month to month and season to season, indicating a lack of constant outliers among the weather stations analysed (Figure 12). It can be concluded that, although with some distinctions, the geographical divisions tend to be consistent with the effects of the NAO index on temperature anomalies (Figure 12).

The relationship between the NAO index and precipitation anomalies shows seasonally high-high clusters, especially in central Italy, where there are many significant weather stations in autumn and winter. Also on a seasonal level in autumn, there are some significant weather stations in the North-East, while it is peculiar to observe that in summer period all the weather stations in Sicily are significant with high-high clusters (Figure 13). The low-low clusters in winter and summer are located in north-western Italy, but in autumn in the South; with regard to the outliers on a seasonal scale, low-high outliers are predominantly found in Northern Italy, especially in spring and autumn. It can be concluded that, although with some distinctions, the geographical divisions tend to be consistent with the effects of the NAO index (Figure 13). On a monthly scale for precipitation anomalies, there are high-high clusters in January and March in northern and central Italy, while in the same months, there is a low-low cluster in the south. In August, there is a low-low cluster in the North-East and parts of the North-West, although there is a high-high cluster in Sardinia. In September, Northern Italy is predominantly the site of high-high clusters with some low-high outliers in the North-East, while in November and December it is the North-East that is site of high-high clusters, with the South and the westernmost part of the North-West constituting low-low clusters (Figure 13).

4. Discussion

4.1. Interpretations and Implications

This study represented a treatment of the influence of the NAO index on precipitation and temperature anomalies in Italy from 1991 to 2020. Clusters and outliers were also assessed in the analysis, as well as the correlation and its intensity, in addition to the existence of the linear relationship and the incidence that the teleconnective index in question may have on the explanation of the variance of the climate parameters (temperatures and precipitation) studied. The analysis of the influence of the NAO index on temperature anomalies revealed some rather surprising outcomes. Southern Italy has very few meteorological stations with a significant correlation for all the periods studied, and only in the month of May is there a greater number of significant weather stations with a discrete correlation intensity. In spring, there is a significant correlation with a discrete intensity throughout Central and Northern Italy, while in winter, although the correlation is always significant, the intensity weakens somewhat in Central Italy. February, March, May, September and especially December are the most correlated months in Central-Northern Italy and the correlation is of good intensity, as well as being always positive, such that a positive NAO corresponds to a positive thermometric anomaly. All of these results are in strong disagreement with previous research on the subject in the study area, so much so that only the correlation in the winter month in northern Italy was found in previous research, whereas this analysis shows a correlation at other times of the year and in other parts of Italy, even a rather intense one [46]. In some research, only the correlation of temperatures with the NAO index in the winter season is wrongly analysed, neglecting important relationships that in some areas, such as southern Italy, are present in other seasons in the case of temperatures, for example in May [47]. As far as precipitation is concerned, here too, there are distinctions to be made with respect to the scientific literature in the area; although, as in the other case, the sense of correlation is concordant among all the research, i.e., a predominantly negative and inverse correlation between precipitation anomalies and the NAO index. Some research in Northern Italy highlights an inverse correlation that should be present especially in the winter and spring months, neglecting autumn which, as shown in the analysis, has discrete correlation values that become even better if September is assessed [48]. Furthermore, the correlation between the NAO index and precipitation becomes direct in many weather stations in the summer months, especially in August. Research carried out in Abruzzo, a region on the border between southern and central Italy, highlights, in accordance with this research, the negative correlations between precipitation and the NAO index in the months of January, February and March, but does not analyse the positive correlations present in summer months [49]. In contrast, research conducted in the same region highlights the significance of the correlation especially in summer, in agreement with what was observed for southern Italy in this study as well [50]. In the literature, not many studies highlight, regardless of correlation, the linear relationship between the NAO index and anomalies in climate parameters, especially in studies conducted in Italy. In particular, a certain linear relationship has been verified in Sardinia showing a coefficient of determination of about 0.3 in the period October to April, the linear relationship was also observed in winter in a hydrological analysis in northern Italy [51,52]. In the present study, fair values of the coefficient of determination were found for temperatures in winter and spring for the North, in spring only for the Centre, while good values are found monthly in the Centre and North Italy in December and slightly less good in September and March. Southern Italy, as also shown by the correlation, does not have a good explanation of variance with regard to temperature anomalies, it follows that the influence of the NAO index in determining temperature anomalies is also quite high in southern Europe, unlike what has been observed in other studies on the subject [22]. For precipitation anomalies, the coefficient of determination is certainly lower than that found with temperatures, so that although many weather stations are still significant throughout Italy, the R² seasonal values are rather low. In this context, the highest values of the coefficient of determination are reached in December and then scaled up in September and March, for the entire North and Central Italy. In contrast, in Southern Italy, good coefficients occur especially in August and only for certain weather stations in November, February and June. The linear relationship between precipitation and the NAO index in summer is also found in the literature in connection with the analysis of the impact of the NAO index on summer droughts [53]. Regarding the analysis of clusters and outliers in the literature, there are no great examples, and basically the winter months are almost exclusively favoured, with emphasis on northern Europe, which certainly has the most sensitive effects at least on precipitation [54]. Also in relation to clusters, our study highlights both the NAO index and the temperature and precipitation anomalies of areas. High-high clusters especially in the North Central and areas with low-low clusters in the South. While as far as outliers are concerned, they are highly variable and not easy to interpret, probably dependent on local atmospheric dynamics.

4.2. Research Limitations

This study, as is natural, inevitably has some limitations that may provide an opportunity for further improvement in the future. In particular, the numerosity of the weather stations could be a limitation that would allow for an improvement in the analysis by favouring better spatialisation in the analysis of the coefficient of determination, but also more indications in the analysis of clusters and outliers. Despite the validation and homogenisation of weather stations, in mountainous environments there may be underestimations of the amount of rainfall due to the presence of strong winds. Without some precautions, they could reduce the rain entering the rain gauge and also the solid precipitation even though the rain gauges are heated [55].

5. Conclusions

This study deals with a well-known topic in the scientific climate literature, namely, the dependence of temperature and precipitation on the NAO index. However, although there is a vast scientific literature on the subject, usually, very small areas with rather accurate sampling or very large areas with rather sparse sampling compared to the area studied have been chosen. In addition, there are mainly climate studies oriented towards defining the effects in Northern Europe, which is certainly the most affected by the phenomenon, or in the Mediterranean to assess the extent of the influence of the phenomenon. This research examined the entire Italian territory, looking for correlations not only in the winter season, which the literature identifies as the most sensitive to fluctuations in the NAO index. In fact, in the other seasons, correlations were found that were, in some cases, even greater than in the winter season, isolating the months that were most correlated in the thirty-year period 1991–2020. The main and innovative results of the study were threefold:

• The correlation between the NAO index and temperature or precipitation anomalies was mapped for the entire Italian territory;
• A linear regression was obtained with the relevant coefficients of determination between the NAO index and temperature or precipitation anomalies;
• The presence of clusters and outliers in the study area was assessed.

This analysis thus provides a better understanding of how pressure differences in the North Atlantic affect the climate in Italy in all seasons, affecting different areas depending on the period. The explanation of the variance of precipitation and temperature anomalies is a topic that would deserve further analysis with other teleconnective indices. Finally, if well calibrated, satellite data could also be used in the future in order to have a homogeneous grid with good detail, such that it would no longer be necessary to perform interpolation for the spatialisation of point data [56].