Using Data-Driven Prediction of Downstream 1D River Flow to Overcome the Challenges of Hydrologic River Modeling
Abstract
:1. Introduction
2. Materials and Methods
2.1. The SSARR Model
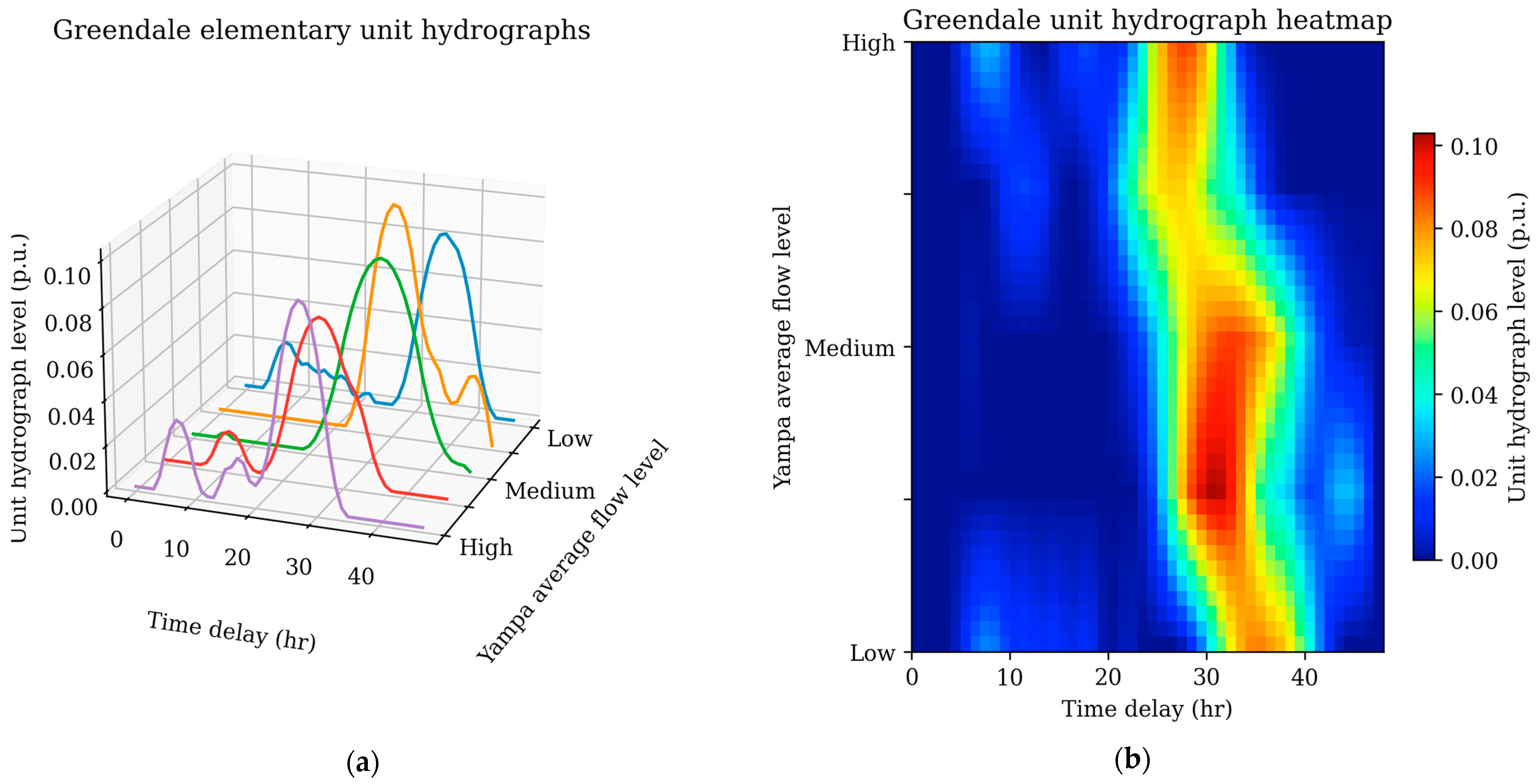
2.2. The Discrete Convolution Approach
2.3. The Linear Programming Model
- Instead of predicting the downstream discharge by identifying the optimal unit hydrograph of a single upstream source, our model simultaneously identifies the optimal unit hydrograph of multiple contributing upstream sources;
- Instead of assuming the unit hydrograph of each upstream source to be static, the model allows the identification of dynamic unit hydrographs;
- Apart from minimizing the error in predicting the downstream flow, the model also maximizes the smoothness of the identified unit hydrographs.
2.4. The Convolutional Neural Network Encoder
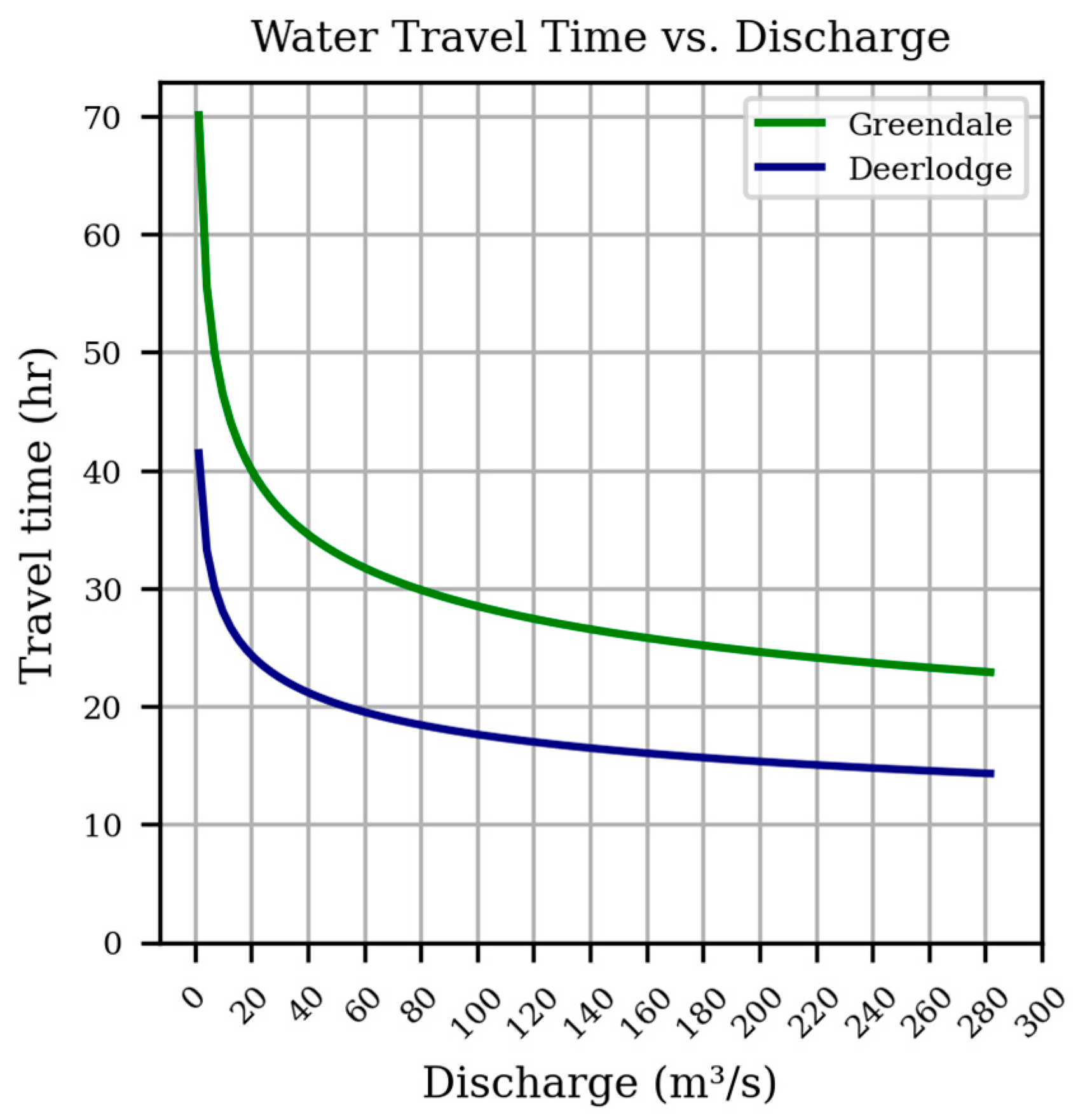
2.5. Discharge-Variant Water Travel Time
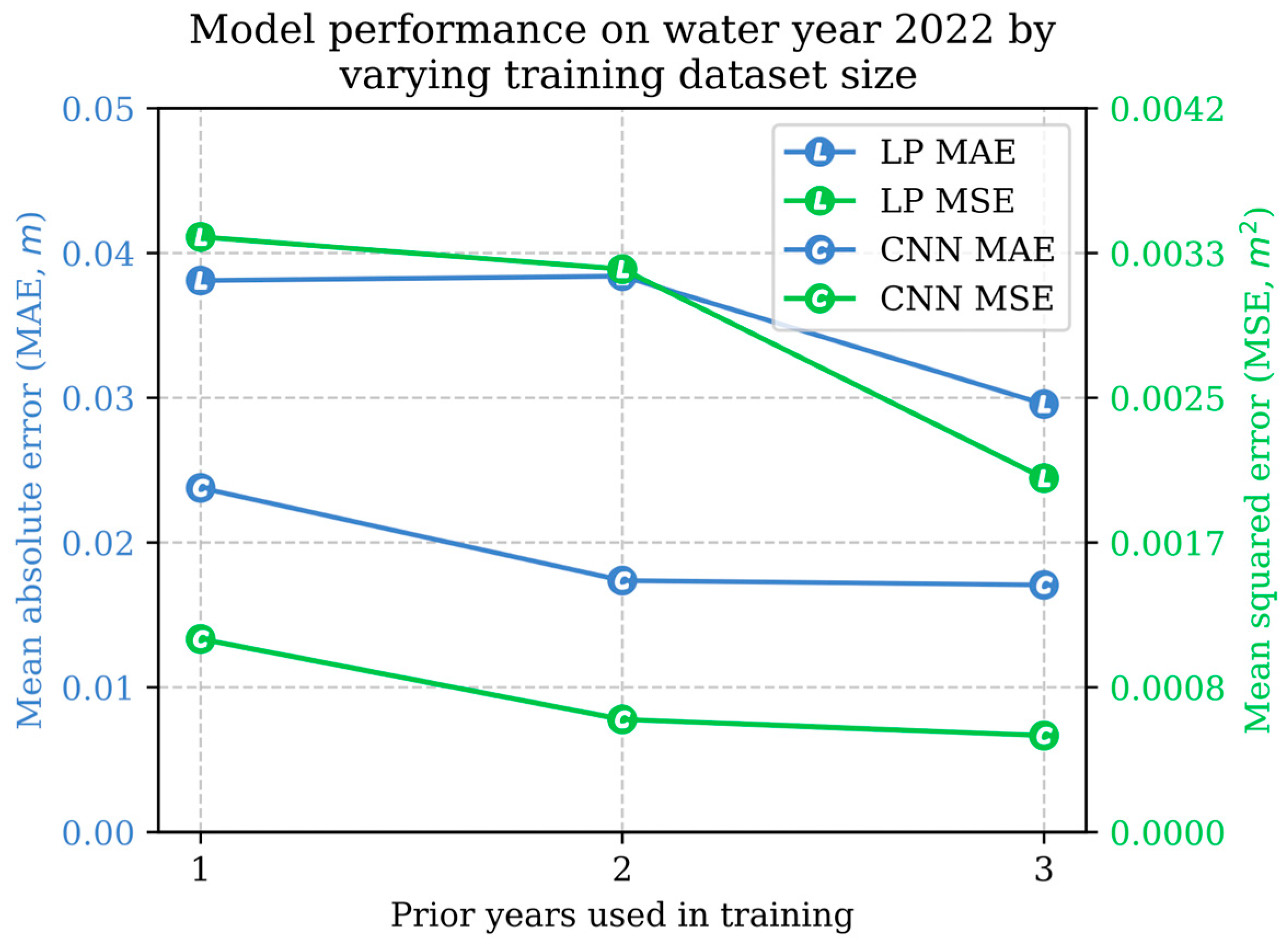
2.6. Model Validation
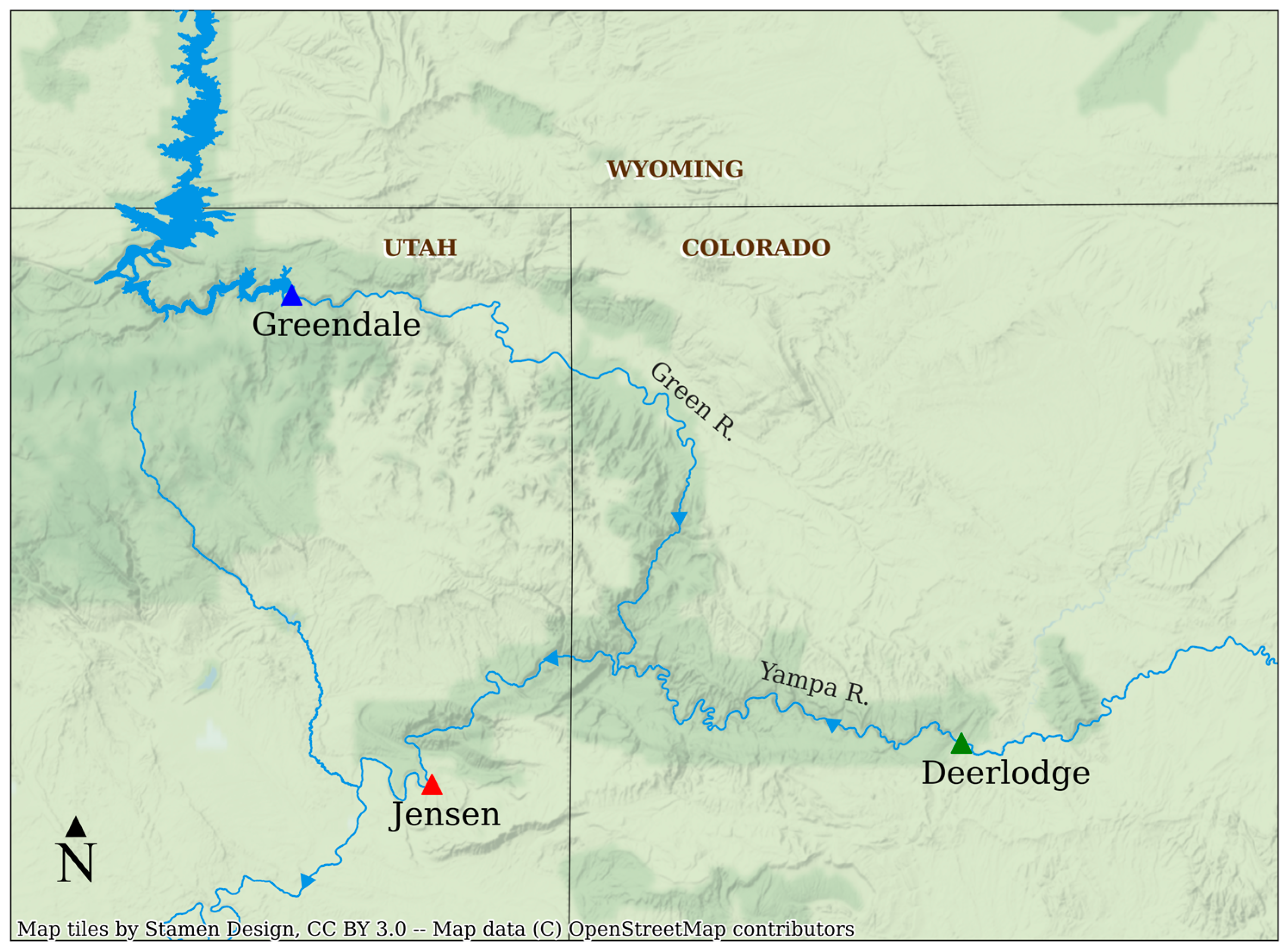
2.7. Site Description
2.8. Datasets
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- Detailed mathematical formulation of the LP method
- Sets
- Parameters
- Variables
- Description
- Unit hydrograph and link to water travel time and mass balance indicator
Appendix B
| Parameter | Type | Domain | Optimized Value | Note |
|---|---|---|---|---|
| Number of convolution layers | Discrete | (1, 10) | 5 | |
| Number of convolution filters | Discrete | {4, 8, 16, 32, 64} | 16 | |
| Kernel size | Discrete | (4, 193) | 24 | Subject to number of convolutions |
| Kernel non-negative constraint | Boolean | {True, False} | False | |
| Kernel regularizer L2 factor | Continuous | (0, 0.1) | 0.03 | |
| Learning rate | Continuous | (0.00001, 0.01) | 0.002 | |
| Batch size | Discrete | {64, 128, 256} | 64 |
References
- Worster, D. Rivers of Empire: Water, Aridity, and the Growth of the American West; Oxford University Press: Oxford, UK, 1992; ISBN 978-0-19-507806-0. [Google Scholar]
- Allan, C.; Xia, J.; Pahl-Wostl, C. Climate Change and Water Security: Challenges for Adaptive Water Management. Curr. Opin. Environ. Sustain. 2013, 5, 625–632. [Google Scholar] [CrossRef]
- Nanditha, J.S.; Mishra, V. On the Need of Ensemble Flood Forecast in India. Water Secur. 2021, 12, 100086. [Google Scholar] [CrossRef]
- Cueto-Felgueroso, L.; Santillán, D.; García-Palacios, J.H.; Garrote, L. Comparison between 2D Shallow-Water Simulations and Energy-Momentum Computations for Transcritical Flow Past Channel Contractions. Water 2019, 11, 1476. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C. Linear Stationary Models. In Time Series Analysis; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2008; pp. 47–91. ISBN 978-1-118-61919-3. [Google Scholar]
- Cryer, J.D.; Chan, K.-S. Time Series Analysis; Springer Texts in Statistics; Springer: New York, NY, USA, 2008; ISBN 978-0-387-75958-6. [Google Scholar]
- Salas, J.D.; Delleur, J.W.; Yevjevich, V.; Lane, W.L. Applied Modeling of Hydrologic Time Series; Water Resources Publications: Littleton, CO, USA, 1980; ISBN 978-0-918334-37-4. [Google Scholar]
- Bisgaard, S.; Kulahci, M. Time Series Analysis and Forecasting by Example; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 2011; ISBN 978-0-470-54064-0. [Google Scholar]
- Pekarova, P.; Pekar, J. Long-Term Discharge Prediction for the Turnu Severin Station (the Danube) Using a Linear Autoregressive Model. Hydrol. Process. 2006, 20, 1217–1228. [Google Scholar] [CrossRef]
- Beyaztas, U.; Shang, H.L.; Yaseen, Z.M. A Functional Autoregressive Model Based on Exogenous Hydrometeorological Variables for River Flow Prediction. J. Hydrol. 2021, 598, 126380. [Google Scholar] [CrossRef]
- Abrahart, R.J.; See, L. Comparing Neural Network and Autoregressive Moving Average Techniques for the Provision of Continuous River Flow Forecasts in Two Contrasting Catchments. Hydrol. Process. 2000, 14, 2157–2172. [Google Scholar] [CrossRef]
- Anderson, P.L.; Meerschaert, M.M.; Zhang, K. Forecasting with Prediction Intervals for Periodic Autoregressive Moving Average Models. J. Time Ser. Anal. 2013, 34, 187–193. [Google Scholar] [CrossRef]
- Mohammadi, K.; Eslami, H.R.; Kahawita, R. Parameter Estimation of an ARMA Model for River Flow Forecasting Using Goal Programming. J. Hydrol. 2006, 331, 293–299. [Google Scholar] [CrossRef]
- Fashae, O.A.; Olusola, A.O.; Ndubuisi, I.; Udomboso, C.G. Comparing ANN and ARIMA Model in Predicting the Discharge of River Opeki from 2010 to 2020. River Res. Appl. 2019, 35, 169–177. [Google Scholar] [CrossRef]
- Lin, J.-Y.; Cheng, C.-T.; Chau, K.-W. Using Support Vector Machines for Long-Term Discharge Prediction. Hydrol. Sci. J. 2006, 51, 599–612. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Zadeh, H.A.; Isazadeh, M.; Terzi, O. A Comparative Study of Artificial Neural Network (MLP, RBF) and Support Vector Machine Models for River Flow Prediction. Environ. Earth Sci. 2016, 75, 476. [Google Scholar] [CrossRef]
- Kişi, Ö. River Flow Modeling Using Artificial Neural Networks. J. Hydrol. Eng. 2004, 9, 60–63. [Google Scholar] [CrossRef]
- Chang, F.-J.; Chen, P.-A.; Lu, Y.-R.; Huang, E.; Chang, K.-Y. Real-Time Multi-Step-Ahead Water Level Forecasting by Recurrent Neural Networks for Urban Flood Control. J. Hydrol. 2014, 517, 836–846. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, Y.-P.; Yang, Z.; Wang, G.; Zhu, Q. Integration of a Parsimonious Hydrological Model with Recurrent Neural Networks for Improved Streamflow Forecasting. Water 2018, 10, 1655. [Google Scholar] [CrossRef]
- Vieux, B.E.; Cui, Z.; Gaur, A. Evaluation of a Physics-Based Distributed Hydrologic Model for Flood Forecasting. J. Hydrol. 2004, 298, 155–177. [Google Scholar] [CrossRef]
- Butler, T.; Graham, L.; Estep, D.; Dawson, C.; Westerink, J.J. Definition and Solution of a Stochastic Inverse Problem for the Manning’s n Parameter Field in Hydrodynamic Models. Adv. Water Resour. 2015, 78, 60–79. [Google Scholar] [CrossRef]
- Yang, D.Y.; Frangopol, D.M. Physics-Based Assessment of Climate Change Impact on Long-Term Regional Bridge Scour Risk Using Hydrologic Modeling: Application to Lehigh River Watershed. J. Bridg. Eng. 2019, 24, 04019099. [Google Scholar] [CrossRef]
- Hussain, F.; Wu, R.-S.; Wang, J.-X. Comparative Study of Very Short-Term Flood Forecasting Using Physics-Based Numerical Model and Data-Driven Prediction Model. Nat. Hazards 2021, 107, 249–284. [Google Scholar] [CrossRef]
- Sepúlveda, U.M.; Mendoza, P.A.; Mizukami, N.; Newman, A.J. Revisiting Parameter Sensitivities in the Variable Infiltration Capacity Model across a Hydroclimatic Gradient. Hydrol. Earth Syst. Sci. 2022, 26, 3419–3445. [Google Scholar] [CrossRef]
- United States Army Corps of Engineers North Pacific Division. Program Description and User Manual for SSARR, Streamflow Synthesis and Reservoir Regulation: Program 724-K5-G0010; Army Engineer Division, North Pacific: Honolulu, HI, USA, 1975.
- Zagona, E.A.; Fulp, T.J.; Shane, R.; Magee, T.; Goranflo, H.M. Riverware: A Generalized Tool for Complex Reservoir System Modeling1. JAWRA J. Am. Water Resour. Assoc. 2001, 37, 913–929. [Google Scholar] [CrossRef]
- Ploussard, Q.; Veselka, T.D.; Palmer, C.S. Economic Analysis of Changes in Hydropower Operations at the Flaming Gorge Dam and the Aspinall Unit Due to the Upper Colorado River Endangered Fish Recovery Program; Argonne National Lab. (ANL): Argonne, IL, USA, 2022.
- U.S. Geological Survey. USGS Water Data for the Nation; U.S. Geological Survey: Reston, VA, USA, 1994. [CrossRef]
- Nash, J.E. Systematic Determination of Unit Hydrograph Parameters. J. Geophys. Res. 1959, 64, 111–115. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Zhao, B.; Tung, Y.-K. Determination of Optimal Unit Hydrographs by Linear Programming. Water Resour. Manag. 1994, 8, 101–119. [Google Scholar] [CrossRef]
- Sauer, V.B. Standards for the Analysis and Processing of Surface-Water Data and Information Using Electronic Methods; Water-Resources Investigations Report; U.S. Geological Survey: Reston, VA, USA, 2002; Volume 2001–4044.
- Gurobi Optimization, LLC. Gurobi Optimization Reference Manual; Gurobi Optimization, LLC: Beaverton, OR, USA, 2023. [Google Scholar]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D Convolutional Neural Networks and Applications: A Survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- The GPyOpt Authors. GPyOpt: A Bayesian Optimization Framework in Python 2016. Available online: http://github.com/SheffieldML/GPyOpt (accessed on 8 October 2023).
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Grippo, M.; LaGory, K.E.; David, W.; Hayse, J.W.; Walston, L.J.; Weber, C.C.; Magnusson, A.K.; Jiang, X.H. Relationships between Flow and the Physical Characteristics of Colorado Pikeminnow Backwater Nursery Habitats in the Middle Green River, Utah; Final Report to Upper Colorado River Endangered Fish Recovery Program; Argonne National Laboratory: Lemont, IL, USA, 2017.
- U.S. Bureau of Reclamation. Record of Decision: Operation of Flaming Gorge Dam Final Environmental Impact Statement; U.S. Bureau of Reclamation: Washington, DC, USA, 2006.
- Muth, R.T.; Crist, L.W.; LaGory, K.E.; Hayse, J.W.; Bestgen, K.R.; Ryan, T.P.; Lyons, J.K.; Valdez, R.A. Flow and Temperature Recommendations for Endangered Fishes in the Green River Downstream of Flaming Gorge Dam; Final Report FG-53 to the Upper Colorado River Endangered Fish Recovery Program; Larval Fish Laboratory Contribution 120; U. S. Fish and Wildlife Service: Denver, CO, USA, 2000.
- Yin, S.C.L.; Tomasko, D.; Cho, H.E.; Williams, G.; McCoy, J.; Palmer, C. Effects of Flaming Gorge Dam Hydropower Operations on Downstream Flow, Stage, and Sediment Transport; Argonne National Lab. (ANL): Argonne, IL, USA, 1996.
- Potra, F.A.; Wright, S.J. Interior-Point Methods. J. Comput. Appl. Math. 2000, 124, 281–302. [Google Scholar] [CrossRef]
| Training Time (Seconds) | Hourly Prediction | Daily Minimum-to-Maximum Prediction | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | MAE (m) | MSE (m2) | R2 | Max Error Residual (m) | MAE (m) | MSE (m2) | R2 | Max Error Residual (m) | |
| SSARR | - | 0.0411 | 0.0030 | 0.987 | 0.295 | 0.027 | 0.0014 | 0.669 | 0.180 |
| LP | 17 | 0.0296 | 0.0020 | 0.991 | 0.210 | 0.016 | 0.00056 | 0.856 | 0.130 |
| CNN | 170 | 0.0171 | 0.00056 | 0.998 | 0.145 | 0.015 | 0.00046 | 0.877 | 0.142 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feinstein, J.; Ploussard, Q.; Veselka, T.; Yan, E. Using Data-Driven Prediction of Downstream 1D River Flow to Overcome the Challenges of Hydrologic River Modeling. Water 2023, 15, 3843. https://doi.org/10.3390/w15213843
Feinstein J, Ploussard Q, Veselka T, Yan E. Using Data-Driven Prediction of Downstream 1D River Flow to Overcome the Challenges of Hydrologic River Modeling. Water. 2023; 15(21):3843. https://doi.org/10.3390/w15213843
Chicago/Turabian StyleFeinstein, Jeremy, Quentin Ploussard, Thomas Veselka, and Eugene Yan. 2023. "Using Data-Driven Prediction of Downstream 1D River Flow to Overcome the Challenges of Hydrologic River Modeling" Water 15, no. 21: 3843. https://doi.org/10.3390/w15213843
APA StyleFeinstein, J., Ploussard, Q., Veselka, T., & Yan, E. (2023). Using Data-Driven Prediction of Downstream 1D River Flow to Overcome the Challenges of Hydrologic River Modeling. Water, 15(21), 3843. https://doi.org/10.3390/w15213843





