Future Joint Probability Characteristics of Extreme Precipitation in the Yellow River Basin
Abstract
:1. Introduction
2. Materials and Methods
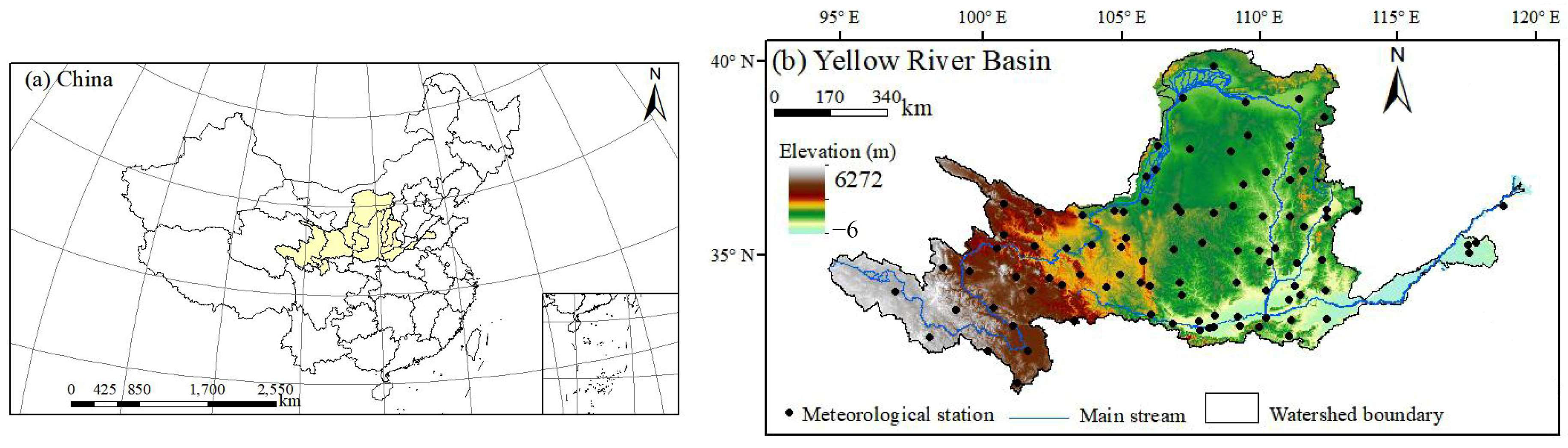
2.1. Study Area
2.2. Datasets
- (1)
- Hydro-Meteorological data
- (2)
- Climate Model Data
2.3. Methodology
2.3.1. Model Establishment and Selection
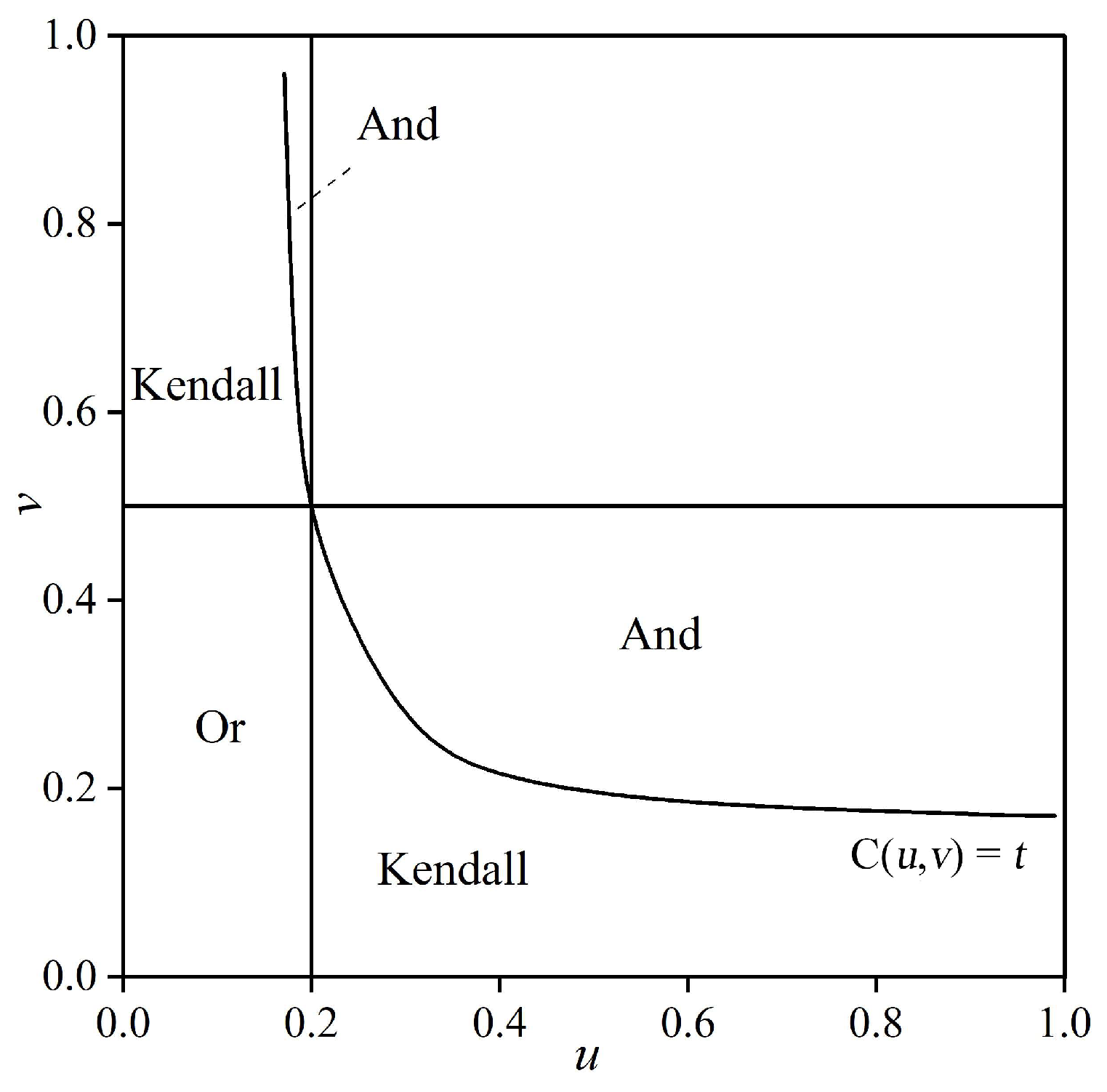
2.3.2. Calculation of Return Periods
2.3.3. Estimation of Design Values
3. Results
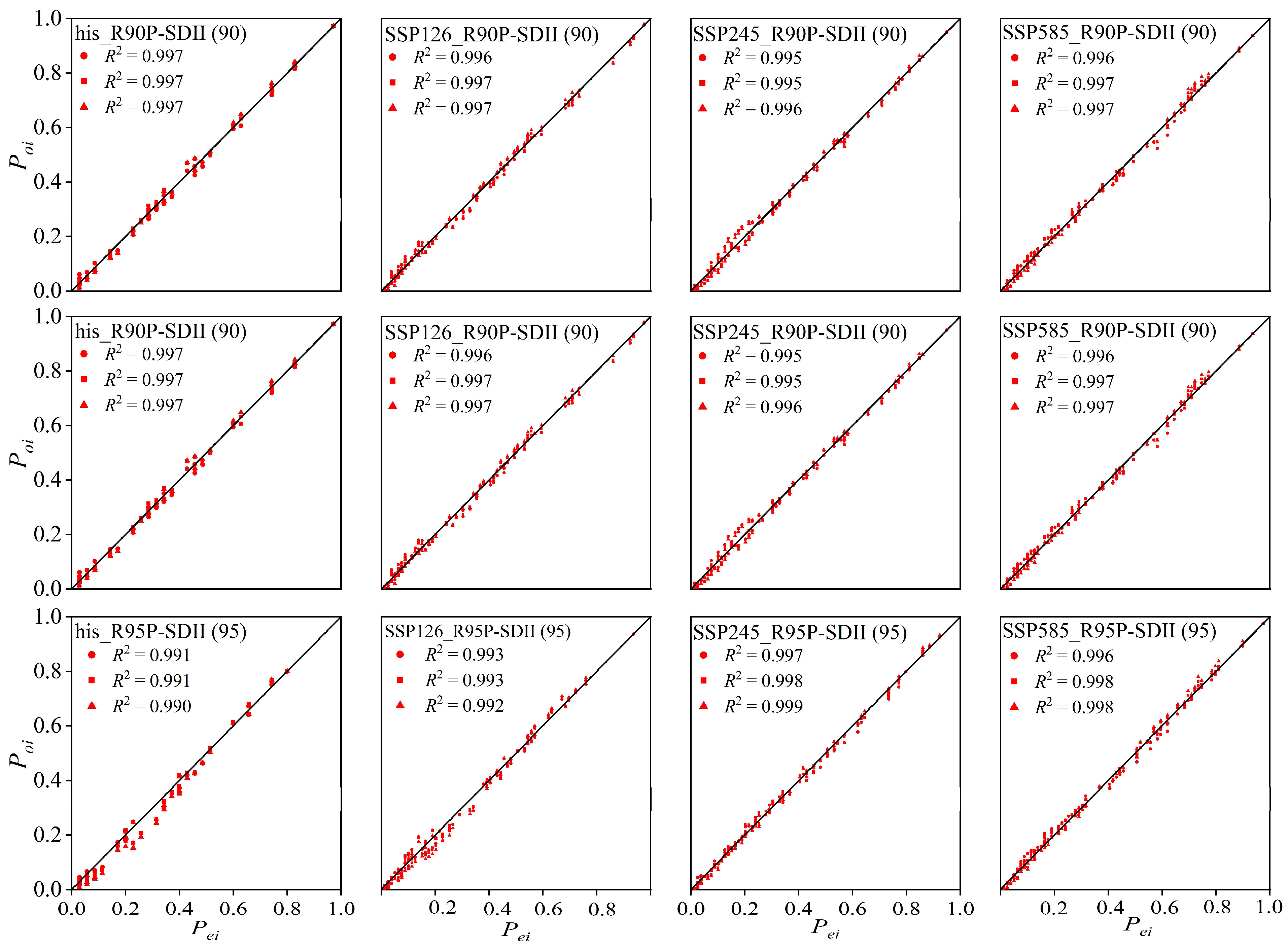
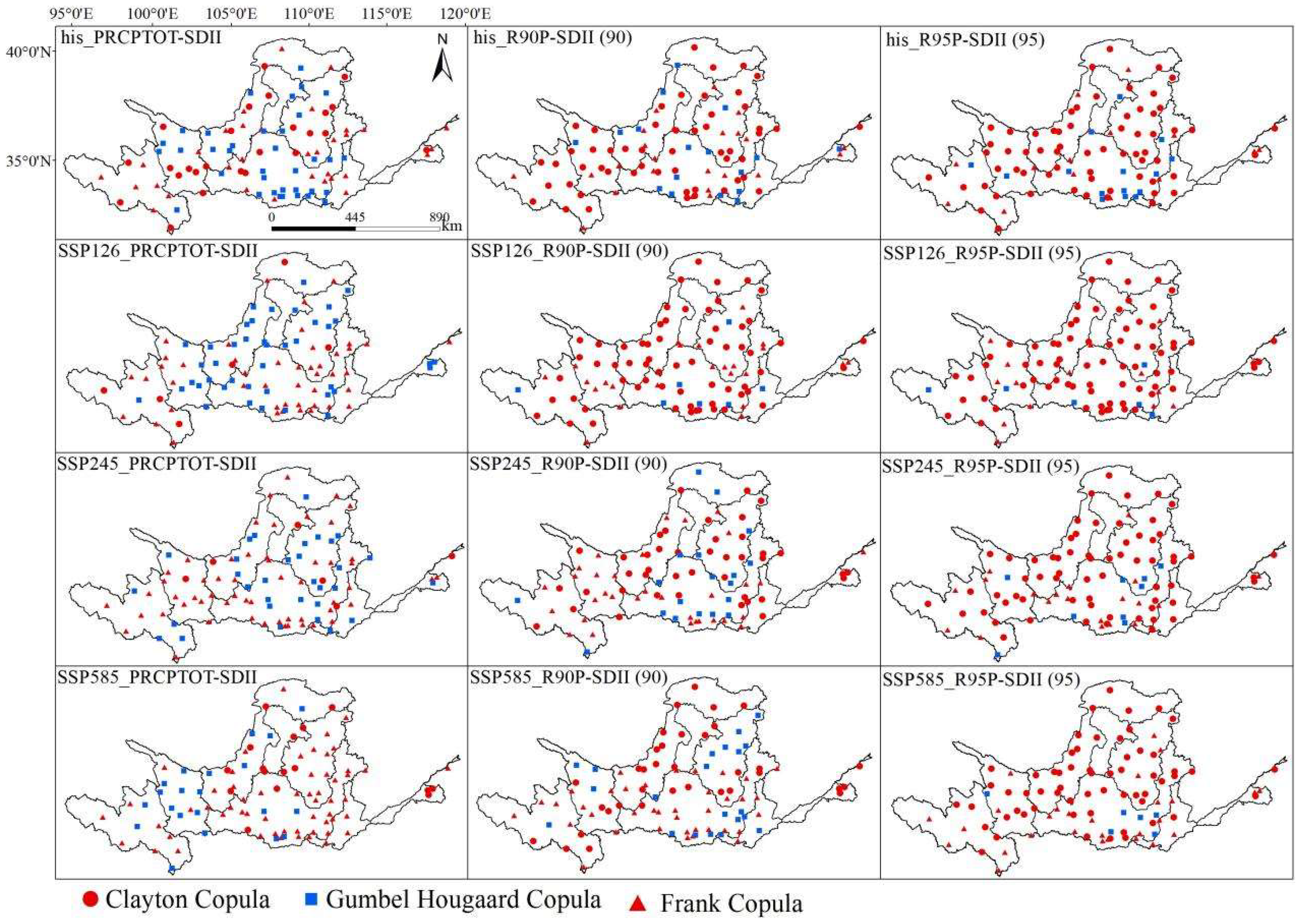
3.1. Optimal Selection and Applicability Analysis of Copula Functions
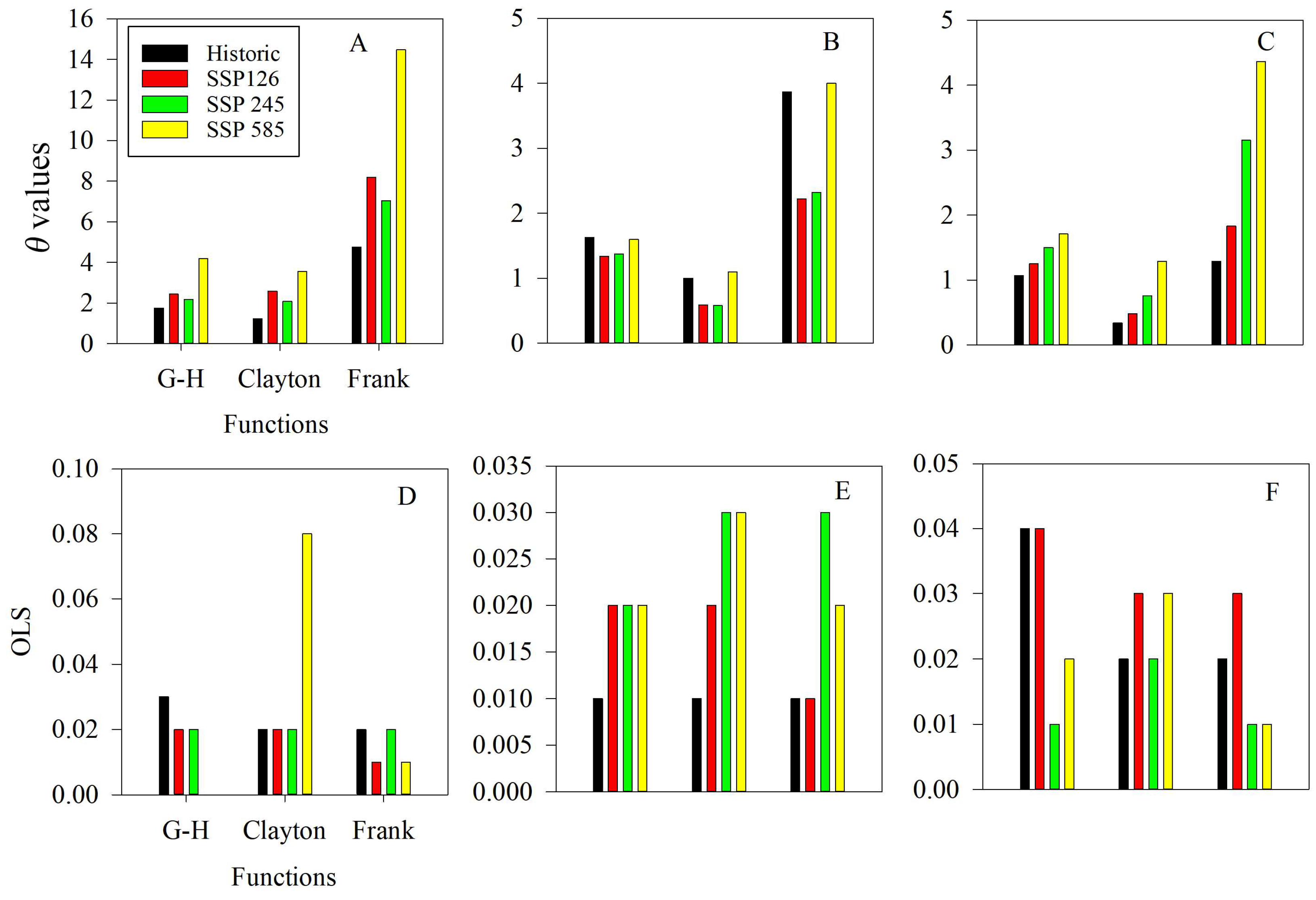
3.2. Bivariate Recurrence Period
3.3. Bivariate Design Values
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, S.; Fu, B.; Piao, S. Reduced sediment transport in the Yellow River due to anthropogenic changes. Nat. Geosci. 2016, 9, 38–41. [Google Scholar] [CrossRef]
- Chen, Y.; Fu, B.; Zhao, Y.; Wang, K.; Zhao, M.; Ma, J.; Wu, J.; Xu, C.; Liu, W.; Wang, H. Sustainable development in the Yellow River Basin: Issues and strategies. J. Clean. Prod. 2020, 263, 121223. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, X.; Huang, W.; Wang, Y.; Xu, Y.; Chen, H.; Kang, Z. Trends in observed mean and extreme precipitation within the Yellow River Basin, China. Theor. Appl. Climatol. 2019, 136, 1387–1396. [Google Scholar] [CrossRef]
- Gao, T.; Wang, H. Trends in precipitation extremes over the Yellow River basin in North China: Changing properties and causes. Hydrol. Process. 2017, 31, 2412–2428. [Google Scholar] [CrossRef]
- Jiang, S.; Cui, H.; Ren, L.; Yan, D.; Yang, X.; Yuan, S.; Liu, Y.; Wang, M.; Xu, C. Will China’s Yellow River basin Suffer More Serious Combined Dry and Wet Abrupt Alternation in the Future? J. Hydrol. 2023, 624, 129871. [Google Scholar] [CrossRef]
- Zhang, Y.; Liang, K.; Liu, C. Time distribution pattern and spatial heterogeneity of hourly scale event-based extreme precipitation in China. J. Hydrol. 2023, 622, 129712. [Google Scholar] [CrossRef]
- Donat, M.G.; Delgado-Torres, C.; De Luca, P.; Mahmood, R.; Ortega, P.; Doblas-Reyes, F.J. How credibly do CMIP6 simulations capture historical mean and extreme precipitation changes? Geophys. Res. Lett. 2023, 50, e2022GL102466. [Google Scholar] [CrossRef]
- Deng, R.; Qiao, S.; Zhu, X.; Dong, T.; Feng, G.; Dong, W. The improvements of sea surface temperature simulation over China Offshore Sea in present climate from CMIP5 to CMIP6 models. Clim. Dyn. 2023, 61, 5111–5130. [Google Scholar] [CrossRef]
- Nooni, I.K.; Ogou, F.K.; Chaibou, A.A.S.; Natoky, F.M.; Gnitou, G.T.; Lu, J. Evaluating CMIP6 Historical Mean Precipitation over Africa and the Arabian Peninsula against Satellite-Based Observation. Atmosphere 2023, 14, 607. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, L.; Zhou, T.; Zheng, J. Assessing the performance of CMIP6 models in simulating droughts across global drylands. Adv. Atmos. Sci. 2023, 1–16. [Google Scholar] [CrossRef]
- Janizadeh, S.; Bateni, S.M.; Jun, C.; Pal, S.C.; Band, S.S.; Chowdhuri, I.; Saha, A.; Tiefenbacher, J.; Mosavi, A. Potential impacts of future climate on the spatio-temporal variability of landslide susceptibility in Iran using machine learning algorithms and CMIP6 climate-change scenarios. Gondwana Res. 2023, 124, 1–17. [Google Scholar] [CrossRef]
- Reddy, N.M.; Saravanan, S. Extreme precipitation indices over India using CMIP6: A special emphasis on the SSP585 scenario. Environ. Sci. Pollut. Res. 2023, 30, 47119–47143. [Google Scholar] [CrossRef] [PubMed]
- Mmame, B.; Ngongondo, C. Evaluation of CMIP6 model skills in simulating tropical climate extremes over Malawi, Southern Africa. Model. Earth. Syst. Environ. 2023, 1–15. [Google Scholar] [CrossRef]
- Ding, Y.; Jiang, C.; Zhou, Z.; Gao, T.; Wang, S.; Zhang, X.; Cai, H.; Shi, H. Evaluation of precipitation and its time series components in CMIP6 over the Yellow River Basin. Clim. Dyn. 2023, 60, 1203–1223. [Google Scholar] [CrossRef]
- Chen, T.; Ao, T.; Zhang, X.; Li, X.; Zhou, L.; Li, M.; Yang, K. Spatial and temporal variation and probability characteristics of extreme precipitation events in the Min River Basin from 1961 to 2016. Appl. Ecol. Environ. Res. 2019, 17, 11375–11394. [Google Scholar] [CrossRef]
- Innocenti, S.; Mailhot, A.; Leduc, M.; Cannon, A.J.; Frigon, A. Projected changes in the probability distributions, seasonality, and spatiotemporal scaling of daily and subdaily extreme precipitation simulated by a 50-member ensemble over northeastern North America. J. Geophys. Res. Atmos. 2019, 124, 10427–10449. [Google Scholar] [CrossRef]
- Murphy, C.; Kettle, A.; Meresa, H.; Golian, S.; Bruen, M.; Mellander, P.; Tsakiris, G. Climate Change Impacts on Irish River Flows: High Resolution Scenarios and Comparison with CORDEX and CMIP6 Ensembles. Water Resour. Manag. 2023, 37, 1841–1858. [Google Scholar] [CrossRef]
- Das, P.; Zhang, Z.; Ghosh, S.; Lu, J.; Ayugi, B.; Ojara, M.; Guo, X. Historical and projected changes in Extreme High Temperature events over East Africa and associated with meteorological conditions using CMIP6 models. Glob. Planet Chang. 2023, 222, 104068. [Google Scholar] [CrossRef]
- Konda, G.; Vissa, N.K. Evaluation of CMIP6 models for simulations of surplus/deficit summer monsoon conditions over India. Clim. Dyn. 2023, 60, 1023–1042. [Google Scholar] [CrossRef]
- Taylor, G.P.; Loikith, P.C.; Aragon, C.M.; Lee, H.; Waliser, D.E. CMIP6 model fidelity at simulating large-scale atmospheric circulation patterns and associated temperature and precipitation over the Pacific Northwest. Clim. Dyn. 2023, 60, 2199–2218. [Google Scholar] [CrossRef]
- Pierce, D.W.; Cayan, D.R.; Feldman, D.R.; Risser, M.D. Future Increases in North American Extreme Precipitation in CMIP6 Downscaled with LOCA. J. Hydrometeorol. 2023, 24, 951–975. [Google Scholar] [CrossRef]
- Sarkar, S.; Maity, S.S.; Maity, R. Precipitation-based Climate Change Hotspots across India through a Multi-model Assessment from CMIP6. J. Hydrol. 2023, 623, 129805. [Google Scholar] [CrossRef]
- Wang, S.; Feng, J.; Liu, X.; Ji, X. Simulation of the long-term variability of the Hadley circulation in CMIP6 models. Atmos. Res. 2023, 287, 106716. [Google Scholar] [CrossRef]
- Gadain, H.; Libanda, B. CMIP6 models simulate heavier future rainfall over the Highlands than across other agricultural areas of Yemen. Model. Earth. Syst. Environ. 2023, 1–13. [Google Scholar] [CrossRef]
- Zhang, Y.; Chiew, F.H.S.; Li, M.; Post, D. Predicting Runoff Signatures Using Regression and Hydrological Modeling Approaches. Water Resour. Res. 2018, 54, 125478. [Google Scholar] [CrossRef]
- Galelli, S.; Castelletti, A. Assessing the predictive capability of randomized tree-based ensembles in streamflow modelling. Hydrol. Earth. Syst. Sci. 2013, 17, 2669–2684. [Google Scholar] [CrossRef]
- Sklar, A. Fonctions de Repartition an Dimensions et Leurs Marges. Publ. Inst. Statist. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Bajracharya, A.R.; Bajracharya, S.R.; Shrestha, A.B.; Maharjan, S.B. Climate change impact assessment on the hydrological regime of the Kaligandaki Basin, Nepal. Sci. Total Environ. 2018, 625, 837–848. [Google Scholar] [CrossRef]
- Shrestha, N.K.; Du, X.; Wang, J. Assessing climate change impacts on fresh water resources of the Athabasca River basin, Canada. Sci. Total Environ. 2017, 601, 425–440. [Google Scholar] [CrossRef]
- Nejc, B.; Mojca, Š.; Matjaž, M. Copula-based IDF curves and empirical rainfall thresholds for flash floods and rainfall-induced landslides. J. Hydrol. 2016, 541, 272–284. [Google Scholar] [CrossRef]
- Salvatore, G.; Francesco, S. Asymmetric copula in multivariate flood frequency analysis. Adv. Water Resour. 2006, 29, 1155–1167. [Google Scholar] [CrossRef]
- Halwatura, D.; Najim, M.M.M. Application of the HEC-HMS model for runoff simulation in a tropical catchment. Environ. Model. Softw. 2013, 46, 155–162. [Google Scholar] [CrossRef]
- Muhammad, A.; Minha, C.; Tae-Woong, K.; Umar, W.L. Hydrological modeling to simulate streamflow under changing climate in a scarcely gauged cryosphere catchment. Environ. Earth Sci. 2016, 75, 186. [Google Scholar] [CrossRef]
- Yuan, W.L.; Liu, M.Q.; Wang, F. Calculation of Critical Rainfall for Small-Watershed Flash Floods Based on the HEC-HMS Hydrological Model. Water Resour. Manag. 2019, 33, 2555–2575. [Google Scholar] [CrossRef]
- Ran, G.; Jian, S.; Wu, Q.; Zhang, L.; Hu, C. Exploring the Dominant Runoff Processes in Two Typical Basins of the Yellow River, China. Water 2020, 12, 3055. [Google Scholar] [CrossRef]
- Luo, L.; Wang, Z.J.; Liu, X.Y.; Zhang, X.C. Changes in characteristics of precipitation in flood season over five typical basins of middle reaches of the yellow River in China. J. Hydraul. Eng. 2013, 44, 848–855, (In Chinese with English abstract). [Google Scholar]
- Ren, Z.; Ma, X.; Wang, K.; Li, Z. Effects of Extreme Precipitation on Runoff and Sediment Yield in the Middle Reaches of the Yellow River. Atmosphere 2023, 14, 1415. [Google Scholar] [CrossRef]
- Chang, D.; Li, S.; Lai, Z. Effects of extreme precipitation intensity and duration on the runoff and nutrient yields. J. Hydrol. 2023, 626, 130281. [Google Scholar] [CrossRef]
- Mohammad, R.R.; Fernanda, H.; Bofu, Y. Individual and combined impacts of urbanization and climate change on catchment runoff in Southeast Queensland, Australia. Sci. Total Environ. 2023, 861, 160528. [Google Scholar] [CrossRef]
- José, Y.G.; Suzana, M.G.; Richarde, M.; Celso, A.G. Modeling the impacts of future LULC and climate change on runoff and sediment yield in a strategic basin in the Caatinga/Atlantic forest ecotone of Brazil. Catena 2021, 203, 105308. [Google Scholar] [CrossRef]
- Utsumi, N.; Kim, H.; Kanae, S.; Oki, T. Relative contributions of weather systems to mean and extreme global precipitation. J. Geophys. Res. Atmos. 2016, 122, 152–167. [Google Scholar] [CrossRef]
- Li, J.; Qian, Y.; Leung, L.R.; Feng, Z. Summer mean and extreme precipitation over the Mid-Atlantic Region: Climatological characteristics and contributions from different precipitation types. J. Geophys. Res. Atmos. 2021, 126, e2021JD035045. [Google Scholar] [CrossRef]
- Gimeno, L.; Sorí, R.; Vázquez, M.; Stojanovic, M.; Algarra, I.; Eiras-Barca, J.; Gimeno-Sotelo, L.; Nieto, R. Extreme precipitation events. WIREs Water 2022, 9, e1611. [Google Scholar] [CrossRef]
- Naz, S.; Jamil, S.S.; Iqbal, M.J. Archimedean copula-based bivariate flood-frequency analysis on Sukkur, Pakistan. Arab J. Geosci. 2020, 13, 282. [Google Scholar] [CrossRef]
- Wable, P.S.; Jha, M.K. Application of Archimedean copulas to the impact assessment of hydro-climatic variables in semi-arid aquifers of western India. Hydrogeol. J. 2018, 26, 89–108. [Google Scholar] [CrossRef]
- Wazneh, H.; Arain, M.A.; Coulibaly, P.; Gachon, P.T.; Rigo, T. Evaluating the dependence between temperature and precipitation to better estimate the risks of concurrent extreme weather events. Adv. Meteorol. 2020, 2020, 8763631. [Google Scholar] [CrossRef]
- Brunner, M.I.; Liechti, K.; Zappa, M. Extremeness of recent drought events in Switzerland: Dependence on variable and return period choice. Nat. Hazards Earth Syst. Sci. 2019, 19, 2311–2323. [Google Scholar] [CrossRef]
- Bender, J.; Wahl, T.; Jensen, J. Multivariate design in the presence of non-stationarity. J. Hydrol. 2014, 514, 123–130. [Google Scholar] [CrossRef]
- Jiang, C.; Xiong, L.; Yan, L.; Dong, J.; Xu, C. Multivariate hydrologic design methods under nonstationary conditions and application to engineering practice. Hydrol. Earth Syst. Sci. 2019, 23, 1683–1704. [Google Scholar] [CrossRef]
- Zhu, X.; Lee, S.Y.; Wen, X.; Ji, Z.; Lin, L.; Zheng, Z.; Xu, D.; Dong, W. Extreme climate changes over three major river basins in China as seen in CMIP5 and CMIP6. Clim. Dyn. 2021, 57, 1187–1205. [Google Scholar] [CrossRef]


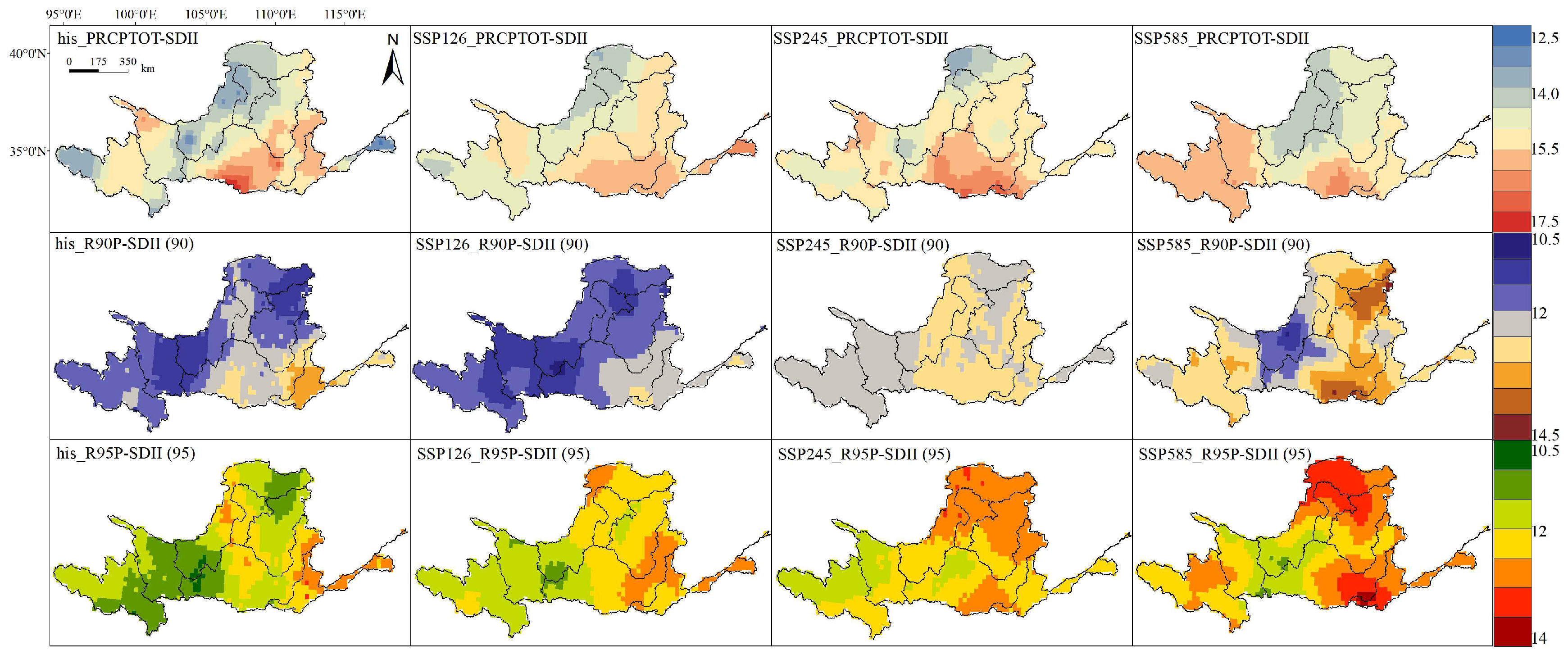
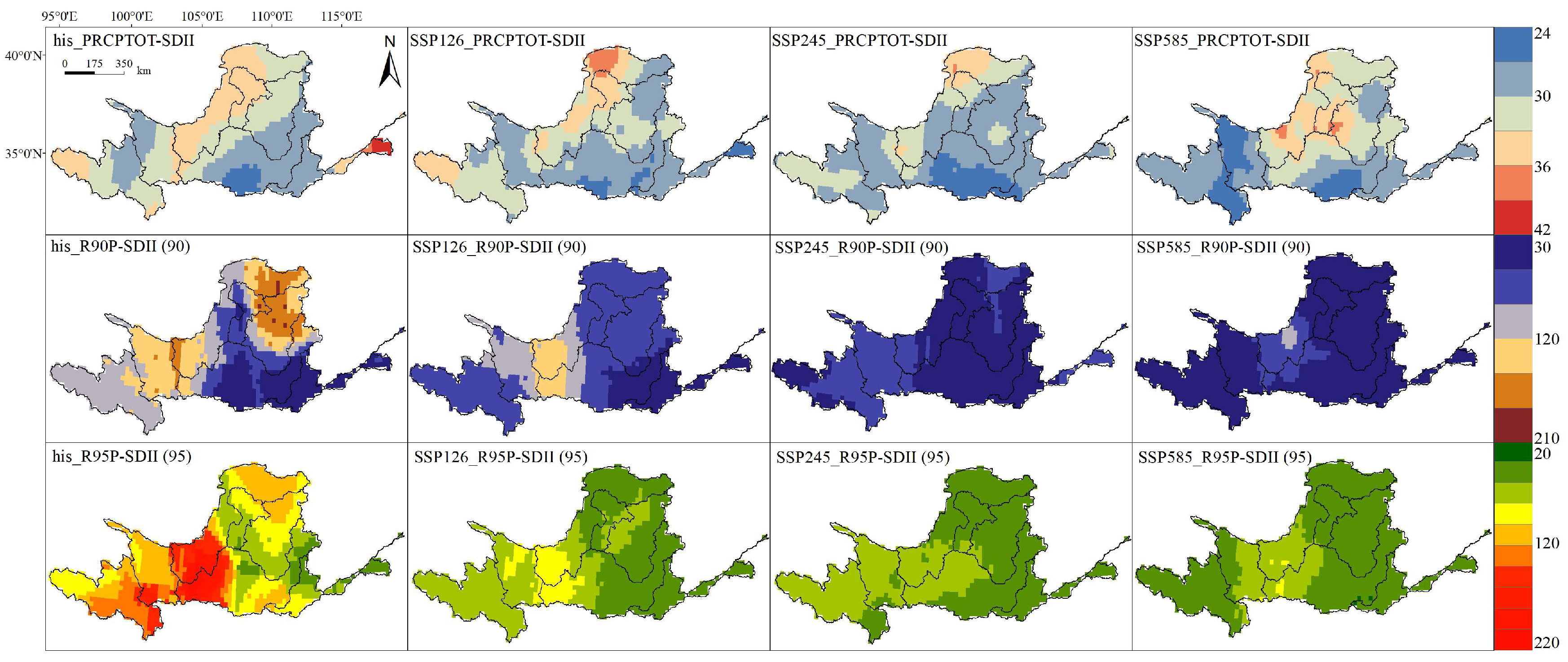


| Abbreviation | Name | Definition | Unit |
|---|---|---|---|
| PRCPTOT | Annual precipitation | ≥1 mm precipitation daily cumulative amount | mm |
| SDII | Precipitation intensity | The ratio of total precipitation ≥1 mm to number of days | mm/d |
| R95P | Heavy precipitation | The sum of 95% quantile values of intense precipitation | mm |
| SDII (95) | Heavy precipitation intensity | The ratio of the sum of heavy precipitation to the number of heavy precipitation days | mm/d |
| R90P | Heavy rainfall | The part of precipitation exceeding the 90th percentile in precipitation events | mm |
| SDII (90) | Heavy precipitation intensity | The sum of rainfall for heavy rain events exceeding the 90th percentile value divided by the number of days with heavy rain | mm/d |
| Numbers | Climate Model | Resolution Ratio | Country |
|---|---|---|---|
| 1 | EC-Earth3 | 100 km | Britain |
| 2 | EC-Earth3-Veg | 100 km | Sweden |
| 3 | GFDL-ESM4 | 100 km | America |
| 4 | MPI-ESM1-2-HR | 100 km | Germany |
| 5 | MRI-ESM2-0 | 100 km | Japan |
| 6 | IPSL-CM6A-LR | 100 km | France |
| Copula Function | Generating Elements | Density Function | Distribution Function |
|---|---|---|---|
| G-H | |||
| Clayton | |||
| Frank |
| Function | Relationship between τ and θ | Kc |
|---|---|---|
| Gumbel | ||
| Clayton | ||
| Frank |
| Index | Recurrence Interval | Design Value | Rate of Change Relative to Historical Period (%) | Rate of Change Relative to Univariate Design Value (%) | |||||
|---|---|---|---|---|---|---|---|---|---|
| His | SSP 126 | SSP 245 | SSP 585 | His | SSP 126 | SSP 245 | SSP 585 | ||
| PRCP TOT (mm) | 100a * | 631.33 | 28.88 | 23.83 | 24.83 | −5.27 | −3.30 | −3.99 | −0.79 |
| 50a | 619.43 | 25.45 | 23.00 | 24.71 | −5.08 | −2.82 | −3.21 | −2.50 | |
| 20a | 601.56 | 20.50 | 21.81 | 24.12 | −4.75 | −2.14 | −2.42 | −5.17 | |
| 10a | 585.02 | 23.90 | 20.76 | 23.47 | −4.45 | −1.74 | −1.92 | −1.60 | |
| 5a | 529.11 | 31.30 | 27.40 | 30.63 | −9.97 | −1.42 | −1.47 | −1.34 | |
| 2a | 529.11 | 20.25 | 15.35 | 18.48 | −1.45 | −1.26 | −1.15 | −1.09 | |
| SDII (mm/day) | 100a | 4.29 | 18.54 | 16.37 | 18.50 | −7.77 | −2.91 | −3.26 | −0.95 |
| 50a | 4.21 | 16.18 | 15.91 | 18.33 | −7.46 | −2.45 | −2.80 | −2.29 | |
| 20a | 4.10 | 15.78 | 15.30 | 18.16 | −7.04 | −1.91 | −2.07 | −1.77 | |
| 10a | 4.00 | 15.48 | 14.75 | 17.89 | −6.71 | −1.51 | −1.48 | −1.40 | |
| 5a | 3.88 | 15.19 | 14.17 | 17.53 | −6.42 | −1.16 | −1.16 | −1.09 | |
| 2a | 3.64 | 14.98 | 13.41 | 16.92 | −6.24 | −0.87 | −0.87 | −0.81 | |
| R90P (mm) | 100a | 247.30 | 24.53 | 26.56 | 32.32 | −14.09 | −15.35 | −14.08 | −11.85 |
| 50a | 237.41 | 23.69 | 24.75 | 30.46 | −13.13 | −13.80 | −12.78 | −11.30 | |
| 20a | 223.13 | 22.37 | 22.14 | 28.55 | −11.61 | −11.50 | −10.81 | −8.53 | |
| 10a | 210.01 | 21.40 | 20.08 | 25.20 | −10.39 | −9.65 | −9.24 | −7.99 | |
| 5a | 185.84 | 25.45 | 22.88 | 23.63 | −12.52 | −7.63 | −7.40 | −9.84 | |
| 2a | 151.60 | 22.43 | 20.99 | 20.99 | −10.75 | −7.42 | −4.68 | −7.49 | |
| SDII (90) (mm/day) | 100a | 13.53 | 8.77 | 11.61 | 13.21 | −8.84 | −7.30 | −7.17 | −6.84 |
| 50a | 13.22 | 9.28 | 11.50 | 13.18 | −7.46 | −6.27 | −6.16 | −5.79 | |
| 20a | 12.79 | 9.95 | 11.42 | 12.95 | −5.76 | −4.90 | −4.78 | −4.59 | |
| 10a | 12.44 | 10.48 | 11.38 | 13.05 | −4.56 | −3.87 | −3.76 | −3.49 | |
| 5a | 12.04 | 10.99 | 11.31 | 12.78 | −3.28 | −2.76 | −2.69 | −2.56 | |
| 2a | 11.31 | 12.34 | 11.35 | 12.33 | −1.51 | −0.61 | −1.12 | −1.24 | |
| R95P (mm) | 100a | 170.64 | 22.67 | 24.52 | 28.55 | −16.61 | −17.69 | −18.67 | −17.65 |
| 50a | 161.08 | 22.48 | 23.38 | 25.20 | −15.10 | −16.15 | −16.67 | −17.88 | |
| 20a | 147.53 | 22.52 | 21.62 | 24.50 | −12.73 | −13.40 | −13.73 | −15.22 | |
| 10a | 135.68 | 17.66 | 19.82 | 23.20 | −10.70 | −14.63 | −11.50 | −13.27 | |
| 5a | 121.53 | 22.27 | 17.89 | 20.53 | −8.14 | −8.56 | −8.79 | −11.49 | |
| 2a | 91.22 | 19.53 | 14.24 | 16.77 | −6.25 | −8.93 | −7.75 | −9.77 | |
| SDII (95) (mm/day) | 100a | 16.75 | 8.17 | 10.70 | 11.84 | −10.54 | −10.46 | −10.53 | −10.04 |
| 50a | 16.30 | 8.52 | 10.82 | 12.10 | −8.96 | −9.00 | −8.73 | −8.35 | |
| 20a | 15.67 | 9.15 | 11.01 | 12.47 | −6.99 | −7.08 | −6.49 | −6.19 | |
| 10a | 15.15 | 9.73 | 11.27 | 12.77 | −5.57 | −5.61 | −4.84 | −4.66 | |
| 5a | 14.58 | 10.20 | 11.44 | 13.05 | −4.05 | −4.23 | −3.29 | −3.12 | |
| 2a | 14.08 | 6.76 | 6.79 | 9.13 | −1.91 | −2.39 | −2.67 | −1.13 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Zhang, G.; Zhang, X. Future Joint Probability Characteristics of Extreme Precipitation in the Yellow River Basin. Water 2023, 15, 3957. https://doi.org/10.3390/w15223957
Li F, Zhang G, Zhang X. Future Joint Probability Characteristics of Extreme Precipitation in the Yellow River Basin. Water. 2023; 15(22):3957. https://doi.org/10.3390/w15223957
Chicago/Turabian StyleLi, Fujun, Guodong Zhang, and Xueli Zhang. 2023. "Future Joint Probability Characteristics of Extreme Precipitation in the Yellow River Basin" Water 15, no. 22: 3957. https://doi.org/10.3390/w15223957
APA StyleLi, F., Zhang, G., & Zhang, X. (2023). Future Joint Probability Characteristics of Extreme Precipitation in the Yellow River Basin. Water, 15(22), 3957. https://doi.org/10.3390/w15223957





