Effect of Flow on the Energy Conversion Characteristics of Multiphase Pumps Based on Energy Transport Theory
Abstract
:1. Introduction
2. Energy Transport Theory
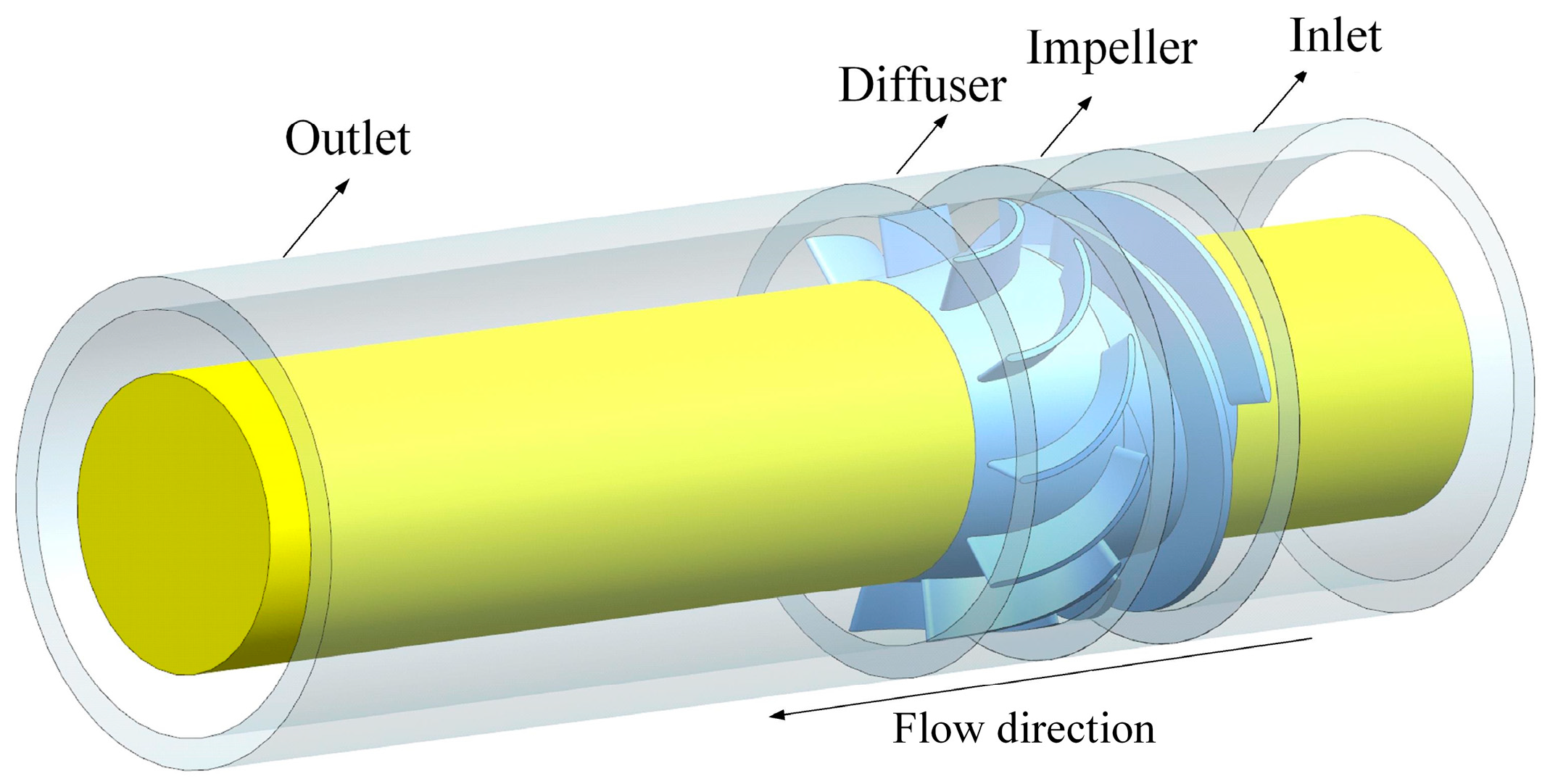
3. Research Target
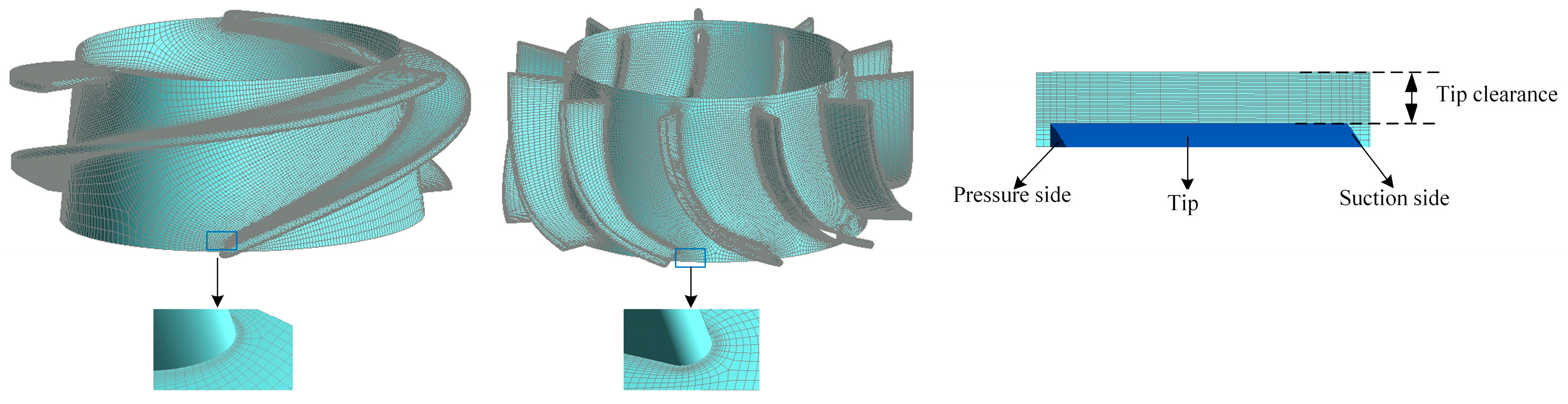
4. Mesh Division and Boundary Condition Setting
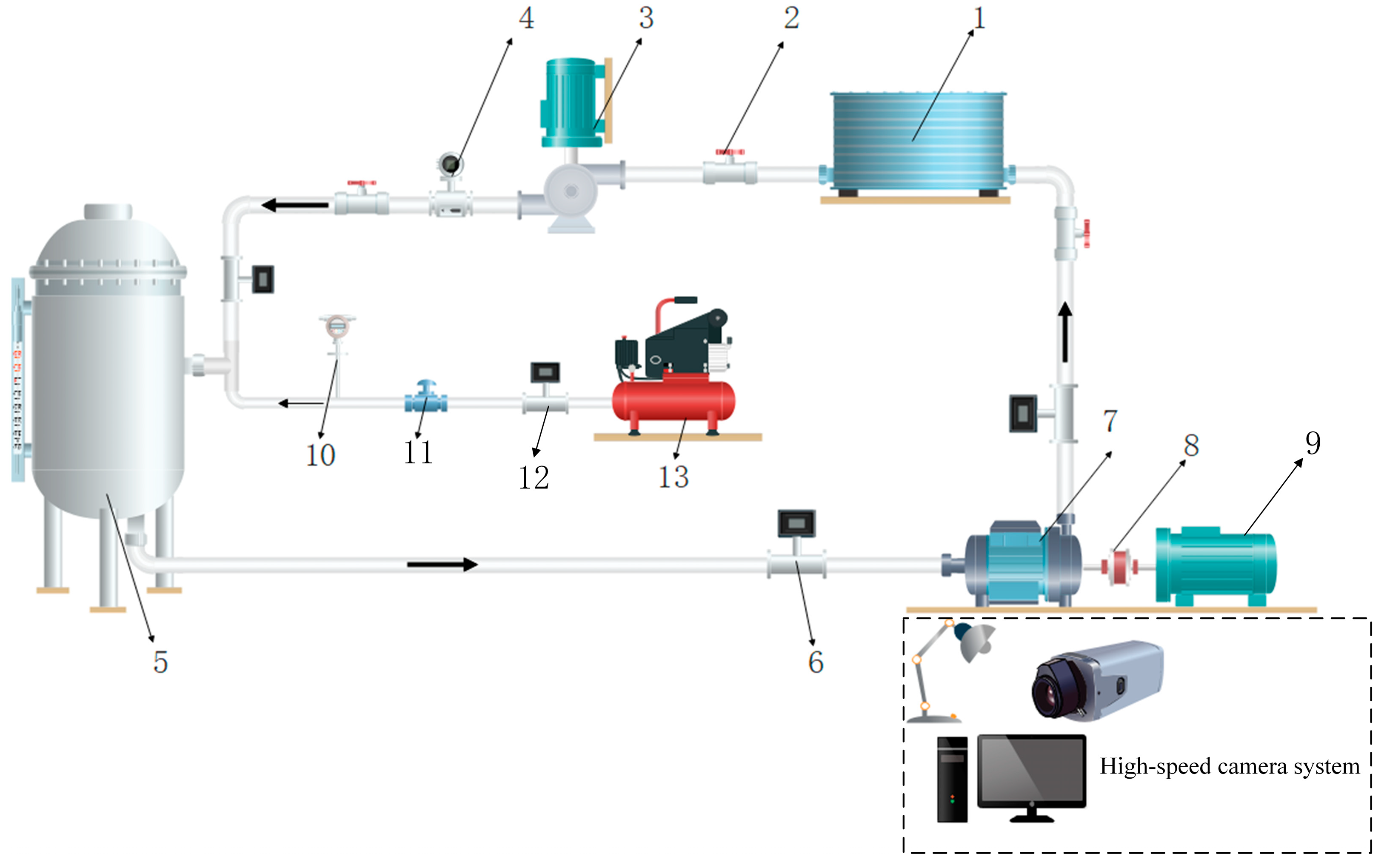
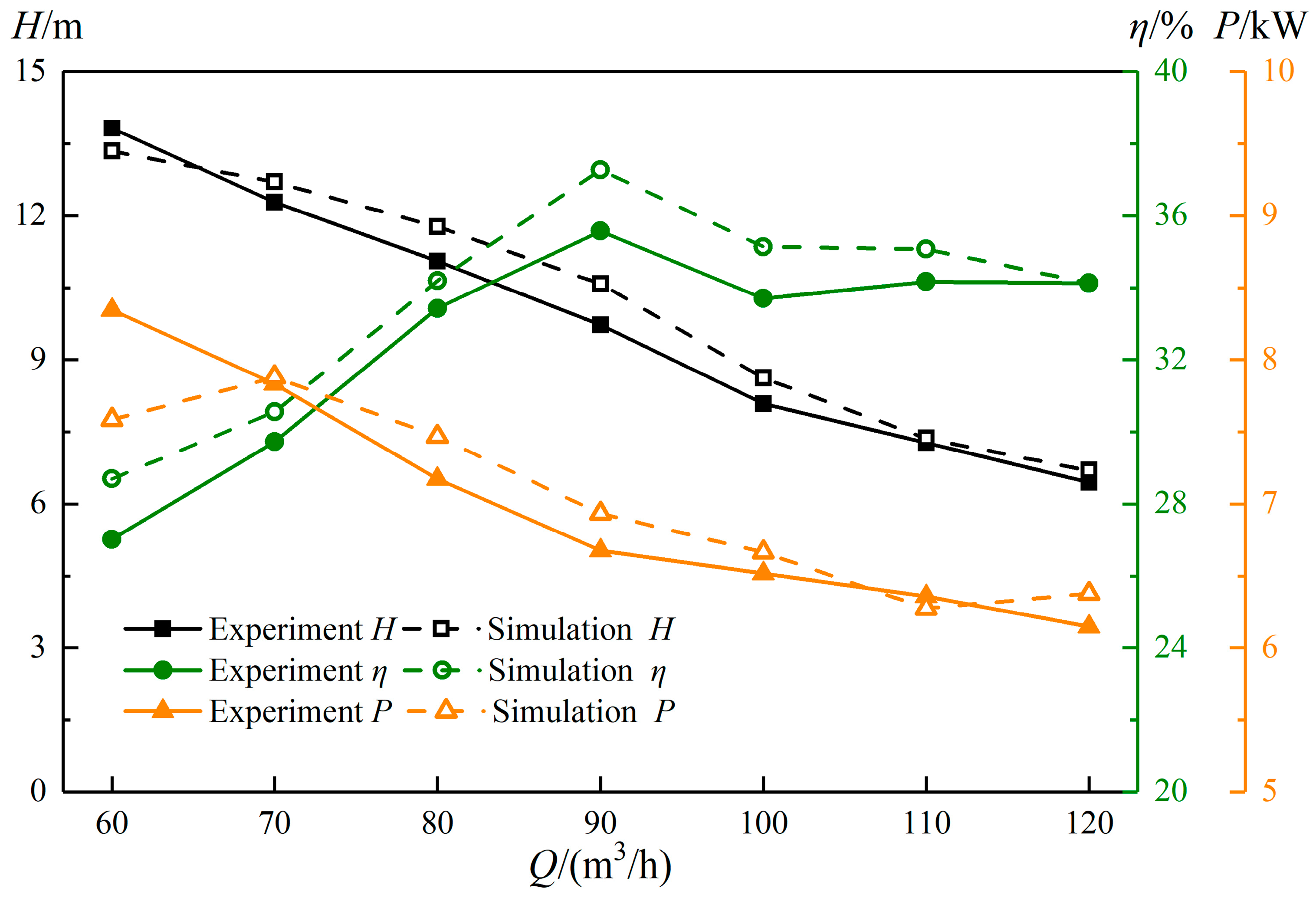
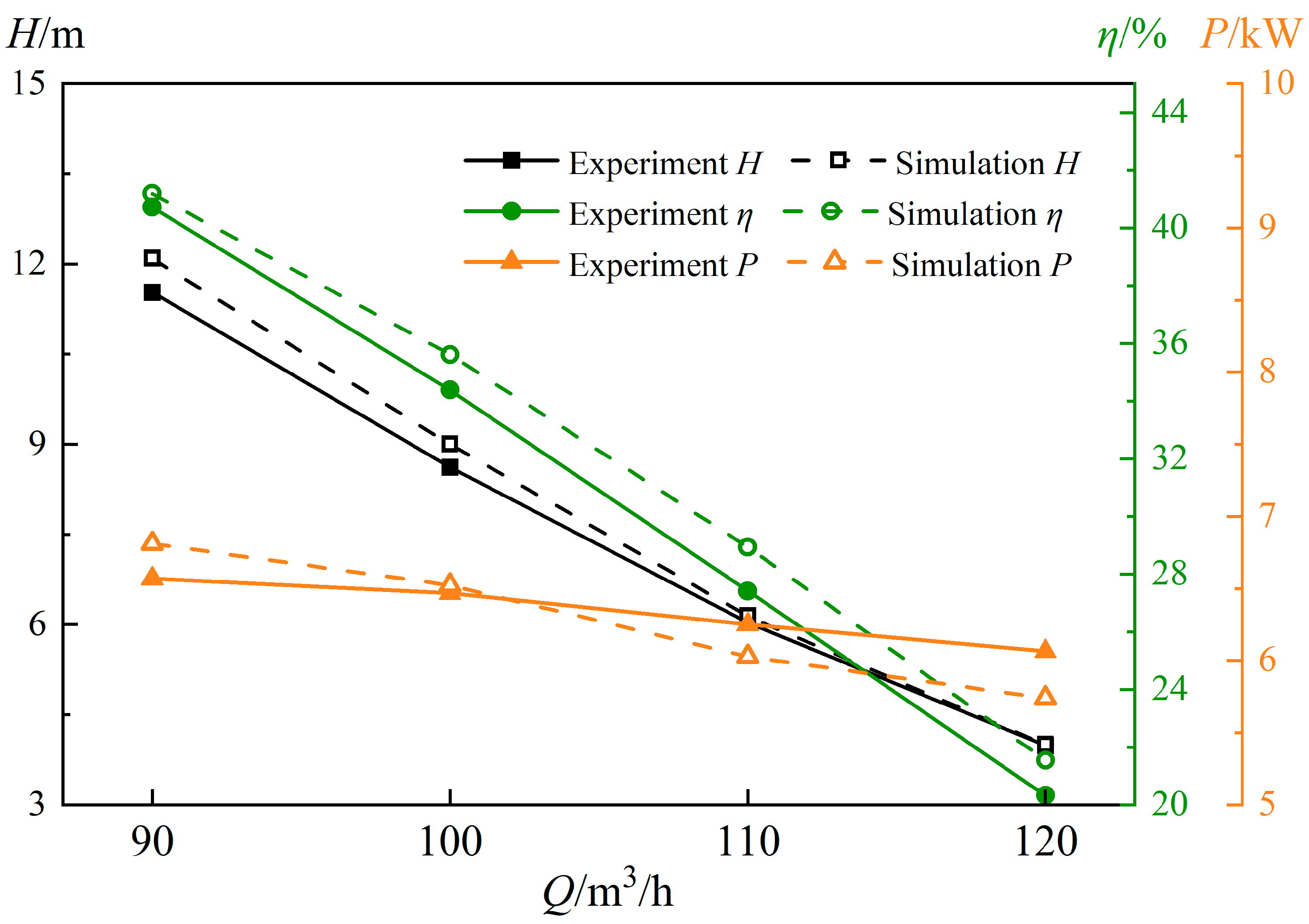
5. Experimental Procedure
6. Analysis of Results
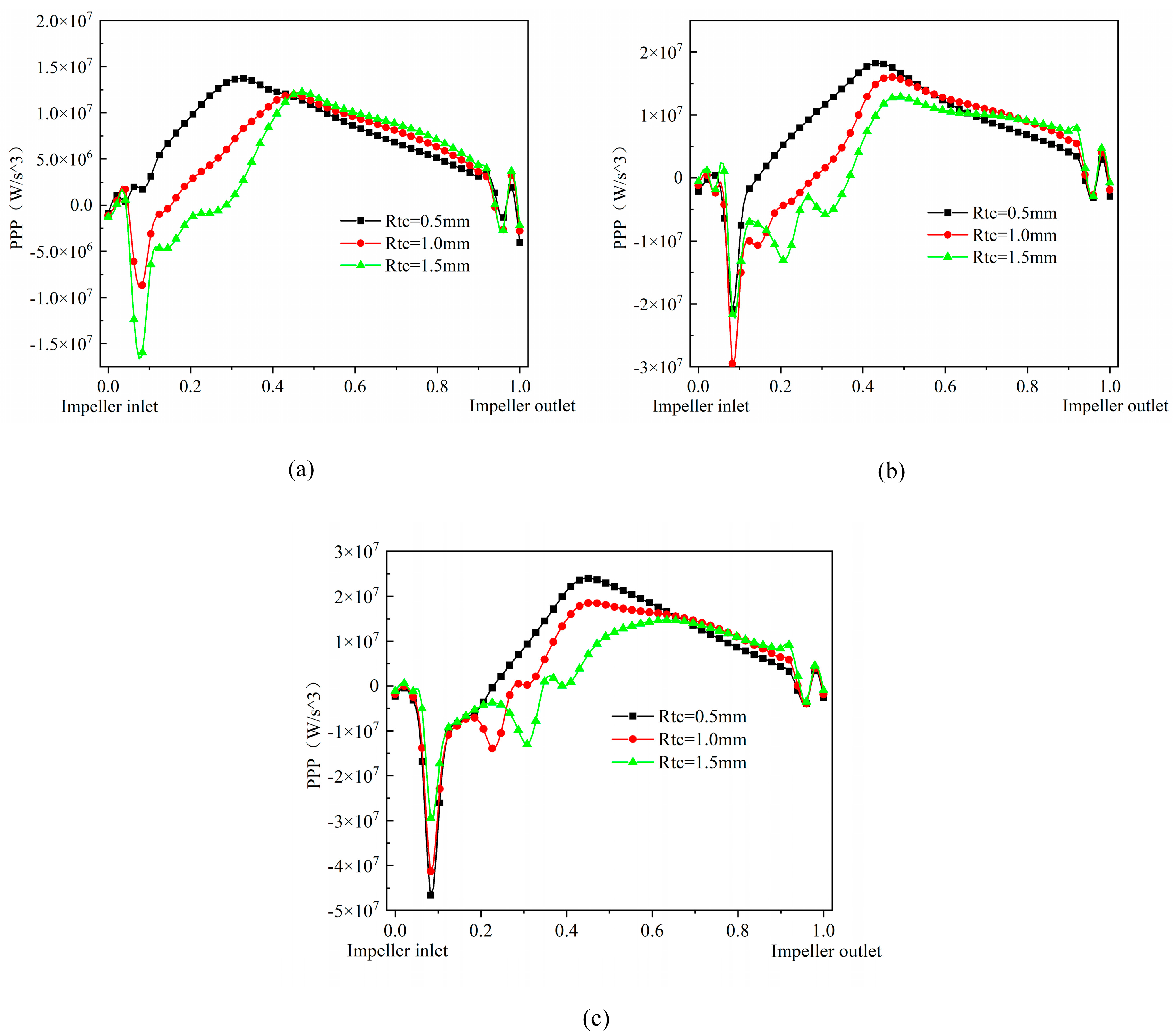
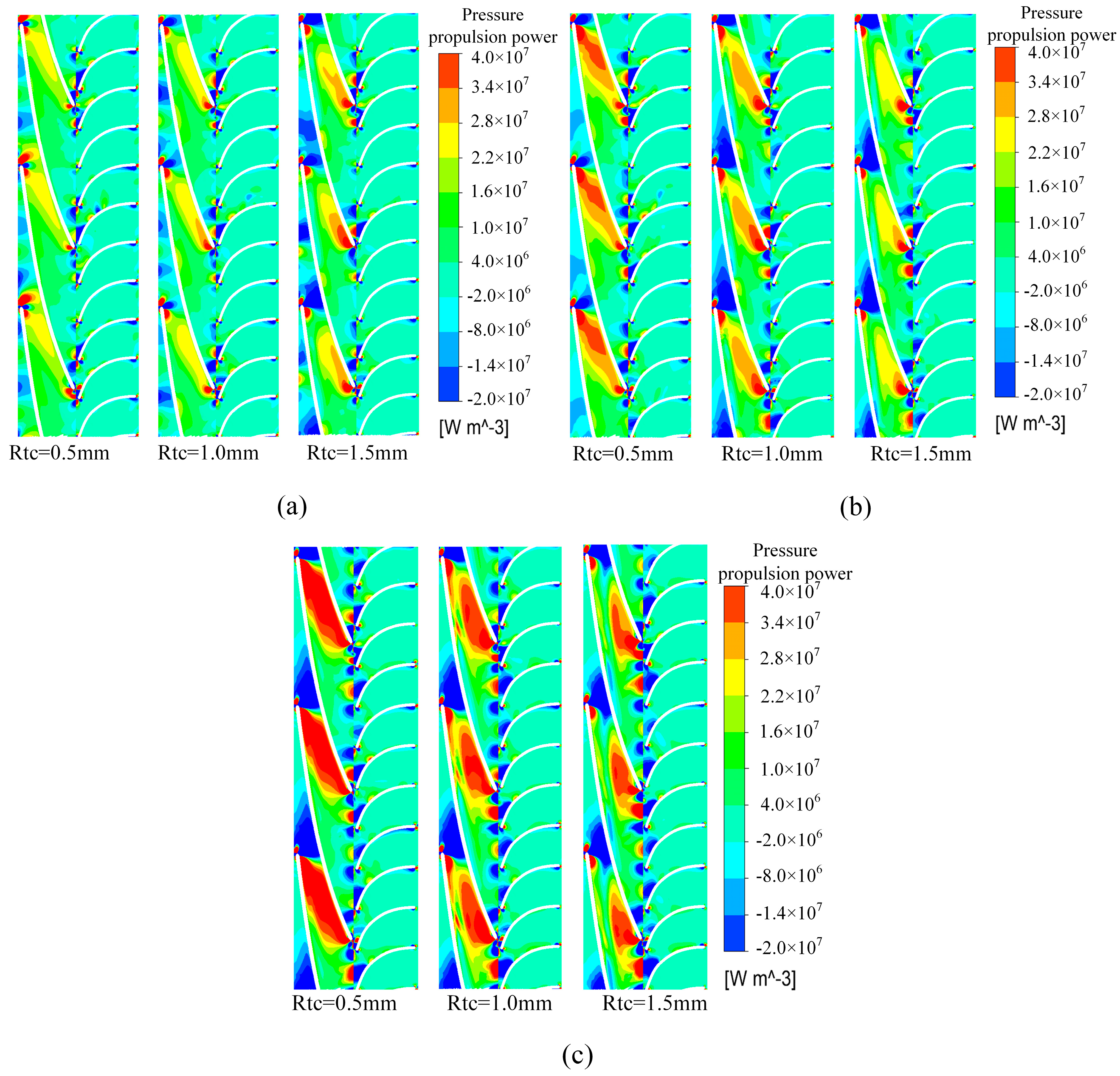
6.1. Effect of Flow on the Pressure Propulsion Power within a Pressurization Unit
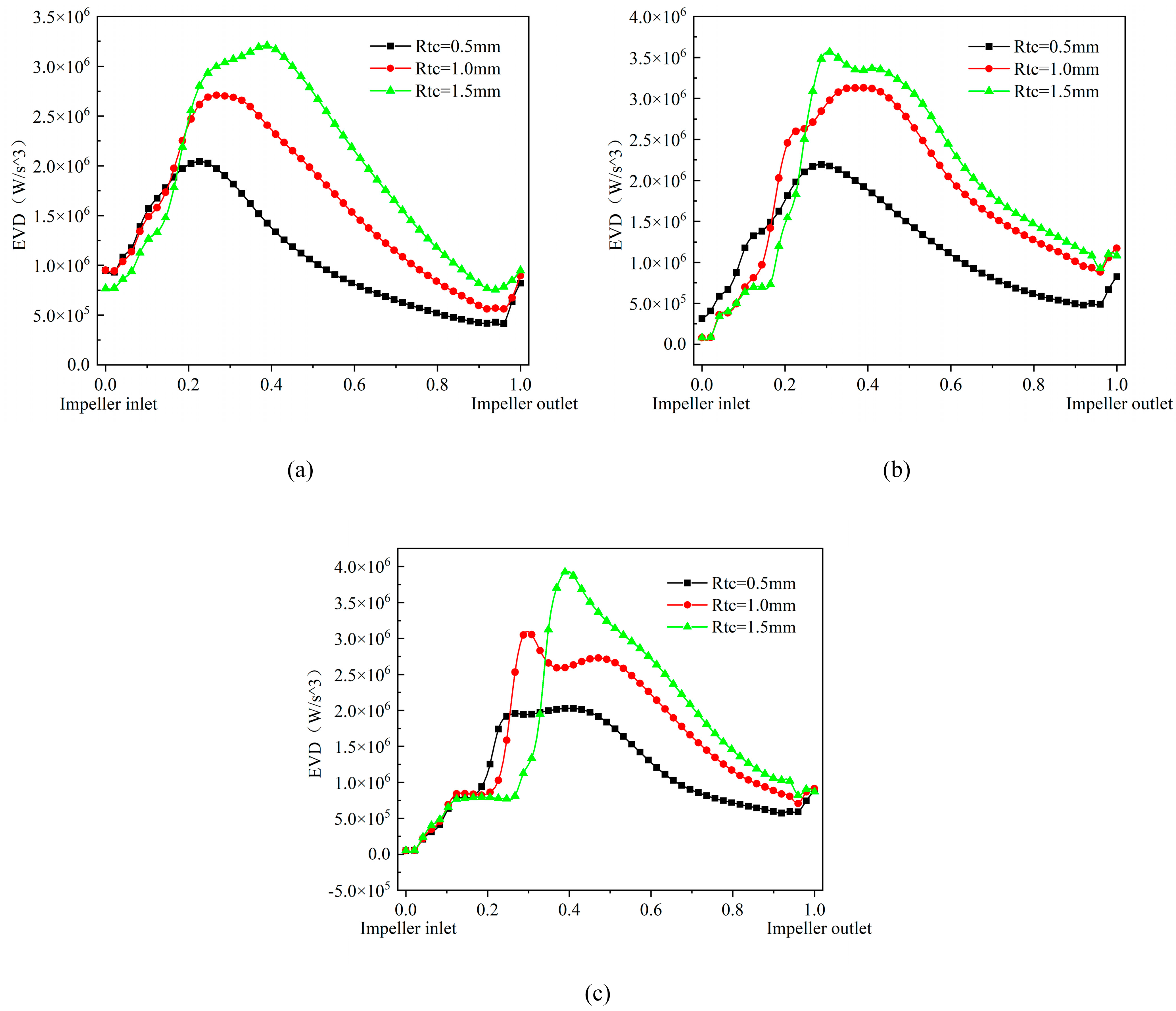
6.2. Effect of Flow on the Lamb Vector Dispersion with a Pressurization Unit
6.3. Effect of Flow on the Vortex Enstrophy Dissipation in the Pressurization Unit
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vysotskii, V.; Dmitrievskii, A. Global Oil and Gas Resources and Their Development. Russ. J. Gen. Chem. 2009, 79, 2477–2485. [Google Scholar] [CrossRef]
- Tong, X.; Zhang, G.; Wang, Z.; Wen, Z.; Tian, Z.; Wang, H.; Ma, F.; Wu, Y. Distribution and Potential of Global Oil and Gas Resources. Pet. Explor. Dev. 2018, 45, 779–789. [Google Scholar] [CrossRef]
- Li, L.; Gu, Z.; Xu, W.; Tan, Y.; Fan, X.; Tan, D. Mixing Mass Transfer Mechanism and Dynamic Control of Gas-Liquid-Solid Multiphase Flow Based on VOF-DEM Coupling. Energy 2023, 272, 127015. [Google Scholar] [CrossRef]
- Xu, Y.; Cao, S.; Sano, T.; Wakai, T.; Reclari, M. Experimental Investigation on Transient Pressure Characteristics in a Helico-Axial Multiphase Pump. Energies 2019, 12, 461. [Google Scholar] [CrossRef]
- Xiao, W.; Tan, L. Design Method of Controllable Velocity Moment and Optimization of Pressure Fluctuation Suppression for a Multiphase Pump. Ocean Eng. 2021, 220, 108402. [Google Scholar] [CrossRef]
- Li, C.; Luo, X.; Feng, J.; Zhu, G.; Xue, Y. Effects of Gas-Volume Fractions on the External Characteristics and Pressure Fluctuation of a Multistage Mixed-Transport Pump. Appl. Sci. 2020, 10, 582. [Google Scholar] [CrossRef]
- Asfora, L.; dos Santos, A.; Duarte, L. Modeling Multiphase Jet Pumps for Gas Compression. J. Pet. Sci. Eng. 2019, 173, 844–852. [Google Scholar] [CrossRef]
- Zhang, W.; Zhu, B.; Zi, D.; Ma, Z.; Wang, F. Transportability Improvement of a Gas-Liquid Rotodynamic Pump Using the Two-Step Multi-Objective Optimization Strategy. Front. Energy Res. 2022, 10, 900182. [Google Scholar] [CrossRef]
- Shi, J.; Tao, S.; Shi, G.; Song, W. Effect of Gas Volume Fraction on the Energy Loss Characteristics of Multiphase Pumps at Each Cavitation Stage. Water 2021, 13, 2293. [Google Scholar] [CrossRef]
- Liu, M.; Tan, L.; Cao, S. Influence of Viscosity on Energy Performance and Flow Field of a Multiphase Pump. Renew. Energy 2020, 162, 1151–1160. [Google Scholar] [CrossRef]
- Quan, H.; Li, R.; Su, Q.; Han, W.; Wang, P. Analysis on Energy Conversion of Screw Centrifugal Pump in Impeller Domain Based on Profile Lines. Adv. Mech. Eng. 2013, 5, 512523. [Google Scholar] [CrossRef]
- Zhang, X.L.; Hu, S.; Shen, Z.; Wu, S.; Li, K. Research on Energy Conversion Mechanism of Rotodynamic Pump and Design of Non-Overload Centrifugal Pump. IOP Conf. Ser. Mater. Sci. Eng. 2016, 129, 012003. [Google Scholar] [CrossRef]
- Liu, Y.; Tan, L. Method of C Groove on Vortex Suppression and Energy Performance Improvement for a NACA0009 Hydrofoil with Tip Clearance in Tidal Energy. Energy 2018, 155, 448–461. [Google Scholar] [CrossRef]
- Miao, S.; Yang, J.; Shi, F.; Wang, X.; Shia, G. Research on Energy Conversion Characteristic of Pump as Turbine. Adv. Mech. Eng. 2018, 10, 1687814018770836. [Google Scholar] [CrossRef]
- Miao, S.; Zhang, H.; Shi, F.; Wang, X.; Ma, X. Study on Energy Conversion Characteristics in Volute of Pump as Turbine. Fluid Dyn. Mater. Process. 2021, 17, 201–214. [Google Scholar] [CrossRef]
- Miao, S.; Zhang, H.; Zhang, J.; Wang, X.; Shi, F. Unsteady Flow Characteristics of Energy Conversion in Impeller of Centrifugal Pump as Turbine. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 1502–1511. [Google Scholar] [CrossRef]
- Zhang, J.; Tan, L. Energy Performance and Pressure Fluctuation of a Multiphase Pump with Different Gas Volume Fractions. Energies 2018, 11, 1216. [Google Scholar] [CrossRef]
- Zhang, J.; Fan, H.; Zhang, W.; Xie, Z. Energy Performance and Flow Characteristics of a Multiphase Pump with Different Tip Clearance Sizes. Adv. Mech. Eng. 2019, 11, 1687814018823356. [Google Scholar] [CrossRef]
- Shi, G.; Wang, S.; Xiao, Y.; Liu, Z.; Li, H.; Liu, X. Effect of Cavitation on Energy Conversion Characteristics of a Multiphase Pump. Renew. Energy 2021, 177, 1308–1320. [Google Scholar] [CrossRef]
- Shi, G.; Liu, Z.; Xiao, Y.; Wang, Z.; Luo, Y.; Luo, K. Energy Conversion Characteristics of Multiphase Pump Impeller Analyzed Based on Blade Load Spectra. Renew. Energy 2020, 157, 9–23. [Google Scholar] [CrossRef]
- Ji, L.; Li, W.; Shi, W.; Chang, H.; Yang, Z. Energy Characteristics of Mixed-Flow Pump under Different Tip Clearances Based on Entropy Production Analysis. Energy 2020, 199, 117447. [Google Scholar] [CrossRef]
- Jin, Y.; Zhang, D.; Song, W.; Shen, X.; Shi, L.; Lu, J. Numerical Study on Energy Conversion Characteristics of Molten Salt Pump Based on Energy Transport Theory. Energy 2022, 244, 122674. [Google Scholar] [CrossRef]
- Zhao, Z.; Song, W.; Jin, Y.; He, L. Numerical Study on Flow Stall and Kinetic Energy Conversion of Low-Specific-Speed Centrifugal Pump. Phys. Fluids 2023, 35, 044104. [Google Scholar] [CrossRef]
- Liu, Y.; Tan, L.; Hao, Y.; Xu, Y. Energy Performance and Flow Patterns of a Mixed-Flow Pump with Different Tip Clearance Sizes. Energies 2017, 10, 191. [Google Scholar] [CrossRef]
- Wang, L.; Lu, J.; Liao, W.; Guo, P.; Feng, J.; Luo, X.; Wang, W. Numerical Investigation of the Effect of T-Shaped Blade on the Energy Performance Improvement of a Semi-Open Centrifugal Pump. J. Hydrodyn. 2021, 33, 736–746. [Google Scholar] [CrossRef]
- Ye, D.; Lai, X.; Chen, J.; Zhai, F.; Wu, J.; Gou, Q. Fluid Energy Conversion Analysis in Hydraulic Channels of Reactor Coolant under Flow Coastdown Transient. Energy Rep. 2022, 8, 9232–9241. [Google Scholar] [CrossRef]



| Geometric Parameter | Work Unit | Numerical Value | |
|---|---|---|---|
| Design flow | Q | m3/h | 100 |
| Design speed | N | rpm | 3600 |
| Number of impeller blades | Z1 | (-) | 3 |
| Number of diffuser blades | Z2 | (-) | 11 |
| External diameter | D | mm | 161 |
| Impeller inlet angle | αh/αs | ° | 9.05/6 |
| Impeller outlet angle | βh/βs | ° | 27.05/24 |
| Inlet angle of diffuser | αh/αs | ° | 0 |
| Outlet angle of diffuser | βh/βs | ° | 35 |
| Parameters | Mesh 1 | Mesh 2 | Mesh 3 | Mesh 4 |
|---|---|---|---|---|
| Mesh number | 2,246,540 | 2,627,229 | 3,093,387 | 4,054,644 |
| Relative head | 1 | 0.9986 | 1.0023 | 1.0104 |
| Relative efficiency | 1 | 1.0052 | 1.0021 | 0.9976 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, M.; Shi, G.; Lv, W.; Peng, X.; Huang, Z. Effect of Flow on the Energy Conversion Characteristics of Multiphase Pumps Based on Energy Transport Theory. Water 2023, 15, 4188. https://doi.org/10.3390/w15234188
Tang M, Shi G, Lv W, Peng X, Huang Z. Effect of Flow on the Energy Conversion Characteristics of Multiphase Pumps Based on Energy Transport Theory. Water. 2023; 15(23):4188. https://doi.org/10.3390/w15234188
Chicago/Turabian StyleTang, Manqi, Guangtai Shi, Wenjuan Lv, Xiaodong Peng, and Zongliu Huang. 2023. "Effect of Flow on the Energy Conversion Characteristics of Multiphase Pumps Based on Energy Transport Theory" Water 15, no. 23: 4188. https://doi.org/10.3390/w15234188
APA StyleTang, M., Shi, G., Lv, W., Peng, X., & Huang, Z. (2023). Effect of Flow on the Energy Conversion Characteristics of Multiphase Pumps Based on Energy Transport Theory. Water, 15(23), 4188. https://doi.org/10.3390/w15234188









