Hydrodynamic Decontamination of Groundwater and Soils Using ZVI
Abstract
:1. Introduction
1.1. Fe0 Particle Size
1.2. Fe0 Catalysis
1.3. Contaminant Plumes
1.4. Permeability Reduction
1.5. Modelling
1.5.1. Contaminant Plume Availability
1.5.2. ZVI Operation
1.5.3. ZVI Definition
1.5.4. Significance of Iron Bacteria
1.6. Aquifer Contaminants
1.7. Reconstruction of the Aquifer Potentiometric Surface
1.7.1. Group 1 and 2 Plumes
1.7.2. Seawater Incursion
1.7.3. Group 4 Aquifers
1.7.4. Group 5 Contaminated Soils
1.8. Study Purpose
2. Materials and Methods
- Firstly, the formation of stationary hydrodynamic plumes (SHP) in both confined and unconfined aquifers. The issues associated with the advection–diffusion migration of pollutants [72] across the hydrodynamic boundaries of the SHP, due to chemical potential gradients, is not addressed in this study; the detailed modelling of the aquifer recharge using wells [73] associated with the periphery of the SHP is outside the scope of this study;
- Secondly, the formation of perched groundwater mounds (PGM) in soils located above an unconfined aquifer or an aquitard [74,75,76]. These stationary plumes (PGM) are designed to decontaminate part of the groundwater contained within an unconfined aquifer or soil. These groundwater mounds are created using a freshwater source. The PGM is used to dissolve salts (contaminant ions) within the soil, or an unconfined aquifer. These ions are then abstracted with the water, from the PGM, to allow for ion recovery using a surface located ZVI reactor, and for the appropriate disposal of the recovered pollutants.
- Appendix A—Process assumptions
- Stationary Hydrodynamic Plume Assumptions
- Example Stationary Hydrodynamic Plume
- Perched Groundwater Mound Assumptions
- Appendix B—Reaction Process Assumptions
- Confined or Unconfined Aquifer Treatment
- Stationary Groundwater Mound Treatment
- Appendix C—ZVI Formation
- Formation via an Fe3O4 Intermediary
- n-Fe0 Formation using Borohydrides
- n-Fe0 Formation using Dithionite or Hydrosulfite Ions (S2O42−)
- n-Fe0 Formation using Hydrazine
- n-Fe0 Formation using Organic Reductants
- Regeneration of n-Fe0
- Appendix D—Contaminant Removal Kinetic Models
- Adsorbent Models
- Appendix E—Contaminant Processing Assumptions
- Redox Remediation
- Appendix F—Reactor Assumptions;
- Appendix G—Creation of a Stationary Hydrodynamic Plume
- Appendix H—Formation of a Groundwater Mound
- Chemical Potential
- Standard Infiltration Groundwater Mound
- Vertically Static, Laterally Expanding Groundwater Mound
- Reconstructing a Perched Groundwater Mound to Remediate the Soil
- Modelling the Remediation of soil using a Groundwater Mound
- Appendix I—Arsenic Removal
- Unsupported n-ZVI
- Active Carbon (AC)-Supported n-ZVI (C0@n/m-Fe0)
- Biochar (BC)-Supported n-ZVI (C0@n/m-Fe0)
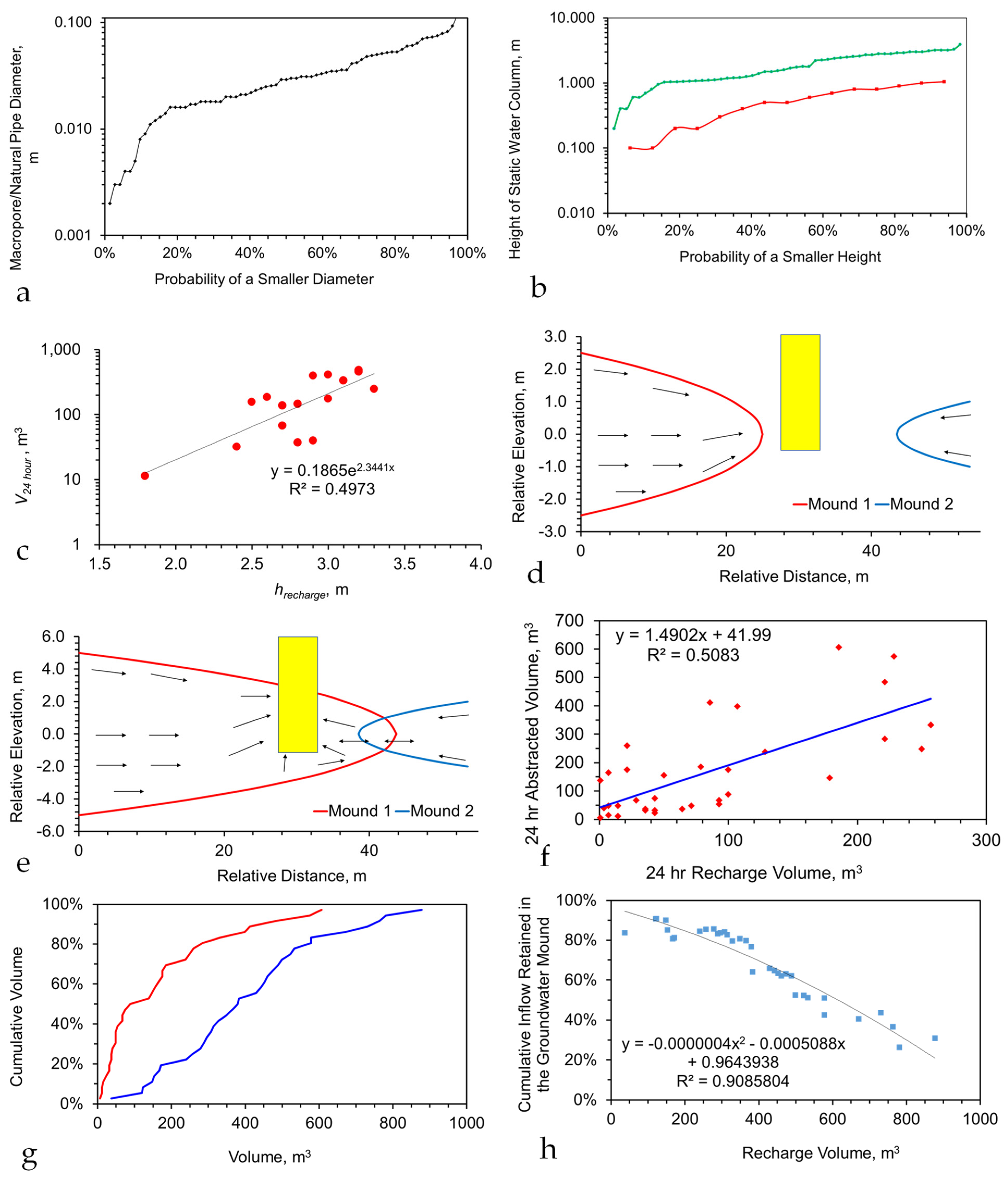
2.1. Data Sources
2.2. Hydrological Modelling
2.3. Aquifer Remediation Modelling
3. Modelling Remediation
3.1. Fe-Reaction, Adsorption and Redox Interpretations
- Assumption 1: ZVI reacts directly with a contaminant ion to remove it. Contaminant removal is by reduction, while the Fe0 is oxidized. The evidence for this interpretation is based on the observation that a soluble contaminant has been reduced to allow its precipitation. At the same time, the Fe0 has been oxidized to form an oxyhydroxide, e.g., [7]. There is no doubt that the two reaction start and end products occur. For example [7]:
- 2.
3.2. Redox Changes
- (i)
- Mode A: On the ZVI surface
- (ii)
- Mode B: In the hydration shell of the ZVI, where the Eh and pH conditions of the shell are intermediate between those in the water body and on the ZVI surface;
- (iii)
- Mode C: In the main water body.
3.2.1. pH Changes
3.2.2. ZVI Characteristics
- (i)
- Its zeta potential in water switches from a positive value to a negative value as the pH increases [100]. The pH (7.5 to 8.5) where this switch occurs (the iso electric point (IEP)) can decrease as the Pw increases. Pw = weight of Fe0 in the water, g L−1.
- (ii)
- For a specific Fe0 particle size and Pw, the product water pH increases with time to an equilibrium level [100]. For a specific reaction time, pH increases as Pw increases [100]. Consequently, in a continuous flow reactor containing a fixed volume of Fe0, the product water pH decreases as the water flow rate increases. i.e., pH is a function of the space velocity, SV:
- (iii)
- For a specific Fe0 particle size and Pw, the product water Eh decreases with time to an equilibrium level [100]. For a specific reaction time, Eh decreases as Pw increases [100]. Consequently, in a continuous flow reactor containing a fixed volume of Fe0, the product water Eh increases as the water flow rate increases. i.e., Eh is a function of the space velocity, SV. This, in turn, establishes that the PSE (Equation (1)) is also a function of SV.
- (iv)
- pH increases and Eh decreases for a specific value of Pw, as as (the particle surface area, m2 g−1) increases, and the particle size decreases. It is not unreasonable to expect that, for a particle size of <50 nm, as of >20 m2 g−1, and a Pw of >0.2 g L−1, the water Eh to reduce by <−0.8 V and the pH to increase by >3 units after approximately 15 min in a batch reactor [100].
3.2.3. Impact of Space Velocity in a Continuous Flow Reactor
3.2.4. Use of Fe0 to Produce Entrained n-Fe(a,b,c) Polymers
3.3. Remediation Rate Constant
3.4. Remediation of Immiscible Liquids (Oils)
3.5. Removal of Ionic Salts (Anions and Cations)
4. Applications
- Identify the contaminant plume and define its extent (Figure A1);
- Establish the nature of the aquifer, in terms of permeability, porosity and fluid flow characteristics for both the water and the contaminant;
- Define a target area, and gross rock (aquifer) volume, for the construction of the stationary hydrodynamic mound (Figure A1 and Figure A17), using a mixture of infiltration and abstraction wells;
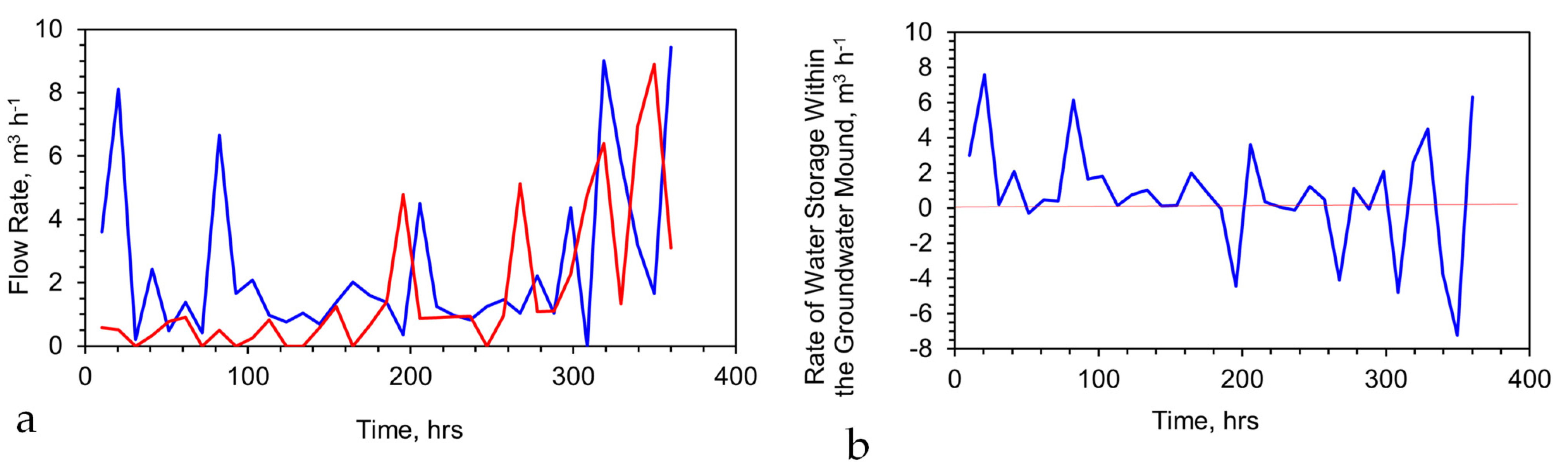
- Insert the required infiltration and abstraction wells (Figure A17). Start abstracting water from the central part of the mound, and reinjecting/infiltrating water around the periphery (Figure 3). The potentiometric surface across the area will reorientate, to create a stationary hydrodynamic mound, e.g., Figure 7. The hydrology of this change is summarized in Appendix A and Appendix I.
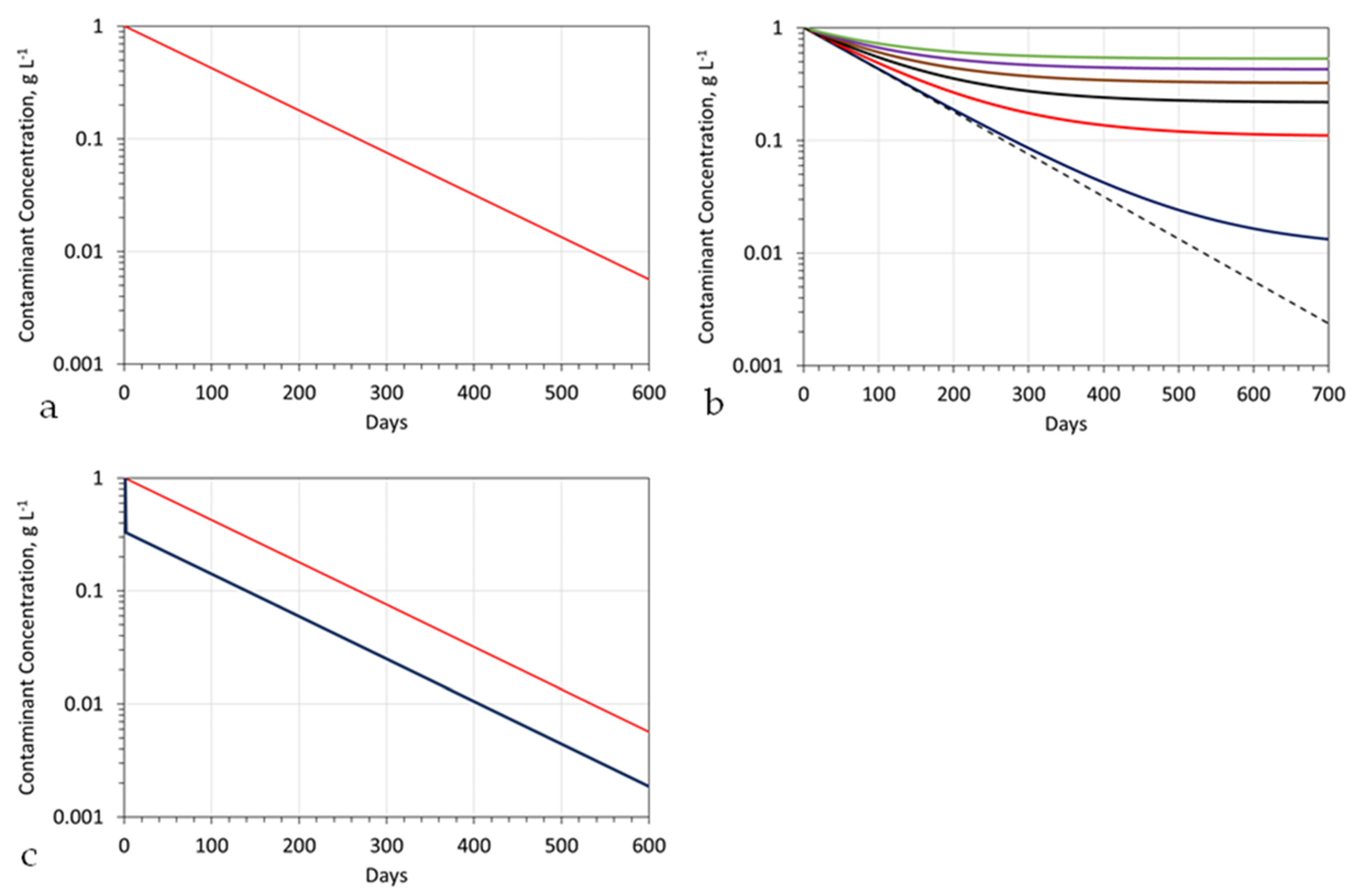
- An idealized mound structure is shown in Figure 7. The idealized mound has no water leakage from the aquifer, into the hydrodynamic mound. In an idealized environment the contaminant concentration will reduce to zero, within the mound, over a short time span (Figure A2a). In reality, there will always be some fluid leakage, from the wider aquifer into the mound. This leakage, will control the amount of remediation, which is possible (e.g., Figure A2b), at a specific aquifer location, when the contaminant, is a natural pollutant (e.g., As). When the contaminant is an anthropogenic pollutant, fluid leakage from the wider aquifer, will not affect the ability of the process to remove the pollutant. The expected pollutant removal profile, in this situation, is shown in Figure A2a.
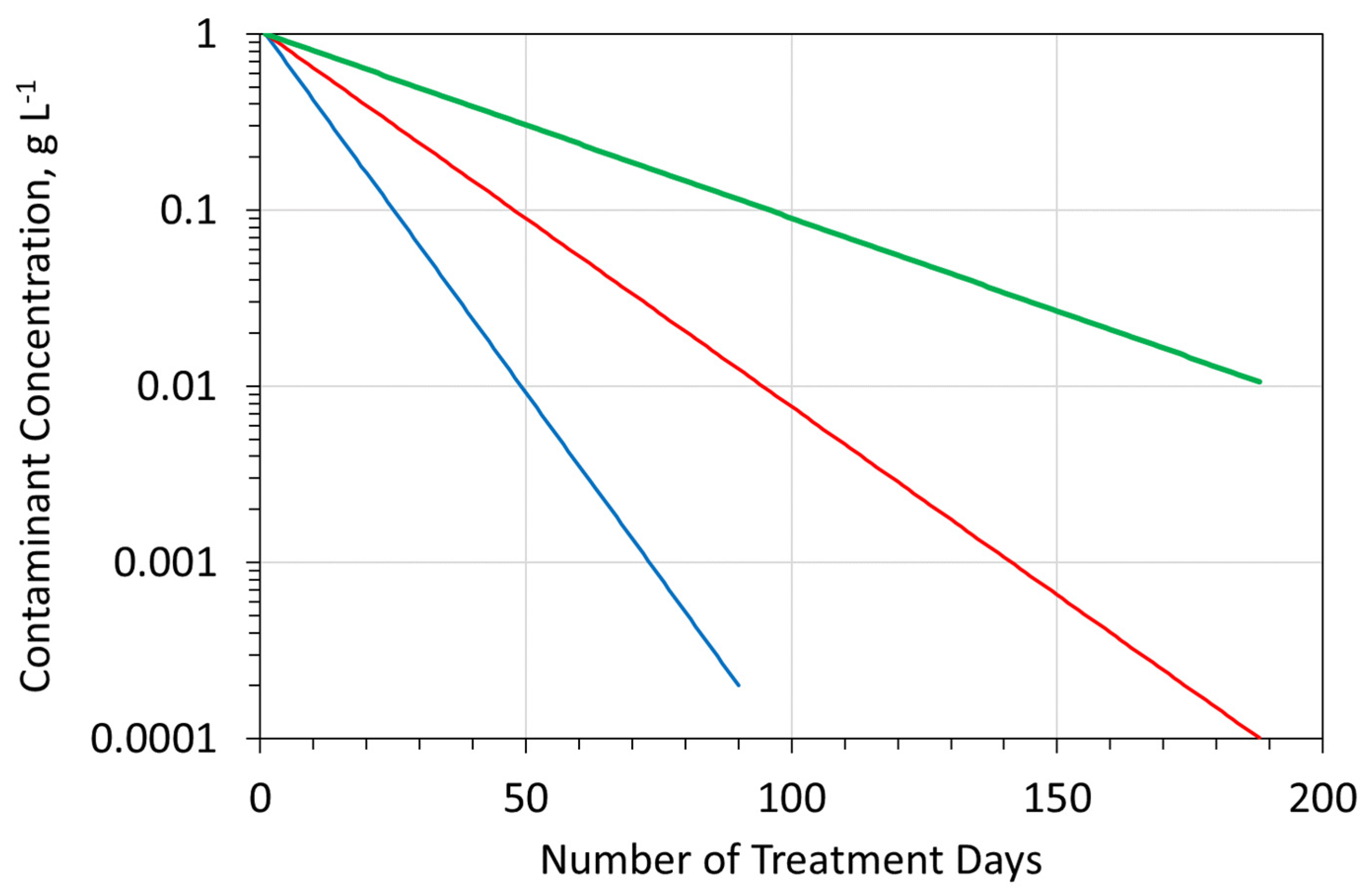
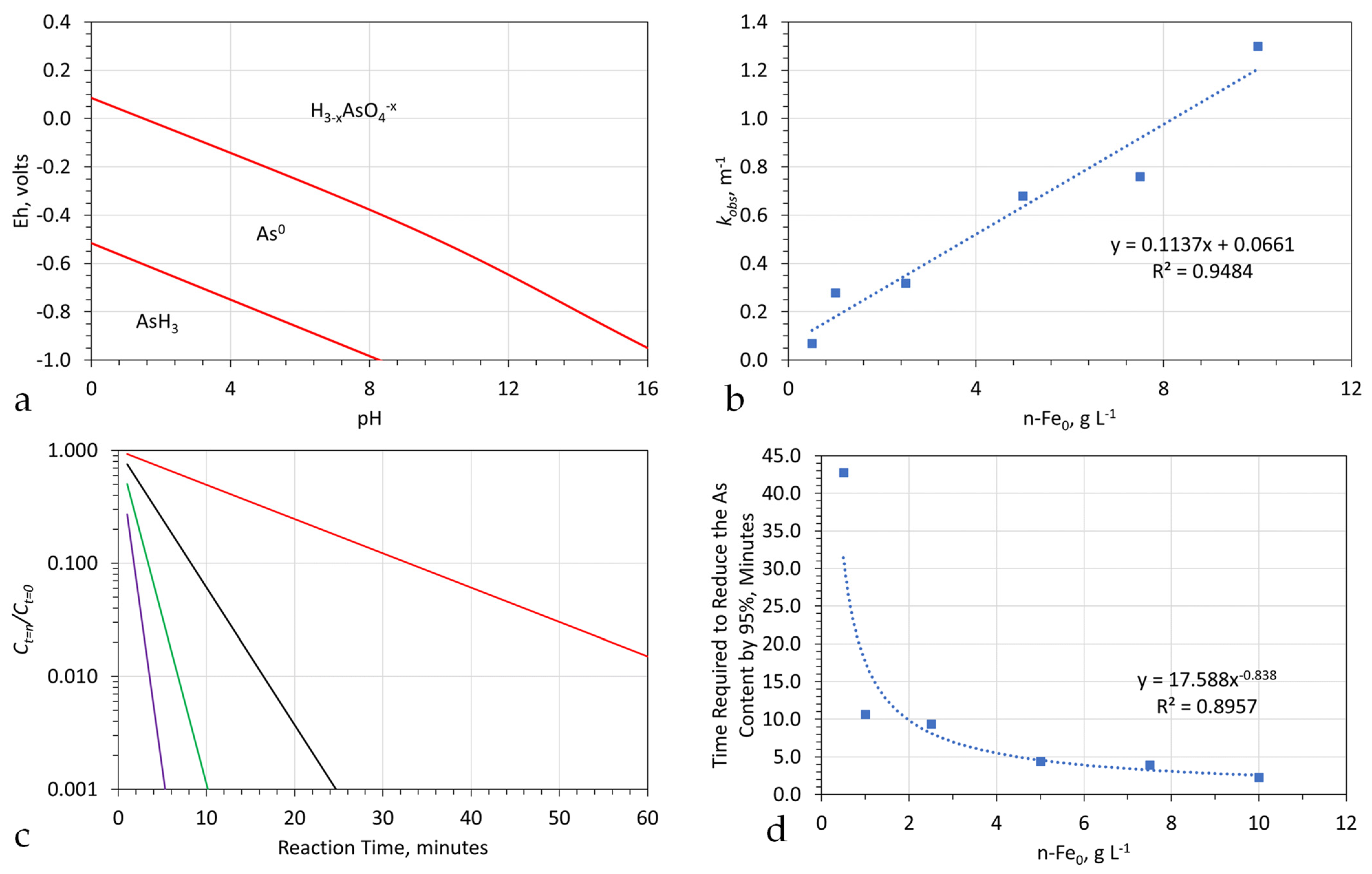
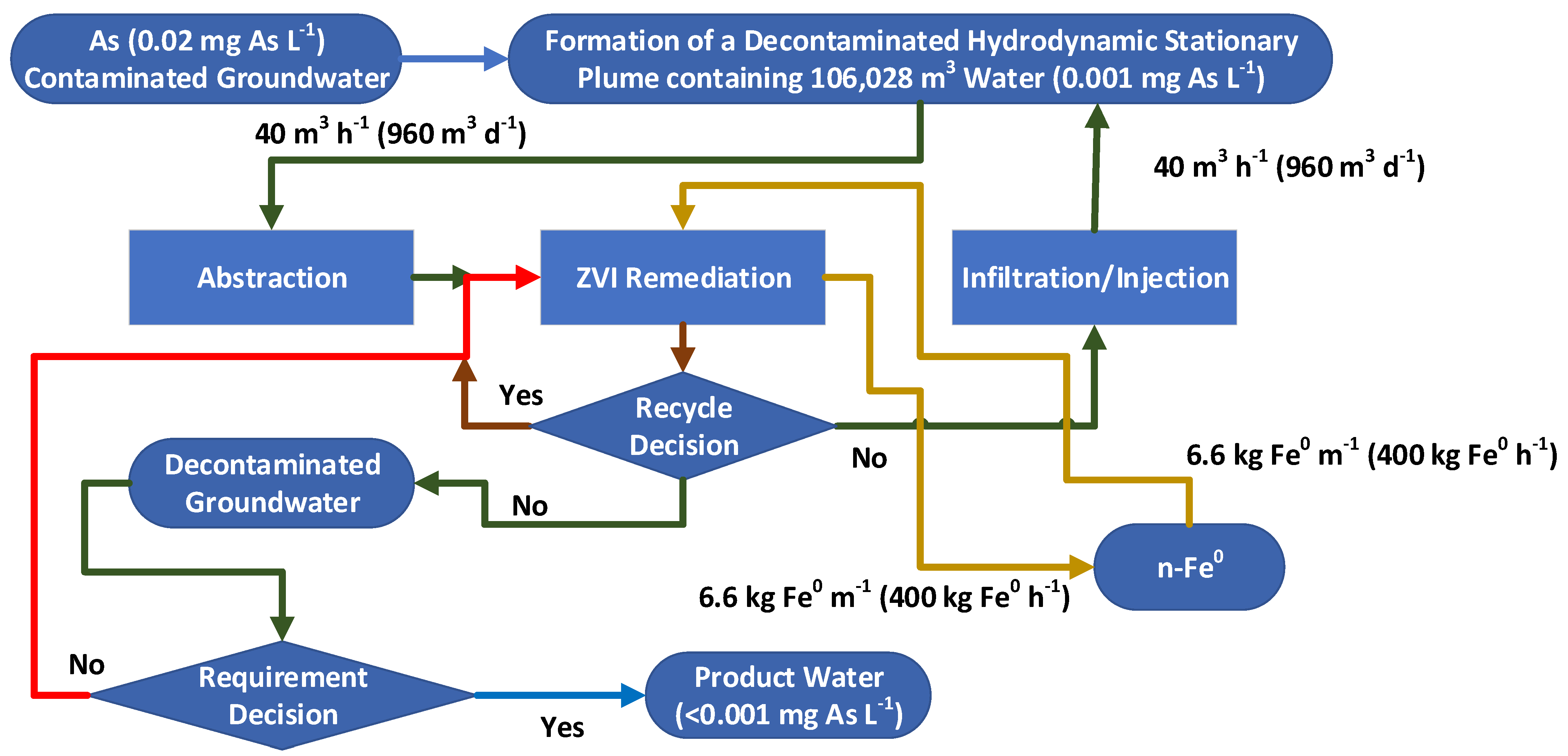
- The choice of ZVI (Appendix C) used in the reactor (Figure A6), and the reactor type selected will define the reactor size required, the amount of ZVI required, the Eh and pH of the product water (Figure A13 and Figure A14), and the amount of water, which can be processed by, a single batch of ZVI. For example, Appendix I examines (e.g., Figure A29) the removal of As, using three different forms of n-Fe0. The same level of removal, could be achieved, with each form of n-Fe0. However, the amount of n-Fe0 varies, by a factor of 10, between the different types of n-Fe0. The example, n-Fe0 formulations in Appendix I, indicate that to achieve the idealized outcome, illustrated in Figure A2a, the reactor, processing 40 m3 h−1, would require 400 kg n-Fe0 h−1, or 40 kg n-Fe0:AC h−1; or 80 kg n-Fe0:BC h−1. Using 400 kg n-Fe0:AC h−1, would significantly reduce the remediation time (e.g., Figure A2c). Therefore, the process economics and remediation duration, is impacted by the type Fe0 selected, and the amount used. These details are site specific.
- The redox modification within the reactor (Figure A13 and Figure A14) will result in the Eh of the stationary mound decreasing with time, while its pH will in-crease with time.
4.1. Example Aquifer Desalination
4.2. Groundwater Mound Decontamination
5. Conclusions
- Immiscible liquids, which are lighter than water, can be abstracted from the aquifer (or soil) using both a water flood and a surfactant flood approach. The liquids are either recovered or are processed in a surface reactor containing ZVI before the residual water is reinjected.
- The miscible liquids and dissolved ionic salts that are contained in contaminant plumes can be abstracted from an aquifer, by converting a part of the aquifer into a stationary plume. This results in both the sub-surface dilution of the contaminant and the surface-based ZVI remediation of the contaminant.
- The miscible liquids and dissolved ionic salts that are contained in naturally contaminated aquifers can be abstracted from an aquifer by converting a part of the aquifer to a stationary plume. This results in surface-based ZVI remediation of the contaminant, followed by the reinjection of the decontaminated water in order to produce a diluted contaminant level. Following a prolonged period of operation, the process will produce a decontaminated aquifer within the stationary plume.
- The miscible liquids and dissolved ionic salts that are contained in naturally (and anthropogenically) contaminated soils can be abstracted from a soil by converting a part of the soil to a perched groundwater mound. This results in the surface-based ZVI remediation of the contaminant, followed by the reinjection of the decontaminated water, which produces a diluted contaminant level. Following a prolonged period of operation, this process produces a decontaminated soil within the groundwater mound.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Process Assumptions
Appendix A.1. Stationary Hydrodynamic Plume in a Confined or Unconfined Aquifer
Appendix A.1.1. Soluble, or Miscible, Contaminant Plume
Appendix A.1.2. Creating a Hydrodynamic Stationary Plume
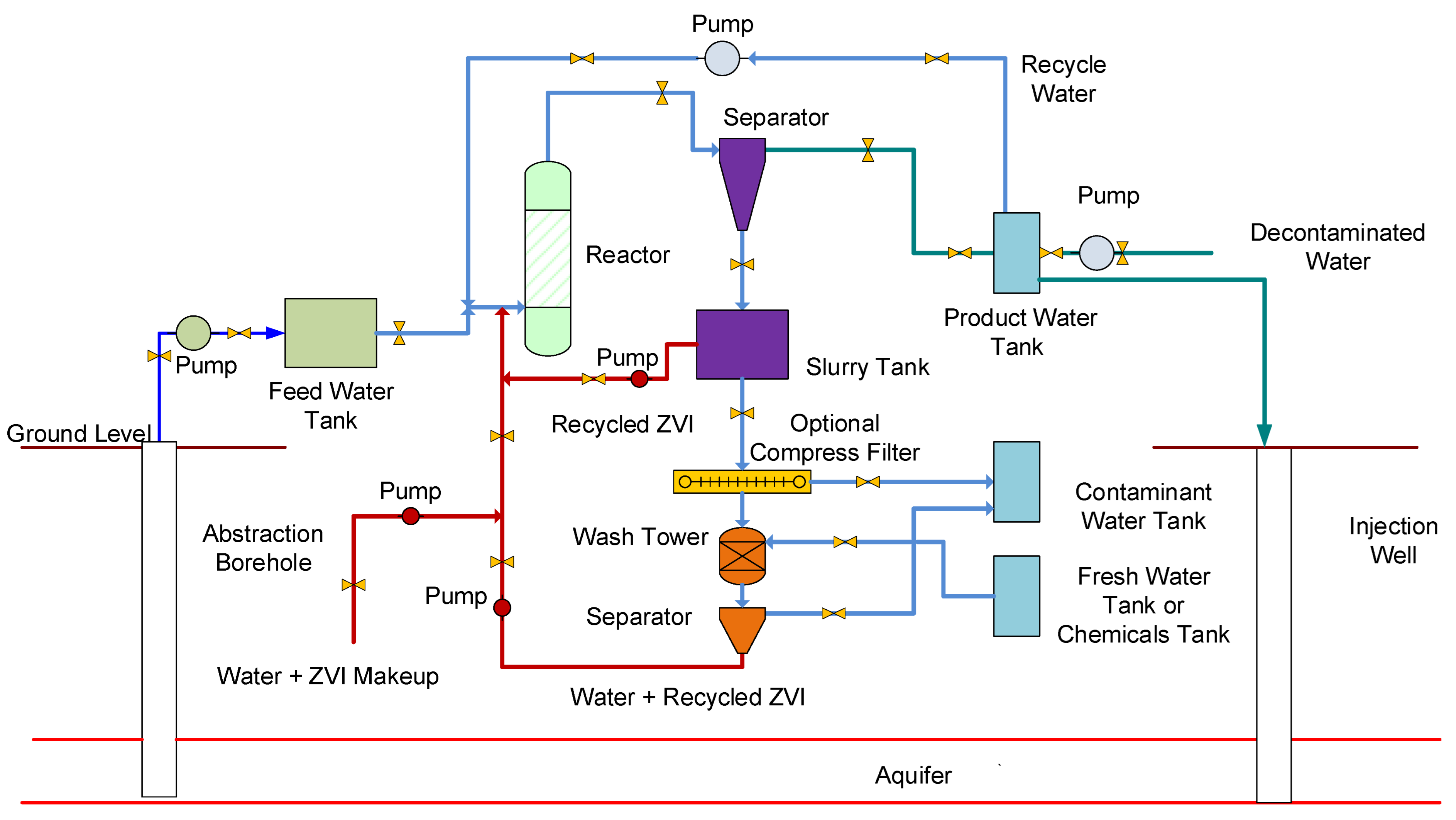
- A volume of water [C] is continuously abstracted from the abstraction well. This water is directed to a storage tank before being processed in a reactor.
- The water exiting the reactor is passed to a storage tank before being distributed and the volume (B) is injected, or infiltrated, back into the aquifer at a number of recharge points.
- The water within the stationary plume (E) comprises water infiltrating from the injection wells/infiltration wells (B), plus makeup water from the surrounding aquifer (A), plus irreducible water, Swir (D) within the aquifer, minus abstracted water (C). Sw = E − Swir (D) = mobile water saturation.
- For base case modelling, it is assumed that A = 0 m3 h−1, and C = 40 m3 h−1.
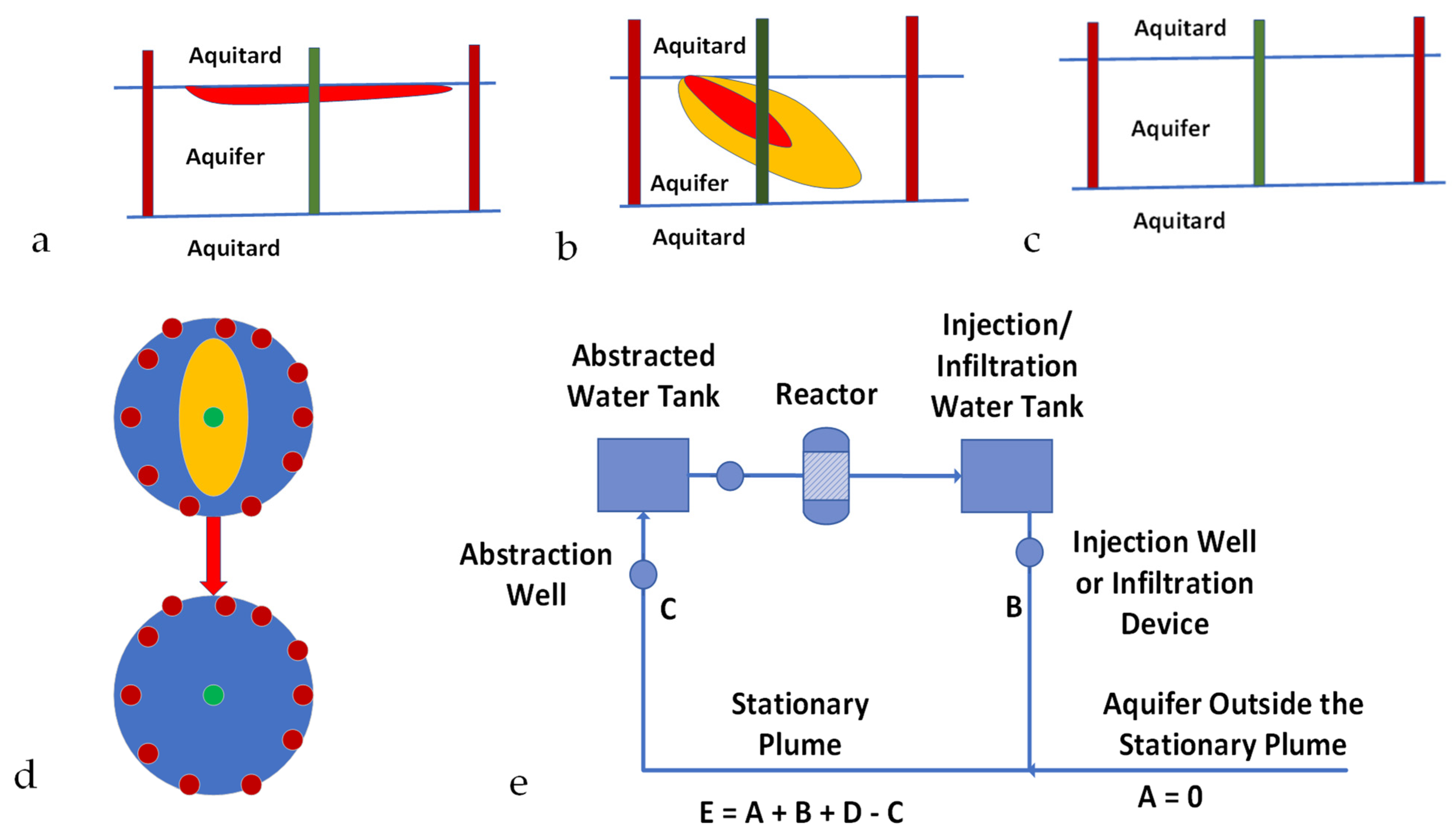
Appendix A.2. Example Operation of a Stationary Plume
Appendix A.3. Stationary Groundwater Mound Created in Soil
- The soil contains a contaminant that is soluble in water;
- The soil either overlies an aquitard, or has a horizontal permeability that is substantially greater than its vertical permeability.
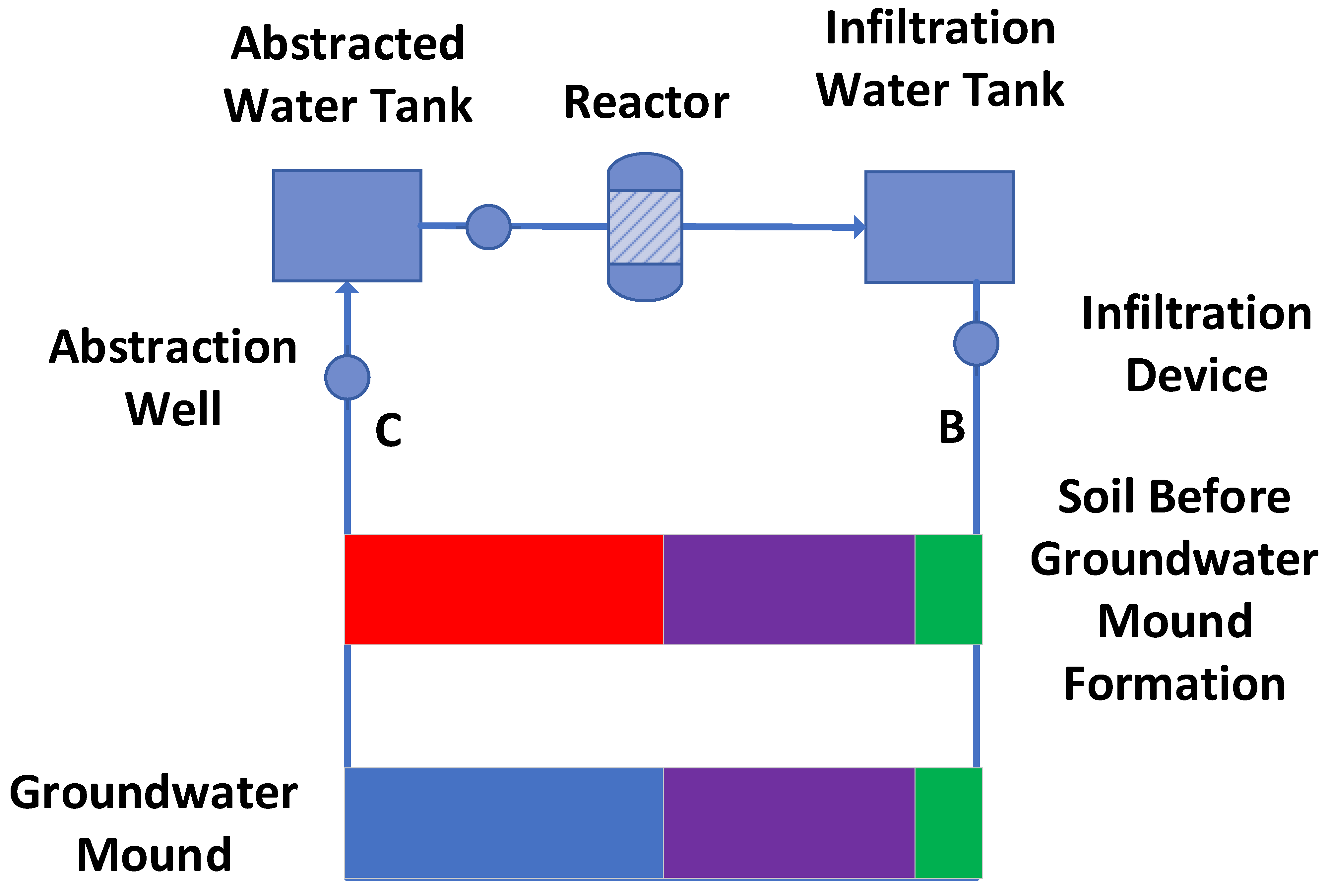
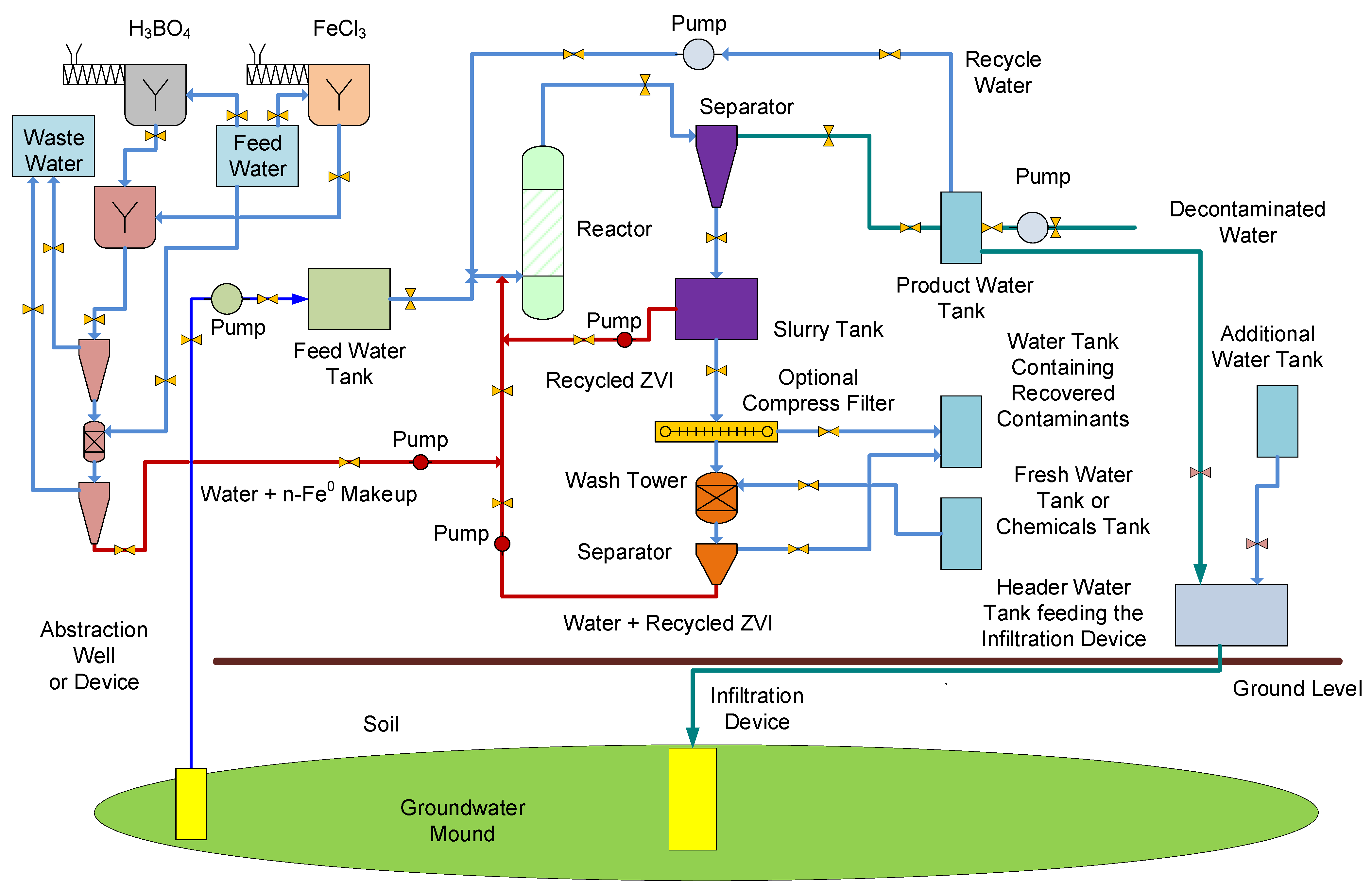
Water Mass Balance During Operation
- A volume of water [C] is continuously abstracted from the aquifer. This water is directed to a storage tank, before being processed in a reactor.
- The water exiting the reactor is passed to a storage tank before being distributed. A water volume [B] is infiltrated or injected back into the groundwater mound.
- Initially [B] > [C]. Following the formation of the groundwater mound, [C] will be approximate to [B]. [C] can, for short periods, exceed [B]. This situation occurs during periods when increases in permeability are associated with increases in ϕsoil, combined with decreases in Swir.
- The total volume of water placed in the groundwater mound will normally be more than the cumulative amount of water abstracted from the groundwater mound. This shortfall will be approximate to the pore volume, occupied by Sw within the groundwater mound.

Appendix B. Reaction Process Assumptions
Appendix B.1. Confined Aquifer, or Unconfined Aquifer, Treatment
Appendix B.2. Stationary Groundwater Mound Treatment
Appendix C. ZVI Formation
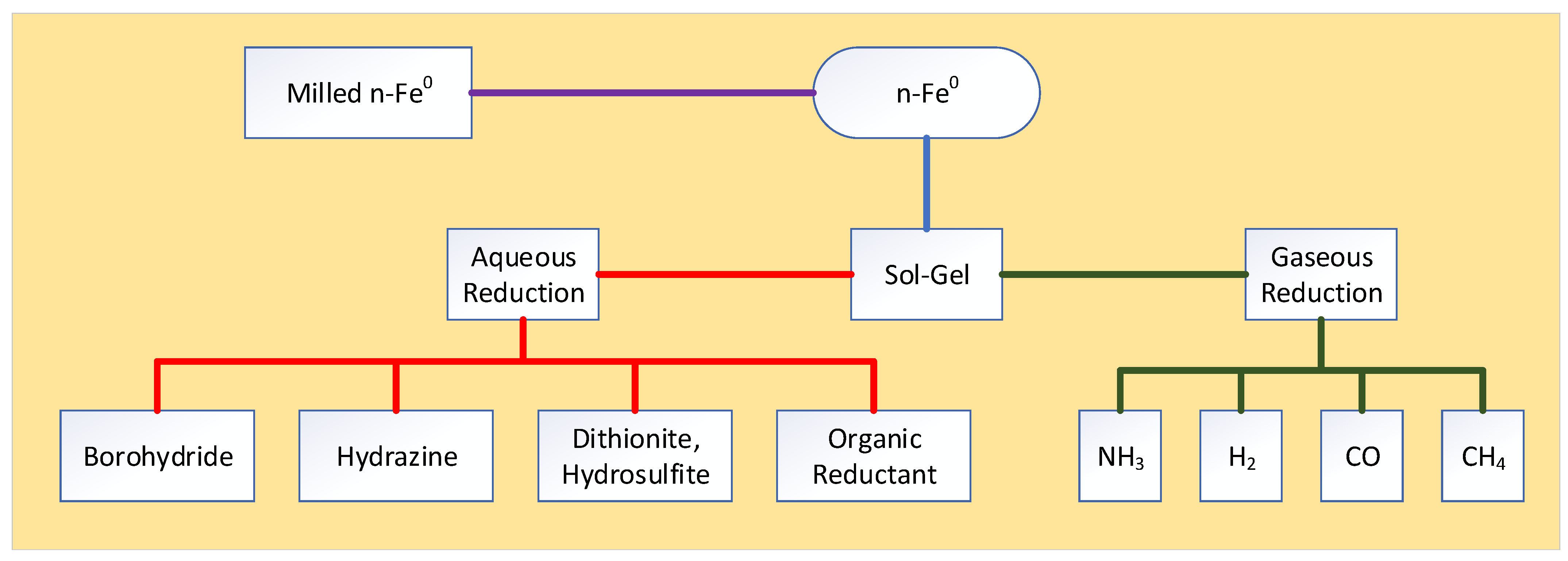
Appendix C.1. Approach 1—Formation via an Fe3O4 Intermediary
Appendix C.1.1. Reduction of n-Fe3O4 Using H and CO to Form n-Fe0
Appendix C.1.2. Methodology Variants
Appendix C.2. Approach 2—n-Fe0 Formation Using Borohydrides
Appendix C.2.1. Basic Construction of Unsupported n-Fe0
KR100975822B1 Manufacturing Method
US20070022839A1 Manufacturing Method
Appendix C.2.2. Active Carbon Supported n-Fe0 [C0@Fe0]
Appendix C.2.3. Biochar Supported n-Fe0
Appendix C.3. Approach 3—n-Fe0 Formation Using Dithionite or Hydrosulfite Ions (S2O42−)
US Patent US8283034B2
Appendix C.4. Approach 4—n-Fe0 Formation Using Hydrazine
Appendix C.5. Approach 5—n-Fe0 Formation Using Organic Reductants
Appendix C.5.1. Canadian Patent CA2728987C
- A metal ion solution is created from ferric chloride (FeCl3), ferrous sulfate (FeSO4), ferric nitrate (Fe(NO3)3, a metal chelate, Fe(III)-EDTA, Fe(III)-citric acid, Fe(III)-EDDS, Fe(I1)-EDTA, Fe(II)-citric acid, and Fe(II)-EDDS);
- An organic reductant solution is created from one or more of the following: tea extract, green tea extract, coffee extract, lemon balm extract, sorghum bran, sorghum bran extract, polyphenolic flavonoid, flavonoid, flavonol, flavone, flavanone, isoflavone, flavans, flavanol, anthocyanins, proanthocyanins, carotenoids, catechins, quercetin, and rutin;
- The metal ion solution is combined with the organic reductant and the plant-based surfactant, in order to produce n-Fe0 particles (20–250 nm);
- A plant-based surfactant is added to the solution containing the n-Fe0 to provide an activated (cationic or anionic) coating to the n-Fe0 particles. The surfactant is selected from one or more of the following: castor oil, coca oil, coconut oil, soy oil, cotton seed oil, naturally occurring plant oil, ethoxylated corn oil, ethoxylated palm oil, ethoxylated soybean oil, ethoxylated castor oil, ethoxylated coconut oil, polyoxyethylene castor oil, polyethylene glycol castor oil, ethoxylated coconut fatty acid, polyethylene glycol ester of coconut fatty acid, ethoxylated coconut oil fatty acid, polyethylene glycol monoester of coconut oil fatty acid, polyethylene glycol monococonut ester, ethoxylated coca oil, ethoxylated coco fatty acid, polyethylene glycol cocoate, polyethylene glycol monococoate, polyethylene glycol monococonut ester, monococoate polyethylene glycol, monococonut oil fatty acid ester of polyethylene glycol, polyoxyethylene monococoate, polyethylene glycol cocamide, polyethylene glycol coconut amide, polyoxyethylene coconut amide, amidified ethoxylated coconut fatty acid, ethoxylated monoethanolamide of a coconut oil fatty acid, yucca extract, soapwood extract, or extracts of other plants that produce saponins.
Appendix C.5.2. US Patent US7963720B2
- A packed bed reactor containing ASTM 20/30 sand is created. The specification example uses a column 3 m long and 0.3 m in diameter (containing 0.21 m3 sand). The expected pore volume is around 0.1 m3 (100 L);
- A 0.1 M iron ion solution of Fe(NO3)3 is created;
- A plant extract is created in deionized water, by heating dried green tea or dried lemon balm leaves to 80 °C;
- The two liquids are injected at a rate of 0.15 cm3 m−1 (each, 0.3 cm3 m−1) into the base of the sand column;
- The n-Fe0 is present in the water within the sand column, and in the product water produced from the sand column;
- The recovered particles can be coated with an organic polymer by mixing the solution containing the n-Fe0 with a solution containing the organic polymer.
Appendix C.5.3. Chinese Patent CN106077624B
- A solution is made of FeSO4, plus the poloxamer (e.g., poloxamer F68, poloxamer F108 and poloxamer F127);
- A second solution is made using either a borohydride or a green tea extract solution, made by soaking tea leaves in water;
- The reductant solution is added to the first solution, to precipitate the formation of PF-nZVI;
Appendix C.5.4. Chinese Patent CN112755963A
- A mixed solution of green tea extract, sodium alginate, and ferrous sulphate is formed. This contains green tea n-Fe0 (GT-nFe0);
- Calcium chloride is added to the solution to precipitate the formation of calcium alginate (CA). This produces GT-nFe0@CA particles. The product is magnetic, does not degrade easily, and can be used to process multiple batches of water.
Appendix C.5.5. Chinese Patent CN109967024B
- A solution of iron sulphate is created;
- A reductant solution of green tea extract plus vitamin C is created;
- The reductant solution is added to the solution containing Fen+ ions to precipitate n-Fe0.
Appendix C.5.6. Chinese Patent CN113477214A
- A solution of green tea text extract is created;
- Its pH is adjusted into the range 6 to 7 using NaOH;
- The residual plant material is carbonized to obtain a residual carbon;
- A ferric salt solution is created;
- The ferric salt solution, green tea extract and the residual carbon are mixed to produce a green n-Fe0-based biomass suspension.
Appendix C.6. Regeneration of n-Fe0
Appendix C.6.1. Gaseous Reduction
Appendix C.6.2. Acidification and Regeneration
Appendix D. Contaminant Removal Kinetic Models
- All published data is normalized to a multi-train plant processing 40 m3 h−1 for the treatment of a stationary plume in an aquifer or unconfined aquifer, or 4 m3 h−1 for the treatment of a stationary groundwater mound in soil;
- Where sufficient data is available, the first order rate constant is determined as a function of ZVI concentration, g L−1. The assumption made [93] is as follows:
Appendix E. Contaminant Processing Assumptions
- Removed by an equilibrium redox reaction [165,166,167,168], when the n-Fe0 adjusts the pH and Eh of the water to favor the precipitation of the pollutant, as one of a hydroxide, oxide, carbonate, sulphate, metal, or non-metal [92]. The precipitate is either entrained in the water or is physically adsorbed on the n-Fe0 particle surface.
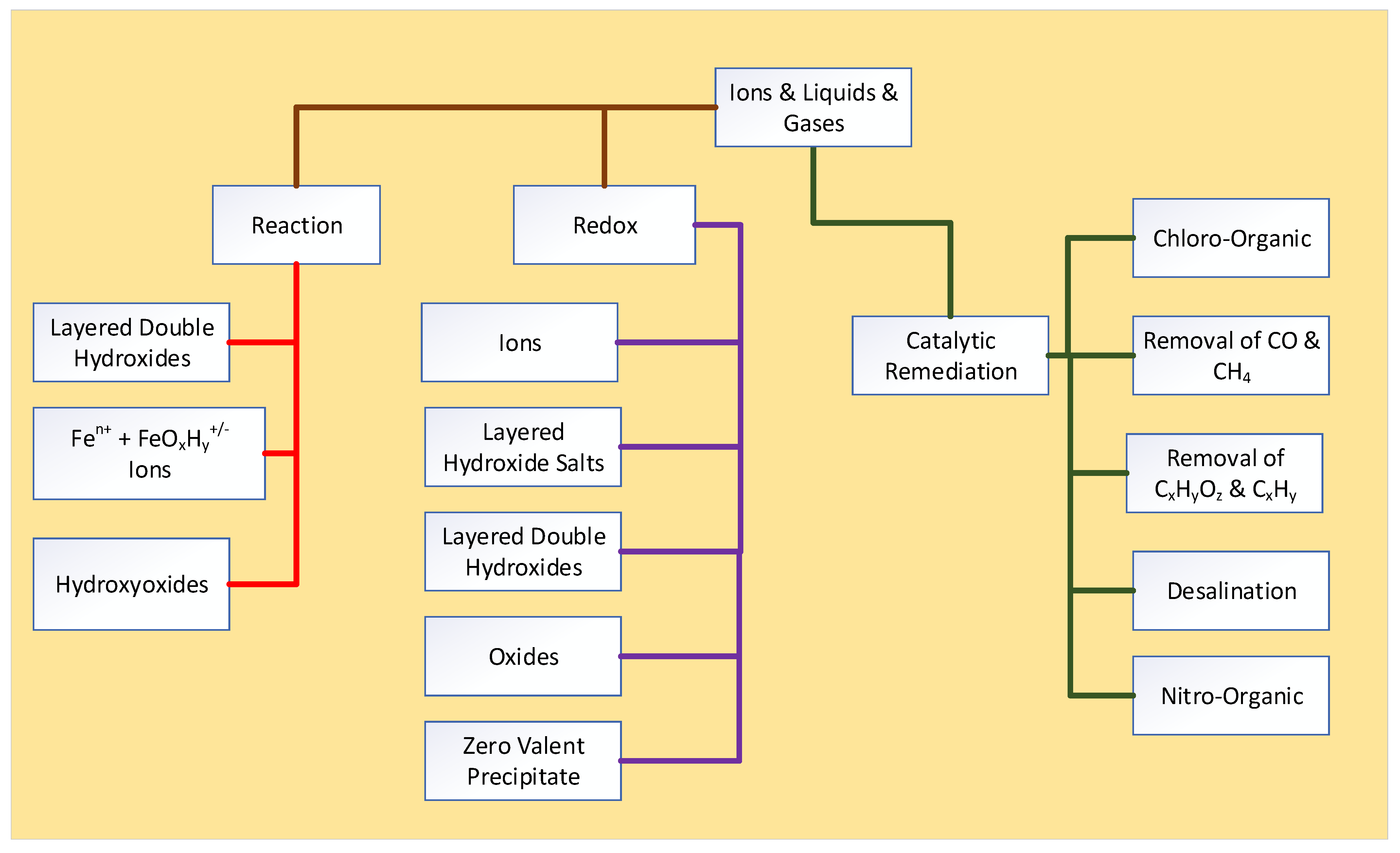
Appendix E.1. Redox Remediation
pH Changes Resulting from the Presence of Fe0
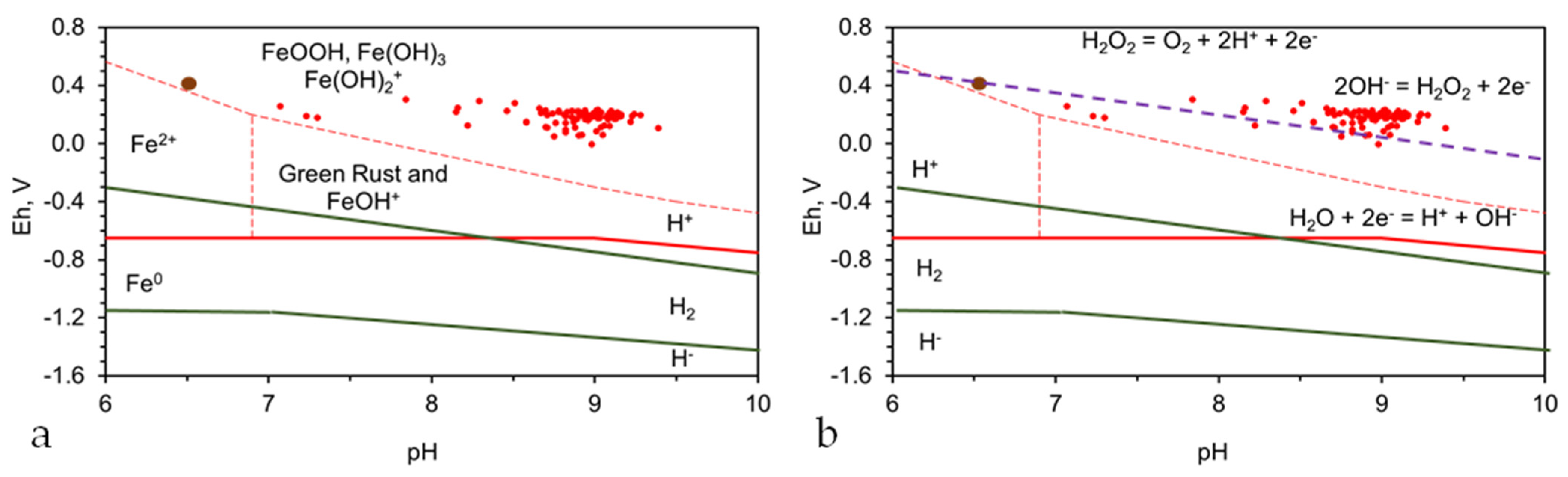
- The Fe0 surface and the water body are in hydrogen stability zone 0;
- The water body is located within the 2OH− = H2O2 + 2e− = O2 + 2H+ + 2e− redox fence zone. Consequently, some of the contaminants within the water may be remediated using a Fenton Type of Reaction.
- Polonium: Po0 will be expected to precipitate on the Fe0 (Figure A11a);
- Tellurium: Te0 will be expected to precipitate on the Fe0 (Figure A11b);
- Selenium: Se0 will be expected to precipitate on the Fe0 (Figure A11c);
- Bismuth: Bi0 will be expected to precipitate on the Fe0 and Bi(OH)3 within the water body (Figure A11d);
- Antimony: Sb0 will be expected to precipitate on the Fe0 (Figure A11e);
- Arsenic: As0 will be expected to precipitate on the Fe0 (Figure A11f);
- Nitrogen: Nitrates and nitrites will expect to reduce to NH4+ or NH4OH on contact with the Fe0 (Figure A11g);
- Lead: Pb0 will be expected to precipitate on the Fe0 (Figure A11h), and Pb(OH)2 and PbO2 within the water body (Figure A11h);
- Thallium: Tl0 will be expected to precipitate on the Fe0 (Figure A11i); the oxygenation of the residual water would be expected to precipitate the residual Tl+ ions as Tl(OH)3 (Figure A11i);
- Cadmium: Cd0 will be expected to precipitate on the Fe0 (Figure A11j) and Cd(OH)2 within the water body (Figure A11j);
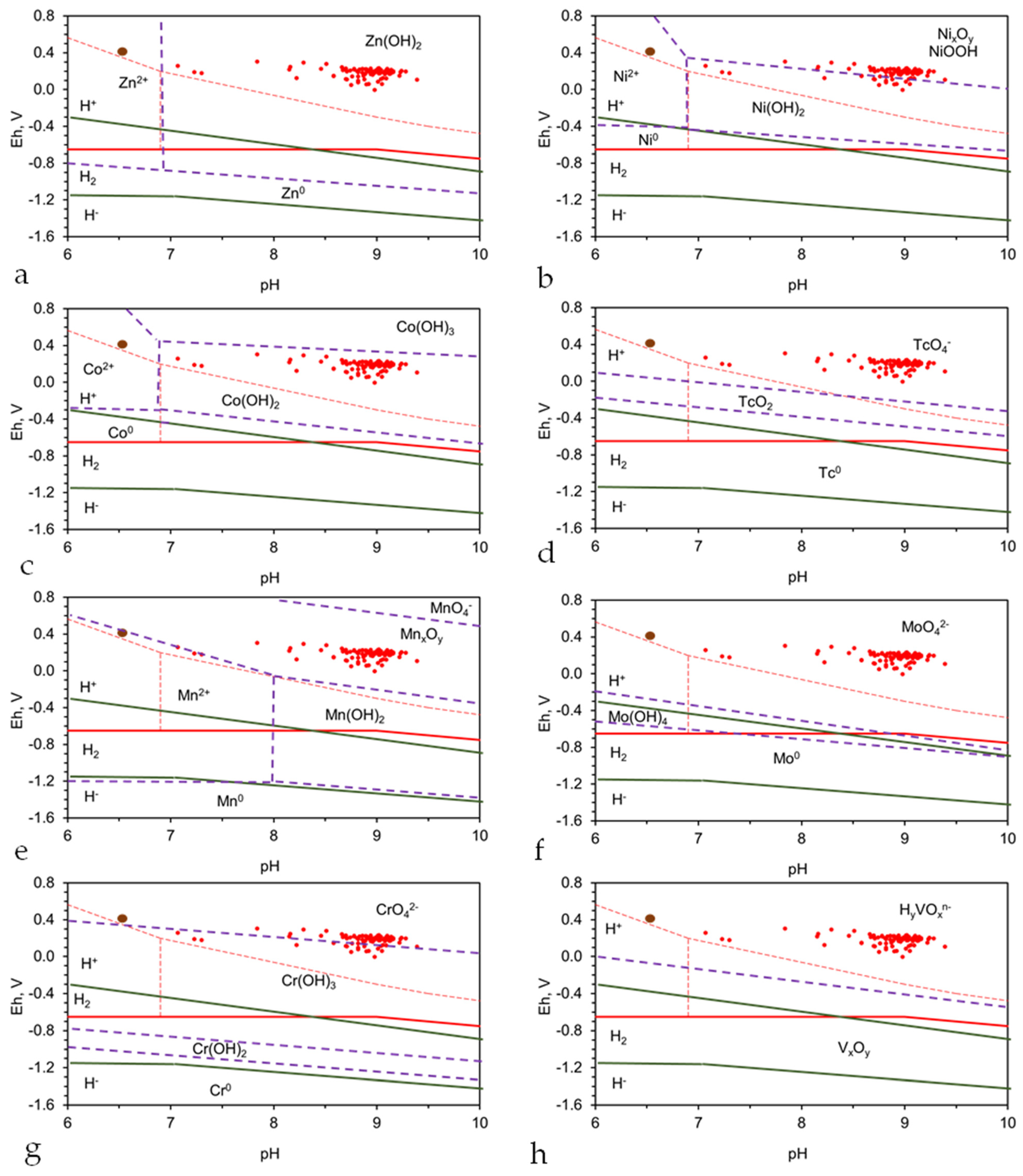
- Zinc: Zn(OH)2 will be expected to precipitate on the Fe0 and within the waterbody (Figure A12a);
- Nickel: Ni0 will be expected to precipitate on the Fe0 (Figure A12b), and on Ni(OH)2, Ni(OH)3, and NiOOH within the water body (Figure A12b);
- Cobalt: Co0 will be expected to precipitate on the Fe0 (Figure A12c) and Co(OH)2 within the water body (Figure A12c);
- Technetium: Tc0 will be expected to precipitate on the Fe0 (Figure A12d);
- Manganese: Mn(OH)2 will be expected to precipitate on the Fe0 (Figure A12e) and MnxOy within the water body (Figure A12e);
- Molybdenum: Mo0, or M(OH)4 will be expected to precipitate on the Fe0 (Figure A12f);
- Chromium: Cr(OH)3 will be expected to precipitate on the Fe0 and in the water (Figure A12g);
- Vanadium: VxOy will be expected to precipitate on the Fe0 (Figure A12h).

Appendix F. Reactor Assumptions
Appendix F.1. Continuous Flow, Fixed Bed Examples
Appendix F.1.1. Train A Construction
- Reactor: 0.5 m × 0.04 m O.D. ABS;
- ZVI: containing 0.5 kg of m-Fe0 powder (2 to 80 micron particle size);
- Operating time period: 1840 h of continuous operation;
- Average flow rate: 0.81 L kg−1 of Fe0 h−1;
- Water volume processed: 745 L train−1.
Appendix F.1.2. Train B Construction
- Reactor: 3 m × 0.04 m O.D. ABS;
- ZVI: containing 0.4 kg of Fe0 on a fibrous support;
- Operating time period: 1840 h of continuous operation;
- Average flow rate: 25 L kg−1 of Fe0 h−1;
- Water volume processed: 18,400 L train−1;
- The continuous flow experiment was repeated using a 3 m long, 0.04 m O.D; reactor containing 0.4 kg of Fe0 held on a fibrous support with 80% porosity;
- The reactor was operated for 1840 h continuously at an average flow rate of 0.81 L kg−1 of Fe0 h−1, processing >1500 m3 water t−1 Fe0.
Appendix F.1.3. Operational Results (Train A)
- The product water Eh was reduced relative to the feed water (Figure A13a) by an average of −221.6 mV (standard deviation = 61.8);
- The product water pH was increased relative to the feed water (Figure A13b) by an average of 1.87 units (standard deviation = 0.92); The principal Eh:pH change impacting the water for the initial cumulative 1100 m3 t−1 Fe0 was Eh;
- The average PSE change, relative to the feed water, was −0.118 V.
- The product water EC was increased initially due to the release of Fe ions (Figure A13c); after about 800 cumulative m3 t−1 had been produced, the EC of the product water started to decline below that of the feed water;
- The fixed-bed reactor was provided with a constant head of 1.3 m and a constant supply of feed water. The expected flow rate, based on particle size and head, was 12–16 m3 h−1 t−1. Initial declines over the first 140 h (and next 400 h) were reversed by particle agitation (Figure A13d). The flow rate decline after 900 h was due solely to the destruction of permeability due to the formation of Fe(OH)x minerals in the Fe0 bed. At the end of 1840 h, the particle bed was solid. This decline in the flow rate was associated with an increase in pH, a decrease in EC, and a decrease in Eh.
Appendix F.1.4. Operational Results (Train B)
- A higher flow rate and cumulative water volume processed is achievable, due to the higher permeability (and porosity) of the ZVI bed;
- The magnitude of the Eh and pH changes observed was lower than those observed in Figure A13, indicating that the change in Eh and pH is a function of the space velocity, SV (where the SV = Volume of water processed per unit time per unit volume or weight of ZVI contained in the reactor).


Appendix F.2. Significance of the Operational Results
Appendix F.2.1. PRB Formed Using Injected n-Fe0

General Porosity Closure Mechanisms

Appendix F.2.2. PRB Formed Using Fe0
Appendix G. Creation of a Stationary Hydrodynamic Plume
- The aquifer parameters, depth to base (and top if confined), potentiometric surface, contaminant plume location, contaminant plume chemistry, chemistry of the surrounding water, aquifer porosity, and aquifer permeability;
- The proposed abstraction well details, including the negative head (or pressure) created by the well;
- The proposed injection well or infiltration device details, including expected positive head (or pressure during recharge);
| Item | Parameter | Value |
|---|---|---|
| 1 | Aquifer Thickness, m | 5 |
| 2 | Aquifer Porosity | 30% |
| 3 | Aquifer Permeability, m3 m−2 s−1 Pa−1 | |
| 3a | Vertical (z) direction | 5 × 10−6 |
| 3b | Horizontal (x) direction | 5 × 10−6 |
| 3c | Horizontal (y) direction | 5 × 10−6 |
| 4 | Stationary plume radius, m | 150 |
| 5 | Gross Rock volume within the plume, m3 | 353,429 |
| 6 | Net to Gross Ratio for the aquifer | 1 |
| 7 | Saturations | |
| 7a | Irreducible Water Saturation | |
| 7aa | Tixier Model | 30.19% |
| 7ab | Timur Model | 3.66% |
| 7ac | Coates Dumanoir Model | 28.70% |
| 7ad | Assumed for Modelling | 30.00% |
| 7b | Reducible Water Saturation | 70.00% |
| 8 | Total Mobile Water volume, m3 | 74,220 |
| 9 | Ground area covered by the stationary plume, ha | 7.07 |

Appendix H. Formation of a Groundwater Mound
Appendix H.1. Chemical Potential
Appendix H.2. Standard Infiltration Groundwater Mound
Appendix H.3. Vertically Static, Laterally Expanding Groundwater Mound
Modelling the Upper Surface of the Mound
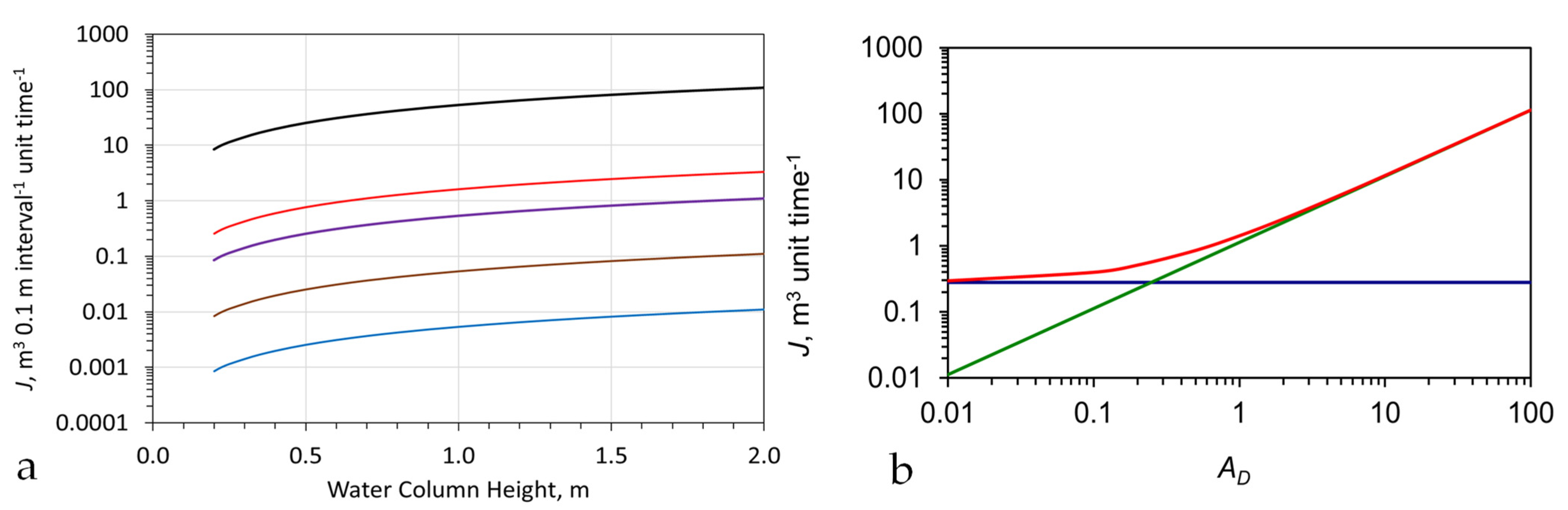
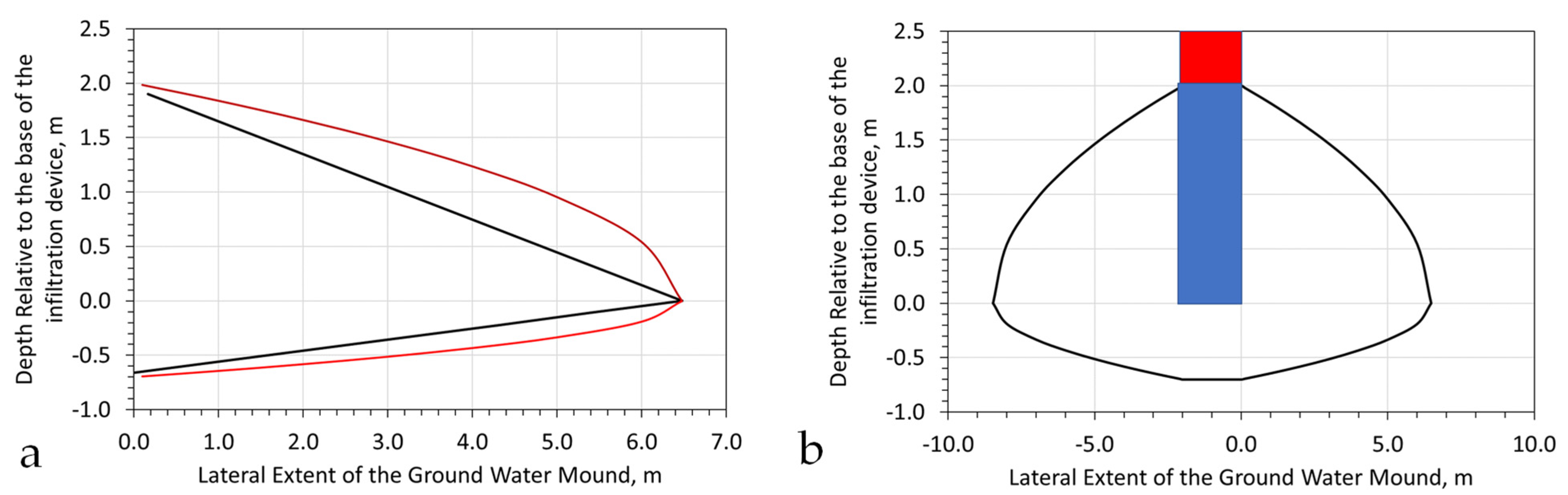
Appendix H.4. Reconstructing a Perched Groundwater Mound to Remediate the Soil
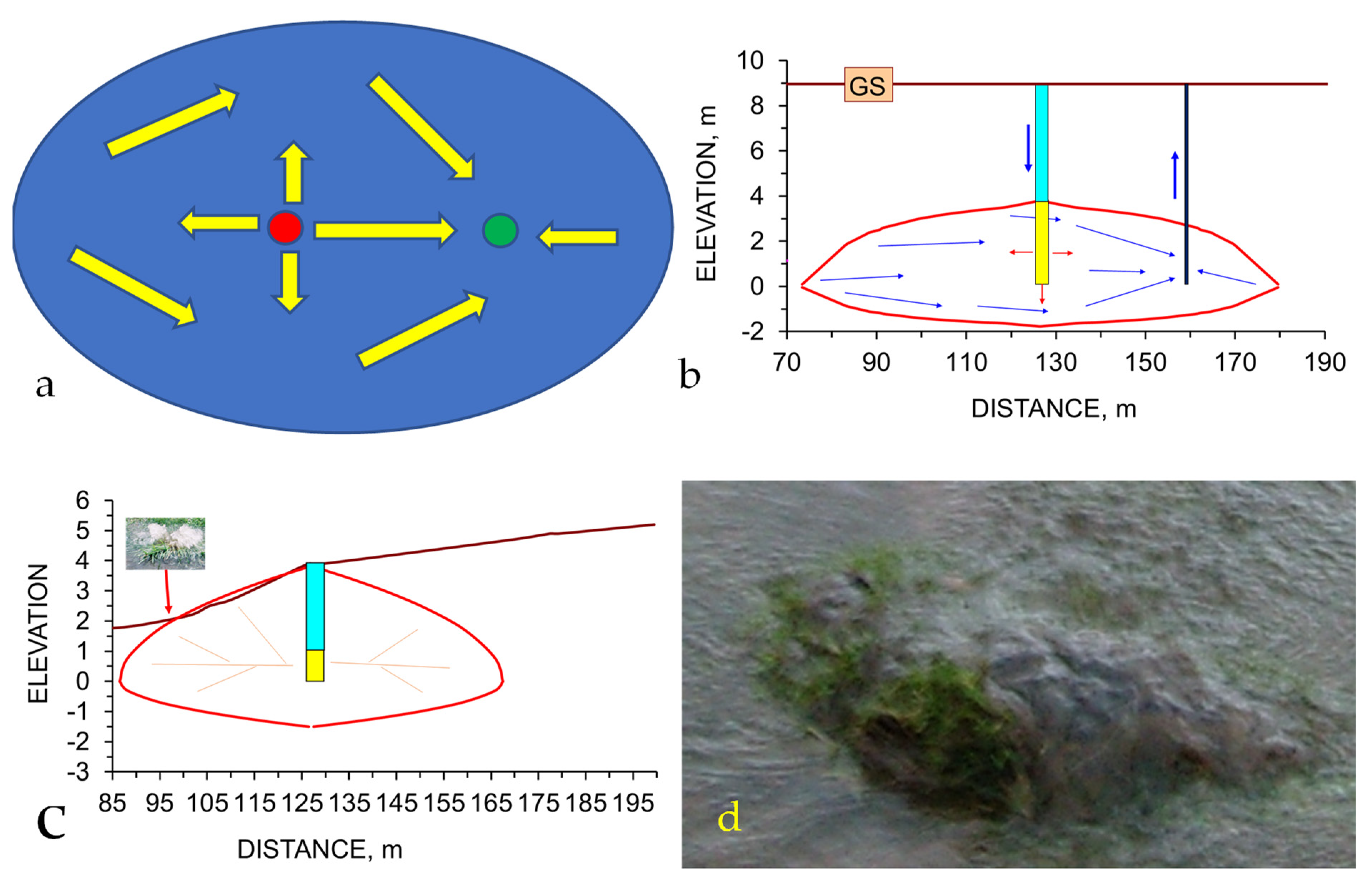
- The local sediment permeability will dictate the parameters of the perched groundwater mound. Its rate of descent is a function of the vertical permeability.
- Infiltration devices are normally designed to discharge the sequestered water, primarily in a z-direction, where the vertical flow rate is as follows:
Appendix H.5. Conceptual Example of Operation
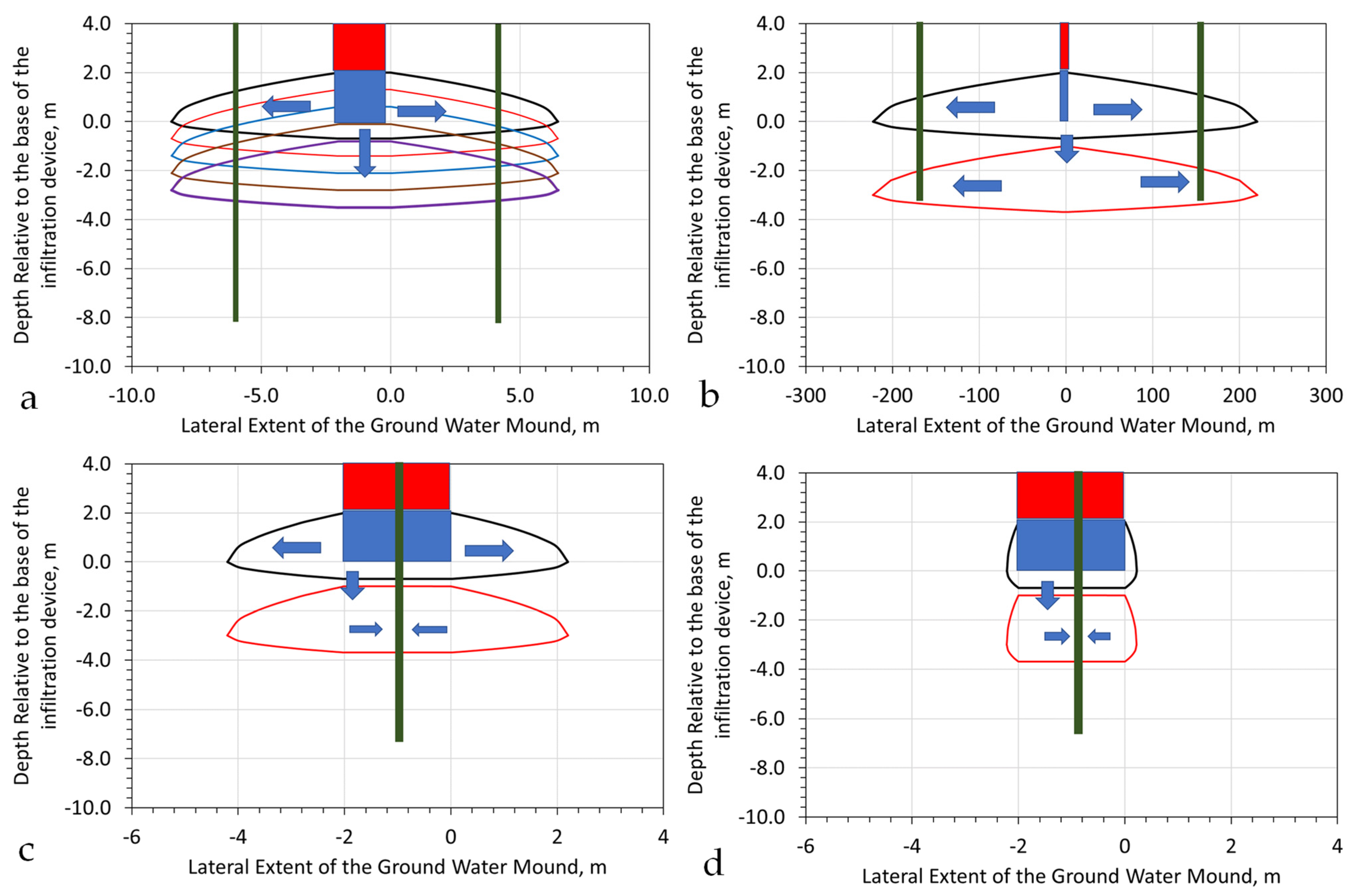
Appendix H.6. Modelling the Remediation of Soil Using a Groundwater Mound
- Placement of an abstraction borehole, or boreholes, at appropriate locations around the margins of the groundwater mound;
- Placement of an abstraction (infiltration) device located at the feather edge of the groundwater mound (Figure A24a). This device is designed to reorientate the flowlines within the groundwater mound towards the infiltration device. This results in the water level rising in the abstraction (infiltration) device (Figure A24b).

- Beryllium, Aluminum, Thorium, Uranium, Zirconium, Hafnium, Rhodium, Gallium—removable provided the groundwater mound has a pH of <3/4;
- Magnesium—removable provided the groundwater mound has a pH of <10;
- Cerium, Dysprosium, Holmium, Terbium, Gadolinium, Europium, Samarium, Scandium, Yttrium, Lanthanum, Praseodymium, Neodymium, Promethium, Thulium, Lutetium, Ytterbium, Erbium, Manganese, Iron, Cobalt, Nickel, Copper, Silver, Zinc, Cadmium, Indium, Lead, Bismuth—removable provided the groundwater mound has a pH of <7/8;
- Vanadium, Molybdenum, Antimony,—removable provided the groundwater mound has a pH of >5/6;
- Chromium, Sodium, Potassium, Lithium, Technetium, Rhenium, Thallium, Carbon, Arsenic, Phosphorous, Sulphur, Selenium, Tellurium, Fluoride, Chloride, Bromide, Iodide—no effective pH constraints.
Appendix I. Arsenic Removal
Appendix I.1. Unsupported n-ZVI
- Leakage volumes (A) into the hydrodynamic stationary plume (Figure A1) from the surrounding aquifer;
- The pH and Eh of the water entering and leaving the reactor (Figure A27);
- The reduction in site availability for the adsorption of As0 on the n-Fe0 following each usage if it is not regenerated following each use.

Appendix I.2. Active Carbon (AC) Supported n-ZVI (C0@n/m-Fe0)
- The initial stage (e.g., 0.3Yt [t0.5]−1 for t0.5 = <3) may relate to adsorption onto Fe0 or sequestration within the AC macropores.
- The second stage (e.g., 0.01Yt [t0.5]−1 + Yt = 0.9, for t0.5 = >3) may relate to adsorption within micro-pores and meso-pores.

Appendix I.3. Biochar (BC) Supported n-ZVI (C0@n/m-Fe0)
References
- Zhu, F.; Tan, X.; Zhao, W.; Feng, L.; He, S.; Wei, L.; Yang, L.; Wang, K.; Zhao, Q. Efficiency assessment of ZVI-based media as fillers in permeable reactive barrier for multiple heavy metal-contaminated groundwater remediation. J. Hazard. Mater. 2022, 424, 127605. [Google Scholar] [CrossRef] [PubMed]
- Medawela, S.; Indraratna, B.; Athuraliya, S.; Lugg, G.; Nghiem, L.D. Monitoring the performance of permeable reactive barriers constructed in acid sulfate soils. Eng. Geol. 2022, 296, 106465. [Google Scholar] [CrossRef]
- Thisani, S.K.; Kallon, D.V.V.; Byrne, P. Co-remediation of acid mine drainage and industrial effluent using passive permeable reactive barrier pre-treatment and active co-bioremediation. Minerals 2022, 12, 565. [Google Scholar] [CrossRef]
- Yang, H.; Liu, Q.; Hu, R.; Ptak, T.; Taherdangkoo, R.; Liu, Y.; Noubactep, C. Numerical case studies on long-term effectiveness of metallic iron based permeable reactive barriers: Importance of porosity heterogeneity of the barrier. J. Hydrol. 2022, 612, 128148. [Google Scholar] [CrossRef]
- Henderson, A.D.; Demond, A.H. Long-term performance of zero-valent iron permeable reactive barriers: A critical review. Environ. Eng. Sci. 2007, 24, 401–423. [Google Scholar] [CrossRef] [Green Version]
- Wilkin, R.T.; Puls, R.W.; Sewell, G.W. Long-term performance of permeable reactive barriers using zero-valent iron: Geochemical and microbiological effects. Groundwater 2003, 41, 493–503. [Google Scholar] [CrossRef]
- Lawrinenko, M.; Kurwadkar, S.; Wilkin, R.T. Long–term performance evaluation of zero-valent iron amended permeable reactive barriers for groundwater remediation—A mechanistic approach. Geosci. Front. 2022, 14, 101494. [Google Scholar] [CrossRef]
- Ahn, J.Y.; Kim, C.; Jun, S.C.; Hwang, I. Field-scale investigation of nanoscale zero-valent iron (NZVI) injection parameters for enhanced delivery of NZVI particles to groundwater. Water Res. 2021, 202, 117402. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Liu, W.; Cai, Z.; Han, B.; Qian, T.; Zhao, D. An overview of preparation and applications of stabilized zero-valent iron nanoparticles for soil and groundwater remediation. Water Res. 2016, 100, 245–266. [Google Scholar] [CrossRef] [Green Version]
- Galdames, A.; Ruiz-Rubio, L.; Orueta, M.; Sánchez-Arzalluz, M.; Vilas-Vilela, J.L. Zero-valent iron nanoparticles for soil and groundwater remediation. Int. J. Environ. Res. Public Health 2020, 17, 5817. [Google Scholar] [CrossRef]
- Su, C.; Puls, R.W.; Krug, T.A.; Watling, M.T.; O’Hara, S.K.; Quinn, J.W.; Ruiz, N.E. Travel distance and transformation of injected emulsified zerovalent iron nanoparticles in the subsurface during two and half years. Water Res. 2013, 47, 4095–4106. [Google Scholar] [CrossRef] [PubMed]
- Molin, J.; Valkenburg, J.; Seech, A.; Oesterreich, R.; Son, J. Long-term evaluation of an EHC injection permeable reactive barrier in a sulfate-rich, high-flow aquifer. Remediat. J. 2019, 29, 17–29. [Google Scholar] [CrossRef]
- Arnason, J.G.; Harkness, M.; Butler-Veytia, B. Evaluating the Subsurface Distribution of Zero-Valent Iron Using Magnetic Susceptibility. Groundw. Monit. Remediat. 2014, 34, 96–106. [Google Scholar] [CrossRef]
- Truex, M.J.; Vermeul, V.R.; Mendoza, D.P.; Fritz, B.G.; Mackley, R.D.; Oostrom, M.; Wietsma, T.W.; Macbeth, T.W. Injection of Zero-Valent Iron into an Unconfined Aquifer Using Shear-Thinning Fluids. Groundw. Monit. Remediat. 2011, 31, 50–58. [Google Scholar] [CrossRef]
- Caré, S.; Crane, R.; Calabrò, P.S.; Ghauch, A.; Temgoua, E.; Noubactep, C. Modeling the permeability loss of metallic iron water filtration systems. Clean–Soil Air Water 2013, 41, 275–282. [Google Scholar] [CrossRef] [Green Version]
- Santisukkasaem, U.; Das, D.B. A non-dimensional analysis of permeability loss in zero-valent iron permeable reactive barrier (PRB). Transp. Porous Media 2019, 126, 139–159. [Google Scholar] [CrossRef] [Green Version]
- Medawela, S.; Indraratna, B.; Rowe, R.K. The reduction in porosity of permeable reactive barriers due to bio-geochemical clogging caused by acidic groundwater flow. Can. Geotech. J. 2022. [Google Scholar] [CrossRef]
- Singh, R.; Chakma, S.; Birke, V. Performance of field-scale permeable reactive barriers: An overview on potentials and possible implications for in-situ groundwater remediation applications. Sci. Total Environ. 2022, 858, 158838. [Google Scholar] [CrossRef]
- Vogan, J.L.; Focht, R.M.; Clark, D.K.; Graham, S.L. Performance evaluation of a permeable reactive barrier for remediation of dissolved chlorinated solvents in groundwater. J. Hazard. Mater. 1999, 68, 97–108. [Google Scholar] [CrossRef] [PubMed]
- Noubactep, C. The suitability of metallic iron for environmental remediation. Environ. Prog. Sustain. Energy 2010, 29, 286–291. [Google Scholar] [CrossRef]
- Stipp, S.L.S.; Hansen, M.; Kristensen, R.; Hochella, M.F., Jr.; Bennedsen, L.; Dideriksen, K.; Balic-Zunic, T.; Leonard, D.; Mathieu, H.J. Behaviour of Fe-oxides relevant to contaminant uptake in the environment. Chem. Geol. 2002, 190, 321–337. [Google Scholar] [CrossRef]
- Mu, Y.; Jia, F.; Ai, Z.; Zhang, L. Iron oxide shell mediated environmental remediation properties of nano zero-valent iron. Environ. Sci. Nano 2017, 4, 27–45. [Google Scholar] [CrossRef]
- Krok, B.; Mohammadian, S.; Noll, H.M.; Surau, C.; Markwort, S.; Fritzsche, A.; Nachev, M.; Sures, B.; Meckenstock, R.U. Remediation of zinc-contaminated groundwater by iron oxide in situ adsorption barriers–From lab to the field. Sci. Total Environ. 2022, 807, 151066. [Google Scholar] [CrossRef] [PubMed]
- Jabbar, K.Q.; Barzinjy, A.A.; Hamad, S.M. Iron oxide nanoparticles: Preparation methods, functions, adsorption and coagulation/flocculation in wastewater treatment. Environ. Nanotechnol. Monit. Manag. 2022, 17, 100661. [Google Scholar] [CrossRef]
- Baby, R.; Hussein, M.Z.; Abdullah, A.H.; Zainal, Z. Nanomaterials for the Treatment of Heavy Metal Contaminated Water. Polymers 2022, 14, 583. [Google Scholar] [CrossRef]
- Singh, R.; Chakma, S.; Birke, V. Numerical modelling and performance evaluation of multi-permeable reactive barrier system for aquifer remediation susceptible to chloride contamination. Groundw. Sustain. Dev. 2020, 10, 100317. [Google Scholar] [CrossRef]
- Obiri-Nyarko, F.; Kwiatkowska-Malina, J.; Malina, G.; Kasela, T. Geochemical modelling for predicting the long-term performance of zeolite-PRB to treat lead contaminated groundwater. J. Contam. Hydrol. 2015, 177, 76–84. [Google Scholar] [CrossRef]
- Ma, L.; Zhang, C.; Liu, S.; Luo, Q.; Zhang, R.; Qian, J. Sensitivity analysis of factors influencing pollutant removal from shallow groundwater by the PRB method based on numerical simulation. Environ. Sci. Pollut. Res. 2022, 29, 82156–82168. [Google Scholar] [CrossRef]
- Zheng, K.; Luo, X.; Tan, Y.; Li, Z.; Wang, H.; Chen, T.; Zhao, L.; Zhan, L. Passive convergence-permeable reactive barrier (PC-PRB): An effective configuration to enhance hydraulic performance. Front. Environ. Sci. Eng. 2022, 16, 156. [Google Scholar] [CrossRef]
- Sarin, P.; Snoeyink, V.L.; Lytle, D.A.; Kriven, W.M. Iron corrosion scales: Model for scale growth, iron release, and colored water formation. J. Environ. Eng. Asce 2004, 130, 364–373. [Google Scholar] [CrossRef]
- Bottero, J.Y.; Manceau, A.; Villieras, F.; Tchoubar, D. Structure and mechanisms of formation of iron oxide hydroxide (chloride) polymers. Langmuir 1994, 10, 316–319. [Google Scholar] [CrossRef]
- Spiro, T.G.; Allerton, S.E.; Renner, J.; Terzis, A.; Bils, R.; Saltman, P. The Hydrolytic Polymerization of Iron(III). J. Am. Chem. Soc. 1966, 88, 2721–2726. [Google Scholar] [CrossRef]
- Dong, H.; Gao, B.; Yue, Q.; Sun, S.; Wang, Y.; Li, Q. Floc properties and membrane fouling of different monomer and polymer Fe coagulants in coagulation–ultrafiltration process: The role of Fe (III) species. Chem. Eng. J. 2014, 258, 442–449. [Google Scholar] [CrossRef]
- Chen, D.-W.; Liu, C.; Lu, J.; Mehmood, T.; Ren, Y.-Y. Enhanced phycocyanin and DON removal by the synergism of H2O2 and micro-sized ZVI: Optimization, performance, and mechanisms. Sci. Total Environ. 2020, 738, 140134. [Google Scholar] [CrossRef] [PubMed]
- Allerton, S.E.; Renner, J.; Colt, S.; Saltman, P. Viscosity studies on the behavior of inorganic iron polymers in aqueous solution. J. Am. Chem. Soc. 1966, 88, 3147–3148. [Google Scholar] [CrossRef]
- Sommer, B.A.; Margerum, D.W.; Renner, J.; Saltman, P.; Spiro, T.G. Reactivity and aging in hydroxy-iron (III) polymers, analogs of ferritin cores. Bioinorg. Chem. 1973, 2, 295–309. [Google Scholar] [CrossRef]
- Du, Q.; Zhang, S.; Pan, B.; Lv, L.; Zhang, W.; Zhang, Q. Effect of spatial distribution and aging of ZVI on the reactivity of resin–ZVI composites for arsenite removal. J. Mater. Sci. 2014, 49, 7073–7079. [Google Scholar] [CrossRef]
- Wang, Q.; Lee, S.; Choi, H. Aging study on the structure of Fe0-nanoparticles: Stabilization, characterization, and reactivity. J. Phys. Chem. C 2010, 114, 2027–2033. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, X.L.; Li, H.; Yang, J.; Zhou, L.Y.; Liu, Y.D. Re-activation of aged-ZVI by iron-reducing bacterium Shewanella putrefaciens for enhanced reductive dechlorination of trichloroethylene. J. Chem. Technol. Biotechnol. 2017, 92, 2642–2649. [Google Scholar] [CrossRef]
- Li, H.; Chen, S.; Ren, L.Y.; Zhou, L.Y.; Tan, X.J.; Zhu, Y.; Belver, C.; Bedia, J.; Yang, J. Biochar mediates activation of aged nanoscale ZVI by Shewanella putrefaciens CN32 to enhance the degradation of Pentachlorophenol. Chem. Eng. J. 2019, 368, 148–156. [Google Scholar] [CrossRef]
- Guiguer, N. Numerical modelling of the fate of residual immiscible fluids in saturated porous media. Water Sci. Technol. 1991, 24, 261–270. [Google Scholar] [CrossRef]
- Corapcioglu, M.Y.; Baehr, A. Immiscible contaminant transport in soils and groundwater with an emphasis on petroleum hydrocarbons: System of differential equations vs single cell model. Water Sci. Technol. 1985, 17, 23–37. [Google Scholar] [CrossRef]
- Corapcioglu, M.Y.; Baehr, A.L. A compositional multiphase model for groundwater contamination by petroleum products: 1. Theoretical considerations. Water Resour. Res. 1987, 23, 91–200. [Google Scholar] [CrossRef]
- Ostendorf, D.W. Long term fate and transport of immiscible aviation gasoline in the subsurface environment. Water Sci. Technol. 1990, 22, 37–44. [Google Scholar] [CrossRef]
- Mercer, J.W.; Cohen, R.M. A review of immiscible fluids in the subsurface: Properties, models, characterization and remediation. J. Contam. Hydrol. 1990, 6, 107–163. [Google Scholar] [CrossRef]
- Liu, H.H.; Dane, J.H. A criterion for gravitational instability in miscible dense plumes. J. Contam. Hydrol. 1996, 23, 233–243. [Google Scholar] [CrossRef]
- Rossabi, J.; Jackson, D.G.; Vermeulen, H.H.; Looney, B.B. Dense non-aqueous phase liquid chlorinated contaminant detected far from the source release area in an aquifer. Commun. Earth Environ. 2022, 3, 223. [Google Scholar] [CrossRef]
- Castro, A.R.; Martins, G.; Salvador, A.F.; Cavaleiro, A.J. Iron Compounds in Anaerobic Degradation of Petroleum Hydrocarbons: A Review. Microorganisms 2022, 10, 2142. [Google Scholar] [CrossRef] [PubMed]
- Takai, S.; Shimada, T.; Takeda, S.; Koike, K. Evaluating the effectiveness of a geostatistical approach with groundwater flow modeling for three-dimensional estimation of a contaminant plume. J. Contam. Hydrol. 2022, 251, 104097. [Google Scholar] [CrossRef] [PubMed]
- Earnden, L.; Marangoni, A.G.; Laredo, T.; Stobbs, J.; Marshall, T.; Pensini, E. Decontamination of water co-polluted by copper, toluene and tetrahydrofuran using lauric acid. Sci. Rep. 2022, 12, 15832. [Google Scholar] [CrossRef]
- Badmus, G.O.; Ogungbemi, O.S.; Enuiyin, O.V.; Adeyeye, J.A.; Ogunyemi, A.T. Delineation of leachate plume migration and appraisal of heavy metals in groundwater around Emirin dumpsite, Ado-Ekiti, Nigeria. Sci. Afr. 2022, 17, e01308. [Google Scholar] [CrossRef]
- Shen, H.; Huang, Y.; Su, Y. Progress in the development and application of permeable reaction barriers for remediation of dissolved oil contaminants in groundwater. Water Environ. J. 2022, 36, 188–198. [Google Scholar] [CrossRef]
- Nugraha, G.U.; Bakti, H.; Lubis, R.F.; Nur, A.A. Seawater intrusion mapping using hydrochemical ionic ratio data: An application in northern part of Jakarta groundwater basins, Indonesia. Arab. J. Geosci. 2022, 15, 1575. [Google Scholar] [CrossRef]
- Manivannan, V.; Manoj, S.; RamyaPriya, R.; Elango, L. Delineation and quantification of groundwater resources affected by seawater intrusion along the east coast of India. Environ. Earth Sci. 2022, 81, 300. [Google Scholar] [CrossRef]
- Yang, J.-S.; Jeong, Y.-W.; Agossou, A.; Sohn, J.-S.; Lee, J.-B. GALDIT Modification for Seasonal Seawater Intrusion Mapping Using Multi Criteria Decision Making Methods. Water 2022, 14, 2258. [Google Scholar] [CrossRef]
- Selvakumar, S.; Chandrasekar, N.; Srinivas, Y.; Selvam, S.; Kaliraj, S.; Magesh, N.S.; Venkatramanan, S. Hydrogeochemical processes controlling the groundwater salinity in the coastal aquifers of Southern Tamil Nadu, India. Mar. Pollut. Bull. 2022, 174, 113264. [Google Scholar] [CrossRef]
- Askri, B.; Ahmed, A.T.; Bouhlila, R. Origins and processes of groundwater salinisation in Barka coastal aquifer, Sultanate of Oman. Phys. Chem. Earth Parts A/B/C 2022, 126, 103116. [Google Scholar] [CrossRef]
- Sarkar, A.; Paul, B.; Darbha, G.K. The groundwater arsenic contamination in the Bengal Basin-A review in brief. Chemosphere 2022, 299, 134369. [Google Scholar] [CrossRef]
- Raju, N.J. Arsenic in the geo-environment: A review of sources, geochemical processes, toxicity and removal technologies. Environ. Res. 2022, 203, 111782. [Google Scholar] [CrossRef]
- Haskell, D.; Heo, J.; Park, J.; Dong, C. Hydrogeochemical Evaluation of Groundwater Quality Parameters for Ogallala Aquifer in the Southern High Plains Region, USA. Int. J. Environ. Res. Public Health 2022, 19, 8453. [Google Scholar] [CrossRef]
- Hao, L.; Zhang, S.; Luo, K. Content of Selenium and Other Elements, Water Quality, Health Risks and Utilization Prospect in Natural Water of Southern Qinling-Daba Mountains, Southern Shaanxi, China. Expo. Health 2022, 14, 29–47. [Google Scholar] [CrossRef]
- Lashari, A.A.; Kazi, T.G.; Baig, J.A.; Afridi, H.I.; Memon, A.A. Speciation of the Selenium in Groundwater Samples of Different Aquifers from Coal Mining Fields: Applied a Green Analytical Technique. Water Air Soil Pollut. 2022, 233, 1–11. [Google Scholar] [CrossRef]
- Ma, X.; Yang, Z.; Yu, T.; Guan, D.X. Probability of cultivating Se-rich maize in Se-poor farmland based on intensive field sampling and artificial neural network modelling. Chemosphere 2022, 309, 136690. [Google Scholar] [CrossRef]
- Usman, M.; Jellali, S.; Anastopoulos, I.; Charabi, Y.; Hameed, B.H.; Hanna, K. Fenton oxidation for soil remediation: A critical review of observations in historically contaminated soils. J. Hazard. Mater. 2022, 424, 127670. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Wang, Z.; Liu, C.; Dong, Y. Technologies for removing heavy metal from contaminated soils on farmland: A review. Chemosphere 2022, 305, 135457. [Google Scholar] [CrossRef] [PubMed]
- Rajendran, S.; Priya, T.A.K.; Khoo, K.S.; Hoang, T.K.; Ng, H.S.; Munawaroh, H.S.H.; Karaman, C.; Orooji, Y.; Show, P.L. A critical review on various remediation approaches for heavy metal contaminants removal from contaminated soils. Chemosphere 2022, 287, 132369. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.H.; Woo, H.; An, S.; Chung, J.; Lee, S.; Lee, S. What determines the efficacy of landfarming for petroleum-contaminated soils: Significance of contaminant characteristics. Chemosphere 2022, 290, 133392. [Google Scholar] [CrossRef]
- Dahlberg, E.C. Applied Hydrodynamics in Petroleum Exploration; Springer: New York, NY, USA, 1982. [Google Scholar]
- Kulatilake, P.H. Probabilistic potentiometric surface mapping. J. Geotech. Eng. 1989, 115, 1569–1587. [Google Scholar] [CrossRef]
- Gunawardhana, L.N.; Al-Harthi, F.; Sana, A.; Baawain, M.S. Analytical and numerical analysis of constant-rate pumping test data considering aquifer boundary effect. Environ. Earth Sci. 2021, 80, 543. [Google Scholar] [CrossRef]
- Momm, H.G.; Bingner, R.L.; Moore, K.; Herring, G. Integrated surface and groundwater modeling to enhance water resource sustainability in agricultural watersheds. Agric. Water Manag. 2022, 269, 107692. [Google Scholar] [CrossRef]
- Alhama, I.; García-Ros, G.; Icardi, M. Non-Stationary Contaminant Plumes in the Advective-Diffusive Regime. Mathematics 2021, 9, 725. [Google Scholar] [CrossRef]
- Fuentes, C.; Chávez, C.; Quevedo, A.; Trejo-Alonso, J.; Fuentes, S. Modeling of Artificial Groundwater Recharge by Wells: A Model Stratified Porous Medium. Mathematics 2020, 8, 1764. [Google Scholar] [CrossRef]
- Currie, D.; Laattoe, T.; Walker, G.; Woods, J.; Smith, T.; Bushaway, K. Modelling Groundwater Returns to Streams from Irrigation Areas with Perched Water Tables. Water 2020, 12, 956. [Google Scholar] [CrossRef] [Green Version]
- Fan, X.; Xu, H.; Jin, G.; Lv, Y.; Wu, S.; Wu, T. Regional differences in influence of intermediate cover permeability on perched leachate in landfill. Urban Clim. 2022, 42, 101094. [Google Scholar] [CrossRef]
- Lu, P.; Sheng, Z.; Zhang, Z.; Miller, G.; Reinert, S.; Huang, M. Effect of multilayered groundwater mounds on water dynamics beneath a recharge basin: Numerical simulation and assessment of surface injection. Hydrol. Process. 2021, 35, e14193. [Google Scholar] [CrossRef]
- Polat, C. Gaussian formulation based correlation for Dietz shape factor. Upstream Oil Gas Technol. 2021, 7, 100059. [Google Scholar] [CrossRef]
- Dake, L.P. Fundamentals of Reservoir Engineering; Elsevier: Amsterdam, The Netherlands, 1998; p. 443. [Google Scholar]
- Johansen, T.E.; Cao, J. A new theory for flow computations in a large class of anisotropic media with applications to well productivity modeling. J. Pet. Sci. Eng. 2022, 208, 109366. [Google Scholar] [CrossRef]
- Kulkarni, N.H. Numerical simulation of groundwater recharge from an injection well. Int. J. Water Resour. Environ. Eng. 2015, 7, 75–83. [Google Scholar]
- Allow, K.A. The use of injection wells and a subsurface barrier in the prevention of seawater intrusion: A modelling approach. Arab. J. Geosci. 2012, 5, 1151–1161. [Google Scholar] [CrossRef]
- Zheng, S.; Sharma, M. Coupling a Geomechanical Reservoir and Fracturing Simulator with a Wellbore Model for Horizontal Injection Wells. Int. J. Multiscale Comput. Eng. 2022, 20, 23–55. [Google Scholar] [CrossRef]
- Khomine, A.; János, S.; Balázs, K. Potential solutions in prevention of saltwater intrusion: A modelling approach. In Advances in the Research of Aquatic Environment; Springer: Berlin/Heidelberg, Germany, 2011; Volume 1, pp. 251–257. [Google Scholar] [CrossRef]
- Luyun, R., Jr.; Momii, K.; Nakagawa, K. Effects of recharge wells and flow barriers on seawater intrusion. Groundwater 2011, 49, 239–249. [Google Scholar] [CrossRef]
- Sriapai, T.; Walsri, C.; Phueakphum, D.; Fuenkajorn, K. Physical model simulations of seawater intrusion in unconfined aquifer. Songklanakarin J. Sci. Technol. 2012, 34, 679–687. [Google Scholar]
- Zhou, L.; Li, Z.; Yi, Y.; Tsang, E.P.; Fang, Z. Increasing the electron selectivity of nanoscale zero-valent iron in environmental remediation: A review. J. Hazard. Mater. 2022, 421, 126709. [Google Scholar] [CrossRef] [PubMed]
- Liang, W.; Wang, G.; Peng, C.; Tan, J.; Wan, J.; Sun, P.; Li, Q.; Ji, X.; Zhang, Q.; Wu, Y.; et al. Recent advances of carbon-based nano zero valent iron for heavy metals remediation in soil and water: A critical review. J. Hazard. Mater. 2022, 426, 127993. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.; Wang, J.; Zhang, S.; Pang, H.; Wang, X.; Chen, Z.; Li, M.; Song, G.; Qiu, M.; Yu, S. Recent advances in nanoscale zero-valent iron-based materials: Characteristics, environmental remediation and challenges. J. Clean. Prod. 2021, 319, 128641. [Google Scholar] [CrossRef]
- Li, Q.; Chen, Z.; Wang, H.; Yang, H.; Wen, T.; Wang, S.; Hu, B.; Wang, X. Removal of organic compounds by nanoscale zero-valent iron and its composites. Sci. Total Environ. 2021, 792, 148546. [Google Scholar] [CrossRef] [PubMed]
- Cao, V.; Bakari, O.; Kenmogne-Tchidjo, J.F.; Gatcha-Bandjun, N.; Ndé-Tchoupé, A.I.; Gwenzi, W.; Njau, K.N.; Noubactep, C. Conceptualizing the Fe0/H2O System: A Call for Collaboration to Mark the 30th Anniversary of the Fe0-Based Permeable Reactive Barrier Technology. Water 2022, 14, 3120. [Google Scholar] [CrossRef]
- Antia, D.D.J. Remediation of Saline Wastewater Producing a Fuel Gas Containing Alkanes and Hydrogen Using Zero Valent Iron (Fe0). Water 2022, 14, 1926. [Google Scholar] [CrossRef]
- Pourbaix, M. Atlas of Electrochemical Equilibria in Aqueous Solutions, 2nd ed.; Library of Congress Catalog Card No. 65-11670; Franklin, J.A., Translator; NACE International: Houston, TX, USA, 1974; p. 644. [Google Scholar]
- Ebbing, D.D.; Gammon, S.D. General Chemistry, 8th ed.; Houghton Mifflin Company: New York, NY, USA, 2005; ISBN 0618399429. [Google Scholar]
- Dehgani, Z.; Ghaedi, M.; Sabzehmeidani, M.M.; Adhami, E. Removal of paraquat from aqueous solutions by a bentonite modified zero-valent iron adsorbent. New J. Chem. 2020, 44, 13368–13376. [Google Scholar] [CrossRef]
- Zhao, X.; Dou, X.; Mohan, D.; Pittman, C.U., Jr.; Ok, Y.S.; Jin, X. Antimonate and antimonite adsorption by a polyvinyl alcohol-stabilized granular adsorbent containing nanoscale zero-valent iron. Chem. Eng. J. 2014, 247, 250–257. [Google Scholar] [CrossRef]
- Xing, M.; Wang, J. Nanoscaled zero valent iron/graphene composite as an efficient adsorbent for Co (II) removal from aqueous solution. J. Colloid Interface Sci. 2016, 474, 119–128. [Google Scholar] [CrossRef] [PubMed]
- Awang, N.A.; Wan Salleh, W.N.; Aziz, F.; Yusof, N.; Ismail, A.F. A review on preparation, surface enhancement and adsorption mechanism of biochar-supported nano zero-valent iron adsorbent for hazardous heavy metals. J. Chem. Technol. Biotechnol. 2022, 98, 22–44. [Google Scholar] [CrossRef]
- Yin, L.; Liu, L.; Lin, S.; Owens, G.; Chen, Z. Synthesis and characterization of Nanoscale Zero-Valent Iron (nZVI) as an adsorbent for the simultaneous removal of As (III) and As (V) from groundwater. J. Water Process Eng. 2022, 47, 102677. [Google Scholar] [CrossRef]
- Ainiwaer, M.; Zeng, X.; Yin, X.; Wen, J.; Su, S.; Wang, Y.; Zhang, Y.; Zhang, T.; Zhang, N. Thermodynamics, Kinetics, and Mechanisms of the Co-Removal of Arsenate and Arsenite by Sepiolite-Supported Nanoscale Zero-Valent Iron in Aqueous Solution. Int. J. Environ. Res. Public Health 2022, 19, 11401. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.P.; Li, X.Q.; Cao, J.; Zhang, W.X.; Wang, H.P. Characterization of zero-valent iron nanoparticles. Adv. Colloid Interface Sci. 2006, 120, 47–56. [Google Scholar] [CrossRef]
- Antia, D.D.J. Water Treatment and Desalination Using the Eco-materials n-Fe0 (ZVI), n-Fe3O4, n-FexOyHz[mH2O], and n-Fex[Cation]nOyHz[Anion]m [rH2O]. In Handbook of Nanomaterials and Nanocomposites for Energy and Environmental Applications, 1st ed.; Kharissova, O.V., Torres-Martínez, L.M., Kharisov, B.I., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; pp. 3159–3242. [Google Scholar] [CrossRef]
- Antia, D.D.J. Provision of Desalinated Irrigation Water by the Desalination of Groundwater Abstracted from a Saline Aquifer. Hydrology 2022, 9, 128. [Google Scholar] [CrossRef]
- Antia, D.D.J. Catalytic Partial Desalination of Saline Water. Water 2022, 14, 2893. [Google Scholar] [CrossRef]
- Varghese, P.; Varma, A. Catalytic reactions in transport-line reactors. Chem. Eng. Sci. 1979, 34, 337–343. [Google Scholar] [CrossRef]
- Carberry, J.J. Chemical and Catalytic Reaction Engineering; Dover Publications, Inc.: New York, NY, USA, 2001. [Google Scholar]
- Twigg, M.V. Catalyst Handbook; Wolfe Publishing, Ltd.: London, UK, 1989. [Google Scholar]
- Wang, X.; Ren, L.; Long, T.; Geng, C.; Tian, X. Migration and remediation of organic liquid pollutants in porous soils and sedimentary rocks: A review. Environ. Chem. Lett. 2022, 20, 1–18. [Google Scholar] [CrossRef]
- Vu, K.A.; Mulligan, C.N. Utilization of a biosurfactant foam/nanoparticle mixture for treatment of oil pollutants in soil. Environ. Sci. Pollut. Res. 2022, 29, 88618–88629. [Google Scholar] [CrossRef]
- Ang, C.C.; Abdul, A.S. Aqueous surfactant washing of residual oil contamination from sandy soil. Groundw. Monit. Remediat. 1991, 11, 121–127. [Google Scholar] [CrossRef]
- Lamont, K.; Marangoni, A.G.; Pensini, E. Emulsion locks’ for the containment of hydrocarbons during surfactant flushing. J. Environ. Sci. 2020, 90, 98–109. [Google Scholar] [CrossRef] [PubMed]
- Harwell, J.H.; Sabatini, D.A.; Knox, R.C. Surfactants for ground water remediation. Colloids Surf. A Physicochem. Eng. Asp. 1999, 151, 255–268. [Google Scholar] [CrossRef]
- Amanat, N.; Barbati, B.; Rossi, M.M.; Bellagamba, M.; Buccolini, M.; Galantini, L.; Petrangeli Papini, M. Synthetic and Natural Surfactants for Potential Application in Mobilization of Organic Contaminants: Characterization and Batch Study. Water 2022, 14, 1182. [Google Scholar] [CrossRef]
- Drzewicz, P.; Perez-Estrada, L.; Alpatova, A.; Martin, J.W.; Gamal El-Din, M. Impact of peroxydisulfate in the presence of zero valent iron on the oxidation of cyclohexanoic acid and naphthenic acids from oil sands process-affected water. Environ. Sci. Technol. 2012, 46, 8984–8991. [Google Scholar] [CrossRef]
- Pourrezaei, P.; Alpatova, A.; Khosravi, K.; Drzewicz, P.; Chen, Y.; Chelme-Ayala, P.; El-Din, M.G. Removal of organic compounds and trace metals from oil sands process-affected water using zero valent iron enhanced by petroleum coke. J. Environ. Manag. 2014, 139, 50–58. [Google Scholar] [CrossRef]
- Nasehi, S.A.; Uromeihy, A.; Nikudel, M.R.; Morsali, A. Use of nanoscale zero-valent iron and nanoscale hydrated lime to improve geotechnical properties of gas oil contaminated clay: A comparative study. Environ. Earth Sci. 2016, 75, 1–20. [Google Scholar] [CrossRef]
- Mu, S.; Chen, X.; Luo, Y.; Zhang, J. Degradation of petroleum hydrocarbons in oil-based drilling cuttings by a zero-valent iron Fenton-like advanced oxidation system. Process. Saf. Environ. Prot. 2022, 168, 883–891. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, L.; Tian, S.; Zhu, S.; Chen, Z.; Si, H. The effect of zero-valent iron/Fe3+ coupling and reuse on the properties of anoxic sludge. J. Clean. Prod. 2022, 344, 131031. [Google Scholar] [CrossRef]
- Haneef, T.; Ul Mustafa, M.R.; Rasool, K.; Ho, Y.C.; Mohamed Kutty, S.R. Removal of polycyclic aromatic hydrocarbons in a heterogeneous Fenton like oxidation system using nanoscale zero-valent iron as a catalyst. Water 2020, 12, 2430. [Google Scholar] [CrossRef]
- Peng, Z.; Xiong, C.; Wang, W.; Tan, F.; Wang, X.; Qiao, X.; Wong, P.K. Hydrophobic modification of nanoscale zero-valent iron with excellent stability and floatability for efficient removal of floating oil on water. Chemosphere 2018, 201, 110–118. [Google Scholar] [CrossRef]
- Antia, D.D.J. Desalination of irrigation water using metal polymers. Water 2022, 14, 3224. [Google Scholar] [CrossRef]
- Antia, D.D.J. Partial Desalination of Saline Groundwater, Including Flowback Water, to Produce Irrigation Water. Hydrology 2022, 9, 219. [Google Scholar] [CrossRef]
- Antia, D.D.J. Purification of Saline Water Using Desalination Pellets. Water 2022, 14, 2639. [Google Scholar] [CrossRef]
- Rotz, R.; Milewski, A.; Rasmussen, T.C. Transient Evolution of Inland Freshwater Lenses: Comparison of Numerical and Physical Experiments. Water 2020, 12, 1154. [Google Scholar] [CrossRef] [Green Version]
- Jazayeri, A.; Werner, A.D.; Wu, H.; Lu, C. Effects of River Partial Penetration on the Occurrence of Riparian Freshwater Lenses: Experimental Investigation. Water Resour. Res. 2021, 57, e2021WR029728. [Google Scholar] [CrossRef]
- Kacimov, A.R.; Obnosov, Y.V. Analytic solutions for fresh groundwater lenses floating on saline water under desert dunes: The Kunin-Van Der Veer legacy revisited. J. Hydrol. 2019, 574, 733–743. [Google Scholar] [CrossRef]
- Anneser, B.; Einsiedl, F.; Meckenstock, R.U.; Richters, L.; Wisotzky, F.; Griebler, C. High-resolution monitoring of biogeochemical gradients in a tar oil-contaminated aquifer. Appl. Geochem. 2008, 23, 1715–1730. [Google Scholar] [CrossRef]
- Gutierrez-Neri, M.; Ham, P.A.S.; Schotting, R.J.; Lerner, D.N. Analytical modelling of fringe and core biodegradation in groundwater plumes. J. Contam. Hydrol. 2009, 107, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Quinn, J.; Geiger, C.; Clausen, C.; Brooks, K.; Coon, C.; O'Hara, S.; Krug, T.; Major, D.; Yoon, W.S.; Gavaskar, A.; et al. Field demonstration of DNAPL dehalogenation using emulsified zero-valent iron. Environ. Sci. Technol. 2005, 39, 1309–1318. [Google Scholar] [CrossRef] [PubMed]
- Bajagain Jeong, S.W. Degradation of petroleum hydrocarbons in soil via advanced oxidation process using peroxymonosulfate activated by nanoscale zero-valent iron. Chemosphere 2021, 270, 128627. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Fang, G.; Zhu, C.; Zhu, F.; Wu, S.; Chen, N.; Wu, T.; Wang, Y.; Gao, J.; Zhou, D. Zero-valent iron activated persulfate remediation of polycyclic aromatic hydrocarbon-contaminated soils: An in situ pilot-scale study. Chem. Eng. J. 2019, 355, 65–75. [Google Scholar] [CrossRef]
- El Sharawy, M.S.; Gaafar, G.R. Impacts of petrophysical properties of sandstone reservoirs on their irreducible water saturation: Implication and prediction. J. Afr. Earth Sci. 2019, 156, 118–132. [Google Scholar] [CrossRef]
- Behrenbruch, P.; Yuan, C.; Truong, N.B.; Do Huu, P.; Hoang, T. Defining irreducible water saturation using global characteristics envelopes and novel correlations. APPEA J. 2016, 56, 1–10. [Google Scholar] [CrossRef]
- Stalheim, S.O.; Eidesmo, T.; Rueslåtten, H. Influence of wettability on water saturation Taktak, F.; Rigane, A.; Boufares, T.; Kharbachi, S.; Bouaziz, S. Modelling approaches for the estimation of irreducible water saturation and heterogeneities of the commercial Ashtart reservoir from the Gulf of Gabès, Tunisia. J. Pet. Sci. Eng. 2011, 78, 376–383. [Google Scholar]
- Shen, J.; Qin, Y.; Wang, G.X.; Fu, X.; Wei, C.; Lei, B. Relative permeabilities of gas and water for different rank coals. Int. J. Coal Geol. 2011, 86, 266–275. [Google Scholar] [CrossRef]
- Sun, C.; McClure, J.E.; Mostaghimi, P.; Herring, A.L.; Shabaninejad, M.; Berg, S.; Armstrong, R.T. Linking continuum-scale state of wetting to pore-scale contact angles in porous media. J. Colloid Interface Sci. 2020, 561, 173–180. [Google Scholar] [CrossRef] [Green Version]
- Moridis, G.J.; Reddell, D.L. Secondary water recovery by air injection: 3. Evaluation of feasibility. Water Resour. Res. 1991, 27, 2369–2379. [Google Scholar] [CrossRef]
- Stalheim, S.O.; Eidesmo, T.; Rueslåtten, H. Influence of wettability on water saturation modelling. J. Pet. Sci. Eng. 1999, 24, 243–253. [Google Scholar] [CrossRef]
- Chen, M.; Al-Maktoumi, A.; Al-Mamari, H.; Izady, A.; Nikoo, M.R.; Al-Busaidi, H. Oxygenation of aquifers with fluctuating water table: A laboratory and modeling study. J. Hydrol. 2020, 590, 125261. [Google Scholar] [CrossRef]
- Dembicki, H., Jr.; Anderson, M.J. Secondary migration of oil: Experiments supporting efficient movement of separate, buoyant oil phase along limited conduits. AAPG Bull. 1989, 73, 1018–1021. [Google Scholar]
- Yahyaoui, S.; Akkal, R.; Khodja, M.; Ahmed Zaid, T. On the Water-Oil Relative Permeabilities of Southern Algerian Sandstone Rock Samples. Energies 2022, 15, 5687. [Google Scholar] [CrossRef]
- Masoomi, R.; Torabi, F. A new computational approach to predict hot-water flooding (HWF) performance in unconsolidated heavy oil reservoirs. Fuel 2022, 312, 122861. [Google Scholar] [CrossRef]
- Antia, D.D.J. Formation and Control of Self-Sealing High Permeability Groundwater Mounds in Impermeable Sediment: Implications for SUDS and Sustainable Pressure Mound Management. Sustainability 2009, 1, 855–923. [Google Scholar] [CrossRef] [Green Version]
- Gui, M.-W.; Alebachew, A.A. Responses of Laterally Loaded Single Piles Subjected to Various Loading Rates in a Poroelastic Soil. Appl. Sci. 2022, 12, 617. [Google Scholar] [CrossRef]
- Vgenopoulou, I.; Beskos, D.E. Dynamic poroelastic soil column and borehole problem analysis. Soil Dyn. Earthq. Eng. 1992, 11, 335–345. [Google Scholar] [CrossRef]
- Coppola, A.; Gerke, H.H.; Comegna, A.; Basile, A.; Comegna, V. Dual-permeability model for flow in shrinking soil with dominant horizontal deformation. Water Resour. Res. 2012, 48, 11376. [Google Scholar] [CrossRef]
- Lu, M.M.; Xie, K.H.; Guo, B. Consolidation theory for a composite foundation considering radial and vertical flows within the column and the variation of soil permeability within the disturbed soil zone. Can. Geotech. J. 2010, 47, 207–217. [Google Scholar] [CrossRef]
- Wilkinson, W.B.; Shipley, E.L. Vertical and horizontal laboratory permeability measurements in clay soils. Dev. Soil Sci. 1972, 2, 285–298. [Google Scholar]
- Phillips, J.; Clausen, B.; Dumesic, J.A. Iron pentacarbonyl decomposition over grafoil. Production of small metallic iron particles. J. Phys. Chem. 1980, 84, 1814–1822. [Google Scholar] [CrossRef]
- Santos, J.; Phillips, J.; Dumesic, J.A. Metal-support interactions between iron and titania for catalysts prepared by thermal decomposition of iron pentacarbonyl and by impregnation. J. Catal. 1983, 81, 147–167. [Google Scholar] [CrossRef]
- Maruyama, T.; Shinyashiki, Y. Iron–iron oxide composite thin films prepared by chemical vapor deposition from iron pentacarbonyl. Thin Solid Film. 1998, 333, 203–206. [Google Scholar] [CrossRef]
- Pour, A.N.; Housaindokht, M.R.; Tayyari, S.F.; Zarkesh, J. Fischer-Tropsch synthesis by nano-structured iron catalyst. J. Nat. Gas Chem. 2010, 19, 284–292. [Google Scholar] [CrossRef]
- Amonette, J.E.; Szecsody, J.E.; Schaef, H.T.; Gorby, Y.A.; Fruchter, J.S.; Templeton, J.C. Abiotic Reduction of Aquifer Materials by Dithionite: A Promising In-Situ Remediation Technology; (No. PNL-SA--24505); Pacific Northwest Lab.: Richland, WA, USA, 1994. [Google Scholar]
- Sun, Q.; Feitz, A.J.; Guan, J.; Waite, T.D. Comparison of the reactivity of nanosized zero-valent iron (nZVI) particles produced by borohydride and dithionite reduction of iron salts. Nano 2008, 3, 341–349. [Google Scholar] [CrossRef]
- Ma, X.; He, D.; Jones, A.M.; Collins, R.N.; Waite, T.D. Reductive reactivity of borohydride-and dithionite-synthesized iron-based nanoparticles: A comparative study. J. Hazard. Mater. 2016, 303, 101–110. [Google Scholar] [CrossRef]
- Xiaomin, N.; Xiaobo, S.; Huagui, Z.; Dongen, Z.; Dandan, Y.; Qingbiao, Z. Studies on the one-step preparation of iron nanoparticles in solution. J. Cryst. Growth 2005, 275, 548–553. [Google Scholar] [CrossRef]
- Runge, F.F. Ueber einige Produkte der Steinkohlendestillation. Ann. Der Phys. Und Chem. 1834, 107, 65–78. [Google Scholar] [CrossRef] [Green Version]
- Edwards, M.; Benjamin, M.M. Regeneration and reuse of iron hydroxide adsorbents in treatment of metal-bearing wastes. J. Water Pollut. Control Fed. 1989, 61, 481–490. [Google Scholar]
- Chen, A.S.; Sorg, T.J.; Wang, L. Regeneration of iron-based adsorptive media used for removing arsenic from groundwater. Water Res. 2015, 77, 85–97. [Google Scholar] [CrossRef]
- Lang, Y.; Yu, Y.; Zou, H.; Ye, J.; Zhang, S. Performance and Mechanisms of Sulfidated Nanoscale Zero-Valent Iron Materials for Toxic TCE Removal from the Groundwater. Int. J. Environ. Res. Public Health 2022, 19, 6299. [Google Scholar] [CrossRef]
- Xiao, M.; Hu, R.; Ndé-Tchoupé, A.I.; Gwenzi, W.; Noubactep, C. Metallic Iron for Water Remediation: Plenty of Room for Collaboration and Convergence to Advance the Science. Water 2022, 14, 1492. [Google Scholar] [CrossRef]
- Curcio, G.M.; Limonti, C.; Siciliano, A.; Kabdaşlı, I. Nitrate Removal by Zero-Valent Metals: A Comprehensive Review. Sustainability 2022, 14, 4500. [Google Scholar] [CrossRef]
- Ullah, S.; Faiz, P.; Leng, S. Synthesis, Mechanism, and Performance Assessment of Zero-Valent Iron for Metal-Contaminated Water Remediation: A Review. Clean–Soil Air Water 2020, 48, 2000080. [Google Scholar] [CrossRef]
- Sun, J.; Tian, A.; Feng, Z.; Zhang, Y.; Jiang, F.; Tang, Q. Evaluation of Zero-Valent Iron for Pb(II) Contaminated Soil Remediation: From the Analysis of Experimental Mechanism Hybird with Carbon Emission Assessment. Sustainability 2021, 13, 452. [Google Scholar] [CrossRef]
- Hu, R.; Yang, H.; Tao, R.; Cui, X.; Xiao, M.; Amoah, B.K.; Cao, V.; Lufingo, M.; Soppa-Sangue, N.P.; Ndé-Tchoupé, A.I.; et al. Metallic Iron for Environmental Remediation: Starting an Overdue Progress in Knowledge. Water 2020, 12, 641. [Google Scholar] [CrossRef] [Green Version]
- Antia, D.D.J. Sustainable Zero-Valent Metal (ZVM) Water Treatment Associated with Diffusion, Infiltration, Abstraction, and Recirculation. Sustainability 2010, 2, 2988–3073. [Google Scholar] [CrossRef] [Green Version]
- Antia, D.D.J. Groundwater water remediation by static diffusion using nano-zero valent metals [ZVM](Fe0, Cu0, Al0), n-FeHn+, n-Fe(OH)x, n-FeOOH, n-Fe-[OxHy](n+/−). In Nanomaterials for Environmental Protection, 1st ed.; Kharisov, B.I., Kharissova, O.V., Dias, H.V.R., Eds.; Wiley Inc.: Hoboken, NJ, USA, 2014; Chapter 1; pp. 3–25. [Google Scholar]
- Xu, Z.; Wan, Z.; Sun, Y.; Gao, B.; Hou, D.; Cao, X.; Komárek, M.; Ok, Y.S.; Tsang, D.C. Electroactive Fe-biochar for redox-related remediation of arsenic and chromium: Distinct redox nature with varying iron/carbon speciation. J. Hazard. Mater. 2022, 430, 128479. [Google Scholar] [CrossRef] [PubMed]
- Pasinszki, T.; Krebsz, M. Synthesis and Application of Zero-Valent Iron Nanoparticles in Water Treatment, Environmental Remediation, Catalysis, and Their Biological Effects. Nanomaterials 2020, 10, 917. [Google Scholar] [CrossRef]
- Antia, D.D.J. ZVI (Fe0) desalination: Catalytic partial desalination of saline aquifers. Appl. Water Sci. 2018, 8, 71. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.E.; Park, Y.-K. Applications of Modified Biochar-Based Materials for the Removal of Environment Pollutants: A Mini Review. Sustainability 2020, 12, 6112. [Google Scholar] [CrossRef]
- Antia, D.D.J. Modification of Aquifer Pore-Water by Static Diffusion Using Nano-Zero-Valent Metals. Water 2011, 3, 79–112. [Google Scholar] [CrossRef] [Green Version]
- Gong, L.; Qi, J.; Lv, N.; Qiu, X.; Gu, Y.; Zhao, J.; He, F. Mechanistic role of nitrate anion in TCE dechlorination by ball milled ZVI and sulfidated ZVI: Experimental investigation and theoretical analysis. J. Hazard. Mater. 2021, 403, 123844. [Google Scholar] [CrossRef] [PubMed]
- Noubactep, C. Metallic iron for the removal of metals and metalloids from aqueous solutions: An old-timer view. Curr. Opin. Environ. Sci. Health 2021, 22, 100256. [Google Scholar] [CrossRef]
- Liu, X.; Wu, M.; Zhao, J. Removal of Trichloroethylene from Water by Bimetallic Ni/Fe Nanoparticles. Water 2022, 14, 1616. [Google Scholar] [CrossRef]
- Wei, J.; Qian, Y.; Liu, W.; Wang, L.; Ge, Y.; Zhang, J.; Yu, J.; Ma, X. Effects of particle composition and environmental parameters on catalytic hydrodechlorination of trichloroethylene by nanoscale bimetallic Ni-Fe. J. Environ. Sci. 2014, 26, 1162–1170. [Google Scholar] [CrossRef] [PubMed]
- Divakar, D.; Romero-Sáez, M.; Pereda-Ayo, B.; Aranzabal, A.; González-Marcos, J.A.; González-Velasco, J.R. Catalytic oxidation of trichloroethylene over Fe-zeolites. Catal. Today 2011, 176, 357–360. [Google Scholar] [CrossRef]
- Liu, J.; Peng, C.; Shi, X. Preparation, characterization, and applications of Fe-based catalysts in advanced oxidation processes for organics removal: A review. Environ. Pollut. 2022, 293, 118565. [Google Scholar] [CrossRef]
- Ma, H.; Ai, J.; Lu, C.; Hansen, H.C.B. Element doping of biochars enhances catalysis of trichloroethylene dechlorination. Chem. Eng. J. 2022, 428, 132496. [Google Scholar] [CrossRef]
- Christiansen, B.C.; Balic-Zunic, T.; Petit, P.O.; Frandsen, C.; Mørup, S.; Geckeis, H.; Katerinopoulou, A.; Stipp, S.S. Composition and structure of an iron-bearing, layered double hydroxide (LDH)–Green rust sodium sulphate. Geochim. Cosmochim. Acta 2009, 73, 3579–3592. [Google Scholar] [CrossRef]
- Platte, T.; Finck, N.; Mangold, S.; Polly, R.; Geckeis, H. Retention of Iodide and Chloride by Formation of a Green Rust Solid Solution GR-Cl1–x I x: A Multiscale Approach. Inorg. Chem. 2021, 60, 10585–10595. [Google Scholar] [CrossRef]
- Al Mamun, A.; Onoguchi, A.; Granata, G.; Tokoro, C. Role of pH in green rust preparation and chromate removal from water. Appl. Clay Sci. 2018, 165, 205–213. [Google Scholar] [CrossRef]
- Perez, J.P.H.; Schiefler, A.A.; Rubio, S.N.; Reischer, M.; Overheu, N.D.; Benning, L.G.; Tobler, D.J. Arsenic removal from natural 2110 groundwater using ‘green rust’: Solid phase stability and contaminant fate. J. Hazard. Mater. 2021, 401, 123327. [Google Scholar] [CrossRef] [PubMed]
- Andrei, F.; Sappa, G.; Boni, M.R.; Mancini, G.; Viotti, P. Mobility of nZVI in a Reconstructed Porous Media Monitored by an Image Analysis Procedure. Water 2021, 13, 2797. [Google Scholar] [CrossRef]
- Hubbert, M.K. Entrapment of petroleum under hydrodynamic conditions. AAPG Bull. 1953, 37, 1954–2026. [Google Scholar]
- Schowalter, T.T. Mechanics of secondary hydrocarbon migration and entrapment. AAPG Bull. 1979, 63, 723–760. [Google Scholar]
- Schowalter, T.T.; Hess, P.D. Interpretation of subsurface hydrocarbon shows. AAPG Bull. 1982, 66, 1302–1327. [Google Scholar]
- Valderrama, M. Secondary migration of heavy oil in low dip basins. AAPG Bull. 2022, 106, 1923–1937. [Google Scholar] [CrossRef]
- Nguindjel, A.D.C.; de Visser, P.J.; Winkens, M.; Korevaar, P.A. Spatial programming of self-organizing chemical systems using sustained physicochemical gradients from reaction, diffusion and hydrodynamics. Phys. Chem. Chem. Phys. 2022, 24, 23980–24001. [Google Scholar] [CrossRef] [PubMed]
- Raychoudhury, T. Transport behaviour of different metal-based nanoparticles through natural sediment in the presence of humic acid and under the groundwater condition. J. Earth Syst. Sci. 2020, 129, 1–12. [Google Scholar]
- Dibyanshu, K.; Chhaya, T.; Raychoudhury, T. A review on the fate and transport behavior of engineered nanoparticles: Possibility of becoming an emerging contaminant in the groundwater. Int. J. Environ. Sci. Technol. 2022, 1–24. [Google Scholar] [CrossRef]
- Antia, D.D.J. Irrigation water desalination using PVP (polyvinylpyrrolidone) coated n-Fe0 (ZVI, zero valent iron). In New Polymer Nanocomposites for Environmental Remediation; Hussain, C.M., Mishra, A., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 541–600. [Google Scholar]
- He, H.; Wu, T.; Chen, Y.F.; Yang, Z. A pore-scale investigation of microplastics migration and deposition during unsaturated flow in porous media. Sci. Total Environ. 2023, 858, 159934. [Google Scholar] [CrossRef]
- Viotti, P.; Sappa, G.; Tatti, F.; Andrei, F. nZVI Mobility and Transport: Laboratory Test and Numerical Model. Hydrology 2022, 9, 196. [Google Scholar] [CrossRef]
- Mondal, A.; Dubey, B.K.; Arora, M.; Mumford, K. Porous media transport of iron nanoparticles for site remediation application: A review of lab scale column study, transport modelling and field-scale application. J. Hazard. Mater. 2021, 403, 123443. [Google Scholar] [CrossRef] [PubMed]
- Bianco, C.; Tosco, T.; Sethi, R. A 3-dimensional micro- and nanoparticle transport and filtration model (MNM3D) applied to the migration of carbon-based nanomaterials in porous media. J. Contam. Hydrol. 2016, 193, 10–20. [Google Scholar] [CrossRef] [Green Version]
- Ma, C.; Huangfu, X.; He, Q.; Ma, J.; Huang, R. Deposition of engineered nanoparticles (ENPs) on surfaces in aquatic systems: A review of interaction forces, experimental approaches, and influencing factors. Environ. Sci. Pollut. Res. 2018, 25, 33056–33081. [Google Scholar] [CrossRef]
- Elimelech, M.; O’Melia, C.R. Effect of Particle Size on Collision Efficiency in the Deposition of Brownian Particles with Electrostatic Energy Barriers. Langmuir 1990, 6, 1153–1163. [Google Scholar] [CrossRef]
- Yang, H.; Hu, R.; Ruppert, H.; Noubactep, C. Modeling porosity loss in Fe0-based permeable reactive barriers with Faraday’s law. Sci. Rep. 2021, 11, 16998. [Google Scholar] [CrossRef]
- Bilardi, S.; Calabrò, P.S.; Moraci, N. Reactive and Hydraulic Behavior of Granular Mixtures Composed of Zero Valent Iron. Water 2022, 14, 3613. [Google Scholar] [CrossRef]
- Domga, R.; Togue-Kamga, F.; Noubactep, C.; Tchatchueng, J.B. Discussing porosity loss of Fe0 packed water filters at ground level. Chem. Eng. J. 2015, 263, 127–134. [Google Scholar] [CrossRef]
- Moraci, N.; Lelo, D.; Bilardi, S.; Calabrò, P.S. Modelling long-term hydraulic conductivity behaviour of zero valent iron column tests for permeable reactive barrier design. Can. Geotech. J. 2016, 53, 946–961. [Google Scholar] [CrossRef]
- Moraci, N.; Bilardi, S.; Calabrò, P.S. Critical aspects related to Fe0 and Fe0/pumice PRB design. Environ. Geotech. 2016, 3, 114–124. [Google Scholar] [CrossRef]
- Bilardi, S.; Calabrò, P.S.; Moraci, N. A Review of the Hydraulic Performance of Permeable Reactive Barriers Based on Granular Zero Valent Iron. Water 2023, 15, 200. [Google Scholar] [CrossRef]
- Yang, H.; Hu, R.; Ndé-Tchoupé, A.I.; Gwenzi, W.; Ruppert, H.; Noubactep, C. Designing the next generation of Fe0-based filters for decentralized safe drinking water treatment. Processes 2020, 8, 745. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, P.; Wang, S.; Finfrock, Y.Z.; Ye, Z.; Feng, Y.; Li, X. Iron-modified biochar-based bilayer permeable reactive barrier for Cr (VI) removal. J. Hazard. Mater. 2022, 439, 129636. [Google Scholar] [CrossRef]
- Plessl, K.; Russ, A.; Vollprecht, D. Application and development of zero-valent iron (ZVI) for groundwater and wastewater treatment. Int. J. Environ. Sci. Technol. 2022, 1–16. [Google Scholar] [CrossRef]
- Njaramba, L.K.; Park, J.B.; Lee, C.S.; Nzioka, A.M.; Kim, Y.J. Permeable reactive barriers with zero-valent iron and pumice for remediation of groundwater contaminated with multiple heavy metals. Environ. Eng. Sci. 2021, 38, 245–255. [Google Scholar] [CrossRef]
- Bilardi, S.; Calabrò, P.S.; Moraci, N.; Madaffari, M.G.; Ranjbar, E. A comparison between Fe0/pumice and Fe0/lapillus mixtures in permeable reactive barriers. Environ. Geotech. 2019, 7, 524–539. [Google Scholar] [CrossRef]
- Calabrò, P.S.; Bilardi, S.; Moraci, N. Advancements in the use of filtration materials for the removal of heavy metals from multicontaminated solutions. Curr. Opin. Environ. Sci. Health 2021, 20, 100241. [Google Scholar] [CrossRef]
- Peng, L.; Zhang, C.; Ma, H.; Pan, H. Estimating irreducible water saturation and permeability of sandstones from nuclear magnetic resonance measurements by fractal analysis. Mar. Pet. Geol. 2019, 110, 565–574. [Google Scholar] [CrossRef]
- Adebayo, T.A. Irreducible water saturation and porosity mathematical models for Kwale sands. Pet. Coal 2015, 57, 412–423. [Google Scholar]
- Castellan, G.W. Physical Chemistry, 3rd ed.; Adison Wesley: Reading, MA, USA, 1983. [Google Scholar]
- Ataie-Ashtiani, B.; Hassanizadeh, S.M.; Celia, M.A. Effects of heterogeneities on capillary pressure–saturation–relative permeability relationships. J. Contam. Hydrol. 2002, 56, 175–192. [Google Scholar] [CrossRef] [PubMed]
- Mufti, S.; Das, A. An advanced pore-scale model for simulating water retention characteristics in granular soils. J. Hydrol. 2022, 615, 128561. [Google Scholar] [CrossRef]
- Bai, X.; Jia, X.; Zhao, C. Prediction of the van Genuchten model soil hydraulic parameters for the 5-m soil profile in China’s Loess Plateau. Catena 2022, 210, 105889. [Google Scholar] [CrossRef]
- Honda, H.; Magara, K. Estimation of irreducible water saturation and effective pore size of mudstones. J. Pet. Geol. 1982, 4, 407–418. [Google Scholar] [CrossRef]
- Kacimov, A.R. Dynamics of groundwater mounds: Analytical solutions and integral characteristics. Hydrol. Sci. J. 1997, 42, 329–342. [Google Scholar] [CrossRef]
- Khan, M.Y.; Kirkham, D.; Handy, R.L. Shapes of steady state perched groundwater mounds. Water Resour. Res. 1976, 12, 429–436. [Google Scholar] [CrossRef]
- Youngs, E.G. An examination of computed steady-state water-table heights in unconfined aquifers: Dupuit-Forchheimer estimates and exact analytical results. J. Hydrol. 1990, 119, 201–214. [Google Scholar] [CrossRef]
- World Health Organization. Guidelines for Drinking-Water Quality: Incorporating the First and Second Addenda, 4th ed.; WHO: Geneva, Switzerland, 2022. [Google Scholar]
- Kanel, S.R.; Manning, B.; Charlet, L.; Choi, H. Removal of arsenic (III) from groundwater by nanoscale zero-valent iron. Environ. Sci. Technol. 2005, 39, 1291–1298. [Google Scholar] [CrossRef]
- Zhu, H.; Jia, Y.; Wu, X.; Wang, H. Removal of arsenic from water by supported nano zero-valent iron on activated carbon. J. Hazard. Mater. 2009, 172, 1591–1596. [Google Scholar] [CrossRef]
- Yang, D.; Wang, L.; Li, Z.; Tang, X.; He, M.; Yang, S.; Liu, X.; Xu, J. Simultaneous adsorption of Cd (II) and As (III) by a novel biochar-supported nanoscale zero-valent iron in aqueous systems. Sci. Total Environ. 2020, 708, 134823. [Google Scholar] [CrossRef]

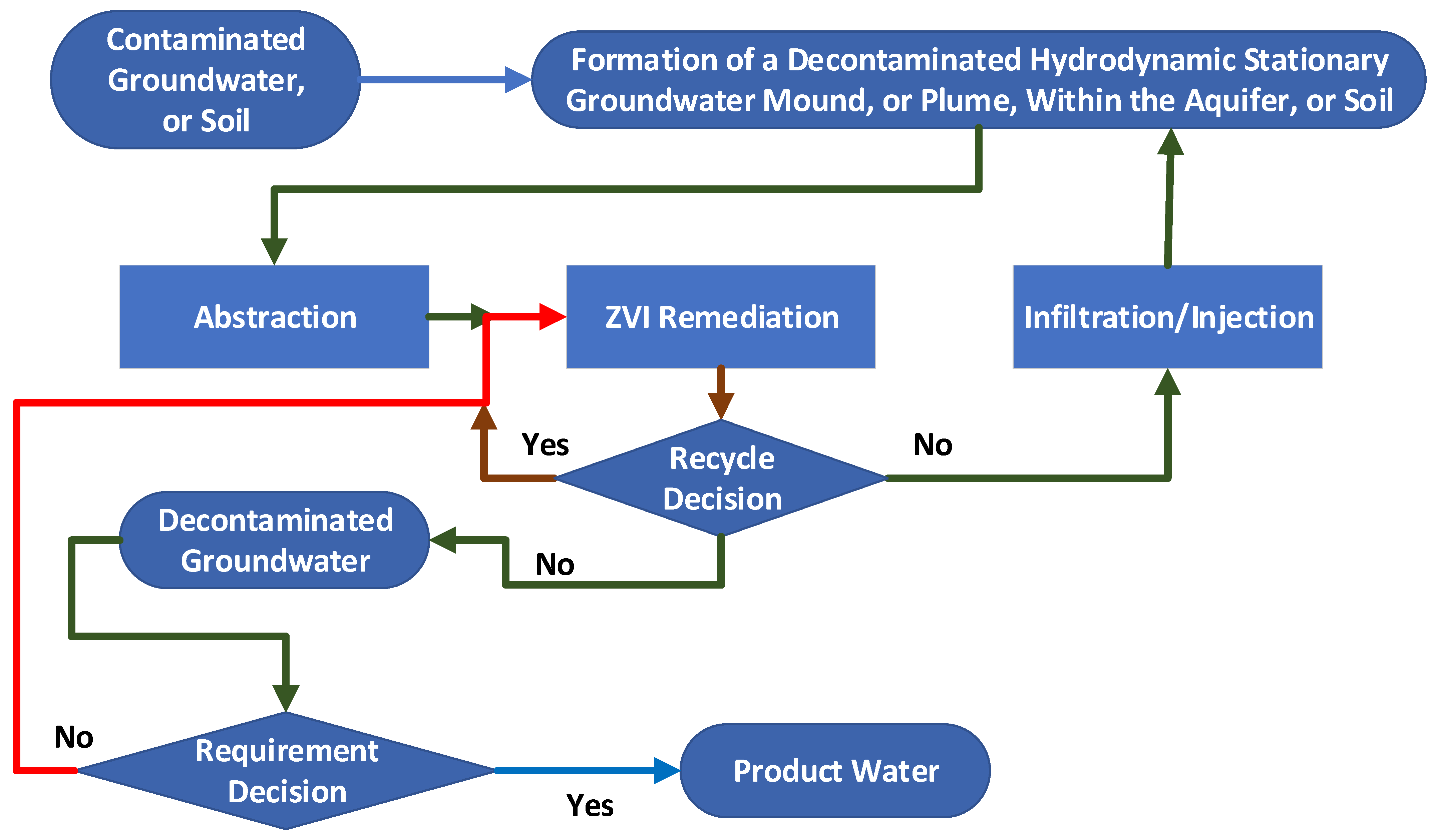
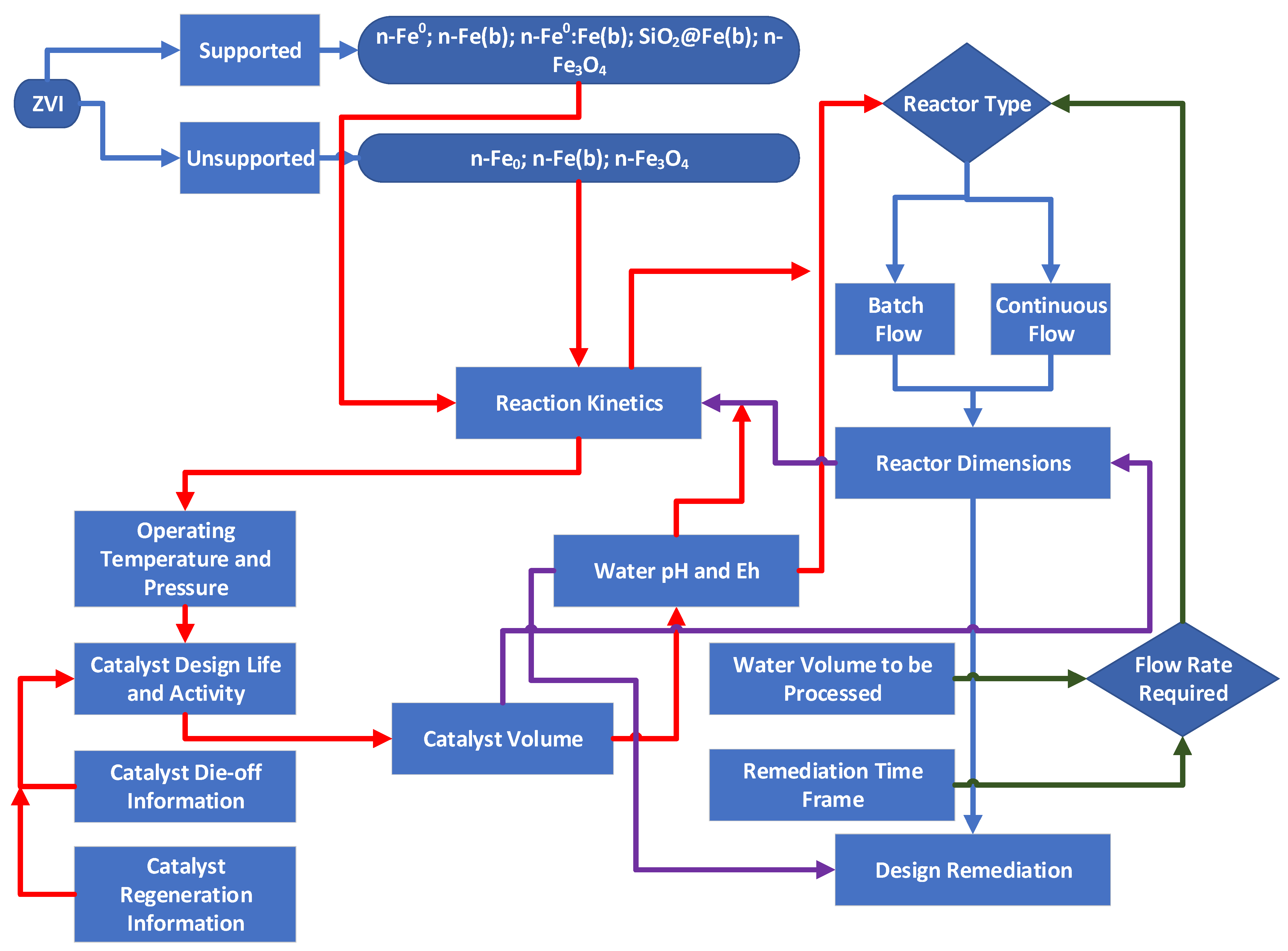


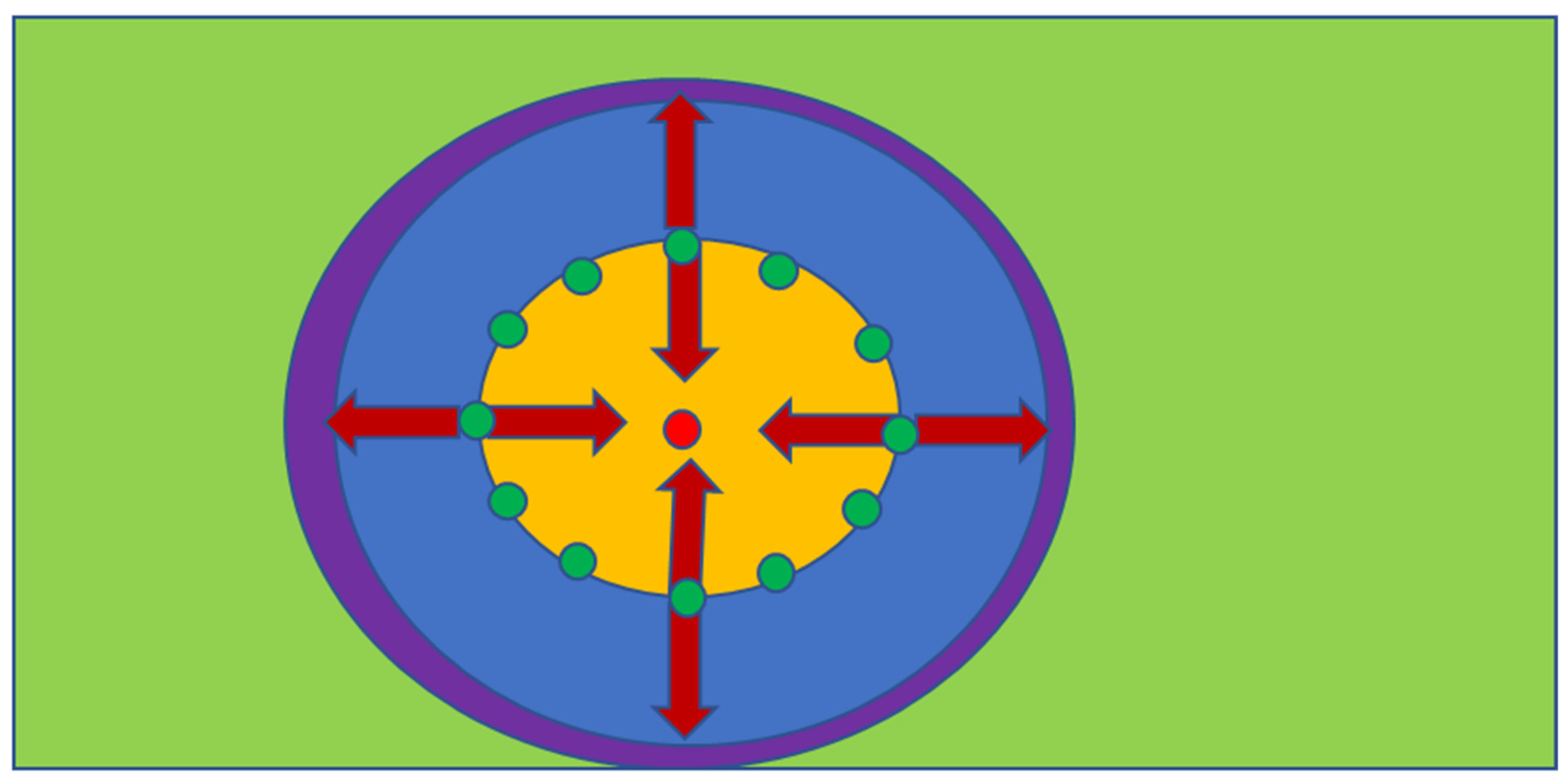
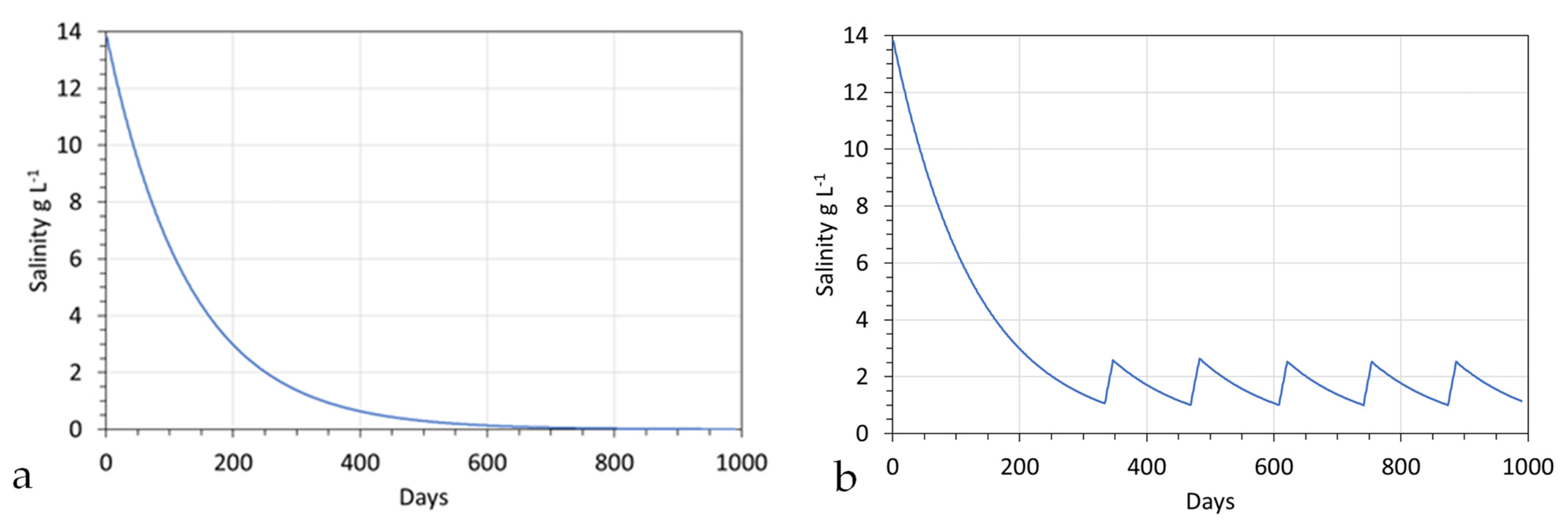
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antia, D.D.J. Hydrodynamic Decontamination of Groundwater and Soils Using ZVI. Water 2023, 15, 540. https://doi.org/10.3390/w15030540
Antia DDJ. Hydrodynamic Decontamination of Groundwater and Soils Using ZVI. Water. 2023; 15(3):540. https://doi.org/10.3390/w15030540
Chicago/Turabian StyleAntia, David D. J. 2023. "Hydrodynamic Decontamination of Groundwater and Soils Using ZVI" Water 15, no. 3: 540. https://doi.org/10.3390/w15030540
APA StyleAntia, D. D. J. (2023). Hydrodynamic Decontamination of Groundwater and Soils Using ZVI. Water, 15(3), 540. https://doi.org/10.3390/w15030540







