Analysis of Optimal Sensor Placement in Looped Water Distribution Networks Using Different Water Quality Models
Abstract
:1. Introduction
2. Materials and Methods
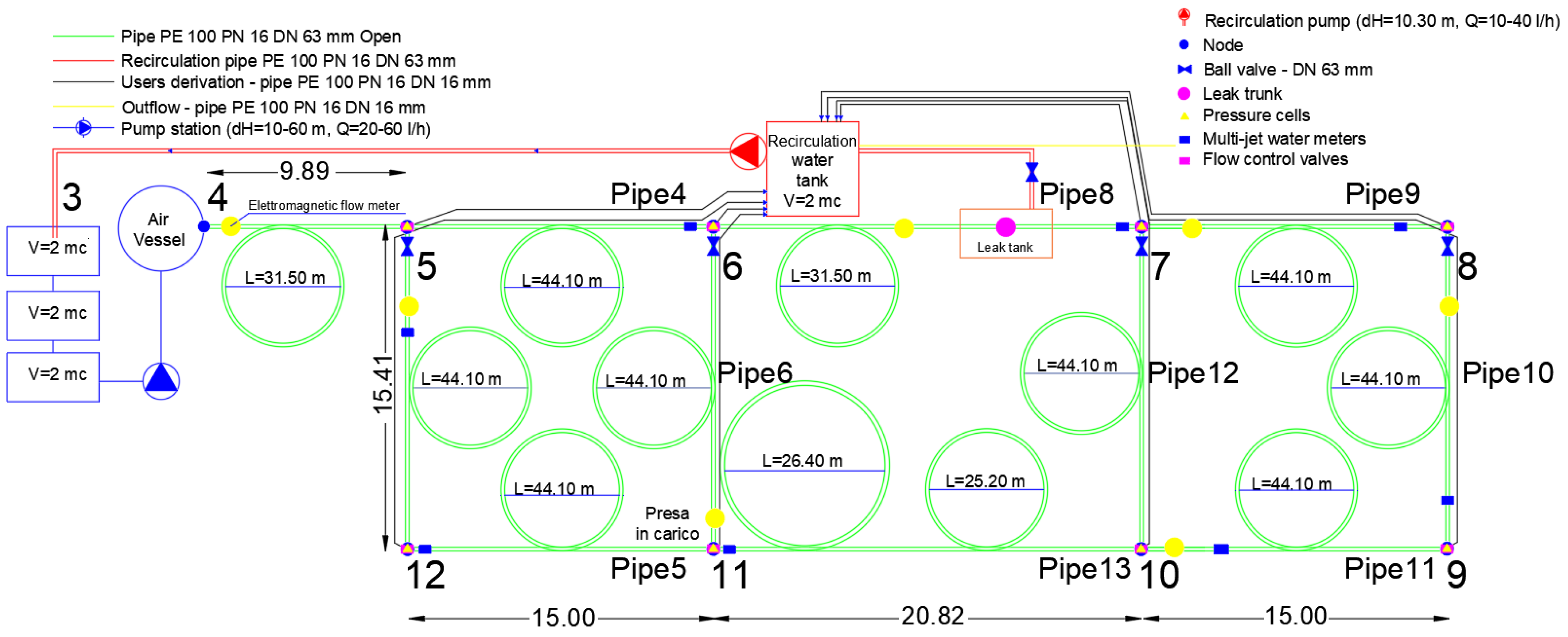
2.1. Experimental Setup and Conditions
2.2. Optimisation of Sensor Placement
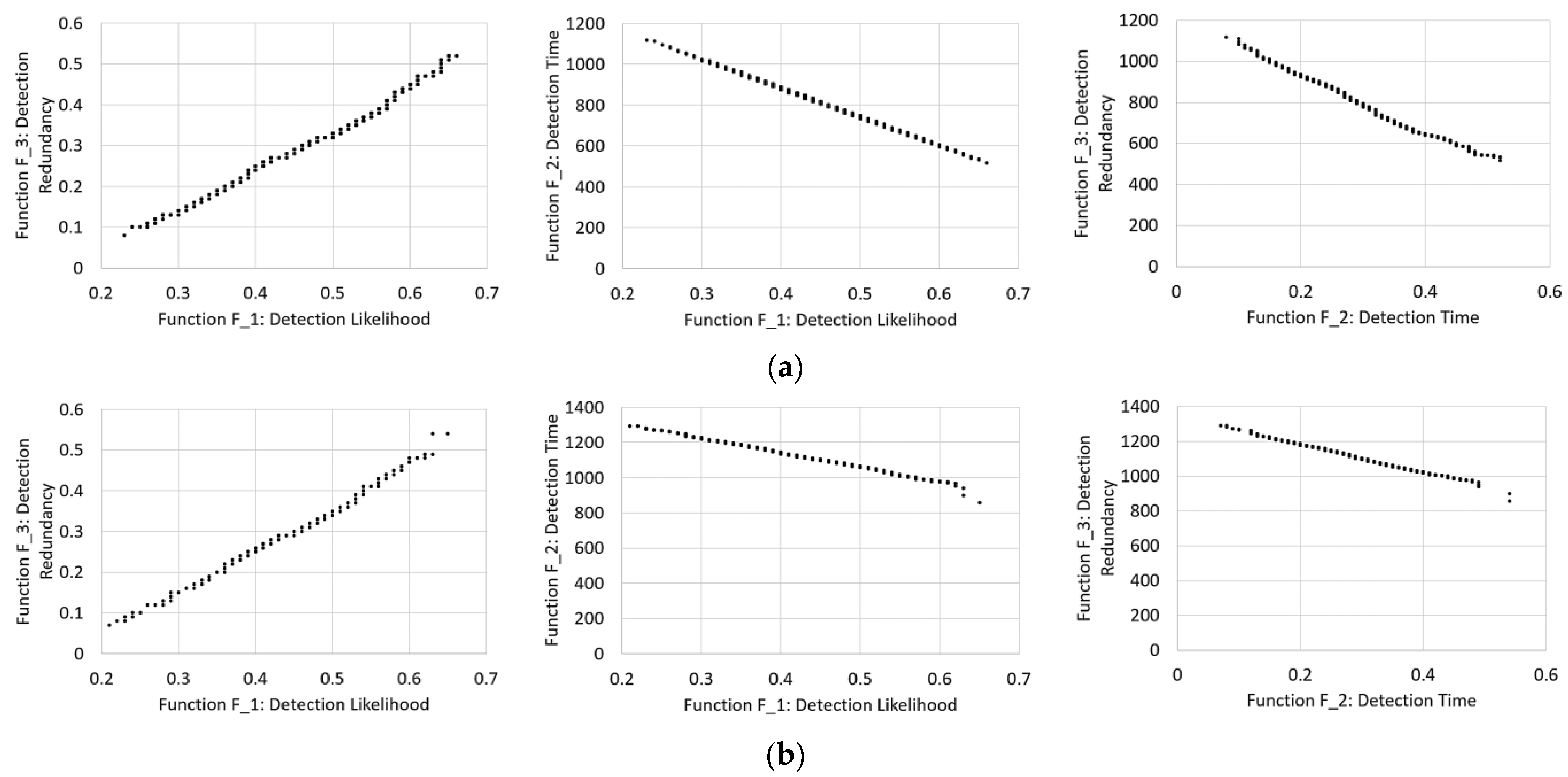
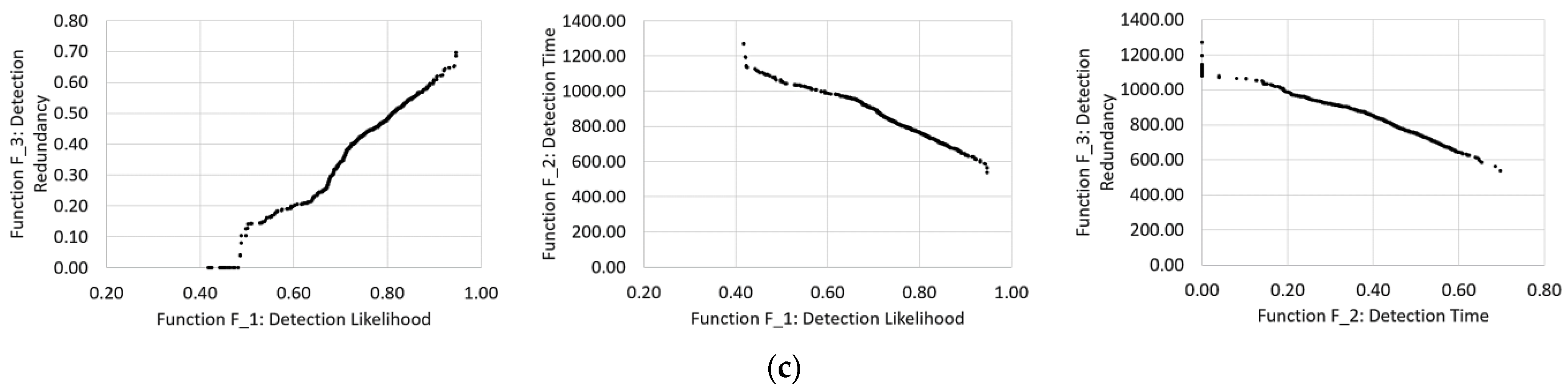
- F_1, the detection likelihood, i.e., the probability that a sensor configuration will detect the contamination;
- F_2, the detection time, i.e., the average time between contamination and detection in 200 simulations;
- F_3, the detection redundancy, i.e., the probability that two sensors detect the contamination within 20 min.
3. Results and Discussions
4. Conclusions
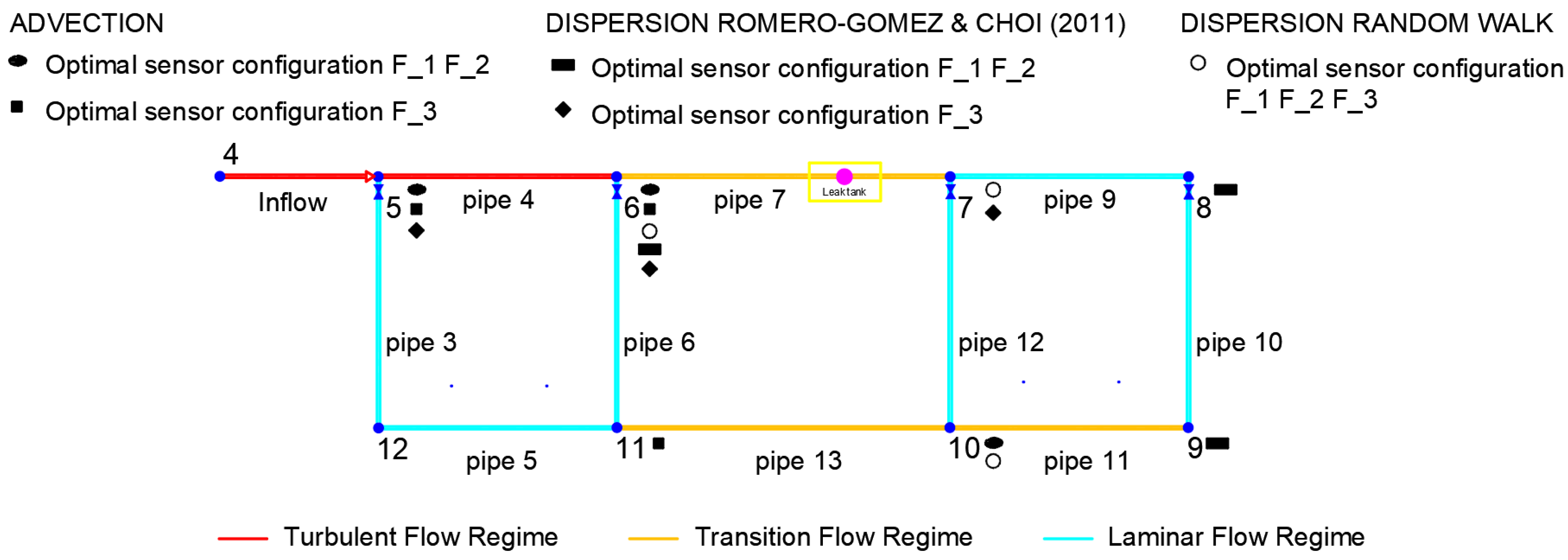
- When the advective approach was used to solve the optimisation problem, the sensors were positioned in areas with high Reynolds numbers, where the flow regimes are predominantly turbulent and transition;
- The sensors were positioned in a linear pattern and covered most of the network using the dispersive AZRED approach;
- The EPANET-DD model provided the best performance, with a contamination event detection likelihood of 95%, a redundancy of 70%, and a detection time of approximately 9 min;
- Different configurations for sensor positions are obtained depending on the model used to solve the optimisation problem, as are different detection efficiencies for the objective functions. For example, the parameter values determined by the advective model are much lower than those determined by the dynamic dispersive model (EPANET-DD).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Singh, R.B.; Kumar, D. Water scarcity. In Handbook of Engineering Hydrology: Environmental Hydrology and Water Management; CRC Press: Boca Raton, FL, USA, 2014; pp. 519–544. [Google Scholar]
- Aisopou, A.; Stoianov, I.; Graham, N.J.D. In-pipe water quality monitoring in water supply systems under steady and unsteady state flow conditions: A quantitative assessment. Water Res. 2012, 46, 235–246. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Winnel, M.; Lin, H.; Panther, J.; Liu, C.; O’Halloran, R.; Wang, K.; An, T.; Wong, P.K.; Zhang, S.; et al. A reliable sewage quality abnormal event monitoring system. Water Res. 2017, 121, 248–257. [Google Scholar] [CrossRef] [PubMed]
- Sambito, M.; Freni, G. Strategies for Improving Optimal Positioning of Quality Sensors in Urban Drainage Systems for Non-Conservative Contaminants. Water 2021, 13, 934. [Google Scholar] [CrossRef]
- Ostfeld, A.; Uber, J.G.; Salomons, E.; Berry, J.W.; Hart, W.E.; Phillips, C.A.; Watson, J.P.; Dorini, G.; Jonkergouw, P.; Kapelan, Z.; et al. The Battle of the Water Sensor Networks (BWSN): A Design Challenge for Engineers and Algorithms. J. Water Resour. Plan. Manag. 2008, 134, 556–568. [Google Scholar] [CrossRef] [Green Version]
- Preis, A.; Ostfeld, A. Multiobjective Contaminant Sensor Network Design for Water Distribution Systems. J. Water Resour. Plan. Manag. 2008, 134, 366–377. [Google Scholar] [CrossRef] [Green Version]
- Villez, K.; Vanrolleghem, P.A.; Corominas, L. Optimal flow sensor placement on wastewater treatment plants. Water Res. 2016, 101, 75–83. [Google Scholar] [CrossRef]
- Weickgenannt, M.; Kapelan, Z.; Blokker, M.; Savic, D.A. Optimal Sensor Placement for the Efficient Contaminat Detection in Water Distribution Systems. In Water Distribution Systems Analysis; ASCE: Reston, VA, USA, 2008. [Google Scholar]
- Murray, R.; Haxton, T.; Janke, R.; Hart, W.E.; Berry, J.; Phillips, C. Sensor Network Design for Drinking Water Contamination Warning Systems: A Compendium of Research Results and Case Studies Using TEVA-SPOT; EPA/600/R-09/141; Office of Research and Development, National Homeland Security Research Center: New Delhi, India, 2009.
- Perelman, L.; Ostfeld, A. Operation of remote mobile sensors for security of drinking water distribution systems. Water Res. 2013, 47, 4217–4226. [Google Scholar] [CrossRef]
- Oliker, N.; Ostfeld, A. Inclusion of Mobile Sensors in Water Distribution System Monitoring Operations. J. Water Resour. Plan. Manag. 2016, 142, 04015044. [Google Scholar] [CrossRef]
- Sankary, N.; Ostfeld, A. Inline Mobile Water Quality Sensors Deployed for Contamination Intrusion Localization. In Computing and Control for the Water Industry; Research Studies Press: Boston, MA, USA, 2017. [Google Scholar]
- Creaco, E.; Campisano, A.; Fontana, N.; Marini, G.; Page, P.R.; Walski, T. Real time control of water distribution networks: A state-of-the-art review. Water Res. 2019, 161, 517–530. [Google Scholar] [CrossRef]
- Isovitsch, S.L.; VanBriesen, J.M. Sensor Placement and Optimization Criteria Dependencies in a Water Distribution System. J. Water Resour. Plan. Manag. 2008, 134, 186–196. [Google Scholar] [CrossRef]
- Ohar, Z.; Lahav, O.; Ostfeld, A. Optimal sensor placement for detecting organophosphate intrusions into water distribution systems. Water Res. 2015, 73, 193–203. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Boccelli, D.L. Dynamic Water-Quality Simulation for Contaminant Intrusion Events in Distribution Systems. J. Water Resour. Plan. Manag. 2016, 142, 04016038. [Google Scholar] [CrossRef]
- Abokifa, A.A.; Xing, L.; Sela, L. Investigating the Impacts of Water Conservation on Water Quality in Distribution Networks Using an Advection-Dispersion Transport Model. Water 2020, 12, 1033. [Google Scholar] [CrossRef] [Green Version]
- Taylor, G. Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. London Ser. A 1953, 219, 186–203. [Google Scholar]
- Taylor, G.I. The dispersion of matter in turbulent flow through a pipe. Proc. R. Soc. London Ser. A 1954, 223, 446–468. [Google Scholar]
- Axworthy, D.H.; Karney, B. Modelling Low Velocity/High Dispersion Flow in Water Distribution Systems. J. Water Resour. Plan. Manag. 1996, 122, 218–221. [Google Scholar] [CrossRef]
- Romeo-Gomez, P.; Choi, C.Y. Axial Dispersion Coefficients in Laminar Flows of Water-Distribution Systems. J. Hydraul. Eng. 2011, 137, 1500–1508. [Google Scholar] [CrossRef]
- Piazza, S.; Blokker, E.J.M.; Freni, G.; Puleo, V.; Sambito, M. Impact of diffusion and dispersion of contaminants in water distribution networks modelling and monitoring. Water Supply 2020, 20, 46–58. [Google Scholar] [CrossRef]
- Rossman, L.A.; Clark, R.M.; Grayman, W.M. Modeling Chorine Residuals in Drinking-Water Distribution Systems. J. Environ. Eng. 1994, 120, 803–820. [Google Scholar] [CrossRef]
- Piazza, S.; Sambito, M.; Freni, G. A Novel EPANET Integration for the Diffusive–Dispersive Transport of Contaminants. Water 2022, 14, 2707. [Google Scholar] [CrossRef]
- Tarantola, A. Monte Carlo Methods. In Inverse Problem Theory and Methods for Model Parameter Estimation; SIAM: Philadelphia, PA, USA, 2004; pp. 41–55. [Google Scholar]
- Rossman, L.A.; Boulos, P.F.; Altman, T. Discrete volume-element method for network water quality models. J. Water Resour. Plan. Manag. 1993, 119, 505–517. [Google Scholar] [CrossRef] [Green Version]
- Lee, Y. Mass Dispersion in Intermittent Laminar Flow; University of Cincinnati: Cincinnati, OH, USA, 2004. [Google Scholar]
- Eliades, D.G.; Kyriakou, M.; Vrachimis, S.; Polycarpou, M.M. EPANET-MATLAB Toolkit: An Open-Source Software for Interfacing EPANET with MATLAB, The Netherlands. In Proceedings of the 14th International Conference on Computing and Control for the Water Industry (CCWI), Amsterdam, The Netherlands, 7–9 November 2016; pp. 1–8. [Google Scholar]
- Delay, F.; Ackerer, P.; Danquigny, C. Simulating Solute Transport in Porous or Fractured Formations Using Random Walk Particle Tracking: A Review. Vadose Zone J. 2005, 4, 360–379. [Google Scholar] [CrossRef]
- Kinzelbach, W.; Uffink, G. The random walk method and extensions in groundwater modelling. Transp. Process. Porous Media 1991, 761–787. [Google Scholar]
- LaBolle, E.M.; Fogg, G.E.; Tompson, A.F.B. Random-walk simulation of transport in heterogeneou porous media: Local mass-conservation problem and implementation methods. Water Resour. Res. 1996, 32, 583–593. [Google Scholar] [CrossRef]


| Advective Model | Romero-Gomez and Choi (2011) Model | EPANET-DD Model | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Objective Functions | Optim. Values | Sensor Node Index | Optim. Values | Sensor Node Index | Optim. Values | Sensor Node Index | ||||||
| Detection Likelihood (F_1) | 0.66 | 5 | 6 | 10 | 0.65 | 6 | 8 | 9 | 0.95 | 6 | 7 | 10 |
| Detection Time [s] (F_2) | 517.13 | 5 | 6 | 10 | 858.54 | 6 | 8 | 9 | 538.96 | 6 | 7 | 10 |
| Redundancy (F_3) | 0.52 | 5 | 6 | 11 | 0.54 | 5 | 6 | 7 | 0.70 | 6 | 7 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piazza, S.; Sambito, M.; Freni, G. Analysis of Optimal Sensor Placement in Looped Water Distribution Networks Using Different Water Quality Models. Water 2023, 15, 559. https://doi.org/10.3390/w15030559
Piazza S, Sambito M, Freni G. Analysis of Optimal Sensor Placement in Looped Water Distribution Networks Using Different Water Quality Models. Water. 2023; 15(3):559. https://doi.org/10.3390/w15030559
Chicago/Turabian StylePiazza, Stefania, Mariacrocetta Sambito, and Gabriele Freni. 2023. "Analysis of Optimal Sensor Placement in Looped Water Distribution Networks Using Different Water Quality Models" Water 15, no. 3: 559. https://doi.org/10.3390/w15030559
APA StylePiazza, S., Sambito, M., & Freni, G. (2023). Analysis of Optimal Sensor Placement in Looped Water Distribution Networks Using Different Water Quality Models. Water, 15(3), 559. https://doi.org/10.3390/w15030559








