ML algorithms are typically categorized into three main groups: supervised, unsupervised, and RL [
5]. A comparison of these is summarized in
Table 2. Supervised learning algorithms employ labeled datasets to train the algorithms to classify or predict the output, where both the input and output values are known beforehand. Unsupervised learning algorithms are trained using unlabeled datasets for clustering. These algorithms discover hidden patterns or data groupings without the need for human intervention. RL is an area of ML that concerns how intelligent an agent is to take action in an environment to obtain the maximum reward. In both supervised and RL, inputs and outputs are mapped such that the agent is informed of the best strategy to take in order to complete a task. In RL, positive and negative behaviors are signaled through incentives and penalties, respectively. As a result, in supervised learning, a machine learns the behavior and characteristics of labeled datasets, detects patterns in unsupervised learning, and explores the environment without any prior training in RL algorithms. Thus, an appropriate category of ML is required based on the engineering application. The major ML learning types in WRM are summarized in
Figure 2, where the first segment covers the core contents of the research reviewed in the following sections.
3.1. Prediction
The term “prediction” refers to any technique that uses data processing to get an estimation of an outcome. This is the outcome of an algorithm that was trained on a prior dataset and is now being applied to new data to assess the likelihood of a certain result in order to generate an output model. Forecasting is the probabilistic version of predicting an event in the future. In this review paper, the terms prediction and forecasting are used interchangeably. ML model predictions can be used to create very accurate estimations of the potential outcomes of a situation based on past data, and they can be about anything. For each record in the new data, the algorithm will generate probability values for an unknown variable, allowing the model builder to determine the most likely value. Prediction models can have either a parametric or non-parametric form; however, most WRM models are parametric. The development steps consist of four phases: data processing, feature selection, hyperparameter tuning, and training. Raw historical operation data are translated to a normalized scale in the data transformation step to increase the accuracy of the prediction model. The feature extraction stage extracts the essential variables that influence the output. These retrieved features are then used to train the model. The model’s hyperparameters are optimized to acquire the best model structure. Finally, the model’s weights are automatically modified to produce the final forecast model, which is of paramount importance for optimal control, performance evaluation, and other purposes.
3.1.1. Essential Data Processing in ML
For prediction purposes, ML algorithms can be applied to a wide variety of data types and formats, including time series, big data, univariate, and multivariate datasets. Time series are observations of a particular variable collected at regular intervals and in chronological order across time. A feature dataset is a collection of feature classes that utilize the same coordinate system and are connected. Its major purpose is to collect similar feature classes into a single dataset, which can be used to generate a network dataset. Many real-world datasets are becoming increasingly multi-featured because the ability to acquire information from a variety of sources is continuously expanding. Big data was first defined in 2005 as a large volume of data that cannot be processed by typical database systems or applications because of its size and complexity. Big data are extremely massive, complex, and challenging to process with the current infrastructure. Big data can be classified as structured, unstructured, or semi-structured. Structured data are the most well-known among hydrologist researchers because of their easy accessibility; they are usually stored in spreadsheets. Unstructured data such as images, video, and audio cannot be directly analyzed with a machine, whereas semi-structured data such as user-defined XML files can be read by a machine. Big data have five distinguishing characteristics (namely, the five Vs): volume, variety, velocity, veracity, and value. Recent developments in graphics processing units (GPUs) have paved the way for ML and its subset to get the advantage of big data and learn the complex and high dimensional environment. The establishment of a prediction model begins with the assimilation of data. It includes the phases of data collection, cleansing, and processing.
After adequate components have been gathered, any dataset needs to be structured. Predefined programs allow for the application of a variety of data manipulation, imputation, and cleaning procedures to achieve this goal. Anomalies and missing data are common in datasets and require special attention throughout the preprocessing phase. Depending on the goals of the prediction and the techniques selected, the clean data will require further processing. Depending on the type of prediction model being used, a dataset may employ a single labeled category or multiple categories. In ML, there are four types of data: numerical, categorical, time series, and text. The selected data category affects the techniques available for feature engineering and modeling, as well as the research questions that can be posed. Depending on how many variables need to be predicted, a prediction model will either be univariate, bivariate, or multivariate. In the processing phase, the raw data are remodeled, combined, reorganized, and reconstructed to meet the needs of the model.
3.1.2. Algorithms and Metrics for Evaluation
Because the outcomes of various ML approaches are not always the same, their performances are assessed by considering the outcomes acquired. Numerous statistical assessment measures have been proposed to measure the efficacy of the ML prediction technique.
Table 3 summarizes some commonly used ML evaluation metrics, classifying them as either magnitude, absolute, or squared error metrics. The mean normalized bias and mean percentage error, which measures the discrepancies between predicted and observed values, fall under the first group. When only the amount by which the data deviate from the norm is of interest, an absolute function can be used to report an absolute error as a positive value, where
,
,
, and
denote the observed, predicted, the mean of the observed, and the mean of the predicted value, respectively.
3.1.3. Applications and Challenges
The metrics used to evaluate the performance of ML models based on the accuracy of the predicted values are presented in
Table 3. Choosing the correct metric to evaluate a model is crucial, as some models may only produce favorable results when evaluated using a specific metric. Researchers’ assessments of the significance of various characteristics in the outcomes are influenced by the metrics they use to evaluate and compare the performances of ML algorithms. Each year, a considerable number of papers are published to share the successes and achievements in the vast area of WRM. In the field of hydrology, some studies employ recorded data such as streamflow, precipitation, and temperature data, whereas others employ processed data such as large-scale atmospheric data, which are generated using gauge and satellite data. When it comes to predictions in the field of WRM, data-driven models perform better than statistical models owing to their higher capability in a complex environment.
Table 4 provides a brief overview of some of the recent applications of ML for WRM prediction, with the relevant abbreviations defined in the glossary.
Today, most countries are putting more pressure on their water resources than ever before. The world’s population is growing quickly, and if things stay the same, there will be a 40% gap between how much water is needed and how much is available by 2030. In addition, extreme weather events like floods and droughts are seen as some of the biggest threats to global prosperity and stability. People are becoming more aware of how water shortages and droughts make fragile situations and conflicts worse. Changes in hydrological cycles due to climate change will exacerbate the problem by making water more volatile and increasing the frequency and severity of floods and droughts. Approximately 1 billion people call monsoonal basins home, while another 500 million call deltas home. In this situation, the lives of millions of people are relying on a sustainable integrated WRM plan, which is an essential issue being handled by engineers and hydrologists. To increase water security in the face of increasing demand, water scarcity, growing uncertainty, and severe natural hazards such as floods and droughts, politicians, governments, and all shareholders will be required to invest in institutional strengthening, data management, and hazard control infrastructure facilities. Institutional instruments such as regulatory frameworks, water prices, and incentives are needed for better allocation, governance, and conservation of water resources. Having open access to information is essential for water resources monitoring, decision-making under uncertainty, hydro-meteorological prediction, and early warning. Ensuring the quick spread and appropriate adaptation or use of these breakthroughs is critical for increasing global water resilience and security. However, the absence of appropriate data sets restricts the accuracy of prediction models, especially in complex real-world applications. Moreover, advanced multi-dimensional prediction models are scarce in hydrology and WRM studies. ML algorithms should be able to self-learn and make accurate predictions based on the provided data. It is anticipated that models that integrate various efficient algorithms into elaborate ML architectures will form the groundwork for future research lines. Some of the difficulties currently encountered in hydrological prediction may be overcome by employing newly emerging networks such as graph neural networks. The lack of widespread adaption of cutting-edge algorithms in the water-resource field, such as those used in image and natural language processing, hampers the creation of cutting-edge multidisciplinary models for integrated WRM.
Table 4 shows no signs of the implementation of attention-based models, CNNs, or even more compatible models with long sequence time-series forecasting (LSTF), such as informer and conformer. Finding an appropriate prediction model and prediction strategy is the primary difficulty in prediction research. The five initial steps for ML prediction models are shown in
Figure 3. If even one of these steps is conducted poorly, it will affect the rest, and as a result, the entire prediction strategy will fail.
3.2. Clustering
The importance of clustering in hydrology cannot be overstated. The clustering of hydrological data provides rich insights into diverse concepts and relations that underline the inherent heterogeneity and complexity of hydrological systems. Clustering is a form of unsupervised ML that can identify hidden patterns in data and classify them into sets of items that share the most similarities. Similarities and differences among cluster members are revealed by the clustering procedure. The intra-cluster similarity is just as important as inter-cluster dissimilarity in cluster analysis. Different clustering algorithms vary in how they detect different types of data patterns and distances. Classification is distinct from clustering. In other words, a machine uses a supervised procedure called classification to learn the pattern, structure, and behavior of the data that it is fed. In supervised learning, the machine is fed with labeled historical data in order to learn the relationships between inputs and outputs, whereas in unsupervised learning, the machine is fed only input data and then asked to discover the hidden patterns. In this method, data is clustered to make models more manageable, decrease their dimensionality, or improve the efficiency of the learning process. Each of these applications, along with the pertinent literature, is discussed in this section.
3.2.1. Algorithms and Metrics for Evaluation
There are numerous discussions of clustering algorithms in the literature. Some studies classify clustering algorithms as monothetic or polythetic. Members of a cluster share a common set of characteristics in monothetic approaches, whereas polythetic approaches are based on a broader measure of similarity [
48]. Depending on the algorithm’s parameters, a clustering algorithm may produce either hard or soft clusters. Hard clustering requires that an element is either a member of a cluster or not. Soft clustering allows for the possibility of cluster overlap. The structure of the resulting clusters may be flat or hierarchical. While some strategies for clustering produce collections of groups, others benefit from a systematic approach. Algorithms for hierarchical clustering may be agglomerative or divisive [
49]. A dataset’s points are clustered by combining them with their neighbors using agglomerative approaches. The desired number of clusters is attained by repeatedly dividing the original unit in divisive approaches.
The well-known clustering algorithms in WRM are shown in
Figure 4. Many clustering algorithms fall into the individual branches of the figure. Some of the famous partitional methods are K-means, K-medians, and K-modes. These algorithms are centroid-based methods that form clusters around known data centroids. Fuzzy sets and fuzzy C-means are soft clustering techniques applied extensively in control systems and reliability studies. The density-based spatial clustering of applications with noise (DBSCAN) and its updated version, distributed density-based clustering for multi-target regression, deals with probabilities while clustering. Divisive clustering analysis (DIANA) and agglomerative nesting (AGNES) are two hierarchical methods and functions that readily visualize the clustering procedure. The performances of these algorithms significantly depend on the distance functions chosen. Distribution-based clustering of large spatial databases (DBCLASD) and Gaussian mixed models are some of the popular distribution-based functions built upon mature experiments. The statistics of support vectors are used by the support vector clustering algorithms to develop data clusters with some margins.
Table 5 lists some of the error functions commonly used to assess the performance of clustering algorithms. These metrics can be used to answer both the question of which clustering method performs better and the question of how many clusters should be used in a given dataset. These issues may be addressed in a variety of ways, such as through the use of graphical inspection and the implementation of an optimization algorithm. Nonetheless, this relies on the clustered dataset, and no comprehensive approaches have yet been proposed.
3.2.2. Clustering in the Field of WRM
Clustering techniques are extensively applied in different WRM fields. It is up to the discretion of the decision maker (DM) to choose the best strategy for the growth and use of water resources. When the DM has access to relevant data, better decisions should follow. However, as more data become available, the DM will have a harder time compiling relevant summaries and settling on a single decision option. Clustering analysis has proven to be a useful method of condensing large amounts of data into manageable chunks for easier analysis and management in a decision-making environment [
56].
Some of the applications of clustering algorithms in hydrology include time series modeling [
57], interpolation and data mining [
58], delineation of homogenous hydro-meteorological regions [
59], catchment classification [
60], regionalization of the catchment for flood frequency analysis and prediction [
61], flood risk studies [
62], hydrological modeling [
63], hydrologic similarity [
64], and groundwater assessment [
65,
66]. Clustering is useful in these situations because it simplifies the creation of effective executive plans and maps by reducing the problem diversity. Furthermore, one of the more traditional uses of clustering analysis is in spotting outliers and other anomalies in the dataset. Any clustering approach can be used for anomaly detection, but the choice will depend on the nature and structure of the data. To sum up, cluster analysis is advantageous for complex projects because it enables accurate dimension reduction for both models and features without compromising accuracy.
3.2.3. Clustering Applications and Challenges in WRM
Some recent applications of clustering algorithms in WRM are summarized in
Table 6. Model simplification, ease of learning, and dimensionality reduction are all areas where K-means variants contribute significantly to hydrological research. Moreover, they are easy to change to fit different types, shapes, and distributions of data, and they are easy to apply and available in most commercial data analysis and statistics packages. As shown in
Table 6, K-means and hierarchical clustering are the most commonly used methods in WRM. The former can handle big data well, while the later cannot. This is because the time complexity of K-means is linear, whereas that of hierarchical clustering is quadratic [
67]. Hierarchical algorithms are predominantly used for dimension reduction [
68]. Data imputation and cleaning are two examples of secondary data analytics applications that benefit from density-based algorithms. Furthermore, a recent study by Gao et al. [
69] reported the capability of density-based algorithms for clustering a dataset with missing features. Most studies report the number of clusters required for the successful application of a clustering algorithm because conventional clustering algorithms cannot efficiently handle real-world data clustering challenges [
70]. As shown in
Table 6, the required number of clusters varies considerably based on the nature of the problem. While the optimal method for determining the number of clusters to employ is discussed in the majority of clustering papers, this is still a topic of debate in the ML community.
Although unsupervised learning performs well in reducing the dimensions of complicated models, the rate at which new clustering algorithms are created has fallen in recent years. Various neural networks can play a role as clustering algorithms. It is anticipated that new ML algorithms will be required to solve multidisciplinary WRM problems, and data clustering will be an important step in defining a constructive problem. After discovering their hidden patterns, ML algorithms are able to autonomously solve these problems. Clustering ensembles, as opposed to single clustering models, are at the forefront of computer science. The effectiveness of diverse ensemble architectures still needs to be investigated. The reliability of probabilistic clustering algorithms, which are an updated version of classic decision-making tools, have also been investigated in recent research. Unsupervised learning-based predictive models and their accuracy evaluation are a new field of research.
3.3. Reinforcement Learning
This section provides an in-depth introduction to RL, covering all the fundamental concepts and algorithms. After years of being ignored, this subfield of ML has recently gained much attention as a result of the successful application of Google DeepMind to learning to play Atari games in 2013 (and, later, learning to play Go at the highest level) [
92]. This modern subfield of ML is a crowning achievement of DL. RL deals with how to learn control strategies to interact with a complex environment. In other words, RL defines how to interact with the environment based on experience (by trial and error) as a framework for learning. Currently, RL is the cutting-edge research topic in the field of modern artificial intelligence (AI), and its popularity is growing in all scientific fields. It is all about taking appropriate action to maximize reward in a particular environment. In contrast to supervised learning, in which the answer key is included in the training data by labeling them, and the model is trained with the correct answer itself, RL does not have an answer; instead, the reinforcement autonomous agent determines what to do in order to accomplish the given task. In other words, unlike supervised learning, where the model is trained on a fixed dataset, RL works in a dynamic environment and tries to explore and interact with that environment in different ways to learn how to best accomplish its tasks in that environment without any form of human supervision [
93,
94]. The Markov decision process (MDP), which is a framework that can be utilized to model sequential decision-making issues, along with the methodology of dynamic programming (DP) as its solution, serves as the mathematical basis for RL [
95]. RL extends mainly to conditions with known and unknown MDP models. The former refers to model-based RL, and the latter refers to model-free RL. Value-based RL, including Monte Carlo (MC) and temporal difference (TD) methods, and policy-search-based RL, including stochastic and deterministic policy gradient methods, fall into the category of model-free RL. State–action–reward–state–action (SARSA) and Q-learning are two well-known TD-based RL algorithms that are widely employed in RL-related research, with the former employing an on-policy method and the latter employing an off-policy method [
90,
91].
When it comes to training agents for optimal performance in a regulated Markovian domain, Q-learning is one of the most popular RL techniques [
96]. It is an off-policy method in which the agent discovers the optimal policy without following the policy. The MDP framework consists of five components, as shown in
Figure 5. To comprehend RL, it is required to understand agents, environments, states, actions, and rewards. An autonomous agent takes action, where the action is the set of all possible moves the agent can take [
97]. The environment is a world through which the agent moves and responds. The agent’s present state and action are inputs, while the environment returns the agent’s reward and its next state as outputs. A state is the agent’s concrete and immediate situation. An action’s success or failure in a given state can be measured through the provision of feedback in the form of a reward, as shown in
Figure 5. Another term in RL is policy, which refers to the agent’s technique for determining the next action based on the current state. The policy could be a neural network that receives observations as inputs and outputs the appropriate action to take. The policy can be any algorithm one can think of and does not have to be deterministic. Owing to inherent dynamic interactions and complex behaviors of the natural phenomena dealt with in WRM, RL could be considered a remedy to solve a wide range of tasks in the field of hydrology. Most real-world WRM challenges can be handled by RL for efficient decision-making, design, and operation, as elucidated in this section.
Water resources have always been vital to human society as sources of life and prosperity [
98]. Owing to social development and uneven precipitation, water resources security has become a global issue, especially in many water-shortage countries where competing demands over water among its users are inevitable [
99]. Complex and adaptive approaches are needed to allocate and use water resources properly. Allocating water resources properly is difficult because many different factors, including population, economic, environmental, ecologic, policy, and social factors, must be considered, all of which interact with and adapt to water resources and related socio-economic and environmental aspects.
RL can be utilized to model the behaviors of agents, simplify the process of modeling human behavior, and locate the optimal solution, particularly in an uncertain decision-making environment, to optimize the long-term reward. Simulating the actions of agents and the feedback corresponding to those actions from the environment is the aim of RL-based approaches. In other words, RL involves analyzing the mutually beneficial relationships that exist between the agents and the system, which is an essential requirement in an optimal water resources allocation and management scenario. Another challenging yet less investigated issue in WRM and allocation is shared resource management. Without simultaneously considering the complicated and challenging social, economic, and political aspects, along with the roles of all the beneficiaries and stakeholders, providing an applicable decision-making plan for water demand management is not possible, especially in countries located in arid regions suffering from water crises. Various frameworks have been proposed to analyze and model such a multi-level, complex, and dynamic environment. In the last two decades, complex adaptive systems (CASs) have received much attention because of their efficacy [
100].
In the realm of WRM, agent-based modeling (ABM) is a popular simulation method for investigating the non-linear adaptive interactions inherent to a CAS [
95]. ABM has been widely used for simulating human decisions when modeling complex natural and socioecological systems. In contrast, the application of ABM in WRM is still relatively new [
101], despite the fact that it can be used to define and simulate water resources wherein individual actors are described as unique and autonomous entities that interact regionally with one another and with a shared environment, thus addressing the complexity of integrated WRM [
102,
103]. In RL water resources-related studies, when addressing water allocation systems, from water infrastructure systems and ecological water consumers to municipal water supply and demand problem management, agents have been conceptualized to represent urban water end-users [
104,
105].
While RL has shown promise in self-driving cars, games, and robot applications, it has not been given widespread attention related to applications in the field of hydrology. However, RL is expected to take over an increasingly wide range of real-world applications in the future, especially to obtain better WRM schemes. Over the past five years, numerous frameworks have emerged, including Tensorforce, which is a useful RL open-source library based on TensorFlow [
106], and Keras-RL [
107]. In addition to these, it is notable that there are now additional frameworks such as TF-agents [
108], RL-coach [
109], acme [
110], dopamine [
111], RLlib [
112], and stable baselines3 [
113]. RL can be integrated with a DNN as a function approximator to improve its performance. Deep reinforcement learning (DRL) is capable of automatically and directly abstracting and extracting high-level features while avoiding complex feature engineering for a specific task. Some trendy DRL algorithms that are modified from Q-learning include the deep Q-network (DQN) [
92], double DQN (DDQN) [
114], and dueling DQN [
115]. Other packages for the Python programming language are available to facilitate the implementation of RL, including the PyTorch-based RL (PFRL) library [
116]. Other fundamental, engineering-focused programming languages such as MATLAB (MathWorks), and Modelica (Modelica Association Project) have also been utilized for the development and instruction of RL agents. The application of RL in WRM and planning will simplify the complexity of all the conflicting interests and their interactions. It will also provide a powerful tool for simulating new management scenarios to understand the consequences of decisions in a more straightforward way [
95]. The categorization of RL algorithms by OpenAI using [
112,
113,
114,
115,
116,
117,
118,
119,
120,
121,
122,
123,
124,
125,
126,
127,
128,
129] was utilized to draw the overall picture in
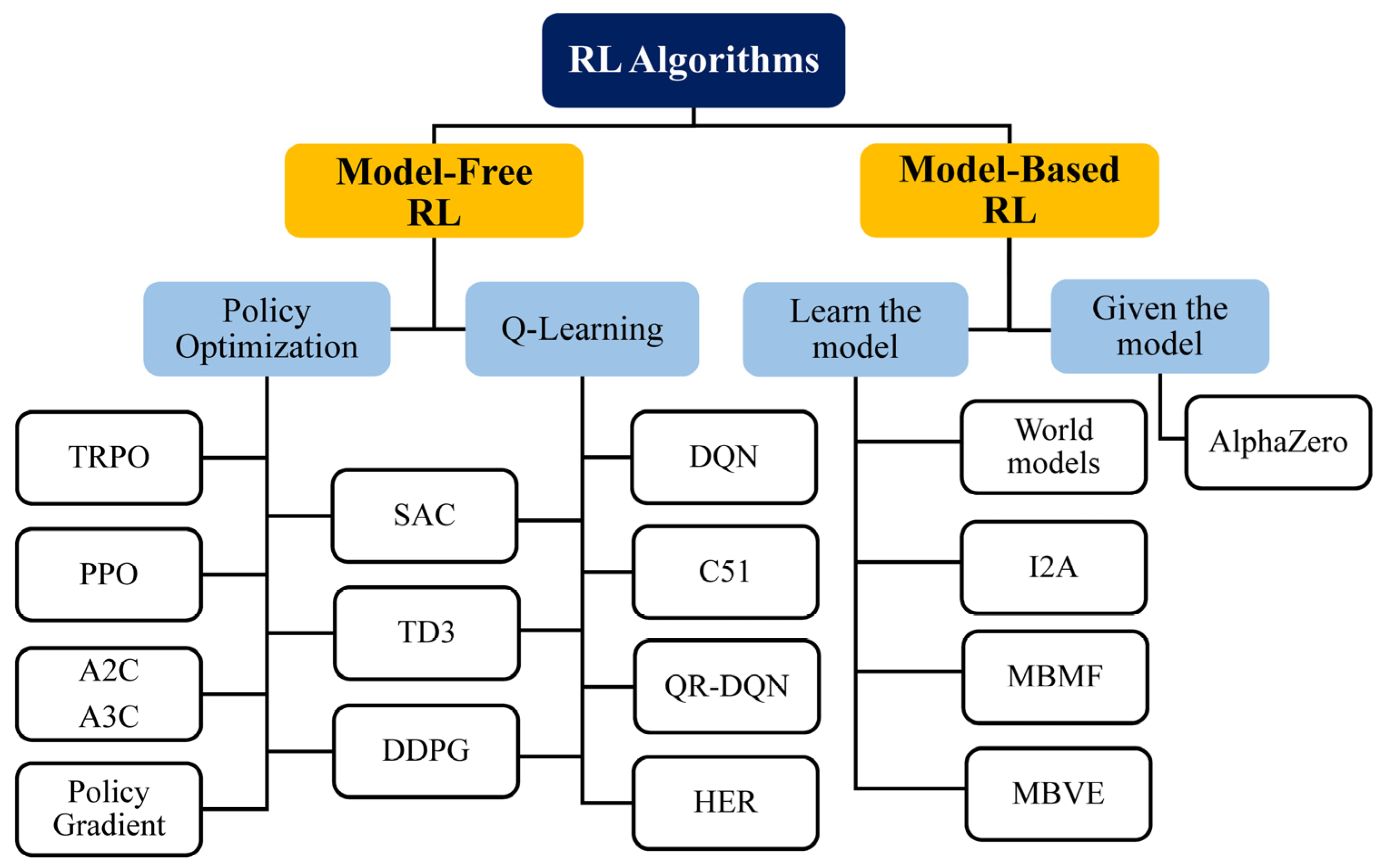
Figure 6.