Spreading of Impacting Water Droplet on Surface with Fixed Microstructure and Different Wetting from Superhydrophilicity to Superhydrophobicity
Abstract
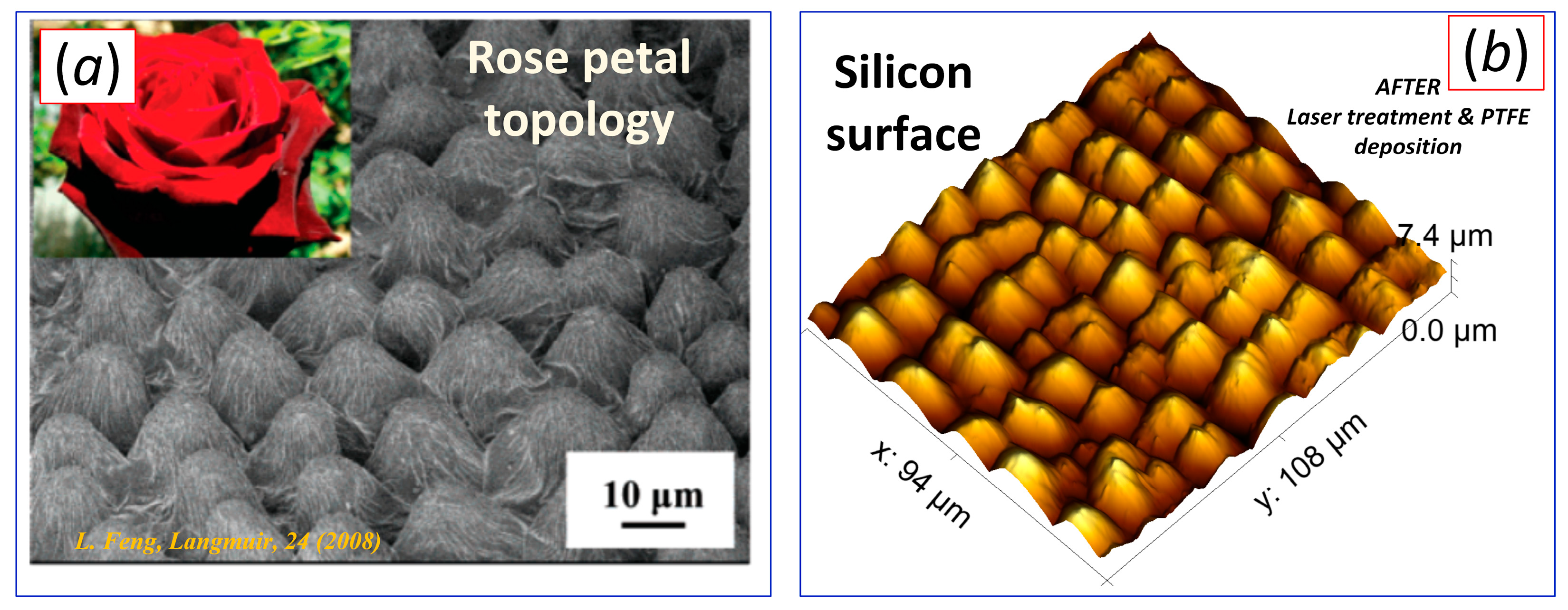
:1. Introduction
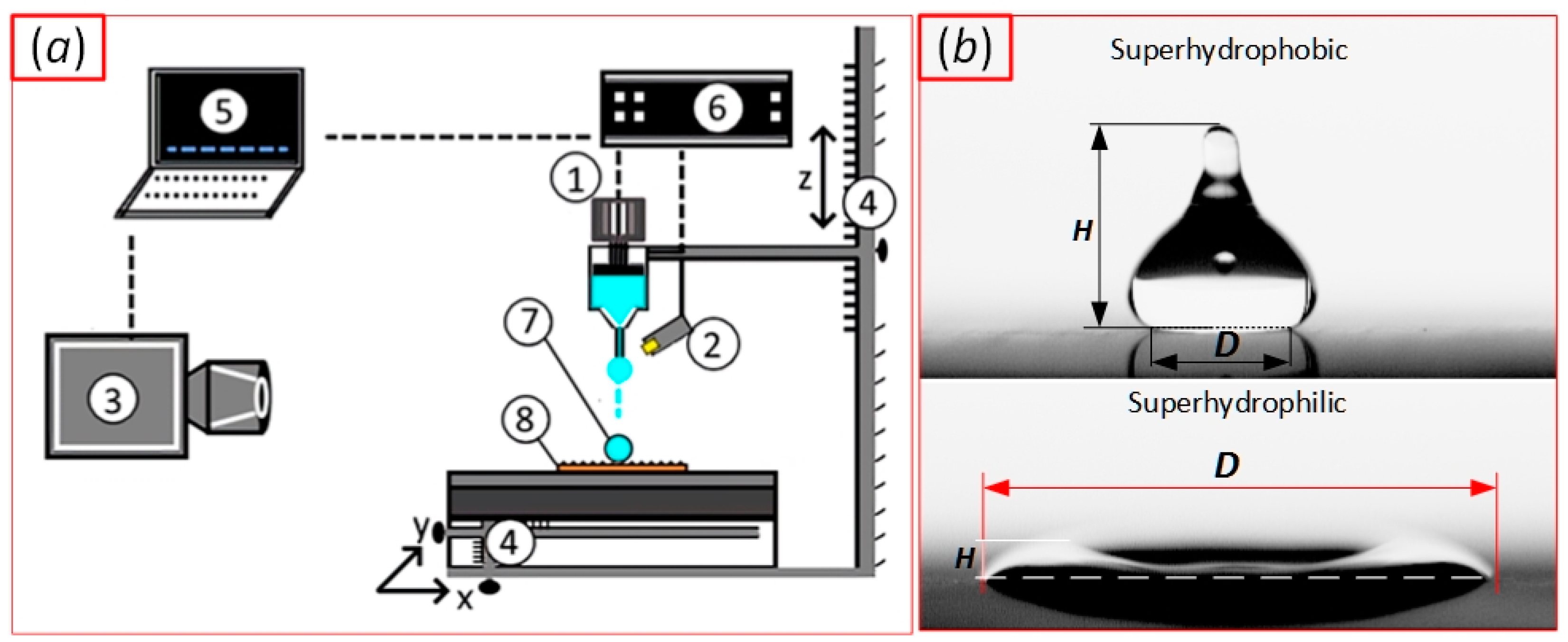
2. Experimental Setup
3. LBM Simulation
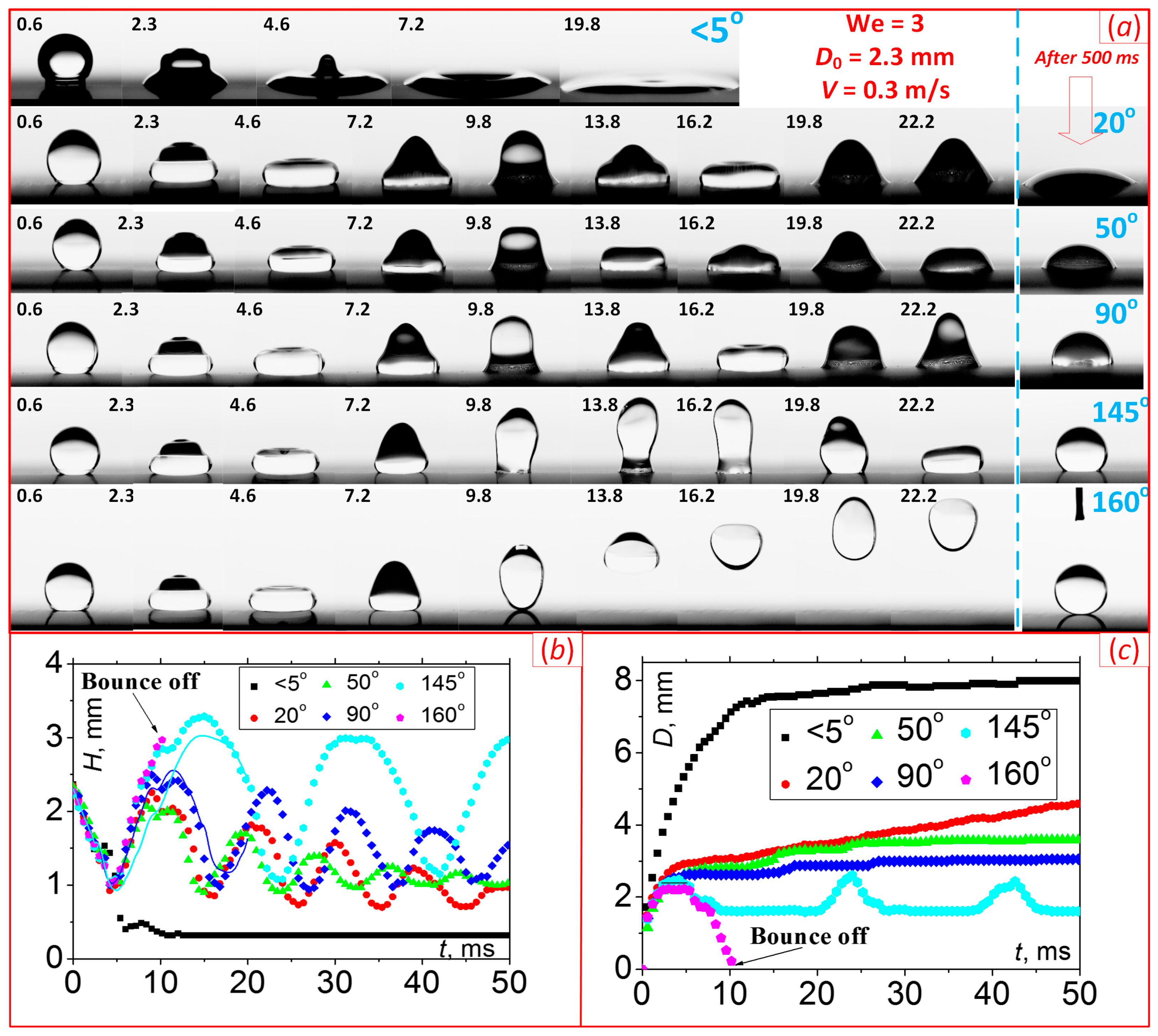
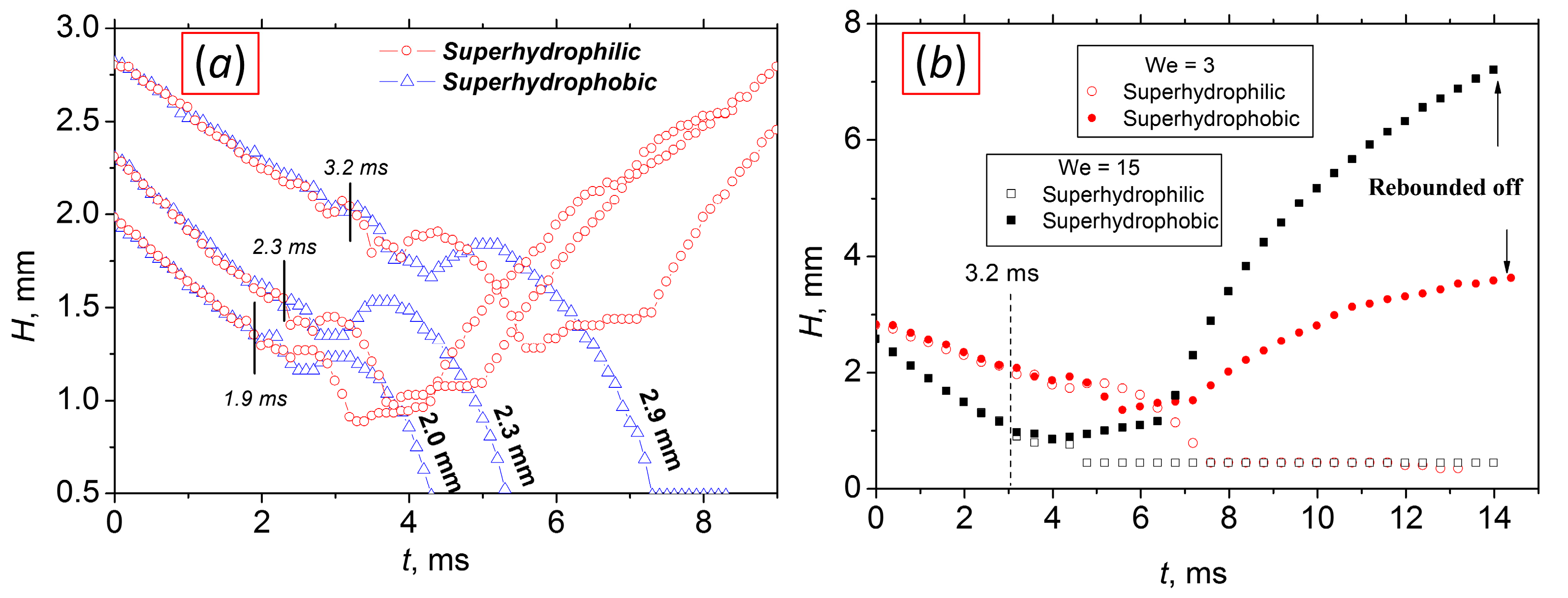
4. Results and Discussion
5. Conclusions
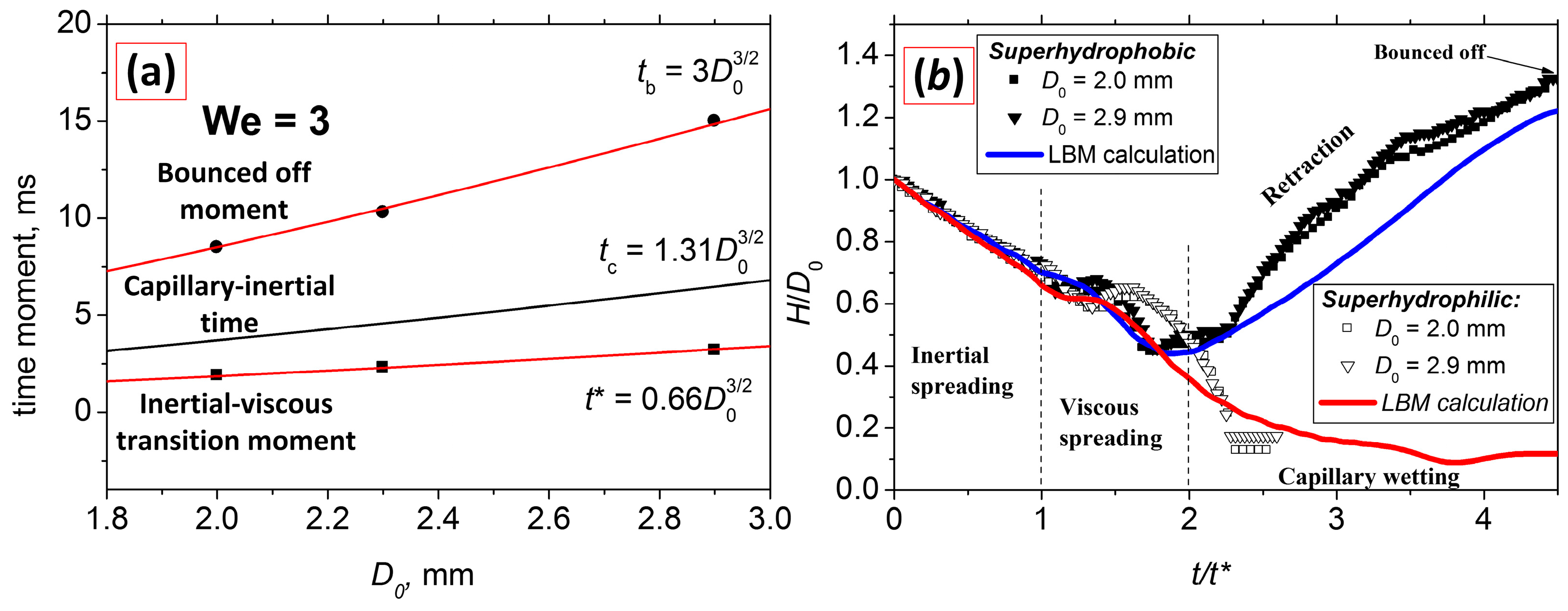
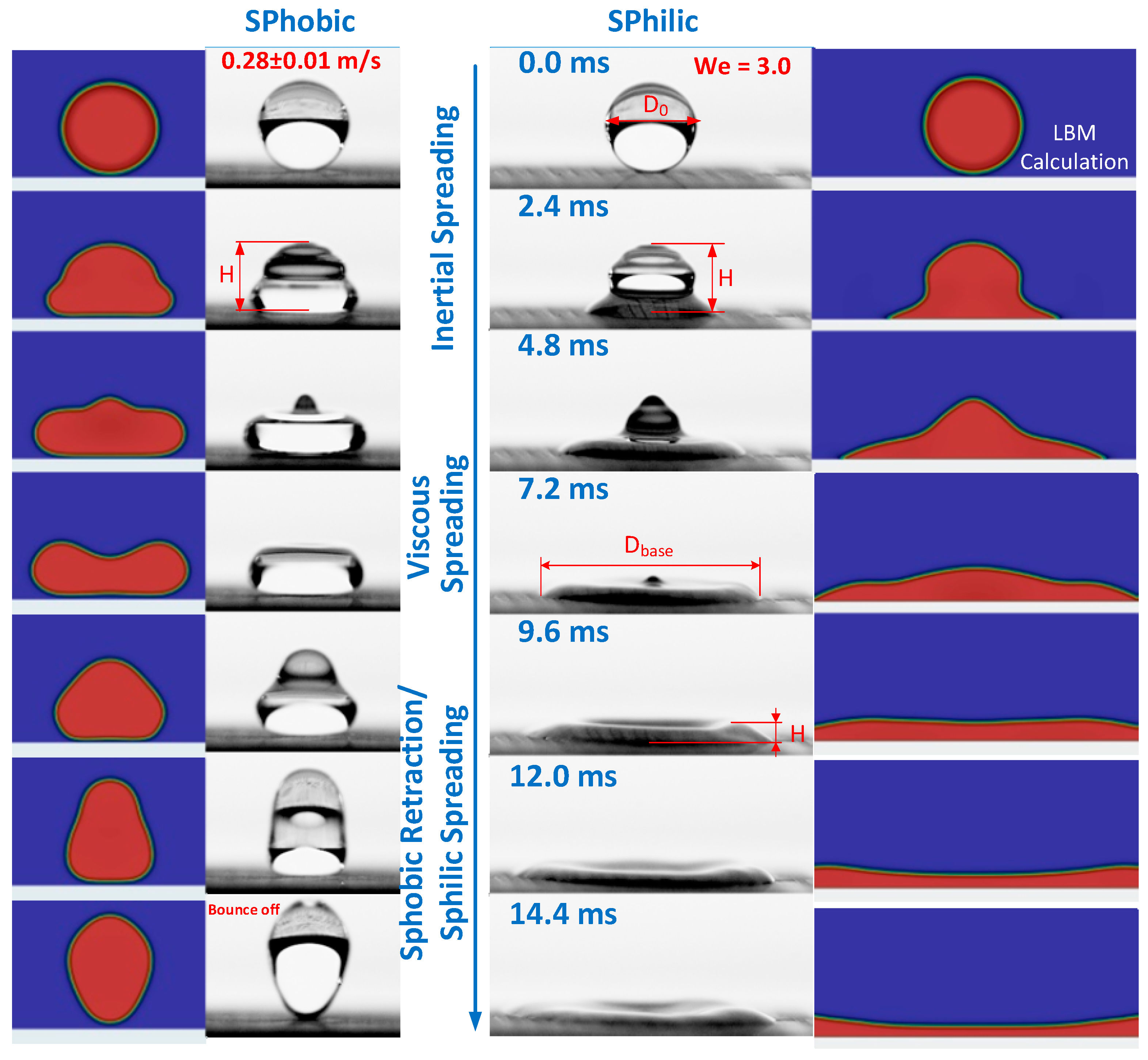
- For the first time, we systematically studied the dynamics of falling water droplets on surfaces with identical hierarchical structures but different wettability in a wide range of contact angles 5–161° for We = 0.3–33.
- We proposed a generalizing parameter—the time value t* = 0.66 D03/2—corresponding to the transition between inertial and viscous flow regimes. We compared the dynamics of water droplets falling at different velocities and onto different surfaces. It was shown that the parameter t* does not depend on the We number in all investigated conditions.
- Analyzing the velocity fields obtained by the LBM, it was found that the inertial spreading regime <t* corresponds to the moment of capillary-surface waves reaching the droplet apex for all surfaces in the considered conditions. The inertial-capillary number tc corresponds to the zeroing of velocity for the superhydrophobic surface. However, for superhydrophilic surfaces, tc has no physical meaning.
- It was shown that surfaces with absolutely different hierarchical structures can provide the identity of the contact line dynamics for falling droplets, regardless of the liquid used, where the contact angles equality is the necessary condition.
- It was found that the droplet spreading over surfaces with high adhesion force (or exhibiting the rose petal effect or, in other words, having very large contact angle hysteresis) is fundamentally different from droplets spreading over a smooth surface despite the equality of contact angles. For the first time, it was shown that the surface structure does not affect the dynamics of the falling droplet spreading if we deal with the rose petal effect, i.e., the key factor is the liquid to the surface adhesion force.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yu, C.; Liu, M.; Zhang, C.; Yan, H.; Zhang, M.; Wu, Q.; Liu, M.; Jiang, L. Bio-Inspired Drag Reduction: From Nature Organisms to Artificial Functional Surfaces. Giant 2020, 2, 100017. [Google Scholar] [CrossRef]
- Weng, W.; Tenjimbayashi, M.; Hu, W.H.; Naito, M. Evolution of and Disparity among Biomimetic Superhydrophobic Surfaces with Gecko, Petal, and Lotus Effect. Small 2022, 18, 2200349. [Google Scholar] [CrossRef]
- Liu, Y.; Li, G. A New Method for Producing “Lotus Effect” on a Biomimetic Shark Skin. J. Colloid Interface Sci. 2012, 388, 235–242. [Google Scholar] [CrossRef] [PubMed]
- Liravi, M.; Pakzad, H.; Moosavi, A.; Nouri-Borujerdi, A. A Comprehensive Review on Recent Advances in Superhydrophobic Surfaces and Their Applications for Drag Reduction. Prog. Org. Coatings 2020, 140, 105537. [Google Scholar] [CrossRef]
- Betz, A.R.; Jenkins, J.; Kim, C.J.; Attinger, D. Boiling Heat Transfer on Superhydrophilic, Superhydrophobic, and Superbiphilic Surfaces. Int. J. Heat Mass Transf. 2013, 57, 733–741. [Google Scholar] [CrossRef]
- Drelich, J.; Marmur, A. Physics and Applications of Superhydrophobic and Superhydrophilic Surfaces and Coatings. Surf. Innov. 2014, 2, 211–227. [Google Scholar] [CrossRef]
- Drelich, J.; Chibowski, E.; Meng, D.D.; Terpilowski, K. Hydrophilic and Superhydrophilic Surfaces and Materials. Soft Matter 2011, 7, 9804–9828. [Google Scholar] [CrossRef]
- Starinskaya, E.; Miskiv, N.; Terekhov, V.; Safonov, A.; Li, Y.; Lei, M.; Starinskiy, S. Evaporation Dynamics of Sessile and Suspended Almost-Spherical Droplets from a Biphilic Surface. Water 2023, 15, 273. [Google Scholar] [CrossRef]
- Wenzel, R.N. Resistance of Solid Surfaces To Wetting By Water. Ind. Eng. Chem. 1936, 28, 988–994. [Google Scholar] [CrossRef]
- Cassie, A.B.D.; Baxter, S. Wettability of Porous Surfaces. Trans. Faraday Soc. 1944, 40, 546. [Google Scholar] [CrossRef]
- Starinskiy, S.V.; Rodionov, A.A.; Shukhov, Y.G.; Safonov, A.I.; Maximovskiy, E.A.; Sulyaeva, V.S.; Bulgakov, A.V. Formation of Periodic Superhydrophilic Microstructures by Infrared Nanosecond Laser Processing of Single-Crystal Silicon. Appl. Surf. Sci. 2020, 512, 145753. [Google Scholar] [CrossRef]
- Yildirim Erbil, H.; Elif Cansoy, C. Range of Applicability of the Wenzel and Cassie-Baxter Equations for Superhydrophobic Surfaces. Langmuir 2009, 25, 14135–14145. [Google Scholar] [CrossRef]
- McHale, G. Cassie and Wenzel: Were They Really so Wrong? Langmuir 2007, 23, 8200–8205. [Google Scholar] [CrossRef]
- Milne, A.J.B.; Amirfazli, A. The Cassie Equation: How It Is Meant to Be Used. Adv. Colloid Interface Sci. 2012, 170, 48–55. [Google Scholar] [CrossRef]
- Feng, L.; Zhang, Y.; Xi, J.; Zhu, Y.; Wang, N.; Xia, F.; Jiang, L. Petal Effect: A Superhydrophobic State with High Adhesive Force. Langmuir 2008, 24, 4114–4119. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, G.; Zhao, X.; Sun, W.; Ma, X. Falling Liquid Film Periodical Fluctuation over a Superhydrophilic Horizontal Tube at Low Spray Density. Int. J. Heat Mass Transf. 2020, 147, 118938. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, J.; Hu, Y.; Yang, D.Q.; Sacher, E. Dynamic Behaviours and Drying Processes of Water Droplets Impacting on Superhydrophilic Surfaces. Surf. Eng. 2021, 37, 1301–1307. [Google Scholar] [CrossRef]
- Hu, Z.; Chu, F.; Wu, X. Double-Peak Characteristic of Droplet Impact Force on Superhydrophobic Surfaces. Extrem. Mech. Lett. 2022, 52, 101665. [Google Scholar] [CrossRef]
- Hu, Z.; Chu, F.; Lin, Y.; Wu, X. Contact Time of Droplet Impact on Inclined Ridged Superhydrophobic Surfaces. Langmuir 2022, 38, 1540–1549. [Google Scholar] [CrossRef] [PubMed]
- Satpathi, N.S.; Malik, L.; Ramasamy, A.S.; Sen, A.K. Drop Impact on a Superhydrophilic Spot Surrounded by a Superhydrophobic Surface. Langmuir 2021, 37, 14195–14204. [Google Scholar] [CrossRef] [PubMed]
- Tilton, D.E.; Kearns, D.A.; Tilton, C.L. Liquid Nitrogen Spray Cooling of a Simulated Electronic Chip. Adv. Cryog. Eng. 1994, 39, 1779–1786. [Google Scholar] [CrossRef]
- Moreira, A.L.N.; Moita, A.S.; Panão, M.R. Advances and Challenges in Explaining Fuel Spray Impingement: How Much of Single Droplet Impact Research Is Useful? Prog. Energy Combust. Sci. 2010, 36, 554–580. [Google Scholar] [CrossRef]
- Singh, M.; Haverinen, H.M.; Dhagat, P.; Jabbour, G.E. Inkjet Printing-Process and Its Applications. Adv. Mater. 2010, 22, 673–685. [Google Scholar] [CrossRef]
- Kwon, H.-M.; Paxson, A.T.; Varanasi, K.K.; Patankar, N.A. Rapid Deceleration-Driven Wetting Transition during Pendant Drop Deposition on Superhydrophobic Surfaces. Phys. Rev. Lett. 2011, 106, 036102. [Google Scholar] [CrossRef]
- Schutzius, T.M.; Jung, S.; Maitra, T.; Eberle, P.; Antonini, C.; Stamatopoulos, C.; Poulikakos, D. Physics of Icing and Rational Design of Surfaces with Extraordinary Icephobicity. Langmuir 2015, 31, 4807–4821. [Google Scholar] [CrossRef] [PubMed]
- Choi, C.; Kim, M. Wettability Effects on Heat Transfer. In Two Phase Flow, Phase Change and Numerical Modeling; InTech: Shanghai, China, 2011; pp. 313–340. Available online: https://cdn.intechopen.com/pdfs/20823/InTech-Wettability_effects_on_heat_transfer.pdf (accessed on 10 February 2021).
- Xu, Q.; Liu, Q.; Zhu, Y.; Luo, X.; Tao, L.; Guo, L. Entropy and Exergy Analysis of the Steam Jet Condensation in Crossflow of Subcooled Water. Ann. Nucl. Energy 2023, 180, 109485. [Google Scholar] [CrossRef]
- Xu, Q.; Yuan, X.; Liu, C.; Wang, X.; Guo, L. Signal Selection for Identification of Multiphase Flow Patterns in Offshore Pipeline-Riser System. Ocean Eng. 2023, 268, 113395. [Google Scholar] [CrossRef]
- Castrejón-Pita, J.R.; Muñoz-Sánchez, B.N.; Hutchings, I.M.; Castrejón-Pita, A.A. Droplet Impact onto Moving Liquids. J. Fluid Mech. 2016, 809, 716–725. [Google Scholar] [CrossRef]
- Dash, S.; Kumari, N.; Garimella, S.V. Characterization of Ultrahydrophobic Hierarchical Surfaces Fabricated Using a Single-Step Fabrication Methodology. J. Micromechanics Microengineering 2011, 21, 105012. [Google Scholar] [CrossRef]
- Lin, S.; Zhao, B.; Zou, S.; Guo, J.; Wei, Z.; Chen, L. Impact of Viscous Droplets on Different Wettable Surfaces: Impact Phenomena, the Maximum Spreading Factor, Spreading Time and Post-Impact Oscillation. J. Colloid Interface Sci. 2018, 516, 86–97. [Google Scholar] [CrossRef]
- Wang, F.; Fang, T. Retraction Dynamics of Water Droplets after Impacting upon Solid Surfaces from Hydrophilic to Superhydrophobic. Phys. Rev. Fluids 2020, 5, 033604. [Google Scholar] [CrossRef]
- Pachchigar, V.; Ranjan, M.; Sooraj, K.P.; Augustine, S.; Kumawat, D.; Tahiliani, K.; Mukherjee, S. Self-Cleaning and Bouncing Behaviour of Ion Irradiation Produced Nanostructured Superhydrophobic PTFE Surfaces. Surf. Coatings Technol. 2021, 420, 127331. [Google Scholar] [CrossRef]
- Pan, Y.; Shi, K.; Duan, X.; Naterer, G.F. Experimental Investigation of Water Droplet Impact and Freezing on Micropatterned Stainless Steel Surfaces with Varying Wettabilities. Int. J. Heat Mass Transf. 2019, 129, 953–964. [Google Scholar] [CrossRef]
- Lv, C.; Hao, P.; Zhang, X.; He, F. Drop Impact upon Superhydrophobic Surfaces with Regular and Hierarchical Roughness. Appl. Phys. Lett. 2016, 108, 141602. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, X.; Wang, X.; Xu, Q.; Geng, T. Wetting and Tribological Properties of Superhydrophobic Aluminum Surfaces with Different Water Adhesion. J. Mater. Sci. 2020, 55, 11658–11668. [Google Scholar] [CrossRef]
- Sun, S.; Li, H.; Guo, Y.; Mi, H.-Y.; He, P.; Zheng, G.; Liu, C.; Shen, C. Superefficient and Robust Polymer Coating for Bionic Manufacturing of Superwetting Surfaces with “Rose Petal Effect” and “Lotus Leaf Effect”. Prog. Org. Coatings 2021, 151, 106090. [Google Scholar] [CrossRef]
- Du, Q.; Zhou, P.; Pan, Y.; Qu, X.; Liu, L.; Yu, H.; Hou, J. Influence of Hydrophobicity and Roughness on the Wetting and Flow Resistance of Water Droplets on Solid Surface: A Many-Body Dissipative Particle Dynamics Study. Chem. Eng. Sci. 2022, 249, 117327. [Google Scholar] [CrossRef]
- Renardy, Y.; Popinet, S.; Duchemin, L.; Renardy, M.; Zaleski, S.; Josserand, C.; Drumright-Clarke, M.A.; Richard, D.; Clanet, C.; Quéré, D. Pyramidal and Toroidal Water Drops after Impact on a Solid Surface. J. Fluid Mech. 2003, 484, 69–83. [Google Scholar] [CrossRef]
- Eggers, J.; Fontelos, M.A.; Josserand, C.; Zaleski, S. Drop Dynamics after Impact on a Solid Wall: Theory and Simulations. Phys. Fluids 2010, 22, 062101. [Google Scholar] [CrossRef]
- Ukiwe, C.; Kwok, D.Y. On the Maximum Spreading Diameter of Impacting Droplets on Well-Prepared Solid Surfaces. Langmuir 2005, 21, 666–673. [Google Scholar] [CrossRef]
- Roisman, I.V.; Lembach, A.; Tropea, C. Drop Splashing Induced by Target Roughness and Porosity: The Size Plays No Role. Adv. Colloid Interface Sci. 2015, 222, 615–621. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, X.; Yi, X.; Du, Y.; He, F.; Niu, F.; Hao, P. How Surface Roughness Promotes or Suppresses Drop Splash. Phys. Fluids 2022, 34, 022111. [Google Scholar] [CrossRef]
- Li, X.; Ma, X.; Lan, Z. Dynamic Behavior of the Water Droplet Impact on a Textured Hydrophobic/Superhydrophobic Surface: The Effect of the Remaining Liquid Film Arising on the Pillars’ Tops on the Contact Time. Langmuir 2010, 26, 4831–4838. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Nam, Y.; Lastakowski, H.; Hur, J.I.; Shin, S.; Biance, A.L.; Pirat, C.; Kim, C.J.; Ybert, C. Two Types of Cassie-to-Wenzel Wetting Transitions on Superhydrophobic Surfaces during Drop Impact. Soft Matter 2015, 11, 4592–4599. [Google Scholar] [CrossRef] [PubMed]
- Cetiner, A.; Evren, B.; Budakli, M.; Arik, M.; Ozbek, A. Spreading Behavior of Droplets Impacting over Substrates with Varying Surface Topographies. Colloids Surfaces A Physicochem. Eng. Asp. 2020, 606, 125385. [Google Scholar] [CrossRef]
- Ding, W.; Dorao, C.A.; Fernandino, M. Improving Superamphiphobicity by Mimicking Tree-Branch Topography. J. Colloid Interface Sci. 2022, 611, 118–128. [Google Scholar] [CrossRef]
- Foltyn, P.; Ribeiro, D.; Silva, A.; Lamanna, G.; Weigand, B. Influence of Wetting Behavior on the Morphology of Droplet Impacts onto Dry Smooth Surfaces. Phys. Fluids 2021, 33, 063305. [Google Scholar] [CrossRef]
- Schiaffino, S.; Sonin, A.A. Molten Droplet Deposition and Solidification at Low Weber Numbers. Phys. Fluids 1997, 9, 3172–3187. [Google Scholar] [CrossRef]
- Almohammadi, H.; Amirfazli, A. Droplet Impact: Viscosity and Wettability Effects on Splashing. J. Colloid Interface Sci. 2019, 553, 22–30. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, D.; Zhang, Y.; Xue, T.; Huang, Y.; Zhang, G. Fabrication and Droplet Impact Performance of Superhydrophobic Ti6Al4V Surface by Laser Induced Plasma Micro-Machining. Appl. Surf. Sci. 2022, 605, 154661. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, X.; Yi, X.; He, F.; Niu, F.; Hao, P. Effect of Wettability on Droplet Impact: Spreading and Splashing. Exp. Therm. Fluid Sci. 2021, 124, 110369. [Google Scholar] [CrossRef]
- Sun, R.; Bai, H.; Ju, J.; Jiang, L. Droplet Emission Induced by Ultrafast Spreading on a Superhydrophilic Surface. Soft Matter 2013, 9, 9285. [Google Scholar] [CrossRef]
- Antonini, C.; Villa, F.; Bernagozzi, I.; Amirfazli, A.; Marengo, M. Drop Rebound after Impact: The Role of the Receding Contact Angle. Langmuir 2013, 29, 16045–16050. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.; Coyle, T.W.; Pershin, L.; Mostaghimi, J. From Lotus Effect to Petal Effect: Tuning the Water Adhesion of Non-Wetting Rare Earth Oxide Coatings. J. Eur. Ceram. Soc. 2020, 40, 1692–1702. [Google Scholar] [CrossRef]
- Roy, D.; Pandey, K.; Banik, M.; Mukherjee, R.; Basu, S. Dynamics of Droplet Impingement on Bioinspired Surface: Insights into Spreading, Anomalous Stickiness and Break-Up. Proc. R. Soc. A Math. Phys. Eng. Sci. 2019, 475, 20190260. [Google Scholar] [CrossRef]
- Serdyukov, V.; Starinskiy, S.; Malakhov, I.; Safonov, A.; Surtaev, A. Laser Texturing of Silicon Surface to Enhance Nucleate Pool Boiling Heat Transfer. Appl. Therm. Eng. 2021, 194, 117102. [Google Scholar] [CrossRef]
- Safonov, A.I.; Sulyaeva, V.S.; Gatapova, E.Y.; Starinskiy, S.V.; Timoshenko, N.I.; Kabov, O.A. Deposition Features and Wettability Behavior of Fluoropolymer Coatings from Hexafluoropropylene Oxide Activated by NiCr Wire. Thin Solid Films 2018, 653, 165–172. [Google Scholar] [CrossRef]
- Starinskiy, S.V.; Bulgakov, A.V.; Gatapova, E.Y.; Shukhov, Y.G.; Sulyaeva, V.S.; Timoshenko, N.I.; Safonov, A.I. Transition from Superhydrophilic to Superhydrophobic of Silicon Wafer by a Combination of Laser Treatment and Fluoropolymer Deposition. J. Phys. D Appl. Phys. 2018, 51, 255307. [Google Scholar] [CrossRef]
- d’Humières, D. Multiple–Relaxation–Time Lattice Boltzmann Models in Three Dimensions. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 2002, 360, 437–451. [Google Scholar] [CrossRef]
- Shan, X.; Chen, H. Lattice Boltzmann Model for Simulating Flows with Multiple Phases and Components. Phys. Rev. E 1993, 47, 1815–1819. [Google Scholar] [CrossRef] [Green Version]
- Shan, X.; Chen, H. Simulation of Nonideal Gases and Liquid-Gas Phase Transitions by the Lattice Boltzmann Equation. Phys. Rev. E 1994, 49, 2941–2948. [Google Scholar] [CrossRef] [PubMed]
- Shen, S.; Bi, F.; Guo, Y. Simulation of Droplets Impact on Curved Surfaces with Lattice Boltzmann Method. Int. J. Heat Mass Transf. 2012, 55, 6938–6943. [Google Scholar] [CrossRef]
- Li, Q.; Luo, K.H.; Li, X.J. Lattice Boltzmann Modeling of Multiphase Flows at Large Density Ratio with an Improved Pseudopotential Model. Phys. Rev. E 2013, 87, 053301. [Google Scholar] [CrossRef] [PubMed]
- Ma, R.; Zhou, X.; Dong, B.; Li, W.; Gong, J. Simulation of Impacting Process of a Saturated Droplet upon Inclined Surfaces by Lattice Boltzmann Method. Int. J. Heat Fluid Flow 2018, 71, 1–12. [Google Scholar] [CrossRef]
- Liu, X.; Cheng, P.; Quan, X. Lattice Boltzmann Simulations for Self-Propelled Jumping of Droplets after Coalescence on a Superhydrophobic Surface. Int. J. Heat Mass Transf. 2014, 73, 195–200. [Google Scholar] [CrossRef]
- Bouzidi, M.; D’Humières, D.; Lallemand, P.; Luo, L.-S. Lattice Boltzmann Equation on a Two-Dimensional Rectangular Grid. J. Comput. Phys. 2001, 172, 704–717. [Google Scholar] [CrossRef]
- Kupershtokh, A.L.; Medvedev, D.A.; Karpov, D.I. On Equations of State in a Lattice Boltzmann Method. Comput. Math. Appl. 2009, 58, 965–974. [Google Scholar] [CrossRef]
- Khajepor, S.; Cui, J.; Dewar, M.; Chen, B. A Study of Wall Boundary Conditions in Pseudopotential Lattice Boltzmann Models. Comput. Fluids 2019, 193, 103896. [Google Scholar] [CrossRef]
- Richard, D.; Clanet, C.; Quéré, D. Contact Time of a Bouncing Drop. Nature 2002, 417, 811. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, X.; Min, J. Spreading of Droplets Impacting Different Wettable Surfaces at a Weber Number Close to Zero. Chem. Eng. Sci. 2019, 207, 495–503. [Google Scholar] [CrossRef]
- Roux, D.C.D.; Cooper-White, J.J. Dynamics of Water Spreading on a Glass Surface. J. Colloid Interface Sci. 2004, 277, 424–436. [Google Scholar] [CrossRef]
- Farshchian, B.; Pierce, J.; Beheshti, M.S.; Park, S.; Kim, N. Droplet Impinging Behavior on Surfaces with Wettability Contrasts. Microelectron. Eng. 2018, 195, 50–56. [Google Scholar] [CrossRef] [PubMed]
- Zhou, M.; Qu, J.; Ji, Y. Dynamic Characteristics of Droplet Impingement on Carbon Nanotube Array Surfaces with Varying Wettabilities. Appl. Surf. Sci. 2021, 554, 149359. [Google Scholar] [CrossRef]
- Tang, C.; Qin, M.; Weng, X.; Zhang, X.; Zhang, P.; Li, J.; Huang, Z. Dynamics of Droplet Impact on Solid Surface with Different Roughness. Int. J. Multiph. Flow 2017, 96, 56–69. [Google Scholar] [CrossRef]

| Sample | ACA, ° | RCA, ° | PTFE Thickness, nm |
|---|---|---|---|
| Surface 1 | <5 | <5 | 0 |
| Surface 2 | 22 | 5 | 2 |
| Surface 3 | 50 | 17 | 5 |
| Surface 4 | 90 | 20 | 12 |
| Surface 5 | 145 | 22 | 25 |
| Surface 6 | 160 | 159 | 50 |
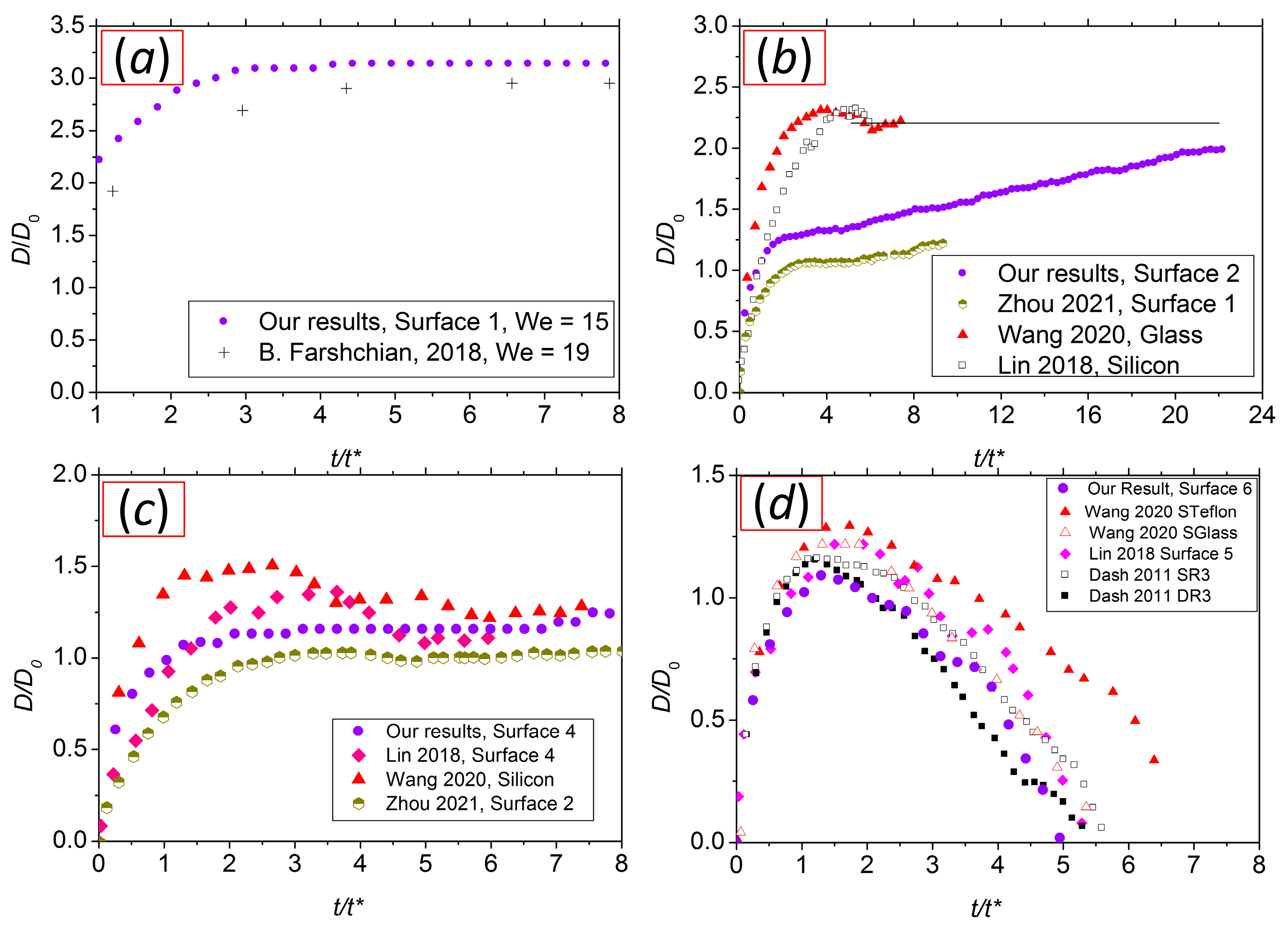
| Reference | We | D0, mm | Surface | ACA, ° | RCA, ° | SCA, ° |
|---|---|---|---|---|---|---|
| S. Dash, et al. 2011, [30] | 2.8 | 2.2 | Single-roughness surface (SR3) | 155 | 122 | 144 |
| S. Dash, et al. 2011, [30] | 2.8 | 2.2 | Double-roughness surface (SR3) | 165 | 155 | 166 |
| S. Lin, et al. 2018, [31] | 2 | 2.3 | Fractal-like network of hydrophobized silica shells on clean glass slides (surface 5) | 163 | 159 | 161 |
| F. Wang, et al. 2020, [32] | 4 | 2.5 | Sanding Teflon (STeflon) | 146 | 137 | - |
| F. Wang, et al. 2020, [32] | 4 | 2.5 | Superhydrophobic solution NeverWet on a piece of clean glass (SGlass) | 158 | 153 | - |
| S. Lin, et al. 2018, [31] | 2 | 2.3 | Silanized silicon wafers (surface 4) | 111 | 100 | 106 |
| F. Wang, et al. 2020, [32] | 4 17 | 2.5 | Silicon | 92 | 74 | - |
| F. Wang, et al. 2020, [32] | 4 | 2.5 | Glass | 46 | 21 | - |
| S. Lin, et al. 2018, [31] | 4 | 2.5 | Silicon | 31 | - | 27 |
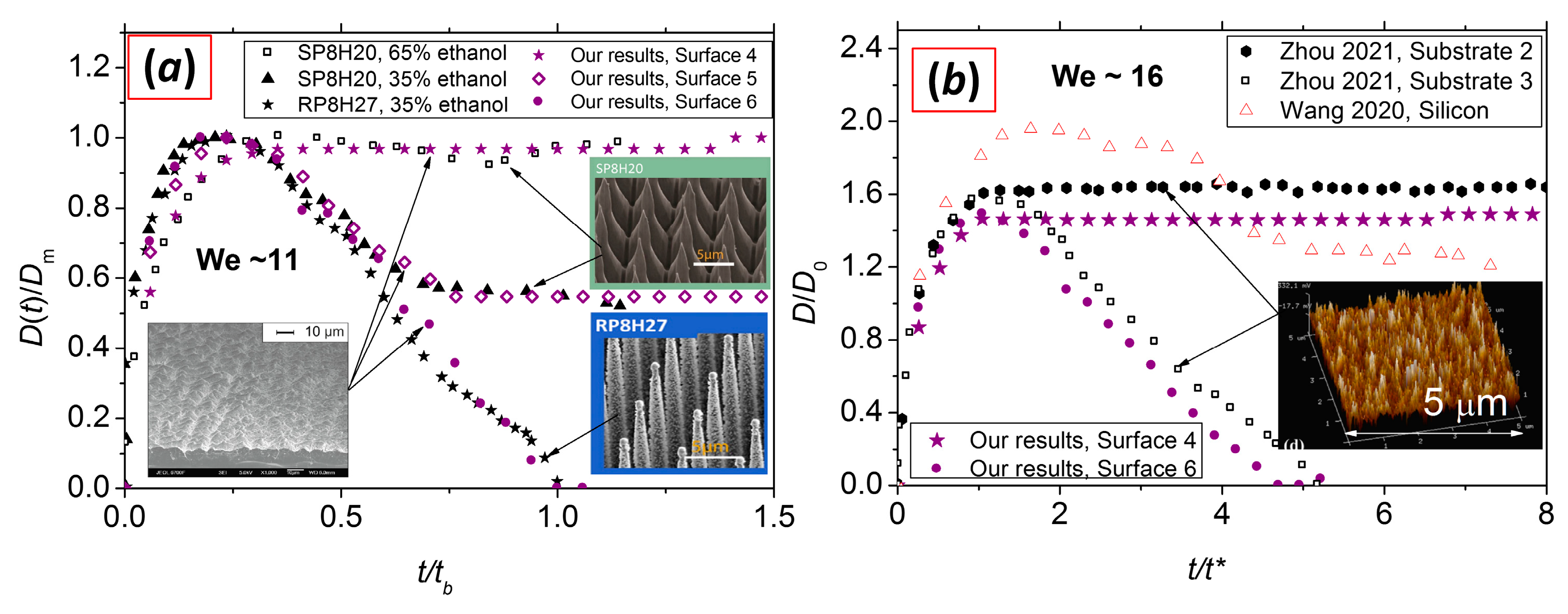
| B. Farshchian, et al. 2018, [73] * | 19 | 2.3 | Plasma-treated nanoparticles on PMMA | - | - | 9 |
| W. Ding, et al. 2022, [47] ** | 10.5 | 2 | Salinized smooth microcones on silicon surface (SP8H20) | - | - | 93 |
| W. Ding, et al. 2022, [47] ** | 10.5 | 2 | Salinized smooth microcones on silicon surface (SP8H20) | - | - | 134 |
| W. Ding, et al. 2022, [47] ** | 10.5 | 2 | Salinized rough microcones on silicon surface (RP8H27) | - | - | 159 |
| M. Zhou, et al. 2021, [74] | 1.5 17.7 | 2 | Carbon nanotube forest treated by plasma (Substrate 1) | - | - | 29 |
| M. Zhou, et al. 2021, [74] | 1.5 17.7 | 2 | Carbon nanotube forest treated by plasma (Substrate 2) | - | - | 84 |
| M. Zhou, et al. 2021, [74] | 1.5 17.7 | 2 | Carbon nanotube forest treated by plasma (Substrate 3) | - | - | 147 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Starinskiy, S.; Starinskaya, E.; Miskiv, N.; Rodionov, A.; Ronshin, F.; Safonov, A.; Lei, M.-K.; Terekhov, V. Spreading of Impacting Water Droplet on Surface with Fixed Microstructure and Different Wetting from Superhydrophilicity to Superhydrophobicity. Water 2023, 15, 719. https://doi.org/10.3390/w15040719
Starinskiy S, Starinskaya E, Miskiv N, Rodionov A, Ronshin F, Safonov A, Lei M-K, Terekhov V. Spreading of Impacting Water Droplet on Surface with Fixed Microstructure and Different Wetting from Superhydrophilicity to Superhydrophobicity. Water. 2023; 15(4):719. https://doi.org/10.3390/w15040719
Chicago/Turabian StyleStarinskiy, Sergey, Elena Starinskaya, Nikolay Miskiv, Alexey Rodionov, Fedor Ronshin, Alexey Safonov, Ming-Kai Lei, and Vladimir Terekhov. 2023. "Spreading of Impacting Water Droplet on Surface with Fixed Microstructure and Different Wetting from Superhydrophilicity to Superhydrophobicity" Water 15, no. 4: 719. https://doi.org/10.3390/w15040719
APA StyleStarinskiy, S., Starinskaya, E., Miskiv, N., Rodionov, A., Ronshin, F., Safonov, A., Lei, M.-K., & Terekhov, V. (2023). Spreading of Impacting Water Droplet on Surface with Fixed Microstructure and Different Wetting from Superhydrophilicity to Superhydrophobicity. Water, 15(4), 719. https://doi.org/10.3390/w15040719






