Double Parameters Generalization of Water-Blocking Effect of Submerged Vegetation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Numerical Simulation of Open Channel Flow with Submerged Vegetation
2.1.1. Mathematical Model
2.1.2. Verification
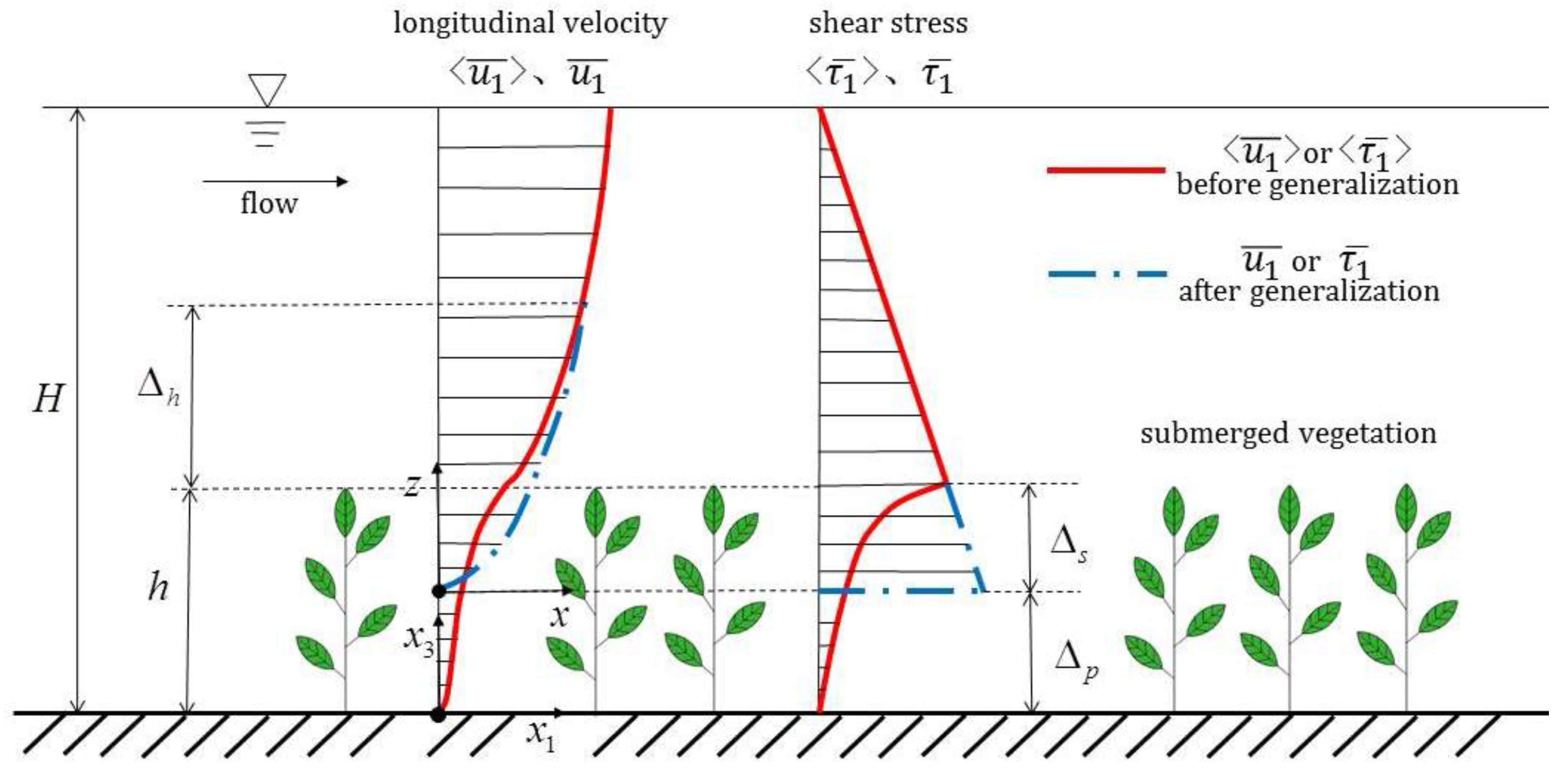
2.2. Study of the Water-Blocking Effect Generalization of Submerged Vegetation
2.2.1. Generalization Model and Principle
2.2.2. Handling of Key Issues
2.2.3. Data for Generalization
3. Results
3.1. Numerical Simulation of Open Channel Flow with Submerged Vegetation
3.1.1. Verification 1
3.1.2. Verification 2
3.2. Water-Blocking Effect Generalization of Submerged Vegetation
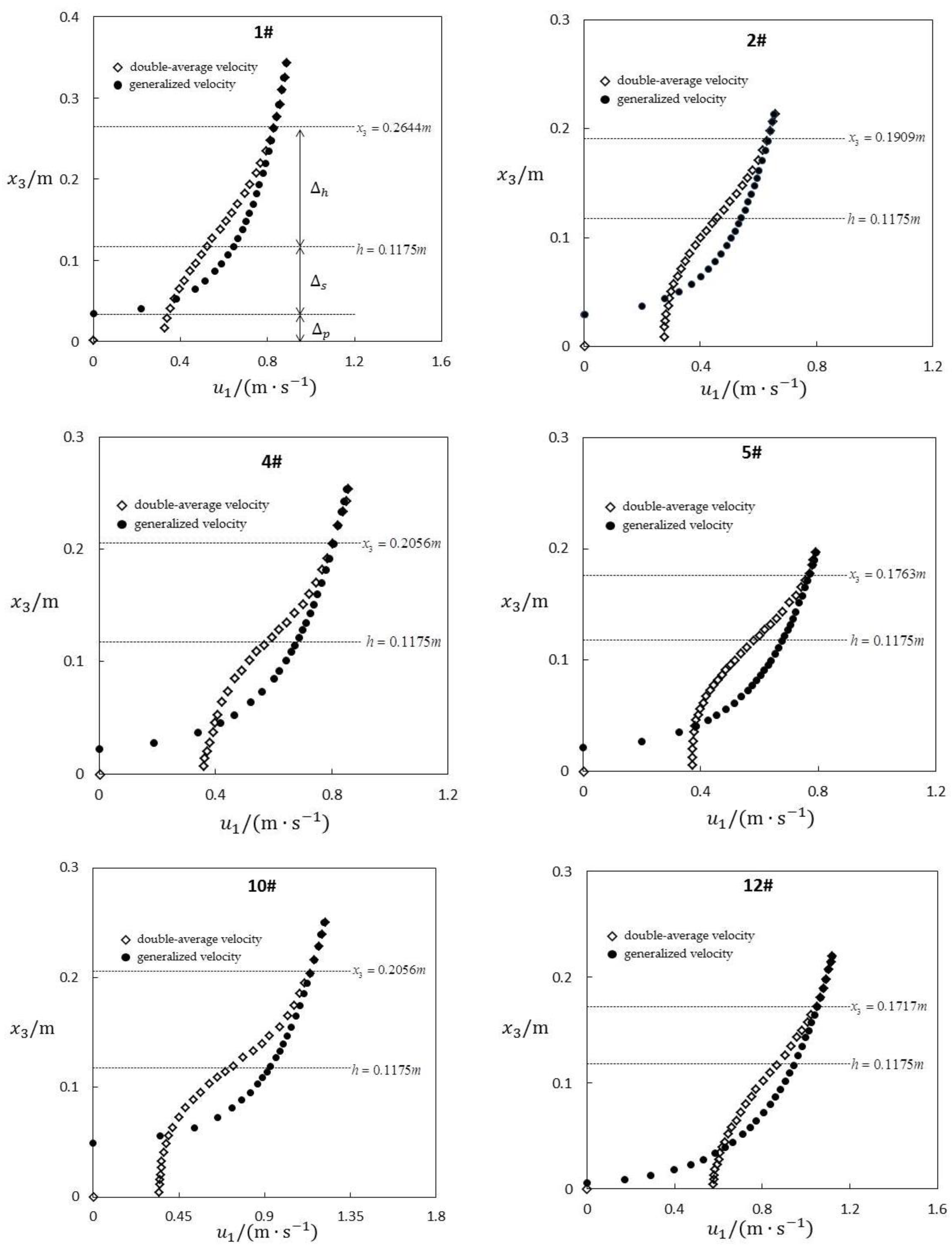
3.2.1. Preliminary Result
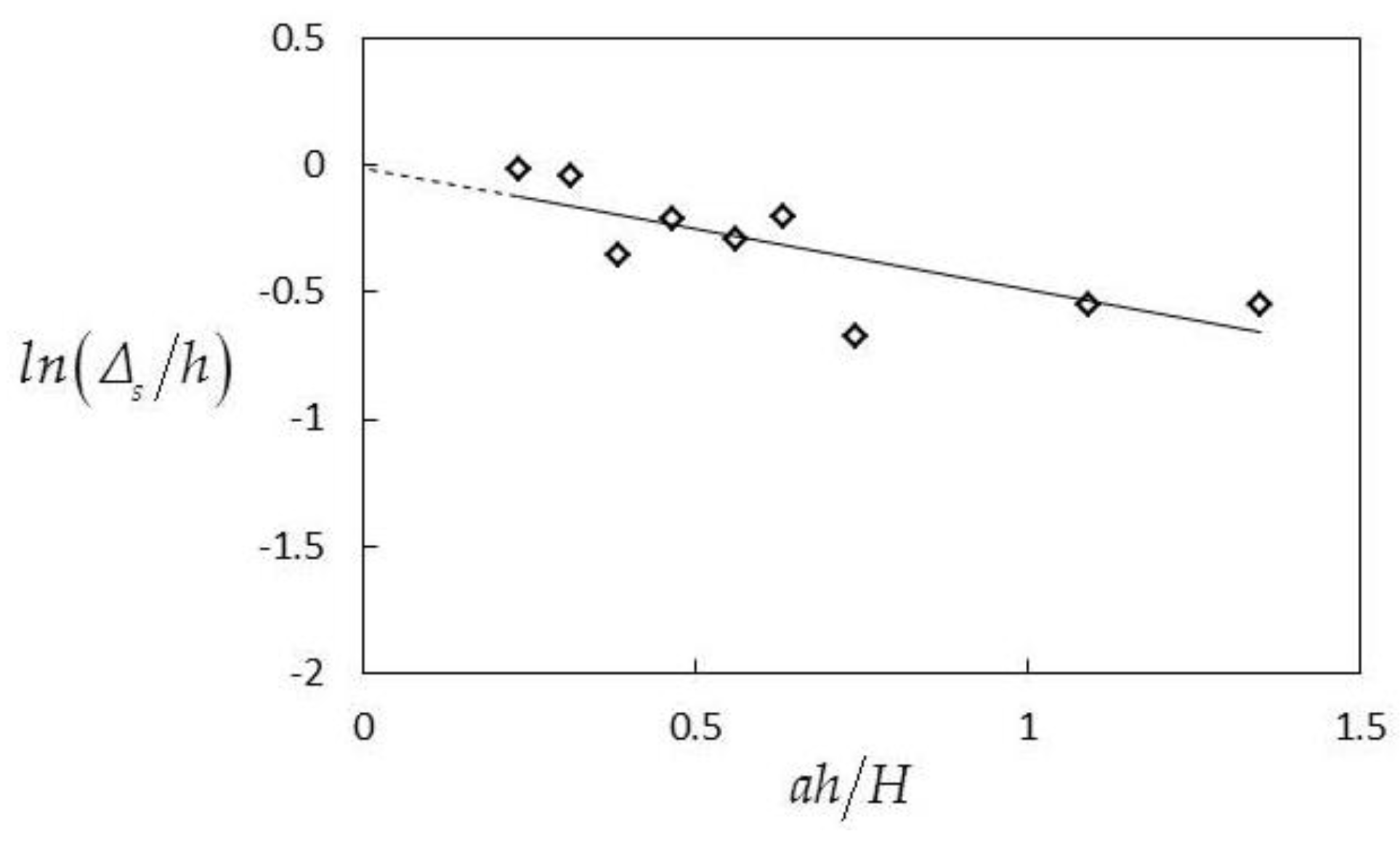
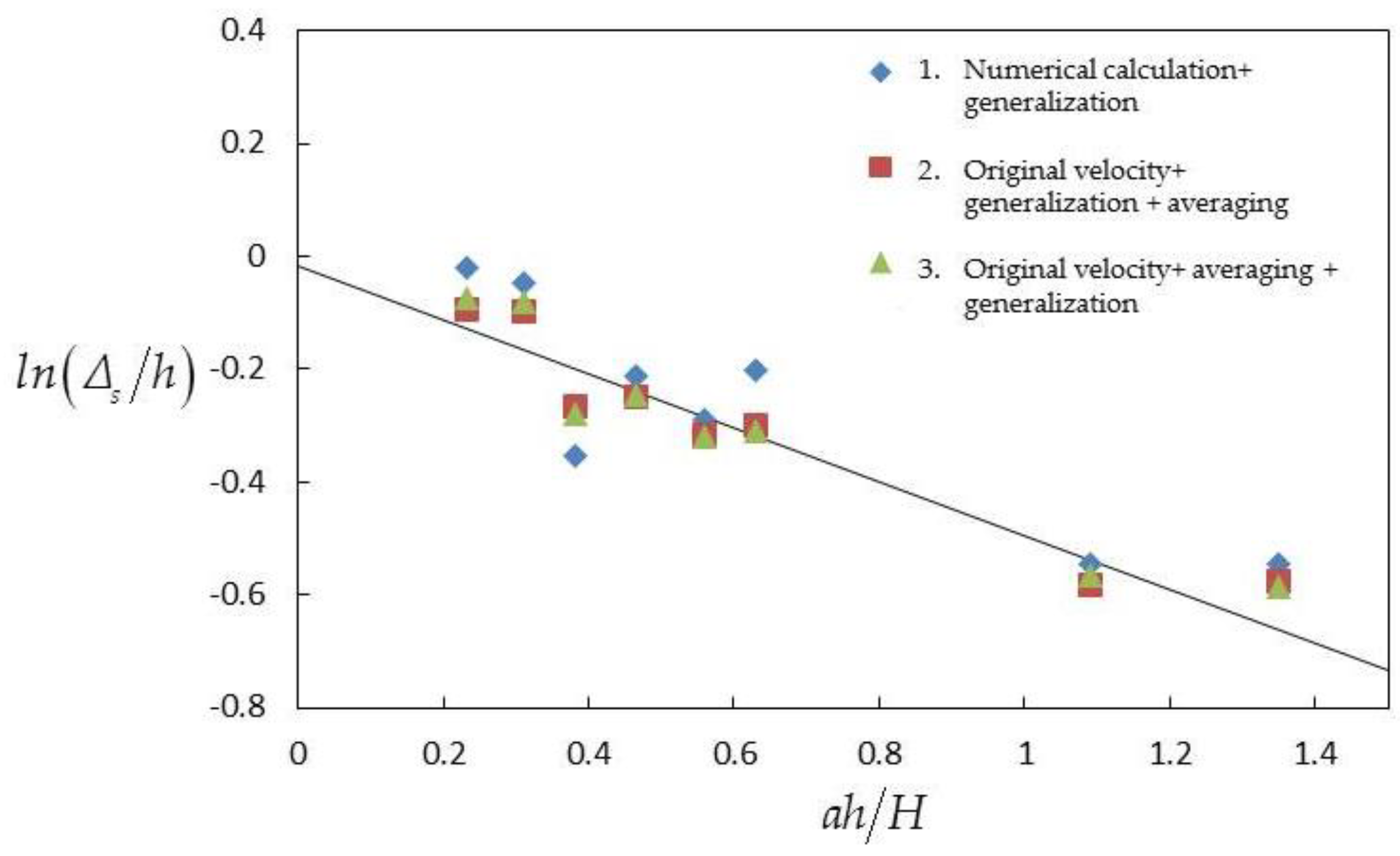
3.2.2. Height of the Theoretical Zero Point Δs
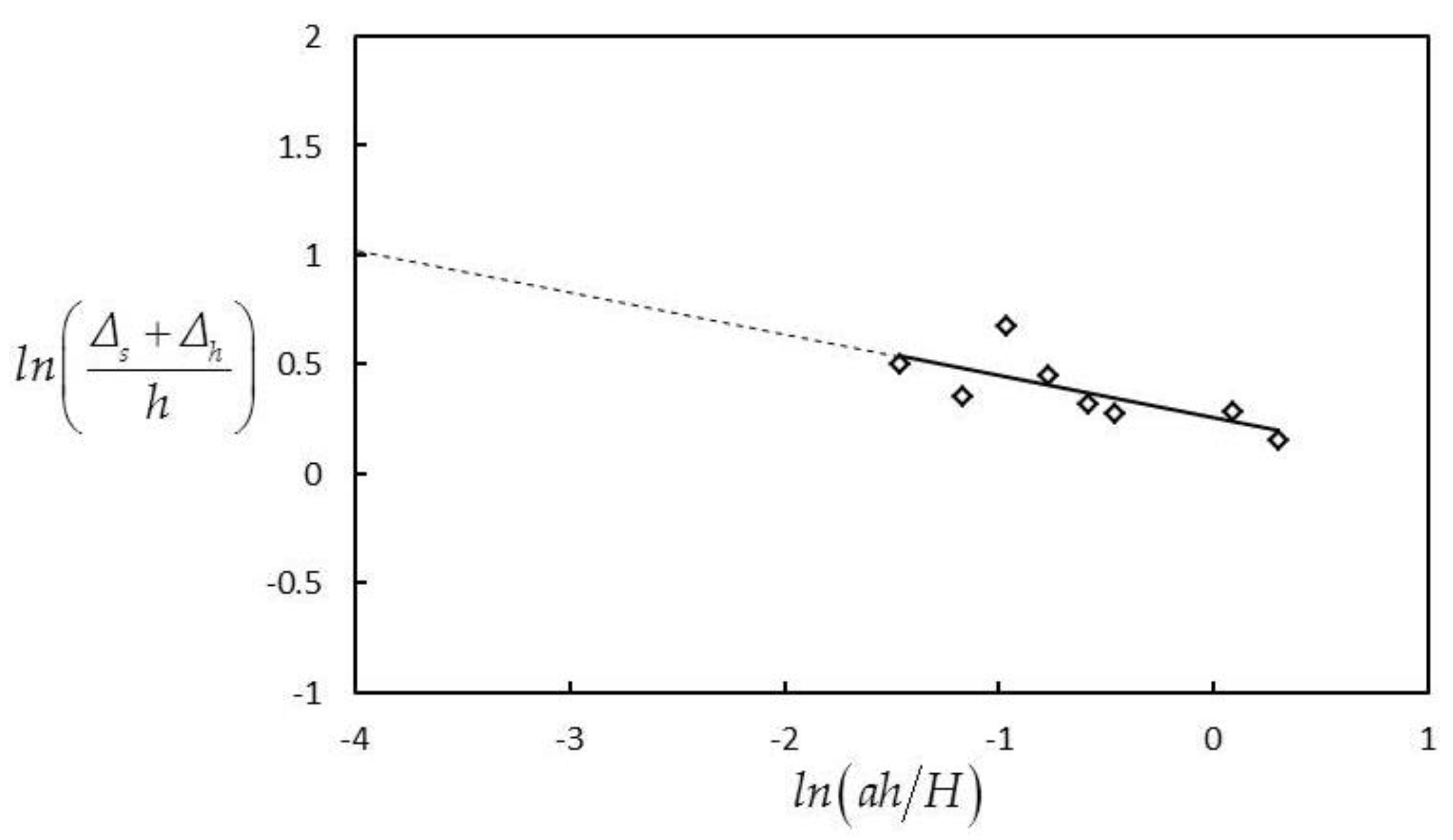
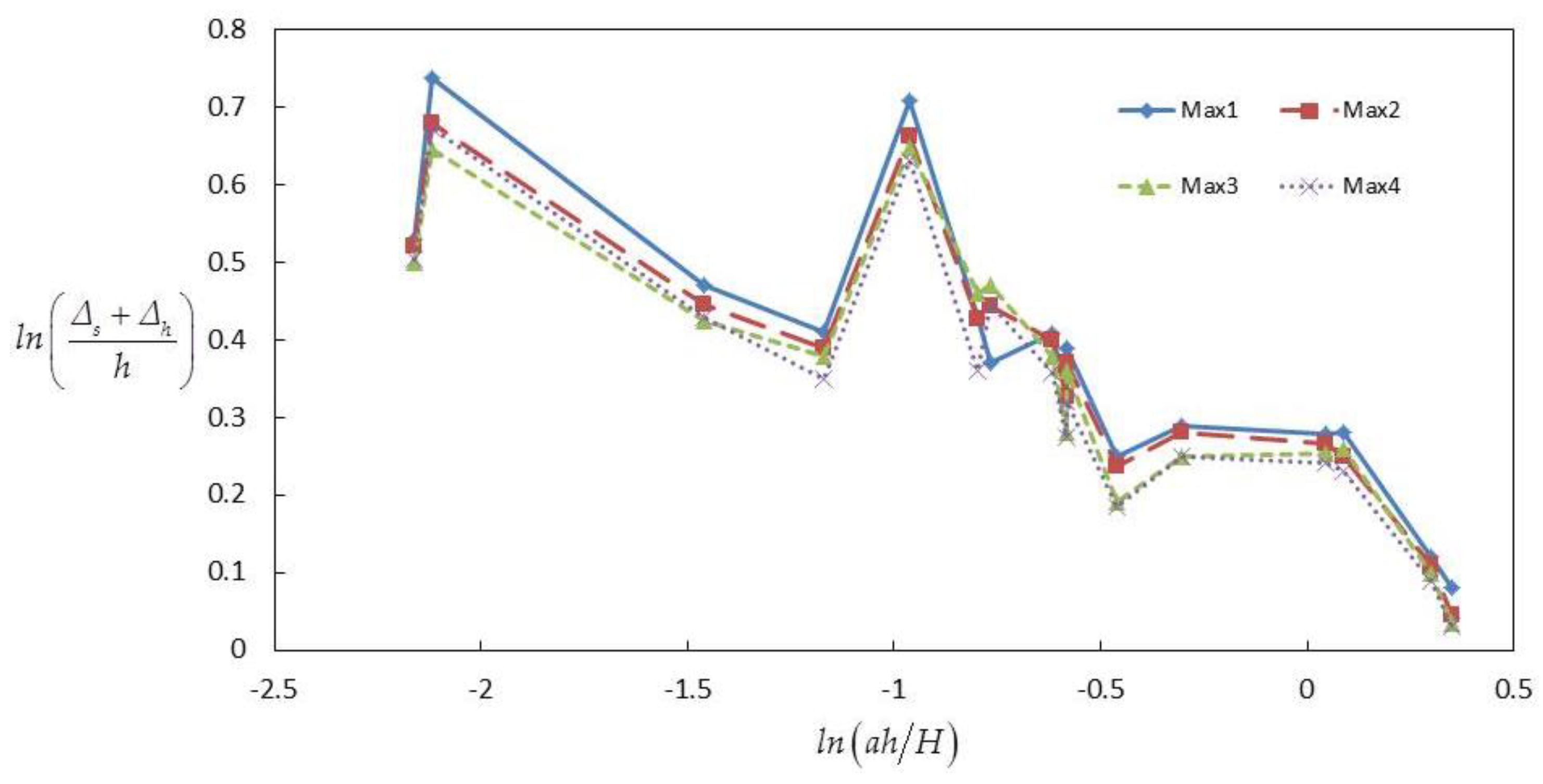
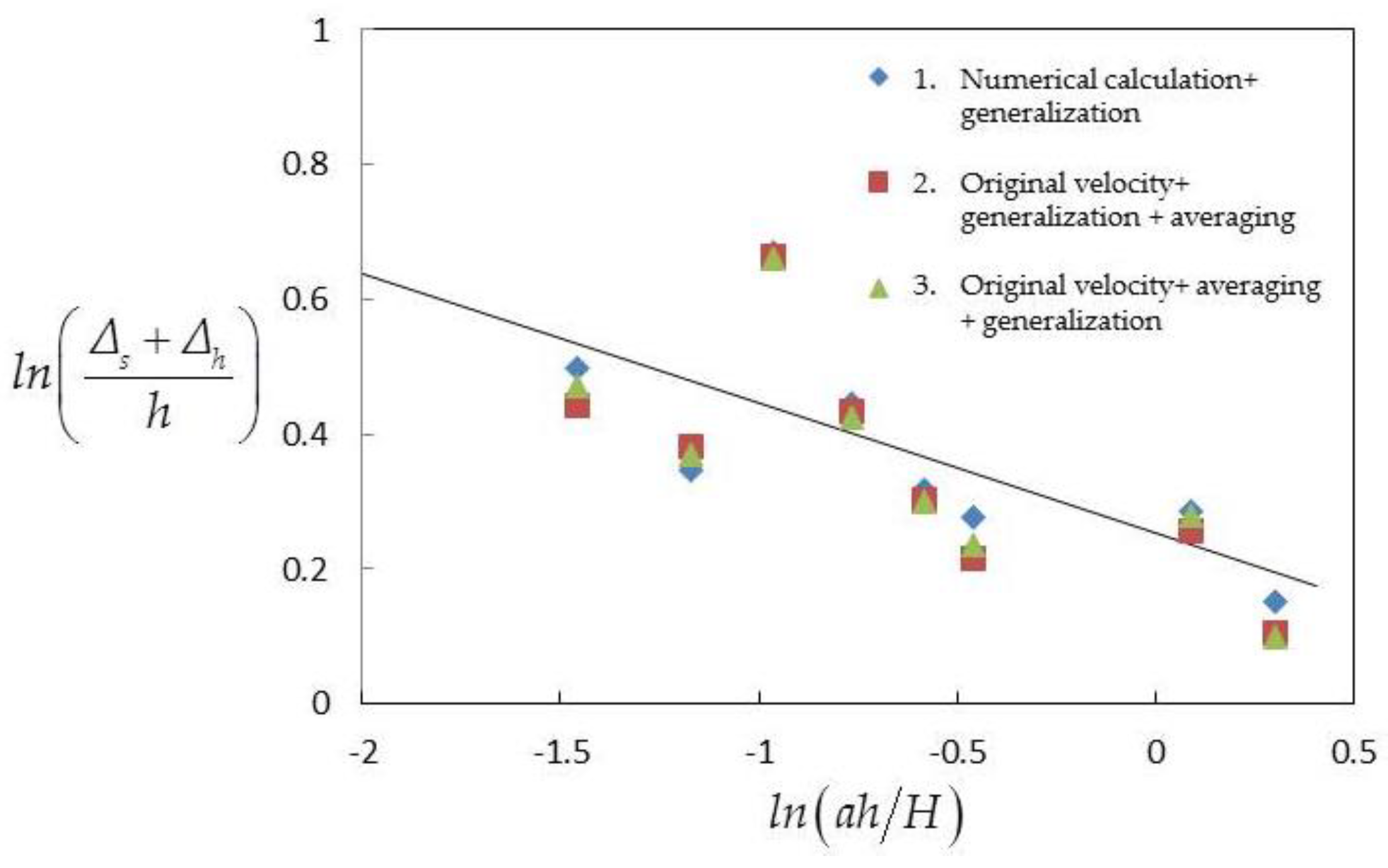
3.2.3. Influence Depth Δs + Δh
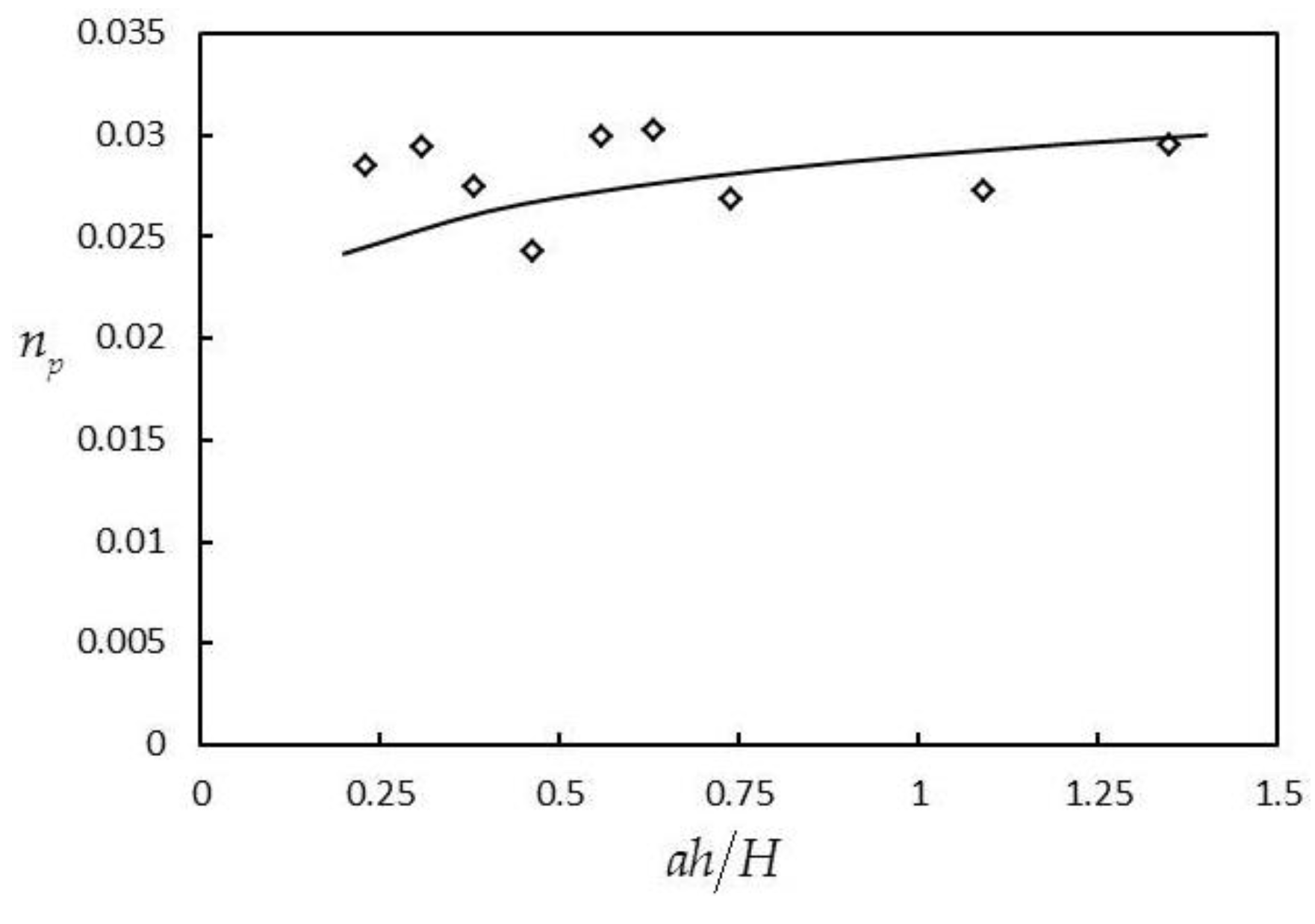
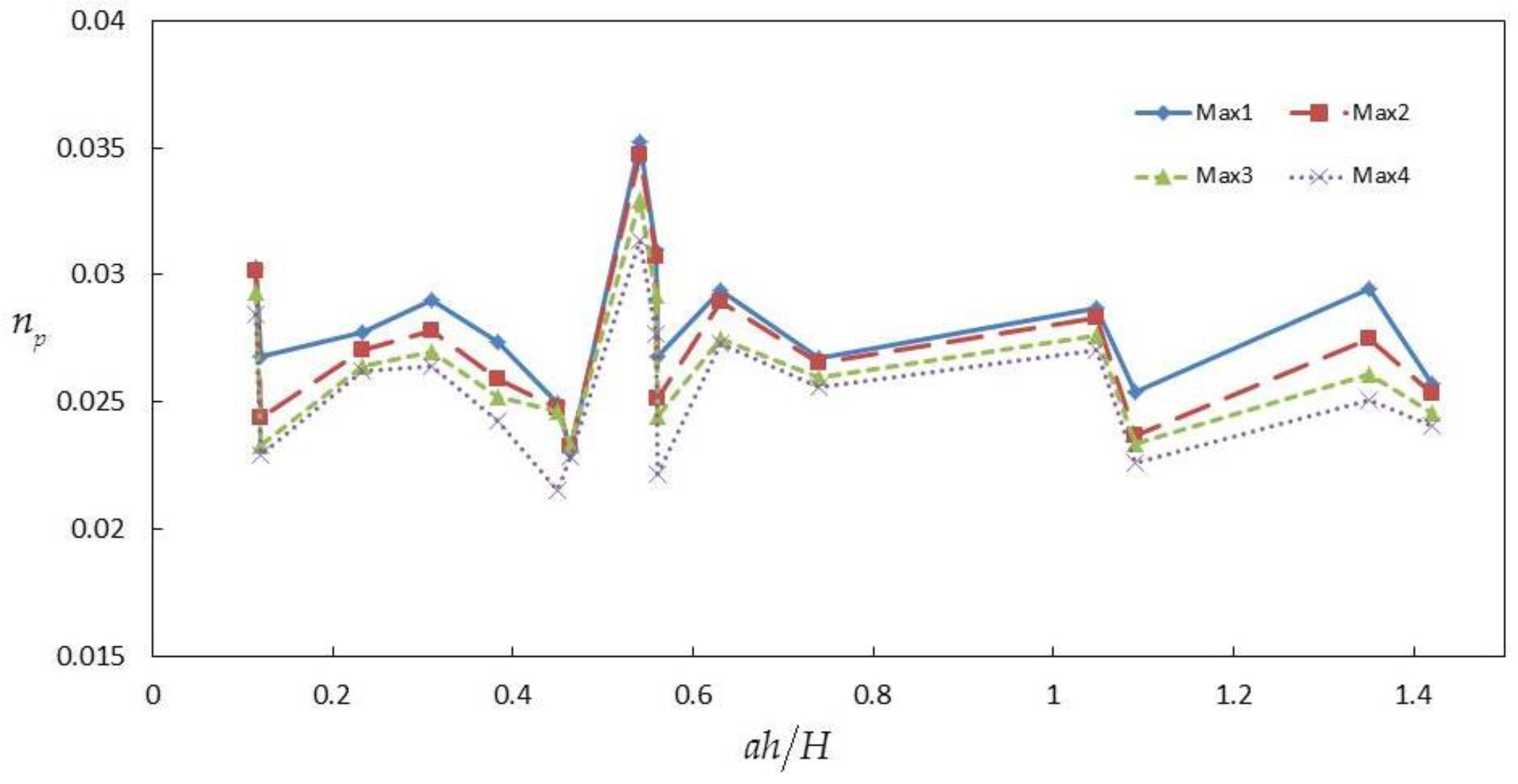
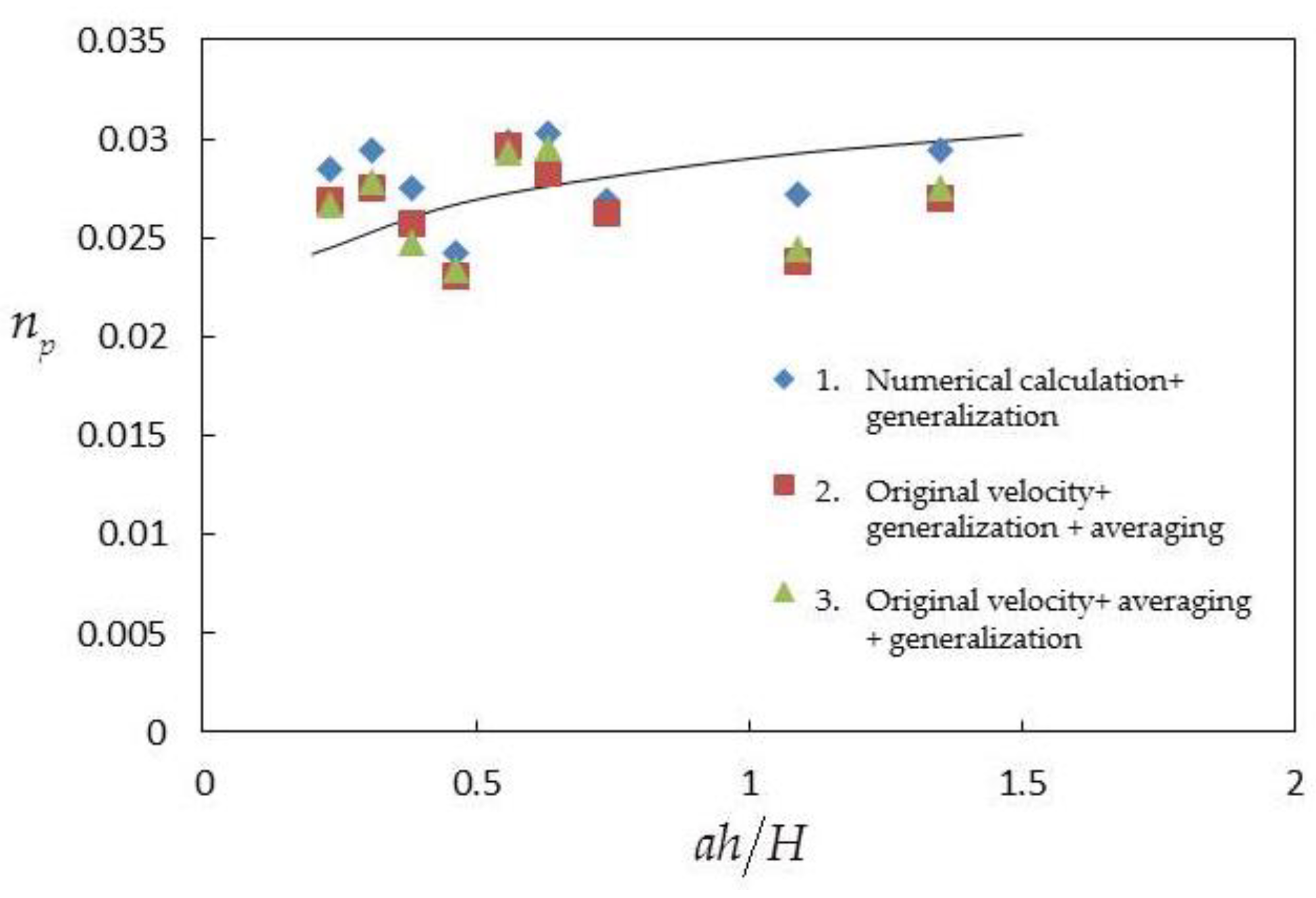
3.2.4. Generalized Roughness Coefficient np
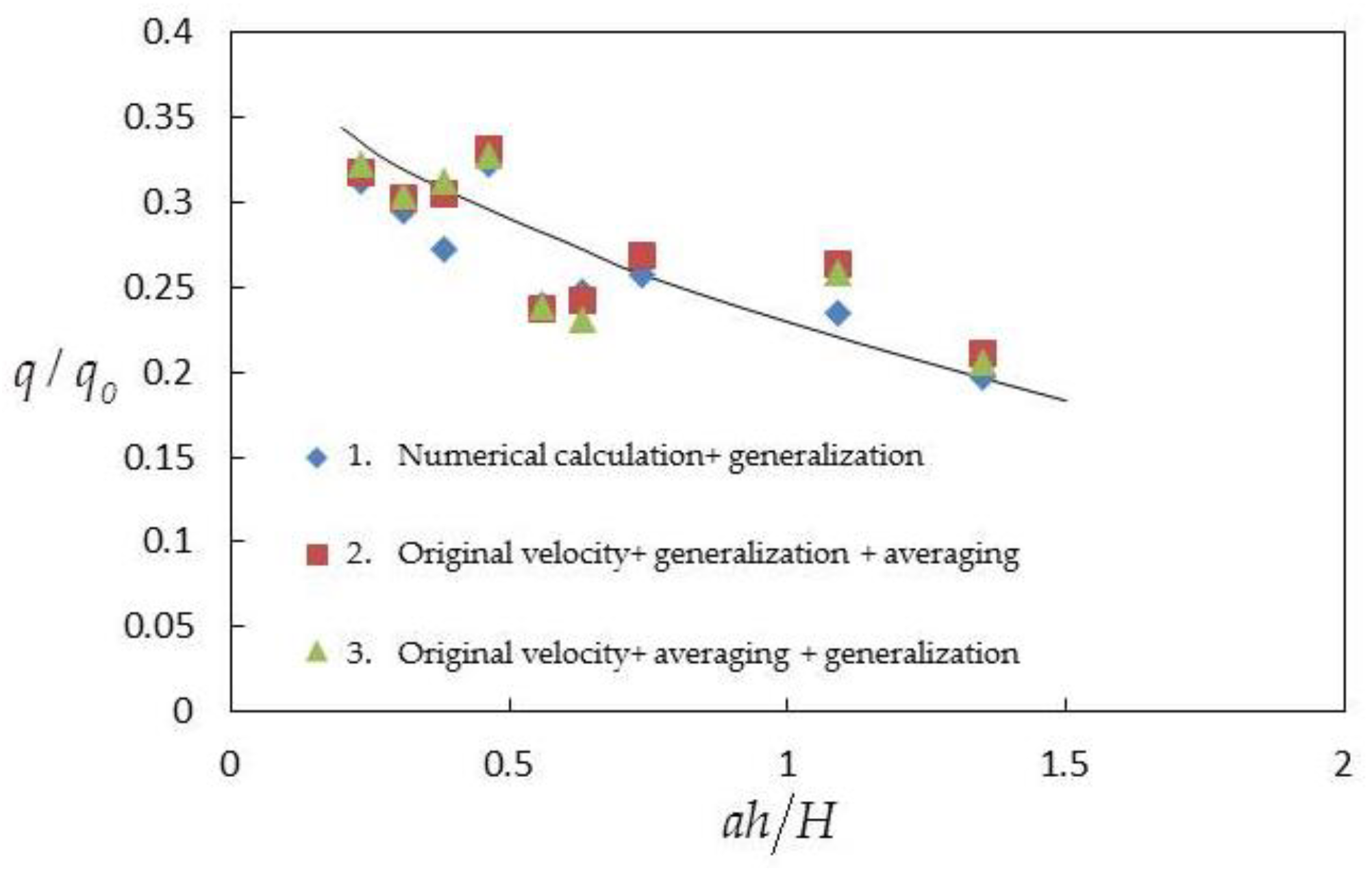
3.2.5. Ratio of Single-Width-Discharges q/q0
3.2.6. Comparison Results Related to Velocity Integration
4. Discussion
4.1. Height of the Theoretical Zero Point Δs in Three Cases
4.2. Influence Depth Δs + Δh in Three Cases
4.3. Generalized Roughness Coefficient np in Three Cases
4.4. Ratio of Single-Width-Discharges q/q0 in Three Cases
4.5. Influences of Arrangement of Vegetation
4.6. Discussion of Implications for Environmental Flows and Hydraulic Engineering Problems
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Symbol Key | |
| instantaneous variable | |
| time mean variable | |
| fluctuation variable | |
| local spatial mean | |
| local spatial pulsation | |
| longitudinal flow velocity after double averaging (m/s) | |
| longitudinal flow velocity after generalization (m/s) | |
| shear stress after double averaging (Pa) | |
| shear stress after generalization (Pa) | |
| bottom slope of the open channel | |
| diameter of submerged vegetation (m) | |
| porosity of the flora | |
| drag coefficient | |
| molecular viscosity coefficient (m2/s) | |
| turbulence viscosity coefficient (m2/s) | |
| k | turbulent kinetic energy |
| ks | turbulent kinetic energy of the large-scale shear turbulence |
| kw | turbulent kinetic energy of the small-scale stem turbulence |
| ε | turbulent kinetic energy dissipation rate |
| εs | turbulent kinetic energy dissipation rate of the large-scale shear turbulence |
| εw | turbulent kinetic energy dissipation rate of the small-scale stem turbulence |
| WD | a term reflecting the transformation of shear turbulent kinetic energy to stem-scale wake kinetic energy |
| νt | turbulent viscosity coefficient |
| vegetation density (1/m) | |
| inflow area of a single cylinder (m2) | |
| volume affected by a single cylinder (m3) | |
| diameter of the cylinder (m) | |
| height of submerged vegetation (m) | |
| length of the volume in direction when averaged locally (m), and can be streamwise direction and spanwise direction, respectively. | |
| length of the volume in direction when averaged locally (m). | |
| ah/H | a comprehensive parameter to describe the water-blocking effect of submerged vegetation on water (1/m) |
| Δs | the height of the theoretical zero point, and the flow velocity here is zero after generalization (m) |
| Δp | the height of the equivalent virtual obstacle after generalization, and it’s called virtual channel height (m) |
| Δh | the thickness of the affected region in which submerged vegetation changes the longitudinal velocity above the top of vegetation (m) |
| Δs + Δh | the influence depth (m) |
| Hm | effective water depth (m), defined as Hm = H − h + Δs |
| τh | shear stress at the top of the vegetation layer before generalization (Pa) |
| τb | shear stress at the top of the virtual channel after generalization (Pa) |
| np | roughness coefficient |
| Q | flow discharge quantity (m3/s) |
| B | channel width (m) |
| g | the acceleration of gravity (m2/s) |
| frictional velocity (m/s), defined as | |
| q | single-width discharge of open channel flow with submerged vegetation (m3/s) |
| q0 | single-width discharge of open channel flow without submerged vegetation (m3/s) |
References
- Chad, D.; Fabian, L.; Marcelo, G. Mean flow and turbulence in a laboratory channel with simulated vegetation. In Civil Engineering Studies; Hydrosystems Laboratory, Department of Civil Engineering, University of Illinois at Urbana–Champaign: Urbana, IL, USA, 1996; Hydraulic Engineering Series No. 51. [Google Scholar]
- Raupach, M.R.; Finnigan, J.J.; Brunei, Y. Coherent eddies and turbulence in vegetation canopies: The mixing-layer analogy. Bound-Layer Meteorol. 1996, 78, 351–382. [Google Scholar] [CrossRef]
- Nepf, H.; Ghisalberti, M.; White, B.; Murphy, E. Retention time and dispersion associated with submerged aquatic canopies. Water Resour. Res. 2007, 43, 436–451. [Google Scholar] [CrossRef]
- Iehisa, N.; Michio, S. Turburence structure and coherent motion in vegetated canopy open-channel flows. J. Hydro-Environ. Res. 2008, 2, 62–90. [Google Scholar]
- Carmelo, J.; Schärer, C.; Jenny, H.; Schleiss, A.J.; Franca, M.J. Floodplain land cover and flow hydrodynamic control of overbank sedimentation in compound channel flows. Water Resour. Res. 2019, 55, 9072–9091. [Google Scholar]
- Vargas-Luna, A.; Duró, G.; Crosato, A.; Uijttewaal, W. Morphological adaptation of river channels to vegetation establishment: A laboratory study. J. Geophys. Res.-Earth 2019, 124, 1981–1995. [Google Scholar] [CrossRef] [Green Version]
- Nepf, H.M.; Vivoni, E.R. Flow structure in depth-limited, vegetated flow. J. Geophys. Res.-Oceans 2000, 105, 28547–28557. [Google Scholar] [CrossRef]
- Ghisalberti, M.; Nepf, H. Shallow flows over a permeable medium: The hydrodynamics of submerged aquatic canopies. Transp. Porous Med. 2009, 78, 309–326. [Google Scholar] [CrossRef]
- Ortiz, A.C.; Ashton, A.; Nepf, H. Mean and turbulent velocity fields near rigid and flexible plants and the implications for deposition. J. Geophys. Res.-Earth 2013, 118, 2585–2599. [Google Scholar] [CrossRef]
- Ghisalberti, M. Mixing layers and coherent structures in vegetated aquatic flows. J. Geophys. Res. 2002, 107, 3011. [Google Scholar] [CrossRef]
- Ghisalberti, M.; Nepf, H.M. The limited growth of vegetated shear layers. Water Resour. Res. 2004, 40, 196–212. [Google Scholar] [CrossRef]
- Ghisalberti, M.; Schlosser, T. Vortex generation in oscillatory canopy flow. J. Geophys. Res.-Oceans 2013, 118, 1534–1542. [Google Scholar] [CrossRef]
- Takaaki, O.; Iehisa, N.; Michio, S. Flow-vegetation interactions: Length-scale of the “monami” phenomenon. J. Hydraul. Res. 2016, 54, 251–262. [Google Scholar]
- Takaaki, O.; Iehisa, N. Spatial evolution of coherent motions in finite-length vegetation patch flow. Environ. Fluid Mech. 2013, 13, 417–434. [Google Scholar]
- Zeng, Y.; Huai, W.; Zhao, M. Flow characteristics of rectangular open channels with compound vegetation roughness. Appl. Math. Mech. 2016, 37, 341–348. [Google Scholar] [CrossRef]
- Coceal, O.; Dobre, A.; Thomas, T.G. Unsteady dynamics and organized structures from dns over an idealized building canopy. Int. J. Climatol. 2007, 27, 1943–1953. [Google Scholar] [CrossRef] [Green Version]
- Ji, C.; Munjiza, A.; Williams, J.J.R. A novel iterative direct-forcing immersed boundary method and its finite volume applications. J. Comput. Phys. 2012, 231, 1797–1821. [Google Scholar] [CrossRef]
- Choi, S.U.; Kang, H. Numerical investigations of mean flow and turbulence structures of partly-vegetated open-channel flows using the Reynolds stress model. J. Hydraul. Res. 2006, 44, 203–217. [Google Scholar] [CrossRef]
- Kang, H.; Choi, S.U. Turbulence modeling of compound open-channel flows with and without vegetation on the floodplain using the Reynolds stress model. Adv. Water Resour. 2006, 29, 1650–1664. [Google Scholar] [CrossRef]
- Coceal, O.; Thomas, T.G.; Castro, I.P.; Belcher, S.E. Mean Flow and Turbulence Statistics over Groups of Urban-like Cubical Obstacles. Bound-Layer Meteorol. 2006, 121, 491–519. [Google Scholar] [CrossRef]
- Defina, A.; Bixio, A.C. Mean flow and turbulence in vegetated open channel flow. Water Resour. Res. 2005, 41, 372–380. [Google Scholar] [CrossRef] [Green Version]
- Huai, W.; Song, S.; Han, J.; Zeng, Y. Prediction of velocity distribution in straight open-channel flow with partial vegetation by singular perturbation method. Appl. Math. Mech. 2016, 37, 1315–1324. [Google Scholar] [CrossRef]
- Bai, F.; Yang, Z.; Huai, W.; Zheng, C. A depth-averaged two dimensional shallow water model to simulate flow-rigid vegetation interactions. In Proceedings of the 12th International Conference on Hydroinformatics (HIC)—Smart Water for the Future, Incheon, Republic of Korea, 21–26 August 2016. [Google Scholar]
- Luhar, M.; Nepf, H.M. From the blade scale to the reach scale: A characterization of aquatic vegetative drag. Adv. Water Resour. 2013, 51, 305–316. [Google Scholar] [CrossRef]
- Murphy, E.; Ghisalberti, M.; Nepf, H. Model and laboratory study of dispersion in flows with submerged vegetation. Water Resour. Res. 2007, 43, 1315–1324. [Google Scholar] [CrossRef]
- Hu, Y.; Huai, W.; Han, J. Analytical solution for vertical profile of streamwise velocity in open-channel flow with submerged vegetation. Environ. Fluid Mech. 2013, 13, 389–402. [Google Scholar] [CrossRef]
- Shi, H.; Liang, X.; Huai, W.; Wang, Y. Predicting the bulk average velocity of open-channel flow with submerged rigid vegetation. J. Hydrol. 2019, 572, 213–225. [Google Scholar] [CrossRef]
- Southard, P.; Johnson, J.; Rempe, D.; Matheny, A. Impacts of Vegetation on Dryland River Morphology: Insights from Spring-Fed Channel Reaches, Henry Mountains, Utah. Water Resour. Res. 2022, 58, e2021WR031701. [Google Scholar] [CrossRef]
- Li, D.; Yang, Z.; Sun, Z.; Huai, W.; Liu, J. Theoretical Model of Suspended Sediment Concentration in a Flow with Submerged Vegetation. Water 2018, 10, 1656. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.; Kimura, I.; Shimizu, Y. Bed morphological changes around a finite patch of vegetation. Earth Surf. Process. Landf. 2015, 40, 375–388. [Google Scholar] [CrossRef]
- Yang, J.; Nepf, H. A Turbulence-Based Bed-Load Transport Model for Bare and Vegetated Channels. Geophys. Res. Lett. 2018, 45, 10428–10436. [Google Scholar] [CrossRef]
- Cotton, J.; Wharton, G.; Bass, J.; Heppell, C.; Wotton, R. The effects of seasonal changes to in-stream vegetation cover on patterns of flow and accumulation of sediment. Geomorphology 2006, 77, 320–334. [Google Scholar] [CrossRef]
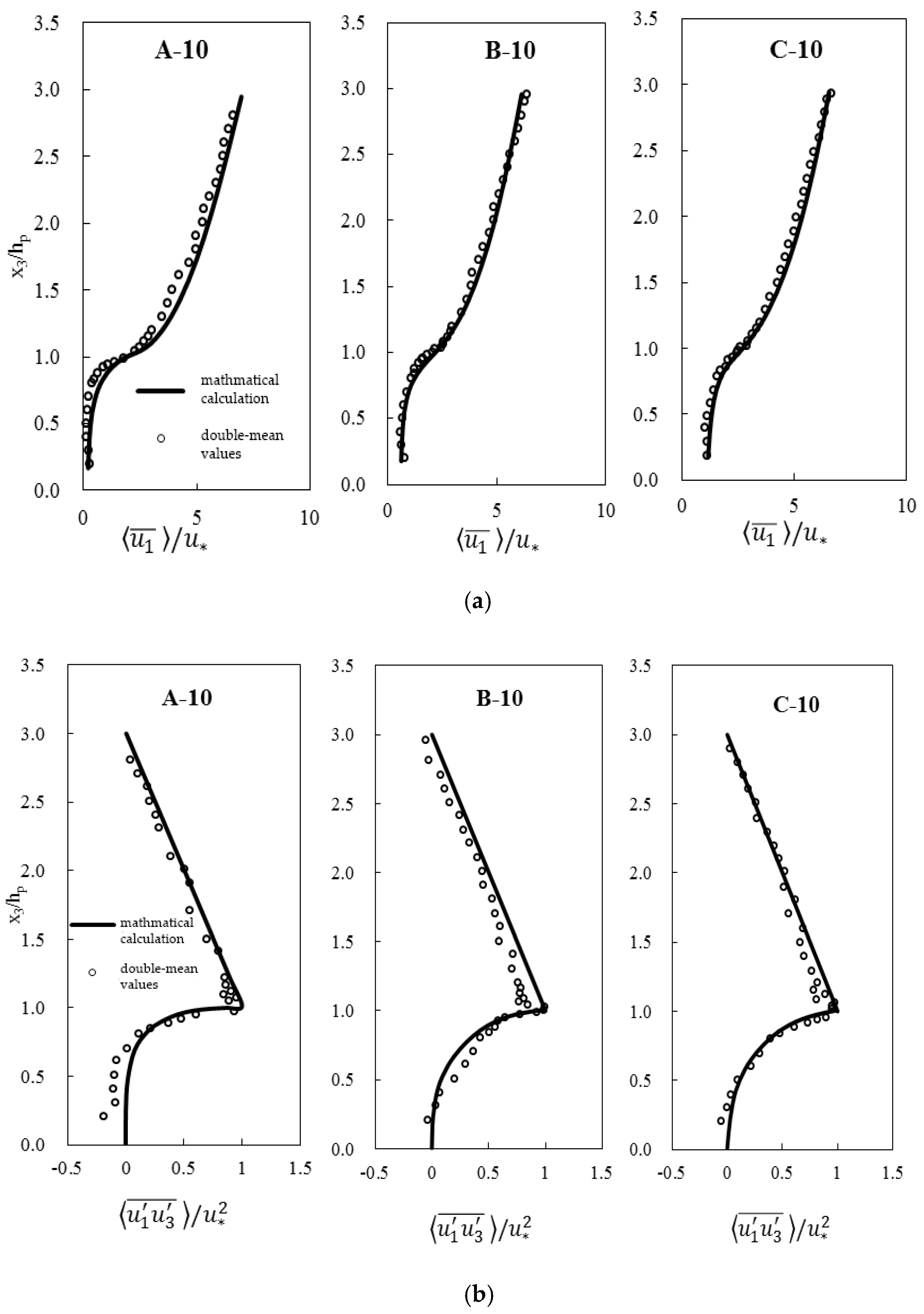





| Case | Water Depth H (cm) | Height of Vegetation Element h (cm) | Mean Bulk Velocity Um (cm/s) | Uh 1 (cm/s) | Friction Velocity U* 2 (cm/s) | Fr | Reynolds Number Re |
|---|---|---|---|---|---|---|---|
| A-10 | 15.0 | 5.0 | 12.0 | 5.83 | 2.76 | 0.10 | 1.8 × 104 |
| B-10 | 15.0 | 5.0 | 12.0 | 5.25 | 2.53 | 0.10 | 1.8 × 104 |
| C-10 | 15.0 | 5.0 | 12.0 | 5.77 | 2.31 | 0.10 | 1.8 × 104 |
| Experiment | Q (L/s) | Bed Slop S (%) | Bulk FlowVelocity (m/s) | Water Depth (m) | Reynolds Number Re | Manning’s n (m1/6) | Fr |
|---|---|---|---|---|---|---|---|
| 1 | 179 | 0.36 | 0.587 | 0.335 | 2.24 × 105 | 0.034 | 0.33 |
| 2 | 88 | 0.36 | 0.422 | 0.229 | 1.13 × 105 | 0.041 | 0.29 |
| 3 | 46 | 0.36 | 0.308 | 0.164 | 0.57 × 105 | 0.048 | 0.24 |
| 4 | 178 | 0.76 | 0.709 | 0.276 | 1.91 × 105 | 0.038 | 0.36 |
| 5 | 98 | 0.76 | 0.531 | 0.203 | 1.25 × 105 | 0.045 | 0.37 |
| 6 | 178 | 0.36 | 0.733 | 0.267 | 1.96 × 105 | 0.025 | 0.39 |
| 7 | 95 | 0.36 | 0.570 | 0.183 | 1.20 × 105 | 0.027 | 0.42 |
| 8 | 180 | 0.36 | 0.506 | 0.391 | 2.58 × 105 | 0.042 | 0.29 |
| 9 | 58 | 0.36 | 0.298 | 0.214 | 0.70 × 105 | 0.056 | 0.19 |
| 10 | 180 | 1.61 | 0.746 | 0.265 | 2.03 × 105 | 0.052 | 0.40 |
| 11 | 177 | 0.36 | 0.625 | 0.311 | 2.22 × 105 | 0.031 | 0.35 |
| 12 | 181 | 1.08 | 0.854 | 0.233 | 2.38 × 105 | 0.036 | 0.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, C.; Huang, J.; Liu, S.; Pan, W. Double Parameters Generalization of Water-Blocking Effect of Submerged Vegetation. Water 2023, 15, 764. https://doi.org/10.3390/w15040764
Qiu C, Huang J, Liu S, Pan W. Double Parameters Generalization of Water-Blocking Effect of Submerged Vegetation. Water. 2023; 15(4):764. https://doi.org/10.3390/w15040764
Chicago/Turabian StyleQiu, Chunlin, Jiesheng Huang, Shihe Liu, and Wenhao Pan. 2023. "Double Parameters Generalization of Water-Blocking Effect of Submerged Vegetation" Water 15, no. 4: 764. https://doi.org/10.3390/w15040764
APA StyleQiu, C., Huang, J., Liu, S., & Pan, W. (2023). Double Parameters Generalization of Water-Blocking Effect of Submerged Vegetation. Water, 15(4), 764. https://doi.org/10.3390/w15040764





