Analysis of Water-Lifting Aerator Performance Based on the Volume of Fluid Method
Abstract
:1. Introduction
2. Numerical Simulation Methods
2.1. VOF Method
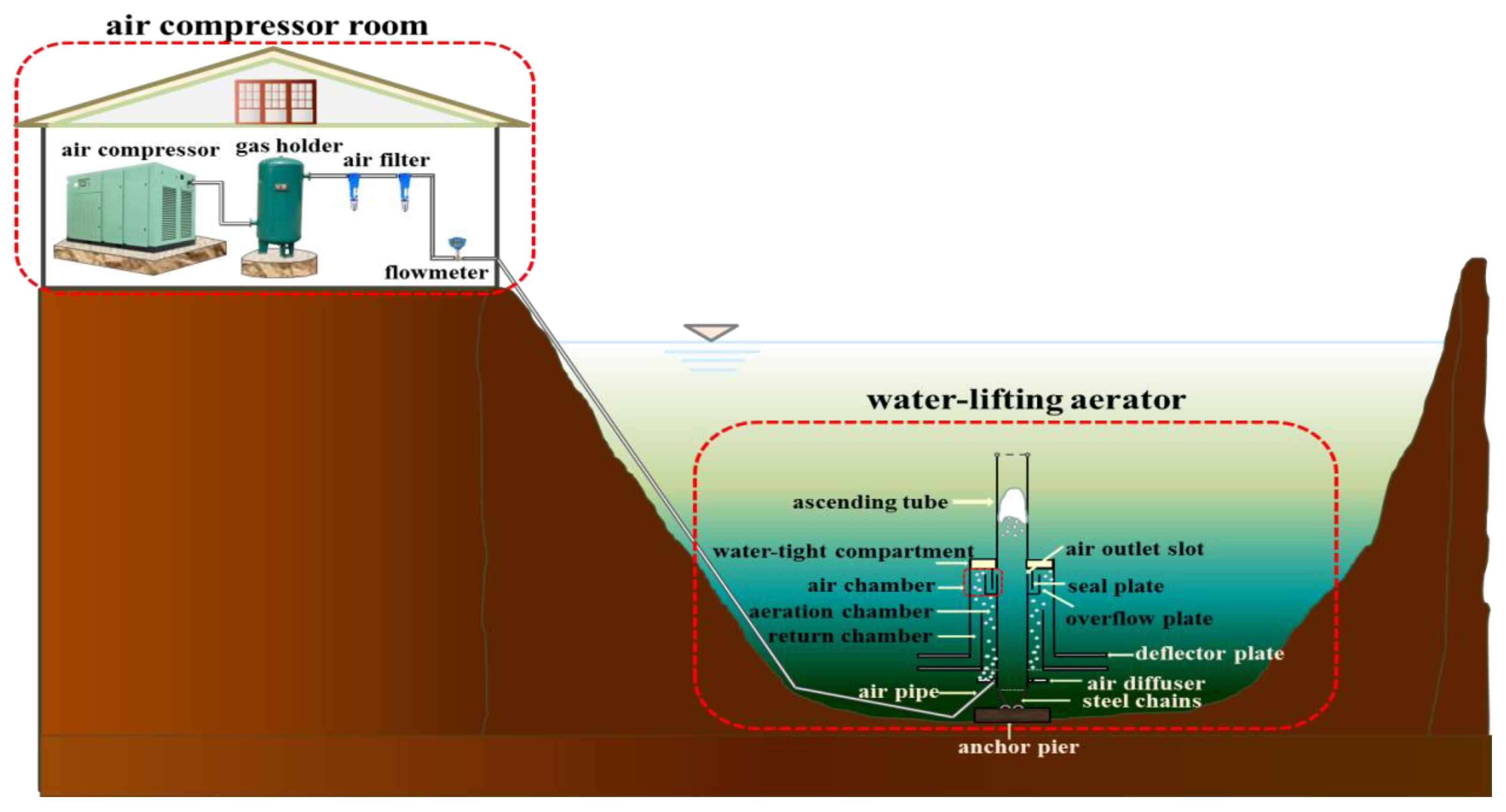
2.2. Computational Model and Boundary Condition
2.3. WLA Performance Indices
3. Results and Discussion
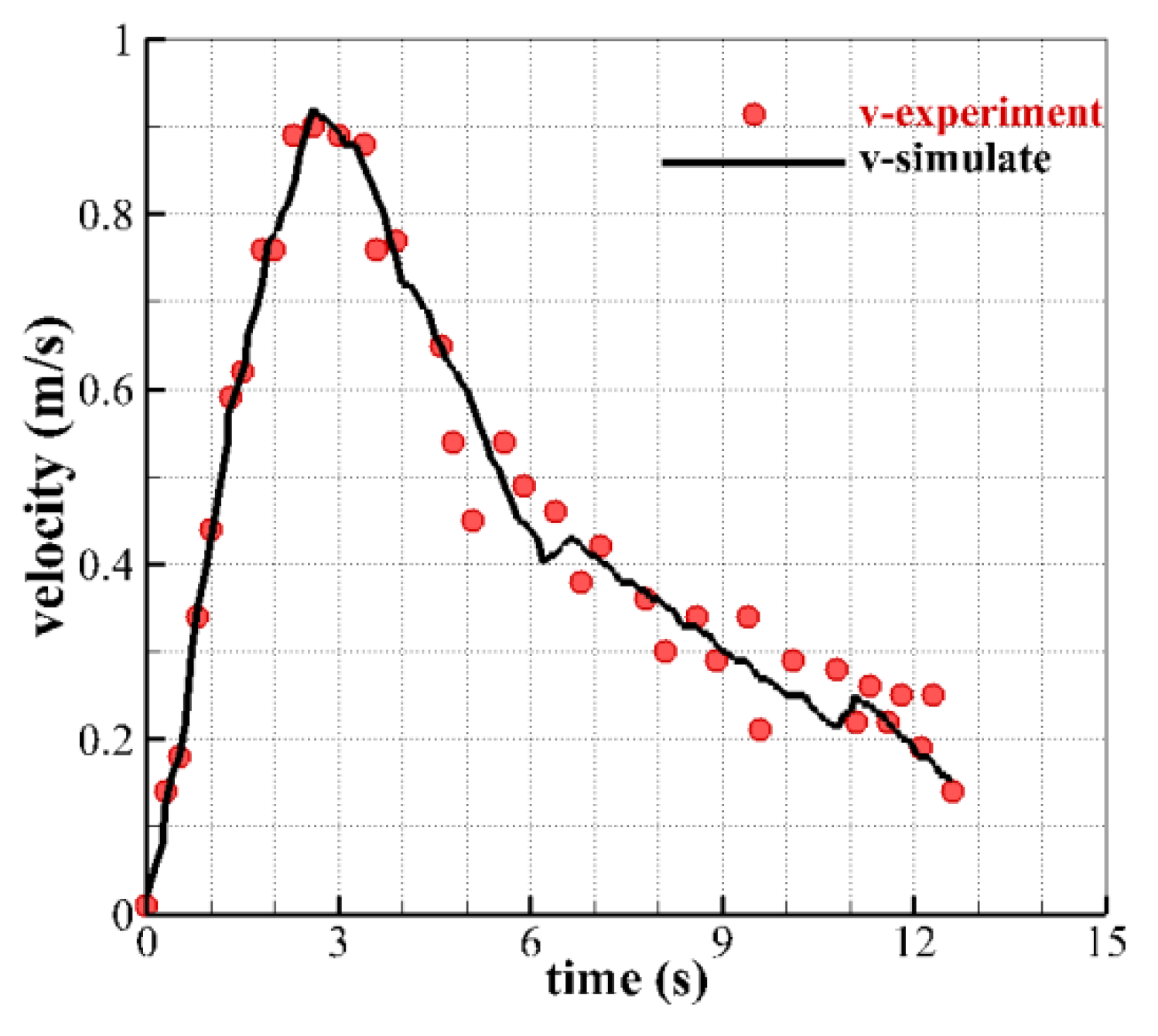
3.1. Numerical Method Verification
3.2. Analysis of the Internal Flow of the Water-Lifting Aerator
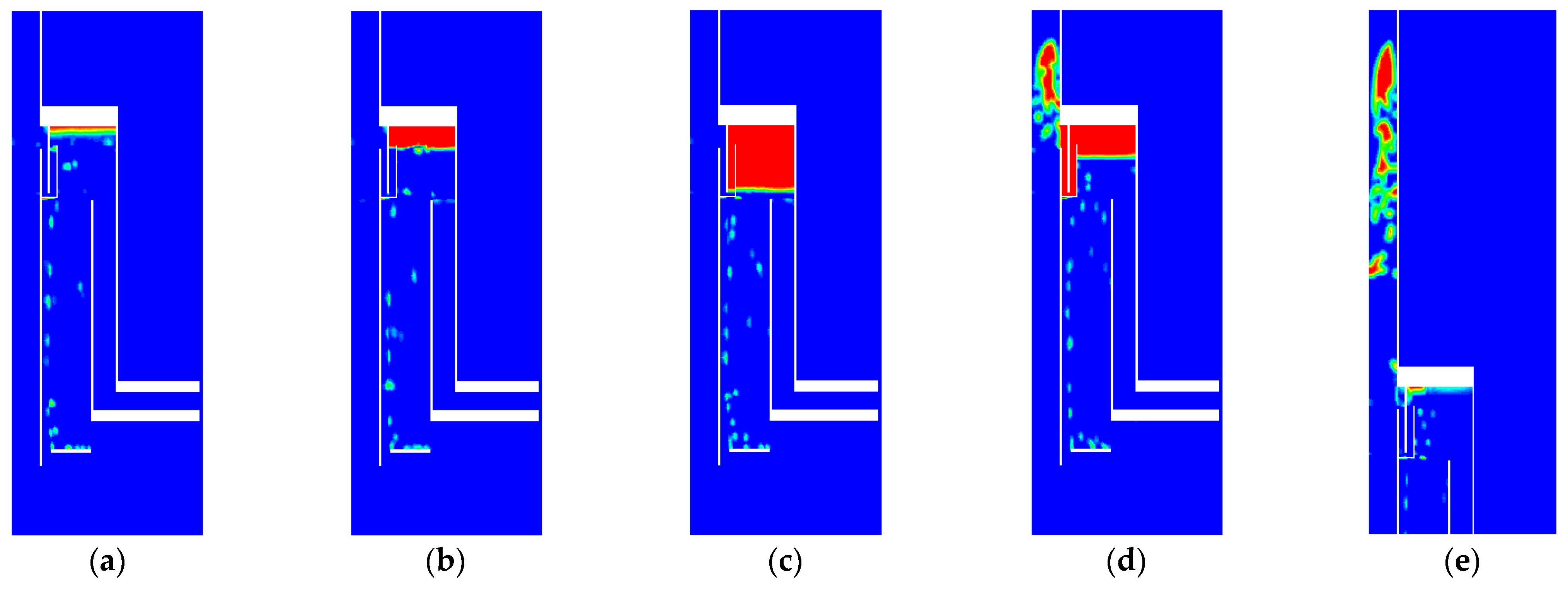
3.2.1. Analysis of the Air Piston Forming Process
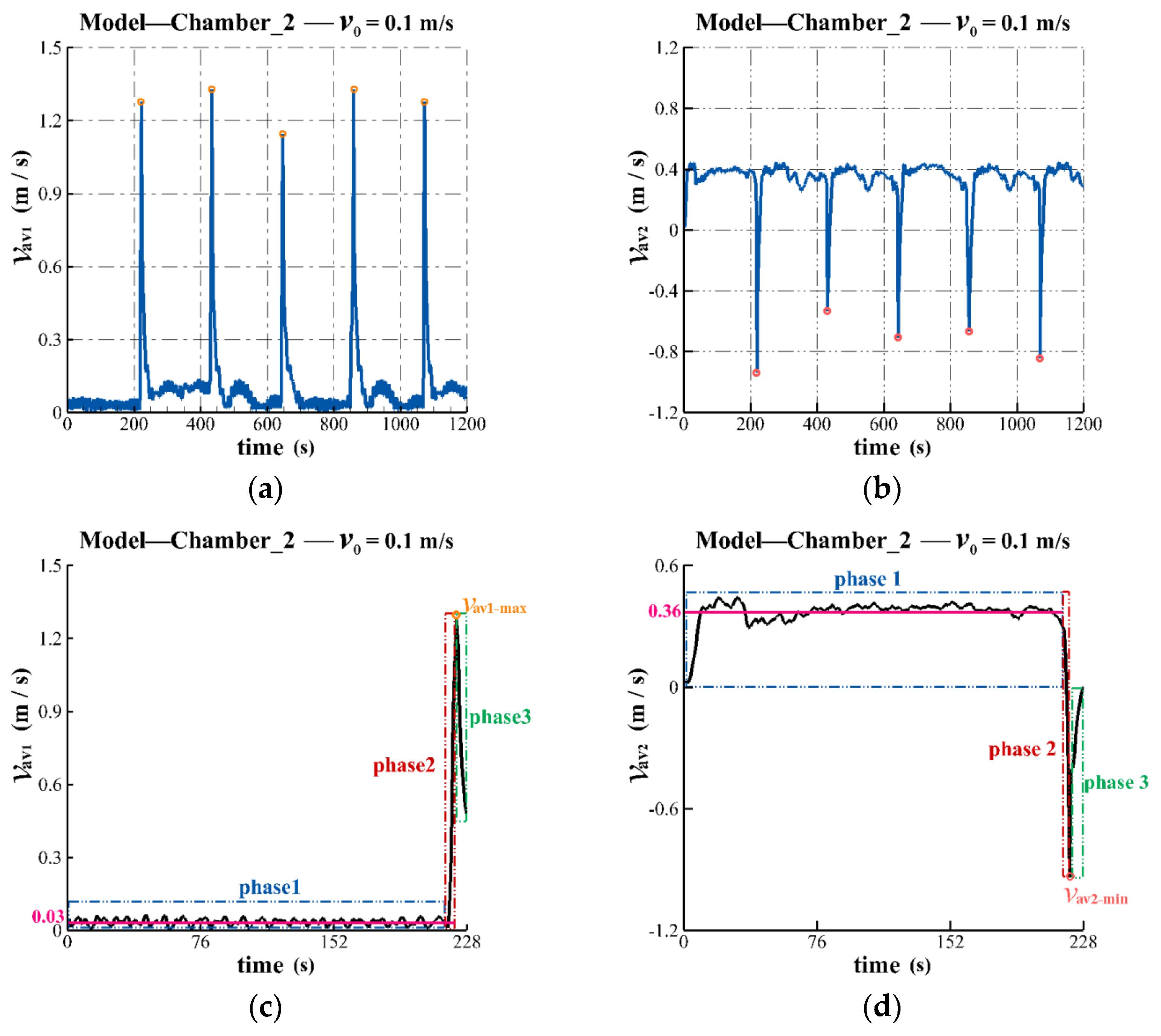
3.2.2. Velocity Analysis of the WLA Outlet
3.3. Analysis of Factors Affecting Water-Lifting Performance
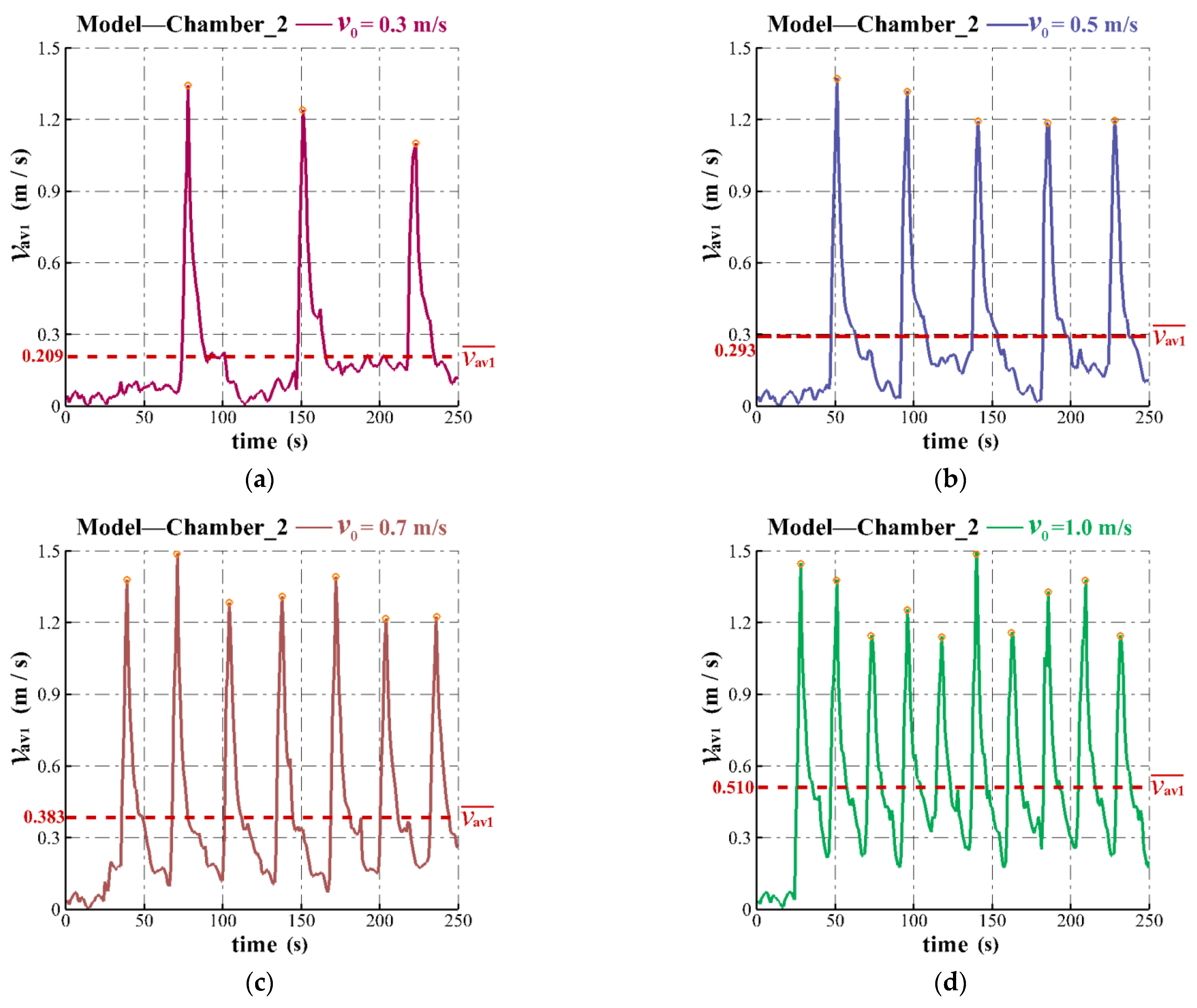
3.3.1. Effect of Air Release Rate
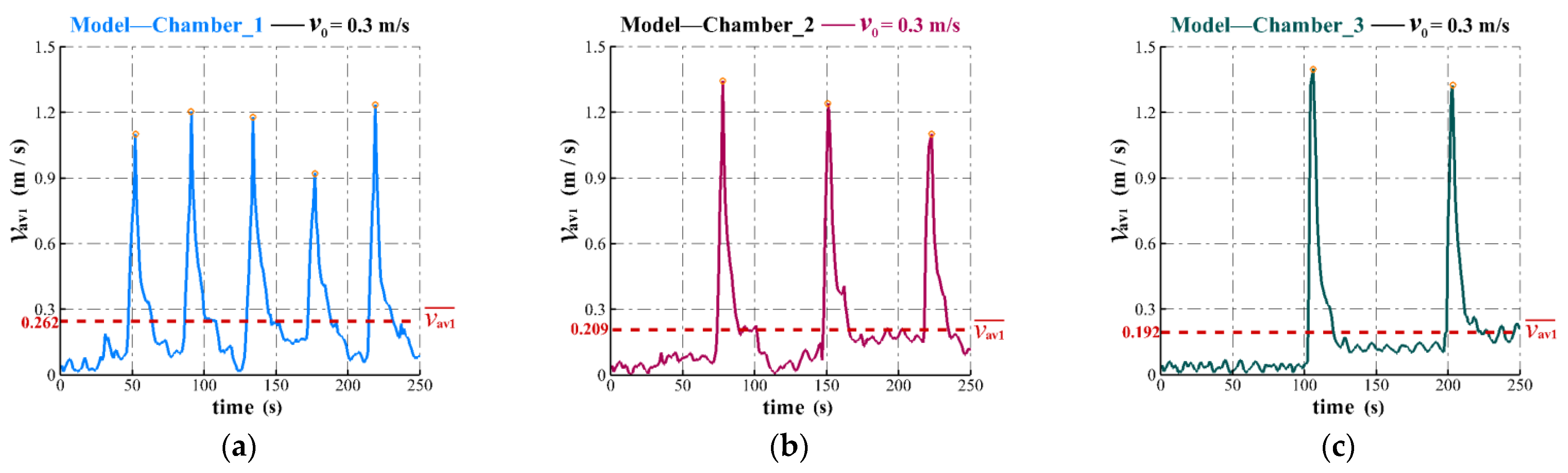
3.3.2. Effect of Air Chamber Volume
3.4. Analysis of Factors Affecting Oxygenation Performance
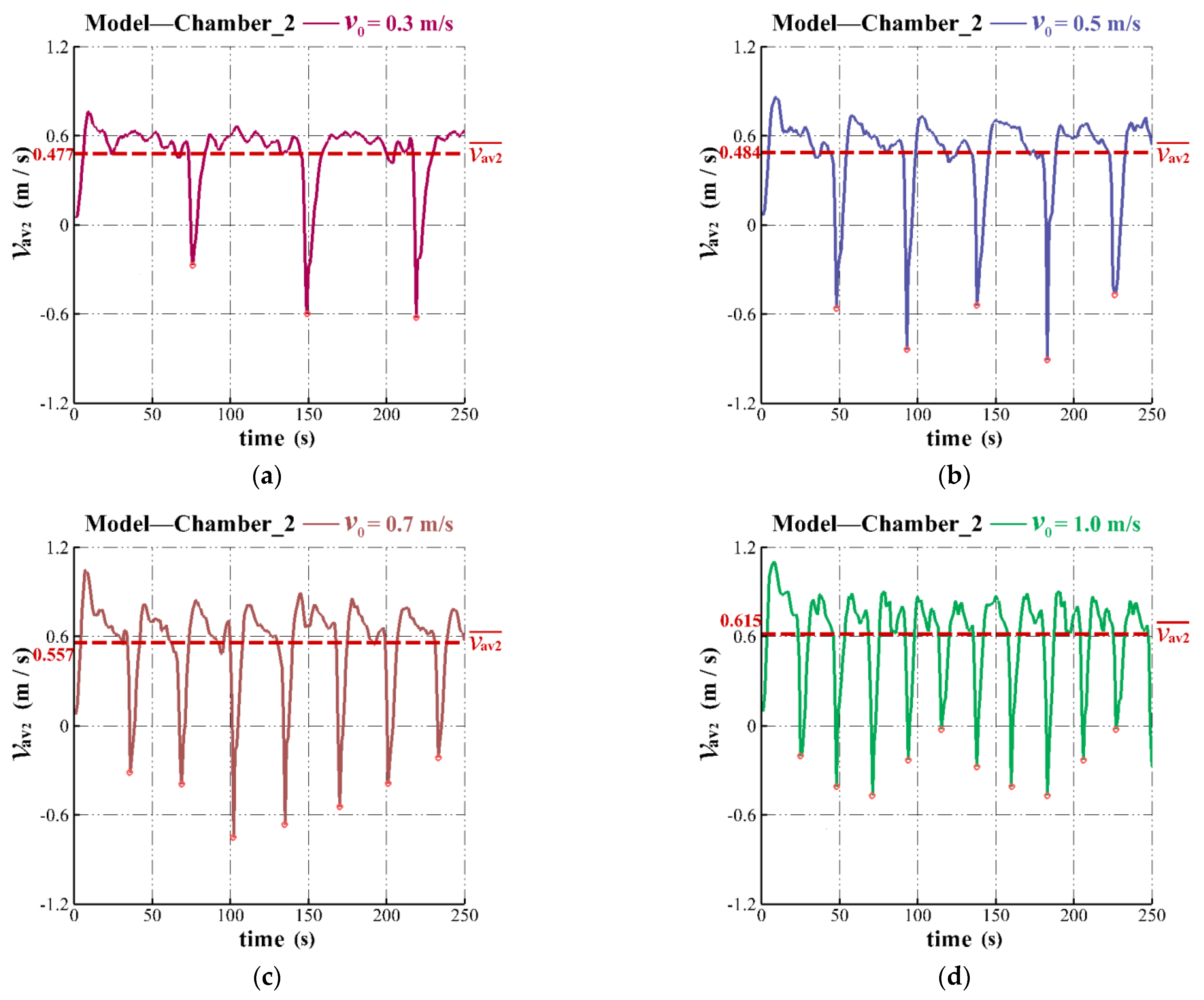
3.4.1. Effect of Air Release Rate
3.4.2. Effect of Air Chamber Volume
3.5. Performance Analysis of Water-Lifting Aerator
4. Conclusions
- The calculation results obtained using the VOF method correlated with the experimental results. This demonstrates the feasibility of the methodology and the reliability of the results, indicating that the proposed method can be used to analyze WLA internal flow details.
- By analyzing the detailed process of air bubble accumulation and air piston formation and release inside the WLA, the effects of air piston release on the flow in the ascending tube and deflector plate were discussed, and the mechanisms of water-lifting and oxygenation to deep water were revealed.
- The effects of different air release rates and air chamber volumes on the water-lifting performance of WLA were analyzed. The results show that an increase in the air release rate shortened the air piston period, increased the time-averaged velocity of the ascending tube outlet, and enhanced the water-lifting performance of the WLA. Additionally, increasing the air chamber volume increased the air piston period, reduced the time-averaged velocity of the ascending tube outlet, and weakened the water-lifting performance of the WLA.
- The effects of different air release rates and air chamber volumes on the oxygenation performance of a deep water body were analyzed. The results show that increasing the air release rate shortened the air piston period and increased the time-averaged velocity of the deflector plate outlet, finally enhancing the oxygenation performance of the WLA. Increasing the air chamber volume prolonged the air piston period, increased the time-averaged velocity of the deflector plate outlet, and improved the oxygenation performance of the bottom water.
- The performance of WLAs with different air chamber volumes and air release rates were compared. The results show that as the air chamber volume increased, the oxygenation performance increased at a relative rate of 27%, and the water-lifting performance decreased by 14%. As the air release rate increased, the oxygenation performance increased at a relative rate of 17%, and the water-lifting performance increased by 47%.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vinçon-Leite, B.; Casenave, C. Modelling eutrophication in lake ecosystems: A review. Sci. Total Environ. 2019, 651, 2985–3001. [Google Scholar] [CrossRef] [PubMed]
- Huang, T.L. In-situ control of water pollution and improvement of water quality in water source reservoirs is the primary precondition for the safety of drinking water. Water Wastewater Eng. 2017, 43, 69. [Google Scholar] [CrossRef]
- Li, N.; Li, J.X.; Li, G.W.; Li, Y.; Xi, B.D.; Wu, Y.W.; Li, C.L.; Li, W.; Zhang, L.Y. The eutrophication and its regional heterogeneity in typical lakes of China. Acta Hydrobiol. Sin. 2018, 42, 854–864. [Google Scholar] [CrossRef]
- Yin, H.X.; Wang, Z.K.; Luo, X.Y.; Wang, M.; Guo, Y.; Li, K. The impact of different growth conditions on chemical characteristics of algal organic matter Variation. Water Wastewater Eng. 2019, 45, 134–140. [Google Scholar] [CrossRef]
- Wen, C.C.; Huang, T.L.; Wen, G.; Li, K.; Yang, S.Y.; Zhang, H.H.; Xu, J.; Wang, Z. Controlling phytoplankton blooms in a canyon-shaped drinking water reservoir via artificial and induced natural mixing: Taxonomic versus functional groups. Chemosphere 2022, 287, 131771. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Lei, C.; Carey, C.C.; Gantzer, P.A.; Little, J.C. A coupled three-dimensional hydrodynamic model for predicting hypolimnetic oxygenation and epilimnetic mixing in a shallow eutrophic reservoir. Water Resour. Res. 2017, 53, 470–484. [Google Scholar] [CrossRef]
- Bryant, L.D.; Gantzer, P.A.; Little, J.C. Increased sediment oxygen uptake caused by oxygenation-induced hypolimnetic mixing. Water Res. 2011, 45, 3692–3703. [Google Scholar] [CrossRef]
- Munger, Z.W.; Carey, C.C.; Gerling, A.B.; Hamre, K.D.; Doubek, J.P.; Klepatzki, S.D.; McClure, R.P.; Schreiber, M.E. Effectiveness of hypolimnetic oxygenation for preventing accumulation of Fe and Mn in a drinking water reservoir. Water Res. 2016, 106, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Hasan, K.; Alam, K.; Chowdhury, S.A.M. The Use of an aeration system to prevent thermal stratification of water bodies: Pond, lake and water supply reservoir. Appl. Ecol. Environ. Sci. 2014, 2, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Toffolon, M.; Serafini, M. Effects of artificial hypolimnetic oxygenation in a shallow lake. Part 2: Numerical modelling. J. Environ. Manag. 2013, 114, 530–539. [Google Scholar] [CrossRef]
- Zhai, Z.Q.; Huang, T.L.; Chen, F. Application of water-lifting aeration technology in water quality improvement of water diversion reservoir. China Water Wastewater 2022, 38, 31–37. [Google Scholar] [CrossRef]
- Huang, T.L.; Cong, H.B.; Chai, B.B. Source Water Quality Pollution and Control; China Architecture & Building Press: Beijing, China, 2009. [Google Scholar]
- Cong, H.B.; Huang, T.L.; Chai, B.B. A Water-Circulating Aerator: Optimizing structure and predicting water flow rate and oxygen transfer. J. Hydraul. Eng. 2011, 137, 659–667. [Google Scholar] [CrossRef]
- Shi, J.C. Variation of Water Quality and the In-Situ Water Quality Improvement of a Stratified, Source Water Reservoir. Ph.D. Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2016. [Google Scholar] [CrossRef]
- Chang, Z.Y.; Huang, T.L. Research on the water-lifting performance of water-lifting aerator based on VOF. J. Xi’an Univ. Archit. Technol. 2021, 53, 117–125. [Google Scholar] [CrossRef]
- Cong, H.B.; Huang, T.L.; Miu, J.G.; He, W.J.; Yin, P.J. Study on water improvement function, capacity of lifting water and oxygenation of a water-lifting aerator. Chin. J. Environ. Eng. 2007, 1, 7–13. [Google Scholar] [CrossRef]
- Zhu, W.F. Numerical Simulations on the Periphery Flow Field of Water-Lifting Aerator and the Flow Field of Aeration Chamber. Master’s Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2008. [Google Scholar] [CrossRef]
- Wang, J.X. Numerical Simulations of Effects of Thermal Stratification and Water Depth on Flow Around Water-Lifting Aerator. Master’s Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2010. [Google Scholar] [CrossRef]
- Sun, X.; Ye, L.L.; Zhao, W.L.; Huang, T.L.; Cong, H.B. Effect of temperature gradient on algae inhibition by in-situ water-lifting aeration in a stratified reservoir. China Environ. Sci. 2014, 34, 352–358. [Google Scholar]
- Sun, X.; Li, X.; Zhang, M.D.; Huang, T.L.; Liu, W. Comparison of water-lifting aerator type for algae inhibition in stratified source water reservoirs. Ecol. Eng. 2014, 73, 624–634. [Google Scholar] [CrossRef]
- Zhang, M.D. System Optimization of Water-Lifting Aeration in Deep-Water Reservoirs. Master’s Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2014. [Google Scholar]
- Hu, P.; Liu, L.H.; Wu, L.X.; Fang, Y.Y. Current research progress and trend on fine pore aeration. Environ. Eng. 2015, 33, 58–61. [Google Scholar] [CrossRef]
- He, Y.P. Numerical Simulation Study on the Position Distribution and the Optimization of the Optimization of the Aeration of the Oxidation Trench Thruster. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2021. [Google Scholar] [CrossRef]
- Zhang, W.L.; Yang, X.M.; Wang, H.L.; Li, Y. Experimental research of oxygenation performance optimization for fine pore aeration system of rivers. Water Resour. Prot. 2022, 38, 154–160. [Google Scholar]
- Amaral, A.; Bellandi, G.; Rehman, U. Towards improved accuracy in modeling aeration efficiency through understanding bubble size distribution dynamics. Water Res. 2018, 131, 346–355. [Google Scholar] [CrossRef]
- Yin, X.F.; Fan, H.T.; Qi, L.; Wang, H.C.; Wei, Y.L.; Jiang, S.Z. Pilot study on influence of airflow rate and diffuser density on oxygenation performance of fine-pore diffuser in air aeration system. Water Pollut. Control 2015, 33, 27–30. [Google Scholar] [CrossRef]
- Liu, X.Y.; Wu, T.; Kang, W.C.; Zhou, X.L.; Bi, X.J. Influence of velocity field distribution on the oxygenation performance of fine bubble aeration in plug-flow reactor. Environ. Sci. Technol. 2020, 43, 12–17. [Google Scholar] [CrossRef]
- Xu, P.; Shan, J.H.; Jin, X.H.; Yu, J.Z.; Sun, Y.; Zhang, J.Z. Performance of impulse-type fine bubble aerator. Chin. J. Environ. Eng. 2015, 9, 4287–4292. [Google Scholar]
- Cheng, X.J.; Xie, Y.N.; Zhu, D.T.; Li, R.; Xie, J. Experiment on effects of microporous diffuser types on aeration oxygenation performance. Trans. Chin. Soc. Agric. Eng. 2017, 33, 226–233. [Google Scholar] [CrossRef]
- Wang, H.B.; Li, C.L.; Qiu, G.M.; Guo, X. Numerical simulation of flow field characteristics in aerated reactor based on VOF. Membr. Sci. Technol. 2016, 36, 70–78. [Google Scholar]
- Gu, Y.J.; Yang, W.D.; Liu, Z.Y.; Luo, Z.G.; Zou, Z.S. Numerical simulation about evolution of bubble wake during bubble rising by VOF method. CIESC J. 2021, 72, 1947–1955. [Google Scholar] [CrossRef]
- Ding, G.D.; Chen, J.Q.; Cai, X.L.; Ye, F.; Li, Z.L.; Ji, Y.P.; Guo, J. Numerical simulation of single bubble breaking behavior in Venturi microbubble generator. Chem. Ind. Eng. Prog. 2020, 39, 2590–2598. [Google Scholar] [CrossRef]
- Zuzio, D.; Orazzo, A.; Estivalèzes, J.-L.; Lagrange, I. A new efficient momentum preserving Level-Set/VOF method for high density and momentum ratio incompressible two-phase flows. J. Comput. Phys. 2020, 410, 109342. [Google Scholar] [CrossRef]
- Wen, H.L.; Yu, C.H.; Sheu, T.W. On the development of LS-assisted VOF method for incompressible interfacial flows. J. Comput. Phys. 2020, 406, 109188. [Google Scholar] [CrossRef]
- Cerqueira, R.F.L.; Paladino, E.E.; Evrard, F.; Denner, F.; van Wachem, B. Multiscale modeling and validation of the flow around Taylor bubbles surrounded with small dispersed bubbles using a coupled VOF-DBM approach. Int. J. Multiph. Flow 2021, 141, 103673. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Giussani, F.; Piscaglia, F.; Saez-Mischlich, G.; Hèlie, J. A three-phase VOF solver for the simulation of in-nozzle cavitation effects on liquid atomization. J. Comput. Phys. 2020, 406, 109068. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- ANSYS. Ansys Fluent 14.0 Theory Guide; ANSYS Inc.: Pittsburgh, PA, USA, 2011. [Google Scholar]
- Ray, J.; Lefantzi, S.; Arunajatesan, S.; Dechant, L. Bayesian Parameter Estimation of a k-epsilon Model for Accurate Jet-in-Crossflow Simulations. AIAA J. 2016, 54, 2432–2448. [Google Scholar] [CrossRef]


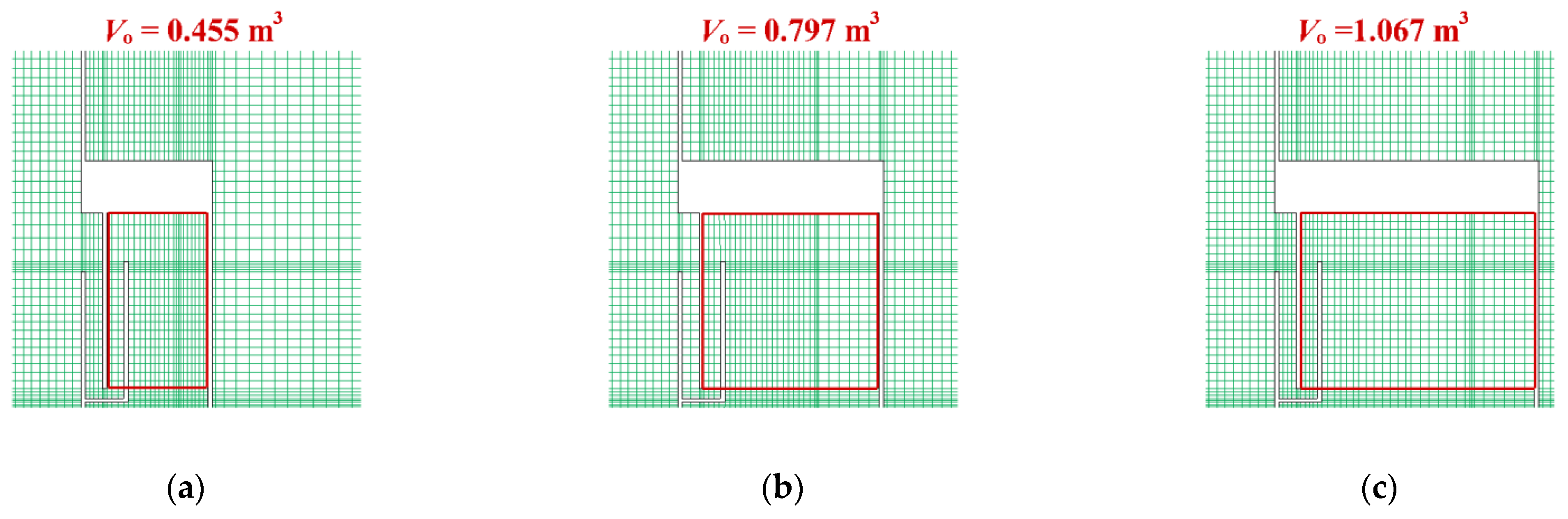
| Working Condition | Computational Model | Air Chamber Volume (m3) | Air Release Rate (m/s) |
|---|---|---|---|
| Working Condition 1 | Chamber_2 | 0.797 | 0.1 |
| Working Condition 2 | Chamber_2 | 0.797 | 0.3 |
| Working Condition 3 | Chamber_2 | 0.797 | 0.5 |
| Working Condition 4 | Chamber_2 | 0.797 | 0.7 |
| Working Condition 5 | Chamber_2 | 0.797 | 1.0 |
| Working Condition 6 | Chamber_1 | 0.455 | 0.3 |
| Working Condition 2 | Chamber_2 | 0.797 | 0.3 |
| Working Condition 7 | Chamber_3 | 1.067 | 0.3 |
| Working Condition 2 | Working Condition 3 | Working Condition 4 | Working Condition 5 | |
|---|---|---|---|---|
| Air release rate, (m/s) | 0.3 | 0.5 | 0.7 | 1.0 |
| Average air piston period, (s) | 73 | 45 | 32 | 23 |
| Average maximum velocity of the ascending tube outlet, (m/s) | 1.296 | 1.345 | 1.373 | 1.422 |
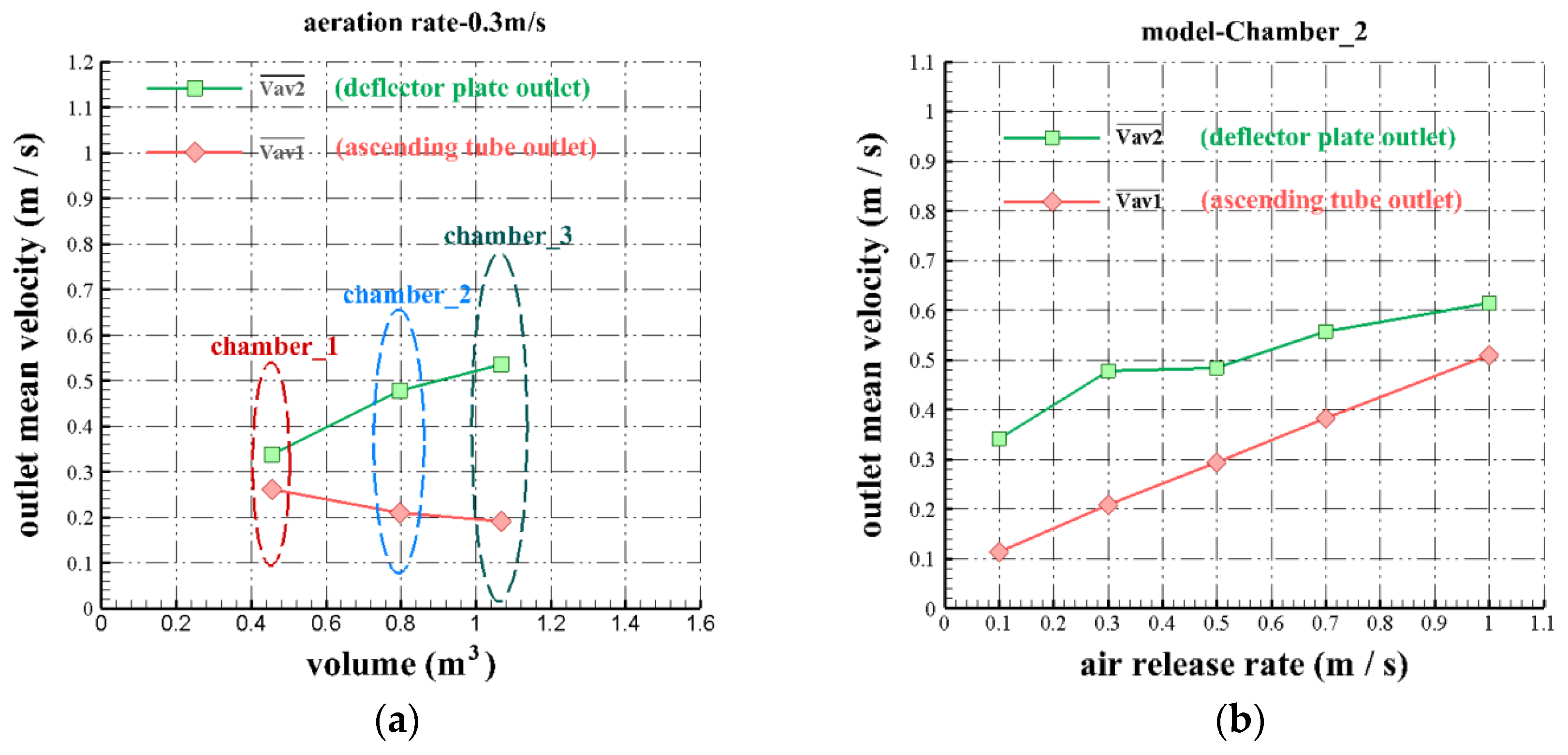
| Time-averaged velocity of the ascending tube outlet, (m/s) | 0.209 | 0.293 | 0.383 | 0.510 |
| Working Condition 6 (Chamber_1) | Working Condition 2 (Chamber_2) | Working Condition 7 (Chamber_3) | |
|---|---|---|---|
| Air chamber volume, (m3) | 0.455 | 0.797 | 1.067 |
| Average air piston period, (s) | 41 | 73 | 97 |
| Average maximum velocity of the ascending tube outlet, (m/s) | 1.136 | 1.296 | 1.333 |
| Time-averaged velocity of the ascending tube outlet, (m/s) | 0.262 | 0.209 | 0.192 |
| Working Condition 2 | Working Condition 3 | Working Condition 4 | Working Condition 5 | |
|---|---|---|---|---|
| Air release rate, (m/s) | 0.3 | 0.5 | 0.7 | 1.0 |
| Average air piston period, (s) | 73 | 45 | 32 | 23 |
| Average minimum velocity of the deflector plate outlet, (m/s) | −0.666 | −0.650 | −0.440 | −0.272 |
| Time-averaged velocity of the deflector plate outlet, (m/s) | 0.477 | 0.484 | 0.557 | 0.615 |
| Working Condition 6 (Chamber_1) | Working Condition 2 (Chamber_2) | Working Condition 7 (Chamber_3) | |
|---|---|---|---|
| Air chamber volume, (m3) | 0.455 | 0.797 | 1.067 |
| Average air piston period, (s) | 41 | 73 | 97 |
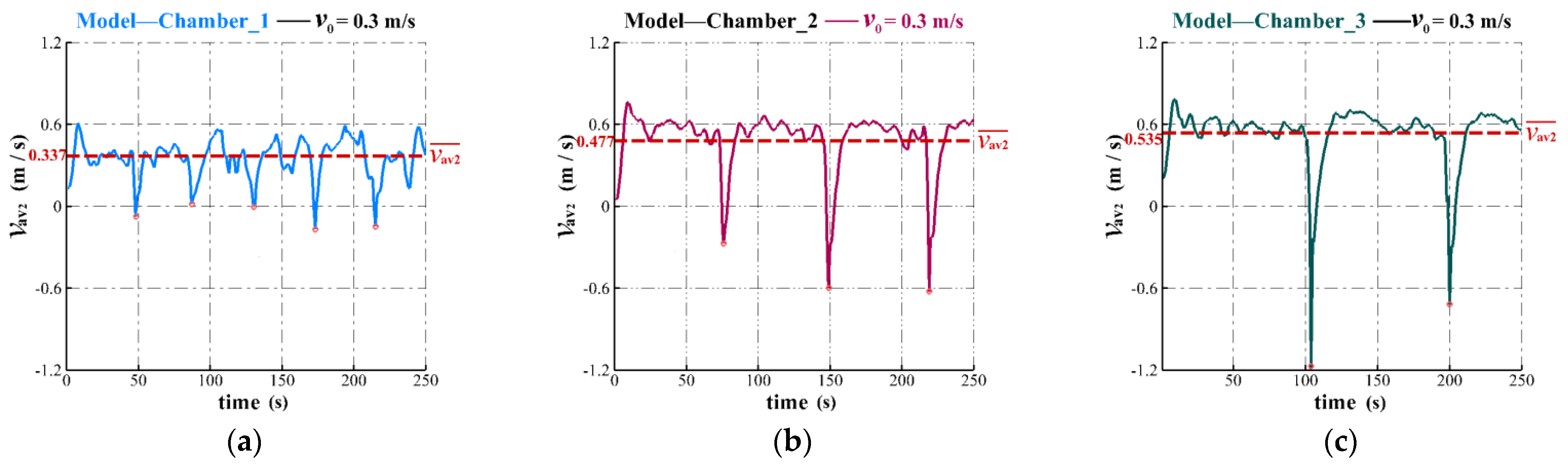
| Average minimum velocity of the deflector plate outlet, (m/s) | −0.100 | −0.666 | −0.829 |
| Time-averaged velocity of the deflector plate outlet, (m/s) | 0.337 | 0.477 | 0.535 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, Z.; Huang, T. Analysis of Water-Lifting Aerator Performance Based on the Volume of Fluid Method. Water 2023, 15, 991. https://doi.org/10.3390/w15050991
Chang Z, Huang T. Analysis of Water-Lifting Aerator Performance Based on the Volume of Fluid Method. Water. 2023; 15(5):991. https://doi.org/10.3390/w15050991
Chicago/Turabian StyleChang, Zhiying, and Tinglin Huang. 2023. "Analysis of Water-Lifting Aerator Performance Based on the Volume of Fluid Method" Water 15, no. 5: 991. https://doi.org/10.3390/w15050991





