Definition of Rainfall Thresholds for Landslides Using Unbalanced Datasets: Two Case Studies in Shaanxi Province, China
Abstract
:1. Introduction
2. Materials and Methods
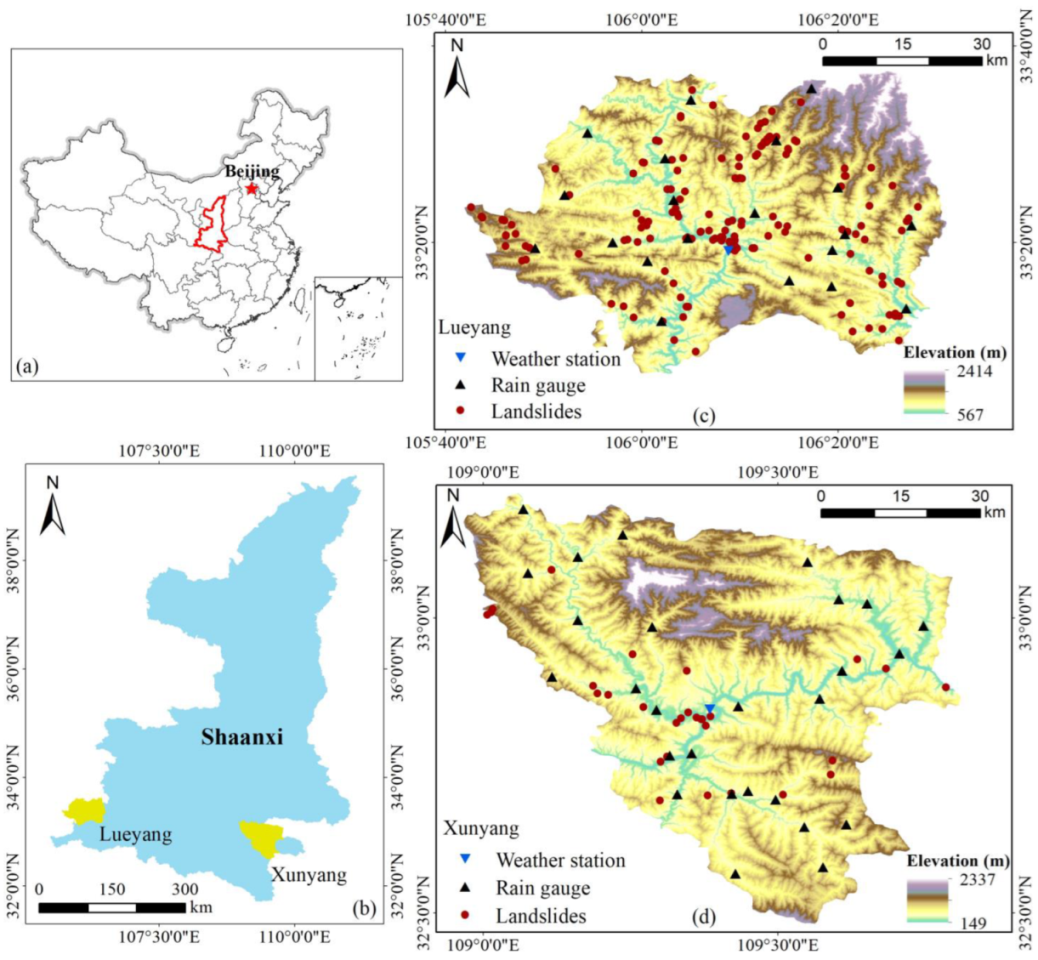
2.1. Study Area
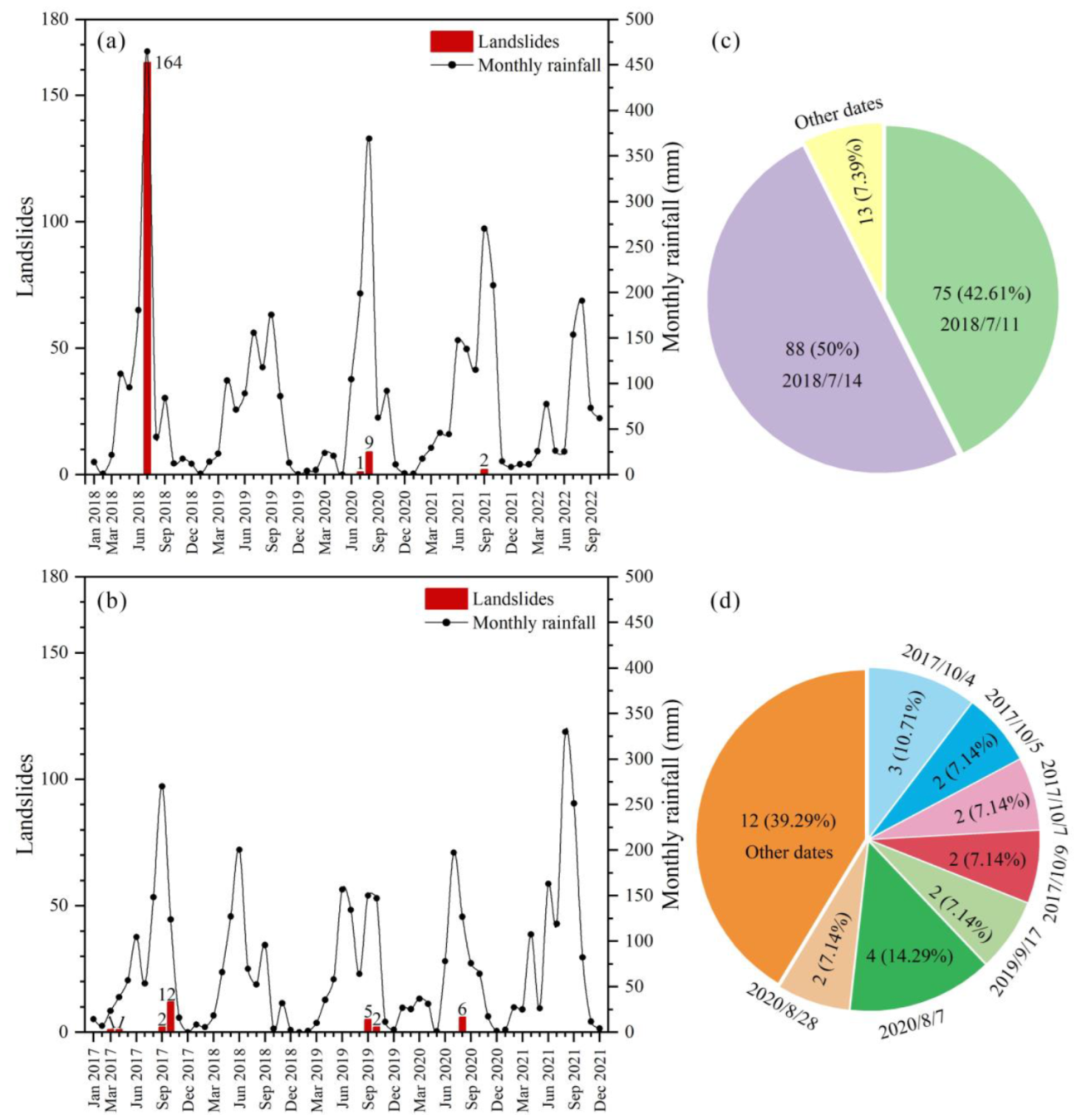
2.2. Datasets
2.3. Methods
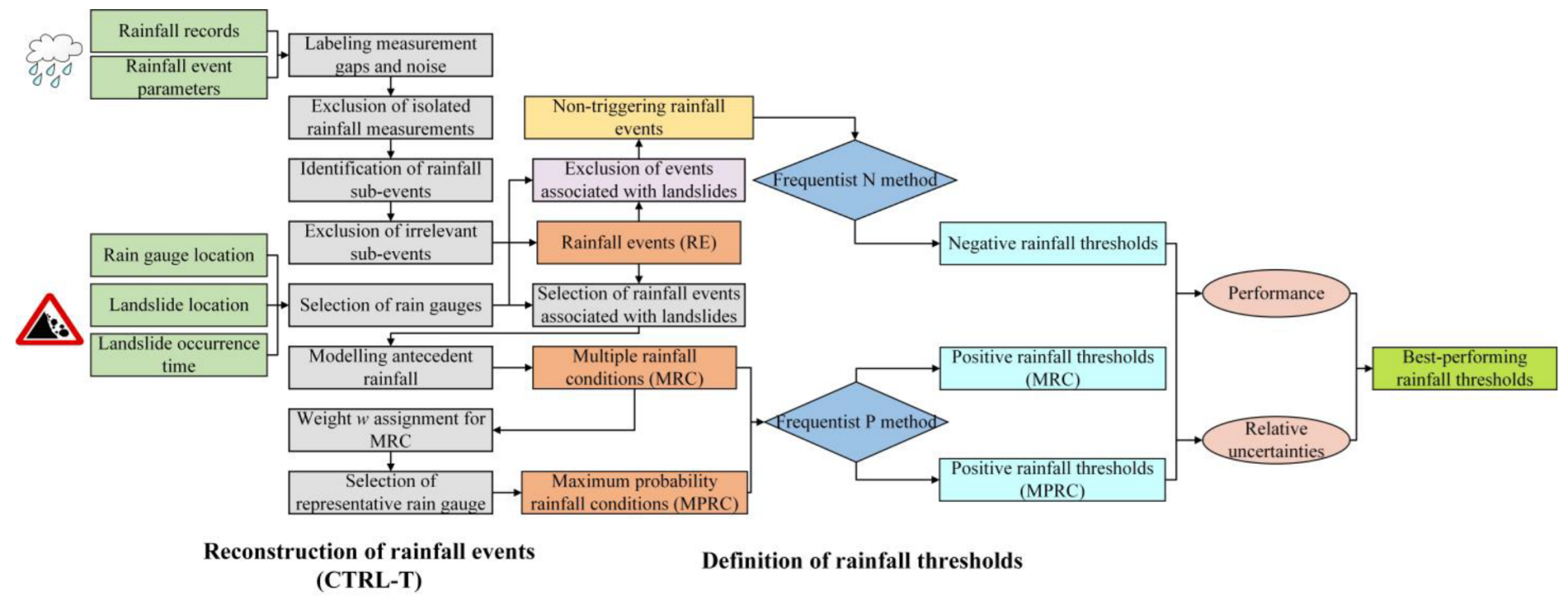
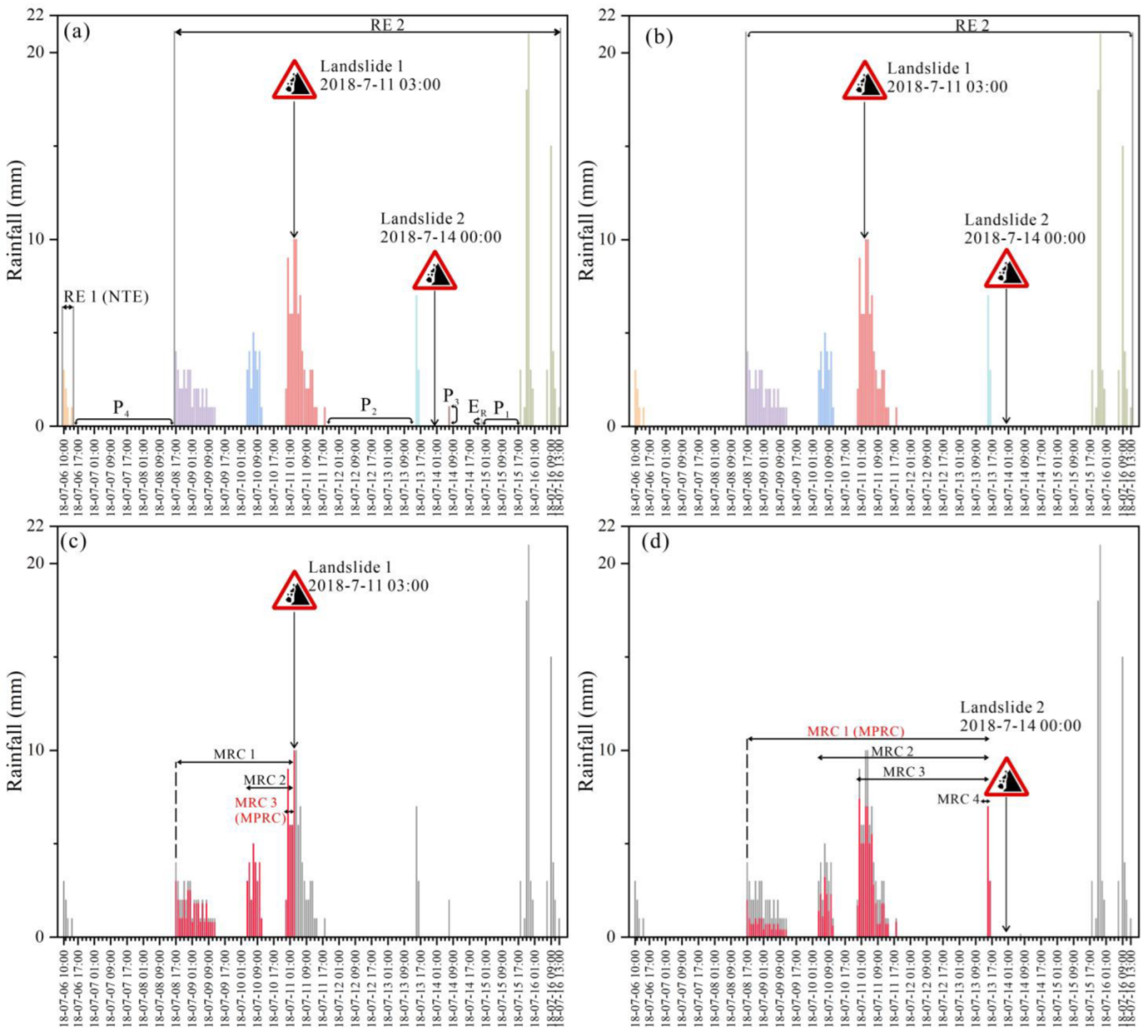
2.3.1. Reconstruction of Rainfall Events
2.3.2. Definition of Rainfall Thresholds
- Efficiency index (Equation (2));
- True positive rate (also referred to as hit rate, probability of detection rate, and sensitivity (Equation (3)));
- False positive rate (also referred to as probability of false detection (Equation (4)));
- Positive predictive value (also referred to as precision (Equation (5)));
3. Results
3.1. Reconstraction of Rainfall Events
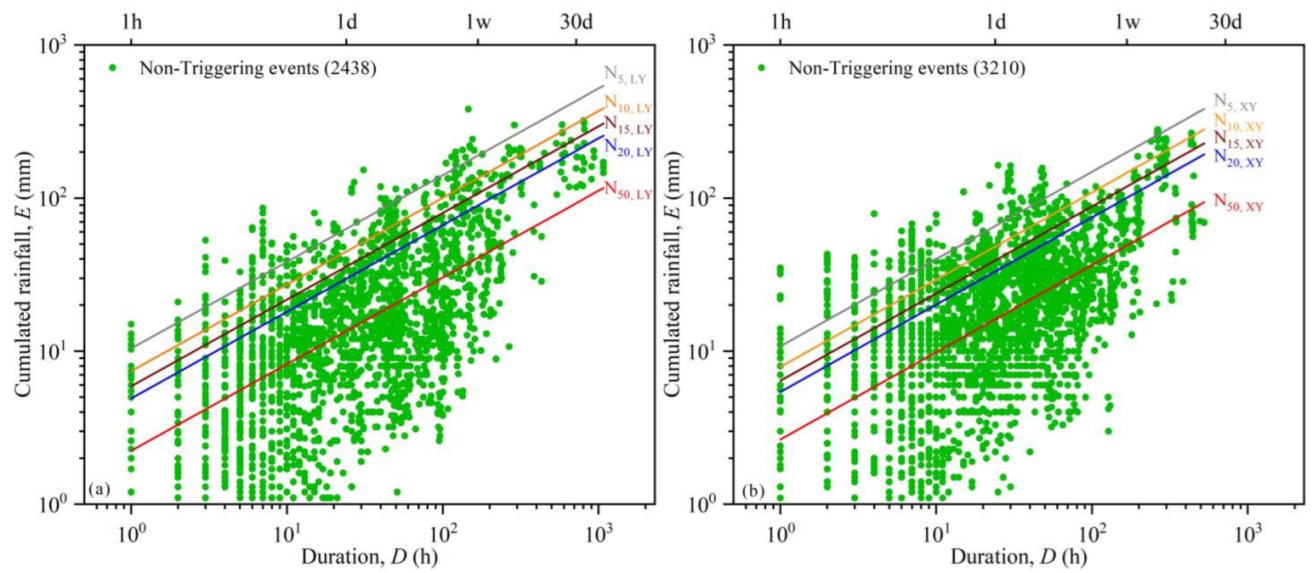
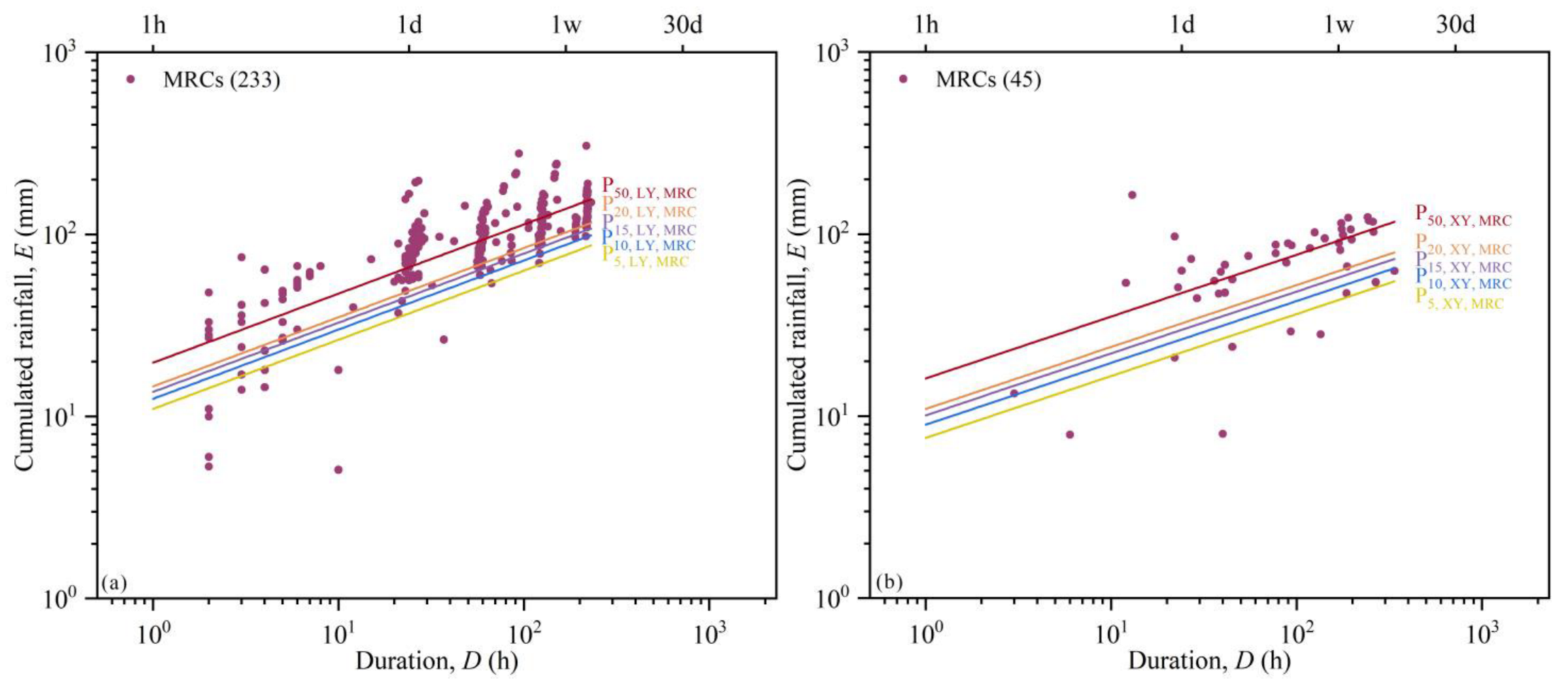
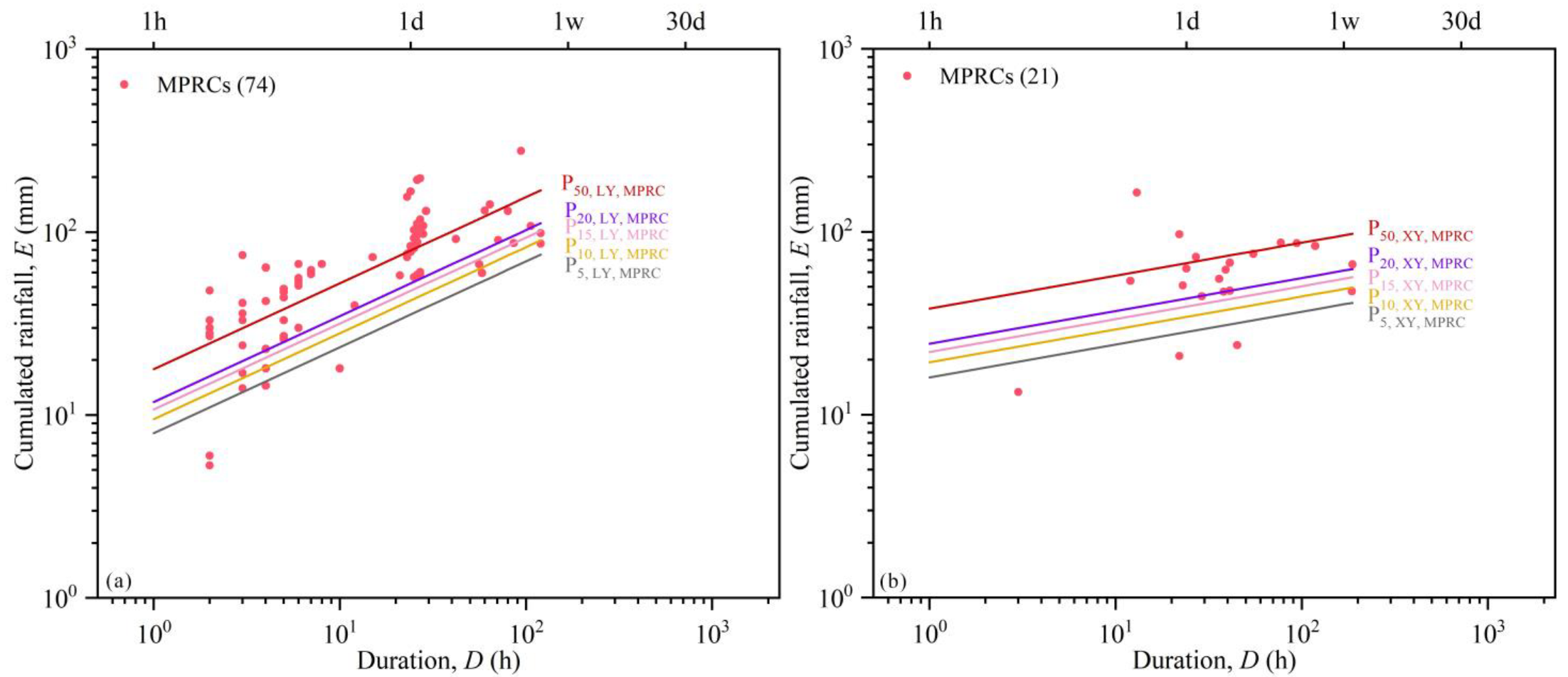
3.2. Definition of Rainfall Thresholds
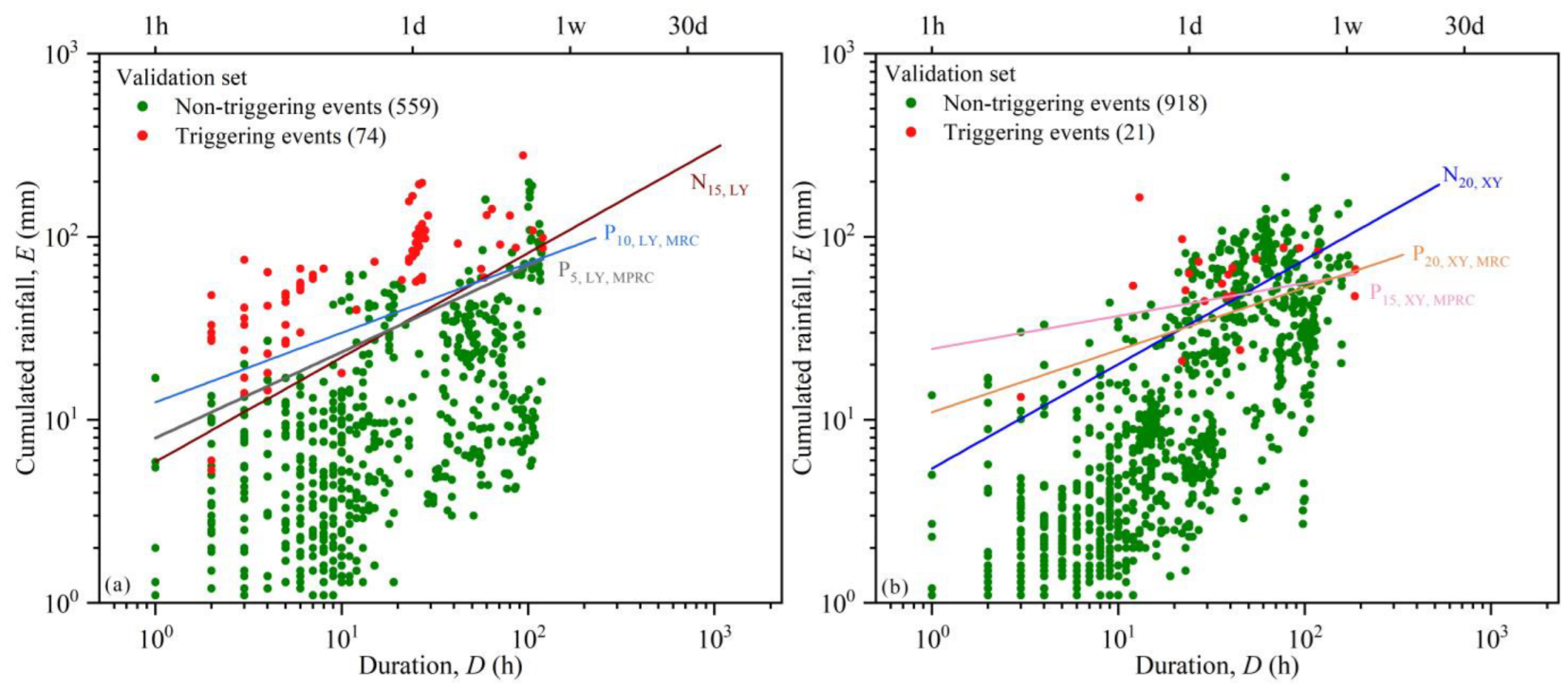
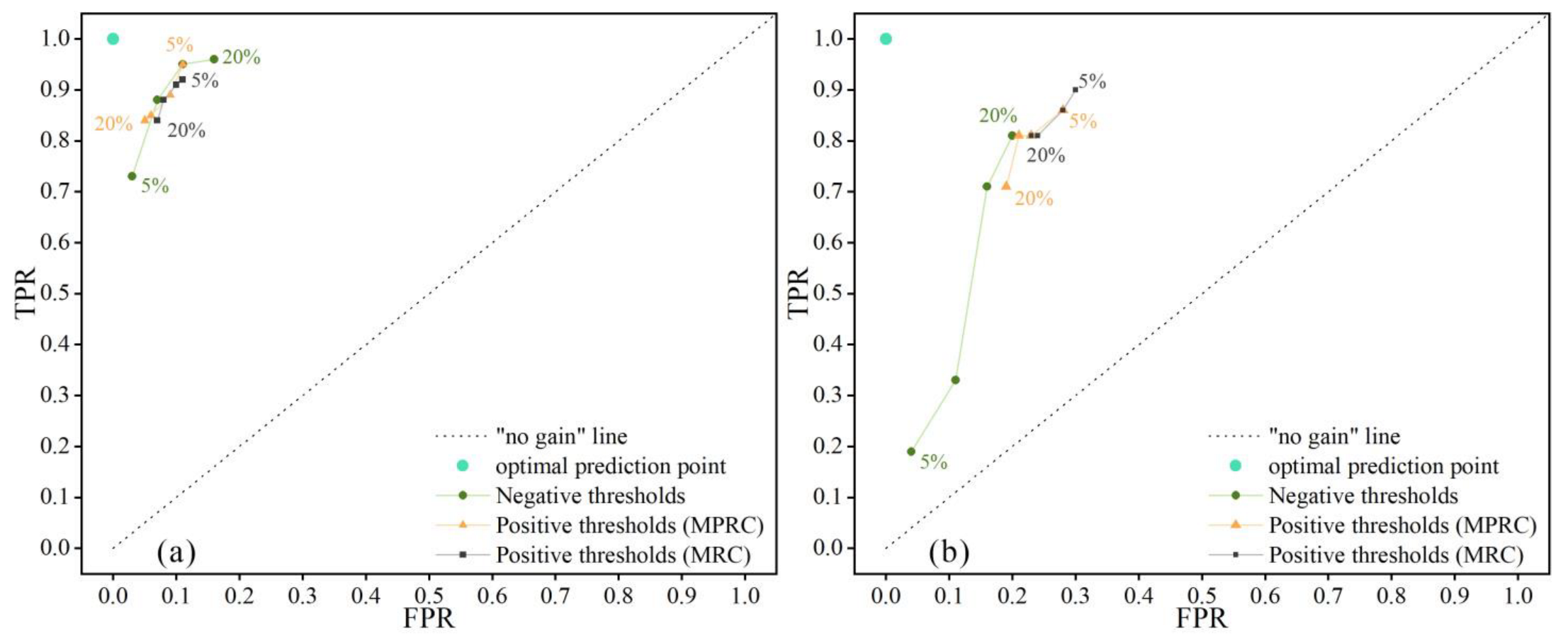
3.3. Performance Evaluation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Intrieri, E.; Gigli, G.; Mugnai, F.; Fanti, R.; Casagli, N. Design and Implementation of a Landslide Early Warning System. Eng. Geol. 2012, 147, 124–136. [Google Scholar] [CrossRef] [Green Version]
- Calvello, M. Early Warning Strategies to Cope with Landslide Risk. Riv. Ital. Geotec. 2017, 2, 63–91. [Google Scholar] [CrossRef]
- Piciullo, L.; Calvello, M.; Cepeda, J.M. Territorial Early Warning Systems for Rainfall-Induced Landslides. Earth-Sci. Rev. 2018, 179, 228–247. [Google Scholar] [CrossRef]
- Pecoraro, G.; Calvello, M.; Piciullo, L. Monitoring Strategies for Local Landslide Early Warning Systems. Landslides 2019, 16, 213–231. [Google Scholar] [CrossRef]
- Piciullo, L.; Gariano, S.L.; Melillo, M.; Brunetti, M.T.; Peruccacci, S.; Guzzetti, F.; Calvello, M. Definition and Performance of a Threshold-Based Regional Early Warning Model for Rainfall-Induced Landslides. Landslides 2017, 14, 995–1008. [Google Scholar] [CrossRef]
- Guzzetti, F.; Gariano, S.L.; Peruccacci, S.; Brunetti, M.T.; Marchesini, I.; Rossi, M.; Melillo, M. Geographical Landslide Early Warning Systems. Earth-Sci. Rev. 2020, 200, 102973. [Google Scholar] [CrossRef]
- Caine, N. The Rainfall Intensity-Duration Control of Shallow Landslides and Debris Flows. Geogr. Ann. Ser. A 1980, 62, 23–27. [Google Scholar] [CrossRef]
- Aleotti, P. A Warning System for Rainfall-Induced Shallow Failures. Eng. Geol. 2004, 73, 247–265. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. Rainfall Thresholds for the Initiation of Landslides in Central and Southern Europe. Meteorol. Atmos. Phys. 2007, 98, 239–267. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. The Rainfall Intensity-Duration Control of Shallow Landslides and Debris Flows: An Update. Landslides 2008, 5, 3–17. [Google Scholar] [CrossRef]
- Segoni, S.; Piciullo, L.; Gariano, S.L. A Review of the Recent Literature on Rainfall Thresholds for Landslide Occurrence. Landslides 2018, 15, 1483–1501. [Google Scholar] [CrossRef]
- Gariano, S.L.; Guzzetti, F. Landslides in a Changing Climate. Earth-Sci. Rev. 2016, 162, 227–252. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Jiang, Q.; Xu, X.; Tao, G.; Zhang, Z.; Gao, X.; He, C. Influence of Soil Mechanical and Hydraulic Parameters on the Definition of Rainfall Intensity and Duration Thresholds Based on Transient Rainfall Infiltration and Grid-Based Regional Slope-Stability Model (TRIGRS). Front. Earth Sci. 2022, 10, 971655. [Google Scholar] [CrossRef]
- Gariano, S.L.; Brunetti, M.T.; Iovine, G.; Melillo, M.; Peruccacci, S.; Terranova, O.; Vennari, C.; Guzzetti, F. Calibration and Validation of Rainfall Thresholds for Shallow Landslide Forecasting in Sicily, Southern Italy. Geomorphology 2015, 228, 653–665. [Google Scholar] [CrossRef]
- Nikolopoulos, E.I.; Borga, M.; Creutin, J.D.; Marra, F. Estimation of Debris Flow Triggering Rainfall: Influence of Rain Gauge Density and Interpolation Methods. Geomorphology 2015, 243, 40–50. [Google Scholar] [CrossRef]
- Rossi, M.; Luciani, S.; Valigi, D.; Kirschbaum, D.; Brunetti, M.T.; Peruccacci, S.; Guzzetti, F. Statistical Approaches for the Definition of Landslide Rainfall Thresholds and Their Uncertainty Using Rain Gauge and Satellite Data. Geomorphology 2017, 285, 16–27. [Google Scholar] [CrossRef]
- Peres, D.J.; Cancelliere, A.; Greco, R.; Bogaard, T.A. Influence of Uncertain Identification of Triggering Rainfall on the Assessment of Landslide Early Warning Thresholds. Nat. Hazards Earth Syst. Sci. 2018, 18, 633–646. [Google Scholar] [CrossRef] [Green Version]
- Gariano, S.L.; Melillo, M.; Peruccacci, S.; Brunetti, M.T. How Much Does the Rainfall Temporal Resolution Affect Rainfall Thresholds for Landslide Triggering? Nat. Hazards 2020, 100, 655–670. [Google Scholar] [CrossRef] [Green Version]
- Xu, Q. Understanding the Landslide Monitoring and Early Warn-Ing: Consideration to Practical Issues. J. Eng. Geol. 2020, 28, 360–374. (In Chinese) [Google Scholar] [CrossRef]
- Jiang, W.; Chen, G.; Meng, X.; Jin, J.; Zhao, Y.; Lin, L.; Li, Y. Probabilistic Rainfall Threshold of Landslides in Data-Scarce Mountainous Areas: A Case Study of the Bailong River Basin, China. Catena 2022, 213, 106190. [Google Scholar] [CrossRef]
- Pan, H.-L.; Jiang, Y.-J.; Wang, J.; Ou, G.-Q. Rainfall Threshold Calculation for Debris Flow Early Warning in Areas with Scarcity of Data. Nat. Hazards Earth Syst. Sci. 2018, 18, 1395–1409. [Google Scholar] [CrossRef] [Green Version]
- Peres, D.J.; Cancelliere, A. Comparing Methods for Determining Landslide Early Warning Thresholds: Potential Use of Non-Triggering Rainfall for Locations with Scarce Landslide Data Availability. Landslides 2021, 18, 3135–3147. [Google Scholar] [CrossRef]
- Brunetti, M.T.; Peruccacci, S.; Rossi, M.; Luciani, S.; Valigi, D.; Guzzetti, F. Rainfall Thresholds for the Possible Occurrence of Landslides in Italy. Nat. Hazards Earth Syst. Sci. 2010, 47, 633–635. [Google Scholar] [CrossRef]
- Peruccacci, S.; Brunetti, M.T.; Luciani, S.; Vennari, C.; Guzzetti, F. Lithological and Seasonal Control on Rainfall Thresholds for the Possible Initiation of Landslides in Central Italy. Geomorphology 2012, 139, 79–90. [Google Scholar] [CrossRef]
- Berti, M.; Martina, M.L.V.; Franceschini, S.; Pignone, S.; Simoni, A.; Pizziolo, M. Probabilistic Rainfall Thresholds for Landslide Occurrence Using a Bayesian Approach. J. Geophys. Res. Earth Surf. 2012, 117, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Staley, D.M.; Kean, J.W.; Cannon, S.H.; Schmidt, K.M.; Laber, J.L. Objective Definition of Rainfall Intensity-Duration Thresholds for the Initiation of Post-Fire Debris Flows in Southern California. Landslides 2013, 10, 547–562. [Google Scholar] [CrossRef]
- Peres, D.J.; Cancelliere, A. Derivation and Evaluation of Landslide-Triggering Thresholds by a Monte Carlo Approach. Hydrol. Earth Syst. Sci. 2014, 18, 4913–4931. [Google Scholar] [CrossRef] [Green Version]
- Postance, B.; Hillier, J.; Dijkstra, T.; Dixon, N. Comparing Threshold Definition Techniques for Rainfall-Induced Landslides: A National Assessment Using Radar Rainfall. Earth Surf. Process Landf. 2018, 43, 553–560. [Google Scholar] [CrossRef] [Green Version]
- Marino, P.; Peres, D.J.; Cancelliere, A.; Greco, R.; Bogaard, T.A. Soil Moisture Information Can Improve Shallow Landslide Forecasting Using the Hydrometeorological Threshold Approach. Landslides 2020, 17, 2041–2054. [Google Scholar] [CrossRef]
- Piciullo, L.; Tiranti, D.; Pecoraro, G.; Cepeda, J.M.; Calvello, M. Standards for the Performance Assessment of Territorial Landslide Early Warning Systems. Landslides 2020, 17, 2533–2546. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, S.; Bao, H.; Zhao, X. Characteristics and Influencing Factors of Rainfall-Induced Landslide and Debris Flow Hazards in Shaanxi Province, China. Nat. Hazards Earth Syst. Sci. 2019, 19, 93–105. [Google Scholar] [CrossRef] [Green Version]
- Mattauer, M.; Matte, P.; Malavieille, J.; Tapponnier, P.; Maluski, H.; Qin, X.Z.; Lun, L.Y.; Qin, T.Y. Tectonics of the Qinling Belt: Build-up and Evolution of Eastern Asia. Nature 1985, 317, 496–500. [Google Scholar] [CrossRef]
- Xue, F.; Lerch, M.F.; Kröner, A.; Reischmann, T. Tectonic Evolution of the East Qinling Mountains, China, in the Palaeozoic: A Review and New Tectonic Model. Tectonophysics 1996, 253, 271–284. [Google Scholar] [CrossRef]
- Li, W.; Liu, C.; Hong, Y.; Zhang, X.; Wan, Z.; Saharia, M.; Sun, W.; Yao, D.; Chen, W.; Chen, S.; et al. A Public Cloud-Based China’s Landslide Inventory Database (CsLID): Development, Zone, and Spatiotemporal Analysis for Significant Historical Events, 1949–2011. J. Mt. Sci. 2016, 13, 1275–1285. [Google Scholar] [CrossRef]
- Qiu, H.; Cui, Y.; Hu, S.; Yang, D.; Pei, Y.; Yang, W. Temporal and Spatial Distributions of Landslides in the Qinba Mountains, Shaanxi Province, China. Geomat. Nat. Hazards Risk 2019, 10, 599–621. [Google Scholar] [CrossRef]
- Liu, J. Analysis of “2018.7” flooding in Lueyang station, Jialing River. Shaanxi Water Resour. 2019, 02, 74–76. (In Chinese) [Google Scholar] [CrossRef]
- Rescuers Rush to Help Rainstorm-Hit County. Available online: http://www.ecns.cn/hd/2018-07-16/detail-ifyvzyvz7264489.shtml (accessed on 16 July 2018).
- Melillo, M.; Brunetti, M.T.; Peruccacci, S.; Gariano, S.L.; Guzzetti, F. An Algorithm for the Objective Reconstruction of Rainfall Events Responsible for Landslides. Landslides 2015, 12, 311–320. [Google Scholar] [CrossRef]
- Melillo, M.; Brunetti, M.T.; Peruccacci, S.; Gariano, S.L.; Roccati, A.; Guzzetti, F. A Tool for the Automatic Calculation of Rainfall Thresholds for Landslide Occurrence. Environ. Model. Softw. 2018, 105, 230–243. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An Approach toward a Rational Classification of Climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Fawcett, T. An Introduction to ROC Analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Vennari, C.; Gariano, S.L.; Antronico, L.; Brunetti, M.T.; Iovine, G.; Peruccacci, S.; Terranova, O.; Guzzetti, F. Rainfall Thresholds for Shallow Landslide Occurrence in Calabria, Southern Italy. Nat. Hazards Earth Syst. Sci. 2014, 14, 317–330. [Google Scholar] [CrossRef] [Green Version]
| Parameter Name | Parameter Value | Unit | |
|---|---|---|---|
| Warm Periods (CW) | Cold Periods (CC) | ||
| Gs | 0.1 | 0.1 | mm |
| ER | 0.2 | 0.2 | mm |
| Rb | 15 | 15 | km |
| P1 | 3 | 6 | h |
| P2 | 6 | 12 | h |
| P3 | 1 | 1 | mm |
| P4 | 48 | 96 | h |
| Actual Events | |||
|---|---|---|---|
| Landslides | No Landslides | ||
| Predicted events | Landslides: E ≥ f(D) | TP | FP |
| No landslides: E < f(D) | FN | TN | |
| Events | Number | Duration (h) | Cumulated Rainfall (mm) | ||
|---|---|---|---|---|---|
| Min | Max | Min | Max | ||
| LY | |||||
| RE | 2467 | 1 | 1075 | 1.1 | 690 |
| RE associated with landslides | 29 | 2 | 383 | 14.5 | 690 |
| MRC total/not considering repetitions | 465/233 | 2 | 230 | 5.1 | 306.8 |
| MPRC total/not considering repetitions | 171/74 | 2 | 120 | 5.3 | 277.9 |
| Non-triggering RE | 2438 | 1 | 1075 | 1.1 | 381.9 |
| XY | |||||
| RE | 3229 | 1 | 669 | 1.1 | 298 |
| RE associated with landslides | 19 | 13 | 669 | 21 | 298 |
| MRC | 45 | 3 | 337 | 7.9 | 163.9 |
| MPRC | 21 | 3 | 187 | 13.3 | 163.9 |
| Non-triggering RE | 3210 | 1 | 526 | 1.1 | 280 |
| Label | Threshold Equation | △α/α (%) | △γ/γ (%) |
|---|---|---|---|
| N5,LY | E = (10.44 ± 0.45) × D(0.57 ± 0.01) | 4% | 2% |
| N10,LY | E = (7.43 ± 0.31) × D(0.57 ± 0.01) | 4% | 2% |
| N15,LY | E = (5.91 ± 0.24) × D(0.57 ± 0.01) | 4% | 2% |
| N20,LY | E = (4.92 ± 0.20) × D(0.57 ± 0.01) | 4% | 2% |
| N50,LY | E = (2.24 ± 0.09) × D(0.57 ± 0.01) | 4% | 2% |
| N5,XY | E = (10.78 ± 0.40) × D(0.57 ± 0.01) | 4% | 2% |
| N10,XY | E = (7.91 ± 0.29) × D(0.57 ± 0.01) | 4% | 2% |
| N15,XY | E = (6.42 ± 0.22) × D(0.57 ± 0.01) | 3% | 2% |
| N20,XY | E = (5.43 ± 0.19) × D(0.57 ± 0.01) | 3% | 2% |
| N50,XY | E = (2.65 ± 0.08) × D(0.57 ± 0.01) | 3% | 2% |
| Label | Threshold Equation | △α/α (%) | △γ/γ (%) |
|---|---|---|---|
| P20,LY,MRC | E = (14.59 ± 1.93) × D(0.38 ± 0.03) | 13% | 8% |
| P15,LY,MRC | E = (13.61 ± 1.84) × D(0.38 ± 0.03) | 14% | 8% |
| P10,LY,MRC | E = (12.48 ± 1.74) × D(0.38 ± 0.03) | 14% | 8% |
| P5,LY,MRC | E = (10.97 ± 1.59) × D(0.38 ± 0.03) | 14% | 8% |
| P50,LY,MRC | E = (19.68 ± 2.35) × D(0.38 ± 0.03) | 12% | 8% |
| P20,XY,MRC | E = (10.98 ± 5.60) × D(0.34 ± 0.10) | 51% | 28% |
| P15,XY,MRC | E = (10.12 ± 5.19) × D(0.34 ± 0.10) | 51% | 28% |
| P10,XY,MRC | E = (8.98 ± 4.53) × D(0.34 ± 0.10) | 50% | 28% |
| P5,XY,MRC | E = (7.61 ± 3.81) × D(0.34 ± 0.10) | 50% | 28% |
| P50,XY,MRC | E = (16.13 ± 8.41) × D(0.34 ± 0.10) | 52% | 28% |
| P20,LY,MPRC | E = (11.80 ± 2.14) × D(0.47 ± 0.05) | 18% | 12% |
| P15,LY,MPRC | E = (10.73 ± 1.99) × D(0.47 ± 0.05) | 19% | 12% |
| P10,LY,MPRC | E = (9.51 ± 1.82) × D(0.47 ± 0.05) | 19% | 12% |
| P5,LY,MPRC | E = (7.96 ± 1.58) × D(0.47 ± 0.05) | 20% | 12% |
| P50,LY,MPRC | E = (17.84 ± 2.92) × D(0.47 ± 0.05) | 16% | 12% |
| P20,XY,MPRC | E = (24.43 ± 19.85) × D(0.18 ± 0.17) | 81% | 96% |
| P15,XY,MPRC | E = (22.04 ± 17.58) × D(0.18 ± 0.17) | 80% | 96% |
| P10,XY,MPRC | E = (19.36 ± 14.91) × D(0.18 ± 0.17) | 77% | 96% |
| P5,XY,MPRC | E = (15.99 ± 11.92) × D(0.18 ± 0.17) | 75% | 96% |
| P50,XY,MPRC | E = (38.10 ± 33.51) × D(0.18 ± 0.17) | 88% | 96% |
| Label | TP | FN | FP | TN |
|---|---|---|---|---|
| N5,LY | 54 | 20 | 16 | 543 |
| N10,LY | 65 | 9 | 37 | 522 |
| N15,LY | 70 | 4 | 60 | 499 |
| N20,LY | 71 | 3 | 92 | 467 |
| P20,LY,MRC | 62 | 12 | 41 | 518 |
| P15,LY,MRC | 65 | 9 | 44 | 515 |
| P10,LY,MRC | 67 | 7 | 54 | 505 |
| P5,LY,MRC | 68 | 6 | 64 | 495 |
| P20,LY,MPRC | 62 | 12 | 29 | 530 |
| P15,LY,MPRC | 63 | 11 | 34 | 525 |
| P10,LY,MPRC | 66 | 8 | 48 | 511 |
| P5,LY,MPRC | 70 | 4 | 61 | 498 |
| Label | TP | FN | FP | TN |
|---|---|---|---|---|
| N5,XY | 4 | 17 | 33 | 885 |
| N10,XY | 7 | 14 | 103 | 815 |
| N15,XY | 14 | 7 | 146 | 772 |
| N20,XY | 17 | 4 | 184 | 734 |
| P20,XY,MRC | 17 | 4 | 210 | 708 |
| P15,XY,MRC | 17 | 4 | 223 | 695 |
| P10,XY,MRC | 18 | 3 | 258 | 660 |
| P5,XY,MRC | 19 | 2 | 279 | 639 |
| P20,XY,MPRC | 15 | 6 | 171 | 747 |
| P15,XY,MPRC | 17 | 4 | 190 | 728 |
| P10,XY,MPRC | 17 | 4 | 214 | 704 |
| P5,XY,MPRC | 18 | 3 | 255 | 663 |
| Label | EI | TPR | FPR | PPV | δ |
|---|---|---|---|---|---|
| N5,LY | 0.94 | 0.73 | 0.03 | 0.77 | 0.271 |
| N10,LY | 0.93 | 0.88 | 0.07 | 0.64 | 0.134 |
| N15,LY | 0.90 | 0.95 | 0.11 | 0.54 | 0.121 |
| N20,LY | 0.85 | 0.96 | 0.16 | 0.44 | 0.165 |
| P20,LY,MRC | 0.92 | 0.84 | 0.07 | 0.60 | 0.175 |
| P15,LY,MRC | 0.92 | 0.88 | 0.08 | 0.60 | 0.411 |
| P10,LY,MRC | 0.90 | 0.91 | 0.10 | 0.55 | 0.135 |
| P5,LY,MRC | 0.89 | 0.92 | 0.11 | 0.52 | 0.136 |
| P20,LY,MPRC | 0.94 | 0.84 | 0.05 | 0.68 | 0.168 |
| P15,LY,MPRC | 0.93 | 0.85 | 0.06 | 0.65 | 0.162 |
| P10,LY,MPRC | 0.91 | 0.89 | 0.09 | 0.58 | 0.142 |
| P5,LY,MPRC | 0.90 | 0.95 | 0.11 | 0.53 | 0.121 |
| Label | EI | TPR | FPR | PPV | δ |
|---|---|---|---|---|---|
| N5,XY | 0.95 | 0.19 | 0.04 | 0.11 | 0.811 |
| N10,XY | 0.88 | 0.33 | 0.11 | 0.06 | 0.679 |
| N15,XY | 0.84 | 0.71 | 0.16 | 0.09 | 0.331 |
| N20,XY | 0.80 | 0.81 | 0.20 | 0.08 | 0.276 |
| P20,XY,MRC | 0.77 | 0.81 | 0.23 | 0.07 | 0.298 |
| P15,XY,MRC | 0.76 | 0.81 | 0.24 | 0.07 | 0.306 |
| P10,XY,MRC | 0.72 | 0.86 | 0.28 | 0.07 | 0.313 |
| P5,XY,MRC | 0.70 | 0.90 | 0.30 | 0.06 | 0.316 |
| P20,XY,MPRC | 0.81 | 0.71 | 0.19 | 0.08 | 0.347 |
| P15,XY,MPRC | 0.79 | 0.81 | 0.21 | 0.08 | 0.283 |
| P10,XY,MPRC | 0.77 | 0.81 | 0.23 | 0.07 | 0.298 |
| P5,XY,MPRC | 0.73 | 0.86 | 0.28 | 0.07 | 0.313 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Pecoraro, G.; Jiang, Q.; Calvello, M. Definition of Rainfall Thresholds for Landslides Using Unbalanced Datasets: Two Case Studies in Shaanxi Province, China. Water 2023, 15, 1058. https://doi.org/10.3390/w15061058
Zhang S, Pecoraro G, Jiang Q, Calvello M. Definition of Rainfall Thresholds for Landslides Using Unbalanced Datasets: Two Case Studies in Shaanxi Province, China. Water. 2023; 15(6):1058. https://doi.org/10.3390/w15061058
Chicago/Turabian StyleZhang, Sen, Gaetano Pecoraro, Qigang Jiang, and Michele Calvello. 2023. "Definition of Rainfall Thresholds for Landslides Using Unbalanced Datasets: Two Case Studies in Shaanxi Province, China" Water 15, no. 6: 1058. https://doi.org/10.3390/w15061058
APA StyleZhang, S., Pecoraro, G., Jiang, Q., & Calvello, M. (2023). Definition of Rainfall Thresholds for Landslides Using Unbalanced Datasets: Two Case Studies in Shaanxi Province, China. Water, 15(6), 1058. https://doi.org/10.3390/w15061058









