Forecasting Monthly Water Deficit Based on Multi-Variable Linear Regression and Random Forest Models
Abstract
:1. Introduction
2. Data and Methodology
2.1. Data Collection
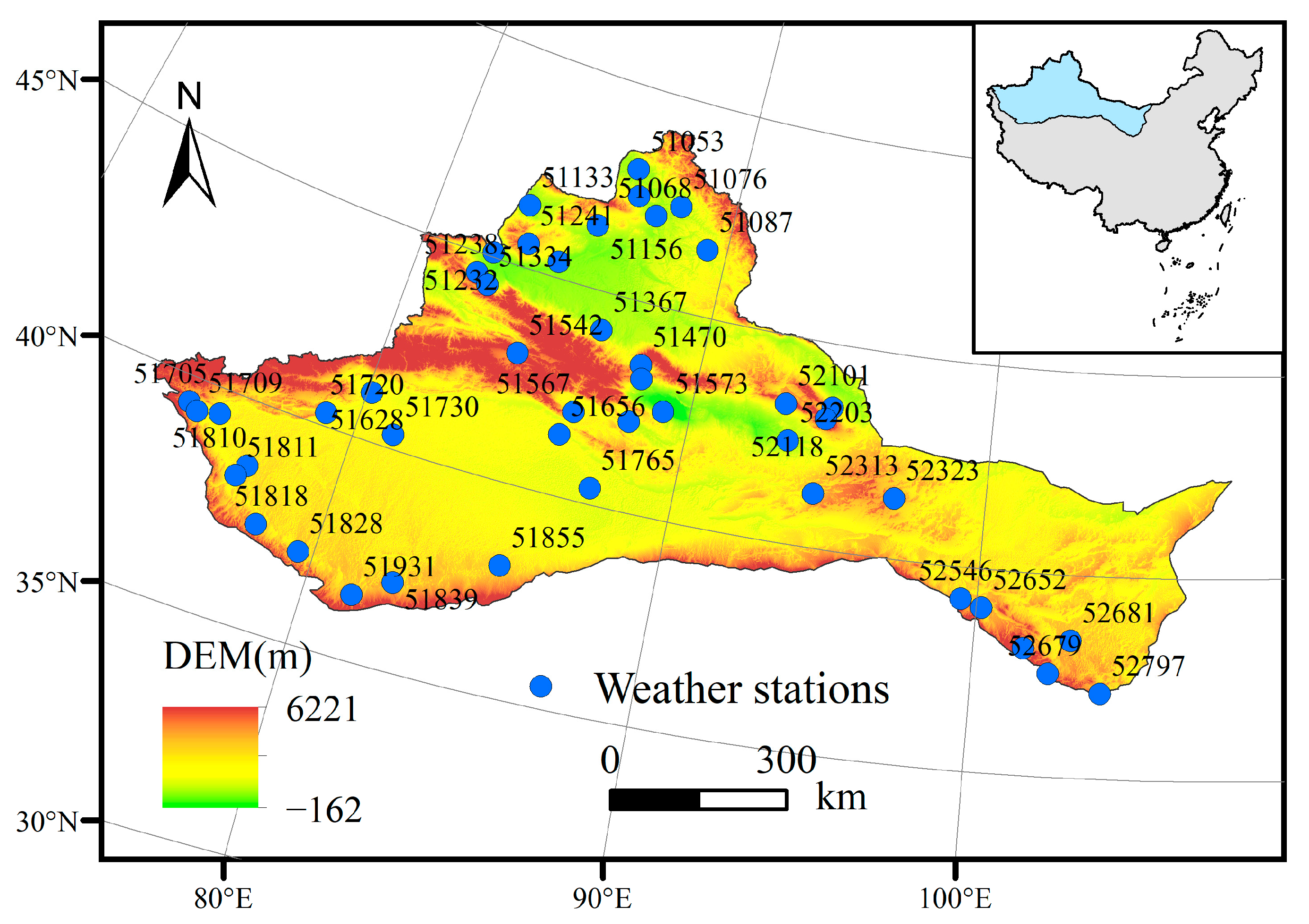
2.1.1. Study Area and Weather Data
2.1.2. The Circulation Indices Data
2.2. Methodology
2.2.1. Variation of Water Deficit
2.2.2. Selection of the Key Circulation Indices
Preliminary Selection of the Independent Circulation Indices
Selection of the Key Circulation Indices
2.2.3. The Quantitative Relationship between D and the Key Circulation Indices
Multi-Variable Linear Regression Model
Random Forest Model
Model Performance Assessment
2.2.4. Prediction of Water Deficit Conditions
3. Results
3.1. Spatiotemporal Variations of Month D
3.2. Relationship between Monthly D and Circulation Indices
3.2.1. Preliminary Selected Circulation Indices Considering Multi-Collinearity
3.2.2. Screen of the Key Circulation Indices
3.3. Quantitative Relationship between Monthly D and the Key Circulation Indices
3.3.1. Model Performance Assessment
3.3.2. Importance Rank of Predictors
3.4. Forecasted Water Deficit Conditions in Northwestern China
4. Discussions
4.1. The Necessity of Selecting Key Circulation Indices from over 100 Indices
4.2. Relative Importance of Climate Drivers to Water Deficit
4.3. Prediction of Water Deficit Conditions
4.4. Limitations and Future Framework
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AO | Artic oscillation |
| D | difference of precipitation and ET0 |
| ET0 | reference crop evapotranspiration |
| ENSO | El Niño Southern Oscillation |
| FAO | Food and Agriculture Organization |
| IOD | Indian Ocean Dipole |
| IPCC | Intergovernmental Panel on Climate Change |
| LCCC | Lin’s Concordance Correlation Coefficient |
| MAPE | mean absolute percentage error |
| MLR | multi-variable linear regression model |
| NAO | North Atlantic Oscillation |
| PDO | Pacific Decade Oscillation |
| Pr | precipitation |
| R2 | coefficient of determination |
| RMSE | root mean square error |
| R | Pearson correlation coefficient |
| SPI | standardized precipitation index |
| SPEI | standardized precipitation and evapotranspiration index |
| VIF | variance inflation factor |
References
- Cook, B.I.; Mankin, J.S.; Anchukaitis, K.J. Climate Change and Drought: From Past to Future. Curr. Clim. Change Rep. 2018, 4, 164–179. [Google Scholar] [CrossRef]
- Wei, Y.; Yu, H.P.; Huang, J.P.; Zhou, T.J.; Zhang, M.; Ren, Y. Drylands climate response to transient and stabilized 2 °C and 1.5 °C global warming targets. Clim. Dyn. 2019, 53, 2375–2389. [Google Scholar] [CrossRef]
- Kurnik, B.; Kajfež-Bogataj, L.; Horion, S. An assessment of actual evapotranspiration and soil water deficit in agricultural regions in Europe. Int. J. Climatol. 2015, 35, 2451–2471. [Google Scholar] [CrossRef]
- Zhao, H.C.; Li, Y.; Chen, X.G.; Wang, H.R.; Yao, N.; Liu, F.G. Monitoring monthly soil moisture conditions in China with temperature vegetation dryness indexes based on an enhanced vegetation index and normalized difference vegetation index. J. Trop. Meteorol. 2021, 143, 159–176. [Google Scholar] [CrossRef]
- King, A.D.; Pitman, A.J.; Henley, B.J.; Ukkola, A.M.; Brown, J.R. The role of climate variability in Australian drought. Nat. Clim. Change 2020, 10, 177–179. [Google Scholar] [CrossRef]
- Dai, A.; Zhao, T.B.; Chen, J. Climate Change and Drought: A Precipitation and Evaporation Perspective. Curr. Clim. Change Rep. 2018, 4, 301–312. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Mihăilă, D.; Bistricean, P.I.; Lazurca, L.G.; Briciu, A.E. Climatic water deficit and surplus between the Carpathian Mountains and the Dniester River (1961–2012). Environ. Monit. Assess. 2017, 189, 545. [Google Scholar] [CrossRef] [PubMed]
- Das, P.K.; Dutta, D.; Sharma, J.R.; Dadhwal, V.K. Trends and behaviour of meteorological drought (1901–2008) over Indian region using standardized precipitation–evapotranspiration index. Int. J. Climatol. 2016, 36, 909–916. [Google Scholar] [CrossRef]
- Somorowska, U. Changes in Drought Conditions in Poland over the Past 60 Years Evaluated by the Standardized Precipitation-Evapotranspiration Index. Acta Geophys. 2016, 64, 2530–2549. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.L.; Wu, X.S.; Xu, C.Y.; Guo, S.L.; Chen, X.H.; Zhang, Z.X. Robust Meteorological Drought Prediction Using Antecedent SST Fluctuations and Machine Learning. Water Resour. Res. 2021, 57, e2020WR029413. [Google Scholar] [CrossRef]
- Jiang, S.H.; Wang, M.H.; Ren, L.L.; Xu, C.Y.; Yuan, F.; Liu, Y.; Lu, Y.G.; Shen, H.R. A framework for quantifying the impacts of climate change and human activities on hydrological drought in a semiarid basin of Northern China. Hydrol. Process. 2019, 3, 1075–1088. [Google Scholar] [CrossRef]
- Feng, P.Y.; Wang, B.; Luo, J.J.; Liu, D.L.; Waters, C.; Ji, F. Using large-scale climate drivers to forecast meteorological drought condition in growing season across the Australian wheatbelt. Sci. Total Environ. 2020, 724, 138162. [Google Scholar] [CrossRef] [PubMed]
- Özger, M.; Mishra, A.K.; Singh, V.P. Low frequency drought variability associated with climate indices. J. Hydrol. 2009, 364, 152–162. [Google Scholar] [CrossRef]
- Talaee, P.H.; Tabari, H.; Ardakani, S.S. Hydrological drought in the west of Iran and possible association with large-scale atmospheric circulation patterns. Hydrol. Process. 2014, 28, 764–773. [Google Scholar] [CrossRef]
- Manzano, A.; Clemente, M.A.; Morata, A.; Luna, M.Y.; Beguería, S.; Vicente-Serranod, S.M.; Martín, M.L. Analysis of the atmospheric circulation pattern effects over SPEI drought index in Spain. Atmos. Res. 2019, 230, 104630. [Google Scholar] [CrossRef]
- Esha, R.I.; Imteaz, M.A. Assessing the predictability of MLR models for long-term streamflow using lagged climate indices as predictors: A case study of NSW (Australia). Hydrol. Res. 2019, 50, 262–281. [Google Scholar] [CrossRef]
- Acharya, N.; Singh, A.; Mohanty, U.C.; Nair, A.; Chattopadhyay, S. Performance of general circulation models and their ensembles for the prediction of drought indices over India during summer monsoon. Nat. Hazards 2013, 66, 851–871. [Google Scholar] [CrossRef]
- Zhu, X.F.; Hou, C.Y.; Xu, K.; Liu, Y. Establishment of agricultural drought loss models: A comparison of statistical methods. Ecol. Indic. 2020, 112, 106084. [Google Scholar] [CrossRef]
- Li, L.C.; Wang, B.; Feng, P.Y.; Wang, H.H.; He, Q.S.; Wang, Y.K.; Liu, D.L.; Li, Y.; He, J.Q.; Feng, H.; et al. Crop yield forecasting and associated optimum lead time analysis based on multi-source environmental data across China. Agric. For. Meteorol. 2021, 308–309, 108558. [Google Scholar] [CrossRef]
- Yao, N.; Li, Y.; Lei, T.; Peng, L.L. Drought evolution, severity and trends in mainland China over 1961–2013. Sci. Total Environ. 2018, 616, 73–89. [Google Scholar] [CrossRef]
- Ummenhofer, C.C.; D’Arrigo, R.D.; Anchukaitis, K.J.; Buckley, B.M.; Cook, E.R. Links between Indo-Pacific climate variability and drought in the Monsoon Asia Drought Atlas. Clim. Dyn. 2013, 40, 1319–1334. [Google Scholar] [CrossRef]
- Xiao, M.; Zhang, Q.; Singh, V.P.; Liu, L. Transitional properties of droughts and related impacts of climate indices in the Pearl River basin, China. J. Hydrol. 2016, 534, 397–406. [Google Scholar] [CrossRef]
- Li, B.F.; Chen, Y.N.; Chen, Z.S.; Xiong, H.G.; Lian, L.S. Why does precipitation in northwest China show a significant increasing trend from 1960 to 2010? Atmos. Res. 2016, 167, 275–284. [Google Scholar] [CrossRef]
- Yao, N.; Li, Y.; Li, N. Bias correction of precipitation data and its effects on aridity and drought assessment in China over 1961–2015. Sci. Total Environ. 2018, 639, 1015–1027. [Google Scholar] [CrossRef]
- Helsel, D.R.; Hirsch, R.M.; Ryberg, K.R.; Archfield, S.A.; Gilroy, E.J. Statistical Methods in Water Resources; Elsevier: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Stine, R.A. Graphical Interpretation of Variance Inflation Factors. Am. Stat. 1995, 49, 53–56. [Google Scholar] [CrossRef]
- Doetterl, S.; Stevens, A.; Six, J.; Merckx, R.; Van Oost, K.; Casanova Pinto, M. Soil carbon storage con-trolled by interactions between geochemistry and climate. Nat. Geosci. 2015, 8, 780–783. [Google Scholar] [CrossRef]
- Liu, D.L.; Ji, F.; Wang, B.; Waters, C.; Feng, P.Y.; Darbyshire, R. The implication of spatial interpolated climate data on biophysical modelling in agricultural systems. Int. J. Climatol. 2020, 40, 2870–2890. [Google Scholar] [CrossRef]
- Chen, X.G.; Li, Y.; Yao, N.; Liu, D.L.; Javed, T.; Liu, C.C.; Liu, F.G. Impacts of multi-timescale SPEI and SMDI variations on winter wheat yields. Agric. Syst. 2020, 185, 102955. [Google Scholar] [CrossRef]
- Wang, B.; Waters, C.; Orgill, S.; Cowie, A.; Clark, A.; Liu, D.L.; Simpson, M.; McGowen, I.; Sides, T. Estimating soil organic carbon stocks using different modelling techniques in the semi-arid rangelands of eastern Australia. Ecol. Indic. 2018, 88, 425–438. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.; Sanchez-Castillo, M.; Chica-Olmo, M.; Chica-Rivas, M. Machine learning predictive models for mineral prospectivity: An evaluation of neural networks, random forest, regression trees and support vector machines. Ore Geol. Rev. 2015, 71, 804–818. [Google Scholar] [CrossRef]
- Eom, Y.S.; Park, B.R.; Shin, H.W.; Kang, D.H. Evaluation of Outdoor Particle Infiltration into Classrooms Considering Air Leakage and Other Building Characteristics in Korean Schools. Sustainability 2021, 13, 7382. [Google Scholar] [CrossRef]
- Srisomkiew, S.; Kawahigashi, M.; Limtong, P. Digital mapping of soil chemical properties with limited data in the Thung Kula Ronghai region, Thailand. Geoderma 2021, 389, 114942. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Feng, P.Y.; Wang, B.; Liu, D.L.; Waters, C.; Xiao, D.P.; Shi, L.J.; Yu, Q. Dynamic wheat yield forecasts are improved by a hybrid approach using a biophysical model and machine learning technique. Agric. For. Meteorol. 2021, 285–286, 107922. [Google Scholar] [CrossRef]
- Miralles, D.G.; Gentine, P.; Seneviratne, S.I.; Teuling, A.J. Land-atmospheric feedbacks during droughts and heatwaves: State of the science and current challenges. Ann. N. Y. Acad. Sci. 2019, 1436, 19–35. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, S.Z.; Huang, Q.; Wang, H.; Fang, W.; Yang, Y.Y.; Wang, L. Assessing socioeconomic drought based on an improved Multivariate Standardized Reliability and Resilience Index. J. Hydrol. 2019, 568, 904–918. [Google Scholar] [CrossRef]
- Irannezhad, M.; Ahmadi, B.; Kløve, B.; Moradkhani, H. Atmospheric circulation patterns explaining climatological drought dynamics in the boreal environment of Finland, 1962–2011. Int. J. Climatol. 2017, 37 (Suppl. S1), 801–807. [Google Scholar] [CrossRef]
- Wu, M.J.; Li, Y.; Hu, W.; Yao, N.; Li, L.C.; Liu, D.L. Spatiotemporal variability of standardized precipitation evapotranspiration index in mainland China over 1961–2016. Int. J. Climatol. 2020, 40, 4781–4799. [Google Scholar] [CrossRef]
- Guan, X.; Yang, L.; Zhang, Y.; Li, J. Spatial distribution, temporal variation, and transport characteristics of atmospheric water vapor over Central Asia and the arid region of China. Glob. Planet. Chang. 2019, 172, 159–178. [Google Scholar] [CrossRef]
- Huang, W.; Feng, S.; Chen, J.; Chen, F. Physical mechanisms of summer precipitation variations in the Tarim Basin in northwestern China. J. Clim. 2015, 28, 3579–3591. [Google Scholar] [CrossRef]
- Zhang, H.D.; Jin, R.H.; Zhang, Y.S. Relationships between summer northern polar vortex with sub-tropical high and their influence on precipitation in north china. J. Trop. Meteorol. 2008, 24, 417–422. (In Chinese) [Google Scholar]
- Chen, C.; Zhang, X.; Lu, H.; Jin, L.; Du, Y.; Chen, F. Increasing summer precipitation in arid central Asia linked to the weakening of the East Asian summer monsoon in the recent decades. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2021, 41, 1024–1038. [Google Scholar] [CrossRef]
- Wu, P.; Ding, Y.; Liu, Y.; Li, X. The characteristics of moisture recycling and its impact on regional precipitation against the background of climate warming over Northwest China. Int. J. Climatol. 2019, 39, 5241–5255. [Google Scholar] [CrossRef]
- Cai, Q.F.; Liu, Y.; Liu, H.; Ren, J.L. Reconstruction of drought variability in North China and its association with sea surface temperature in the joining area of Asia and Indian–Pacific Ocean. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2015, 417, 554–560. [Google Scholar] [CrossRef]
- Yao, N.; Li, Y.; Li, L.C.; Feng, P.Y.; Feng, H.; Liu, D.L.; Liu, Y.; Jiang, K.T.; Hu, X.T.; Li, Y. Projections of drought characteristics in China based on a standardized precipitation and evapotranspiration index and multiple GCMs. Sci. Total Environ. 2020, 704, 135245. [Google Scholar] [CrossRef]
- Feng, P.Y.; Wang, B.; Liu, D.L.; Waters, C.; Yu, Q. Incorporating machine learning with biophysical model can improve the evaluation of climate extremes impacts on wheat yield in southeastern Australia. Agric. For. Meteorol. 2019, 275, 100–113. [Google Scholar] [CrossRef]
- Forootan, E.; Khaki, M.; Schumacher, M.; Wulfmeyer, V.; Mehrnegar, N.; van Dijke, A.I.J.M. Understanding the global hydrological droughts of 2003–2016 and their relationships with teleconnections. Sci. Total Environ. 2019, 650, 2587–2604. [Google Scholar] [CrossRef] [PubMed]
- Hosseini-Moghari, S.M.; Araghinejad, S. Monthly and seasonal drought forecasting using statistical neural networks. Environ. Earth Sci. 2015, 74, 397–412. [Google Scholar] [CrossRef]
- Xu, L.; Chen, N.C.; Zhang, X.; Chen, Z.Q. An evaluation of statistical, NMME and hybrid models for drought prediction in China. J. Hydrol. 2018, 566, 235–249. [Google Scholar] [CrossRef]
- Gao, Q.G.; Kim, J.S.; Chen, J.; Chen, H.; Lee, J.H. Atmospheric T eleconnection-Based Extreme Drought Prediction in the Core Drought Region in China. Water 2019, 11, 232. [Google Scholar] [CrossRef]
- Bibi, N.; Shah, I.; Alsubie, A.; Ali, S.; Lone, S.A. Electricity Spot Prices Forecasting Based on Ensemble Learning. IEEE Access 2021, 9, 150984–150992. [Google Scholar] [CrossRef]







| Initially Selected Circulation Indices | |||||
|---|---|---|---|---|---|
| NAHAI | WPSH | EPSH | NANRP | EPRP | SSRP |
| WHWRP | APVA | PPVA | NAPVA | AEPVA | PPVI |
| AEPVI | NVCL | NVCLI | EMC | AZC | AMC |
| EATP | IBTI | AO | AAO | NAO | PNA |
| EA | WP | EAWR | POL | SCA | 50ZW |
| MPZW | WPTW | CPTW | EPTA | ACCP | NINO1 + 2 |
| NINOW | NINOA | NINOB | TSA | WHWP | IOWPA |
| WPWPA | AMO | OC | WWDC | EM | NE |
| TIOD | SIOD | WNPTN | NLTC | TSN | SOI |
| AMM | QBO | NAT | |||
| No. of Site | Fitted MLR Equation | R2 | LCCC | MAPE (%) | RMSE (mm) |
|---|---|---|---|---|---|
| 51053 | 0.0088PPVI12 + 0.21NAHAI6 − 1.68SSRP10 − 1.13NANRP11 − 3.32PPVA6 − 0.76MPZW5 + 3.10WPWPA4 − 1.10EPRP11 + 0.0046AEPVI12 − 2.06WNPTN10 − 36.57 | 0.863 | 0.927 | 44.3 | 22.4 |
| 51238 | +0.0071PPVI12−1.41SSRP11 + 3.43WPWPA4 + 4.13 PPVA12 − 0.84NANRP11 + 0.0045AEPVI12 − 0.60MPZW5 − 0.77NAHAI12 − 2.07WNPTN10 − 0.17EPRP11 − 186.38 | 0.872 | 0.931 | 28.8 | 19.0 |
| 51334 | − 0.50NAHAI12 − 1.08NANRP11 − 0.78EPRP11 − 1.34SSRP10 + 4.55NAPVA12 + 0.0082PPVI12 + 0.0056AEPVI12 − 0.67 MPZW5 + 3.96WPWPA4 − 2.14WNPTN10 − 211.16 | 0.919 | 0.958 | 11.2 | 17.1 |
| 51811 | − 0.0073PPVI6 + 4.78PPVA11 − 0.19SSRP10 − 1.55EPRP11 + 0.50IOWPA9 + 0.75NAHAI5 + 1.92WPWPA4 − 1.28 NANRP10 + 0.007AEPVI12 − 2.29WNPTN10 − 0.02MPZW5 − 147.04 | 0.900 | 0.948 | 28.7 | 17.5 |
| 51573 | − 2.29SSRP10 + 0.012PPVI12 + 5.70PPVA11 − 0.95WPWPA10 − 1.55NANRP11 + 0.79NAHAI11 − 0.62MPZW5 − 0.92 EPRP11 − 0.09IOWPA3 + 0.0113AEPVI12 − 4.59WNPTN10 − 150.71 | 0.903 | 0.949 | 27.6 | 21.9 |
| 51477 | − 0.0078PPVI6 − 2.30SSRP10 + 2.62NANRP5 − 0.0068 AEPVI6 − 3.98PPVA6 − 0.37IOWPA9 − 1.12EPRP10 + 0.03 NAHAI6 + 1.63WPWPA4 − 2.05WNPTN10 − 0.54MPZW5 + 10.87 | 0.891 | 0.942 | 21.3 | 21.0 |
| 52203 | − 0.0087PPVI6 + 0.52IOWPA9 − 1.76SSRP10 − 0.0086 AEPVI6 + 0.15NAHAI5 + 2.85WPWPA4 − 2.09APVA6 − 2.51 WNPTN10 − 0.46MPZW5 − 4.56PPVA5 − 1.03NANRP10 − 0.69EPRP10 +88.96 | 0.905 | 0.950 | 36.7 | 19.8 |
| 52112 | − 0.01PPVI6 − 5.51WNPTN10 − 3.32SSRP10 + 0.0169 AEPVI12 − 0.28IOWPA9 + 3.26WPWPA4 − 6.71PPVA6 − 1.61NANRP10 − 0.31APVA6 + 1.13NAHAI5 − 0.59MPZW5 − 0.72EPRP10 + 53.11 | 0.930 | 0.964 | 19.2 | 26.8 |
| 51567 | − 1.96NAPVA5 − 0.0053PPVI6 + 1.75SSRP4 + 0.0092 AEPVI12 + 0.31IOWPA9 − 0.61MPZW5 + 1.48WPWPA4 − 1.21NANRP10 + 0.12NAHAI5 − 1.66APVA6 + 2.66 WNPTN4 − 0.74EPRP10 − 48.82 | 0.895 | 0.945 | 21.1 | 17.4 |
| No. of Site | Predictor Variables Importance Ranking (%) |
|---|---|
| 51053 | PPVI12 (37.1), NAHAI6 (30), SSRP10 (29.3), NANRP11 (29.1), PPVA6 (28.4), MPZW5 (25), WPWPA4 (24.2), EPRP11 (22.1), AEPVI12 (21.7), WNPTN10 (17.5) |
| 51060 | IOWPA9 (32.5), PPVI12 (32.5), SSRP10 (31.7), NANRP6 (27.4), NAHAI11 (26.9), PPVA6 (26.8), WPWPA4 (24.1), EPRP12 (23.7), AEPVI11 (23), MPZW5 (22.8), WNPTN10 (14.3) |
| 51068 | PPVI12 (35.5), WPWPA10 (35.2), SSRP4 (33.9), EPRP12 (28.8), NANRP11 (26), PPVA11 (25.6), MPZW5 (23.5), WNPTN12 (22.7), AEPVI10 (21), NAHAI11 (19.9) |
| 51076 | NAHAI6 (33.5), SSRP10 (32.8), NANRP12 (31.5), AEPVI11 (31.1), PPVI6 (30.9), MPZW5 (29.4), WPWPA4 (26.4), PPVA6 (23.8), EPRP11 (21), WNPTN10 (13.2) |
| 51087 | PPVA11 (34.2), PPVI12 (33.8), NANRP12 (32.7), SSRP10 (32), MPZW5 (25), EPRP11 (24.8), WPWPA10 (22.4), AEPVI10 (15.9), NAHAI12 (14.1), WNPTN11 (13) |
| 51133 | PPVI6 (36.5), AEPVI12 (36.4), SSRP11 (33.9), PPVA10 (25.8), WPWPA11 (25.5), NANRP12 (24.6), NAHAI11 (18.8), EPRP12 (18.4), WNPTN10 (12.9) |
| 51156 | PPVI12 (36.5), SSRP10 (34.4), MPZW5 (32.6), WPWPA10 (30.5), PPVA12 (23.9), NANRP12 (22.8), AEPVI11 (22.4), WNPTN10 (17.7), EPRP11 (15.3) |
| 51232 | PPVI12 (41.2), WPWPA4 (36.3), NAHAI6 (33.1), SSRP12 (31.7), AEPVI11 (29.2), NANRP11 (27.9), PPVA6 (27.6), MPZW5 (26.2), EPRP11 (21.2), WNPTN10 (16.3) |
| 51238 | PPVI12 (40.6), SSRP11 (32.2), WPWPA4 (31.6), PPVA12 (27.6), NANRP11 (27.3), AEPVI5 (25.8), MPZW12 (23.9), NAHAI12 (21.2), WNPTN11 (17.2), EPRP10 (16.6) |
| 51241 | AEPVI6 (43), PPVI12 (36.8), SSRP11 (30.9), NANRP11 (20), EPRP11 (18.9), PPVA12 (18.6), WNPTN10 (11.8) |
| 51243 | PPVI6 (42.5), IOWPA11 (31.2), NAHAI9 (30.1), NANRP6 (29.8), SSRP10 (25.3), EPRP11 (22.2), PPVA6 (21), AEPVI5 (15.8), WPWPA6 (15.7), MPZW4 (15), WNPTN10 (6.1) |
| 51334 | PPVI12 (37.8), SSRP10 (36.9), WPWPA4 (34.3), PPVA11 (30.6), NANRP5 (28.3), NAHAI12 (27.8), AEPVI12 (26.9), MPZW12 (26.6), EPRP11 (21.4), WNPTN10 (12.6) |
| 51367 | WPWPA4 (40.3), SSRP11 (39.4), PPVI12 (36.7), AEPVI12 (31.4), MPZW5 (30.3), NANRP11 (26.3), PPVA12 (24), NAHAI12 (22.1), IOWPA3 (20.2), EPRP11 (15.9), WNPTN10 (14.9) |
| 51477 | PPVI6 (37.4), SSRP10 (29.1), NANRP6 (28.8), AEPVI5 (25.3), PPVA9 (25.1), IOWPA6 (24.2), EPRP6 (17.6), NAHAI10 (17.4), WPWPA4 (15), WNPTN10 (13.1), MPZW5 (11.1) |
| 51526 | PPVI4 (34.9), SSRP6 (34.7), PPVA12 (28.7), NANRP9 (28.4), IOWPA5 (25), WPWPA10 (23.2), AEPVI6 (23), NAHAI5 (19.9), EPRP10 (18.8), MPZW6 (17.3), APVA5 (16.7), WNPTN4 (11.6) |
| 51567 | PPVI6 (37.1), SSRP4 (32), AEPVI12 (31.1), IOWPA9 (29.8), MPZW5 (25), WPWPA4 (24.1), NANRP5 (22.3), NAHAI5 (21.5), APVA10 (20.4), PPVA6 (19.7), WNPTN4 (17.9), EPRP10 (16) |
| 51573 | SSRP10 (39.5), PPVI12 (36.7), PPVA10 (31.8), WPWPA11 (31.3), NANRP11 (29.5), NAHAI11 (28.2), MPZW3 (26), EPRP11 (24.8), IOWPA5 (24.3), AEPVI10 (24.1), WNPTN12 (21.7) |
| 51628 | WNPTN4 (37.9), PPVI12 (37.7), SSRP10 (31.5), PPVA11 (30.4), WPWPA10 (27.6), NANRP11 (24.9), MPZW10 (24), EPRP10 (21.9), NAHAI11 (20.7), AEPVI12 (19.3), APVA12 (15) |
| 51656 | WPWPA4 (36.8), SSRP4 (34.6), PPVI6 (33.6), IOWPA9 (33.1), MPZW5 (28.9), PPVA5 (26), NANRP4 (24.6), WNPTN4 (24.4), NAHAI5 (21.8), APVA6 (21), AEPVI6 (17.7), EPRP4 (17.5) |
| 51704 | PPVI6 (39.9), NANRP11 (32.2), IOWPA10 (28.9), SSRP9 (28), AEPVI10 (23.8), NAHAI4 (23.4), WNPTN6 (21.6), WPWPA5 (19.6), EPRP11 (18.1), MPZW6 (16.9), PPVA6 (16.5) |
| 51705 | EPRP11 (37), PPVI10 (35.4), SSRP12 (34.1), WNPTN10 (31.5), AEPVI12 (26.1), NANRP11 (22.2) |
| 51709 | PPVI12 (37.5), WPWPA11 (36.9), SSRP10 (33.8), PPVA5 (33.6), MPZW10 (30.2), EPRP10 (29.1), WNPTN11 (28.9), NANRP11 (25.2), AEPVI3 (21.9), IOWPA12 (21), NAHAI11 (19.4) |
| 51720 | PPVI6 (36.3), WPWPA4 (36), NANRP4 (26.4), SSRP9 (26), AEPVI5 (23.9), IOWPA6 (23.7), PPVA6 (23.1), NAHAI10 (21.2), WNPTN5 (20.3), EPRP5 (14.7) |
| 51730 | PPVI6 (38.2), IOWPA10 (35.8), SSRP9 (28.6), WNPTN10 (27.4), AEPVI4 (23.3), WPWPA6 (23), NAHAI5 (21.7), NANRP10 (20.7), PPVA6 (18.1), MPZW5 (17.8), APVA10 (17.3), EPRP5 (15.5) |
| 51765 | PPVI6 (38.2), IOWPA9 (32), SSRP4 (31), NANRP4 (29.3), WPWPA10 (28.7), WNPTN4 (24.8), PPVA5 (24.3), MPZW6 (23.6), AEPVI6 (23.1), APVA5 (20.2), NAHAI5 (18.6), EPRP10 (16.8) |
| 51810 | PPVI6 (43.8), IOWPA4 (38.8), WPWPA11 (31.8), PPVA9 (30.3), SSRP10 (25.9), WNPTN10 (25.7), AEPVI12 (20.6), MPZW5 (18.1), NANRP10 (18), NAHAI11 (17.5), EPRP10 (11.5) |
| 51811 | PPVI6 (46.9), PPVA9 (28.8), SSRP11 (27.5), EPRP5 (26.8), IOWPA10 (25.8), NAHAI11 (25), WPWPA4 (22.2), NANRP10 (20.1), AEPVI12 (19.5), WNPTN10 (18.9), MPZW5 (14.3) |
| 51818 | NANRP6 (36.7), PPVI5 (34.1), SSRP4 (31.9), AEPVI12 (27.9), PPVA11 (27.3), NAHAI11 (25.8), MPZW10 (21.2), WPWPA5 (21.1), EPRP10 (16.8), WNPTN4 (13.7) |
| 51828 | AEPVI5 (33.6), SSRP6 (32.9), PPVI12 (32.6), NANRP4 (32.5), NAHAI11 (27.2), MPZW5 (22.9), PPVA11 (21.9), WPWPA10 (21.1), IOWPA9 (17.2), EPRP12 (15.5), APVA10 (13.7), WNPTN4 (13) |
| 51839 | AEPVI12 (36.5), PPVI6 (34.3), PPVA11 (33.6), SSRP4 (33.4), NANRP5 (31.6), WPWPA10 (28.2), IOWPA5 (23.1), APVA6 (22), NAHAI10 (20.8), EPRP9 (18.3), WNPTN4 (16), MPZW5 (12.5) |
| 51855 | WPWPA4 (35.7), SSRP4 (34.1), PPVI6 (31.1), IOWPA9 (29), NANRP5 (26.6), AEPVI6 (25.9), PPVA5 (24.3), EPRP5 (23.8), APVA6 (21.8), NAHAI5 (18.8), MPZW5 (16.8), WNPTN4 (9.8) |
| 51931 | PPVI5 (35.7), SSRP6 (33.7), NANRP4 (31.6), APVA4 (25.1), AEPVI6 (24.7), WPWPA9 (23.9), IOWPA6 (23.3), PPVA5 (23.3), MPZW10 (22.7), EPRP5 (21.3), NAHAI5 (19.8), WNPTN4 (11.4) |
| 52101 | WNPTN4 (38.8), PPVI12 (36.6), WPWPA10 (25.3), EPRP10 (23.8), SSRP10 (23.3), PPVA6 (22.5), MPZW10 (17), NANRP5 (16.5), AEPVI12 (14.2) |
| 52112 | PPVI6 (43.2), WNPTN9 (33.4), SSRP10 (29.5), AEPVI12 (28.8), IOWPA10 (28.5), WPWPA4 (26.7), PPVA6 (26.1), NANRP10 (20.8), APVA5 (20.4), NAHAI6 (15.5), MPZW10 (14.7), EPRP5 (13.7) |
| 52118 | PPVI6 (45), IOWPA9 (31.6), PPVA10 (28.3), AEPVI6 (25.8), SSRP12 (25.4), MPZW5 (22.9), WNPTN5 (20.9), NAHAI10 (19), NANRP10 (17.1), WPWPA10 (14.7), EPRP4 (13.8) |
| 52203 | PPVI6 (41.1), IOWPA9 (33.5), SSRP10 (27.8), AEPVI5 (24.9), NAHAI4 (24.2), WPWPA6 (23.7), APVA5 (23.2), WNPTN10 (22.3), MPZW10 (20.2), PPVA6 (20.2), NANRP5 (16.5), EPRP10 (12) |
| 52313 | EPRP11 (39.2), PPVI6 (38.6), SSRP4 (34.5), NANRP5 (28.1), MPZW10 (21.4), WPWPA6 (21.1), WNPTN10 (20.5), AEPVI6 (20.4), NAHAI6 (19.4), PPVA5 (17.5), APVA6 (14.4) |
| 52323 | WNPTN4 (48), SSRP10 (33.7), PPVI12 (32.7), MPZW5 (32.7), EPRP11 (28.6), WPWPA10 (26.8), AEPVI11 (24.6), NANRP12 (24.2), NAHAI12 (22.5), APVA12 (20.5), PPVA12 (18.3) |
| 52546 | PPVI6 (40.5), IOWPA9 (28), NAHAI5 (26.9), WNPTN12 (24.4), AEPVI11 (23.4), SSRP4 (23.3), PPVA10 (22.8), NANRP10 (20.5), MPZW5 (17.3), WPWPA10 (16.8), EPRP4 (16.3) |
| 52652 | WNPTN4 (48.1), PPVA11 (31.9), SSRP10 (29.2), PPVI12 (28.6), AEPVI10 (27), MPZW5 (25.4), EPRP12 (24.8), WPWPA10 (23.1), NANRP10 (22.7), NAHAI11 (10.7) |
| 52674 | EPRP10 (55.5), NANRP10 (49.2) |
| 52679 | EPRP10 (31.7), PPVA11 (31.2), SSRP10 (28.6), NANRP10 (25.9), NAHAI11 (19.9), AEPVI12 (15.7), PPVI11 (14.9) |
| 52681 | PPVA11 (33.6), WPWPA12 (31.3), APVA10 (29.1), PPVI10 (28.6), NANRP12 (28), SSRP10 (26.4), EPRP10 (25.2), WNPTN10 (22.5), NAHAI5 (18.6), MPZW11 (16.3), AEPVI12 (15.7) |
| 52797 | SSRP10 (42.2), EPRP10 (35.4), NANRP10 (31.9), PPVI11 (27.2) |
| Circulation Index | PPVI | SSRP | WPWPA | NANRP | PPVA | IOWPA | AEPVI | WNPTN | NAHAI | MPZW | EPRP | APVA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rankid,NW | 2.959 | 1.928 | 1.135 | 0.962 | 0.941 | 0.900 | 0.856 | 0.631 | 0.507 | 0.406 | 0.401 | 0.141 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Wei, K.; Chen, K.; He, J.; Zhao, Y.; Yang, G.; Yao, N.; Niu, B.; Wang, B.; Wang, L.; et al. Forecasting Monthly Water Deficit Based on Multi-Variable Linear Regression and Random Forest Models. Water 2023, 15, 1075. https://doi.org/10.3390/w15061075
Li Y, Wei K, Chen K, He J, Zhao Y, Yang G, Yao N, Niu B, Wang B, Wang L, et al. Forecasting Monthly Water Deficit Based on Multi-Variable Linear Regression and Random Forest Models. Water. 2023; 15(6):1075. https://doi.org/10.3390/w15061075
Chicago/Turabian StyleLi, Yi, Kangkang Wei, Ke Chen, Jianqiang He, Yong Zhao, Guang Yang, Ning Yao, Ben Niu, Bin Wang, Lei Wang, and et al. 2023. "Forecasting Monthly Water Deficit Based on Multi-Variable Linear Regression and Random Forest Models" Water 15, no. 6: 1075. https://doi.org/10.3390/w15061075
APA StyleLi, Y., Wei, K., Chen, K., He, J., Zhao, Y., Yang, G., Yao, N., Niu, B., Wang, B., Wang, L., Feng, P., & Yang, Z. (2023). Forecasting Monthly Water Deficit Based on Multi-Variable Linear Regression and Random Forest Models. Water, 15(6), 1075. https://doi.org/10.3390/w15061075











