Comparison of Size Distribution of Fish Obtained from Gill Netting and the Distributions of Echoes from Hydroacoustics in Lake Dejguny (Poland)
Abstract
:1. Introduction
2. Materials and Methods
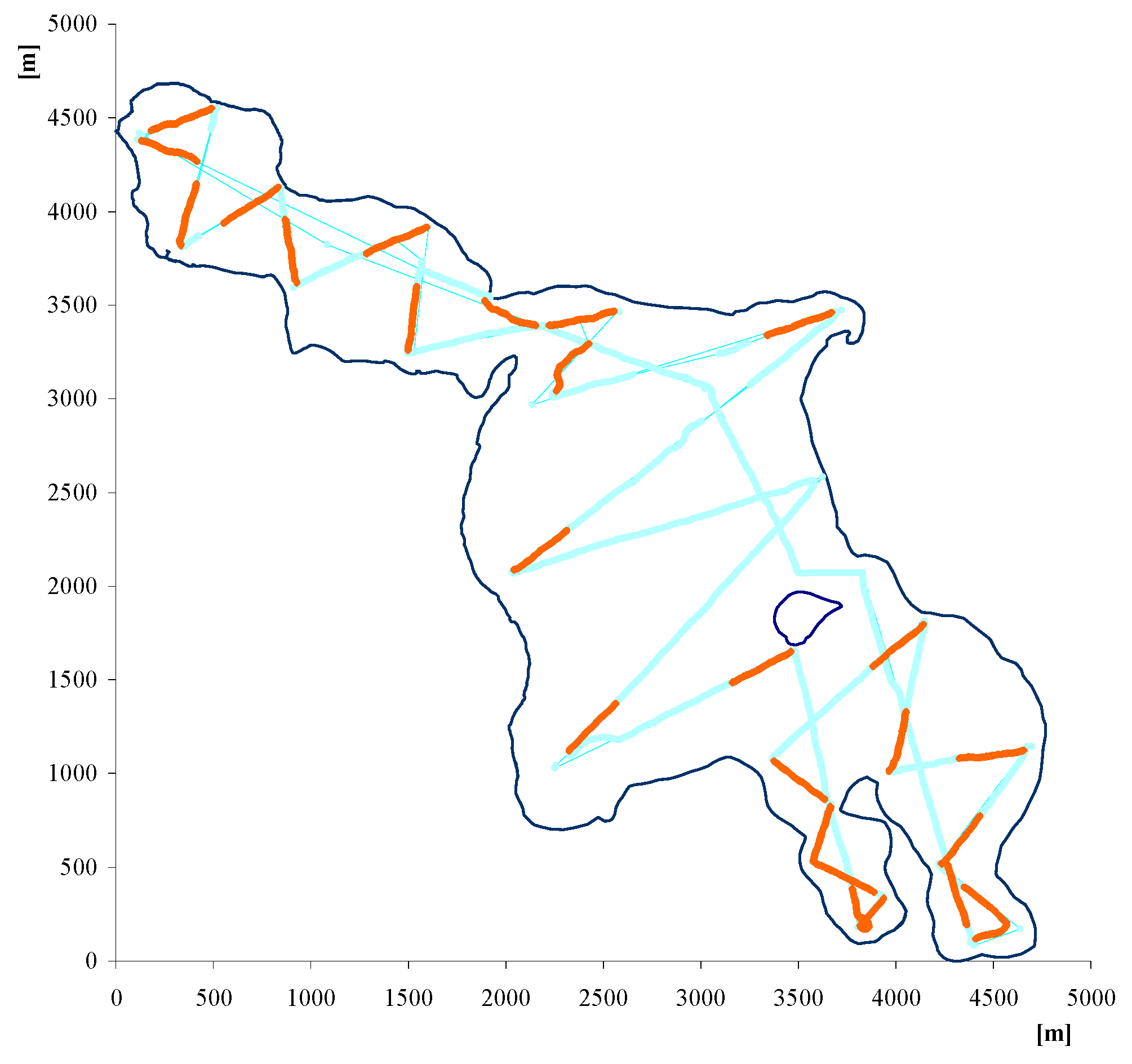
2.1. Gillnet Sampling
2.2. Hydroacoustic
2.2.1. Data Collection
2.2.2. Data Post-Processing
2.2.3. Statistics
2.2.4. Meta-Analysis
3. Results
3.1. Gillnet Catches
3.2. Hydroacoustics
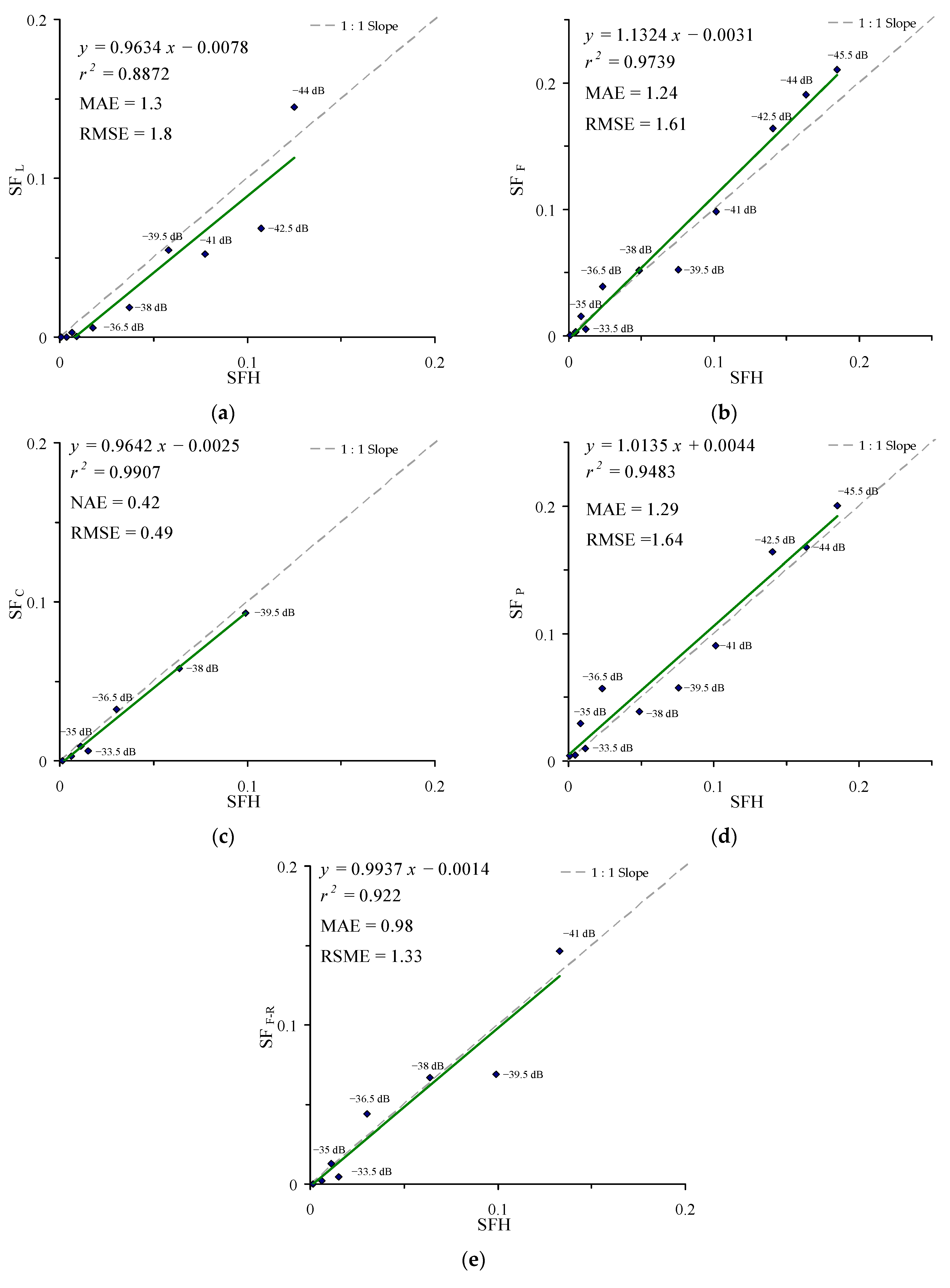
3.3. Analysis
3.4. Meta-Analysis
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Godlewska, M.; Długoszewski, B.; Doroszczyk, L.; Jóźwik, A. The relationship between sampling intensity and sampling error—Empirical results from acoustic surveys in Polish vendace lakes. Fish. Res. 2009, 96, 17–22. [Google Scholar] [CrossRef]
- Frouzová, J.; Kubečka, J.; Balk, H.; Frouz, J. Target strength of some European fish species and its dependence on fish body parameters. Fish. Res. 2005, 75, 86–96. [Google Scholar] [CrossRef]
- Foote, K.G. Fish target strengths for use in echo integrator surveys. J. Acoust. Soc. Am. 1987, 82, 981–987. [Google Scholar] [CrossRef] [Green Version]
- Horppila, J.; Malinen, T.; Peltonen, H. Density and habitat shifts of a roach (Rutilus rutilus) stock assessed within one season with cohort analysis, depletion methods and echosounding. Fish. Res. 1996, 28, 151–161. [Google Scholar] [CrossRef]
- Świerzowski, A.; Doroszczyk, L. Seasonal differences in situ measurements of the target strength of vendace (Coregonus albula L.) in lake Pluszne. Hydroacoustics 2004, 7, 217–226. [Google Scholar]
- Mehner, T. Prediction of hydroacoustic target strength of vendace (Coregonus albula) from concurrent trawl catches. Fish. Res. 2006, 79, 162–169. [Google Scholar] [CrossRef]
- Love, R.H. Dorsal-Aspect target strength of an individual fish. J. Acoust. Soc. Am. 1971, 49, 816–823. [Google Scholar] [CrossRef]
- Love, R.H. Target strength of an individual fish at any aspect. J. Acoust. Soc. Am. 1977, 62, 1397–1403. [Google Scholar] [CrossRef]
- Mehner, T.; Schulz, M. Monthly variability of hydroacoustic fish stock estimates in a deep lake and its correlation to gillnet catches. J. Fish Biol. 2002, 61, 1109–1121. [Google Scholar] [CrossRef]
- Mehner, T.; Gassner, H.; Schulz, M. Comparative fish stock estimates in Lake Stechlin by parallel split-beam echosounding with 120 kHz. Arch. Hydrobiol. Spec. Issues Advanc. Limnol. 2003, 68, 227–236. [Google Scholar]
- Ona, E. Physiological factors causing natural variations in acoustic target strength of fish. J. Mar. Biol. Assoc. United Kingd. 1990, 70, 107–127. [Google Scholar] [CrossRef]
- Hazen, E.L.; Horne, J.K. A method for evaluating the effects of biological factors on fish target strength. J. Mar. Sci. 2003, 60, 555–562. [Google Scholar] [CrossRef]
- Emmrich, M.; Winfield, I.J.; Guillard, J.; Rustadbakken, A.; Vergès, C.; Volta, P.; Jeppesen, E.; Lauridsen, T.L.; Brucet, S.; Holmgren, K.; et al. Strong correspondence between gillnet catch per unit effort and hydroacoustically derived fish biomass in stratified lakes. Freshw. Biol. 2012, 57, 2436–2448. [Google Scholar] [CrossRef] [Green Version]
- Achleitner, D.; Gassner, H.; Luger, M. Comparison of three standardised fish sampling methods in 14 alpine lakes in Austria. Fish. Manag. Ecol. 2012, 19, 352–361. [Google Scholar] [CrossRef]
- Tušer, M.; Guillard, J.; Rustadbakken, A.; Mehner, T. Comparison of fish size spectra obtained from hydroacoustics and gillnets across seven European natural lakes. Can. J. Fish. Aquat. Sci. 2022, 79, 2179–2190. [Google Scholar] [CrossRef]
- Tátrai, I.; Specziár, A.; György, A.I.; Bíró, P. Comparison of fish size distribution and fish abundance estimates obtained with hydroacoustics and gill netting in the open water of a large shallow Lake. Ann. Limnol.-Int. J. Lim. 2008, 44, 231–240. [Google Scholar] [CrossRef] [Green Version]
- DuFour, M.R.; Qian, S.S.; Mayer, C.M.; Vandergoot, C.S. Evaluating catchability in a large-scale gillnet survey using hydroacoustics: Making the case for coupled surveys. Fish. Res. 2019, 211, 309–318. [Google Scholar] [CrossRef]
- Baran, R.; Blabolil, P.; Čech, M.; Draštík, V.; Frouzová, J.; Holubová, M.; Jůza, T.; Koliada, I.; Muška, M.; Peterka, J.; et al. New way to investigate fish density and distribution in the shallowest layers of the open water. Fish. Res. 2021, 238, 105907. [Google Scholar] [CrossRef]
- Braun, L.-M.; Mehner, T. Size Spectra of Pelagic Fish Populations in a Deep Lake—Methodological Comparison between Hydroacoustics and Midwater Trawling. Water 2021, 13, 1559. [Google Scholar] [CrossRef]
- DuFour, M.R.; Mayer, C.M.; Kocovsky, P.M.; Qian, S.S.; Warner, D.M.; Kraus, R.T.; Vandergoot, C.S. Sparse targets in hydroacoustic surveys: Balancing quantity and quality of in situ target strength data. Fish. Res. 2017, 188, 173–182. [Google Scholar] [CrossRef] [Green Version]
- Borisenko, E.S.; Degtev, A.I.; Mochek, A.D.; Pavlov, D.S. Hydroacoustic characteristics of mass fhishes of the Ob–Irtysh Basin. J. Ichthyol. 2006, 46 (Suppl. 2), S227–S234. [Google Scholar] [CrossRef]
- Doroszczyk, L. Wykorzystanie Metod Hydroakustycznych do Oceny Populacji Sielawy na Przykładzie Jeziora Pluszne. Ph.D. Thesis, Instytut Rybactwa Śródlądowego, Olsztyn, Poland, 2011. [Google Scholar]
- CEN. Water Quality—Sampling of Fish with Multi-Mesh Gillnets (EN 14757); CEN: Brussels, Belgium, 2015. [Google Scholar]
- Chybowski, Ł.; Białokoz, W.; Wołos, A.; Draszkiewicz-Mioduszewska, H.; Szlakowski, J. Przewodnik Metodyczny do Monitoringu Ichtiofauny w Jeziorach; Biblioteka Monitoringu Środowiska: Warszawa, Poland, 2016; pp. 1–52. [Google Scholar]
- Malinen, T.; Tuomaala, A.; Peltonen, H. Hydroacoustic fish stock assessment in the presence of dense aggregations of Chaoborus lartvae. Can. J. Fish. Aquat. Sci. 2005, 62, 245–249. [Google Scholar] [CrossRef]
- Jurvelius, J.; Knudsen, F.R.; Balk, H.; Maejomäki, T.J.; Peltonen, H.; Taskinen, J.; Tuomaala, A.; Viljanen, M. Echo-sounding can discriminate between fish and macroinvertebrates in freshwater. Freshwat. Biol. 2008, 53, 912–923. [Google Scholar] [CrossRef]
- Simrad EP 500, Echo processing system, 1997. Instruction Manual. To jest instrukcja dołączona do sonaru EY 500. Została wydana w 1997 roku. Obecnie nie jest dostępna online.
- Prchalová, M.; Kubečka, J.; Říha, M.; Mrkvička, T.; Vašeka, M.; Jůza, T.; Kratochvíl, M.; Peterka, J.; Draštíka, V.; Křížekd, J. Size selectivity of standardized multimesh gillnets in sampling coarse European species. Fish. Res. 2009, 96, 51–57. [Google Scholar] [CrossRef]
- Olin, M.; Malinen, T.; Ruuhijärvi, J. Gillnet catch in estimating the density and structure of fish community—Comparison of gillnet and trawl samples in a eutrophic lake. Fish. Res. 2009, 96, 88–94. [Google Scholar] [CrossRef]
- Malinen, T. Hydroacoustic Fish Stock Assessment in Southern and Northern Boreal Lakes–Potential and Constraints. Ph.D. Thesis, Faculty of Biological and Environmental Sciences, University of Helsinki, Hansaprint Oy, Turenki, 2018. Available online: https://helda.helsinki.fi/bitstream/handle/10138/239247/hydroaco.pdf?sequence=2 (accessed on 24 February 2023).
- Probst, W.N.; Thomas, G.; Eckmann, R. Hydroacoustic observations of surface shoaling behaviour of young-of-the-year perch Perca fluviatilis (Linnaeus, 1758) with a towed upward-facing transducer. Fish. Res. 2009, 96, 133–138. [Google Scholar] [CrossRef] [Green Version]
- Gooding, P. Consumer Price Inflation Basket of Goods and Services: 2021. Available online: https://backup.ons.gov.uk/wp-content/uploads/sites/3/2021/03/Consumer-price-inflation-basket-of-goods-and-services-2021.pdf (accessed on 18 November 2022).
- Maksymiuk, A.; Furmańczyk, K.; Ignar, S.; Krupa, J.; Okruszko, T. Analiza zmienności parametrów klimatycznych i hydrologicznych w dolinie rzeki Biebrzy [Analysis of climatic and hydrologic parameters variability in the Biebrza River basin]. Przegląd Nauk. Inżynieria I Kształtowanie Sr. 2008, 3, 59–68. [Google Scholar]
- Białokoz, W.; Chybowski, Ł. Ichtiofauna. In Ecological Status Assessment of the Waters in the Wel River Catchment. Guidelines for Integrated Assessment of Ecological Status of River and Lakes to Support River Basin Management Plans; Soszka, H., Ed.; Wydawnictwo Instytutu Rybactwa Śródlądowego: Olsztyn, Poland, 2011; pp. 217–234. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the use of “goodness-of-fit”measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef] [Green Version]
- Julien, G.A.; Emmanuel, L.; Clement, A.; Akiyo, R.O.L.; Sinsin, B.A. Modelling of solar energy transfer through roof material in Africa Sub-Saharan regions. Renew. Energy 2013, 34, 632–645. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Motovilov, Y.G.; Gottschalk, L.; Engeland, K.; Rodhe, A. Validation of a distributed hydrological model against spatial observations. Agric. For. Meteorol. 1999, 98–99, 257–277. [Google Scholar] [CrossRef]
- Van Liew, M.W.; Arnold, J.G.; Bosc, D.D. Problems and potential of autocalibrating a hydrologic model. Trans. ASAE Am. Soc. Agric. Eng. 2005, 48, 1025–1040. [Google Scholar] [CrossRef] [Green Version]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in as sessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Chai1, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)? Geosci. Model Dev. Discuss. 2014, 7, 1525–1534. [Google Scholar] [CrossRef] [Green Version]
- Kushwaha, N.L.; Rajput, J.; Elbeltagi, A.; Elnaggar, A.Y.; Sena, D.R.; Vishwakarma, D.K.; Mani, I.; Hussein, E.E. Data Intelligence Model and Meta-Heuristic Algorithms-Based Pan Evaporation Modelling in Two Different Agro-Climatic Zones: A Case Study from Northern India. Atmosphere 2021, 12, 1654. [Google Scholar] [CrossRef]
- Knudsena, F.R.; Sægrovb, H. Benefits from horizontal beaming during acoustic survey: Application to three Norwegian lakes. Fish. Res. 2002, 56, 205–211. [Google Scholar] [CrossRef]
- Draštík, V.; Kubečka, J.; Čech, M.; Frouzová, J.; Říha, M.; Jůza, T.; Tušer, M.; Jarolím, O.; Prchalová, M.; Peterka, J.; et al. Hydroacoustic estimates of fish stocks in temperate reservoirs: Day or night surveys? Aquat. Living Resour. 2009, 22, 69–77. [Google Scholar] [CrossRef]


| Species | Abundance (%) |
|---|---|
| perch (Perca fluviatilus L.) | 36.0 |
| European smelt (Osmerus eperlanus L.) | 21.1 |
| roach (Rutilus rutilus L.) | 17.7 |
| bream (Blicca bjoerkna L.) | 10.4 |
| freshwater bream (Abramis brama L.) | 4.6 |
| ruffe (Gymnocephalus cernuus L.) | 4.5 |
| vendance (Coregonus albula L.) | 4.1 |
| bleak (Alburnus alburnus L.) | 1.1 |
| rudd (Scardinius erythrophthalmus L.) | 0.2 |
| pike (Esox lucius L.) | 0.2 |
| tench (Tinca tinca L.) | <0.1 |
| bitterling (Rhodeus amarus L.) | <0.1 |
| spined loach (Cobitis taenia L.) | <0.1 |
| burbot (Lota lota L.) | <0.1 |
| TS [dB] | −56.0 | −54.5 | −53.0 | −51.5 | −50.0 | −48.5 | −47.0 | −45.5 | −44.0 | −42.5 | −41.0 | −39.5 | −38.0 | −36.5 | −35.0 | −33.5 | −32.0 | −30.5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NH | 1718 | 1723 | 1623 | 1385 | 1146 | 796 | 612 | 479 | 424 | 364 | 263 | 196 | 126 | 60 | 22 | 30 | 12 | 3 |
| NL | 5 | 84 | 18 | 18 | 63 | 1362 | 352 | 1125 | 631 | 298 | 228 | 239 | 82 | 26 | 12 | 1 | 0 | 0 |
| NF | 1 | 39 | 57 | 10 | 17 | 55 | 739 | 919 | 832 | 715 | 430 | 228 | 225 | 170 | 68 | 23 | 14 | 2 |
| NC | 89 | 16 | 7 | 32 | 137 | 1436 | 133 | 481 | 1076 | 442 | 152 | 250 | 156 | 87 | 25 | 17 | 8 | 0 |
| NP | 5 | 42 | 58 | 7 | 25 | 51 | 771 | 872 | 730 | 715 | 394 | 250 | 168 | 247 | 129 | 42 | 21 | 17 |
| NF-R | 0 | 0 | 1 | 46 | 58 | 17 | 49 | 1158 | 574 | 1127 | 640 | 302 | 293 | 193 | 57 | 20 | 9 | 0 |
| NF-P | 112 | 25 | 26 | 191 | 1012 | 408 | 149 | 896 | 457 | 247 | 293 | 133 | 127 | 183 | 115 | 90 | 37 | 43 |
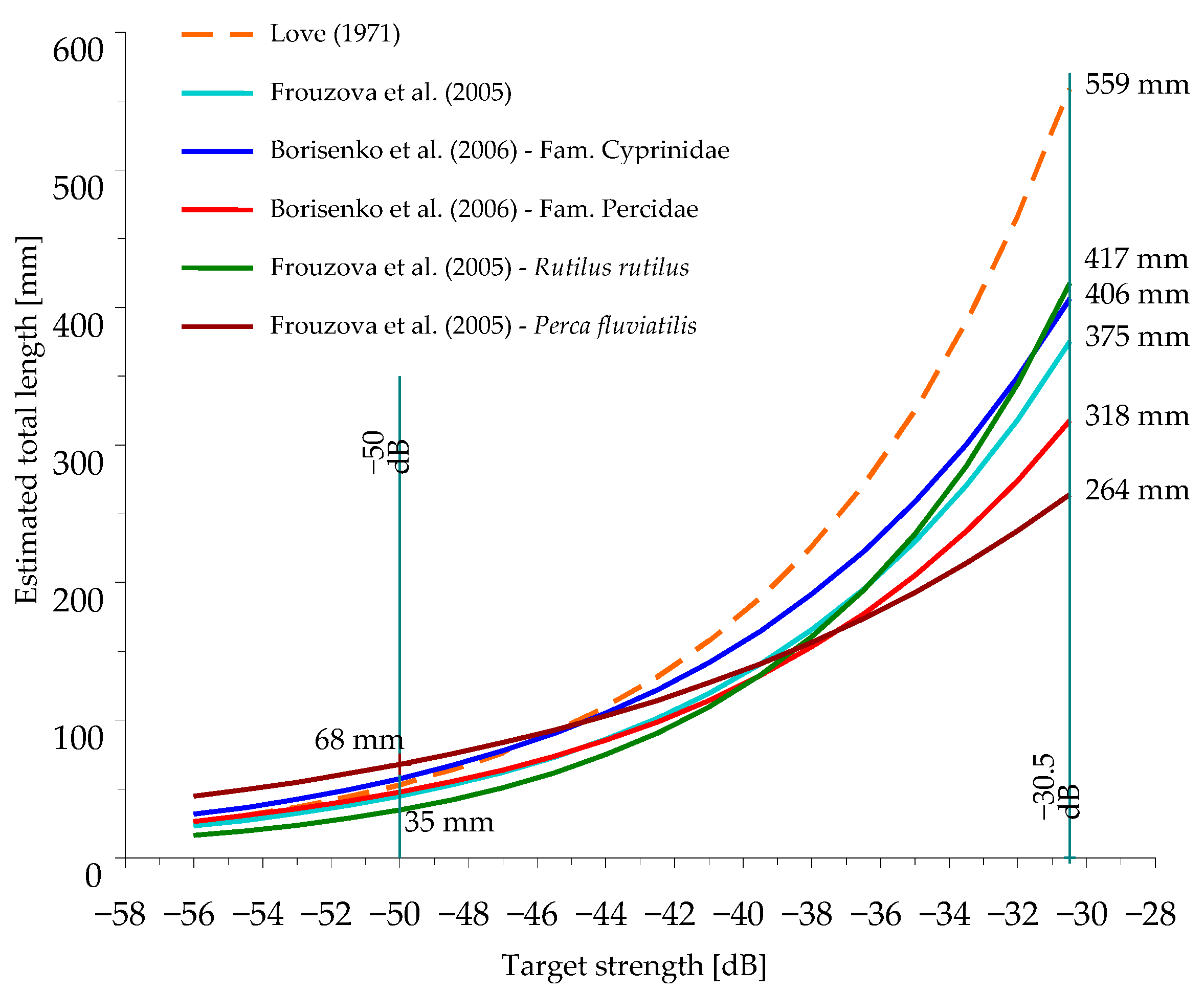
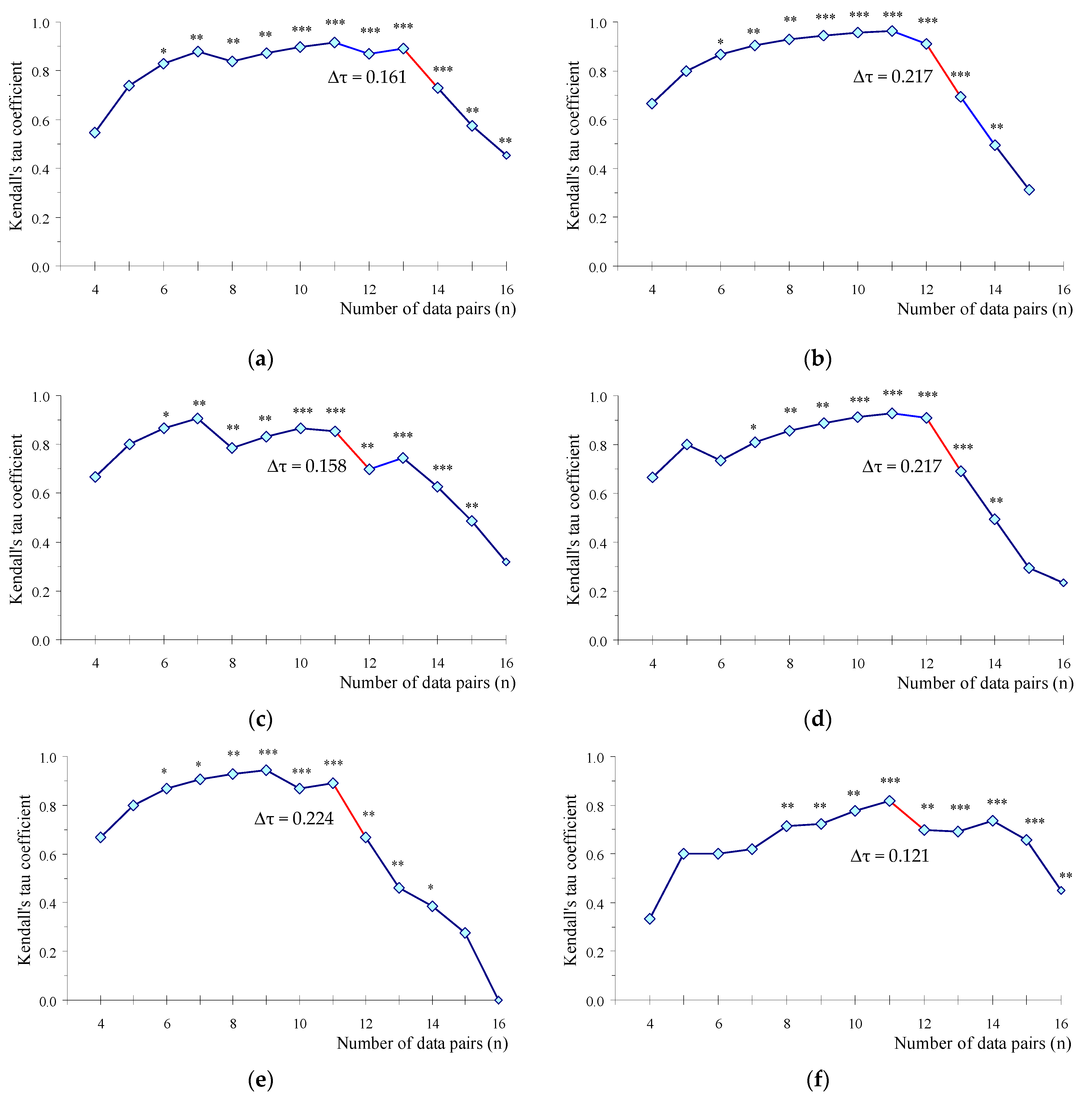
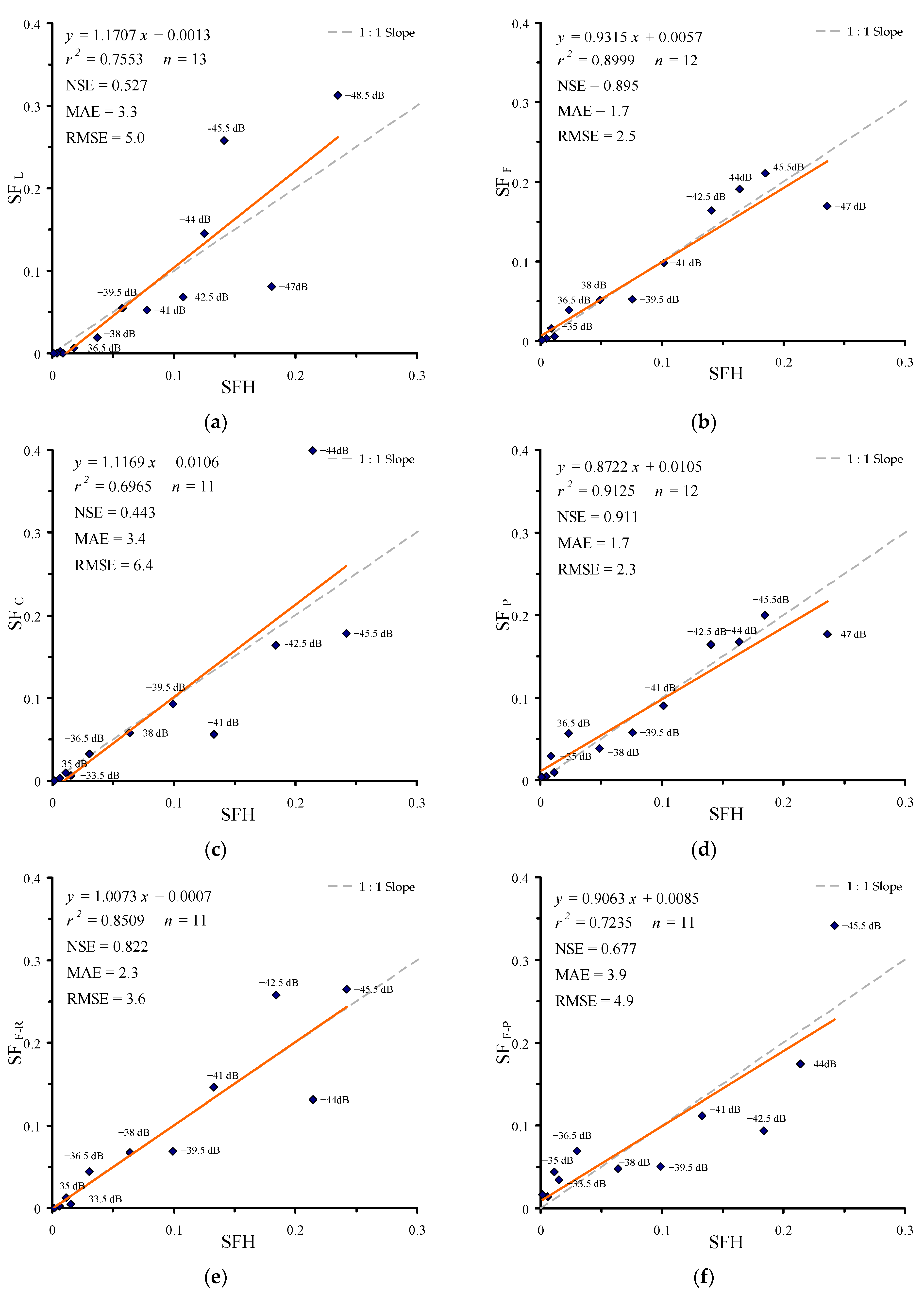
| Equation (1) | Equation (2) | Equation (3) for Family Cyprinidae | Equation (4) for Family Percidae | Equation (5) for Roach | Equation (6) for Perch | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TS (dB) | TLE (mm) | NSE | TLE (mm) | NSE | TLE (mm) | NSE | TLE (mm) | NSE | TLE (mm) | NSE | TLE (mm) | NSE |
| −48.5 | 63.8 | 0.527 | ||||||||||
| −47.0 | 76.4 | 0.367 | 62.3 | 0.899 | 64.0 | 0.911 | 62.0 | 0.822 | 93.0 | 0.677 | ||
| −45.5 | 91.6 | 0.387 | 73.3 | 0.939 | 74.0 | 0.443 | 74.0 | 0.937 | 75.0 | 0.751 | 103.3 | 0.711 |
| −44.0 | 109.7 | 0.833 | 86.3 | 0.932 | 85.6 | 0.262 | 85.6 | 0.916 | 90.8 | 0.797 | 114.6 | 0.576 |
| −42.5 | 131.5 | 0.762 | 101.6 | 0.926 | 99.0 | 0.810 | 99.0 | 0.863 | 109.9 | 0.915 | 127.2 | 0.622 |
| −41.0 | 157.6 | 0.784 | 119.7 | 0.907 | 114.6 | 0.639 | 114.6 | 0.780 | 133.0 | 0.842 | 141.2 | 0.252 |
| −39.5 | 188.8 | 0.780 | 140.9 | 0.803 | 132.5 | 0.978 | 132.5 | 0.558 | 160.9 | 0.873 | 159.7 | −0.332 |
| −38.0 | 226.2 | 0.359 | 165.9 | 0.773 | 153.3 | 0.951 | 153.3 | −0.092 | 194.7 | 0.334 | ||
| −36.5 | 271.1 | −0.440 | 195.3 | −0.201 | 177.4 | 0.800 | 235.6 | −0.266 | ||||
| −35.0 | 205.2 | 0.116 | ||||||||||
| −33.5 | 237.4 | 0.065 | ||||||||||
| −32.0 | 274.7 | −0.151 | ||||||||||
| Citation | Equation in This Study | Number of Fish | Length Range (mm) | Number of Species | Environment |
|---|---|---|---|---|---|
| [7] | 1 | 36 | 48–224 | 8 | Marine-brackish—44% Marine-brackish-Freshwater—25% Freshwater—31% |
| [2] | 2 | 40 | 72–710 | 6 | Freshwater (from the Rimov reservoir and local fish farms) |
| [20] | 3 | 39 | 60–360 | 4 | Freshwater (from Irtysh River) |
| [20] | 4 | 19 | 120–390 | 2 | Freshwater (from Irtysh River) |
| [2] | 5 | 8 | 117–305 | 1 (Roach) | Freshwater |
| [2] | 6 | 5 | 101–290 | 1 (Perch) | Freshwater |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hutorowicz, A.; Ulikowski, D.; Tunowski, J. Comparison of Size Distribution of Fish Obtained from Gill Netting and the Distributions of Echoes from Hydroacoustics in Lake Dejguny (Poland). Water 2023, 15, 1117. https://doi.org/10.3390/w15061117
Hutorowicz A, Ulikowski D, Tunowski J. Comparison of Size Distribution of Fish Obtained from Gill Netting and the Distributions of Echoes from Hydroacoustics in Lake Dejguny (Poland). Water. 2023; 15(6):1117. https://doi.org/10.3390/w15061117
Chicago/Turabian StyleHutorowicz, Andrzej, Dariusz Ulikowski, and Jacek Tunowski. 2023. "Comparison of Size Distribution of Fish Obtained from Gill Netting and the Distributions of Echoes from Hydroacoustics in Lake Dejguny (Poland)" Water 15, no. 6: 1117. https://doi.org/10.3390/w15061117
APA StyleHutorowicz, A., Ulikowski, D., & Tunowski, J. (2023). Comparison of Size Distribution of Fish Obtained from Gill Netting and the Distributions of Echoes from Hydroacoustics in Lake Dejguny (Poland). Water, 15(6), 1117. https://doi.org/10.3390/w15061117