Effect of Unbalanced Magnetic Pull of Generator Rotor on the Dynamic Characteristics of a Pump—Turbine Rotor System
Abstract
:1. Introduction
2. Finite Element Calculation Model
2.1. Mathematical Model of Rotor Dynamics
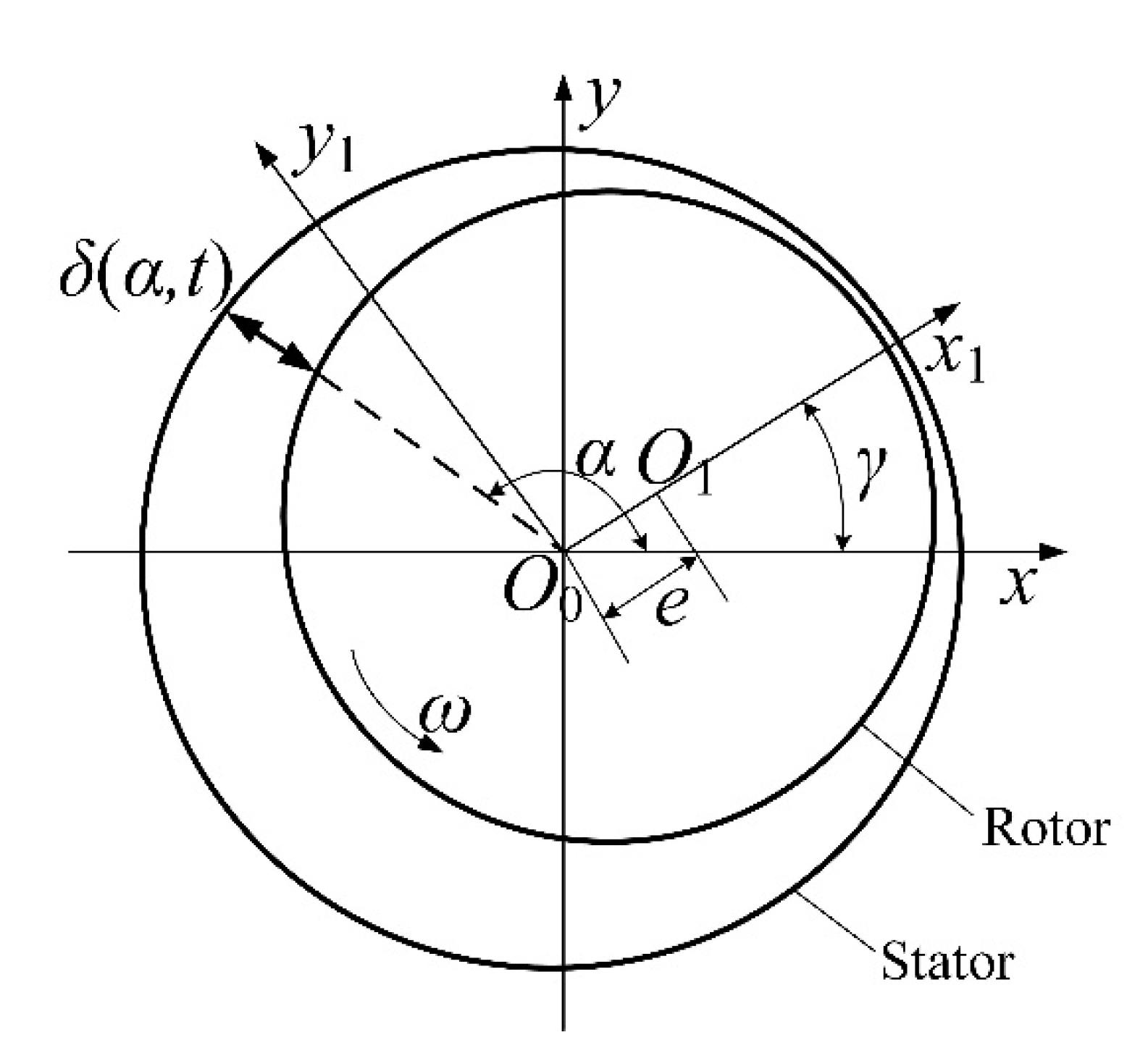
2.2. Generator Air Gap Unbalance Magnetic Pull Model
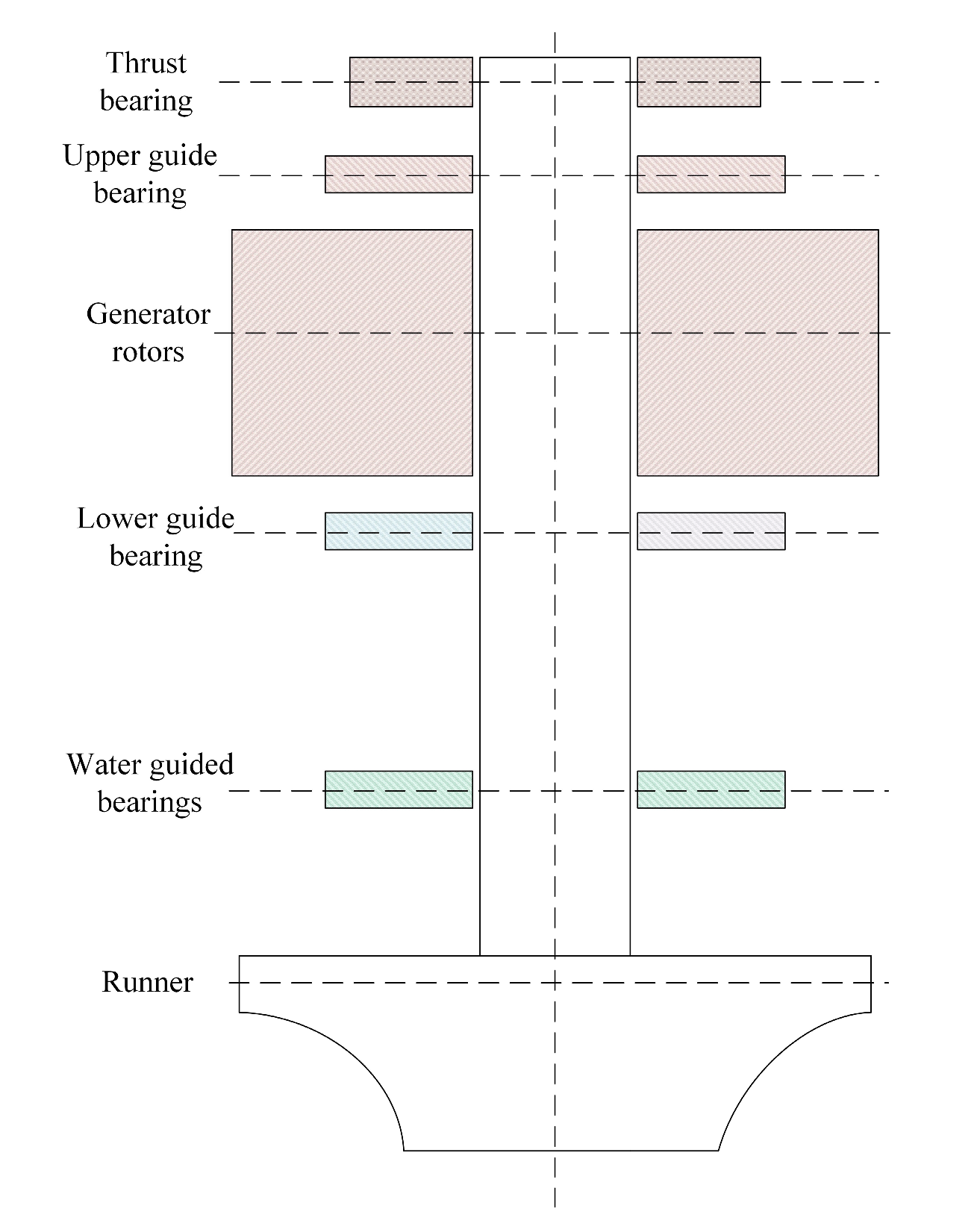
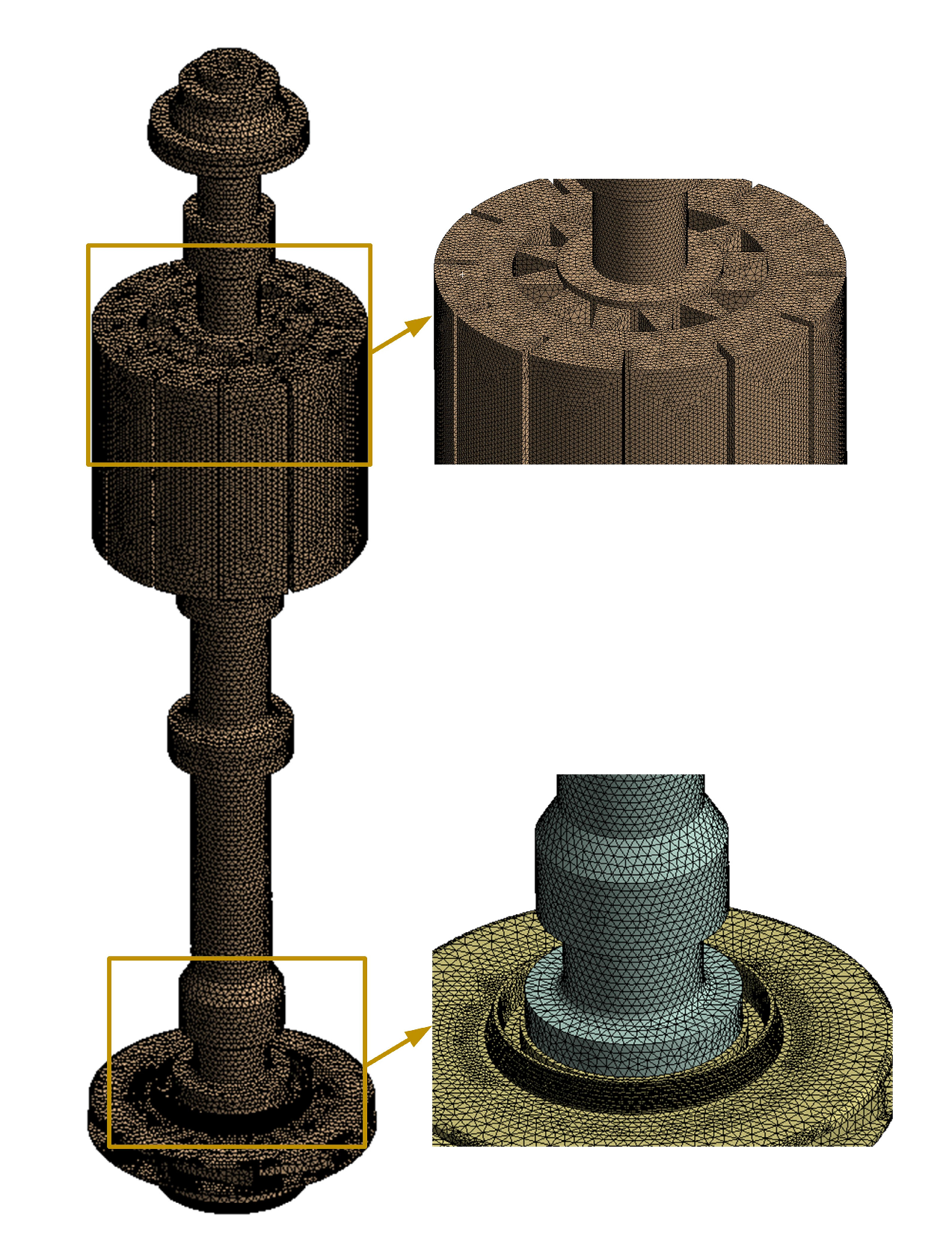
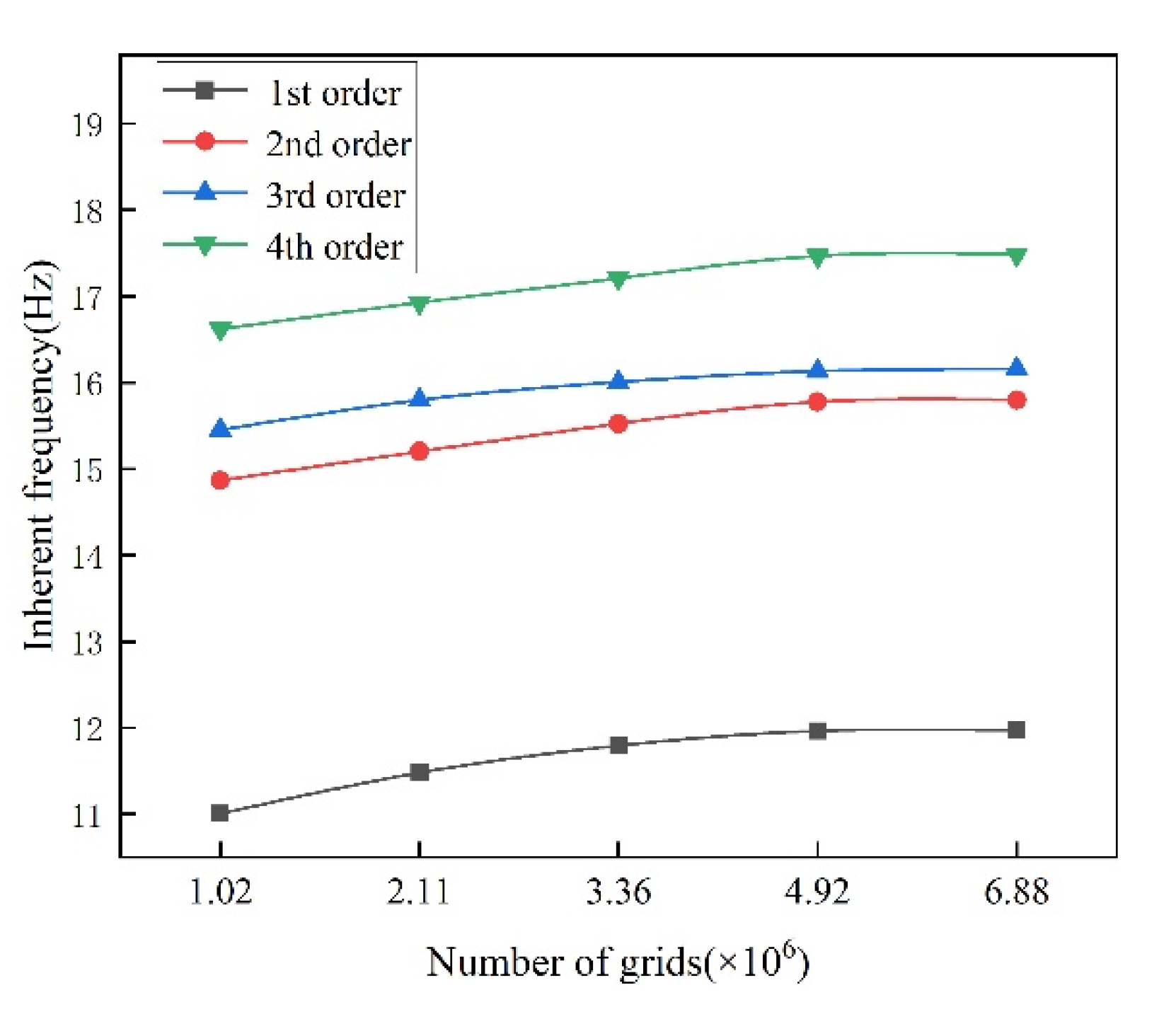
2.3. D Model and Mesh Model of the Rotor-Bearing EM System
3. Analysis of Unbalanced Magnetic Pull on the Rotor of a Pumped Storage Unit Generator
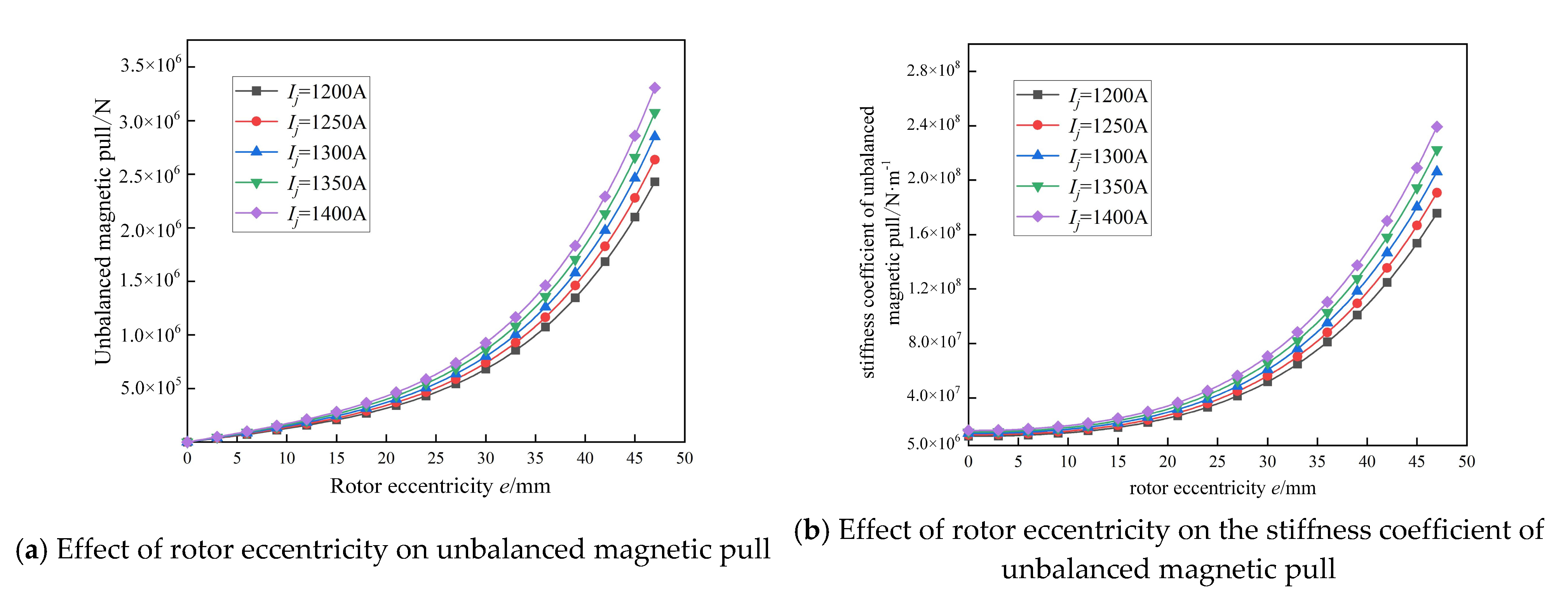
3.1. Effect of Rotor Eccentricity on Unbalanced Magnetic Pull
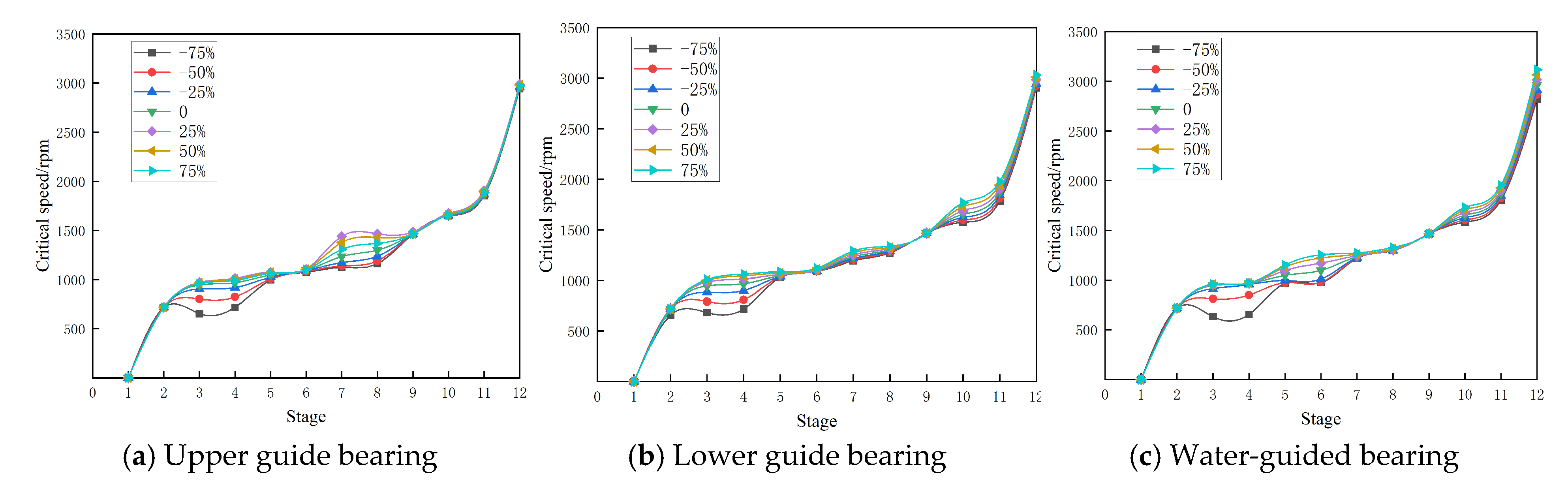
3.2. Influence of Bearing Stiffness on Critical Speed
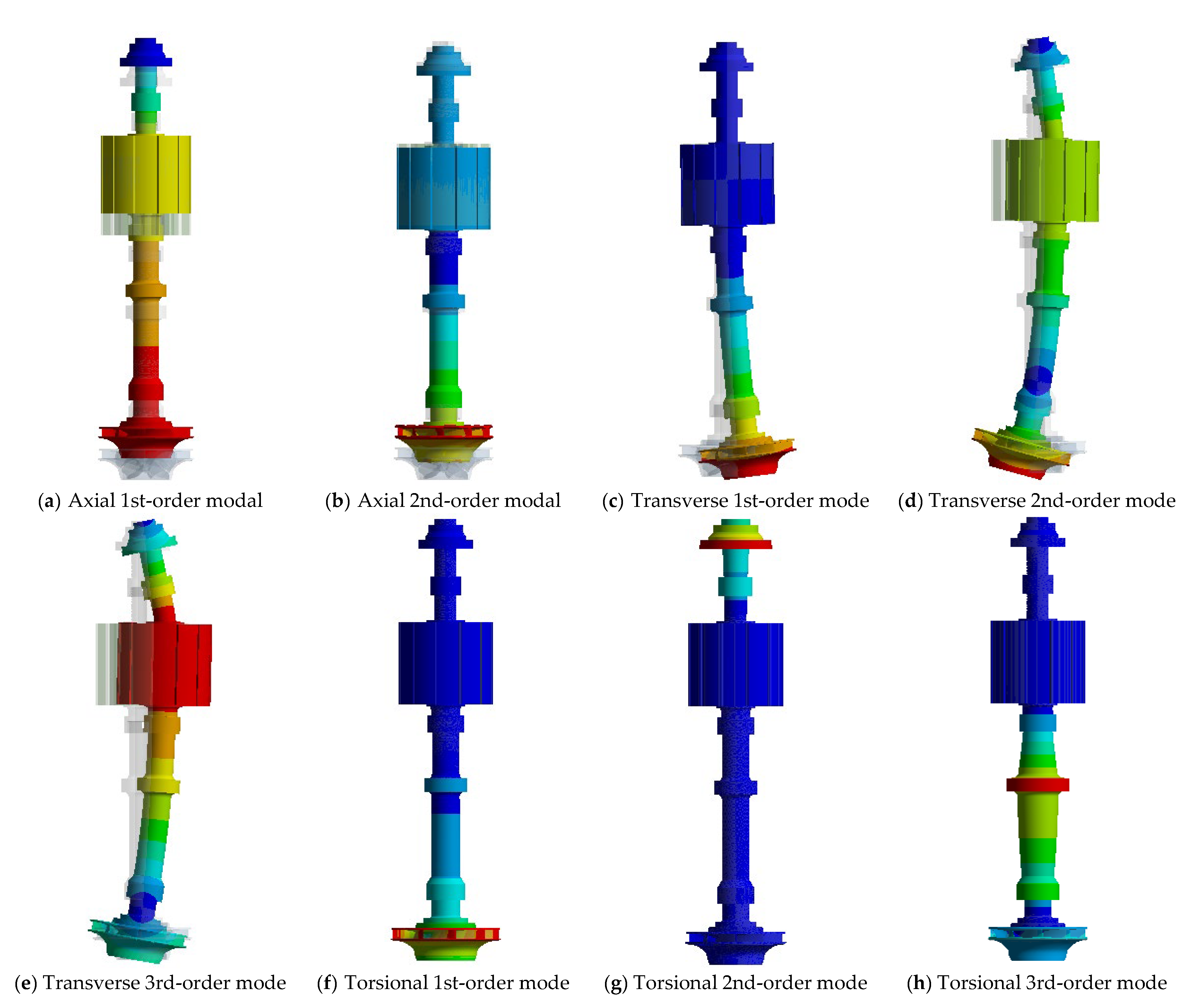
3.3. Effect of Unbalanced Magnetic Pull on the Dynamic Characteristics of Rotor Systems
4. Conclusions
- (1)
- The unbalanced magnetic pull increases non-linearly with the increase in excitation current and rotor eccentricity. During stable operation, the generator rotor vibration oscillation is small and the unbalance magnetic pull increases linearly. During the transition process, excessive rotor vibration may cause the rotor eccentricity to increase, and the unbalance magnetic pull increases with an obvious non-linear trend.
- (2)
- Changes in the stiffness coefficients of the upper guide bearing, lower guide bearing, and water guide bearing all have a significant effect on the critical speed of the rotor system at each stage. Changes in the stiffness coefficients of the three guide bearings have the greatest effect on the critical speed of the rotor system at the third and fourth stages, and the minimum bearing stiffness coefficients for stable operation of the different guide bearings of the rotor system are obtained.
- (3)
- The unbalanced magnetic tension has an impact on the intrinsic frequency of transverse oscillation in the first-order mode vibration pattern, with the intrinsic frequency amplitude dropping by 34.65%, which is lower than the rotational frequency of the unit, and strong vibration may occur during the unit load increase. The axial mode vibration pattern is characterized by up and down movements of different parts of the rotor system, the transverse mode vibration pattern is characterized by transverse oscillations of different parts, and the torsional mode is characterized by the radial enlargement or reduction in the generator rotor, runner, and coupling parts of the rotor system.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Feng, F.; Chu, F.; Zhang, Z.; Li, C. Analysis and Calculation of Dynamic Characteristics of the Shaft System of a Hydro-Turbine Generator Unit. J. Vib. Meas. Diagn. 1999, 3–9+68. [Google Scholar] [CrossRef]
- Zhai, L.; Yao, Z.; Huang, Q.; Yan, Z.; Wang, Z. 3D Dynamic Characteristics of Rotor System of Pump Storage Generator Set. Trans. Chin. Soc. Agric. Mach. 2014, 45, 107–111+137. [Google Scholar]
- Wang, T.; Wang, F. Critical Speeds and Vibration Modes of Shafting for High-Speed Permanent-Magnet Machines. Eng. Mech. 2012, 29, 264–269. [Google Scholar]
- Wang, Z.; Yu, J.; Fang, Y.; Wen, X.; Cao, J.; Shi, Q. The characteristic analysis of rotor dynamics of large hydraulic generating uint. J. Hydroelectr. Eng. 2005, 4, 62–66. [Google Scholar]
- Tenhunen, T.P.; Holopainen, A.A. Spatial linearity of an unbalanced magnetic pull in induction motors during eccentric rotor motions. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2003, 22, 862–876. [Google Scholar] [CrossRef] [Green Version]
- Holopainen, T.P.; Tenhunen, A.; Lantto, E.; Arkkio, A. Unbalanced magnetic pull induced by arbitrary eccentric motion of cage rotor in transient operation. Part 1: Analytical model. Electr. Eng. 2005, 88, 13–24. [Google Scholar] [CrossRef]
- Holopainen, T.P.; Tenhunen, A.; Lantto, E.; Arkkio, A. Unbalanced magnetic pull induced by arbitrary eccentric motion of cage rotor in transient operation. Part 2: Verification and numerical parameter estimation. Electr. Eng. 2005, 88, 25–34. [Google Scholar] [CrossRef]
- Guo, D.; Chu, F.; Chen, D. The Unbalanced Magnetic Pull and Its Effects On Vibration In a Three-Phase Generator With Eccentric Rotor. J. Sound Vib. 2002, 254, 297–312. [Google Scholar] [CrossRef]
- Subbiah, R.; Rieger, N.F. On the Transient Analysis of Rotor-Bearing Systems. J. Vib. Acoust. Stress Reliab. Des. 1988, 110, 515–520. [Google Scholar] [CrossRef]
- Bhat RBSubbiah RSankar, T.S. Dynamic Behavior of a Simple Rotor with Dissimilar Hydrodynamic Bearings by Modal Analysis. J. Vib. Acoust. Stress Reliab. Des. 1985, 107, 267–269. [Google Scholar] [CrossRef]
- Subbiah RBhat RBSankar, T.S. Response of Rotors Subjected to Random Support Excitations. J. Vib. Acoust. Stress Reliab. Des. 1985, 107, 453–459. [Google Scholar] [CrossRef]
- Wang, T.; Wang, F.; Bai, H.; Cui, H. Stiffness and Critical Speed Calculation of Magnetic Bearing-rotor System Based on FEA. In Proceedings of the 11th International Conference on Electrical Machines and Systems, Wuhan, China, 17–20 October 2008; Volume 2, pp. 75–78. [Google Scholar]
- Wei, F.; Zhang, K.; Liu, Z.; Liu, B.; Zhang, H.; Mei, J.; Wu, L. Modeling and analysis of unbalanced magnetic pull in synchronous motorized spindle considering magneto-thermal coupling. Int. J. Appl. Electromagn. Mech. 2022, 70, 303–321. [Google Scholar]
- Ma, C.; Zhao, D.; Liao, W.; Sun, W.; Guo, P.; Xu, Y. Effect of the unbalanced magnetic pull force and oil-film force on nonlinearity of a dual-rotor bearing system. Proc. Inst. Mech. Eng. Part K: J. Multi-Body Dyn. 2022, 236, 623–638. [Google Scholar] [CrossRef]
- Huang, L.; Shen, G.; Hu, N.; Chen, L.; Yang, Y. Coupled Electromagnetic-Dynamic Modeling and Bearing Fault Characteristics of Induction Motors considering Unbalanced Magnetic Pull. Entropy 2022, 24, 1386. [Google Scholar] [CrossRef]
- Zhang, L.; Ma, Z.; Song, B. Characteristics Analysis of Hydroelectric Generating Set under Unbalanced Magnetic Pull and Sealing Force of Runner. Water Resour. Power 2010, 28, 117–120. [Google Scholar]
- Song, Z.; Ma, Z. Nonlinear vibration analysis of an eccentric rotor with unbalance magnetic pull. J. Vib. Shock 2010, 29, 169–173+250. [Google Scholar] [CrossRef]
- Perers, R.; Lundin, U.; Leijon, M. Saturation Effects on Unbalanced Magnetic Pull in a Hydroelectric Generator With an Eccentric Rotor. IEEE Trans. Magn. 2007, 43, 3884–3890. [Google Scholar] [CrossRef]
- Perers, R.; Lundin, U.; Leijon, M. Development of synchronous generators for Swedish hydropower: A review. Renew. Sustain. Energy Rev. 2005, 11, 1008–1017. [Google Scholar] [CrossRef]
- Wallin, M.; Lundin, U. Dynamic Unbalanced Pull from Field Winding Turn Short Circuits in Hydropower Generators. Electr. Power Compon. Syst. 2013, 41, 1672–1685. [Google Scholar] [CrossRef]
- Wallin, M.; Bladh, J.; Lundin, U. Damper Winding Influence on Unbalanced Magnetic Pull in Salient Pole Generators With Rotor Eccentricity. IEEE Trans. Magn. 2013, 49, 5158–5165. [Google Scholar] [CrossRef]
- Wallin, M.; Ranlof, M.; Lundin, U. Reduction of Unbalanced Magnetic Pull in Synchronous Machines due to Parallel Circuits. IEEE Trans. Magn. 2011, 47, 4827–4833. [Google Scholar] [CrossRef]
- Nave, O.; Sharma, M. Singular Perturbed Vector Field (SPVF) Applied to Complex ODE System with Hidden Hierarchy Application to Turbocharger Engine Model. Int. J. Nonlinear Sci. Numer. Simul. 2020, 21, 99–113. [Google Scholar] [CrossRef]
- Pang, J.; Liu, H.; Liu, X.; Yang, H.; Peng, Y.; Zeng, Y.; Yu, Z. Study on sediment erosion of high head Francis turbine runner in Minjiang River basin. Renew. Energy 2022, 192, 849–858. [Google Scholar] [CrossRef]
- Shi, D. Calculation of UMP and Analysis of Rotor Dynamic Characteristics of Large Induction Motor; Harbin University of Science and Technology: Harbin, China, 2016. [Google Scholar]
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Generator stator radius R0/m | 2.45 | Air gap fundamental magnetic momentum coefficient ki | 7 |
| Rotor radius of generators R/m | 2.403 | Air magnetic permeability μ0 | 4π × 10−7 |
| Rotor length of generators L/m | 3.665 | Excitation current Ij/A | 1200–1400 |
| Average length of air gap δ0/m | 0.047 | Eccentric distance of generator rotor e/mm | 0–47 |
| Components | Materials | Density/(kg/m3) | Modulus of Elasticity/Pa | Poisson’s Ratio |
|---|---|---|---|---|
| Coils | Copper | 8900 | 1.15 × 109 | 0.33 |
| Magnetic yoke poles | Magnetic yoke materials | 7830 | 2.06 × 109 | 0.3 |
| Other | steel | 7850 | 2.10 × 1011 | 0.3 |
| Modal | Number of Steps | No Consideration of Unbalanced Magnetic Pull | Consideration of Unbalanced Magnetic Pull (e = 5 mm) | Consideration of Unbalanced Magnetic Pull (e = 15 mm) | Consideration of Unbalanced Magnetic Pull (e = 46.5 mm) | |||
|---|---|---|---|---|---|---|---|---|
| Values (Hz) | Values (Hz) | Deviation/% | Values (Hz) | Deviation/% | Values (Hz) | Deviation/% | ||
| Axial | 1 | 15.778 | 12.017 | −23.86 | 12.017 | −23.86 | 12.017 | −23.86 |
| 2 | 89.321 | 90.437 | 1.25 | 90.437 | 1.25 | 90.437 | 1.25 | |
| Horizontal | 1 | 11.966 | 7.82 | −34.65 | 7.82 | −34.65 | 7.82 | −34.65 |
| 2 | 16.136 | 16.079 | −0.35 | 16.064 | −0.45 | 15.661 | −2.94 | |
| 3 | 17.477 | 16.369 | −6.34 | 16.351 | −6.44 | 15.886 | −9.10 | |
| Turning | 1 | 24.443 | 24.595 | 0.62 | 24.595 | 0.62 | 24.595 | 0.62 |
| 2 | 56.331 | 56.657 | 0.58 | 56.657 | 0.58 | 56.657 | 0.58 | |
| 3 | 133.04 | 134.770 | 1.3 | 134.77 | 1.3 | 134.77 | 1.3 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, W.; Pang, J.; Liu, X.; Zhao, W.; Lu, Z.; Yan, D.; Zhou, L.; Wang, Z. Effect of Unbalanced Magnetic Pull of Generator Rotor on the Dynamic Characteristics of a Pump—Turbine Rotor System. Water 2023, 15, 1120. https://doi.org/10.3390/w15061120
Wu W, Pang J, Liu X, Zhao W, Lu Z, Yan D, Zhou L, Wang Z. Effect of Unbalanced Magnetic Pull of Generator Rotor on the Dynamic Characteristics of a Pump—Turbine Rotor System. Water. 2023; 15(6):1120. https://doi.org/10.3390/w15061120
Chicago/Turabian StyleWu, Weidong, Jiayang Pang, Xuyang Liu, Weiqiang Zhao, Zhiwei Lu, Dandan Yan, Lingjiu Zhou, and Zhengwei Wang. 2023. "Effect of Unbalanced Magnetic Pull of Generator Rotor on the Dynamic Characteristics of a Pump—Turbine Rotor System" Water 15, no. 6: 1120. https://doi.org/10.3390/w15061120








