A Deforming Mixed-Hybrid Finite Element Model for Robust Groundwater Flow Simulation in 3D Unconfined Aquifers with Unstructured Layered Grids

Abstract

Determining the water table shape and position in unconfined aquifers is fundamental to many groundwater flow assessment studies. The commonly used industry-standard fixed mesh models, contrary to popular belief, do not provide an accurate description of the phreatic surface. When using such models, the water table position is post-processed from the simulated groundwater heads, leading to an approximation error. This error becomes larger for coarse vertical grids. This paper introduces a novel moving mesh technique to simulate the groundwater table in three-dimensional unconfined aquifers under steady-state or transient conditions. We adopt the face-based mixed-hybrid finite element discretization approach in space, leading to a more accurate approximation of the specific discharge field. The model uses an adaptive unstructured but layered mesh which is iteratively adjusted until its top fits the phreatic surface. The developed algorithm accounts for a linearized form of the kinematic boundary condition prescribed on the moving boundary and also supports usual boundary conditions as well. The model was compared to the existing analytical, fixed mesh, and previously published solutions. The obtained results show that the developed model is superior in terms of its numerical stability, convergence behavior, and accuracy. Furthermore, the simulated phreatic surface is free from a cellwise interpolation error and independent of the vertical grid size as used in fixed mesh methods. We also found that the robustness of the moving mesh method cannot be surpassed by a fixed mesh alternative. The model’s efficiency is supported by an almost quadratic rate of convergence of the outer iteration loop.

1. Introduction

Nearly half of the world population is supplied by groundwater aquifers [1], while the percentage of the U.S. population relying exclusively on groundwater is estimated to be between 40% and 50% [2]. Groundwater flow modeling is a widespread technique to sustainably manage these resources [3]. Indeed, many groundwater modeling tools are readily available [4,5]. The numerical modeling of groundwater flow in unconfined aquifers is much more involved than in confined aquifers. This is because the governing equation (i.e., Richard’s equation) is highly nonlinear and is subject to nonlinear boundary conditions as well. The nonlinearity in Richard’s equation is related to the dependence of the relative permeability and the water retention in the unsaturated zone on the pressure head [6,7]. Moreover, fully saturated models are typically associated with boundary conditions such as constant head, pumping/injection flow rates, and leakage flux through a semi-confining bed. These are essentially linear and do not pose additional challenges to standard numerical solution techniques. This is not the case for unconfined flow models where some boundary conditions are nonlinear and therefore are unknowns a priori; thus, they are an integral part of the numerical solution. A typical example is the free and moving water table boundary. Another complication in modeling unconfined groundwater flow is to locate the position of seepage faces when the water table reaches the land surface. The seepage boundary faces are not known prior to the numerical solution and are, therefore, not fixed as typically done with other boundary conditions. Additionally, wells pumping groundwater from unconfined aquifers might become dry as the water table drops below the well screens, and natural or artificial drains may stop draining groundwater as the levels drop below predefined elevations. These are typical examples that necessitate additional bookkeeping procedures during the nonlinear iterative solution process when solving for an unconfined groundwater flow model.

Natural groundwater flow occurs mostly in highly heterogeneous and anisotropic materials, thus increasing the nonlinearity of the resulting discrete algebraic systems of the equations. Hence, robust and advanced numerical methods are needed in this context.

For unconfined aquifers, a decision has to be, very often, made for the choice of the groundwater modeling approach. The most rigorous approach selects a numerical discretization of Richard’s equation which explicitly accounts for the processes in the unsaturated zone (Figure 1B). These are, for instance, the occurrence of a capillary barrier above the saturated zone where the soil moisture is variably distributed, and gravity routing of infiltrated surface water to confined storage. The second choice is to use an approach that simplifies the underlying physics in the porous medium. Hence, the water table is viewed as a sharp interface whose position in space and time is sought, and the flow in the unsaturated zone is neglected. The last approach, although not free from limitations, is by far the most used in practice when dealing with regional-scale modeling studies. This is because the more detailed and accurate approach requires much more field data which are frequently not available on a large scale. Hence, groundwater modeling of the unsaturated zone is, very often, performed on a local scale of a site where experimental data are available. For some projects, the two approaches might advantageously be used concurrently to understand the local behavior in the unsaturated zone, thus enabling a better parametrization of an unconfined flow model built with the simplified approach. This paper deals exclusively with the second approach; modeling the unsaturated zone will not be discussed further.

Modeling unconfined groundwater flow subject to free and moving boundaries is performed using two broad classes of methods. The first category assumes a fixed mesh as illustrated in Figure 1C. Within this class, an algorithm should determine the spatial and temporal distribution of three types of cells: wet, dry, and partially wet cells (i.e., crossed by the water table). The second category considers a moving mesh that adapts to the dynamics of the water table boundary (Figure 1D). Hence, unlike for a fixed mesh method, the dry zone (i.e., approximate unsaturated zone) is not part of the computational domain. The main advantage of an adaptive mesh technique is to solve a saturated groundwater flow equation, hence a linear system of algebraic equations, during each iteration of the mesh adaption process. Meanwhile, more elaborate algorithms are needed for mesh adaption and the interpolation of hydraulic properties between moving cells.

The fixed mesh approach is probably the most widespread owing to the availability of many computer implementations such as MODFLOW developed by the USGS [4,8,9]. Legacy versions of MODFLOW [8] were criticized for an unphysical representation of unconfined groundwater flow dynamics, leading to a numerical instability for highly nonlinear problems [10,11]. This was due, in part, to the heuristics upon which the decision to rewet a previously dry cell are based. Second, Picard iteration for some highly nonlinear problems may converge at a very slow rate or not at all. The latest releases include, however, a new Newton–Raphson-based formulation that substantially improves the computational stability [4,9]. Another known difficulty within the fixed mesh approach derives from the way to artificially hide the flow patterns in the dry cells. Because this is not possible as the mesh is fixed, different approaches have been developed to tackle this problem. Desai [12] developed a two-dimensional finite element model that linearizes the relative permeability function and recast it as a function of hydraulic head. The same approach was used by [13,14] in the framework of three-dimensional finite element models. Other authors [15] used a sharp representation of this function; that is, the hydraulic conductivity in all dry cells is multiplied by a small residual factor (i.e., $~$10⁻²–10⁻³). New developments presented the numerical solution of 3D unconfined seepage problems with the smoothed finite element method borrowed from solid mechanics [16]. A limitation of the fixed mesh approach is that the exact position and shape of the water table could only be determined by post-processing computed groundwater heads. Hence, it is expected that a moving mesh technique will always lead to a more accurate position and a smooth shape of the phreatic surface when compared with a fixed mesh approach using the same resolution.

The second class of methods solve a series of linear equations on a deforming mesh. The mesh is adapted iteratively to fit the water table position. Here, again, many sub-approaches have been developed that could be categorized as rigorous or simplified. As described in standard textbooks [6], the phreatic surface does not only fulfill the zero-pressure condition, but it is a kinematic boundary condition too. In other words, it is an interface through which the effects of unconfined storage, net recharge, and nonlinear effects related to the changing shape of the surface geometry are balanced. To the best of our knowledge, the only published numerical model taking into account both conditions was presented by [10]. As we will demonstrate later, even under steady-state conditions, the kinematic boundary condition cannot be neglected.

Previous works in the literature using a moving mesh approach were developed using standard finite difference (FDM), finite volume (FVM), and finite element (FEM) methods. This is because, within a FDM framework, the grid should remain orthogonal and fixed, so the groundwater flow equation is rewritten in a rectangular computational domain using a coordinates transformation technique. An example of this is the so-called boundary-fitted coordinates (BFC) method [17,18]. The same method was also used by [10] for an application to the Delaware Basin of south-eastern New Mexico. This approach leads to a transformed groundwater flow equation which is of the advection-diffusion type, leading to more computational storage as the resulting system matrix is unsymmetric. Additionally, the numerical solution of this equation type is not only more involved than the standard groundwater flow equation, but it sounds unnatural to many groundwater modelers. Another method’s disadvantage is using ghost cells close to the water table boundary because it is not possible to discretize the kinematic condition exactly on the phreatic surface.

Owing to the limitations of the FDM method, the standard FEM is a more attractive alternative. An FEM-based moving mesh approach has been introduced by [19,20] for groundwater applications for the first time. A two-dimensional cross-section model using triangular finite elements was developed for heterogeneous alluvial aquifers and applied to simulating irrigation and drainage in California’s western San Joaquin Valley [21]. In this model, the stratigraphic domain was cut from the top along the new position of the water table curve, and the updated computational domain was re-meshed prior to finding a new groundwater head distribution. In [22], a nonlinear programming minimization algorithm was coupled with an adaptive finite element procedure to determine the location of the phreatic line in earth dams. This model solves a steady-state two-dimensional seepage problem using bilinear triangular finite elements. A parallel three-dimensional adaptive mesh finite element model was presented for a steady-state unconfined flow in subsurface aquifers [23]. An initially coarse unstructured mesh is iteratively adapted along the horizontal direction to refine the mesh in areas of a high hydraulic gradient, but also along the vertical direction to fit the upper slice of the mesh to the phreatic surface.

In [24], a moving curvilinear finite volume grid was used for solving steady-state seepage flow in two-dimensional homogeneous and isotropic earth dams subject to nonlinear boundary conditions. The developed algorithm was favorably validated against the experimental results.

As described earlier, solving unconfined groundwater flow with a moving mesh technique using a finite difference method has some limitations. These problems do not exist when using a conforming (i.e., nodal-based) finite element technique such as the Galerkin weighted residual approach [25,26]. However, while the groundwater head and the water table shape obtained by the conforming FEM using a moving mesh method might be accurate, it is well known that this is not the case for the specific discharge field. Moreover, the conforming FEM is not exactly mass conservative, which is problematic for nodes sharing elements with a high contrast of hydraulic conductivities. Post-processing techniques were introduced to derive continuous nodal-specific discharge fields, but it was reported that this procedure has a high computational cost [27,28,29,30]. Mixed finite element methods were introduced to simultaneously approximate a scalar variable and its first-order derivative fields [31]. Promising results highlighting a higher accuracy of this approximation technique when compared with alternative techniques were obtained for flow problems [32]. The mixed finite element method leads, however, to an indefinite system of algebraic equations which is difficult to solve with direct or iterative methods. A hybridization technique avoids this problem by reformulating the mixed problem with primary unknowns on the faces of the mesh and using local algebraic relationships to recover the cell-centered heads and the normal specific discharge components [33]. This gives rise to a method formally known as the mixed-hybrid finite element method (MHFEM). Previous works established the outstanding behavior of this method to tackle groundwater flow problems in highly heterogeneous and anisotropic formations [28,34,35]. While the MHFEM approximation was used for many classes of groundwater flow problems such as unsaturated flow [36,37,38,39] and two-phase flow [40,41], to the best of the authors’ knowledge, this is the first time that it has been used in combination with a deforming mesh approach to solve an unconfined flow in phreatic aquifers.

The objective of this paper is to introduce a new state-of-the-art three-dimensional MHFEM numerical model for confined–unconfined groundwater flow in complex aquifer systems characterized by irregular geometries, heterogeneous and anisotropic materials, and nonlinear boundary conditions of a practical relevance. These include, in particular, the nonlinear kinematic and seepage face boundary conditions generally ignored or weakly dealt with in previous studies. The model formulation and numerical discretization on layered unstructured grids are presented in detail in the next sections. Several theoretical and realistic examples are provided to demonstrate the model’s accuracy, efficiency, and capability to successfully simulate unconfined groundwater flow with a moving mesh technique.

The manuscript is organized as follows. We start by exposing the theory of unconfined groundwater flow in a deforming mesh, namely, how the free and moving boundary conditions are formulated in this particular case. The next section shows the discrete form of the three-dimensional mixed-hybrid finite element model when a moving mesh approach is used. Notably, the numerical implementation of the associated boundary conditions, which is tricky in some cases, is presented in sufficient detail. Section 4 presents the numerical algorithm that iteratively solves a steady-state or transient unconfined flow problem with a deforming mesh. The next section validates the developed model on a series of available analytical and numerical solutions of an increasing complexity. They demonstrate the model’s accuracy, efficiency, robustness, and applicability to a wide range of hydrogeological problems typically encountered in practice. Finally, a summary and concluding remarks section closes the paper.

2. Theory

When modeling unconfined groundwater flow in three-dimensions using a moving mesh approach, there are two domains of interest. The first is the stratigraphic domain (known also as the physical or geological model) where the hydrogeological units and their hydraulic properties are defined. The second is the moving computational domain where the top surface is adjusted to fit the unknown water table position. The stratigraphic domain is inherently static and is used mainly in the background to map the hydraulic properties into the deforming domain when needed. One advantage of the moving mesh approach is to solve a series of linear problems on the deforming domain using a saturated flow equation. The non-linearity is, therefore, moved from the governing equation to the process of mesh adaption.

2.1. Governing Equations

The governing equation for confined groundwater flow in the porous medium filling the deforming domain is presented as in [6,7]:

$$S_p\frac{\partial h}{\partial t}+\nabla .\mathit{q}={\mathit{q}}_s$$

(1)

where $S_p$ [L⁻¹] is the specific storage coefficient, $h$ [L] is the hydraulic head, $t$ [T] is the time, ${\mathit{q}}_s$ [T⁻¹] denotes the source/sink strength term positive for sources and negative for sinks, $\nabla$ [L⁻¹] is the differential operator, and $\mathit{q}$ [LT⁻¹] is the specific groundwater discharge, following Darcy’s law:

$$\mathit{q}=-K.\nabla h$$

(2)

where $K$ [LT⁻¹] is the hydraulic conductivity tensor. In the presented model, we use a full tensor for each soil type in the stratigraphic domain:

$$K=\left[\begin{array}{ccc}{k}_{xx}& k_{xy}& k_{xz}\\ k_{yx}& k_{yy}& k_{yz}\\ k_{zx}& k_{zy}& k_{zz}\end{array}\right]$$

(3)

Supporting a full hydraulic conductivity tensor allows for modeling of the groundwater flow in cases where the stratigraphic domain is highly heterogeneous and anisotropic, but also in the frequent situation where there is a mismatch between the scales of the geological model and the computational domain. Using static or dynamic upscaling approaches may produce non-zero off-diagonal equivalent hydraulic conductivities even if the original (i.e., fine scale) hydraulic conductivity tensor is aligned with the principal directions [42].

By inserting Equation (2) in Equation (1), we obtain the governing equation for three-dimensional groundwater flow in the heterogeneous and anisotropic deforming domain:

$$S_p\frac{\partial h}{\partial t}=\nabla .\left(K.\nabla h\right)+{\mathit{q}}_s$$

(4)

This equation is subject to the initial and boundary conditions of Dirichlet, Neumann, and Cauchy types, as will be further discussed in the next subsection.

2.2. Boundary Conditions

In the framework of a moving mesh approach, some boundary conditions require a special treatment. The conceptual approaches behind such boundary conditions when using the fixed mesh approach are discussed in many references [3,4,8]. Special attention is paid to these boundary conditions because they are part of the solution and, second, they affect the final solution inside the computational domain. The numerical implementation of these boundary conditions is discussed in the following section once the discrete numerical model has been obtained.

2.2.1. Phreatic Surface

The sharp phreatic surface, ${\Gamma }_{WT}$, delimiting the water and air phases, is of special interest here. This is because the shape and location of this interface is unknown a priori. Hence, additional constraints on the free surface are needed. The theory of unconfined groundwater flow [6] (pp. 252–259) stipulates the existence of two distinct boundary conditions. The first states that the pressure at the water table is atmospheric, hence:

$$h\left(x,y,z_{WT},t\right)=z_{WT}\left(x,y,t\right)$$

(5)

where $z_{WT}$ [L] is the water table elevation. Second, the kinematic boundary condition is a statement of the continuity of the mass flux across the phreatic surface. According to [6], it is provided as:

$$S_y\frac{\partial h}{\partial t}=\left(K.\nabla h+N\right).\nabla \left(h-z\right)$$

(6)

where $S_y$ [L⁻¹] is the specific yield and $N\left(x,y,t\right)=-N\nabla z$ [LT⁻¹] is the flux associated with net recharge (i.e., inflows such as recharge minus outflows such as evapotranspiration) across the surface. The kinematic condition is nonlinear, owing, first, to the occurrence of the quadratic terms in $\nabla h$ and, second, because the conductivity coefficients depend upon the location of the water table inside the stratigraphic domain. It indicates that the flux vector across the water table is not entirely vertical. It is a combination of linear and nonlinear flux terms. The nonlinearity derives from the changing shape of the deforming computational domain volume. A direct numerical discretization of Equation (4) subject to boundary conditions (5) and (6), in particular, increases the model’s nonlinearity and impacts its efficiency. Alternatively, we use a linearized version of Equation (6) borrowed from Dagan [43] that was used also by Neuman [44]:

$$S_y\frac{\partial h}{\partial t}=-\left(K_z+N\right)\frac{\partial h}{\partial z}+N$$

(7)

where $K_z$ is the vertical component of a diagonal hydraulic conductivity tensor. The linearized flux in Equation (7) does not only neglect the quadratic terms, but it also neglects the horizontal flux components because a diagonal hydraulic conductivity tensor was adopted to derive this expression. The simplified kinematic boundary condition in Equation (7) stipulates that the head rate of change at the water table equals $N/S_y$, excluding a term which is proportional to the vertical hydraulic gradient $\partial h/\partial z$.

When a full hydraulic conductivity tensor is used as adopted herein, the development of Equation (6), while still neglecting the quadratic terms, yields:

$${\mathit{q}}_z=-N+N\frac{\partial h}{\partial z}+S_y\frac{\partial h}{\partial t}$$

(8)

$${\mathit{q}}_z=-\left(K_{zx}\frac{\partial h}{\partial x}+K_{zy}\frac{\partial h}{\partial y}+K_{zz}\frac{\partial h}{\partial z}\right)$$

(9)

where ${\mathit{q}}_z$ is the vertical component of the specific discharge vector. Equation (8) relates the vertical specific discharge to net recharge, the vertical hydraulic head gradient, and the unconfined storage owing to the water table displacement. This is in sharp contrast to an unconfined flow model relying on a fixed mesh where ${\mathit{q}}_z$ would be, naturally, equal to $-N$. Prescribing the net recharge flux for a moving mesh approach in this way would result in an erroneous estimation of the specific discharge at the interface. This error equals to $\left|N\frac{\partial h}{\partial z}+S_y\frac{\partial h}{\partial t}\right|$, which accounts for contributions from the vertical hydraulic head gradient and the unconfined storage. It vanishes only in the particular case when considering a steady-state regime with a zero net recharge.

Under steady-state conditions, Equation (8) becomes:

$${\mathit{q}}_z=-N+N\frac{\partial h}{\partial z}$$

(10)

enforcing the vertical specific discharge component to scale with the net recharge across the water table interface. Here, again, prescribing the recharge directly on the moving water table would result in an erroneous estimation of the vertical flux component of the specific discharge.

The form of the kinematic condition provided in Equation (8) is suitable for a face-based finite element technique such as the mixed-hybrid finite element method. The numerical implementation of the kinematic condition is described in detail in the next section.

2.2.2. Seepage Face

Another complication arises when modeling unconfined flow with a moving water table approach. Rising groundwater levels may seep through the land surface as often happens in earth dams and trench drains. This interaction between the free-surface and the basin topography is approached using the seepage boundary condition [6]:

$$h\left(x,y,z_{WT},t\right)=z_{TOP}\left(x,y\right)$$

(11)

where $z_{TOP}$ [L] is the land surface elevation. This is essentially a switching Dirichlet boundary condition that applies to a set of unknown locations, adding further nonlinearity to the model. Indeed, a numerical implementation iteratively checks for the occurrence of this condition. When the computed free-surface elevation is above $z_{TOP}$, Equation (11) replaces Equations (5) and (8) as they apply only when the water table is below the land surface. The kinematic condition provided by Equation (8) is not prescribed at seepage faces. The complete numerical implementation of the seepage face boundary conditions is provided in the next section. The numerical treatment of seepage faces is identical under steady-state and transient conditions.

2.2.3. Recharge

The downward recharge flux, $RE\left(x,y,t\right)$ [LT⁻¹], is prescribed directly on the moving water table boundary, as presented in Equations (8) and (10), for transient and steady-state regimes, respectively. Under transient conditions, the recharge may take a non-negligible time to reach the saturated zone from the land surface. This is known as the unsaturated zone time lag, $t_u\left(x,y\right)$, which is site-specific and depends on many parameters, such the water table depth, layered heterogeneity in the unsaturated zone, rainfall intensity, crops water demand, etc. Many approaches have been developed in the literature [45,46,47] to provide first-order estimates of this parameter which can be provided as a model input to delay the recharge flux prescribed at the horizontal coordinates $\left(x,y\right)$ and time $t$ as $RE\left(x,y,t-t_u\left(x,y\right)\right)$. Obviously, a delayed recharge flux is not needed under steady-state conditions. Based on observed rainfall and water levels time series in six chalk aquifers, ref. [48] concluded that for shallower water tables, a linear relationship exists between the lag time and the depth to the water table. In [49], simple analytical methods based on a steady-state assumption and rigorous one-dimensional transient simulations were compared to assess the travel time in unsaturated zone profiles. The authors found that none of the results obtained with the simplified methods matched the transient simulations.

2.2.4. Evapotranspiration

The evapotranspiration flux, $ET(x,y,t$) [LT⁻¹], is prescribed directly on the moving water table boundary, such that the net recharge in Equations (8) and (10) is $N=RE-ET$. This condition is characterized by two conceptual parameters. The extinction elevation, $z_{EXT}$, below which evapotranspiration from the water table ceases. Next, the ET surface elevation, $z_{ET}>z_{EXT}$, above which the evapotranspiration loss from the water table occurs at a fixed rate, $E{T}_{max}$. In between, it is assumed that the $ET$ flux varies linearly with the water table elevation. Hence,

$$ET\left(x,y,t\right)=\{\begin{array}{cc}0\hfill & \hfill z_{WT}\le z_{EXT}\\ \frac{z_{WT}-z_{EXT}}{z_{ET}-z_{EXT}}E{T}_{max}\hfill & \hfill z_{EXT}<z_{WT}<z_{ET}\\ E{T}_{max}\hfill & \hfill z_{WT}\ge z_{ET}\end{array}$$

(12)

2.2.5. Pumping and Injection Wells

Any vertical well is provided by the top, $z_{top}^w$, and bottom, $z_{\mathit{b}ot}^w$, vertical positions of the strainer. The prescribed flow rate, $Q_w$ [L³T⁻¹], depends on the position of the water table relative to the well screen. When the water table position is higher than $z_{top}^w$, the flow rate is distributed among the formations perforated by the well screen; otherwise, when it intersects, the well screen length the flow rate is distributed among the formations lying between the water table position and the bottom of the well screen. A third case corresponds to the situation when the water table is below the bottom of the well screen, leading to shutting-down the well (i.e., $Q_w=0$). Additionally, we have implemented an option for a gradual decrease in the prescribed flow rate of a pumping well when the water table position starts to decrease below a threshold elevation, $z_{thr}^w, (z_{\mathit{b}ot}^w<z_{thr}^w<z_{top}^w)$, as was introduced in [9]. To summarize, the well boundary condition is formulated as follows:

$$Q_w=\{\begin{array}{cc}{f}_Q{Q}_w^0\hfill & \hfill Q_w^0<0\\ Q_w^0\hfill & \hfill Q_w^0>0\end{array}$$

(13)

$$f_Q=\{\begin{array}{cc}{s}_w{}^2\left(-\frac{2}{{\zeta }^3}{s}_w+\frac{3}{{\zeta }^2}\right)\hfill & \hfill z_{\mathit{b}ot}^w\le z_{WT}\le z_{thr}^w\\ 1\hfill & \hfill z_{WT}>z_{thr}^w\\ 0\hfill & \hfill z_{WT}<z_{\mathit{b}ot}^w\end{array}$$

(14)

where $Q_w^0$ is the initially prescribed flow rate, $f_Q$ is a flow rate scaling factor for a pumping well, $s_w=z_{WT}-z_{\mathit{b}ot}^w$ is the saturated length in the well, and $\zeta =z_{thr}^w-z_{\mathit{b}ot}^w$ is the critical well length triggering a declining pumping flow rate.

2.2.6. River

The conceptualization of river–aquifer interactions assumes that a gaining or losing reach of the river is characterized by three constant parameters defining flow into or from the aquifer through a leaky riverbed layer. These are the river stage, $h_R$, the bottom elevation of the riverbed layer, $z_{RB}$, and the hydraulic conductance of the riverbed material, $C_R$. When the water table elevation is above $z_{RB}$, flow is directed towards the river using a mixed boundary condition where the negative flow rate depends linearly on the water table elevation. Otherwise, the flow rate $Q_R$ is directed towards the aquifer and a constant positive flow rate is prescribed at the water table directly, such that $N=RE-ET+Q_R$ is just beneath the riverbed. To sum up, this boundary condition is expressed as:

$$Q_R=\{\begin{array}{cc}{C}_R\left(h_R-z_{WT}\right)\hfill & \hfill z_{WT}>z_{RB}\\ C_R\left(h_R-z_{RB}\right)\hfill & \hfill z_{WT}\le z_{RB}\end{array}$$

(15)

An inherent assumption when the water table is below the riverbed is that the depth of the unsaturated zone is relatively thin, such that surface water enters the aquifer without a significant delay. Otherwise, similar to the recharge condition, we can estimate the unsaturated zone time lag, and, consequently, the time-dependent flow rate, $Q_R$, is delayed.

2.2.7. Drain

The conceptualization of aquifer drainage using natural or artificial structures is somewhat similar in nature to the preceding condition type. A mixed boundary condition is usually adopted to estimate a drain flow rate, $Q_{DRN}$, coming from the aquifer as the water table elevation remains above the drain elevation $z_{DRN}$. When the water table elevation drops below the drain, this one exerts no action on the groundwater flow such that $Q_{DRN}=0$. A mathematical statement of this condition reads:

$$Q_{DRN}=\{\begin{array}{cc}{C}_{DRN}\left(z_{DRN}-z_{WT}\right)\hfill & \hfill z_{WT}>z_{DRN}\\ 0\hfill & \hfill z_{WT}\le z_{DRN}\end{array}$$

(16)

where $C_{DRN}$ is the hydraulic conductance of the drain.

3. The Discrete Moving Mesh Model

3.1. Mixed-Hybrid Finite Element Approximation (MHFEM)

We consider a spatial discretization of the groundwater flow, in Equation (4), using a mixed-hybrid finite element approximation on unstructured hexahedral grids. Let nf and ne be the total number of faces and elements in the mesh, respectively. The basic idea of the MHFEM is to simultaneously approximate the dependent variable and its first-order derivative [31,33]. Hence, a simultaneous discrete representation of the groundwater head and the specific discharge will be considered. According to [33], $\nabla .\mathit{q}$ is constant inside each element, e, and facet, f, of the mesh. ${\mathit{q}}_e$ is uniquely determined when all normal fluxes through the six faces of a hexahedral element are perfectly known, such that:

$${\mathit{q}}_e={\displaystyle \sum }_{j=1}^6{\mathit{q}}_{e,j} {\mathit{b}}_j$$

(17)

where ${\mathit{q}}_{e,j}$ is the normal component of the groundwater discharge across the jth face of the hexahedral element e, and ${\mathit{b}}_j$ are the lowest-order Raviart–Thomas (RT0) basis functions, provided in Appendix A, and satisfying the fundamental relationship:

$${{\displaystyle \int }}_e^{}\nabla .{\mathit{b}}_j de={{\displaystyle \int }}_{f_i}^{}{\mathit{b}}_j.n_i d{f}_i={\delta }_{ij} i, j=1, \dots , 6$$

(18)

where $n_i$ is the outward normal unit vector to the face, f_i, of element e. This implies that the basis function ${\mathit{b}}_i$ contributes a unit flux to face number i, and a null flux to all others.

The variational formulation of Darcy′s law is obtained by taking the scalar product of Equation (2) with test functions ${\mathit{b}}_i$, integrating over the element, and using Green’s formula [33], yielding:

$${{\displaystyle \int }}_e^{}\left(K_e^{-1}.{\mathit{q}}_e\right).{\mathit{b}}_i de=h_e{{\displaystyle \int }}_e^{}\nabla .{\mathit{b}}_i de-{{\displaystyle \sum }}_{j=1}^{6}T{h}_{e,j} {{\displaystyle \int }}_{f_j}^{}{\mathit{b}}_i.n_j d{f}_j i=1, \dots , 6$$

(19)

where $T{h}_{e,j}$ is the trace of the groundwater head at face number j of element e, and h_e is the cell-centered groundwater head.

Inserting Equations (17) and (18) into Equation (19) yields:

$${{\displaystyle \sum }}_{j=1}^6{\mathit{q}}_{e,j}{{\displaystyle \int }}_e^{}\left(K_e^{-1}.{\mathit{b}}_j\right).{\mathit{b}}_i de=h_e-T{h}_{e,i} i=1, \dots , 6$$

(20)

Next, we introduce the local symmetric matrix $\left[A_e\right]\in {ℝ}^6\mathrm{x}{ℝ}^6$ with entries:

$$A_{ij}={{\displaystyle \int }}_e^{}\left(K_e^{-1}.{\mathit{b}}_j\right).{\mathit{b}}_i de$$

(21)

Appendix D provides a pseudo-code for assembly of the local mixed-hybrid finite element matrix $\left[A_e\right]$. Hence, Equation (19) is rewritten as:

$${\mathit{q}}_{e,i}={\alpha }_{e,i}{h}_e-{\displaystyle \sum }_{j=1}^6{A}_{ij}^{-1} T{h}_j$$

(22)

$${\alpha }_{e,i}={\displaystyle \sum }_{j=1}^6{A}_{ij}^{-1}$$

(23)

where the shape factor ${\alpha }_{e,i}$ is the sum at row number i of the inverse of the local resistance matrix A_e. From Equation (21), it is clear that this shape factor depends only on the geometry and the hydraulic conductivity components of the hexahedral element e.

The continuity of the normal component of the specific discharge is expressed for all internal faces, f_i, shared by two neighbor elements, e₁ and e₂, such that:

$${\mathit{q}}_{e_1,i}+{\mathit{q}}_{e_2,i}=0$$

(24)

Equation (22) substituted twice (for e₁ and e₂) into Equation (24) yields:

$${\alpha }_{e_1,i}{h}_{e_1}+{\alpha }_{e_2,i}{h}_{e_2}-{\displaystyle \sum }_{j=1}^6\left[{\left(A_{ij}^{-1}\right)}_{e_1}-{\left(A_{ij}^{-1}\right)}_{e_2}\right] T{h}_j=0$$

(25)

Notably, when a constant flux ${\mathit{q}}_N$ is prescribed on Neumann boundary faces lying in a portion of the domain boundary ${\Gamma }_N$ (i.e., $Q_w$ in Equation (13) or $Q_{DRN}$ in Equation (16)), Equation (25) reduces to:

$${\alpha }_{e,i}{h}_e-{\displaystyle \sum }_{j=1}^6{A}_{ij}^{-1} T{h}_j={\mathit{q}}_N$$

(26)

Likewise, we consider a Cauchy-type or general head boundary condition provided as ${\mathit{q}}_C=\lambda \left(h-h_0\right)$, where ${\mathit{q}}_C$ is a head-dependent flux, $\lambda$ is a hydraulic conductance (i.e., $C_R$ in Equation (15)), and $h_0$ is a prescribed head [L] (i.e., $z_{WT}$ or $z_{RB}$ in Equation (15)). ${\mathit{q}}_C$ is prescribed on all Cauchy boundary faces lying in a portion of the domain boundary ${\Gamma }_C$. In this case, Equation (25) is rewritten as:

$${\alpha }_{e,i}{h}_e-{\displaystyle \sum }_{j=1}^6{A}_{ij}^{-1} T{h}_j-{\lambda }_{i}T{h}_i=-{\lambda }_{i}T{h}_{i,0}$$

(27)

where ${\lambda }_i$ and $T{h}_{i,0}$ are the prescribed conductance and head values at face i being part of ${\Gamma }_C$.

Dirichlet boundary conditions of faces lying in ${\Gamma }_D$ (a portion of the domain boundary) are handled by simply moving the Dirichlet terms in the second term of Equation (27) to the right-hand side for rows belonging to non-Dirichlet faces, and directly substituting Equation (27) by the Dirichlet conditions (i.e., $T{h}_i=T{h}_{i,0}$) for all Dirichlet rows.

Merging the continuity of the specific discharge provided by Equation (25), and the specific equations for Dirichlet, Neumann, and Cauchy boundary conditions presented by Equations (26) and (27), leads to the following matrix equation:

$$\left[G\right]\left\{h\right\}-\left[H\right]\left\{\mathit{Th}\right\}=\left\{D\right\}+\left\{N\right\}+\left\{C\right\}$$

(28)

Entries of the globally assembled conductance matrices $\left[G\right]\in {ℝ}^{nf}\mathrm{x}{ℝ}^{ne}$ and $\left[H\right]\in {ℝ}^{nf}\mathrm{x}{ℝ}^{nf}$ are:

$$G_{ij}=\{\begin{array}{cc}{\alpha }_{e_j,i}\hfill & \hfill f_i\in \partial e_j\\ 0\hfill & \hfill f_i\notin \partial e_j\end{array}$$

(29)

$$H_{ij}=\{\begin{array}{cc}{\displaystyle \sum }_{f_i, f_j\in \partial e}{\left(A_{ij}^{-1}\right)}_e-{\lambda }_i\hfill & \hfill f_i\in {\Gamma }_C\\ {\displaystyle \sum }_{f_i, f_j\in \partial e}{\left(A_{ij}^{-1}\right)}_e\hfill & \hfill f_i\notin {\Gamma }_C\end{array}$$

(30)

Entries of the right-hand side column vectors $\left\{D\right\}$, $\left\{N\right\}$, and $\left\{C\right\}$ resulting from prescribed Dirichlet, Neumann, and Cauchy boundary conditions on faces ${\Gamma }_D$, ${\Gamma }_N$, and ${\Gamma }_C$, respectively, are:

$$D_i=\{\begin{array}{cc}{H}_{ij} T{h}_{i,0}\hfill & \hfill f_i\in {\Gamma }_D\\ 0\hfill & \hfill f_i\notin {\Gamma }_D \end{array}$$

(31)

$$N_i=\{\begin{array}{cc}{\mathit{q}}_i\hfill & \hfill f_i\in {\Gamma }_N\\ 0\hfill & \hfill f_i\notin {\Gamma }_N\end{array}$$

(32)

$$C_i=\{\begin{array}{cc}{\lambda }_{i}T{h}_{i,0}\hfill & \hfill f_i\in {\Gamma }_C\\ 0\hfill & \hfill f_i\notin {\Gamma }_C\end{array}$$

(33)

Integration of Equation (1), using a first-order fully implicit Euler discretization in time, and making use of the special properties of the RT0 basis functions as presented in Equation (18), yields:

$$\left|V_e\right|S_{p,e}\frac{h_e^{n+1}-h_e^n}{\Delta t^n}+{\displaystyle \sum }_{j=1}^6{\mathit{q}}_{e,j}^{n+1}=Q_s^{n+1}$$

(34)

where $V_e$ [L³] is the volume of element e, $n$ is a time index, $\Delta t^n=t^{n+1}-t^n$ [T] is the time step at time level $n$, and $Q_s^{n+1}={\mathit{q}}_s^{n+1}{V}_e$ [L³T⁻¹] is a volumetric source/sink term.

The insertion of Equation (22) into Equation (34) yields:

$$h_e^{n+1}-\left(1-{\beta }_e\right)h_e^n-{\beta }_e{\displaystyle \sum }_{j=1}^6\frac{{\alpha }_{e,j}}{{\alpha }_e}T{h}_j^{n+1}=\frac{{\beta }_e{Q}_s^{n+1}}{{\alpha }_e}$$

(35)

where ${\beta }_e=\frac{{\omega }_e}{1+{\omega }_e}$, ${\omega }_e=\frac{{\alpha }_e\Delta t^n}{\left|V_e\right|S_{p,e}}$, and ${\alpha }_e={\displaystyle \sum }_{i=1}^6{\alpha }_{e,i}$ are the sum of all the entries of the inverse of the local matrix A_e. Equation (35) is rewritten in globally assembled matrix form as:

$${\left\{h\right\}}^{n+1}-\left[M\right]{\left\{h\right\}}^n-\left[T\right]{\left\{\mathit{Th}\right\}}^{n+1}={\left\{R\right\}}^{n+1}+{\left\{Q\right\}}^{n+1}$$

(36)

where entries of the diagonal mass matrix $\left[M\right]\in {ℝ}^{ne}\mathrm{x}{ℝ}^{ne}$ and the trace matrix $\left[T\right]\in {ℝ}^{ne}\mathrm{x}{ℝ}^{nf}$ are:

$$M_{ij}=\{\begin{array}{cc}1-{\beta }_i\hfill & \hfill e_i=e_j\\ 0\hfill & \hfill e_i\ne e_j\end{array}$$

(37)

$$T_{ij}=\{\begin{array}{cc}\frac{{\beta }_i{\alpha }_{e_i,j}}{{\alpha }_i}\hfill & \hfill f_j\in \partial e_i\\ 0\hfill & \hfill f_j\notin \partial e_i\end{array}$$

(38)

Entries of the right-hand side column vector $\left\{R\right\}\in {ℝ}^{ne}$ result from the Dirichlet face boundaries in ${\Gamma }_D$ whose terms are moved to the right-hand side, such that:

$$R_i={\displaystyle \sum }_{f_j\in \left(\partial e_i{\displaystyle \cap }{\Gamma }_D\right)}\frac{{\beta }_i{\alpha }_{e_i,j}}{{\alpha }_i}T{h}_{j,0}$$

(39)

The source–sink column vector $\left\{Q\right\}\in {ℝ}^{ne}$ has the following entries:

$$Q_i=\frac{Q_{S_i}{\beta }_{e_i}}{{\alpha }_{e_i}}$$

(40)

Combining Equations (28) and (36) eliminates the cell-centered head unknowns and yields a linear system where the head traces at the faces of the mesh are the primary unknowns:

$$\begin{array}{c}\left(\left[H\right]-\left[G\right]\left[T\right]\right){\left\{\mathit{Th}\right\}}^{n+1}=\left[G\right]\left(\left[M\right]{\left\{h\right\}}^n+{\left\{R\right\}}^{n+1}+{\left\{Q\right\}}^{n+1}\right)\\ -{\left\{D\right\}}^{n+1}-{\left\{N\right\}}^{n+1}-{\left\{C\right\}}^{n+1}\end{array}$$

(41)

The global sparse matrix $\left(\left[H\right]-\left[G\right]\left[T\right]\right)\in {ℝ}^{nf}\mathrm{x}{ℝ}^{nf}$ is symmetric. Appendix E provides a pseudo-code to assembly of the global mixed-hybrid finite element matrix. A standard preconditioned conjugate gradient technique, such as ILU(0) preconditioning, is a suitable solver [50]. In situations where the matrix is not positive-definite owing to highly stretched elements or the occurrence of small dihedral angles, an M-matrix transformation always guaranties the existence of an ILU(0) preconditioner [50,51].

Once the linear system in Equation (41) is solved, the obtained trace heads vector, ${\left\{Th\right\}}^{n+1}$, is substituted into Equation (36) to obtain the cell-centered heads at the current time level, ${\left\{h\right\}}^{n+1}$, and, consequently, the specific discharge on all faces of the mesh using Equation (22) on a cell-by-cell basis. This post-processing step does not require, therefore, any linear system solution. Appendix F provides a pseudo-code for the hybridization procedure.

Notably, the assembled linear system for steady-state groundwater flow could be obtained simply by letting $\Delta t\to +\infty$, thus the coefficients ${\beta }_i$ are equal to 1 in Equations (37)–(39), and consequently the mass matrix, M, vanishes. Therefore, under steady-state conditions, Equation (41) simplifies to:

$$\left(\left[H\right]-\left[G\right]\left[T\right]\right)\left\{\mathit{Th}\right\}=\left[G\right]\left(\left\{R\right\}+\left\{Q\right\}\right)-\left\{D\right\}-\left\{N\right\}-\left\{C\right\}$$

(42)

where the ${\beta }_i$ coefficients cancel out in the entries of the trace matrix $\left[T\right]$ and the right-hand side vector $\left\{R\right\}$.

The global matrix $\left(\left[H\right]-\left[G\right]\left[T\right]\right)$ resulting from the MHFEM approximation is sparser than the global matrix resulting from a conforming finite element approximation. To illustrate this, we first recall that the non-zero entries of row number i in the global MHFEM and FEM assembled matrices result from face/node neighbors to face/node number i, respectively. In the finite element method, this neighborhood relationship is naturally defined as the faces or nodes shared by the same elements containing the target face or node. For a structured three-dimensional problem considering the conforming FEM on a hexahedral mesh, each node has 27 neighbors, including itself. Owing to the symmetry of the global conductance matrix, at most, 14 non-zeros are stored for each row of the sparse matrix. Alternatively, when considering an MHFEM for the same problem, each face has 11 neighbors, including itself. Therefore, because the matrix is symmetric, only (at most) six non-zero entries in each row of the resulting sparse matrix need to be stored. We conclude that even if the number of unknowns for an MHFEM approximation are greater than those for a conforming FEM for the same problem (as $2 nn<nf<3 nn$ for a three-dimensional hexahedral mesh), the resulting global matrix associated with an MHFEM approximation is sparser and, therefore, not necessarily slower to process with sparse linear algebra operations such as matrix–vector multiplication, triangular solves, incomplete factorization, etc.

When the spatial grid is orthogonal and the hydraulic conductivity tensor is diagonal, the MHFEM approximation becomes equivalent to the standard FDM approximation (See Appendix B and Appendix C for demonstration).

3.2. Mesh Adaption to Water Table Movement

The computational stencil is a three-dimensional hexahedral mesh that is optionally unstructured in the plane and made from many layers to concept the aquifer geometry. Generally, then the given slices of the mesh conform with the stratigraphy of the aquifers’ bottoms and the land surface as much as possible. Hence, the mesh is composed of vertical columns and the mesh adaption proceeds independently in each column. This simplifies the interpolation (linear or harmonic) of the materials’ properties from the background geological mesh to the moving computational mesh. This also makes this process fast and practically tractable.

The phreatic surface position is locally updated using the boundary condition provided by Equation (5) at the nodal points in the surface. Prior to this, the computed head traces at the face centers of the upper slice of the mesh are interpolated to the nodal points of the same slice. This is because, usually, the coordinates of a finite element mesh are generally provided at the nodal points and not the face centers. If this updated value is above the land surface elevation, then the corresponding face is marked as a seepage face and Equation (11) takes place.

After updating the phreatic surface, it is necessary to do so for other moving nodes in the mesh. Only a set of the upper mesh slices is allowed to change their position while the others remain fixed. As suggested by other authors [10,23], a linear interpolation proves to work satisfactorily to find the position of the moving mesh slices. Optionally, a Laplacian smoothing technique is applied to the free nodes of the mesh. Those are the nodes not subject to any boundary condition. This operation is necessary for extreme situations where the vertical-to-horizontal scales ratio is higher than 1, which is typical for civil engineering structures such as earth dams (see Section 4.3).

3.3. Numerical Implementation of Boundary Conditions

The discrete systems of Equations (41) and (42) for groundwater flow under transient and steady-state conditions, respectively, have provisions for Dirichlet (i.e., constant or fixed head), Neuman, and Cauchy boundary conditions. Herein, we will discuss the numerical implementation for all the boundary conditions encountered in Section 2.2.

Notably, all discrete boundary conditions can use time series functions to allow for time-dependent variables. Spatial variability of any boundary condition parameter is dictated by the mesh resolution. Hence, each boundary face may have a different set of boundary conditions parameters.

3.3.1. Phreatic Surface

Any face on the top slice of the mesh is a phreatic surface boundary governed by Equation (8). At these boundaries, we have ${\frac{\partial h}{\partial z}|}_{{\mathsf{\Gamma }}_{WT}}=-{K_{zz}^{-1}|}_{{\mathsf{\Gamma }}_{WT}}{\mathit{q}}_z$, where $K_{zz}^{-1}$ is the component of the inverse of the hydraulic conductivity tensor, $K$, along the third dimension. Notably, this hydraulic conductivity tensor belongs to the stratigraphic element, which is crossed by the moving surface. Additionally, the z-component of the specific discharge, ${\mathit{q}}_z$, is related to the normal component through the face, $\mathit{q}$, by the relationship ${\mathit{q}}_z=\mathit{q}\cos \theta$, where $\theta$ is the cosine angle between the face normal and the vertical axis. Inserting the two previous relationships into Equation (8) yields:

$$\mathit{q}=\frac{1}{\cos \theta \left(1+N{K}_{zz}^{-1}\right)}\left(-N+S_y\frac{\partial h}{\partial t}\right)$$

(43)

Using an implicit first-order discretization of the time derivative term in Equation (43) as ${\left(\frac{\partial h}{\partial t}\right)}^{n+1}\cong \frac{T{h}^{n+1}-T{h}^n}{\Delta t^n}$ shows that a kinematic boundary face is a Cauchy-type boundary condition where the face hydraulic conductance and specified head are:

$$\lambda =\frac{S_y}{\Delta t^n\cos \theta \left(1+N{K}_{zz}^{-1}\right)}$$

(44)

$$T{h}_0=\frac{N+\frac{S_{y}T{h}^n}{\Delta t^n}}{\cos \theta \left(1+N{K}_{zz}^{-1}\right)}$$

(45)

Under steady-state conditions, the kinematic boundary condition reduces to a fixed flux on the given face, whose magnitude is presented as:

$$\mathit{q}=\frac{-N}{\cos \theta \left(1+N{K}_{zz}^{-1}\right)}$$

(46)

As stated earlier, a kinematic condition is dependent on other boundary conditions which are the components of the net recharge through recharge, evapotranspiration, and river faces.

3.3.2. Seepage Face

All the free top faces of the mesh are marked as potential candidates as seepage faces. The model implements equally an option where only a restricted set of these faces is included. This helps the algorithm to be faster, as areas where the groundwater depth is known to be significant are safely excluded (i.e., in high valleys, hills, etc.). Next, at each outer iteration, marked faces retain their phreatic surface conditions if the head is lower than the land surface position, $z_{TOP}$, at the same horizontal coordinates. If the head exceeds this position, a constant head boundary condition, $T{h}_i=z_{TOP}$, is prescribed, where $i$ is the face number. The numerical treatment of a constant head boundary is described in the next sub-section.

3.3.3. Constant Head

The head in any boundary face of the finite element mesh may be fixed during the simulation. The fixed head terms of a Dirichlet face, whose number is $i$, are moved to the right-hand side in all matrix rows, $j\ne i$, according to Equation (39). It turns out that these are the rows for faces, $j$, who can share the same element with face $i$ and that are not Dirichlet boundaries too. Furthermore, the coefficient matrix of the ith diagonal of the global matrix is set equal to one. In this way, the size of the matrix equations does not need to be modified prior or next to an iterative sparse matrix solution.

3.3.4. Recharge and Evapotranspiration

Recharge and evapotranspiration boundary conditions are directly applied on the water table boundary to calculate the net recharge through all its faces. Those are Neuman-type boundary conditions. The flux is internally multiplied by the face surface area prior to prescribing the boundary condition. Any recharge boundary condition is optionally delayed in time, while an evapotranspiration condition is applicable only when the calculated head in the face is higher than the specified extinction elevation at the horizontal coordinates of this face center.

3.3.5. Pumping/Injection Well

There are two alternatives to setup boundary conditions for a pumping/injection well when using an MHFEM numerical approximation. First, the flow rate boundary condition could be assigned to a group of boundary faces from which the fluid is extracted/injected. This is the case for a tubular geometry that represents a fictive well diameter. Another representation is possible by adding a source/sink term to an element containing the well. The first schematization is more flexible when greater accuracy at the proximity of the well is needed, such as when interpreting pumping tests. The second option allows the well effects to be incorporated at the regional scale without additional constraints on the mesh stencil near the wells, which is practical for field studies with a large number of wells. Both well’s representations are used in this paper. However, only the second option is supported within a moving mesh approach.

When representing a well boundary condition with a source/sink term, the difficulty with the moving mesh approach is to iteratively relocate the cells lying between the bottom and top screens of the well along a vertical column of cells. Provision is made to fit the bottom of the lower element in this column with the bottom of the well screen. Additionally, the flow rate is distributed among the cells in this column lying in the saturated interval of the well screen. In particular, for a pumping well, when the position of the water table in the well (i.e., the position of the upper surface in the well vertical column of cells) is below a given fraction of the well screen length, the flow rate is smoothly decreased according to Equation (14). In the preceding two situations, a source/sink term is added to the right-hand side vector $\left\{Q\right\}$ in the discrete mass balance in Equation (36) according to Equation (40). Because the vector $\left\{Q\right\}$ is multiplied by the matrix $\left[G\right]$ in Equation (41) to obtain the final system of the equations on the mesh faces, during the assembly of the right-hand side of this system, a source/sink term such as in Equation (41) is distributed among the six j-faces of cell number $i$ with the weighting shape factor ${\alpha }_{e_i,j}$. When the water table position at the well falls below its screen bottom, this condition is deactivated.

The cellwise injection/pumping rates are adjusted, therefore, iteratively during each outer iteration of the overall algorithm.

3.3.6. River

A river boundary condition is applied to any face in the upper slice of the finite element mesh. When the water table position is above the riverbed elevation, $z_{RB}$, of a river face, whose number is $i$, this results in a third type of boundary condition. The prescribed hydraulic conductance, $C_R$, at this face is added to the ith diagonal of the global matrix according to Equation (30), and the product $C_R{h}_R$ is added to the ith entry of the right-hand side column vector according to Equation (33). Otherwise, when the water table falls below the riverbed elevation of the face, we switch the boundary condition to the Neuman type with a prescribed flow rate that equals $C_R\left(h_R-z_{RB}\right)>0$. Hence, a river boundary condition is essentially a switching boundary condition. This status is updated at each outer (i.e., mesh level) iteration prior to solving a new linear system of equations and after updating the water table elevations.

3.3.7. Drain

Conceptually, there is two distinct ways to setup drains within an MHFEM approach. First, boundary faces could drain groundwater when the explicit geometric details of the structures, such as underground tunnels, are a part of the mesh. A second representation of this boundary condition may use a sink term to model drained water, such that all the drain geometric details are lumped at the cell center of an element. The first representation, while offering more flexibility, is more appropriate at detailed local scale models. The second representation is more flexible for regional scale studies. The first approach has some limitations when using the moving mesh method because of the difficulty to adjust or complete the details of the drain geometry when crossed by the water table. Hence, this representation could be used only when the drain is guaranteed to remain in the saturated zone during the simulation. Both methods are implemented in the developed simulator, but only the second one is used in this paper, and is therefore described as follows. When considering the second method, we search for the element center with the closest coordinates to the drain at $\left(x_{DRN}, y_{DRN}, z_{DRN}\right)$. If this element exists (i.e., is inside the actual saturated region), a prescribed negative flow rate equal to $C_{DRN}\left(z_{DRN}-z_{WT}\right)<0$ is attributed to this element, where $z_{WT}$ is the water table elevation at coordinates $\left(x_{DRN}, y_{DRN}\right)$, that is the highest vertical elevation of the mesh column containing the drain element, and $C_{DRN}$ is the hydraulic conductance of the drain. Otherwise, when the element is not found (i.e., is inside the virtual unsaturated region), this condition is inactive (i.e., no prescribed flow rate).

3.4. Computer Code

HydroTec^© is the computer code implementing the adaptive MHFEM method presented in this paper. It is entirely programmed using the object-oriented (OO) C++ language. Although there was an increasing support of OO methodologies in other widely used computer languages by the groundwater modeling community, such as the Fortran 2003 standard, C++ was preferred because it is tightly integrated to high-level scripting languages (i.e., such as Python), which are planned to be used in the future to accelerate the addition of new features. Furthermore, the extended support of OO features and template-based metaprogramming were other features needed in this project. The core computational framework includes classes for sparse linear algebra, structured/unstructured mesh management, iterative sparse linear solvers, and boundary condition packages. Similar to MODFLOW, all supported types of boundary conditions could be loaded on-the-fly from their input files to the discrete sparse system of the equations. This flexibility supports the flexible and modular testing of groundwater flow models using different sets of hypothetical boundary conditions when using several conceptual models.

Finite element analysis is supported by a hierarchy of polymorphic face and element classes. For instance, any instance of an element class refers to either a quadrilateral or hexahedral object depending on the dimension of the problem being solved. The FEM assembly routines directly use the element class, enhancing the code genericity and leading to a less duplicate code.

A set of utility classes was designed to support input/output to different file formats, the management of time stress periods, and time series datasets (i.e., piezometric records, time-dependent boundary conditions, and time-dependent hydraulic conductivity or storage coefficients).

The code is under active development to support many groundwater modeling projects. A new MHFEM simulator for solute/heat transport was recently developed using the same framework and will be documented elsewhere.

4. Results

Five examples are presented to illustrate and validate the deforming mesh MHFEM model developed in this paper. The first evaluates the model by comparison with a two-dimensional analytical solution for drawdown in an infinite anisotropic confined aquifer. The second problem compares the model’s accuracy with MODFLOW + MODFPATH simulations for a two-dimensional highly heterogeneous formation. The third problem simulates the water table and seepage face on a rectangular earth dam, where the obtained results are compared with those of other authors. The fourth example uses a two-dimensional cross-section model of an unconfined aquifer to compare the free surface computed by HydroTec^© with the same solution obtained by MODFLOW. The last example is an adapted three-dimensional model of an alluvial aquifer which is used as a test bed to compare the two models’ performance when simulating an unconfined groundwater flow.

4.1. Pumping in a Two-Dimensional Anisotropic Aquifer

Papadopulos provided an analytical solution for the hydraulic head drawdown, s, in an infinite anisotropic confined aquifer [52]. This analytical solution features a full anisotropic transmissivity tensor, $T$, and is used in this section for model verification. The radial drawdown resulting from the pumping well action depends on the pumping flow rate, $Q_w$, the components of the transmissivity tensor, $T$, and the well function, $W\left(u\right)$ as:

$$s\left(x,y,t\right)=\frac{Q_w}{4\pi \sqrt{T_{xx}{T}_{yy}-T_{xy}^2}}W\left(u\right)$$

(47)

where $u$ depends on the observation point coordinates (x, y), the aquifer specific storage, $S_p$, the components of the transmissivity tensor, $T$, and the pumping time, $t$, such that:

$$u\left(x,y,t\right)=\frac{S_p\left(T_{xx}{y}^2+T_{yy}{x}^2-2T_{xy}xy\right)}{4t\left(T_{xx}{T}_{yy}-T_{xy}^2\right)}$$

(48)

The well function, known also as the negative exponential integral, reads:

$$W\left(u\right)={{\displaystyle \int }}_u^{+\infty }\frac{e^{-\xi }}{\xi } d\xi$$

(49)

Notably, when $T_{xx}=T_{yy}$, and $T_{xy}=0$, Equation (47) reduces to the well-known analytical solution provided by Theis for non-leaky confined aquifers [53].

The computational domain has an extension of 100 m in each side of the XY plane and has a uniform depth at 1 m. The physical parameters of the problem are provided in

Table 1. Physical parameters used in the pumping test problem. Case 1 and 2 correspond to diagonal and fully symmetric transmissivity tensors, respectively.

Parameter	Value—Case 1	Value—Case 2
$\mathrm{Transmissivity} \mathrm{along} \mathrm{X}, T_{xx}$ m2.s−1	2.93 × 10−5	2.57 × 10−5
$\mathrm{Transmissivity} \mathrm{along} \mathrm{Y}, T_{yy}$ m2.s−1	1.47 × 10−5	1.84 × 10−5
$\mathrm{Transmissivity} \mathrm{along} \mathrm{XY}, T_{xy}=T_{yx}$ m2.s−1	0	6.36 × 10−6
$\mathrm{Specific} \mathrm{storage}, S_p$ m−1	1.957 × 10−3	1.957 × 10−3
$\mathrm{Pumping} \mathrm{flow} \mathrm{rate}, Q_w$ m3.s−1	5 × 10−3	5 × 10−3

. Two cases are selected. The first corresponds to a diagonal transmissivity tensor, while the second case uses a full symmetric transmissivity tensor. Transmissivity components in the second case are obtained by rotating the main axes of the tensor ellipsoid, taken in the first case, by 30° in the anti-clockwise direction.

An automatically generated quality single-layer hexahedral mesh honoring the internal geometrical features of the model and the target maximal subdomain size is shown in Figure 2a. These mesh constraints are 1 m in the area bounded by a 10 m circle centered on the pumping well position, as shown in Figure 2b. Next, a second refinement zone is considered in the area enclosed by a circle with a radius of 1 m, as depicted in Figure 2c. Notably, a well radius of 0.1 m is adopted, and the well circumference is approximated with a regular pentagon (Figure 2c) and is located at the center of the domain. The hexahedral mesh contains a total of 3778 facets and 1876 elements.

The two transient simulations span a single stress period whose length equals 10³ s. A constant time step of 2 s is selected. The hydraulic head drawdown is monitored at two piezometers, P₁ and P₂, as shown in Figure 2b. Figure 3a,b show the evolution of the numerically computed drawdowns with those analytically evaluated using Equation (47) at piezometers P₁ and P₂ for the diagonal and fully symmetric transmissivity tensors, respectively. In all cases, the MHFEM and analytical solutions are in good agreement. For the second case, it is clear that the hydraulic head drawdown is higher in P₂ and lower in P₁ than in the first case as expected, at least qualitatively, from the change in the transmissivity values provided in Table 1.

4.2. Flow in a Heterogeneous Porous Medium

Here, we consider a previously published model from the literature [28]. The authors illustrated the accuracy of the MHFEM approximation when compared to the conforming FEM using a hypothetical two-dimensional problem as shown in Figure 4. Their results suggested using particle tracking shape as a metric to evaluate the accuracy of the underlying numerical methods. In this work, we additionally use the particles forward travel time, $\tau$, as a second metric for these accuracy assessments.

Figure 4 shows the 100 m by 100 m conceptual model considered in this test case. The domain comprises four hydraulic conductivity zones ranging from 10² m.d⁻¹ to 10⁻³ m.d⁻¹. Groundwater flows from north to south between two fixed head boundaries at 100 m and 99 m, respectively. A total of 19 particles were placed at an equal distance of 5 m at the top boundary tracing their flow paths. MODPATH simulation uses a semi-analytical particle tracking method [54]. Meanwhile, particle tracking simulation using the continuous specific discharge fields obtained by the MHFEM approximation is based on previously published algorithms [34].

The steady-state flow and particle tracking simulations are approximated with the MHFEM and the finite difference method (FDM) approximations. Their results refer to implementations in the HydroTec^© and MODFLOW/MODPATH computer codes, respectively. In the first column of Figure 5, the simulated path lines using the MHFEM approximation with increasing grid resolutions from top to bottom are shown for the 10 × 10, 20 × 20, and 30 × 30 grid resolutions. Similarly, the second column shows the path lines simulated with MODPATH with identical grid resolutions. Notably, in all subfigures, the reference path lines are plotted with a red color for a direct comparison of both MHFEM and FDF approximations. These reference path lines are identical to the reference solution presented by the authors in the original publication [28].

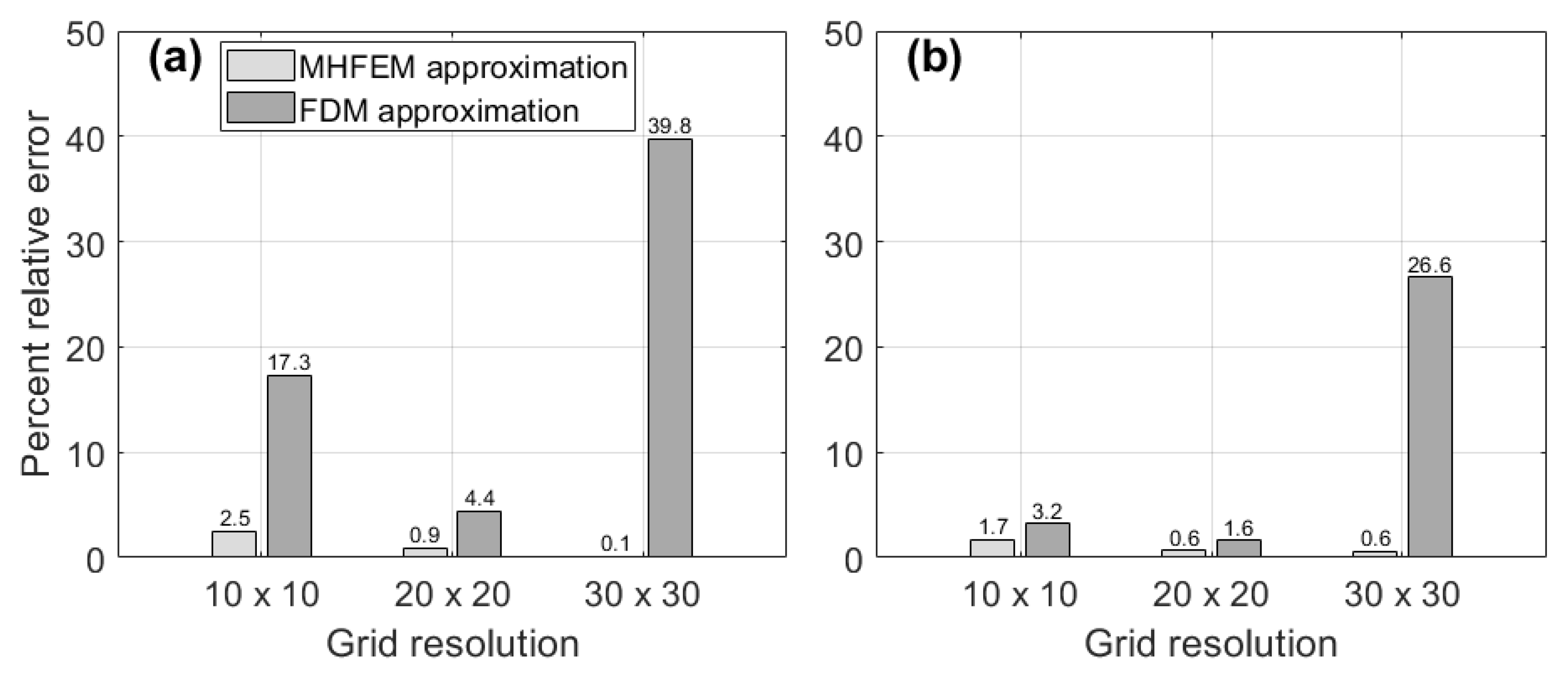
Comparing Figure 5a,d indicates that the path lines resulting from the MHFEM approximation are closer to the reference solution than those computed with the FDM approximation. Particularly, it can be noticed that all flow paths which start traveling from the points located above the northmost least permeable block are penetrating it. This should not be the case according to the reference solution.

The same above-mentioned remarks hold for the other grid resolutions considered in this study. This can be concluded by comparing Figure 5b,e, then Figure 5c,f.

The improvement in the path lines shape is much better for the MHFEM approximation when the grid resolution steadily increases. For instance, Figure 5c shows that a 30 × 30 grid resolution using the MHFEM method is deemed sufficient for accurate particle tracking as the resulting flow paths follow very closely the reference solution that requires a much higher resolution (i.e., 320 × 320 grid). Notably, the mixed approximation yields a more accurate solution at a 20 × 20 grid resolution than a finite difference approximation at a 30 × 30 resolution. Hence, this confirms the superiority of the MHFEM method as a more appropriate choice when using coarse grids for particle tracking simulations, as concluded in previous works [28,34].

It Is worth noting that the FDM approximation necessitates a higher resolution than a 30 × 30 grid resolution to simulate accurate particle tracks. This is because one particle path is still penetrating the uppermost most impermeable block (Figure 5f), which is physically unrealistic.

As mentioned earlier, in reference [28], the authors did not consider the forward travel time as a metric for comparative assessments of the MHFEM with an alternative spatial approximation technique. This is performed in this work by calculating the percent relative error in the simulated travel time of a flowing particle at the exit boundary as:

$$\mathrm{error}(\%)=100\times \left|{\tau }_{ref}-\tau \right|/{\tau }_{ref}$$

(50)

where ${\tau }_{ref}$ is the travel time of the reference flow path at the exit boundary simulated on the 320 × 320 fine grid resolution with a mixed approximation, while $\tau$ is a similar quantity evaluated at the grid resolution of interest.

Figure 6a,b depict the relative errors obtained from the MHFEM and FDM approximations for different grid resolutions for particles released at coordinates (25, 100) m and (95, 100) m, respectively. They show that travel time errors for the MHFEM approximation are small even for the lowest resolution. Indeed, they do not exceed 2.5% and 1.7% for the considered flow lines, respectively. These errors are much smaller than those obtained when using an FDM approximation. Moreover, the relative error in the MHFEM decreases monotonically as the grid resolution increases, confirming the suitability and superiority of this numerical scheme for particle tracking analysis on coarse grids. This is unlikely the case with the FDM approximation as the travel time convergence when increasing the grid resolutions is erratic.

4.3. Two-Dimensional Free Surface in a Homogeneous Earth Dam

In this third example, a homogeneous cross-section model of a regular earth dam is considered. The model domain has a length of 5 m and a height of 10 m. This area is divided into uniform quadrilateral elements at 0.1 m on each side. Therefore, the mesh stencil contains 5000 elements and 10,150 edges. The hydraulic conductivity equals 1 m/d everywhere. The flow occurs between two fixed head boundaries. On the left, the head was fixed to 10 m, while this was set to 2 m on the right side. All nodes in the mesh, except those lying at the bottom, and fixed head faces were allowed to change their position. Notably, in this problem, Laplacian mesh smoothing was enabled because simply moving the nodes along the vertical lines could result in highly distorted elements or even elements with self-intersecting edges owing to the high vertical-to-horizontal aspect ratio of the problem.

Figure 7 shows the newly obtained mesh and the position of the steady-state phreatic surface. The length of the seepage face results directly from the water table height on the right side. There was no need to specify potential seepage faces at this boundary prior to the simulation as would be the case within a fixed mesh approach. The simulated water table height is compared with other numerical solutions gathered from the literature. There was a good agreement with the solutions provided by [55,56]. The first solution developed in [55] uses a bilinear fixed mesh conforming FEM model. The second solution from [56] was computed with an FDM technique implemented in a spreadsheet.

4.4. Two-Dimensional Free Surface in a Pumped Phreatic Aquifer

In this third example, we consider a 6 Km long and 50 m deep vertical section of a phreatic aquifer bounded by two constant head boundaries at 50 m and 35 m from west to east, respectively. The aquifer is assumed to be homogeneous and isotropic with a hydraulic conductivity at 5 m/d. The mean groundwater recharge was assumed to linearly increase from 0 to 0.05 m/d between the ground surface and a depth of 35 m following previous observations [48]. A partially penetrating well located at the center of the model extension withdraws groundwater with a flow rate equal to 62.5 m³/d. The well is screened in the lower half of the aquifer thickness. Owing to the aquifer homogeneity, the flow rate is equally divided among the cells lying along the well perforation.

A structured mesh was adopted to enable a fair comparison with MODFLOW 2005 [8]. The grid has 120 columns and 10 layers. Hence, the finite-difference simulation with MODFLOW solves a nonlinear problem with 1200 unknowns, while the MHFEM simulation with HydroTec^© solves a problem with 2530 unknowns using the deforming mesh algorithm developed in this paper.

The two compared codes use the same preconditioned iterative method, and the same convergence control parameters, for the inner linear systems in the outer iteration loop, facilitating a fair intercomparison. Namely, the maximum number of iterations (i.e., 900) and the tolerance of inner convergence of groundwater heads (i.e., 10⁻¹²). In the FDM- based simulation, a Picard iteration is adopted with a convergence closure equal to 10⁻³ m. The same parameter was used as a convergence closure for the heads in the mesh adaption loop. Likewise, a maximum number of 100 outer iterations was similarly taken for both algorithms. All 10 upper horizontal lines of the 2D mesh were allowed to move during the iterative adaption process.

Figure 8 shows the final mesh shape and head distribution after the convergence of the adaptive MHFEM solution. In particular, the groundwater surface is smooth and all its nodes (i.e., the med-edges) explicitly satisfy the prescribed external convergence criteria. This is not the case for MODFLOW’s FDM solution, because the water table is inside the grid blocks and must be found by post-processing (i.e., interpolation) from the simulated groundwater heads in the center of their cells. This explains why the moving mesh solution always provides directly a much more accurate position of the water table.

The convergence behavior of mesh adaptation is shown in Figure 9. This is about 3.2 and is therefore faster than a linear trend. More importantly, it outperforms the convergence rate of Picard’s method and even the well-known quadratic rate of Newton’s iteration method. Only 8 iterations were needed in the adaptive mesh MHFEM model, while 32 Picard iterations were performed by MODFLOW. In this case, even for this simple problem, convergence was more difficult to reach with the chosen external stopping criterion. It was necessary to move to a small under-relaxation factor (i.e., 0.25) for MODFLOW to converge.

On the other hand, the MHFEM model took less than 2 s CPU time for this steady-state simulation, while the FDM solution with a fixed mesh took about 11 s.

Figure 10 shows the simulated water table with the MHFEM and FDM approximations. While there is a good agreement between the drawdowns calculated with the two methods, small discrepancies are observed far from the well. The maximum error does not exceed 0.74 m, which amounts to 15% of the vertical grid size (i.e., 5 m). As concluded earlier, the differences are due to interpolation artifacts inside the fixed mesh. This error would be greater as the mesh becomes coarser along the vertical direction. Furthermore, the MHFEM approximation with an adaptive mesh is always more accurate in the particular case of groundwater abstraction. This is because the mesh density becomes higher than the initial fixed mesh when it contracts due to pumping. This observation would also apply to the groundwater head distribution in the moving saturated region.

We conclude from the obtained results relative to this third test problem that the moving mesh method is an attractive technique to accurately simulate groundwater flow in unconfined aquifers subject to stresses such as pumping, recharge, etc. The next test problem could be regarded as a three-dimensional extension that would serve as a basis to consolidate these findings.

4.5. Three-Dimensional Free Surface in a Pumped Phreatic Aquifer

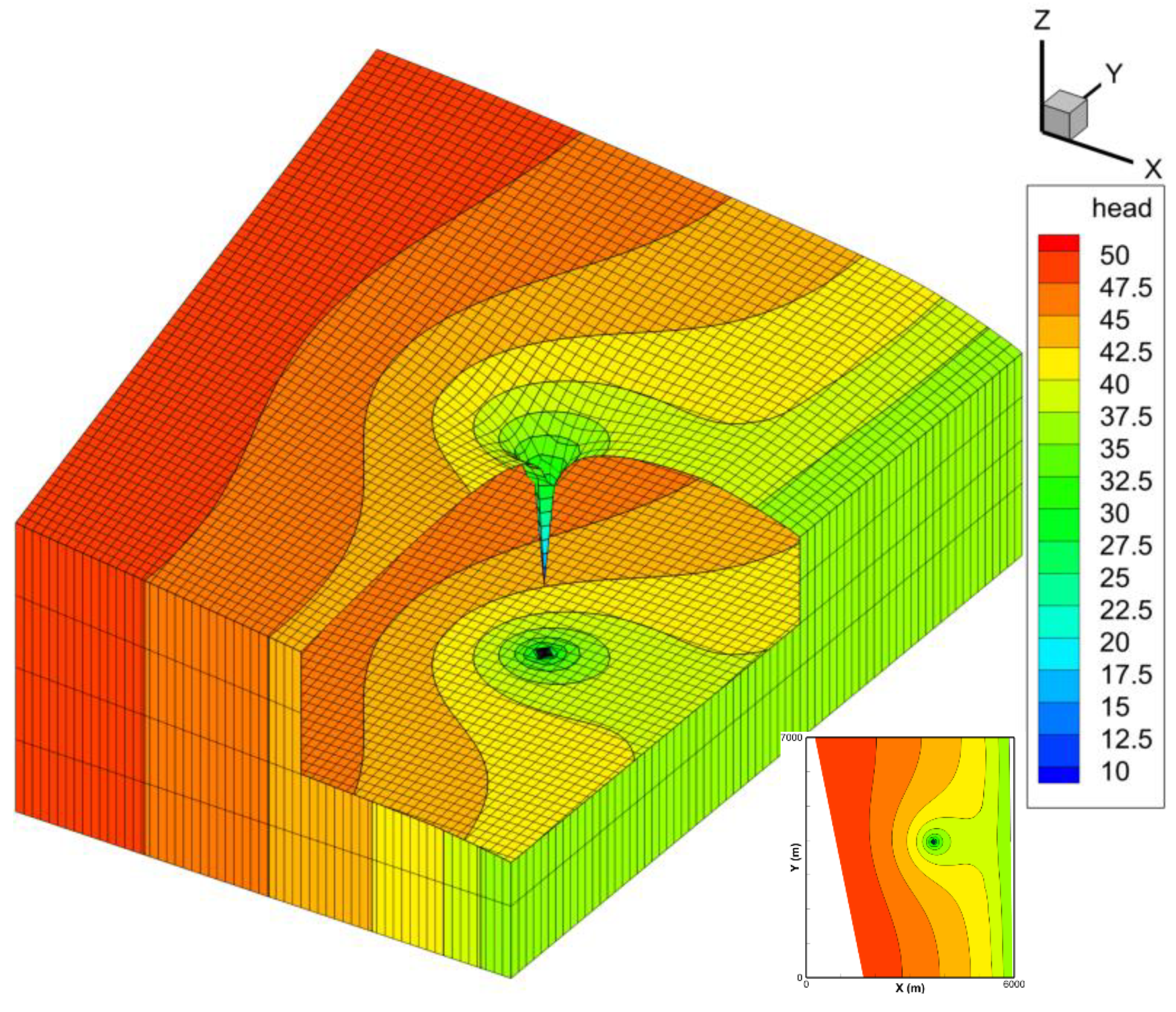
This problem is adapted from a field case study in a small alluvial aquifer. The domain geometry is shown in the inset of Figure 11. Except for the left constant head boundary, this three-dimensional problem inherits many characteristics of the previous example. A second difference concerns the well properties including its position, well rate, and perforated length. The well is positioned at coordinates x = 3700 m and y = 4000 m. The pumping rate equals 6000 m³/d. The well is screened in the lower 10 m of the aquifer.

As in the previous example, a structured and relatively coarse mesh was adopted to enable a direct comparison with MODFLOW 2005. The grid has 60 columns, 70 rows, and 4 layers. Hence, when the mesh is fixed, the horizontal cell dimension is close to 100 m and the vertical cell size is uniform at 12.5 m. The finite-difference simulation with MODFLOW solves a nonlinear problem with 16,284 unknowns, while the MHFEM simulation with HydroTec^© solves a problem with 53,435 unknowns.

The convergence control parameters for the two simulations are identical to those selected in the previous problem, except for the nonlinear/mesh convergence closure criterion, which is equal to 10⁻² m. This is because the MODFLOW simulation does not converge when the last parameter was increased up to 10⁻³ m. Contrarily, a higher outer convergence criterion does not pose any challenge to the adaptive mesh model as only three more mesh iterations were required. All four upper horizontal slices of the 3D mesh were allowed to move during the iterative adaption process.

Figure 11 shows a cutaway view of the final mesh shape and head distribution at steady-state conditions. Even with a coarse mesh, the model successfully computes and visualizes the cone of depression with a rapidly changing curvature of the free surface. As expected, and also depicted in Figure 11, the hydraulic gradient is the highest in this zone.

The convergence behavior of mesh adaptation is shown in Figure 12. This is about 1.9 and is therefore faster than a linear trend and close to the quadratic rate of Newton’s iteration method. Only 13 iterations were needed by the adaptive mesh MHFEM model, while 54 Picard iterations were performed by MODFLOW. The MHFEM model took 32 s CPU time for this steady-state simulation, while the FDM solution with a fixed mesh took about 48 s.

Figure 13 shows the simulated water table profile with the MHFEM and FDM approximations. This profile is parallel to the X-axis and crosses the well position. The drawdowns calculated with the two methods are not in good agreement at the well as the difference amounts to 2.65 m. This is a consequence of the coarse vertical discretization of the fixed mesh. Hence, post-processing the water table position, including the drawdown at the well, can lead to higher errors as the vertical cell size increases. The results of this test problem confirm the ability of the MHFEM approximation with an adaptive mesh to deliver an accurate representation of the water table geometry, which is free from interpolation errors and less prone to the vertical discretization of the mesh.

5. Discussion

The adaptive meshing technique developed in this paper is relatively simple to implement into the framework of an existing code for modeling saturated groundwater flow. This upgrading effort is somewhat equivalent to upgrading an FEM fixed mesh model to support unconfined flow using a Picard loop. For the moving mesh technique, this outer loop corresponds to mesh iteration. Hence, the nonlinearity is removed from the flow process in favor of mesh adaption. The provided examples demonstrate that this approach enhances the model’s robustness, provided that the geological model complexity can survive the layered mesh adaption methodology. When this process succeeds, the moving mesh approach is unbeatable. This is because the underlying preconditioned linear systems using the M-matrix transformation for the intermediate linear systems are always guaranteed to converge. Another robustness aspect of the moving mesh approach is its resilience with respect to the outer tolerance or mesh convergence closure. As can be seen from the provided examples, convergence is no problem for values up to 10⁻³ m, while this impacts even the simplest models with a fixed mesh approach.

The provided problems in this work support that the moving mesh technique is more efficient than the fixed mesh. Indeed, the convergence rate is higher than linear and is close to quadratic for three-dimensional models. There is even room for improvement as the PCG iteration could be replaced with a more efficient algebraic multigrid preconditioner when targeting large-scale discrete problems [57].

The chief advantage of the moving mesh approach is obtaining an accurate water table interface shape, which is free from the uncertainties related to coarse discretization and spatial interpolation from groundwater heads. The water table interface is derived naturally because it is part of the adapted mesh geometry.

The moving mesh method has few limitations with regard to the current state-of-the-art method. The most challenging obstacle to its universal application is the occurrence of the random heterogeneity of the porous medium. This is the case of hydraulic conductivity realizations mapped from geostatistical techniques. When the hydraulic conductivity is different from cell to cell along all directions, it becomes almost impossible to find any practical guidelines to correctly adapt the mesh. Another minor limitation is the inability to simulate perched water table aquifers. This is because the continuity of the saturated and unsaturated zones is implicitly taken as an initial assumption. Furthermore, the simple mesh adaption scheme used in this work cannot handle the extreme situation when the water table becomes nearly vertical, spanning a large number of vertical cells in the model. This is the case of a heterogeneous earth dam where, for instance, two pile sheet materials are placed along a vertical discontinuous interface. However, this event is impossible to occur in realistic unconfined aquifers characterized by their large horizontal-to-vertical aspect ratio.

Overall, we think that any widely used groundwater modeling software should support not only the fixed mesh approach. This will not only enlarge its scope and usability, but it will advantageously enable users to cross-check the two approaches for the same application.

An interesting extension of the moving mesh approach is handling the general case of multiple free and moving groundwater interfaces. A typical example is the situation of two exploited aquifers separated by an impermeable layer where a dewatered zone results from extensive pumping of the lower aquifer. In this case, not only the mesh geometry accounts but also its topology (i.e., connectivity) should be adapted accordingly to exclude the dewatered volume from the mesh. Advances in this direction are awaited in future works.

6. Conclusions

This paper deals with a novel moving mesh approach for modeling unconfined groundwater flow with a mixed-hybrid finite element approximation. A layered mesh is adjusted to fit with the water table interface modeled as a kinematic boundary condition. The model accounts for many types of boundary conditions needed in practical applications. This approach has been validated using analytical solutions and numerical solutions computed with industry-standard groundwater FDM modeling codes such as MODFLOW. The following conclusions can be drawn from this study:

• The mixed-hybrid finite element approximation is suitable for highly heterogeneous and anisotropic aquifers. It provides accurate solutions for the discharge fields even for coarser grids than the FDMs. Therefore, it is a suitable approximation technique prior to advective particle tracking or solute/heat transport simulations.
• The moving mesh technique based on the MHFEM approximations provides an accurate solution for the water table interface, groundwater heads, and specific discharge fields. The water table is accurate because it is free from cellwise interpolation and independent of the vertical grid size, as used in fixed mesh methods.
• The robustness of the moving mesh method cannot be surpassed by a fixed mesh alternative. The nonlinearity associated with the latter is replaced by a series of saturated flow problems which are always guaranteed to converge for some preconditioners. Moreover, the moving mesh outer iteration loop accepts higher convergence closure parameters.
• Owing to the simplicity of the mesh adaption scheme, the moving mesh model proves to be equally efficient. For all of the studied problems, it was faster than the Picard loop-based FDM solutions when using the same resolution.
• The efficiency of the moving mesh MHFEM model is supported by an almost quadratic rate of convergence.
• The presented samples prove that it is possible to confidently develop practical groundwater applications using HydroTec^© code. Nevertheless, additional benchmarks and testing will strengthen users’ confidence.