Two-Phase MPM Simulation of Surge Waves Generated by a Granular Landslide on an Erodible Slope
Abstract
:1. Introduction
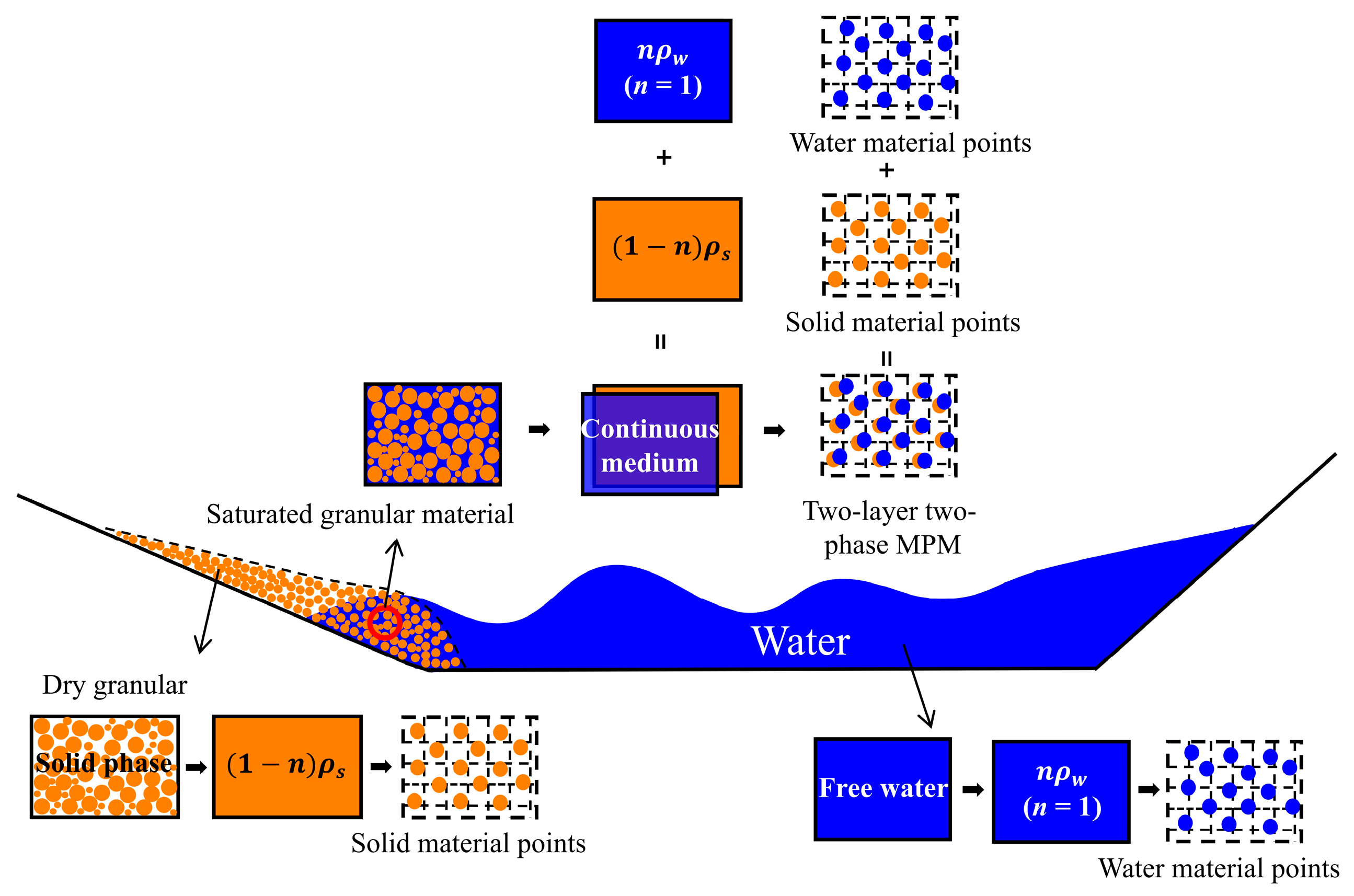
2. The Governing Equations
2.1. Mass Balance Equations
2.2. Momentum Balance Equations
2.3. Constitutive Models
3. Numerical Examples
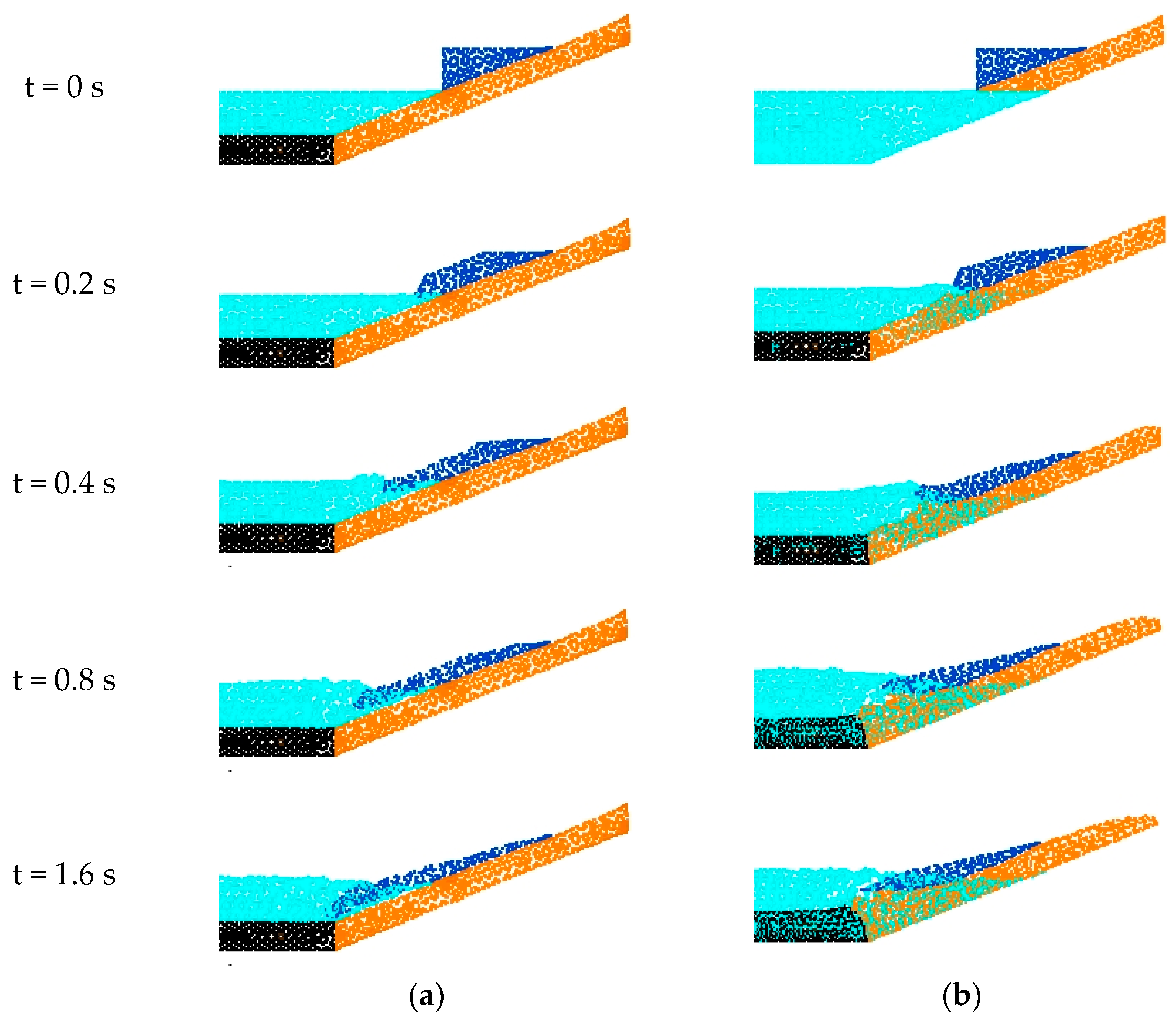
3.1. Topsoil Erosion by Granular Landslides
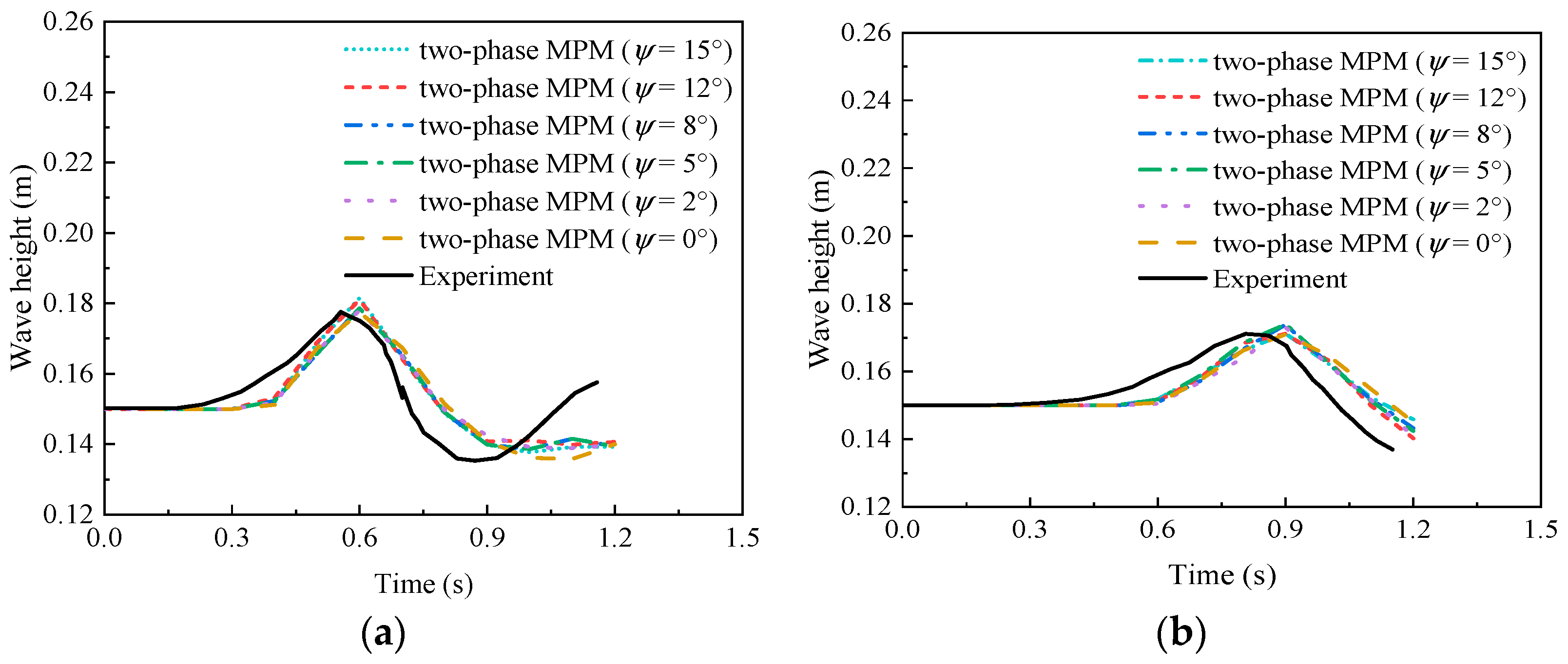
3.2. Surge Waves by Dry Granules Sliding on a Rigid Slope
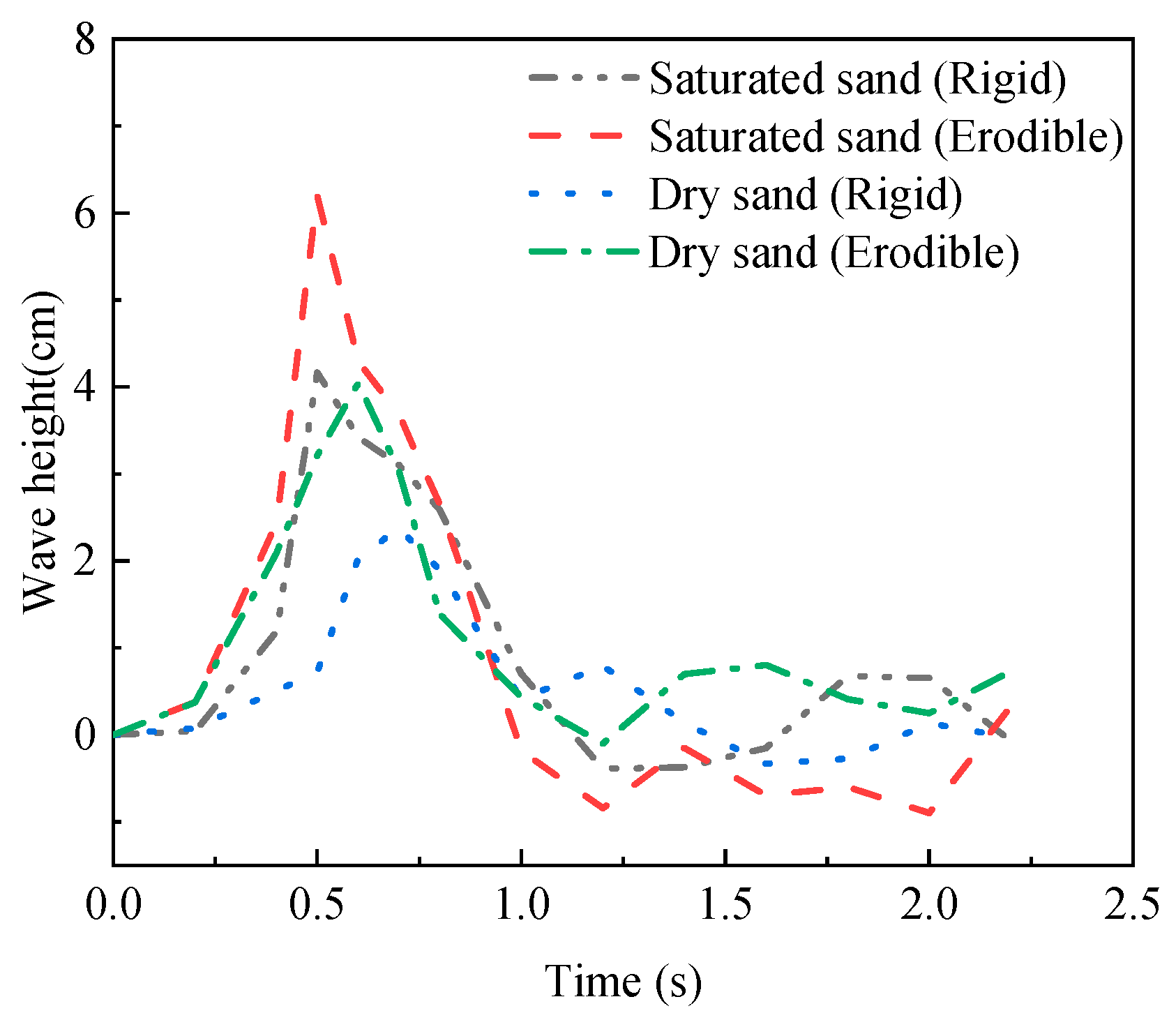
3.3. Surge Waves by Dry and Saturated Granules Sliding on Erodible Slope
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Iverson, R.M. The physics of debris flows. J. Rev. Geophys. 1997, 35, 245–296. [Google Scholar] [CrossRef] [Green Version]
- Evans, S.G. The 1946 Mount Colonel Foster rock avalanche and associated displacement wave, Vancouver Island, British Columbia. Can. Geotech. J. 1989, 26, 447–452. [Google Scholar] [CrossRef]
- Miller, D.J. Giant waves in Lituya Bay, Alaska. J. Geophys. Res. 1959, 64, 692. [Google Scholar] [CrossRef]
- Fritz, H.M.; Hager, W.H.; Minor, H. Lituya Bay case; rockslide impact and wave run-up. Sci. Tsunami Hazards 2001, 19, 3–22. [Google Scholar]
- Alonso, E.E.; Pinyol, N.M. Criteria for rapid sliding I. A review of Vaiont case. Eng. Geol. 2010, 114, 198–210. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Wang, P.Y.; Yu, T.; Zhang, F.; Men, Y.Q. Model test research on soil-landslide surge by river channel reservoir. Appl. Mech. Mater. 2013, 353–356, 2610–2613. [Google Scholar] [CrossRef]
- Wang, R.; Ding, M.; Wang, Y.; Xu, W.; Yan, L. Field characterization of landslide-induced surge waves based on computational fluid dynamics. Front. Physics. 2022, 9, 1–11. [Google Scholar] [CrossRef]
- Viroulet, S.; Cebron, D.; Kimmoun, O.; Kharif, C. Shallow water waves generated by subaerial solid landslides. Geophys. J. Int. 2013, 193, 747–762. [Google Scholar] [CrossRef] [Green Version]
- Jin, Y.C.; Guo, K.; Tai, Y.C.; Lu, C.H. Laboratory and numerical study of the flow field of subaqueous block sliding on a slope. Ocean Eng. 2016, 124, 371–383. [Google Scholar] [CrossRef]
- Qiu, L.; Tian, L.; Liu, X.; Han, Y. A 3D multiple-relaxation-time LBM for modeling landslide-induced surge waves. Eng. Anal. Bound. Elem. 2019, 102, 51–59. [Google Scholar] [CrossRef]
- Lynett, P.; Liu, P. A numerical study of the run-up generated by three-dimensional landslides. J. Geophys. Res.-Oceans 2005, 110, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Basu, D.; Das, K.; Green, S.; Janetzke, R.; Stamatakos, J. Numerical simulation of surface waves generated by a subaerial landslide at Lituya Bay Alaska. J. Offshore Mech. Arct. Eng. Trans. ASME 2010, 132, 041101. [Google Scholar] [CrossRef] [Green Version]
- Cremonesi, M.; Frangi, A.; Perego, U. A lagrangian finite element approach for the simulation of water-waves induced by landslides. Comput. Struct. 2011, 89, 1086–1093. [Google Scholar] [CrossRef]
- Xu, W.J.; Dong, X.Y. Simulation and verification of landslide tsunamis using a 3D SPH-DEM coupling method. Comput. Geotech. 2021, 129, 103803. [Google Scholar] [CrossRef]
- Xue, H.C.; Ma, Q.; Diao, M.J.; Jiang, L. Propagation characteristics of subaerial landslide-generated impulse waves. Environ. Fluid Mech. 2019, 19, 203–230. [Google Scholar] [CrossRef]
- Si, P.F.; Shi, H.B.; Yu, X.P. A general numerical model for surface waves generated by granular material intruding into a water body. Coast. Eng. 2018, 142, 42–51. [Google Scholar] [CrossRef]
- Rzadkiewicz, S.A.; Mariotti, C.; Heinrich, P. Numerical simulation of submarine landslides and their hydraulic effects. J. Waterw. Port Coast. Ocean. Eng.-ASCE 1997, 123, 149–157. [Google Scholar] [CrossRef]
- Zhao, L.; You, G. Rainfall affected stability analysis of maddingley brown coal eastern batter using plaxis 3D. Arab. J. Geosci. 2020, 13, 1071. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and applications to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Sulsky, D.; Chen, Z.; Schreyer, H.L. A particle method for history-dependent materials. Comput. Meth. Appl. Mech. Eng. 1994, 118, 179–196. [Google Scholar] [CrossRef]
- Koshizuka, S.; Oka, Y. Moving-particle semi-implicit method for fragmentation of incompressible fluid. Nucl. Sci. Eng. 1996, 123, 421–434. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef] [Green Version]
- Idelsohn, S.R.; Onate, E.; Del Pin, F. The particle finite element method: A powerful tool to solve incompressible flows with free-surfaces and breaking waves. Int. J. Numer. Methods Eng. 2004, 61, 964–989. [Google Scholar] [CrossRef] [Green Version]
- Jin, Y.F.; Yin, Z.Y.; Zhou, X.W.; Liu, F.T. A stable node-based smoothed PFEM for solving geotechnical large deformation 2d problems. Comput. Meth. Appl. Mech. Eng. 2021, 387, 114179. [Google Scholar] [CrossRef]
- Fu, L.; Jin, Y.C. Investigation of non-deformable and deformable landslides using meshfree method. Ocean Eng. 2015, 109, 192–206. [Google Scholar] [CrossRef]
- Qi, Y.T.; Chen, J.Y.; Zhang, G.B.; Xu, Q.; Li, J. An improved multi-phase weakly-compressible SPH model for modeling various landslides. Powder Technol. 2022, 397, 117120. [Google Scholar] [CrossRef]
- Qiu, L.C.; Jin, F.; Lin, P.Z.; Liu, Y.; Han, Y. Numerical simulation of submarine landslide tsunamis using particle based methods. J. Hydrodyn. 2017, 29, 542–551. [Google Scholar] [CrossRef]
- Zhao, K.L.; Qiu, L.C.; Liu, Y. Two-layer two-phase material point method simulation of granular landslides and generated tsunami waves. Phys. Fluids 2022, 34, 123312. [Google Scholar] [CrossRef]
- Nabian, M.A.; Farhadi, L. Multiphase mesh-free particle method for simulating granular flows and sediment transport. J. Hydraul. Eng. 2017, 143. [Google Scholar] [CrossRef]
- Bandara, S.; Soga, K. Coupling of soil deformation and pore fluid flow using material point method. Comput. Geotech. 2015, 63, 199–214. [Google Scholar] [CrossRef]
- Mangeney, A.; Roche, O.; Hungr, O.; Mangold, N.; Faccanoni, G.; Lucas, A. Erosion and mobility in granular collapse over sloping beds. J. Geophys. Res.-Earth Surf. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Mangeney, A.; Tsimring, L.S.; Volfson, D.; Aranson, I.S.; Bouchut, F. Avalanche mobility induced by the presence of an erodible bed and associated entrainment. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef] [Green Version]
- Yerro, A.; Soga, K.; Bray, J. Runout evaluation of oso landslide with the material point method. Can. Geotech. J. 2019, 56, 1304–1317. [Google Scholar] [CrossRef] [Green Version]
- Soga, K.; Alonso, E.; Yerro, A.; Kumar, K.; Bandara, S. Trends in large-deformation analysis of landslide mass movements with particular emphasis on the material point method. Geotechnique. 2016, 66, 248–273. [Google Scholar] [CrossRef] [Green Version]
- Du, W.J.; Sheng, Q.; Fu, X.D.; Chen, J.; Zhou, Y.Q. Extensions of the two-phase double-point material point method to simulate the landslide-induced surge process. Eng. Anal. Bound. Elem. 2021, 133, 362–375. [Google Scholar] [CrossRef]
- Abe, K.; Soga, K.; Bandara, S. Material point method for coupled hydromechanical problems. J. Geotech. Geoenviron. Eng. 2014, 140. [Google Scholar] [CrossRef]
- Bandara, S.; Soga, K. Coupling of soil deformation and pore fluid flow using material point method. Comput. Geotech. 2015, 65, 302. [Google Scholar] [CrossRef]
- Truesdell, C.; Toupin, R. The classical field theories. In Handbuch der Physik; Springer: Berlin/Heidelberg, Germany, 1960; Volume 2. [Google Scholar]
- Vardoulakis, I. Fluidisation in artesian flow conditions: Hydromechanically stable granular media. Geotechnique 2004, 54, 117–130. [Google Scholar] [CrossRef]
- Forchheimer, P. Wasserbewegung durch boden. Z. Ver. Dtsch. Ing. 1901, 45, 1782–1788. [Google Scholar]
- Ergun, S. Fluid flow through packed columns. J. Mater. Sci. Chem. Eng. 1952, 48, 89–94. [Google Scholar]
- Topin, V.; Monerie, Y.; Perales, F.; Radjai, F. Collapse dynamics and runout of dense granular materials in a fluid. Phys. Rev. Lett. 2012, 109, 188001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Viroulet, S.; Sauret, A.; Kimmoun, O.; Kharif, C. Granular collapse into water: Toward tsunami landslides. J. Vis. 2013, 16, 189–191. [Google Scholar] [CrossRef]
- Viroulet, S.; Sauret, A.; Kimmoun, O. Tsunami generated by a granular collapse down a rough inclined plane. EPL-Europhys Lett. 2014, 105, 34004. [Google Scholar] [CrossRef] [Green Version]
- Shi, C.Q.; An, Y.; Wu, Q.; Liu, Q.Q.; Cao, Z.X. Numerical simulation of landslide-generated waves using a soil-water coupling smoothed particle hydrodynamics model. Adv. Water Resour. 2016, 92, 130–141. [Google Scholar] [CrossRef] [Green Version]
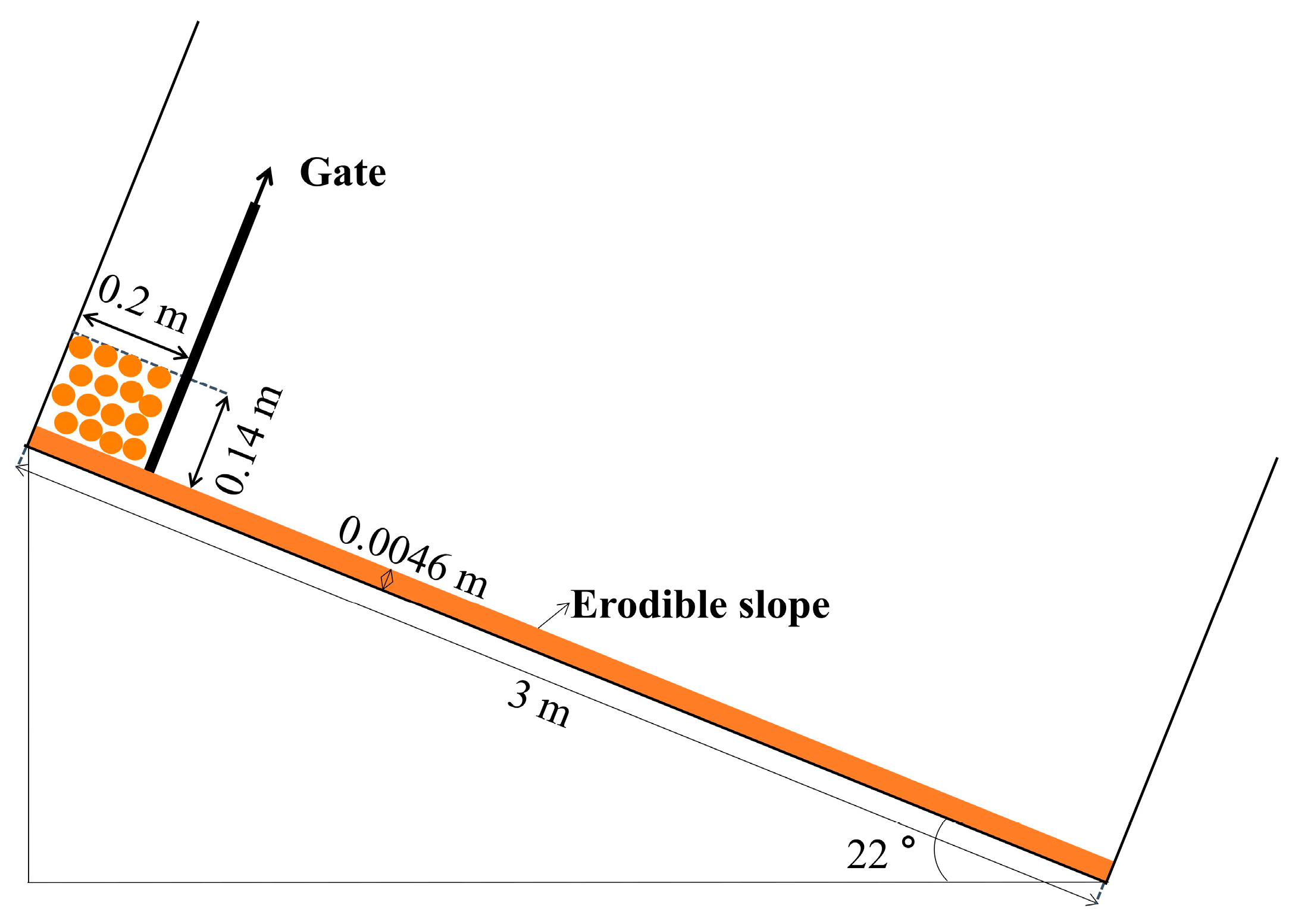
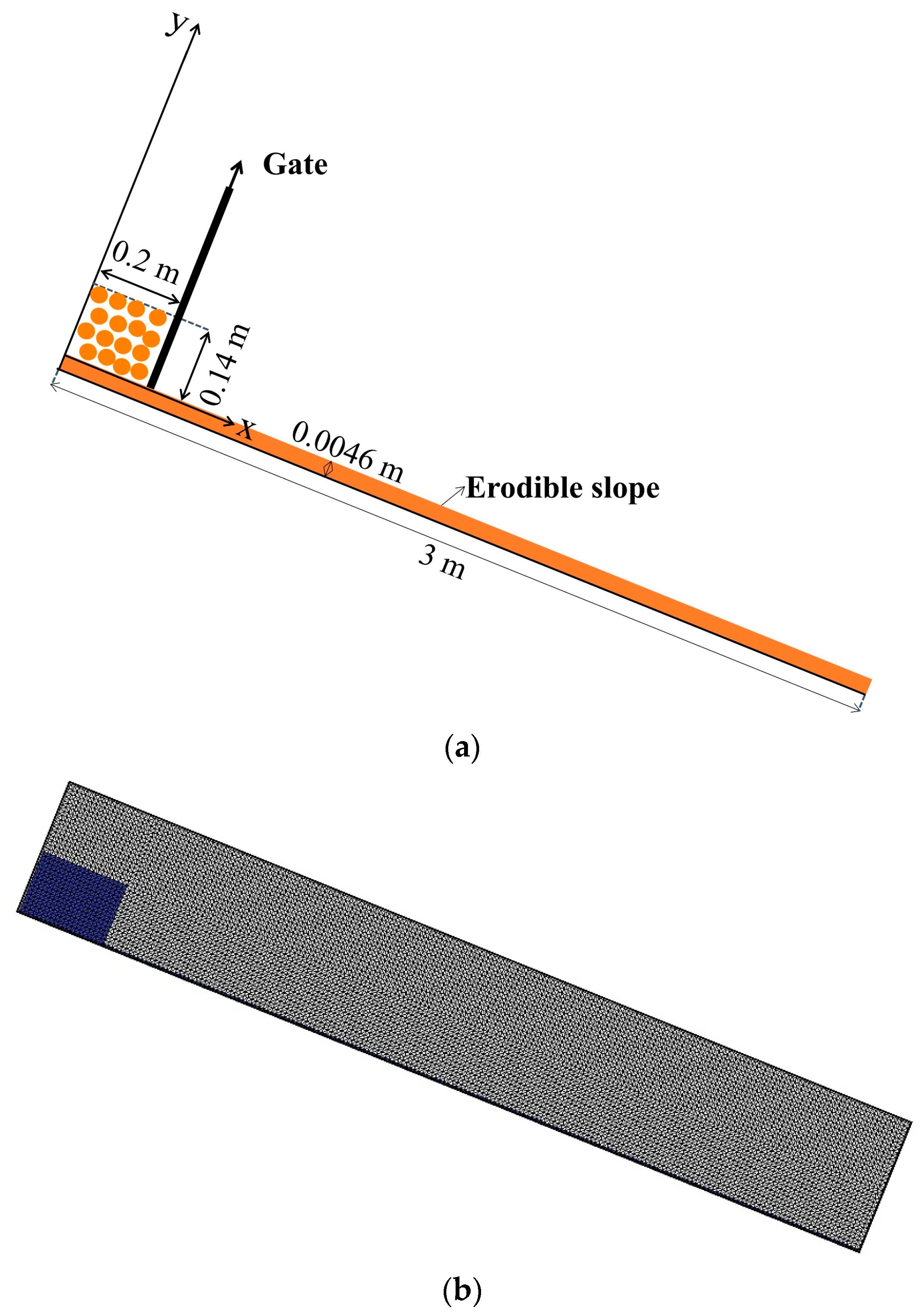
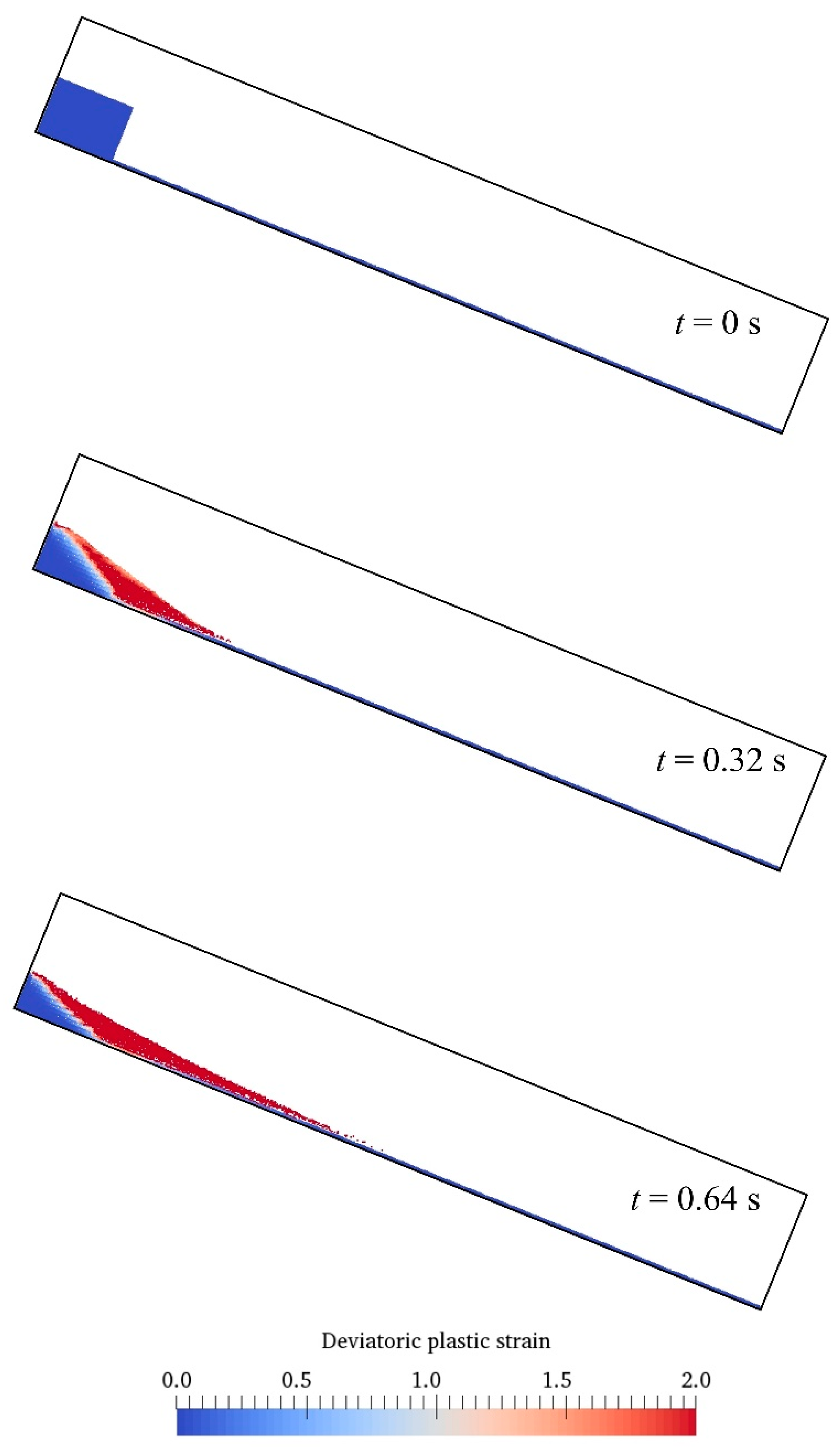
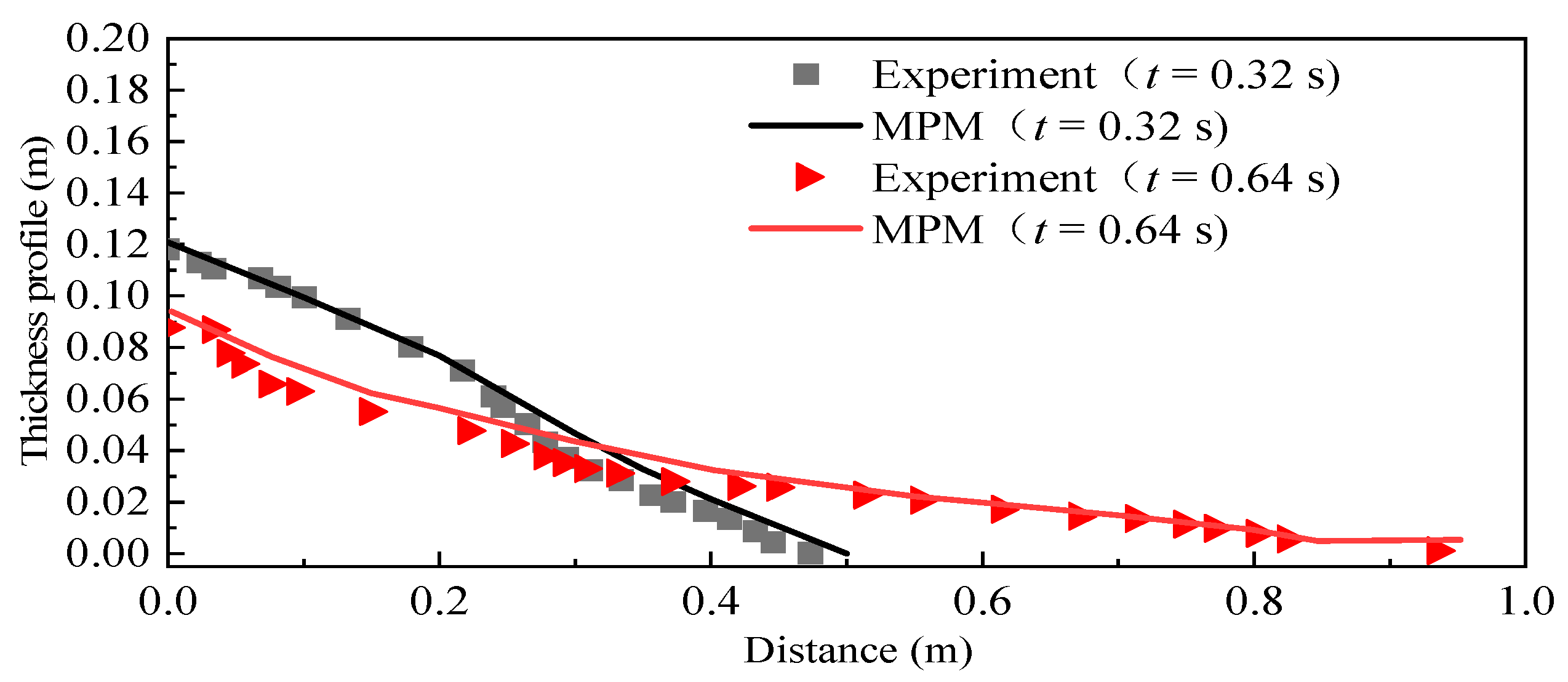
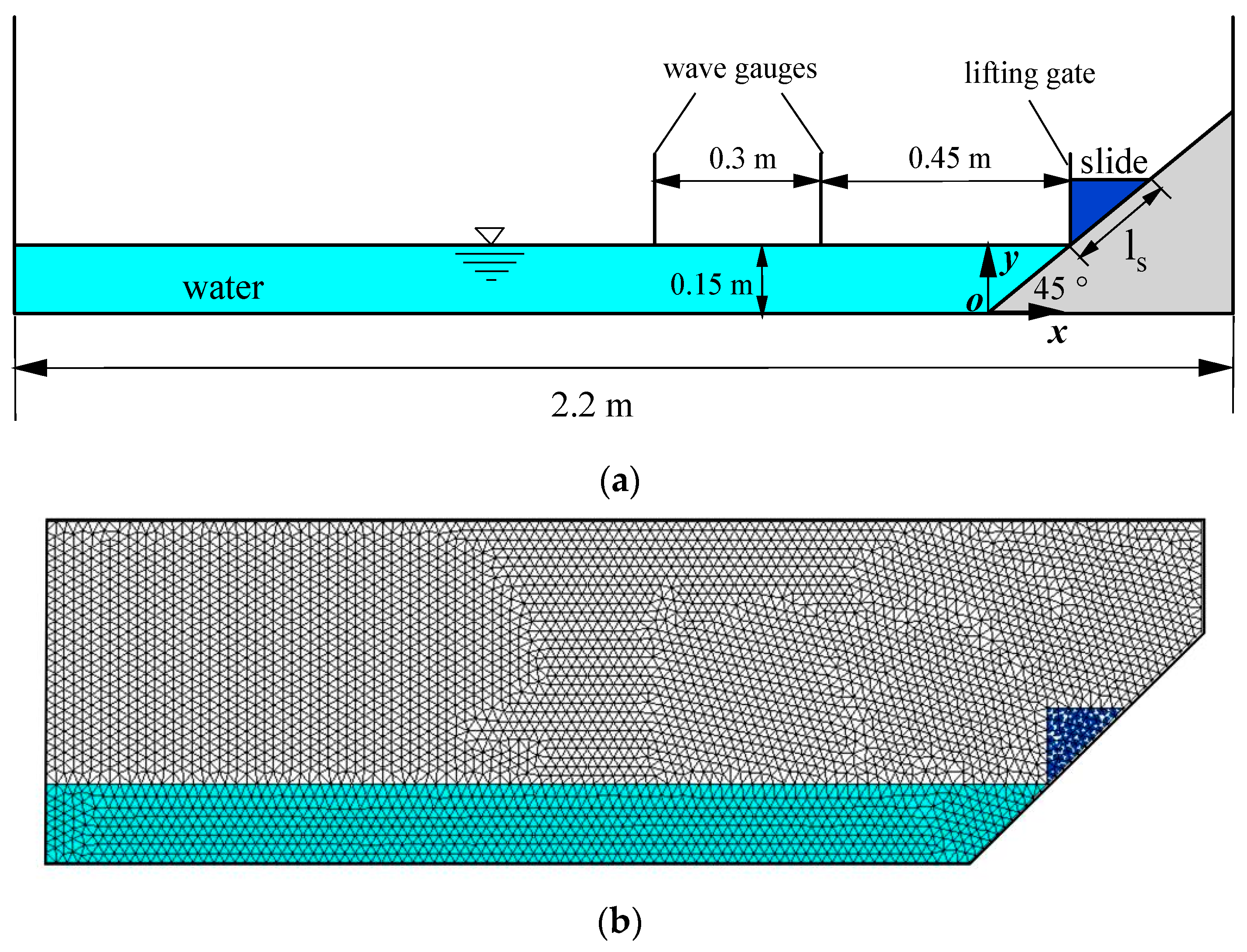
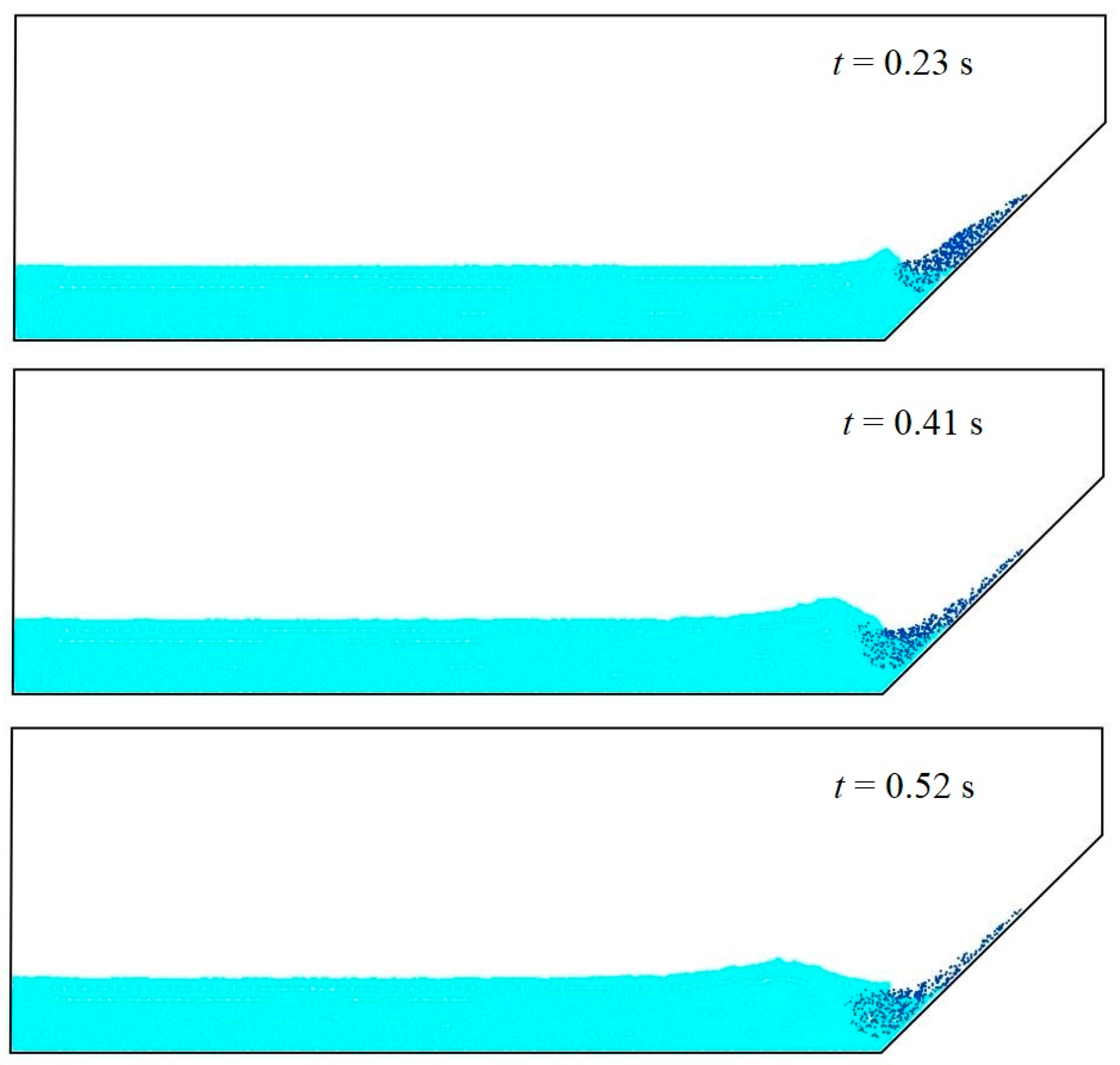
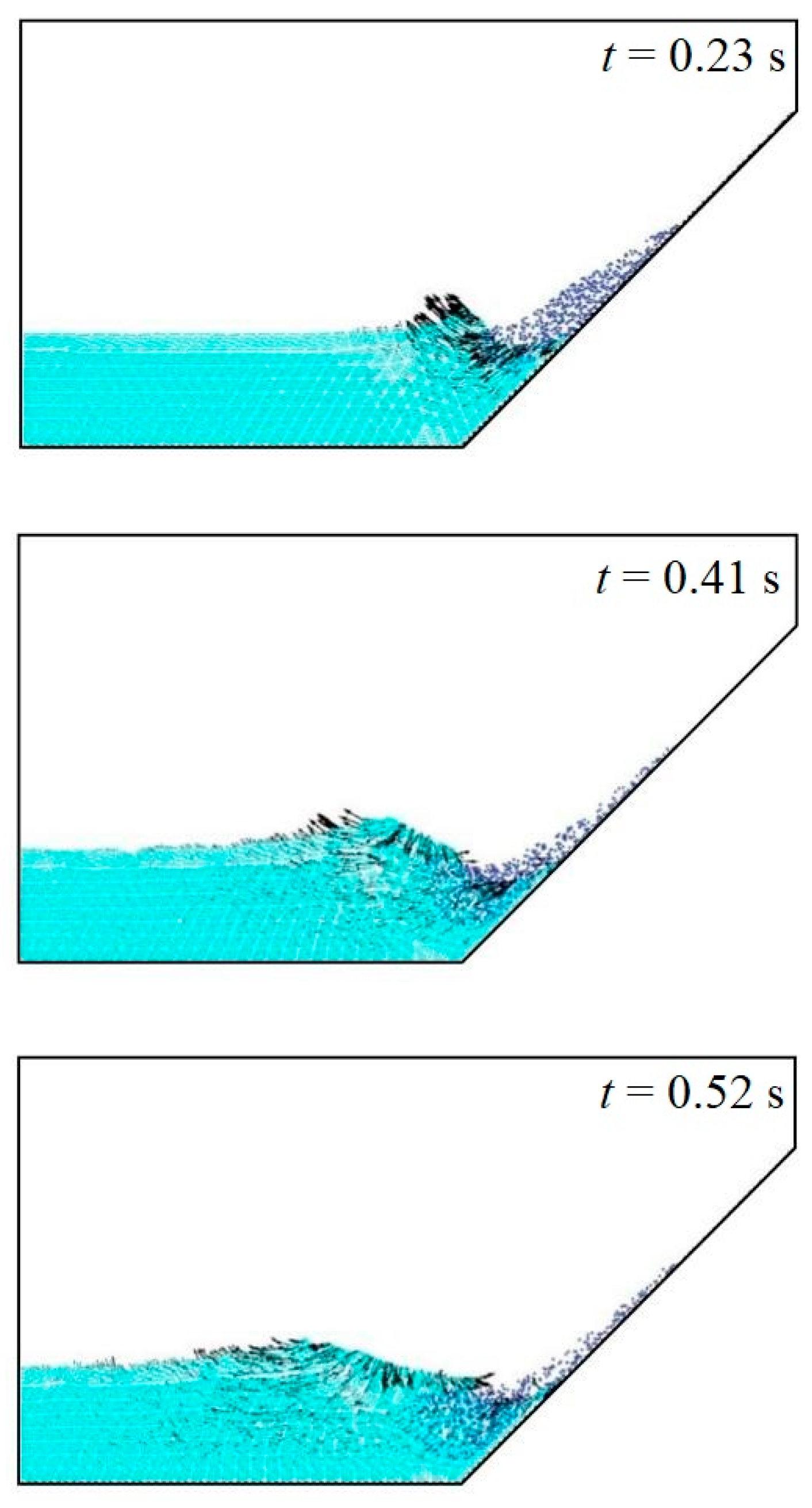
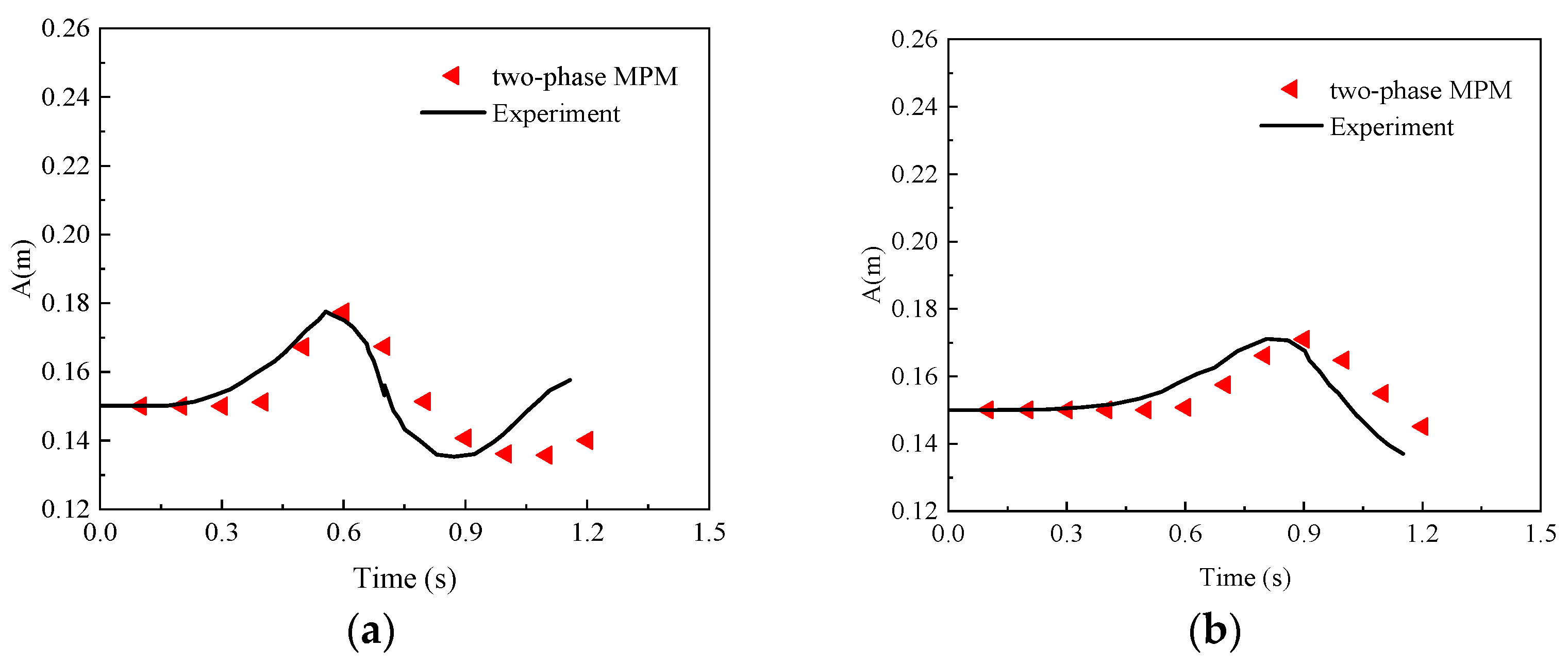
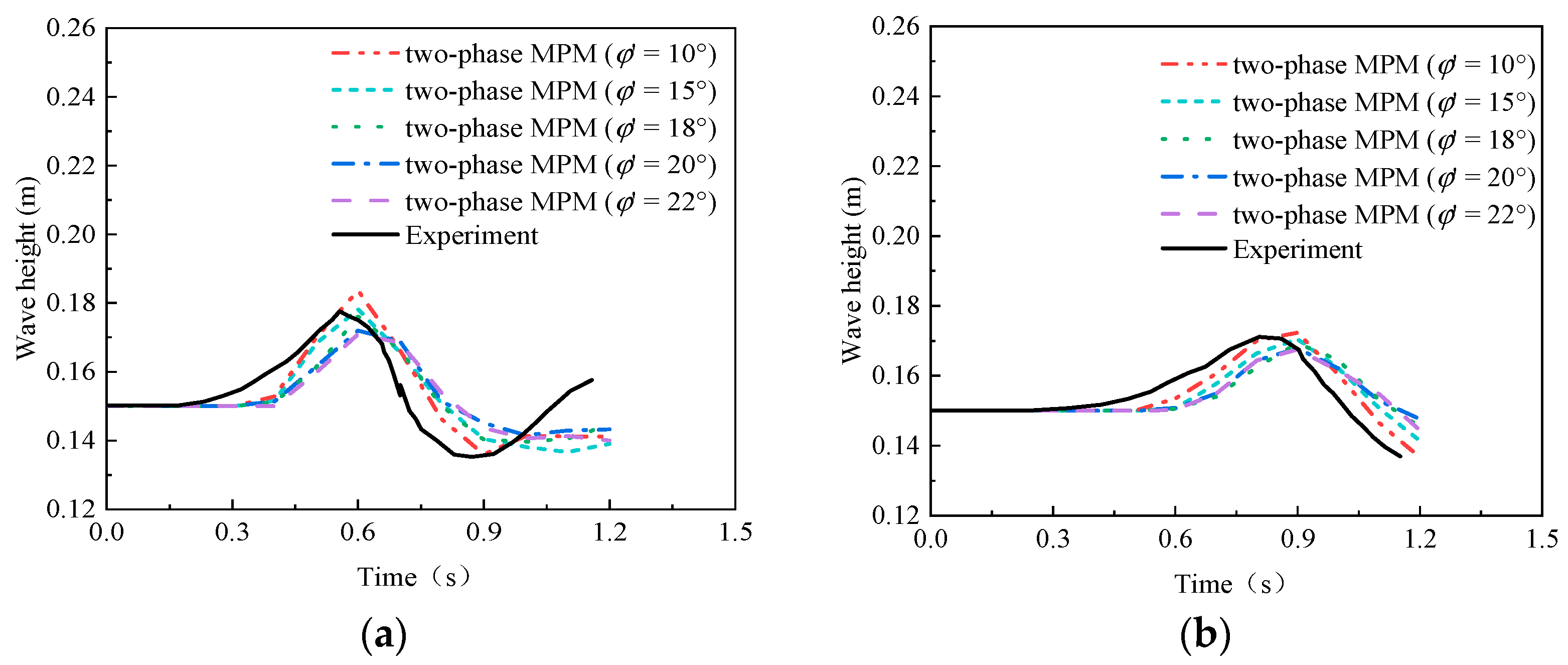
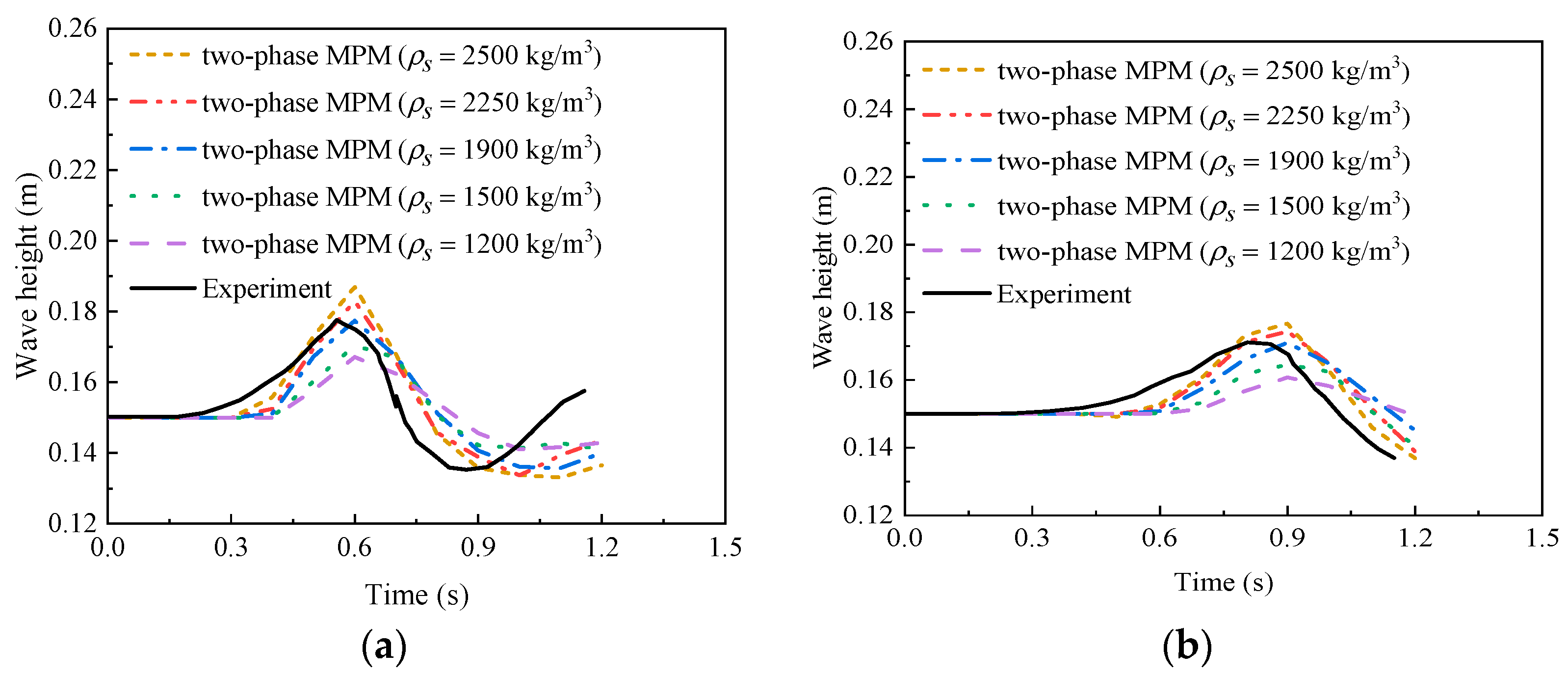

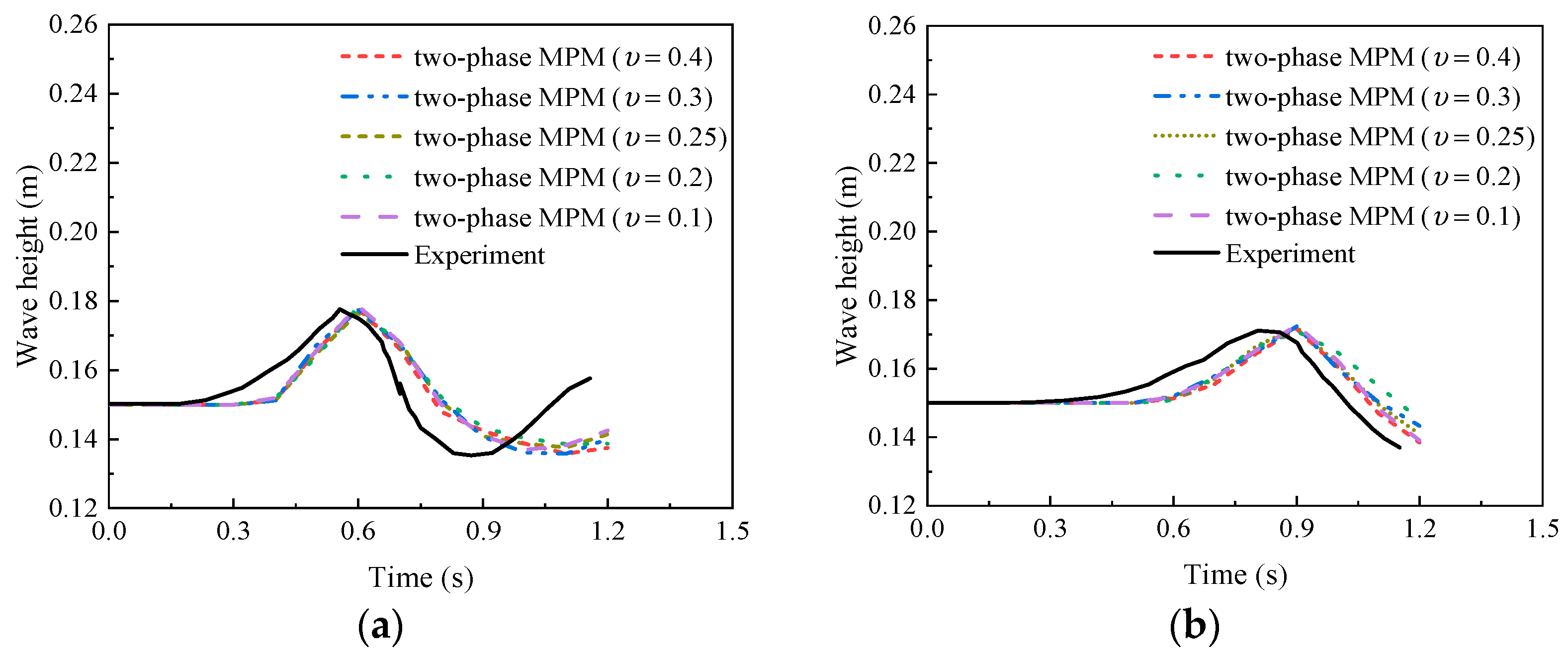



| Case | Slope Type | Elevation of Water Surface (m) | Tank Bottom Length (m) | The Dimensions of a Triangular Deposit (cm) | Slope Angle (°) |
|---|---|---|---|---|---|
| 1 | Rigid | 0.15 | 2.9 | 14.4 × 38 (dry/saturated) | 22 |
| 2 | Erodible | 0.15 | 2.9 | 14.4 × 38 (dry/saturated) | 22 |
| Material | Parameter | Numerical Values |
|---|---|---|
| Landslides | Density (kg/m3) | 1900 |
| Modulus of elasticity (kPa) | 1.0 × 104 | |
| Poisson ratio | 0.3 | |
| Internal friction angle (°) | 15 | |
| Expansion angle (°) | 0 | |
| Cohesion (kPa) | 0 | |
| Initial porosity | 0.4 | |
| Maximum porosity | 0.5 | |
| Mean diameter (mm) | 2 | |
| Rigid slope | Density (kg/m3) | 1900 |
| Modulus of elasticity (kPa) | 1.0 × 104 | |
| Poisson ratio | 0.3 | |
| Erodible slope | Density (kg/m3) | 1900 |
| Modulus of elasticity (kPa) | 1.0 × 104 | |
| Poisson ratio | 0.3 | |
| Expansion angle (°) | 0 | |
| Internal friction angle (°) | 15 | |
| Cohesion (kPa) | 0.1 | |
| Water | Density (kg/m3) | 1000 |
| Bulk modulus (kPa) | 2.15 × 104 | |
| Dynamic viscosity (kPa·s) | 1.00 × 10−6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, K.-L.; Qiu, L.-C.; Yuan, T.-J.; Wang, Y.; Liu, Y. Two-Phase MPM Simulation of Surge Waves Generated by a Granular Landslide on an Erodible Slope. Water 2023, 15, 1307. https://doi.org/10.3390/w15071307
Zhao K-L, Qiu L-C, Yuan T-J, Wang Y, Liu Y. Two-Phase MPM Simulation of Surge Waves Generated by a Granular Landslide on an Erodible Slope. Water. 2023; 15(7):1307. https://doi.org/10.3390/w15071307
Chicago/Turabian StyleZhao, Kai-Li, Liu-Chao Qiu, Tang-Jin Yuan, Yang Wang, and Yi Liu. 2023. "Two-Phase MPM Simulation of Surge Waves Generated by a Granular Landslide on an Erodible Slope" Water 15, no. 7: 1307. https://doi.org/10.3390/w15071307
APA StyleZhao, K.-L., Qiu, L.-C., Yuan, T.-J., Wang, Y., & Liu, Y. (2023). Two-Phase MPM Simulation of Surge Waves Generated by a Granular Landslide on an Erodible Slope. Water, 15(7), 1307. https://doi.org/10.3390/w15071307








