Changes in Tidal and Barometric Response of Groundwater during Earthquakes—A Review with Recommendations for Better Management of Groundwater Resources
Abstract
:1. Introduction
2. Groundwater Response to Earth Tides
2.1. Earth Tides
2.2. Tidal Response of Groundwater Level in Wells
2.3. Interpretation of Tidal Response of Groundwater in Aquifers
2.4. Assessing Earthquake Impact on Groundwater from Its Response to Earth Tides
3. Barometric Pressure and Barometric Response
3.1. Barometric Response
3.2. Barometric Response of the Groundwater Level in Wells
3.3. Assessing Earthquake Impact on Groundwater with Barometric Response
4. Mechanisms
5. Suggested Future Studies
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Castellano, C.; Cucci, L.; Tertulliani, A. Reappraisal of data of hydrological changes associated with some strong historical Italian earthquakes. Geosciences 2023, 13, 55. [Google Scholar] [CrossRef]
- Institute of Geophysics. CAS (China Earthquake Administration) China Earthquake Catalog; Center for Chinese Research Materials: Washington, DC, USA, 1976; p. 500. (In Chinese) [Google Scholar]
- Wakita, H. Water wells as possible indicators of tectonic strain. Science 1975, 189, 553–555. [Google Scholar] [CrossRef] [PubMed]
- Brodsky, E.E.; Roeloffs, E.; Woodcock, D.; Gall, I.; Manga, M. A mechanism for sustained water pressure changes induced by distant earthquakes. J. Geophys. Res. 2003, 108, 2390. [Google Scholar] [CrossRef] [Green Version]
- Chia, Y.P.; Wang, Y.S.; Wu, H.P.; Chiu, J.J.; Liu, C.-W. Changes of groundwater level due to the 1999 Chi-Chi earthquake in the Choshui River fan in Taiwan. Bull. Seismol. Soc. Am. 2001, 91, 1062–1068. [Google Scholar] [CrossRef] [Green Version]
- Hurst, A.; Scott, A.; Vigorito, M. Physical characteristics of sand injectites. Earth Sci. Rev. 2011, 106, 215–246. [Google Scholar] [CrossRef]
- Jonsson, S.; Segall, P.; Pedersen, R.; Björnsson, G. Postearthquake ground movements correlated to porepressure transients. Nature 2003, 424, 179–183. [Google Scholar] [CrossRef]
- Kitagawa, Y.; Koizumi, N.; Takahashi, M.; Matsumoto, N.; Sato, N. Changes in water levels or pressures associated with the 2004 earthquake off the west coast of northern Sumatra (M9.0). Earth Planets Space 2006, 58, 173–179. [Google Scholar] [CrossRef] [Green Version]
- Matsumoto, N.; Kitagawa, G.; Roeloffs, E.A. Hydrological response to earthquakes in the Haibara well, central Japan—I. Water level changes revealed using state space decomposition of atmospheric pressure, rainfall and tidal responses. Geophys. J. Int. 2003, 155, 885–898. [Google Scholar] [CrossRef] [Green Version]
- Quilty, E.; Roeloffs, E. Water level changes in response to the December 20, 1994, M4.7 earthquake near Parkfield California. Bull. Seismol. Soc. Am. 1997, 87, 310–317. [Google Scholar] [CrossRef]
- Roeloffs, E.A. Poroelastic techniques in the study of earthquake-related hydrogeologic phenomena. Adv. Geophys. 1996, 37, 135–195. [Google Scholar]
- Roeloffs, E.A. Persistent water level changes in a well near Parkfield, California, due to local and distant earthquakes. J. Geophys. Res. 1998, 103, 869–889. [Google Scholar] [CrossRef]
- Rojstaczer, S. Determination of fluid flowproperties from the response ofwater levels in wells to atmospheric loading. Water Resour. Res. 1988, 24, 1927–1938. [Google Scholar] [CrossRef] [Green Version]
- Rojstaczer, S.; Wolf, S. Permeability changes associated with large earthquakes: An example from Loma Prieta, California, 10/17/89 earthquake. Geology 1992, 20, 211–214. [Google Scholar] [CrossRef]
- Rojstaczer, S.; Wolf, S.; Michel, R. Permeability enhancement in the shallow crust as a cause of earthquake-induced hydrological changes. Nature 1995, 373, 237–239. [Google Scholar] [CrossRef]
- Sato, T.; Matsumoto, N.; Kitagawa, Y.; Koizumi, N.; Takahashi, M.; Kuwahara, Y.; Ito, H.; Cho, A.; Satoh, T.; Ozawa, K.; et al. Changes in water level associated with the 2003 Tokachi-oki earthquake. Earth Planets Space 2004, 56, 395–400. [Google Scholar] [CrossRef] [Green Version]
- Sil, S.; Freymueller, J.T. Well water level changes in Fairbanks, Alaska, due to the great Sumatra-Andaman earthquake. Earth Planets Space 2006, 58, 181–184. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.Y.; Cheng, L.H.; Chin, C.V.; Yu, S.-B. Coseismic hydrologic response of an alluvial fan to the 1999 Chi-Chi earthquake, Taiwan. Geology 2001, 29, 831–834. [Google Scholar] [CrossRef]
- Wang, C.Y.; Chia, Y. Mechanism of water-level changes during earthquakes near field versus intermediate field. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Wang, C.Y.; Manga, M.; Shirzaei, M.; Weingarten, M.; Wang, L.-P. Induced seismicity in Oklahoma affects shallow groundwater. Seismol. Res. Lett. 2017, 88, 956–962. [Google Scholar] [CrossRef]
- Whitehead, R.L.; Harper, R.W.; Sisco, H.G. Hydrologic changes associated with the October 28, 1983, Idaho earthquake. Pure Appl. Geophys. 1984, 122, 280–293. [Google Scholar] [CrossRef]
- Cox, S.C.; van Ballegooy, S.; Rutter, H.K.; Harte, D.S.; Holden, C.; Gulley, A.K.; Lacrosse, V.; Manga, M. Can artesian groundwater and earthquake-induced aquifer leakage exacerbate the manifestation of liquefaction? Eng. Geol. 2021, 281, 1059982. [Google Scholar] [CrossRef]
- Galli, P. New empirical relationships between magnitude and distance for liquefaction. Tectonophysics 2000, 324, 169–187. [Google Scholar] [CrossRef]
- Guliyev, I.S.; Huseynov, D.A. Relics of Mud Volcanoes in the Sedimentary Cover of the South Caspian Basin. Lithol. Miner. Resour. 2015, 50, 311–321. [Google Scholar] [CrossRef]
- Hosono, T.; Yamada, C.; Shibata, T.; Tawara, Y.; Wang, C.Y.; Manga, M.; Rahman, A.T.M.S.; Shimada, J. Coseismic groundwater drawdown along crustal ruptures during the 2016 Mw 7.0 Kumamoto earthquake. Water Resour. Res. 2019, 55, 5891–5903. [Google Scholar] [CrossRef] [Green Version]
- Manga, M. Origin of postseismic streamflow changes inferred from baseflow recession and magnitude-distance relation. Geophys. Res. Lett. 2001, 28, 2133–2136. [Google Scholar] [CrossRef] [Green Version]
- Muir-Wood, R.; King, G.C. Hydrological signatures of earthquake strain. J. Geophys. Res. Solid Earth 1993, 98, 22035–22068. [Google Scholar] [CrossRef]
- Wang, C.Y.; Manga, M. New streams and springs after the 2014 Mw6.0 South Napa earthquake. Nat. Commun. 2015, 6, 7597. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Waller, R.M.; Thomas, H.E.; Vorhis, R.C. Effects of the good friday earthquake on water supplies. J. Am. Water Work Assoc. 1965, 57, 123–131. [Google Scholar] [CrossRef]
- Wang, C.Y.; Barbour, A.J. Influence of pore pressure change on coseismic volumetric strain. Earth Planet. Sci. Lett. 2017, 475, 152–159. [Google Scholar] [CrossRef]
- Wang, C.Y.; Liao, X.; Wang, L.P.; Wang, C.-H.; Manga, M. Large earthquakes create vertical permeability by breaching aquitards. Water Resour. Res. 2016, 52, 5923–5937. [Google Scholar] [CrossRef] [Green Version]
- Geballe, Z.M.; Wang, C.Y.; Manga, M. A permeability-change model for water-level changes triggered by teleseismic waves. Geofluids 2011, 11, 302–308. [Google Scholar] [CrossRef]
- Wang, C.Y.; Wang, C.H.; Manga, M. Coseismic release of water from mountains: Evidence from the 1999 (Mw = 7.5) Chi-Chi, Taiwan, earthquake. Geology 2004, 32, 769–772. [Google Scholar] [CrossRef] [Green Version]
- Mohr, C.H.; Manga, M.; Wang, C.Y.; Kirchner, J.W.; Bronstert, A. Shaking water out of soil. Geology 2015, 43, 207–210. [Google Scholar] [CrossRef]
- Mohr, C.H.; Manga, M.; Wang, C.Y.; Korup, O. Regional changes in streamflow after a megathrust earthquake. Earth Planet Sci. Lett. 2017, 458, 418–428. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.Y.; Wang, C.H.; Kuo, C.Y. Temporal change in groundwater level following the 1999 Mw 7.5 Chi-Chi earthquake, Taiwan. Geofluids 2004, 4, 210–220. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.Y.; Manga, M. Water and Earthquake; Springer: Cham, Switzerland, 2021; Available online: https://link.springer.com/book/10.1007/978-3-030-64308-9 (accessed on 22 February 2023).
- Wang, C.Y.; Doan, M.L.; Xue, L.; Barbour, A.J. Tidal response of groundwater in a leaky aquifer—Application to Oklahoma. Water Resour. Res. 2018, 54, 8019–8033. [Google Scholar] [CrossRef]
- Zhang, S.C.; Shi, Z.M.; Wang, G.C. Comparison of aquifer parameters inferred from water level changes induced by slug test, earth tide and earthquake—A case study in the three Gorges area. J. Hydrol. 2019, 579, 124169. [Google Scholar] [CrossRef]
- Zhang, S.; Shi, Z.; Wang, G.; Zhang, Z.; Guo, H. The origin of hydrological responses following earthquakes in confined aquifer: Insight from water level, flow rate and temperature observations. Hydrol. Earth Syst. Sci. 2023, 27, 401–415. [Google Scholar] [CrossRef]
- Barbour, A.J.; Xue, L.; Roeloffs, E.; Rubinstein, J.L. Leakage and increasing fluid pressure detected in Oklahoma’s wastewater disposal reservoir. J. Geophys. Res. Solid Earth 2019, 124, 2896–2919. [Google Scholar] [CrossRef]
- Elkhoury, J.E.; Brodsky, E.E.; Agnew, D.C. Seismic waves increase permeability. Nature 2006, 441, 1135–1138. [Google Scholar] [CrossRef] [Green Version]
- Liao, X.; Wang, C.-Y.; Liu, C.-P. Disruption of groundwater systems by earthquakes. Geophys. Res. Lett. 2015, 42, 9758–9763. [Google Scholar] [CrossRef]
- Wang, C.Y. A new mechanism for earthquake-enhanced permeability. Water Resour. Res. 2022, 58, e2021WR031503. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, C.Y.; Fu, L.Y.; Yang, Q.Y. Are deep aquifers really confined? Water Resour. Res. 2021, 57, e2021WR030195. [Google Scholar] [CrossRef]
- Allègre, V.; Brodsky, E.E.; Xue, L.; Nale, S.M.; Parker, B.L.; Cherry, J.A. Using earthtide induced water pressure changes to measure in situ permeability: A comparison with longterm pumping tests. Water Resour. Res. 2016, 52, 3113–3126. [Google Scholar] [CrossRef]
- Hung, R.J.; Weingarten, M. Persistent groundwater reduction induced by dynamic stresses from the 2019 Ridgecrest earthquake observed within a fractured aquifer near Ash Meadows, Nevada, USA. Earth Planet. Sci. Lett. 2023, 605, 118034. [Google Scholar] [CrossRef]
- Qi, Z.; Shi, Z.; Rasmussen, T.C. Time- and frequency-domain determination of aquifer hydraulic properties using water-level responses to natural perturbations: A case study of the Rongchang Well, Chongqing, southwestern China. J. Hydrol. 2023, 617, 128820. [Google Scholar] [CrossRef]
- Shi, Z.; Wang, G.; Minga, M.; Wang, C.Y. Mechanism of co-seismic water level change following four great earthquakes—Insights from co-seismic responses throughout the Chinese mainland. Earth Planet. Sci. Lett. 2015, 430, 66–74. [Google Scholar] [CrossRef] [Green Version]
- Shi, Z.M.; Wang, G.C. Aquifers switched from confined to semiconfined by earthquakes. Geophys. Res. Lett. 2016, 43, 11166–111172. [Google Scholar] [CrossRef]
- Shi, Z.; Wang, C.-Y.; Yan, R. Frequency-dependent groundwater response to earthquakes. J. Hydrol. 2021, 603, 127153. [Google Scholar] [CrossRef]
- Xue, L.; Li, H.B.; Brodsky, E.E.; Xu, Z.-Q.; Kano, Y.; Wang, H.; Mori, J.J.; Si, J.-L.; Pei, J.-L.; Zhang, W. continuous permeability measurements record healing inside the Wenchuan earthquake fault zone. Science 2013, 340, 1555–1559. [Google Scholar] [CrossRef] [PubMed]
- Xue, L.; Brodsky, E.E.; Erskine, J.; Fulton, P.M.; Carter, R. A permeability and compliance contrast measured hydrogeologically on the San Andreas Fault. Geochem. Geophys. Geosyst. 2016, 17, 858–871. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Wang, C.Y.; Fu, L.Y.; Zhao, B.; Ma, Y. Unexpected far-field hydrological response to a great earthquake. Earth Planet. Sci. Lett. 2019, 519, 202–212. [Google Scholar] [CrossRef]
- Zhang, Y.; Manga, M.; Fu, L.Y.; Yang, Q.Y.; Cui, Z.D.; Huang, Y. Changes of Hydraulic Transmissivity Orientation Induced by Tele-Seismic Waves. Water Resour. Res. 2022, 58, e2022WR033272. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, L.-Y.; Zhu, A.; Zhao, L.; Qi, S.; Huang, T.; Ma, Y.; Zhang, W. Anisotropy and heterogeneity induced by shale in aquifer lithology—Influence of aquifer shale on the leaky model with tidal response analysis. Water Resour. Res. 2023, 59, e2021WR031451. [Google Scholar] [CrossRef]
- He, A.; Singh, R.P. Coseismic groundwater temperature response associated with the Wenchuan earthquake. Pure Appl. Geophys. 2020, 177, 109–120. [Google Scholar] [CrossRef]
- Hwang, J.-H.; Yang, C.-W.; Chen, C.-H. Investigations on soil liquefaction during the Chi-Chi earthquake. Soils Found. 2003, 43, 107–123. [Google Scholar] [CrossRef] [Green Version]
- Jacob, C.E. The flow of water in an elastic artesian aquifer. EOS Trans. AGU 1940, 21, 574–586. [Google Scholar] [CrossRef]
- Thomas, A.; Fortin, J.; Vitteecoq, B.; Liolette, S. Earthquake and heavy rainfall influence on aquifer properties: A new coupled earth and barometric tidal response model in a confined bi-layer aquifer. Water Resour. Res. 2023; in review. [Google Scholar] [CrossRef]
- Valois, R.; Rau, G.C.; Vouillamoz, J.-M.; Derode, B. Estimating hydraulic properties of the shallow subsurface using the groundwater response to Earth and atmospheric tides: A comparison with pumping tests. Water Resour. Res. 2022, 58, e2021WR031666. [Google Scholar] [CrossRef]
- Zhang, H.; Shi, Z.M.; Wang, G.C.; Yan, X.; Liu, C.L.; Sun, X.L.; Ma, Y.C.; Wen, D.G. Different sensitivities of earthquake-ihnduced water level and ydrogeological property variations in two aquifer systems. Water Resour. Res. 2021, 57, e2020WR028217. [Google Scholar] [CrossRef]
- Doan, M.L.; Brodsky, E.E.; Prioul, R.; Signer, C. Tidal Analysis of Borehole Pressure: A Tutorial; Schlumberger-Doll Research Report; Schlumberger: Cambridge, MA, USA, 2006. [Google Scholar]
- Wilhelm, H.; WZürn; Wenzel, H.-G. (Eds.) Tidal Phenomena; Lecture Notes in Earth Sciences; Springer: Berlin/Heidelberg, Germany, 1997; Volume 66. [Google Scholar]
- Agnew, D.C. Earth tides. Treatise Geophys. 2007, 3, 163–195. [Google Scholar]
- Beaumont, C.; Berger, J. An analysis of tidal strain observations from the United States of America: I. The laterally homogeneous tide. Bull. Seismol. Soc. Am. 1975, 65, 1613–1629. [Google Scholar] [CrossRef]
- Harrison, J.C. Cavity and topography effects on the measurement of tilt and strain. EOS. Trans. Am. Geophys. Union 1974, 56, 1151. [Google Scholar]
- Hsieh, P.; Bredehoeft, J.; Farr, J. Determination of aquifer permeability from earthtide analysis. Water Resour. Res. 1987, 23, 1824–1832. [Google Scholar] [CrossRef]
- Wang, H.F. Theory of Linear Poroelasticity with Applications to Geomechanics and Hydrogeology; Princeton University Press: Princeton, NJ, USA, 2000. [Google Scholar]
- McMillan, T.C.; Rau, G.C.; Timms, W.A.; Andersen, M.S. Utilizing the impact of Earth and atmospheric tides on groundwater systems: A review reveals the future potential. Rev. Geophys. 2019, 57, 281–315. [Google Scholar] [CrossRef] [Green Version]
- Cutillo, P.A.; Bredehoeft, J.D. Estimating aquifer properties from the water level response to earth tides. Groundwater 2011, 49, 600–610. [Google Scholar] [CrossRef]
- Galloway, D.L.; Rojstaczer, S.A. Inferences about formation elastic and fluid flow properties from the frequency response of water levels to atmospheric loads and earth tides: 4th Canadian/American conference on hydrogeology: Fluid flow. In Proceedings of the Heat Transfer and Mass Transport in Fractured Rocks, Banff, AB, Canada, 21–24 June 1988; pp. 100–113. [Google Scholar]
- Ingebritsen, S.E.; Sanford, W.E.; Neuzil, C.E. Groundwater in Geologic Processes, 2nd ed.; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Hantush, M.S.; Jacob, C.E. Non-steady Green’s functions for an infinite strip of leaky aquifers. Trans. Am. Geophys. Union 1955, 36, 101–112. [Google Scholar] [CrossRef]
- Yang, Q.-Y.; Zhang, Y.; Fu, L.-Y.; Ma, Y.; Hu, J. Vertical leakage occurred after an earthquake: Suggestions for utilizing the mixed flow model. Lithosphere 2021, 2021, 8281428. [Google Scholar] [CrossRef]
- Hanson, J.M.; Owen, L.B. Fracture orientation analysis by the solid earth tidal strain method. In Spe Annual Technical Conference and Exhibition; OnePetro: Richardson, TX, USA, 1982. [Google Scholar]
- Liao, X.; Wang, C.-Y.; Wang, Z.-Y. Seasonal change of groundwater response to Earth tides. J. Hydrol. 2022, 612, 128118. [Google Scholar] [CrossRef]
- Odling, N.E.; Serrano, R.P.; Hussein, M.E.A.; Riva, M.; Guadagnini, A. Detecting the vulnerability of groundwater in semi-confined aquifers using barometric response functions. J. Hydrol. 2015, 520, 143–156. [Google Scholar] [CrossRef]
- He, G.; Shi, Z.; Rasmussen, T.C.; Qi, Z. Fault zone hydraulic parameter estimation by passive methods using natural forces. Water Resour. Res. 2023, 59, e2022WR033377. [Google Scholar] [CrossRef]
- Hussein, M.E.; Odling, N.E.; Clark, R.A. Borehole water level response to barometric pressure as an indicator of aquifer vulnerability. Water Resour. Res. 2013, 49, 7102–7119. [Google Scholar] [CrossRef]
- Obermeier, S.F.; Dickenson, S.E. Liquefaction evidence for the strength of ground motions resulting from late Holocene Cascadia subduction earthquakes, with emphasis on the event of 1700 A.D. Bull. Seismol. Soc. Am. 2000, 90, 876–896. [Google Scholar] [CrossRef]
- Zhang, H.; Shi, Z.; Wang, G.; Sun, X.; Yan, R.; Liu, C. Large earthquake reshapes the groundwater flow system: Insight from the water-level response to Earth tides and atmospheric pressure in a deep well. Water Resour. Res. 2019, 55, 4207–4219. [Google Scholar] [CrossRef] [Green Version]
- Beresnev, I.; Gaul, W.; Vigil, R.D. Direct pore-level observation of permeability increase in two-phase flow by shaking. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef] [Green Version]
- Crews, J.B.; Cooper, C.A. Experimental evidence for seismically initiated gas bubble nucleation and growth in groundwater as a mechanism for coseismic borehole water level rise and remotely triggered seismicity. J. Geophys. Res. Solid Earth 2014, 119, 7079–7091. [Google Scholar] [CrossRef]
- Deng, W.; Cardenas, M.B. Dynamics and dislodgment from pore constrictions of a trapped nonwetting droplet stimulated by seismic waves. Water Resour. Res. 2013, 49, 4206–4218. [Google Scholar] [CrossRef]
- National Research Council. State of the Art and Practice in the Assessment of Earthquake-Induced Soil Liquefaction and Its Consequences; National Academies Press: Washington, DC, USA, 2016. [Google Scholar] [CrossRef]
- Manga, M.; Beresnev, I.; Brodsky, E.E.; Elkhoury, J.E.; Elsworth, D.; Ingebritsen, S.E.; Mays, D.C.; Wang, C.-Y. Changes in permeability caused by transient stresses: Field observations, experiments, and mechanics. Rev. Geophys. 2012, 50, RG2004. [Google Scholar] [CrossRef]
- Candela, T.; Marone, E.E.B.C.; Elsworth, D. Laboratory evidence for particle mobilization as a mechanism for permeability enhancement via dynamic stressing. Earth Planet. Sci. Lett. 2014, 392, 279–291. [Google Scholar] [CrossRef] [Green Version]
- Elkhoury, J.E.; Niemeijer, A.; Brodsky, E.E.; Marone, C. Laboratory observations of permeability enhancement by fluid pressure oscillation of in-situ fractured rock. J. Geophys. Res. 2011, 116, B02311. [Google Scholar] [CrossRef] [Green Version]
- Faoro, I.; Elsworth, D.; Marone, C. Permeability evolution during dynamic stressing of dual permeability media. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.Y. Liquefaction beyond the near field. Seismol. Res. Lett. 2007, 78, 512–517. [Google Scholar] [CrossRef]
- Obermeir, S.F. The New Madrid Earthquakes: An Engineering-Geologic Interpretation of Relic Liquefaction Features; US Geological Survey Professional Paper; USGS: New Madrid, MO, USA, 1989; p. 114, 1336-B.
- Alvarez, W.; Staley, E.; O’Connor, D.; Chan, M.A. Synsedimentary deformation in the Jurassic of southeastern Utah—A case of impact shaking? Geology 1998, 26, 579–582. [Google Scholar] [CrossRef]
- Huuse, M.; Jackson, C.A.-L.; Van Rensbergen, P.; Davies, R.; Felmings, P.B.; Dixon, R.J. Subsurface sediment remobilization and fluid flow in sedimentary basins: An overview. Basin Res. 2010, 22, 342–360. [Google Scholar] [CrossRef]
- Sherry, T.J.; Rowe, C.D.; Kirkpatrick, J.D.; Brodsky, E.E. Emplacement and dewatering of the world’s largest exposed sand injectite complex. Geochem. Geophys. Geosys. 2012, 13. [Google Scholar] [CrossRef] [Green Version]
- Thompson, B.J.; Moore, J.C.; Garrison, R.E. A Reservoir-scale Miocene Injectite near Santa Cruz, California. AAPG Mem. 2007, 87, 151–162. [Google Scholar]
- Andresen, K.J. Fluid flow features in hydrocarbon plumbing systems: What do they tell us about the basin evolution? Marine Geol. 2012, 332–334, 89–108. [Google Scholar] [CrossRef]
- Cartwirght, J. Regionally extensive emplacement of sandstone intrusions: A brief review. Basin Res. 2010, 22, 502–516. [Google Scholar] [CrossRef]
- Che, Y.-T.; Yu, J.-Z.; Liu, C.-L.; Wan, Y.-F.; Luo, S.-Q.; He, Y.-Q.; Xiao, Z.-D. Investigation and analysis to co-seismic blowout in Chagan well. Seismol. Geol. 2009, 31, 226–232. [Google Scholar] [CrossRef]
- Wang, C.Y.; Manga, M. Hydrogeologic responses to earthquakes and a general metric. Geofluids 2010, 10, 206–216. [Google Scholar]
- Yan, X.; Shi, Z.; Wang, C.Y.; Ingebritsen, S.E.; Manga, M. Violent groundwater eruption triggered by a distant earthquake. Geophys. Res. Lett. 2022, 49, e2022GL101239. [Google Scholar] [CrossRef]
- Gao, X.; Sato, K.; Horne, R. N General solution for tidal behavior in confined and semiconfined aquifers considering skin and–wellbore storage effects. Water Resour. Res. 2020, 56, e2020WR027195. [Google Scholar] [CrossRef]
- Beroza, G.C.; Segou, M.; Mostafa Mousavi, S. Machine learning and earthquake forecasting—Next steps. Nat. Commun. 2021, 12, 4761. [Google Scholar] [CrossRef]
- Galkina, A.; Grafeeva, N. Machine Learning Methods for Earthquake Prediction: A Survey. In Proceedings of the Fourth Conference on Software Engineering and Information Management (SEIM-2019), Saint Petersburg, Russia, 13 April 2019; full papers. p. 25. [Google Scholar]
- Mignan, A.; Broccardo, M. Neural Network Applications in Earthquake Prediction (1994–2019): Meta- Analytic and Statistical Insights on Their Limitations. Seismol. Res. Lett. 2020, 91, 2330–2342. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Ellsworth, W.L.; Zhu, W.; Chuang, L.Y.; Beroza, G.C. Earthquake transformer—An attentive deep-learning model for simultaneous earthquake detection and phase picking. Nat. Commun. 2020, 11, 3952. [Google Scholar] [CrossRef] [PubMed]
- Perol, T.; Gharbi, M.; Denolle, M. Convolutional neural network for earthquake detection and location. Sci. Adv. 2018, 4, e1700578. [Google Scholar] [CrossRef] [Green Version]
- Yokoo, K.; Ishida, K.; Nagasato, T.; Kawagoshi, Y.; Ito, H. Reconstruction of groundwater level at Kumamoto, Japan by means of deep learning to evaluate its increase by the 2016 earthquake. In IOP Conference Series: Earth and Environmental Science; Iop Science: Bristol, UK, 2021; Volume 851, p. 012032. [Google Scholar]
- Wang, C.Y.; Zhu, A.Y.; Liao, X.; Manga, M.; Wang, L. Capillary effects on groundwater response to Earth tides. Water Resour. Res. 2019, 55, 6886–6895. [Google Scholar] [CrossRef]
- Yan, X.; Shi, Z.; Wang, G.; Zhang, H.; Bi, E. Detection of possible hydrological precursor anomalies using long short-term memory: A case study of the 1996 Lijiang earthquake. J. Hydrol. 2021, 599, 126369. [Google Scholar] [CrossRef]
- Gitis, V.G.; Derendyaev, A.B. Machine learning methods for seismic hazards forecast. Geosciences 2019, 9, 308. [Google Scholar] [CrossRef] [Green Version]
- Scorzini, A.R.; Bacco, M.D.; De Luca, G.; Tallini, M. Deep learning for earthquake hydrology? Insights from the karst Gran Sasso aquifer in central Italy. J. Hydrol. 2023, 617, 129002. [Google Scholar] [CrossRef]
- Liang, X.Y.; Wang, C.Y.; Ma, E.Z.; Zhang, Y.K. Effects of unsaturated flow on hydraulic head response to Earth tides—An analytical model. Water Resour. Res. 2022, 58, e2021WR030337. [Google Scholar] [CrossRef]
- Zhang, J.; Liang, X.; Wang, C.Y. Capillary impact on tidal response of groundwater in two-dimensional unconfined aquifers with finite thickness, anisotropy, and borehole storage—An analytical model. Water Resour. Res. 2023; in press. [Google Scholar]
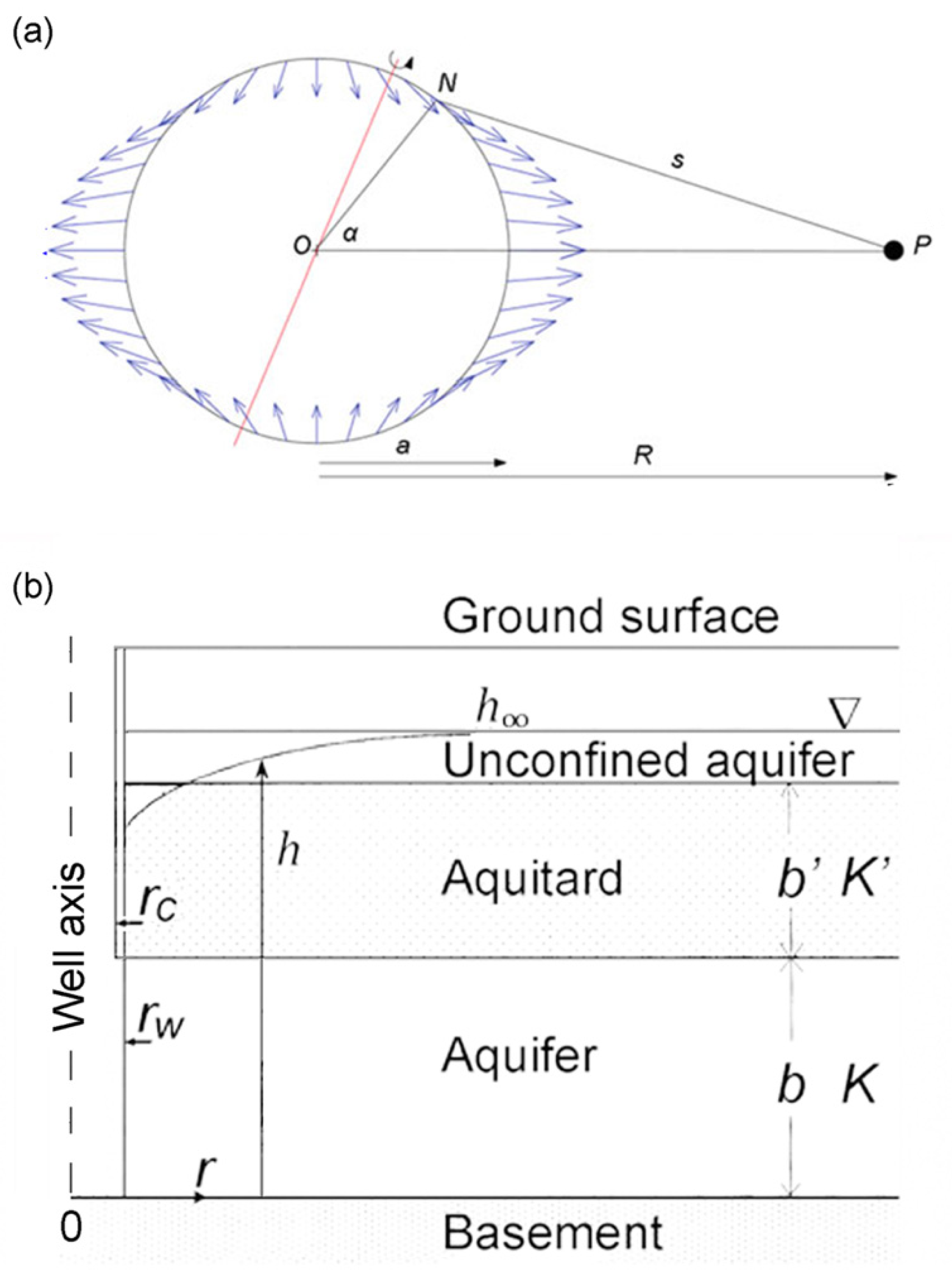

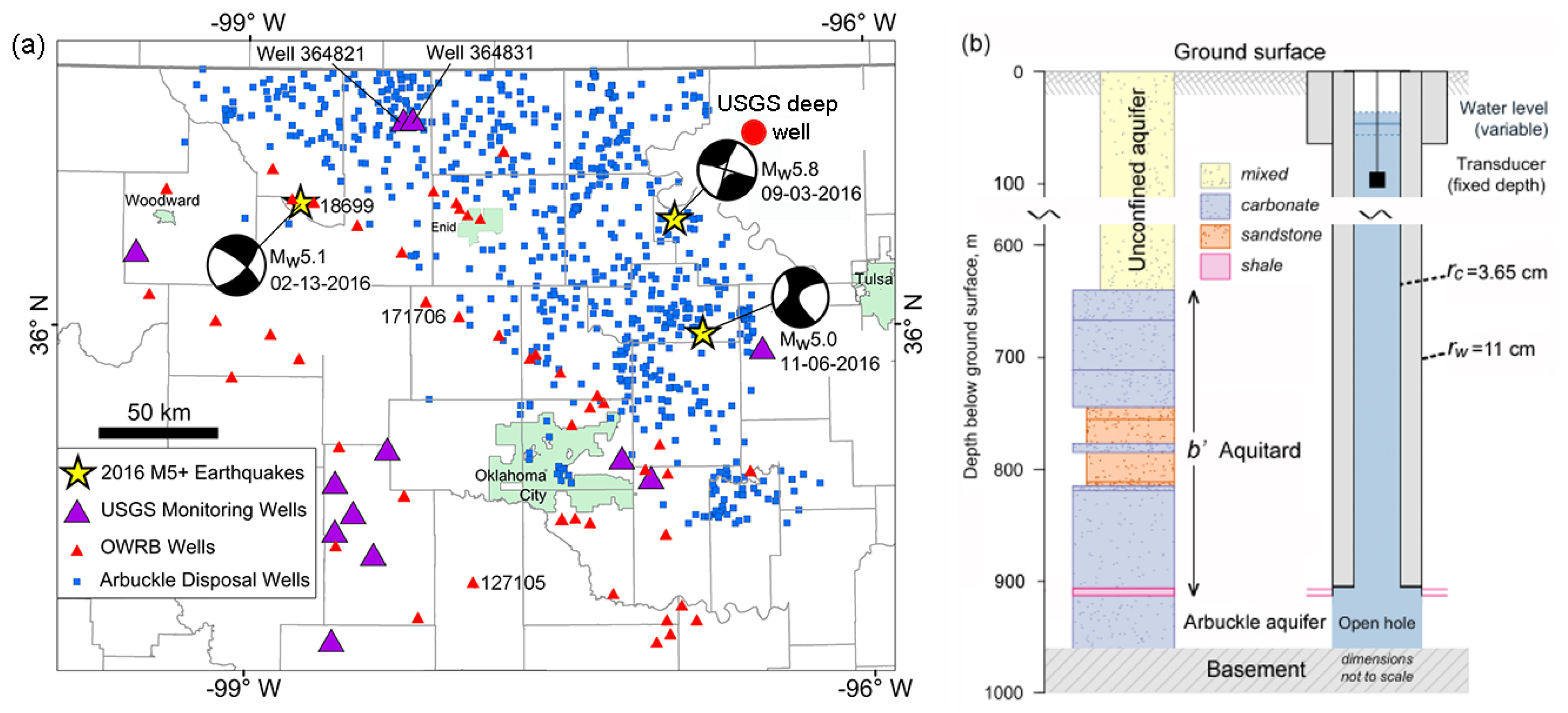
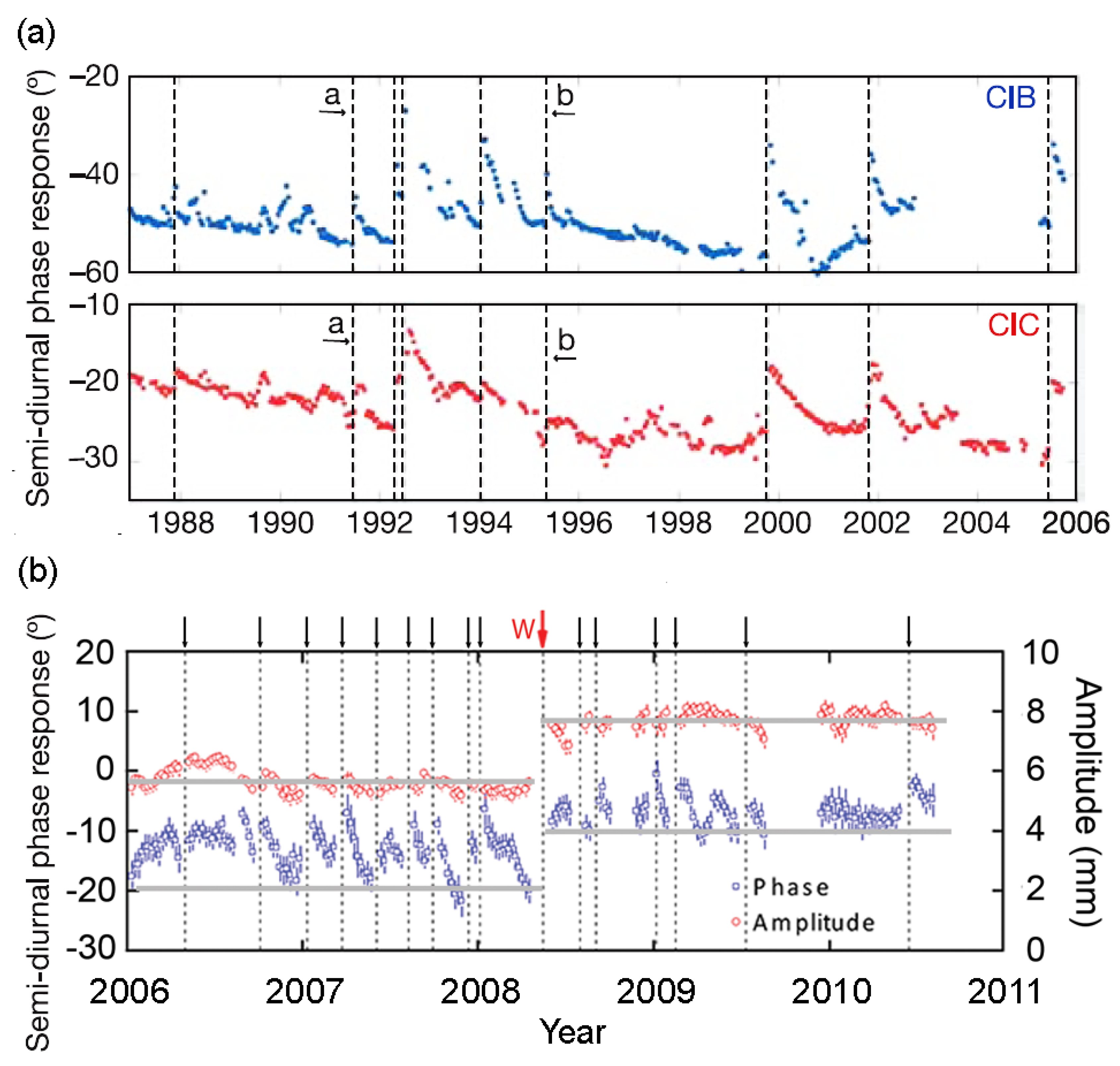
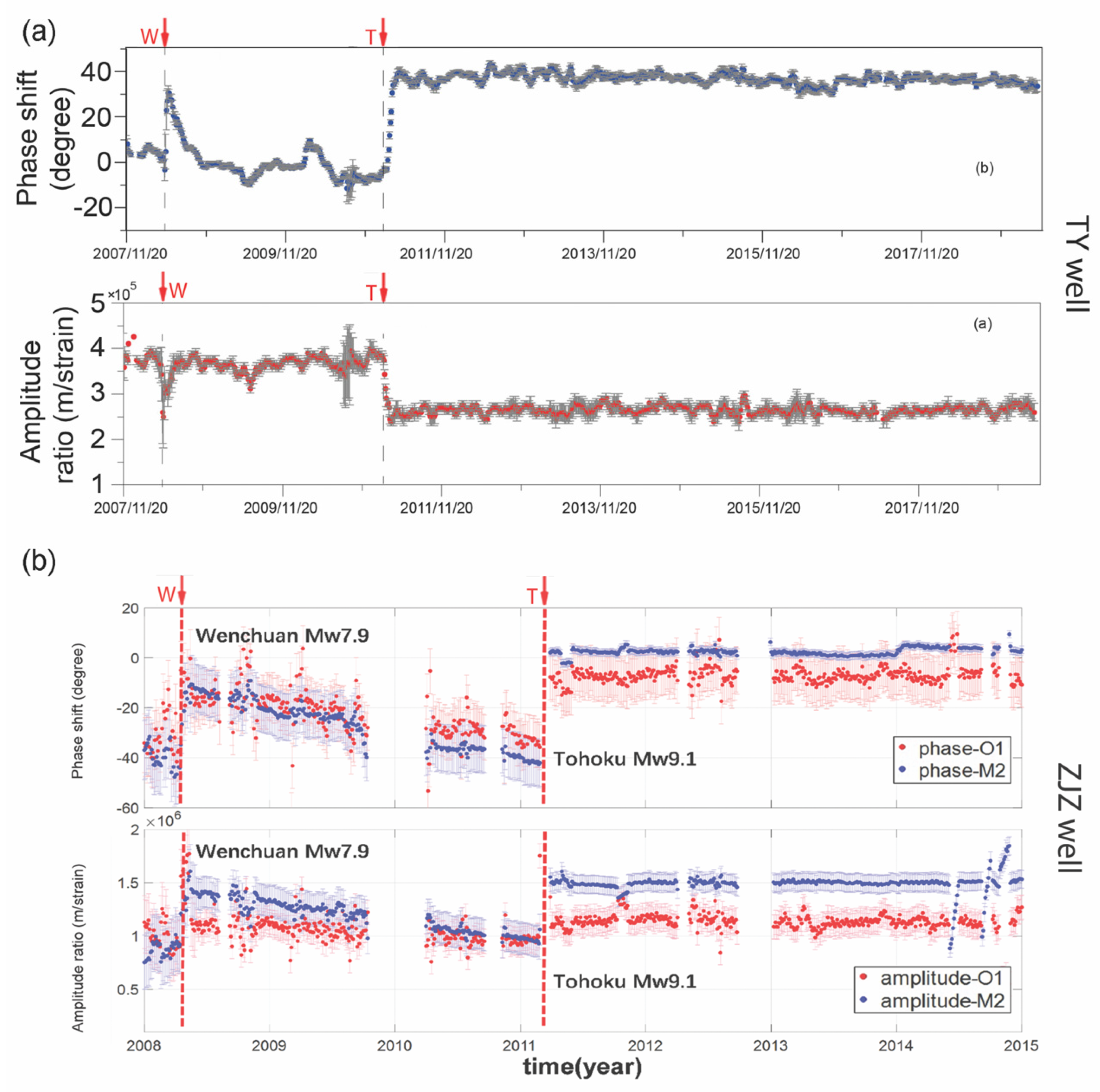
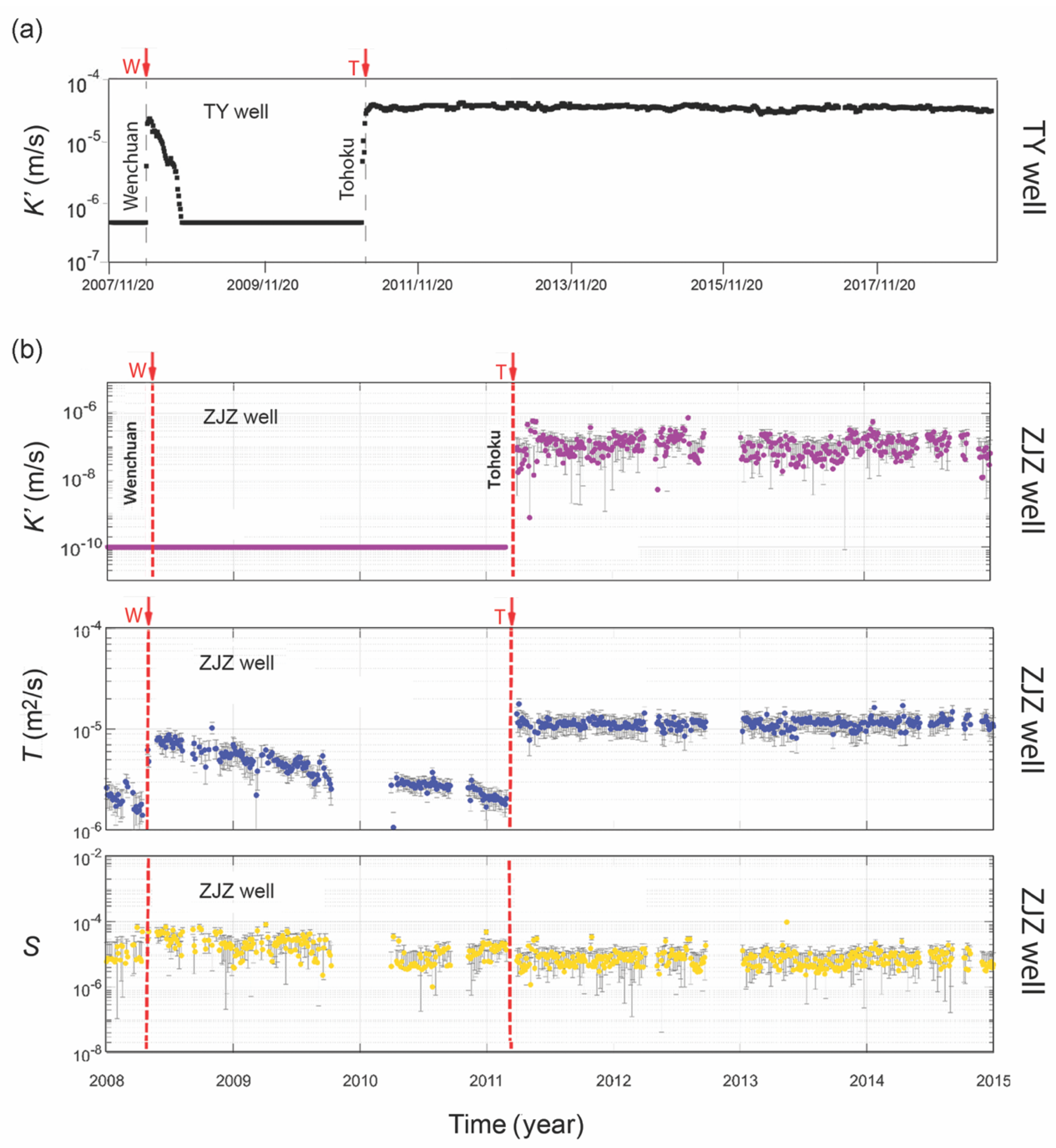
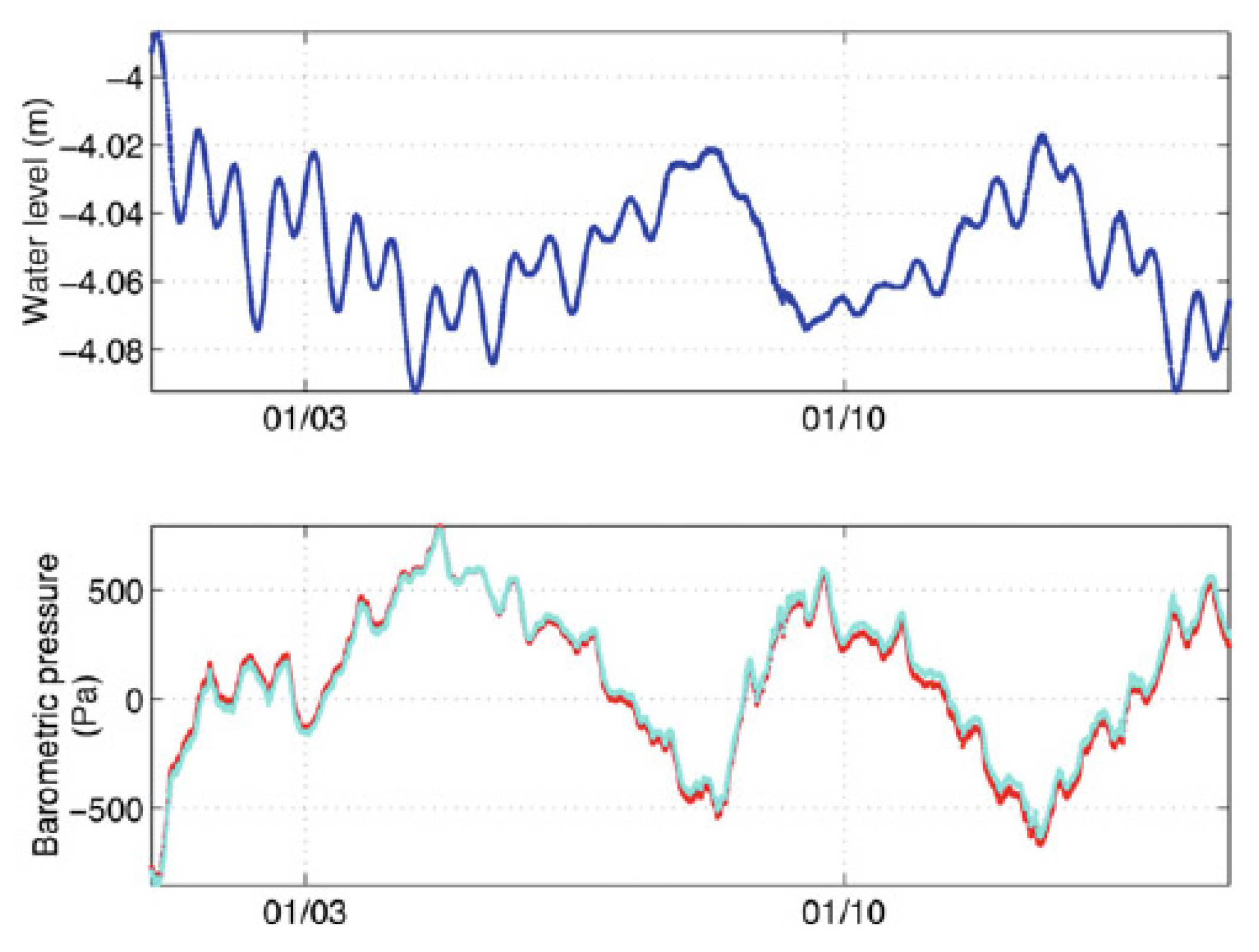
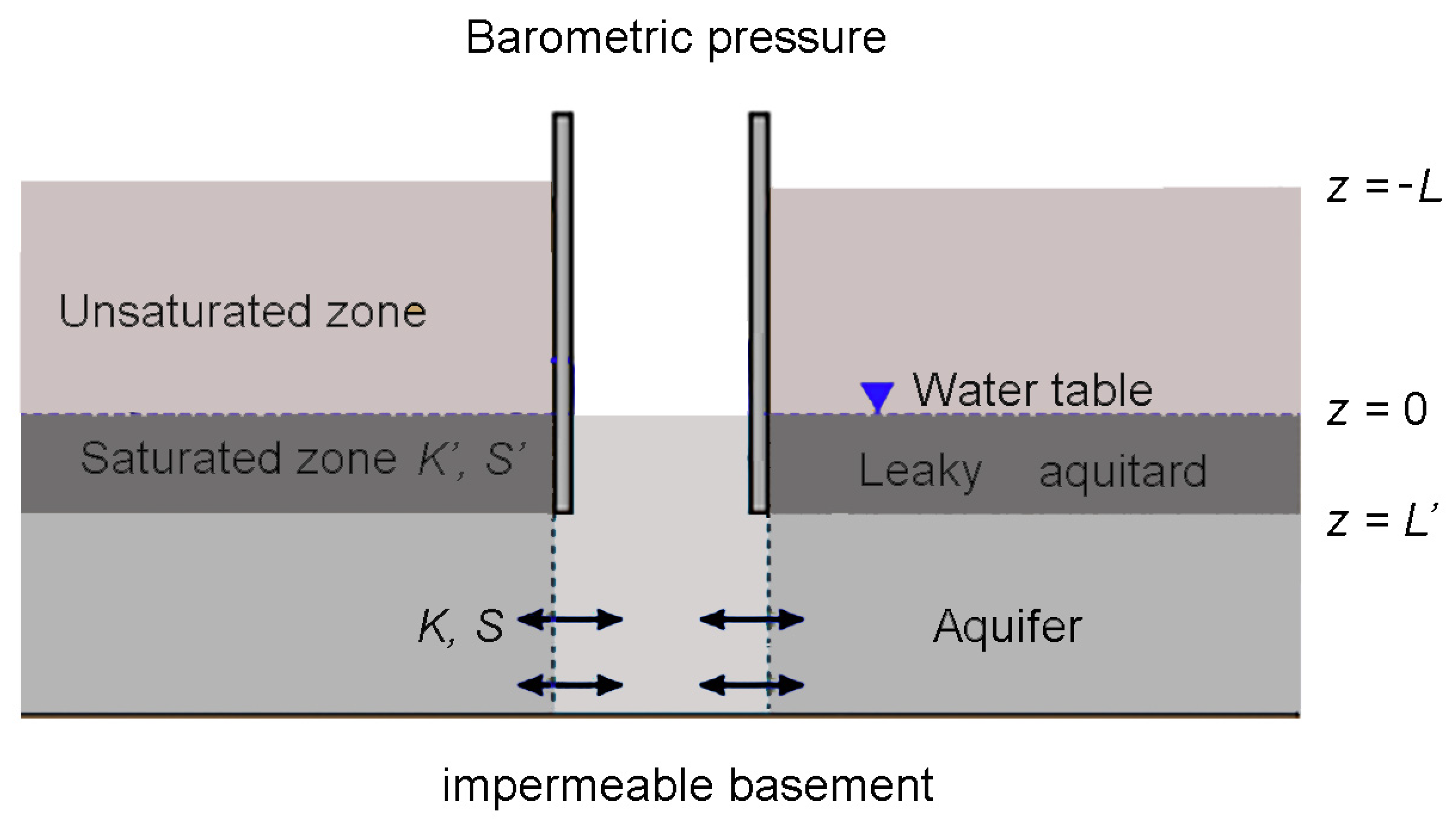

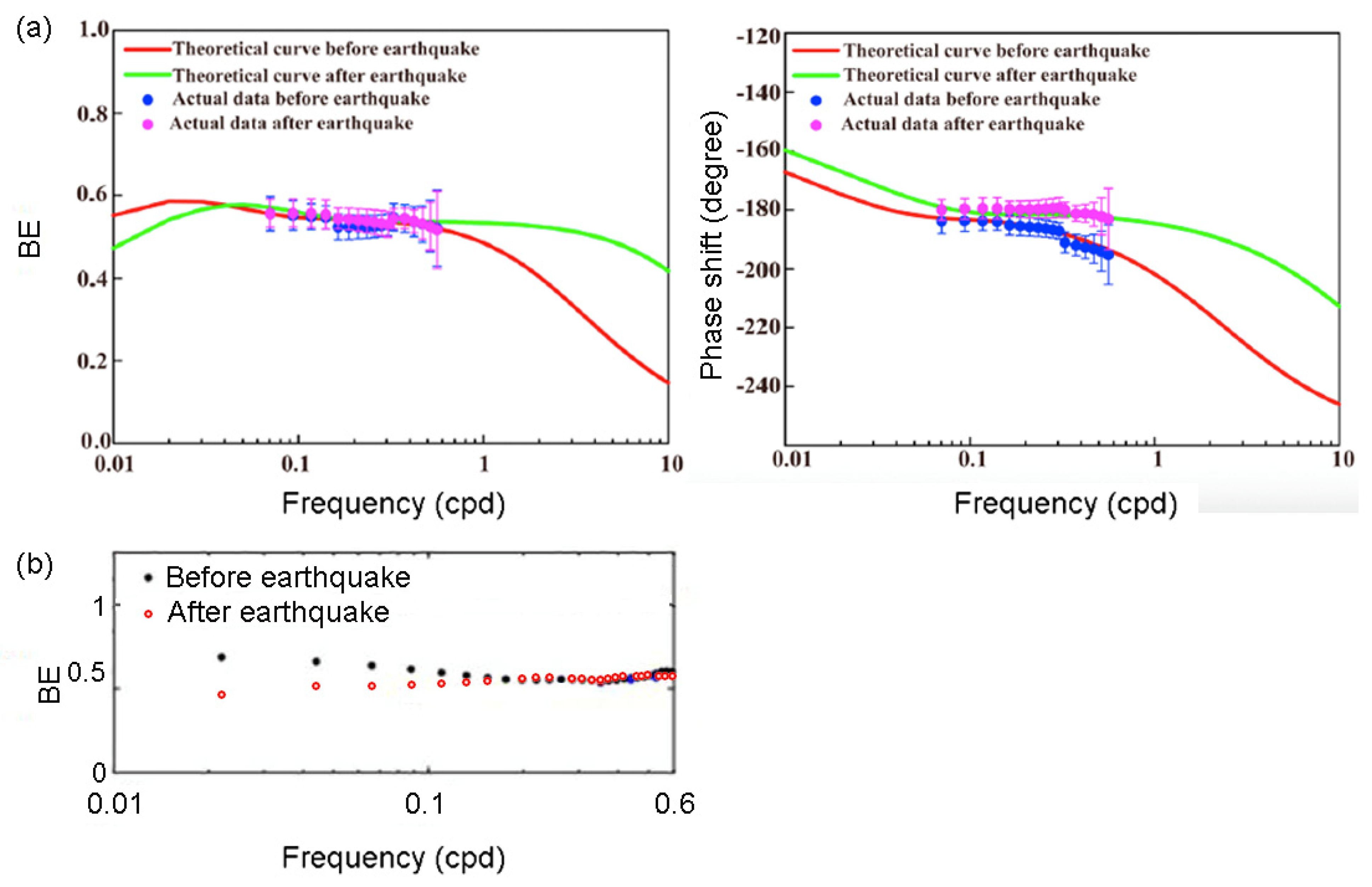
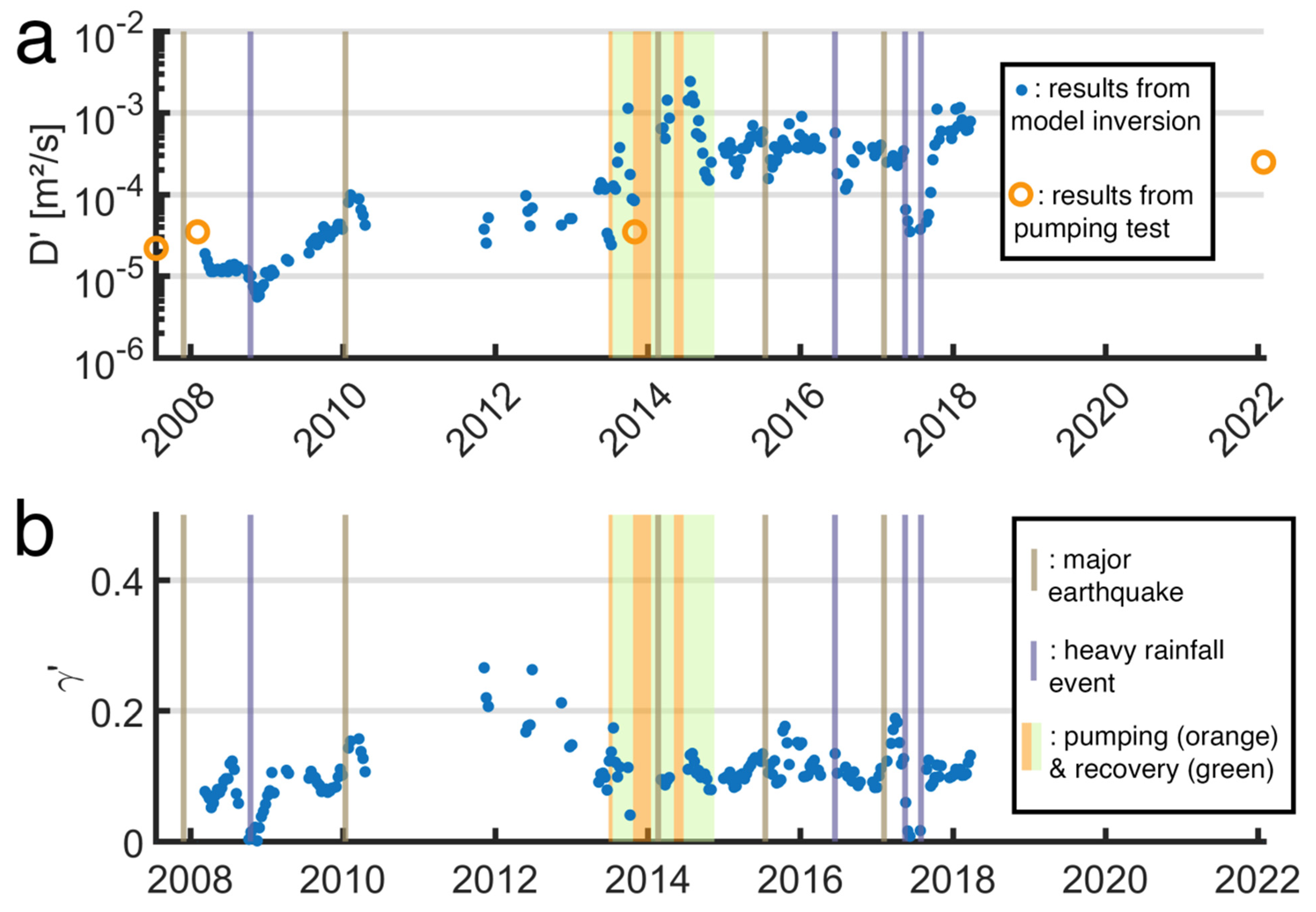
| Darwin Name | Period (Day) | Frequency (cpd) | Origin | Vertical Displacement (mm) |
|---|---|---|---|---|
| Mm | 27.554 | 0.0363 | Moon | 7 |
| Mf | 13.660 | 0.0732 | Moon | 14 |
| Q1 | 1.1195 | 0.8933 | Moon | 19 |
| O1 | 1.0758 | 0.9295 | Moon | 100 |
| M1 | 1.0347 | 0.9665 | Moon | 8 |
| P1 | 1.0027 | 0.9973 | Sun | 47 |
| S1 | 1.0000 | 1.000 | Sun | 1 |
| K1 | 0.9973 | 1.0027 | Moon/Sun | 141 |
| J1 | 0.9624 | 1.0391 | Moon | 8 |
| OO1 | 0.9294 | 1.0760 | Moon | 4 |
| 2N2 | 0.5377 | 1.8598 | Moon | 3 |
| N2 | 0.5274 | 1.8961 | Moon | 21 |
| M2 | 0.5175 | 1.9324 | Moon | 108 |
| L2 | 0.5080 | 1.9685 | Moon | 21 |
| S2 | 0.5000 | 2.0000 | Sun | 50 |
| K2 | 0.4986 | 2.0056 | Moon/Sun | 14 |
| M3 | 0.3450 | 2.8986 | Moon | 1 |
| Well Names | Locations | Well Depth (m) | Aquifer Lithology | Aquitard Lithology | Epicentral Distance (km) | |
|---|---|---|---|---|---|---|
| Wenchuan Earthquake | Tohoku Earthquake | |||||
| USGS Oklahoma deep well | 36.73 N, 96.53 W | 960 | Carbonates | Shale, sandstone, carbonates | (Not studied) | (Not studied) |
| Piñor Flat Observatory 1 | 33.61 N, 116.46 W | 211 (CIB) 137 (CIC) | Fractured granodiorite | Unfractured granodiorite | (Not studied) | (Not studied) |
| JY 2 (Jiangyou) | 31.82 N, 104.76 E, | 4000 | Sandstone | Shale | 21 km from ruptured fault | 3480 |
| ZJZ 3 (Zuojiazhuang) | 39.95 N, 116.45 E | 2600 | Dolomite | Shale, mudstone | 1532 | 2260 |
| TY 4 (Taiyuan) | 37.72 N, 112.43 E | 765 | Limestone dolomite | Marlstone | 1115 | 2614 |
| Fond Lahaye borehole 5 | ~14.6 N ~61.1 W | 62 | Fractured andesite | Altered andesite | (Not studied) | (Not studied) |
| Parameter | Value |
|---|---|
| Barometric efficiency, BE (no units) | 0.5 |
| Saturated aquitard thickness, L′ (m) | 18 |
| Unsaturated aquitard thickness, L (m) | 2 |
| Saturated aquitard hydraulic diffusivity, D′ (m2/d) | 50 |
| Unsaturated aquitard pneumatic diffusivity, D (m2/d) | 10 |
| Aquifer specific storage, Ss(aqf) (m−1) | 2.76 × 10−6 |
| Aquitard specific storage, Ss(aqt) (m−1) | 6.71 × 10−4 |
| Well radius, rw (m) | 0.075 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.-Y.; Manga, M. Changes in Tidal and Barometric Response of Groundwater during Earthquakes—A Review with Recommendations for Better Management of Groundwater Resources. Water 2023, 15, 1327. https://doi.org/10.3390/w15071327
Wang C-Y, Manga M. Changes in Tidal and Barometric Response of Groundwater during Earthquakes—A Review with Recommendations for Better Management of Groundwater Resources. Water. 2023; 15(7):1327. https://doi.org/10.3390/w15071327
Chicago/Turabian StyleWang, Chi-Yuen, and Michael Manga. 2023. "Changes in Tidal and Barometric Response of Groundwater during Earthquakes—A Review with Recommendations for Better Management of Groundwater Resources" Water 15, no. 7: 1327. https://doi.org/10.3390/w15071327
APA StyleWang, C.-Y., & Manga, M. (2023). Changes in Tidal and Barometric Response of Groundwater during Earthquakes—A Review with Recommendations for Better Management of Groundwater Resources. Water, 15(7), 1327. https://doi.org/10.3390/w15071327






