Evaluating the Effect of Deforestation on Decadal Runoffs in Malaysia Using the Revised Curve Number Rainfall Runoff Approach
Abstract
:1. Introduction
2. Materials and Methods
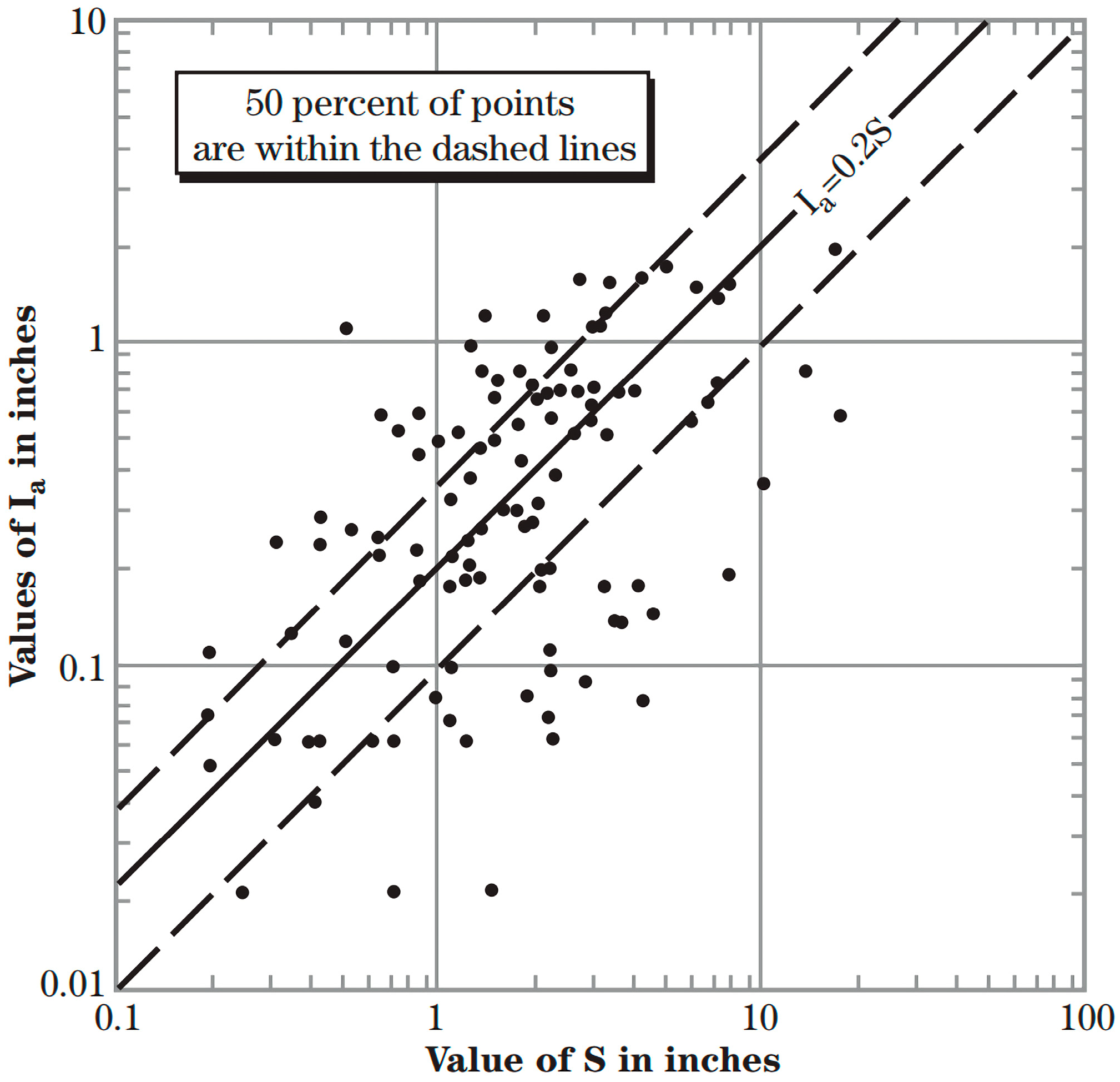
2.1. New Power Correlation of Ia = SL
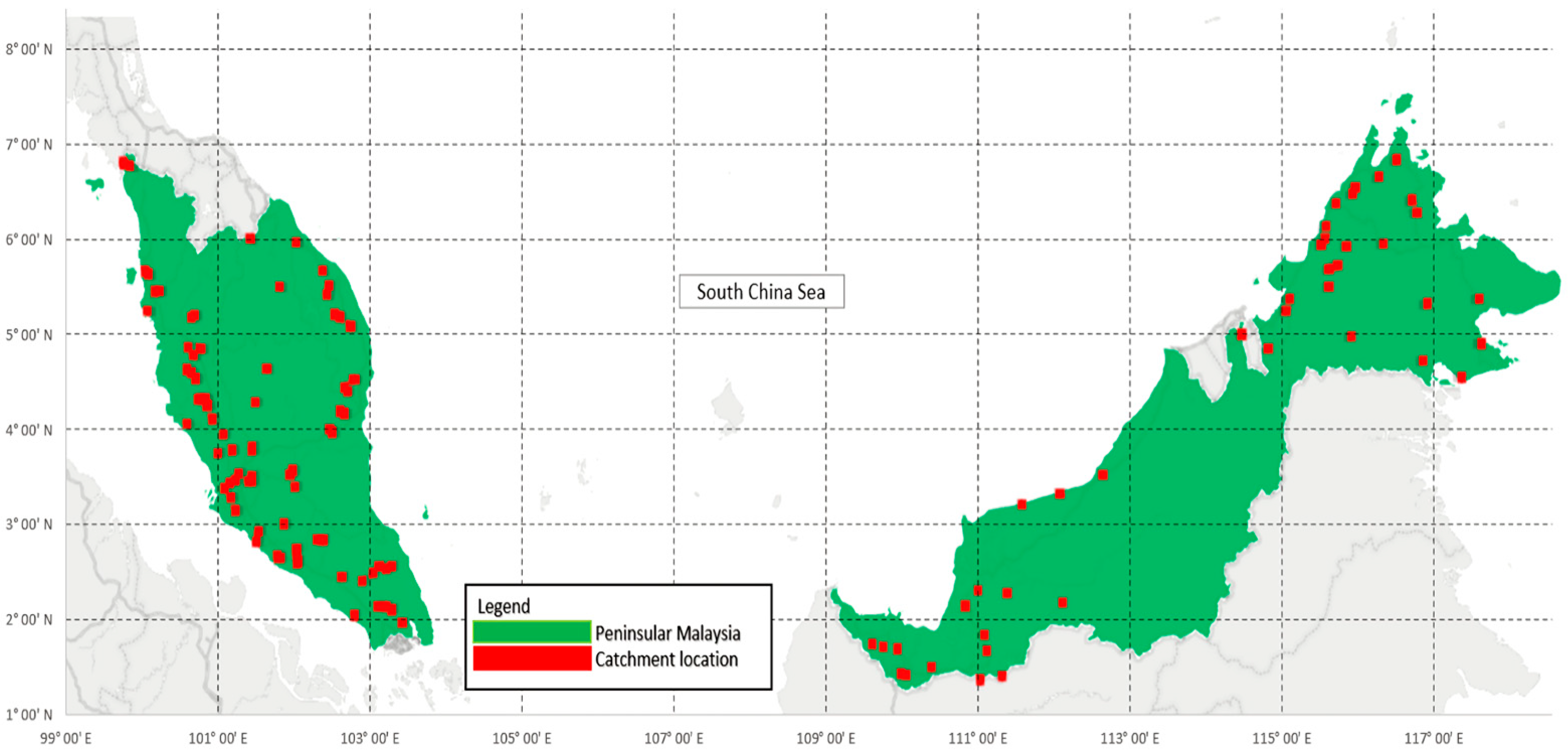
2.2. Study Sites in Malaysia
2.3. Decadal Analysis of Rainfall Runoff Models in Malaysia
2.4. Analysis of the Impact of Deforestation on the Rainfall Runoff Conditions in Malaysia
3. Results
3.1. Decadal Analysis of Runoff Trends in Peninsular Malaysia and East Malaysia
3.2. Impact of Human Activities on Runoff Amount in Malaysia
4. Discussion
4.1. Validity of Ia = 0.2S and the Newly Proposed Correlation of Ia = SL
4.2. Application of Newly Calibrated Runoff Predictive Models
4.3. Decadal Runoff Trend Analaysis in Both Peninsular Malaysia and East Malaysia
4.4. Exploring the Application of Machine Learning for Rainfall Runoff Prediction
5. Conclusions
- This study demonstrated the unreliability of the SCS’s proposed relation of Ia = 0.2S, indicating a need to update the SCS runoff prediction model. The new power correlation of Ia = SL shows improved accuracy in runoff prediction. The results align with previous global studies, indicating an Ia to S ratio of around 5% or less, which is significantly different from the traditional value of 0.2 (20%) proposed by the SCS. On average, the power regression model exhibits a 138% higher predictive accuracy than the conventional SCS-CN model, as measured by the KGE index.
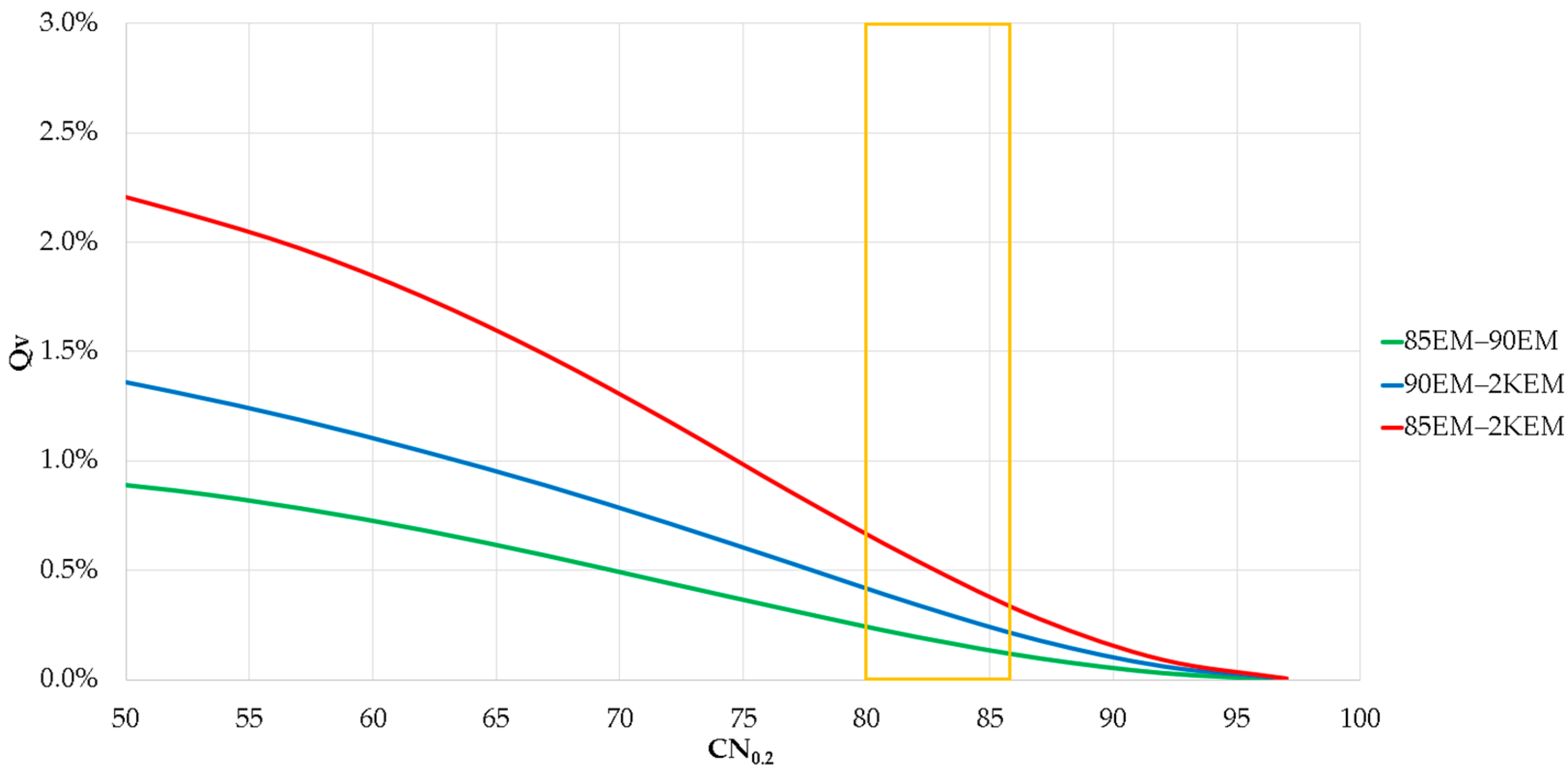
- This study emphasizes designing flood control infrastructure based on the maximum estimated runoff amount. Not using this estimate could result in a 50,100 m3 underestimation of the runoff volume per 1 km2 watershed area in Malaysia, as indicated by the difference between the optimum CN0.2 values and the upper limit of the BCa 99% CI for CN0.2.
- This study found a strong correlation between decreasing forest area and increasing runoff difference in Malaysia over time. Peninsular Malaysia saw a 25% reduction in forest area from the 1970s to the 1990s, and East Malaysia experienced a 9% reduction from the 1980s to the 2010s. This was accompanied by an increase in decadal runoff difference, with the most significant increases of 108% in Peninsular Malaysia from the 1970s to the 1990s and 32% in East Malaysia from the 1980s to the 2010s.
- The proposed methodology requires a minimum dataset of 25 data pairs for accurate inferential results and relies on the bootstrap BCa method for optimizing key variables and formulating a new runoff predictive model. Therefore, using statistical software with this method is essential. Future studies may consider incorporating machine learning methods to further enhance the model’s performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B. Refer to Section 2.4, Equation (6) in [47] and Section 2, Equation (8) in [56]
Appendix C
- The SCS stated that Ia = λS, while the effective rainfall (Pe) = P − Ia, and therefore Equation (1) () can be expressed as:
- 2.
- Given a P–Q dataset, the corresponding Li and Si values to Pi and Qi can be calculated through numerical analysis technique with Equation (6) or (A1). To date, there is no closed form for the general equation for S. Therefore, a numerical analysis technique will be used to solve for the corresponding Si values.
- 3.
- With bootstrap, a BCa procedure (selects 95–99% confidence interval level) to generate the confidence interval (CI) for derived Li and Si datasets and check for its dataset normality in SPSS (or other statistical software):
- (a)
- If the dataset is normally distributed, the optimum S and L values are found from the mean BCa CI to formulate a new runoff predictive model.
- (b)
- Otherwise, the S and L optimization process will refer to the median BCa CI (denote the optimum value of both parameters as Loptimum and Soptimum).
- 4.
- To formulate the new SCS-CN rainfall runoff model, both Loptimum and Soptimum values are substituted into Equation (1) with Ia = SL.
- 5.
- The corresponding Si values with the same P–Q dataset are computed, along with the Loptimum value with Equations (A1) or (6) through numerical analysis technique.
- 6.
- Given (Pi, Qi) data pairs and λ = 0.2, S0.2i values are computed with Equations (A3) or (7).
- 7.
- S0.2i (from step 6) and Si (from step 5) values are correlated to obtain a correlation equation between S0.2i and Si via SPSS for curve number (CN0.2) value derivation.
- 8.
- The S correlation equation from step 7 is substituted into the SCS curve number formula () to derive the CN0.2 value.
Appendix D
| Decadal Model | Power Regressed Model | Conventional SCS-CN Model | ||||
|---|---|---|---|---|---|---|
| E | Bias | KGE | E | Bias | KGE | |
| 70PM | 0.941 | 0 | 0.968 | 0.876 | 12.29 | 0.579 |
| 80PM | 0.906 | 0.497 | 0.947 | 0.506 | 24.85 | 0.346 |
| 90PM | 0.892 | 0 | 0.925 | 0.801 | 10.75 | 0.733 |
| 85EM | −0.387 | −1.910 | 0.307 | −0.108 | 9.49 | −0.401 |
| 90EM | 0.788 | 0 | 0.713 | 0.316 | 12.22 | 0.195 |
| 2KEM | 0.730 | 0 | 0.866 | 0.302 | 12.72 | 0.391 |
| Decadal Model | Std. Dev. | 95% BCa CI for λ | 99% BCa CI for λ | ||||
|---|---|---|---|---|---|---|---|
| Lower | Upper | Variation | Lower | Upper | Variation | ||
| 70PM | 0.123 | 0.057 | 0.082 | 44.04% | 0.053 | 0.089 | 66.32% |
| 80PM | 0.088 | 0.014 | 0.018 | 27.48% | 0.014 | 0.020 | 40.91% |
| 90PM | 0.132 | 0.032 | 0.046 | 46.07% | 0.032 | 0.054 | 69.27% |
| 85EM | 0.259 | 0.028 | 0.072 | 158.77% | 0.025 | 0.080 | 218.59% |
| 90EM | 0.078 | 0.006 | 0.009 | 42.03% | 0.006 | 0.009 | 66.27% |
| 2KEM | 0.176 | 0.014 | 0.053 | 274.04% | 0.014 | 0.061 | 349.23% |
Appendix E
| Peninsular Malaysia | |
|---|---|
| Decadal Datasets | Decadal Model Equations |
| 1970s (70PM) | |
| 1980s (80PM) | |
| 1990s (90PM) | |
| East Malaysia | |
| 1985s (85EM) | |
| 1990s (90EM) | |
| 2000s (2KEM) | |
Appendix F
Appendix G


References
- Yang, T.H.; Liu, W.C. A General Overview of the Risk-Reduction Strategies for Floods and Droughts. Sustainability 2020, 12, 2687. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Luo, M.; Gao, S.; Chen, W.; Hari, V.; Khouakhi, A. Compound Hydrometeorological Extremes: Drivers, Mechanisms and Methods. Front. Earth Sci. 2021, 9, 673495. [Google Scholar] [CrossRef]
- Garner, G.; van Loon, A.F.; Prudhomme, C.; Hannah, D.M. Hydroclimatology of Extreme River Flows. Freshw. Biol. 2015, 60, 2461–2476. [Google Scholar] [CrossRef]
- Morin, E.; Harats, N.; Jacoby, Y.; Arbel, S.; Getker, M.; Arazi, A.; Grodek, T.; Ziv, B.; Dayan, U. Studying the Extremes: Hydrometeorological Investigation of a Flood-Causing Rainstorm Over Israel. Adv. Geosci. 2007, 12, 107–114. [Google Scholar] [CrossRef] [Green Version]
- Nyeko-Ogiramoi, P.; Willems, P.; Ngirane-Katashaya, G. Trend and Variability in Observed Hydrometeorological Extremes in the Lake Victoria Basin. J. Hydrol. 2013, 489, 56–73. [Google Scholar] [CrossRef]
- Fattorelli, S.; Fontana, G.D.; Ros, D. Flood Hazard Assessment and Mitigation. In Floods and Landslides: Integrated Risk Assessment; Springer: Berlin/Heidelberg, Germany, 1999; pp. 19–38. [Google Scholar]
- Tsakiris, G. Flood Risk Assessment: Concepts, Modelling, Applications. Nat. Hazards Earth Syst. Sci. 2014, 14, 1361–1369. [Google Scholar] [CrossRef] [Green Version]
- Sitterson, J.; Knightes, C.; Parmar, R.; Wolfe, K.; Avant, B.; Muche, M. An Overview of Rainfall-Runoff Model Types. In Proceedings of the International Congress on Environmental Modelling and Software, Collins, CO, USA, 24–28 June 2018; p. 41. [Google Scholar]
- Nagure, A.S.; Shahapure, S.S. Effect of Watershed Characteristics on a Rainfall Runoff Analysis and Hydrological Model Selection-A Review. In Proceedings of the 2021 International Conference on Computing, Communication and Green Engineering (CCGE), Pune, India, 23–25 September 2021; IEEE: New York, NY, USA, 2021. [Google Scholar]
- Rezaie-Balf, M.; Zahmatkesh, Z.; Kim, S. Soft Computing Techniques for Rainfall-Runoff Simulation: Local Non–Parametric Paradigm vs. Model Classification Methods. Water Resour. Manag. 2017, 31, 3843–3865. [Google Scholar] [CrossRef]
- Vafakhah, M.; Janizadeh, S.; Bozchaloei, S.K. Application of Several Data-Driven Techniques for Rainfall-Runoff Modeling. Ecopersia 2014, 2, 455–469. [Google Scholar]
- Lee, K.K.F.; Ling, L.; Yusop, Z. The Revised Curve Number Rainfall-Runoff Methodology for an Improved Runoff Prediction. Water 2023, 15, 491. [Google Scholar] [CrossRef]
- N.E.D.C. Engineering Hydrology Training Series. In Module 205-SCS Runoff Equation; N.E.D.C.: London, UK, 1997; Available online: https://d32ogoqmya1dw8.cloudfront.net/files/geoinformatics/steps/nrcs_module_runoff_estimation.pdf (accessed on 8 July 2022).
- Soil Conservation Service (S.C.S.). National Engineering Handbook; Section 4; US Soil Conservation Service: Washington, DC, USA, 1964; Chapter 10. Available online: https://directives.sc.egov.usda.gov/RollupViewer.aspx?hid=17092 (accessed on 10 July 2022).
- USDA; NRCS. National Engineering Handbook, Part 630 Hydrology; US Soil Conservation Service: Washington, DC, USA, 1964; Chapter 10. [Google Scholar]
- Mishra, S.K.; Suresh Babu, P.; Singh, V.P. SCS-CN Method Revisited. In Advances in Hydraulics and Hydrology; Water Resources Publications: Littleton, CO, USA, 2007. [Google Scholar]
- Tan, W.J.; Ling, L.; Yusop, Z.; Huang, Y.F. New Derivation Method of Region Specific Curve Number for Urban Runoff Prediction at Melana Watershed in Johor, Malaysia. IOP Conf. Ser. Mater. Sci. Eng. 2018, 401, 012008. [Google Scholar] [CrossRef]
- Yuan, L.; Sinshaw, T.; Forshay, K.J. Review of Watershed-Scale Water Quality and Nonpoint Source Pollution Models. Geosciences 2020, 10, 25. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mosavi, A.; Ozturk, P.; Chau, K. Flood Prediction Using Machine Learning Models: Literature Review. Water 2018, 10, 1536. [Google Scholar] [CrossRef] [Green Version]
- Fu, M.; Fan, T.; Ding, Z.; Salih, S.Q.; Al-Ansari, N.; Yaseen, Z.M. Deep Learning Data-Intelligence Model Based on Adjusted Forecasting Window Scale: Application in Daily Streamflow Simulation. IEEE Access 2020, 8, 32632–32651. [Google Scholar] [CrossRef]
- Kaya, C.M.; Tayfur, G.; Gungor, O. Predicting Flood Plain Inundation for Natural Channels Having No Upstream Gauged Stations. J. Water Clim. Chang. 2019, 10, 360–372. [Google Scholar] [CrossRef] [Green Version]
- Hawkins, R.H.; Moglen, G.E.; Ward, T.J.; Woodward, D.E. Updating the Curve Number: Task Group Report. In Proceedings of the Watershed Management 2020, Henderson, NV, USA, 20–21 May 2020; American Society of Civil Engineers: Reston, VA, USA, 2020; pp. 131–140. [Google Scholar]
- Hawkins, R.H.; Yu, B.; Mishra, S.K.; Singh, V.P. Another Look at SCS-CN Method. J. Hydrol. Eng. 2001, 6, 451–452. [Google Scholar] [CrossRef]
- Hawkins, R.; Ward, T.J.; Woodward, E.; van Mullem, J.A. Continuing Evolution of Rainfall-Runoff and the Curve Number Precedent. In Proceedings of the 2nd Joint Federal Interagency Conference, Las Vegas, NV, USA; 2010; pp. 1–12. [Google Scholar]
- Qin, T. Urban Flooding Mitigation Techniques: A Systematic Review and Future Studies. Water 2020, 12, 3579. [Google Scholar] [CrossRef]
- Cooper, R.J.; Hiscock, K.M.; Lovett, A.A. Mitigation Measures for Water Pollution and Flooding. In Landscape Planning with Ecosystem Services; von Haaren, C., Lovett, A., Albert, C., Eds.; Landscape series; Volume 24, Springer: Dordrecht, The Netherlands, 2019. [Google Scholar] [CrossRef]
- Xie, J.; Chen, H.; Liao, Z.; Gu, X.; Zhu, D.; Zhang, J. An Intergrated Assessment of Urban Flooding Mitigation Strategies for Robust Decision Making. Environ. Model. Softw. 2017, 95, 143–155. [Google Scholar] [CrossRef]
- Danáčová, M.; Földes, G.; Labat, M.M.; Kohnová, S.; Hlavčová, K. Estimating the Effect of Deforestation on Runoff in Small Mountainous Basins in Slovakia. Water 2020, 12, 3113. [Google Scholar] [CrossRef]
- Li, Y.; Liu, C.; Zhang, D.; Liang, K.; Li, X.; Dong, G. Reduced Runoff Due to Anthropogenic Intervention in the Loess Plateau, China. Water 2016, 8, 458. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Xia, J.; Yu, J.; Randall, M.; Zhang, Y.; Zhao, T.; Pan, X.; Zhai, X.; Shao, Q. Simulation and Assessment of Urbanization Impacts on Runoff Metrics: Insights from Landuse Changes. J. Hydrol. 2018, 560, 247–258. [Google Scholar] [CrossRef]
- Zhai, R.; Tao, F. Contributions of Climate Change and Human Activities to Runoff Change in Seven Typical Catchments across China. Sci. Total Environ. 2017, 605–606, 219–229. [Google Scholar] [CrossRef]
- Li, C.; Liu, M.; Hu, Y.; Shi, T.; Qu, X.; Walter, M.T. Effects of Urbanization on Direct Runoff Characteristics in Urban Functional Zones. Sci. Total Environ. 2018, 643, 301–311. [Google Scholar] [CrossRef]
- Miyamoto, M.; Mohd Parid, M.; Noor Aini, Z.; Michinaka, T. Proximate and Underlying Causes of Forest Cover Change in Peninsular Malaysia. Policy Econ. 2014, 44, 18–25. [Google Scholar] [CrossRef] [Green Version]
- Tan, W.J.; Ling, L.; Yusop, Z.; Huang, Y.F. Claim Assessment of a Rainfall Runoff Model with Bootstrap. In Proceedings of the Third International Conference on Computing, Mathematics and Statistics (iCMS2017); Springer: Singapore, 2019; pp. 287–293. [Google Scholar]
- Hawkins, R.H.; Khojeini, A.V. Initial Abstraction and Loss in the Curve Number Method. In Proceedings of the Arizona State Hydrological Society Proceedings, Las Vegas, NV, USA, 15 April 1980; Arizona-Nevada Academy of Science: Las Vegas, NV, USA, 1980; pp. 115–119. [Google Scholar]
- DID. Hydrological Procedure 27 Design Hydrograph Estimation for Rural Catchments in Malaysia; JPS, DID: Kuala Lumpur, Malaysia, 2010. Available online: https://www.water.gov.my/jps/resources/PDF/Hydrology%20Publication/Hydrological_Procedure_No_27_(HP_27).pdf (accessed on 24 February 2023).
- DID. Hydrological Procedure 11 Design Flood Hydrograph Estimation for Rural Catchments in Malaysia; JPS, DID: Kuala Lumpur, Malaysia, 2018. Available online: http://h2o.water.gov.my/man_hp1/HP11_2018.pdf (accessed on 24 February 2023).
- Ling, L.; Lai, S.H.; Yusop, Z.; Chin, R.J.; Ling, J.L. Formulation of Parsimonious Urban Flash Flood Predictive Model with Inferential Statistics. Mathematics 2022, 10, 175. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman and Hall/CRC: Boca Raton, FL, USA, 1993; ISBN 978-0-412-04231-7. [Google Scholar]
- Davison, A.C. Cambridge Series In Statistical And Probabilistic; Cambridge University Press: New York, NY, USA, 1997; ISBN 978-0-511-67299-6. [Google Scholar]
- Efron, B. Large-Scale Inference: Empirical Bayes Methods for Estimation, Testing, and Prediction; Cambridge University Press: New York, NY, USA, 2010; ISBN 978-1-107-61967-8. [Google Scholar]
- Rochowicz, J.A.J. Bootstrapping Analysis, Inferential Statistics and EXCEL. Spreadsheets Edu. (Ejsie) 2010, 4, 1–23. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Knoben, W.J.M.; Freer, J.E.; Woods, R.A. Technical Note: Inherent Benchmark or Not? Comparing Nash–Sutcliffe and Kling–Gupta Efficiency Scores. Hydrol. Earth Syst. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef] [Green Version]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the Mean Squared Error and NSE Performance Criteria: Implications for Improving Hydrological Modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Ling, L.; Yusop, Z.; Ling, J.L. Statistical and Type II Error Assessment of a Runoff Predictive Model in Peninsula Malaysia. Mathematics 2021, 9, 812. [Google Scholar] [CrossRef]
- Hawkins, R.H.; Ward, T.J.; Woodward, D.E.; van Mullem, J.A. Curve Number Hydrology: State of the Practice; American Society of Civil Engineers: Reston, VA, USA, 2009. [Google Scholar]
- Tedela, N.H.; McCutcheon, S.C.; Rasmussen, T.C.; Hawkins, R.H.; Swank, W.T.; Campbell, J.L.; Adams, M.B.; Jackson, C.R.; Tollner, E.W. Runoff Curve Numbers for 10 Small Forested Watersheds in the Mountains of the Eastern United States. J. Hydrol. Eng. 2012, 17, 1188–1198. [Google Scholar] [CrossRef] [Green Version]
- Miles, J. R Squared, Adjusted R Squared. In Wiley StatsRef: Statistics Reference Online; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Hawkins, R.H.; Theurer, F.D.; Rezaeianzadeh, M. Understanding the Basis of the Curve Number Method for Watershed Models and TMDLs. J. Hydrol. Eng. 2019, 24, 06019003. [Google Scholar] [CrossRef]
- Baltas, E.A.; Dervos, N.A.; Mimikou, M.A. Technical Note: Determination of the SCS Initial Abstraction Ratio in an Experimental Watershed in Greece. Hydrol. Earth Syst. Sci. 2007, 11, 1825–1829. [Google Scholar] [CrossRef] [Green Version]
- Mishra, S.K.; Singh, V.P. Another Look at SCS-CN Method. J. Hydrol. Eng. 1999, 4, 257–264. [Google Scholar] [CrossRef]
- Yu, B. Discussion of “Another Look at SCS-CN Method” by Bofu Yu. J. Hydrol. Eng. 2001, 6, 451. [Google Scholar] [CrossRef]
- Jackson, T.J.; Rawls, W.J. SCS URBAN CURVE NUMBERS FROM A LANDSAT DATA BASE. J. Am. Water Resour. Assoc. 1981, 17, 857–862. [Google Scholar] [CrossRef]
- Ling, L.; Yusop, Z.; Yap, W.S.; Tan, W.L.; Chow, M.F.; Ling, J.L. A Calibrated, Watershed-Specific SCS-CN Method: Application to Wangjiaqiao Watershed in the Three Gorges Area, China. Water 2020, 12, 60. [Google Scholar] [CrossRef] [Green Version]

| Decadal Model | L | SL (mm) | Ia/S | E | BIAS | KGE |
|---|---|---|---|---|---|---|
| 70PM | 0.168 | 187.81 | 0.013 | 0.941 | 0 | 0.968 |
| 80PM | 0.228 | 183.31 | 0.018 | 0.906 | 0.497 | 0.947 |
| 90PM | 0.232 | 175.30 | 0.019 | 0.892 | 0 | 0.925 |
| Decadal Model | L | SL (mm) | Ia/S | E | BIAS | KGE |
|---|---|---|---|---|---|---|
| 85EM | 0.332 | 152.23 | 0.035 | −0.387 | −1.910 | 0.307 |
| 90EM | 0.274 | 121.11 | 0.031 | 0.788 | 0 | 0.713 |
| 2KEM | 0.316 | 152.40 | 0.032 | 0.730 | 0 | 0.866 |
| Decadal Model | Correlation Equation | R2adj | p-Value |
|---|---|---|---|
| 70PM | S0.2 = S0.1680.851 | 0.987 | <0.001 |
| 80PM | S0.2 = S0.2280.881 | 0.998 | <0.001 |
| 90PM | S0.2 = S0.2320.889 | 0.998 | <0.001 |
| Decadal Model | Correlation Equation | R2adj | p-Value |
|---|---|---|---|
| 85EM | S0.2 = S0.3320.891 | 0.997 | <0.001 |
| 90EM | S0.2 = S0.2740.887 | 0.998 | <0.001 |
| 2KEM | S0.2 = S0.3160.896 | 0.998 | <0.001 |
| Peninsular Malaysia | ||||||
|---|---|---|---|---|---|---|
| Decadal Model | BCa 99% CI for S (mm) | BCa 99% CI for CN0.2 | ||||
| Optimum S (mm) | Lower | Upper | Optimum CN0.2 | Lower | Upper | |
| 70PM | 187.81 | 137.59 | 194.85 | 74.69 | 74.09 | 79.36 |
| 80PM | 183.31 | 137.60 | 183.31 | 72.04 | 72.04 | 76.83 |
| 90PM | 175.30 | 120.37 | 191.21 | 71.99 | 70.41 | 78.22 |
| East Malaysia | ||||||
| 85EM | 152.23 | 50.89 | 152.23 | 74.26 | 74.26 | 88.45 |
| 90EM | 121.11 | 63.55 | 127.29 | 78.29 | 77.53 | 86.47 |
| 2KEM | 152.40 | 50.49 | 166.95 | 73.76 | 72.15 | 88.32 |
| Peninsular Malaysia | ||||
|---|---|---|---|---|
| Decadal Model (Appendix E) | Highest Rainfall Depth Recorded (mm) | Estimated Runoff Depth based on the Optimum CN0.2 (mm) | Maximum Runoff Depth Estimated with Upper CN0.2 Limit (mm) | Estimated Runoff Depth Difference (mm) |
| 70PM | 485 | 353.46 | 380.50 | 27.04 |
| 80PM | 420 | 290.27 | 314.15 | 23.88 |
| 90PM | 306 | 192.29 | 217.31 | 25.02 |
| East Malaysia | ||||
| 85EM | 175 | 88.13 | 131.33 | 43.20 |
| 90EM | 575 | 472.20 | 515.16 | 42.96 |
| 2KEM | 224 | 129.48 | 179.58 | 50.10 |
| Interdecadal Period | Forest Area | Model Runoff Difference, Qv, observed | ||
|---|---|---|---|---|
| (‘000 Ha) | (%) | (mm) | (%) | |
| 1970s–1980s | −1736.47 | −21.69% | 5.71 | 42.26% |
| 1980s–1990s | −381.18 | −6.00% | 8.91 | 46.36% |
| 1970s–1990s | −2032.94 | −25.39% | 14.62 | 108.22% |
| Interdecadal Model | Forest Area | Runoff Difference, Qv, observed | ||
|---|---|---|---|---|
| (‘000 Ha) | % | (mm) | (%) | |
| 1987s–1990s | −771 | −5.71% | 0.25 | 1.75% |
| 1991s–2000s | −1057 | −7.89% | 4.35 | 29.90% |
| 1987s–2010s | −1167 | −9.24% | 4.60 | 32.17% |
| Study Site | Dataset | Best Correlation Model | R2adj |
|---|---|---|---|
| Peninsular Malaysia | Runoff and FA | 0.947 | |
| East Malaysia | Runoff and FA | 0.949 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khor, J.F.; Lim, S.; Ling, L. Evaluating the Effect of Deforestation on Decadal Runoffs in Malaysia Using the Revised Curve Number Rainfall Runoff Approach. Water 2023, 15, 1392. https://doi.org/10.3390/w15071392
Khor JF, Lim S, Ling L. Evaluating the Effect of Deforestation on Decadal Runoffs in Malaysia Using the Revised Curve Number Rainfall Runoff Approach. Water. 2023; 15(7):1392. https://doi.org/10.3390/w15071392
Chicago/Turabian StyleKhor, Jen Feng, Steven Lim, and Lloyd Ling. 2023. "Evaluating the Effect of Deforestation on Decadal Runoffs in Malaysia Using the Revised Curve Number Rainfall Runoff Approach" Water 15, no. 7: 1392. https://doi.org/10.3390/w15071392
APA StyleKhor, J. F., Lim, S., & Ling, L. (2023). Evaluating the Effect of Deforestation on Decadal Runoffs in Malaysia Using the Revised Curve Number Rainfall Runoff Approach. Water, 15(7), 1392. https://doi.org/10.3390/w15071392







