Analysis of Flow Characteristics around a Square Cylinder with Boundary Constraint
Abstract
:1. Introduction
2. Numerical Simulation Method for Flow around a Square Cylinder
2.1. Mathematical Model
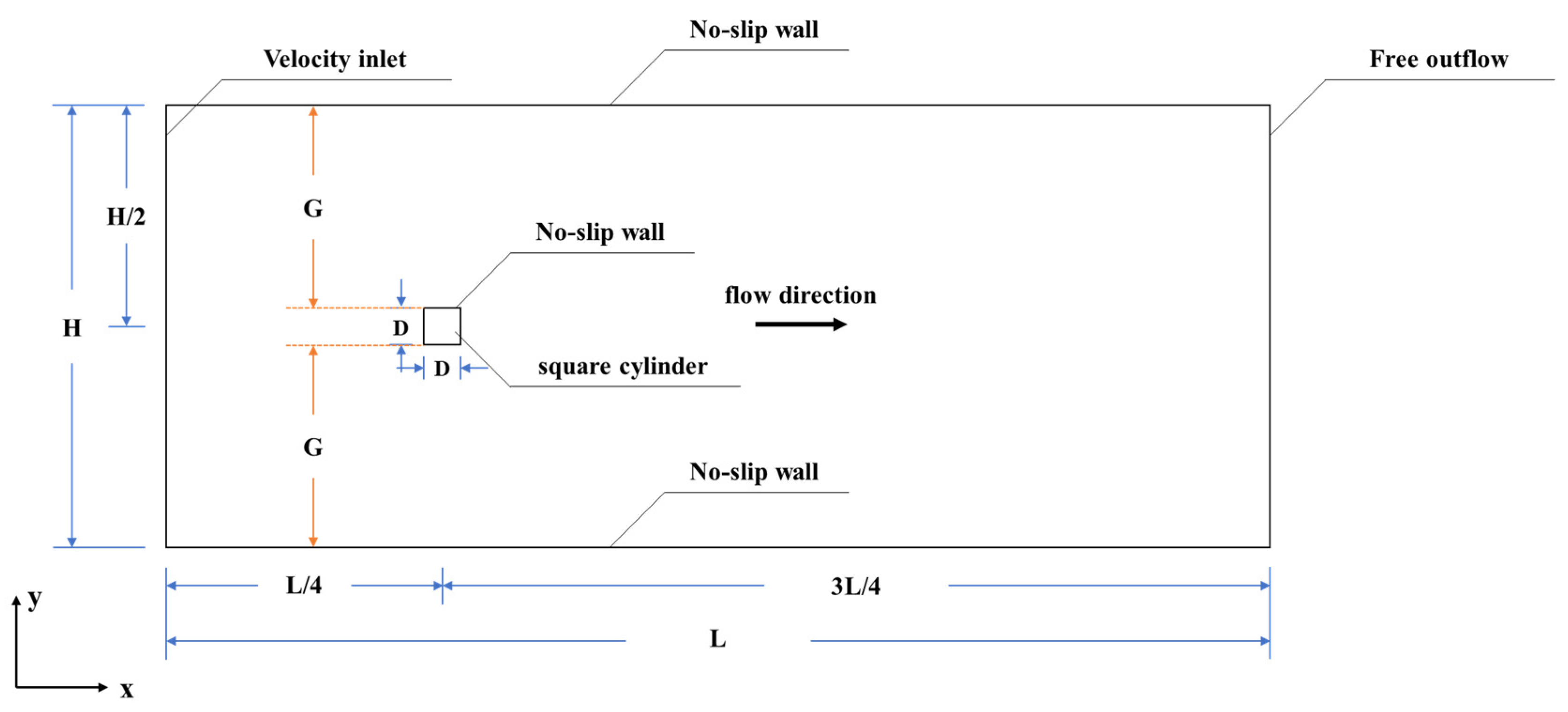
2.2. Computational Domain and Boundary Conditions
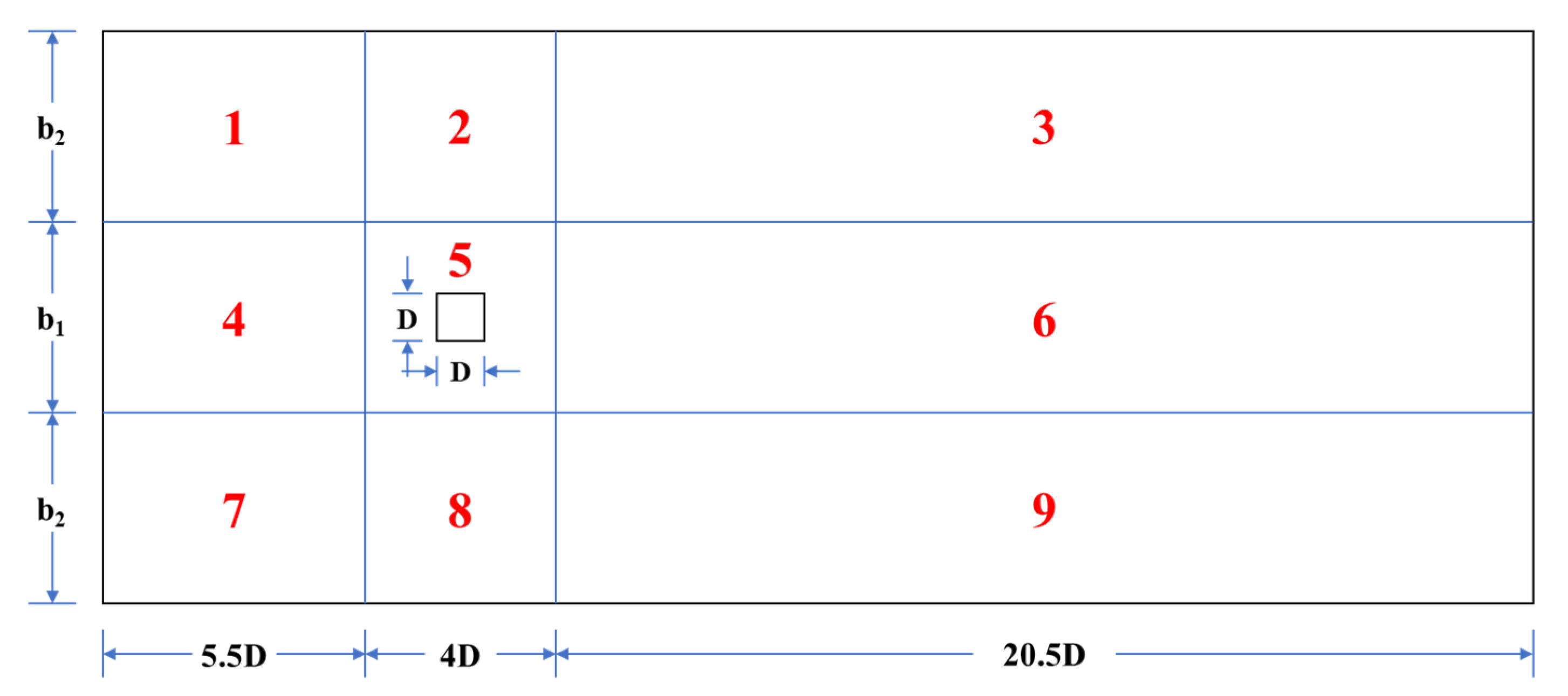
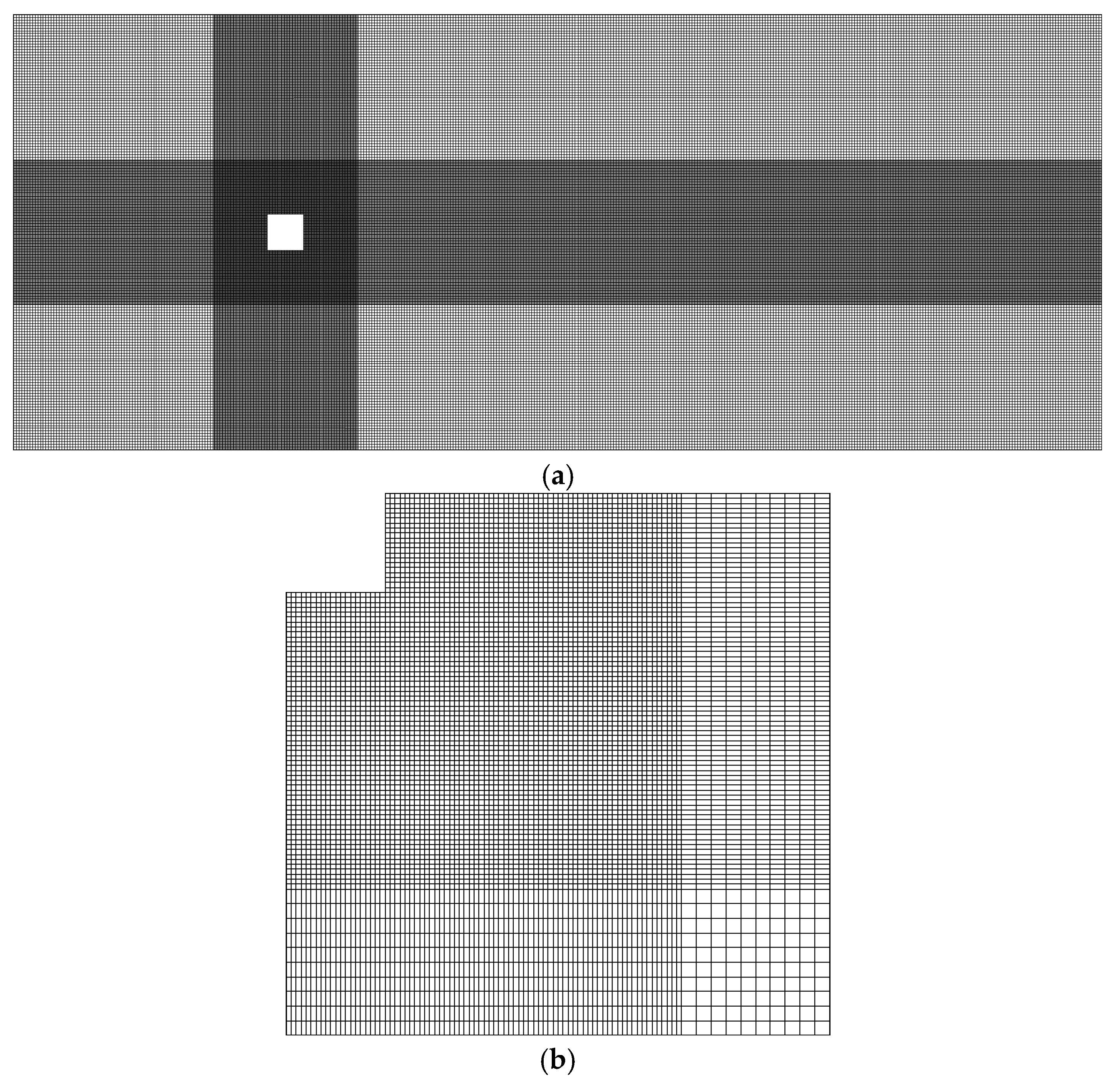
2.3. Computational Grids
2.4. Model Analysis
3. Characteristics of the Flow around a Square Cylinder under Boundary Constraint
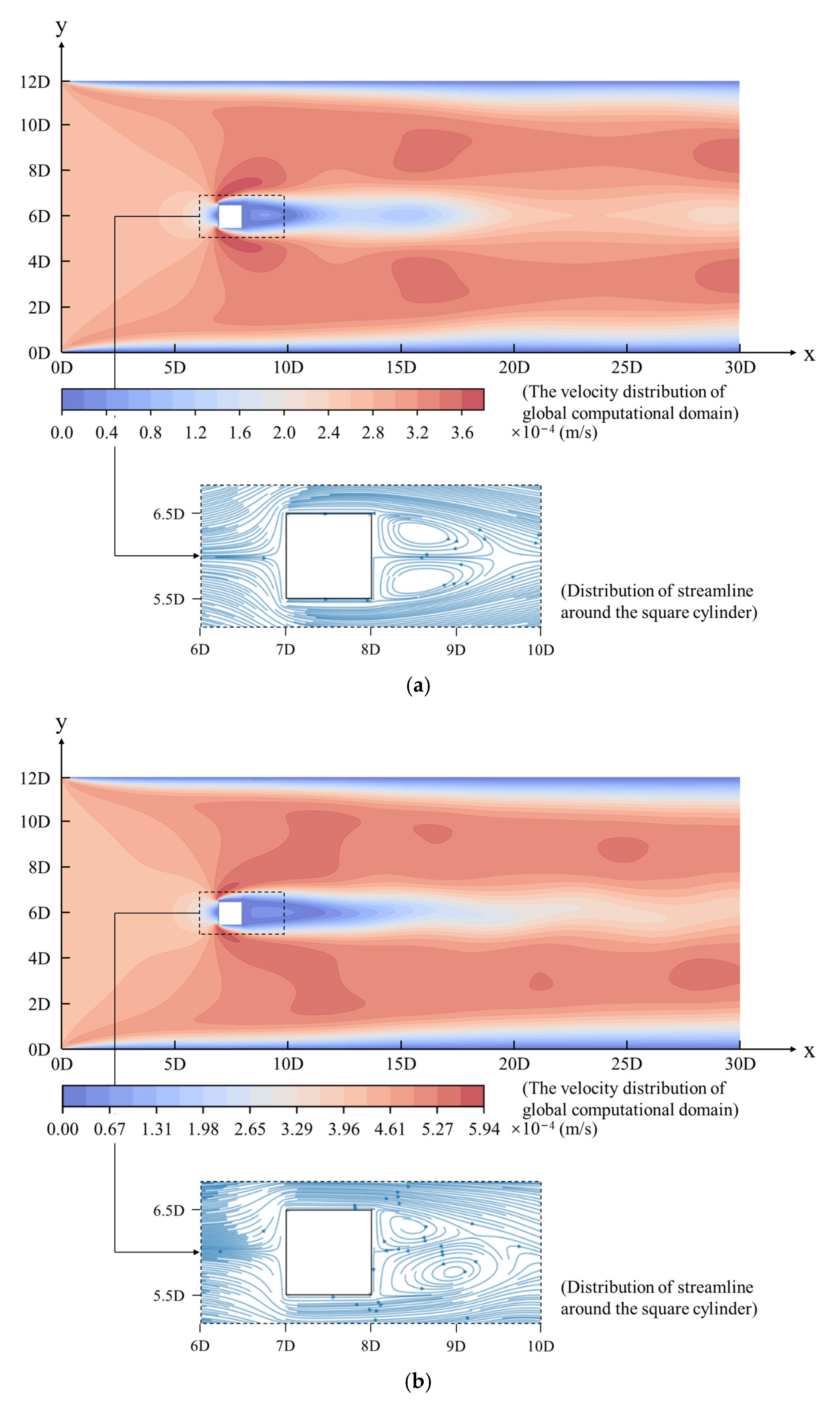
3.1. Feature of Wake Flow Patterns of the Flow around a Square Cylinder
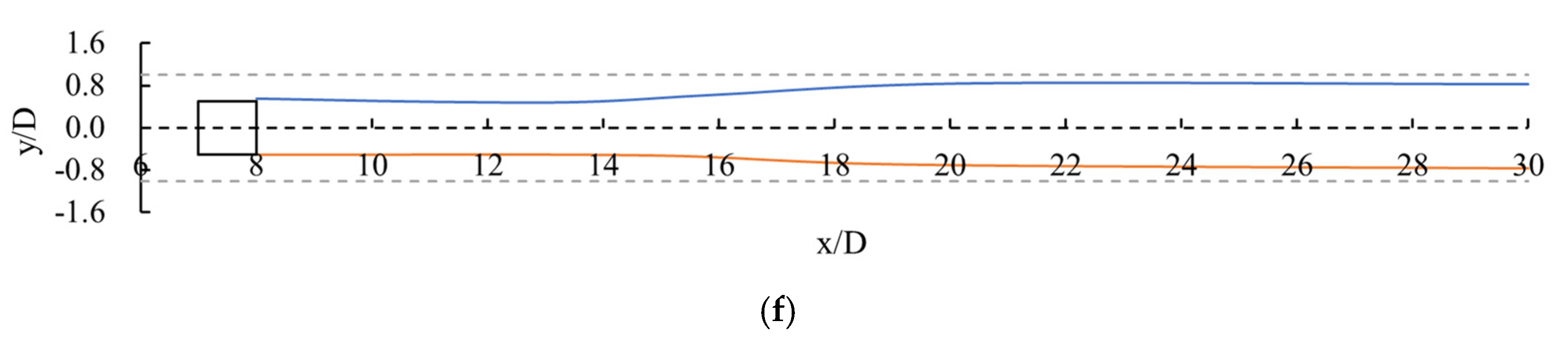
3.2. Boundary Constraint Effect in Vortex Street Flow
3.3. Fluid Characteristics of the Flow around a Square Cylinder
3.4. Flow Pattern Division of Flow around a Square Cylinder
4. Conclusions
- (1)
- The flow pattern around a square cylinder can be divided into four types under different Reynolds numbers: L1 (stable attached vortex phase), L2 (unstable attached vortex phase), L3 (laminar vortex street phase), and T (turbulence phase). The boundary constraint does not change the flow pattern around a square cylinder.
- (2)
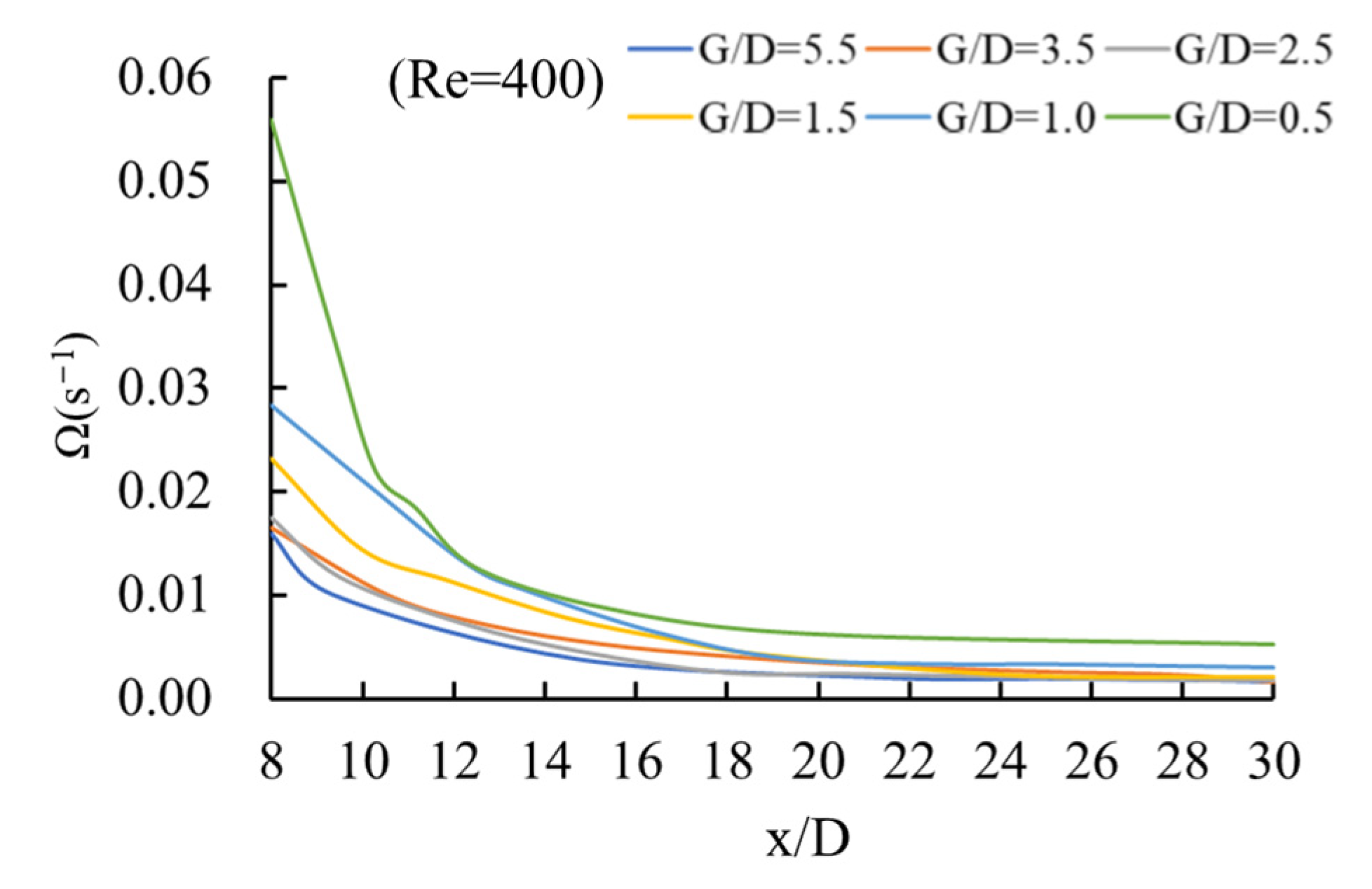
- In the flow pattern of a laminar vortex street, the boundary constraint squeezes the vortex shapes, pushes the vortex centres to the channel boundaries, and reduces the distance between the vortices along the flow direction, but the boundary constraint cannot change the attenuation law and magnitude of the vorticity along the flow direction.
- (3)
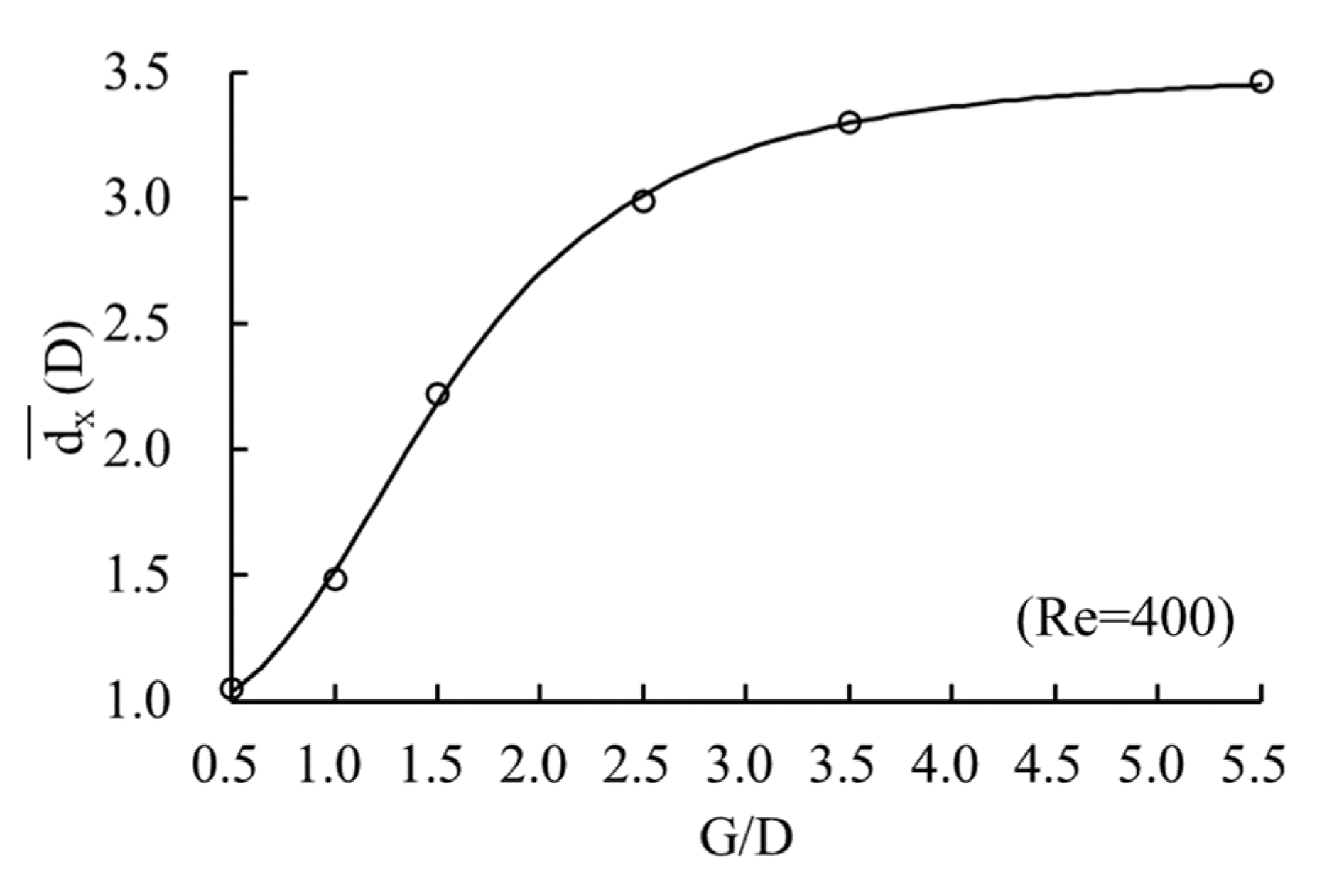
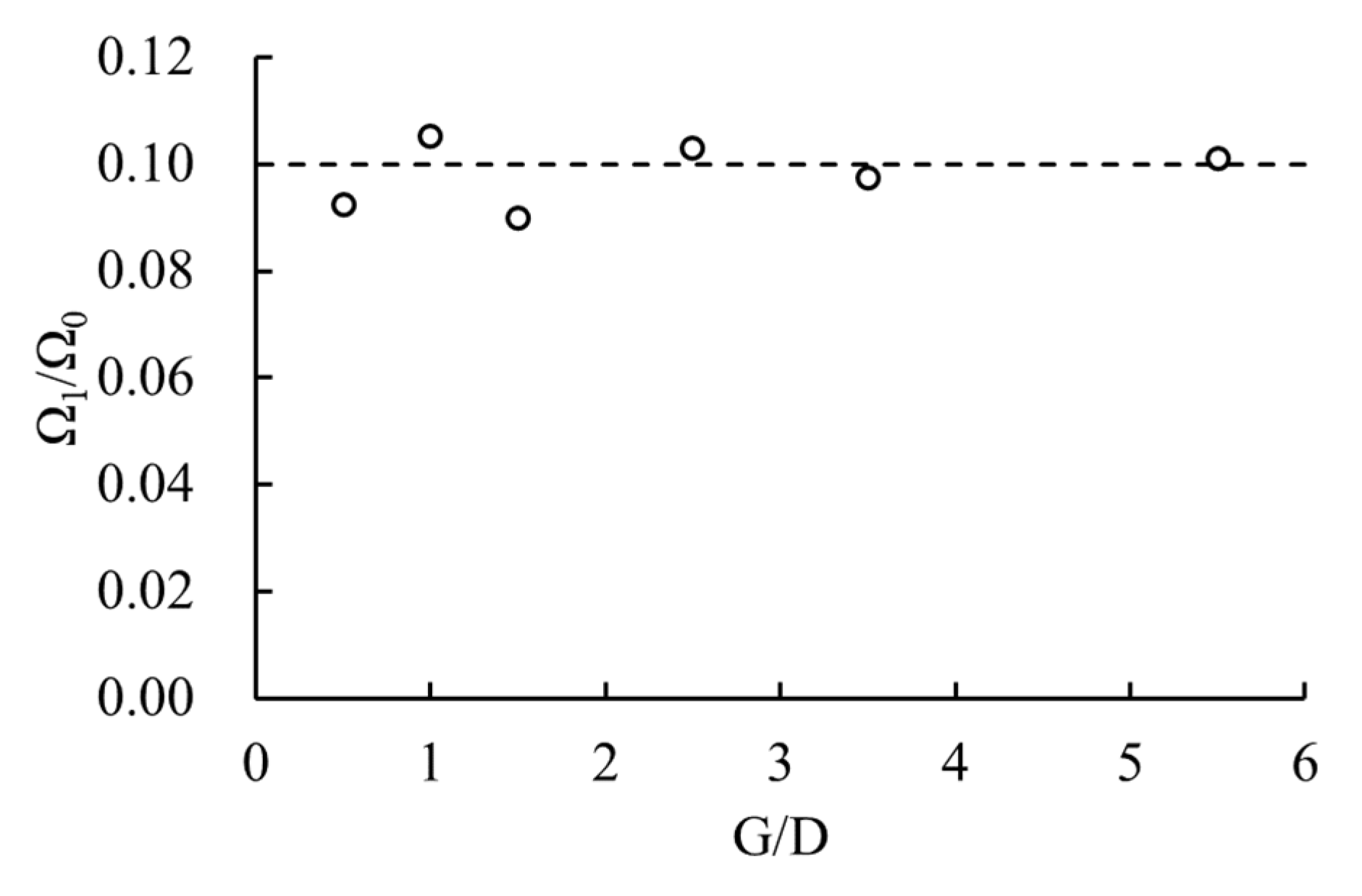
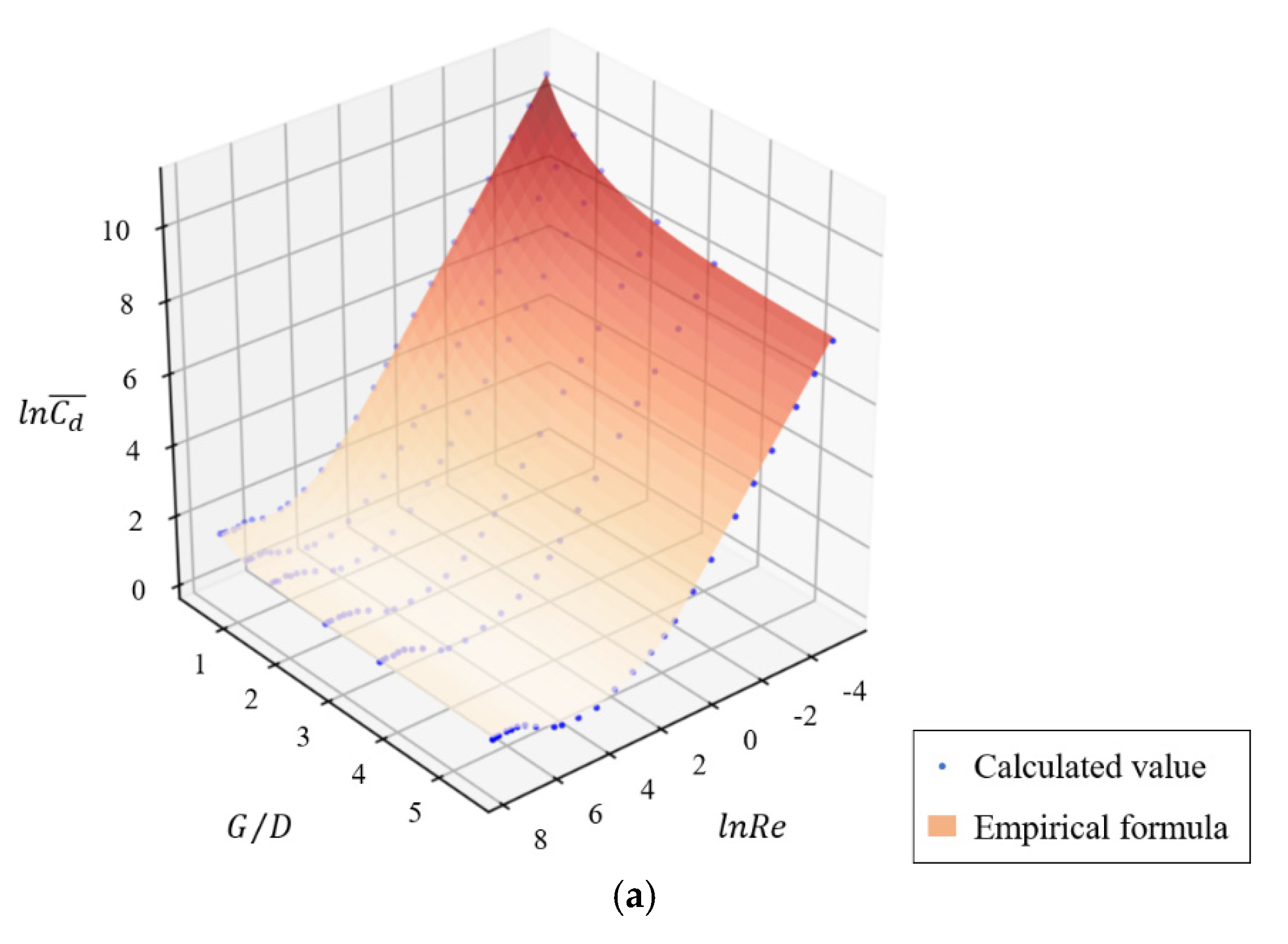
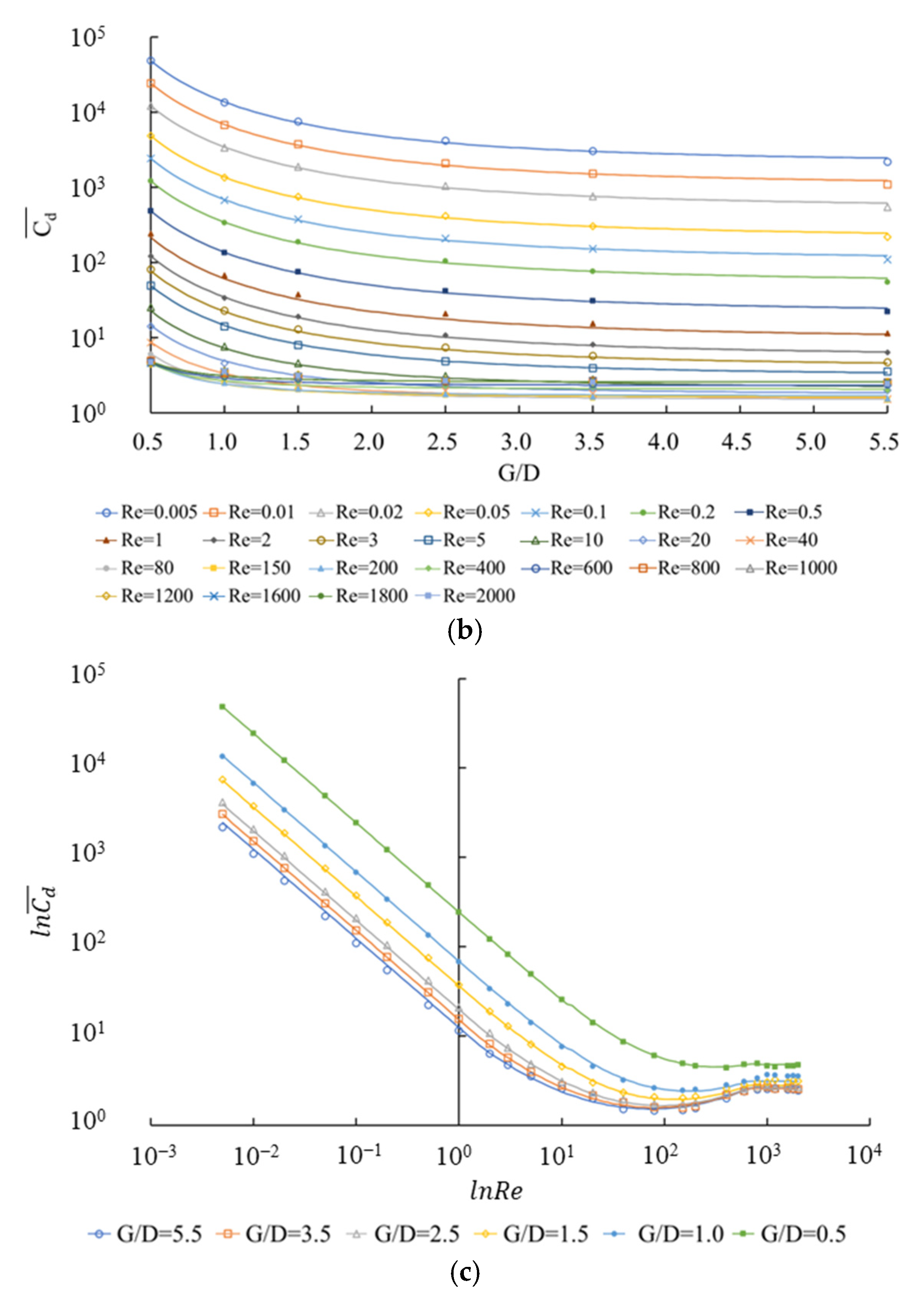
- When the constraint degree of boundaries exceeds a specific level (G/D < 3.5), the time-averaged drag coefficient of the cylinder and the shedding frequency of the attached vortices can increase significantly.
- (4)
- The variation law of the drag coefficient of the flow around a square cylinder and the shedding frequency of attached vortices with the Reynolds number will not be affected by the boundary constraint degree.
- (5)
- The boundary constraint rectifies the wake flow pattern around a square cylinder, and the appearance of turbulence requires a larger Reynolds number. With the increase of boundary constraint degree, the expansion of the of Reynolds number range corresponding to the flow pattern of the laminar vortex street is the most significant.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Williamson, C.H.K. Defining a universal and continuous Strouhal–Reynolds number relationship for the laminar vortex shedding of a circular cylinder. Phys. Fluids 1988, 31, 2742–2744. [Google Scholar] [CrossRef]
- Wang, Y.L.; Liu, Y.Z.; Miao, G.P. Three-Dimensional Numerical Simulation of Viscous Flow around Circular Cylinder. J. Shanghai Jiaotong Univ. 2001, 2001, 1461–1469. [Google Scholar]
- Behara, S.; Mittal, S. Wake transition in flow past a circular cylinder. Phys. Fluids 2010, 22, 114104. [Google Scholar] [CrossRef]
- Taneda, S. Experimental investigation of the wakes behind cylinders and plates at low Reynolds numbers. J. Phys. Soc. Jpn. 1956, 11, 302–307. [Google Scholar] [CrossRef]
- Coutanceau, M.; Bouard, R. Experimental determination of the main features of the viscous flow in the wake of a circular cylinder in uniform translation. Part 1. Steady flow. J. Fluid Mech. 1977, 79, 231–256. [Google Scholar] [CrossRef]
- Thoman, D.C.; Szewczyk, A.A. Time-dependent viscous flow over a circular cylinder. Phys. Fluids 1969, 12, II-76–II-86. [Google Scholar] [CrossRef]
- Collins, W.M.; Dennis, S.C.R. Flow past an impulsively started circular cylinder. J. Fluid Mech. 1973, 60, 105–127. [Google Scholar] [CrossRef]
- Coutanceau, M.; Defaye, J.R. Circular cylinder wake configurations: A flow visualization survey. Apply Mech. Rev. 1991, 44, 255–305. [Google Scholar] [CrossRef]
- Wu, M.H.; Wen, C.Y.; Yen, R.H.; Weng, M.C.; Wang, A.B. Experimental and numerical study of the separation angle for flow around a circular cylinder at low Reynolds number. J. Fluid Mech. 2004, 515, 233–260. [Google Scholar] [CrossRef] [Green Version]
- Couder, Y. The observation of a shear flow instability in a rotating system with a soap membrane. J. De Phys. Lett. 1981, 42, 429–431. [Google Scholar] [CrossRef]
- Chomaz, J.M. The dynamics of a viscous soap film with soluble surfactant. J. Fluid Mech. 2001, 442, 387–409. [Google Scholar] [CrossRef] [Green Version]
- Beizaie, M.; Gharib, M. Fundamentals of a liquid (soap) film tunnel. Exp. Fluids 1997, 23, 130–140. [Google Scholar] [CrossRef]
- Kim, N.; Kim, H.; Park, H. An experimental study on the effects of rough hydrophobic surfaces on the flow around a circular cylinder. Phys. Fluids 2015, 27, 85113. [Google Scholar] [CrossRef]
- Palau-Salvador, G.; Stoesser, T.; Fröhlich, J.; Kappler, M.; Rodi, W. Large eddy simulations and experiments of flow around finite-height cylinders. Flow Turbul. Combust. 2010, 84, 239–275. [Google Scholar] [CrossRef]
- Sen, S.; Mittal, S.; Biswas, G. Flow past a square cylinder at low Reynolds numbers. Int. J. Numer. Methods Fluids 2011, 67, 1160–1174. [Google Scholar] [CrossRef]
- Tong, B.; Zhu, B.; Zhou, B.K. Numerical Simulation of Flow around Square Cylinder. Chin. Q. Mech. 2002, 23, 77–81. [Google Scholar]
- Yang, F.; Zhou, Z.; Tang, G.; Lu, L. Steady flow around a square cylinder near a plane boundary. Ocean Eng. 2021, 222, 108599. [Google Scholar] [CrossRef]
- Prsic, M.A.; Ong, M.C.; Pettersen, B.; Myrhaug, D. Large Eddy Simulations of flow around a circular cylinder close to a flat seabed. Mar. Struct. 2016, 46, 127–148. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.F.; Wu, G.X. Boundary shear flow past a cylinder near a wall. Appl. Ocean Res. 2019, 92, 101923. [Google Scholar] [CrossRef]
- Lei, C.; Cheng, L.; Kavanagh, K. Re-examination of the effect of a plane boundary on force and vortex shedding of a circular cylinder. J. Wind Eng. Ind. Aerodyn. 1999, 80, 263–286. [Google Scholar] [CrossRef]
- Nishino, T.; Roberts, G.T.; Zhang, X. Vortex shedding from a circular cylinder near a moving ground. Phys. Fluids 2007, 19, 25103. [Google Scholar] [CrossRef] [Green Version]
- Lei, C.; Cheng, L.; Armfield, S.W.; Kavanagh, K. Vortex shedding suppression for flow over a circular cylinder near a plane boundary. Ocean Eng. 2000, 27, 1109–1127. [Google Scholar] [CrossRef]
- Khabbouchi, I.; Guellouz, M.S.; Nasrallah, S.B. A study of the effect of the jet-like flow on the near wake behind a circular cylinder close to a plane wall. Exp. Therm. Fluid Sci. 2013, 44, 285–300. [Google Scholar] [CrossRef]
- Durao, D.F.G.; Gouveia, P.S.T.; Pereira, J.C.F. Velocity characteristics of the flow around a square cross section cylinder placed near a channel wall. Exp. Fluids 1991, 11, 341–350. [Google Scholar] [CrossRef]
- Martinuzzi, R.J.; Bailey, S.C.C.; Kopp, G.A. Influence of wall proximity on vortex shedding from a square cylinder. Exp. Fluids 2003, 34, 585–596. [Google Scholar] [CrossRef]
- Bailey, S.C.C.; Kopp, G.A.; Martinuzzi, R.J. Vortex shedding from a square cylinder near a wall. J. Turbul. 2002, 3, 3. [Google Scholar] [CrossRef]
- Bearman, P.W.; Zdravkovich, M.M. Flow around a circular cylinder near a plane boundary. J. Fluid Mech. 1978, 89, 33–47. [Google Scholar] [CrossRef]
- Grass, A.J.; Raven, P.W.J.; Stuart, R.J.; Bray, J.A. The influence of boundary layer velocity gradients and bed proximity on vortex shedding from free spanning pipelines. J. Energy Resour. Technol. 1984, 106, 70–78. [Google Scholar] [CrossRef]
- Shi, L.L.; Liu, Y.Z.; Wan, J.J. Influence of wall proximity on characteristics of wake behind a square cylinder: PIV measurements and POD analysis. Exp. Therm. Fluid Sci. 2010, 34, 28–36. [Google Scholar] [CrossRef]
- Zhou, J.; Qiu, X.; Li, J.; Liu, Y. Vortex evolution of flow past the near-wall circular cylinder immersed in a flat-plate turbulent boundary layer. Ocean Eng. 2022, 260, 112011. [Google Scholar] [CrossRef]
- Price, S.J.; Sumner, D.; Smith, J.G.; Leong, K.; Païdoussis, M.P. Flow visualization around a circular cylinder near to a plane wall. J. Fluids Struct. 2002, 16, 175–191. [Google Scholar] [CrossRef]
- Zhang, Z.; Ji, C.; Alam, M.M.; Xu, D. DNS of vortex-induced vibrations of a yawed flexible cylinder near a plane boundary. Wind Struct. 2020, 30, 465–474. [Google Scholar] [CrossRef]
- Trias, F.X.; Gorobets, A.; Oliva, A. Turbulent flow around a square cylinder at Reynolds number 22,000: A DNS study. Comput. Fluids 2015, 123, 87–98. [Google Scholar] [CrossRef] [Green Version]
- Dong, S.; Karniadakis, G.E.; Ekmekci, A.; Rockwell, D. A combined direct numerical simulation–particle image velocimetry study of the turbulent near wake. J. Fluid Mech. 2006, 569, 185–207. [Google Scholar] [CrossRef] [Green Version]
- Behera, S.; Saha, A.K. Characteristics of the flow past a wall-mounted finite-length square cylinder at low Reynolds number with varying boundary layer thickness. J. Fluids Eng. 2019, 141, 1–17. [Google Scholar] [CrossRef]
- Ji, C.N.; Zhang, Z.M.; Alam, M.M.; Xu, D. Three-dimensional DNS of vortex-induced vibrations of an inclined flexible cylinder near a plane boundary. In Proceedings of the 2019 World Congress on Advances in Structural Engineering and Mechanics, Jeju Island, Republic of Korea, 17–21 September 2019. [Google Scholar]
- Rodi, W.; Ferziger, J.H.; Breuer, M.; Pourquié, M. Status of large eddy simulation: Results of a workshop. Trans. -Am. Soc. Mech. Eng. J. Fluids Eng. 1997, 119, 248–262. [Google Scholar] [CrossRef]
- Voke, P.R. Flow past a square cylinder: Test case LES2. In Direct and Large-Eddy Simulation II; Springer: Dordrecht, The Netherlands, 1997; pp. 355–373. [Google Scholar] [CrossRef]
- Kahil, Y.; Benhamadouche, S.; Berrouk, A.S.; Afgan, I. Simulation of subcritical-Reynolds-number flow around four cylinders in square arrangement configuration using LES. Eur. J. Mech.-B/Fluids 2019, 74, 111–122. [Google Scholar] [CrossRef]
- Rodi, W. Comparison of LES and RANS calculations of the flow around bluff bodies. J. Wind Eng. Ind. Aerodyn. 1997, 69, 55–75. [Google Scholar] [CrossRef]
- Grigoriadis, D.G.E.; Bartzis, J.G.; Goulas, A. LES of the flow past a rectangular cylinder using the immersed boundary concept. Int. J. Numer. Methods Fluids 2003, 41, 615–632. [Google Scholar] [CrossRef]
- Khan, N.B.; Ibrahim, Z.; Bin Mohamad Badry, A.B.; Jameel, M.; Javed, M.F. Numerical investigation of flow around cylinder at Reynolds number = 3900 with large eddy simulation technique: Effect of spanwise length and mesh resolution. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2019, 233, 417–427. [Google Scholar] [CrossRef]
- Kanaris, N.; Grigoriadis, D.; Kassinos, S. Three dimensional flow around a circular cylinder confined in a plane channel. Phys. Fluids 2011, 23, 64106. [Google Scholar] [CrossRef] [Green Version]
- Norberg, C. Flow around rectangular cylinders: Pressure forces and wake frequencies. J. Wind Eng. Ind. Aerodyn. 1993, 49, 187–196. [Google Scholar] [CrossRef]
- Blackburn, H.M.; Henderson, R.D. A study of two-dimensional flow past an oscillating cylinder. J. Fluid Mech. 1999, 385, 255–286. [Google Scholar] [CrossRef] [Green Version]
- Sadeque, M.A.; Rajaratnam, N.; Loewen, M.R. Flow around cylinders in open channels. J. Eng. Mech. 2008, 134, 60–71. [Google Scholar] [CrossRef]
- Yuce, M.I.; Kareem, D.A. A numerical analysis of fluid flow around circular and square cylinders. J. -Am. Water Work. Assoc. 2016, 108, E546–E554. [Google Scholar] [CrossRef]
- Zaid, M.; Yazdanfar, Z.; Chowdhury, H.; Alam, F. Numerical modeling of flow around a pier mounted in a flat and fixed bed. Energy Procedia 2019, 160, 51–59. [Google Scholar] [CrossRef]
- Lan, X.J.; Zhao, W.W.; Wan, D.C.; Zou, L. Numerical simulation of low-Re flow around a square cylinder by MPS method. Ocean Eng. 2002, 40, 83–92. [Google Scholar] [CrossRef] [Green Version]
- Gera, B.; Sharma, P.K. CFD analysis of 2D unsteady flow around a square cylinder. Int. J. Appl. Eng. Res. 2010, 1, 602. [Google Scholar]
- Okajima, A. Strouhal numbers of rectangular cylinders. J. Fluid Mech. 1982, 123, 379–398. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.C. Direct Numerical Simulation of Medium Reynolds Flow Past Square Cylinder. Master’s Thesis, China Ship Research and Development Academy, Beijing, China, 2016. [Google Scholar]
- Lyn, D.A. Phase-averaged turbulence measurements in the separated shear layer region of flow around a square cylinder. In Proceedings of the 23rd Congress of the International Association for Hydraulic Research, Ottawa, ON, Canada, 21–25 August 1989. [Google Scholar]
- Bouris, D.; Bergeles, G. 2D LES of vortex shedding from a square cylinder. J. Wind Eng. Ind. Aerodyn. 1999, 80, 31–46. [Google Scholar] [CrossRef]
- Fureby, C.; Tabor, G.; Weller, H.G.; Gosman, A.D. Large eddy simulations of the flow around a square prism. AIAA J. 2000, 38, 442–452. [Google Scholar] [CrossRef]
- Cao, Y.; Tamura, T. Large-eddy simulations of flow past a square cylinder using structured and unstructured grids. Comput. Fluids 2016, 137, 36–54. [Google Scholar] [CrossRef]
- Bearman, P.W.; Obasaju, E.D. An experimental study of pressure fluctuations on fixed and oscillating square-section cylinders. J. Fluid Mech. 1982, 119, 297–321. [Google Scholar] [CrossRef]
- Lee, B.E. The effect of turbulence on the surface pressure field of a square prism. J. Fluid Mech. 1975, 69, 263–282. [Google Scholar] [CrossRef]
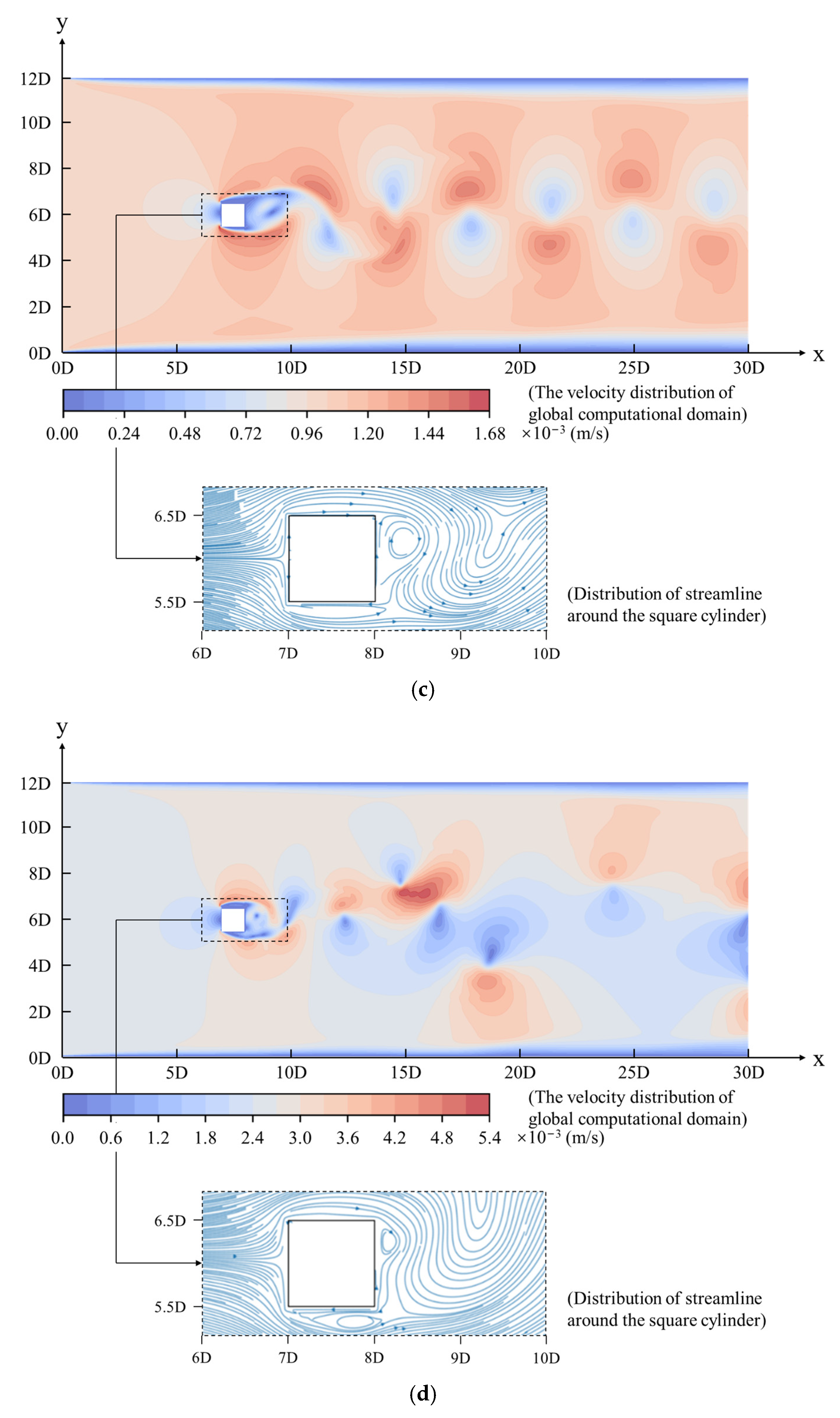
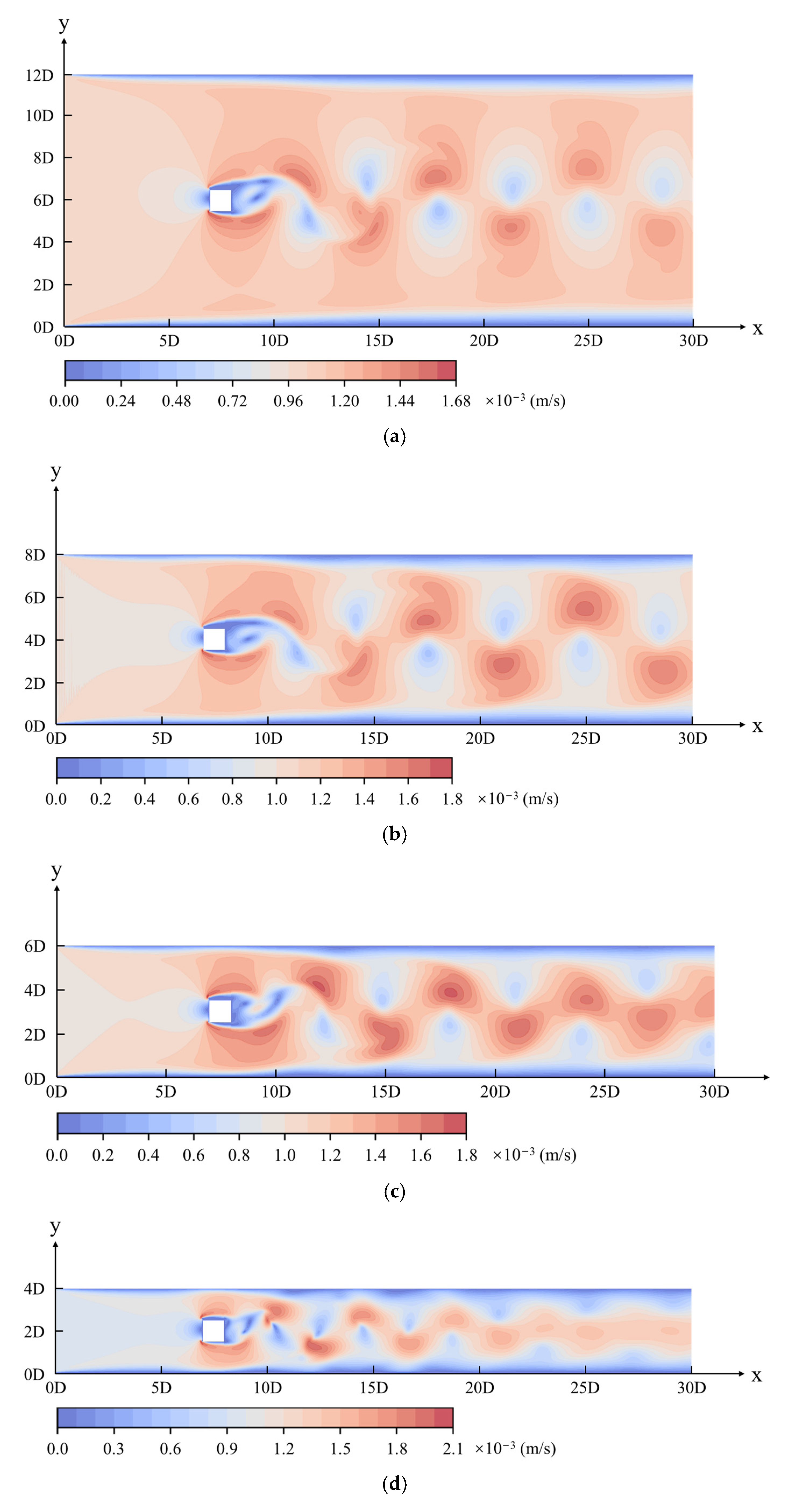


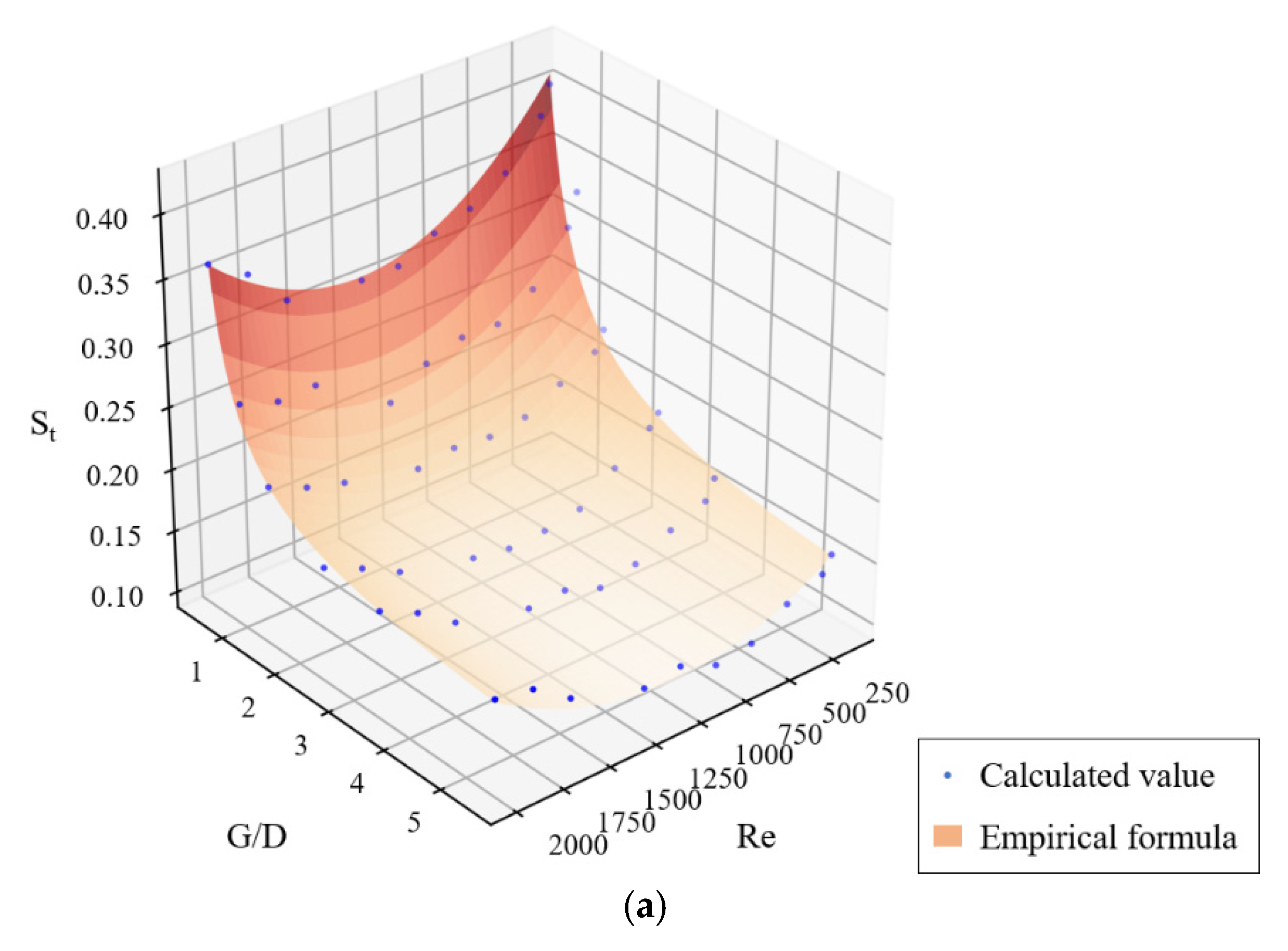
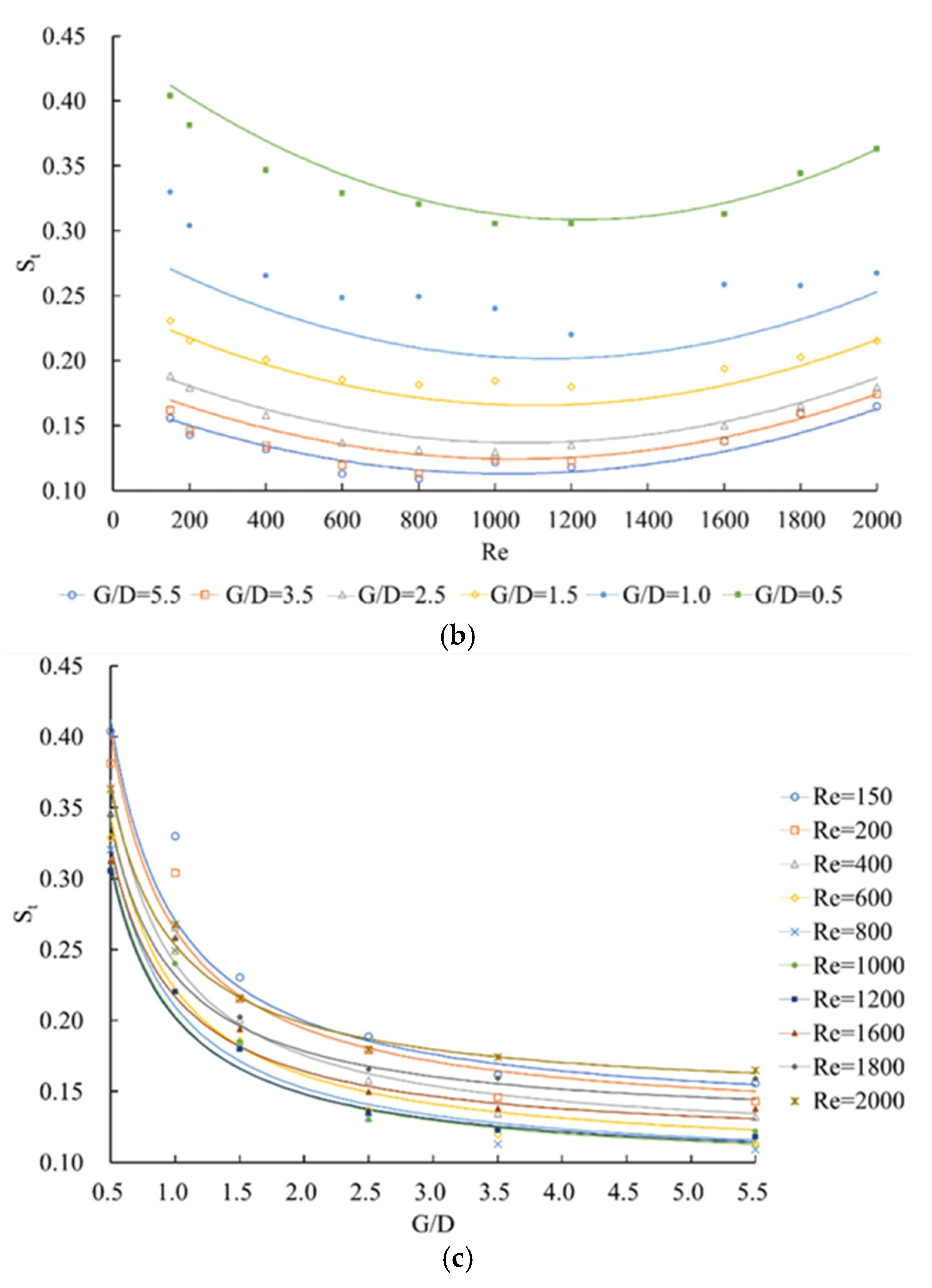
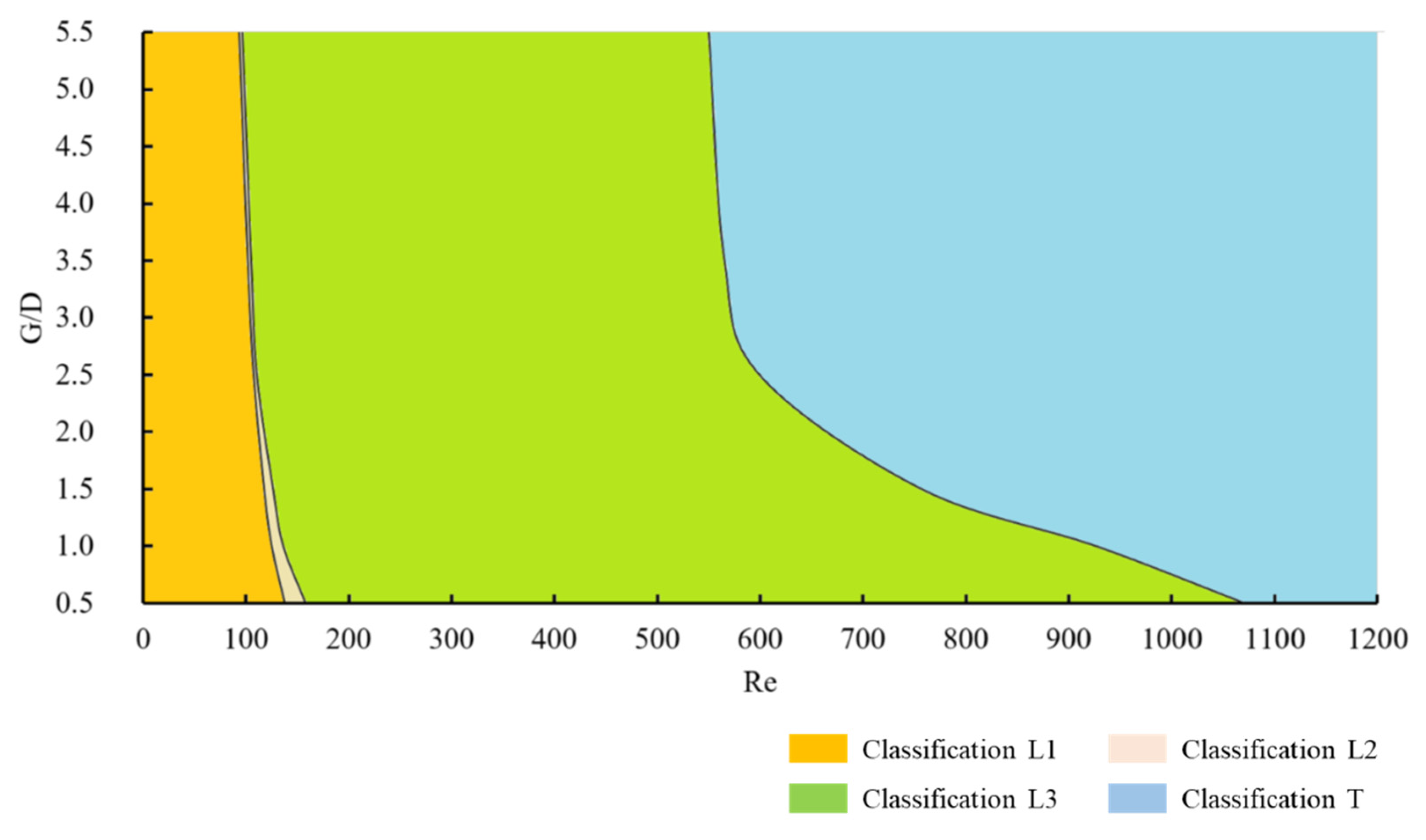
| Flow Pattern Classification | Flow Characteristics | |
|---|---|---|
| L1 | Stable attached vortex phase | Stable and symmetrical attached vortices formed by the separated flow behind a cylinder (Taneda, 1956 [4]; Coutanceau and Bouard, 1977 [5]). |
| L2 | Unstable attached vortex phase | The attached vortices behind a cylinder are asymmetric, fluctuating sinusoidally. |
| L3 | Laminar vortex street phase | Attached vortex shedding appearing behind a cylinder and forming periodic laminar vortex streets (Thoman and Szewczyk, 1969 [6]; Collins and Dennis, 1973 [7]). |
| T | Turbulence phase | Vortex streets are unstable, attached vortex shedding appearing non-sinusoidally, and turbulence is formed behind a cylinder. |
| Zone | Grid Length | Grid Width |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 |
| Grids | Total Elements | Re = 40 | Re = 1000 | ||
|---|---|---|---|---|---|
| G1 | 0.125 | 5444 | 1.49 | 1.88 | 0.117 |
| G2 | 0.075 | 15,194 | 1.54 | 2.02 | 0.120 |
| G3 | 0.050 | 33,636 | 1.59 | 2.17 | 0.121 |
| G4 | 0.025 | 134,544 | 1.64 | 2.29 | 0.121 |
| G5 | 0.0125 | 535,076 | 1.67 | 2.39 | 0.122 |
| G6 | 0.0075 | 1,487,034 | 1.69 | 2.42 | 0.122 |
| Source | |||
|---|---|---|---|
| 40 | Sen et al. [15] | 1.67 | - |
| Lan et al. [49] | 1.72 | - | |
| Present | 1.67 | - | |
| 200 | Lan et al. [49] | 1.49 | 0.143 |
| Gera et al. [50] | - | 0.145 | |
| Okajima [51] | 1.50 | 0.141 | |
| Present | 1.49 | 0.141 | |
| 1000 | Lan et al. [49] | 2.23 | 0.122 |
| Okajima [51] | 2.10 | 0.120~0.130 | |
| Wang [52] | 2.40 | 0.124 | |
| Present | 2.39 | 0.122 | |
| 22,000 | Trias et al. [33] | 2.19 | 0.132 |
| Lyn [53] | 2.18 | 0.134 | |
| Bouris et al. [54] | 2.10 | 0.135 | |
| Fureby et al. [55] | 2.11–2.30 | 0.126~0.138 | |
| Cao et al. [56] | - | 0.130 | |
| Bearman et al. [57] | 2.05 | 0.122 | |
| Lee [58] | 2.18 | 0.132 | |
| Present | 2.06 | 0.124 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Wu, S.; Wu, X.; Xue, W.; Wang, F.; Gao, A.; Zhang, W. Analysis of Flow Characteristics around a Square Cylinder with Boundary Constraint. Water 2023, 15, 1507. https://doi.org/10.3390/w15081507
Xu Z, Wu S, Wu X, Xue W, Wang F, Gao A, Zhang W. Analysis of Flow Characteristics around a Square Cylinder with Boundary Constraint. Water. 2023; 15(8):1507. https://doi.org/10.3390/w15081507
Chicago/Turabian StyleXu, Zhun, Shiqiang Wu, Xiufeng Wu, Wanyun Xue, Fangfang Wang, Ang Gao, and Weile Zhang. 2023. "Analysis of Flow Characteristics around a Square Cylinder with Boundary Constraint" Water 15, no. 8: 1507. https://doi.org/10.3390/w15081507
APA StyleXu, Z., Wu, S., Wu, X., Xue, W., Wang, F., Gao, A., & Zhang, W. (2023). Analysis of Flow Characteristics around a Square Cylinder with Boundary Constraint. Water, 15(8), 1507. https://doi.org/10.3390/w15081507









