WINDS Model Demonstration with Field Data from a Furrow-Irrigated Cotton Experiment
Abstract
:1. Introduction
2. Materials and Methods
2.1. Cotton Field Experiment Layout
2.2. Field Experiment Irrigation Scheduling and Crop ET Evaluation
2.3. WINDS Model
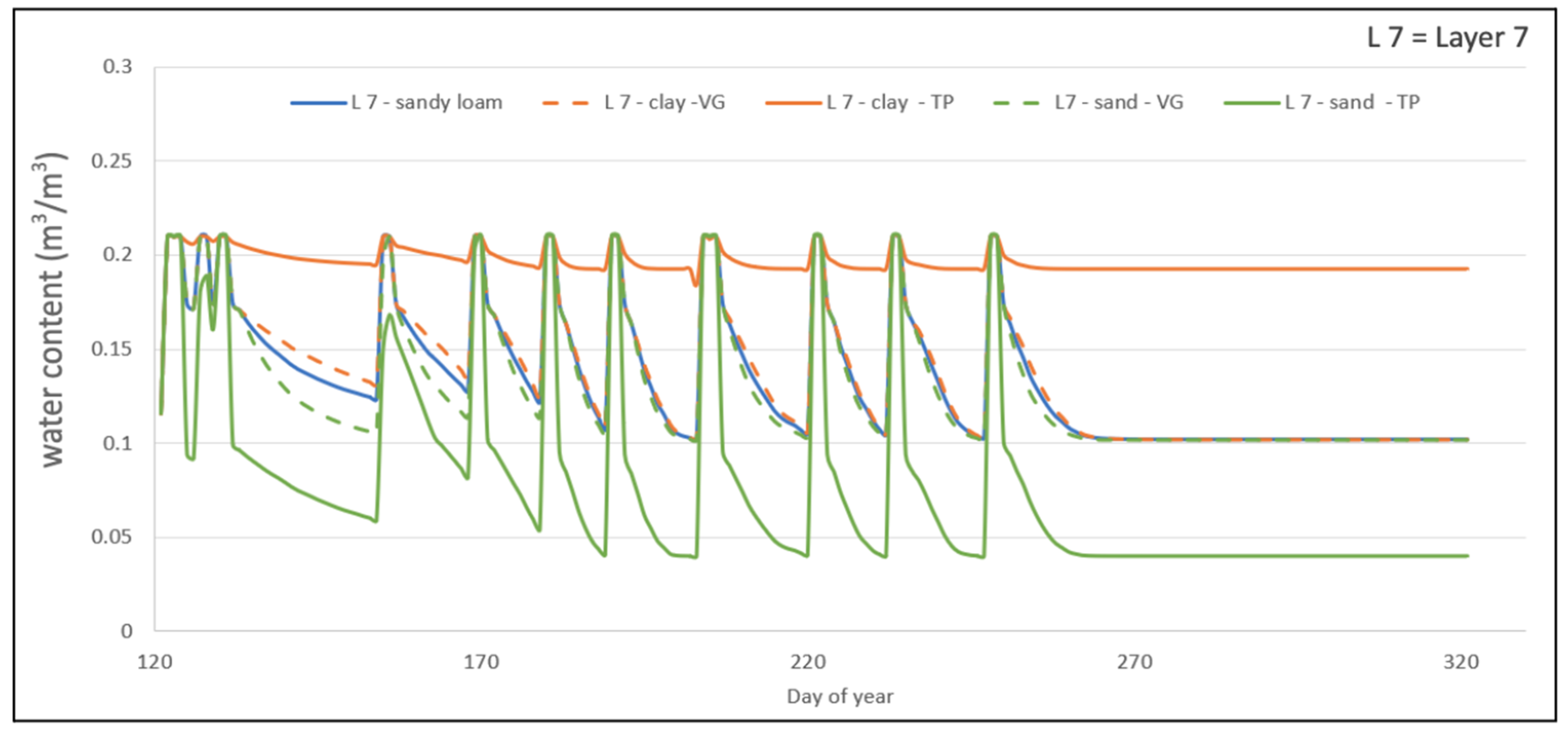
2.4. Sensitivity Analysis
3. Results
3.1. Field Experiment Results
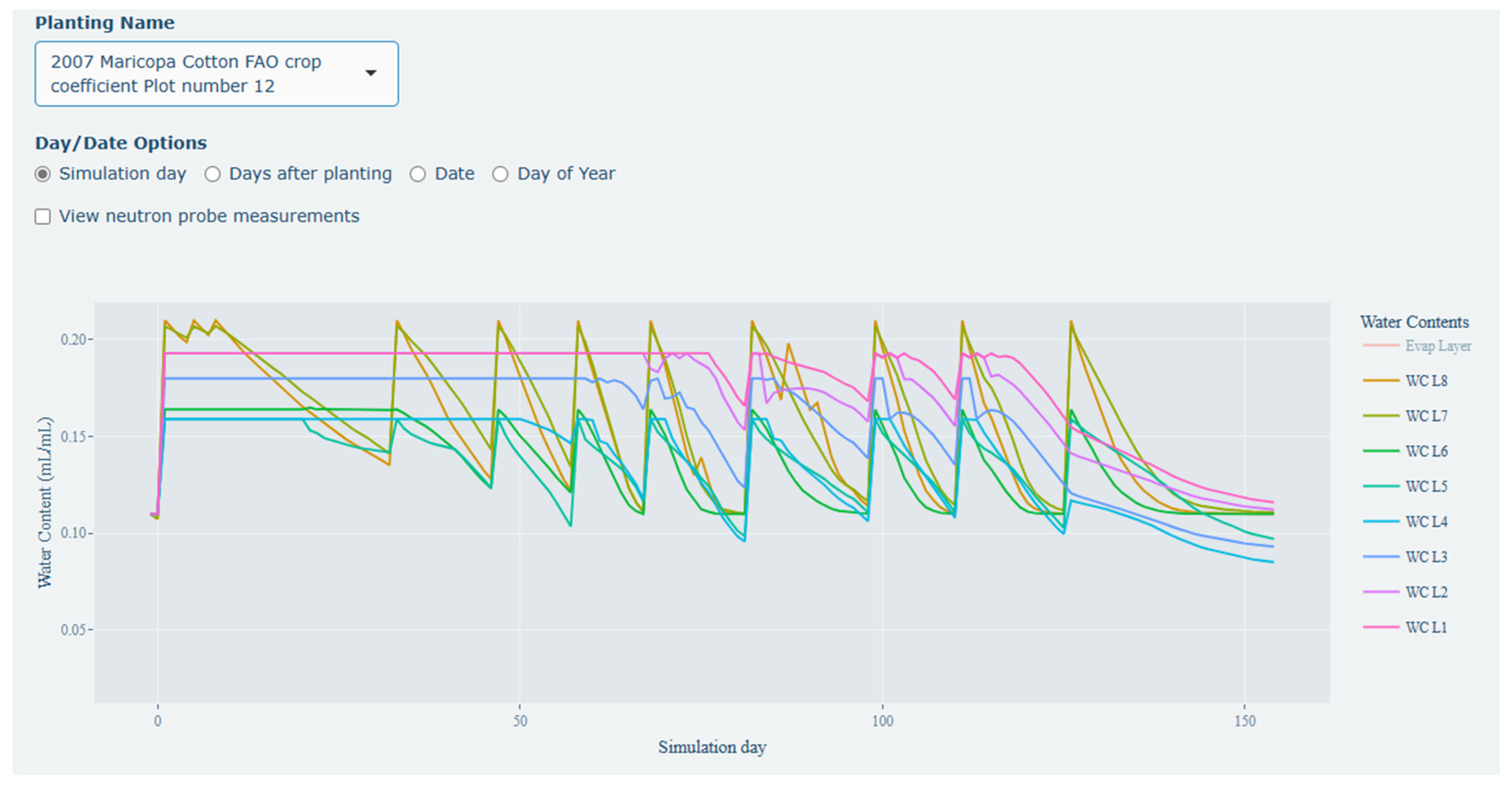
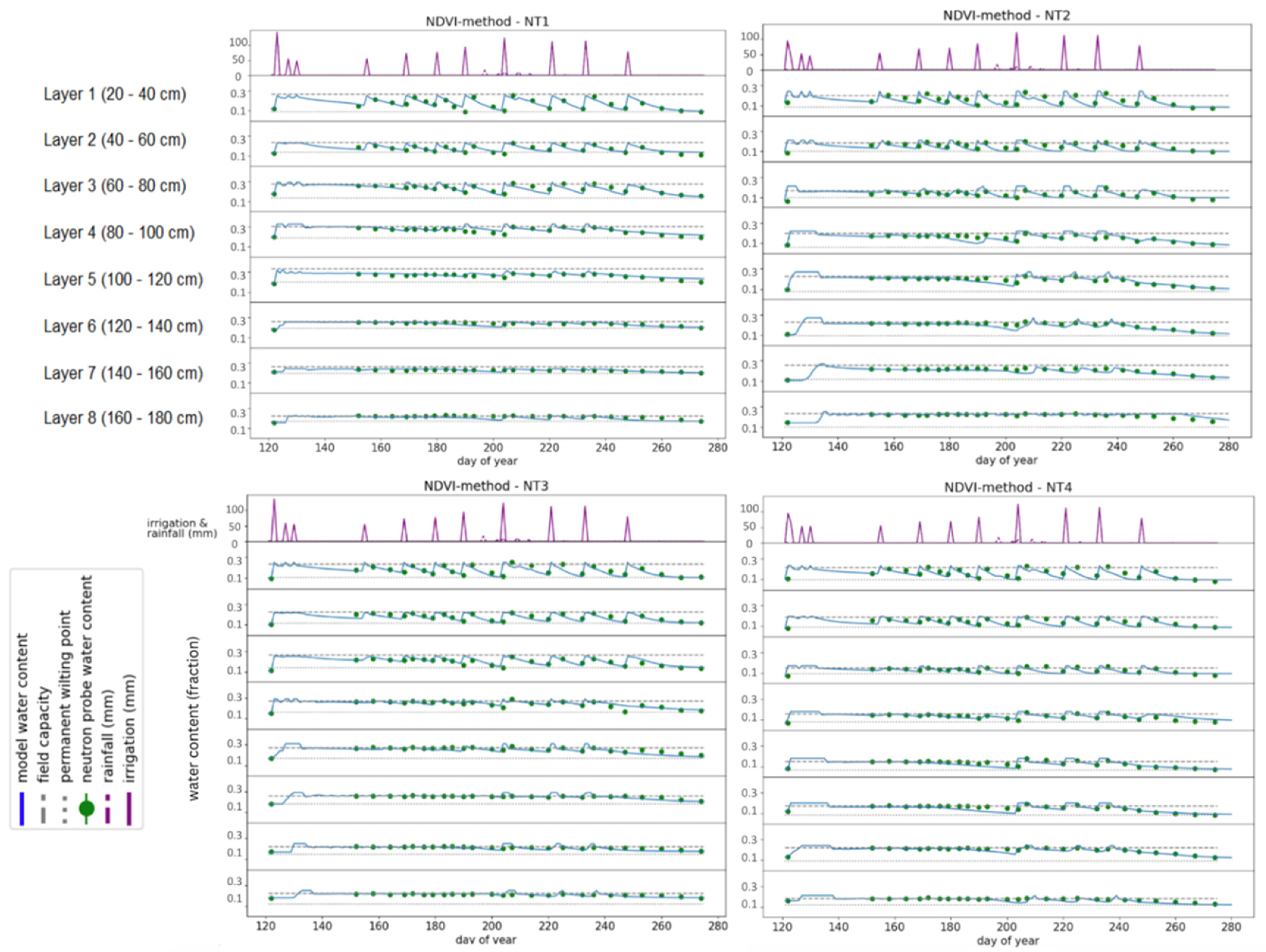
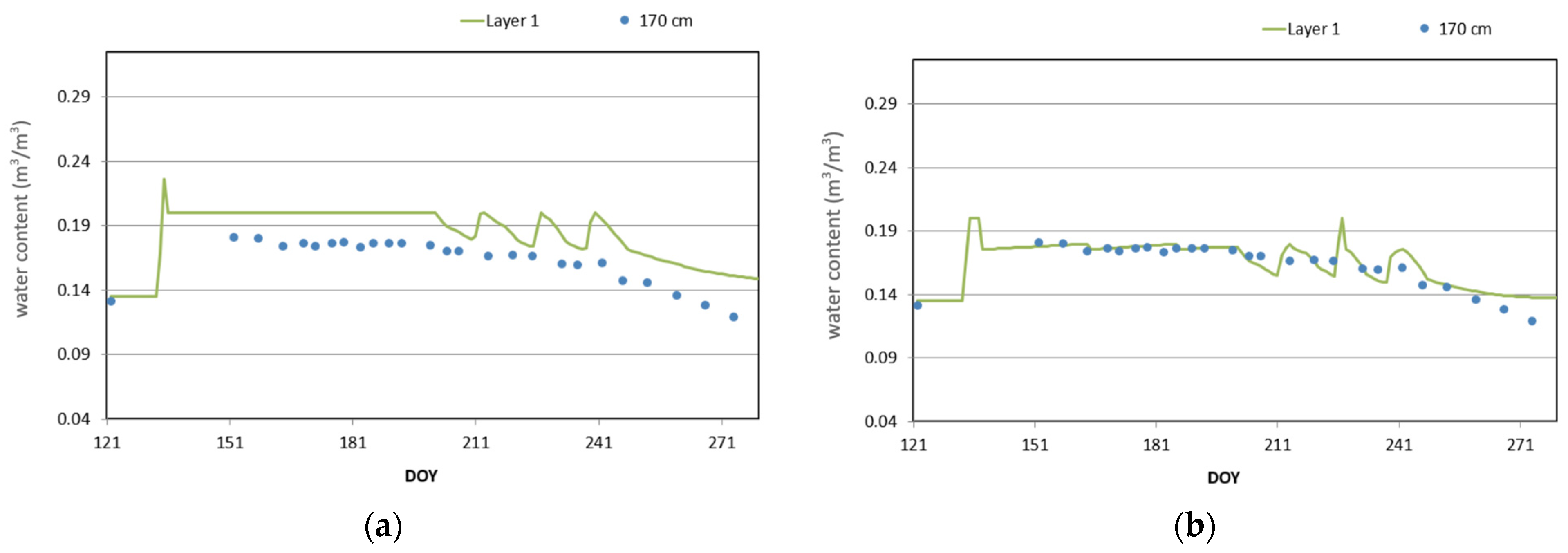
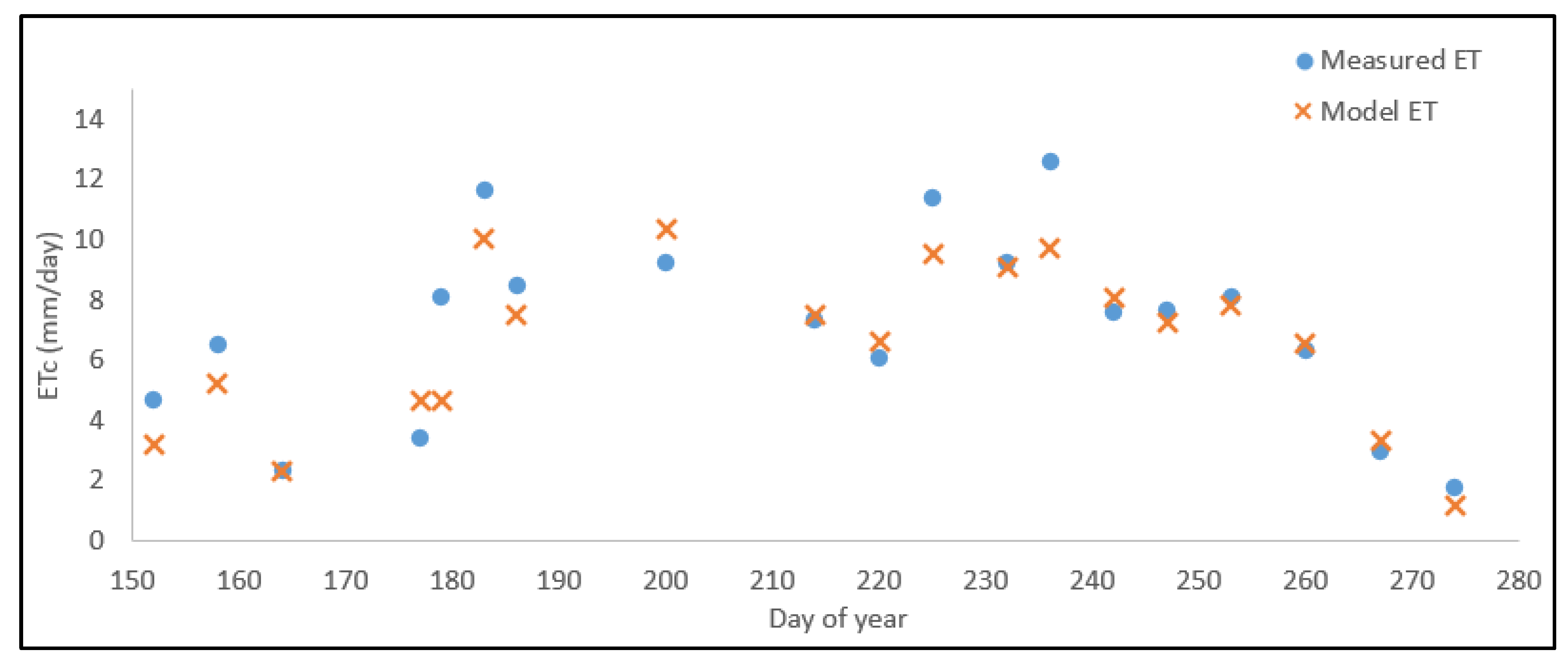
3.2. Model Results
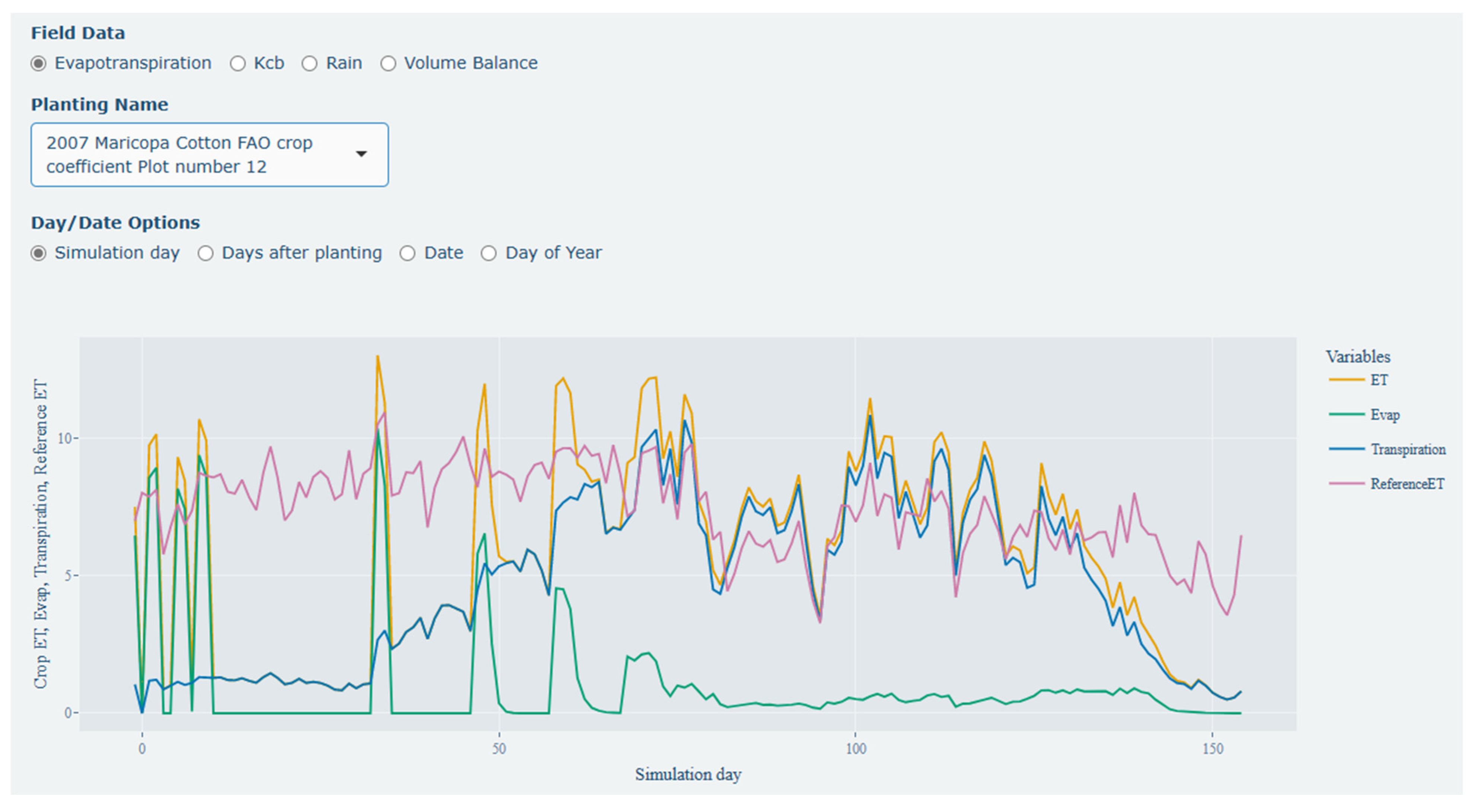
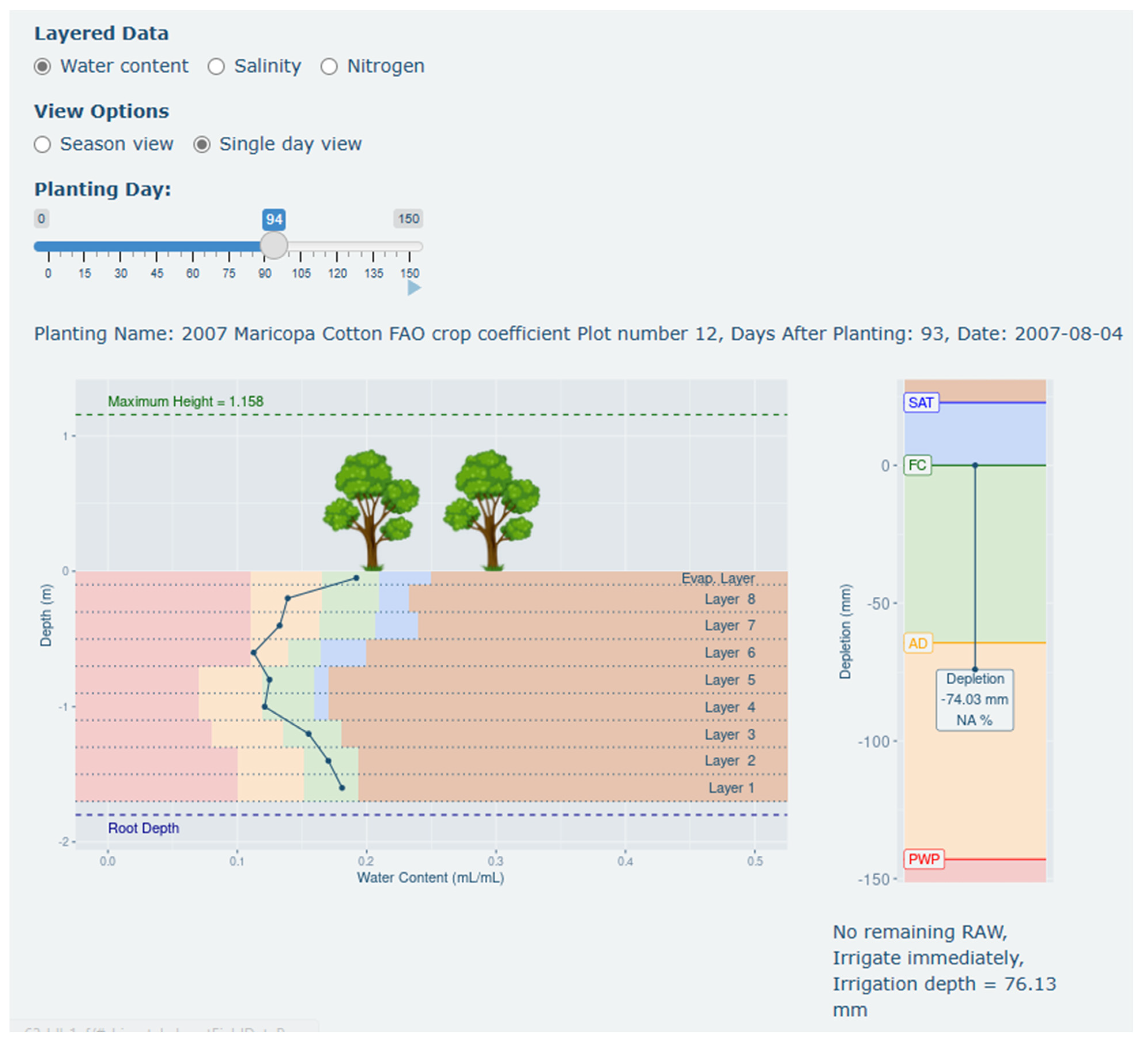
3.3. Irrigation Scheduling and Visualization Tool
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Holdren, G.C.; Turner, K. Characteristics of lake mead, Arizona–Nevada. Lake Reserv. Manag. 2010, 26, 230–239. [Google Scholar] [CrossRef] [Green Version]
- Prein, A.F.; Holland, G.J.; Rasmussen, R.M.; Clark, M.P.; Tye, M.R. Running dry: The U.S. Southwest’s drift into a drier climate state. Geophys. Res. Lett. 2016, 43, 1272–1279. [Google Scholar] [CrossRef]
- Castle, S.L.; Reager, J.T.; Thomas, B.F.; Purdy, A.J.; Lo, M.; Famiglietti, J.S.; Tang, Q. Remote detection of water management impacts on evapotranspiration in the Colorado River Basin. Geophys. Res. Lett. 2016, 43, 5089–5097. [Google Scholar] [CrossRef] [Green Version]
- Bennett, K.; Talsma, C.; Boero, R. Concurrent Changes in Extreme Hydroclimate Events in the Colorado River Basin. Water 2021, 13, 978. [Google Scholar] [CrossRef]
- Bucks, D.A.; Allen, S.G.; Roth, R.L.; Gardner, B.R. Short staple cotton under micro and level-basin irrigation methods. Irrig. Sci. 1988, 9, 161–176. [Google Scholar] [CrossRef]
- Hunsaker, D.J.; Pinter, P.J.; Cai, H. Alfalfa basal crop coefficients for FAO–56 procedures in the desert regions of the southwestern US. Trans. ASAE 2002, 45, 1799. [Google Scholar] [CrossRef]
- French, A.N.; Hunsaker, D.J.; Bounoua, L.; Karnieli, A.; Luckett, W.E.; Strand, R. Remote Sensing of Evapotranspiration over the Central Arizona Irrigation and Drainage District, USA. Agronomy 2018, 8, 278. [Google Scholar] [CrossRef] [Green Version]
- Elshikha, D.E.M.; Waller, P.M.; Hunsaker, D.J.; Dierig, D.; Wang, G.; Cruz, V.M.V.; Thorp, K.R.; Katterman, M.E.; Bronson, K.F.; Wall, G.W. Growth, water use, and crop coefficients of direct-seeded guayule with furrow and subsurface drip irrigation in Arizona. Ind. Crop. Prod. 2021, 170, 113819. [Google Scholar] [CrossRef]
- Hunsaker, D.; Bronson, K. FAO56 crop and water stress coefficients for cotton using subsurface drip irrigation in an arid US climate. Agric. Water Manag. 2021, 252, 106881. [Google Scholar] [CrossRef]
- Pereira, L.; Paredes, P.; Jovanovic, N. Soil water balance models for determining crop water and irrigation requirements and irrigation scheduling focusing on the FAO56 method and the dual Kc approach. Agric. Water Manag. 2020, 241, 106357. [Google Scholar] [CrossRef]
- Svedin, J.D.; Hansen, N.C.; Kerry, R.; Hopkins, B.G. Modeling spatio-temporal variations in crop water stress for variable-rate irrigation. In Precision Agriculture’19; Wageningen Academic Publishers: Wageningen, The Netherlands, 2019; pp. 155–206. [Google Scholar]
- Martínez-Romero, A.; López-Urrea, R.; Montoya, F.; Pardo, J.; Domínguez, A. Optimization of irrigation scheduling for barley crop, combining AquaCrop and MOPECO models to simulate various water-deficit regimes. Agric. Water Manag. 2021, 258, 107219. [Google Scholar] [CrossRef]
- Wale, A.; Dessie, M.; Kendie, H. Evaluating the Performance of AquaCrop Model for Potato Production Under Deficit Irrigation. Air Soil Water Res. 2022, 15, 11786221221108216. [Google Scholar] [CrossRef]
- Hassanli, M.; Ebrahimian, H.; Mohammadi, E.; Rahimi, A.; Shokouhi, A. Simulating maize yields when irrigating with saline water, using the AquaCrop, SALTMED, and SWAP models. Agric. Water Manag. 2016, 176, 91–99. [Google Scholar] [CrossRef]
- Akinbile, C.O. Crop water requirements, biomass and grain yields estimation for upland rice using CROPWAT, AQUA-CROP and CERES simulation models. Agric. Eng. Int. CIGR J. 2020, 22, 1–20. [Google Scholar]
- Smith, M. CROPWAT: A Computer Program for Irrigation Planning and Management (No. 46); Food & Agriculture Organization: Rome, Italy, 1992. [Google Scholar]
- Steduto, P.; Hsiao, T.C.; Raes, D.; Fereres, E. AquaCrop—The FAO crop model to simulate yield response to water: I. Concepts and underlying principles. Agron. J. 2009, 101, 426–437. [Google Scholar] [CrossRef] [Green Version]
- Sandhu, R.; Irmak, S. Performance of AquaCrop model in simulating maize growth, yield, and evapotranspiration under rainfed, limited and full irrigation. Agric. Water Manag. 2019, 223, 105687. [Google Scholar] [CrossRef]
- Simunek, J.; Huang, K.; Van Genuchten, M.T. The SWMS_3D Code for Simulating Water Flow and Solute Transport in Three-Dimensional Variably-Saturated Media; US Salinity Laboratory Agricultural Research Service: Riverside, CA, USA, 1995; p. 139. [Google Scholar]
- Simunek, J.; Van Genuchten, M.T.; Šejna, M. HYDRUS: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1263–1274. [Google Scholar]
- Iqbal, M.; Kamal, R.; Mohd, F.M.; Man, H.C.; Wayayok, A. HYDRUS-1D Simulation of Soil Water Dynamics for Sweet Corn under Tropical Rainfed Condition. Appl. Sci. 2020, 10, 1219. [Google Scholar] [CrossRef] [Green Version]
- Karandish, F.; Šimůnek, J. A comparison of the HYDRUS (2D/3D) and SALTMED models to investigate the influence of various water-saving irrigation strategies on the maize water footprint. Agric. Water Manag. 2018, 213, 809–820. [Google Scholar] [CrossRef] [Green Version]
- Waller, P.; Yitayew, M. Irrigation and Drainage Engineering; Springer: New York, NY, USA, 2016; p. 742. [Google Scholar]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper; FAO: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Pinter, P.J., Jr.; Hatfield, J.L.; Schepers, J.S.; Barnes, E.M.; Moran, M.S.; Daughtry, C.S.; Upchurch, D.R. Remote sensing for crop management. Photogramm. Eng. Remote Sens. 2003, 69, 647–664. [Google Scholar] [CrossRef] [Green Version]
- Hunsaker, D.J.; Barnes, E.M.; Clarke, T.R.; Fitzgerald, G.J.; Pinter, P.J., Jr. Cotton irrigation scheduling using remotely sensed and FAO-56 basal crop coefficients. Trans. ASAE 2005, 48, 1395–1407. [Google Scholar] [CrossRef]
- Kothari, K.; Ale, S.; Bordovsky, J.P.; Thorp, K.R.; Porter, D.O.; Munster, C.L. Simulation of efficient irrigation manage-ment strategies for grain sorghum production over different climate variability classes. Agric. Syst. 2019, 170, 49–62. [Google Scholar] [CrossRef]
- Pôças, I.; Calera, A.; Campos, I.; Cunha, M. Remote sensing for estimating and mapping single and basal crop coefficients: A review on spectral vegetation indices approaches. Agric. Water Manag. 2020, 233, 106081. [Google Scholar] [CrossRef]
- Elshikha, D.E.; Hunsaker, D.J.; Waller, P.M.; Thorp, K.R.; Dierig, D.; Wang, G.; Cruz, V.M.V.; Katterman, M.E.; Bronson, K.F.; Wall, G.W.; et al. Estimation of direct-seeded guayule growth, crop coefficient and yield parameters using UAS-based multispectral and RGB data. Agric. Water Manag. 2022, 265, 107540. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W.; Harlan, J.C. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation; NASA/GSFC Type III Final Report; NASA: Greenbelt, MD, USA, 1974; p. 371.
- Alface, A.B.; Pereira, S.B.; Filgueiras, R.; Cunha, F.F. Sugarcane spatial-temporal monitoring and crop coefficient estima-tion through NDVI. Rev. Bras. Eng. Agrícola E Ambient. 2019, 23, 330–335. [Google Scholar] [CrossRef]
- Dingre, S.K.; Gorantiwar, S.D.; Kadam, S.A. Correlating the field water balance derived crop coefficient (Kc) and canopy reflectance-based NDVI for irrigated sugarcane. Precis. Agric. 2021, 22, 1134–1153. [Google Scholar] [CrossRef]
- Ramachandran, J.; Lalitha, R.; Kannan, S.V. Estimation of site-specific crop coefficients for major crops of lalgudi block in tamil nadu using remote sensing based algorithms. J. Agric. Eng. 2021, 58, 62–72. [Google Scholar] [CrossRef]
- Ayars, J.; Hutmacher, R.; Schoneman, R.; Soppe, R.; Vail, S.; Dale, F. Realizing the Potential of Integrated Irrigation and Drainage Water Management for Meeting Crop Water Requirements in Semi-Arid and Arid Areas. Irrig. Drain. Syst. 1999, 13, 321–347. [Google Scholar] [CrossRef]
- Ayars, J.; Fulton, A.; Taylor, B. Subsurface drip irrigation in California—Here to stay? Agric. Water Manag. 2015, 157, 39–47. [Google Scholar] [CrossRef]
- Grismer, M. Regional cotton lint yield, ETc and water value in Arizona and California. Agric. Water Manag. 2002, 54, 227–242. [Google Scholar] [CrossRef]
- Radin, J.; Reaves, L.; Mauney, J.; French, O. Yield Enhancement in Cotton by Frequent Irrigations during Fruiting. Agron. J. 1992, 84, 551–557. [Google Scholar] [CrossRef]
- Hunsaker, D.; Clemmens, A.; Fangmeier, D. Cotton response to high frequency surface irrigation. Agric. Water Manag. 1998, 37, 55–74. [Google Scholar] [CrossRef]
- Thorp, K.; Thompson, A.; Bronson, K. Irrigation rate and timing effects on Arizona cotton yield, water productivity, and fiber quality. Agric. Water Manag. 2020, 234, 106146. [Google Scholar] [CrossRef]
- Post, D.F.; Mack, C.; Camp, P.D.; Suliman, A.S. Mapping and Characterization of the Soils on the University of Arizona Maricopa Agricultural Center; Arizona-Nevada Academy of Science: Tucson, AZ, USA, 1988. [Google Scholar]
- Hunsaker, D.J.; French, A.N.; Clarke, T.R.; El-Shikha, D.M. Water use, crop coefficients, and irrigation management criteria for camelina production in arid regions. Irrig. Sci. 2010, 29, 27–43. [Google Scholar] [CrossRef]
- Bonan, G. Climate change and Terrestrial Ecosystem Modeling; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]

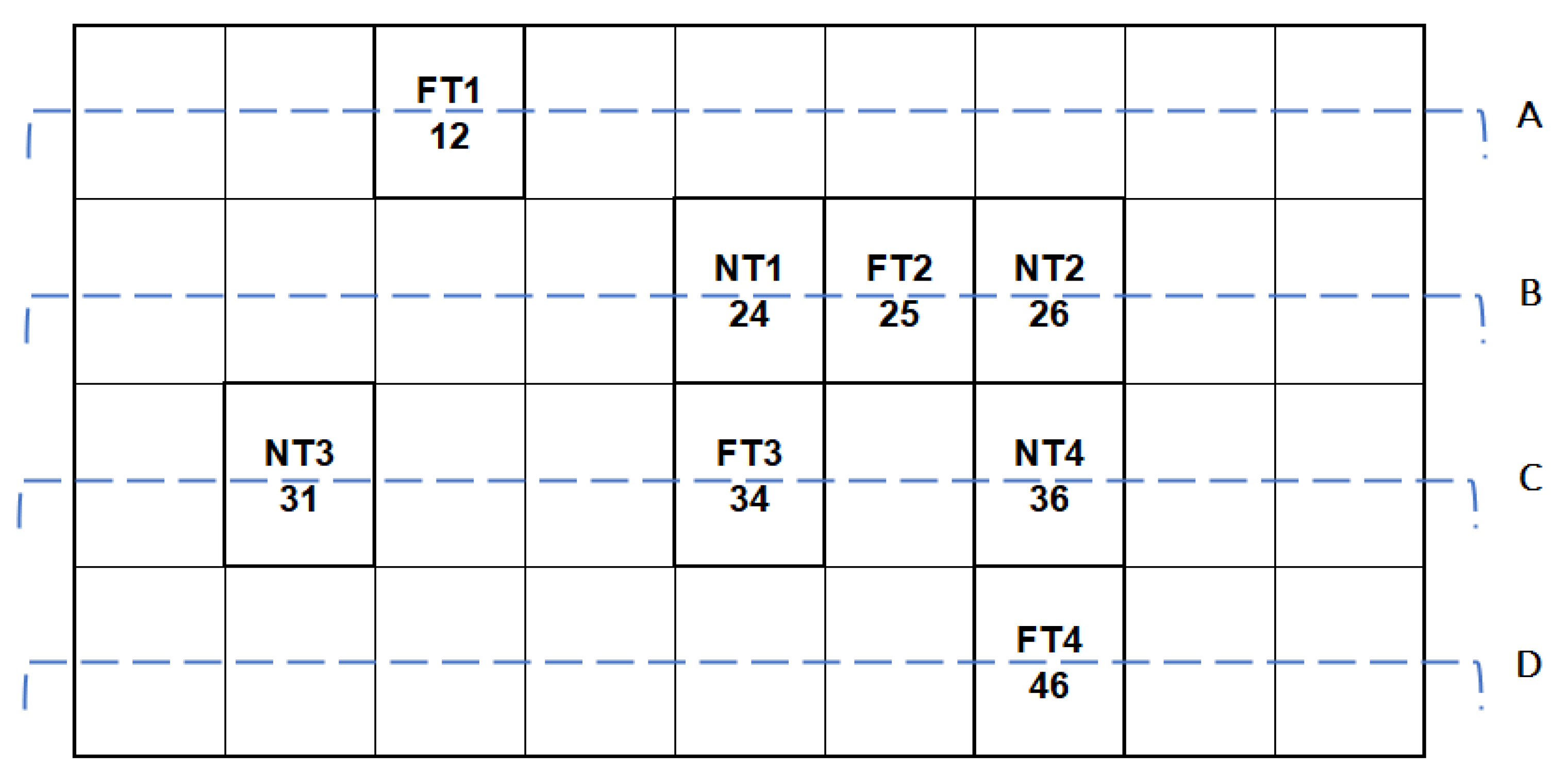



| Treatment | Plot Number | Title 3 |
|---|---|---|
| FAO method | 12 | FT1 |
| 25 | FT2 | |
| 34 | FT3 | |
| 46 | FT4 | |
| NDVI method | 24 | NT1 |
| 26 | NT2 | |
| 31 | NT3 | |
| 36 | NT4 |
| Month | Max Temp (°C) | Min Temp (°C) | Rainfall (mm) | ETo (mm) | Wind Speed 2 m (m/s) |
|---|---|---|---|---|---|
| May | 35.5 | 16.9 | 0.0 | 245.5 | 2.1 |
| June | 40.4 | 21.0 | 0.0 | 265.3 | 2.1 |
| July | 40.4 | 25.4 | 45.0 | 244.4 | 2.2 |
| August | 40.1 | 25.6 | 9.7 | 210.1 | 1.7 |
| September | 37.5 | 20.4 | 2.3 | 185.9 | 1.9 |
| Total growing period ave. | 37.7 | 20.3 | 60.0 | 1151 | 2.0 |
| Estimated Kcb | Estimated Crop ET (mm) | |||||
|---|---|---|---|---|---|---|
| Growth Stage | Day of Year | Growth Stage Length (days) | FAO56 | NDVI | FAO56 a | NDVI a |
| Initial stage | 122–151 | 30 | 0.15 | 0.16 | 95.8 ± 4.9 | 103.7 ± 7.3 |
| Development | 152–203 | 52 | 0.17–1.18 | 0.28–1.16 | 362.3 ± 3.1 | 359.3 ± 15.5 |
| Mid-season | 204–253 | 50 | 1.20 | 1.21 | 400.7 ± 2.7 | 399.4 ± 1.2 |
| Late season | 254–276 | 23 | 1.17–0.51 | 1.20–0.26 | 83.1 ± 15.8 | 91.3 ± 1.3 |
| Total | 122–276 | 155 | 941.8 ± 24.5 | 953.8 ± 12.1 | ||
| NDVI-based Kcb criteria | ||||||
| Growth stage | Kcb-NDVI relationship b | |||||
| Initial through mid-season | Kcb = −0.21 + 5.0 × NDVI − 12.2 × NDVI2 + 14.9 × NDVI3 − 6.2 × NDVI4 | |||||
| Late season | Kcb = −125 + 498 × NDVI − 662 × NDVI2 + 294 × NDVI3 | |||||
| Mualem–Van Genuchten Parameters | |||
|---|---|---|---|
| Sand a | Sandy Loam b | Clay b | |
| α (m−1) | 14.5 | 7.5 | 0.8 |
| N (dimensionless) | 2.6 | 1.89 | 1.09 |
| θr (%) | 4.5 | 6.5 | 6.8 |
| Ksat (m/day) | 7.128 | 1.061 | 0.038 |
| L (dimensionless) | 0.5 | 0.5 | 0.5 |
| Tipping bucket parameters | |||
| Sand a | Sandy loam c | Clay c | |
| Field Capacity (%) | 10 | 18.2 | 25.7 |
| Wilting point (%) | 4 | 10.2 | 19.2 |
| Kcb | ||||||||
|---|---|---|---|---|---|---|---|---|
| Treatment | Initial | Mid | End | ETc [E] (mm) | Crop height (m) | I (mm) | ETc [m] (mm) | LY (kg/ha) |
| FT-1 | 0.150 | 1.20 | 0.51 | 936 | 1.16 | 953 | 988 | 1957 |
| FT-2 | 0.150 | 1.20 | 0.51 | 910 | 1.23 | 928 | 977 | 2016 |
| FT-3 | 0.150 | 1.20 | 0.51 | 955 | 1.19 | 988 | 1012 | 1876 |
| FT-4 | 0.150 | 1.20 | 0.51 | 966 | 1.29 | 972 | 981 | 1876 |
| FT avg | 0.150 | 1.20 | 0.51 | 942 | 1.22 | 960 | 990 | 1931 |
| NT-1 | 0.152 | 1.22 | 0.30 | 961 | 1.19 | 971 | 1007 | 1947 |
| NT-2 | 0.152 | 1.21 | 0.18 | 937 | 1.30 | 954 | 974 | 2040 |
| NT-3 | 0.152 | 1.21 | 0.38 | 964 | 1.06 | 976 | 961 | 1972 |
| NT-4 | 0.152 | 1.21 | 0.27 | 953 | 1.12 | 969 | 1009 | 1851 |
| NT avg | 0.152 | 1.216 | 0.28 | 954 | 1.17 | 967 | 988 | 1953 |
| Treatment Name | Plot Code | Soil Type |
|---|---|---|
| FT Replicate 1 | FT-1 | Sandy clay loam |
| FT Replicate 2 | FT-2 | Sandy loam |
| FT Replicate 3 | FT-3 | Sandy clay loam |
| FT Replicate 4 | FT-4 | Sandy clay loam |
| NT Replicate 1 | NT-1 | Sandy clay loam |
| NT Replicate 2 | NT-2 | Sandy loam |
| NT Replicate 3 | NT-3 | Sandy clay loam |
| NT Replicate 4 | NT-4 | Sandy loam |
| Kcb Method | Replicate 1 | Replicate 2 | Replicate 3 | Replicate 4 | Average | |
|---|---|---|---|---|---|---|
| RMSE | FAO | 0.022 | 0.026 | 0.026 | 0.032 | 0.026 |
| NDVI | 0.025 | 0.032 | 0.029 | 0.029 | 0.028 | |
| R2 | FAO | 0.87 | 0.86 | 0.98 | 0.97 | 0.92 |
| NDVI | 0.94 | 0.90 | 0.89 | 0.95 | 0.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maqsood, H.; Hunsaker, D.J.; Waller, P.; Thorp, K.R.; French, A.; Elshikha, D.E.; Loeffler, R. WINDS Model Demonstration with Field Data from a Furrow-Irrigated Cotton Experiment. Water 2023, 15, 1544. https://doi.org/10.3390/w15081544
Maqsood H, Hunsaker DJ, Waller P, Thorp KR, French A, Elshikha DE, Loeffler R. WINDS Model Demonstration with Field Data from a Furrow-Irrigated Cotton Experiment. Water. 2023; 15(8):1544. https://doi.org/10.3390/w15081544
Chicago/Turabian StyleMaqsood, Hadiqa, Douglas J. Hunsaker, Peter Waller, Kelly R. Thorp, Andrew French, Diaa Eldin Elshikha, and Reid Loeffler. 2023. "WINDS Model Demonstration with Field Data from a Furrow-Irrigated Cotton Experiment" Water 15, no. 8: 1544. https://doi.org/10.3390/w15081544
APA StyleMaqsood, H., Hunsaker, D. J., Waller, P., Thorp, K. R., French, A., Elshikha, D. E., & Loeffler, R. (2023). WINDS Model Demonstration with Field Data from a Furrow-Irrigated Cotton Experiment. Water, 15(8), 1544. https://doi.org/10.3390/w15081544







