Study on the Carrying Capacity and Change Trend of Groundwater Resources in Coal Mining Area: A Case Study of a Coal Mine in Northwest China

Abstract

The groundwater resources carrying capacity is a comprehensive metric that assesses the ability of groundwater resources in a region to support industrial production and socioeconomic development. In arid regions, the calculation and analysis of the carrying capacity of groundwater resources are of paramount importance for guiding sustainable mining practices in coal mines. This study utilized a combination of the Fuzzy Comprehensive Evaluation (FCE) method and the Analytic Hierarchy Process (AHP) method to analyze the carrying capacity of groundwater resources in the coal mine located in northwest China. The results showed that the groundwater resources carrying capacity in the study coal mine was at a low level from 2011 to 2020 and the development and utilization of groundwater will reach its limit. The change trend of the carrying capacity showed a slight increase following a decline, with the highest value 0.5021 and the lowest 0.3518. The factors that significantly impacted the size of the carrying capacity included the total groundwater resources, the degree of groundwater development and utilization, and the per unit GDP of water consumption. To ensure sustainable development, the optimization of coal mining technology and the improvement of groundwater utilization efficiency should be promoted, while the rate of groundwater development should be slowed. The findings of this study offer valuable insights for guiding the sustainable development of groundwater resources in the coal mine of arid areas in the future and have practical implications.

1. Introduction

The coal resources in the northwest region of China are abundant and make up a substantial proportion of the total coal resources in the country, accounting for approximately 80% [1,2,3,4]. However, the water resources in the same region are quite limited, making up only 9.4% of the total water resources in the country [5,6,7]. With rich coal and poor water in northwest China, a large amount of mine water will be produced in the process of coal mining, which leads to water loss. Many coal mines in arid areas are faced with the problem of unclear carrying capacity of groundwater resources, which makes it impossible to escape the dilemma of groundwater loss and water shortage. The dry and arid climate, with low precipitation and high evaporation levels, has made water resources scarcity a key challenge to the development of the coal industry in this region. At present, the research on water resources carrying capacity has been widely carried out, but mainly concentrated on surface water resources. The study on the carrying capacity of groundwater resources is still insufficient, especially the research on coal mines in arid areas is rarely carried out. Groundwater, as a crucial water source, directly influences the mining prospects and construction directions in a region due to its carrying capacity. An analysis of groundwater carrying capacity can provide insight into the relationship between limited groundwater resources, population, environment, and economic development, thereby identifying the factors and conditions that restrict the sustainable development of the mining area. Conducting an evaluation of groundwater carrying capacity is of great significance for comprehending the endowment of groundwater resources in the mining area and other arid regions. The coal mine in Lingwu City selected in this paper is the first to carry out an analysis of groundwater resource carrying capacity. As a case study, this study opens a window to understanding the characteristics of groundwater endowment in northwest China arid region.

The fuzzy comprehensive evaluation method (FCE) is a systematic evaluation approach that leverages the principles of fuzzy mathematics to address complex and non-quantifiable issues [8,9,10]. Its comprehensiveness and ability to produce clear outcomes have led to its widespread application in various domains [11]. Zhu et al. [12] utilized the FCE in conjunction with the Analytic Hierarchy Process (AHP) to develop a coal burst prediction model for a coal mine in Shanxi Province, resulting in a successful evaluation of the coal burst risk level. Chen et al. [13] proposed a framework for the evaluation of teaching performance that incorporates both the AHP and FCE, demonstrating the effectiveness, reasonableness, and accuracy of the evaluation results. Guo et al. [14] employed the FCE in the evaluation of road pavement performance for the Xinglin section of Taihang Mountain Expressway reconstruction and expansion project, providing a quantitative assessment of the old pavement’s performance level through fuzzy mathematical iteration calculations. Wang et al. [15] developed an improved version of the FCE for the evaluation of desulfurization technology based on the principle of maximum membership degree, and obtained an effective solution. Fuzzy theory is based on the fuzzy set, which is a class of objects with continuous membership levels [16]. Such a set is represented by a membership (feature) function that assigns each object a membership rank between 0 and 1 [17]. Fuzzy sets and theory have been applied in many ways. Yang et al. [18] evaluated the geological environment quality of heavy metal mines in Zhaotong City based on the fuzzy set theory, and divided the evaluation into four grades: excellent, good, common, and inferior, which provided a reference for decision-making of current geological environment protection. In this paper, the groundwater carrying capacity of the mining area was calculated based on the FCE, and the changes in the groundwater carrying capacity and evaluation index membership in the mining area from 2011 to 2020 were analyzed, providing support for the follow-up exploitation and construction of the coal mine.

The accuracy of evaluation results in the FCE critically depends on the proper determination of the weights of the evaluation indicators [19,20]. AHP is a decision analysis method which is widely used because of its simplicity and systematism. Compared with other mathematical-based approaches, it combines qualitative and quantitative methods to solve complex multi-objective problems, especially in the allocation of weights [21,22,23,24]. In addition, AHP can determine the weight by layers and combine subjective and objective factors to make the decision more scientific and reasonable [21,22,23,24]. Wang et al. [25] introduced a variable weight factor into the traditional AHP process and presented a novel and improved weight distribution technique. The finding indicates that the AHP method is effective in managing the dynamic interactions between indicators. Guo et al. [26] proposed a social vulnerability assessment model based on the rough AHP method, where the standard weights were established using the rough AHP process and the social vulnerability of different regions was evaluated. Zhu et al. [27] utilized the AHP and life cycle assessment methods to rank the evaluation indicators and examine the assessment methods of public and some rural toilets from design to decommissioning, thereby enhancing the comprehensiveness of toilet evaluation under varying conditions. This study adopts the AHP method to determine the weights of the indicators for evaluating groundwater carrying capacity, thereby ensuring the accuracy of carrying capacity computation.

One of the preconditions for the calculation of FCE is to determine the weight of each evaluation index, that is the weight vector, which is generally directly specified by the decision-maker. However, for complex problems, such as many evaluation indexes and mutual influence relationships, it is difficult to directly give the weight of each evaluation index, which is exactly what AHP is good at. FCE and AHP have successful practice cases in the situation of combined use, and have achieved the expected effect. In this study, the combined method of FCE and AHP is used to analyze the groundwater resources carrying capacity of coal mines in arid areas. The present study first constructed an evaluation index system for the carrying capacity of groundwater resources based on the actual situation of the coal mine area and the collection of measured and statistical data from the coal mine. Subsequently, the weights of the evaluation indicators were assigned using the AHP. Next, the evaluation level grading criteria were determined based on the actual situation of the study mining area, and a fuzzy relationship matrix was established based on the membership function. Finally, the comprehensive value for the carrying capacity of groundwater resources was calculated, and the changes in the carrying capacity of groundwater from 2011 to 2020 and in the membership of important indicators were analyzed. This study provides a basis for strengthening the protection of coal mine groundwater resources. In addition, different from other similar studies, the highlight of this paper lies in the specificity and certainty of the research object, which can provide ideas for the development of coal mining industry in arid areas and provide references for coal mines to improve the carrying capacity of groundwater resources.

2. Research Methodology

2.1. Study Area and Data

The selected study mine area in this paper is located in Lingwu City, Ningxia Hui Autonomous Region (Figure 1).

The north–south length of the mine is about 11 km, the east–west width is about 2.48 km, and the area is 27.4937 km². The mine has a production capacity of 3.2 million tons per year, and the average salinity of mine water is 5610 mg/L, which is typical of high-salinity mining water. The area has a dense distribution of mines and is representative of coal mines in arid regions. By selecting the coal mine as the study area, this study provides reference for exploring the size of the carrying capacity of groundwater resources in coal mines in arid regions and the long-term temporal changes.

The data used in this study were primarily sourced from the actual monitoring and statistical data of the coal mine, and partially from local reports on the national economy and social development statistics.

2.2. Fuzzy Comprehensive Evaluation

2.2.1. Evaluation Index System

The selection of indicators for the evaluation of the carrying capacity of groundwater resources is a critical factor in determining the validity and applicability of the evaluation results. The chosen indicators should reflect the specific characteristics of the groundwater environment in the mine area and take into account the actual conditions of the study mining area. The selection of the index layer in this study was based on the availability and representativeness of the indicator and the degree of correlation between the indicator and groundwater resource carrying capacity. The indicators selected for the evaluation of the carrying capacity of groundwater resources in the mine area must effectively and unambiguously reflect the capability of the water resources to sustain coal mining activities while preserving the ecological environment.

Based on the analysis of the actual situation of the groundwater environment in the mining area from 2011 to 2020, an evaluation index system was established with expert opinions. We invited five experts to guide the study, during which we consulted with them when they had different opinions. In this paper, the consent of all experts has been obtained where expert guidance is needed, such as weight determination. The index system consists of three layers: the objective layer, the criteria layer, and the indicator layer. The criteria layer is divided into three parts, namely the groundwater resources part, the socioeconomic part, and the ecological environment part. The purpose of establishing the part of groundwater resource is to analyze the groundwater resource endowment of the mine area and the impact of mining on the amount of groundwater resources. A total of 4 indicators are included under this part. The socioeconomic part contains 5 indicators, which reflect the impact on groundwater under different production conditions at the mine area. The eco-environmental part contains 3 indicators, which mainly reveal the relationship between surface ecological quality and groundwater resources. The evaluation index system is shown in

Table 1. Evaluation index system of groundwater resources carrying capacity.

Objective Layer (A)	Criteria Layer (B)	Indicator Layer (P)
Groundwater resources carrying capacity (A)	Groundwater resources (B1)	P1 Coal mine seepage volume/(m3/h)
		P2 Total groundwater resources/(107 m3)
		P3 Groundwater dewatering volume/(104 m3)
		P4 Degree of groundwater development and utilization/%
	Socioeconomic (B2)	P5 Comprehensive water consumption/(m3/t)
		P6 Total population
		P7 Water price/yuan
		P8 Per unit GDP of water consumption/(m3/10,000 yuan)
		P9 Daily domestic water consumption per capita/L
	Ecological environment (B3)	P10 Sewage treatment rate/%
		P11 Average mineralization degree of groundwater/(mg/L)
		P12 Vegetation coverage rate/%

.

The weight of indicators P1–P12 in Table 1 are determined by AHP, denoted as $p_1,p_2,p_3,\cdots ,p_{12}$. The field data of indicators P1–P12 in the mining area are shown in

Table 2. Field data of indicators P1–P12.

Indicator Layer (P)	Time/Year
	2011	2012	2013	2014	2015	2016	2017	2018	2019	2020
P1/(m3/h)	378	344	365	397	390	465	467	480	509	534
P2/(107 m3)	16.19	15.79	15.46	15.47	15.19	15.01	14.87	14.87	14.92	15.15
P3/(104 m3)	95.84	32.39	192.41	163.73	257.05	239.53	261.01	237.63	267.85	270.12
P4/%	38.56	39.12	40.34	41.78	42.55	43.1	43.31	43.46	43.12	42.85
P5/(m3/t)	0.61	0.69	0.67	0.59	0.66	0.54	0.55	0.71	0.58	0.34
P6/people	1365	1365	1371	1375	1370	1366	1366	1355	1352	1350
P7/yuan	3.84	3.69	3.84	3.81	3.79	3.78	4.24	3.728	3.66	4.01
P8/ (m3/10,000 yuan)	15.20	15.80	16.20	15.40	14.60	13.80	13.00	12.80	11.70	11.10
P9/L	195.40	196.20	196.10	196.70	199.80	201.70	204.30	203.80	203.60	198.50
P10/%	95.21	95.23	97.52	98.83	99.70	100	100	100	100	100
P11/(mg/L)	4530	4752	4858	4869	4987	5061	5102	4986	5007	4989
P12/%	44.21	44.04	43.25	41.07	39.57	36.24	33.21	31.78	29.47	28.01

, in which the data is represented by the annual average.

2.2.2. Indicator Grading Criteria

The grading criteria of index evaluation levels in this study are carried out on the basis of fully analyzing the coal mine field data and combining expert opinions. The grading criteria value is closely related to the local specific of the mining area. The indicators were categorized into three evaluation levels, where level V1 represents a relatively high carrying capacity for the groundwater resources and level V3 signifies a near-capacity carrying limit and limited residual development. Level V2, positioned between the two, indicates that the groundwater resources have undergone significant development but still have some potential. In the development process, emphasis should be placed on the protection and responsible utilization of the groundwater resources. For quantitative calculations later, V1, V2, and V3 are assigned values between 0 and 1. V1 receives a value of 0.95, V2 receives a value of 0.50, and V3 receives a value of 0.05.

The criteria for categorizing each indicator in the mining area are presented in

Table 3. Grading criteria of indicators evaluation level.

Criteria	Indicators	Indicator Type	Evaluation Level
			V1	V2	V3
B1	P1/(m3/h)	Negative	<300	300–600	>600
	P2/107 m3	Positive	>25	15–25	<15
	P3/104 m3	Negative	<100	100–300	>300
	P4/%	Negative	<24	24–27	>27
B2	P5/(m3/t)	Negative	<0.6	0.6–0.7	>0.7
	P6/(m3/10,000 yuan)	Negative	<10	10–20	>20
	P7/yuan	Negative	<3.0	3.0–4.0	>4.0
	P8/people	Negative	<1300	1300–1400	>1400
	P9/L	Negative	<190	190–200	>200
B3	P10/%	Positive	>99	90–99	<90
	P11/(mg/L)	Negative	<1000	1000–5000	>5000
	P12/%	Positive	>60	40–60	<40
	Evaluation value ($\alpha$)		0.95	0.5	0.05

. Indicators are divided into two types: the first type is a positive indicator, the higher the index value, the closer to V1, and the better the carrying capacity. The second type is a negative indicator, the higher the index value, the closer to V3, and the worse the carrying capacity.

2.2.3. Membership Degree Functions

Determining the membership degree of indicators to different evaluation levels is a key aspect in fuzzy comprehensive evaluation. The membership degree functions of indicators to different evaluation levels are shown in Equations (1)–(3) [12,13,14]. A fuzzy relationship matrix of the carrying capacity of groundwater resources in mining areas from 2011 to 2020 was established based on the calculation results of the membership degree functions.

$$\text{Positive indicator}\text{Negative indicator}$$

$$UV1\left(ui\right)=\left\{\begin{array}{ccc}0.5\left(1+\frac{ui-k1}{ui-k2}\right)& ui\ge k1& \hfill ui<k1\\ 0.5\left(1-\frac{k1-ui}{k1-k2}\right)& k1>ui\ge k2& \hfill k2>ui\ge k1\\ 0& ui<k2& \hfill ui\ge k2\end{array}\right.$$

(1)

$$UV2\left(ui\right)=\left\{\begin{array}{ccc}0.5\left(1-\frac{ui-k1}{ui-k2}\right)\hfill & \hfill ui\ge k1& \hfill ui<k1\\ 0.5\left(1+\frac{k1-ui}{k1-k2}\right)\hfill & \hfill k1>ui\ge k2& \hfill k2>ui\ge k1\\ 0.5\left(1+\frac{ui-k3}{k2-k3}\right)\hfill & \hfill k2>ui\ge k3& \hfill k3>ui\ge k2\\ 0.5\left(1-\frac{ui-k3}{ui-k2}\right)\hfill & \hfill ui<k3& \hfill ui\ge k3\end{array}\right.$$

(2)

$$UV3\left(ui\right)=\left\{\begin{array}{ccc}0.5\left(1-\frac{ui-k3}{k2-k3}\right)& k2>ui\ge k3& \hfill k3>ui\ge k2\\ 0.5\left(1+\frac{k3-ui}{k2-ui}\right)& ui<k3& \hfill ui\ge k3\\ 0& ui\ge k2& \hfill ui<k2\end{array}\right.$$

(3)

In the equation, k1 represents the critical value between membership levels V1 and V2; k3 represents the critical value between membership levels V2 and V3; and k2 represents the midpoint value of membership level V2, that is, k2 = (k1 + k3)/2.

2.2.4. Carrying Capacity Calculation

The comprehensive evaluation matrix is obtained by multiplying the evaluation index comprehensive weight matrix A and the fuzzy relationship matrix R, as shown in the following equation [13]:

$$B=A·R$$

(4)

In the equation, $A=\left(p_1,p_2,p_3,\cdots ,p_{12}\right)$, $p_1,p_2,p_3,\cdots ,p_{12}$: Weight values of indicators P1–P12; B: Comprehensive evaluation matrix

The equation for calculating the comprehensive value of the carrying capacity of groundwater resources in the coal mine from 2011 to 2020 is shown as follows [15]:

$$a=\frac{{{\displaystyle \sum }}_{j=1}^3{b}_j^P·{\alpha }_j}{{{\displaystyle \sum }}_{j=1}^3{b}_j^P}$$

(5)

In the equation, $j=1,2,3$: evaluation level V1, V2, V3; ${\alpha }_j$: evaluation value of evaluation level; $b_j^P$: the membership degree of indicators P in the comprehensive evaluation matrix B corresponding to the evaluation level $j$. $P=1,2,3\cdots ,12$.

2.3. Analytical Hierarchy Process

The Analytical Hierarchy Process (AHP), introduced by American operations researcher A. L. Saaty in the 1970s, is a systematic approach for analyzing decision-making factors [25]. This method decomposes the factors into various levels, such as objectives, criteria, and indicators, and engages in both qualitative and quantitative analysis [26,27]. The AHP approach is notable for its clear thought process, simple methodology, and strong systematic nature and serves as a robust tool for analyzing complex systems with multiple objectives, factors, and criteria. In this analysis of the carrying capacity of groundwater resources in the study mining area, the AHP method was utilized to determine the evaluation indicator weights, with four distinct steps: formation of the hierarchy structure model, creation of the paired comparison matrix, weight determination, and consistency assessment.

2.3.1. Hierarchy Structure Model

In order to understand the influence of the various factors on the groundwater resources carrying capacity in the coal mine, it is necessary to determine the relationships between these relevant factors [28]. This can be accomplished by classifying these factors into three hierarchical layers, namely the objective layer, criteria layer, and indicator layer [29]. The categorization is based on the distinctive attributes of each factor [30]. The factors within a particular layer are interdependent, in that they either depend on the factors in the higher layer or have an impact on these higher-layer factors, while also exerting dominance over the factors in the lower layer or being subject to the influence of the lower-layer factors [31].

2.3.2. Paired Comparison Matrix

It is crucial to compare the significance of each factor within a given level with respect to a criterion in the preceding level. This is achieved by utilizing the 9-point scale method to arrive at a judgment value. Subsequently, a comparative matrix is constructed, referred to as [32,33,34]:

$$A={\left(a_{ij}\right)}_{n\times n}$$

(6)

The above equation must satisfy the following condition: $a_{ij}>0$; $a_{ii}=1$; $a_{ij}=1/a_{ji}$; $a_{ij}$ is to be valued according to the 9-point scale table (

Table 4. 9-point scale table.

${\mathit{a}}_{\mathit{i}\mathit{j}}$	Meaning of Values
1	$a_i$ and $a_j$ have the same effect
3	$a_i$ has a slightly stronger effect than and $a_j$
5	$a_i$ has a stronger effect than $a_j$
7	$a_i$ has a significantly stronger effect than $a_j$
9	$a_i$ has an absolutely stronger effect than $a_j$
2, 4, 6, 8	The middle value between the above two adjacent evaluations
reciprocal	The judgment value of comparison between $a_j$ and $a_i$, $a_{ij}=1/a_{ji}$

). $A$ represents the comparative matrix; $n$ represents the number of factors; and $a_{ij}$ represents the relative importance ratio of factor $a_i$ compared to factor $a_j$ with respect to a certain criterion.

2.3.3. Indicator Weight Determination

The maximum eigenvalue ${\lambda }_{max}$ and its corresponding eigenvector $W$ of each comparative matrix are solved by using the eigenvalue method [35,36].

(1)

Matrix $A$ is normalized by columns, referred to as:

$$M={\left(\overline{a_{ij}}\right)}_{n\times n}$$

(7)

$$\overline{a_{ij}}=\frac{a_{ij}}{{{\displaystyle \sum }}_{k=1}^n{a}_{kj}}\left(i,j=1,2,3\cdots ,n\right)$$

(8)

(2)

Vector $N$ is obtained by adding the rows of matrix $M$, referred to as:

$$N={\left(N_1,N_2,N_3\cdots N_n\right)}^T$$

(9)

$$N_i={\displaystyle \sum }_{j=1}^n\overline{a_{ij}}\left(i=1,2,3\cdots ,n\right)$$

(10)

(3)

Eigenvector $W$ is obtained after normalizing the vector $N$ and referred to as:

$$W={\left(W_1,W_2,W_3\cdots W_n\right)}^T$$

(11)

$$W_i=\frac{N_i}{{{\displaystyle \sum }}_{j=1}^n{N}_j} \left(i=1,2,3\cdots ,n\right)$$

(12)

(4)

Calculate the maximum eigenvalue ${\lambda }_{max}$ of the paired comparison matrix:

$${\lambda }_{max}={\displaystyle \sum }_{i=1}^n\frac{{\left(AW\right)}_i}{n{W}_i}$$

(13)

The eigenvector $W_i$ corresponding to the maximum eigenvalue ${\lambda }_{max}$ represents the relative weight of the factors; however, a consistency check of the paired comparison matrix is still required. Only the $W_i$ calculated from the matrix that passes the consistency check is the final weight of the factors, otherwise, the paired comparison matrix needs to be reconstructed and recalculated.

2.3.4. Consistency Check

The consistency of the pairwise comparison matrix is checked by the consistency index (CI) and the consistency ratio (CR), and the calculation of CI and CR is as follows [21]:

$$CI=\frac{{\lambda }_{max}-n}{n-1}$$

(14)

$$CR=\frac{CI}{RI}$$

(15)

In Equation (14), RI is the average consistency index of the pairwise comparison matrix, which can be obtained by referring to

Table 5. The average random consistency index.

Matrix order	1	2	3	4	5	6	7	8
RI	0	0	0.52	0.89	1.12	1.26	1.36	1.41

.

The higher the CI, the worse the consistency of the pairwise comparison matrix. When CI = 0, the matrix is completely consistent. The lower the CR, the better the consistency of the matrix. When CR is less than 0.1, the pairwise comparison matrix has satisfactory consistency; otherwise, the matrix needs to be adjusted until it has satisfactory consistency.

3. Results and Discussion

3.1. Indicator Weight Assignment

Using the AHP to assign weights to the evaluation indicators of the groundwater resources carrying capacity in the coal mine. The paired comparison matrix for the objective layer (A) and the criteria layer (B) can be seen in

Table 6. A-B comparison matrix.

A	B1	B2	B3	ωi	Aωi
B1	1	2	3	0.54	1.62
B2	1/2	1	2	0.30	0.89
B3	1/3	1/2	1	0.16	0.49

Note(s): ${\mathsf{\lambda }}_{\max }=3.0092$, CI = 0.0046, RI = 0.52, CR = 0.0088 < 0.1, consistency check passed.

.

The comparison matrices for the criterion layer and each indicator layer can be seen in

Table 7. B1-P comparison matrix.

B1	P1	P2	P3	P4	ωi	Aωi
P1	1	1/4	2	1/2	0.11	0.51
P2	4	1	7	2	0.56	2.22
P3	1/2	1/7	1	1/4	0.09	0.27
P4	2	1/3	4	1	0.24	0.93

Note(s): ${\mathsf{\lambda }}_{\max }$ = 4.0445, CI = 0.0148, RI = 0.89, CR = 0.017 < 0.1, consistency check passed.

,

Table 8. B2-P comparison matrix.

B2	P5	P6	P7	P8	P9	ωi	Aωi
P5	1	1/3	6	2	1/3	0.15	0.79
P6	3	1	9	6	2	0.44	2.36
P7	1/6	1/9	1	1/5	1/8	0.03	0.16
P8	1/2	1/6	5	1	1/2	0.11	0.55
P9	3	1/2	8	2	1	0.27	1.41

Note(s): ${\mathsf{\lambda }}_{\max }$ = 5.208, CI = 0.052, RI = 1.12, CR = 0.046 < 0.1, consistency check passed.

and

Table 9. B3-P comparison matrix.

B3	P10	P11	P12	ωi	Aωi
P10	1	1/2	1/4	0.14	0.43
P11	2	1	1/2	0.29	0.86
P12	4	2	1	0.57	1.71

Note(s): ${\mathsf{\lambda }}_{\max }$ = 3, CI = 0, RI = 0.52, CR = 0 < 0.1, consistency check passed.

.

The summary of the weights of evaluation indicators can be seen in

Table 10. Indicator weight assignment.

Criteria Layer (B)	Criteria Layer Weight (B)	Indicator Layer (P)	Indicator Layer Weight	Indicator Weight
B1	0.54	P1/(m3/h)	0.11	0.059
		P2/(107 m3)	0.56	0.302
		P3/(104 m3)	0.09	0.049
		P4/%	0.24	0.130
B2	0.30	P5/(m3/t)	0.15	0.045
		P6/(m3/10,000 yuan)	0.44	0.132
		P7/yuan	0.03	0.010
		P8	0.11	0.033
		P9/L	0.27	0.081
B3	0.16	P10/%	0.14	0.022
		P11/(mg/L)	0.29	0.046
		P12/%	0.57	0.091

.

3.2. Fuzzy Relationship Matrix

Based on the membership degree functions 1–3 and based on the data and evaluation index system of the mining area, the fuzzy relationship matrix of indicator from 2011 to 2020 is calculated as shown below.

$$\mathrm{R}2011\left[\begin{array}{ccc}0.24\hfill & 0.76\hfill & 0.00\hfill \\ 0.00\hfill & 0.62\hfill & 0.38\hfill \\ 0.52\hfill & 0.48\hfill & 0.00\hfill \\ 0.74\hfill & 0.26\hfill & 0.00\hfill \\ 0.40\hfill & 0.60\hfill & 0.00\hfill \\ 0.00\hfill & 0.98\hfill & 0.02\hfill \\ 0.00\hfill & 0.66\hfill & 0.34\hfill \\ 0.00\hfill & 0.85\hfill & 0.15\hfill \\ 0.23\hfill & 0.77\hfill & 0.00\hfill \\ 0.08\hfill & 0.92\hfill & 0.00\hfill \\ 0.00\hfill & 0.62\hfill & 0.38\hfill \\ 0.00\hfill & 0.71\hfill & 0.29\hfill \end{array}\right]R2012\left[\begin{array}{ccc}0.35& 0.65& 0.00\\ 0.00& 0.58& 0.42\\ 0.70& 0.30& 0.00\\ 0.68& 0.32& 0.00\\ 0.00& 0.60& 0.40\\ 0.00& 0.92& 0.08\\ 0.00& 0.81& 0.19\\ 0.00& 0.85& 0.15\\ 0.19& 0.81& 0.00\\ 0.08& 0.92& 0.00\\ 0.00& 0.56& 0.44\\ 0.00& 0.70& 0.30\end{array}\right]\mathrm{R}2013\left[\begin{array}{ccc}0.28& 0.72& 0.00\\ 0.00& 0.55& 0.45\\ 0.04& 0.96& 0.00\\ 0.39& 0.61& 0.00\\ 0.00& 0.80& 0.20\\ 0.00& 0.88& 0.12\\ 0.00& 0.66& 0.34\\ 0.00& 0.79& 0.21\\ 0.20& 0.80& 0.00\\ 0.33& 0.67& 0.00\\ 0.00& 0.54& 0.46\\ 0.00& 0.66& 0.34\end{array}\right]$$

$$\mathrm{R}2014\left[\begin{array}{ccc}0.18\hfill & 0.82\hfill & 0.00\hfill \\ 0.00\hfill & 0.55\hfill & 0.45\hfill \\ 0.18\hfill & 0.82\hfill & 0.00\hfill \\ 0.00\hfill & 0.91\hfill & 0.09\hfill \\ 0.58\hfill & 0.42\hfill & 0.00\hfill \\ 0.00\hfill & 0.96\hfill & 0.04\hfill \\ 0.00\hfill & 0.69\hfill & 0.31\hfill \\ 0.00\hfill & 0.75\hfill & 0.25\hfill \\ 0.17\hfill & 0.83\hfill & 0.00\hfill \\ 0.48\hfill & 0.52\hfill & 0.00\hfill \\ 0.00\hfill & 0.53\hfill & 0.47\hfill \\ 0.00\hfill & 0.55\hfill & 0.45\hfill \end{array}\right]R2015\left[\begin{array}{ccc}0.20\hfill & 0.80\hfill & 0.00\hfill \\ 0.00\hfill & 0.52\hfill & 0.48\hfill \\ 0.00\hfill & 0.71\hfill & 0.29\hfill \\ 0.00\hfill & 0.65\hfill & 0.35\hfill \\ 0.00\hfill & 0.90\hfill & 0.10\hfill \\ 0.04\hfill & 0.96\hfill & 0.00\hfill \\ 0.00\hfill & 0.71\hfill & 0.29\hfill \\ 0.00\hfill & 0.80\hfill & 0.20\hfill \\ 0.01\hfill & 0.99\hfill & 0.00\hfill \\ 0.57\hfill & 0.43\hfill & 0.00\hfill \\ 0.00\hfill & 0.50\hfill & 0.50\hfill \\ 0.00\hfill & 0.48\hfill & 0.52\hfill \end{array}\right]\mathrm{R}2016\left[\begin{array}{ccc}0.00& 0.95& 0.05\\ 0.00& 0.50& 0.50\\ 0.00& 0.80& 0.20\\ 0.00& 0.47& 0.53\\ 0.77& 0.23& 0.00\\ 0.12& 0.88& 0.00\\ 0.00& 0.72& 0.28\\ 0.00& 0.84& 0.16\\ 0.00& 0.92& 0.08\\ 0.57& 0.43& 0.00\\ 0.00& 0.49& 0.51\\ 0.00& 0.36& 0.64\end{array}\right]$$

$$\mathrm{R}2017\left[\begin{array}{ccc}0.00\hfill & 0.94\hfill & 0.06\hfill \\ 0.00\hfill & 0.51\hfill & 0.49\hfill \\ 0.00\hfill & 0.69\hfill & 0.31\hfill \\ 0.00\hfill & 0.41\hfill & 0.59\hfill \\ 0.75\hfill & 0.25\hfill & 0.00\hfill \\ 0.20\hfill & 0.80\hfill & 0.00\hfill \\ 0.00\hfill & 0.34\hfill & 0.66\hfill \\ 0.00\hfill & 0.84\hfill & 0.16\hfill \\ 0.00\hfill & 0.78\hfill & 0.12\hfill \\ 0.58\hfill & 0.42\hfill & 0.00\hfill \\ 0.00\hfill & 0.48\hfill & 0.52\hfill \\ 0.00\hfill & 0.30\hfill & 0.70\hfill \end{array}\right]R2018\left[\begin{array}{ccc}0.00& 0.90& 0.10\\ 0.00& 0.53& 0.47\\ 0.00& 0.81& 0.19\\ 0.00& 0.38& 0.62\\ 0.00& 0.42& 0.58\\ 0.22& 0.78& 0.00\\ 0.00& 0.77& 0.23\\ 0.00& 0.95& 0.05\\ 0.00& 0.81& 0.19\\ 0.59& 0.41& 0.00\\ 0.00& 0.50& 0.50\\ 0.00& 0.27& 0.73\end{array}\right]\mathrm{R}2019\left[\begin{array}{ccc}0.00& 0.80& 0.20\\ 0.00& 0.51& 0.49\\ 0.00& 0.66& 0.34\\ 0.00& 0.46& 0.54\\ 0.64& 0.36& 0.00\\ 0.33& 0.67& 0.00\\ 0.00& 0.84& 0.16\\ 0.00& 0.98& 0.02\\ 0.00& 0.82& 0.18\\ 0.59& 0.41& 0.00\\ 0.00& 0.50& 0.50\\ 0.00& 0.24& 0.76\end{array}\right]$$

$$\mathrm{R}2020\left[\begin{array}{ccc}0.00\hfill & 0.72\hfill & 0.28\hfill \\ 0.00\hfill & 0.51\hfill & 0.49\hfill \\ 0.00\hfill & 0.65\hfill & 0.35\hfill \\ 0.00\hfill & 0.55\hfill & 0.45\hfill \\ 0.92\hfill & 0.08\hfill & 0.00\hfill \\ 0.39\hfill & 0.61\hfill & 0.00\hfill \\ 0.00\hfill & 0.49\hfill & 0.51\hfill \\ 0.00\hfill & 1.00\hfill & 0.00\hfill \\ 0.08\hfill & 0.92\hfill & 0.00\hfill \\ 0.59\hfill & 0.41\hfill & 0.00\hfill \\ 0.00\hfill & 0.50\hfill & 0.50\hfill \\ 0.00\hfill & 0.23\hfill & 0.77\hfill \end{array}\right]$$

As shown by the above data, the three indices of total groundwater resources, the degree of groundwater development and utilization, and per unit GDP of water consumption have relatively high weights in the evaluation index system. The changes in the membership degree of these three indices over time can be seen in Figure 2.

The magnitude of the groundwater resources in a mining area has a direct impact on its carrying capacity. As depicted in Figure 2a, the membership degree of the total groundwater resources index to V3 gradually increased during 2011–2018. Combined with the field data, the decrease in the groundwater carrying capacity in the mining area is related to the decrease in the total groundwater resources from 2011 to 2018. With the increase in total groundwater resources from 2018 to 2020, the carrying capacity of groundwater resources has a recovery trend. The analysis of total groundwater resource index shows that groundwater carrying capacity is closer to V3 level. The degree of groundwater development and utilization also underwent a transformation, with 74% belonging to the V1 level in 2011, transitioning to 91% belonging to the V2 level in 2014, and eventually evolving to 59% belonging to the V3 level in 2017 (Figure 2b). This demonstrates that the utilization of groundwater resources has continuously intensified from 2011 to 2017, reaching its limit.

As a socioeconomic indicator, per unit GDP of water consumption reflects the production conditions of the mining area. As shown in Figure 2c, during the period of 2011–2013, the coal mining was relatively rough, with 88% belonging to the V2 level and 12% belonging to the V3 level. From 2014 to 2020, the coal mine continuously improved its production process and technology to increase efficiency, resulting in the indicator gradually shifting from the V2 level to the V1 level.

3.3. Carrying Capacity Calculation Results

According to the Equations (4) and (5), the results of the calculation for the groundwater resources carrying capacity in the mining area from 2011 to 2020 are shown in

Table 11. Groundwater resources carrying capacity calculation results.

Time	Evaluation Level			Comprehensive Evaluation Value	Rank
	V1	V2	V3
2011	0.1748	0.6551	0.1701	0.5021	1
2012	0.1614	0.6287	0.2100	0.4781	2
2013	0.0920	0.6831	0.2245	0.4402	3
2014	0.0694	0.7027	0.2278	0.4287	4
2015	0.0304	0.6806	0.2891	0.3836	6
2016	0.0631	0.6078	0.3291	0.3803	7
2017	0.0728	0.5684	0.3588	0.3713	9
2018	0.0420	0.5866	0.3714	0.3518	10
2019	0.0855	0.5592	0.3553	0.3786	8
2020	0.1119	0.5506	0.3371	0.3985	5

.

Based on the evaluation results and the principle of maximum membership degree, it can be seen that from 2011 to 2020, the carrying capacity of groundwater resources in the mining area is the highest for V2 level, followed by V3 level, and the lowest for V1 level. This indicates that the carrying capacity of groundwater resources in the mine area will reach the limit and the remaining development potential can be ignored. The subsequent mining construction should focus on the protection of groundwater resources and reduce groundwater exploitation.

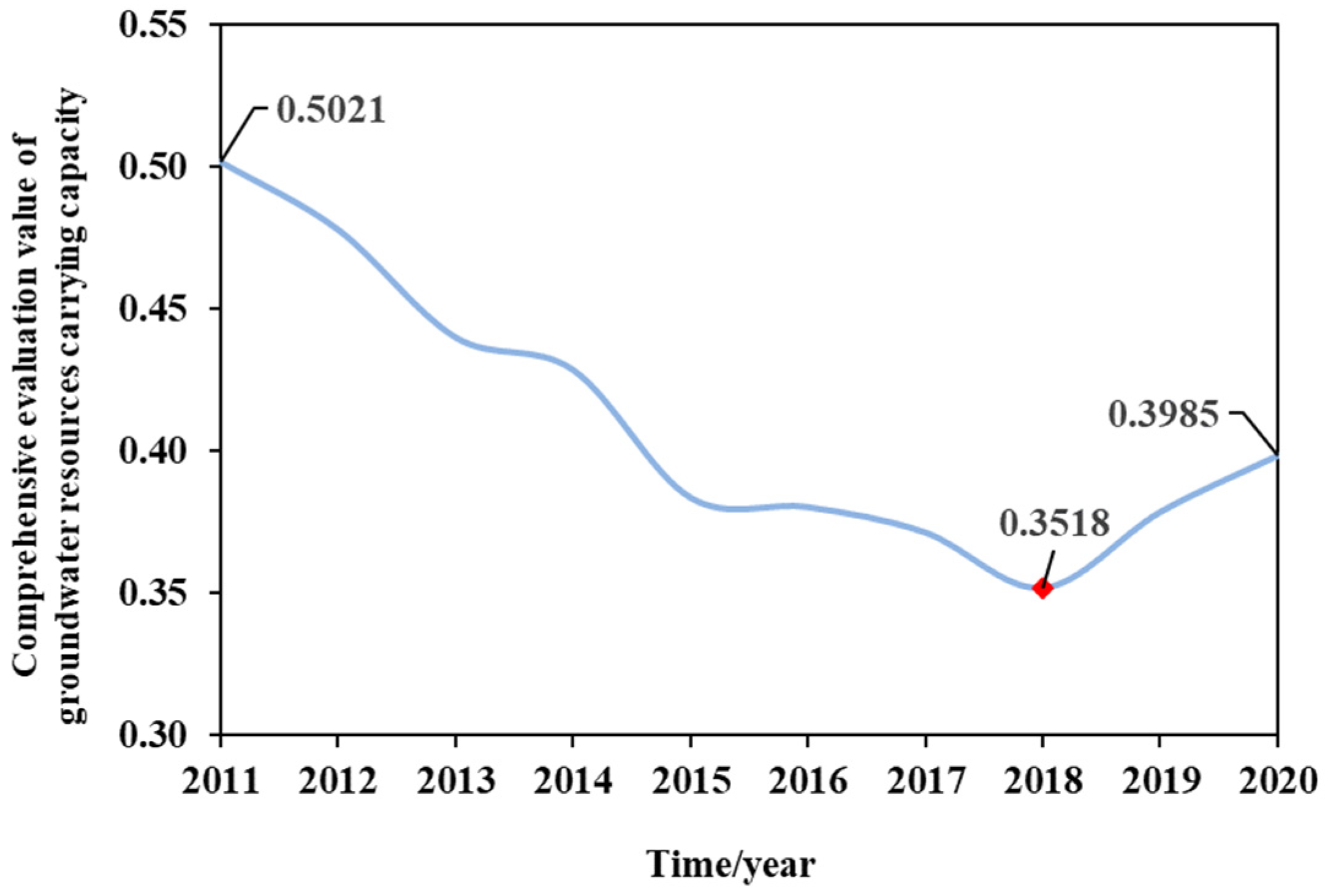
The trend of the comprehensive evaluation value of groundwater resources carrying capacity in the mining area from 2011 to 2020 is shown in Figure 3.

As shown in Figure 3, the groundwater resources carrying capacity in the mining area changed from a large decline to a slight increase during the period of 2011–2020. The groundwater resource carrying capacity was low between 2011 and 2018, with a minimum value of 0.3518, and generally declining. The decrease may be due to the increasing scale of production in the mining area, which caused a short-term increase in the groundwater drainage, resulting in a groundwater funnel. In addition, the study mining area is located in the northwest arid region of China, with sparse rainfall and strong evaporation. The combined effect of climate factors and unstable groundwater recharge sources has led to a downward trend in the total amount of groundwater resources in the study period.

The groundwater resources were effectively protected during the period of 2018–2020 and the total groundwater resources increased. The carrying capacity of groundwater resources in mining area was partially recovered to a certain extent, but it was still necessary to ensure that the groundwater resources were within a reasonable range during coal mining. The carrying capacity of groundwater resources increased slightly from 2018 to 2020, with a value of 0.3985 in 2020. This may be due to the continuous use of advanced mining equipment and improved production technology in the research mining area, and the application of water-conserving mining technology has greatly improved the utilization efficiency of groundwater. The continuous improvement of clean production management and system in mining areas also guarantees the multilevel utilization of domestic water. At the same time, new engineering measures such as the construction of an underground concentrated brine reservoir have been taken to improve the production efficiency, bringing in a decrease in the per unit GDP water consumption from 16.2 m³/10,000 yuan to 11.1 m³/10,000 yuan, a decrease of 31.48%. In addition, the extent of groundwater development and utilization in mining areas has also been reduced, from 43.46% to 42.85%. During the period when coal mining capacity increases sharply, the amount of groundwater outflow caused by coal mining remains relatively stable. This can also reveal that the mining area has greatly realized the reuse of groundwater, reduced unnecessary waste, and realized the recovery of groundwater resource carrying capacity. With the enhancement of people’s awareness of environmental protection, the concept of building green mines is gradually applied to the entire mining process. During 2018–2020, the study area implemented large-scale greening actions, greatly improving the ecological environment of the mine and its surrounding areas. The decline in vegetation coverage has been reversed, and the ability to replenish groundwater has been enhanced, leading to an increase in the total groundwater resources from 14.867 × 10⁷ m³ in 2018 to 15.146 × 10⁷ m³ in 2020. This is an important reason for the increase in the carrying capacity of groundwater resources.

This study indicates that the size and temporal variation of the groundwater resources carrying capacity in the mining area can provide direction and basis for the subsequent mining production in coal mining in arid areas. The groundwater resources in the study coal mining area are scarce, the development intensity at a high level, and the carrying capacity at a low level. Therefore, in the subsequent development, efforts should continue to be made to protect groundwater resources, optimize production processes to improve the efficiency of groundwater utilization, strengthen the construction of environmental protection infrastructure in the mining area, and slow down the development and utilization of groundwater.

4. Conclusions

In this paper, a coal mine in the arid area of northwest China is selected as the research object, and the combination of FCE and AHP is selected to evaluate the mining area’s groundwater resource carrying capacity and its change trend during 2011–2020, which provides method selection and technical support for the analysis of the coal mine groundwater resource carrying capacity in the arid area of northwest China. The conclusions are as follows:

• Over the 2011–2020 period, the coal mine witnessed a decline in its groundwater resource carrying capacity, followed by a modest recovery (Figure 3). From 2011 to 2018, the carrying capacity decreased from 0.5021 to 0.3518, possibly due to a decrease in the total groundwater resources resulting from extensive production practices and increased drainage and discharge of groundwater during 2011–2018. Subsequently, a rebound in the groundwater resource carrying capacity occurred during 2018–2020 due to enhanced production efficiency, better utilization of groundwater, and an improved ecological environment (Figure 3). Although the carrying capacity increased to 0.3985, it still remains low level.
• The total groundwater resources, the degree of groundwater development and utilization, and the per unit GDP of water consumption are three critical indicators affecting the groundwater resources carrying capacity in the mining area, which have significant impacts on its variations (Table 10). The membership degree of evaluation level of above mentioned three indicators have all shifted from V2 level to V3 level (Figure 2). To improve the carrying capacity sustainably, the coal mine should promote innovative water-conserving mining technologies, reduce groundwater drainage and discharge, and increase the reuse of groundwater in subsequent mining and construction activities. Additionally, promoting vegetation restoration and enhancing ecological restoration and compensation plans are crucial measures for preserving the ecosystem.
• This research has been strongly supported by the competent authorities of groundwater resources in the mining area, and the research methods and results have also been unanimously recognized by the department leaders. The future research on how to improve the carrying capacity of groundwater resources in coal mines in arid areas should also be put on the agenda.

AHP is based on experience and has some limitations. Therefore, there is uncertainty in the weight assignment of indicators in this study. In the follow-up research, more objective and accurate weight assignment methods can be adopted to make up for the above limitations.