Influence of Installation Deviation of Thrust Bearing on Oil Film Flow of 1000 MW Hydraulic Turbine Unit
Abstract
:1. Introduction
2. Numerical Techniques
2.1. Continuity Equation
2.2. Navier–Stokes Equations
2.3. Energy Equation
2.4. SST k-ω Turbulence Model
2.5. Viscosity Temperature Equation
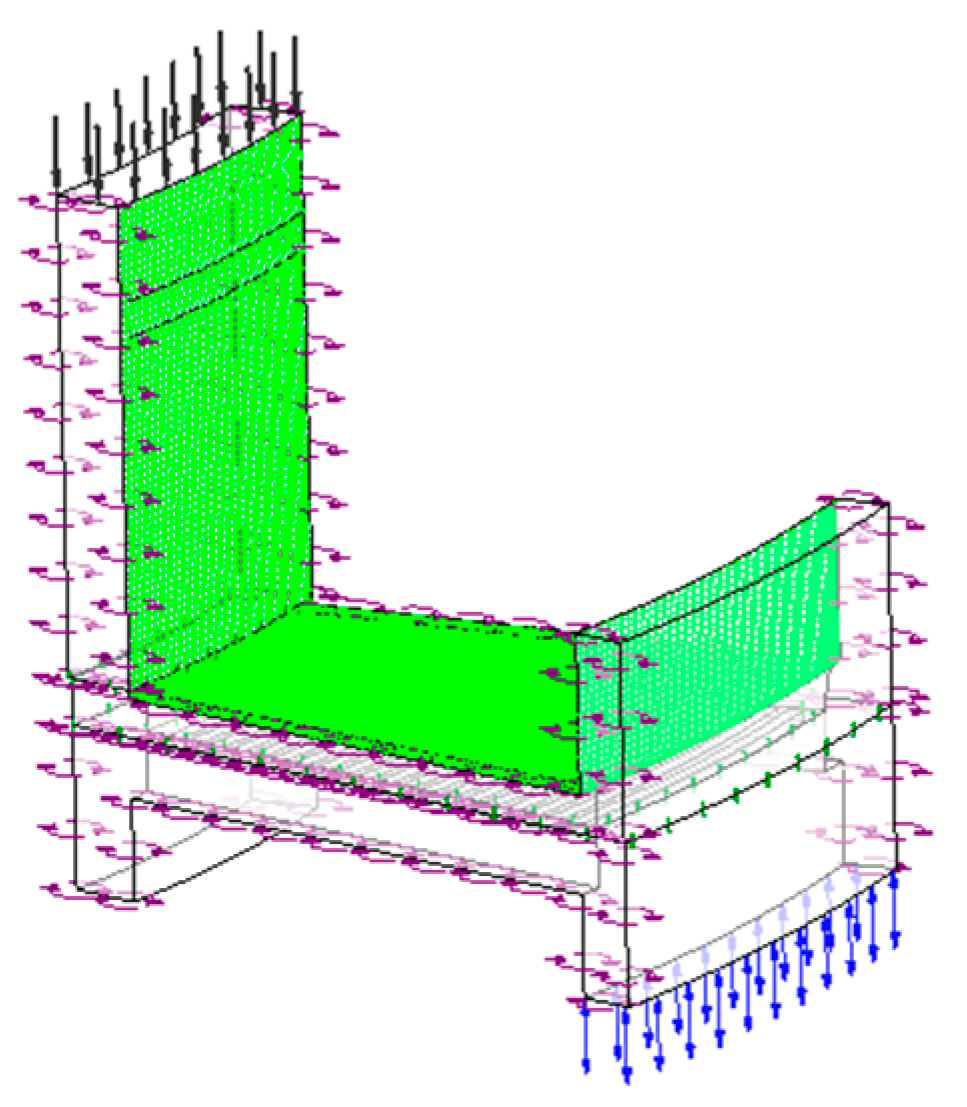
3. Theoretical Model
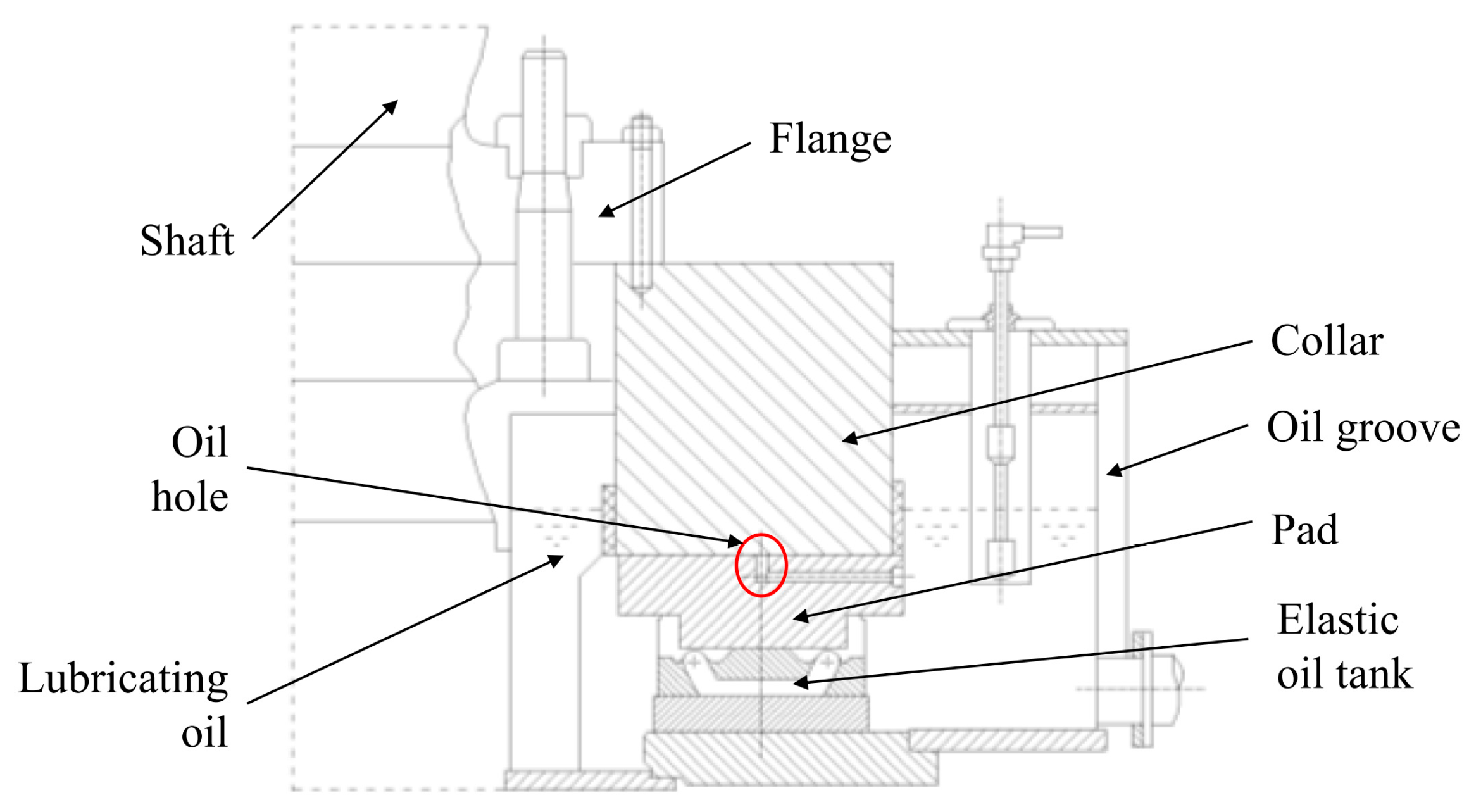
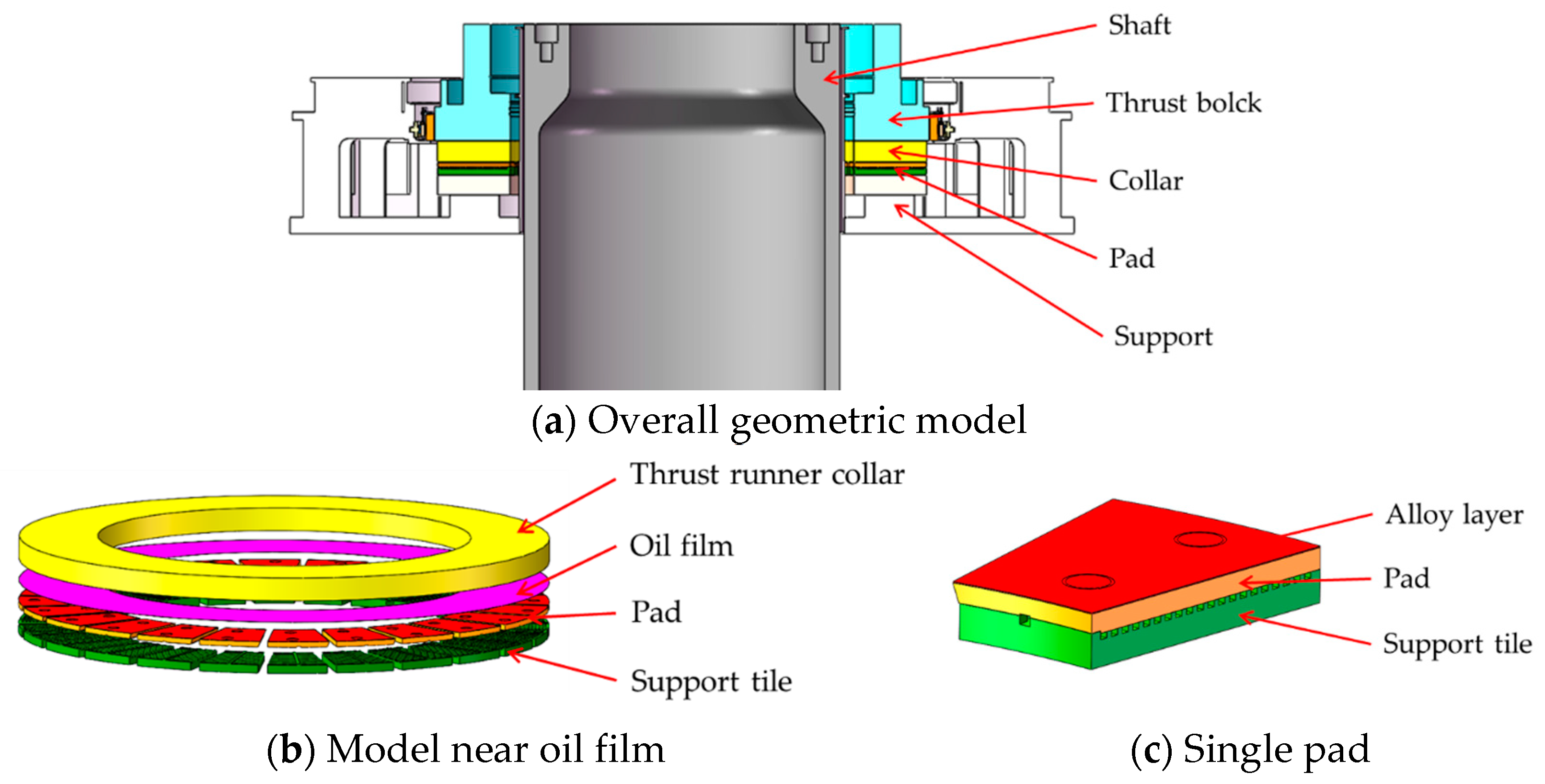
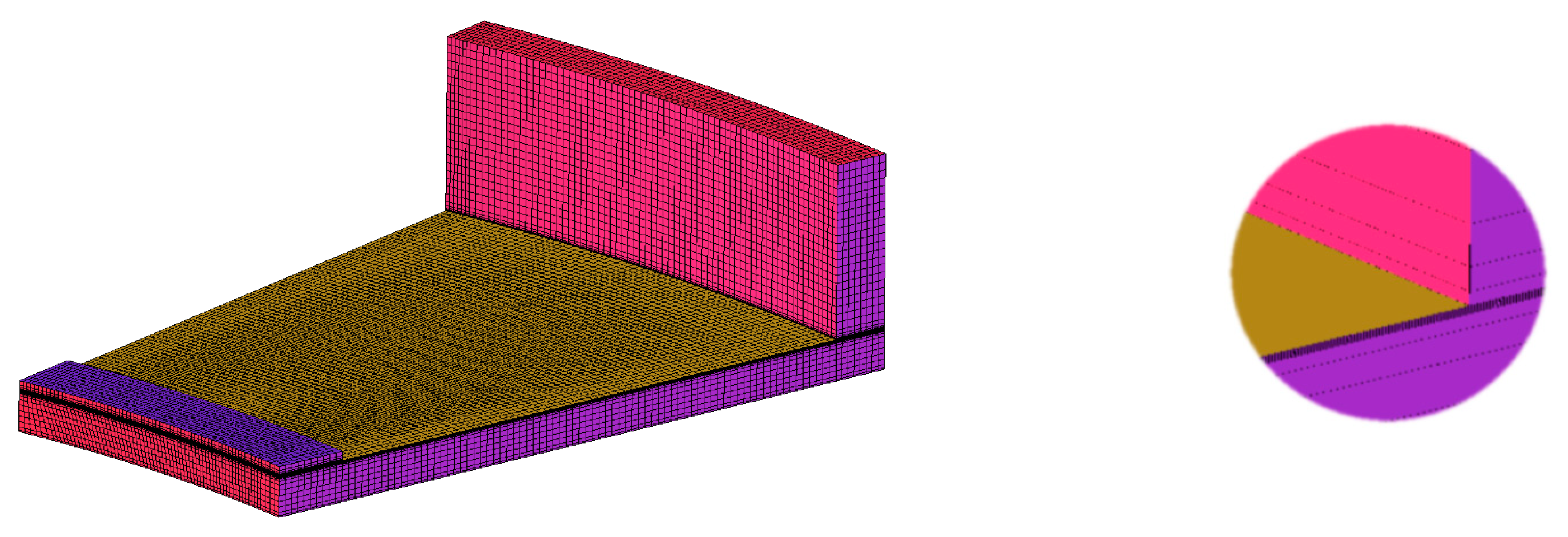
3.1. Model of the Oil Film
3.2. Thrust Bearing THD Model
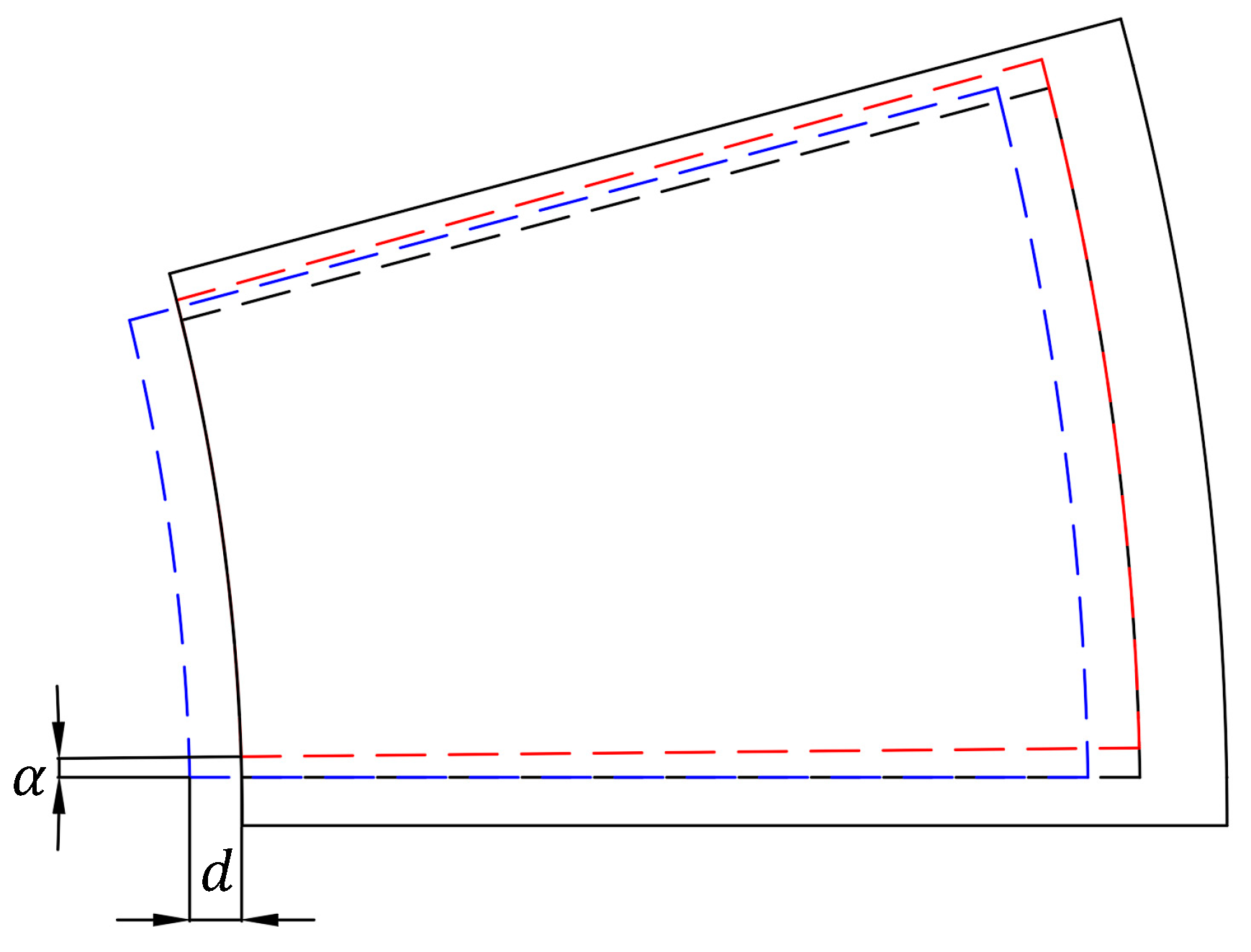
3.3. Model Considering Radial and Circumferential Deviation
4. Results and Discussion
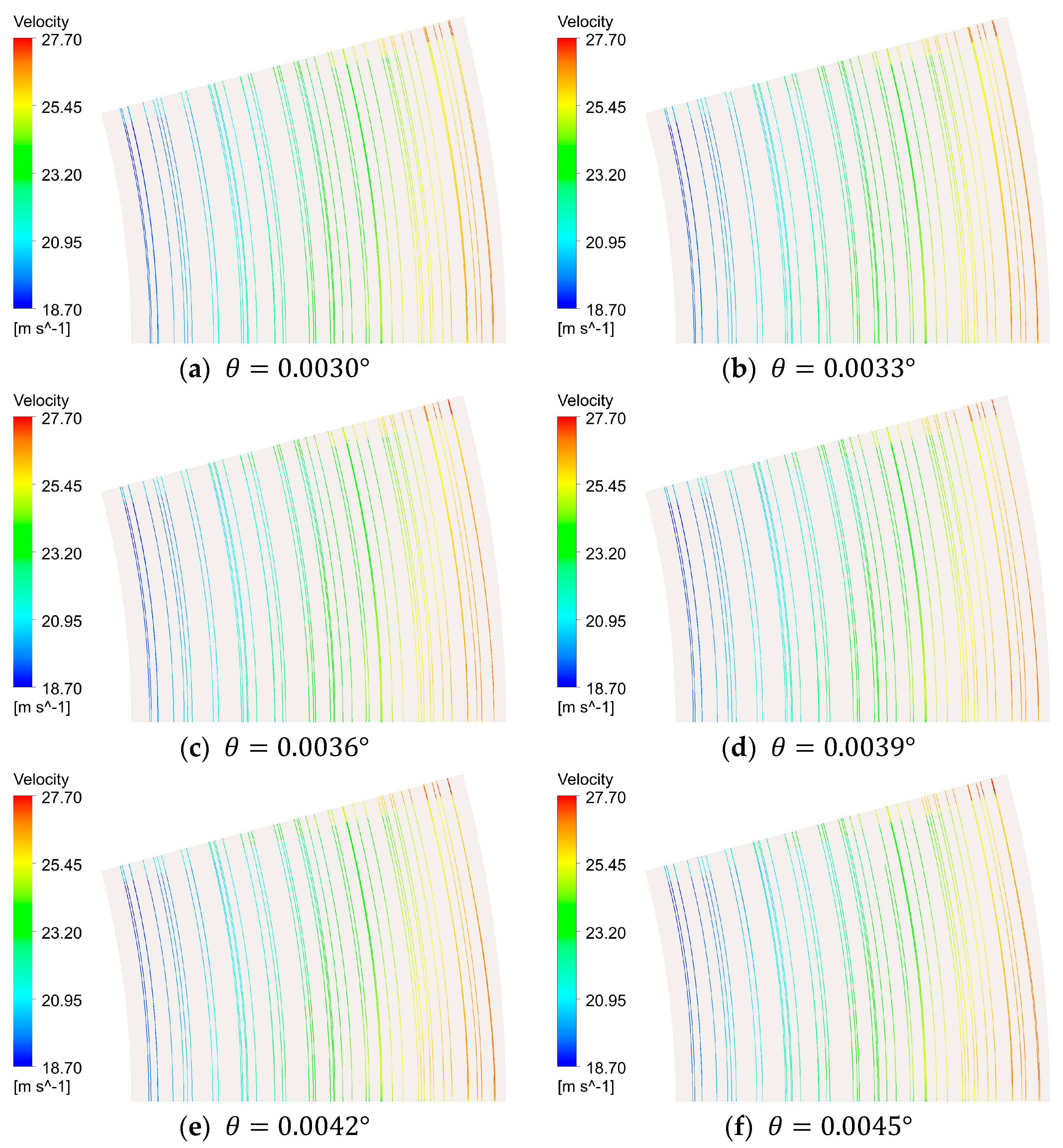
4.1. Flow Characteristics
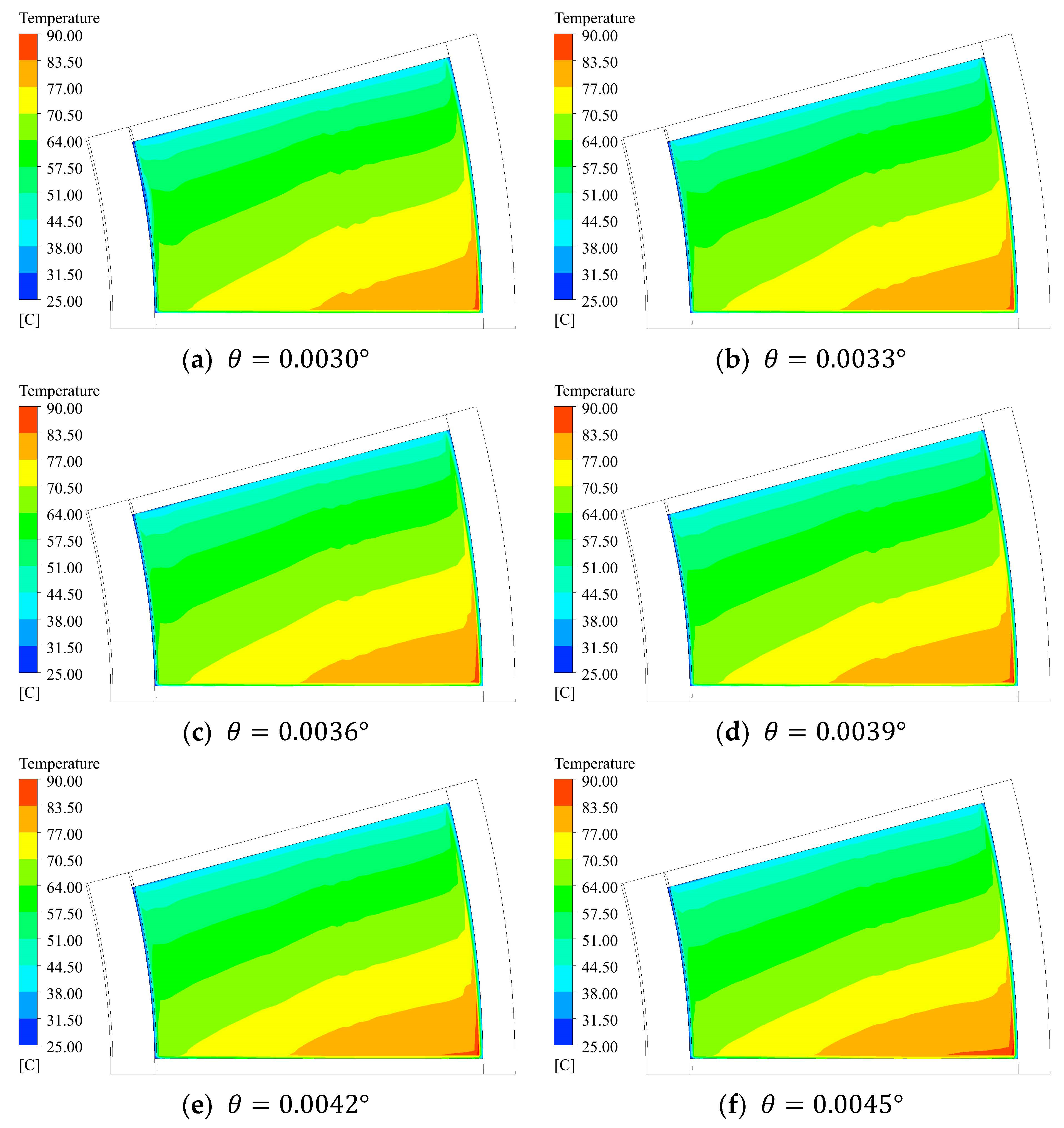
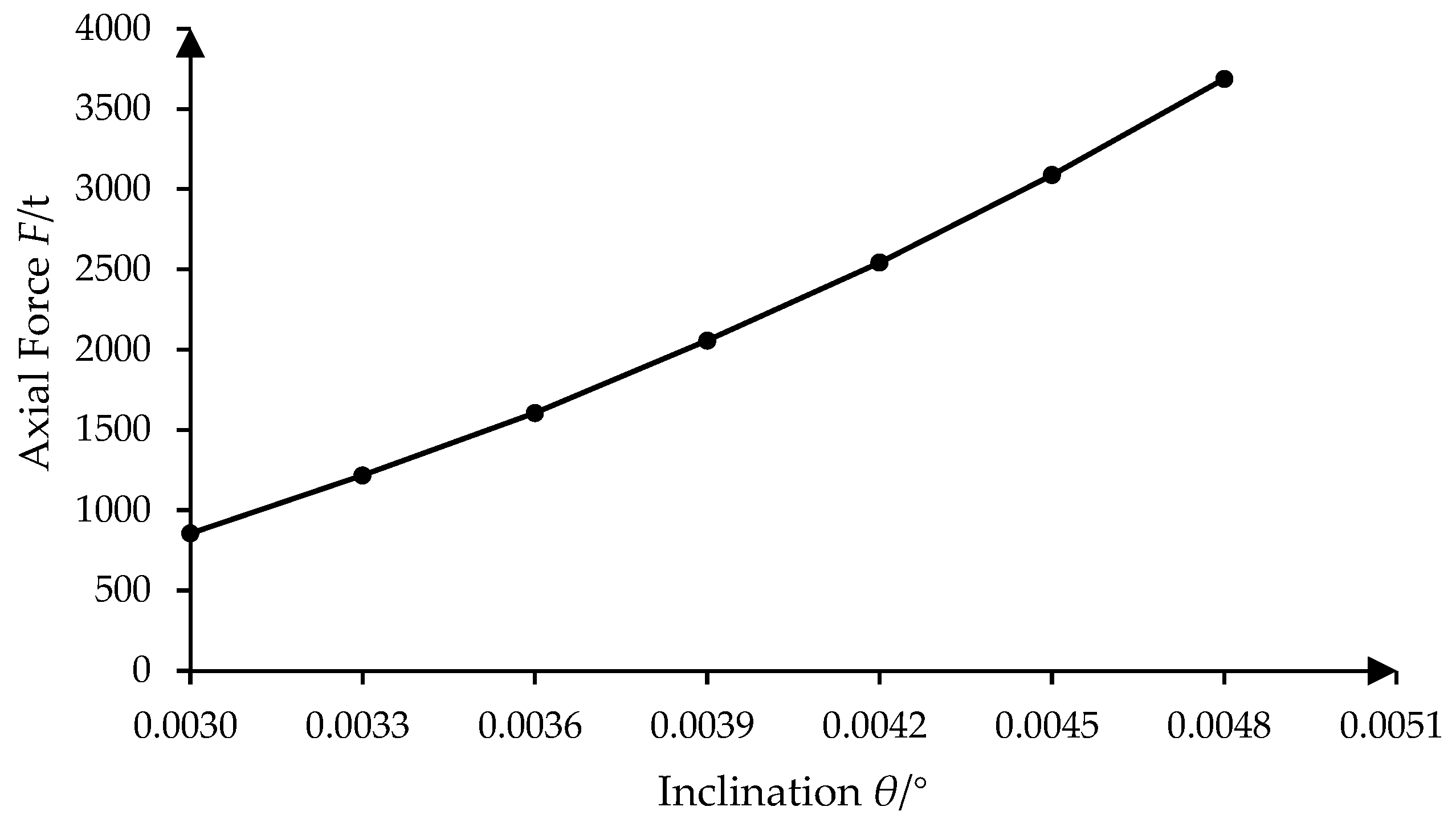
4.2. Relationship between Load and Inclination Angle
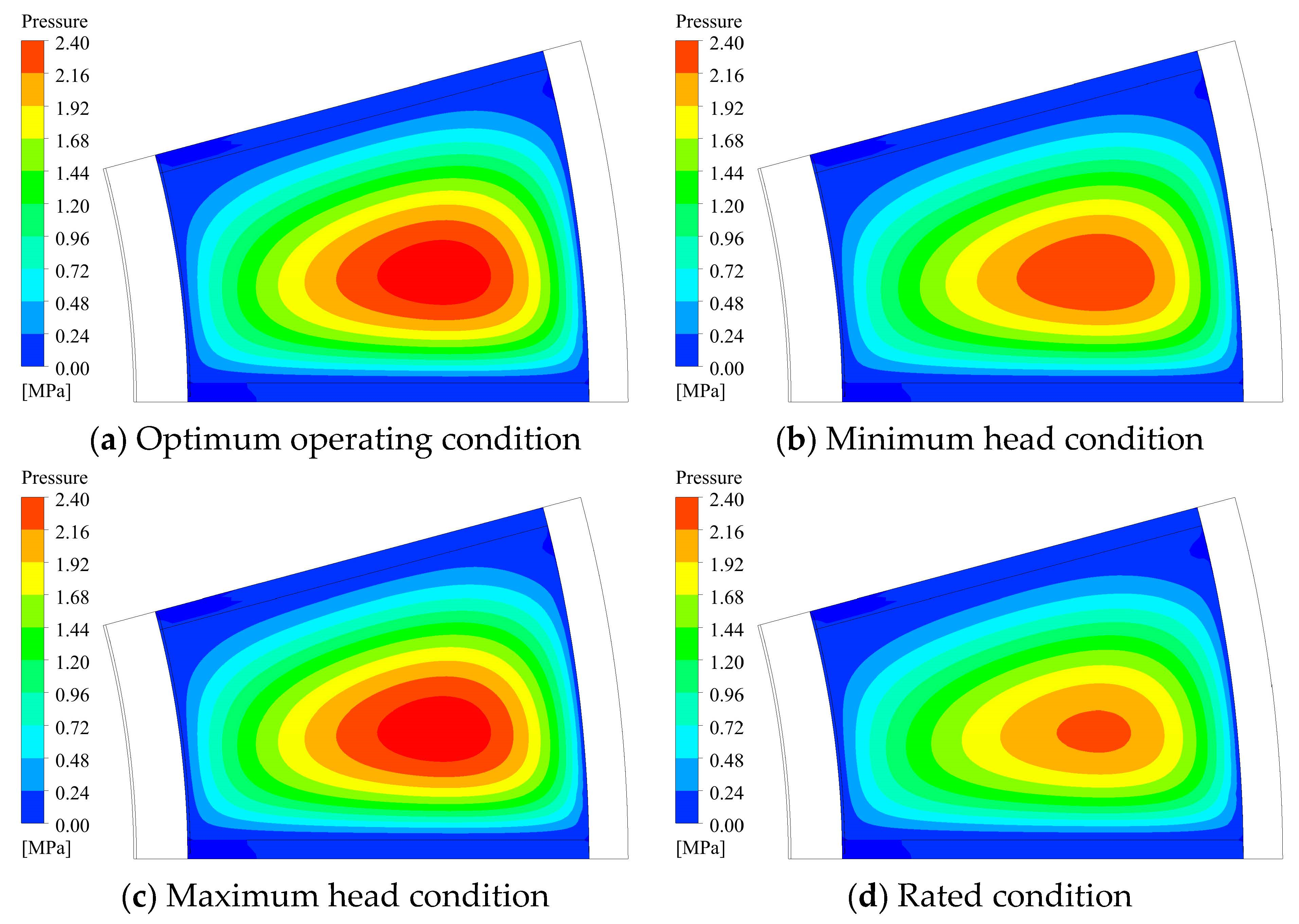
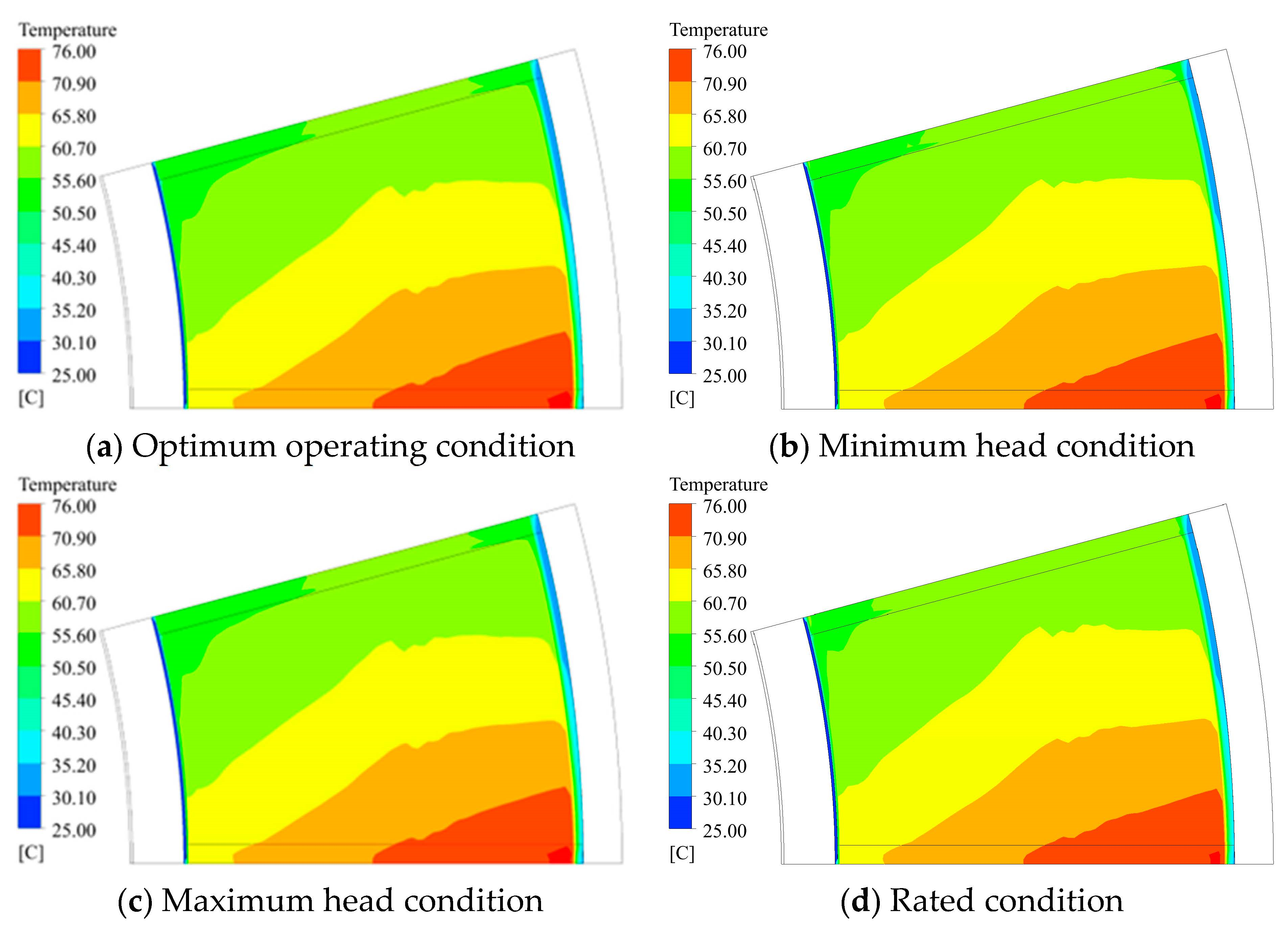
4.3. Oil Film Characteristics under Different Working Conditions
4.4. Influence of Deviation
5. Conclusions
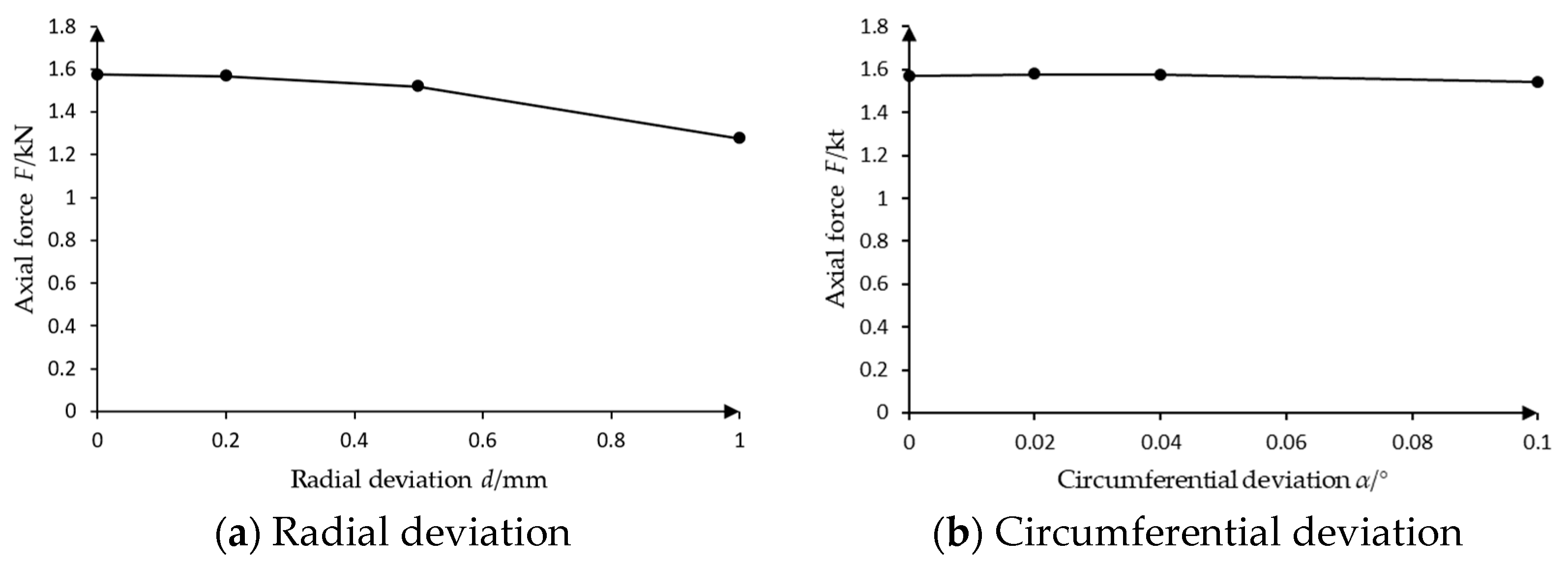
- (a)
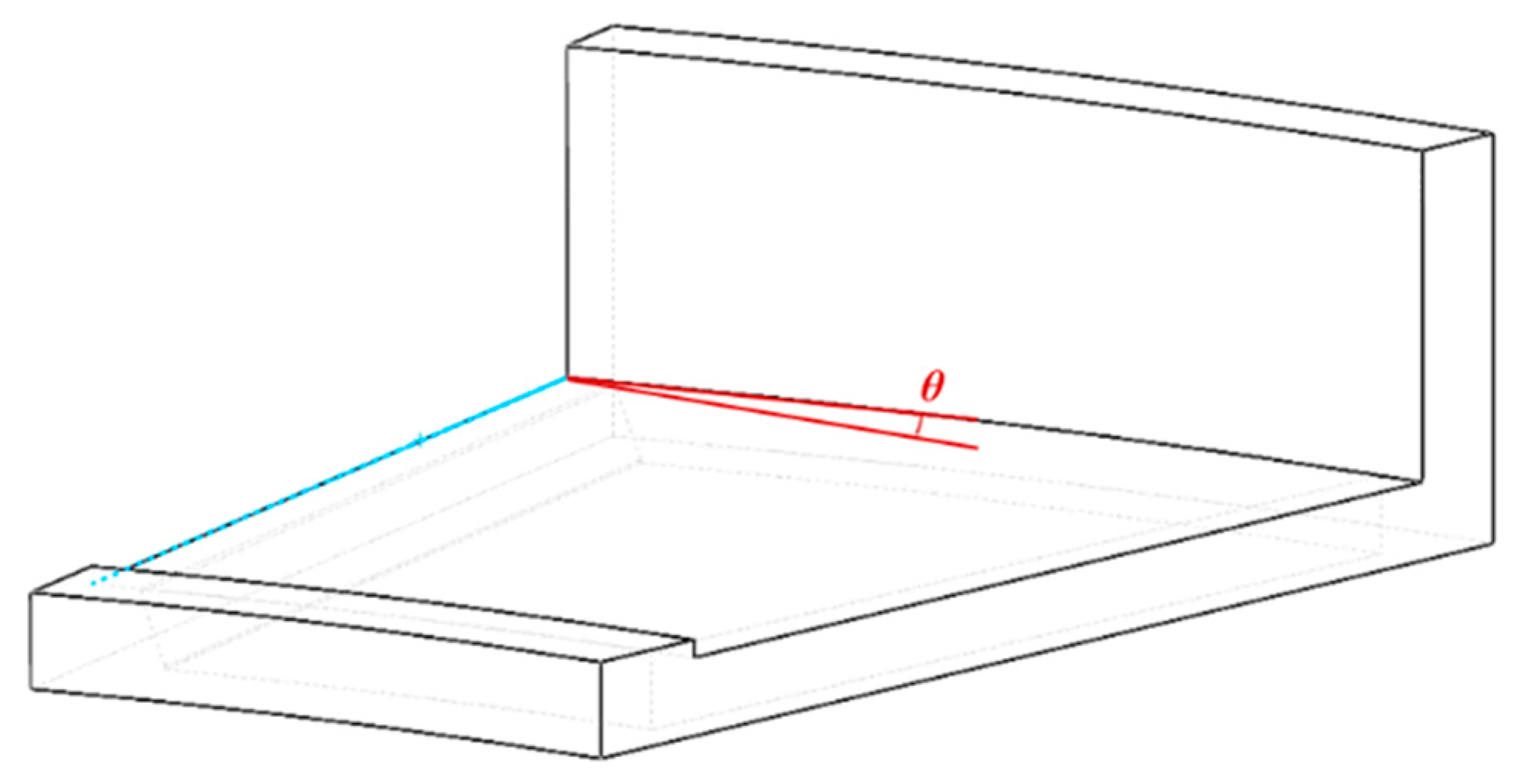
- Under the action of wedge-shaped oil film, the axial force increases with the increase of the inclination angle, but the temperature and pressure also increase, which may lead to safety risks to a certain extent. Through calculation, under the optimum operating condition, the inclination angle is 0.0039 degrees; under rated condition, the inclination angle is 0.0037 degrees.
- (b)
- The numerical results show that the axial force of the bearing decreases with the increase of radial installation deviation . The axial force is basically constant with the increase of circumferential deviation . Therefore, it is more important to pay attention to the radial installation deviation during the installation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Funan, C. Research on the Dynamic Characteristics of Key Components of Pump Turbine in Transient Processes Based on Fluid-Structure Interaction. Ph.D. Thesis, Tsinghua University, Beijing, China, 2021. [Google Scholar]
- Zhang, Y.; Sun, J.; Zheng, Y.; Ge, X.; Peng, X.; Hong, Y.; Fernandez-Rodriguez, E. Unsteady characteristics of lubricating oil in thrust bearing tank under different rotational speeds in pumped storage power station. Renew. Energy 2022, 201, 904–915. [Google Scholar] [CrossRef]
- Kong, L.; Cao, J.; Li, X.; Zhou, X.; Hu, H.; Wang, T.; Gui, S.; Lai, W.; Zhu, Z.; Wang, Z.; et al. Numerical Analysis on the Hydraulic Thrust and Dynamic Response Characteristics of a Turbine Pump. Energies 2022, 15, 1580. [Google Scholar] [CrossRef]
- Ji, X.-Y.; Li, X.-B.; Su, W.-T.; Lai, X.; Zhao, T.-X. On the hydraulic axial thrust of Francis hydro-turbine. J. Mech. Sci. Technol. 2016, 30, 2029–2035. [Google Scholar] [CrossRef]
- Cao, J.; Luo, Y.; Mirza Umar, B.; Wang, W.; Wang, Z. Influence of structural parameters on the modal characteristics of a Francis runner. Eng. Fail. Anal. 2022, 131, 105853. [Google Scholar] [CrossRef]
- Yu, X. Characteristic Information of Pressure Pulsation in Draft Tube of Francis Turbine; China Institute of Water Resources and Hydropower Research: Beijing, China, 2018. [Google Scholar]
- Sun, L. Investigation on Vortex Characteristics in Francis Turbine Operation at Part Load Conditons. Ph.D. Thesis, Xi’an University of Technology, Xi’an, China, 2020. [Google Scholar]
- Hwang, Y.-C.; Chen, Z.; Choi, Y.-D.; Lee, Y.-H. Runner Design and Internal Flow Characteristics Analysis for an Ns = 200 Francis Hydro Turbine Model. J. Korean Soc. Mar. Eng. 2016, 40, 698–703. [Google Scholar] [CrossRef]
- Chambers, W.S.; Mikula, A.M. Operational data for a large vertical thrust bearing in a pumped storage application. Tribol. Trans. 1988, 31, 61–65. [Google Scholar] [CrossRef]
- Zhang, Z.; Meng, F.; Mo, Y.; Hu, K.; Chen, Y.; Zhao, F.; Zhou, D. Numerical simulation of oil film dynamic characteristics in the bidirectional thrust bearing of a pumped storage unit. J. Phys. Conf. Ser. 2022, 2310, 012029. [Google Scholar] [CrossRef]
- Qu, F.; Li, S.; Liu, X.; Liu, Y.; Zhang, J. Research on ultrasonic testing technology of lubricating film thickness of tilting pad thrust bearing. Lubr. Eng. 2022, 47, 141–146. [Google Scholar]
- Can, H.; Jun, X.; Bin, X. Research on Film Force of Hydrodynamic Bearing in Different Oil-film Flow State. Lubr. Eng. 2012, 37, 50–53, 90. [Google Scholar]
- Xu, Z.; Sun, J.; Zheng, Z.; Zhao, J. Status and Prospect for Thermohydrodynamic Lubrication. Anal. J. Bear. 2016, 412, 58–63. [Google Scholar] [CrossRef]
- Cao, J.; Zhai, L.; Luo, Y.; Ahn, S.-H.; Wang, Z.; Liu, Y. Transient thermo-elasto-hydrodynamic analysis of a bidirectional thrust bearing in start-up and shutdown processes. Eng. Comput. 2021, 39, 1511–1533. [Google Scholar] [CrossRef]
- Reynolds, O. On the theory of lubrication and its application to Mr Tower’s. Phil. Trans. Soc. 1886, 177, 154–234. [Google Scholar]
- Charitopoulos, A. Computational Fluid Dynamics Study of Heavily Loaded Fixed-Pad Thrust Bearings Operating under Thermoelastohydrodynamic Regime. Ph.D. Thesis, Université de Poitiers, Athens, Greece, 2020. [Google Scholar]
- Pei, H. Research on Oil Film Characteristics of Thrust Bearing of Plastic Shingle for Hydropower Unit Based on Finite Element Analysis. Master’s Thesis, Changchun Institute of Technology, Changchun, China, 2021; 72p. [Google Scholar]
- Dowson, D. A generalized Reynolds equation for fluid-film lubrication. Int. J. Mech. Sci. 1962, 4, 159–170. [Google Scholar] [CrossRef]
- Wentao, Z.; Songlin, Z.; Baixin, C. Thermohydrodynamics Analysis of the Slope-platform Pad Thrust Bearing. Mech. Drive 2018, 42, 106–110. [Google Scholar]
- Tieu, A. A numerical simulation of finite-width thrust bearings, taking into account viscosity variation with temperature and pressure. J. Mech. Eng. Sci. 1975, 17, 1–10. [Google Scholar] [CrossRef]
- Michaud, P.; Souchet, D.; Bonneau, D. Thermohydrodynamic lubrication analysis for a dynamically loaded journal bearing. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2007, 221, 49–61. [Google Scholar] [CrossRef]
- Ahmadkhah, A.; Kakaee, A.H. Three-dimensional thermohydrodynamic analysis of the effects of textured main bearing on lubricant density and viscosity in internal combustion engines. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 236, 386–404. [Google Scholar] [CrossRef]
- Li, B.; Sun, J.; Zhu, S.; Fu, Y.; Zhao, X.; Wang, H.; Teng, Q.; Ren, Y.; Li, Y.; Zhu, G. Thermohydrodynamic lubrication analysis of misaligned journal bearing considering the axial movement of journal. Tribol. Int. 2019, 135, 397–407. [Google Scholar] [CrossRef]
- Yang, Y. Reynolds-Averaged Navier-Stokes Simulation of the Flow around Ship’s Hull. Master’s Thesis, Dalian Maritime University, Dalian, China, 2016; 78p. [Google Scholar]
- Zhang, C. Size Optimization of Thrust Bearing Oil Groove of Hydro-Generator Unit Based on CFD; Changchun Institute of Technology: Changchun, China, 2020; 62p. [Google Scholar]
- He, P.; Chen, T.; Zhao, R.; Zou, Y. Characteristic Analysis of Oil Film in Thrust Bearing with Plastic Pad Based on Finite Element Method. J. Chang. Inst. Technol. (Nat. Sci. Ed.) 2021, 22, 57–61. [Google Scholar]


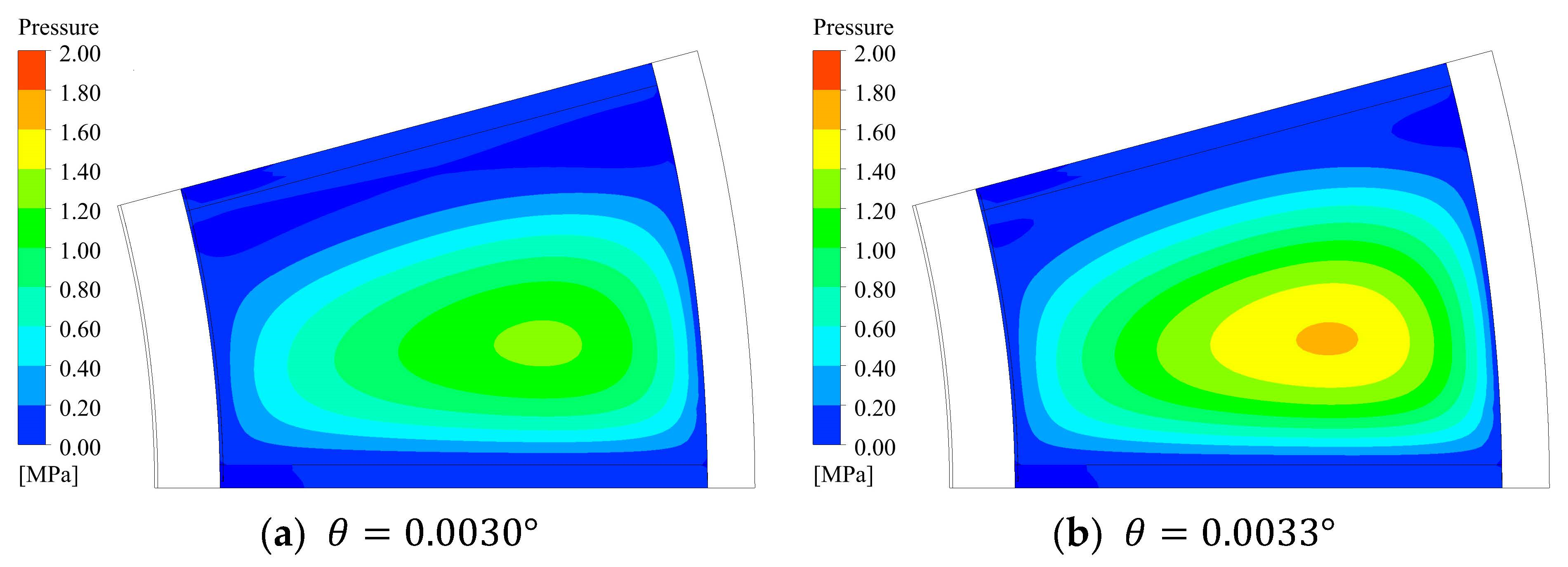
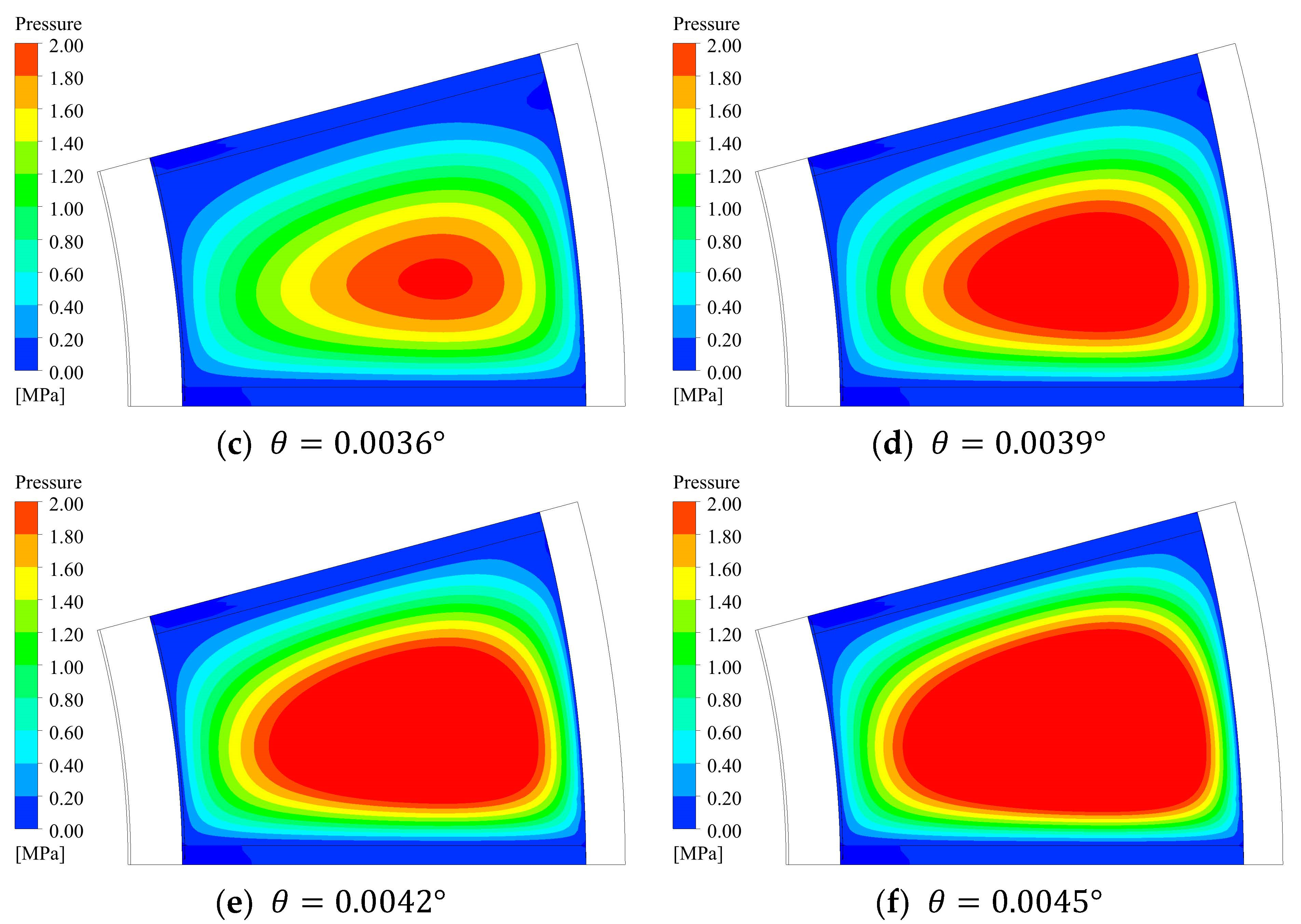
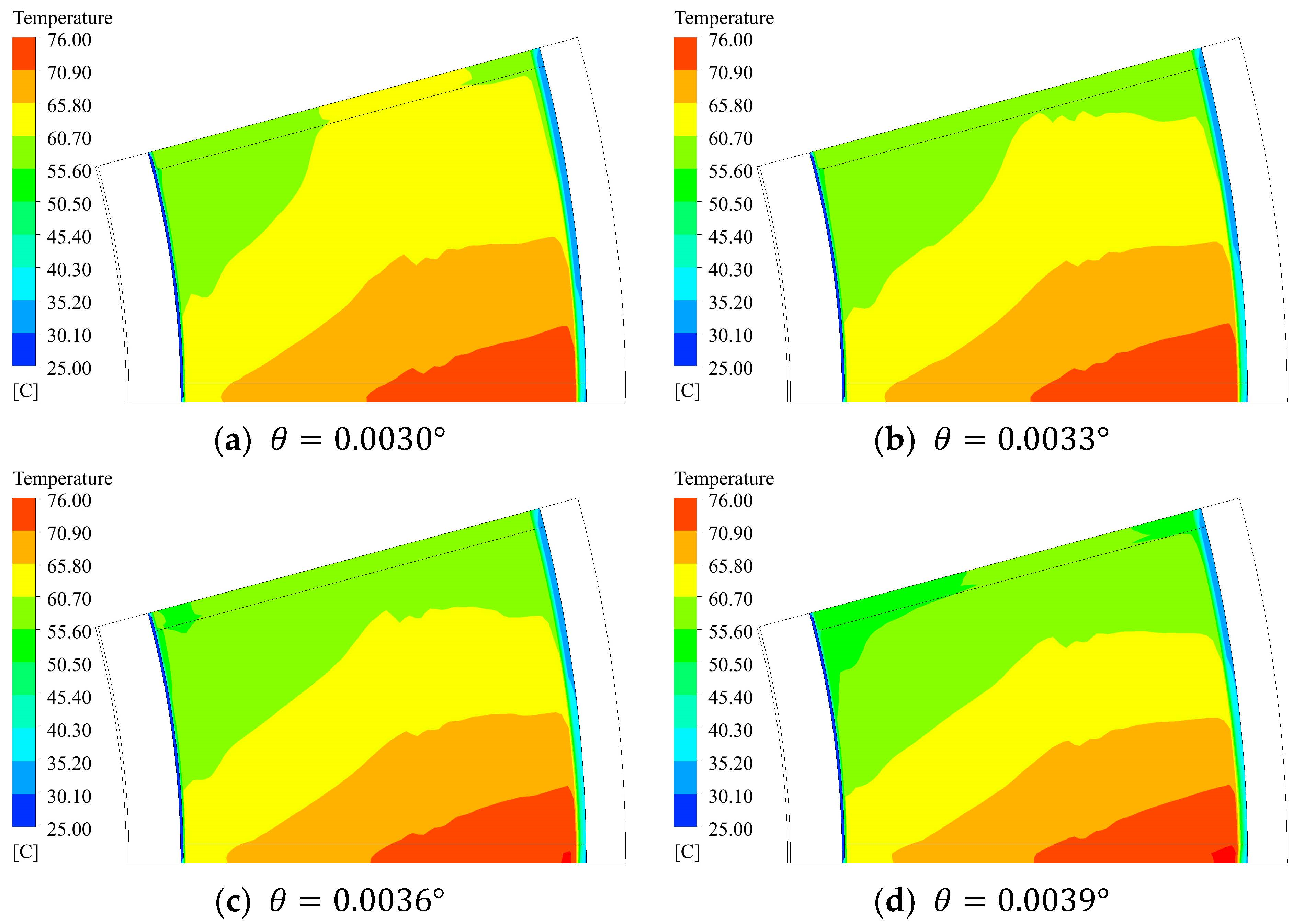

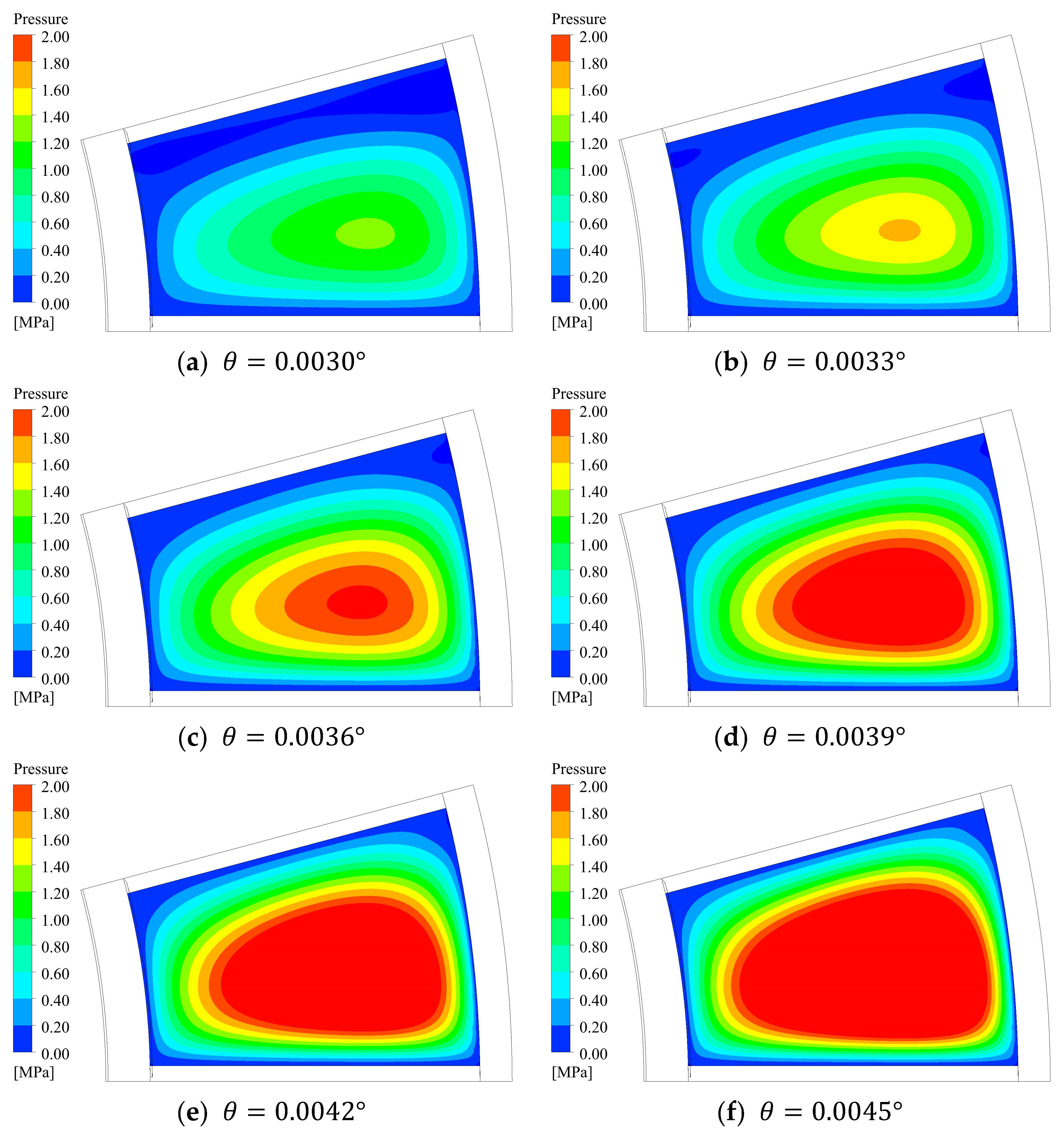
| Item | Value |
|---|---|
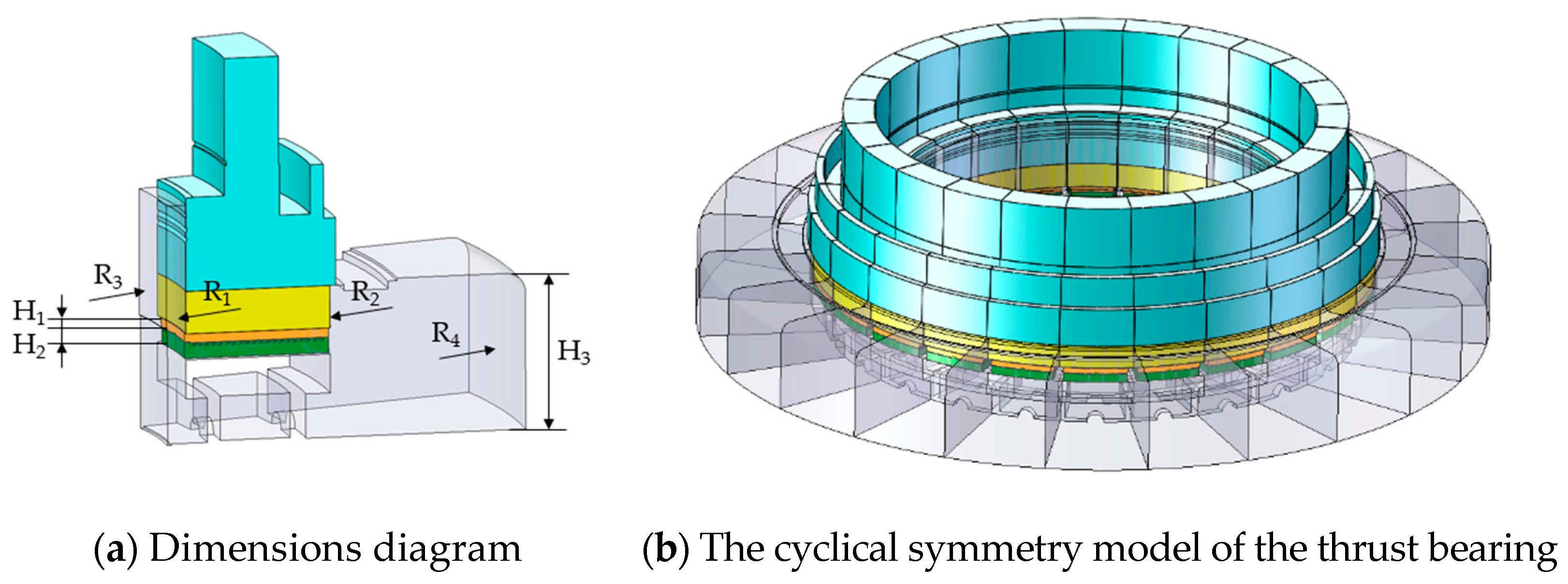
| Pad inner radius R1/mm | 1770 |
| Pad outer radius R2/mm | 2515 |
| Fluid domain inner radius R3/mm | 1670 |
| Fluid domain outer radius R4/mm | 3525 |
| Pad thickness H1/mm | 55 |
| Support tile thickness H2/mm | 80 |
| Tank height H3/mm | 811 |
| Inclination | Maximum Thickness/mm (Left) | Minimum Thickness/mm (Right) |
|---|---|---|
| 0.0030 | 0.1 | 0.066 |
| 0.0033 | 0.1 | 0.063 |
| 0.0036 | 0.1 | 0.059 |
| 0.0039 | 0.1 | 0.056 |
| 0.0042 | 0.1 | 0.052 |
| 0.0045 | 0.1 | 0.049 |
| Number of Oil Film Mesh Layers | Mesh Number | Axial Force /t |
|---|---|---|
| 12-layer | 204,534 | 2108.31 |
| 10-layer | 152,960 | 2057.23 |
| 7-layer | 132,155 | 1864.51 |
| 6-layer | 125,220 | 1732.93 |
| 3-layer | 104,415 | 1573.12 |
| Conditions | Hydraulic Thrust /t | Axial Force /t | Inclination /° |
|---|---|---|---|
| Optimum operating condition | 653 | 2027 | 0.0039 |
| Minimum head condition | 786 | 1895 | 0.0038 |
| Maximum head condition | 694 | 1987 | 0.0039 |
| Rated condition | 1020 | 1660 | 0.0037 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, Z.; Shi, Y.; Da, X.; Cao, J.; Gong, Q.; Wang, Z.; Huang, X. Influence of Installation Deviation of Thrust Bearing on Oil Film Flow of 1000 MW Hydraulic Turbine Unit. Water 2023, 15, 1649. https://doi.org/10.3390/w15091649
Ji Z, Shi Y, Da X, Cao J, Gong Q, Wang Z, Huang X. Influence of Installation Deviation of Thrust Bearing on Oil Film Flow of 1000 MW Hydraulic Turbine Unit. Water. 2023; 15(9):1649. https://doi.org/10.3390/w15091649
Chicago/Turabian StyleJi, Zhenwei, Yishu Shi, Xinming Da, Jingwei Cao, Qijun Gong, Zhengwei Wang, and Xingxing Huang. 2023. "Influence of Installation Deviation of Thrust Bearing on Oil Film Flow of 1000 MW Hydraulic Turbine Unit" Water 15, no. 9: 1649. https://doi.org/10.3390/w15091649
APA StyleJi, Z., Shi, Y., Da, X., Cao, J., Gong, Q., Wang, Z., & Huang, X. (2023). Influence of Installation Deviation of Thrust Bearing on Oil Film Flow of 1000 MW Hydraulic Turbine Unit. Water, 15(9), 1649. https://doi.org/10.3390/w15091649








