Impact of Explicitly Parameterized Mid-to-Low Level Latent Heating on the Simulation of a Squall Line in South China
Abstract
:1. Introduction
2. Overview of the 18–19 April 2019 Squall Line Case
3. Model Configuration and Experimental Design
3.1. Model Configuration
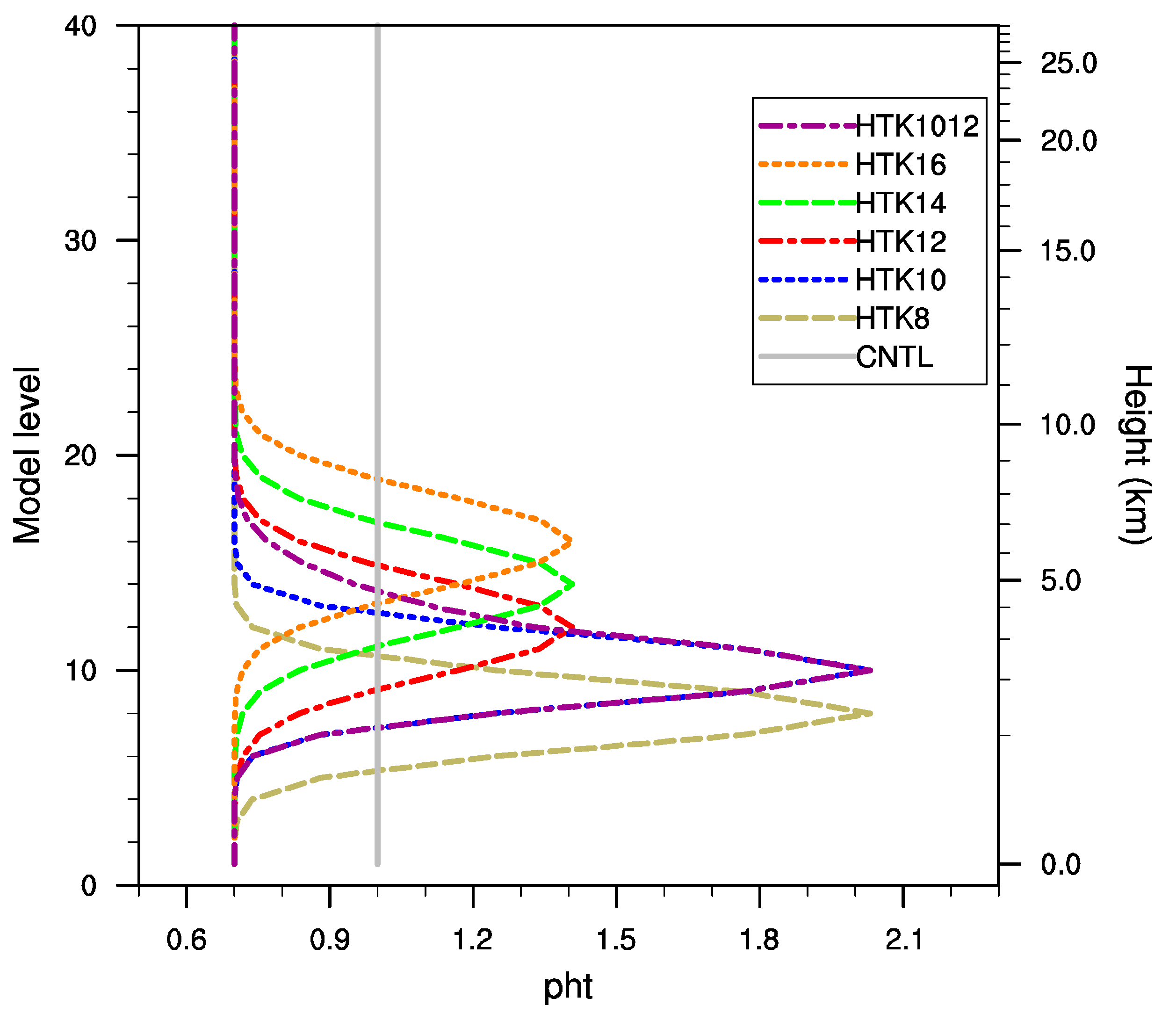
3.2. Experiment Design
4. Simulation Results
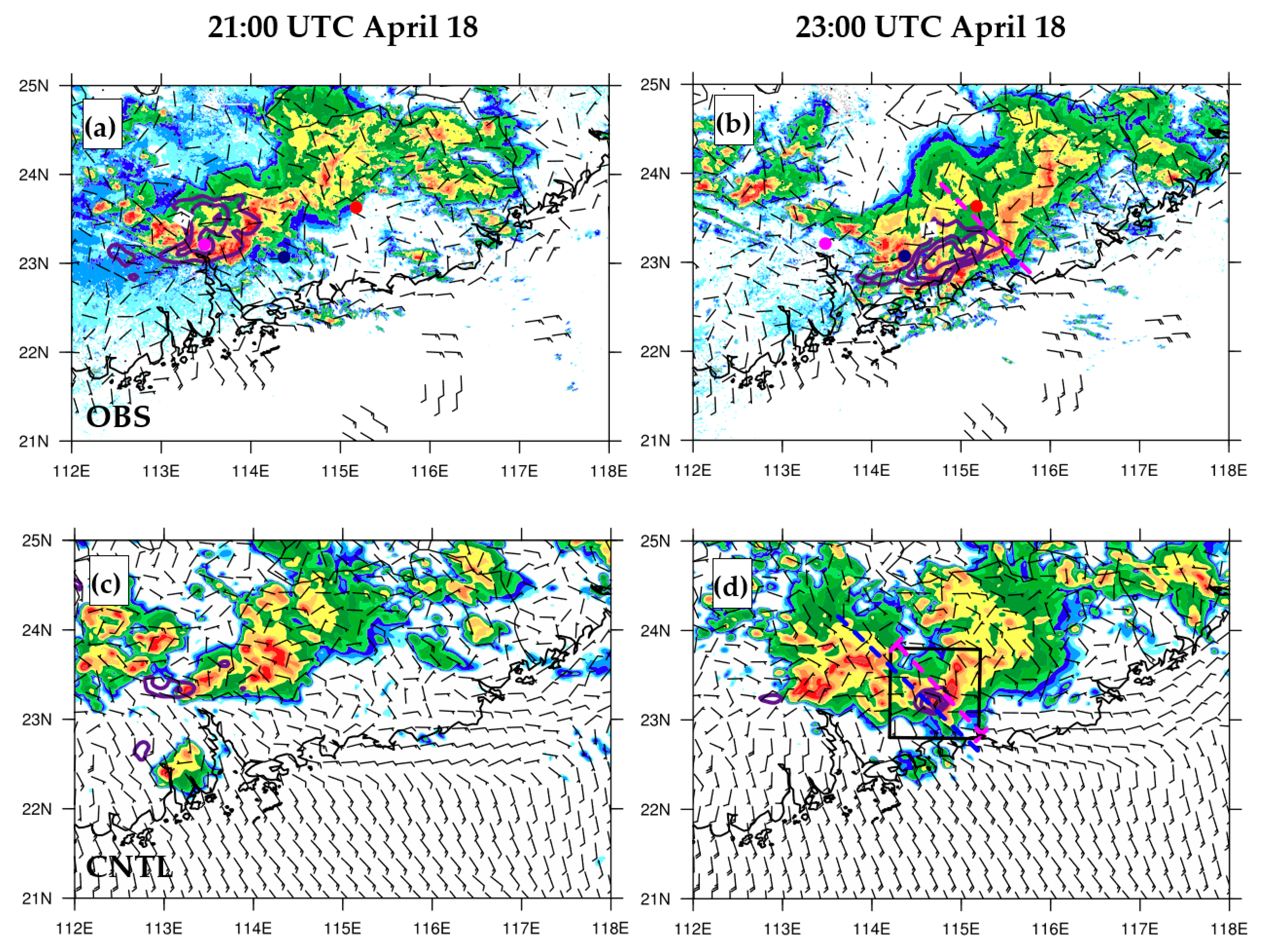
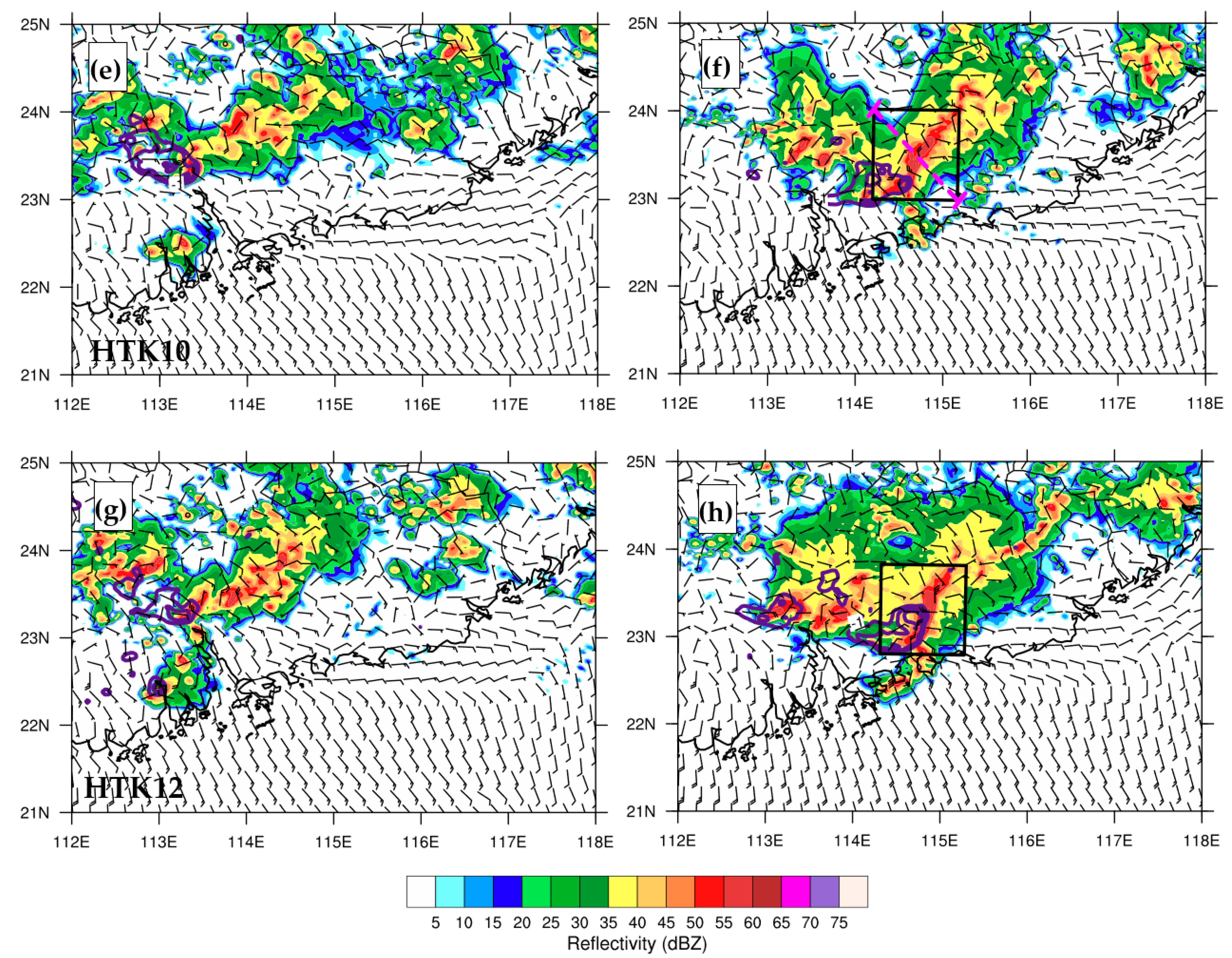
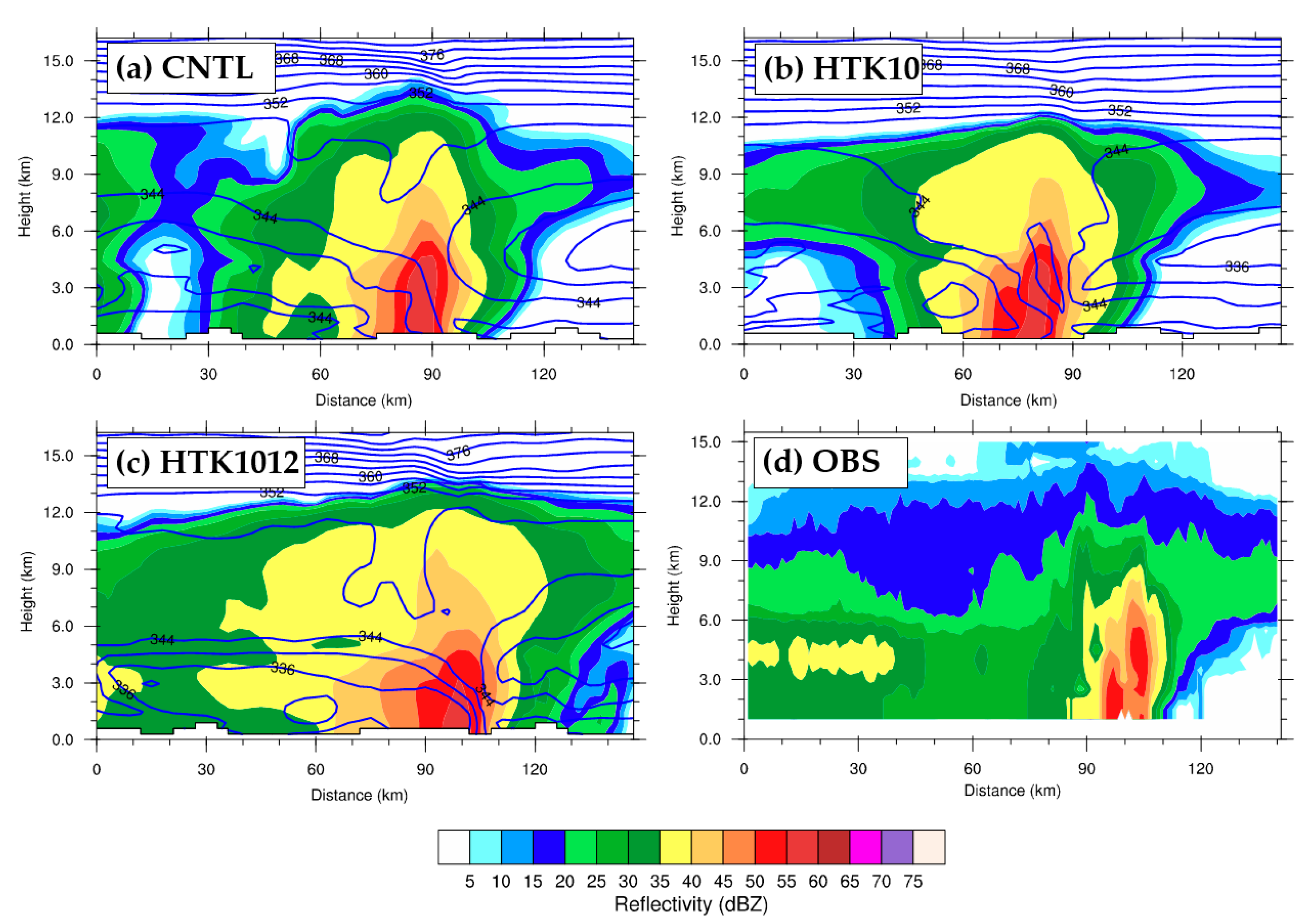
4.1. Convection Evolution
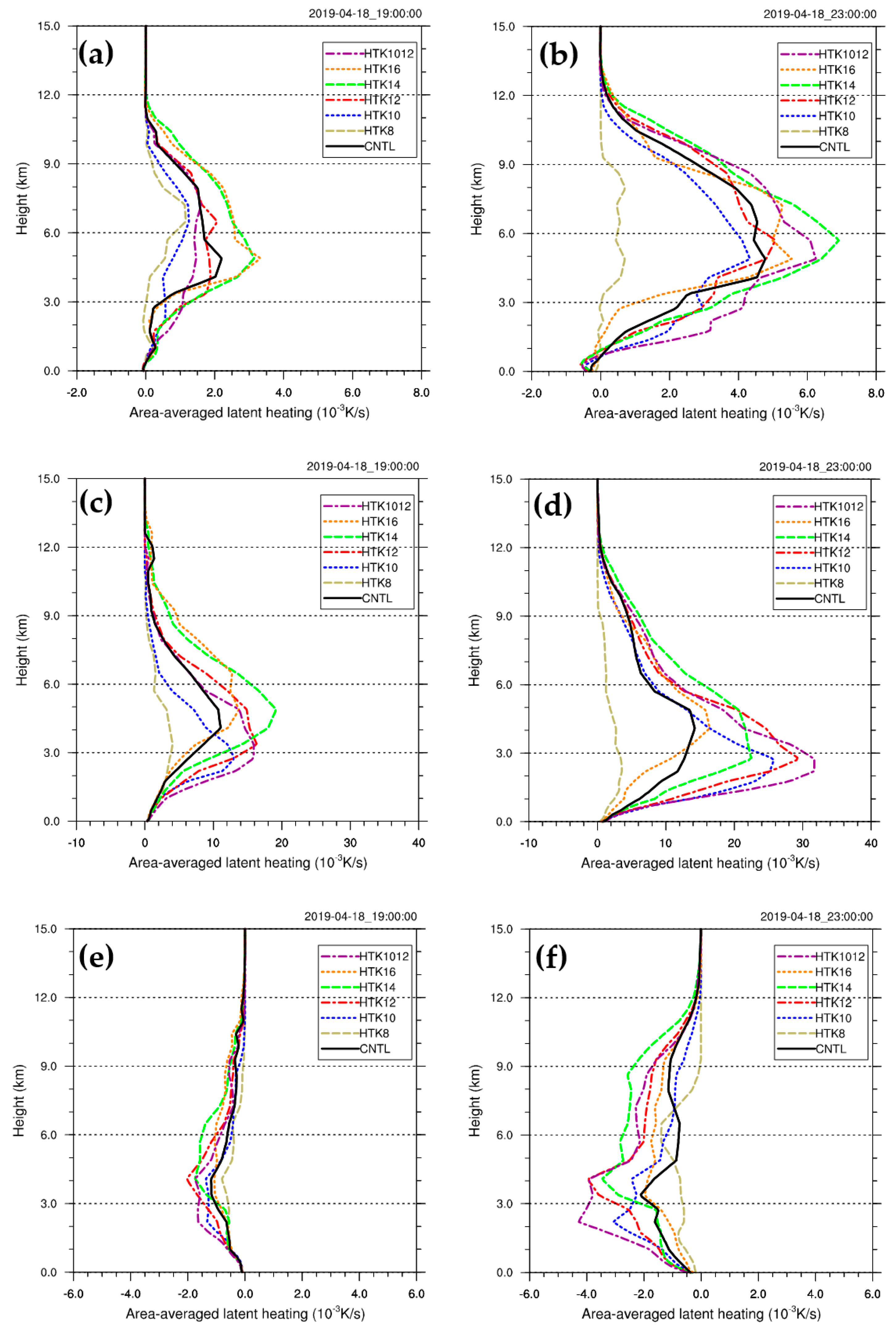
4.2. LH Profiles within the Convection System
5. Convection Structures and Conceptual Model
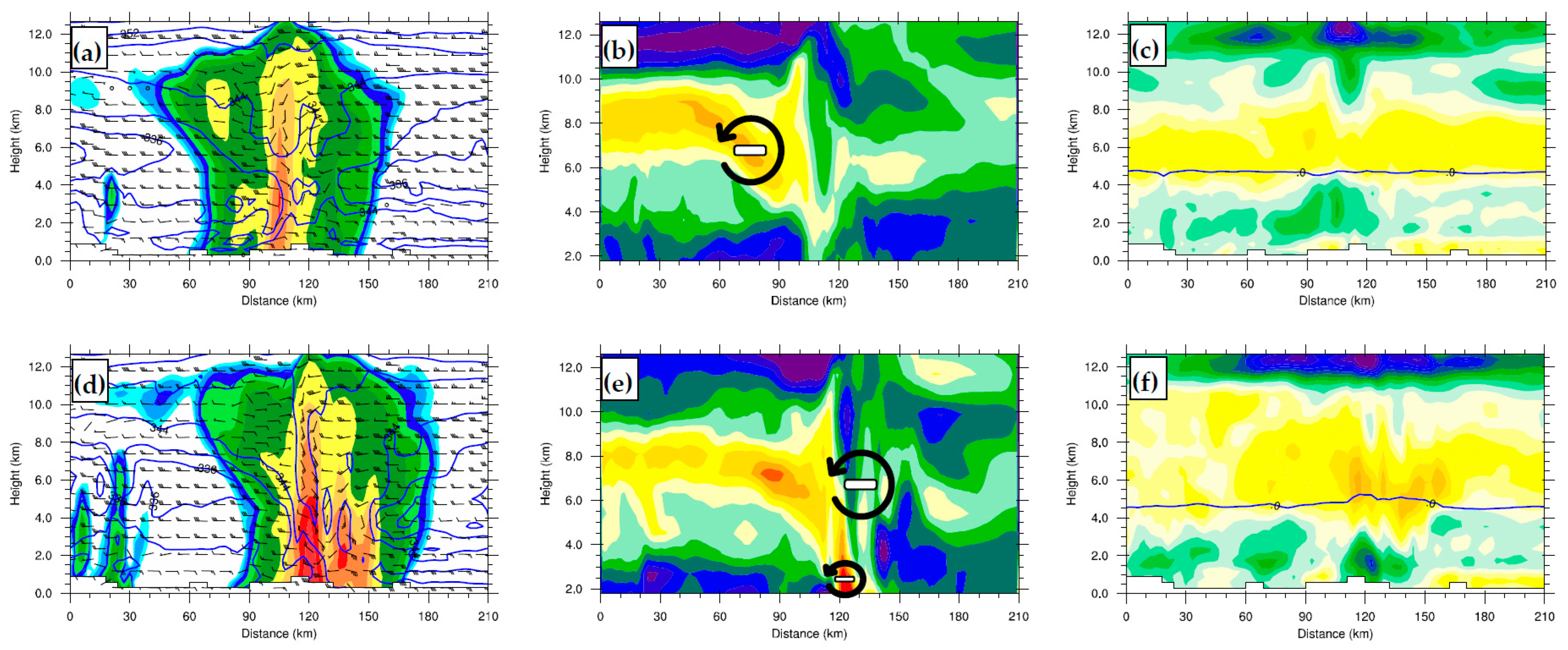
5.1. Characteristic Flows during Storm Evolution
5.1.1. Rear-to-Front (RTF) Flows at Different Scales
5.1.2. Differences in the Tilted Upward Flows
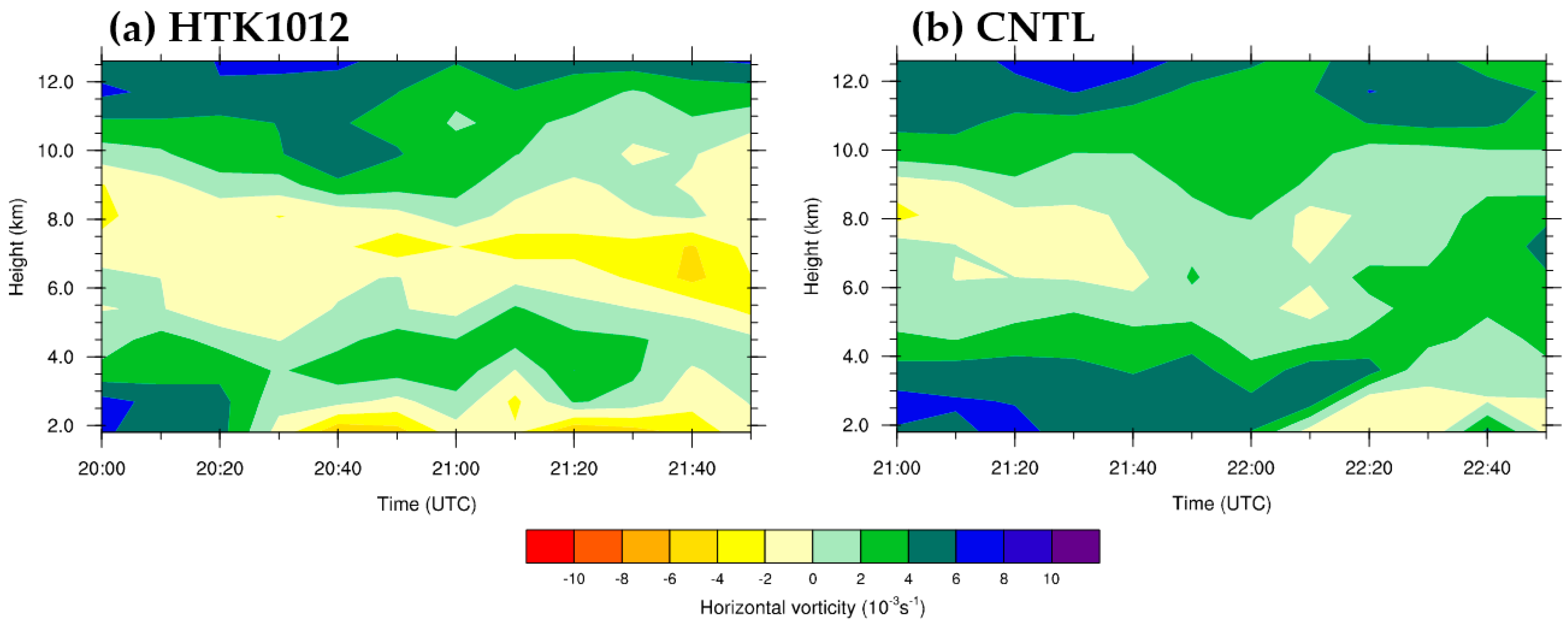
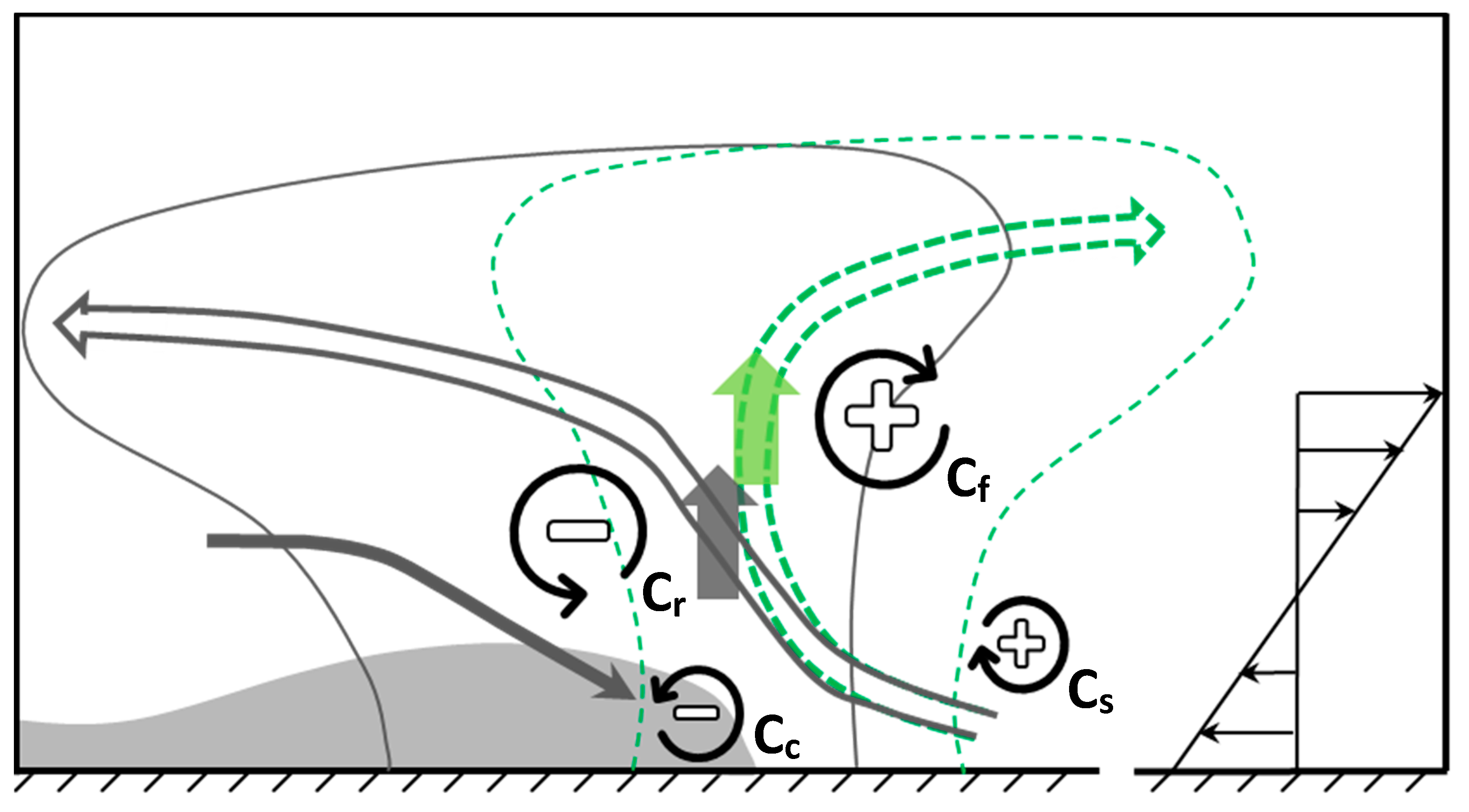
5.2. Horizontal Vorticity, Cold Pool, and Conceptual Model
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Houze, R.A., Jr. Mesoscale Convective Systems. Rev. Geophys. 2004, 42, RG4003. [Google Scholar] [CrossRef]
- Lawson, J.; Gallus, W.A. On Contrasting Ensemble Simulations of Two Great Plains Bow Echoes. Weather Forecast. 2016, 31, 787–810. [Google Scholar] [CrossRef]
- Bretherton, C. Group Velocity and the Linear Response of Stratified Fluids to Internal Heat or Mass Sources. J. Atmos. Sci. 1988, 45, 81–94. [Google Scholar] [CrossRef]
- Cram, J.M.; Pielke, R.A.; Cotton, W.R. Numerical Simulation and Analysis of a Prefrontal Squall Line. Part II: Propagation of the Squall Line as an Internal Gravity Wave. J. Atmos. Sci. 1992, 49, 209–225. [Google Scholar] [CrossRef]
- Mapes, B.E. Gregarious Tropical Convection. J. Atmos. Sci. 1993, 50, 2026–2037. [Google Scholar] [CrossRef]
- Pandya, R.E.; Durran, D.R. The Influence of Convectively Generated Thermal Forcing on the Mesoscale Circulation around Squall Lines. J. Atmos. Sci. 1996, 53, 2924–2951. [Google Scholar] [CrossRef]
- Yanai, M.; Esbensen, S.; Chu, J.-H. Determination of Bulk Properties of Tropical Cloud Clusters from Large-Scale Heat and Moisture Budgets. J. Atmos. Sci. 1973, 30, 611–627. [Google Scholar] [CrossRef]
- Johnson, R.H.; Ciesielski, P.E. Characteristics of the 1998 Summer Monsoon Onset over the Northern South China Sea. J. Meteorol. Soc. Jap. 2006, 80, 561–578. [Google Scholar] [CrossRef]
- Hagos, S.; Zhang, C.; Tao, W.-K.; Lang, S.; Takayabu, Y.N.; Shige, S.; Katsumata, M.; Olson, B.; L’Ecuyer, T. Estimates of Tropical Diabatic Heating Profiles: Commonalities and Uncertainties. J. Clim. 2010, 23, 542–558. [Google Scholar] [CrossRef]
- Tao, W.-K.; Smith, E.A.; Adler, R.F.; Haddad, Z.S.; Hou, A.Y.; Iguchi, T.; Kakar, R.; Krishnamurti, T.N.; Kummerow, C.D.; Lang, S.; et al. Retrieval of Latent Heating from TRMM Measurements. Bull. Am. Meteorol. Soc. 2006, 87, 1555–1572. [Google Scholar] [CrossRef]
- Zhang, C.; Ling, J.; Hagos, S.; Tao, W.-K.; Lang, S.; Takayabu, Y.N.; Shige, S.; Katsumata, M.; Olson, W.S.; L’Ecuyer, T. MJO Signals in Latent Heating: Results from TRMM Retrievals. J. Atmos. Sci. 2010, 67, 3488–3508. [Google Scholar] [CrossRef]
- Barnes, H.C.; Zuluaga, M.D.; Houze, R.A., Jr. Latent Heating Characteristics of the MJO Computed from TRMM Observations. J. Geophys. Res. Atmos. 2015, 120, 1322–1334. [Google Scholar] [CrossRef]
- Shige, S.; Takayabu, Y.N.; Kida, S.; Tao, W.-K.; Zeng, X.; Yokoyama, C.; L’Ecuyer, T. Spectral Retrieval of Latent Heating Profiles from TRMM PR Data. Part IV: Comparisons of Lookup Tables from Two- and Three-Dimensional Cloud-Resolving Model Simulations. J. Clim. 2009, 22, 5577–5594. [Google Scholar] [CrossRef]
- Tao, W.-K.; Takayabu, Y.N.; Lang, S.; Shige, S.; Olson, W.; Hou, A.; Skofronick-Jackson, G.; Jiang, X.; Zhang, C.; Lau, W.; et al. TRMM Latent Heating Retrieval: Applications and Comparisons with Field Campaigns and Large-Scale Analyses. Meteorol. Monogr. 2016, 56, 2.1–2.34. [Google Scholar] [CrossRef]
- Marinescu, P.J.; van den Heever, S.C.; Saleeby, S.M.; Kreidenweis, S.M. The Microphysical Contributions to and Evolution of Latent Heating Profiles in Two MC3E MCSs. J. Geophys. Res. Atmos. 2016, 121, 7913–7935. [Google Scholar] [CrossRef]
- Palmer, T.N.; Buizza, R.; Doblas-Reyes, F.; Jung, T.; Leutbecher, M.; Shutts, G.J.; Steinheimer, M.; Weisheimer, A. Stochastic parametrization and model uncertainty. ECMWF Tech. Memo. 2009, 598, 42. [Google Scholar]
- Hally, A.; Richard, E.; Fresnay, S.; Lambert, D. Ensemble Simulations with Perturbed Physical Parametrizations: Pre-HyMeX Case Studies. Q. J. R. Meteorol. Soc. 2014, 140, 1900–1916. [Google Scholar] [CrossRef]
- Fresnay, S.; Hally, A.; Garnaud, C.; Richard, E.; Lambert, D. Heavy Precipitation Events in the Mediterranean: Sensitivity to Cloud Physics Parameterisation Uncertainties. Nat. Hazards Earth Syst. Sci. 2012, 12, 2671–2688. [Google Scholar] [CrossRef]
- Qiao, X.; Wang, S.; Min, J. The Impact of a Stochastically Perturbing Microphysics Scheme on an Idealized Supercell Storm. Mon. Weather Rev. 2018, 146, 95–118. [Google Scholar] [CrossRef]
- Buizza, R.; Milleer, M.; Palmer, T.N. Stochastic Representation of Model Uncertainties in the ECMWF Ensemble Prediction System. Q. J. R. Meteorol. Soc. 1999, 125, 2887–2908. [Google Scholar] [CrossRef]
- Witte, M.K.; Morrison, H.; Davis, A.B.; Teixeira, J. Limitations of Bin and Bulk Microphysics in Reproducing the Observed Spatial Structure of Light Precipitation. J. Atmos. Sci. 2022, 79, 161–178. [Google Scholar] [CrossRef]
- Schumacher, C.; Houze, R.A.; Kraucunas, I. The Tropical Dynamical Response to Latent Heating Estimates Derived from the TRMM Precipitation Radar. J. Atmos. Sci. 2004, 61, 1341–1358. [Google Scholar] [CrossRef]
- Choudhury, A.D.; Krishnan, R. Dynamical Response of the South Asian Monsoon Trough to Latent Heating from Stratiform and Convective Precipitation. J. Atmos. Sci. 2011, 68, 1347–1363. [Google Scholar] [CrossRef]
- Eitzen, Z.A.; Xu, K.-M. A Statistical Comparison of Deep Convective Cloud Objects Observed by an Earth Observing System Satellite and Simulated by a Cloud-Resolving Model. J. Geophys. Res. Atmos. 2005, 110, D15S14. [Google Scholar] [CrossRef]
- Varble, A.; Zipser, E.J.; Fridlind, A.M.; Zhu, P.; Ackerman, A.S.; Chaboureau, J.-P.; Collis, S.; Fan, J.; Hill, A.; Shipway, B. Evaluation of Cloud-Resolving and Limited Area Model Intercomparison Simulations Using TWP-ICE Observations: 1. Deep Convective Updraft Properties. J. Geophys. Res. Atmos. 2014, 119, 13891–13918. [Google Scholar] [CrossRef]
- Vendrasco, E.P.; Machado, L.A.T.; Ribeiro, B.Z.; Freitas, E.D.; Ferreira, R.C.; Negri, R.G. Cloud-Resolving Model Applied to Nowcasting: An Evaluation of Radar Data Assimilation and Microphysics Parameterization. Weather Forecast. 2020, 35, 2345–2365. [Google Scholar] [CrossRef]
- Ding, Y.H.; Chan, J.C.L. The East Asian Summer Monsoon: An Overview. Meteorol. Atmos. Phys. 2005, 89, 117–142. [Google Scholar] [CrossRef]
- Gu, W.; Wang, L.; Hu, Z.-Z.; Hu, K.; Li, Y. Interannual Variations of the First Rainy Season Precipitation over South China. J. Clim. 2018, 31, 623–640. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.; Dudhia, J.; Gill, D.; Barker, D.M.; Duda, M.G.; Huang, X.Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3 (NCAR Tech. Note TN-4751STR, pp. 113). 2008. Available online: http://www.mmm.ucar.edu/wrf/users/docs/arw_v3_bw.pdf (accessed on 1 January 2020).
- Powers, J.G.; Klemp, J.B.; Skamarock, W.C.; Davis, C.A.; Dudhia, J.; Gill, D.O.; Coen, J.L.; Gochis, D.J.; Ahmadov, R.; Peckham, S.E.; et al. The Weather Research and Forecasting Model: Overview, System Efforts, and Future Directions. Bull. Amer. Meteor. Soc. 2017, 98, 1717–1737. [Google Scholar] [CrossRef]
- Hu, M.; Shao, H.; Stark, D.; Newman, K.; Zhou, C.; Ge, G.; Zhang, X. Grid-Point Statistical Interpolation (GSI) User’s Guide Version 3.6. Developmental Testbed Center, p. 149. 2017. Available online: http://www.dtcenter.org/com-GSI/users/docs/index.php (accessed on 1 January 2020).
- Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.D. Explicit Forecasts of Winter Precipitation Using an Improved Bulk Microphysics Scheme. Part II: Implementation of a New Snow Parameterization. Mon. Weather Rev. 2008, 136, 5095–5115. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an Advanced Land Surface–Hydrology Model with the Penn State–NCAR MM5 Modeling System. Part I: Model Implementation and Sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an Advanced Land Surface–Hydrology Model with the Penn State–NCAR MM5 Modeling System. Part II: Preliminary Model Validation. Mon. Weather Rev. 2001, 129, 587–604. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Dudhia, J.; González-Rouco, J.F.; Navarro, J.; Montávez, J.P.; García-Bustamante, E. A Revised Scheme for the WRF Surface Layer Formulation. Mon. Weather Rev. 2012, 140, 898–918. [Google Scholar] [CrossRef]
- Grell, G.A.; Freitas, S.R. A Scale and Aerosol Aware Stochastic Convective Parameterization for Weather and Air Quality Modeling. Atmos. Chem. Phys. 2014, 14, 5233–5250. [Google Scholar] [CrossRef]
- Bretherton, C.S.; Park, S. A New Moist Turbulence Parameterization in the Community Atmosphere Model. J. Clim. 2009, 22, 3422–3448. [Google Scholar] [CrossRef]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative Forcing by Long-Lived Greenhouse Gases: Calculations with the AER Radiative Transfer Models. J. Geophys. Res. Atmos. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical Study of Convection Observed during the Winter Monsoon Experiment Using a Mesoscale Two-Dimensional Model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Qian, Q.; Lin, Y.; Luo, Y.; Zhao, X.; Zhao, Z.; Luo, Y.; Liu, X. Sensitivity of a Simulated Squall Line During Southern China Monsoon Rainfall Experiment to Parameterization of Microphysics. J. Geophys. Res. Atmos. 2018, 123, 4197–4220. [Google Scholar] [CrossRef]
- Zhang, D.-L.; Gao, K. Numerical Simulation of an Intense Squall Line during 10–11 June 1985 PRE-STORM. Part II: Rear Inflow, Surface Pressure Perturbations and Stratiform Precipitation. Mon. Weather Rev. 1989, 117, 2067–2094. [Google Scholar] [CrossRef]
- Rotunno, R.; Klemp, J.B.; Weisman, M.L. A Theory for Strong, Long-Lived Squall Lines. J. Atmos. Sci. 1988, 45, 463–485. [Google Scholar] [CrossRef]
- Weisman, M.L. The Role of Convectively Generated Rear-Inflow Jets in the Evolution of Long-Lived Mesoconvective Systems. J. Atmos. Sci. 1992, 49, 1826–1847. [Google Scholar] [CrossRef]
- Xue, L.; Fan, J.; Lebo, Z.J.; Wu, W.; Morrison, H.; Grabowski, W.W.; Chu, X.; Geresdi, I.; North, K.; Stenz, R.; et al. Idealized Simulations of a Squall Line from the MC3E Field Campaign Applying Three Bin Microphysics Schemes: Dynamic and Thermodynamic Structure. Mon. Weather Rev. 2017, 145, 4789–4812. [Google Scholar] [CrossRef]
- Adams-Selin, R.D.; van den Heever, S.C.; Johnson, R.H. Impact of Graupel Parameterization Schemes on Idealized Bow Echo Simulations. Mon. Weather Rev. 2013, 141, 1241–1262. [Google Scholar] [CrossRef]












| Coff | B | A | σ | k0 | |
|---|---|---|---|---|---|
| Experiment | |||||
| CNTL | 1.0 | 0.0 | - | - | |
| HTK8 | 0.7 | 5.0 | 1.5 | 8 | |
| HTK10 | 0.7 | 5.0 | 1.5 | 10 | |
| HTK12 | 0.7 | 3.9 | 2.2 | 12 | |
| HTK14 | 0.7 | 3.9 | 2.2 | 14 | |
| HTK16 | 0.7 | 3.9 | 2.2 | 16 | |
| HTK1012 | Blending HTK10 and HTK12. See Equation (3). | ||||
| Experiment | CNTL | HTK8 | HTK10 | HTK12 | HTK14 | HTK16 | HTK1012 | OBS |
|---|---|---|---|---|---|---|---|---|
| Ls (km) | 163 | - | 235 | 242 | 262 | 150 | 332 | 358 |
| Vs (ms−1) | 14 | - | 17 | 18 | 15 | 12 | 19 | 21 |
| Corr | 0.636 | 0.668 | 0.666 | 0.694 | 0.680 | 0.642 | 0.718 | 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, H.; Liu, M.; Ma, L.; Bao, X.; Zou, L.; Zhu, J. Impact of Explicitly Parameterized Mid-to-Low Level Latent Heating on the Simulation of a Squall Line in South China. Water 2023, 15, 1743. https://doi.org/10.3390/w15091743
Chu H, Liu M, Ma L, Bao X, Zou L, Zhu J. Impact of Explicitly Parameterized Mid-to-Low Level Latent Heating on the Simulation of a Squall Line in South China. Water. 2023; 15(9):1743. https://doi.org/10.3390/w15091743
Chicago/Turabian StyleChu, Hai, Mengjuan Liu, Leiming Ma, Xuwei Bao, Lanjun Zou, and Jiakai Zhu. 2023. "Impact of Explicitly Parameterized Mid-to-Low Level Latent Heating on the Simulation of a Squall Line in South China" Water 15, no. 9: 1743. https://doi.org/10.3390/w15091743
APA StyleChu, H., Liu, M., Ma, L., Bao, X., Zou, L., & Zhu, J. (2023). Impact of Explicitly Parameterized Mid-to-Low Level Latent Heating on the Simulation of a Squall Line in South China. Water, 15(9), 1743. https://doi.org/10.3390/w15091743









