Numerical Analyses of Slope Stability Considering Grading and Seepage Prevention
Abstract
:1. Introduction
2. Method and Theory
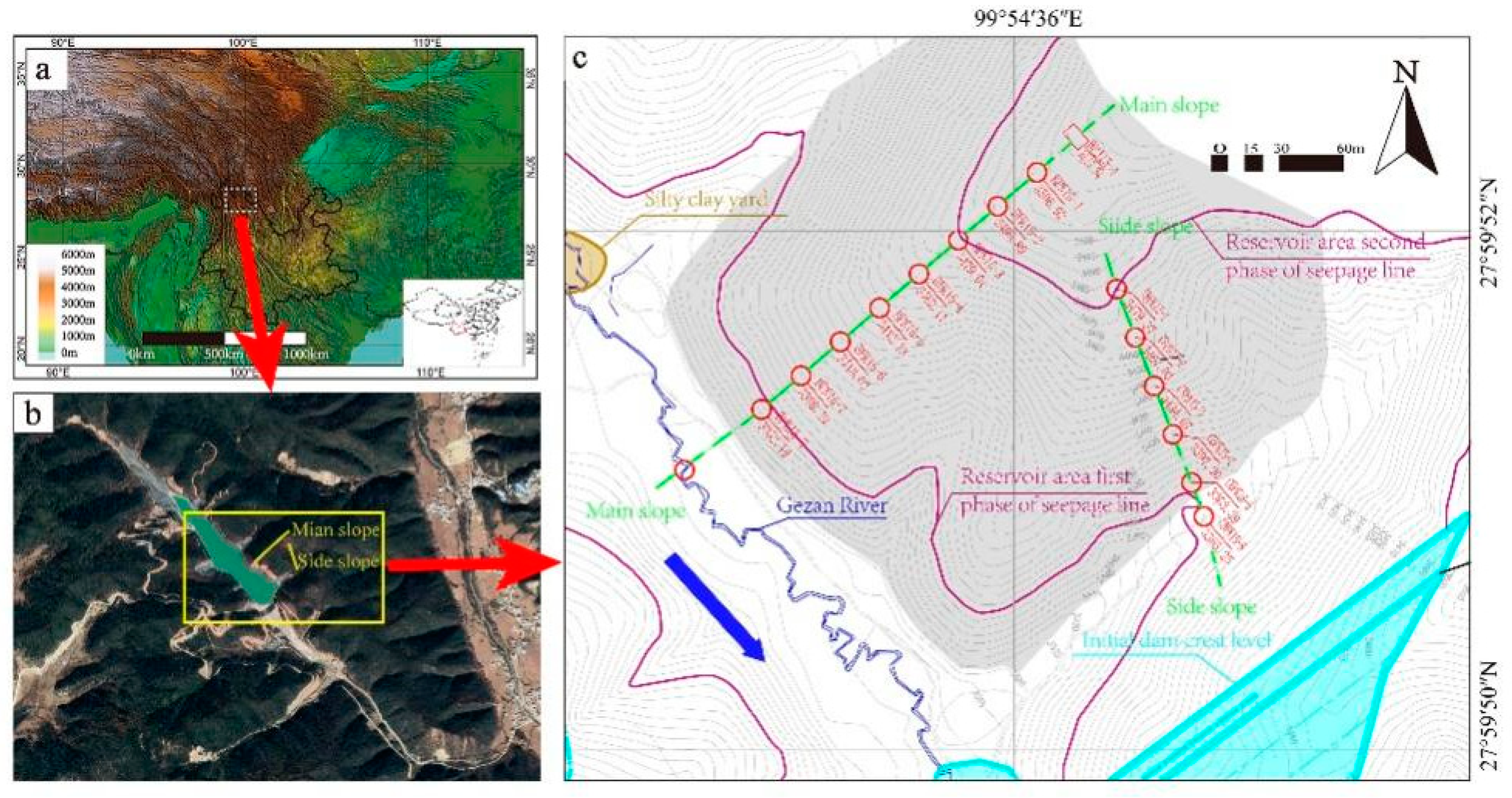
2.1. Theoretical Model Construction
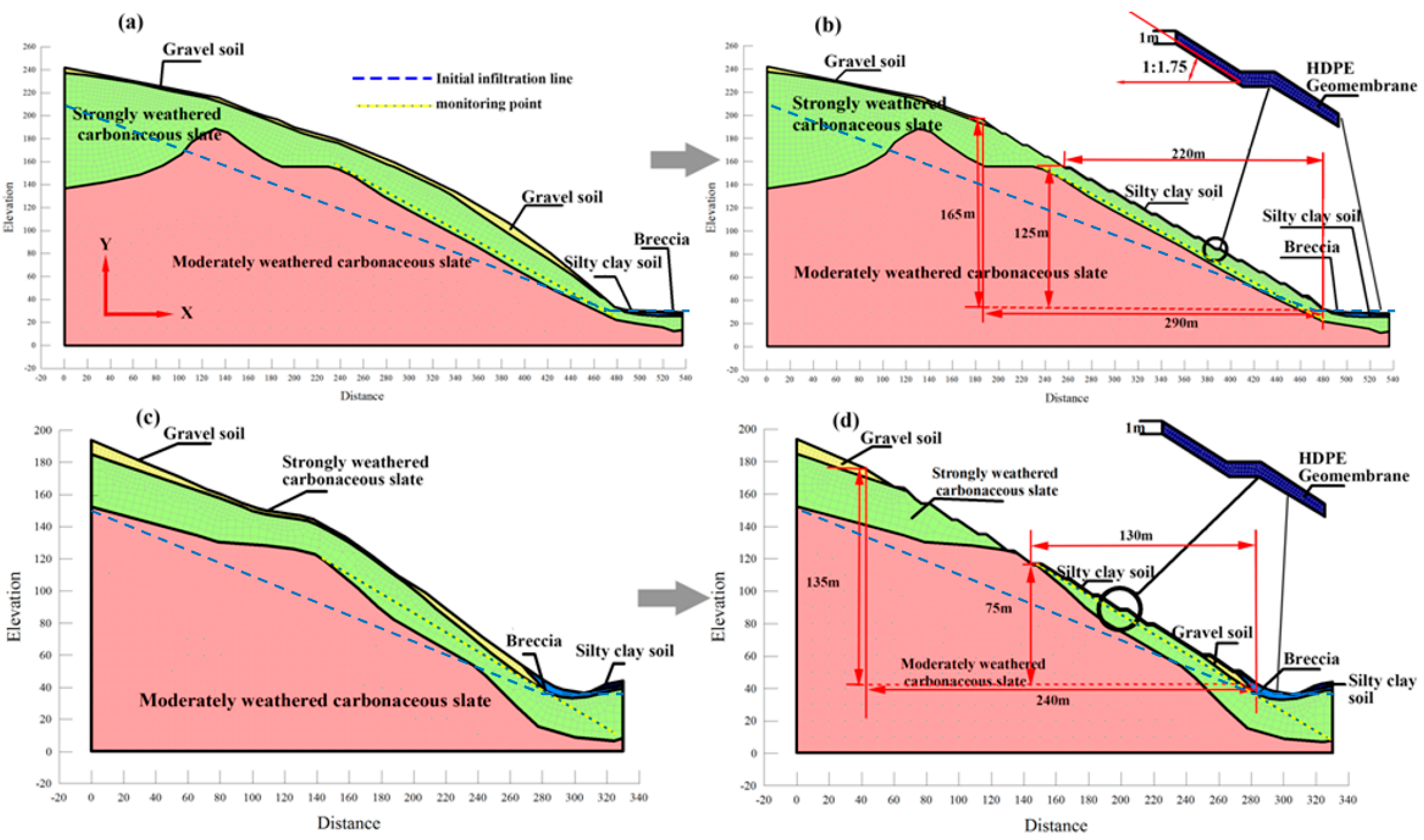
2.2. The Numerical Calculation Model
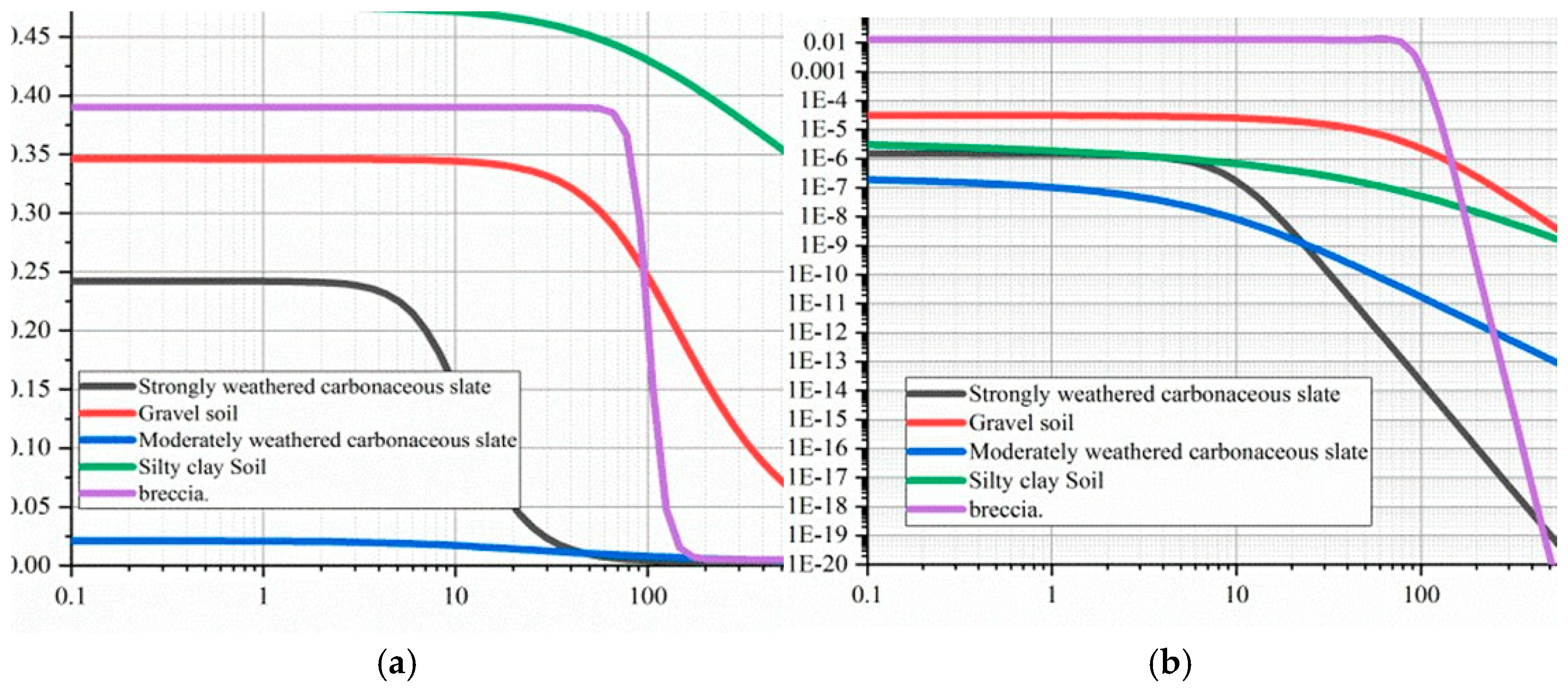
2.3. Calculation Parameters
2.4. Model Boundary Conditions
3. Simulation Analysis
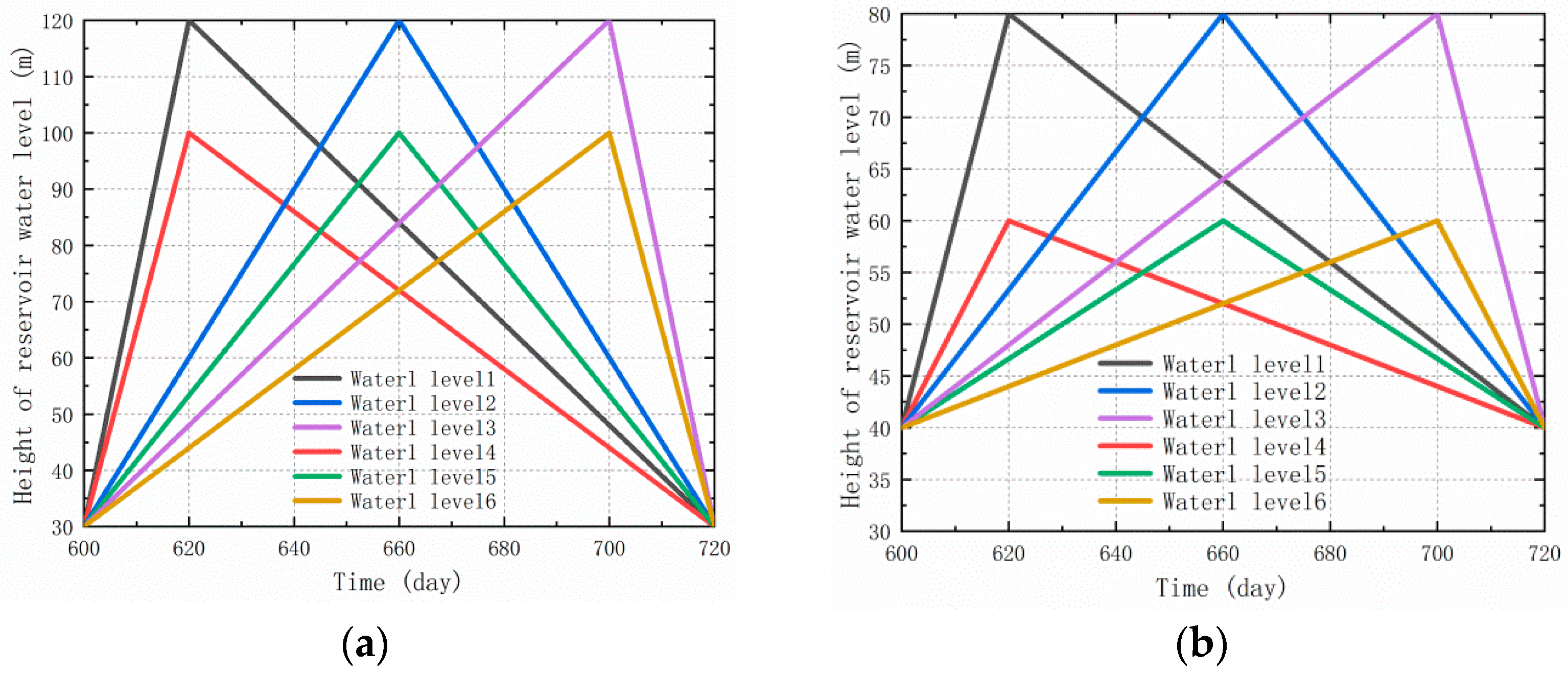
3.1. Simulation Analysis 1
3.2. Simulation Analysis 2
3.3. Simulation Analysis 3
4. Conclusions
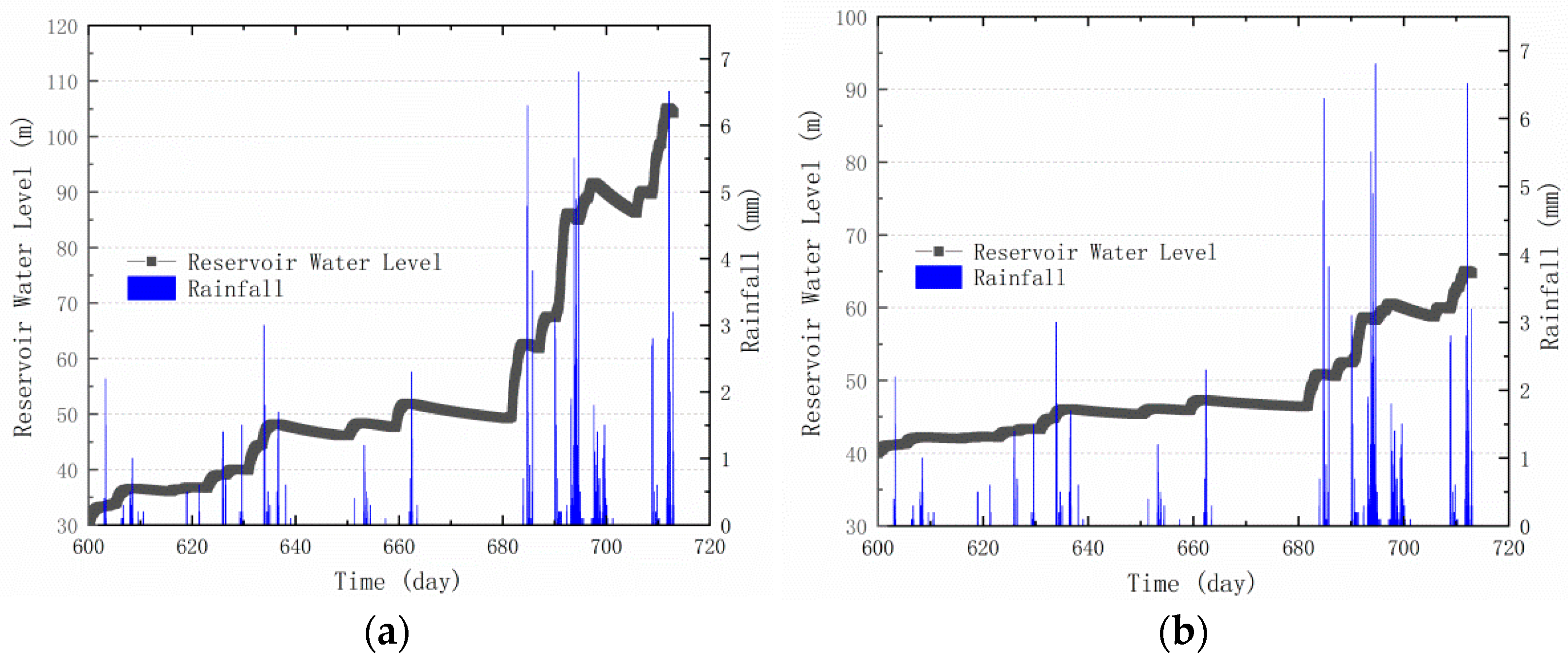
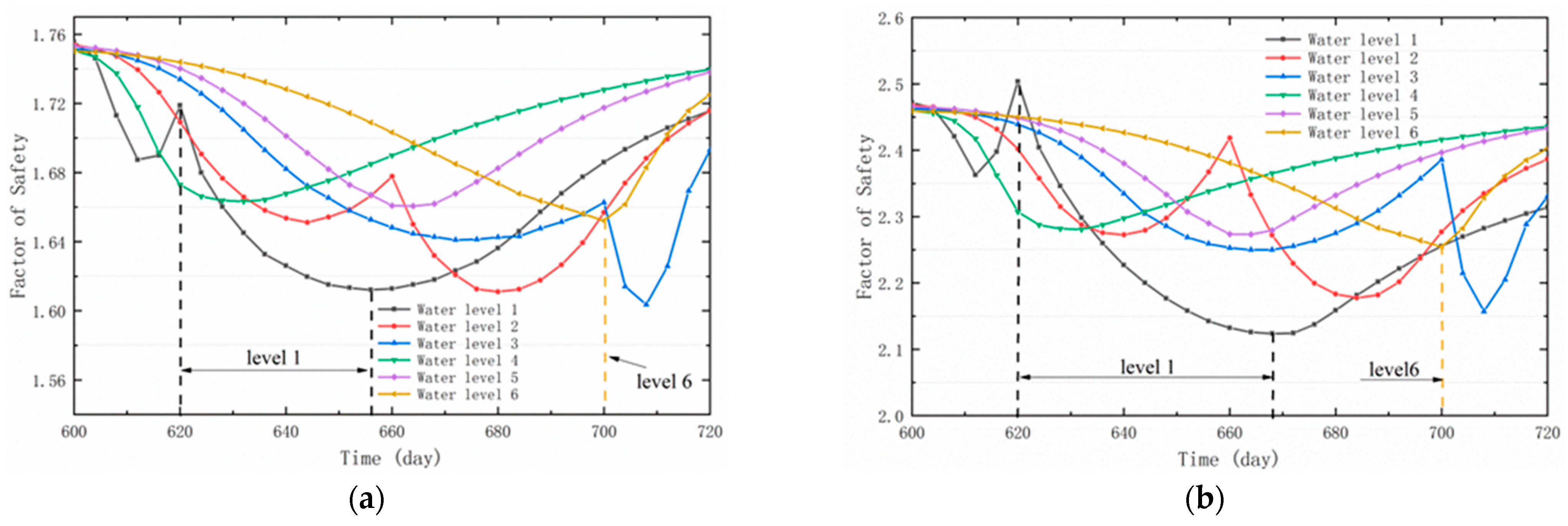
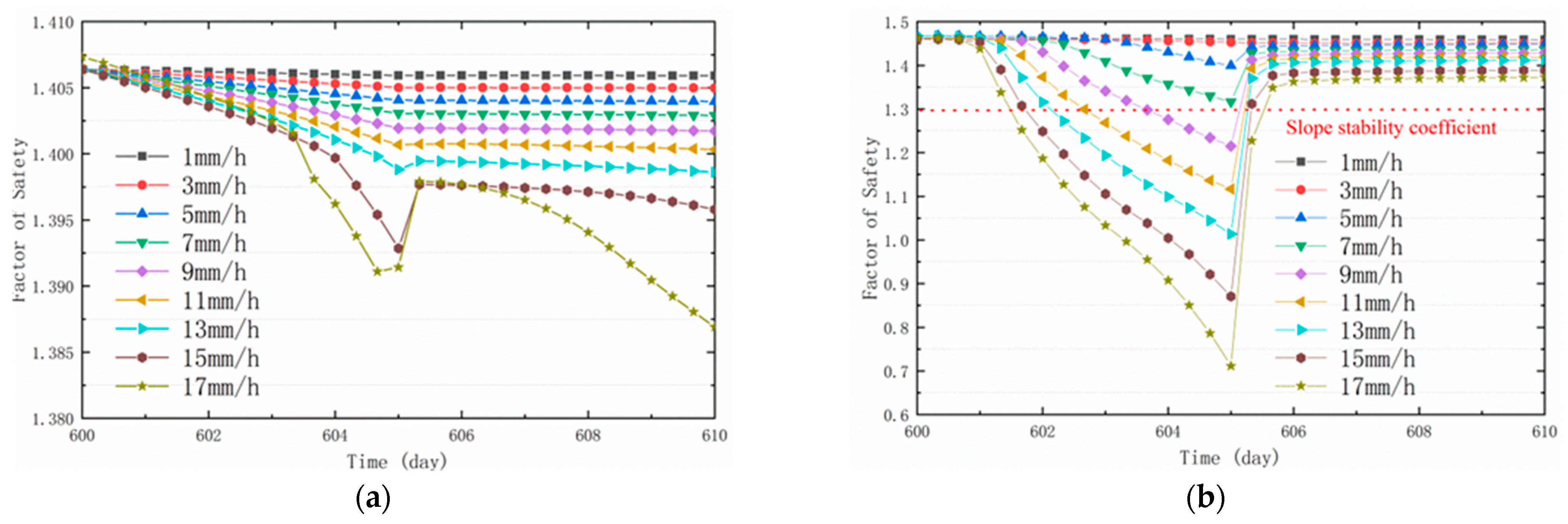
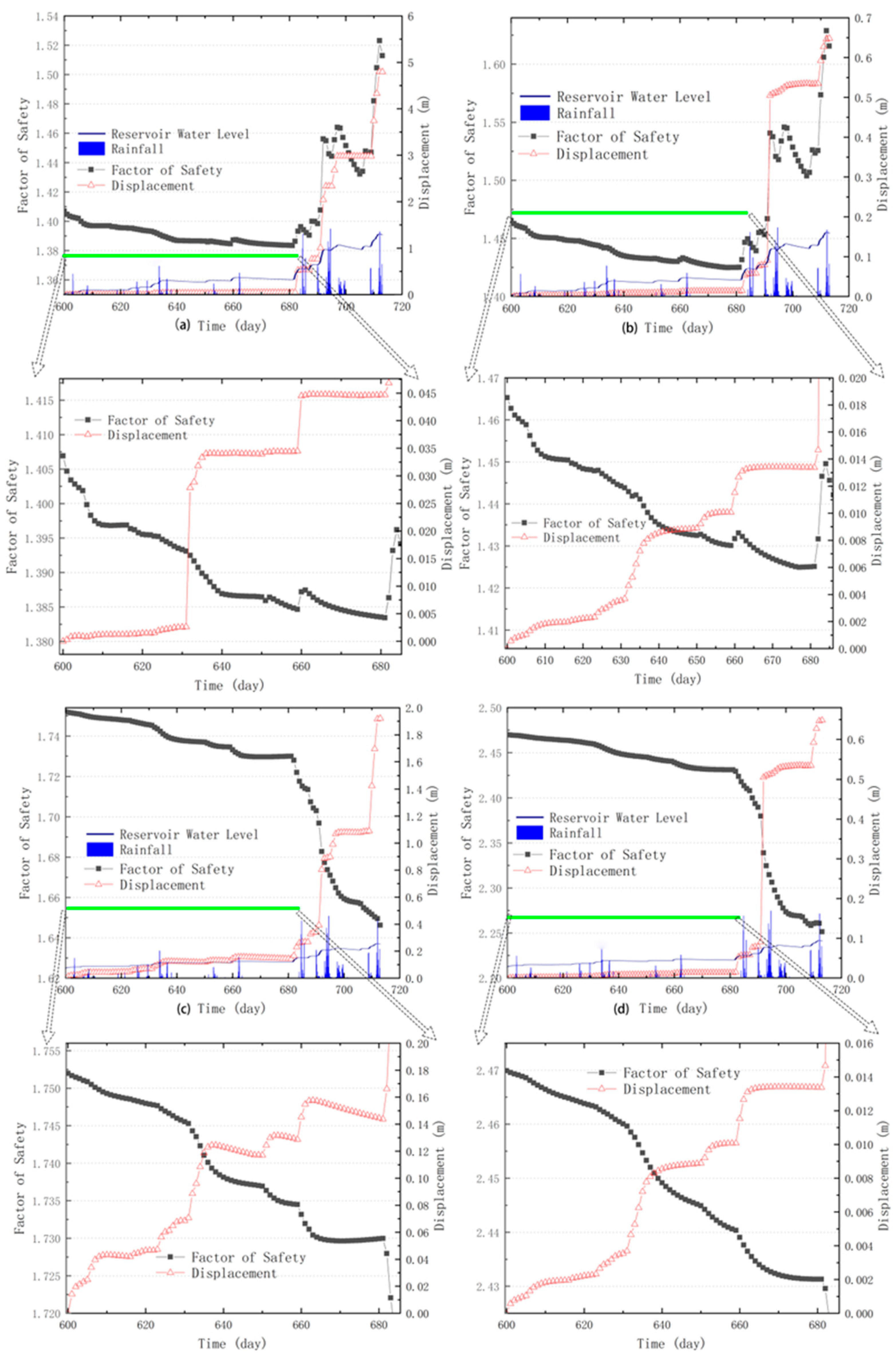
- Under the combined effects of two reservoir water levels and three different rising and falling speeds, the change in the bank slope FS occurs later than the water level change. Such a lag expands as the water level rises faster and higher, and slower water level declines occur. Meanwhile, the PFS of the three water level modes increases when the water level rises faster and higher.
- When there is rainfall, the FS decreases faster with higher rainfall intensity. In addition, the FS increases after the rainfall stops. The initial stability of the bank slope under different conditions was improved after the GSP measures, but the main slope was more sensitive to the changes in rainfall and water level.
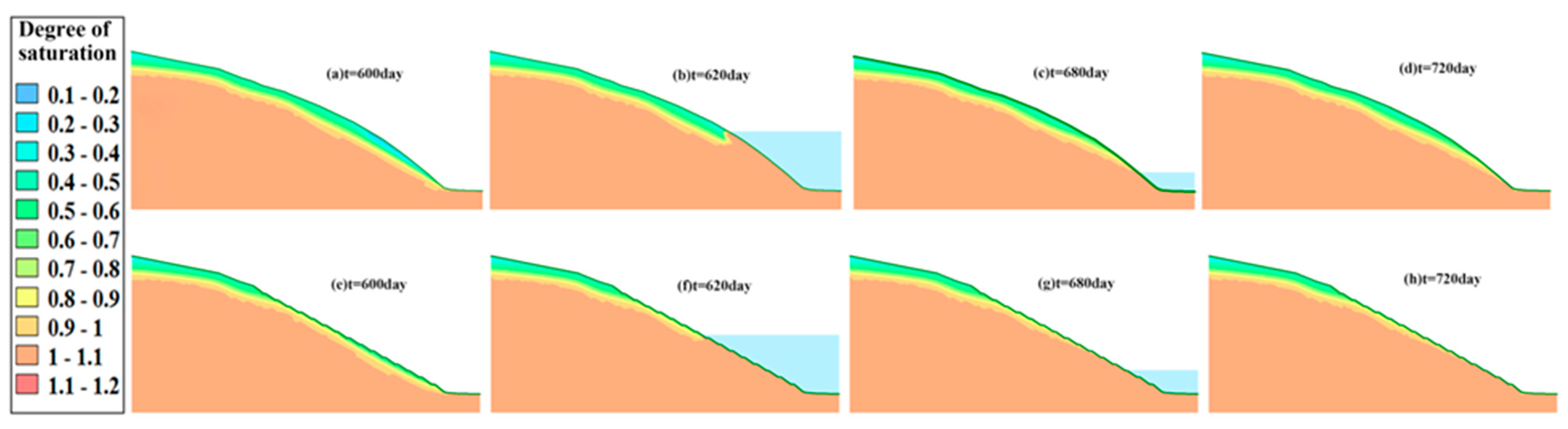
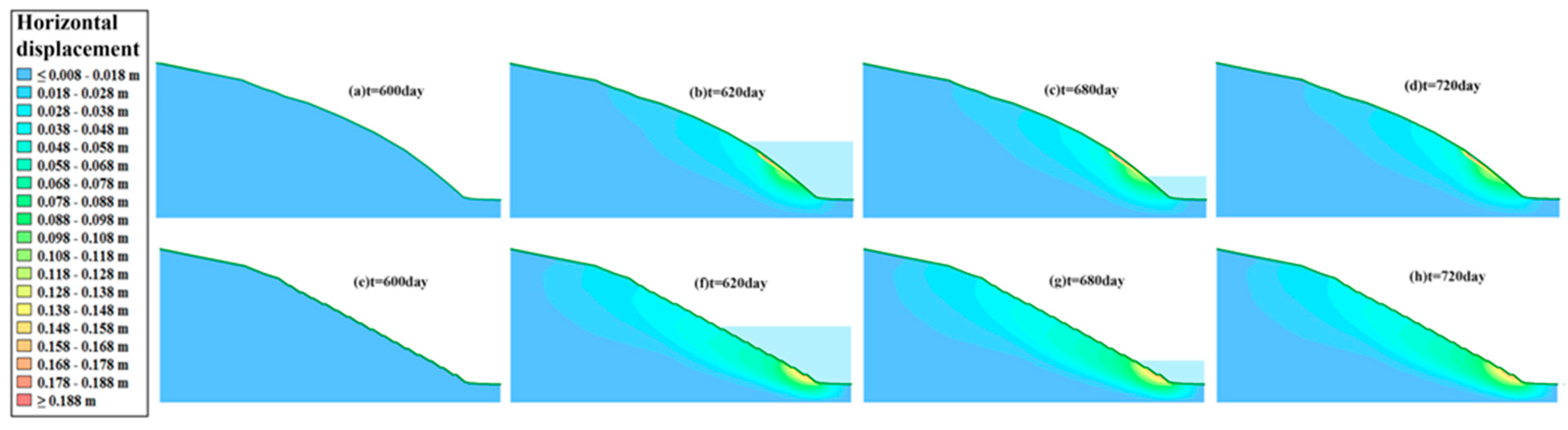
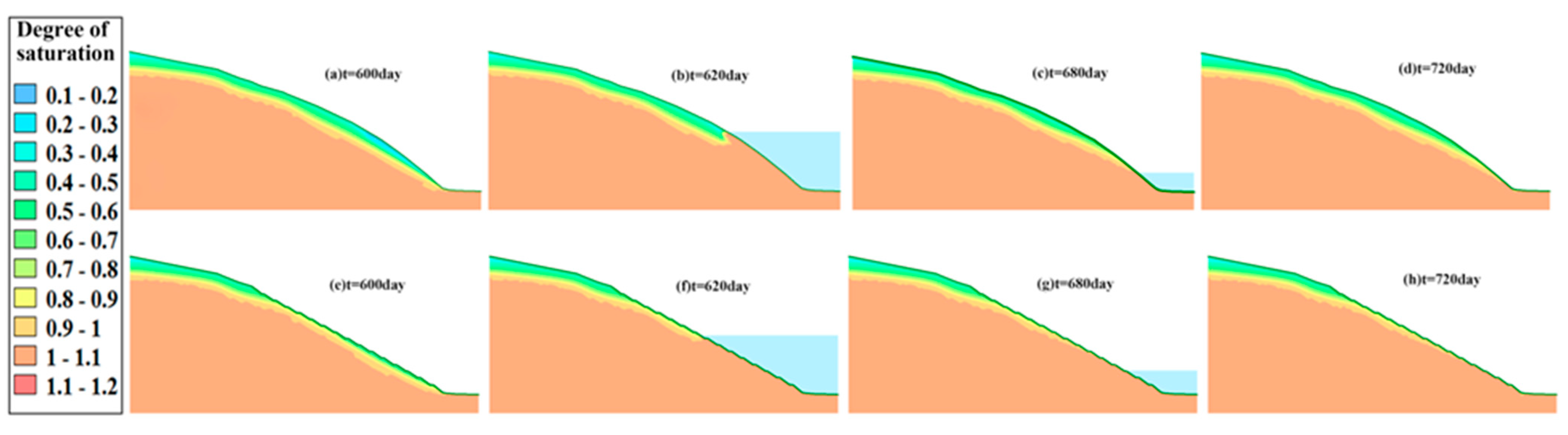
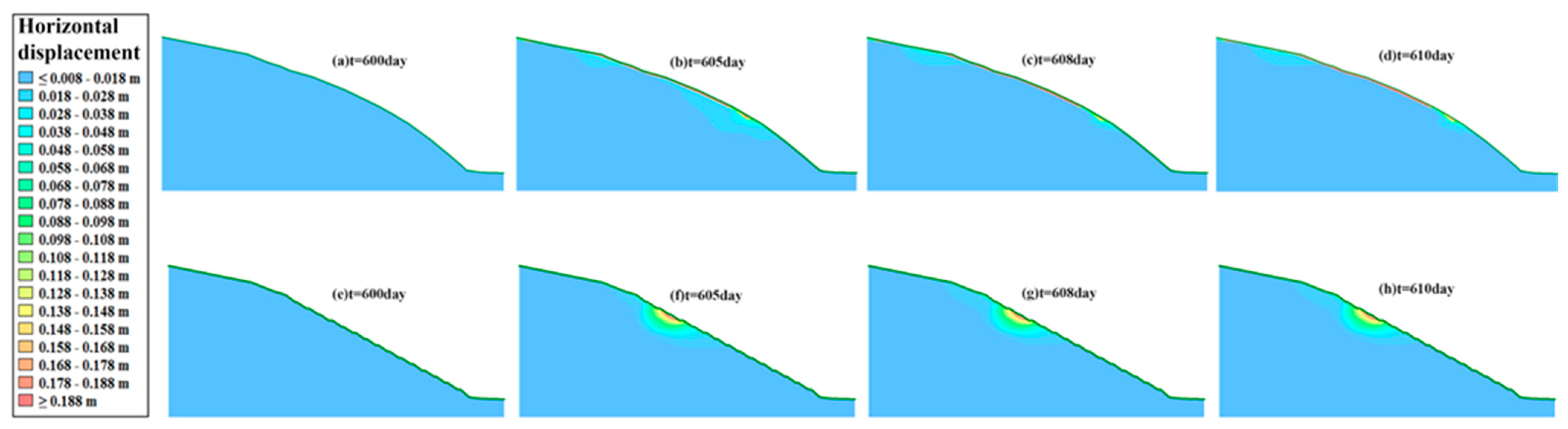
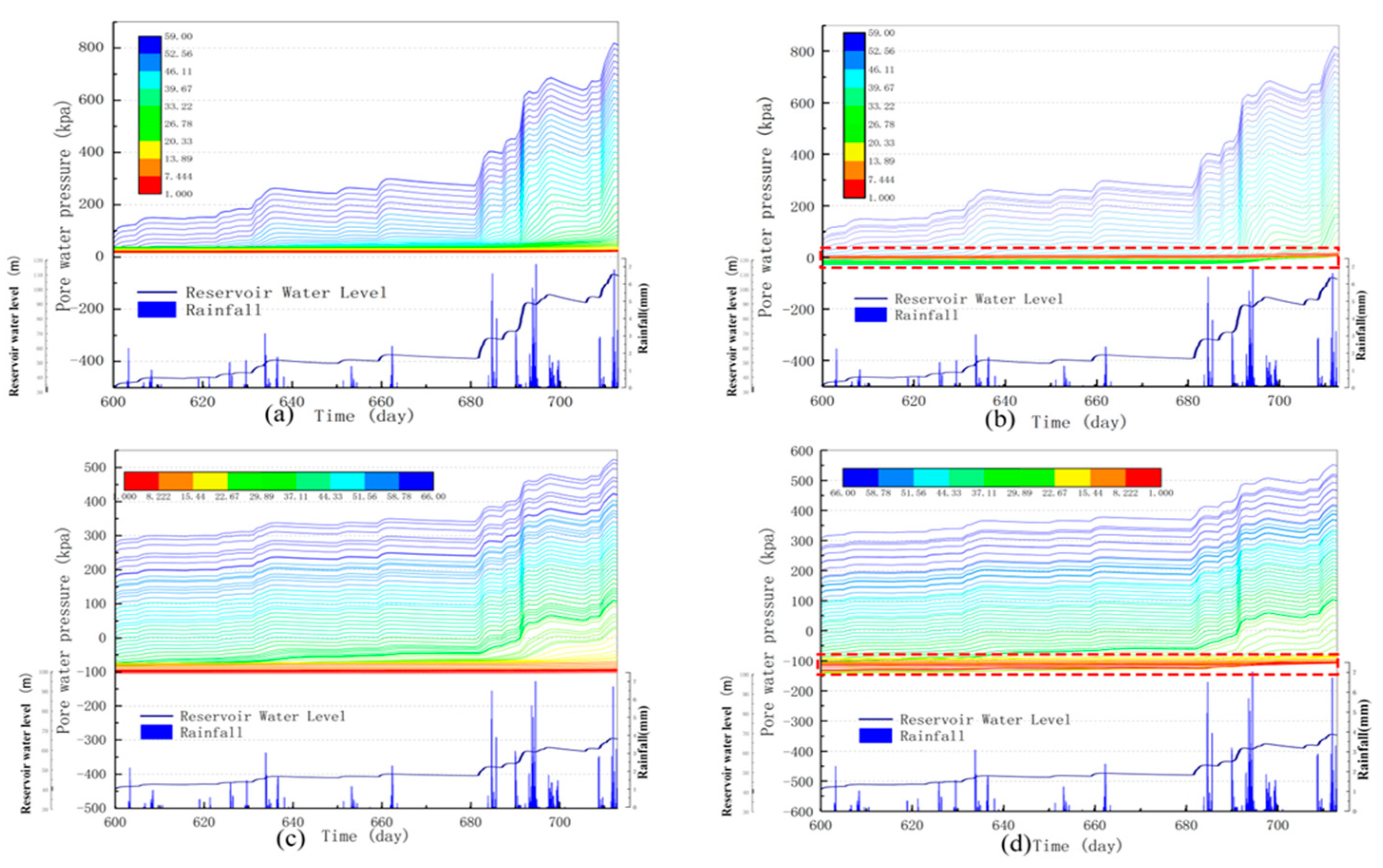
- Under the coupling effects of real rainfall infiltration and reservoir water fluctuation from 1 to 27 July 2019, the PWP changed. The farther the monitoring point from the highest water level, the lower the PWP, and vice versa. The displacement is positively correlated with the rainfall intensity and concentration.
- Simulations for all three conditions indicate that GSP improves the FS of the slopes with no significant improvement to the main slopes but a significant improvement to their total displacement.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fourniadis, I.G.; Liu, J.G.; Mason, P. Regional assessment of landslide impact in the Three Gorges area, China, using ASTER data: Wushan-Zigui. Landslides 2007, 4, 267–278. [Google Scholar] [CrossRef]
- Cojean, R.; Caï, Y. Analysis and Modeling of Slope Stability in the Three-Gorges Dam Reservoir (China)—The Case of Huangtupo Landslide. J. Mt. Sci.-Engl. 2011, 8, 166–175. [Google Scholar] [CrossRef]
- Acharya, K.P.; Bhandary, N.P.; Dahal, R.K.; Yatabe, R. Numerical analysis on influence of principal parameters of topography on hillslope instability in a small catchment. Environ. Earth Sci. 2015, 73, 5643–5656. [Google Scholar] [CrossRef]
- Reid, I.; Parkinson, R.J. The wetting and drying of a grazed and ungrazed clay soil. Eur. J. Soil Sci. 1984, 35, 607–614. [Google Scholar] [CrossRef]
- Take, W.A.; Beddoe, R.A.; Davoodi-Bilesavar, R.; Phillips, R. Effect of antecedent groundwater conditions on the triggering of static liquefaction landslides. Landslides 2015, 12, 469–479. [Google Scholar] [CrossRef]
- Pender, M.J.; Orense, R.P.; Wotherspoon, L.M.; Storie, L.B. Effect of permeability on the cyclic generation and dissipation of pore pressures in saturated gravel layers. Géotechnique 2016, 66, 313–322. [Google Scholar] [CrossRef]
- Wei, Z.; Yin, G.; Wang, J.; Wan, L.; Jin, L. Stability analysis and supporting system design of a high-steep cut soil slope on an ancient landslide during highway construction of Tehran–Chalus. Environ. Earth Sci. 2012, 67, 1651–1662. [Google Scholar] [CrossRef]
- Wen, B.-P.; He, L. Influence of lixiviation by irrigation water on residual shear strength of weathered red mudstone in Northwest China: Implication for its role in landslides’ reactivation. Eng. Geol. 2012, 151, 56–63. [Google Scholar] [CrossRef]
- Chen, J.D.; Ge, X.R.; Song, D.Q.; Cai, J. Deformation and mechanical characteristics of bedding rock slope in tunnel excavation. J. Water Resour. Archit. Eng. 2018, 16, 149–154. (In Chinese) [Google Scholar]
- Ran, T.; Liu, D.A.; Mei, S.H.; Wang, W.; Tan, L. Intelligent feedback analysis on a deep excavation for the gravity anchorage foundation of a super suspension bridge. Chin. J. Rock Mech. Eng. 2019, 38, 2898–2912. (In Chinese) [Google Scholar]
- Singh, J.; Banka, H.; Verma, A. Analysis of slope stability and detection of critical failure surface using gravitational search algorithm. In Proceedings of the 2018 4th International Conference on Recent Advances in Information Technology (RAIT) 2018, Dhanbad, India, 15–17 March 2018; pp. 1–6. [Google Scholar]
- Kang, Z.J.; Tan, Y.; Deng, G.; Bin, W. Impact of Soil Reinforcement in Passive Zone on the Deformation Behaviors of Deep Excavation. J. Yangtze River Sci. Res. Inst. 2017, 34, 119–123. [Google Scholar]
- Zhou, Z.; Wang, X.-Q.; Wei, Y.-F.; Shen, J.-H.; Shen, M. Simulation study of the void space gas effect on slope instability triggered by an earthquake. J. Mt. Sci. 2019, 16, 1300–1317. [Google Scholar] [CrossRef]
- Javdanian, H.; Pradhan, B. Assessment of earthquake-induced slope deformation of earth dams using soft computing techniques. Landslides 2018, 16, 91–103. [Google Scholar] [CrossRef]
- Gomberg, J. Cascadia Onshore-Offshore Site-Response, Submarine Sediment Mobilization, and Earthquake Recurrence. J. Geophys. Res. Solid Earth 2018, 123, 1381–1404. (In Chinese) [Google Scholar] [CrossRef]
- Tang, H.; Hu, X.; Xu, C.; Li, C.; Yong, R.; Wang, L. A novel approach for determining landslide pushing force based on landslide-pile interactions. Eng. Geol. 2014, 182, 15–24. [Google Scholar] [CrossRef]
- VanWoert, N.D.; Rowe, D.B.; Andresen, J.A.; Rugh, C.L.; Fernandez, R.T.; Xiao, L. Green Roof Stormwater Retention: Effects of Roof Surface, Slope, and Media Depth. J. Environ. Qual. 2005, 34, 1036–1044. [Google Scholar] [CrossRef]
- Zhuang, X.; Wang, W.; Ma, Y.; Huang, X.; Lei, T. Spatial distribution of sheet flow velocity along slope under simulated rainfall conditions. Geoderma 2018, 321, 1–7. [Google Scholar] [CrossRef]
- Zhao, L.; Hou, R.; Wu, F.; Keesstra, S. Effect of soil surface roughness on infiltration water, ponding and runoff on tilled soils under rainfall simulation experiments. Soil Tillage Res. 2018, 179, 47–53. [Google Scholar] [CrossRef]
- Fu, X.T. Characteristics of flow pattern and sediment transport processes on loessal soil slope in western Shanxi Province. J. Hydraul. Eng. 2017, 48, 738–747. [Google Scholar]
- Fan, H.M.; Huang, D.H.; Zhou, L.L.; Jin, L. Effects of Seasonal Freeze-thaw Action on Phosphorus Loss of Slope in Black Soil. J. Soil Water Conserv. 2014, 28, 151–152. [Google Scholar]
- Cheng, Y.T.; Li, P.; Xu, G.C.; Li, G.; Zhanbin, W.T. Effect of soil erodibility on nitrogen and phosphorus loss under condition of freeze-thaw. Trans. Chin. Soc. Agric. Eng. 2017, 33, 141–149. [Google Scholar]
- Mandal, A.K.; Li, X.; Shrestha, R. Influence of Water Level Rise on the Bank of Reservoir on Slope Stability: A Case Study of Dagangshan Hydropower Project. Geotech. Geol. Eng. 2019, 37, 5187–5198. [Google Scholar] [CrossRef]
- Sun, G.; Zheng, H.; Tang, H.; Dai, F. Huangtupo landslide stability under water level fluctuations of the Three Gorges reservoir. Landslides 2015, 13, 1167–1179. [Google Scholar] [CrossRef]
- Wei, J.; Deng, J.; Tham, L.; Lee, C.F. Unsaturated seepage analysis for a reservoir landslide during impounding. In Landslides and Engineered Slopes. From the Past to the Future; CRC Press: Boca Raton, FL, USA, 2008; pp. 999–1004. [Google Scholar]
- Xiong, Y.; Bao, X.; Ye, B.; Zhang, F. Soil–water–air fully coupling finite element analysis of slope failure in unsaturated ground. Soils Found. 2014, 54, 377–395. [Google Scholar] [CrossRef]
- Kitamura, R.; Sako, K. Contribution of “Soils and Foundations” to Studies on Rainfall-Induced Slope Failure. Soils Found. 2010, 50, 955–964. [Google Scholar] [CrossRef]
- Lu, N.; Godt, J. Infinite Slope Stability under Steady Unsaturated Seepage Conditions. Water Resour. Res. 2008, 44, 63–75. [Google Scholar] [CrossRef]
- GEO-SLOPE International Ltd. Seepage Modeling with SEEP/W 2007; GEO-SLOPE International Ltd.: Calgary, AB, Canada, 2010; pp. 1–207. [Google Scholar]
- Genuchten, V.M. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Cen, W.J.; Wang, M.; Yang, Z.X. Partial saturated seepage properties of(composite) geomembrane earthrock dams. Adv. Sci. Technol. Water Resour. 2012, 32, 6–9. (In Chinese) [Google Scholar]
- Chen, Y.-F.; Yu, H.; Ma, H.-Z.; Li, X.; Hu, R.; Yang, Z. Inverse modeling of saturated-unsaturated flow in site-scale fractured rocks using the continuum approach: A case study at Baihetan dam site, Southwest China. J. Hydrol. 2020, 584, 124693. [Google Scholar] [CrossRef]
- Wu, Y.; Miao, F.; Li, L.; Xie, Y.; Chang, B. Time-varying reliability analysis of Huangtupo Riverside No.2 Landslide in the Three Gorges Reservoir based on water-soil coupling. Eng. Geol. 2017, 226, 267–276. [Google Scholar] [CrossRef]
- Jiao, Y.-Y.; Zhang, H.-Q.; Tang, H.-M.; Zhang, X.-L.; Adoko, A.C.; Tian, H.-N. Simulating the process of reservoir-impoundment-induced landslide using the extended DDA method. Eng. Geol. 2014, 182, 37–48. [Google Scholar] [CrossRef]
- Zhang, D.; Jian, W.B.; Ye, Q.; Lin, W. A time-varying analytic model of tailings slope and its application. Yantu Lixue/Rock Soil Mech. 2014, 35, 835–840. [Google Scholar] [CrossRef]


| Materials | Elastic Modulus (MPa) | Poisson Ratio | Unit Weight (kN/m3) | Cohesion (kPa) | Friction Angle (°) |
|---|---|---|---|---|---|
| Gravel soil | 261.6 | 0.4 | 20.5 | 15 | 32 |
| Strongly weathered carbonaceous slate | 2644.9 | 0.38 | 22.4 | 93.6 | 33.3 |
| Moderately weathered carbonaceous slate | 5561 | 0.35 | 26.5 | 120 | 35 |
| Silty clay soil | 179.8 | 0.42 | 18.5 | 35 | 15 |
| Breccia | 222.7 | 0.42 | 20 | 15 | 30 |
| Materials | SWCC Parameters | Hydraulic Conduction Coefficient | ||||
|---|---|---|---|---|---|---|
| a/kPa | m | n | θs | θr | kx (m/s) | |
| Gravel soil | 100 | 0.5 | 2 | 0.346 | 0.005 | 3.14 × 10−3 |
| Strongly weathered carbonaceous slate | 10 | 0.31 | 1.45 | 0.242 | 0.001 | 8.08 × 10−5 |
| Moderately weathered carbonaceous slate | 10 | 0.31 | 1.45 | 0.021 | 0.001 | 2.47 × 10−6 |
| Silty clay soil | 100 | 0.145 | 1.17 | 0.476 | 0.001 | 6.51 × 10−6 |
| Breccia | 100 | 0.5 | 2 | 0.39 | 0.005 | 1.28 × 10−2 |
| HDPE geomembrane | 1 × 10−15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Y.; Yan, F.; Wu, L.; Lu, G.; Liu, T. Numerical Analyses of Slope Stability Considering Grading and Seepage Prevention. Water 2023, 15, 1745. https://doi.org/10.3390/w15091745
Feng Y, Yan F, Wu L, Lu G, Liu T. Numerical Analyses of Slope Stability Considering Grading and Seepage Prevention. Water. 2023; 15(9):1745. https://doi.org/10.3390/w15091745
Chicago/Turabian StyleFeng, Yuting, Fuyu Yan, Lianrong Wu, Guangyin Lu, and Taoying Liu. 2023. "Numerical Analyses of Slope Stability Considering Grading and Seepage Prevention" Water 15, no. 9: 1745. https://doi.org/10.3390/w15091745
APA StyleFeng, Y., Yan, F., Wu, L., Lu, G., & Liu, T. (2023). Numerical Analyses of Slope Stability Considering Grading and Seepage Prevention. Water, 15(9), 1745. https://doi.org/10.3390/w15091745





