Improvement Design of a Two-Stage Double-Suction Centrifugal Pump for Wide-Range Efficiency Enhancement

Abstract

Two-stage double-suction centrifugal pumps have both a large flow and high head. However, due to the complexity of their flow passage components, efficiency has always been a major problem, and the corresponding head is also prone to insufficiency. In this study, an improved design for a two-stage double-suction centrifugal pump unit with a specific speed of 25.9 was developed with the help of a computer. The computational fluid dynamics (CFD) method was used to evaluate the performance and loss of the unit in the process of improvement. The unit’s inlet division section, two semi-spiral suction chambers, two impellers for the first stage, two inter-stage channels, a double-suction impeller for the second stage, and the volute were able to be improved. Through a total of 39 improvements, the efficiency under multiple working conditions was comprehensively improved, and the head had a reasonable margin in meeting the requirements. After the improvements, the flow pattern in the inter-stage channel and volume were significantly improved through the check of the streamline. This research successfully improved the performance of a two-stage double-suction centrifugal pump unit, and it has significant engineering value.

1. Introduction

Large-scale water transfer is crucial for industrial and agricultural areas. China is building a national water network. This is a comprehensive engineering system based on natural rivers and lakes, with diversion and drainage projects as channels, regulation and storage projects as nodes, and intelligent regulation as means. It integrates functions such as optimized allocation of water resources, flood control and disaster reduction in river basins, and protection of water ecosystems. In this system, a power system is required to drive the flow and circulation of water, which cannot be separated from the key equipment of water pumps. For the application of high head and large flow, the double-suction centrifugal pump has become one of the main pump types [1,2]. The most obvious advantage of the double-suction centrifugal pump is its low axial force, which is related to the symmetrical arrangement of the unit and the form of inflow on both sides. However, in order to meet the requirements of inflow on two sides, it is necessary to configure the semi-spiral suction chamber and volute as diffusers [3]. When the head is further increased, two-stage or multi-stage double-suction centrifugal pumps can also be designed, which are connected by inter-stage flow channels to meet the demand [4]. The complex flow passage components have an impact on the efficiency, stability, and reliability of double-suction centrifugal pumps. If the design is poor, energy loss may increase and the efficiency may drop, and problems such as the increase in the pressure pulsation may weaken the stability of the unit [5,6,7].

Many researchers have focused on double-suction centrifugal pumps. The main research objects include the internal flow, hydraulic characteristics, flow field pulsation, structural component stress and dynamic response, vibration, and other issues of the double-suction centrifugal pump units. An et al. simulated the flow details in a double-suction centrifugal pump [8]. The internal flow in impellers, such as the flow separation, pressure loss, flow unsteadiness, and performance, were investigated to evaluate the operation of the pump unit. Peng et al. conducted research on unsteady flow in multi-stage double-suction centrifugal pumps based on the DES method, laying the foundation for the optimization of multi-stage double-suction centrifugal pumps [9]. Škerlavaj et al. aimed to maximize hydraulic efficiency and optimized the double-suction pump using the modeFRONTIER optimization platform, obtaining the five design variables that have the most significant impact on the hydraulic efficiency of the double-suction pump [10]. Wang et al. addressed the issue of traditional impeller design methods often leading to design results that do not meet the operational needs under non-design conditions. They optimized the hub and shroud inlet angles of the double-suction centrifugal pump impeller, and the optimized model significantly improved the cavitation performance of the double-suction centrifugal pump at non-design points [11,12]. Zhang et al. optimized a double-suction centrifugal pump using a simulation-kriging model-experiment method [13]. The Pareto solution was used for a balanced optimal scheme. Tao et al. optimized the double-suction centrifugal pump by using multi-objective optimization with a genetic algorithm [14]. The performance of the unit was comprehensively improved. Wang et al. optimized the double-suction centrifugal pump by using the efficiency-house optimization method [15]. The operation range of the pump unit was widened. Zhao et al. selected nine main design parameters of the impeller and double volute as design variables, based on artificial neural networks, for energy-saving optimization design of the impeller and volute of a multi-stage double-suction centrifugal pump [16]. Overall, the performance improvement design of water pumps can utilize optimization algorithms. However, this series of methods needs to be established on the basis of parameterization. Only with good parameterization can the algorithm be successfully applied. For some pumps with special structural forms, their inlet and outlet flow channels are not standard geometric shapes but rather complex curved shapes. Thus, parameterization is not easy accomplished. At this point, there may be situations where there are too many parameters or inaccurate geometric descriptions, making it impossible to combine optimization algorithms with pump performance improvement. Improvement work needs to be carried out based on an understanding of the flow inside the pump to meet the needs of engineering projects.

In summary, many researchers have conducted in-depth studies on the internal flow state and optimization of single-stage double-suction centrifugal pumps, but there has been relatively little research on bipolar double-suction pumps. Compared to single-stage double-suction centrifugal pumps, the internal flow of bipolar double-suction centrifugal pumps is more complex due to the increase in flow channel components. The coordination and unity of various components have a more prominent impact on the performance of bipolar double-suction pumps, and the optimization of bipolar double-suction pumps faces significant challenges. A two-stage double-suction centrifugal pump was considered in this study. It had insufficient efficiency, requiring improvement. Computational fluid dynamics (CFD) were used as the evaluator of performance. The maximum efficiency, high efficiency range, and head of different operation conditions were considered. The improved solution met the requirements of design. Through the research in this article, we can gain a deeper understanding of the design of pumps with special flow channel shapes.

2. Research Objective

The research object was a two-stage double-suction centrifugal pump. The design flow rate Q_d was 0.83 m³/s, the design head H_d was 143.4 m, the rotational speed n_d was 990 r/min, and the fluid medium was 25 °C liquid water. The specific speed n_q of the double-suction centrifugal pump was calculated according to the following formula for comparison between similar pump designs [17]:

$$n_q=\frac{n\sqrt{Q_d/c_q}}{{\left(H_d/c_h\right)}^{3/4}}$$

(1)

where c_q and c_h are the special coefficient of flow rate and head. For the double-suction pump, c_q is 2. For the two-stage pump, c_h is 2. In this case, the value of n_q is 25.9.

As shown in Figure 1, the flow passage of the two-stage double-suction centrifugal pump was complex. It consisted of an inlet division section, two semi-spiral suction chambers, two impellers for the first stage, two inter-stage channels, a double-suction impeller for the second stage, and a volute. The blade number of the first and second impellers was 5. The outlet diameter D out of the first and second impellers was 749 mm.

3. Setup of Improvement Design

3.1. Design Target

The two-stage double-suction centrifugal pump was operated under complex conditions. The actual case required head and efficiency for five flow rate points, as listed in

Table 1. Design target.

Relative Flow Rate Point	Flow Rate (m3/s)	Head Requirement (m)	Efficiency Requirement (%)
0.30	0.250	171.0	-
0.65	0.537	158.1	80.0
0.86	0.715	143.4	84.5
1.00	0.830	132.7	82.5
1.15	0.953	113.6	81.0

. Overall, the design requirements of this pump cover a wide range. There are clear requirements for the head (i.e., pressurizing performance) and efficiency over a large flow range. For bladed pumps, a specific blade design scheme cannot easily balance different operating conditions. There are significant difficulties in improving the design. Therefore, this pump unit needed a comprehensive design. The formula for calculating the head and efficiency of the water pump was as follows:

$$H=\frac{P_{\mathrm{out}}-P_{in}}{\rho g}$$

(2)

$$\eta =\frac{\rho gQH}{M\cdot \omega }$$

(3)

where P_out and P_in represent the total pressure at the pump outlet and the pump inlet, respectively, including the sum of static and dynamic pressures; M is the torque of the impeller around the axis of rotation of the impeller; and ω is the rotational speed of the impeller.

3.2. CFD Setup

To evaluate the performance of the pump, computational fluid dynamics (CFD) were used. The fluid medium studied was 25 °C water, and the reference pressure was 1 Atm. The SST k-ω model [18,19,20] was chosen for the turbulence model. It is a zonal-hybrid model of a standard k-ε model and Wilcox k-ω model. The near-wall region can be solved directly in k-ω mode if the near-wall mesh is refined properly. The strong shear flow can be well solved. Otherwise, the wall function can be used for coarse mesh cases with a reasonable result. In the main flow region in pump with large adverse pressure gradient, the k-ε mode is activated for a better solution. The k and ω equations of SST k-ω model are written as:

$$\frac{\partial (\rho k)}{\partial t}+\frac{\partial \left(\rho u_{i}k\right)}{\partial x_i}=P-\frac{\rho k^{3/2}}{l_{k-\omega }}+\frac{\partial }{\partial x_i}\left[\left(\mu +{\sigma }_k{\mu }_i\right)\frac{\partial k}{\partial x_i}\right]$$

(4)

$$\frac{\partial (\rho \omega )}{\partial t}+\frac{\partial \left(\rho u_i\omega \right)}{\partial x_i}=C_{\omega }P-\beta \rho {\omega }^2+\frac{\partial }{\partial x_i}\left[\left(\mu +{\sigma }_{\alpha }{\mu }_i\right)\frac{\partial \omega }{\partial x_i}\right]+2\left(1-F_1\right)\frac{\rho {\sigma }_{\omega 2}}{\omega }\frac{\partial k}{\partial x_i}\frac{\partial \omega }{\partial x_i}$$

(5)

where x is the coordinate, t is time, u is velocity, and μ is viscosity. P is the production term in the k and ω equations, and F₁ is the blending function. σ_k and σ_ω are constants of the turbulence model. l_k-ω is the parameter for evaluating the turbulence scale, which can be written as l_k-ω = k^1/2β_kω, and β_k is also the model constant.

In the setup of the numerical simulation, the inlet of the division section of the double-suction centrifugal pump was set as the total pressure type inlet boundary condition, and the total inlet pressure was set to 121,131 Pa. The velocity condition at inlet boundary is the zero-gradient type. The volute outlet was set as the flow rate (velocity) type outlet boundary condition to control the flow rate, and the velocity magnitude was determined by the flow in the corresponding operating condition. The pressure condition at the outlet boundary is the zero-gradient type. All the wall boundaries in the computational domain were set as no-slip wall boundaries. The multiple reference frame (MRF) model was used, with the impellers as a rotating reference system and the speed set to 990 r/min, and the other components were stationary. Given the intersection interface between different components, data transfer based on the General Grid Interface (GGI) model was set to transfer data among domains.

In the steady simulation process, the minimum number of iteration steps was set to 300 and the maximum to 1000. The convergence criterion of the momentum energy and continuity equations was less than 0.00001. This is to ensure a good solution with high accuracy and stable results. The steady simulation was used in the performance evaluation in the improvement process. Transient simulation was used to check the initial and final solution for a more accurate result. The flow analysis of the initial and final solutions in this article was based on the results of a specific moment in unsteady simulations. A total of 360 steps were given for each impeller revolution. The convergence criterion was 0.00001.

In this study, tetrahedral unstructured mesh elements were adopted, which were easier to generate automatically and met the requirements for improved design. The different grid parts were verified for independence based on the residual of the calculated head at the design point. As shown in Figure 2, when the number of mesh nodes reached about 3.2 million or more, the residual value was less than 1%. Therefore, considering the calculation cost and accuracy comprehensively, this mesh was finally selected for the improvement design and performance evaluation.

Table 2. Mesh details of the components and the entire pump unit.

Component	Inlet Division Section	Semi-Spiral Suction Chambers	First-Stage Impellers	Inter-Stage Channels	Second-Stage Impeller	Volute	Total
Mesh Node Number	227,143	1,061,812	279,590	794,134	317,946	558,224	3,238,849

lists the details of the mesh node number of these components and the entire pump unit.

3.3. Performance Evaluation

Based on the suggestions of the handbook, the initial solution was designed. By using the CFD setup above, the performance was evaluated as shown in Figure 3, including the head H and efficiency η changing with flow rate Q. Head H represents the pressurizing ability of the pump from inlet to outlet, which is completely required in actual cases. Efficiency η with higher value means the same working target with less energy consumption. This is important for green and low carbon-emission operation. As shown, both the head and efficiency failed to meet the target. Especially at the position that deviated from the design point, the efficiency decreased significantly. Similarly, the head was also lower than the target value under the deviating condition, which meant that the pump was unable to work. The improvement is required to solve the problems and insufficiencies.

To determine the cause of insufficient head and efficiency, the hydraulic loss between the inlet and outlet of different components was statistically analyzed under three off-design conditions, as shown in Figure 4 (the loss was analyzed by using the proportion of total head). It can be seen that the inlet division section and semi-spiral section chambers had little loss and should not be the focus for improving the design. The inter-stage channels and volume had greater losses (more than 14%), which should be reduced by improving the design. By analyzing the efficiency of the first- and second-stage impellers, we found that the efficiencies of the two stages were 86.7% and 86.1%, respectively, at Q = 0.572 m³/s, which were not at a high level. At Q = 0.715 m³/s, the efficiencies of the two stages were 92.5% and 91.3%, which were also not high enough. Therefore, this two-stage double-suction centrifugal pump still has significant margin for improvement. Figure 4 also provides the proportion of first and second stage of impellers in terms of capacity. This represents the pressurization performance of the two-stage impeller under different flow rate conditions. At small flow rate, the second-stage impeller has higher capacity. At middle flow rate, the two stages are equal. At large flow rate, the first-stage impeller has higher capacity. This provides assistance for optimizing and improving the matching of flow channels.

4. Improvement History

The process of improving the pump design was mainly carried out through the judgment of CFD on the flow and pump performance and constantly modifying the design scheme. In the process of improvement, the design was continuously modified and its performance continuously improved, and a temporary scheme was obtained. We analyzed the flow pattern (streamlines) for the temporary scheme to determine whether the distribution rule of the flow regime was reasonable, and then determined the final design scheme. The determination of the final scheme needs to meet the condition that after intensive modifications and scheme attempts, the performance improvement is no longer significant, and there is no significant decrease in performance at specific operating points. The flow chart is shown in Figure 5.

According to this flow chart, the performance of the pump was continuously improved until 39 improvements had been achieved. Efficiency increased with fluctuations. The most obvious phenomenon was that when the efficiency of the large flow rate increased, the efficiency of the small flow rate decreased. There are contradictions between the two, which is also the difficulty in the design. The improvement design work continued, taking into account various working conditions, and continued to find good compromise solutions. At the same time, as the efficiency increased, the head became stable, meeting the requirements without exceeding them, to avoid unnecessary power increases. Figure 6 shows the performance changes of three typical operating points during the improvement process.

5. Comparative Analysis

5.1. Geometry Comparison

Figure 7 shows the geometry of the final solution of this two-stage double-suction centrifugal pump, with a comparison between it and the initial solution. Figure 8 shows the details of the changed components. The inlet division section was changed, adding a plate at the center. The semi-spiral suction chambers were not modified. The size of the volute was made smaller, and the cross-sections became circular instead of rounded rectangles. Notable changes were made to the shape of the inter-stage channels. The blade shape of the first- and second-stage impellers was also changed, without modification of the meridional view. The blade number of the first and second impellers was increased to seven. In addition, in the final solution, the blades of the first- and second-stage impellers had different hydraulic designs. This is to provide different solutions for adapting the different upstream and downstream diffusers. The incoming flow and outflow should have a good adaptation and conditions.

5.2. Performance Comparison

Figure 9 shows the comparison of the initial solution and final solution in terms of performance. The efficiency η was comprehensively improved in the final solution. Especially under the working conditions deviating from the design point, the efficiency improvement was obvious, which meant the expansion of the high efficiency range. In terms of head H, the value of all points was improved by a margin higher than the required value to meet the actual requirements. Figure 10 shows the hydraulic loss of the final solution (loss was analyzed by using the proportion of total head). Compared with the initial solution (see Figure 4), hydraulic loss was significantly reduced, especially in the volute and inter-stage channel (from more than 14% to less than 6%). This is why the efficiency and head were improved in the final solution. Figure 10 also compares the proportion of first and second-stage of impellers in terms of capacity. At small flow rate, the second-stage impeller has higher capacity. At middle flow rate and large flow rate, the first-stage impeller has higher capacity. This is consistent with the law before the improvement, but it does not mean it is unreasonable but rather provides good performance.

5.3. Flow Pattern Comparison

Figure 11 and Figure 12 compare and analyze the flow in the pump before the improvement and after the improvement, mainly considering two points far away from the design point, with a low initial efficiency and an insufficient head. Therefore, flow rates of Q = 0.572 and 0.953 m³/s were both considered. The streamlines are used as the main comparative object to reflect the distribution of vortexes, secondary flow, and the quality of flow patterns, helping to reveal the reasons for performance differences. The streamline is colored with the magnitude of velocity, reflecting the magnitude of local flow velocity and also representing the uniformity of flow to a certain extent.

For the initial solution, the flow in the inlet section and suction chamber was smooth. This is why the local loss was very low. However, complex flow patterns, such as vortexes and secondary flow, can be seen in the inter-stage channel. This caused high hydraulic loss and reduced the efficiency and head. In the volute, a large-scale vortex was observed when the section area was suddenly exaggerated. Comparing a large flow rate and small flow rate, the non-uniformity of the velocity distribution under a small flow was stronger. Especially at the outlet of the impeller, the relative velocity was high at Q = 0.572 m³/s.

For the final solution, the flow in the inlet section and suction chamber was still smooth. After improvement, the flow pattern in the inter-stage channel was strongly optimized, without obvious vortexes or secondary flow. In the volute, a large-scale vortex still existed in the diffusion section at Q = 0.572 m³/s. However, compared with the initial solution, the flow pattern in the volute was greatly improved at Q = 0.953 m³/s. The large-scale vortex was eliminated. The non-uniformity of the relative velocity became weaker. Flow near the first and second impeller outlets became much more uniform. This is why the efficiency became much higher and the high-efficiency range became wider after improvement. The head of the pump rose when the loss became lower. The overall operating efficiency and stability of the pump were positively improved.

6. Experimental–Numerical Verification

After improvement, the prototype pump was tested using an experiment based on a closed hydraulic machinery test rig, as shown in Figure 13a. In the experiment, the flow rate Q was measured by an electro-magnetic flow meter. The accuracy of the flow meter is 0.18%. The pump head H was calculated by H = ρg·Δp, where ρ is the density, g is the acceleration of gravity, and Δp is the pressure difference between the pump inlet and outlet. The pressure difference was measured by pressure sensors at the inlet and volute outlet with the accuracy of 0.05%. Shaft power P was measured by a power meter which had the rotational angular speed ω and shaft torque M and was calculated by P = Mω. The accuracy of the power meter for both rotational angular speed and torque was 1%. The efficiency of pump η was calculated by η = ρgQH/P. The measurement and calculation methods for the above parameters were consistent with the methods for CFD in Equations (2) and (3). Figure 13b shows the data comparison of the experimental and numerical results. As shown in the figure, the flow rate head curve still shows a monotonic decreasing trend. The flow rate efficiency curve first increases and then decreases, with an obvious range of high efficiency areas with higher energy conversion ability. The two sets of data showed good matching and captured the trend of head and efficiency changing with flow, which also verified the success of the improvement.

7. Conclusions

This study was based on computational fluid dynamics to improve the design of a two-stage double-suction centrifugal pump, meeting the design requirements by improving the efficient range of the unit and reducing the head loss. Conclusions were able to be drawn as follows:

(1)

The process of improving a pump design is mainly through the judgment of CFD on flow and pump performance and through constantly modifying the design scheme. In this study, a total of 39 improvements were made to the two-stage double-suction centrifugal pump. The efficiency of the pump increased with fluctuations in the 39 improvements, until the performance of the pump finally met the design requirements. This proved that the improvement was feasible.

(2)

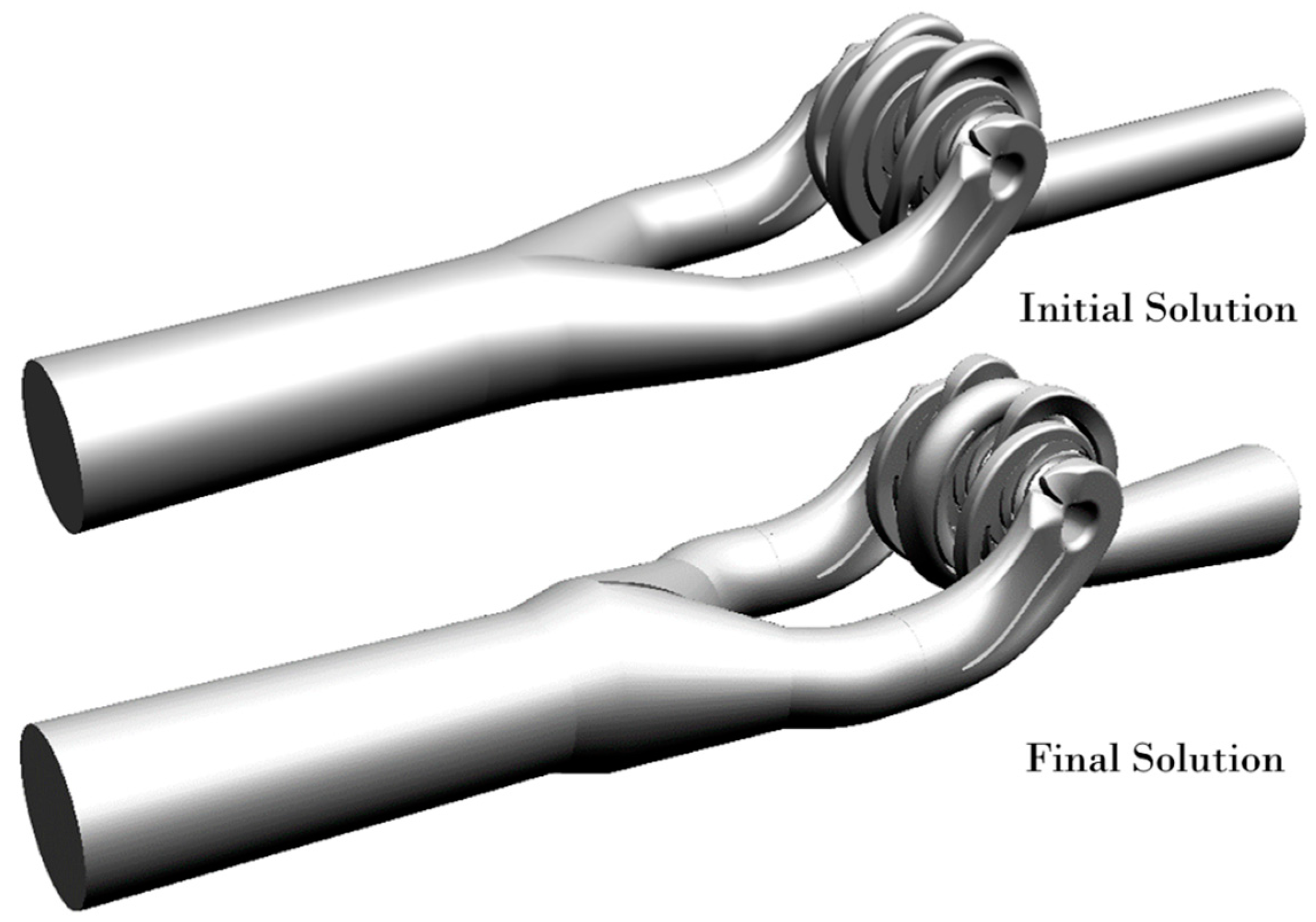
By comparing the geometry, performance, and flow pattern of the original scheme and the final scheme of the two-stage double-suction centrifugal pump, the geometry of the final scheme was shown to be more suitable for the operating conditions, the internal flow was more stable, and the performance was significantly improved. After improvement, the pump head was increased by 10~15 m, and the efficiency was increased by 4~9% within the operation range.

(3)

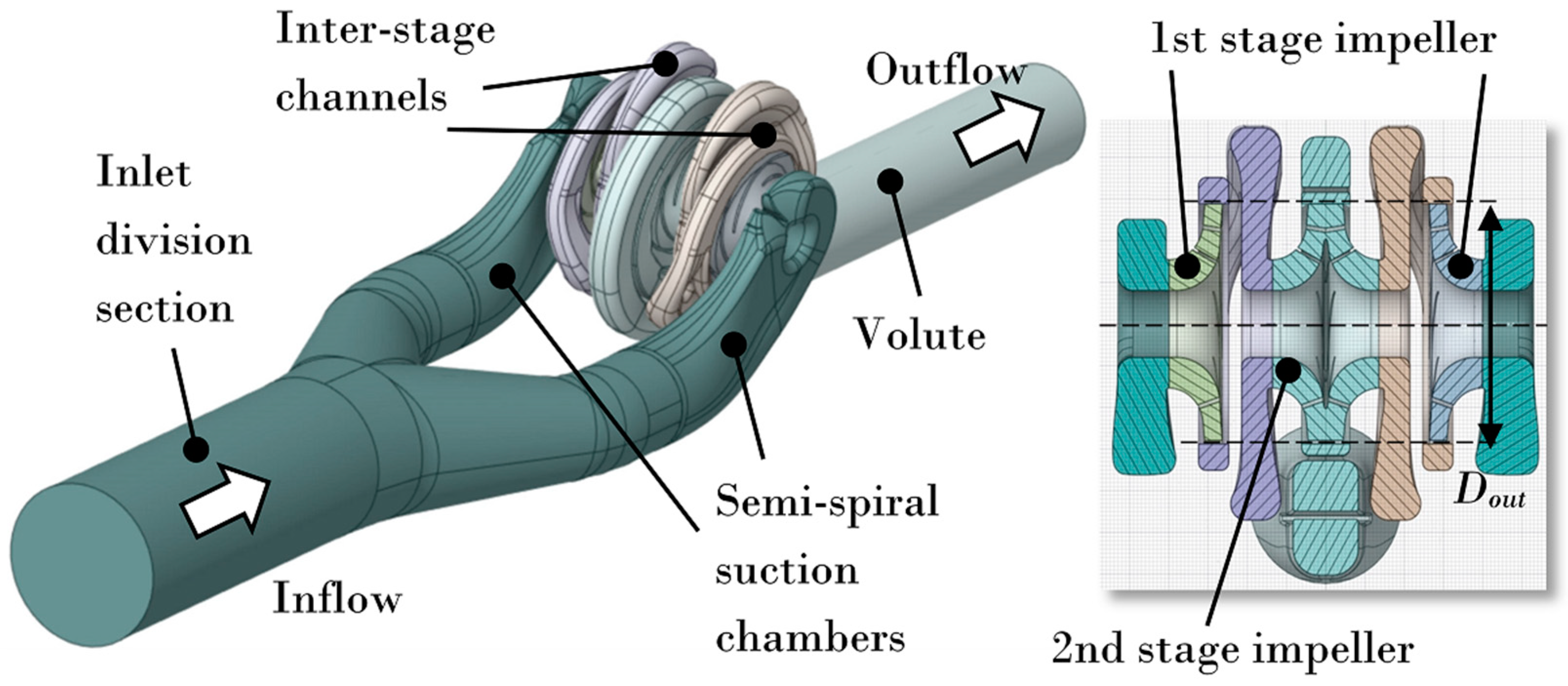
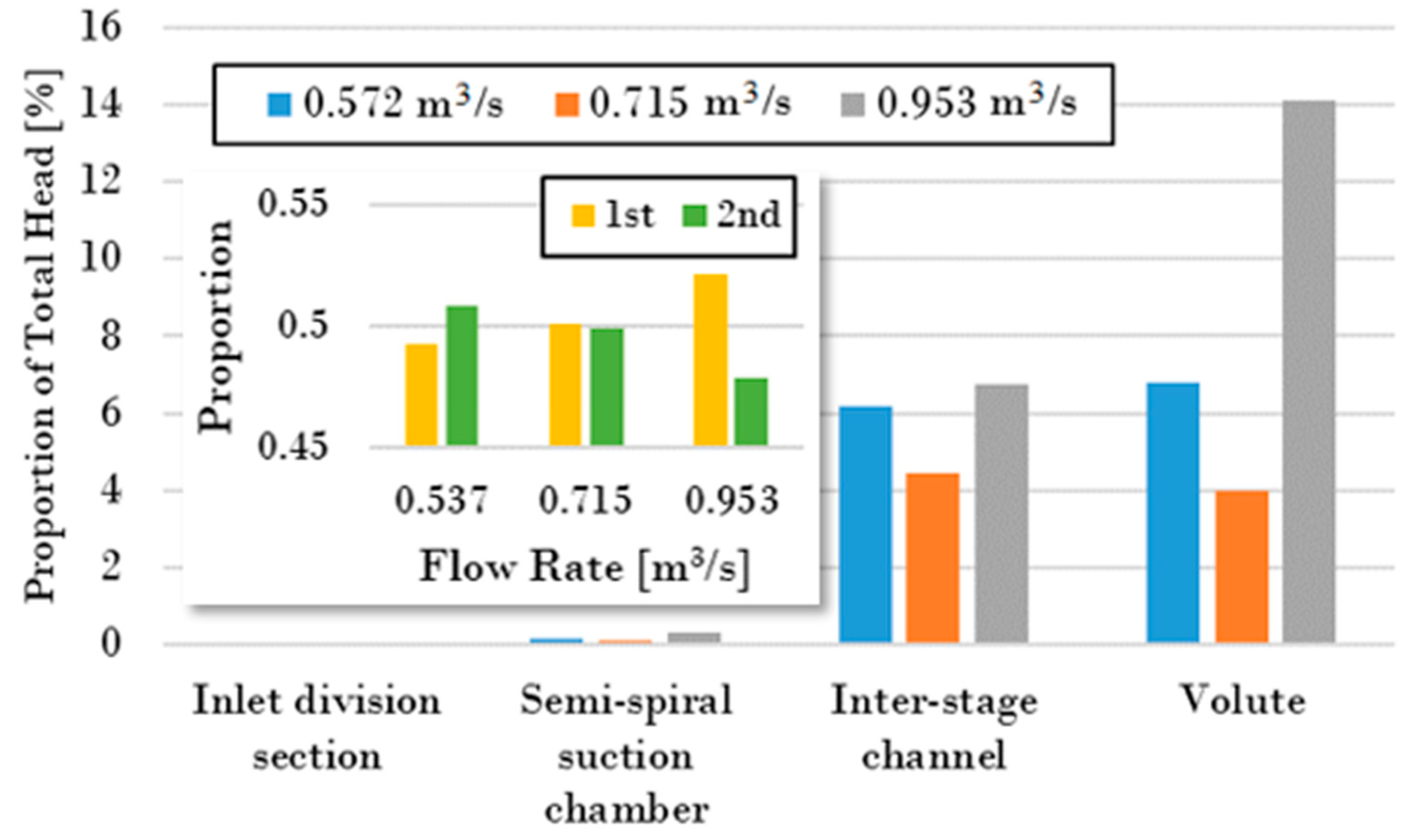
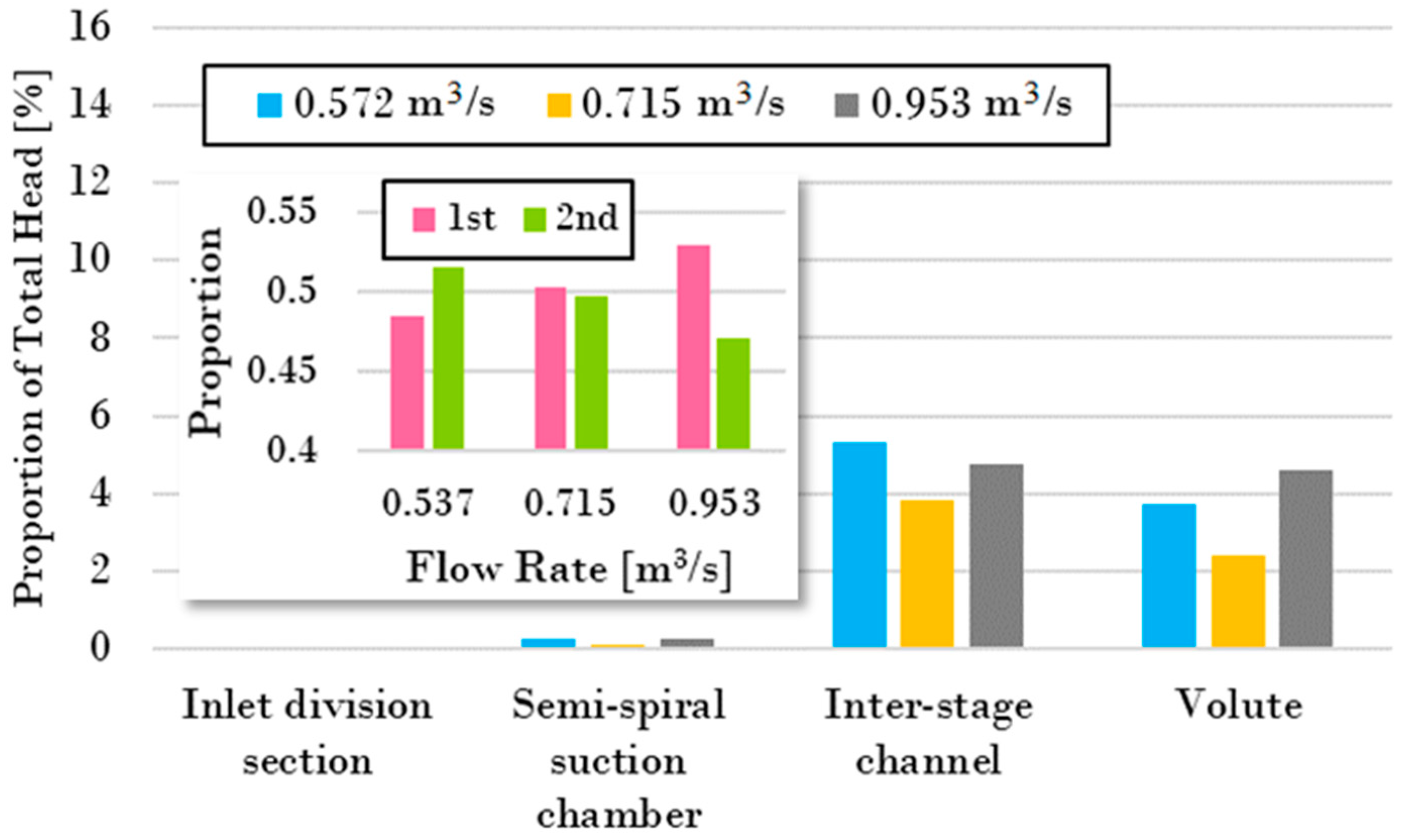
To achieve this improvement, all the components except the semi-spiral suction chamber were modified for a better performance. The inlet division section was modified by adding a baffle at the fork. The trailing-edge blade angle of the first- and second-stage impellers were increased to a higher head. The section area of the inter-stage channel was reduced because the initial areas were too large, with vortexes and flow separation. The volute section area was increased to reduce the friction loss because of the insufficient area in the original. The hydraulic losses were reduced from about 14% to less than 6% after modification.

In general, this study provides a reference for the improved design of a two-stage double-suction centrifugal pump, and it has great scientific significance and engineering value.