Towards Groundwater-Level Prediction Using Prophet Forecasting Method by Exploiting a High-Resolution Hydrogeological Monitoring System

Abstract

Forecasting of water availability has become of increasing interest in recent decades, especially due to growing human pressure and climate change, affecting groundwater resources towards a perceivable depletion. Numerous research papers developed at various spatial scales successfully investigated daily or seasonal groundwater level prediction starting from measured meteorological data (i.e., precipitation and temperature) and observed groundwater levels, by exploiting data-driven approaches. Barely a few research combine the meteorological variables and groundwater level data with unsaturated zone monitored variables (i.e., soil water content, soil temperature, and bulk electric conductivity), and—in most of these—the vadose zone is monitored only at a single depth. Our approach exploits a high spatial-temporal resolution hydrogeological monitoring system developed in the Conero Mt. Regional Park (central Italy) to predict groundwater level trends of a shallow aquifer exploited for drinking purposes. The field equipment consists of a thermo-pluviometric station, three volumetric water content, electric conductivity, and soil temperature probes in the vadose zone at 0.6 m, 0.9 m, and 1.7 m, respectively, and a piezometer instrumented with a permanent water-level probe. The monitored period started in January 2022, and the variables were recorded every fifteen minutes for more than one hydrologic year, except the groundwater level which was recorded on a daily scale. The developed model consists of three “virtual boxes” (i.e., atmosphere, unsaturated zone, and saturated zone) for which the hydrological variables characterizing each box were integrated into a time series forecasting model based on Prophet developed in the Python environment. Each measured parameter was tested for its influence on groundwater level prediction. The model was fine-tuned to an acceptable prediction (roughly 20% ahead of the monitored period). The quantitative analysis reveals that optimal results are achieved by expoiting the hydrological variables collected in the vadose zone at a depth of 1.7 m below ground level, with a Mean Absolute Error (MAE) of 0.189, a Mean Absolute Percentage Error (MAPE) of 0.062, a Root Mean Square Error (RMSE) of 0.244, and a Correlation coefficient of 0.923. This study stresses the importance of calibrating groundwater level prediction methods by exploring the hydrologic variables of the vadose zone in conjunction with those of the saturated zone and meteorological data, thus emphasizing the role of hydrologic time series forecasting as a challenging but vital aspect of optimizing groundwater management.

1. Introduction

Water is indisputably one of the most important natural resources since its availability sustains life, agriculture, industry, and its dependent ecosystems [1,2,3]. A continuously increasing strain on freshwater supplies is observed due to world population growth and climate change [4,5], hence water conservation practice and water availability prediction emerge as a vital objective [6,7]. Indeed, while the causes of climate change are still debated and often divergent, the produced effects are globally recognized. The most common include a rise in dry periods and an increase in intense rainfall events. Those phenomena have a strong impact on both groundwater and surface water resources. In fact, while large amounts of rainfall occurring in a few hours can cause floods, a gradual depletion of groundwater available for human consumption is observed. In this context, some authors suggest that a shift in monitoring focus from the groundwater to the vadose zone is necessary to understand the processes that regulate the decreasing of aquifer recharge [8,9,10,11]. During the last decades, special attention has been paid to monitor the unsaturated zone layers to characterize infiltration processes and thus estimate groundwater recharge vs. run-off generation [12,13]. The unsaturated zone represents the portion that encompasses the topographic surface until the top of the groundwater body, where most of the biogeochemical processes take place and where rainwater infiltrates [14]. At the beginning of the 21st century, the unsaturated zone was included, according to the US National Research Council, in the more elaborated concept of “Critical Zone”, because of the extreme complexity of the phenomena that regulate it [15]. The various heterogeneities in the unsaturated zone (presence of roots, lenses of fine or coarse materials, different gas phases, and redox conditions) are reflected in a heterogeneous response in terms of recharge, transport of pollutants, and their attenuation. Hence, understanding unsaturated-zone processes is crucial to determine the amount and quality of groundwater that is available for human and ecosystem use [16,17]. In this context, the growing interest in groundwater level (GWL) prediction to support water management operations was accompanied by a proliferation of advanced sensors and data collection technologies [18,19]. Usually, Time Domain Reflectometry (TDR) moisture probes are used to monitor the soil hydrologic variables such as water content, soil temperature, and bulk electric conductivity, providing useful information to understand aquifer recharge mechanisms. These sensors can gather vast amounts of hydrologic data at different scales. However, few hydrogeological studies still analyze the aquifer response to meteoric inflow by investigating the vadose zone. Most of the studies deal with precipitation and air temperature data to perform water balance by exploiting the most known empirical methods [20,21,22] or more complex physically based methods [23,24]. A recent work by Berthelin et al., 2023 [25] exploits soil moisture content only measured at a single depth (20 cm) at different locations, to determine the aquifer recharge of the investigated catchment.

The increasing improvement of monitoring systems and the large amount of hydrologic data collected by the scientific community fostered the development of data-driven methods to characterize and understand complex natural phenomena [26]. Several studies are based on the application of machine learning approaches in geosciences and related subjects [27,28,29,30,31]. Utilizing data-driven approaches toward the prediction of groundwater level is not a new phenomenon, and traditionally, numerical methods have been used for groundwater level modeling [32,33,34]. However, recent studies have extensively employed Artificial Intelligence (AI) based techniques [35,36,37]. Due to the inherent non-linear and non-stationary nature of groundwater level time series, intelligent data-driven methodologies have showcased promising results. Across the literature, various popular forecasting approaches have been tested on specific applications of groundwater level forecasting, including Auto-Regressive Integrated Moving Average (ARIMA), Artificial Neural Networks (ANN), Long Short-Term Memory (LSTM) as well as hybrid approaches such as ARIMA-LSTM [38,39,40,41]. Comparative studies have consistently shown that machine learning-based methods outperform traditional numerical approaches [42] with superior prediction performance and capturing complex and non-linear relationships between input and output variables [43]. In a bibliometric study of machine learning and mathematical modeling techniques of forecasting using piezometric data [44], authors find that machine learning techniques such as Random Forest (RF), Support Vector Machine (SVM), and deep learning techniques like ANN achieve higher accuracies if compared to mathematical model techniques. Ren et al. [45] investigated that though deep learning performs well in filling high dynamic gaps, it struggles with reconstructing trends and seasonality-based gaps. On the other hand, ARIMA, a traditional machine learning model, excels in capturing trends and seasonality.

This suggests that traditional models, designed to handle time series with seasonal effects and trends, may be more suitable for groundwater level forecasting tasks. While RFs and SVMs lack built-in mechanisms to handle the temporal nature of groundwater data and explicitly capture seasonality and holiday effects in groundwater-level time series, ANNs require careful architecture design, training, and tuning for time series forecasting. A pressing need exists for a fast, accurate, and tunable forecasting procedure that works best with time series with strong seasonal effects due to the nature of groundwater level oscillation during the hydrologic years. Further, it should also have an easy mechanism of incorporation of exogenous variables while maintaining interpretability. Prophet is an open-source machine learning model specifically designed for time series forecasting, with a particular emphasis on capturing seasonality, trends, and holiday effects [46]. Prophet is robust in automatically handling missing data and outliers, is flexible in incorporating domain knowledge, and can capture seasonality and holiday effects with simplicity. Moreover, Prophet incorporates uncertainty estimation, which is crucial for decision-making in groundwater management. Researchers have tested it for groundwater level estimation, and it has been compared with other models like ARIMA, Multivariate Adaptive Regression (MARS), and Error Trend and Seasonality (ETS) using satellite data to analyze and forecast groundwater level in the Urmia Lake basin (Northwestern Iran) [47]. Prophet consistently outperformed the other models, achieving higher coefficients of determination ($R^2$) ranging from 0.81 to 0.85, as well as lower Mean Absolute Error (MAE) and Root Mean Squared Error (RMSE). Aguilera [48] conducted a similar study at the Ramsar wetland area of Doñana (Spain) and found that Prophet exhibited strong prediction capabilities for groundwater level time series. The study compared Prophet with various statistical and intelligent models commonly used in time series forecasting, suggesting that methods with additive schemes, such as ARIMA and Prophet, are suitable for modeling groundwater time series. Though it has demonstrated superior performance, the existing literature only focuses on a simple implementation based on regressors such as air temperature and precipitation, which are not the most robust representations of the actual groundwater recharging mechanism.

As far as our best knowledge, no previous research aims to estimate future groundwater availability by combining a vadose zone monitoring system collecting data at different depths into the soil and machine learning approaches. Only a few studies in the literature exploit the Prophet forecasting method to estimate future groundwater levels by exploiting just previously observed groundwater level data [47,48] or precipitation data [42]. To fill this gap in the literature, this research explores the additive machine learning model Prophet (not specifically developed for hydrological purposes) to predict the groundwater level of an alluvial aquifer exploited for drinking purposes by using the vadose zone monitored data. The study site is located in the Conero Mt. Regional Park (central Italy). The monitoring strategy consists of a thermo-pluviometric station, three soil water content, electric conductivity, soil temperature probes, and a piezometer instrumented by a water depth probe. All the variables collected from the monitoring system are tested for their influence on groundwater level prediction. Towards this approach, the proposed research tries to address the following open-ended questions:

• How do unsaturated zone variables, like soil volumetric water content, bulk electric conductivity, and soil temperature improve groundwater level predictions compared to precipitation and air temperature data and previously observed groundwater levels?
• Can our proposed Prophet model accurately forecast groundwater levels in a shallow aquifer by integrating high-resolution hydrological monitoring, both from meteorological data and both from the vadose zone data?
• What is the impact of monitoring the vadose zone at different depths on groundwater level predictions in the study area?

2. Materials and Methods

This section presents the materials and methods employed in the investigation of advanced groundwater level prediction by applying the Prophet forecasting method, leveraging the capabilities of a high-resolution hydrological monitoring system. The subsections encompass a comprehensive overview of our research, starting with a description of the study area, the monitoring strategy, and the collected dataset. Subsequently, we delve into the forecasting method and the choice of predictive regressors. Through these carefully integrated methodologies, we aim to contribute to developing an accurate and originally applied forecasting system for groundwater availability and management.

2.1. Hydrogeological Features of the Study Site

The study site is located in the central Mediterranean basin. The research is focused on a sub-catchment (about 5 km²) of the Aspio watershed, situated within the Conero Mt. Regional Park (central Italy) (Figure 1a). The Conero Mt. hydrostructure has been the objective of several studies during past years [49]. Fronzi et al., 2022 [50] identified two main aquifers in the area. The first one, named Scaglia Calcarea aquifer is hosted in the Scaglia Rossa and Scaglia Bianca geological Formations (Fms.), while the second one is hosted in the terraced and alluvial deposits of the Quaternary age (Figure 1b). The Scaglia Calcarea represents the main aquifer and is constituted by stratified mycritic limestones, marly, and flinty limestones [49]. Its hydraulic conductivity is regulated by the presence of fissures and microkarst features, typical of such carbonate geological Fms. [51]. The Scaglia Calcarea aquifer is inferiorly confined by the marly units of the Marne a Fucoidi Fm., (not outcropping in the analyzed basin). At the top, the Scaglia Calcarea aquifer is semi-confined by the presence of a low permeability complex of the Scaglia Variegata Fm., Scaglia Cinerea Fm., the Bisciaro Fm. and the Schlier Fm., which constitute a single aquiclude. This hydrogeological complex, together with Pliocene and Pleistocene clay layers, hydraulically separates the Scaglia Calcarea aquifer from the shallow alluvial aquifer mainly comped by silty-sands, sandy-silts and gravels with sand layers. The alluvial aquifer is responsible for the presence of perennial surface water in the tributaries of the Aspio River and feeds the watercourses through a well-explored groundwater-surface water interaction [50]. As a result, the groundwater body hosted in the alluvial aquifer is responsible for sustaining the aquatic ecosystem of the Regional natural park. The aquifers’ recharge is entirely due to meteoric precipitation which accounts for an average precipitation of about 900 mm/year [49]. Both aquifers play an important role in the drinking water supply. Indeed, they are tapped by the local water management company, providing good quality water in the small towns nearby. However, the meteoric regime of the years 2019, 2020, and 2021 has impacted the groundwater resources in the area with severe groundwater depletion effects and a concomitant drying up of the water course for a prolonged period [50]. This aspect provided the impetus for an in-depth assessment of future groundwater availability by characterizing the infiltration processes and the water movement in the vadose zone towards the alluvial aquifer to support local management companies and authorities. For this reason, starting in January 2022, a high-resolution hydrogeological monitoring system has been set up in the basin. The following chapter describes the implemented monitoring system and the data collection strategy.

2.2. Monitoring System and Data Collection

Starting from November 2021, field operations have been made to implement the monitoring site. Three holes of diameter 0.1 m were manually drilled at a distance of 2 m from each other and inclined 45 degrees to the horizontal. The holes were drilled at 0.6, 0.9, and 1.7 m depth, respectively, into the soil deposits of the alluvial aquifer in the proximity of the wells field employed for drinking water supply (Figure 1b). In the holes, the advanced soil moisture, temperature, and electric conductivity (EC) sensors TEROS 12 (Meter Group Inc., Pullman, WA, USA) were installed at the bottom, taking care to refill and compact the soil previously extracted from the hole over the sensors. This procedure, together with the drilling orientation (45°), was made to minimize the impact of the hole on preferential infiltration flow paths into the soil toward the sensors. The TEROS 12 are advanced sensors that exploit the TDR principle to monitor the vadose zone hydro-physical properties. The soil moisture is expressed as volumetric water content (VWC), measured in m${}^3$/m${}^3$, with a resolution of 0.001 m${}^3$/m${}^3$ and accuracy ±0.03 m${}^3$/m${}^3$. The soil temperature (T${}_{soil}$) operational range is −10 to +60 °C, with resolution of 0.1 °C, and accuracy ±0.5 °C from −10 to 0 °C and ±0.3 °C from 0 to 60 °C. The Bulk electrical conductivity (EC) range is 0–20 mS/cm with 0.001 mS/cm resolution and ±5 percent accuracy. The precipitation (P) regime and the air temperature (T${}_{air}$) in the area are monitored through a thermo-pluviometric station, while a standpipe piezometer located in the alluvial aquifer (about 200 m downstream from the vadose zone monitoring point) was equipped with a hydrometric pressure transducer (TD-Diver Eijkelkamp, accuracy ±0.5 cmH₂O and resolution 0.2 cmH₂O) compensated by atmospheric pressure, for continuously monitoring groundwater level fluctuation (Figure 1b). The monitored period effectively started on 1 January 2022, and all the hydrological parameters were recorded every fifteen minutes for more than one hydrologic year until 30 April 2023, except for the GWL, which was recorded every day at noon. We utilize IoT technology to automatically collect data on the cloud robustly and efficiently, as demonstrated by Galdelli et al., 2019; Galdelli et al., 2021 and Tassetti et al., 2022 [52,53,54]. The obtained high spatial and temporal resolution dataset was used to develop the GWL prediction model, as shown in the next chapter.

2.3. Groundwater Level Forecasting

The implementation of the forecasting algorithm was preceded by a schematic simplification of the natural conditions, according to which the system was divided into three virtual boxes: Box 1 = Atmosphere (and related variables), Box 2 = Vadose zone (and related variables collected at different depths), and Box 3 = Saturated zone (and related variables), following the scheme proposed in Figure 2. The implementation is split into four distinct scenarios that comprehensively assess the model’s predictive capabilities. Initially, variables from Box 1, encapsulating atmospheric conditions, were employed to predict the GWL in Box 3. Subsequently, three additional tests were conducted using variables from Box 2 at depths of 0.6 m, 0.9 m, and 1.7 m, independently to forecast the GWL in Box 3. Each of these scenarios provides valuable insights into the relationships between specific environmental variables and groundwater levels, contributing to an understanding and optimization of the forecasting model for diverse conditions within the system.

Considering the state of the art across the literature we designed a Prophet-based system for forecasting purposes [46]. Prophet is a time series forecasting model developed by the core data science team at Facebook and is an open-source project for analyzing and forecasting time series. Prophet offers numerous strengths, including the robustness of the model in the case of missing data, frequent trend changes, and promising performance even in the presence of outliers. The convenient methods to add additional regressors and robust cross-validation process make it a promising forecasting mechanism in our case study. Prophet represents the time series as the sum of three components: (i) trend, (ii) seasonality, and (iii) holidays, as seen below:

$$y\left(t\right)=g\left(t\right)+s\left(t\right)+h\left(t\right)+{ϵ}_t$$

(1)

where:

• g(t): trend function, models non-periodic changes, it can be logarithmic;
• s(t): seasonality function, relying on the Fourier series, provides a flexible model of periodic effects to model changes that are repeated at regular time intervals (e.g., weekly and yearly seasonality); it is also possible to have more than one seasonality in the same series;
• h(t): holidays, models irregular events that temporarily alter the time series;
• ${ϵ}_t$: error term, represents changes in the time series that the model does not capture, ${ϵ}_t$ is regarded as a normal distribution.

Prophet adopts a unique approach to forecasting, treating it as a curve-fitting problem in contrast to other methods like ARIMA [55]. Unlike ARIMA or SARIMAX, which relies on autocorrelation and partial autocorrelation to capture temporal dependencies, Prophet decomposes the input time series into additive components. It models trends using a piecewise linear logistic growth curve and incorporates seasonality through Fourier series expansion. The data needs to be converted to a proper time series format to facilitate effective utilization, as the model relies on a structured temporal sequence for accurate trend and seasonality identification. Due to the disparity in temporal resolution between the hydrological variables recorded at fifteen-minute intervals (i.e., P, T${}_{air}$, VWC, T${}_{soil}$ and EC) and the GWL observations, collected at daily scale, a data treatment has deemed necessary. Specifically, the hydrological variables of Box 1 and Box 2 were resampled at the daily scale as follows. The daily mean T${}_{air}$ and daily cumulative P were computed. Similarly, the daily mean VWC, T${}_{soil}$ and EC were computed for all different depths, (i.e., 0.6 m, 0.9 m, and 1.7 m). Consequently, the method ensured that all the collected hydrological variables were converted into a consistent daily format, aligning them temporally with the observed GWL.

Training the model involves a combination strategy utilizing grid search for hyperparameter tuning and cross-validation for predictive error assessment on validation data, as depicted in Figure 3. The grid search algorithm systematically explores a range of hyperparameter values, as detailed in

Table 1. Hyperparameters grid optimized using rolling cross-validation strategy for different scenarios: Atmosphere to Saturated zone (Box 1 to Box 3) and Vadose zone to Saturated zone (Box 2 to Box 3).

Scenario	Hyperparameters	Values
Box 1 to Box 3	changepoint_prior_scale	[0.01, 0.05, 0.1, 0.7, 0.9]
	seasonality_mode	[’additive’, ’multiplicative’]
	seasonality_prior_scale	[0.01, 2.0, 12.0, 15.0, 75.0]
	prior_scale_temperature	[0.000001, 0.01, 0.5, 0.7, 1.0]
	prior_scale_rain	[0.000001, 0.01, 0.5, 0.7, 1.0]
	changepoint_range	[0.70, 0.85, 0.90, 0.95]
	daily_seasonality	[’True’, ’False’]
	weekly_seasonality	[’True’, ’False’]
	yearly_seasonality	[’True’, ’False’]
Box 2 to Box 3	changepoint_prior_scale	[0.01, 0.05, 0.1, 0.7, 0.9]
	seasonality_mode	[’additive’, ’multiplicative’]
	seasonality_prior_scale	[0.01, 2.0, 12.0, 15.0, 75.0]
	prior_scale_water_content	[0.000001, 0.01, 0.5, 0.7, 1.0]
	prior_scale_soil_temperature	[0.000001, 0.01, 0.5, 0.7, 1.0]
	prior_scale_electric_conductivity	[0.000001, 0.01, 0.5, 0.7, 1.0]
	changepoint_range	[0.70, 0.85, 0.90, 0.95]
	daily_seasonality	[’True’, ’False’]
	weekly_seasonality	[’True’, ’False’]
	yearly_seasonality	[’True’, ’False’]

, exhaustively testing all possible combinations for optimization. Hyperparameters such as prior_scale_temperature, prior_scale_rain for the atmosphere, prior_scale_soil_temperature, prior_scale_water_content, and prior_scale_ electric_conductivity and were optimized for this investigation. Moreover, depending on the specific forecasting scenario, weights for exogenous variables acting as regressors were introduced. Such exogenous variables are not directly influenced by the groundwater level, but are important factors affecting it. Introducing these exogenous variables as regressors and assigning weights through hyperparameter tuning, our model can account for external influences, providing a more comprehensive and accurate prediction of GWL. Therefore, to incorporate these variables, depending on the forecasting scenario, hyperparameters such as prior_scale_temperature, prior_scale_rain for the atmosphere (Box 1), prior_scale_soil_temperature, prior_scale_water_content, and prior_scale_electric_conductivity for the vadose zone (Box 2) were defined and custom integrated into the model. These weights allow the model to assign varying degrees of importance to different exogenous variables, enhancing its adaptability to the specific dynamics of the saturated zone (Box 3) namely the GWL prediction task. The systematic selection of optimal hyperparameters, combined with the introduction of these weights, ensures the model’s robust performance and facilitates accurate forecasts for different scenarios.

Cross-validation evaluates the model’s performance across multiple training and validation sets based on forecasting requirements. The determination of the training data, which is used for cross-validation, is guided by key parameters: initial, period, and horizon. These parameters are built into the Prophet and play a crucial role in defining the size of the initial training period and the duration of the forecast window. The period parameter specifies the length of a seasonal cycle, and the horizon parameter defines the duration for which future predictions are made. The initial parameter determines the size of the initial training period. During each cross-validation fold, the model is trained on this initial period, allowing it to learn from historical data. The process iterates across the entire time series, providing a robust assessment of the model’s performance across different data segments. Specifically, our cross-validation approach involves dividing the time series into segments, each equivalent to roughly 10% of the total time series into validation and testing. In the validation process, a timeframe of 2 months was established, mirroring the identified seasonal patterns and effectively capturing the recurring nature of the observed data. Additionally, the test dataset spans 2 months, ensuring a comprehensive evaluation of the model’s performance.

A period of 7 days was deemed appropriate in line with the identified seasonal patterns, and this duration captures the recurring nature of the observed data and aligns with the underlying cyclicality. Additionally, a horizon of 14 days was chosen to represent the forecast window. This window length meets the local groundwater management company’s request to operate in time to ensure the availability of drinking water for the population living nearby. Furthermore, the selection of 14 days ensures that each cross-validation fold covers a significant portion of the time series while allowing for a robust assessment of the model’s performance. This choice allows for a two-week projection, providing a meaningful time frame for anticipating near-future trends and variations without significant loss in forecast accuracy. Therefore, in case of a predicted significant groundwater level decrease the management company can locate water pumps at different depths within the wells, or integrate the amount of extracted groundwater from emergency well fields or different water plants.

2.4. RAPS Method

The Rescaled Adjusted Partial Sums (RAPS) method is a fundamental analytical technique within the realm of hydrogeological time series since it can discern nuanced fluctuations within collected data, making it an essential tool for groundwater studies [56,57]. RAPS works by aggregating the deviations from a specified mean level of hydrological variables and adjusting them against the data’s standard deviation, as reported in Equation (2).

$${RAPS}_N=\sum _{i=1}^N\frac{Y_i-\overline{Y}}{S_Y}$$

(2)

where:

• N: the amount of data in the time series;
• $Y_i$: the value of an individual sample i = 1, 2, …, N;
• $\overline{Y}$: average value of the observed sample;
• $S_Y$: the value of the standard deviation of the time series.

The RAPS method was used to analyze observed GWL and the predicted ones at a daily scale by using two time-series lengths. The first one considers the duration of the whole monitoring period, while the second one considers only the testing dataset. This approach was employed to compare trends, periodicities, and fluctuations [58] on observed vs. predicted GWL.

3. Results

3.1. Hydrological Characterization and Collected Dataset

The collected hydrological variables during the monitoring period (1 January 2022–30 April 2023) are reported in the graphs of Figure 4. When examining the graphs, it is possible to observe that the precipitation regime in the area is characterized by wet periods during winter and spring and less rainer periods during summer and early autumn. The summer is marked by sporadic but heavy rainfall events that frequently exceed 10 mm/15 min, while the wet periods are characterized by more continuous rainfall events persisting for several hours to days. The most intense rainfall event can be depicted on 15 September 2022 (12 mm/15 min), recognized also by other authors to be one of the most intense precipitation events affecting the northern Marche Region during the last century [59,60,61].

Concerning the air temperature, it ranges between 0 and 35 °C during the hydrologic year. The higher values are observed during the summer (in July), and the lower are recorded during the winter periods between January and February. The soil temperature mimics the trend of the air temperature at all the monitored depths with a time lag between T${}_{air}$ and T${}_{soil}$ increasing as the depth increases. Three thermal stationary periods can be observed in April and October 2022 and between March and April 2023. During the other months, the soil temperature is higher at 0.6 m and lower at 1.7 m during summer. On the contrary, during winter, an inverse temperature gradient is observed, as expected. Indeed, the T${}_{soil}$ at 0.6 m reflects changes in T${}_{air}$ faster, while deeper down, the thermal inertia of the soil becomes more sizeable, smoothing temperature variations. T${}_{soil}$ at 0.6 m ranges between 6.7 and 25.5 °C, T${}_{soil}$ at 0.9 m ranges between 8.3 and 23.4 °C, while T${}_{soil}$ at 1.7 m ranges from 10 °C to 20.8 °C (

Table 2. Basic statistics of the considered time-series.

Box n°	Hydrological Variable	Measurement Unit	Mean	Min	25th	Median	75th	Max
1	P	mm/15min	0.02	0	0	0	0	12
	T${}_{air}$	°C	14.1	0	7.12	12.53	19.61	35
2	T${}_{soil}$ 0.6 m	°C	14.6	6.7	9.7	12.7	19.2	25.5
	VWC 0.6 m	m3/m3	0.31	0.22	0.27	0.33	0.35	0.4
	EC 0.6 m	mS/cm	0.4	0.22	0.29	0.46	0.49	0.64
	T${}_{soil}$ 0.9 m	°C	14.5	8.3	10.1	12.7	18.8	23.4
	VWC 0.9 m	m3/m3	0.32	0.24	0.28	0.33	0.35	0.4
	EC 0.9 m	mS/cm	0.51	0.31	0.42	0.55	0.58	0.79
	T${}_{soil}$ 1.7 m	°C	14.5	10	11.4	13.3	18.1	20.8
	VWC 1.7 m	m3/m3	0.29	0.24	0.25	0.3	0.32	0.36
	EC 1.7 m	mS/cm	0.51	0.24	0.26	0.46	0.65	1.05
3	GWL	m	−6.39	−9.7	−9.2	−6.42	−4.19	−2.5

). A peculiar thermal response to the rainfall events is observed at 0.6 and 0.9 m where precipitation falling in winter tends to increase the soil temperature. In contrast, an opposite trend can be observed after the precipitation events occurring in summer, producing a decrease in soil temperature at both depths. The thermal influence of infiltrating water into the soil is lost at 1.7 m both in the summer and winter periods, as well. As regards the VWC, an increase in its values is observed after rainfall events between January and February 2022, when the vadose zone is near the saturated conditions. Starting from March, the soil progressively dries until September in all the monitored depths. The rainfall events occurring between March and September 2022 do not produce any increase in VWC, and starting from September 2022 the VWC starts to increase at the shallow soils’ layers (0.6 m) and only in October 2022 the infiltration process involve the soil at 0.9 m. Starting from December, the soil at 0.6 and 0.9 m behaves similarly under the effect of precipitation events with a fast increase of the VWC. Only in January 2023, the three monitored depths reach the complete saturated conditions. VWC at 0.6 m ranges between 0.22 and 0.4 m${}^3$/m${}^3$, VWC at 0.9 m ranges between 0.24 and 0.4 m${}^3$/m${}^3$, while VWC at 1.7 m ranges from 0.24 to 0.36 m${}^3$/m${}^3$ (Table 2). Regarding the bulk EC, it mimics the VWC behavior at all the monitored depths, with an increase in its values as the VWC increases, except for the depth 1.7 m in which sporadic infiltration events are marked by a decrease in EC values. EC at 0.6 m ranges between 0.22 and 0.64 mS/cm, EC at 0.9 m ranges between 0.31 and 0.79 mS/cm, while EC at 1.7 m ranges from 0.24 to 1.05 mS/cm (Table 2). Eventually, the GWL reach its maximum values during winter (January, February) and early spring (March), and then a depletion phase can be observed starting from April 2022, with sparse recharge effects on May 2022.

The GWL reaches its minimum values during the summer and stands at about −9.7 m below ground level until the beginning of November. Then an increase in GWL is observed until February 2023, under the influence of the rainfall events at different stages, when the vadose zone is completely saturated. The GWL ranges between −2.5 and −9.7 m below ground level during the monitored period. Basic statistics for the monitored hydrological variables are reported in Table 2.

3.2. Forecasting Scenarios

The implementation, which is split into four distinct scenarios as described earlier, is considered for prediction purposes, ensuring a robust comparison against atmospheric and vadose zone variables at different depths. Each scenario utilizes the optimized Prophet-based model, which includes components for trend, seasonality, and additional regressors chosen from the specific to three virtual boxes to capture the particular influences of the chosen input variables at a given depth. The testing period is set from the start of March 2023 to the end of April 2023, and therefore, the model makes 61 prediction intervals (days) representing the GWL into the future. The forecasted groundwater level is then compared with actual values to calculate performance metrics. The forecasting performance was evaluated through the following reported metrics:

• Mean Absolute Error (MAE), which is the absolute value of the difference between paired accurate and predicted data;
• Mean Absolute Percentage Error (MAPE), which is the percentage expression of MAE obtained through the normalization by the real data;
• Root Mean Squared Error (RMSE) is the average difference between predicted and real data;
• Correlation is the strength and direction of the linear relationship between predicted and actual values.

The quantitative results for all the scenarios are presented in

Table 3. Performance metrics of the model in different scenarios.

Scenario	Depth	Additive Regressors	MAE	MAPE	RMSE	Correlation
Box 1 to Box 3	Surface	P, T${}_{air}$	0.299	0.101	0.356	0.857
Box 2 to Box 3	Depth 0.6 m	T${}_{soil}$ 0.6 m, VWC 0.6 m, EC 0.6 m	0.255	0.086	0.270	0.850
Box 2 to Box 3	Depth 0.9 m	T${}_{soil}$ 0.9 m, VWC 0.9 m, EC 0.9 m	0.274	0.090	0.374	0.833
Box 2 to Box 3	Depth 1.7 m	T${}_{soil}$ 1.7 m, VWC 1.7 m, EC 1.7 m	0.189	0.062	0.244	0.923

.

These independent scenarios offer a comprehensive approach to understanding and predicting groundwater levels under different conditions. We ran a total of four tests, and the results of each scenario will be presented as the virtual boxes defined earlier.

3.2.1. From Atmosphere (Box 1) to Saurated Zone (Box 3)

The regressors used in this scenario are T${}_{air}$ and P. The resulting plot is observed in Figure 5, and the observed values of MAE, MAPE, RMSE, and correlation are 0.299, 0.101, 0.356, and 0.857. As determined by cross-validation, the best hyperparameters were a changepoint prior scale of 0.05, a changepoint range of 0.9, daily seasonality enabled, a prior scale for precipitation of 0.1, and a prior scale for temperature (air) of 0.01. The seasonality mode was set to ‘multiplicative’ with a seasonality prior scale of 12.0, and both weekly and yearly seasonality enabled. There is a positive correlation between observed and predicted values, and considering the errors, the results are promising.

3.2.2. From Vadose Zone (Box 2) to Saurated Zone (Box 3)

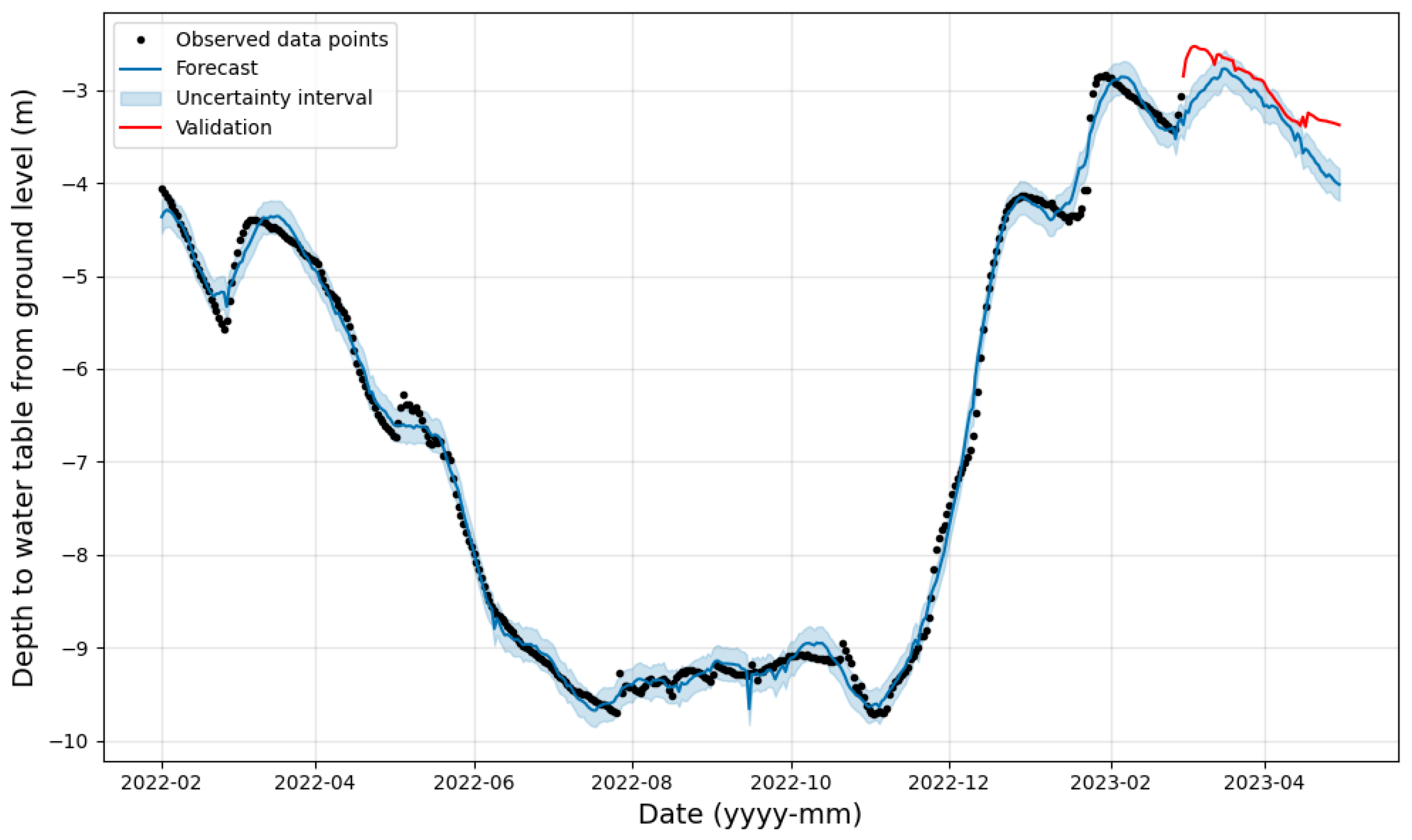
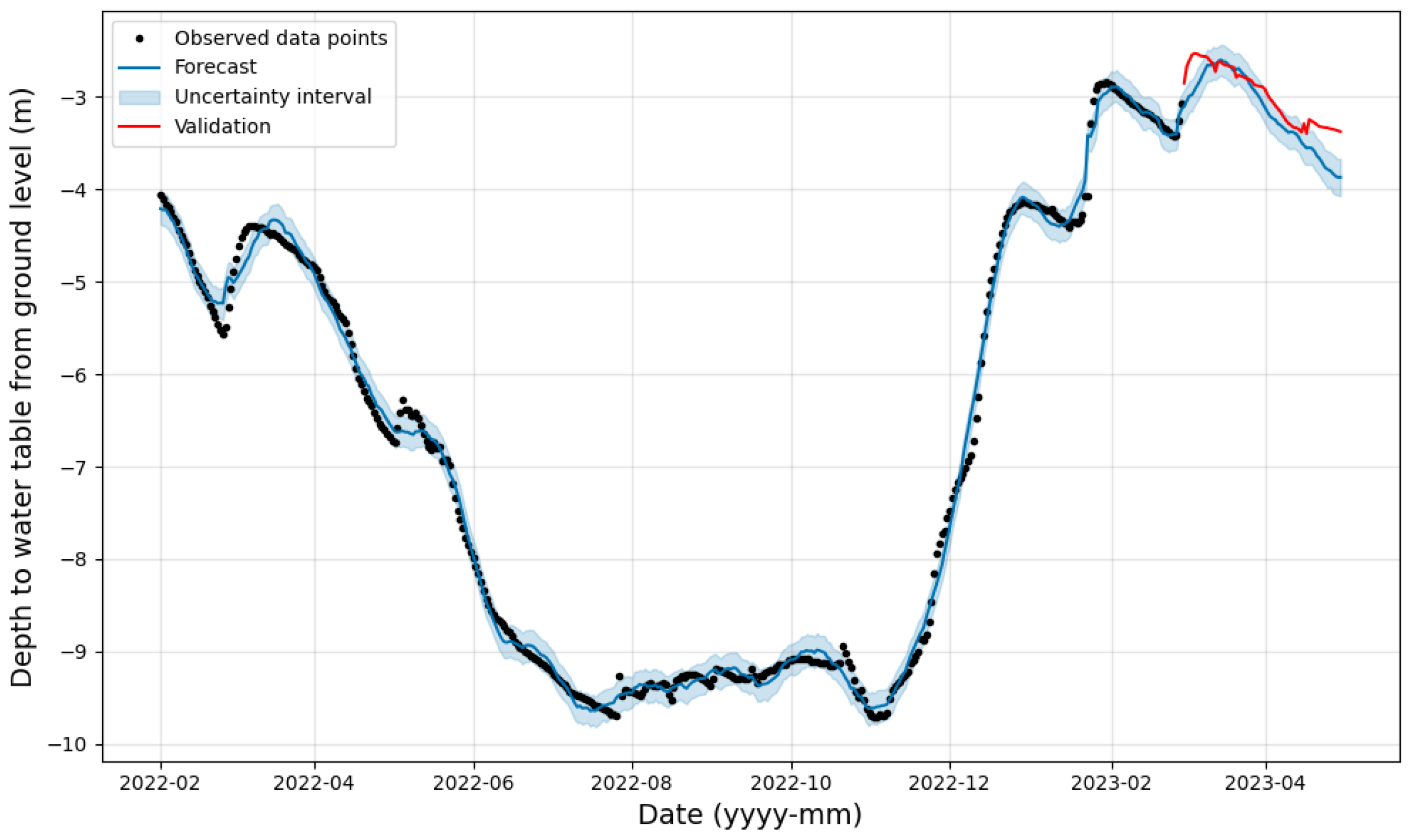
• Depth 0.6 m: The regressors used in this scenario are T${}_{soil}$ 0.6 m, VWC 0.6 m and EC 0.6 m. The resulting plot is observed in Figure 6, and the observed values of MAE, MAPE, RMSE, and correlation are 0.255, 0.086, 0.270, and 0.850, where the errors are lesser than the atmospheric variables. The optimal hyperparameters marked a changepoint prior scale of 0.9, a changepoint range of 0.9, a prior scale for electric conductivity of 0.5, a prior scale for soil temperature of 0.000001, a prior scale for water content of 1.0, a seasonality mode set to ‘multiplicative’ a seasonality prior scale of 15.0. The daily, weekly, and yearly seasonality are set to ‘True’. On visually observing, the forecasted values follow a very similar trend to the observed data points.
• Depth 0.9 m: Further increasing the depth till 0.9 m, we use the regressors as T${}_{soil}$ 0.9 m, VWC 0.9 m and EC 0.9 m, respectively. The resulting plot is observed in Figure 7, and the observed values of MAE, MAPE, RMSE, and correlation are 0.274, 0.090, 0.374, and 0.833. The overall performance has been depreciated compared to 0.6 m depth; however, the performance is slightly better than the atmospheric variables. The optimal hyperparameters marked a changepoint prior scale of 0.9, a changepoint range of 0.95, a prior scale for electric conductivity of 0.7, a prior scale for soil temperature of 0.000001, a prior scale for water content of 1.0, a seasonality mode set to ‘additive’ a seasonality prior scale of 0.01. The daily, weekly, and yearly seasonality are set to ‘True’.
• Depth 1.7 m: The final scenario is implemented at 1.7 m, and here we utilize the regressors T${}_{soil}$ 1.7 m, VWC 1.7 m, and EC 1.7 m. The resulting plot is observed in Figure 8. The observed values of MAPE, MAE, and correlation are 0.189, 0.062, 0.244 and 0.923. The calculated errors are considerably lower and offer the most efficient performance when compared between different depths of the vadose zone. The hyperparameters used to produce the forecast included a changepoint prior scale of 0.7, a changepoint range of 0.95, a prior scale for electric conductivity of 0.000001, a prior scale for soil temperature of 0.5, a prior scale for water content of 0.5, a seasonality mode set to ‘additive’ a seasonality prior scale of 0.01. The daily, weekly, and yearly seasonality are set to ‘True’.

3.2.3. RAPS Method and Trend Analysis

The analysis of the time series of RAPS data for observed GWL vs. predicted ones for the entire dataset (Figure 9) indicates the existence of three sub-periods. The first sub-period is characterized by an upward trend until May 2022, the second sub-period is marked by a downward trend until December 2022, while the last sub-period is characterized again by an upward trend.

The RAPS data for all the analyzed time series follow the same trend, periodicity, and oscillation along the entire timespan. When analyzing the time series of RAPS data of the observed GWL vs. forecasted ones for the testing period (Figure 10) it is possible to observe a general congruence between the obtained graphs with an upward trend until March 2023 and a decreasing trend in all the analyzed time series starting from the second half of March 2023. However, even if marked by the same trends, the periodicity and the oscillation of the RAPS data obtained from the analysis display different results between the analyzed variables. The periodicity and the oscillation of RAPS for the predicted GWL obtained by exploiting Box 2 at 1.7 m (dashed green line) seem to be the most correlated with the observed one (black line). On the contrary, the RAPS for the predicted GWL, obtained by exploiting Box 1 and Box 2 at 0.9 m depth (dashed red line and dashed blue line respectively), display a shift of about 10 days in their peak if compared to the RAPS of the observed GWL. Eventually, the RAPS data for the predicted GWL, obtained by exploiting Box 2 at 0.6 m depth (dashed pink line), deviates more from the RAPS data of observed GWL especially in the first two weeks (i.e., until 15 March 2023).

4. Discussion

The present work shows an AI-based application to GWL prediction focused on the Prophet forecasting method. Interestingly, the best prediction is obtained by using the sensor placed in the vadose zone (Box 2) at 1.7 m. Indeed, as reported in Table 3 this scenario is characterized by maximum correlation values (0.923) and minimum associated errors. On the other hand, the prediction obtained by exploiting the regressors collected from Box 1 (P and T${}_{air}$) and Box 2 (VWC, EC, and T${}_{soil}$ at 0.6 and 0.9 m) are comparable if considering only the correlation values, and slightly better for the Box 2 regressors’ if considering the associated errors. The obtained results match the observed hydrological processes. In fact, if using Box 1 regressors (P and T${}_{air}$) to forecast the GWL, the effective infiltration processes through the unsaturated layers towards the aquifer are not taken into account. By exploiting the surface data the prediction (even if accurate) is not as accurate as the ones obtained by exploiting Box 2 collected hydrological variables, supporting the fact that not all the precipitation events are correlated by effective recharge processes, due to the evapotranspiration occurring between April and October in our study site. On the other hand the prediction increases by observing the relationship between Box 2 and Box 3, as the probes installed in the vadose zone can catch the effective infiltration patterns occurring in the saturated zone. However, considering Box 2 at 0.6 and 0.9 m two different processes can be observed: (1) the shallower portion of the soil is still influenced by the evapotranspiration effects, with a decreasing influence as the depth increases; (2) T${}_{soil}$ acts as a nonlinear regressor during the hydrologic year (i.e., increasing after rainfall events in winter and decreasing with the same magnitude under the effect of similar rainfall events occurring in summer). This aspect supports the prior scale for T${}_{soil}$ automatically obtained by the forecasting method equal to 0.000001 proving that the T${}_{soil}$ at 0.6 and 0.9 m impact on GWL prediction is lower, or in other terms, it generates noise. The best prediction is obtained by using all the regressors (VWC, EC, and T${}_{soil}$) of Box 2 at 1.7 m. At this depth, the T${}_{soil}$ variations under the effect of single rainfall events are not caught by the TDR due to the fact that the temperature is recognized as a non-conservative tracer and the T${}_{soil}$ variations are smoothed during the infiltration processes [62,63]. At this depth, only the seasonal thermal effect can be observed and those are much more correlated to the seasonal GWL oscillation. In fact, the last scenario (Box 2 to Box 3 at 1.7 m) is characterized by a prior scale for T${}_{soil}$ automatically obtained by the forecasting method equal to 0.5, higher than the ones obtained for the other depths, strengthening the fact that the seasonal GWL oscillation is linked to the seasonal temperature of the soil recorded at 1.7 m. On the contrary, the VWC at 1.7 m impact on the prediction is lower (0.5) with respect to the other depths because the VWC variations at lower depths are slow, and once the saturated conditions are reached the VWC still remains high and constant for a prolonged period. The opposite behavior is observed during summer when the VWC still remains low for a prolonged period and no sudden variations of VWC are recorded under the effect of rainfall events. The EC affects the prediction at all depths in a non-conservative way. This outcome can be related to the heterogeneous dissolution processes occurring in the soil at different depths when the percolation occurs. In fact, when the water infiltrates into the soil it can produce an effective solute transport whose magnitude is related to the rainfall intensity and duration, the soil’s granulometric size, and the bio-geochemical processes occurring during the monitored period, resulting in a non-linear behavior of the EC under the effect of each single precipitation event at different depth.

Generally, in our study site, the water infiltrating into the soil produces an increase in EC at all the monitored depths except at 1.7 m where the EC sometimes decreases after the precipitation. Eventually, we exploited two “virtual boxes” (Box 1 and Box 2) with their collected hydrological variables fetched as a time series and used to predict GWL. The findings underscore the significance of hydrological variables from the vadose zone, revealing their capacity to enhance prediction accuracy when compared to the thermo-pluviometric variables. This observation highlights the added value of vadose zone variables in refining GWL forecasting. Our analysis indicates that the optimum performance within the vadose zone is achieved at a depth of 1.7 m, emphasizing the critical influence of this specific depth on the predictive accuracy of GWL models in our study site. The RAPS method applied to the entire dataset (Figure 9) demonstrates the efficiency of the exploited forecasted method highlighting a general correlation both in trends, periodicities, and oscillations along the training, validation, and testing periods. If focusing on the testing dataset (Figure 10) the best correlation of RAPS data for observed GWL is obtained with the TDR placed at 1.7 m depth into the vadose zone, highlighting and strengthening how this specific depth affects the predictive accuracy of the GWL in our case study. While this research has provided valuable insights by concentrating on a singular model and employing grid search optimization, it is essential to acknowledge its limitations. Future remarks may lay in a more comprehensive understanding of the forecasting that can be achieved by exploring different approaches to hyperparameter tuning. This implies that the study could be extended to investigate alternative methods beyond grid search, such as Bayesian optimization [64], to identify the most effective configuration for the Prophet model.

Future developments may lie in comparing the obtained results with other state-of-the-art time series models like ARIMA and SARIMAX, and obtain benchmarks for the selected site [42]. Additionally, incorporating emerging deep learning techniques like NeuralProphet or transformer-based models would contribute to a more comprehensive evaluation [65,66,67]. These models have garnered global attention for their ability to capture complex temporal dependencies and patterns, potentially offering alternative solutions to time series forecasting challenges. The suggested benchmarking across various models may enhance a broader perspective on the strengths and weaknesses of different approaches. Another limitation of the study lies in the duration of the monitoring period. Indeed, since the exploited time series is 16 months long, they cannot catch year seasonality on the observed hydrological processes. This aspect may infer the forecasting process and limit the forecasting time period. Further development of the study can be done only if two or more complete hydrologic years of data are collected. Eventually, a further approach may involve the use of effective precipitation as a regressor of Box 1 by excluding the contribution of evapotranspiration, which can be calculated at a daily scale exploiting the Hargreaves and Samani method [68], starting from the collected P and T${}_{air}$ data. However, it has to be pointed out that at this stage, the characterization of the aquifer recharge processes occurring in the study area is out of the scope of the present research, which aims to improve and explore the Prophet forecasting method by using hydrological variables collected in the vadose zone.

5. Conclusions

The implemented high-resolution monitoring system coupled with the Prophet forecasting method, allows for the early detection of changes and trends in groundwater level, offering a proactive approach to managing this valuable resource. This capability is vital in promptly identifying and addressing declining water levels and groundwater availability, facilitating more effective and sustainable groundwater resource management practices. Indeed, water management companies can proactively respond by strategically placing water pumps at increased depths within wells or by supplementing the aqueduct system through integrated or emergency water plants. Besides, in this study, a high-resolution hydrogeological monitoring system has been demonstrated imperative because it provided precise and quantitative data on crucial hydrological processes. Such monitoring offers unparalleled accuracy in predicting groundwater levels. The ultimate goal of this study is to highlight the importance of combining continuous field monitoring of the unsaturated zone to understand the recharge mechanisms occurring in heterogeneous media in a continuously changing climatic context characterized by an increase in hydrogeological extremes.