Batch Settling and Low-Pressure Consolidation Behaviors of Dredged Mud Slurry: Steady-State Evaluation and Mechanism Study
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experiment Preparation
2.1.1. The Study Area and Sample Preparation
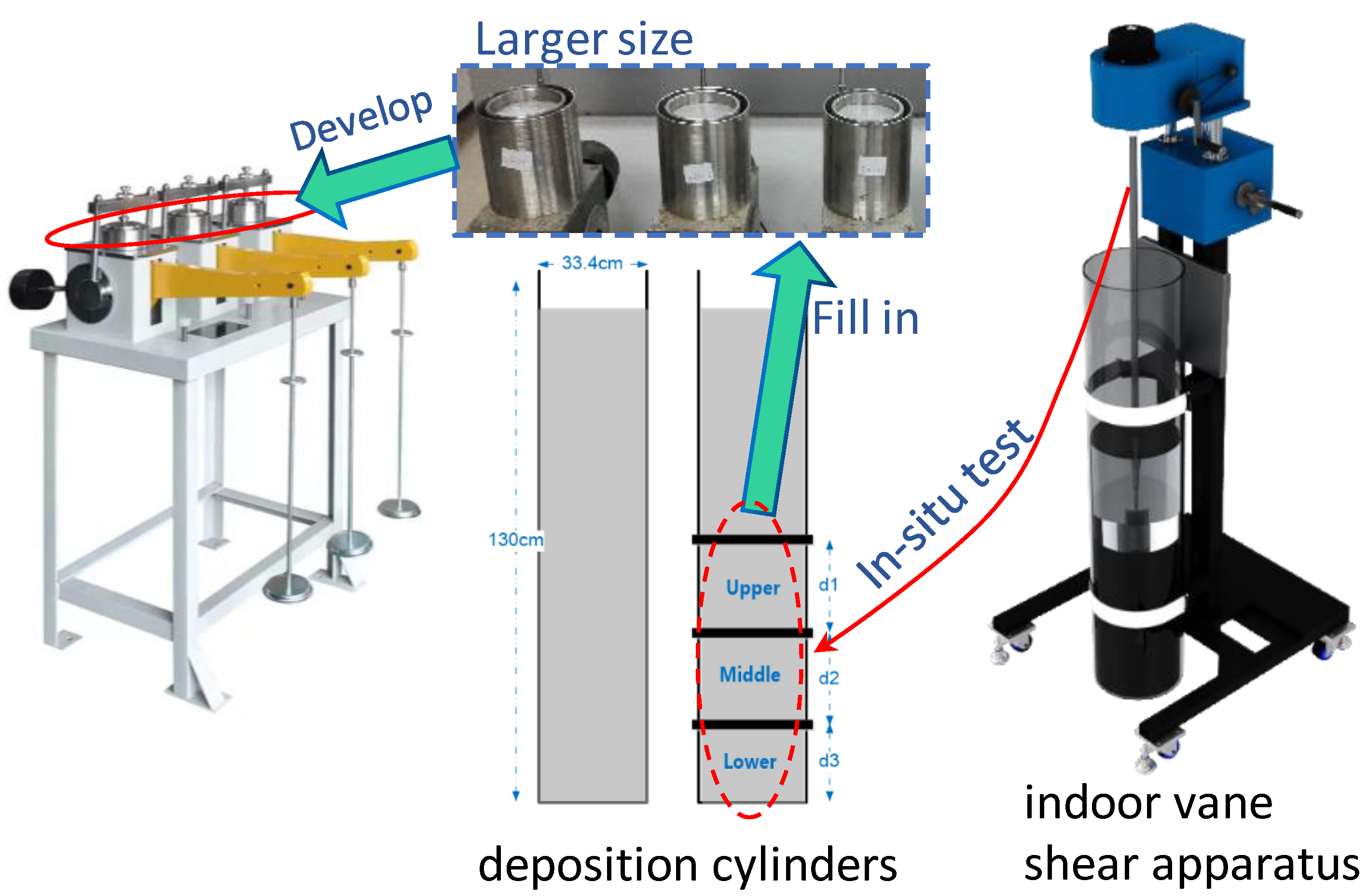
2.1.2. Experiment Apparatus
2.2. Experiment Methodology
2.2.1. Laboratory Experiment of the Batch Sedimentation Process
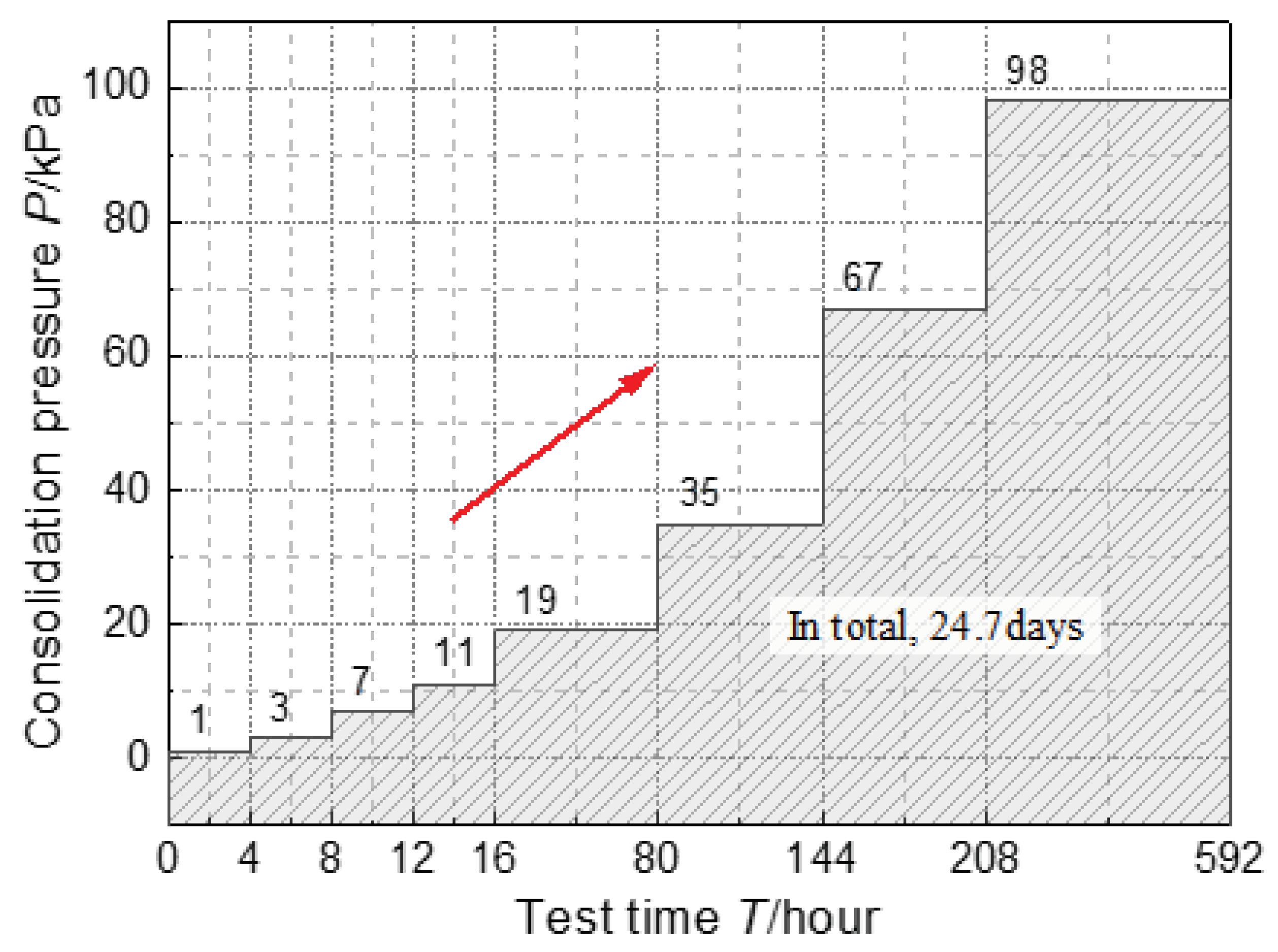
2.2.2. Low-Pressure Consolidation Test
- In engineering practice, the vacuum preloading treatment is usually carried out before the batch sedimentation process can reach a stable state, so the sampling time herein was determined to be about half of the time required for the batch sedimentation to be stable.
- The sampling depth was picked at the middle of the middle section (100 cm from the top) of the I-2 cylinder and the middle of the lower section (120 cm from the top) of the II-2 cylinder.
- The method of obtaining the sample at the corresponding depth is as follows: first, the deposition cylinder above the flange position was removed; then, the in situ shear strength of the sample at the corresponding position was measured by the indoor vane shear apparatus in the target segment, and the rest of the undisturbed samples at the corresponding position were obtained for the low-pressure consolidation tests.
3. Results
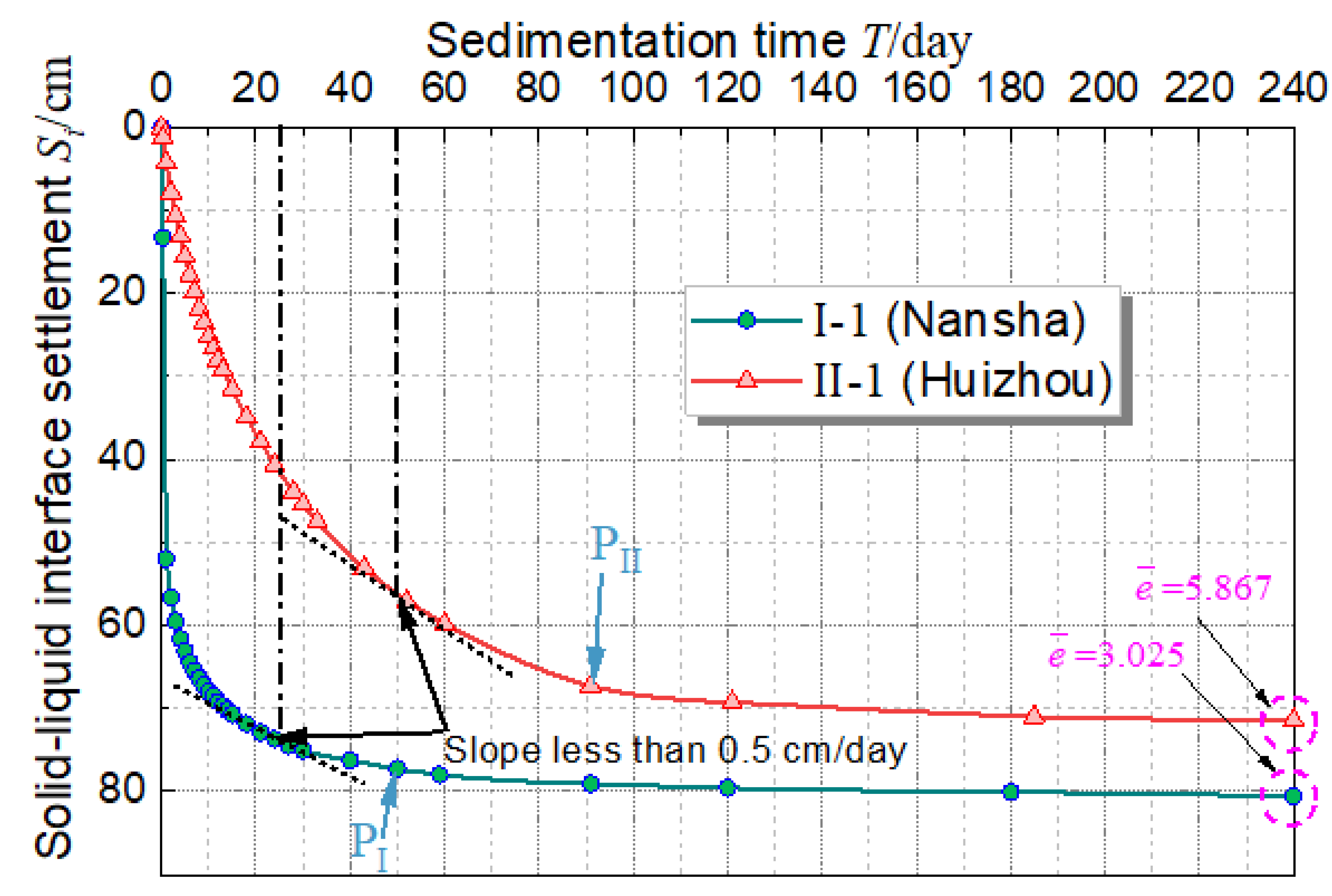
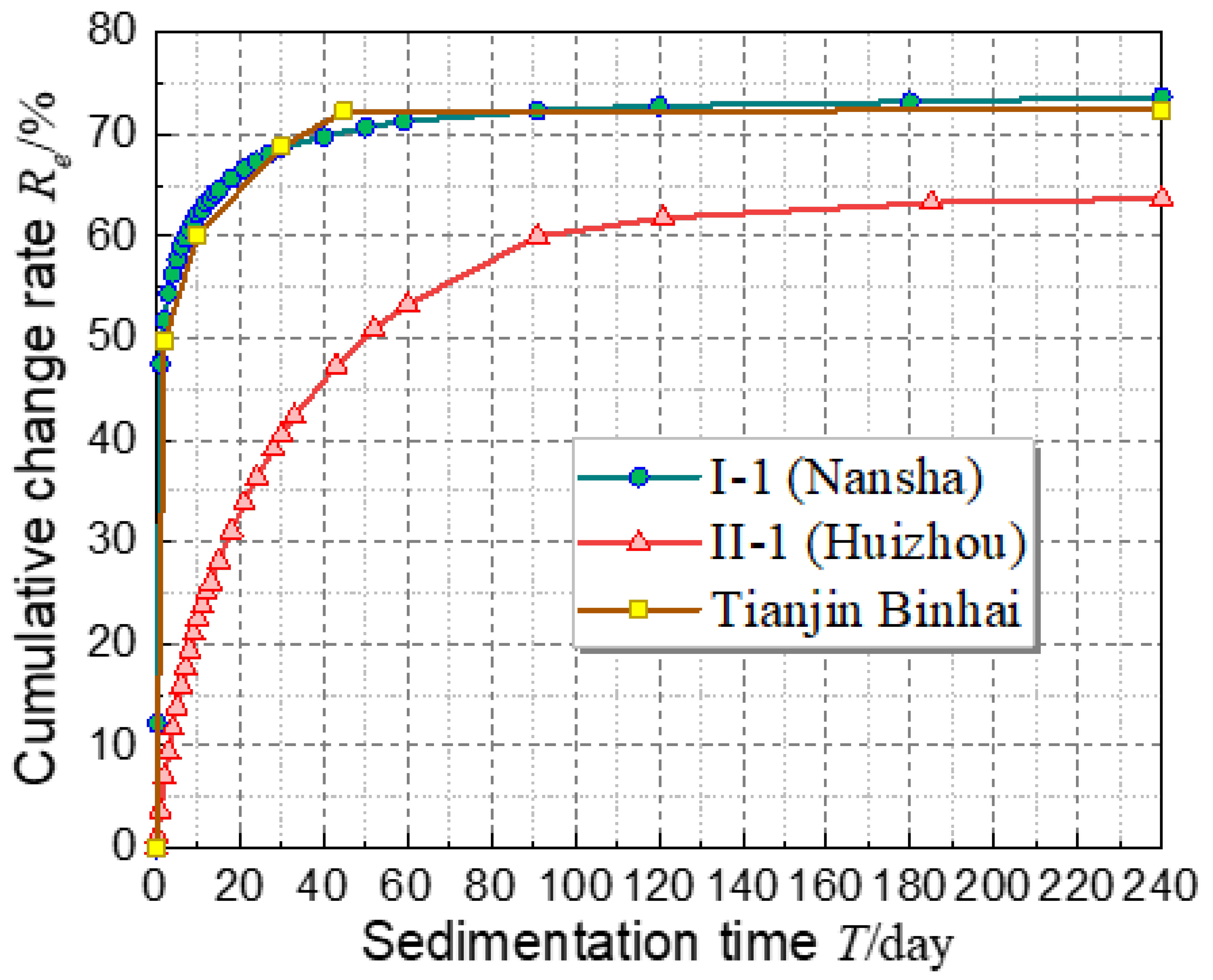
3.1. The Results of the Batch Sedimentation Experiments
3.2. The Results of the Low-Pressure Consolidation and In Situ Shear Tests
4. Theoretical Analyses
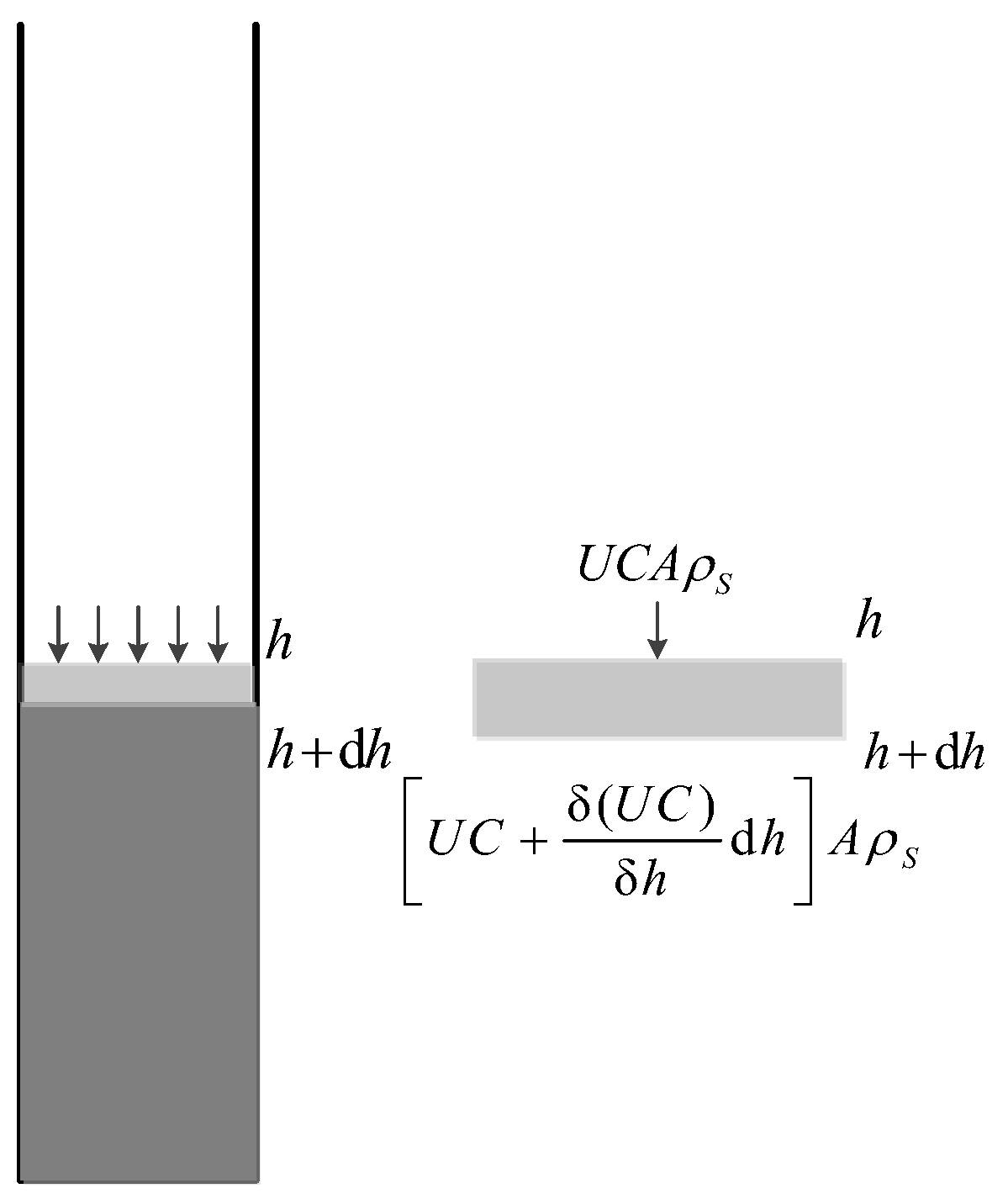
4.1. Characteristics Analysis and Stable Evaluation Criteria of the Batch Sedimentation Process
4.2. Characteristics Analysis of the Low-Pressure Consolidation
4.3. Settlement Prediction Method on the Batch Sedimentation and the Low-Pressure Consolidation Processes
5. Conclusions
- (1)
- The clay (d < 0.005 mm) content is a main factor affecting the batch settlement and consolidation characteristics of dredged mud slurry; dredged mud slurry with higher clay content will have greater drainage resistance; thus, the consolidation effect will be worse.
- (2)
- It was suggested that, for dredged fill whose clay content is within 40~60%, the cumulative change rate of average pore ratio of 60~75% could be used as the steady-state evaluation criteria for the batch sedimentation process, which can also be used to predict the best starting time for vacuum preloading treatment.
- (3)
- The compression curves e-P and e-lgP of the dredged mud slurry during the batch sedimentation have clear concave turning points, which are quite different from those of ordinary soft soil.
- (4)
- A settlement prediction method that considers both the batch sedimentation and the low-pressure consolidation processes was developed. The prediction can easily be realized by using the initial physical parameters of the dredged mud slurry along with the cumulative rate Re of the average void ratio of the laboratory sedimentation experiment and the compression index CC-low of the low-pressure consolidation experiment.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Imai, G. Experimental studies on sedimentation mechanism and sediment formation of clay materials. Soils Found. 1981, 21, 7–20. [Google Scholar] [CrossRef]
- Zhu, W.; Min, F.L.; Lü, Y.Y.; Wang, S.; Sun, Z.; Zhang, C.; Li, L. Subject of “mud science and application technology” and its research progress. Rock Soil Mech. 2013, 34, 3041–3054. (In Chinese) [Google Scholar]
- Bao, S.-F.; Lou, Y.; Dong, Z.-L.; Mo, H.-H.; Chen, P.-S.; Zhou, R.-B. Causes and countermeasures for vacuum consolidation failure of newly-dredged mud foundation. Chin. J. Geotech. Eng. 2014, 36, 1350–1359. (In Chinese) [Google Scholar]
- Shi, L.; Wang, J.; Wang, X.; Sun, H.; Yu, Y.; Cai, Y. How energy is consumed in vacuum preloading treatment of soft ground. Géotechnique 2023, 1–13. [Google Scholar] [CrossRef]
- Balmforth, N.J.; Frigaard, I.A.; Ovarlez, G. Yielding to stress: Recent developments in viscoplastic fluid mechanics. Annu. Rev. Fluid Mech. 2014, 46, 121–146. [Google Scholar] [CrossRef]
- Indraratna, B.; Sathananthan, I.; Rujikiatkamjorn, C.; Balasubramaniam, A.S. Analytical and numerical modeling of soft soil stabilized by prefabricated vertical drains incorporating vacuum preloading. Int. J. Geomech. 2005, 5, 114–124. [Google Scholar] [CrossRef]
- Homede, E.; Zigelman, A.; Abezgauz, L.; Manor, O. Signatures of van der Waals and Electrostatic Forces in the Deposition of Nanoparticle Assemblies. J. Phys. Chem. Lett. 2018, 9, 5226–5232. [Google Scholar] [CrossRef]
- Fang, Y.; Guo, L.; Huang, J. Mechanism test on inhomogeneity of dredged fill during vacuum preloading consolidation. Mar. Georesources Geotechnol. 2019, 37, 1007–1017. [Google Scholar] [CrossRef]
- Terzaghi, K.; Peck, R.B.; Mesri, G. Soil Mechanics in Engineering Practice; John Wiley & Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Shan, W.; Chen, H.-E.; Yuan, X.; Ma, W.; Li, H. Mechanism of pore water seepage in soil reinforced by step vacuum preloading. Bull. Eng. Geol. Environ. 2021, 80, 2777–2787. [Google Scholar] [CrossRef]
- Wang, J.; Ni, J.; Cai, Y.; Fu, H.; Wang, P. Combination of vacuum preloading and lime treatment for improvement of dredged fill. Eng. Geol. 2017, 227, 149–158. [Google Scholar] [CrossRef]
- Wang, P.; Han, Y.; Zhou, Y.; Wang, J.; Cai, Y.; Xu, F.; Pu, H. Apparent clogging effect in vacuum-induced consolidation of dredged soil with prefabricated vertical drains. Geotext. Geomembr. 2020, 48, 524–531. [Google Scholar] [CrossRef]
- Xu, B.H.; He, N.; Jiang, Y.B.; Zhou, Y.Z.; Zhan, X.J. Experimental study on the clogging effect of dredged fill surrounding the PVD under vacuum preloading. Geotext. Geomembr. 2020, 48, 614–624. [Google Scholar] [CrossRef]
- Cai, Y.-Q. Consolidation mechanism of vacuum preloading for dredged slurry and anti-clogging method for drains. Yantu Gongcheng Xuebao/Chin. J. Geotech. Eng. 2021, 43, 201–225. (In Chinese) [Google Scholar]
- Nguyen, V.-T.; Le, V.-A. Fluid mud properties and nautical depth estimation: A case study in navigation channel of Duyen Hai Port, Vietnam. Ocean Eng. 2023, 284, 115163. [Google Scholar] [CrossRef]
- Kirsch, K.; Bell, A. Ground Improvement; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Liu, H.L.; Peng, J.; Chen, Y.H. Simplified method of ground settlement under vacuum combined surcharge preloading. Yantu Lixue (Rock Soil Mech.) 2006, 27, 745–748. (In Chinese) [Google Scholar]
- Zhang, X.-W.; Yang, A.-W.; Kong, L.-W.; Zhou, Q.; Wang, T. Self-weight sedimentation and consolidation characteristics of hydraulic-dredged slurry in Tianjin Binhai District. Chin. J. Geotech. Eng. 2016, 38, 769–776. (In Chinese) [Google Scholar]
- Guo, W.; Chu, J. New observational method for prediction of one-dimensional consolidation settlement. Géotechnique 2017, 67, 516–522. [Google Scholar] [CrossRef]
- François, B.; Corda, G. Experimental characterization and numerical modeling of the self-weight consolidation of a dredged mud. Geomech. Energy Environ. 2022, 29, 100274. [Google Scholar] [CrossRef]
- Ngo, D.H.; Horpibulsuk, S.; Suddeepong, A.; Hoy, M.; Udomchai, A.; Doncommul, P.; Rachan, R.; Arulrajah, A. Consolidation behavior of dredged ultra-soft soil improved with prefabricated vertical drain at the Mae Moh mine, Thailand. Geotext. Geomembr. 2020, 48, 561–571. [Google Scholar] [CrossRef]
- Loginov, M.; Citeau, M.; Lebovka, N.; Vorobiev, E. Evaluation of low-pressure compressibility and permeability of bentonite sediment from centrifugal consolidation data. Sep. Purif. Technol. 2012, 92, 168–173. [Google Scholar] [CrossRef]
- He, B.; Qin, X.; Zhou, Z.; Xu, B.; Yu, S.; Qin, G.; Liu, K.; Peng, X.; Nie, X.; Ma, F.; et al. Experimental study on composite flocculant-electroosmosis combined with seg-mented solidification treatment of high-water-content slurry. Constr. Build. Mater. 2023, 400, 132729. [Google Scholar] [CrossRef]
- Chen, X.; Qi, S.; Simms, P.; Zhou, J.-W.; Yang, X.-G. Characterization of large strain consolidation parameters of soft materials with time-variant compressibility at low effective stress. Soils Found. 2022, 62, 101240. [Google Scholar] [CrossRef]
- Qin, J.; Zheng, J.; Li, L. An analytical solution to estimate the settlement of tailings or backfill slurry by considering the sedimentation and consolidation. Int. J. Min. Sci. Technol. 2021, 31, 463–471. [Google Scholar] [CrossRef]
- Das, B.M. Soil Mechanics Laboratory Manual, 6th ed.; Oxford University Press: New York, NY, USA, 2002. [Google Scholar]
- ASTM D2487-17; Standard Practice for Classification of Soils for Engineering Purposes (Unified Soil Classification System). ASTM International: West Conshohocken, PA, USA, 2017.
- Islam, S.; Williams, D.J.; Bhuyan, M.H. Consolidation testing of tailings in a slurry consolidometer using constant rate and accelerated loading. Proc. Inst. Civ. Eng.-Geotech. Eng. 2021, 176, 295–305. [Google Scholar] [CrossRef]
- ASTM D7181-20; Standard Test Method for Consolidated Drained Triaxial Compression Test for Soils. ASTM International: West Conshohocken, PA, USA, 2020.
- GB/T 50123–2019; Standard for Geotechnical Testing Method. National Standards of People’s Republic of China, China Planning Press: Beijing, China, 2019.
- Raheena, M.; Robinson, R.G. End-of-primary consolidation parameters using inflection point method. Géotechnique 2021, 71, 645–654. [Google Scholar] [CrossRef]
- Oliveira, F.S.; Martins, I.S.M.; Guimarães, L.J.N. A model for one-dimensional consolidation of clayey soils with non-linear viscosity. Comput. Geotech. 2023, 159, 105426. [Google Scholar] [CrossRef]
- Le, T.; Airey, D. Mechanical behaviour of a weakly structured soil at low confining stress. Géotechnique 2023, 73, 128–142. [Google Scholar] [CrossRef]
- Tan, T.S.; Yong, K.Y.; Leong, E.C.; Lee, S.L. Sedimentation of clayey slurry. J. Geotech. Eng. 1990, 116, 885–898. [Google Scholar] [CrossRef]
- Holdich, R.G.; Rushton, A.; Ward, A.S. Solid-Liquid Filtration and Separation Technology; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Wills, B.A.; Finch, J. Wills’ Mineral Processing Technology: An Introduction to the Practical Aspects of Ore Treatment and Mineral Recovery; Butterworth-Heinemann: Oxford, UK, 2015. [Google Scholar]
- Kynch, G.J. A theory of sedimentation. Trans. Faraday Soc. 1952, 48, 166–176. [Google Scholar] [CrossRef]
- Richardson, J.F.; Zaki, W.N. Sedimentation and fluidization: Part I. Chem. Eng. Res. Des. 1997, 75, S82–S100. [Google Scholar] [CrossRef]
- Yang, A.W.; Du, D.J.; Lu, L.Q. Study on sediment characteristics and micro-structure of soft dredger soil of Tianjin. Hydrogeol. Eng. Geol. 2010, 37, 83–87. (In Chinese) [Google Scholar]






| Property or Composition | Unit | Sample I (Nansha) | Sample II (Huizhou) |
|---|---|---|---|
| Specific gravity Gs | - | 2.712 | 2.703 |
| Water content w | % | 380.0 | 548.0 |
| Density ρ | g/cm3 | 1.15 | 1.12 |
| Liquid limit wL | % | 50.8 | 56.9 |
| Plastic limit wP | % | 24.4 | 40.6 |
| Medium sand (d = 0.50~0.25 mm) | % | 1.45 | 1.25 |
| Fine sand (d = 0.25~0.075 mm) | % | 20.75 | 0.90 |
| Silt (d = 0.075~0.005 mm) | % | 37.10 | 36.95 |
| Clayey particles (d < 0.005 mm) | % | 40.70 | 60.90 |
| Samples | Parameters for Calculations | Error | ||||||
|---|---|---|---|---|---|---|---|---|
| H0/m | w0/% | Gs | Re | Cc-low | ||||
| Sample I | 1.2 | 380 | 2.712 | 73.7 | 1.326 | 1.023 | 1.022 | 0.1% |
| Sample II | 1.2 | 548 | 2.703 | 63.7 | 2.180 | 0.967 | 1.027 | 5.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, S.; Guo, L.; Dong, Z.; Zhou, R.; Zhou, S.; Chen, J. Batch Settling and Low-Pressure Consolidation Behaviors of Dredged Mud Slurry: Steady-State Evaluation and Mechanism Study. Water 2024, 16, 7. https://doi.org/10.3390/w16010007
Bao S, Guo L, Dong Z, Zhou R, Zhou S, Chen J. Batch Settling and Low-Pressure Consolidation Behaviors of Dredged Mud Slurry: Steady-State Evaluation and Mechanism Study. Water. 2024; 16(1):7. https://doi.org/10.3390/w16010007
Chicago/Turabian StyleBao, Shufeng, Lingfeng Guo, Zhiliang Dong, Ruibo Zhou, Shuangxi Zhou, and Jian Chen. 2024. "Batch Settling and Low-Pressure Consolidation Behaviors of Dredged Mud Slurry: Steady-State Evaluation and Mechanism Study" Water 16, no. 1: 7. https://doi.org/10.3390/w16010007
APA StyleBao, S., Guo, L., Dong, Z., Zhou, R., Zhou, S., & Chen, J. (2024). Batch Settling and Low-Pressure Consolidation Behaviors of Dredged Mud Slurry: Steady-State Evaluation and Mechanism Study. Water, 16(1), 7. https://doi.org/10.3390/w16010007








