Optimization of Injection Methods in the Microbially Induced Calcite Precipitation Process by Using a Field Scale Numerical Model
Abstract
:1. Introduction
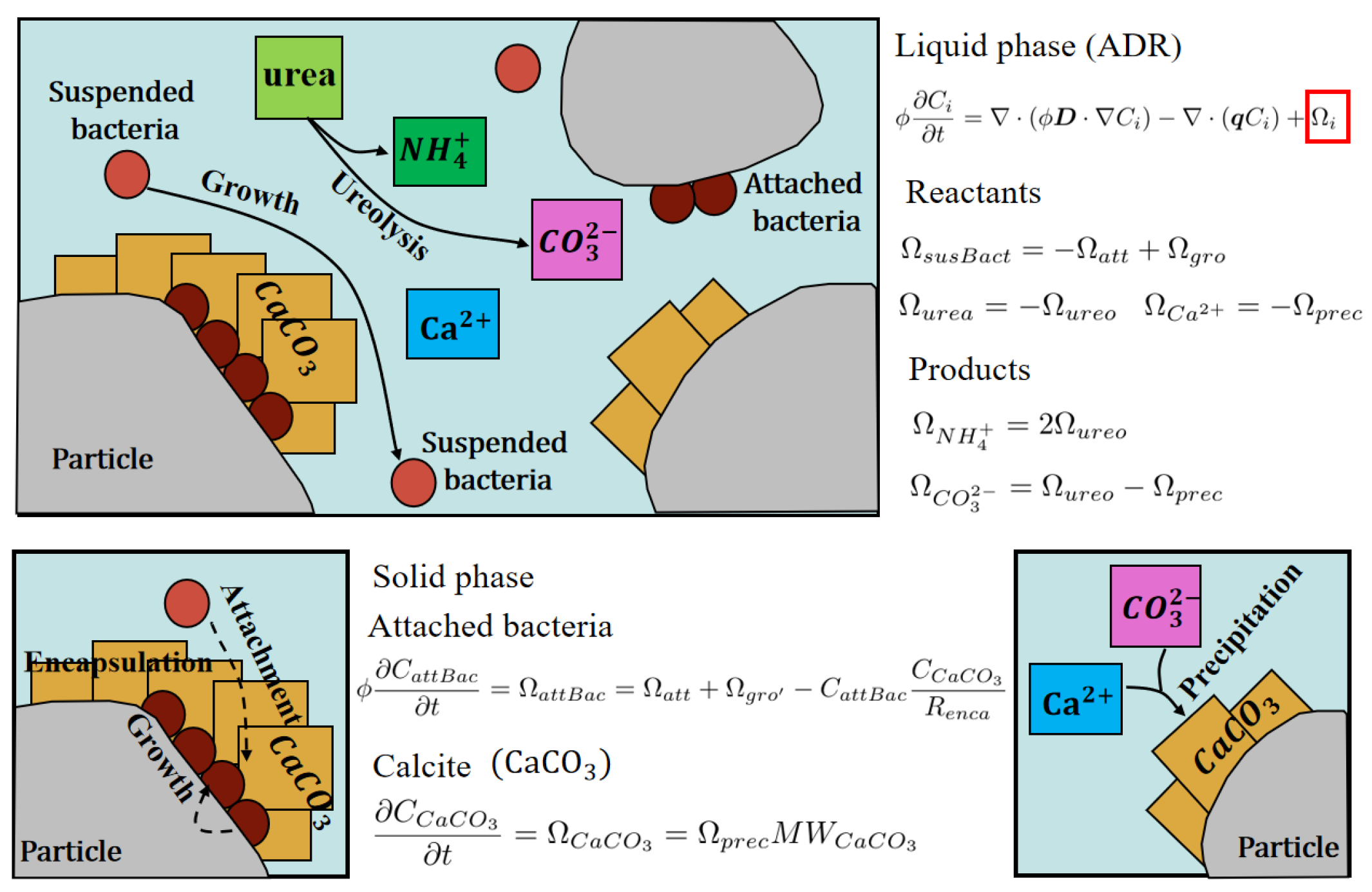
2. Model Concept
2.1. Model Assumptions
- The flow in porous media is fully saturated and incompressible, with constant viscosity. Additionally, simulations of unsaturated flow are not taken into account.
- The reaction process is only divided into two phases: the liquid phase and the solid phase. In the liquid phase, the metabolism of suspended bacteria and ureolysis take place, while in the solid phase, the attached bacteria metabolism and precipitation occur.
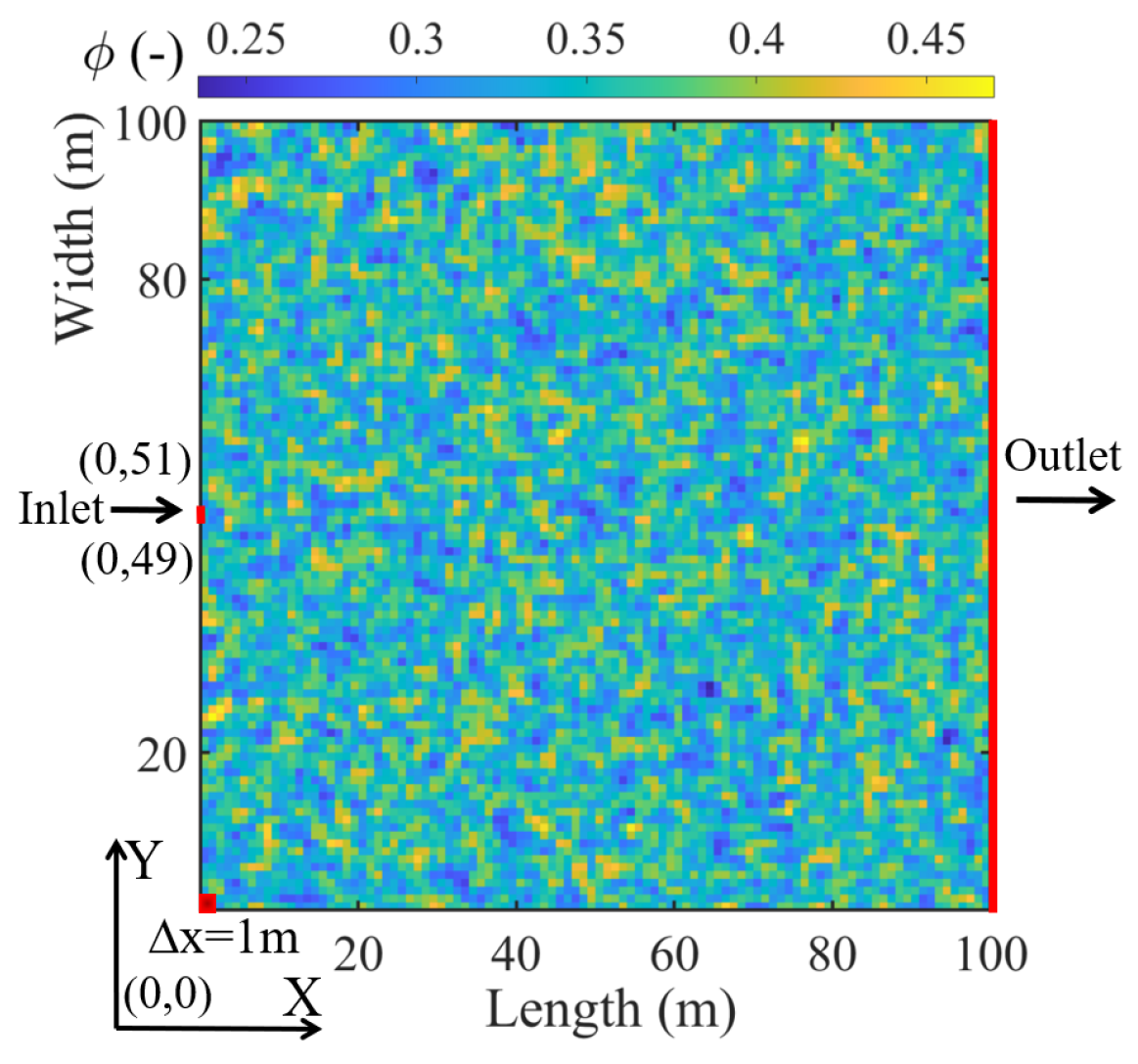
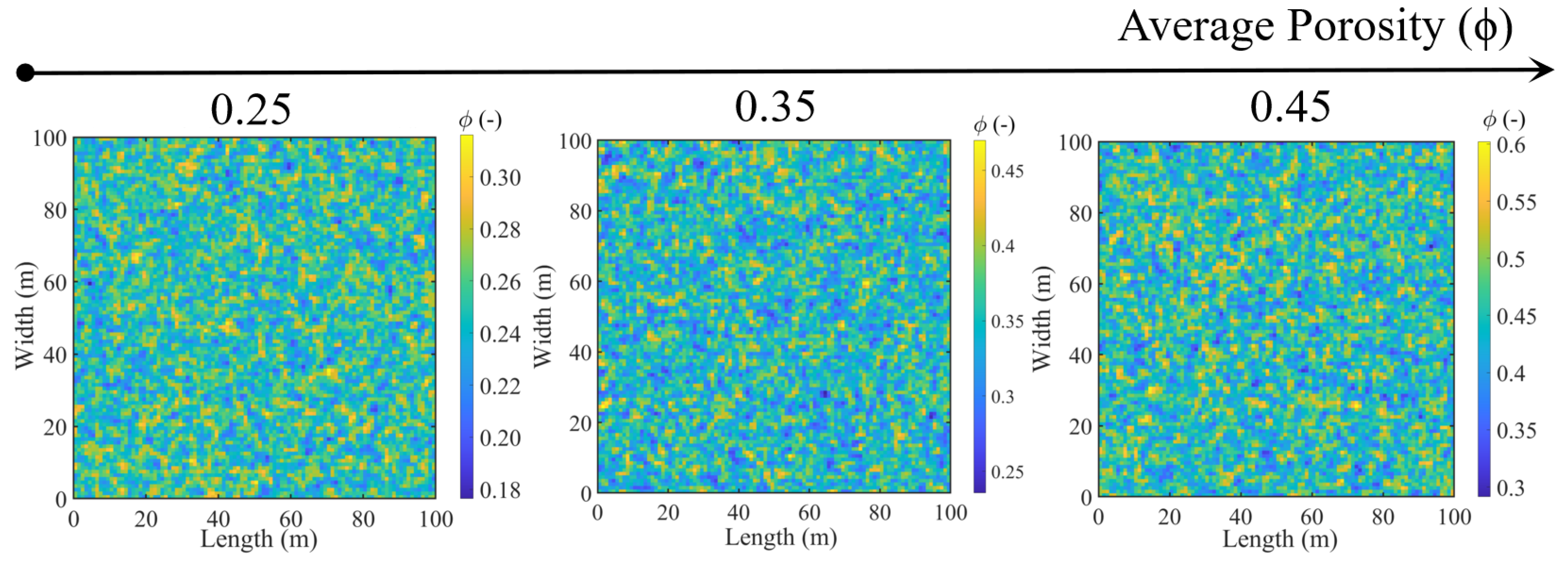
- To effectively investigate the influence of injection strategies, the initial pH and temperature are the same in the following simulated tests. The initial pH is 7, and the temperature is 25 °C [43]. The influence of pH, temperature, and gravity on the reaction process is not considered. The porous media are quantified by porosity in heterogeneity.
2.2. Flow Model
2.3. Mass Transport and Biochemical Reaction Model
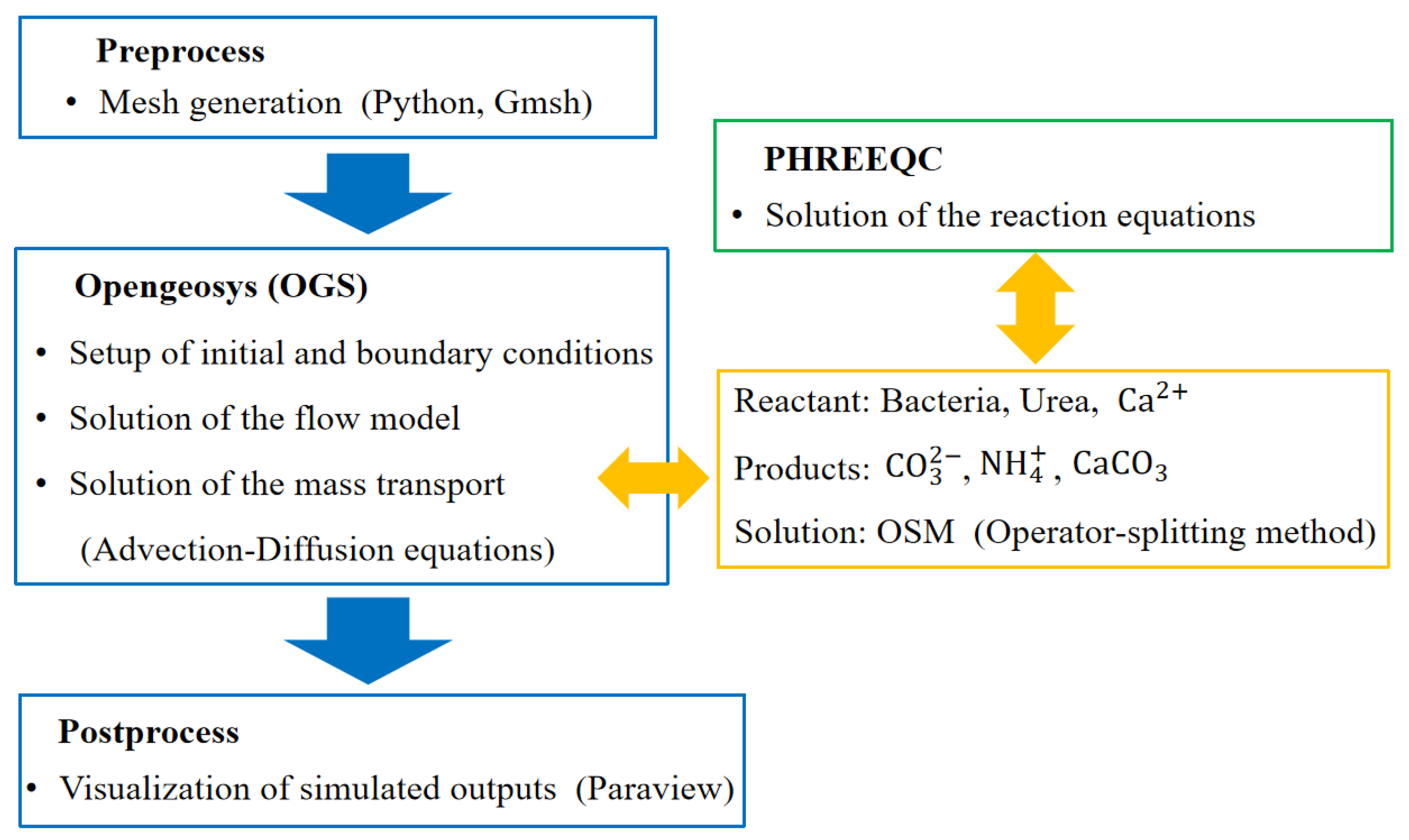
2.4. Numerical Simulation Scheme
3. Results
3.1. Effect of Injection Methods (Case 1)
3.2. Effect of Soil Types under Different Injection Methods (Case 2)
3.3. Effect of Substance Concentrations under Different Injection Methods (Case 3)
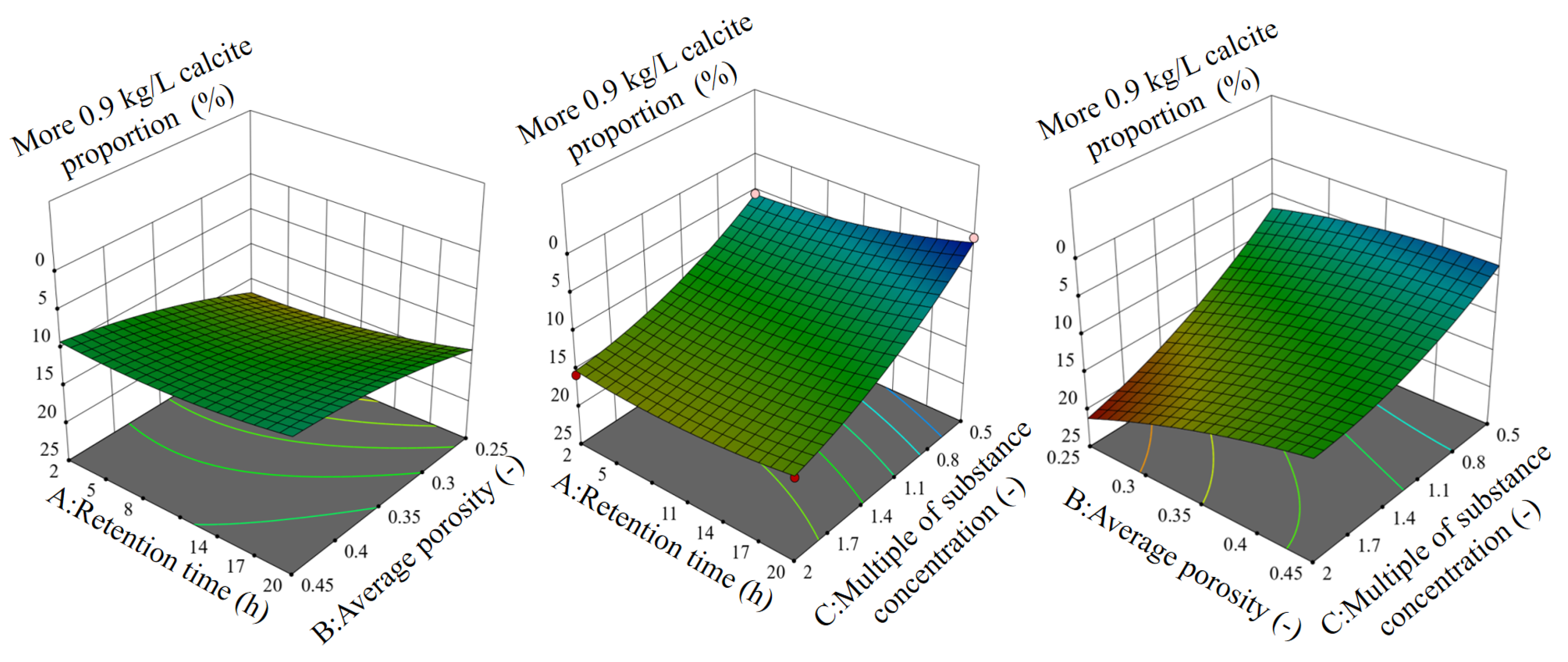
3.4. Analysis by the Orthogonal Experiments
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Information in the Simulation
| Inlet Boundary | Outlet Boundary | |
|---|---|---|
| Flow |
| Parameter | Unit | Description | Value | Reference | |
|---|---|---|---|---|---|
| Model design | A | m2 | Computed domain | Assumed | |
| m | Mesh length | ||||
| L · h−1 | Flow rate | 0.35 | [69] | ||
| m · s−1 | Inflow velocity | ||||
| OD600 | Attached bacteria concentration | 1.538 | |||
| M | Urea concentration | 1.1 | |||
| M | concentration | 1.1 | |||
| Hydrodynamics | m2 · s−1 | Diffusion coefficient | [49] | ||
| m | Longitudinal dispersion length | 0.001 | [62] | ||
| P | Pa | Reference pressure | |||
| Permeability | - | Original effective porosity | 0.35 | Assumed | |
| Pa · s | Kinematic viscosity of liquid | [62] | |||
| m2 | Basic permeability | [49] | |||
| Bacteria | s−1 | Attachment rate | Validated | ||
| metabolism | s−1 | Straining rate | |||
| s−1 | Growth rate | ||||
| kg · m−3 · s−1 | Encapsulation rate constant | 12 | [49] | ||
| − | Velocity dependence | 1 | |||
| − | Neighbor attachment cells | 1 | |||
| Ureolysis | s−1 | Ureolysis rate | Validated | ||
| M | Half saturation constant | 0.301 | [49] | ||
| M | Ammonium inhibition constant | 0.22 | |||
| Precipitation | s−1 | Precipitation rate constant | 0.01 | ||
| kg · m−3 | Bulk density of calcite | 1620 | Standard value | ||
| kg · m−3 · M−1 | Calcite molecular weight | 100.0869 |
Appendix B. Information in the Orthogonal Experiments
| Simulated | A: Retention | B: Average | C: Multiple of | D: Additional | Y1: Total Calcite | Y2: More 0.9 kg/L Calcite |
|---|---|---|---|---|---|---|
| Group | Time (h) | Porosity (-) | Concentration (-) | Time (h) | Mass (kg) | Concentration Proportion (%) |
| 1 | 10 | 0.25 | 2 | 15 | 2408.36 | 21.2 |
| 2 | 2 | 0.35 | 2 | 15 | 1903.31 | 16.49 |
| 3 | 10 | 0.35 | 1 | 15 | 1160.83 | 9.74 |
| 4 | 10 | 0.45 | 0.5 | 15 | 553.86 | 3.95 |
| 5 | 10 | 0.35 | 2 | 30 | 1752.43 | 15.36 |
| 6 | 20 | 0.35 | 0.5 | 15 | 687.59 | 0.52 |
| 7 | 2 | 0.25 | 1 | 15 | 1794.93 | 15.24 |
| 8 | 20 | 0.35 | 1 | 30 | 1210.85 | 7.27 |
| 9 | 10 | 0.45 | 2 | 15 | 1349.38 | 11.72 |
| 10 | 10 | 0.35 | 2 | 0 | 1636.63 | 14.19 |
| 11 | 10 | 0.35 | 0.5 | 0 | 526.45 | 3.72 |
| 12 | 10 | 0.35 | 1 | 15 | 1160.83 | 9.74 |
| 13 | 10 | 0.35 | 0.5 | 30 | 718.47 | 5.19 |
| 14 | 2 | 0.35 | 1 | 0 | 1141.42 | 9.53 |
| 15 | 20 | 0.45 | 1 | 15 | 930.99 | 5.66 |
| 16 | 10 | 0.45 | 1 | 30 | 913.17 | 7.62 |
| 17 | 2 | 0.35 | 0.5 | 15 | 776.48 | 6.02 |
| 18 | 20 | 0.35 | 1 | 0 | 1134.6 | 6.98 |
| 19 | 10 | 0.25 | 1 | 30 | 1629.93 | 13.7 |
| 20 | 10 | 0.25 | 0.5 | 15 | 992.48 | 7.16 |
| 21 | 10 | 0.35 | 1 | 15 | 1160.83 | 9.74 |
| 22 | 2 | 0.35 | 1 | 30 | 1428.52 | 12.08 |
| 23 | 10 | 0.35 | 1 | 15 | 1160.83 | 9.74 |
| 24 | 20 | 0.25 | 1 | 15 | 1626.67 | 9.56 |
| 25 | 20 | 0.35 | 1 | 15 | 1709.93 | 14.26 |
| 26 | 10 | 0.35 | 1 | 15 | 1160.83 | 9.74 |
| 27 | 10 | 0.25 | 1 | 0 | 1542.76 | 13.07 |
| 28 | 10 | 0.45 | 1 | 0 | 862.07 | 7.1 |
| 29 | 2 | 0.45 | 1 | 15 | 1002.1 | 8.3 |
| Std. Dev. | C.V. (%) | R | Adjusted R | Predicted R | |
|---|---|---|---|---|---|
| Y1 | 31.47 | 2.58 | 0.9974 | 0.9947 | 0.9834 |
| Y2 | 0.4364 | 4.53 | 0.9950 | 0.9900 | 0.9669 |
References
- Morgan, R.P.C. Soil Erosion and Conservation; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Huang, J.; Yu, H.; Guan, X.; Wang, G.; Guo, R. Accelerated dryland expansion under climate change. Nat. Clim. Chang. 2016, 6, 166–171. [Google Scholar] [CrossRef]
- Chung, H.; Kim, S.H.; Nam, K. Application of microbially induced calcite precipitation to prevent soil loss by rainfall: Effect of particle size and organic matter content. J. Soils Sediments 2021, 21, 2744–2754. [Google Scholar] [CrossRef]
- Zhang, K.; Tang, C.S.; Jiang, N.J.; Pan, X.H.; Liu, B.; Wang, Y.J.; Shi, B. Microbial-induced carbonate precipitation (MICP) technology: A review on the fundamentals and engineering applications. Environ. Earth Sci. 2023, 82, 229. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Xu, X.; Liu, J.; Mao, W. Centrifuge modeling of seismic response and failure mode of a slope reinforced by a pile-anchor structure. Soil Dyn. Earthq. Eng. 2020, 131, 106037. [Google Scholar] [CrossRef]
- Domènech, G.; Fan, X.; Scaringi, G.; van Asch, T.W.; Xu, Q.; Huang, R.; Hales, T.C. Modelling the role of material depletion, grain coarsening and revegetation in debris flow occurrences after the 2008 Wenchuan earthquake. Eng. Geol. 2019, 250, 34–44. [Google Scholar] [CrossRef]
- Kou, H.L.; Wu, C.Z.; Ni, P.P.; Jang, B.A. Assessment of erosion resistance of biocemented sandy slope subjected to wave actions. Appl. Ocean. Res. 2020, 105, 102401. [Google Scholar] [CrossRef]
- Gong, W.; Juang, C.H.; Wasowski, J. Geohazards and human settlements: Lessons learned from multiple relocation events in Badong, China–Engineering geologist’s perspective. Eng. Geol. 2021, 285, 106051. [Google Scholar] [CrossRef]
- Huang, Y.; He, Z.; Yashima, A.; Chen, Z.; Li, C. Multi-objective optimization design of pile-anchor structures for slopes based on reliability theory considering the spatial variability of soil properties. Comput. Geotech. 2022, 147, 104751. [Google Scholar] [CrossRef]
- Huang, Y.; Xu, X.; Mao, W. Numerical performance assessment of slope reinforcement using a pile-anchor structure under seismic loading. Soil Dyn. Earthq. Eng. 2020, 129, 105963. [Google Scholar] [CrossRef]
- Singh, A.K. Bioengineering techniques of slope stabilization and landslide mitigation. Disaster Prev. Manag. Int. J. 2010, 19, 384–397. [Google Scholar] [CrossRef]
- Liu, J.; Shi, B.; Jiang, H.; Huang, H.; Wang, G.; Kamai, T. Research on the stabilization treatment of clay slope topsoil by organic polymer soil stabilizer. Eng. Geol. 2011, 117, 114–120. [Google Scholar] [CrossRef]
- Salifu, E.; MacLachlan, E.; Iyer, K.R.; Knapp, C.W.; Tarantino, A. Application of microbially induced calcite precipitation in erosion mitigation and stabilisation of sandy soil foreshore slopes: A preliminary investigation. Eng. Geol. 2016, 201, 96–105. [Google Scholar] [CrossRef]
- Giupponi, L.; Borgonovo, G.; Giorgi, A.; Bischetti, G.B. How to renew soil bioengineering for slope stabilization: Some proposals. Landsc. Ecol. Eng. 2019, 15, 37–50. [Google Scholar] [CrossRef]
- Gowthaman, S.; Mitsuyama, S.; Nakashima, K.; Komatsu, M.; Kawasaki, S. Biogeotechnical approach for slope soil stabilization using locally isolated bacteria and inexpensive low-grade chemicals: A feasibility study on Hokkaido expressway soil, Japan. Soils Found. 2019, 59, 484–499. [Google Scholar] [CrossRef]
- Archibong, G.; Sunday, E.; Akudike, J.; Okeke, O.; Amadi, C. A review of the principles and methods of soil stabilization. Int. J. Adv. Acad. Res. Sci. 2020, 6, 2488–9849. [Google Scholar]
- Moghal, A.A.B.; Rasheed, R.M.; Mohammed, S.A.S. Sorptive and desorptive response of divalent heavy metal ions from EICP-treated plastic fines. Indian Geotech. J. 2023, 53, 315–333. [Google Scholar] [CrossRef]
- Chittoori, B.C.; Rahman, T.; Burbank, M.; Moghal, A.A.B. Evaluating shallow mixing protocols as application methods for microbial induced calcite precipitation targeting expansive soil treatment. In Eighth International Conference on Case Histories in Geotechnical Engineering; American Society of Civil Engineers: Reston, VA, USA, 2019; pp. 250–259. [Google Scholar]
- Punetha, P.; Samanta, M.; Sarkar, S. Bioengineering as an effective and ecofriendly soil slope stabilization method: A review. In Landslides: Theory, Practice and Modelling; Springer: Berlin/Heidelberg, Germany, 2019; pp. 201–224. [Google Scholar]
- Harran, R.; Terzis, D.; Laloui, L. Mechanics, Modeling, and Upscaling of Biocemented Soils: A Review of Breakthroughs and Challenges. Int. J. Geomech. 2023, 23, 03123004. [Google Scholar] [CrossRef]
- Shan, Y.; Zhao, J.; Tong, H.; Yuan, J.; Lei, D.; Li, Y. Effects of activated carbon on liquefaction resistance of calcareous sand treated with microbially induced calcium carbonate precipitation. Soil Dyn. Earthq. Eng. 2022, 161, 107419. [Google Scholar] [CrossRef]
- Dejong, J.T.; Soga, K.; Kavazanjian, E.; Burns, S.; Van Paassen, L.; Al Qabany, A.; Aydilek, A.; Bang, S.; Burbank, M.; Caslake, L.F.; et al. Biogeochemical processes and geotechnical applications: Progress, opportunities and challenges. In Bio- and Chemo-Mechanical Processes in Geotechnical Engineering: Géotechnique Symposium in Print 2013; Ice Publishing: Washington, DC, USA, 2014; pp. 143–157. [Google Scholar]
- Mujah, D.; Cheng, L.; Shahin, M.A. Microstructural and geomechanical study on biocemented sand for optimization of MICP process. J. Mater. Civ. Eng. 2019, 31, 04019025. [Google Scholar] [CrossRef]
- Osinubi, K.; Eberemu, A.; Ijimdiya, T.; Yakubu, S.; Gadzama, E.; Sani, J.; Yohanna, P. Review of the use of microorganisms in geotechnical engineering applications. SN Appl. Sci. 2020, 2, 207. [Google Scholar] [CrossRef]
- Wang, Y.; Konstantinou, C.; Soga, K.; DeJong, J.T.; Biscontin, G.; Kabla, A.J. Enhancing strength of MICP-treated sandy soils: From micro to macro scale. arXiv 2020, arXiv:2006.15760. [Google Scholar]
- Wani, K.S.; Mir, B. Influence of microbial geo-technology in the stabilization of dredged soils. Int. J. Geotech. Eng. 2021, 15, 235–244. [Google Scholar] [CrossRef]
- Yu, T.; Souli, H.; Péchaud, Y.; Fleureau, J.M. Optimizing protocols for microbial induced calcite precipitation (MICP) for soil improvement–a review. Eur. J. Environ. Civ. Eng. 2022, 26, 2218–2233. [Google Scholar] [CrossRef]
- Lee, M.; Kolbus, C.M.; Yepez, A.D.; Gomez, M.G. Investigating ammonium by-product removal following stimulated ureolytic microbially-induced calcite precipitation. In Proceedings of the Eighth International Conference on Case Histories in Geotechnical Engineering, Philadelphia, PA, USA, 24–27 March 2019; pp. 260–272. [Google Scholar]
- Mohsenzadeh, A.; Aflaki, E.; Gowthaman, S.; Nakashima, K.; Kawasaki, S.; Ebadi, T. A two-stage treatment process for the management of produced ammonium by-products in ureolytic bio-cementation process. Int. J. Environ. Sci. Technol. 2022, 19, 449–462. [Google Scholar] [CrossRef]
- Wang, X.; Nackenhorst, U. A coupled bio-chemo-hydraulic model to predict porosity and permeability reduction during microbially induced calcite precipitation. Adv. Water Resour. 2020, 140, 103563. [Google Scholar] [CrossRef]
- Rajasekar, A.; Wilkinson, S.; Moy, C.K. MICP as a potential sustainable technique to treat or entrap contaminants in the natural environment: A review. Environ. Sci. Ecotechnol. 2021, 6, 100096. [Google Scholar] [CrossRef]
- Whiffin, V.S. Microbial CaCO3 Precipitation for the Production of Biocement. Ph.D. Thesis, Murdoch University, Murdoch, Australia, 2004. [Google Scholar]
- Terzis, D.; Laloui, L. Cell-free soil bio-cementation with strength, dilatancy and fabric characterization. Acta Geotech. 2019, 14, 639–656. [Google Scholar] [CrossRef]
- Cheng, L.; Cord-Ruwisch, R.; Shahin, M.A. Cementation of sand soil by microbially induced calcite precipitation at various degrees of saturation. Can. Geotech. J. 2013, 50, 81–90. [Google Scholar] [CrossRef]
- van Paassen, L.A.; Ghose, R.; van der Linden, T.J.; van der Star, W.R.; van Loosdrecht, M.C. Quantifying biomediated ground improvement by ureolysis: Large-scale biogrout experiment. J. Geotech. Geoenviron. Eng. 2010, 136, 1721–1728. [Google Scholar] [CrossRef]
- Liu, L.; Liu, H.; Stuedlein, A.W.; Evans, T.M.; Xiao, Y. Strength, stiffness, and microstructure characteristics of biocemented calcareous sand. Can. Geotech. J. 2019, 56, 1502–1513. [Google Scholar] [CrossRef]
- Terzis, D.; Laloui, L. A decade of progress and turning points in the understanding of bio-improved soils: A review. Geomech. Energy Environ. 2019, 19, 100116. [Google Scholar] [CrossRef]
- Almajed, A.; Lateef, M.A.; Moghal, A.A.B.; Lemboye, K. State-of-the-art review of the applicability and challenges of microbial-induced calcite precipitation (MICP) and enzyme-induced calcite precipitation (EICP) techniques for geotechnical and geoenvironmental applications. Crystals 2021, 11, 370. [Google Scholar] [CrossRef]
- Hammes, F.; Boon, N.; de Villiers, J.; Verstraete, W.; Siciliano, S.D. Strain-specific ureolytic microbial calcium carbonate precipitation. Appl. Environ. Microbiol. 2003, 69, 4901–4909. [Google Scholar] [CrossRef] [PubMed]
- Park, S.J.; Park, Y.M.; Chun, W.Y.; Kim, W.J.; Ghim, S.Y. Calcite-forming bacteria for compressive strength improvement in mortar. J. Microbiol. Biotechnol. 2010, 20, 782–788. [Google Scholar] [PubMed]
- Lv, C.; Tang, C.S.; Zhang, J.Z.; Pan, X.H.; Liu, H. Effects of calcium sources and magnesium ions on the mechanical behavior of MICP-treated calcareous sand: Experimental evidence and precipitated crystal insights. Acta Geotech. 2023, 18, 2703–2717. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, H.; Cheng, X. Role of calcium sources in the strength and microstructure of microbial mortar. Constr. Build. Mater. 2015, 77, 160–167. [Google Scholar] [CrossRef]
- Tang, C.S.; Yin, L.y.; Jiang, N.j.; Zhu, C.; Zeng, H.; Li, H.; Shi, B. Factors affecting the performance of microbial-induced carbonate precipitation (MICP) treated soil: A review. Environ. Earth Sci. 2020, 79, 1–23. [Google Scholar] [CrossRef]
- Sharma, A.; Ramkrishnan, R. Study on effect of microbial induced calcite precipitates on strength of fine grained soils. Perspect. Sci. 2016, 8, 198–202. [Google Scholar] [CrossRef]
- Kim, G.; Kim, J.; Youn, H. Effect of temperature, pH, and reaction duration on microbially induced calcite precipitation. Appl. Sci. 2018, 8, 1277. [Google Scholar] [CrossRef]
- Peng, J.; Feng, Q.-P.; Sun, Y.-C. Influences of temperatures on MICP-treated soils. Chin. J. Geotech. Eng. 2018, 40, 1048–1055. [Google Scholar]
- Fu, T.; Saracho, A.C.; Haigh, S.K. Microbially induced carbonate precipitation (MICP) for soil strengthening: A comprehensive review. Biogeotechnics 2023, 2023, 100002. [Google Scholar] [CrossRef]
- Kadhim, F.J.; Zheng, J. Review of the factors that influence on the microbial induced calcite precipitation. Civ. Environ. Res. 2016, 8, 69–76. [Google Scholar]
- Minto, J.M.; Lunn, R.J.; El Mountassir, G. Development of a reactive transport model for field-scale simulation of microbially induced carbonate precipitation. Water Resour. Res. 2019, 55, 7229–7245. [Google Scholar] [CrossRef]
- Stocks-Fischer, S.; Galinat, J.K.; Bang, S.S. Microbiological precipitation of CaCO3. Soil Biol. Biochem. 1999, 31, 1563–1571. [Google Scholar] [CrossRef]
- Gebru, K.A.; Kidanemariam, T.G.; Gebretinsae, H.K. Bio-cement production using microbially induced calcite precipitation (MICP) method: A review. Chem. Eng. Sci. 2021, 238, 116610. [Google Scholar] [CrossRef]
- Whiffin, V.S.; Van Paassen, L.A.; Harkes, M.P. Microbial carbonate precipitation as a soil improvement technique. Geomicrobiol. J. 2007, 24, 417–423. [Google Scholar] [CrossRef]
- Wang, Y.; Konstantinou, C.; Soga, K.; Biscontin, G.; Kabla, A.J. Use of microfluidic experiments to optimize MICP treatment protocols for effective strength enhancement of MICP-treated sandy soils. Acta Geotech. 2022, 17, 3817–3838. [Google Scholar] [CrossRef]
- Cheng, L.; Shahin, M.A.; Cord-Ruwisch, R. Surface percolation for soil improvement by biocementation utilizing in situ enriched indigenous aerobic and anaerobic ureolytic soil microorganisms. Geomicrobiol. J. 2017, 34, 546–556. [Google Scholar] [CrossRef]
- Feng, K.; Montoya, B. Influence of confinement and cementation level on the behavior of microbial-induced calcite precipitated sands under monotonic drained loading. J. Geotech. Geoenviron. Eng. 2016, 142, 04015057. [Google Scholar] [CrossRef]
- Soon, N.W.; Lee, L.M.; Khun, T.C.; Ling, H.S. Factors affecting improvement in engineering properties of residual soil through microbial-induced calcite precipitation. J. Geotech. Geoenviron. Eng. 2014, 140, 04014006. [Google Scholar] [CrossRef]
- Martinez, B.; DeJong, J.; Ginn, T.; Montoya, B.; Barkouki, T.; Hunt, C.; Tanyu, B.; Major, D. Experimental optimization of microbial-induced carbonate precipitation for soil improvement. J. Geotech. Geoenviron. Eng. 2013, 139, 587–598. [Google Scholar] [CrossRef]
- Faeli, Z.; Montoya, B.M.; Gabr, M.A. Elucidating factors governing MICP biogeochemical processes at macro-scale: A reactive transport model development. Comput. Geotech. 2023, 160, 105514. [Google Scholar] [CrossRef]
- Dawoud, O.; Chen, C.; Soga, K. Microbial-induced calcite precipitation (MICP) using surfactants. In Proceedings of the Geo-Congress 2014: Geo-Characterization and Modeling for Sustainability, Atlanta, GA, USA, 23–26 February 2014; pp. 1635–1643. [Google Scholar]
- Choi, S.G.; Chang, I.; Lee, M.; Lee, J.H.; Han, J.T.; Kwon, T.H. Review on geotechnical engineering properties of sands treated by microbially induced calcium carbonate precipitation (MICP) and biopolymers. Constr. Build. Mater. 2020, 246, 118415. [Google Scholar] [CrossRef]
- Saricicek, Y.E.; Gurbanov, R.; Pekcan, O.; Gozen, A.G. Comparison of microbially induced calcium carbonate precipitation eligibility using sporosarcina pasteurii and bacillus licheniformis on two different sands. Geomicrobiol. J. 2019, 36, 42–52. [Google Scholar] [CrossRef]
- Van Wijngaarden, W.; Van Paassen, L.; Vermolen, F.; Van Meurs, G.; Vuik, C. A reactive transport model for biogrout compared to experimental data. Transp. Porous Media 2016, 111, 627–648. [Google Scholar] [CrossRef]
- GGNN, A.; Kawasaki, S. Factors affecting sand solidification using MICP with Pararhodobacter sp. Mater. Trans. 2018, 59, 72–81. [Google Scholar]
- Wang, X.; Nackenhorst, U. Micro-feature-motivated numerical analysis of the coupled bio-chemo-hydro-mechanical behaviour in MICP. Acta Geotech. 2022, 17, 4537–4553. [Google Scholar] [CrossRef]
- Kolditz, O.; Bauer, S.; Bilke, L.; Böttcher, N.; Delfs, J.O.; Fischer, T.; Görke, U.J.; Kalbacher, T.; Kosakowski, G.; McDermott, C.; et al. OpenGeoSys: An open-source initiative for numerical simulation of thermo-hydro-mechanical/chemical (THM/C) processes in porous media. Environ. Earth Sci. 2012, 67, 589–599. [Google Scholar] [CrossRef]
- Charlton, S.R.; Parkhurst, D.L. Modules based on the geochemical model PHREEQC for use in scripting and programming languages. Comput. Geosci. 2011, 37, 1653–1663. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Appelo, C. Description of input and examples for PHREEQC version 3—A computer program for speciation, batch-reaction, one-dimensional transport, and inverse geochemical calculations. US Geol. Surv. Tech. Methods 2013, 6, 497. [Google Scholar]
- Feng, D.; Wang, X.; Nackenhorst, U.; Zhang, X.; Pan, P. A comparative study of using two numerical strategies to simulate the biochemical processes in microbially induced calcite precipitation. J. Rock Mech. Geotech. Eng. 2022, 14, 592–602. [Google Scholar] [CrossRef]
- Van Paassen, L.A. Biogrout, Ground Improvement by Microbial Induced Carbonate Precipitation. Doctoral Thesis, TU Delft, Delft, The Netherlands, 2009. [Google Scholar]
- Yan, D.; Qu, N.; Li, H.; Wang, X. Significance of dimple parameters on the friction of sliding surfaces investigated by orthogonal experiments. Tribol. Trans. 2010, 53, 703–712. [Google Scholar] [CrossRef]
- Xu, C.; Nie, W.; Yang, S.; Peng, H.; Liu, Z.; Ma, Q.; Guo, C.; Liu, Q. Numerical simulation of the multi-index orthogonal experiments on the spray dust-settling devices. Powder Technol. 2020, 371, 217–230. [Google Scholar] [CrossRef]
- Konstantinou, C.; Biscontin, G.; Jiang, N.J.; Soga, K. Application of microbially induced carbonate precipitation to form bio-cemented artificial sandstone. J. Rock Mech. Geotech. Eng. 2021, 13, 579–592. [Google Scholar] [CrossRef]
- Konstantinou, C.; Wang, Y.; Biscontin, G. A systematic study on the influence of grain characteristics on hydraulic and mechanical performance of MICP-treated porous media. Transp. Porous Media 2023, 147, 305–330. [Google Scholar] [CrossRef]

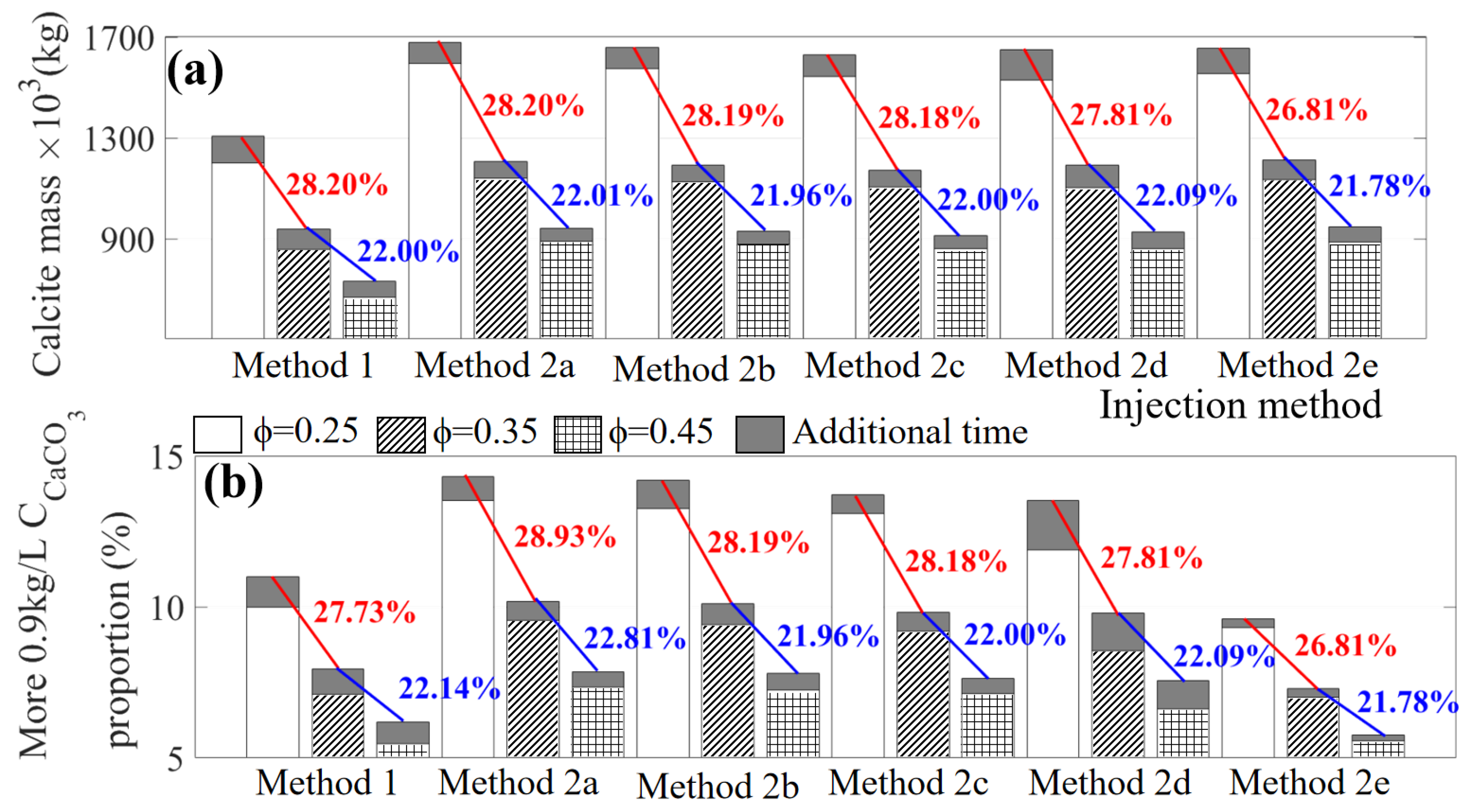
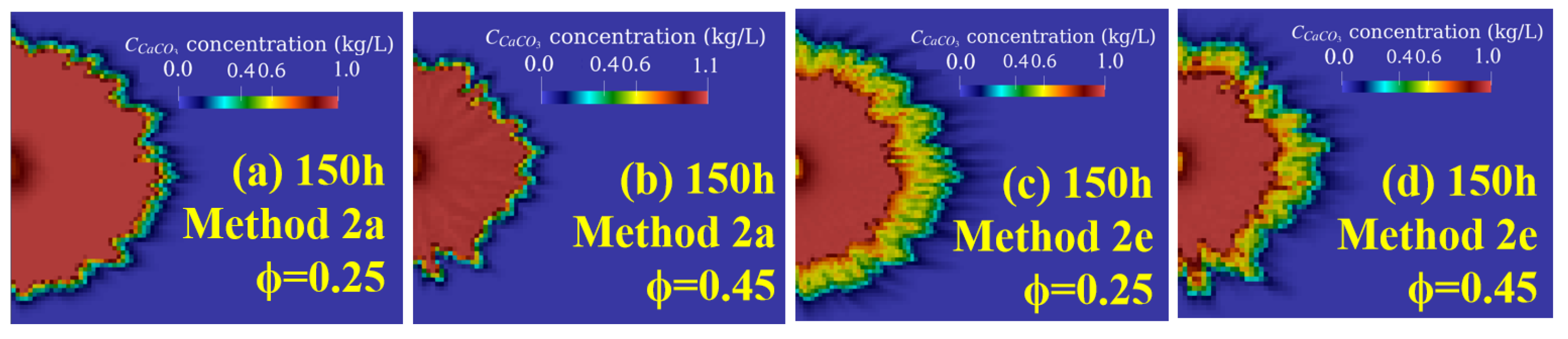
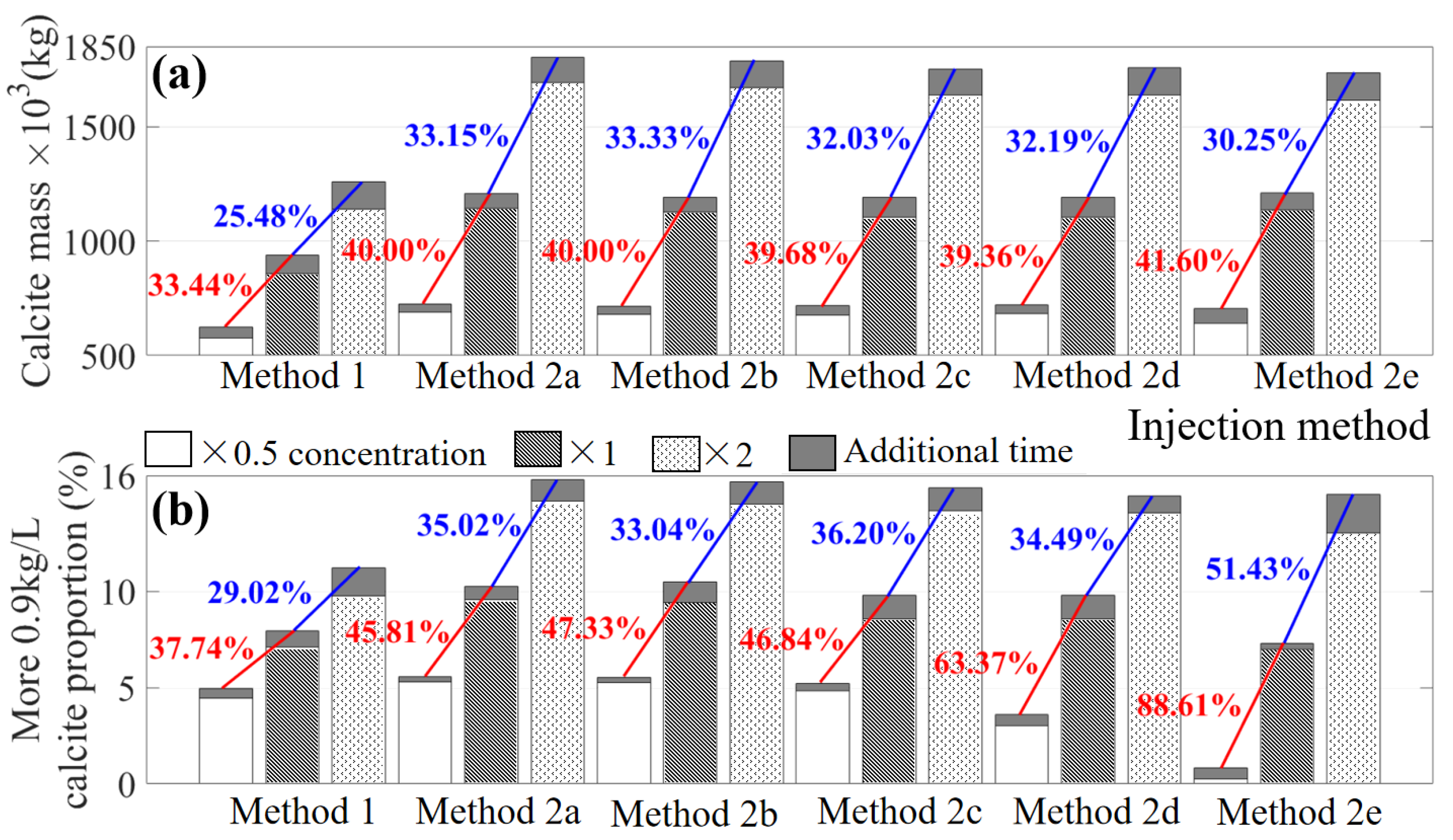
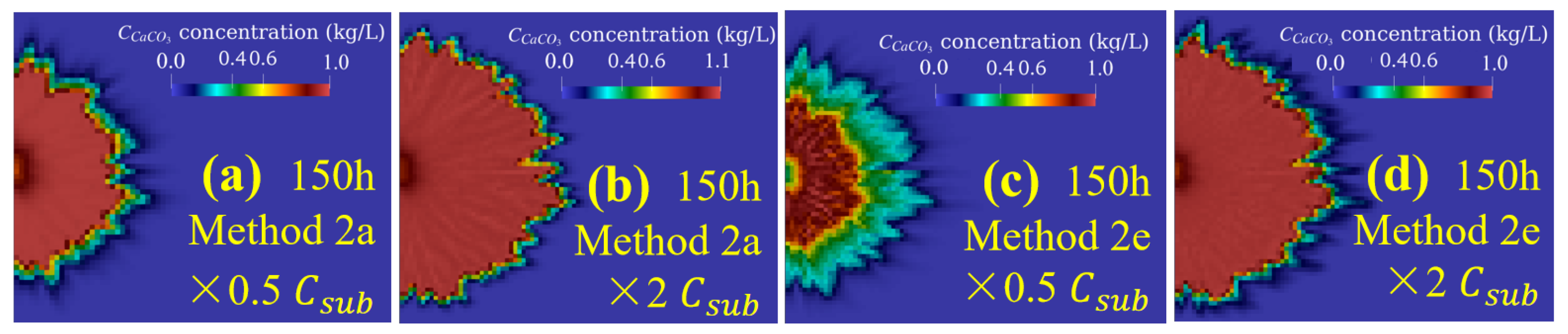

| Injection | Injection | Total Injection Time | Injection Numbers | Retention Time | Additional Time |
|---|---|---|---|---|---|
| Method | Type | (h) | (Bacteria/Cementation) | (h) | (h) |
| Method 1 | Continuous | 60 | - | - | |
| Method 2a | Phased | 120 | 2 | ||
| Method 2b | Phased | 120 | 5 | ||
| Method 2c | Phased | 120 | 10 | ||
| Method 2d | Phased | 120 | 15 | ||
| Method 2e | Phased | 120 | 20 |
| Injection Method | After the Injection (60 h or 120 h) | With the Additional Time (30 h) | Difference in Calcite Mass | ||
|---|---|---|---|---|---|
| 0.9 kg/L Calcite | Total Calcite Mass | 0.9 kg/L Calcite | Total Calcite Mass | ||
| (%) | ×10(kg) | (%)×10(kg) | ×10(kg) | ||
| Method 1 | 7.11 | 7.95 | |||
| Method 2a | 9.55 | 10.26 | 64.54 | ||
| Method 2b | 9.41 | 10.50 | 63.95 | ||
| Method 2c | 9.20 | 9.83 | |||
| Method 2d | 8.54 | 9.80 | |||
| Method 2e | 7.00 | 7.29 | |||
| Level | Factor A: Retention | Factor B: Average | Factor C: Multiple of Substance | Factor D: Additional |
|---|---|---|---|---|
| Time (h) | Porosity (-) | Concentration (-) | Time (h) | |
| −1 | 2 | 0.25 | 0.5 | 0 |
| 0 | 10 | 0.35 | 1 | 15 |
| 1 | 20 | 0.45 | 2 | 30 |
| Source of | Total Calcite Mass | Proportion of High-Concentration Calcite | ||||
|---|---|---|---|---|---|---|
| Variance | Mean Square | F-Value | p-Value (Significance) | Mean SQUARE | F-Value | p-Value (Significance) |
| Factor | 378.83 | <0.0001 ** | 37.88 | 198.87 | <0.0001 ** | |
| A | 2875.81 | 2.9 | 0.1105 | 18.99 | 99.67 | <0.0001 ** |
| B | 1618.68 | <0.0001 ** | 107.12 | 562.35 | <0.0001 ** | |
| C | 3426.94 | <0.0001 ** | 368.87 | 1936.46 | <0.0001 ** | |
| D | 22,939.55 | 23.16 | 0.0003 ** | 1.56 | 8.17 | 0.0127 * |
| AB | 284.85 | 0.2875 | 0.6002 | 1.62 | 8.52 | 0.0112 * |
| AC | 1189.85 | 1.2 | 0.2912 | 3.38 | 17.76 | 0.0009 ** |
| AD | 6.63 | 0.0067 | 0.936 | 0.0401 | 0.2107 | 0.6533 |
| BC | 94,856.89 | 95.75 | <0.0001 ** | 10.07 | 52.86 | <0.0001 ** |
| BD | 325.26 | 0.3283 | 0.5757 | 0.0030 | 0.0159 | 0.9015 |
| CD | 349.61 | 0.3529 | 0.562 | 0.0007 | 0.0034 | 0.9542 |
| A² | 5936.92 | 5.99 | 0.0282 * | 5.85 | 30.69 | <0.0001 ** |
| B² | 79,555.53 | 80.3 | <0.0001 ** | 4.67 | 24.51 | 0.0001 ** |
| C² | 119.82 | <0.0001 ** | 14.49 | 76.04 | <0.0001 ** | |
| D² | 6322.54 | 6.38 | 0.0242 * | 0.4107 | 2.16 | 0.1641 |
| Residual | 990.68 | 0.1905 | ||||
| Lack of Fit | 1386.95 | 0.2667 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Shao, H.; Yi, C.; Huang, Y.; Feng, D. Optimization of Injection Methods in the Microbially Induced Calcite Precipitation Process by Using a Field Scale Numerical Model. Water 2024, 16, 82. https://doi.org/10.3390/w16010082
Wang L, Shao H, Yi C, Huang Y, Feng D. Optimization of Injection Methods in the Microbially Induced Calcite Precipitation Process by Using a Field Scale Numerical Model. Water. 2024; 16(1):82. https://doi.org/10.3390/w16010082
Chicago/Turabian StyleWang, Lingxiang, Huicao Shao, Can Yi, Yu Huang, and Dianlei Feng. 2024. "Optimization of Injection Methods in the Microbially Induced Calcite Precipitation Process by Using a Field Scale Numerical Model" Water 16, no. 1: 82. https://doi.org/10.3390/w16010082
APA StyleWang, L., Shao, H., Yi, C., Huang, Y., & Feng, D. (2024). Optimization of Injection Methods in the Microbially Induced Calcite Precipitation Process by Using a Field Scale Numerical Model. Water, 16(1), 82. https://doi.org/10.3390/w16010082








