A Conceptual Model to Quantify the Water Balance Components of a Watershed in a Continuous Permafrost Region
Abstract
:1. Introduction
- -
- Simulation of seasonal thaw depths;
- -
- Comparison between the existing model and the proposed model;
- -
- Establishment of the water balance components of the catchment.
2. Materials and Methods
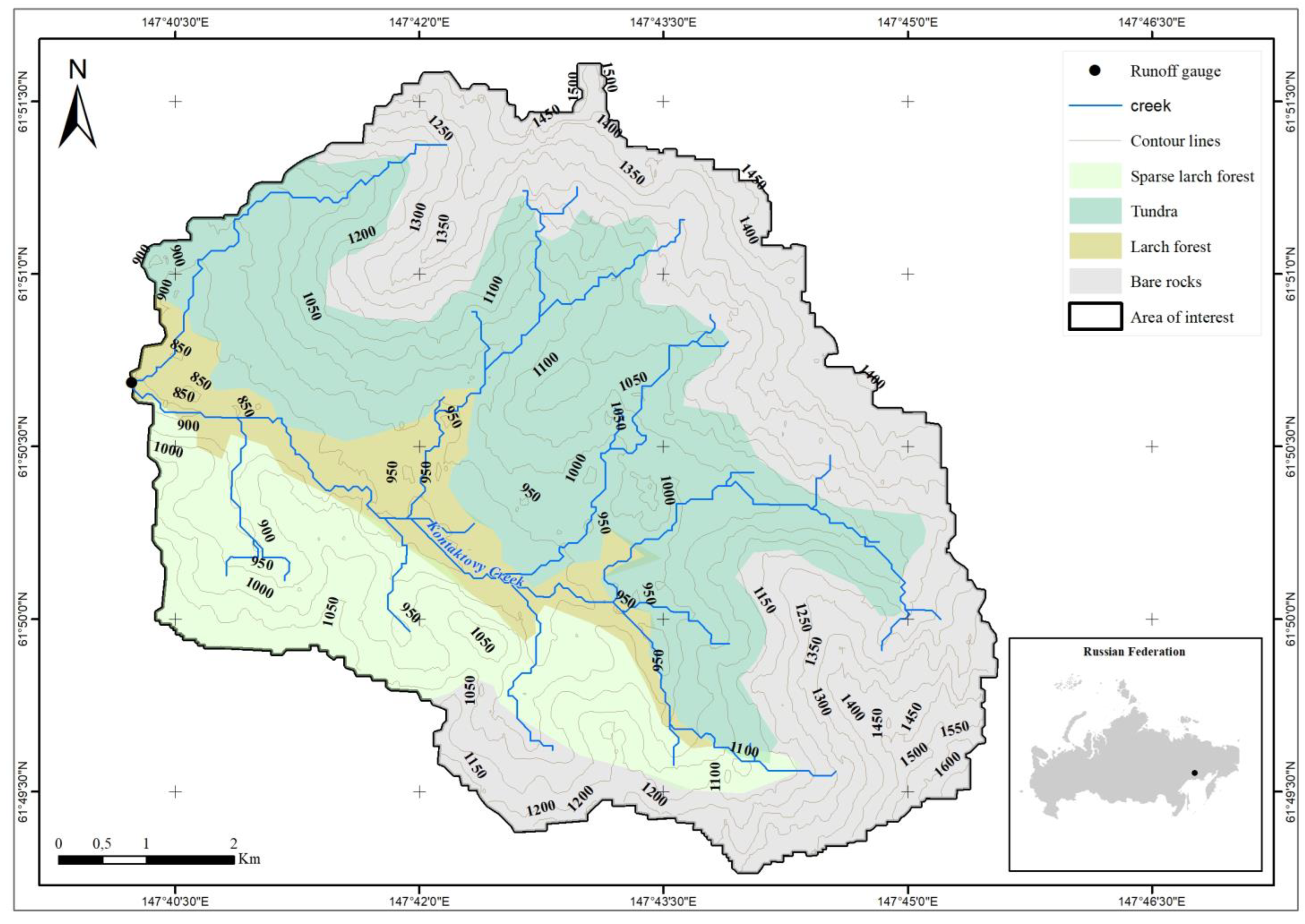
2.1. Study Area
2.2. Description of the HBV Model
2.3. Data Collection and Processing
2.3.1. Meteorological Data
2.3.2. Runoff
2.4. Heat Transfer Model
2.4.1. Heat Transfer Model Description
2.4.2. Soil Physical Properties
2.4.3. Measured Active-Layer Depth
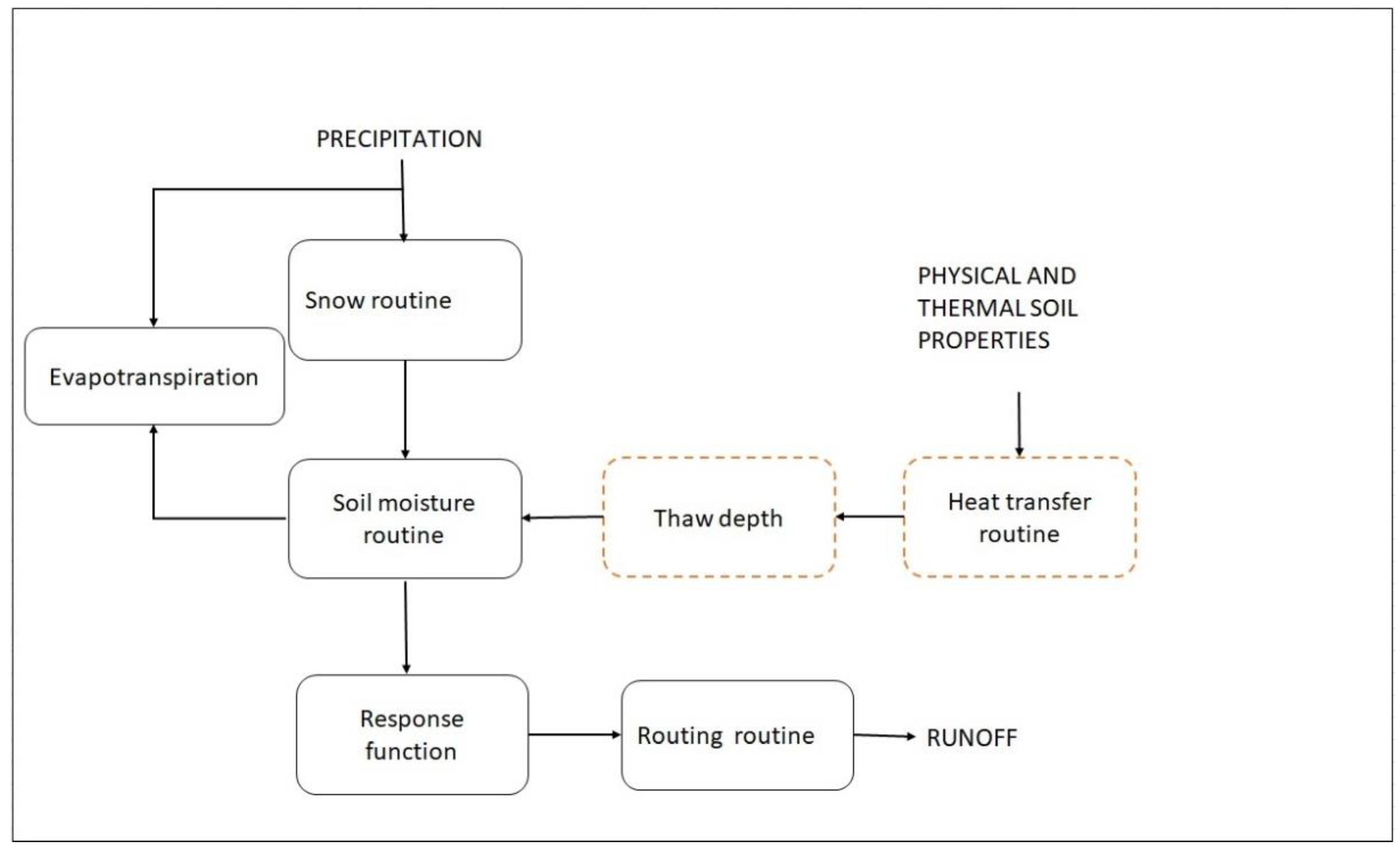
2.5. Integrating Thaw Depth Calculations with HBV
2.6. Model Calibration
2.7. Model Validation
3. Results
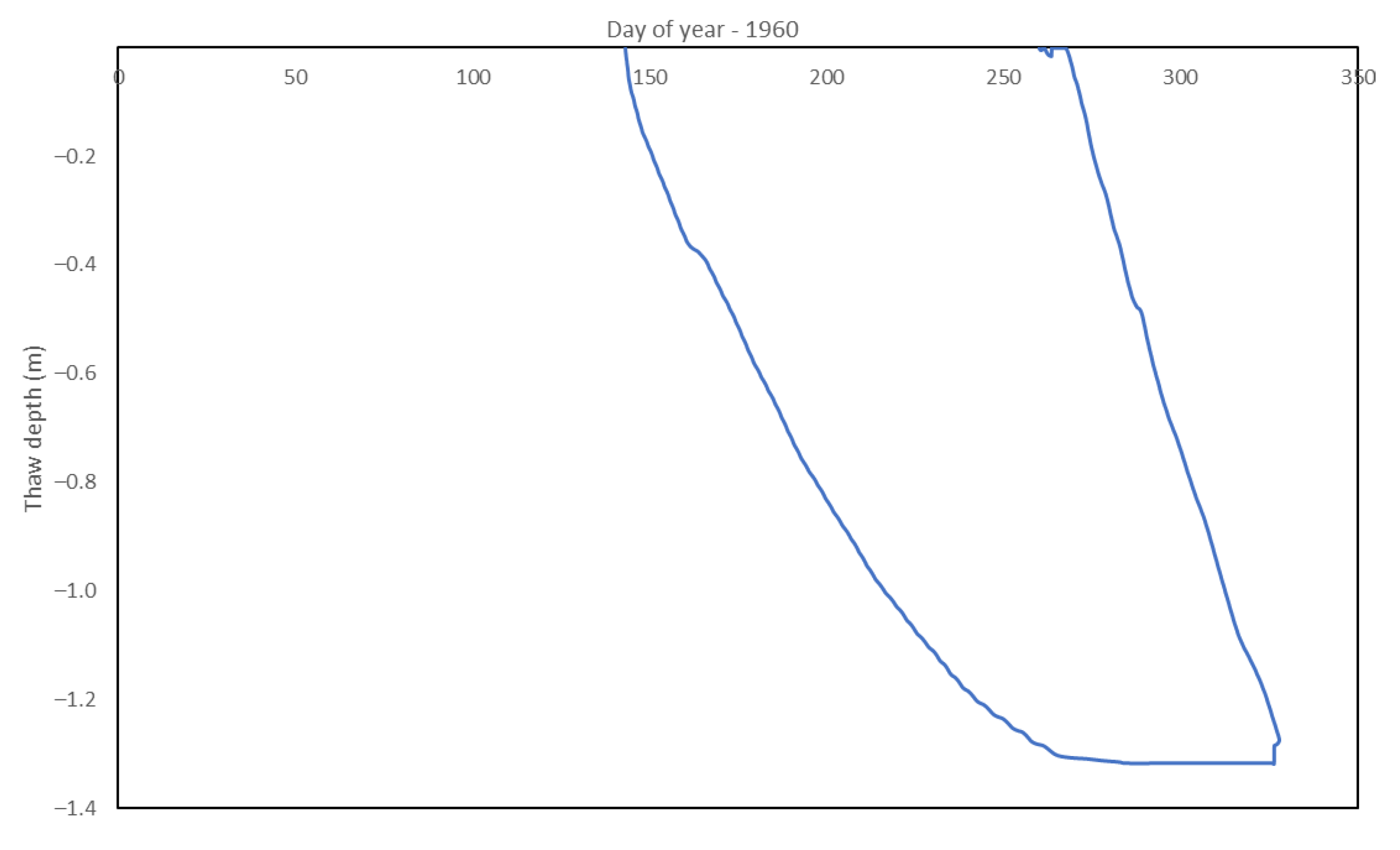
3.1. Simulated Thaw Depth
3.2. Proposed Model
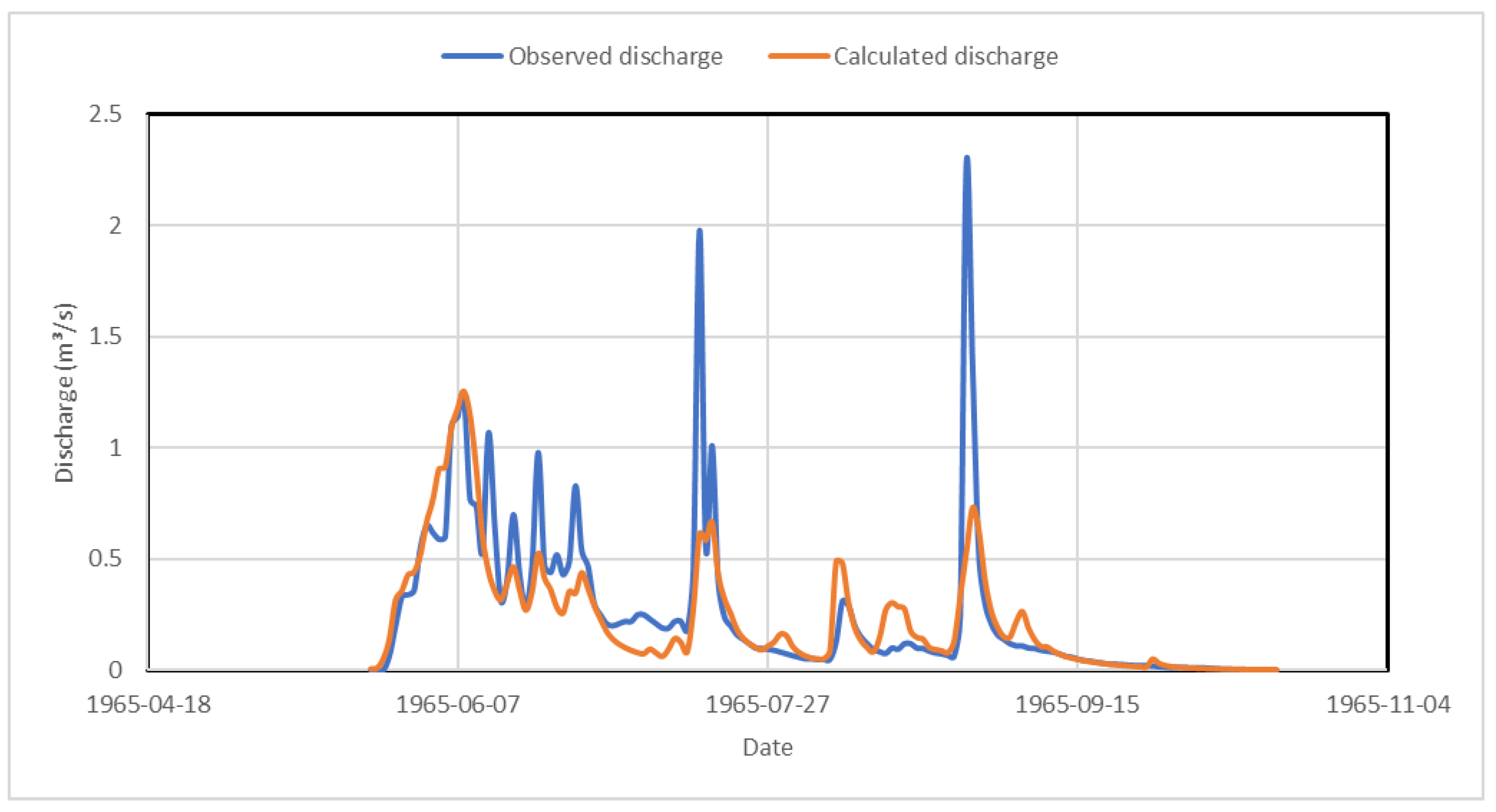
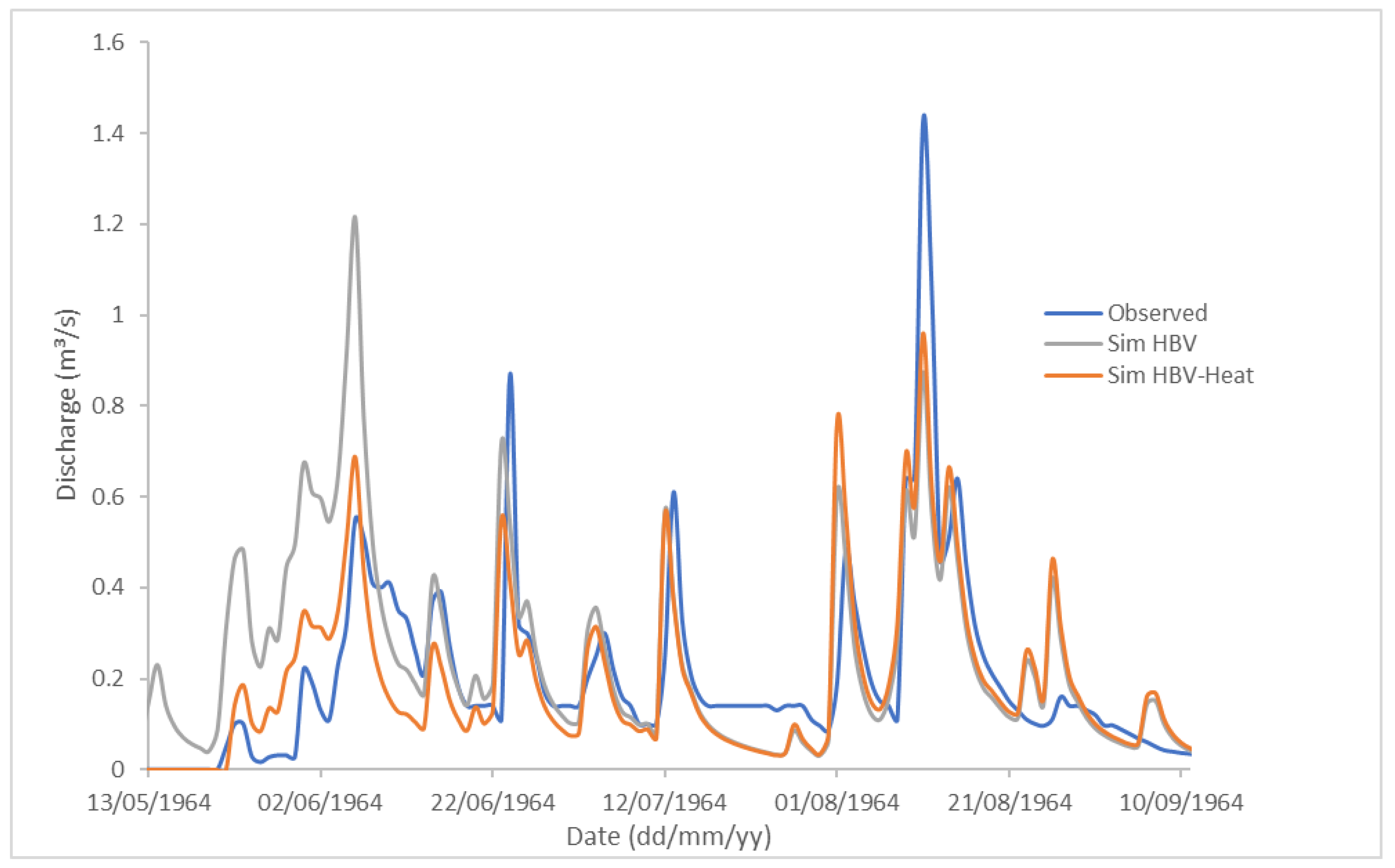
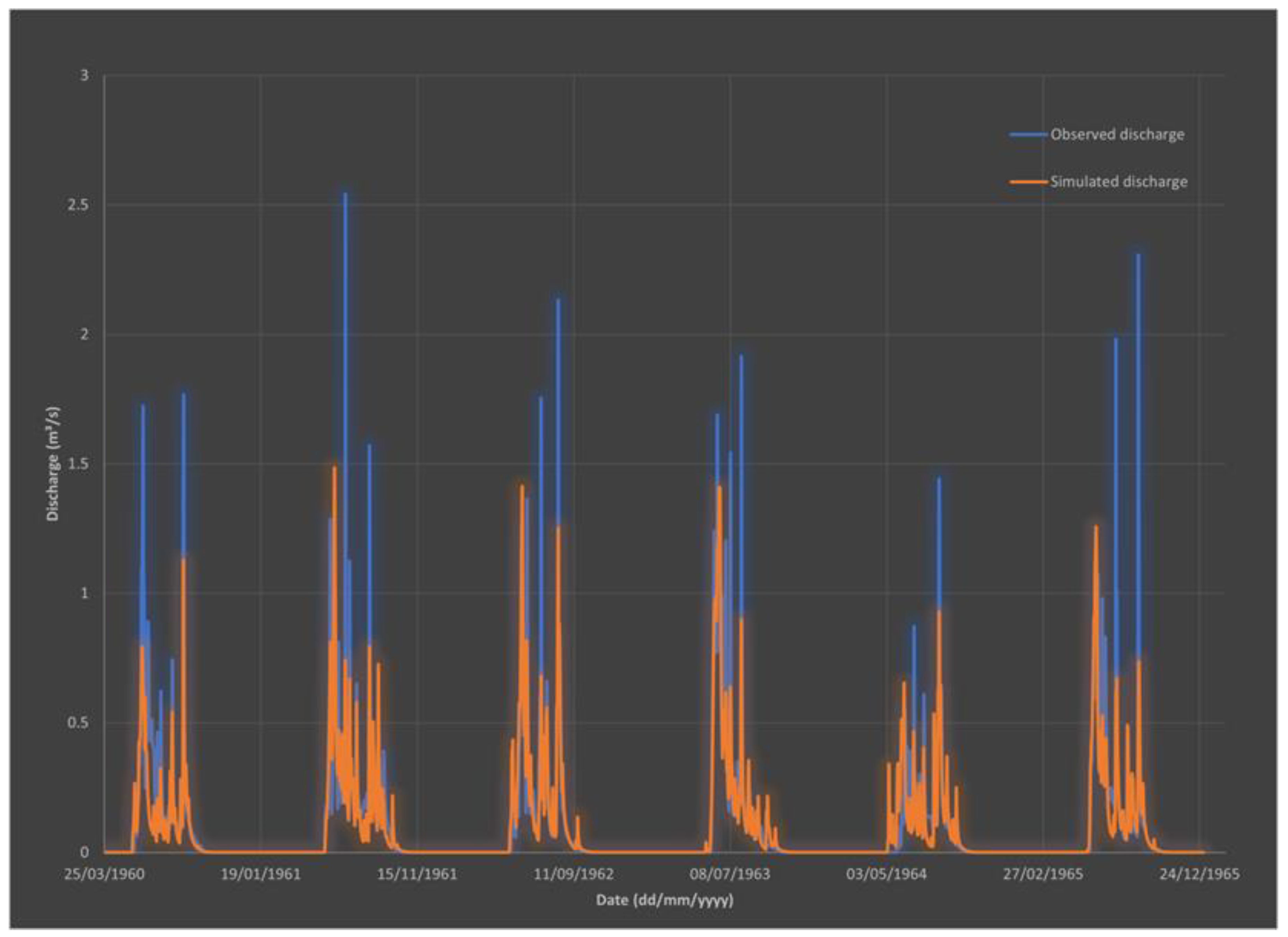
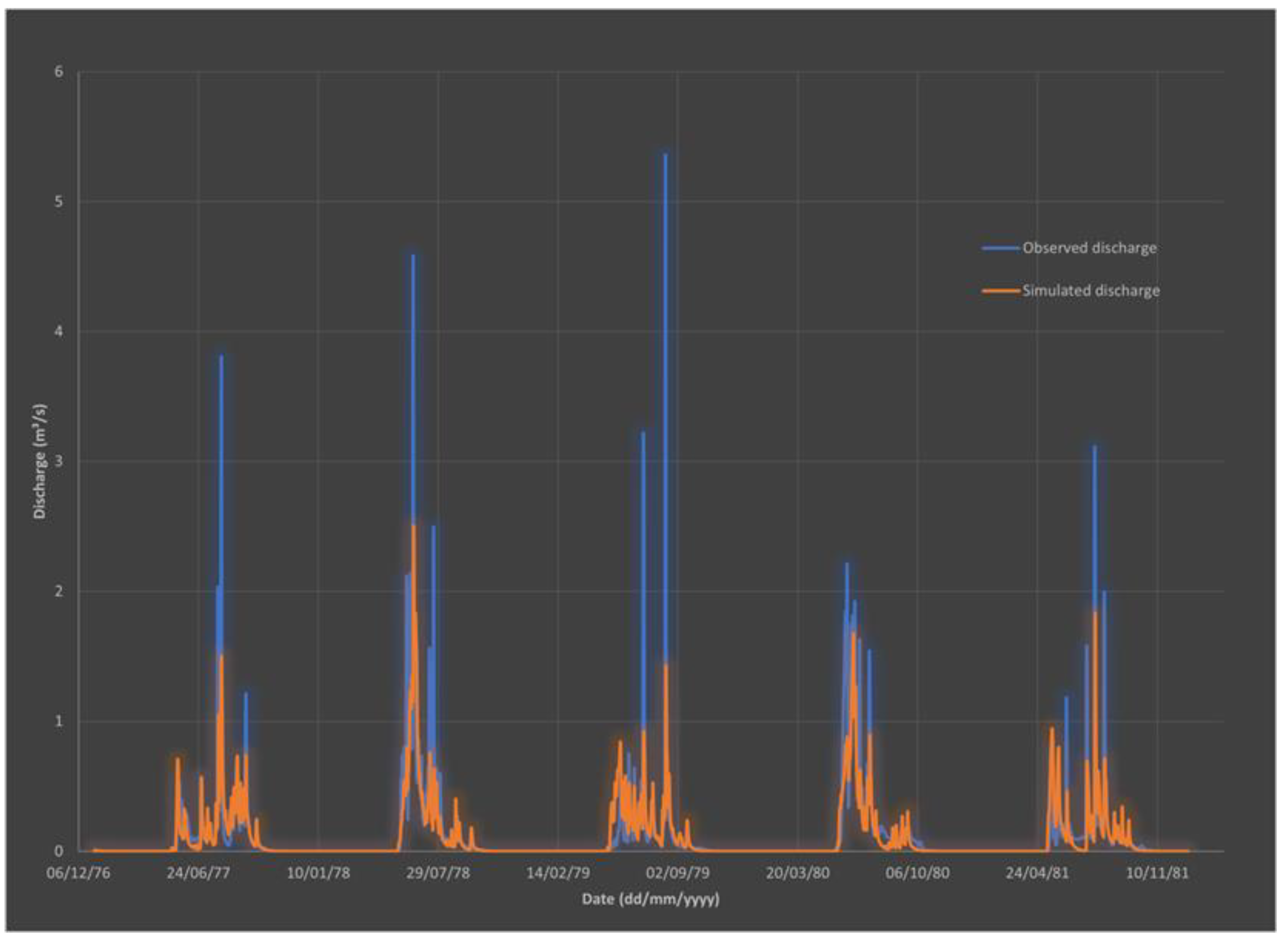
3.3. Simulated Hydrographs for the Calibration and Validation Periods
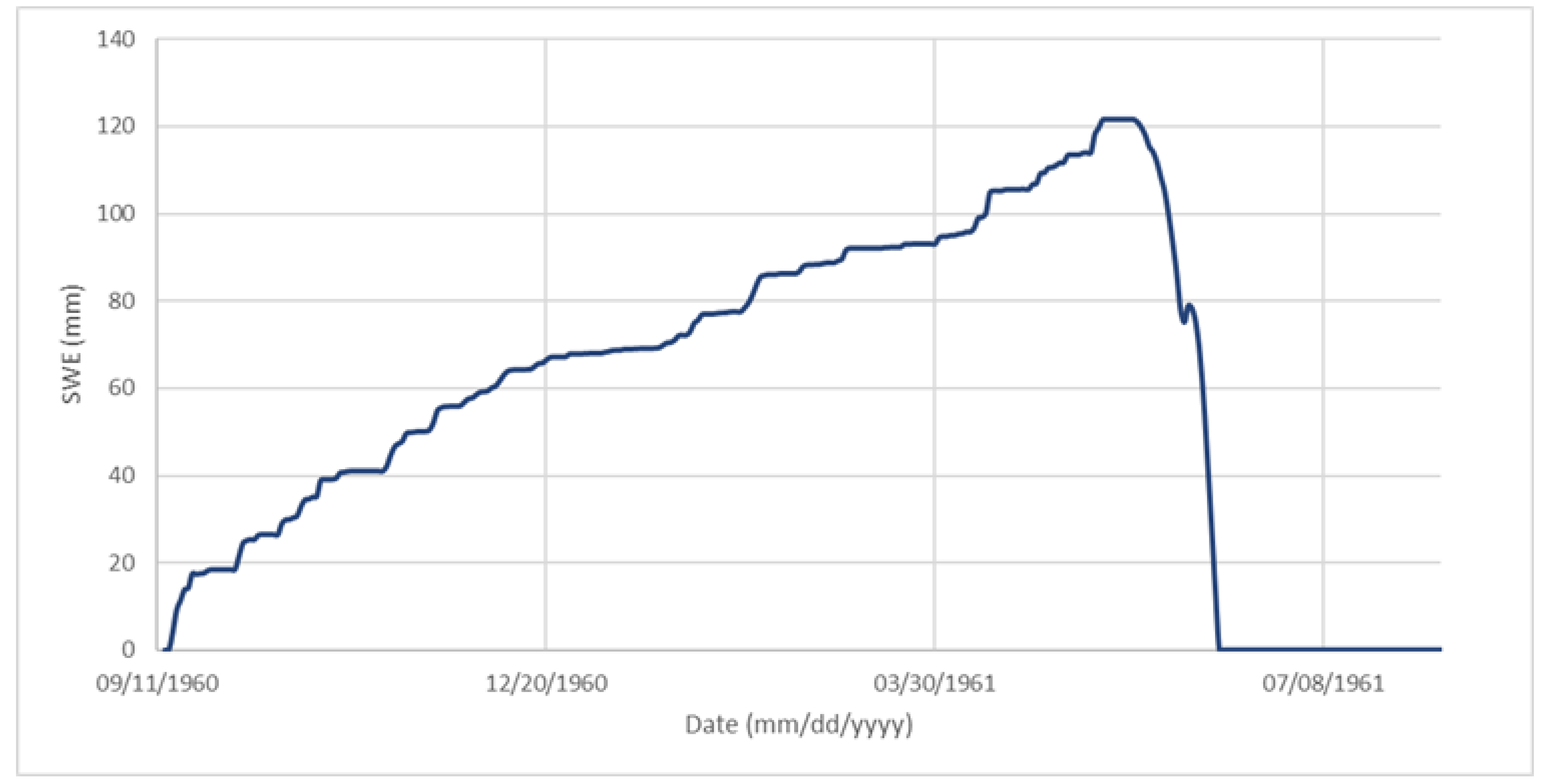
3.4. Simulated Snowmelt
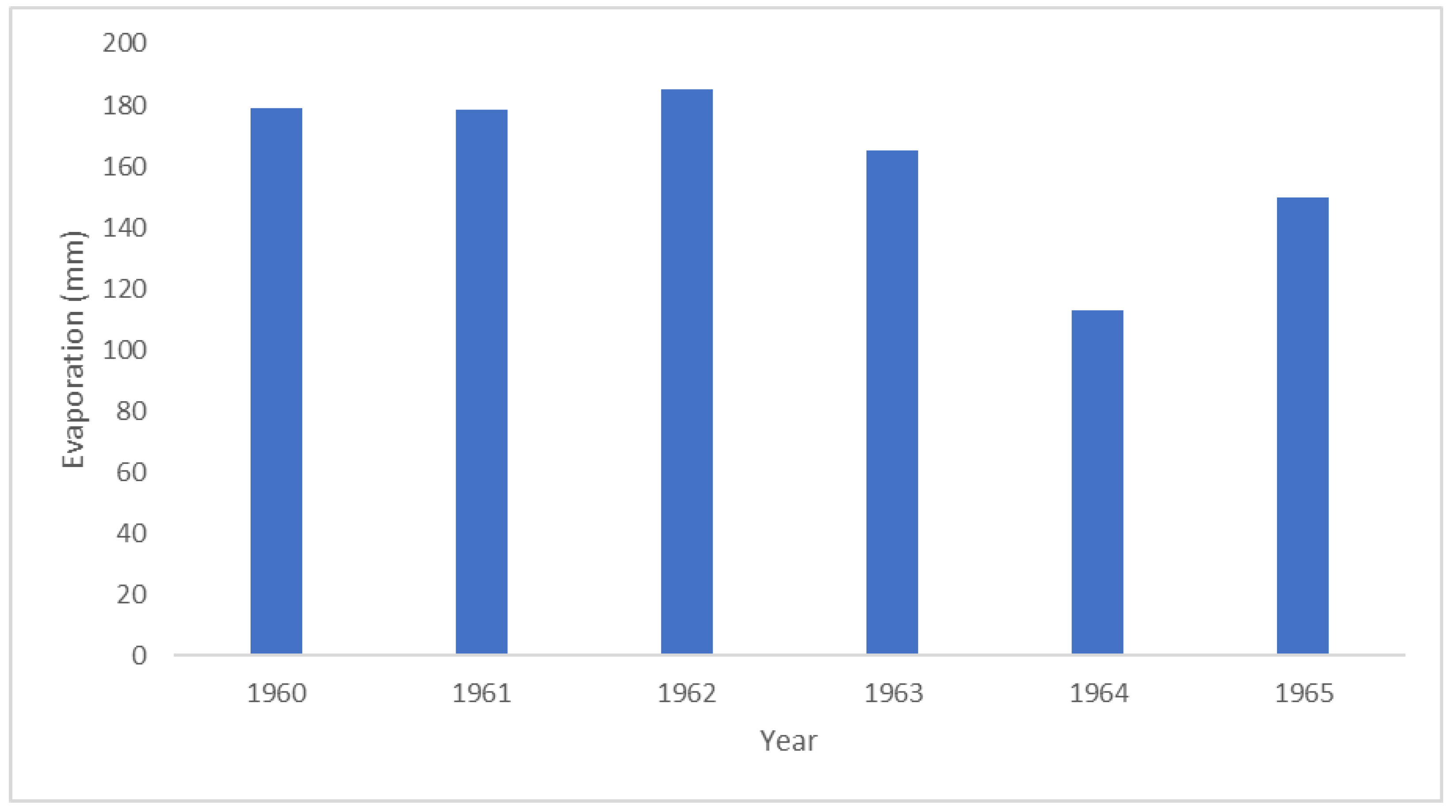
3.5. Evaporation
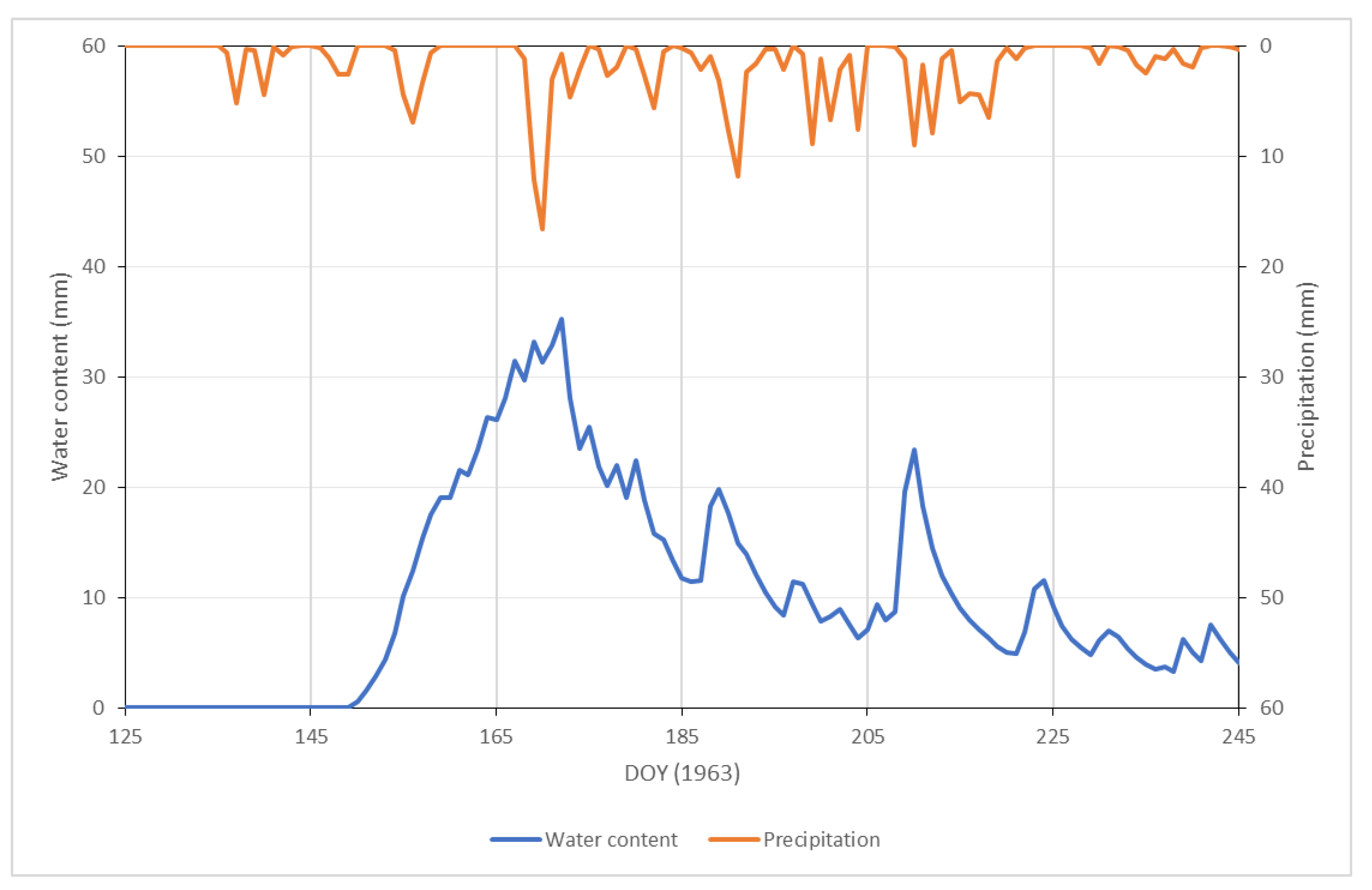
3.6. Calculated Soil Moisture
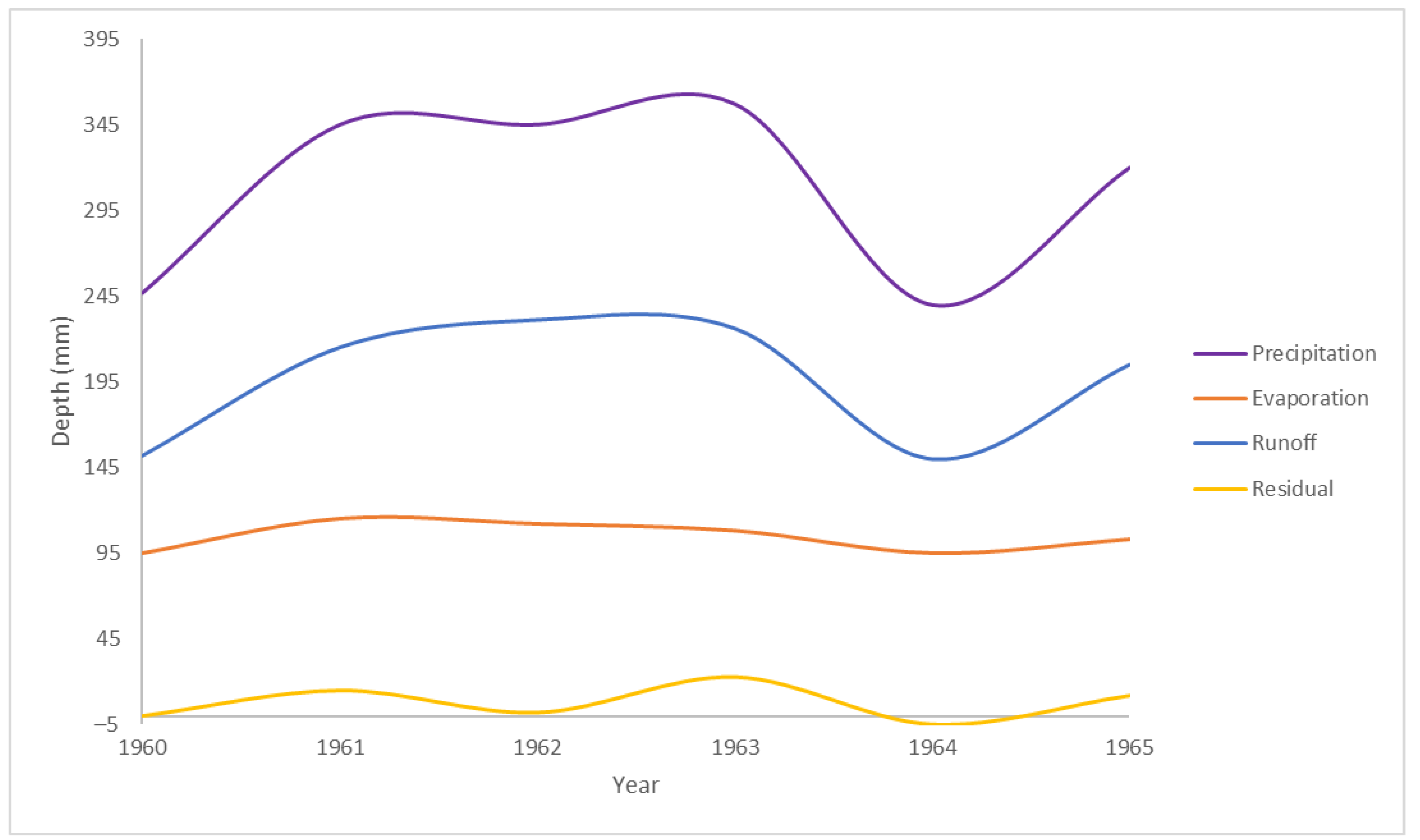
3.7. Water Balance
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Model Parameters
| Parameters | Explanation |
|---|---|
| TT | Threshold temperature |
| DD | Degree-day factor |
| PWP | Permanent wilting point |
| FC | Field capacity |
| L | Threshold water level |
| BETA | Shape coefficient |
| C | Correction factor for potential evaporation |
| K_0 | Near-surface flow storage |
| K_1 | Interflow storage coefficient |
| K_2 | Baseflow storage coefficient |
| K_P | Percolation storage coefficient |
Appendix B. Hydrographs from 1960 to 1965
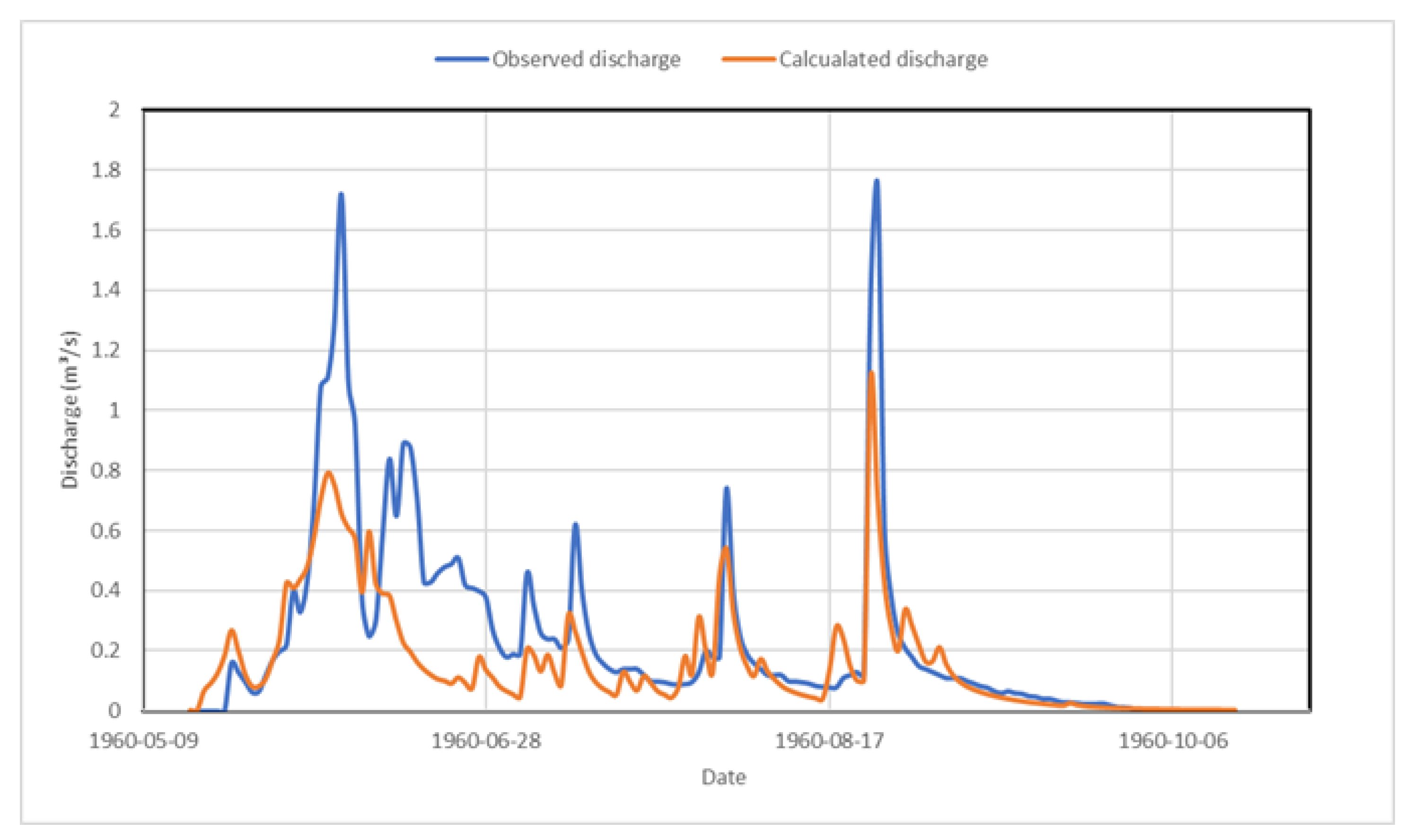
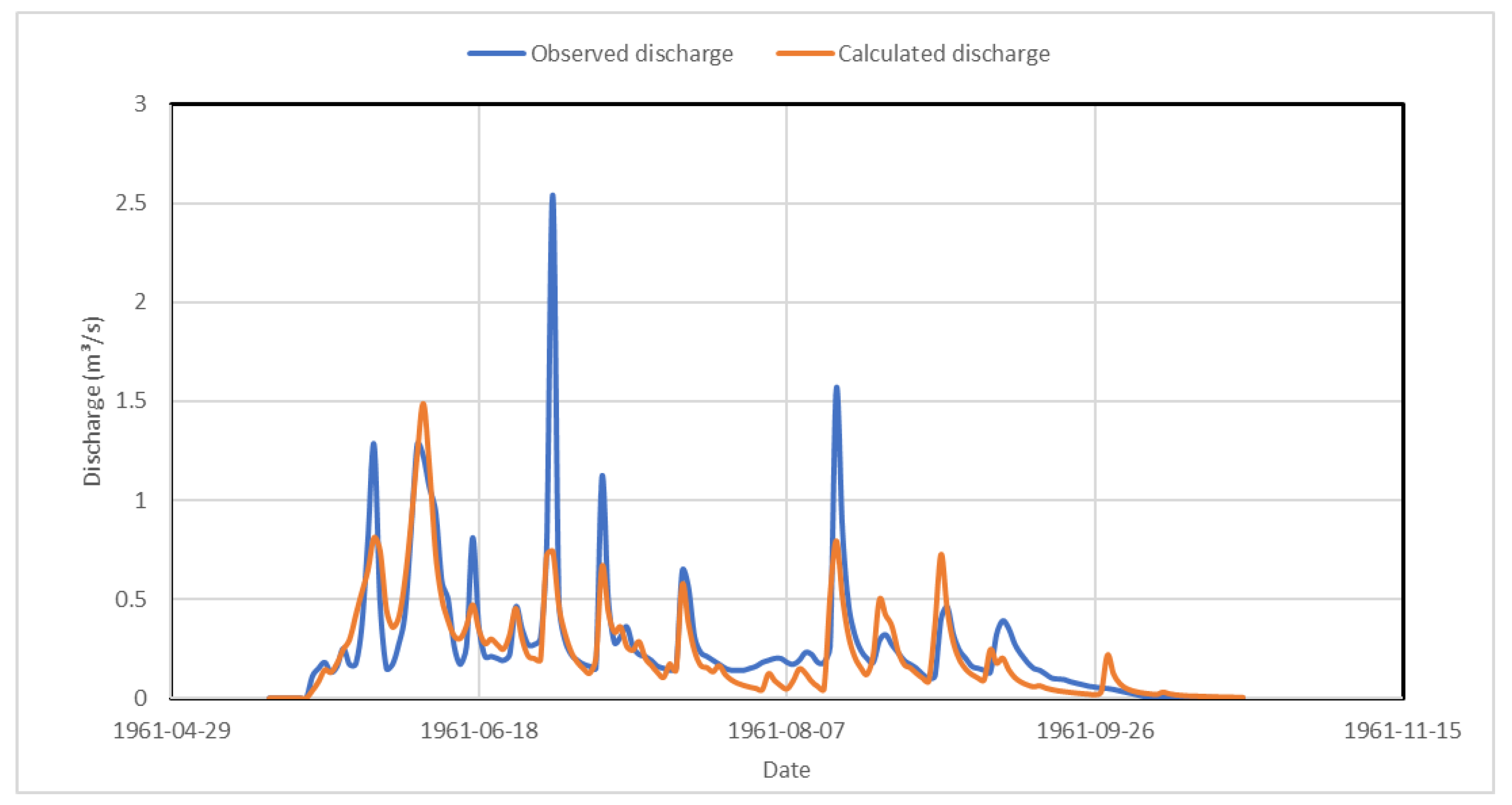
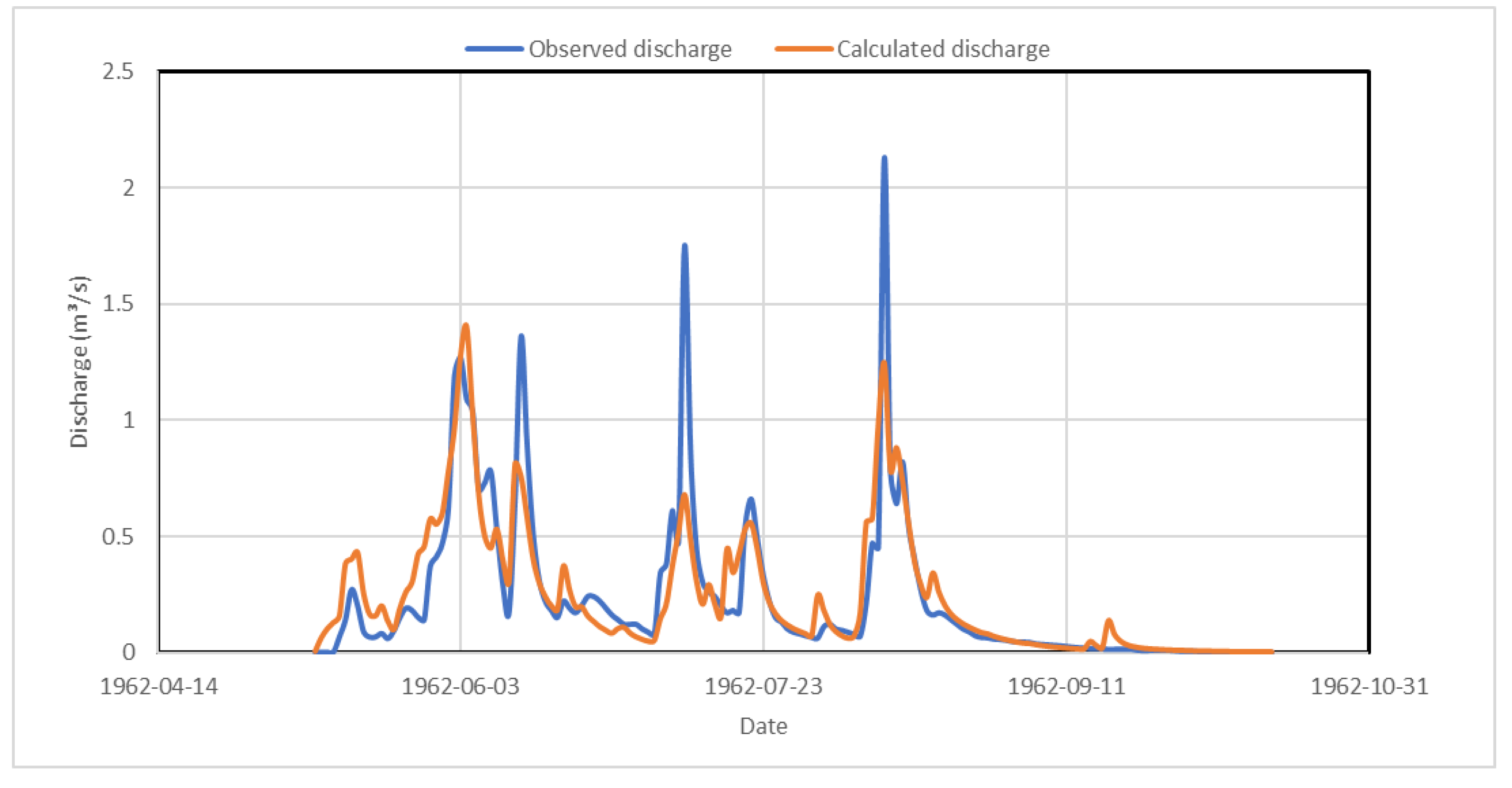

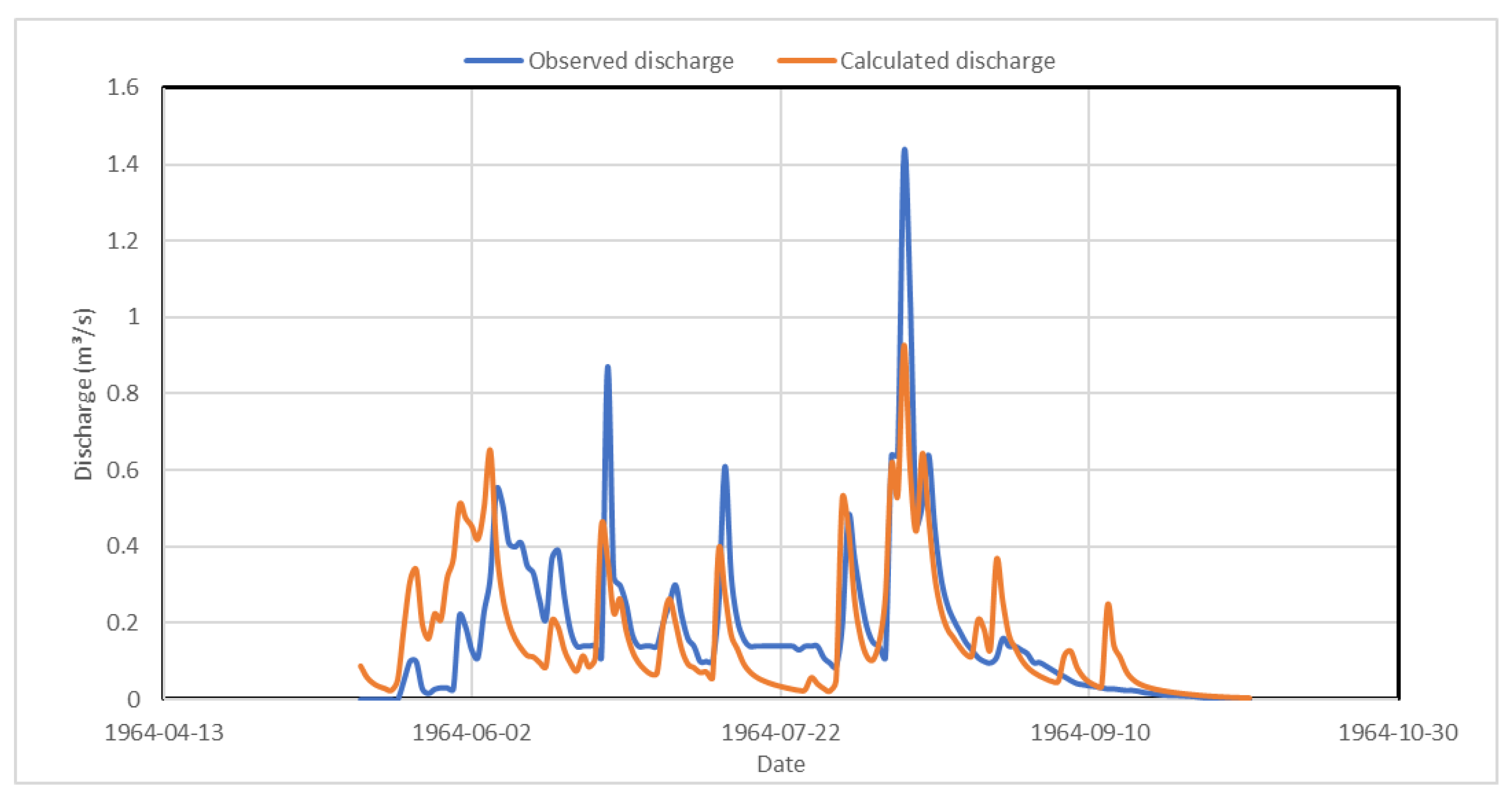
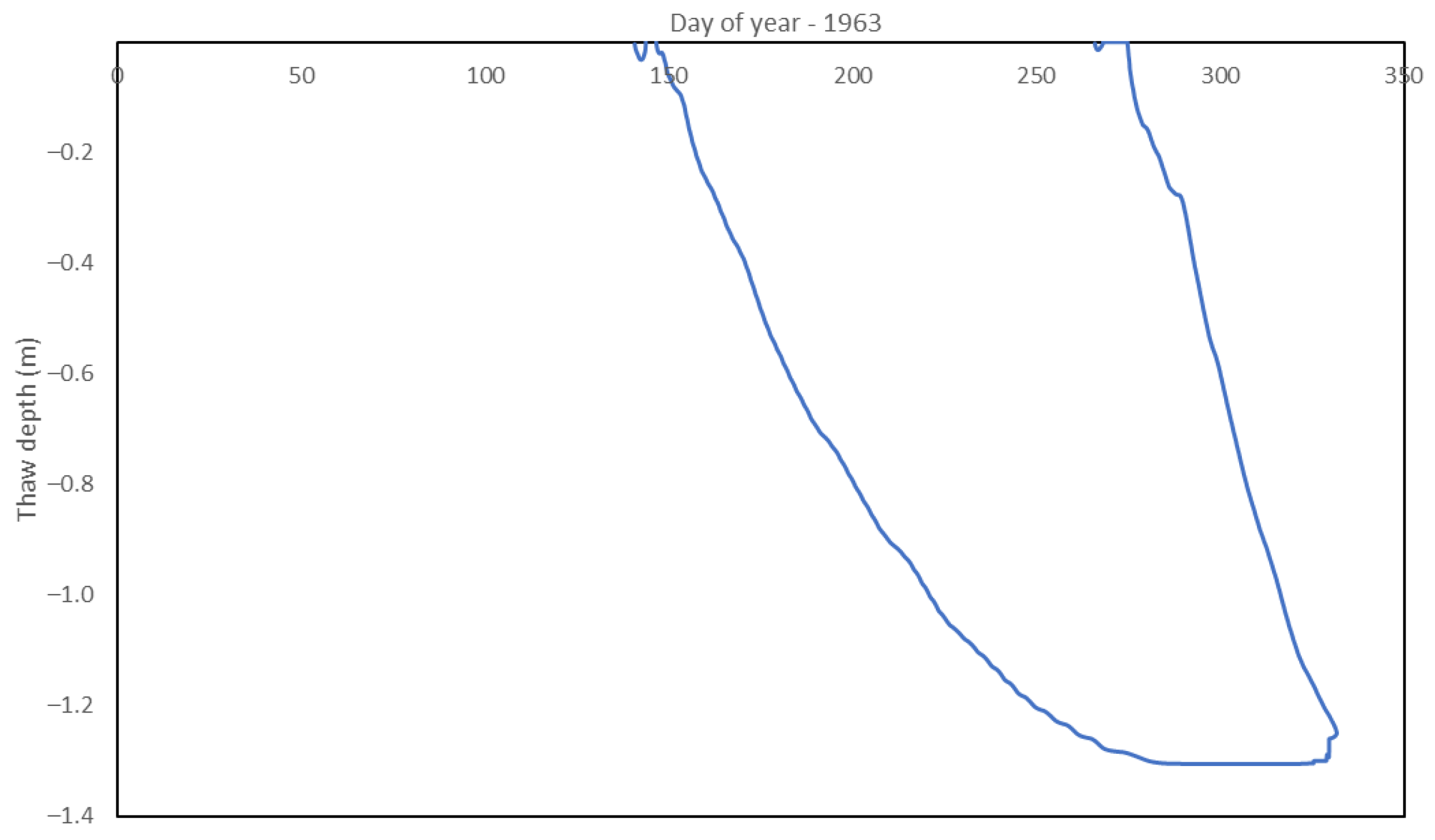
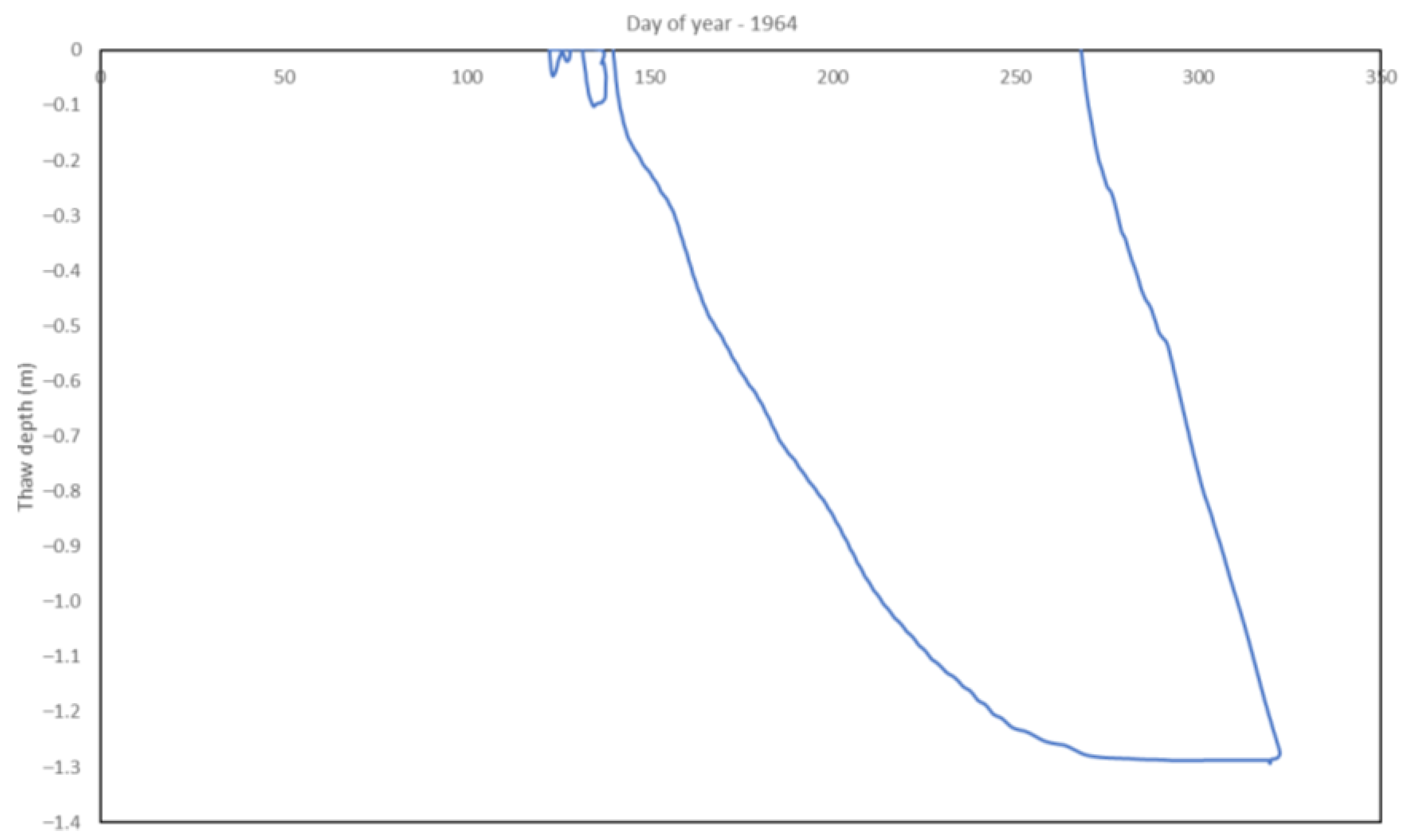
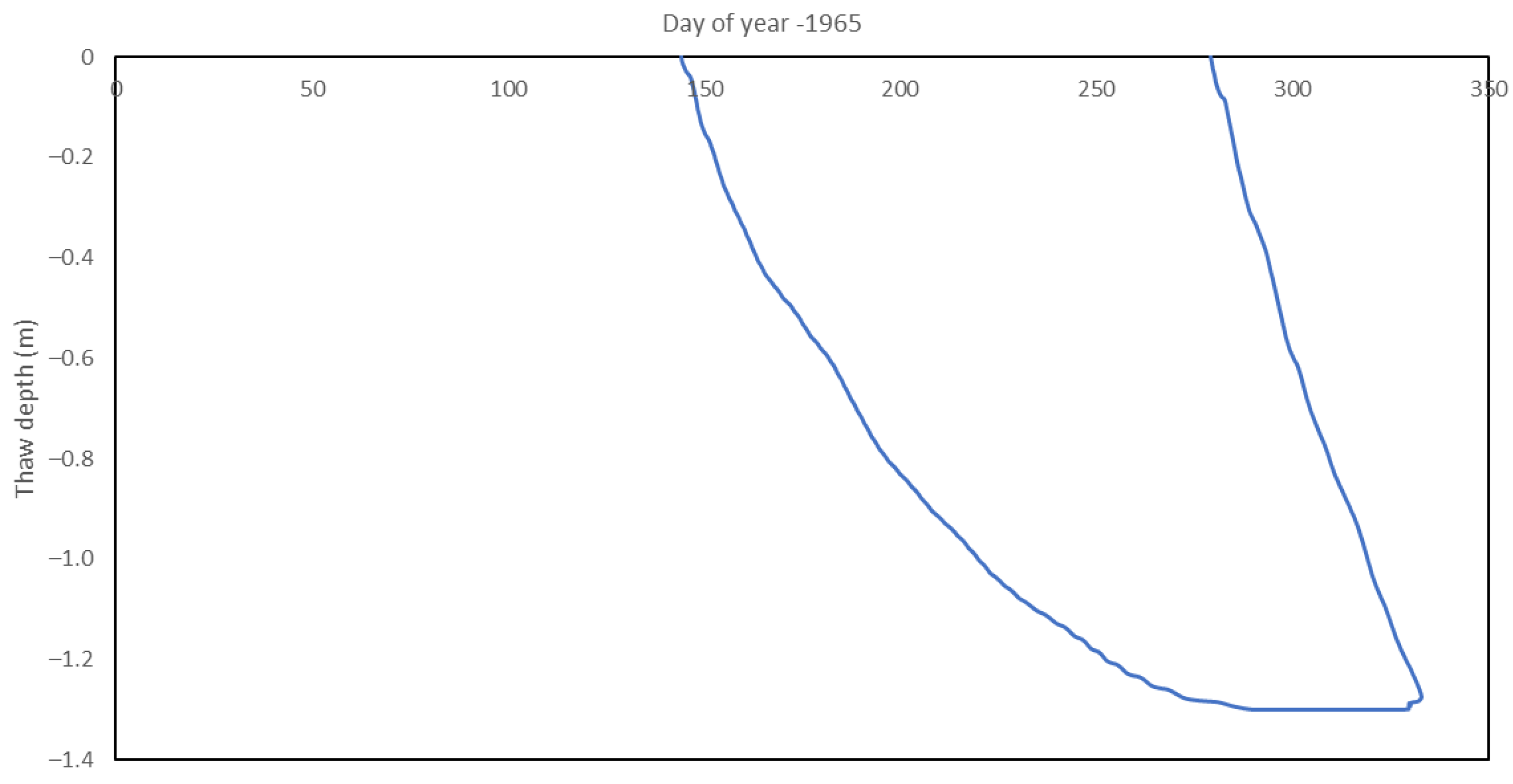
Appendix C. Simulated Thaw Depths
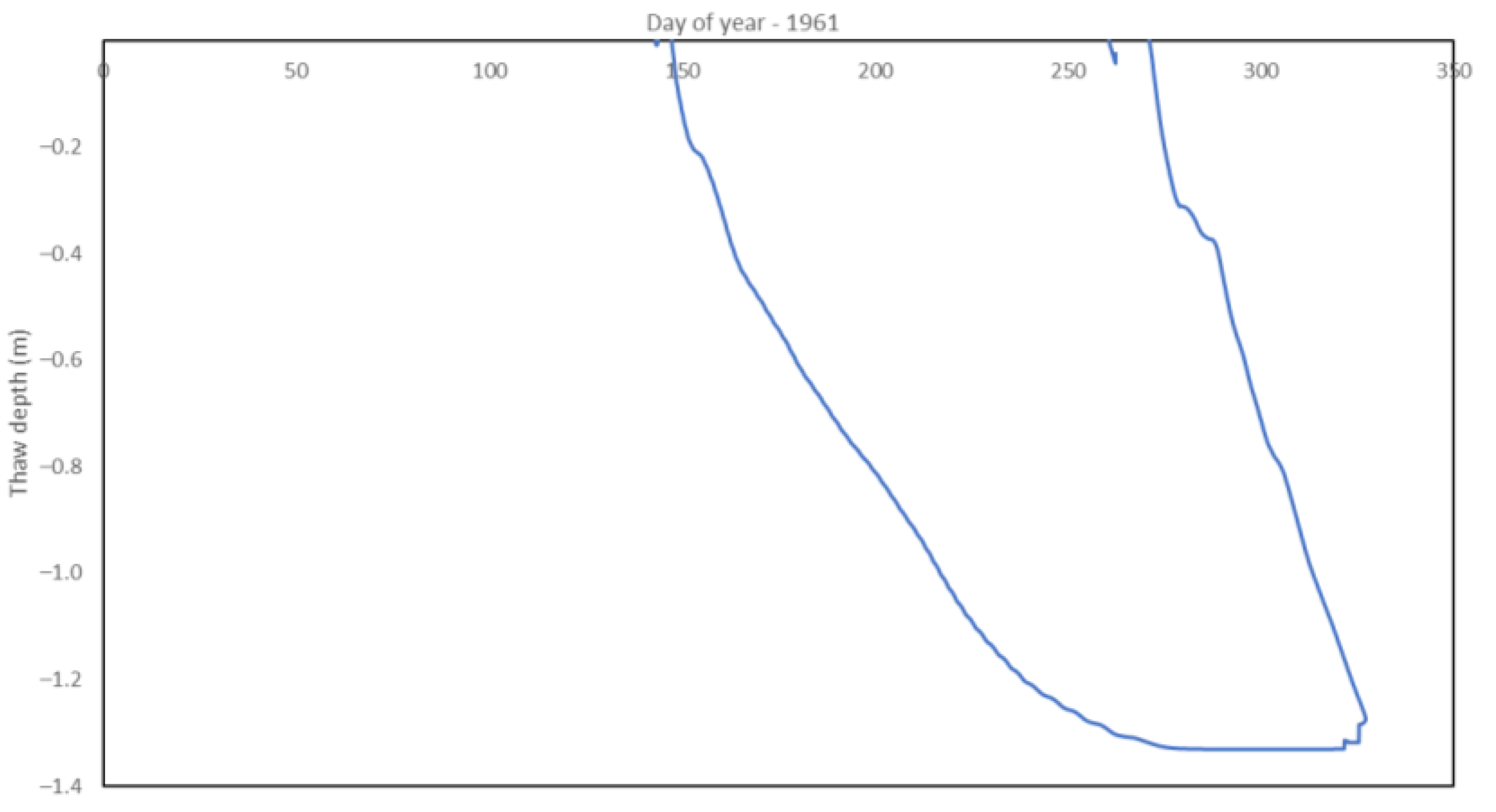
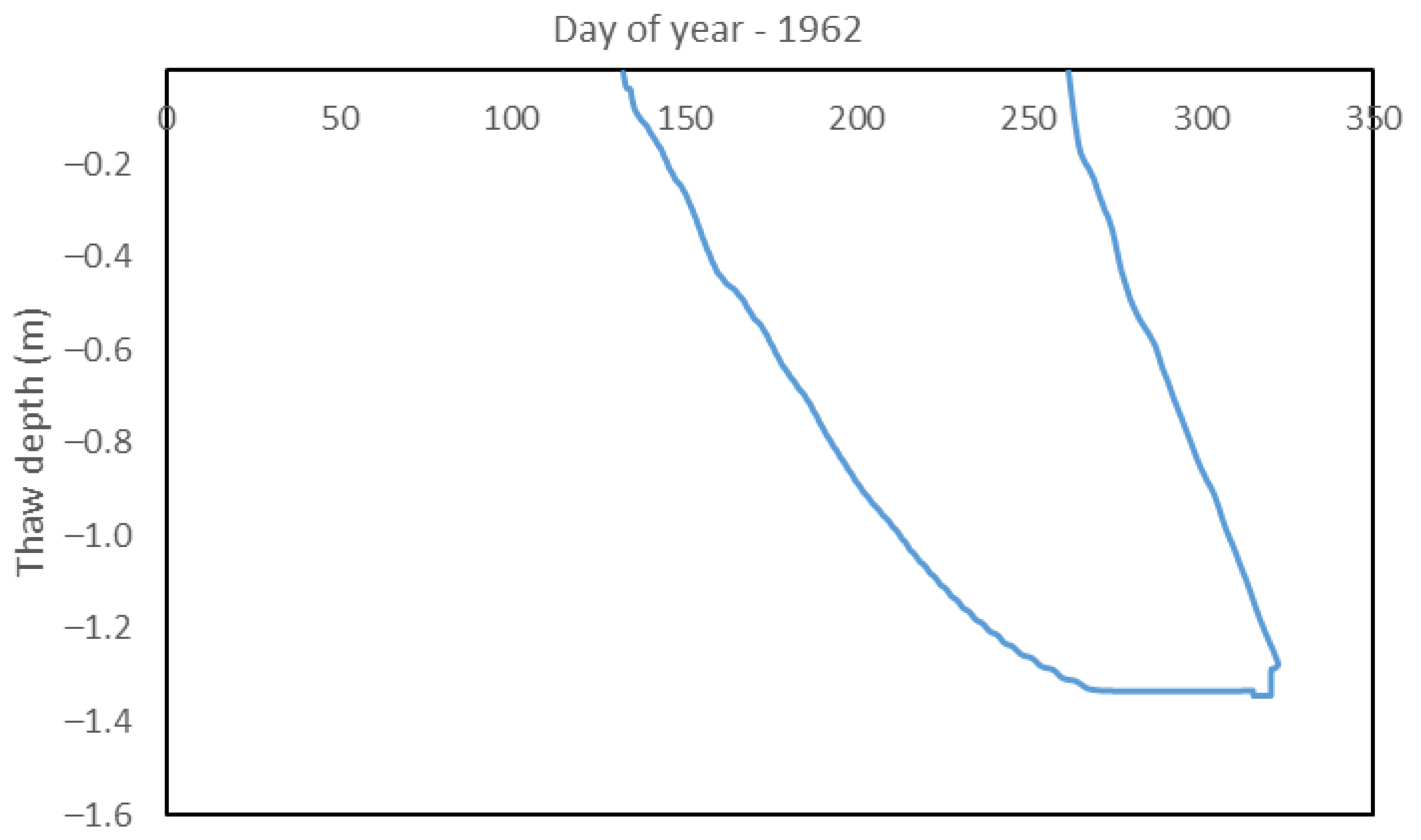
References
- Painter, S.L.; Coon, E.T.; Atchley, A.L.; Berndt, M.; Garimella, R.; Moulton, J.D.; Svyatskiy, D.; Wilson, C.J. Integrated surface/subsurface permafrost thermal hydrology: Model formulation and proof-of-concept simulations. Water Resour. Res. 2016, 52, 6062–6077. [Google Scholar] [CrossRef]
- Woo, M. Permafrost hydrology in North America. Atmos. Ocean 1986, 24, 201–234. [Google Scholar] [CrossRef]
- Zhao, L.; Gray, D.M. A parametric expression for estimating infiltration into frozen soils. Hydrol. Process 1997, 11, 1761–1775. [Google Scholar] [CrossRef]
- Gao, H.; Wang, J.; Yang, Y.; Pan, X.; Ding, Y.; Duan, Z. Permafrost Hydrology of the Qinghai-Tibet Plateau: A Review of Processes and Modeling. Front Earth Sci. 2021, 8, 576838. [Google Scholar] [CrossRef]
- Walvoord, M.A.; Kurylyk, B.L. Hydrologic Impacts of Thawing Permafrost-A Review. Vadose Zone J. 2016, 15, vzj2016.01.0010. [Google Scholar] [CrossRef]
- Shiklomanov, N.I.; Nelson, F.E. Active-layer mapping at regional scales: A 13-year spatial time series for the Kuparuk region, north-central Alaska. Permafr. Periglac. Process 2002, 13, 219–230. [Google Scholar] [CrossRef]
- Zhang, Y.; Carey, S.K.; Quinton, W.L. Evaluation of the algorithms and parameterizations for ground thawing and freezing simulation in permafrost regions. J. Geophys. Res. Atmos. 2008, 113, 1–17. [Google Scholar] [CrossRef]
- Kersten, M.S. Frost penetration: Relationship to air temperature and other factors. Highw. Res. Board Bull. 1959, 225, 45–80. [Google Scholar]
- Jumikis, A.R. The Frost Penetration Problem in Highway Engineering; Rutgers University Press: New Brunswick, NJ, USA, 1955. [Google Scholar]
- Lunardini, V.J. Heat Transfer in Cold Climates; Litton Educational Publishing, Inc.: New York, NY, USA, 1981. [Google Scholar]
- Woo, M.K.; Arain, M.A.; Mollinga, M.; Yi, S. A two-directional freeze and thaw algorithm for hydrologic and land surface modelling. Geophys. Res. Lett. 2004, 31, L12501. [Google Scholar] [CrossRef]
- Hayashi, M.; Goeller, N.; Quinton, W.L.; Wright, N. A simple heat-conduction method for simulating the frost-table depth in hydrological models. Hydrol. Process 2007, 21, 2610–2622. [Google Scholar] [CrossRef]
- Kurylyk, B.L.; McKenzie, J.M.; MacQuarrie, K.T.B.; Voss, C.I. Analytical solutions for benchmarking cold regions subsurface water flow and energy transport models: One-dimensional soil thaw with conduction and advection. Adv. Water Resour. 2014, 70, 172–184. [Google Scholar] [CrossRef]
- Changwei, X.; Gough, W.A. A simple thaw-freeze algorithm for a multi-layered soil using the stefan equation. Permafr. Periglac. Process 2013, 24, 252–260. [Google Scholar] [CrossRef]
- Semenova, O.M.; Vinogradova, T.A. A universal approach to runoff processes modelling: Coping with hydrological predictions in data-scarce regions. IAHS-AISH Publ. 2009, 333, 11–19. [Google Scholar]
- Kurylyk, B.L.; Macquarrie, K.T.B. A new analytical solution for assessing climate change impacts on subsurface temperature. Hydrol. Process 2014, 28, 3161–3172. [Google Scholar] [CrossRef]
- Kurylyk, B.L.; Hayashi, M. Improved Stefan Equation Correction Factors to Accommodate Sensible Heat Storage during Soil Freezing or Thawing. Permafr. Periglac. Process 2016, 27, 189–203. [Google Scholar] [CrossRef]
- Kurylyk, B.L.; Watanabe, K. The mathematical representation of freezing and thawing processes in variably-saturated, non-deformable soils. Adv. Water Resour. 2013, 60, 160–177. [Google Scholar] [CrossRef]
- Gouttevin, I.; Krinner, G.; Ciais, P.; Polcher, J.; Legout, C. Multi-scale validation of a new soil freezing scheme for a land-surface model with physically-based hydrology. Cryosphere 2012, 6, 407–430. [Google Scholar] [CrossRef]
- Rawlins, M.A.; Nicolsky, D.J.; McDonald, K.C.; Romanovsky, V.E. Simulating soil freeze/thaw dynamics with an improved pan-Arctic water balance model. J. Adv. Model. Earth Syst. 2013, 5, 659–675. [Google Scholar] [CrossRef]
- Zhang, Y.; Cheng, G.; Li, X.; Han, X.; Wang, L.; Li, H.; Chang, X.; Flerchinger, G.N. Coupling of a simultaneous heat and water model with a distributed hydrological model and evaluation of the combined model in a cold region watershed. Hydrol. Process 2013, 27, 3762–3776. [Google Scholar] [CrossRef]
- Lubini Tshumuka, A.; Krimi, A.; Fuamba, M. Modeling Heat Transfer through Permafrost Soil Subjected to Seasonal Freeze-Thaw. Land 2022, 11, 1770. [Google Scholar] [CrossRef]
- Bergström, S. Development and Application of a Conceptual Runoff Model for Scandinavian Catchments. SMHI 1976, RHO 7, 134. [Google Scholar]
- Seibert, J.; Bergström, S. A retrospective on hydrological catchment modelling based on half a century with the HBV model. Hydrol. Earth Syst. Sci. 2022, 26, 1371–1388. [Google Scholar] [CrossRef]
- Bergström, S. The HBV Model: Its Structure and Applications; Swedish Metorological and Hydrological Institute (SMHI): Norrköping, Sweden, 1992. [Google Scholar]
- Lebedeva, L.; Semenova, O.; Vinogradova, T. Simulation of active layer dynamics, Upper Kolyma, Russia, using the hydrograph hydrological model. Permafr. Periglac. Process 2014, 25, 270–280. [Google Scholar] [CrossRef]
- Lebedeva, L.; Semenova, O. Coupled modelling of soil thaw/freeze dynamics and runoff generation in permafrost landscapes, Upper Kolyma, Russia. IAHS-AISH Proc. Rep. 2013, 360, 118–124. [Google Scholar]
- Semenova, O.; Vinogradov, Y.; Vinogradova, T.; Lebedeva, L. Simulation of soil profile heat dynamics and their integration into hydrologic modelling in a permafrost zone. Permafr. Periglac. Process 2014, 25, 257–269. [Google Scholar] [CrossRef]
- Sushansky, S.I. History of creation, methods, objects and some results of studies in the Kolyma water balance station (in Russian). In Factors Affecting the Formation of a General Drainage System of Minor Mountain Rivers in Sub-Arctic Areas; Glotov, V., Ukhov, N., Eds.; Svkniidvoran: Magadan, Russia, 2002; pp. 18–35. [Google Scholar]
- Makarieva, O.; Nesterova, N.; Lebedeva, L.; Sushansky, S. Water balance and hydrology research in a mountainous permafrost watershed in upland streams of the Kolyma River, Russia: A database from the Kolyma Water-Balance Station, 1948–1997. Earth Syst. Sci. Data 2018, 10, 689–710. [Google Scholar] [CrossRef]
- Bergström, S.; Forsman, A. Development of a conceptual deterministic rainfall-runoff model. Nord. Hydrol. 1973, 4, 147–170. [Google Scholar] [CrossRef]
- Jansen, K.F.; Teuling, A.J.; Craig, J.R.; Dal Molin, M.; Knoben, W.J.M.; Parajka, J.; Vis, M.; Melsen, L.A. Mimicry of a Conceptual Hydrological Model (HBV): What’s in a Name? Water Resour. Res. 2021, 57, e2020WR029143. [Google Scholar] [CrossRef]
- Hidalgo, I.G.; Paredes-Arquiola, J.; Andreu, J.; Lerma-Elvira, N.; Lopes, J.E.G.; Cioffi, F. Hydropower generation in future climate scenarios. Energy Sustain. Dev. 2020, 59, 180–188. [Google Scholar] [CrossRef]
- Wijayarathne, D.B.; Coulibaly, P. Identification of hydrological models for operational flood forecasting in St. John’s, Newfoundland, Canada. J. Hydrol. Reg. Stud. 2020, 27, 100646. [Google Scholar] [CrossRef]
- Bui, M.T.; Lu, J.; Nie, L. A review of hydrological models applied in the permafrost-dominated Arctic region. Geoscience 2020, 10, 1–27. [Google Scholar] [CrossRef]
- Seibert, J.; Vis, M.J.P. Teaching hydrological modeling with a user-friendly catchment-runoff-model software package. Hydrol. Earth Syst. Sci. 2012, 16, 3315–3325. [Google Scholar] [CrossRef]
- Makarieva, O.; Nesterova, N.; Lebedeva, L.; Sushansky, S. Water-balance and hydrology database for a mountainous permafrost watershed in the up-streams of the Kolyma River, Russia—The Kolyma Water-Balance Station 1948–1997. PANGAEA 2017. [Google Scholar] [CrossRef]
- Gusev, E.M.; Nasonova, O.N.; Dzhogan, L.Y. The simulation of runoff from small catchments in the permafrost zone by the SWAP model. Water Resour. 2006, 33, 115–126. [Google Scholar] [CrossRef]
- Kuchment, L.; Gelfan, A. Assessing parameters of physically-based models for poorly gauged basins. IAHS-AISH Publ. 2009, 333, 3–10. [Google Scholar]
- Aghakouchak, A.; Nakhjiri, N.; Habib, E. An educational model for ensemble streamflow simulation and uncertainty analysis. Hydrol. Earth Syst. Sci. 2013, 17, 445–452. [Google Scholar] [CrossRef]
- Hinzman, L.D.; Kane, D.L. Snow hydrology of a headwater Arctic basin: 2. Conceptual analysis and computer modeling. Water Resour. Res. 1991, 27, 1111–1121. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, T.; Wahr, J. InSAR measurements of surface deformation over permafrost on the North Slope of Alaska. J. Geophys. Res. Earth Surf. 2010, 115, F03023. [Google Scholar] [CrossRef]
- Chen, J.; Wu, Y.; O’Connor, M.; Cardenas, M.B.; Schaefer, K.; Michaelides, R.; Kling, G. Active layer freeze-thaw and water storage dynamics in permafrost environments inferred from InSAR. Remote Sens. Environ. 2020, 248, 112007. [Google Scholar] [CrossRef]
- Woo, M.; Steer, P. Slope hydrology as influenced by thawing of the active layer, Resolute, N.W.T. Can. J. Earth Sci. 1983, 20, 978–986. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- ASCE. Criteria for Evaluation of Watershed Models. J. Irrig. Drain. Eng. 1993, 119, 429–442. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of Automatic Calibration for Hydrologic Models: Comparison with Multilevel Expert Calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Singh, J.; Knapp, H.V.; Arnold, J.G.; Demissie, M. Hydrological Modeling of The Iroquois River Watershed Using Hspf And Swat. J. Am. Water Resour. Assoc. 2005, 41, 343–360. [Google Scholar] [CrossRef]
- Zhuravin, S.A. Features of water balance for small mountainous watersheds in East Siberia: Kolyma Water Balance Station case study. In Northern Research Basins Water Balance; Series of Proceedings and Reports; Douglas, L.K., Daqing, Y., Eds.; IAHS Publication: Oxfordshire, UK, 2004; pp. 28–40. [Google Scholar]
- Armstrong, R.N.; Pomeroy, J.W.; Martz, L.W. Estimating evaporation in a prairie landscape under drought conditions. Can. Water Resour. J. 2010, 35, 173–186. [Google Scholar] [CrossRef]
- Lebedeva, L.S.; Makarieva, O.M.; Vinogradova, T.A. Spatial variability of the water balance elements in mountain catchments in the North-East Russia (case study of the Kolyma Water Balance Station). Meteorol. Hydrol. 2017, 4, 90–101. [Google Scholar]
- Vinogradov, Y.B.; Semenova, O.M.; Vinogradova, T.A. An approach to the scaling problem in hydrological modelling: The deterministic modelling hydrological system. Hydrol. Process 2011, 25, 1055–1073. [Google Scholar] [CrossRef]
- Semenova, O.; Lebedeva, L.; Vinogradov, Y. Simulation of subsurface heat and water dynamics, and runoff generation in mountainous permafrost conditions, in the Upper Kolyma River basin, Russia. Hydrogeol. J. 2013, 21, 107–119. [Google Scholar] [CrossRef]
- Sugimoto, A.; Naito, D.; Yanagisawa, N.; Ichiyanagi, K.; Kurita, N.; Kubota, J.; Kotake, T.; Ohata, T.; Maximov, T.C.; Fedorov, A.N. Characteristics of soil moisture in permafrost observed in East Siberian taiga with stable isotopes of water. Hydrol. Process 2003, 17, 1073–1092. [Google Scholar] [CrossRef]
- Vionnet, V.; Verville, M.; Fortin, V.; Brugman, M.; Abrahamowicz, M.; Lemay, F.; Thériault, J.M.; Lafaysse, M.; Milbrandt, J.A. Snow Level from Post-Processing of Atmospheric Model Improves Snowfall Estimate and Snowpack Prediction in Mountains. Water Resour. Res. 2022, 58, e2021WR031778. [Google Scholar] [CrossRef]
- Kane, D.L.; Yang, D. Northern Research Basins Water Balance; International Association of Hydrological Science: Oxfordshire, UK, 2004. [Google Scholar]
- Lebedeva, L.; Semenova, O. Use of soil thawfreeze depth data to verify hydrological_Lebedeva. Bodenkultur 2013, 64, 53–59. [Google Scholar]
| Soil Layer | Porosity (m³/m³) | Density (Kg/m³) | Heat Capacity (J/Kg °C) | Heat Conductivity (W/m° C) | Maximum Water Holding Capacity (m³/m³) |
|---|---|---|---|---|---|
| Moss | 0.9 | 500 | 1930 | 0.8 | 0.60 |
| Bedrock | 0.35 | 2610 | 750 | 2.3 | 0.07 |
| Depth (cm) | Soil Profile Composition |
|---|---|
| 0–9.99 | Moss |
| 10–150 | Bedrock |
| Error Measures | Description | Range |
|---|---|---|
| Nash–Sutcliffe Percent bias | ||
| Root mean squared error |
| Year | Thaw Depth (cm) | |
|---|---|---|
| Simulated | Measured | |
| 1960 | 129.70 | >120 |
| 1961 | 132.16 | - |
| 1962 | 132.28 | - |
| 1963 | 128.57 | 136 |
| 1964 | 126.72 | 126 |
| 1965 | 129.04 | 131 |
| Average | 129.75 | - |
| Model | NSE | ||||||
|---|---|---|---|---|---|---|---|
| 1960 | 1961 | 1962 | 1963 | 1964 | 1965 | Average | |
| HBV | 0.66 | 0.49 | 0.54 | 0.74 | 0.08 | 0.46 | 0.50 |
| HBV-Heat | 0.59 | 0.62 | 0.72 | 0.77 | 0.57 | 0.62 | 0.65 |
| Parameters | DD | FC | Beta | C | L | K_0 | K_1 | K_2 | K_P | TT |
|---|---|---|---|---|---|---|---|---|---|---|
| Values | 1.06 | 156.9 | 0.21 | 0.79 | 70.2 | 0.79 | 0.33 | 0.11 | 0.20 | 1.20 |
| Period | Years | Goodness of Fit | ||
|---|---|---|---|---|
| NSE | RMSE | PBIAS | ||
| Calibration | 1960–1964 | 0.74 | 0.12 | −11.6 |
| Validation | 1977–1981 | 0.55 | 0.24 | −14.4 |
| Year | SWE (mm) | |
|---|---|---|
| Observed | Simulated | |
| 1960 | 114 | 62 |
| 1961 | 113 | 121 |
| 1962 | 120 | 111 |
| 1963 | 122 | 139 |
| 1964 | 59 | 61 |
| 1965 | 119 | 123 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lubini Tshumuka, A.; Fuamba, M. A Conceptual Model to Quantify the Water Balance Components of a Watershed in a Continuous Permafrost Region. Water 2024, 16, 83. https://doi.org/10.3390/w16010083
Lubini Tshumuka A, Fuamba M. A Conceptual Model to Quantify the Water Balance Components of a Watershed in a Continuous Permafrost Region. Water. 2024; 16(1):83. https://doi.org/10.3390/w16010083
Chicago/Turabian StyleLubini Tshumuka, Alain, and Musandji Fuamba. 2024. "A Conceptual Model to Quantify the Water Balance Components of a Watershed in a Continuous Permafrost Region" Water 16, no. 1: 83. https://doi.org/10.3390/w16010083
APA StyleLubini Tshumuka, A., & Fuamba, M. (2024). A Conceptual Model to Quantify the Water Balance Components of a Watershed in a Continuous Permafrost Region. Water, 16(1), 83. https://doi.org/10.3390/w16010083






