Study on Seismic Source Parameter Characteristics of Baihetan Reservoir Area in the Lower Reaches of the Jinsha River
Abstract
:1. Introduction
2. Study Area and Background
3. Method and Data
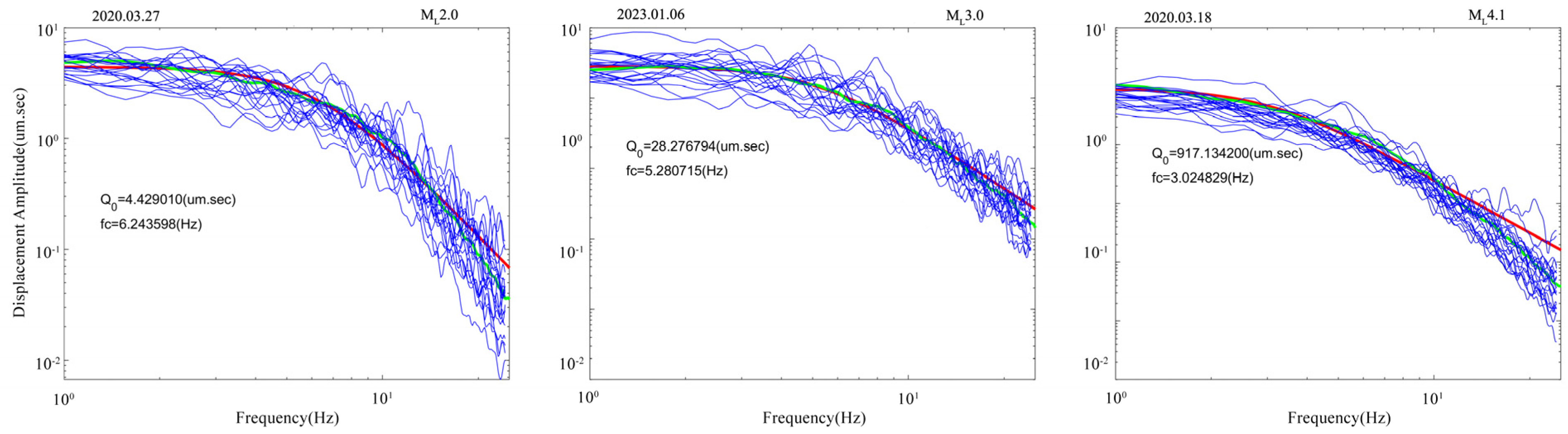
3.1. Method
3.2. Data
4. Results and Analysis of Seismic Source Parameter Calculation
5. Analysis and Discussion
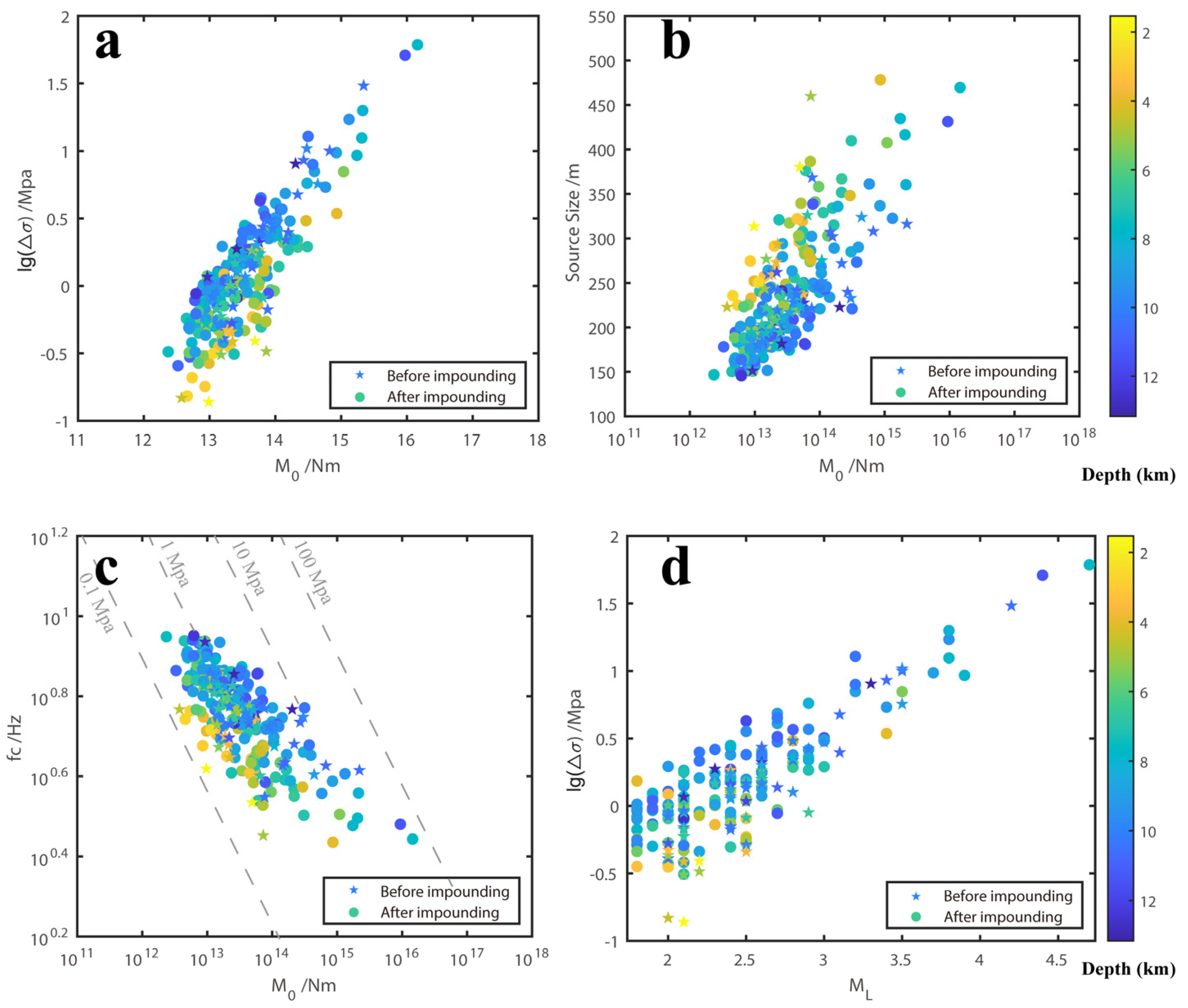
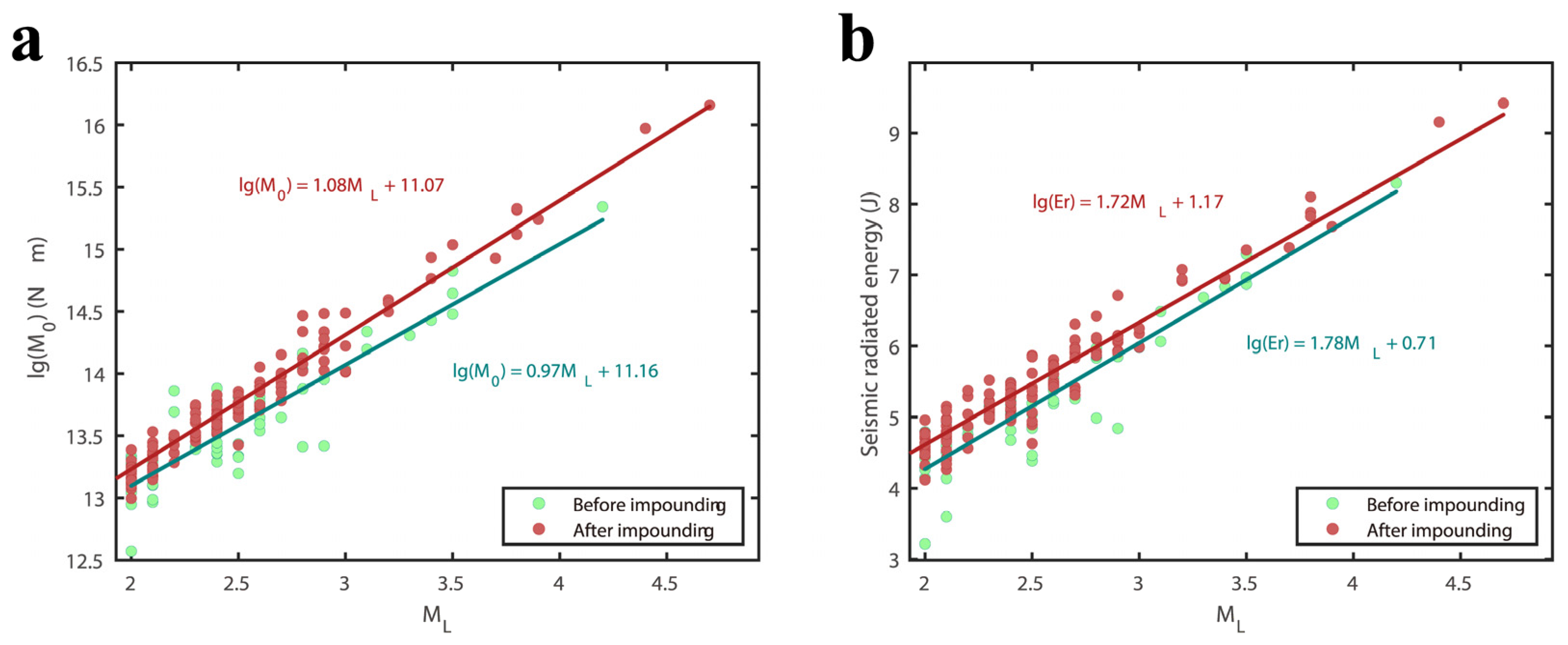
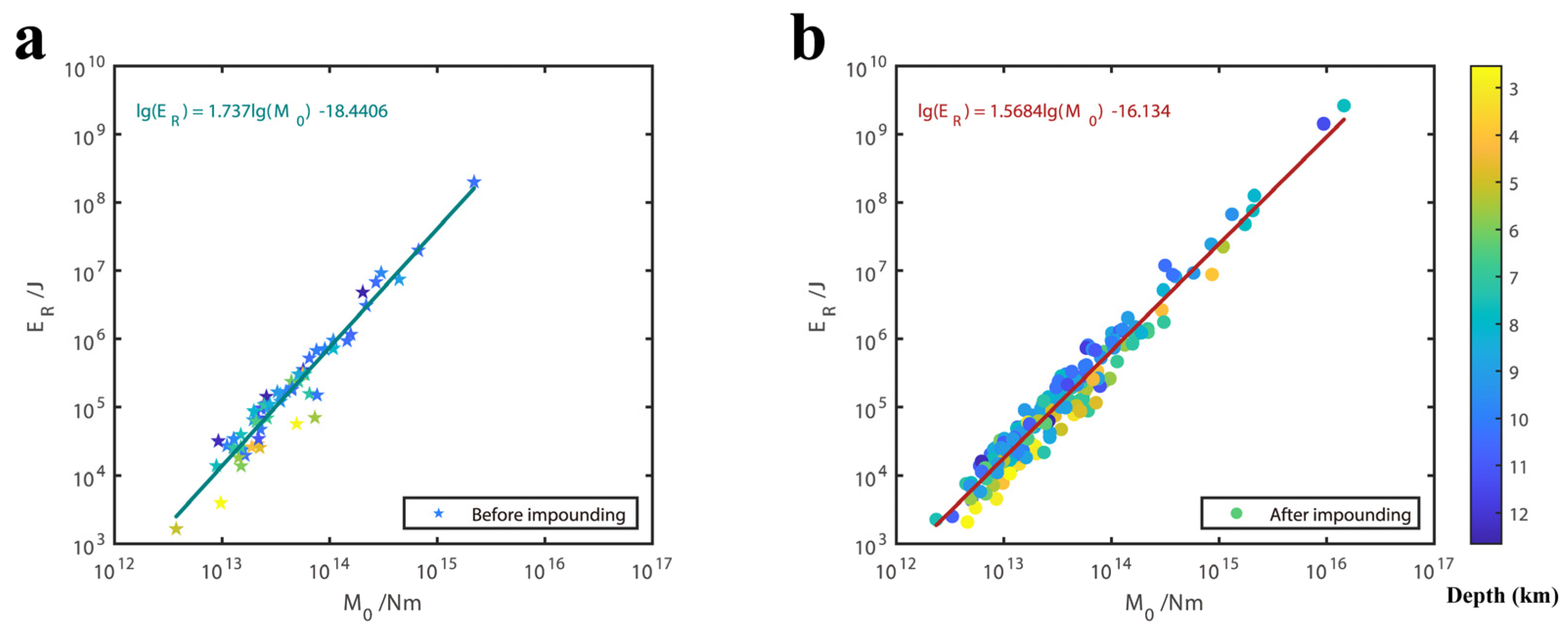
5.1. The Relationship between Source Parameters
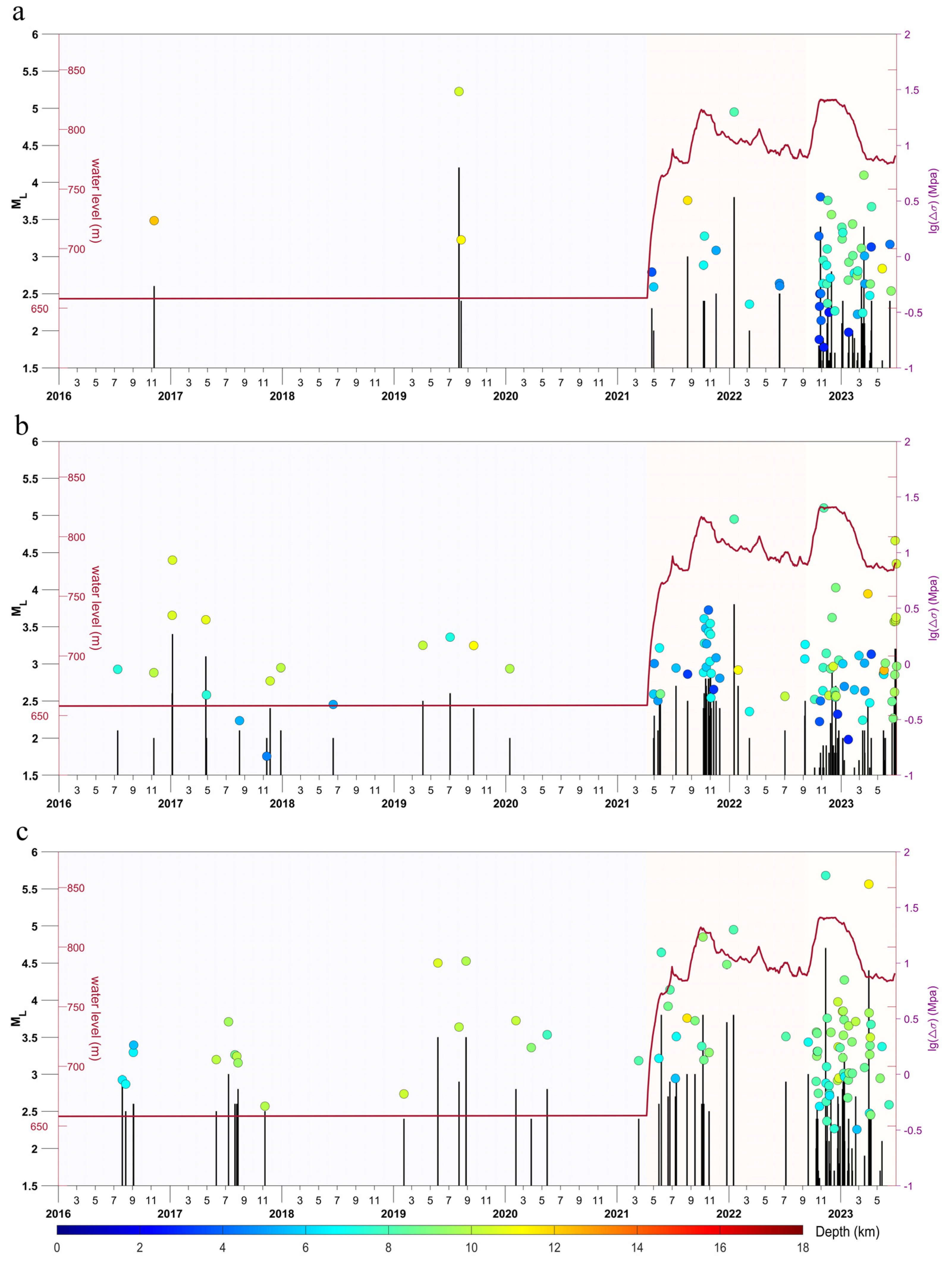
5.2. The Relationship between Stress Drops and Earthquake Magnitude and Water Storage
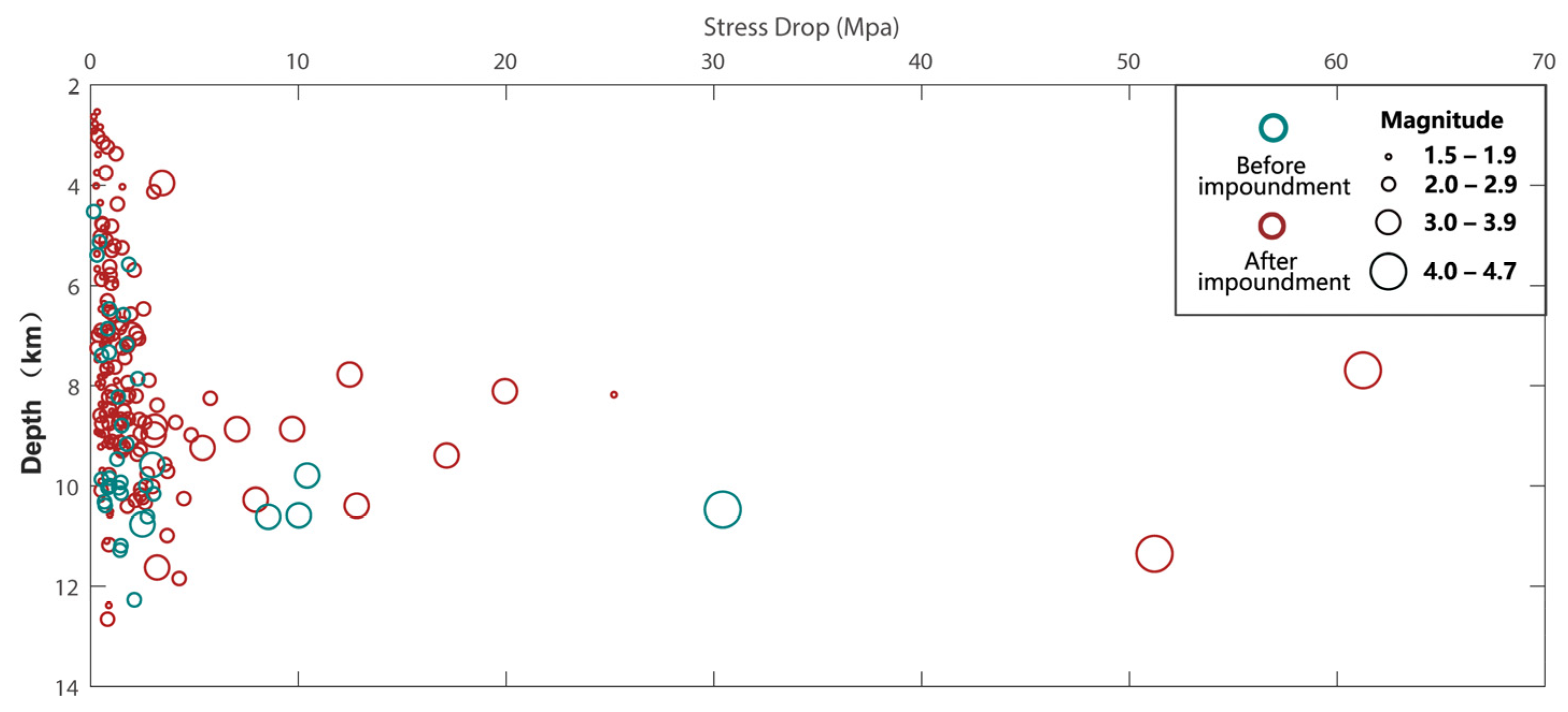
5.3. The Relationship between Stress Drops and Depth
5.4. Time Distribution Characteristics of Seismic Source Parameters
6. Conclusions
- (1)
- Based on the derived seismic wave attenuation model and station’s site response model for the Baihetan Reservoir area, we have recovered the source spectrum and further computed the source parameters for a total of 459 earthquakes within the magnitude range ML1.5 to 4.7 in the Baihetan reservoir region. The results obtained show that the earthquake moments M0 vary between 2.03 × 1012~1.45 × 1016 N·m, corner frequencies span from 2.0 to 10.0 Hz, the source dimensions range from 130 to 480 m, and stress drops fall within the interval of 0.12 to 61.24 MPa.
- (2)
- A positive correlation was observed between seismic stress drop, corner frequency, and source dimension with respect to earthquake magnitude. This means that both stress drop and rupture size generally increase as the magnitude of the earthquake increases. Additionally, for earthquakes of the same magnitude, those occurring at shallower depths tend to have smaller stress drops, lower corner frequencies, but larger rupture dimensions. The corner frequency and rupture scale of earthquakes in the Baihetan Reservoir area are relatively small, which may be the common characteristics of reservoir earthquakes. The reason for the low corner frequency may be caused by the development of reservoir fractures, reservoir water infiltration, and rock strength reduction. We found that the radiation energy of earthquakes below ML3.0 magnitude after impounding was significantly higher than that before impounding, roughly one order of magnitude higher, revealing that the seismic intensity and seismic feeling of earthquakes with the same magnitude are higher than those before impounding.
- (3)
- In the Baihetan Reservoir area of the Jinsha River, earthquakes following reservoir impoundment can be categorized into relatively shallow karst collapse events and deeper earthquakes induced by regional fault structures. Over the two-and-a-half years since water storage began, as the Baihetan Reservoir’s water level has significantly risen and undergone annual adjustments at high levels, earthquakes occurring near the reservoir have exhibited higher stress drops compared to those prior to impoundment. In particular, for earthquakes above magnitude 3 in Zones B and C, the stress drop values are notably greater after the reservoir is filled, with a gradual increase in released stress drops observed. With the Baihetan Dam continuing its annual water level regulation at high elevations, it is estimated that triggered seismic activity will persist, and there may remain a risk of inducing tectonic earthquakes within the reservoir area over the next several years. The dynamic changes in reservoir water levels, coupled with the inherent geological characteristics and loading effects on underlying faults, indicate an ongoing potential for seismically active periods during the operation of the dam.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RIS | Reservoir-induced seismicity |
| M0 | Seismic moments |
| ML | Richter magnitude scale |
| MS | Surface wave magnitude |
| MW | Moment magnitude scale |
References
- Ding, Y. The Reservoir Induced Earthquake. South China Seismol. 1989, 9, 64–72. [Google Scholar] [CrossRef]
- Nikolaev, N.I. Tectonic Conditions Favourable for Causing Earthquakes Occurring in Connection with Reservoir Filling. Eng. Geol. 1974, 8, 171–189. [Google Scholar] [CrossRef]
- Gupta, H.K. Reservoir Induced Earthquakes. Currentence 1992, 62, 183–198. [Google Scholar] [CrossRef]
- Gupta, H.K.; Rastogi, B.K. Developments in Geotechnical Engineering 11: Dams and Earthquakes. 1976. Available online: https://trid.trb.org/View/48488 (accessed on 1 March 2024).
- Rastogi, B.K.; Mandal, P. Foreshocks and Nucleation of Small- to Moderate-Sized Koyna Earthquakes (India). Bull. Seismol. Soc. Am. 1999, 89, 829–836. [Google Scholar] [CrossRef]
- Yadav, A.; Shashidhar, D.; Mallika, K.; Rao, N.P.; Rohilla, S.; Satyanarayana, H.V.S.; Srinagesh, D.; Gupta, H. Source Parameters of Earthquakes in the Reservoir-Triggered Seismic (RTS) Zone of Koyna–Warna, Western India. Nat. Hazards 2013, 69, 965–979. [Google Scholar] [CrossRef]
- Mahato, C.R.; Shashidhar, D. Stress Drop Variations of Triggered Earthquakes at Koyna–Warna, Western India: A Case Study. J. Earth Syst. Sci. 2022, 131, 106. [Google Scholar] [CrossRef]
- Tomic, J.; Abercrombie, R.E.; Do Nascimento, A.F. Source Parameters and Rupture Velocity of Small M ≤ 2.1 Reservoir Induced Earthquakes. Geophys. J. Int. 2009, 179, 1013–1023. [Google Scholar] [CrossRef]
- Saadalla, H.; El-Aal, A.E.-A.K.A.; Mohamed, A.; El-Faragawy, K. Determination of Earthquake Source Parameters Using the Inversion of Waveform Data: A Case of Small Earthquakes around High Dam Lake, Aswan Region, Egypt. J. Afr. Earth Sci. 2019, 151, 403–416. [Google Scholar] [CrossRef]
- Li, P.; Wang, L. Research on Basic Seismological Characteristics of Yunnan and Western Sichuan Region. Sci. Geol. Sin. 1975, 4, 308–325. [Google Scholar]
- She, Y.; Fu, G.; Zhao, Q.; Guo, L. Simulating Changes of Gravity and Coulomb Stress Caused by the Impoundment of the Baihetan Hydropower Station. Chin. J. Geophys. 2021, 64, 1925–1936. [Google Scholar]
- Guo, W.; Zhao, C.; Zuo, K.; Zhao, C. Characteristics of Seismicity before and after Impoundment of Baihetan Dam in the Lower Reaches of Jinsha River. Chin. J. Geophys. 2022, 65, 4659–4671. [Google Scholar]
- Guo, W.; Zhao, C. Focal Mechanisms and Stress Field Characteristics of Microearthquakes in Baihetan Reservoir in the Downstream Area of Jinsha River. Water 2023, 15, 709. [Google Scholar] [CrossRef]
- Abercrombie, R.E. Resolution and Uncertainties in Estimates of Earthquake Stress Drop and Energy Release. Phil. Trans. R. Soc. A 2021, 379, 20200131. [Google Scholar] [CrossRef] [PubMed]
- Hartzell, S.H. Earthquake Aftershocks as Green’s Functions. Geophys. Res. Lett. 1978, 5, 1–4. [Google Scholar] [CrossRef]
- Hua, W.; Chen, Z.; Zheng, S. Source Parameters and Scaling Relations for Reservoir Induced Seismicity in the Longtan Reservoir Area. Pure Appl. Geophys. 2013, 170, 767–783. [Google Scholar] [CrossRef]
- Liu, J.; Zheng, S.; Huang, Y. The Inversion of Anelastic Coefficient, Source Parameters and Site Respond Using Genetic Algorithm. Acta Seismol. Sin. 2003, 16, 226–232. [Google Scholar] [CrossRef]
- Zhao, C.; Chen, Z.; Hua, W.; Wang, Q.; Li, Z.; Zheng, S. Study on Source Parameters of Small to Moderate Earthquakes in the Main Seismic Active Regions, China Mainland. Chin. J. Geophys. 2011, 54, 1478–1489. [Google Scholar]
- Hua, W.; Chen, Z.; Zheng, S.; Yan, C. A Study on Characteristics of Source Parameters in Three Gorges Reservoir Area. Seismol. Geol. 2010, 32, 533–542. [Google Scholar]
- Atkinson, G.M.; Mereu, R.F. The Shape of Ground Motion Attenuation Curves in Southeastern Canada. Bull. Seismol. Soc. Am. 1992, 82, 2014–2031. [Google Scholar] [CrossRef]
- Moya, A.; González, J.; Irikura, K. Inversion of Source Parameters and Site Effects from Strong Ground Motion Records Using Genetic Algorithms. Bull. Seismol. Soc. Am. 2000, 90, 977–992. [Google Scholar] [CrossRef]
- Brune, J. Seismic Sources, Fault Plane Studies and Tectonics. Eos Trans. Am. Geophys. Union 1971, 52, IUGG 178–IUGG 187. [Google Scholar] [CrossRef]
- Stork, A.; Ito, H. Source Parameter Scaling for Small Earthquakes Observed at the Western Nagano 800-m-Deep Borehole, Central Japan. Bull. Seismol. Soc. Am. 2004, 94, 1781–1794. [Google Scholar] [CrossRef]
- Zuo, K.; Lei, H.; Zhao, C.; Zhao, C.; Zhang, H. 3D VP, VS, and VP/VS Structures and Seismicity of the Lower Reaches of the Jinsha River, China. Seismol. Res. Lett. 2023, 94, 2384–2396. [Google Scholar] [CrossRef]
- Jiang, N.; Wu, W.; Hong, Z. Review of International Research Progress in Source Stress Drop. J. Seismol. Res. 2024, 47, 163–177. [Google Scholar]
- Hardebeck, J.L.; Aron, A. Earthquake Stress Drops and Inferred Fault Strength on the Hayward Fault, East San Francisco Bay, California. Bull. Seismol. Soc. Am. 2009, 99, 1801–1814. [Google Scholar] [CrossRef]
- Marone, C.; Vidale, J.; Ellsworth, W. Fault Healing Inferred from Time Dependent Variations in Source Properties of Repeating Earthquake. Geophys. Res. Lett. 1995, 22, 3095–3098. [Google Scholar] [CrossRef]
- Atkinson, G.M. Empirical Attenuation of Ground-Motion Spectral Amplitudes in Southeastern Canada and the Northeastern United States. Bull. Seismol. Soc. Am. 2004, 94, 1079–1095. [Google Scholar] [CrossRef]
- Shi, J.; Kim, W.-Y.; Richards, P.G. The Corner Frequencies and Stress Drops of Intraplate Earthquakes in the Northeastern United States. Bull. Seismol. Soc. Am. 1998, 88, 531–542. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, X. The Transition of Apparent Stress Scaling Law before and after Impounding in Zipingpu Reservoir Region. Chin. J. Geophys. 2010, 53, 2861–2868. [Google Scholar]
- Abercrombie, R.; Leary, P. Source Parameters of Small Earthquakes Recorded at 2.5 Km Depth, Cajon Pass, Southern California: Implications for Earthquake Scaling. Geophys. Res. Lett. 1993, 20, 1511–1514. [Google Scholar] [CrossRef]
- Hua, W.; Zheng, S.; Yan, C.; Wang, M. Attenuation, Site Effects, and Source Parameters in the Three Gorges Reservoir Area, China. Bull. Seismol. Soc. Am. 2013, 103, 371–382. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, C. Study of Attenuation Characteristics, Site Response and Seismic Source Parameters of the Zipingpu Reservoir Region. Seismol. Geol. 2009, 31, 664–675. [Google Scholar]
- Zhong, Y.; Zhu, X.; Zhang, Z. Source Parameter Characteristics of ML3.9 Earthquake Swarm Occurred in Shanxi Reservoir, Wenzhou, Zhejiang Province. Earthquake 2004, 24, 107–114. [Google Scholar]
- Yao, L.; Zhong, Y.; Zhang, Z. Influence of Impregnated Rock Mass on the Corner Frequency. Northwestern Seismol. J. 2004, 26, 315–321. [Google Scholar]
- Choy, G.; Mcgarr, A.; Kirby, S.; Boatwright, J. An Overview of the Global Variability in Radiated Energy and Apparent Stress. Geophys. Monogr. Ser. 2006, 170, 43–57. [Google Scholar] [CrossRef]
- Goebel, T.H.W.; Hauksson, E.; Shearer, P.M.; Ampuero, J.P. Stress-Drop Heterogeneity within Tectonically Complex Regions: A Case Study of San Gorgonio Pass, Southern California. Geophys. J. Int. 2015, 202, 514–528. [Google Scholar] [CrossRef]
- Goertz-Allmann, B.; Goertz, A.; Wiemer, S. Stress Drop Variations of Induced Earthquakes at the Basel Geothermal Site. Geophys. Res. Lett. 2011, 38, L09308. [Google Scholar] [CrossRef]




| Magnitude | A | B | C | E | ||||
|---|---|---|---|---|---|---|---|---|
| Before | After | Before | After | Before | After | Before | After | |
| 2.0–2.9 | 1.759 | 1.300 | 1.005 | 1.393 | 1.527 | 2.131 | 1.454 | 1.701 |
| 3.0–3.9 | —— | 7.992 | 5.52 | 13.562 | 7.801 | 8.617 | 5.532 | 5.247 |
| 4.0–4.7 | 30.423 | —— | —— | —— | —— | 56.221 | 15.938 | —— |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Zhao, C.; Yang, Z.; Xu, L. Study on Seismic Source Parameter Characteristics of Baihetan Reservoir Area in the Lower Reaches of the Jinsha River. Water 2024, 16, 1370. https://doi.org/10.3390/w16101370
Shi J, Zhao C, Yang Z, Xu L. Study on Seismic Source Parameter Characteristics of Baihetan Reservoir Area in the Lower Reaches of the Jinsha River. Water. 2024; 16(10):1370. https://doi.org/10.3390/w16101370
Chicago/Turabian StyleShi, Jing, Cuiping Zhao, Zhousheng Yang, and Lisheng Xu. 2024. "Study on Seismic Source Parameter Characteristics of Baihetan Reservoir Area in the Lower Reaches of the Jinsha River" Water 16, no. 10: 1370. https://doi.org/10.3390/w16101370
APA StyleShi, J., Zhao, C., Yang, Z., & Xu, L. (2024). Study on Seismic Source Parameter Characteristics of Baihetan Reservoir Area in the Lower Reaches of the Jinsha River. Water, 16(10), 1370. https://doi.org/10.3390/w16101370






