Digital Flow in a Pool Induced by a Vertical Jet
Abstract
:1. Introduction
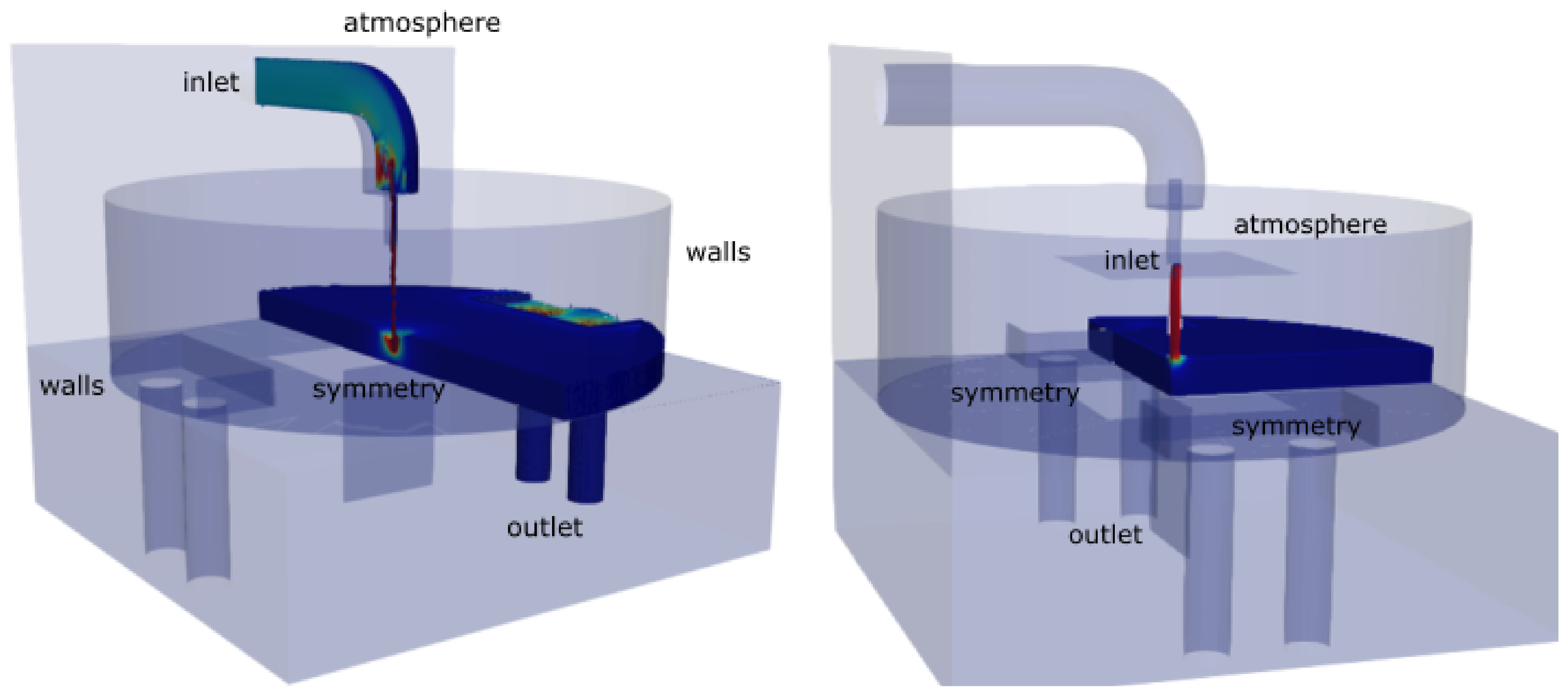
2. Physical Model—Experimental Installation at the EPFL
3. Numerical Modelling
3.1. Numerical Solver
3.2. Numerical Set
3.3. Data Analysis
4. Results and Discussion
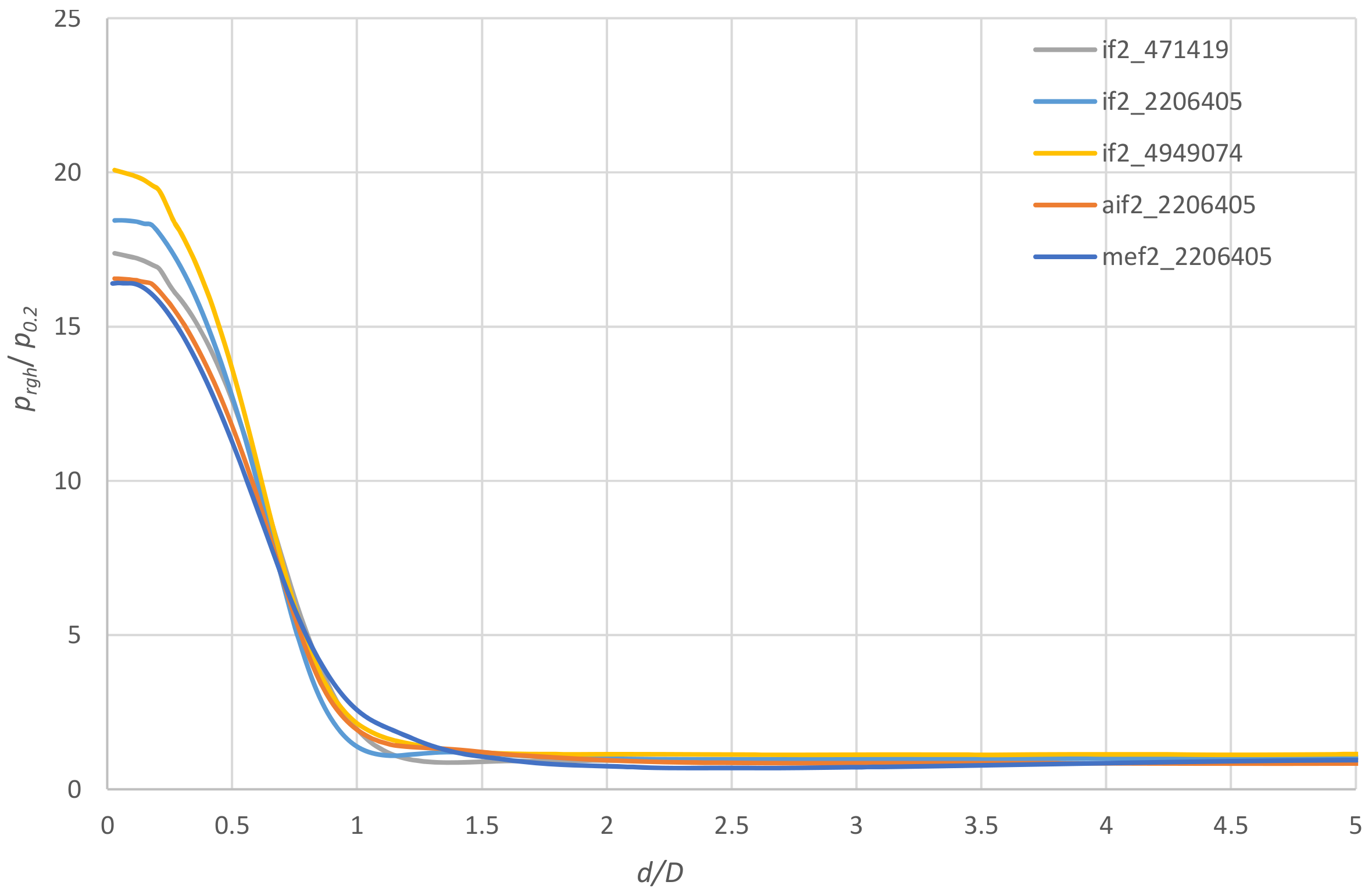
4.1. Grid Sensitivity
4.2. Solver Sensitivity
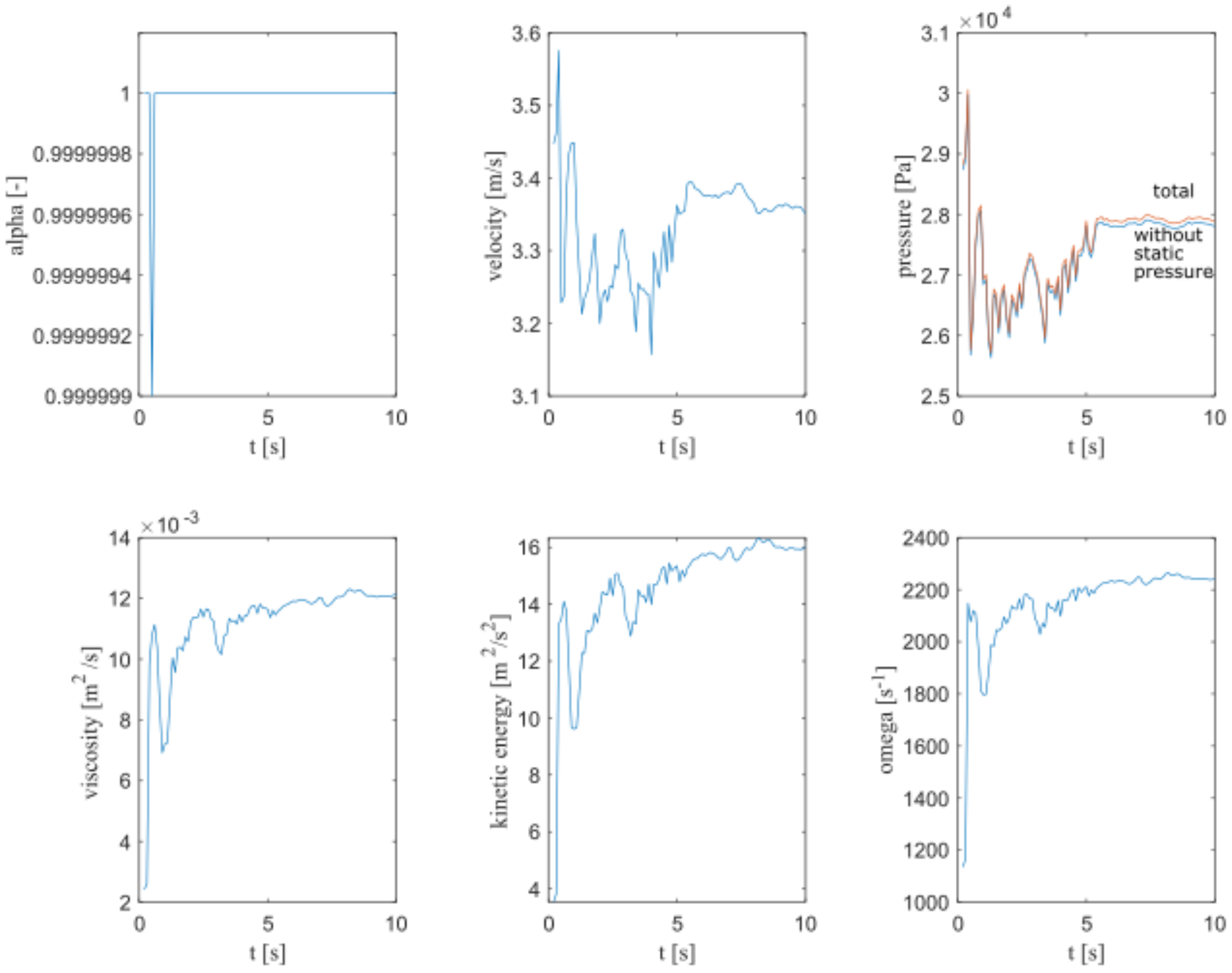
4.3. Unsteady Character
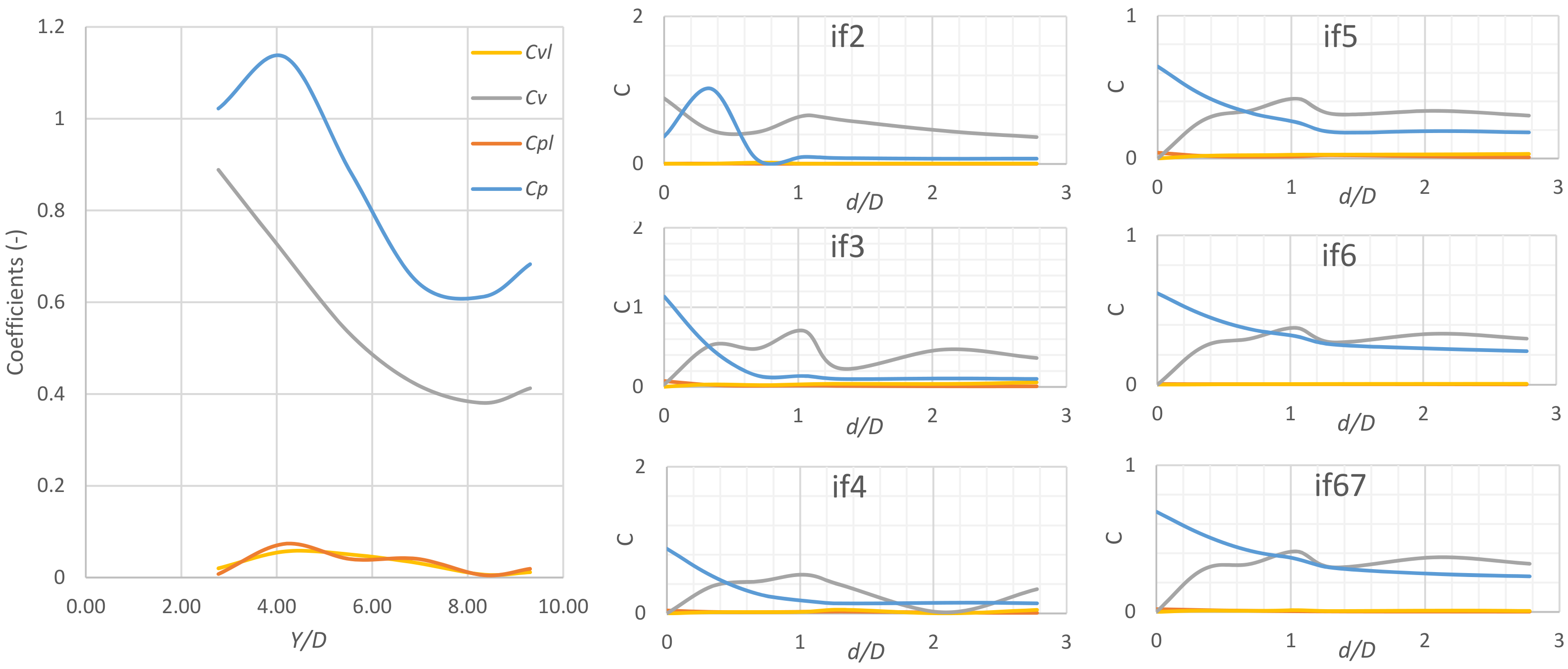
4.4. Statistical Characteristics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| c | general quantity for defining transport equations (k, for turbulent variables in |
| RANS models, turbulence model) | |
| Non-dimensional mean dynamic pressure coefficient | |
| Fluctuating pressure coefficients | |
| Mean velocity coefficient | |
| Fluctuating pressure coefficients | |
| d | Distance from the pool center |
| D | Nozzle diameter |
| Cross-diffusion term of quantity c ( = 0) | |
| F | Volume of Fluid Function |
| Froude number (=) | |
| g | Acceleration due to gravity |
| k | Turbulent kinetic energy |
| L | Jet length from nozzle to water surface, jet travel distance in the air |
| Distance from nozzle to pool’ bottom |
| Pressure resulting by removing the hydrostatic component to total pressure | |
| Hydrostatic pressure at a 0.2 water depth bottom | |
| Dynamic pressure at the pool bottom | |
| Q | Discharge Flow |
| Reynolds number (=) | |
| Source term for gaseous air at the free-surface | |
| t | Time |
| Compression velocity | |
| Velocity of the gaseous air fluid | |
| Velocity of the fluid k | |
| U | Velocity |
| Average velocity at the nozzle exit, jet initial velocity | |
| x | Main horizontal coordinate |
| y | Other horizontal coordinate |
| Y | Water pool depth |
| Dissipation term of quantity c | |
| z | Vertical coordinate |
| Volume of liquid fluid in a control volume (water) | |
| Volume of gaseous air fluid in a control volume | |
| Volume of fluid k in a control volume | |
| t | Time step |
| Effective diffusivity of c (k or ) | |
| Diffusivity tensor of | |
| Production/generation term of quantity c | |
| Kinematic viscosity | |
| Kinematic viscosity of the gaseous air fluid | |
| Kinematic viscosity of the fluid k | |
| Kinematic viscosity of the water | |
| Specific dissipation rate | |
| Density (for the mixing fluid) | |
| Density of the gaseous air fluid | |
| Density of the fluid k | |
| Density of the water |
References
- Albertson, M.L.; Dai, Y.B.; Jensen, R.A.; Rouse, H. Difusion of submerged jets. Proc. Am. Soc. Civ. Eng. 1948, 74, 639–663. [Google Scholar]
- Bertola, N.J.; Wang, H.; Chanson, H. Air Bubble Entrainment at Vertical Plunging Jets: A Large-Scale Experimental Study; Hydraulic Model Report No.CH104/17; School of Civil Engineering, The University of Queensland: Brisbane, QLD, Australia, 2017; 256p. [Google Scholar]
- Bollaert, E.; Schleiss, A. Scour of rock due to the impact of plunging high velocity jets Part I: A state-of-the-art review. J. Hydraul. Res. 2003, 41, 451–464. [Google Scholar] [CrossRef]
- Bonetto, F.; Lahey, R. An experimental study on air carry under due to a plunging liquid jet. Int. J. Multiph. Flow 1993, 19, 281–294, Discussion: 1994, 20, 667–770. [Google Scholar] [CrossRef]
- Brattberg, T.; Chanson, H. Air entrapment and air bubble dispersion at two-dimensional plunging water jets. Chem. Eng. Sci. 1998, 53, 4113–4127. [Google Scholar] [CrossRef]
- Carrillo, J.M.; Castillo, L.G.; Marco, F.; García, J.T. Experimental and Numerical Analysis of Two-Phase Flows in Plunge Pools. J. Hydraul. Eng. 2020, 146, 04020044. [Google Scholar] [CrossRef]
- Castillo, L.G.; Carrillo, J.M. Experimental and numerical analysis of velocities in plunge pools of free falling spillways. In Proceedings of the E-Proceedings of the 36th IAHR World Congress, The Hague, The Netherlands, 28 June–3 July 2015. [Google Scholar]
- Cummings, P.D.; Chanson, H. Air entrainment in the developing flow region of plunging jets—Part 1: Theoretical development. J. Fluids Eng. 1997, 119, 597–602. [Google Scholar] [CrossRef]
- Cummings, P.D.; Chanson, H. Air entrainment in the developing flow region of plunging jets—Part 2: Experimental. J. Fluids Eng. 1997, 119, 603–608. [Google Scholar] [CrossRef]
- Ervine, D.A. Effects of Turbulence intensity on the rate of air-entrainment by plunging water jets. Proc. Inst. Civ. Eng. 1980, 69, 425–445. [Google Scholar] [CrossRef]
- Ervine, D.A.; Falvey, H.T. Behaviour of turbulent water jets in the atmosphere and in plunge pools. Proc. Inst. Civ. Eng. 1987, 83, 295–314. [Google Scholar] [CrossRef]
- Manso, P.A.; Bollaert, E.F.R.; Schleiss, A.J. Impact pressures of turbulent high-velocity jets plunging in pools with flat bottom. Exp. Fluids 2007, 42, 49–60. [Google Scholar] [CrossRef]
- Pinheiro, A.N.; Melo, J.F.; Ramos, C.M. Forces on Plunge Poll Slabs: Influence of Joints Location and Width. J. Hydraul. Eng. 2006, 132, 49–60. [Google Scholar]
- Pfister, M.; Hager, W.H. Deflector-generated jets. J. Hydraul. Res. 2009, 47, 466–475. [Google Scholar] [CrossRef]
- Rajaratnam, N. Turbulent Jet. In Development in Water Science; Elsevier Scientific Publishing Company: New York, NY, USA, 1976; Volume 5. [Google Scholar]
- Volkart, P. The mechanism of air buble entrainment in self aerated flows. Int. J. Multiph. Flow 1980, 6, 411–423. [Google Scholar] [CrossRef]
- Wang, H.; Slamet, N.S.; Zhang, G.; Chanson, H. Intrusive measurements of air-water flow properties in highly turbulent supported plunging jets and effects of inflow jet conditions. Chem. Eng. Sci. 2018, 177, 245–260. [Google Scholar] [CrossRef]
- Wood, I.R. Air entrainment in free-surface flows. In IAHR Hydraulic Structures Design Manual. 4. Hydraulic Design Considerations; Balkema Publisher: Rotterdam, The Netherlands, 1991; p. 149. [Google Scholar]
- Lopes, P.; Tabor, G.; Carvalho, R.F.; Leandro, J. Explicit calculation of natural aeration using a Volume-of-Fluid model. Appl. Math. Model. 2016, 40, 7504–7515. [Google Scholar] [CrossRef]
- Moreira, A.; Leroy, A.; Violeau, D.; Taveira-Pinto, F. Dam spillways and the SPH method: Two case studies in Portugal. J. Appl. Water Eng. Res. 2021, 7, 228–245. [Google Scholar] [CrossRef]
- Lopes, P.; Carvalho, R.F.; Leandro, J. Numerical and experimental study of the fundamental flow characteristics of a 3D gully box under drainage. Water Sci. Technol. 2017, 75, 2204–2215. [Google Scholar] [CrossRef] [PubMed]
- Lopes, P.; Leandro, J.; Carvalho, R.F. Self-Aeration Modelling Using a Sub-Grid Volume-Of-Fluid Model. Int. J. Nonlinear Sci. Numer. Simul. 2017, 18, 559–574. [Google Scholar] [CrossRef]
- Almelanda, S.K.; Mukhab, T.; Bensow, R.E. An improved air entrainment model for stepped spillways. Appl. Math. Model. 2021, 100, 170–191. [Google Scholar] [CrossRef]
- Carvalho, R.F.; Lemos, C.M.; Ramos, C.M. Numerical computation of the flow in hydraulic jump stilling basins. J. Hydraul. Res. 2008, 46, 739–752. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Rusche, H. Computational Fluid Dynamics of Dispersed Two-Phase Flows at High Phase Fractions. Ph.D. Thesis, University of London, London, UK, 2002. [Google Scholar]
- Weller, H. A New Approach to VOF-Based Interface Capturing Methods for Incompressible and Compressible Flows; Report TR/HGW/04; OpenCFD Ltd.: Bracknell, UK, 2008. [Google Scholar]
- Anez, J.; Puggelli, S.; Hecht, N.; Andreini, A.; Reveillon, J.; Demoulin, F.X. Liquid Atomization Modeling in OpenFOAM®; Springer: Berlin/Heidelberg, Germany, 2019; pp. 297–308. [Google Scholar]
- McGinn, P.; Tretola, G.; Vogiatzaki, K. Three-component volume of fluid method coupling with interface compression method and Eulerian—Lagrangian spray atomization surface density model for prediction of cavitating sprays. Phys. Fluids 2024, 36, 022118. [Google Scholar] [CrossRef]
- Gärtner, J.W.; Kronenburg, A. A novel ELSA model for flash evaporation. Int. J. Multiph. Flow 2024, 174, 104784. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar]

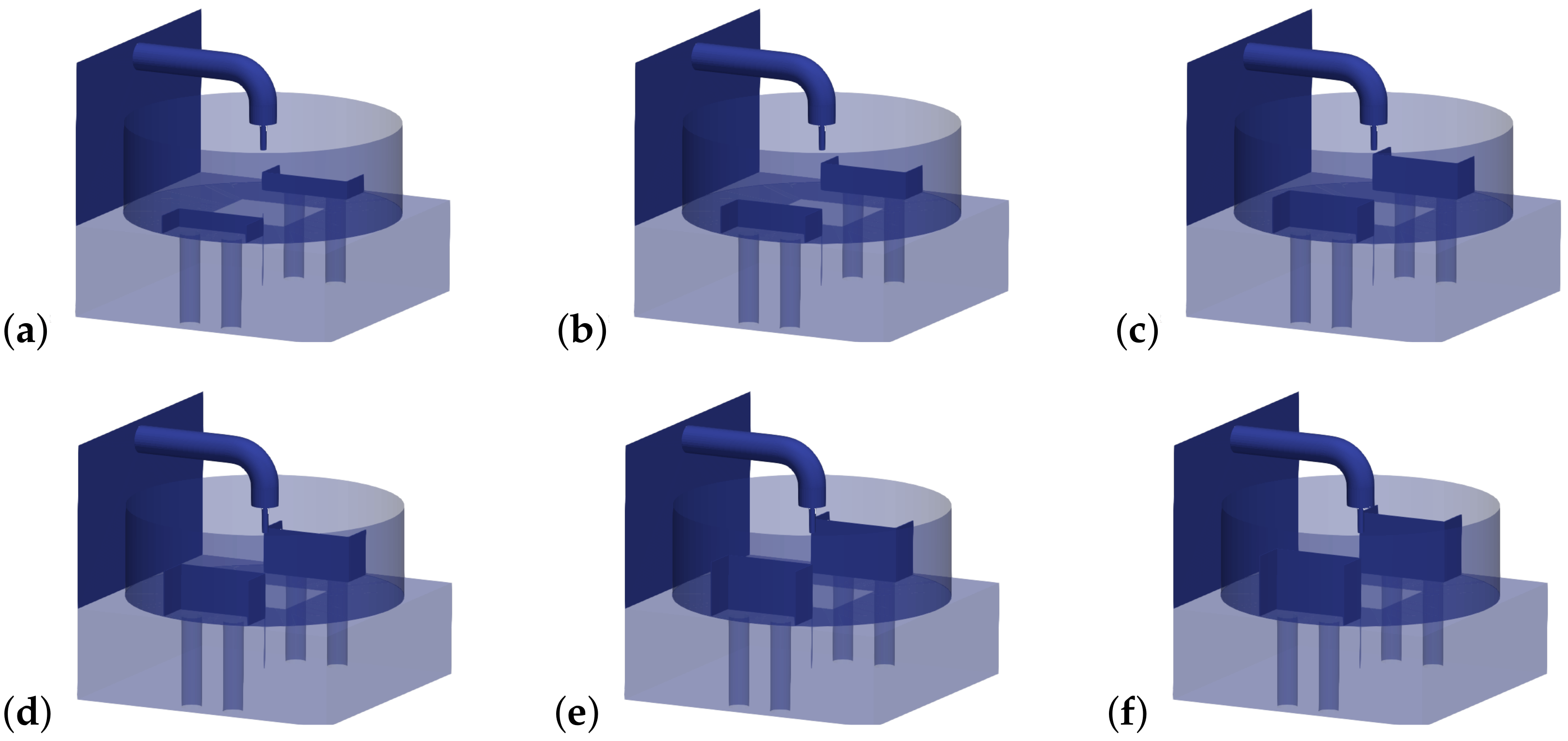




| 30 L/s; 7.4 m/s; 4.6 ; 8.8 | |||
|---|---|---|---|
| (m) | (–) | (m) | (–) |
| 0.2 | 2.8 | 0.5 | 0.32–0.35 |
| 0.3 | 4.2 | 0.4 | 0.26–0.28 |
| 0.4 | 5.6 | 0.3 | 0.19–0.21 |
| 0.5 | 6.9 | 0.2 | 0.13–0.14 |
| 0.6 | 8.3 | 0.1 | 0.06–0.07 |
| 0.67 | 9.3 | 0.03 | 0.02 |
| Pool Water Depth (m) | Number of Cells () |
|---|---|
| 0.2 | 471,419 (25 × 25 × (10 + 25)); |
| 2,206,405 (50 × 50 × (20 + 50)); | |
| 4,949,074 (100 × 100 × (40 + 100)) | |
| 0.3 | 4,263,456 |
| 0.4 | 4,421,496 |
| 0.5 | 4,579,536 |
| 0.6 | 4,737,576 |
| 0.67 | 4,848,204 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carvalho, R.F.; Lopes, P.M.; Beg, M.N.A. Digital Flow in a Pool Induced by a Vertical Jet. Water 2024, 16, 1386. https://doi.org/10.3390/w16101386
Carvalho RF, Lopes PM, Beg MNA. Digital Flow in a Pool Induced by a Vertical Jet. Water. 2024; 16(10):1386. https://doi.org/10.3390/w16101386
Chicago/Turabian StyleCarvalho, Rita F., Pedro M. Lopes, and Md Nazmul A. Beg. 2024. "Digital Flow in a Pool Induced by a Vertical Jet" Water 16, no. 10: 1386. https://doi.org/10.3390/w16101386
APA StyleCarvalho, R. F., Lopes, P. M., & Beg, M. N. A. (2024). Digital Flow in a Pool Induced by a Vertical Jet. Water, 16(10), 1386. https://doi.org/10.3390/w16101386









