Quantifying the Impacts of Dry–Wet Combination Events on Vegetation Vulnerability in the Loess Plateau under a Changing Environment
Abstract
:1. Introduction
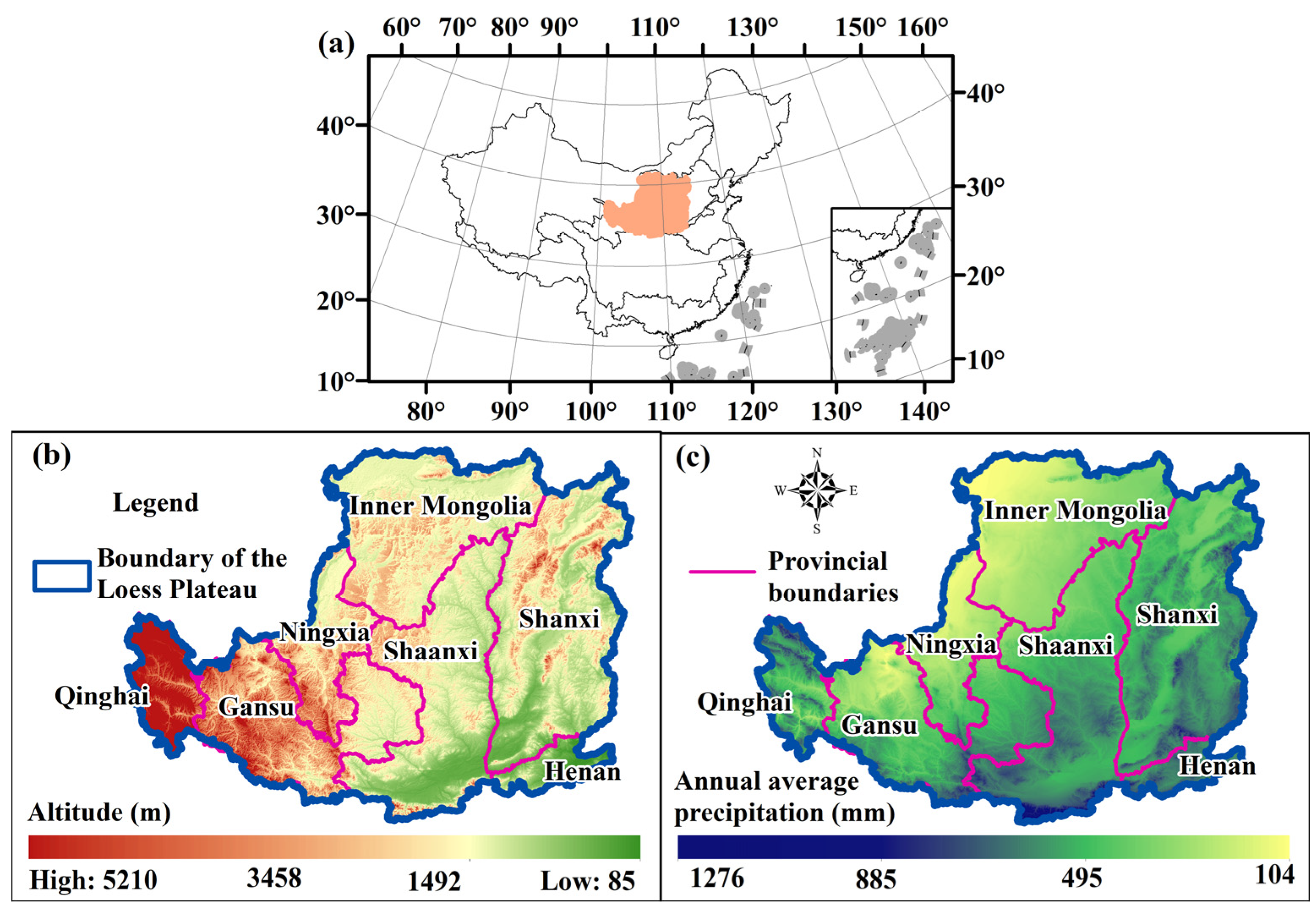
2. Study Area and Data
3. Methods
3.1. Mann–Kendall Trend Test
3.2. The Response Time of Vegetation on Dry and Wet Variation
3.3. Frequency Statistical Method for Vegetation Vulnerability
3.4. Probability Assessment Model for Vegetation Loss
- Univariate marginal distribution
- 2.
- Binary copula joint distribution function
- 3
- Three-dimensional copula joint distribution function
- 4
- Probability of vegetation loss under DWCE stress
4. Results
4.1. The Spatial Distribution Characteristics of NDVI
4.2. Response Time of NDVI to SPI
4.3. The Impact of DWCEs on Vegetation Vulnerability
4.3.1. The Impact on Summer Vegetation Vulnerability
4.3.2. The Impact on Autumn Vegetation Vulnerability
4.4. Probability of Vegetation Loss under DWCEs Stress
4.4.1. Probability of Vegetation Loss in Summer
4.4.2. Probability of Vegetation Loss in Autumn
5. Discussion
6. Conclusions
- NDVI in spring, summer, and autumn showed a significant upward trend, with an area ratio of 90.5%, 86.2%, and 95.4%, respectively. However, the trend of NDVI changes in winter is not significant. The response time of vegetation changes to precipitation changes ranges from one to two seasons.
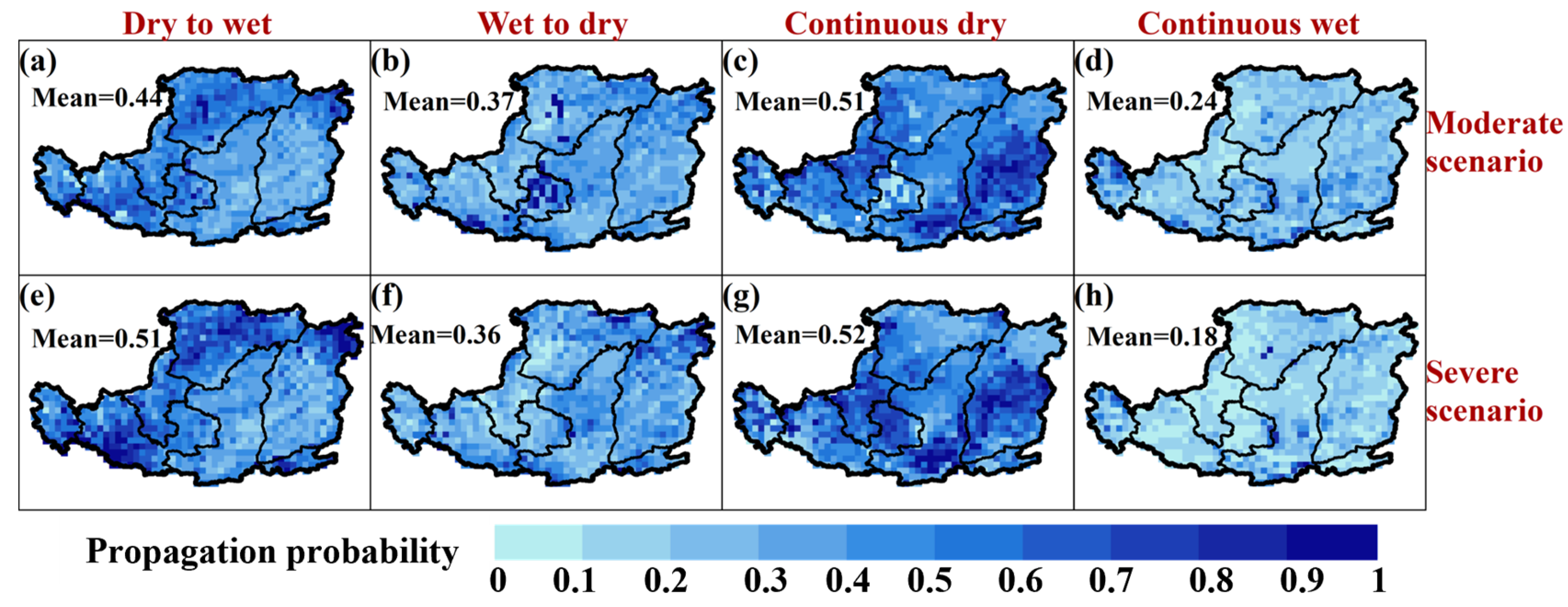
- The impact of DWCEs on vegetation vulnerability is greater in moderate scenarios than in severe scenarios. Specifically, DWEs, WDEs, and CDEs in spring–summer have a significant impact on the summer vegetation of Ningxia and Shanxi, and WDEs and CDEs have a higher impact on autumn vegetation.
- According to the mean value of the vegetation loss probability, the CDEs in the moderate scenario and DWEs and CDEs in the severe scenario cause significant losses to summer vegetation, with loss probabilities of 0.51, 0.51, and 0.52, respectively. WDEs and CDEs under moderate and severe scenarios have a significant impact on autumn vegetation loss, with a probability of loss ranging from 0.44 to 0.56. This study facilitates a better understanding of vegetation loss under DWCE stress. Furthermore, it provides a new framework for quantitatively assessing vegetation vulnerability, which is also applicable to other regions of the world.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Penning-Rowsell, E.C.; Yanyan, W.; Watkinson, A.R.; Jiang, J.; Thorne, C. Socioeconomic scenarios and flood damage assessment methodologies for the Taihu Basin, China. J. Flood Risk Manag. 2013, 6, 23–32. [Google Scholar] [CrossRef]
- Elsey-Quirk, T.; Lynn, A.; Jacobs, M.D.; Diaz, R.; Cronin, J.T.; Wang, L.; Huang, H.; Justic, D. Vegetation dieback in the Mississippi River Delta triggered by acute drought and chronic relative sea-level rise. Nat. Commun. 2024, 15, 3518. [Google Scholar] [CrossRef] [PubMed]
- Qiao, X.; Straight, B.; Ngo, D.; Hilton, C.E.; Owuor Olungah, C.; Naugle, A.; Lalancette, C.; Needham, B.L. Severe drought exposure in utero associates to children’s epigenetic age acceleration in a global climate change hot spot. Nat. Commun. 2024, 15, 4140. [Google Scholar] [CrossRef] [PubMed]
- Dong, B.Q.; Qin, T.L.; Liu, S.S.; Liu, F.; Nie, H.J.; Wang, J.W.; Lv, Z.Y.; Shi, X.Q. Disentangling the Mutual Feedback Relationship between Extreme Drought and Flood Events and Ecological Succession of Vegetation. Pol. J. Environ. Stud. 2021, 30, 1003–1016. [Google Scholar] [CrossRef] [PubMed]
- Meehl, G.A.; Tebaldi, C. More intense, more frequent, and longer lasting heat waves in the 21st century. Science 2004, 305, 994–997. [Google Scholar] [CrossRef] [PubMed]
- Su, B.D.; Huang, J.L.; Fischer, T.; Wang, Y.J.; Kundzewicz, Z.W.; Zhai, J.Q.; Sun, H.M.; Wang, A.Q.; Zeng, X.F.; Wang, G.J.; et al. Drought losses in China might double between the 1.5 °C and 2.0 °C warming. Proc. Natl. Acad. Sci. USA 2018, 115, 10600–10605. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Weng, Z.H.; Chen, H.; Yang, J.W. Analysis of the Evolution of Drought, Flood, and Drought-Flood Abrupt Alternation Events under Climate Change Using the Daily SWAP Index. Water 2020, 12, 1969. [Google Scholar] [CrossRef]
- Bi, W.X.; Li, M.; Weng, B.S.; Yan, D.H.; Dong, Z.Y.; Feng, J.M.; Wang, H. Drought-flood abrupt alteration events over China. Sci. Total Environ. 2023, 875, 162529. [Google Scholar] [CrossRef]
- Hrdinka, T.; Novicky, O.; Hanslík, E.; Rieder, M. Possible impacts of floods and droughts on water quality. J. Hydro-Environ. Res. 2012, 6, 145–150. [Google Scholar] [CrossRef]
- He, X.G.; Sheffield, J. Lagged Compound Occurrence of Droughts and Pluvials Globally Over the Past Seven Decades. Geophys. Res. Lett. 2020, 47, e2020GL087924. [Google Scholar] [CrossRef]
- Verhoeven, E.; Wardle, G.M.; Roth, G.W.; Greenville, A.C. Characterising the spatiotemporal dynamics of drought and wet events in Australia. Sci. Total Environ. 2022, 846, 157480. [Google Scholar] [CrossRef] [PubMed]
- Parry, S.; Marsh, T.; Kendon, M. 2012: From drought to floods in England and Wales. Weather 2013, 68, 268–274. [Google Scholar] [CrossRef]
- Son, R.; Wang, S.Y.S.; Tseng, W.L.; Schuler, C.B.W.; Becker, E.; Yoon, J.H. Climate diagnostics of the extreme floods in Peru during early 2017. Clim. Dyn. 2020, 54, 935–945. [Google Scholar] [CrossRef]
- Jin, G. Similarities and differences of hydrologic frequency distribution models and their parameter estimation problems. Adv. Water Sci. 2010, 21, 466–470. [Google Scholar]
- Mu, W.B.; Yu, F.L.; Xie, Y.B.; Liu, J.; Li, C.Z.; Zhao, N.N. The Copula Function-Based Probability Characteristics Analysis on Seasonal Drought & Flood Combination Events on the North China Plain. Atmosphere 2014, 5, 847–869. [Google Scholar] [CrossRef]
- Chen, J.; Dai, A.; Zhang, Y. Projected Changes in Daily Variability and Seasonal Cycle of Near-Surface Air Temperature over the Globe during the Twenty-First Century. J. Clim. 2019, 32, 8537–8561. [Google Scholar] [CrossRef]
- Myoung, B.; Nielsen-Gammon, J.W. Sensitivity of monthly convective precipitation to environmental conditions. J. Clim. 2010, 23, 166–188. [Google Scholar] [CrossRef]
- Shan, L.; Zhang, L.; Song, J.; Zhang, Y.; She, D.; Xia, J. Characteristics of dry-wet abrupt alternation events in the middle and lower reaches of the Yangtze River Basin and the relationship with ENSO. J. Geogr. Sci. 2018, 28, 1039–1058. [Google Scholar] [CrossRef]
- Shi, X.; Guo, W.; Li, W.; Dai, S.; Lu, H. The sudden turn of drought and flood in spring in northern Qinghai Province, 2013: Characteristics and cause of formation. J. Glaciol. Geocryol. 2015, 37, 376–386. [Google Scholar]
- Sun, C.; Yang, S. Persistent severe drought in southern China during winter–spring 2011: Large-scale circulation patterns and possible impacting factors. J. Geophys. Res. Atmos. 2012, 117, D10112. [Google Scholar] [CrossRef]
- De Luca, P.; Messori, G.; Wilby, R.L.; Mazzoleni, M.; Di Baldassarre, G. Concurrent wet and dry hydrological extremes at the global scale. Earth Syst. Dyn. 2020, 11, 251–266. [Google Scholar] [CrossRef]
- Zhang, X.; Alexander, L.; Hegerl, G.C.; Jones, P.; Tank, A.K.; Peterson, T.C.; Trewin, B.; Zwiers, F.W. Indices for monitoring changes in extremes based on daily temperature and precipitation data. WIREs Clim. Chang. 2011, 2, 851–870. [Google Scholar] [CrossRef]
- Fang, W.; Huang, S.; Huang, G.; Huang, Q.; Wang, H.; Wang, L.; Zhang, Y.; Li, P.; Ma, L. Copulas-based risk analysis for inter-seasonal combinations of wet and dry conditions under a changing climate. Int. J. Climatol. 2019, 39, 2005–2021. [Google Scholar] [CrossRef]
- Broich, M.; Tulbure, M.G.; Verbesselt, J.; Xin, Q.C.; Wearne, J. Quantifying Australia’s dryland vegetation response to flooding and drought at sub-continental scale. Remote Sens. Environ. 2018, 212, 60–78. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, Z.; Li, J.; Zhong, R.; Huang, W. Assessing impacts of meteorological drought on vegetation at catchment scale in China based on SPEI and NDVI. Trans. Chin. Soc. Agric. Eng. 2016, 32, 177–186. [Google Scholar]
- Gao, Y.; Hu, T.; Yuan, H.; Yang, J. Analysis on yield reduced law of rice in Huaibei plain under drought-flood abrupt alternation. Trans. Chin. Soc. Agric. Eng. 2017, 33, 128–136. [Google Scholar]
- Zhang, Q.; Han, L.Y.; Zeng, J.; Wang, X.; Lin, J.J. Climate factors during key periods affect the comprehensive crop losses due to drought in Southern China. Clim. Dyn. 2020, 55, 2313–2325. [Google Scholar] [CrossRef]
- Chen, H.L.; Liang, Z.Y.; Liu, Y.; Jiang, Q.S.; Xie, S.G. Effects of drought and flood on crop production in China across 1949–2015: Spatial heterogeneity analysis with Bayesian hierarchical modeling. Nat. Hazards 2018, 92, 525–541. [Google Scholar] [CrossRef]
- Zhang, B.; He, C.; Burnham, M.; Zhang, L. Evaluating the coupling effects of climate aridity and vegetation restoration on soil erosion over the Loess Plateau in China. Sci. Total Environ. 2016, 539, 436–449. [Google Scholar] [CrossRef]
- Deng, L.; Kim, D.-G.; Li, M.; Huang, C.; Liu, Q.; Cheng, M.; Shangguan, Z.; Peng, C. Land-use changes driven by ‘Grain for Green’ program reduced carbon loss induced by soil erosion on the Loess Plateau of China. Glob. Planet. Chang. 2019, 177, 101–115. [Google Scholar] [CrossRef]
- Sun, W.; Shao, Q.; Liu, J.; Zhai, J. Assessing the effects of land use and topography on soil erosion on the Loess Plateau in China. Catena 2014, 121, 151–163. [Google Scholar] [CrossRef]
- Ullah, R.; Khan, J.; Ullah, I.; Khan, F.; Lee, Y. Assessing Impacts of Flood and Drought over the Punjab Region of Pakistan Using Multi-Satellite Data Products. Remote Sens. 2023, 15, 1484. [Google Scholar] [CrossRef]
- Elagib, N.A.; Al Zayed, I.S.; Khalifa, M.; Rahma, A.E.; Ali, M.M.A.; Schneider, K. Drought versus flood: What matters more to the performance of Sahel farming systems? Hydrol. Process. 2023, 37, e14978. [Google Scholar] [CrossRef]
- Marumbwa, F.M.; Cho, M.A.; Chirwa, P.W. An assessment of remote sensing-based drought index over different land cover types in southern Africa. Int. J. Remote Sens. 2020, 41, 7368–7382. [Google Scholar] [CrossRef]
- Shi, W.Z.; Huang, S.Z.; Zhang, K.; Liu, B.J.; Liu, D.F.; Huang, Q.; Fang, W.; Han, Z.M.; Chao, L.J. Quantifying the superimposed effects of drought-flood abrupt alternation stress on vegetation dynamics of the Wei River Basin in China. J. Hydrol. 2022, 612, 128105. [Google Scholar] [CrossRef]
- Shiau, J.T. Fitting Drought Duration and Severity with Two-Dimensional Copulas. Water Resour. Manag. 2006, 20, 795–815. [Google Scholar] [CrossRef]
- Yang, W.T.; Zhang, L.Y.; Gao, Y. Drought and flood risk assessment for rainfed agriculture based on Copula-Bayesian conditional probabilities. Ecol. Indic. 2023, 146, 109812. [Google Scholar] [CrossRef]
- Nie, M.; Huang, S.; Duan, W.; Leng, G.; Bai, G.; Wang, Z.; Huang, Q.; Fang, W.; Peng, J. Meteorological drought migration characteristics based on an improved spatiotemporal structure approach in the Loess Plateau of China. Sci. Total Environ. 2024, 912, 168813. [Google Scholar] [CrossRef] [PubMed]
- Shi, H.; Shao, M. Soil and water loss from the Loess Plateau in China. J. Arid Environ. 2000, 45, 9–20. [Google Scholar] [CrossRef]
- Song, H.; Zhu, Z.; Li, Y. Validation of land data assimilation and reanalysis precipitation datasets over Inner Mongolia. Arid Zone Res. 2021, 38, 1624–1636. [Google Scholar]
- Brehaut, L.; Danby, R.K. Inconsistent relationships between annual tree ring-widths and satellite- measured NDVI in a mountainous subarctic environment. Ecol. Indic. 2018, 91, 698–711. [Google Scholar] [CrossRef]
- Yan, J.J.; Zhang, G.P.; Ling, H.B.; Han, F.F. Comparison of time-integrated NDVI and annual maximum NDVI for assessing grassland dynamics. Ecol. Indic. 2022, 136, 108611. [Google Scholar] [CrossRef]
- Mckee, T.B.; Doesken, N.J.; Kleist, J.R. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993. [Google Scholar]
- Adnan, S.; Ullah, K.; Shuanglin, L.; Gao, S.; Khan, A.H.; Mahmood, R. Comparison of various drought indices to monitor drought status in Pakistan. Clim. Dyn. 2018, 51, 1885–1899. [Google Scholar] [CrossRef]
- Pearson, K. Mathematical contributions to the theory of evolution—On a form of spurious correlation which may arise when indices are used in the measurement of organs. Proc. R. Soc. Lond. 1897, 60, 489–498. [Google Scholar] [CrossRef]
- Xiao, M.X.; Yu, Z.B.; Zhu, Y.L. Copula-based frequency analysis of drought with identified characteristics in space and time: A case study in Huai River basin, China. Theor. Appl. Climatol. 2019, 137, 2865–2875. [Google Scholar] [CrossRef]
- Mortuza, M.R.; Moges, E.; Demissie, Y.; Li, H.Y. Historical and future drought in Bangladesh using copula-based bivariate regional frequency analysis. Theor. Appl. Climatol. 2019, 135, 855–871. [Google Scholar] [CrossRef]
- De Michele, C.; Salvadori, G.; Passoni, G.; Vezzoli, R. A multivariate model of sea storms using copulas. Coast. Eng. 2007, 54, 734–751. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, S.; Mu, Z.; Leng, G.; Duan, W.; Ling, H.; Xu, J.; Zheng, X.; Li, P.; Li, Z.; et al. Relative humidity and solar radiation exacerbate snow drought risk in the headstreams of the Tarim River. Atmos. Res. 2024, 297, 107091. [Google Scholar] [CrossRef]
- Wei, X.; Huang, S.; Li, J.; Huang, Q.; Leng, G.; Liu, D.; Guo, W.; Zheng, X.; Bai, Q. The negative-positive feedback transition thresholds of meteorological drought in response to agricultural drought and their dynamics. Sci. Total Environ. 2024, 906, 167817. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiang, L.; Sun, Q.; Chen, Q. Bayesian Probabilistic Forecasting of Seasonal Hydrological Drought Based on Copula Function. Sci. Geogr. Sin. 2016, 36, 1437–1444. [Google Scholar]
- Long, Y.N.; Tang, R.; Wang, H.; Jiang, C.B. Monthly precipitation modeling using Bayesian Non-homogeneous Hidden Markov Chain. Hydrol. Res. 2019, 50, 562–576. [Google Scholar] [CrossRef]
- Fan, Y.; Huang, K.; Huang, G.H.; Li, Y.P. A factorial Bayesian copula framework for partitioning uncertainties in multivariate risk inference. Environ. Res. 2020, 183, 109215. [Google Scholar] [CrossRef] [PubMed]
- Conover, W.J. Practical Nonparametric Statistics; Technometrics; John Wiley & Sons: New York, NY, USA, 1980; Volume 23. [Google Scholar]
- Shi, W.Z.; Huang, S.Z.; Liu, D.F.; Huang, Q.; Han, Z.M.; Leng, G.Y.; Wang, H.; Liang, H.; Li, P.; Wei, X.T. Drought-flood abrupt alternation dynamics and their potential driving forces in a changing environment. J. Hydrol. 2021, 597, 126179. [Google Scholar] [CrossRef]
- Hasebe, T. Copula-based maximum-likelihood estimation of sample-selection models. Stata J. 2013, 13, 547–573. [Google Scholar] [CrossRef]
- Ayantobo, O.O.; Wei, J.H.; Wang, G.Q. Modeling Joint Relationship and Design Scenarios Between Precipitation, Surface Temperature, and Atmospheric Precipitable Water over Mainland China. Earth Space Sci. 2021, 8, e2020EA001513. [Google Scholar] [CrossRef]
- Li, J.; She, D.; Zhang, L.; Xia, J.; Liu, Z.; Wang, L.; Qi, G.; Deng, C. Multi-scale Response Characteristics and Mechanism of Vegetation to Meteorological Drought on the Loess Plateau. J. Soil Water Conserv. 2022, 36, 280–289. [Google Scholar]
- Miao, C.; Sun, Q.; Duan, Q.; Wang, Y. Joint analysis of changes in temperature and precipitation on the Loess Plateau during the period 1961–2011. Clim. Dyn. 2016, 47, 3221–3234. [Google Scholar] [CrossRef]
- Wang, D.; Lu, S.; Han, B.; Meng, X.; Li, Z.; Zhang, J. The Characteristics of Spring Vegetation Cover and Its Response to Spring Drought over the Loess Plateau. Plateau Meteorol. 2018, 37, 1208–1219. [Google Scholar]
- Liu, J.; Wen, Z.; Gang, C. Normalized difference vegetation index of different vegetation cover types and its responses to climate change in the Loess Plateau. Acta Ecol. Sin. 2020, 40, 678–691. [Google Scholar]
- Deng, Y.H.; Wang, S.J.; Bai, X.Y.; Luo, G.J.; Wu, L.H.; Chen, F.; Wang, J.F.; Li, C.J.; Yang, Y.J.; Hu, Z.Y.; et al. Vegetation greening intensified soil drying in some semi-arid and arid areas of the world. Agric. For. Meteorol. 2020, 292, 108103. [Google Scholar] [CrossRef]








| SPI Value | Dry–Wet Degree |
|---|---|
| SPI ≤ −2.0 | Extreme drought |
| −2.0 < SPI ≤ −1.5 | Severe drought |
| −1.5 < SPI ≤ −1.0 | Moderate drought |
| −1.0 < SPI ≤ 1.0 | Near normal |
| 1.0 < SPI ≤ 1.5 | Moderate moist |
| 1.5 < SPI ≤ 2.0 | Severe moist |
| SPI > 2.0 | Extreme moist |
| Copulas | Parameter Range | |
|---|---|---|
| Clayton-Copula | ||
| Frank-Copula | ||
| Gumbel-Copula | ||
| Gaussian-Copula | ||
| t-Copula |
| Combinations | Moderate Scenario | Severe Scenario |
|---|---|---|
| From dry to wet | P (–1.5 < X ≤ –1, 1 < Y ≤ 1.5) | P (–2 < X ≤ –1.5, 1.5 < Y ≤ 2) |
| From wet to dry | P (1 < X ≤ 1.5, –1.5 < Y ≤ –1) | P (1.5 < X ≤ 2, –2 < Y ≤ –1.5) |
| Continuous dry | P (–1.5 < X ≤ –1, –1.5 < Y ≤ –1) | P (–2 < X ≤ –1.5, –2 < Y ≤ –1.5) |
| Continuous wet | P (1 < X ≤ 1.5, 1 < Y ≤ 1.5) | P (1.5 < X ≤ 2, 1.5 < Y ≤ 2) |
| Combinations | Scenario | Gansu | Henan | Inner Mongolia | Ningxia | Qinghai | Shanxi | Shaanxi |
|---|---|---|---|---|---|---|---|---|
| Dry to wet | Moderate | 0.11 | 0.52 | 0.09 | 0.55 | 0.09 | 0.16 | 0.08 |
| Severe | 0.00 | 0.00 | 0.00 | 0.10 | 0.00 | 0.03 | 0.02 | |
| Wet to dry | Moderate | 0.02 | 0.39 | 0.13 | 0.04 | 0.13 | 0.22 | 0.14 |
| Severe | 0.08 | 0.06 | 0.01 | 0.00 | 0.00 | 0.05 | 0.09 | |
| Continuous dry | Moderate | 0.15 | 0.23 | 0.23 | 0.63 | 0.00 | 0.27 | 0.07 |
| Severe | 0.11 | 0.06 | 0.07 | 0.22 | 0.02 | 0.16 | 0.00 | |
| Continuous wet | Moderate | 0.07 | 0.00 | 0.07 | 0.08 | 0.04 | 0.01 | 0.03 |
| Severe | 0.00 | 0.00 | 0.02 | 0.00 | 0.00 | 0.00 | 0.01 |
| Combinations | Scenario | Gansu | Henan | Inner Mongolia | Ningxia | Qinghai | Shanxi | Shaanxi |
|---|---|---|---|---|---|---|---|---|
| Dry to wet | Moderate | 0.02 | 0.19 | 0.05 | 0.29 | 0.05 | 0.08 | 0.01 |
| Severe | 0.00 | 0.06 | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 | |
| Wet to dry | Moderate | 0.04 | 0.34 | 0.21 | 0.05 | 0.15 | 0.25 | 0.20 |
| Severe | 0.09 | 0.10 | 0.16 | 0.03 | 0.02 | 0.13 | 0.04 | |
| Continuous dry | Moderate | 0.14 | 0.19 | 0.22 | 0.60 | 0.00 | 0.13 | 0.11 |
| Severe | 0.11 | 0.06 | 0.08 | 0.24 | 0.01 | 0.06 | 0.00 | |
| Continuous wet | Moderate | 0.11 | 0.00 | 0.16 | 0.24 | 0.00 | 0.02 | 0.10 |
| Severe | 0.00 | 0.00 | 0.02 | 0.00 | 0.00 | 0.00 | 0.04 |
| Combinations | Scenario | Gansu | Henan | Inner Mongolia | Ningxia | Qinghai | Shanxi | Shaanxi |
|---|---|---|---|---|---|---|---|---|
| Dry to wet | Moderate | 0.50 | 0.46 | 0.54 | 0.47 | 0.45 | 0.38 | 0.36 |
| Severe | 0.61 | 0.59 | 0.61 | 0.52 | 0.58 | 0.45 | 0.38 | |
| Wet to dry | Moderate | 0.42 | 0.35 | 0.38 | 0.28 | 0.35 | 0.35 | 0.36 |
| Severe | 0.34 | 0.41 | 0.36 | 0.25 | 0.34 | 0.40 | 0.37 | |
| Continuous dry | Moderate | 0.43 | 0.49 | 0.46 | 0.59 | 0.45 | 0.58 | 0.50 |
| Severe | 0.53 | 0.40 | 0.44 | 0.63 | 0.47 | 0.55 | 0.53 | |
| Continuous wet | Moderate | 0.24 | 0.21 | 0.19 | 0.16 | 0.37 | 0.25 | 0.26 |
| Severe | 0.14 | 0.13 | 0.18 | 0.11 | 0.27 | 0.18 | 0.22 |
| Combinations | Scenario | Gansu | Henan | Inner Mongolia | Ningxia | Qinghai | Shanxi | Shaanxi |
|---|---|---|---|---|---|---|---|---|
| Dry to wet | Moderate | 0.28 | 0.30 | 0.36 | 0.33 | 0.32 | 0.28 | 0.30 |
| Severe | 0.27 | 0.36 | 0.37 | 0.30 | 0.33 | 0.31 | 0.30 | |
| Wet to dry | Moderate | 0.52 | 0.49 | 0.49 | 0.44 | 0.48 | 0.45 | 0.41 |
| Severe | 0.64 | 0.65 | 0.56 | 0.47 | 0.57 | 0.56 | 0.46 | |
| Continuous dry | Moderate | 0.44 | 0.39 | 0.42 | 0.54 | 0.52 | 0.55 | 0.38 |
| Severe | 0.43 | 0.31 | 0.38 | 0.58 | 0.50 | 0.50 | 0.36 | |
| Continuous wet | Moderate | 0.23 | 0.25 | 0.21 | 0.19 | 0.32 | 0.27 | 0.37 |
| Severe | 0.17 | 0.16 | 0.21 | 0.14 | 0.25 | 0.22 | 0.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, H.; Gao, Y.; Huang, S.; Liu, T.; Huang, Q.; Cao, Q. Quantifying the Impacts of Dry–Wet Combination Events on Vegetation Vulnerability in the Loess Plateau under a Changing Environment. Water 2024, 16, 1660. https://doi.org/10.3390/w16121660
Dong H, Gao Y, Huang S, Liu T, Huang Q, Cao Q. Quantifying the Impacts of Dry–Wet Combination Events on Vegetation Vulnerability in the Loess Plateau under a Changing Environment. Water. 2024; 16(12):1660. https://doi.org/10.3390/w16121660
Chicago/Turabian StyleDong, Haixia, Yuejiao Gao, Shengzhi Huang, Tiejun Liu, Qiang Huang, and Qianqian Cao. 2024. "Quantifying the Impacts of Dry–Wet Combination Events on Vegetation Vulnerability in the Loess Plateau under a Changing Environment" Water 16, no. 12: 1660. https://doi.org/10.3390/w16121660
APA StyleDong, H., Gao, Y., Huang, S., Liu, T., Huang, Q., & Cao, Q. (2024). Quantifying the Impacts of Dry–Wet Combination Events on Vegetation Vulnerability in the Loess Plateau under a Changing Environment. Water, 16(12), 1660. https://doi.org/10.3390/w16121660







