Research on a Multi-Objective Optimization Method for Transient Flow Oscillation in Multi-Stage Pressurized Pump Stations
Abstract
:1. Introduction
2. Materials and Methods
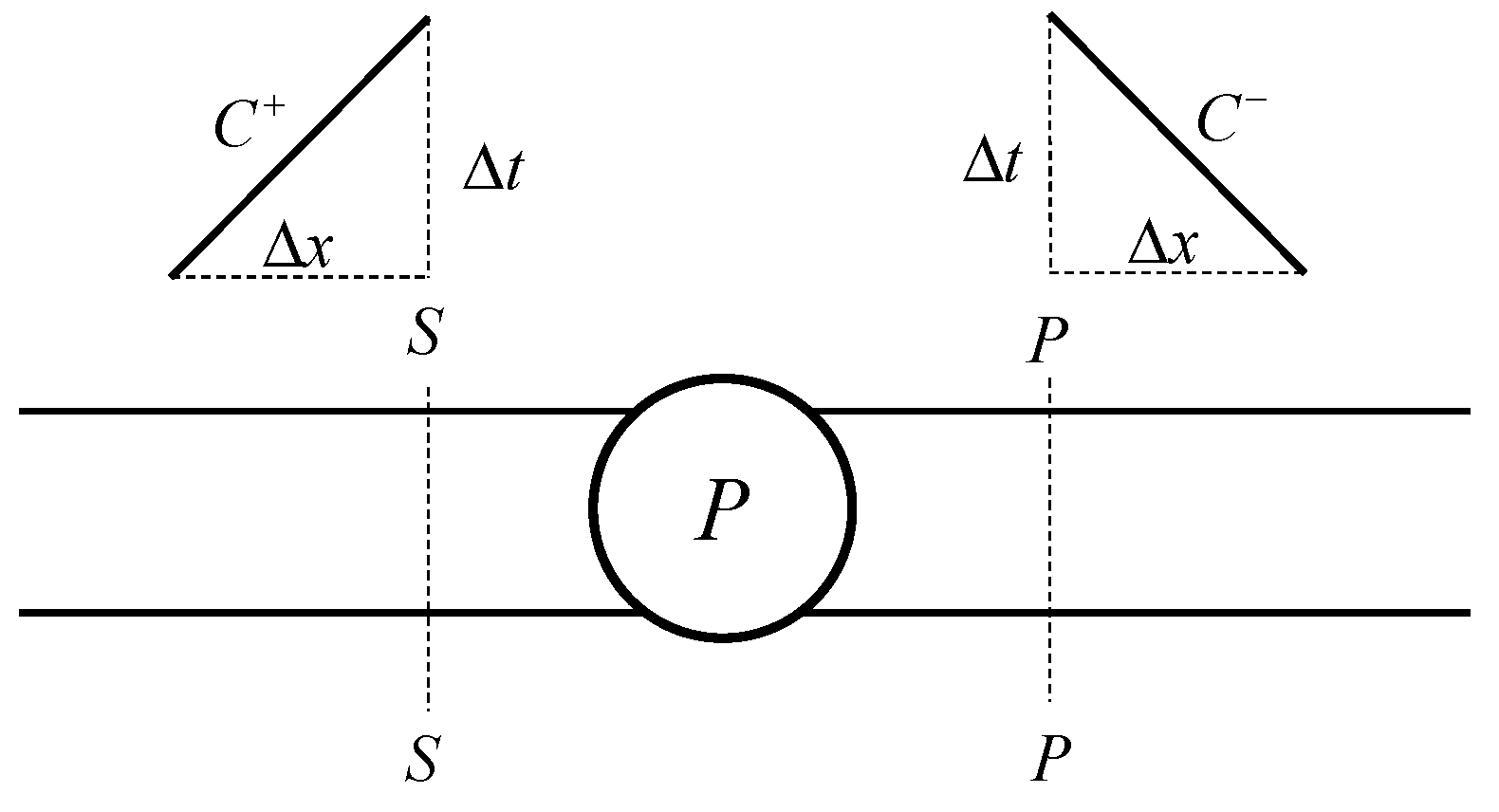
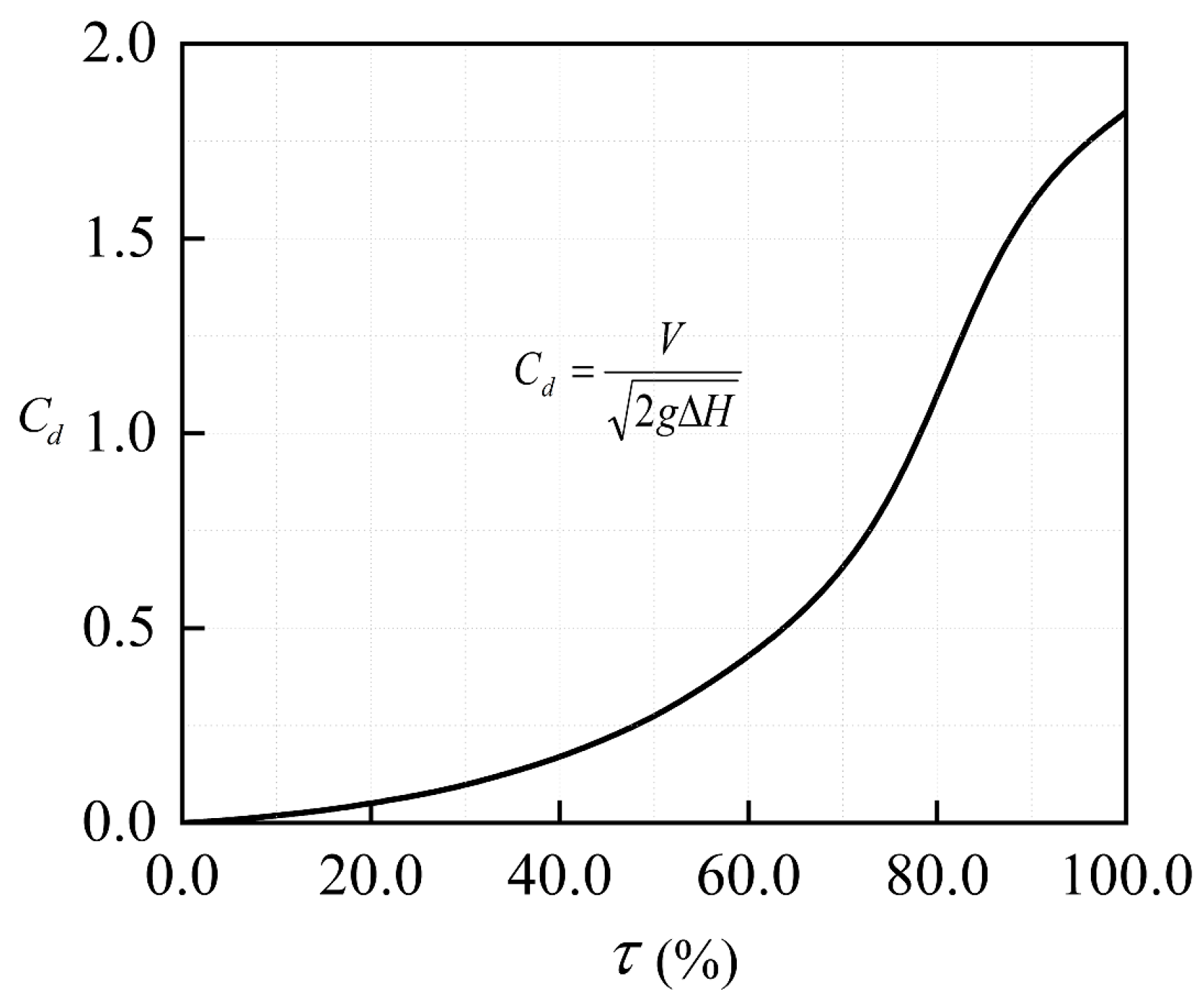
2.1. Calculation Theory of the Method of Characteristics for Transient Flow
2.2. Multi-Objective Optimization Method for Water Hammer Protection
2.2.1. Constructing the Sample Set Based on LHS-MCS
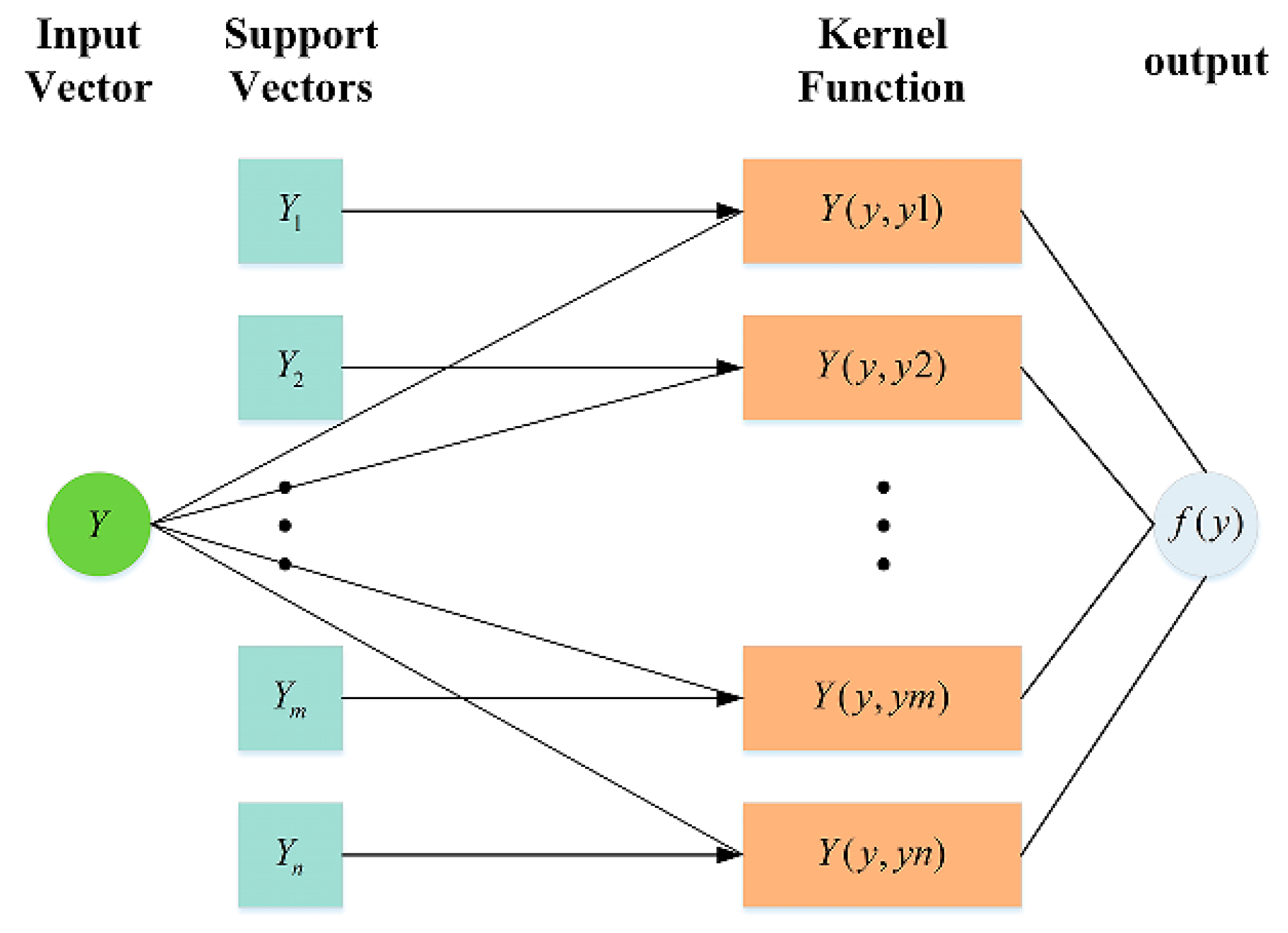
2.2.2. Support Vector Regression (SVR)
2.2.3. Combined Weighting Method
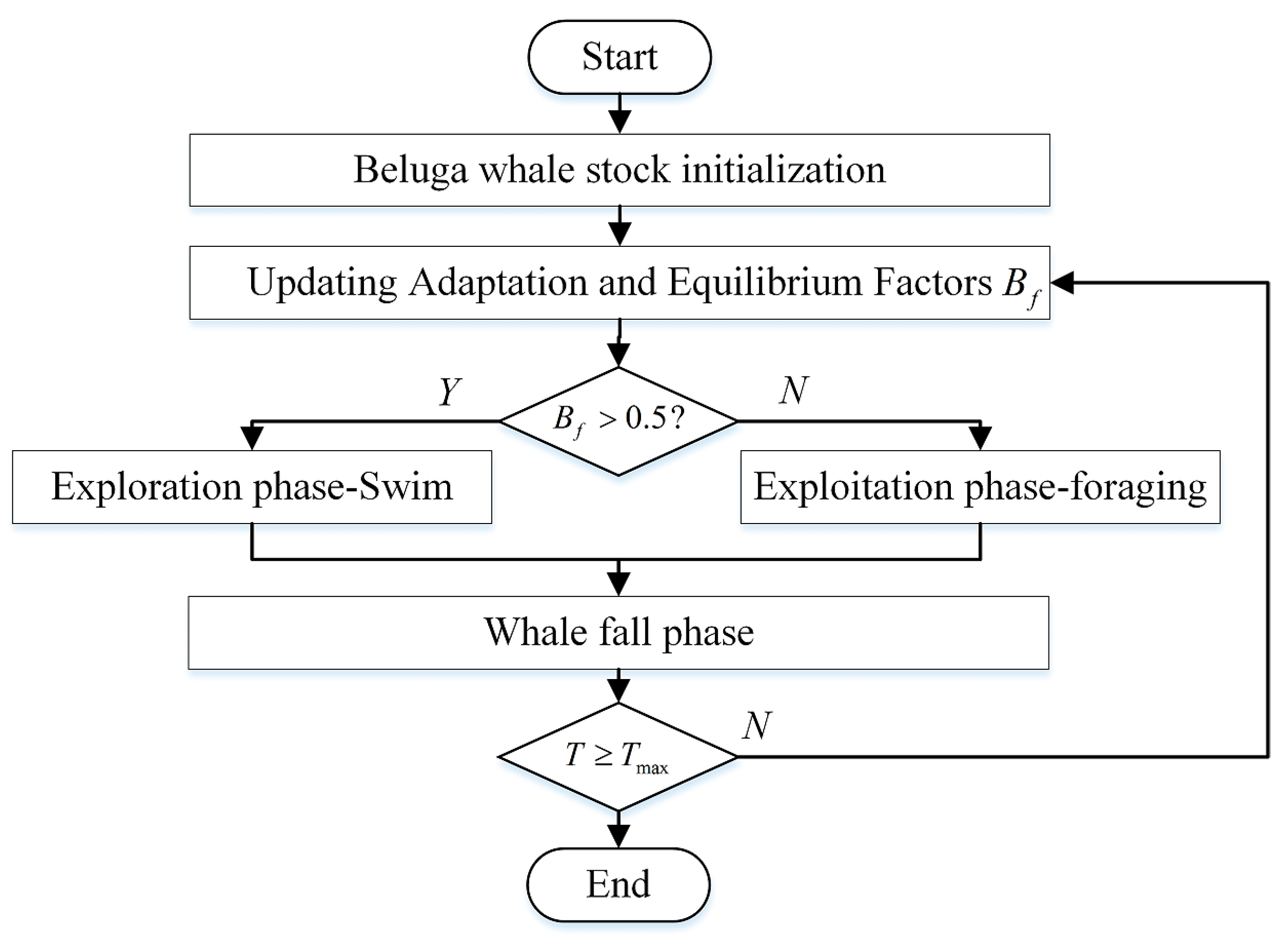
2.2.4. Beluga Whale Optimization (BWO)
2.3. Multi-Objective Optimization Function
2.4. Multi-Objective Optimization Model
3. Results and Discussion
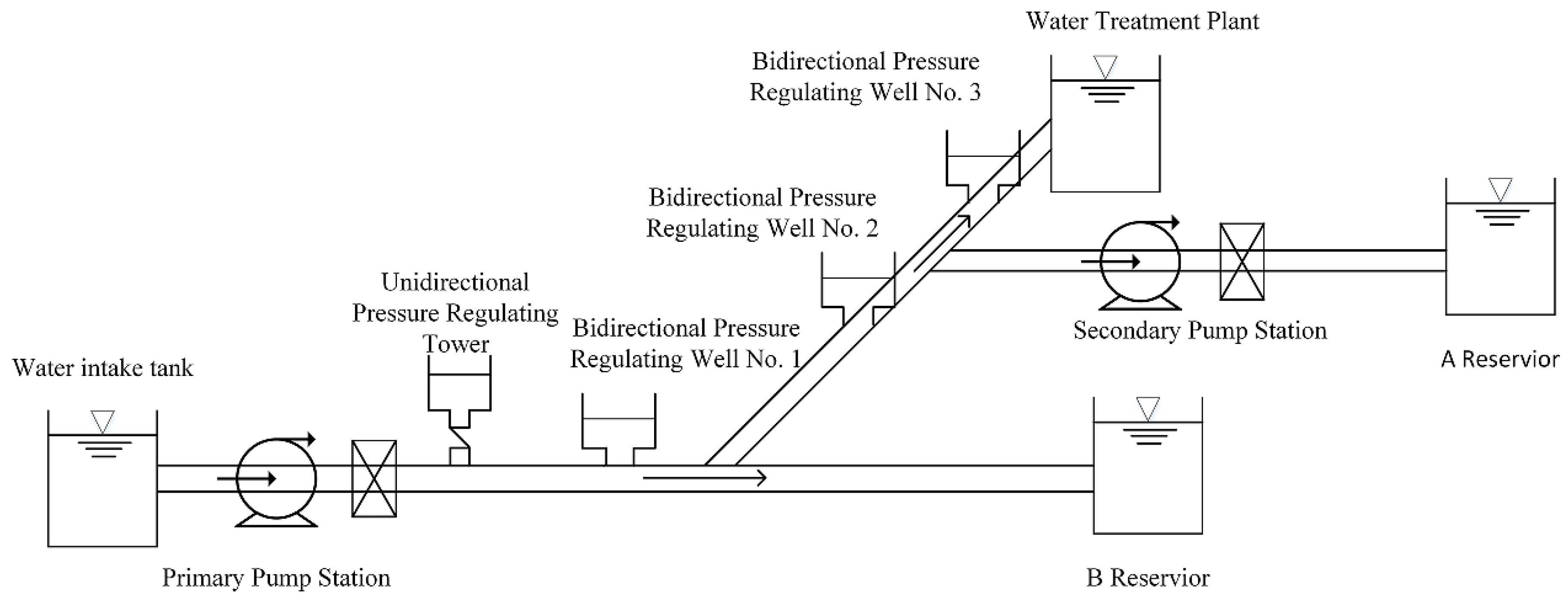
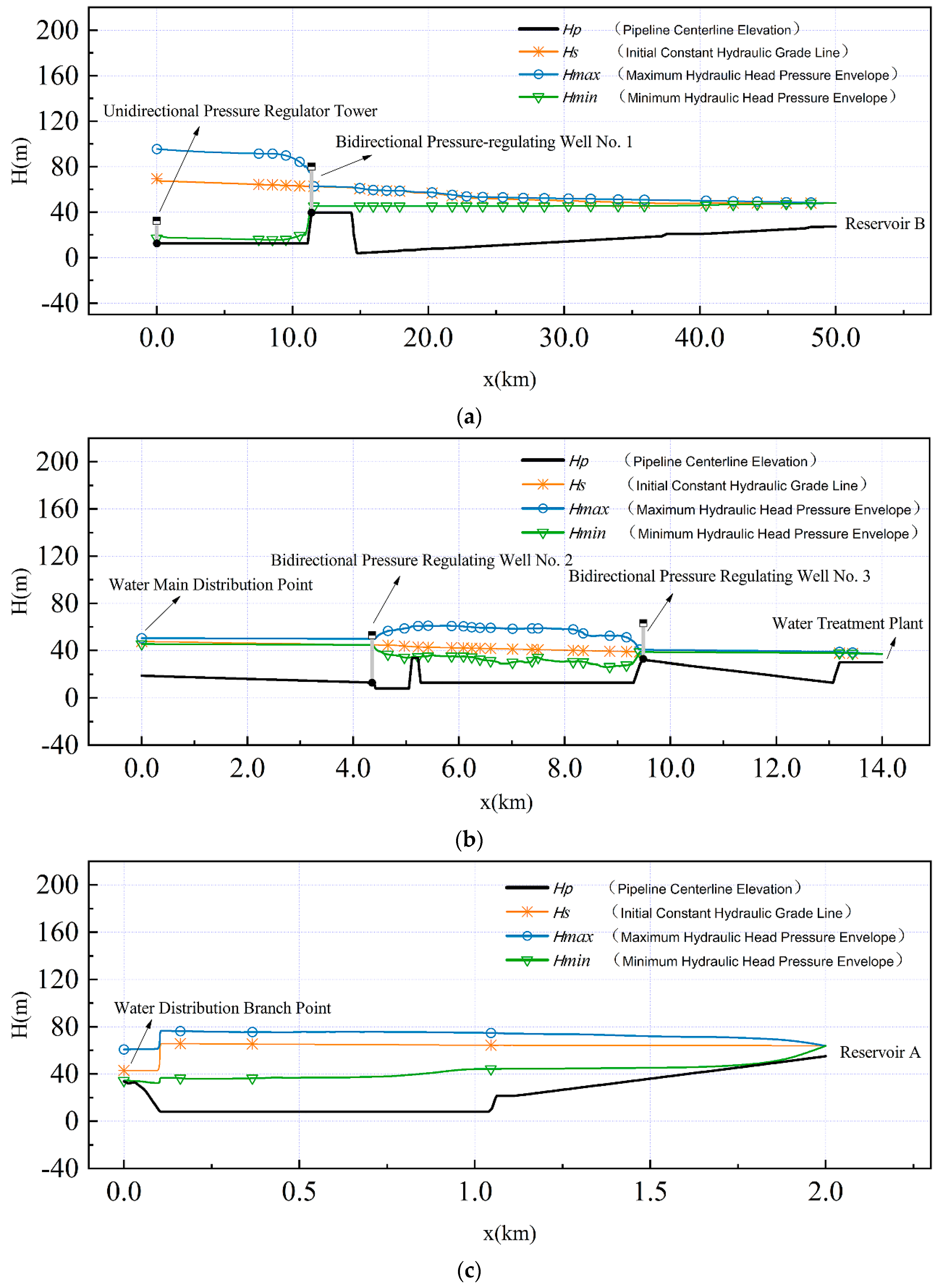
3.1. Project Introduction
3.2. Comparison of Prediction Regression Models
3.2.1. Dataset Construction
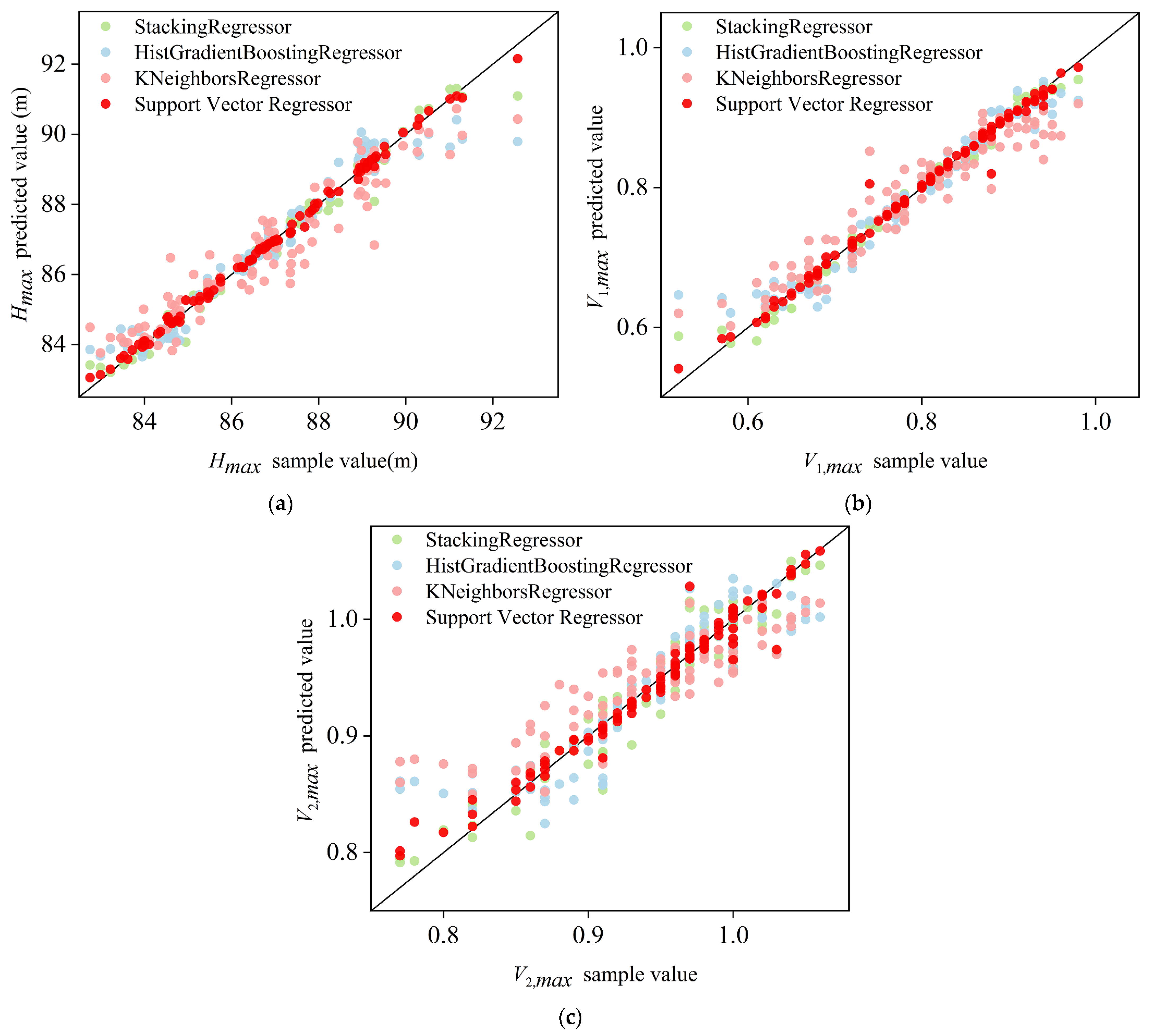
3.2.2. Comparison of Regression Algorithms
3.3. Comparison of Optimization Algorithms
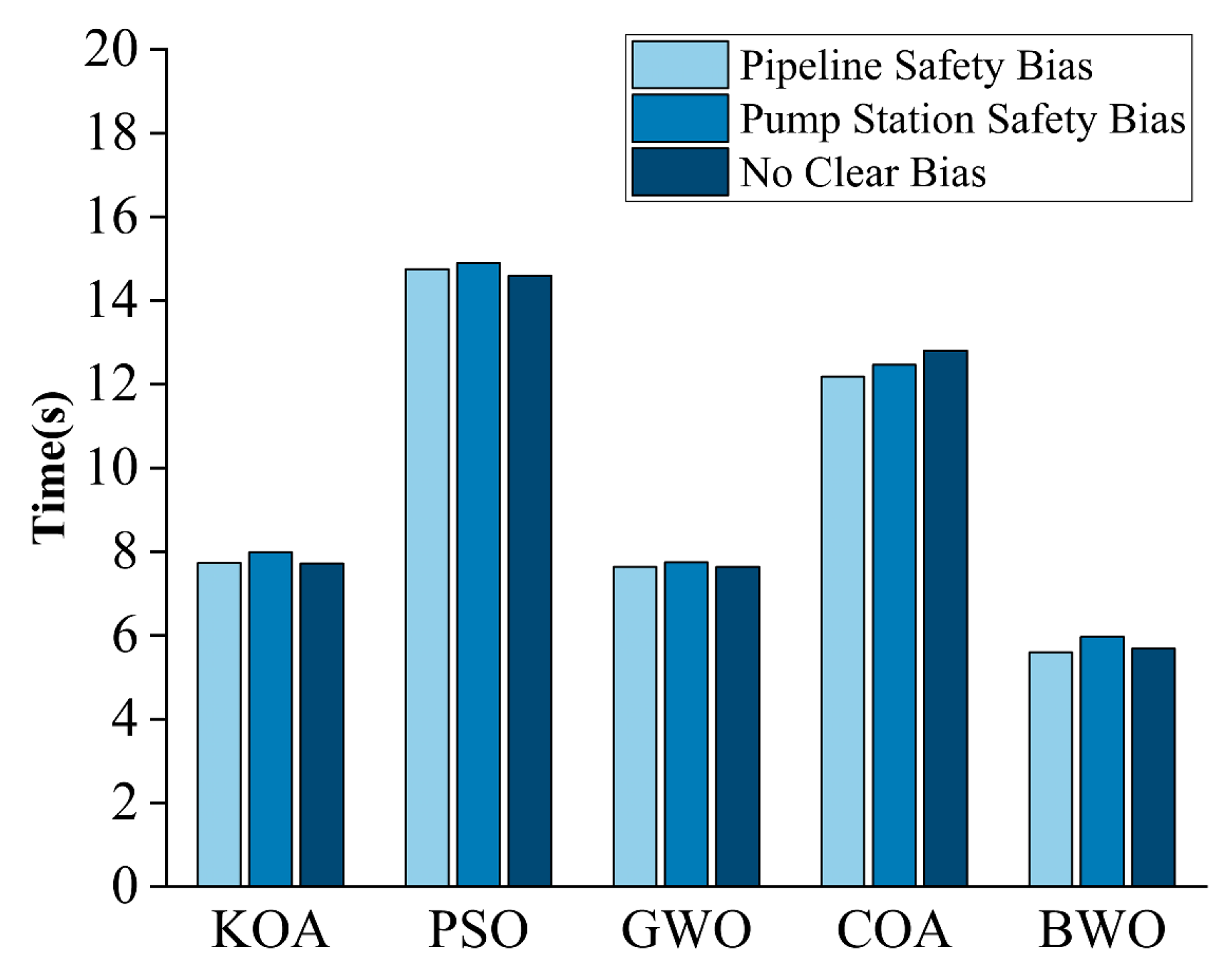
3.3.1. Weights Based on Different Biases
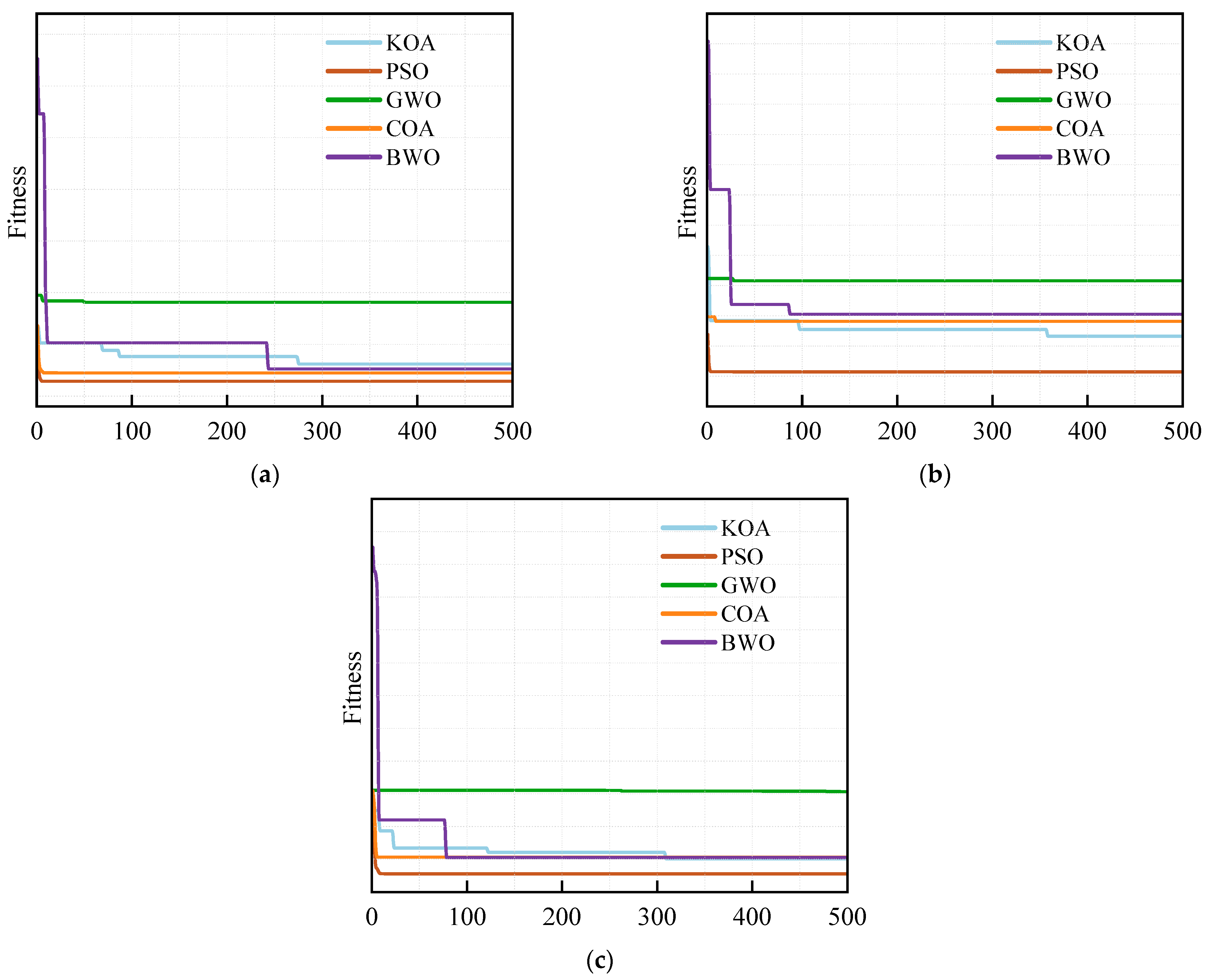
3.3.2. Effects of Different Optimization Algorithms
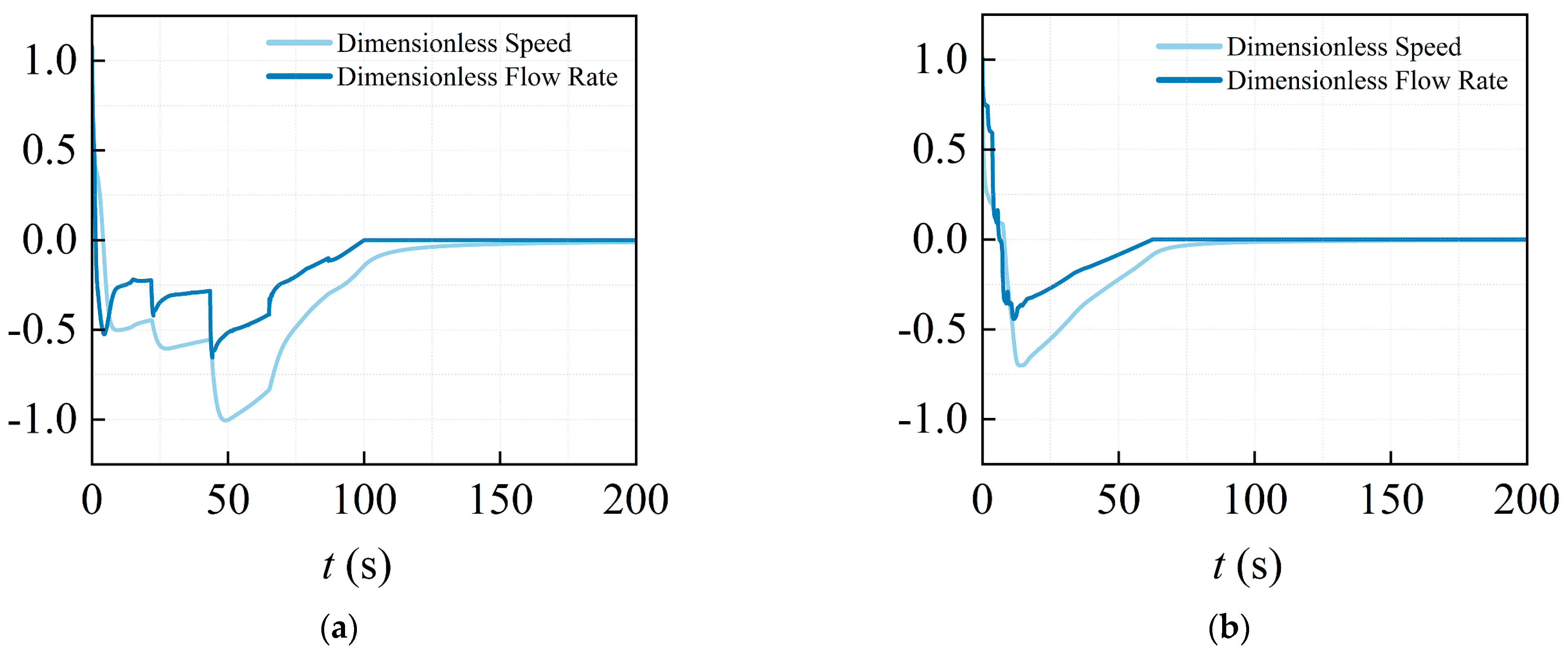
3.4. Verification of Theoretical Solution
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Panov, L.V.; Chirkov, D.V.; Cherny, S.G.; Pylev, I.M. Numerical simulation of pulsation processes in hydraulic turbine based on 3d model of cavitating flow. Thermophys. Aeromech. 2014, 21, 31–43. [Google Scholar] [CrossRef]
- Leishear, R.A. Water hammer causes water main breaks. J. Press. Vessel Technol. 2020, 142, 021402. [Google Scholar] [CrossRef]
- Chen, T.; Ren, Z.; Xu, C.; Loxton, R. Optimal boundary control for water hammer suppression in fluid transmission pipelines. Comput. Math. Appl. 2015, 69, 275–290. [Google Scholar] [CrossRef]
- Bergant, A.; Simpson, A.; Sijamhodzic, E. Water hammer analysis of pumping systems for control of water in underground mines. In Proceedings of the Mine Water Congress, Ljubljana, Slovenia, 25–30 September 1991; pp. 9–20. [Google Scholar]
- Sciamarella, D.; Artana, G. A water hammer analysis of pressure and flow in the voice production system. Speech Commun. 2009, 51, 344–351. [Google Scholar] [CrossRef]
- Asli, K.H.; Naghiyev, F.B.O.; Haghi, A.K. Some aspects of physical and numerical modeling of water hammer in pipelines. Nonlinear Dyn. 2010, 60, 677–701. [Google Scholar] [CrossRef]
- Erath, W.; Nowotny, B.; Maetz, J. Modelling the fluid structure interaction produced by a waterhammer during shutdown of high-pressure pumps. Nucl. Eng. Des. 1999, 193, 283–296. [Google Scholar] [CrossRef]
- Fu, X.; Li, D.; Wang, H.; Qin, D.; Wei, X. Cavitation mechanism and effect on pump power-trip transient process of a pumped-storage unit. J. Energy Storage 2023, 66, 107405. [Google Scholar] [CrossRef]
- Wan, W.; Lian, J.; Li, Y. Influence of valve system discharge coefficient on hydraulic transients. J. Tsinghua Univ. (Sci. Technol.) 2005, 45, 1198–1201. [Google Scholar]
- Romuald, B.; Jian, Z.; Dong, Y.X.; Claire, D. Assessment and performance evaluation of water hammer in hydroelectric plants with hydropneumatic tank and pressure regulating valve. J. Press. Vessel Technol. 2021, 143, 041401. [Google Scholar] [CrossRef]
- Liu, W.; Tan, P.; Yang, J. Study on two-stage closure of valve stroking for water hammer protection of unexpected pump-stop. Fluid Mach. 2020, 48, 53–57. [Google Scholar]
- Wan, W.Y.; Li, F.Q. Sensitivity analysis of operational time differences for a pump-valve system on a water hammer response. J. Press. Vessel Technol. 2016, 138, 011303. [Google Scholar] [CrossRef]
- Lu, M.; Liu, X.; Xu, G.; Tian, Y. Optimal pump-valve coupling operation strategy of complex long-distance water-conveyance systems based on moc. Ain Shams Eng. J. 2024, 15, 102318. [Google Scholar] [CrossRef]
- Han, Y.; Shi, W.D.; Xu, H.; Wang, J.B.; Zhou, L. Effects of closing times and laws on water hammer in a ball valve pipeline. Water 2022, 14, 1497. [Google Scholar] [CrossRef]
- Neyestanaki, M.K.; Dunca, G.; Jonsson, P.; Cervantes, M.J. A comparison of different methods for modelling water hammer valve closure with cfd. Water 2023, 15, 1510. [Google Scholar] [CrossRef]
- Zhao, S.G.; Wang, M.N.; Yi, W.H.; Yang, D.; Tong, J.J. Intelligent classification of surrounding rock of tunnel based on 10 machine learning algorithms. Appl. Sci. 2022, 12, 2656. [Google Scholar] [CrossRef]
- Dhakal, R.; Zhou, J.X.; Palikhe, S.; Bhattarai, K.P. Hydraulic optimization of double chamber surge tank using nsga-ii. Water 2020, 12, 455. [Google Scholar] [CrossRef]
- Hao, R.A.; Bai, Z.X. Comparative study for daily streamflow simulation with different machine learning methods. Water 2023, 15, 1179. [Google Scholar] [CrossRef]
- Lu, M.S.; Hou, Q.Y.; Qin, S.J.; Zhou, L.H.; Hua, D.; Wang, X.X.; Cheng, L. A stacking ensemble model of various machine learning models for daily runoff forecasting. Water 2023, 15, 1265. [Google Scholar] [CrossRef]
- Li, J.Y.; Yuan, X. Daily streamflow forecasts based on cascade long short-term memory (lstm) model over the yangtze river basin. Water 2023, 15, 1019. [Google Scholar] [CrossRef]
- Xu, C.; Hux, L.; Wang, R.; Wang, X.; Tian, J. Multi-objective optimzation study of flow field characteristics in forward intake structure of pumping station. Shuili Xuebao/J. Hydraul. Eng. 2024, 55, 167–178. [Google Scholar]
- Brunton, S.L.; Noack, B.R.; Koumoutsakos, P. Machine Learning for Fluid Mechanics. Annu. Rev. Fluid Mech. 2020, 52, 477–508. [Google Scholar] [CrossRef]
- Bazargan-Lari, M.R.; Kerachian, R.; Afshar, H.; Bashi-Azghadi, S.N. Developing an optimal valve closing rule curve for real-time pressure control in pipes. J. Mech. Sci. Technol. 2013, 27, 215–225. [Google Scholar] [CrossRef]
- Lai, X.; Li, C.; Zhou, J.; Zhang, N. Multi-objective optimization of the closure law of guide vanes for pumped storage units. Renew. Energy 2019, 139, 302–312. [Google Scholar] [CrossRef]
- Cao, Z.; Xia, Q.; Guo, X.J.; Lu, L.; Deng, J.Q. A novel surge damping method for hydraulic transients with operating pump using an optimized valve control strategy. Water 2022, 14, 1576. [Google Scholar] [CrossRef]
- Lei, L.; Chen, D.; Ma, C.; Chen, Y.; Wang, H.; Chen, H.; Zhao, Z.; Zhou, Y.; Mahmud, A.; Patelli, E. Optimization and decision making of guide vane closing law for pumped storage hydropower system to improve adaptability under complex conditions. J. Energy Storage 2023, 73, 109038. [Google Scholar] [CrossRef]
- Wylie, E.B.; Streeter, V.L. Fluid Transients; McGraw-Hill International Book Co.: New York, NY, USA, 1978. [Google Scholar]
- Shields, M.D.; Zhang, J.X. The generalization of latin hypercube sampling. Reliab. Eng. Syst. Saf. 2016, 148, 96–108. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, X.Q.; Qin, H. A data-driven model based on fourier transform and support vector regression for monthly reservoir inflow forecasting. J. Hydro-Environ. Res. 2018, 18, 12–24. [Google Scholar] [CrossRef]
- Saaty, R.W. The analytic hierarchy process—what it is and how it is used. Math. Model. 1987, 9, 161–176. [Google Scholar] [CrossRef]
- Zhu, Y.X.; Tian, D.Z.; Yan, F. Effectiveness of entropy weight method in decision-making. Math. Probl. Eng. 2020, 2020, 3564835. [Google Scholar] [CrossRef]
- Zhong, C.T.; Li, G.; Meng, Z. Beluga whale optimization: A novel nature-inspired metaheuristic algorithm. Knowl.-Based Syst. 2022, 251, 109215. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November 27–1 December 1995. [Google Scholar]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, MHS’95, Nagoya, Japan, 4–6 October 1995. [Google Scholar]
- Abdel-Basset, M.; Mohamed, R.; Azeem, S.A.A.; Jameel, M.; Abouhawwash, M. Kepler optimization algorithm: A new metaheuristic algorithm inspired by kepler’s laws of planetary motion. Knowl.-Based Syst. 2023, 268, 110454. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Trojovská, E.; Trojovský, P. Coati optimization algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems. Knowl.-Based Syst. 2023, 259, 110011. [Google Scholar] [CrossRef]
| Serial Number | t1 | t2 | t3 | t4 | Hmax (m) | V1,max | V2,max | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 9.72 | 87.58 | 89.77 | 10.23 | 7.51 | 58.97 | 89.22 | 10.78 | 92.57 | 0.52 | 0.78 |
| 2 | 8.10 | 85.31 | 85.73 | 14.27 | 7.39 | 60.15 | 86.1 | 13.9 | 88.27 | 0.73 | 0.92 |
| 3 | 6.06 | 89.93 | 86.42 | 13.58 | 6.28 | 60.08 | 87.13 | 12.87 | 88.9 | 0.69 | 0.87 |
| 4 | 6 | 86.55 | 86.06 | 13.94 | 9.5 | 57.76 | 85.15 | 14.85 | 89.3 | 0.69 | 1 |
| 5 | 11.68 | 87.94 | 84.97 | 15.03 | 7.78 | 56.3 | 84.5 | 15.5 | 85.5 | 0.83 | 0.97 |
| 6 | 10.66 | 86.18 | 87.31 | 12.69 | 7.31 | 61.8 | 87.03 | 12.97 | 88.94 | 0.68 | 0.88 |
| 7 | 10.21 | 89.27 | 86.85 | 13.15 | 9.19 | 58.89 | 84.54 | 15.46 | 87.91 | 0.72 | 1 |
| 8 | 10.38 | 86.35 | 83.3 | 16.7 | 8.46 | 60.08 | 87.73 | 12.27 | 84.67 | 0.88 | 0.87 |
| 9 | 12.09 | 87.62 | 81.94 | 18.06 | 8.83 | 58.18 | 84.42 | 15.58 | 87.35 | 0.94 | 0.99 |
| 10 | 6.57 | 87.68 | 84.24 | 15.76 | 7.84 | 59.24 | 84.8 | 15.2 | 86.75 | 0.8 | 0.96 |
| 11 | 11.06 | 88.54 | 87.78 | 12.22 | 8.26 | 57.1 | 82.61 | 17.39 | 88.96 | 0.67 | 1.02 |
| 12 | 10.37 | 87.62 | 82.1 | 17.9 | 8.52 | 60.07 | 88.8 | 11.2 | 83.46 | 0.93 | 0.82 |
| 13 | 9.95 | 89.07 | 89.2 | 10.8 | 6.84 | 63.73 | 85.09 | 14.91 | 91.3 | 0.57 | 0.95 |
| 14 | 7.8 | 87.63 | 83.41 | 16.59 | 7.98 | 57.64 | 86.24 | 13.76 | 85.45 | 0.85 | 0.92 |
| 15 | 7.55 | 85.51 | 86.09 | 13.91 | 5.92 | 57.95 | 84.01 | 15.99 | 88.91 | 0.7 | 0.97 |
| … | … | … | … | … | … | … | … | … | … | … | … |
| 91 | 10.93 | 86.06 | 85.65 | 14.35 | 7.5 | 63.98 | 85.71 | 14.29 | 86.83 | 0.78 | 0.93 |
| 92 | 10.44 | 88.59 | 83.9 | 16.1 | 6.72 | 59.35 | 85.48 | 14.52 | 84.81 | 0.87 | 0.93 |
| 93 | 6.55 | 86.86 | 83.95 | 16.05 | 8.81 | 63.02 | 85.59 | 14.41 | 86.64 | 0.8 | 0.96 |
| 94 | 11.81 | 86.5 | 81.92 | 18.08 | 5.3 | 57.45 | 85.76 | 14.24 | 82.99 | 0.94 | 0.91 |
| 95 | 7.27 | 87.33 | 82.91 | 17.09 | 6.68 | 62.89 | 83.96 | 16.04 | 85.28 | 0.86 | 0.98 |
| 96 | 12.5 | 86.24 | 84.17 | 15.83 | 6.66 | 61.29 | 82.83 | 17.17 | 84.73 | 0.87 | 1 |
| 97 | 7.44 | 88.14 | 81.5 | 18.5 | 5.63 | 60.22 | 86.83 | 13.17 | 83.87 | 0.92 | 0.87 |
| 98 | 9.56 | 88.58 | 83.25 | 16.75 | 9.07 | 63.86 | 88.71 | 11.29 | 84.52 | 0.88 | 0.86 |
| 99 | 14.34 | 88.36 | 84.94 | 15.06 | 9.88 | 59.63 | 85.27 | 14.73 | 84.54 | 0.86 | 1 |
| 100 | 7.98 | 87.12 | 82.41 | 17.59 | 6.55 | 60.05 | 84.93 | 15.07 | 84.63 | 0.89 | 0.95 |
| Regression Model | Hmax | V1,max | V2,max | |||
|---|---|---|---|---|---|---|
| RMSE | R2 | RMSE | R2 | RMSE | R2 | |
| Random Forest Regressor | 0.69 | 0.71 | 0.02 | 0.92 | 0.02 | 0.89 |
| Support Vector Regressor | 0.12 | 0.99 | 0.01 | 0.99 | 0.01 | 0.97 |
| GradientBoostingRegressor | 0.79 | 0.65 | 0.02 | 0.94 | 0.02 | 0.93 |
| LinearRegression | 0.75 | 0.69 | 0.02 | 0.96 | 0.02 | 0.93 |
| Ridge | 0.68 | 0.84 | 0.03 | 0.88 | 0.03 | 0.79 |
| HistGradientBoostingRegressor | 0.53 | 0.92 | 0.02 | 0.94 | 0.02 | 0.8 |
| AdaBoostRegressor | 0.37 | 0.95 | 0.03 | 0.88 | 0.02 | 0.81 |
| ExtraTreesRegressor | 0.67 | 0.73 | 0.02 | 0.95 | 0.06 | 0.31 |
| StackingRegressor | 0.27 | 0.98 | 0.02 | 0.98 | 0.02 | 0.88 |
| RidgeCV | 1.37 | 0.33 | 0.03 | 0.9 | 0.02 | 0.94 |
| Lasso | 1.3 | 0.39 | 0.06 | 0.57 | 0.06 | 0.22 |
| KNeighborsRegressor | 0.74 | 0.83 | 0.04 | 0.83 | 0.03 | 0.68 |
| PoissonRegressor | 0.62 | 0.76 | 0.02 | 0.91 | 0.02 | 0.91 |
| GammaRegressor | 0.98 | 0.69 | 0.05 | 0.69 | 0.03 | 0.72 |
| ElasticNet | 0.98 | 0.69 | 0.05 | 0.68 | 0.03 | 0.72 |
| HuberRegressor | 0.97 | 0.69 | 0.05 | 0.69 | 0.03 | 0.72 |
| Design Bias | Hmax | V1,max | V2,max |
|---|---|---|---|
| Pipeline Safety Priority | 0.403 | 0.34 | 0.257 |
| Station Safety Priority | 0.163 | 0.509 | 0.328 |
| No Clear Bias | 0.269 | 0.408 | 0.323 |
| Protection Schemes under Different Biases | Optimization Algorithm | t1 | t2 | t3 | t4 | ||||
| Optimal Scheme Under Pipeline Safety Bias | KOA | 14.09 | 86.39 | 80 | 20 | 7.64 | 63.42 | 83.88 | 16.12 |
| PSO | 14.5 | 89.62 | 80 | 20 | 8.05 | 61.2 | 86.96 | 13.04 | |
| GWO | 10.41 | 88.03 | 84.33 | 15.67 | 7.04 | 58.37 | 85.5 | 14.5 | |
| COA | 13.4 | 85 | 80 | 20 | 5 | 55 | 88.4 | 11.6 | |
| BWO | 14.82 | 89.81 | 80 | 20 | 7.85 | 61.37 | 87.6 | 12.4 | |
| Optimal Scheme Under Pump Station Safety Bias | KOA | 12.23 | 86.87 | 80 | 20 | 7.74 | 57.7 | 85.26 | 14.74 |
| PSO | 13.32 | 86.35 | 80.02 | 19.98 | 6.58 | 61.34 | 89.83 | 10.17 | |
| GWO | 8.87 | 88.84 | 89.3 | 10.7 | 7.81 | 64.22 | 82.55 | 17.45 | |
| COA | 13.93 | 87.75 | 82.39 | 17.61 | 5 | 61.29 | 90 | 10 | |
| BWO | 15 | 85 | 80 | 20 | 5 | 55 | 90 | 10 | |
| Optimal Scheme Under No Clear Bias | KOA | 13.01 | 85 | 80 | 20 | 5.33 | 58.69 | 83.77 | 16.23 |
| PSO | 12.82 | 89.85 | 80.47 | 19.53 | 7.5 | 61.28 | 88.67 | 11.33 | |
| GWO | 9.68 | 86.25 | 80.6 | 19.4 | 8.07 | 62.93 | 89.27 | 10.73 | |
| COA | 11.64 | 89.82 | 81.68 | 18.32 | 5 | 65 | 88.96 | 11.04 | |
| BWO | 15 | 85 | 80 | 20 | 5 | 57.5 | 90 | 10 |
| Protection Schemes under Different Biases | Optimization Algorithm | Hmax (m) | V1,max | V2,max | F(x) |
|---|---|---|---|---|---|
| Optimal Scheme Under Pipeline Safety Bias | KOA | 84.25 | 1 | 0.987 | 34.54 |
| PSO | 83.48 | 1.014 | 0.893 | 34.22 | |
| GWO | 85.32 | 0.844 | 0.932 | 34.91 | |
| COA | 85.25 | 1.027 | 0.925 | 34.94 | |
| BWO | 83.26 | 1.029 | 0.79 | 34.11 | |
| Optimal Scheme Under Pump Station Safety Bias | KOA | 85.31 | 0.989 | 0.945 | 14.72 |
| PSO | 84.79 | 0.995 | 0.735 | 14.57 | |
| GWO | 91.92 | 0.545 | 1.026 | 15.59 | |
| COA | 86.61 | 0.948 | 0.706 | 14.83 | |
| BWO | 84.2 | 1 | 0.697 | 14.46 | |
| Optimal Scheme Under No Clear Bias | KOA | 85.28 | 0.989 | 0.967 | 23.66 |
| PSO | 84.23 | 0.992 | 0.811 | 23.32 | |
| GWO | 88.22 | 0.949 | 0.787 | 24.37 | |
| COA | 86.4 | 0.954 | 0.775 | 23.88 | |
| BWO | 84.2 | 1 | 0.701 | 23.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Y.; Shen, G.; Wan, W. Research on a Multi-Objective Optimization Method for Transient Flow Oscillation in Multi-Stage Pressurized Pump Stations. Water 2024, 16, 1728. https://doi.org/10.3390/w16121728
Ding Y, Shen G, Wan W. Research on a Multi-Objective Optimization Method for Transient Flow Oscillation in Multi-Stage Pressurized Pump Stations. Water. 2024; 16(12):1728. https://doi.org/10.3390/w16121728
Chicago/Turabian StyleDing, Yuxiang, Guiying Shen, and Wuyi Wan. 2024. "Research on a Multi-Objective Optimization Method for Transient Flow Oscillation in Multi-Stage Pressurized Pump Stations" Water 16, no. 12: 1728. https://doi.org/10.3390/w16121728
APA StyleDing, Y., Shen, G., & Wan, W. (2024). Research on a Multi-Objective Optimization Method for Transient Flow Oscillation in Multi-Stage Pressurized Pump Stations. Water, 16(12), 1728. https://doi.org/10.3390/w16121728







