Risk Assessment and Control for Geohazards at Multiple Scales: An Insight from the West Han River of Gansu Province in China
Abstract
1. Introduction
2. Study Area and Data Preparation
2.1. Risk Results and Assessment at Regional Scale
2.2. Wujiagou Debris Flow
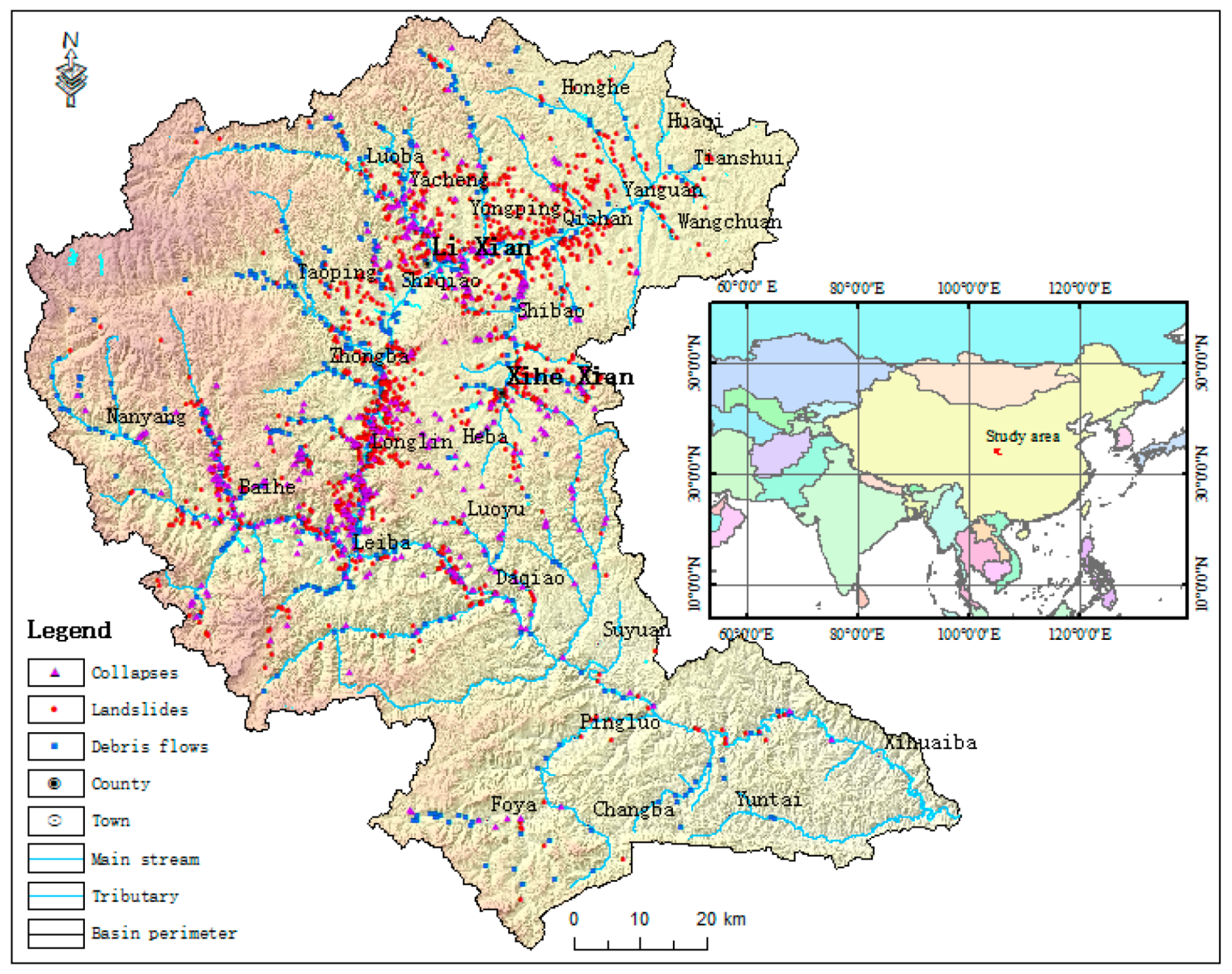
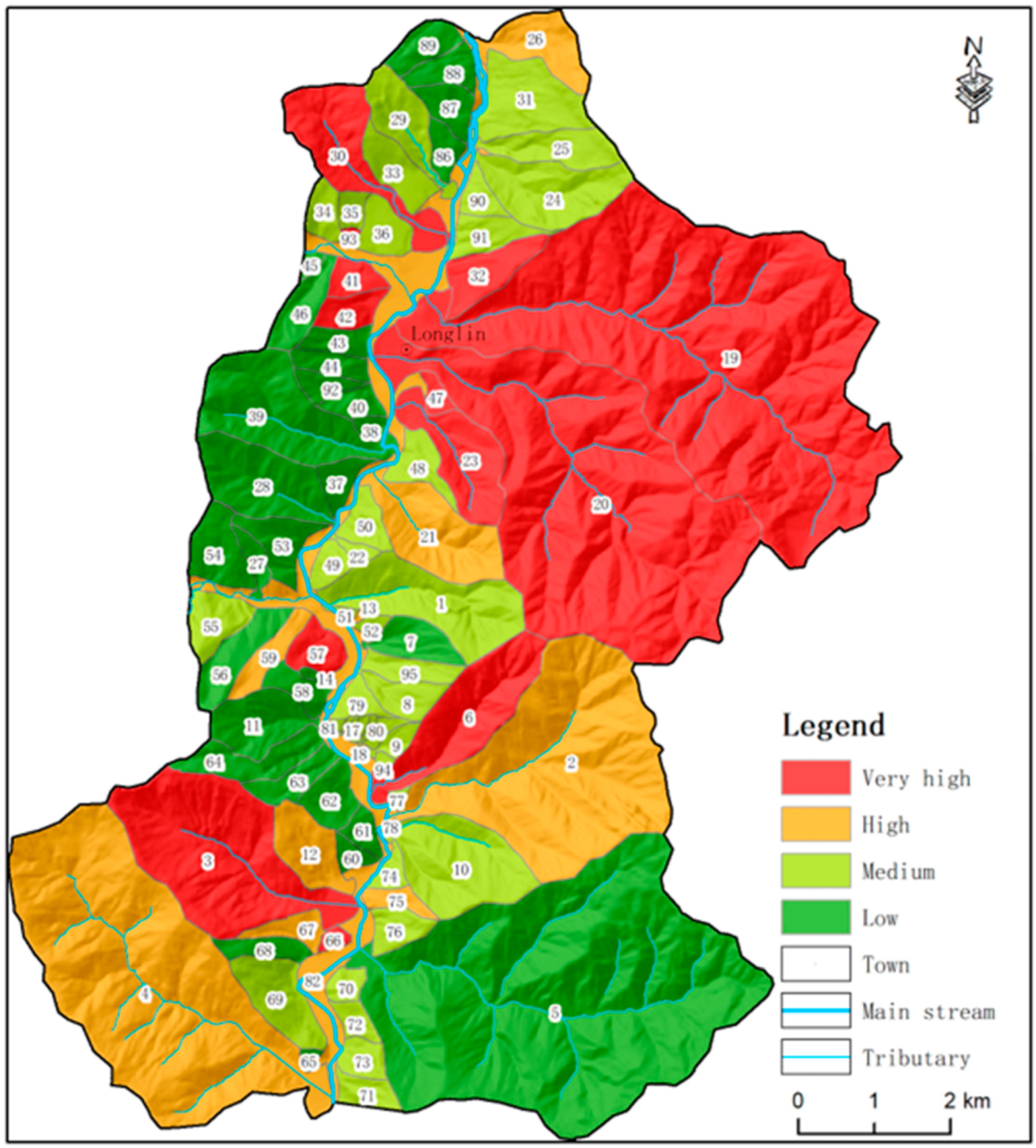
2.3. Overview of Geological Hazards in the Study Area
2.4. Overview of Geological Hazards in the Study Area
3. Methods
3.1. Hazard Evaluation Model
3.1.1. Regional Scale
3.1.2. Local Scale
3.1.3. Site Scale
3.2. Vulnerability Evaluation Methods
3.2.1. Regional Scale
3.2.2. Local Scale
3.2.3. Site Scale
3.3. Risk Assessment Methods
3.3.1. Regional Scale
3.3.2. Local Scale
3.3.3. Site Scale
4. Results
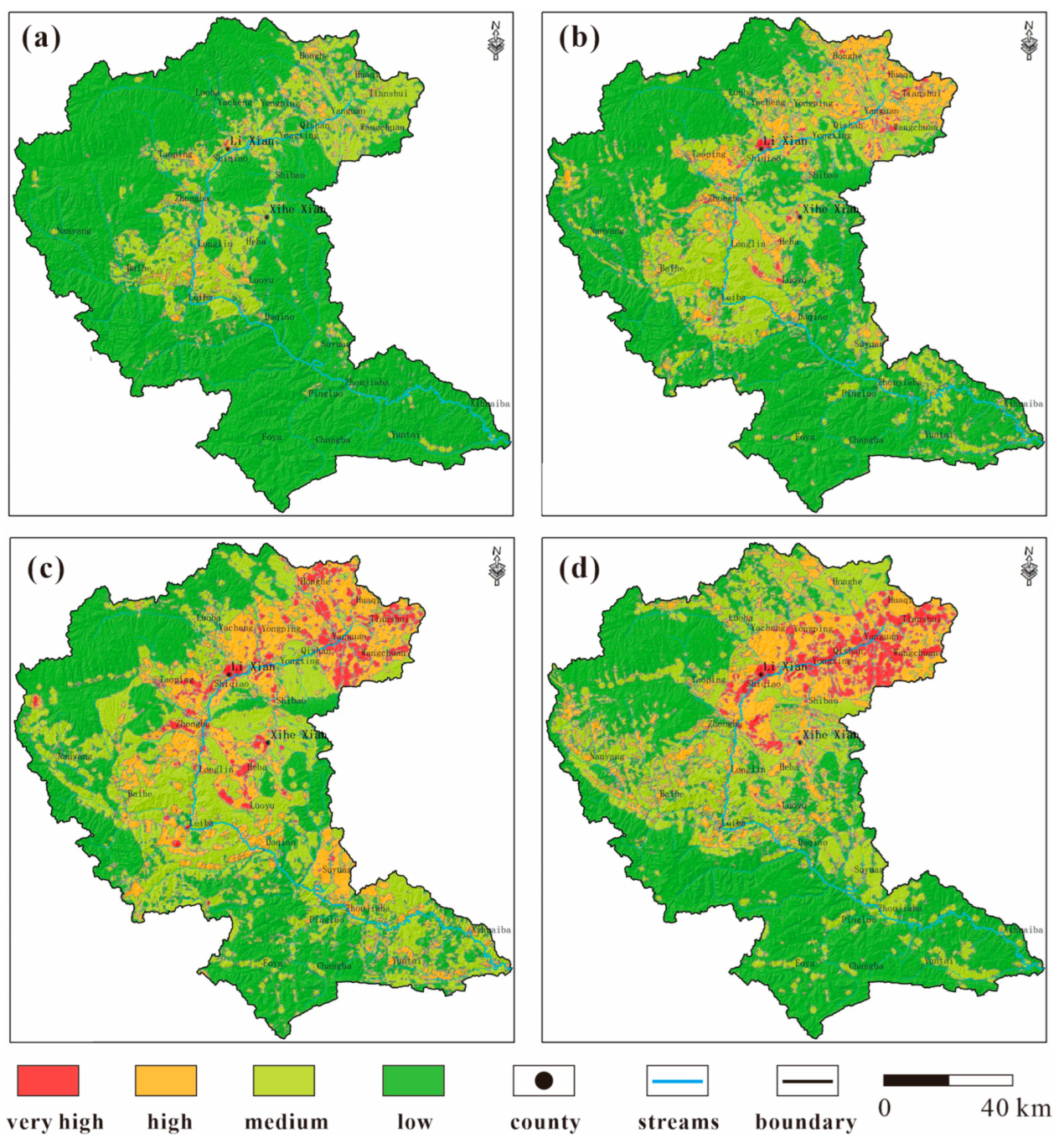
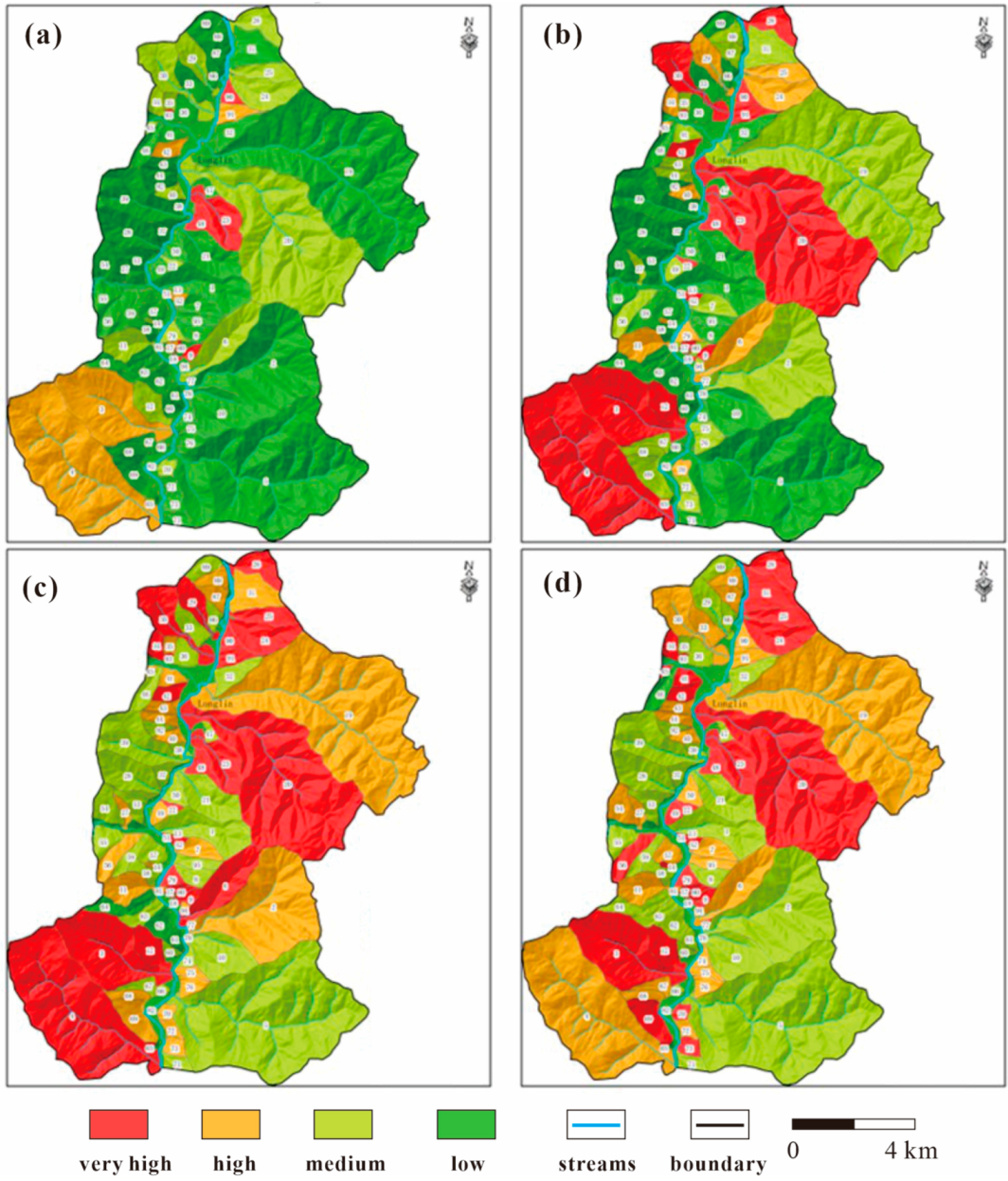
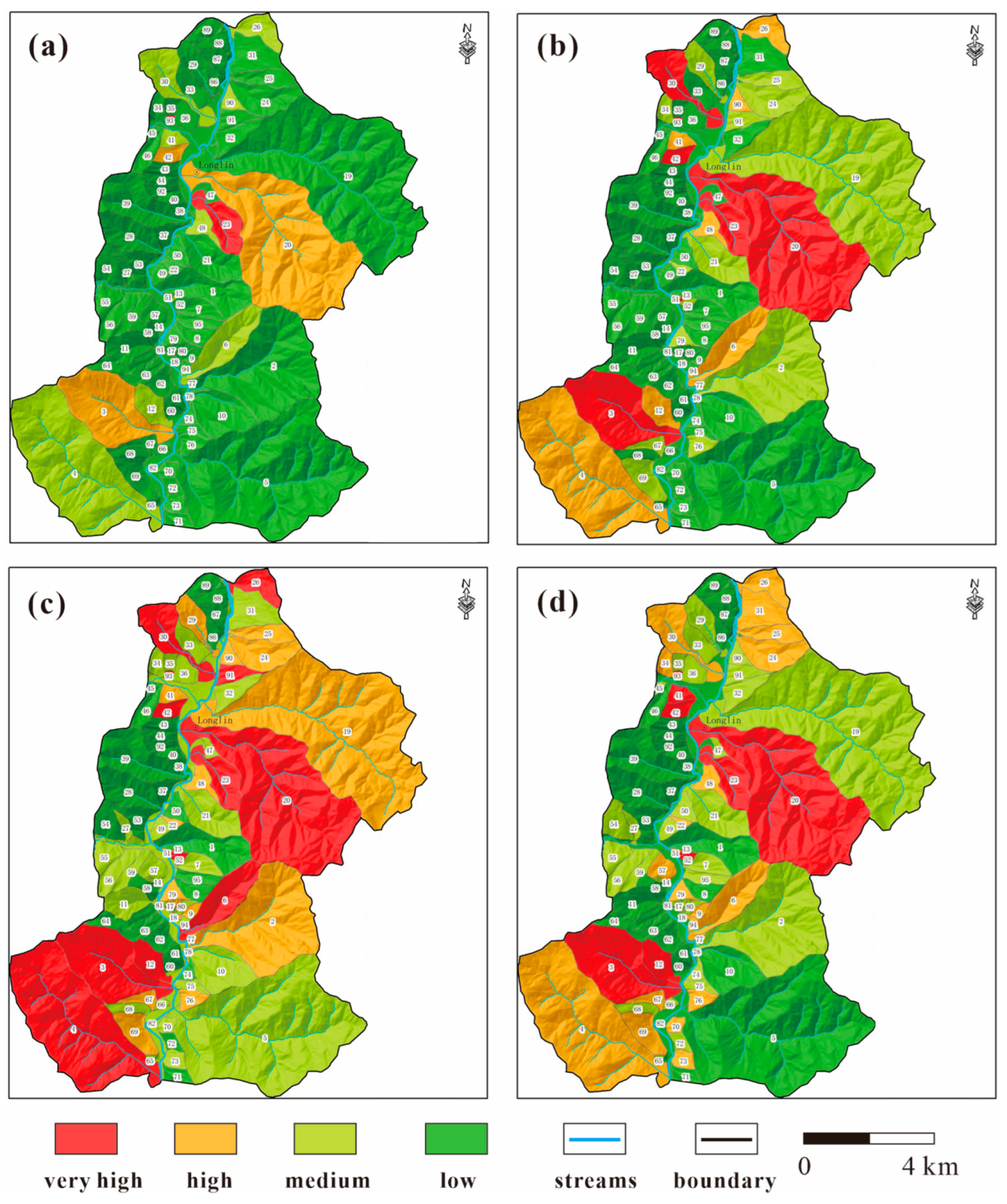
4.1. Risk Results and Assessment at a Regional Scale
4.2. Risk Results and Assessment at Local Scale
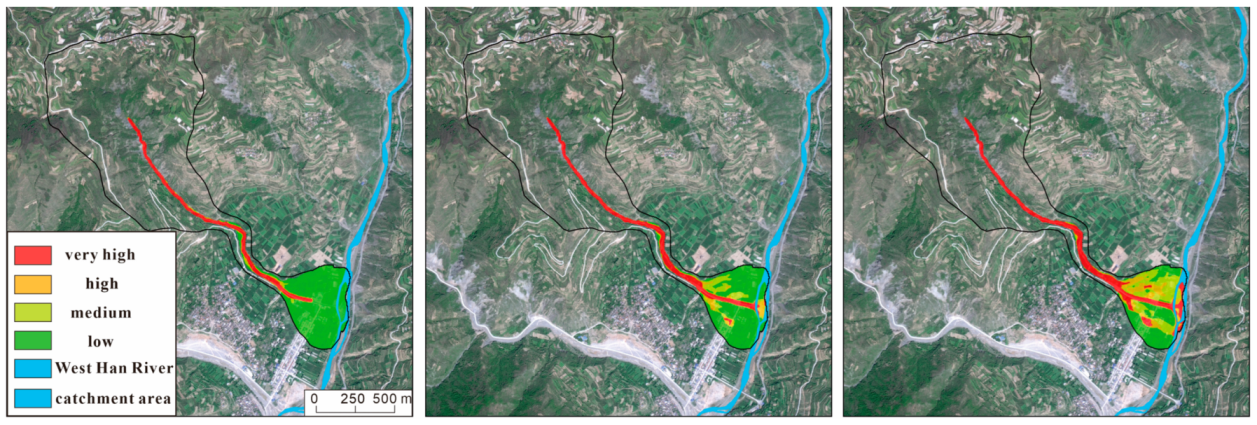
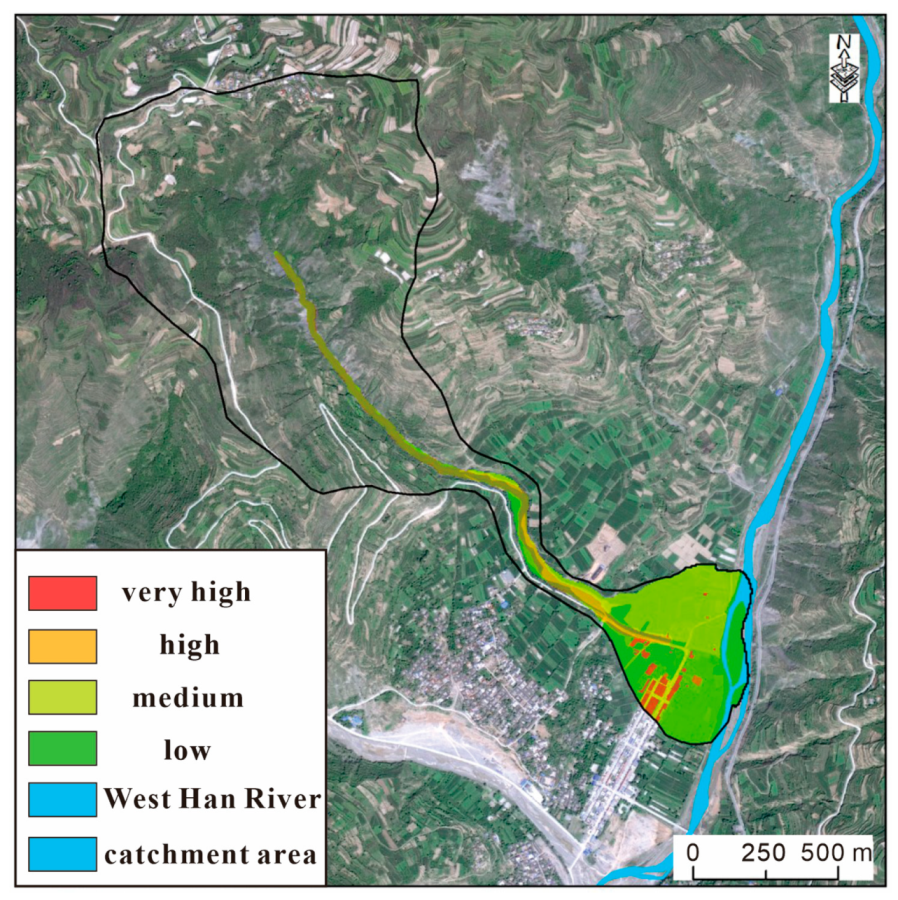
4.3. Risk Results and Assessment for Wujiagou Debris Flow
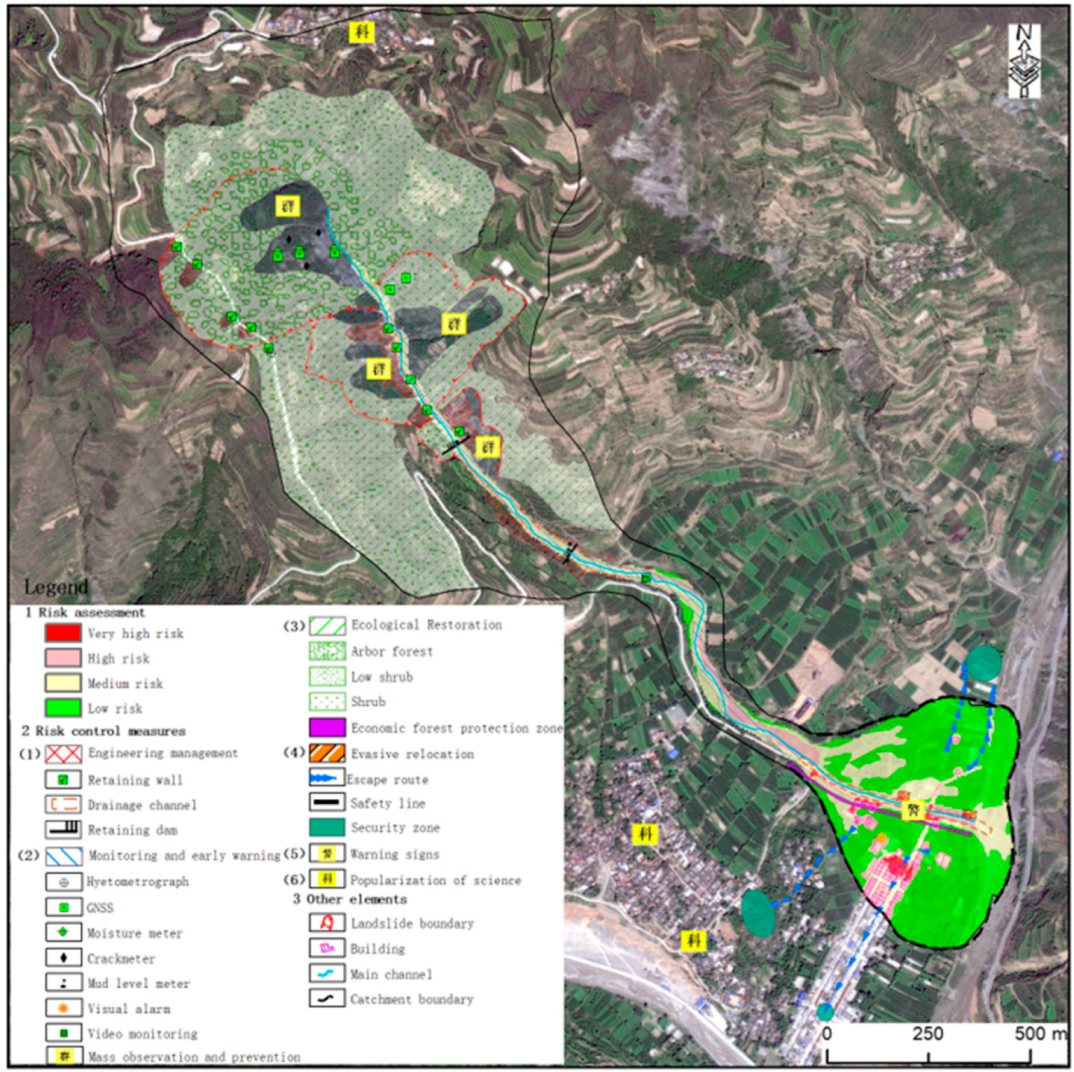
4.4. Multi-Scale Geological Disaster Risk Control
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Catani, F.; Casagli, N.; Ermini, L.; Righini, G.; Menduni, G. Landslide hazard and risk mapping at catchment scale in the Arno River basin. Landslides 2005, 2, 329–342. [Google Scholar] [CrossRef]
- Calvello, M.; Papa, M.N.; Pratschke, J.; Crescenzo, M.N. Landslide risk perception: A case study in Southern Italy. Landslides 2016, 13, 349–360. [Google Scholar] [CrossRef]
- Corominas, J.; van Westen, C.J.; Frattini, P.; Cascini, L.; Malet, J.; Fotopoulou, S. Recommendations for the quantitative analysis of landslide risk. Bull. Eng. Geol. Environ. 2013, 73, 209–263. [Google Scholar] [CrossRef]
- Chen, L.; van Weatern, C.J.; Hussin, H.; Ciurean, R.L.; Turkington, T.; Chavarro-Rincon, D.; Shrestha, D.P. Integrating expert opinion with modelling for quantitative multi-hazard risk assessment in the Eastern Italian Alps. Geomorphology 2016, 273, 150–167. [Google Scholar] [CrossRef]
- Wu, C.Y.; Chen, S.C. Integrating spatial, temporal, and size probabilities for the annual landslide hazard maps in the Shihmen watershed, Taiwan. Nat. Hazards Earth Syst. Sci. 2013, 13, 2353–2367. [Google Scholar] [CrossRef]
- Hürlimann, M.; Guo, Z.; Puig-Polo, C.; Medina, V. Impacts of future climate and land cover changes on landslide susceptibility: Regional scale modelling in the Val d’ Aran region (Pyrenees, Spain). Landslides 2022, 19, 99–118. [Google Scholar] [CrossRef]
- Chen, S.C.; Wu, C.Y. Annual landslide risk and effectiveness of risk reduction measures in Shihmen watershed, Taiwan. Landslides 2016, 13, 551–563. [Google Scholar] [CrossRef]
- Jaiswal, P.; van Western, C.J. Use of quantitative landslide hazard and risk information for local disaster risk reduction along a transportation corridor: A case study from Nilgiri district, India. Nat. Hazards 2013, 65, 887–913. [Google Scholar] [CrossRef]
- Guo, Z.; Torra, O.; Hürlimann, M.; Medina, V.; Puig-Polo, C. FSLAM: A QGIS plugin for fast regional susceptibility assessment of rainfall-induced landslides. Environ. Model. Softw. 2022, 150, 105354. [Google Scholar] [CrossRef]
- Guo, Z.; Tian, B.; Li, G.; Huang, D.; Zeng, T.; He, J.; Song, D. Landslide susceptibility mapping in the Loess Plateau of northwest China using three data-driven techniques-a case study from middle Yellow River catchment. Front. Earth Sci. 2023, 10, 1033085. [Google Scholar] [CrossRef]
- Deschepper, E.; Thas, O.; Ottoy, J.P. Regional residual plots for assessing the fit of linear regression models. Comput. Stat. Data Anal. 2006, 8, 1995–2013. [Google Scholar] [CrossRef]
- Silva, A.; Brito, J.; Gaspar, P.L. Deterministic Models. In Methodologies for Service Life Prediction of Buildings; Green Energy and Technology; Springer: Cham, Switzerland, 2016; Volume 4, pp. 67–162. [Google Scholar]
- König, T.; Kux, H.J.H.; Mendes, R.M. Shalstab mathematical model and WorldView-2 satellite images to identification of landslide-susceptible areas. Nat. Hazards 2019, 97, 1127–1149. [Google Scholar] [CrossRef]
- Tien, B.D.; Tran, H.T.; Bui, X.N. (Eds.) Proceedings of the International Conference on Innovations for Sustainable and Responsible Mining; Springer: Cham, Switzerland, 2021; Volume 108, pp. 210–229. [Google Scholar]
- Nie, Y.; Li, X.; Xu, R. Dynamic hazard assessment of debris flow based on TRIGRS and flow-R coupled models. Stoch. Environ. Res. Risk Assess. 2022, 36, 97–114. [Google Scholar] [CrossRef]
- Gatto, M.P.A.; Lentini, V.; Montrasio, L.; Castelli, F. A simplified semi-quantitative procedure based on the SLIP model for landslide risk assessment: The case study of Gioiosa Marea (Sicily, Italy). Landslides 2023, 20, 1381–1403. [Google Scholar] [CrossRef]
- Medina, V.; Hürlimann, M.; Guo, Z.; Lloret, A.; Vaunat, J. Fast physically-based model for rainfall-induced landslide susceptibility assessment at regional scale. Catena 2021, 201, 105213. [Google Scholar] [CrossRef]
- Sezer, E.A.; Nefeslioglu, H.A.; Osna, T. An expert-based landslide susceptibility mapping (LSM) module developed for Netcad Architect Software. Comput. Geosci. 2017, 98, 26–37. [Google Scholar] [CrossRef]
- Guo, Z.; Tian, B.; He, J.; Xu, C.; Zeng, T.; Zhu, Y. Hazard assessment for regional typhoon-triggered landslides by using physically-based model -A case study from southeastern China. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2023, 17, 740–754. [Google Scholar] [CrossRef]
- Remondo, J.; Bonachea, J.; Cendrero, A. A statistical approach to landslide risk modelling at basin scale: From landslide susceptibility to quantitative risk assessment. Landslides 2005, 2, 321–328. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Pradhan, B. A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using GIS. Comput. Geosci. 2013, 51, 350–365. [Google Scholar] [CrossRef]
- Guo, Z.; Tian, B.; Zhu, Y.; He, J.; Zhang, T. How do the landslide and non-landslide sampling strategies impact landslide susceptibility assessment?—A case study at catchment scale from China. J. Rock. Mech. Geotech. Eng. 2024, 16, 877–894. [Google Scholar] [CrossRef]
- Althuwaynee, O.F.; Pradhan, B.; Park, H.J.; Lee, J.H. A novel ensemble decision tree-based CHi-squared Automatic Interaction Detection (CHAID) and multivariate logistic regression models in landslide susceptibility mapping. Landslides 2014, 11, 1063–1078. [Google Scholar] [CrossRef]
- Goetz, J.N.; Brenning, A.; Petschko, H.; Leopold, P. Evaluating machine learning and statistical prediction techniques for landslide susceptibility modeling. Comput. Geosci. 2015, 81, 1–11. [Google Scholar] [CrossRef]
- Zeng, T.; Guo, Z.; Wang, L.; Jin, B.; Wu, F.; Guo, R. Tempo-Spatial Landslide Susceptibility Assessment from the Perspective of Human Engineering Activity. Remote Sens. 2023, 15, 4111. [Google Scholar] [CrossRef]
- Li, Z.; Nadim, F.; Huang, H.; Uzielli, M.; Lacasse, S. Quantitative vulnerability estimation for scenario-based landslide hazards. Landslides 2010, 7, 125–134. [Google Scholar] [CrossRef]
- Ciurean, R.L.; Hussin, H.; van Weatern, C.J.; Jaboyedoff, M.; Nicolet, P.; Chen, L.; Frigerio, S.; Glade, T. Multi-scale debris flow vulnerability assessment and direct loss estimation of buildings in the Eastern Italian Alps. Nat. Hazards 2017, 85, 929–957. [Google Scholar] [CrossRef]
- Singh, A.; Kanungo, D.P.; Pal, S. Physical vulnerability assessment of buildings exposed to landslides in India. Nat. Hazards 2019, 96, 753–790. [Google Scholar] [CrossRef]
- Luo, H.Y.; Zhang, L.M.; Zhang, L.L.; He, J.; Yin, K.S. Vulnerability of buildings to landslides: The state of the art and future needs. Earth-Sci. Rev. 2023, 238, 104329. [Google Scholar] [CrossRef]
- Peduto, D.; Ferlisi, S.; Nicodemo, G.; Reale, D.; Gullà, G. Empirical fragility and vulnerability curves for buildings exposed to slow-moving landslides at medium and large scales. Landslides 2017, 14, 1993–2007. [Google Scholar] [CrossRef]
- Xing, Z.; Yang, S.; Zan, X.; Dong, X.; Yao, Y.; Liu, Z.; Zhang, X. Flood vulnerability assessment of urban buildings based on integrating high-resolution remote sensing and street view images. Suatain Cities Soc. 2023, 92, 104467. [Google Scholar] [CrossRef]
- Ouyang, Y.; Daivd, L.A.; Vincent, P.D. Seismic Vulnerability Assessment of Bridges on Earthquake Priority Routes in Western Kentucky II Lifeline Earthquake Engineering. In Proceedings of the 3rd U.S. Conference on Lifeline Earthquake Engineering, Los Angeles, CA, USA, 22–23 August 1991. [Google Scholar]
- Mander, J.B.; Basgz, N. Seismic Fragility Curve Theory for Highway Bridges II Optimizing Post-Earthquake Lifeline System Reliability Seattle. In Optimizing Post-Earthquake Lifeline System Reliability, Proceedings of the 5th U.S. Conference on Lifeline Earthquake Engineering, Seattle, WA, USA, 12–14 August 1999; ASCE: Reston, VA, USA, 1999. [Google Scholar]
- Pan, Y.; Agrawal, A.K.; Ghosn, M. Seismic fragility of continuous steel highway bridges in New York State. J. Bridge Eng. 2007, 12, 689–699. [Google Scholar] [CrossRef]
- Zhang, J.; Huo, Y. Evaluating effectiveness and optimum design of isolation devices for highway bridges using the fragility function method. Eng. Struct. 2009, 31, 1648–1660. [Google Scholar] [CrossRef]
- Jaiswal, P.; van Western, C.J.; Jetten, V. Quantitative estimation of landslide risk from rapid debris slides on natural slopes in the Nilgiri hills, India. Nat. Hazards Earth Syst. Sci. 2011, 11, 1723–1743. [Google Scholar] [CrossRef]
- Guo, Z.; Chen, L.; Yin, K.; Shrestha, D.P.; Zhang, L. Quantitative risk assessment of slow-moving landslides from the viewpoint of decision-making: A case study of the Three Gorges Reservoir in China. Eng. Geol. 2020, 273, 105667. [Google Scholar] [CrossRef]
- Guillard-Gonçalves, C.; Zêzere, J.L.; Pereira, S.; Garcia, R.A.C. Assessment of physical vulnerability of buildings and analysis of landslide risk at the municipal scale: Application to the Loures municipality, Portugal. Nat. Hazards Earth Syst. Sci. 2016, 16, 311–331. [Google Scholar] [CrossRef]
- Zêzere, J.L.; Oliveira, S.C.; Garcia, R.A.C.; Reis, E. Landslide risk analysis in the area North of Lisbon (Portugal): Evaluation of direct and indirect costs resulting from a motorway disruption by slope movements. Landslides 2007, 4, 123–136. [Google Scholar] [CrossRef]
- Van Westen, C.J.; van Asch, T.W.J.; Soeters, R. Landslide hazard and risk zonation—Why is it still so difficult? Bull. Eng. Geol. Environ. 2006, 65, 167–184. [Google Scholar] [CrossRef]
- Peng, L.; Xu, S.; Hou, J.; Peng, J. Quantitative risk analysis for landslides: The case of the Three Gorges area, China. Landslides 2015, 12, 943–960. [Google Scholar] [CrossRef]
- Yin, Y.; Huang, B.; Wang, W.; Wei, Y.; Ma, X.; Ma, F.; Zhao, C. Reservoir-induced landslides and risk control in Three Gorges Project on Yangtze River, China. J. Rock. Mech. Geotech. Eng. 2016, 8, 577–595. [Google Scholar] [CrossRef]
- Segoni, S.; Tofani, V.; Rosi, A.; Catani, F.; Casagli, N. Combination of Rainfall Thresholds and Susceptibility Maps for Dynamic Landslide Hazard Assessment at Regional Scale. Front. Earth Sci. 2018, 6, 85. [Google Scholar] [CrossRef]
- Lee, S.; Pradhan, B. Landslide hazard mapping at Selangor, Malaysia using frequency ratio and logistic regression models. Landslides 2007, 4, 33–41. [Google Scholar] [CrossRef]
- Meten, M.; Bhandary, N.P.; Yatabe, R. GIS-based frequency ratio and logistic regression modeling for landslide susceptibility mapping of Debre Sina area in central Ethiopia. J. Mt. Sci. 2015, 12, 1355–1372. [Google Scholar] [CrossRef]
- Chandak, P.G.; Sayyed, S.S.; Kulkarni, Y.U.; Devtale, M.K. Landslide hazard zonation mapping using information value method near Parphi village in Garhwal Himalaya. Ljemas 2016, 4, 228–236. [Google Scholar]
- Wubalem, A.; Meten, M. Landslide susceptibility mapping using information value and logistic regression models in Goncha Siso Eneses area, northwestern Ethiopia. SN Appl. Sci. 2020, 2, 807. [Google Scholar] [CrossRef]
- Tang, Y.; Feng, F.; Guo, Z.; Feng, W.; Li, Z.; Wang, J.; Sun, Q.; Ma, H.; Li, Y. Integrating principal component analysis with statistically-based models for analysis of causal factors and landslide susceptibility mapping: A comparative study from the loess plateau area in Shanxi (China). J. Clean. Prod. 2020, 277, 124159. [Google Scholar] [CrossRef]
- Akamatsu, K.; Nishino, T.; Miyawaki, Y. Spatiotemporal bias of the human gaze toward hierarchical visual features during natural scene viewing. Sci. Rep. 2023, 13, 104. [Google Scholar] [CrossRef] [PubMed]
- Baccalá, L.A.; Sameshima, K. Partial directed coherence: A new concept in neural structure determination. Biol. Cybern. 2001, 84, 463–474. [Google Scholar] [CrossRef] [PubMed]
- Faes, L.; Porta, A. Nollo G Mutual nonlinear prediction as a tool to evaluate coupling strength and directionality in bivariate time series: Comparison among different strategies based on k nearest neighbors. Phys. Rev. E 2008, 78, 026201. [Google Scholar] [CrossRef] [PubMed]
- Barrett, A.B.; Barnett, L.; Seth, A.K. Multivariate granger causality and generalized variance. Phys. Rev. E 2010, 81, 041907. [Google Scholar] [CrossRef]
- Liu, X.; Tang, C.; Zhu, J.; Zhang, S. The drainage background forecast on the risk range of debris flow. J. Nat. Disasters 1992, 1, 56–67, (In Chinese with English abstract). [Google Scholar]
- Tang, Y.; Guo, Z.; Wu, L.; Hong, B.; Feng, W.; Su, X.; Li, Z.; Zhu, Y. Assessing debris flow risk at a catchment scale for an economic decision based on the LiDAR DEM and numerical simulation. Front. Earth Sci. 2022, 10, 821735. [Google Scholar] [CrossRef]
- Sitotaw, H.; Erena, H.W.; Francesco, D.P. Flood hazard mapping using FLO-2D and local management strategies of Dire Dawa city, Ethiopia. J. Hydrol. Reg. Stud. 2010, 19, 224–239. [Google Scholar]
- Liu, D.; Jiang, X.; Li, B. Movement characteristics and risk assessment of mine debris flow based on flo-2d simulation: A Case Study of the Debris Flow in Bojigou Mine of Minxian County, Gansu Province. Geol. Resour. 2022, 31, 693–699. [Google Scholar]
- Zhang, J.; Yin, K.; Wang, J.; Liu, L.; Huang, F. Evaluation of landslide susceptibility for Wanzhou district of Three Gorges Reservoir. Chin. J. Rock. Mech. Eng. 2016, 35, 284–296, (In Chinese with English abstract). [Google Scholar]
- Bulmer, M.H.; Barnouin-Jha, O.S.; Peitersen, M.N.; Bourke, M. An empirical approach to studying debris flows: Implications for planetary modeling studies. J. Geophys.Res. Planets 2002, 107, 9-1–9-14. [Google Scholar] [CrossRef]
- Federico, F.; Cesali, C. An energy-based approach to predict debris flow mobility and analyze empirical relationships. Can. Geotech. J. 2015, 52, 2113–2133. [Google Scholar] [CrossRef]
- Jaiswal, P.; Van Westen, C.J.; Jetten, V. Quantitative Assessment of Direct and Indirect Landslide Risk along Transportation Lines in Southern India. Nat. Hazards Earth Syst. Sci. 2010, 10, 1253–1267. [Google Scholar] [CrossRef]
- Bell, R.; Glade, T. Quantitative Risk Analysis for Landslides—Examples from Bíldudalur, NW-Iceland. Nat. Hazards Earth Syst. Sci. 2004, 4, 117–131. [Google Scholar] [CrossRef]
- Fu, S.; Chen, L.; Woldai, T.; Yin, K.; Gui, L.; Li, D.; Du, J.; Zhou, C.; Xu, Y.; Lian, Z. Landslide hazard probability and risk assessment at the community level: A case of western Hubei, China. Nat. Hazards Earth Syst. Sci. 2020, 20, 581–601. [Google Scholar] [CrossRef]
- Segoni, S.; Piciullo, L.; Gariano, S.L. A review of the recent literature on rainfall thresholds for landslide occurrence. Landslides 2018, 15, 1483–1501. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, H.; Park, H.J.; Heo, J.H. Temporal prediction modeling for rainfall-induced shallow landslide hazards using extreme value distribution. Landslides 2021, 18, 321–338. [Google Scholar] [CrossRef]








| Base Data | Data Source and Production | Data Format |
|---|---|---|
| DEM | Geospatial data used to extract slope, gully density, and specific drop of debris-flow gully bed, etc. | National Geographic Information Center: 5 m × 5 m raster data |
| DOM/DLG | Land use type data | National Geographic Information Center: 5 m × 5 m raster and vector data |
| Geological data | Lithological zoning and fracture structure | 1:200,000 regional geological map, vector data |
| Remote sensing data | For risk source identification, disaster-bearing body types, etc. | Interpretation of P-star and UAV data, raster data |
| Geological disaster data | According to the “Longnan West Han River Basin Disaster Geological Survey” (2019–2021) project database | 1:10,000 precision vector data |
| Rainfall data | Lanzhou central meteorological station and Longnan city geological disaster professional monitoring network | Point cloud (vector) data |
| Survey and test data | Geotechnical density/capacity, water content/permeability coefficient, and physical and mechanical indicators such as angle of internal friction and cohesion for model calculation and analysis | Text data format |
| Risk Classification | Very High Vulnerability | High Vulnerability | Medium Vulnerability | Low Vulnerability |
|---|---|---|---|---|
| Very high hazard | H | H | M | L |
| High hazard | H | M | M | L |
| Medium hazard | M | M | L | L |
| Low hazard | L | L | L | VL |
| Frequency | Evaluation Result Grading Area (km2) | Evaluation Result Grading Ratio (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| Low Zone | Medium Zone | High Zone | Very High Zone | Low Zone | Medium Zone | High Zone | Very High Zone | |
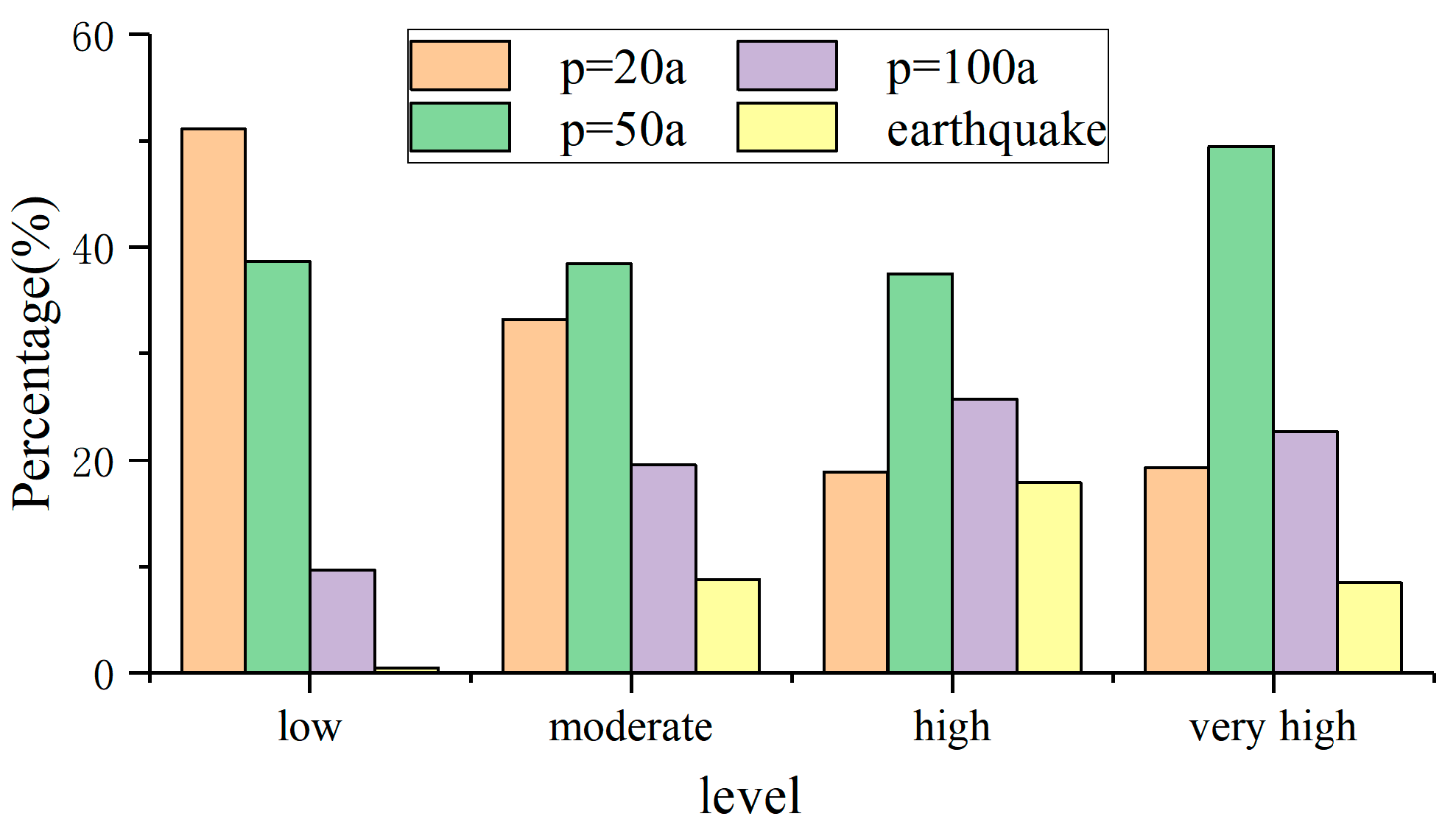
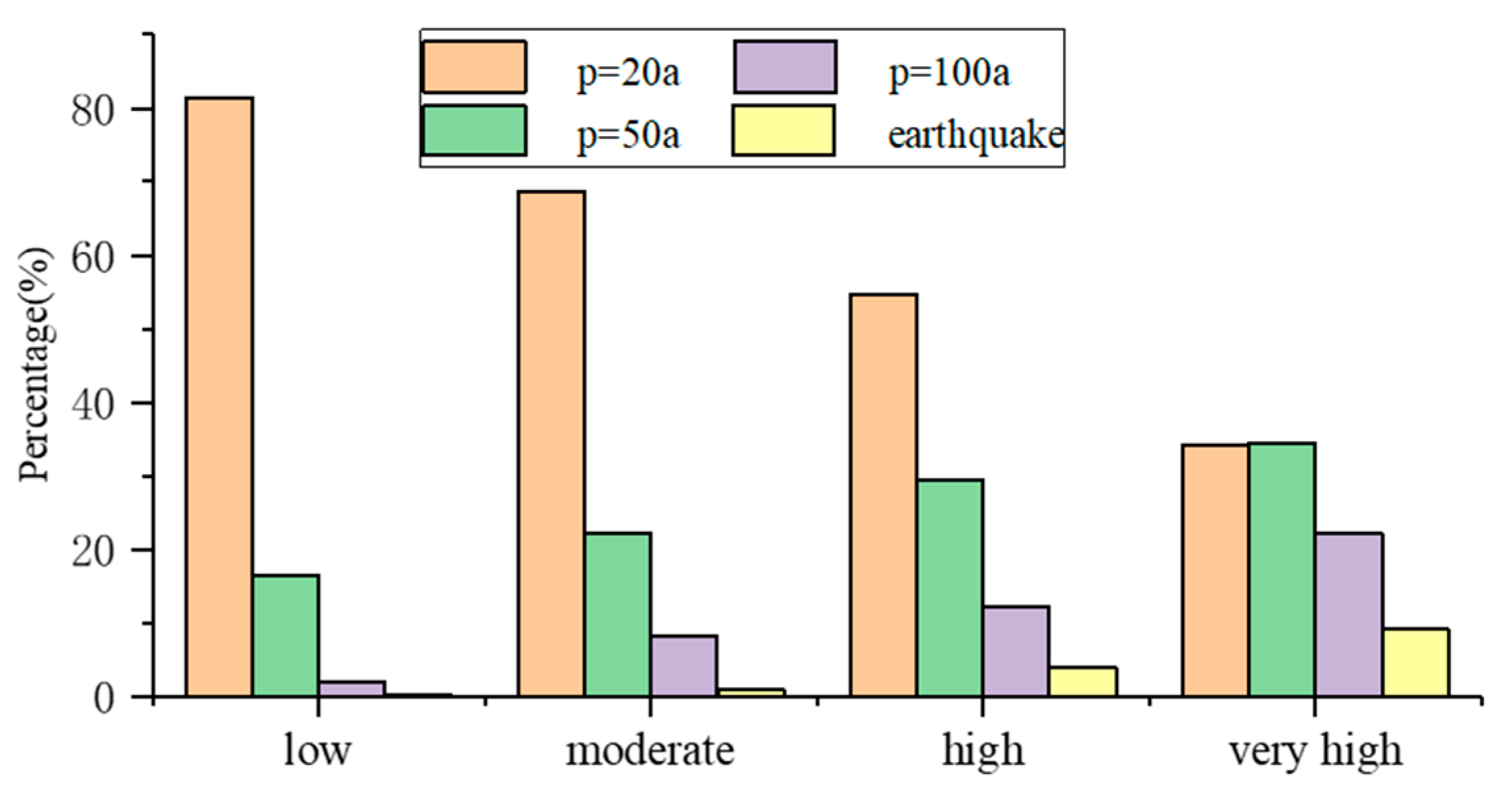
| 20-year event | 64.32 | 21.06 | 13.76 | 2.17 | 63.49 | 20.79 | 13.58 | 2.14 |
| 50-year event | 35.82 | 28.66 | 6.79 | 30.04 | 35.36 | 28.29 | 6.70 | 29.65 |
| 100-year event | 5.27 | 30.86 | 29.69 | 35.49 | 5.20 | 30.46 | 29.31 | 35.03 |
| Seismic conditions | 4.41 | 36.12 | 35.05 | 25.73 | 4.35 | 35.65 | 34.60 | 25.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Z.; Tian, Y.; Li, H.; Shao, C.; Gao, Y.; Wang, G. Risk Assessment and Control for Geohazards at Multiple Scales: An Insight from the West Han River of Gansu Province in China. Water 2024, 16, 1764. https://doi.org/10.3390/w16131764
Ye Z, Tian Y, Li H, Shao C, Gao Y, Wang G. Risk Assessment and Control for Geohazards at Multiple Scales: An Insight from the West Han River of Gansu Province in China. Water. 2024; 16(13):1764. https://doi.org/10.3390/w16131764
Chicago/Turabian StyleYe, Zhennan, Yuntao Tian, Hao Li, Changqing Shao, Youlong Gao, and Gaofeng Wang. 2024. "Risk Assessment and Control for Geohazards at Multiple Scales: An Insight from the West Han River of Gansu Province in China" Water 16, no. 13: 1764. https://doi.org/10.3390/w16131764
APA StyleYe, Z., Tian, Y., Li, H., Shao, C., Gao, Y., & Wang, G. (2024). Risk Assessment and Control for Geohazards at Multiple Scales: An Insight from the West Han River of Gansu Province in China. Water, 16(13), 1764. https://doi.org/10.3390/w16131764





