Guidelines for the Energetic Characterization of a Portable Drip-Type Rainfall Simulator for Soil Erosion Research
Abstract
:1. Introduction
2. Materials and Methods
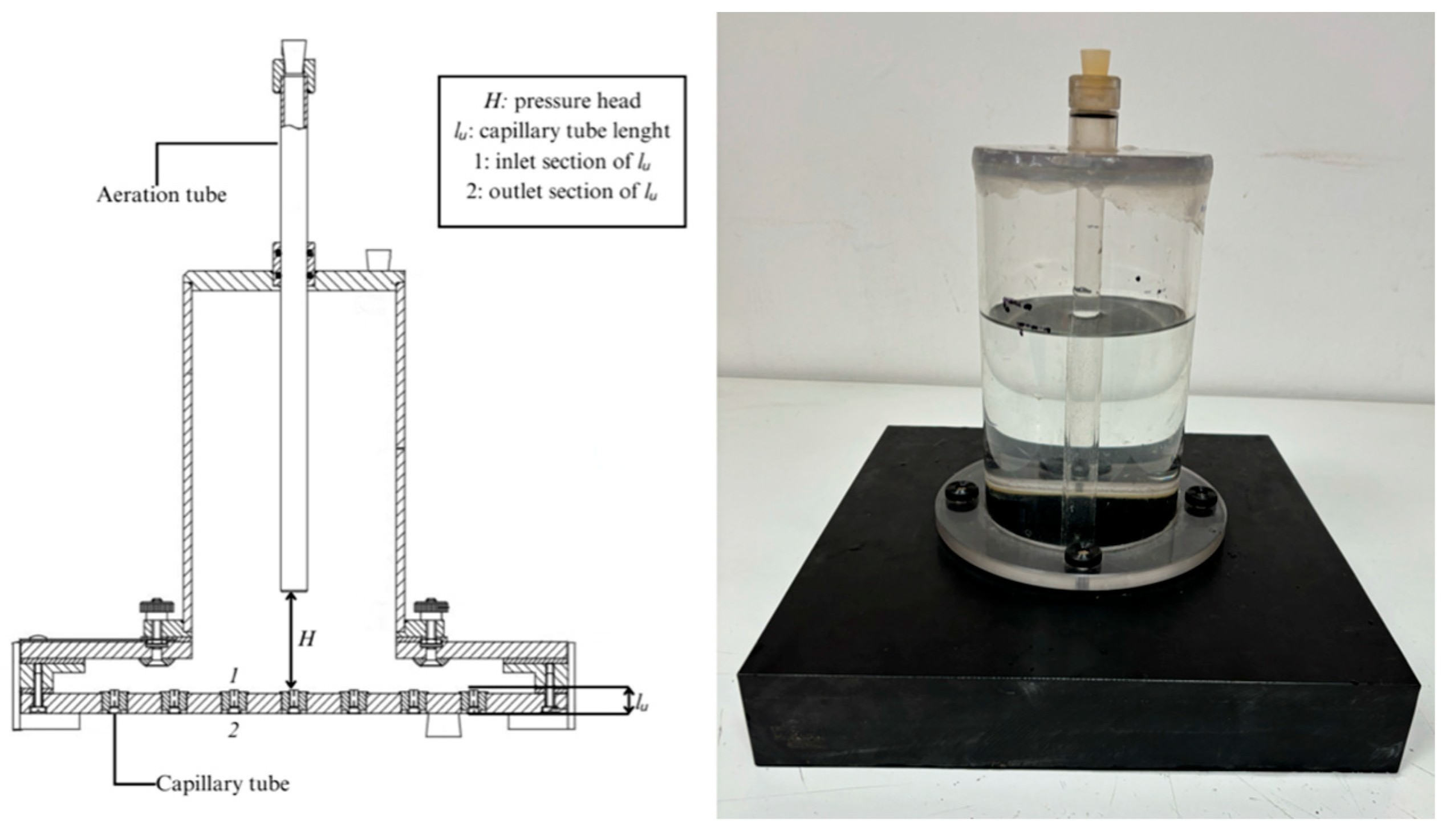
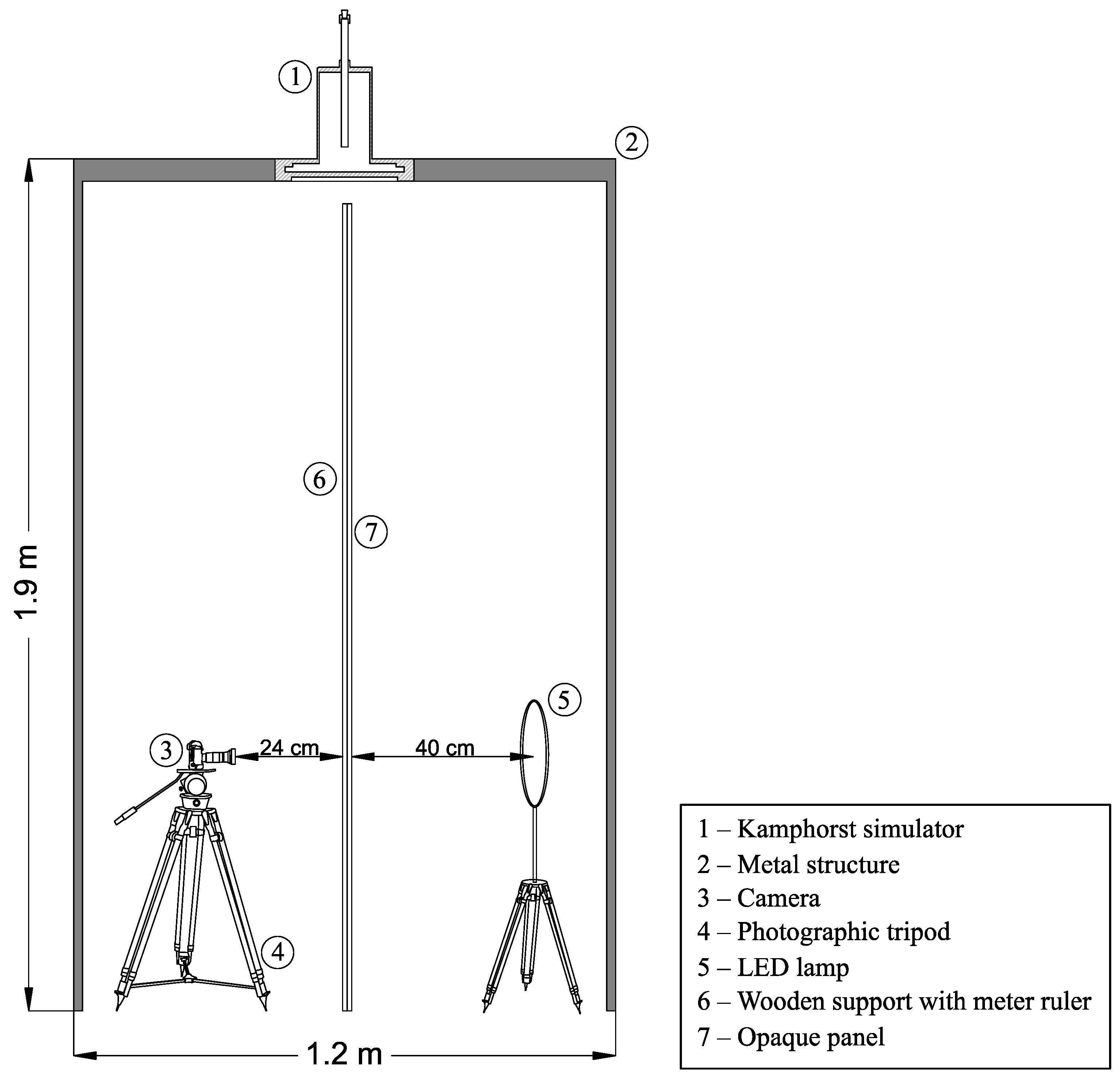
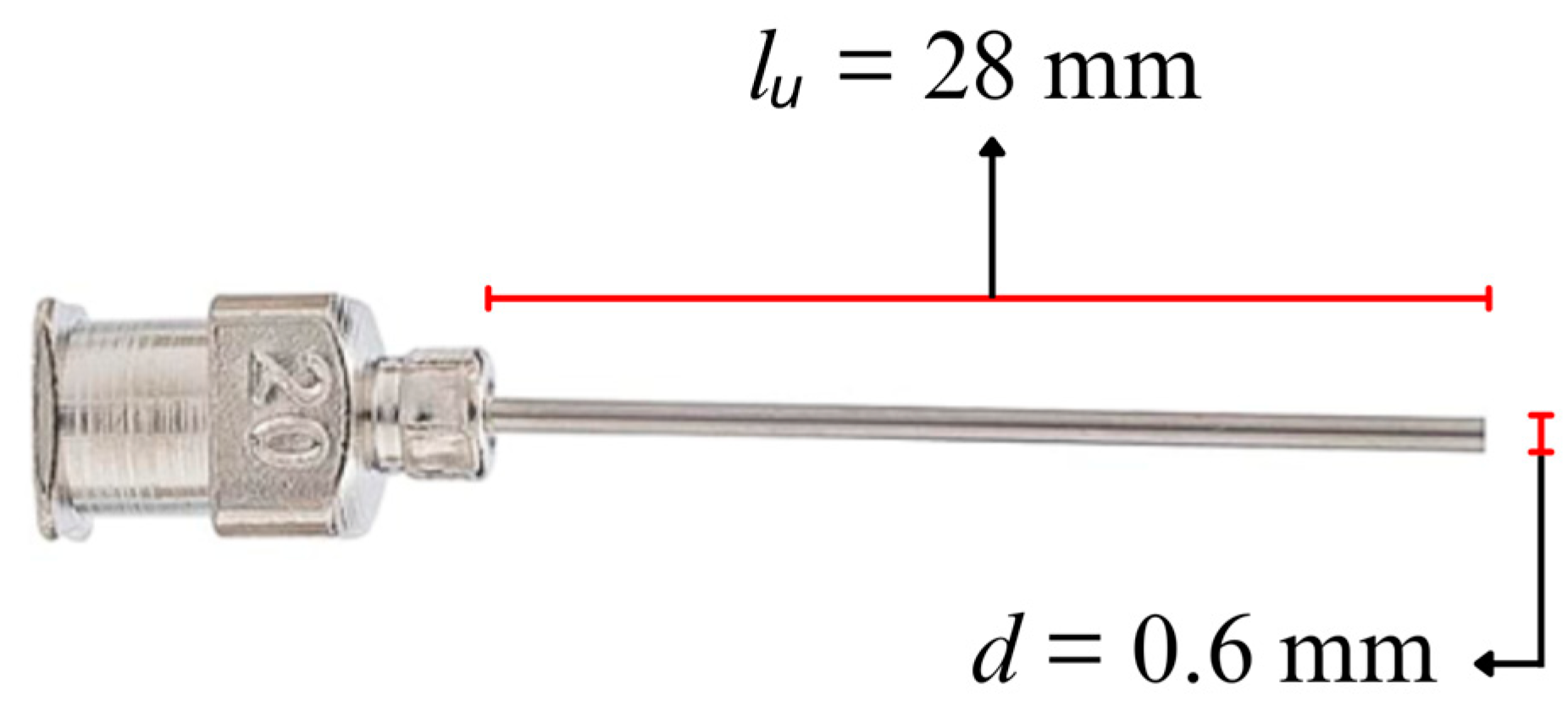
2.1. Experimental Set-Up
2.2. Test Procedure to Determine Rainfall Characteristics and Calculate Rainfall Kinetic Power and Momentum
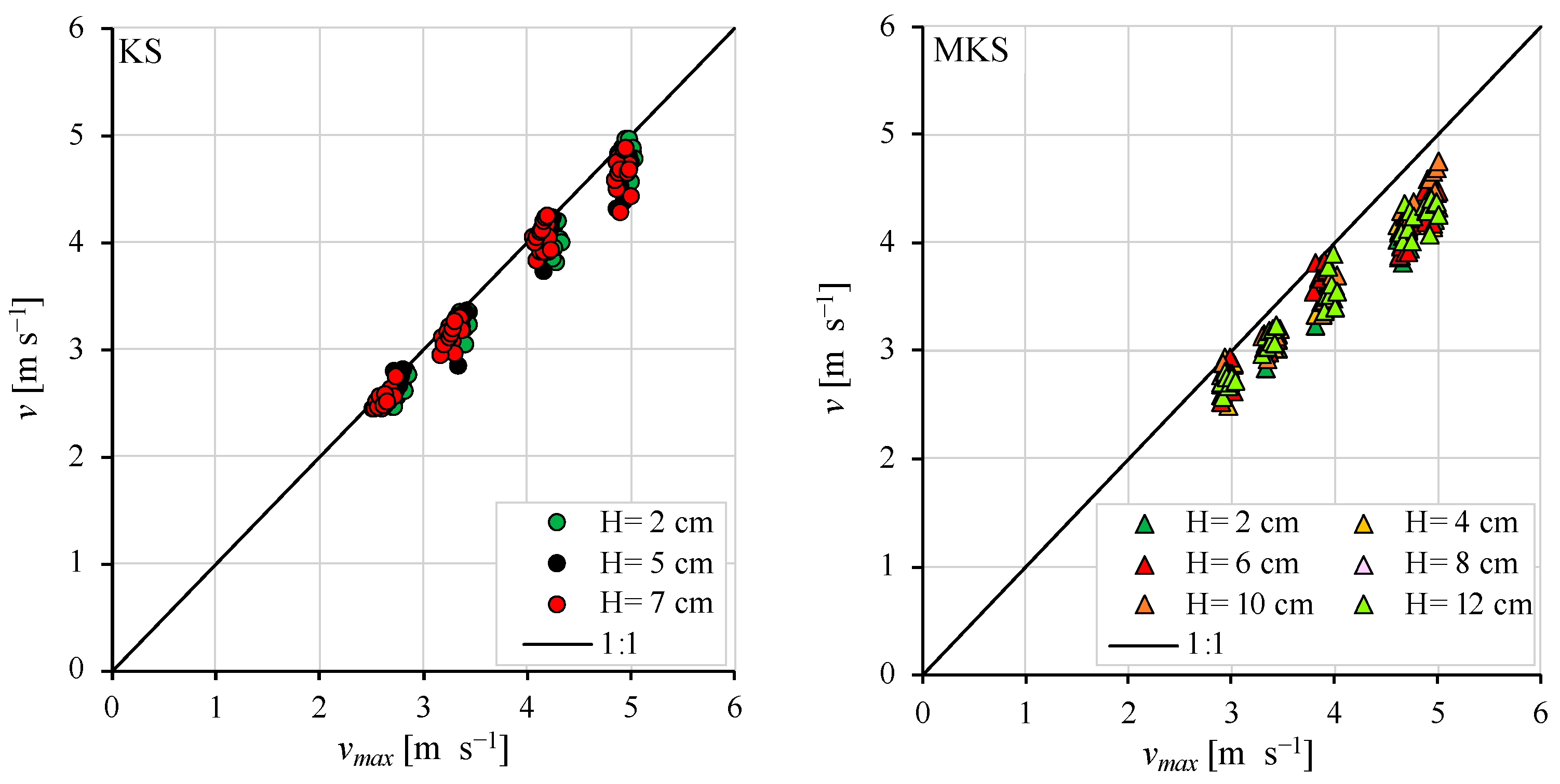
3. Results
4. Discussion
Operative Instructions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Description | Units |
| aS | Parameter of Equation (1) depending on raindrop falling height | cm−1 |
| d | Capillary tube inner diameter | m |
| D | Raindrop equivalent diameter | m |
| g | Gravity acceleration | m s−2 |
| h | Raindrop falling height | m |
| H | Pressure head | m |
| IS | Rainfall intensity | mm h−1 |
| lu | Capillary tube length | m |
| m | Weight of the water volume | kg |
| mSD | Mean mass of a single raindrop | kg |
| M | Rainfall momentum per unit time and area | N m−2 |
| MCalc | Rainfall momentum per unit time and area calculated by Equation (12) | N m−2 |
| nD | Number of drops | - |
| Pn | Rainfall kinetic power per unit time and area | J m−2 s−1 |
| PnCalc | Rainfall kinetic power per unit time and area calculated by Equation (11) | J m−2 s−1 |
| R2 | Coefficient of determination | - |
| t | Sampling time | s |
| T | Water temperature | °C |
| v | Raindrop fall velocity | m s−1 |
| vCalc | Raindrop fall velocity calculated by Equation (10) | m s−1 |
| vmax | Maximum velocity of a raindrop falling freely in a vacuum, starting from rest | m s−1 |
| vt | Raindrop terminal velocity | m s−1 |
| VS | Parameter of Equation (1) depending on raindrop falling height | m s−1 |
| VSD | Mean volume of a single raindrop | m3 |
| α | Parameter of Equation (8) | cm−1 m−β |
| β | Parameter of Equation (8) | - |
| γ | Parameter of Equation (9) | m s−1 |
| δ | Parameter of Equation (9) | mε |
| ε | Parameter of Equation (9) | - |
| ρ | Water density | kg m−3 |
| σ | Surface area assigned to a single capillary tube | m2 |
Acronyms
| Acronym | Meaning |
| DSD | Drop size distribution |
| FPS | Frames per second |
| KS | Kamphorst rainfall simulator |
| LED | Light-emitting diode |
| MAE | Mean absolute error |
| MKS | Modified Kamphorst rainfall simulator |
| USLE | Universal Soil Loss Equation |
References
- Arunrat, N.; Sereenonchai, S.; Kongsurakan, P.; Hatano, R. Assessing soil organic carbon, soil nutrients and soil erodibility under terraced paddy fields and upland rice in Northern Thailand. Agronomy 2022, 12, 537. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, Z.; Dong, F.; Fu, Y.; Hou, L.; Liu, J.; Wang, Y. Research on the Features of Rainfall Regime and Its Influence on Surface Runoff and Soil Erosion in the Small Watershed, the Lower Yellow River. Water 2023, 15, 2651. [Google Scholar] [CrossRef]
- Leone, A.; Pica, M. Caratteristiche dinamiche e simulazione delle piogge. Parte prima: Fondamenti teorici. Riv. Ing. Agrar. 1993, 3, 167–175. [Google Scholar]
- Imeson, A.C. A simple field-portable rainfall simulator for difficult terrain. Earth Surf. Process. 1977, 2, 431–436. [Google Scholar] [CrossRef]
- Luk, S.H. Effect of antecedent soil moisture content on rainwash erosion. Catena 1985, 12, 129–139. [Google Scholar] [CrossRef]
- Roth, C.H.; Meyer, B.; Frede, H.G. A portable rainfall simulator for studying factors affecting runoff, infiltration and soil loss. Catena 1985, 12, 79–85. [Google Scholar] [CrossRef]
- Kamphorst, A. A small rainfall simulator for the determination of soil erodibility. Neth. J. Agric. Sci. 1987, 35, 407–415. [Google Scholar] [CrossRef]
- Poesen, J.; Ingelmo-Sanchez, F.; Mucher, H. The hydrological response of soil surfaces to rainfall as affected by cover and position of rock fragments in the top layer. Earth Surf. Process. Landf. 1990, 15, 653–671. [Google Scholar] [CrossRef]
- Cerdà, A.; Ibáñez, S.; Calvo, A. Design and operation of a small and portable rainfall simulator for rugged terrain. Soil Technol. 1997, 11, 163–170. [Google Scholar] [CrossRef]
- Torri, D.; Regüés, D.; Pellegrini, S.; Bazzoffi, P. Within-storm soil surface dynamics and erosive effects of rainstorms. Catena 1999, 38, 131–150. [Google Scholar] [CrossRef]
- Battany, M.C.; Grismer, M.E. Development of a portable field rainfall simulator for use in hillside vineyard runoff and erosion studies. Hydrol. Process. 2000, 14, 1119–1129. [Google Scholar] [CrossRef]
- Regmi, T.P.; Thompson, A.L. Rainfall simulator for laboratory studies. Appl. Eng. Agric. 2000, 16, 641–647. [Google Scholar] [CrossRef]
- Loch, R.J.; Robotham, B.G.; Zeller, L.; Masterman, N.; Orange, D.N.; Bridge, B.J.; Sheridan, G.J.; Bourke, J.J. A multi-purpose rainfall simulator for field infiltration and erosion studies. Soil Res. 2001, 39, 599–610. [Google Scholar] [CrossRef]
- Humphry, J.B.; Daniel, T.C.; Edwards, D.R.; Sharpley, A.N. A portable rainfall simulator for plot–scale runoff studies. Appl. Eng. Agric. 2002, 18, 199. [Google Scholar] [CrossRef]
- Regüés, D.; Gallart, F. Seasonal patterns of runoff and erosion responses to simulated rainfall in a badland area in Mediterranean mountain conditions (Vallcebre, southeastern Pyrenees). Earth Surf. Process. Landf. 2004, 29, 755–767. [Google Scholar] [CrossRef]
- Birt, L.N.; Persyn, R.A.; Smith, P.K. Evaluation of an indoor nozzle-type rainfall simulator. Appl. Eng. Agric. 2007, 23, 283–287. [Google Scholar] [CrossRef]
- Clarke, M.A.; Walsh, R.P. A portable rainfall simulator for field assessment of splash and slopewash in remote locations. Earth Surf. Process. Landf. 2007, 32, 2052–2069. [Google Scholar] [CrossRef]
- Alves Sobrinho, T.; Gómez-Macpherson, H.; Gómez, J.A. A portable integrated rainfall and overland flow simulator. Soil Use Manag. 2008, 24, 163–170. [Google Scholar] [CrossRef]
- Nadal-Romero, E.; Regüés, D. Detachment and infiltration variations as consequence of regolith development in a Pyrenean badland system. Earth Surf. Process. Landf. 2009, 34, 824–838. [Google Scholar] [CrossRef]
- Abudi, I.; Carmi, G.; Berliner, P. Rainfall simulator for field runoff studies. J. Hydrol. 2012, 454, 76–81. [Google Scholar] [CrossRef]
- Iserloh, T.; Ries, J.B.; Arnáez, J.; Boix-Fayos, C.; Butzen, V.; Cerdà, A.; Echeverría, M.T.; Fernández-Gálvez, J.; Fister, W.; Geißler, C.; et al. European small portable rainfall simulators: A comparison of rainfall characteristics. Catena 2013, 110, 100–112. [Google Scholar] [CrossRef]
- Lascelles, B.; Favis-Mortlock, D.T.; Parsons, A.J.; Guerra, A.J.T. Spatial and temporal variation in two rainfall simulators: Implications for spatially explicit rainfall simulation experiments. Earth Surf. Process. Landf. 2000, 25, 709–721. [Google Scholar] [CrossRef]
- Boulal, H.; Gómez-Macpherson, H.; Gómez, J.A.; Mateos, L. Effect of soil management and traffic on soil erosion in irrigated annual crops. Soil Tillage Res. 2011, 115, 62–70. [Google Scholar] [CrossRef]
- Ries, J.B.; Iserloh, T.; Seeger, M.; Gabriels, D. Rainfall simulations-constraints, needs and challenges for a future use in soil erosion research. Z. Für Geomorphol. 2013, 57 (Suppl. S1), 1–10. [Google Scholar] [CrossRef]
- Eijkelkamp. Rainfall Simulator—Operating Instructions, M-0906E. 2022. Available online: https://www.royaleijkelkamp.com/media/1awdmlno/m-0906e-rainfall-simulator.pdf (accessed on 13 June 2024).
- Bagarello, V.; Baiamonte, G.; Ferro, V.; Giordano, G. Contributo alla valutazione dei fattori elementari dell’erosione negli studi a scala di bacino. Quad. Idronomia Mont. 1996, 15, 47–82. [Google Scholar]
- Serio, M.A.; Carollo, F.G.; Ferro, V. Raindrop size distribution and terminal velocity for rainfall erosivity studies. A review. J. Hydrol. 2019, 576, 210–228. [Google Scholar] [CrossRef]
- Beard, K.V. Terminal velocity and shape of cloud and precipitation drops aloft. J. Atmos. Sci. 1976, 33, 851–864. [Google Scholar] [CrossRef]
- Jayawardena, A.W.; Rezaur, R.B. Drop size distribution and kinetic energy load of rainstorms in Hong Kong. Hydrol. Process. 2000, 14, 1069–1082. [Google Scholar] [CrossRef]
- Laws, J.O. Measurements of the fall-velocity of water-drops and raindrops. Eos Trans. Am. Geophys. Union 1941, 22, 709–721. [Google Scholar] [CrossRef]
- Gunn, R.; Kinzer, G.D. The terminal velocity of fall for water droplets in stagnant air. J. Atmos. Sci. 1949, 6, 243–248. [Google Scholar] [CrossRef]
- Blanchard, D.C. The behavior of water drops at terminal velocity in air. Eos Trans. Am. Geophys. Union 1950, 31, 836–842. [Google Scholar] [CrossRef]
- Epema, G.F.; Riezebos, H.T. Fall velocity of waterdrops at different heights as a factor influencing erosivity of simulated rain. Catena Supp. 1983, 4, 1–17. [Google Scholar]
- Ries, J.B.; Seeger, M.; Iserloh, T.; Wistorf, S.; Fister, W. Calibration of simulated rainfall characteristics for the study of soil erosion on agricultural land. Soil Tillage Res. 2009, 106, 109–116. [Google Scholar] [CrossRef]
- Ries, J.B.; Langer, M. Runoff generation on abandoned fields in the Central Ebro Basin. Results from rainfall simulation experiments. Cuad. Investig. Geográf. Geogr. Res. Lett. 2001, 27, 61–78. [Google Scholar] [CrossRef]
- Seeger, M. Uncertainty of factors determining runoff and erosion processes as quantified by rainfall simulations. Catena 2007, 71, 56–67. [Google Scholar] [CrossRef]
- Carollo, F.G.; Caruso, R.; Palmeri, V.; Serio, M.A. Rainfall energy characteristics of a Kamphorst’s simulator. Quad. Idronomia Mont. 2024, 37, 367–374. [Google Scholar]
- Davies, C.N. Unpublished Ministry of Supply Reports Quoted by Sutton in Air Ministry Report, M.R.P. No. 40. 1942.
- Spilhaus, A.F. Raindrop size, shape and falling speed. J. Atmos. Sci. 1948, 5, 108–110. [Google Scholar] [CrossRef]
- Best, A.C. Empirical formulae for the terminal velocity of water drops falling through the atmosphere. Q. J. R. Meteorol. Soc. 1950, 76, 302–311. [Google Scholar] [CrossRef]
- Kessler, E.; Wilk, K.E. Radar Measurement of Precipitation for Hydrological Purposes; World Meteorological Organization: Geneva, Switzerland, 1968. [Google Scholar]
- Liu, J.Y.; Orville, H.D. Numerical modeling of precipitation and cloud shadow effects on mountain-induced cumuli. J. Atmos. Sci. 1969, 26, 1283–1298. [Google Scholar] [CrossRef]
- Sekhon, R.S.; Srivastava, R.C. Doppler radar observations of drop-size distributions in a thunderstorm. J. Atmos. Sci. 1971, 28, 983–994. [Google Scholar] [CrossRef]
- Atlas, D.; Ulbrich, C.W. Path-and area-integrated rainfall measurement by microwave attenuation in the 1–3 cm band. J. Appl. Meteorol. Climatol. 1977, 16, 1322–1331. [Google Scholar] [CrossRef]
- Uplinger, W.G. A new formula for raindrop terminal velocity. In Proceedings of the 20th Conference on Radar Meteorology, Boston, MA, USA, 30 November–3 December 1981; pp. 389–391. [Google Scholar]
- Grosh, R.C. Weighted fall speed parameters. In Proceedings of the 26th International Conference on Radar Meteorology, Boston, MA, USA, 24–28 May 1993; pp. 607–610. [Google Scholar]
- Ferro, V. Tecniche di misura e monitoraggio dei processi erosivi. Quad. Idronomia Mont. 2001, 21, 63–128. [Google Scholar]
- Assouline, S.; El Idrissi, A.; Persoons, E. Modelling the physical characteristics of simulated rainfall: A comparison with natural rainfall. J. Hydrol. 1997, 196, 336–347. [Google Scholar] [CrossRef]
- Wolfs, J.L. Contribution à L’étude de L’erosion par Simulation de Pluie. MSc Thesis, University Catholique de Louvain-La-Nueve, Louvain-la-Neuve, Belgium, 1981. [Google Scholar]
- Pruppacher, H.R.; Pitter, R.L. A semi-empirical determination of the shape of cloud and rain drops. J. Atmos. Sci. 1971, 28, 86–94. [Google Scholar] [CrossRef]
- Serio, M.A.; Carollo, F.G.; Ferro, V. A method for evaluating rainfall kinetic power by a characteristic drop diameter. J. Hydrol. 2019, 577, 123996. [Google Scholar] [CrossRef]
- Carollo, F.G.; Ferro, V.; Serio, M.A. Reliability of rainfall kinetic power–intensity relationships. Hydrol. Process. 2017, 31, 1293–1300. [Google Scholar] [CrossRef]
- Carollo, F.G.; Ferro, V.; Serio, M.A. Predicting rainfall erosivity by momentum and kinetic energy in Mediterranean environment. J. Hydrol. 2018, 560, 173–183. [Google Scholar] [CrossRef]
- Carollo, F.G.; Serio, M.A.; Ferro, V.; Cerdà, A. Characterizing rainfall erosivity by kinetic power-Median volume diameter relationship. Catena 2018, 165, 12–21. [Google Scholar] [CrossRef]


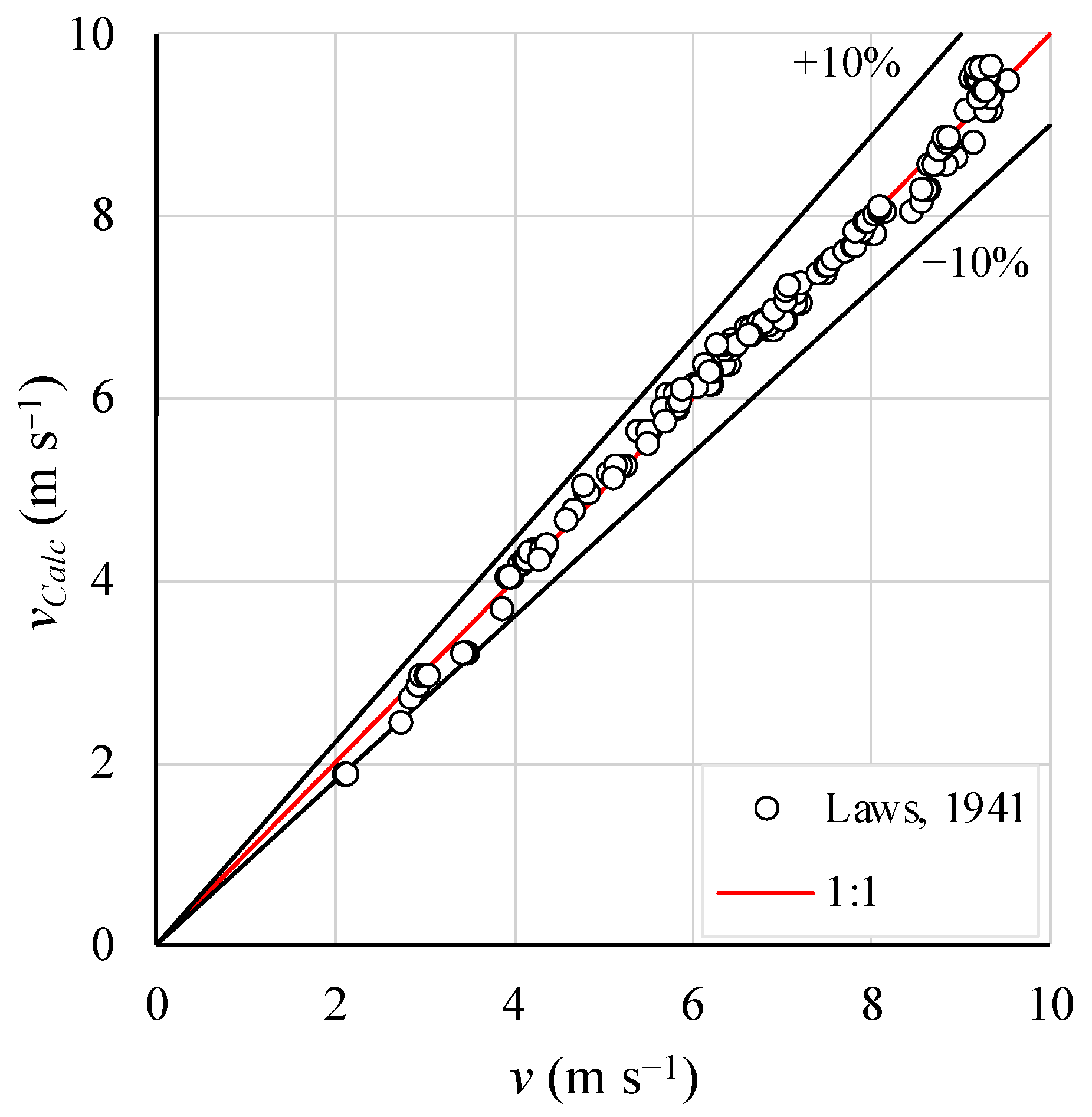
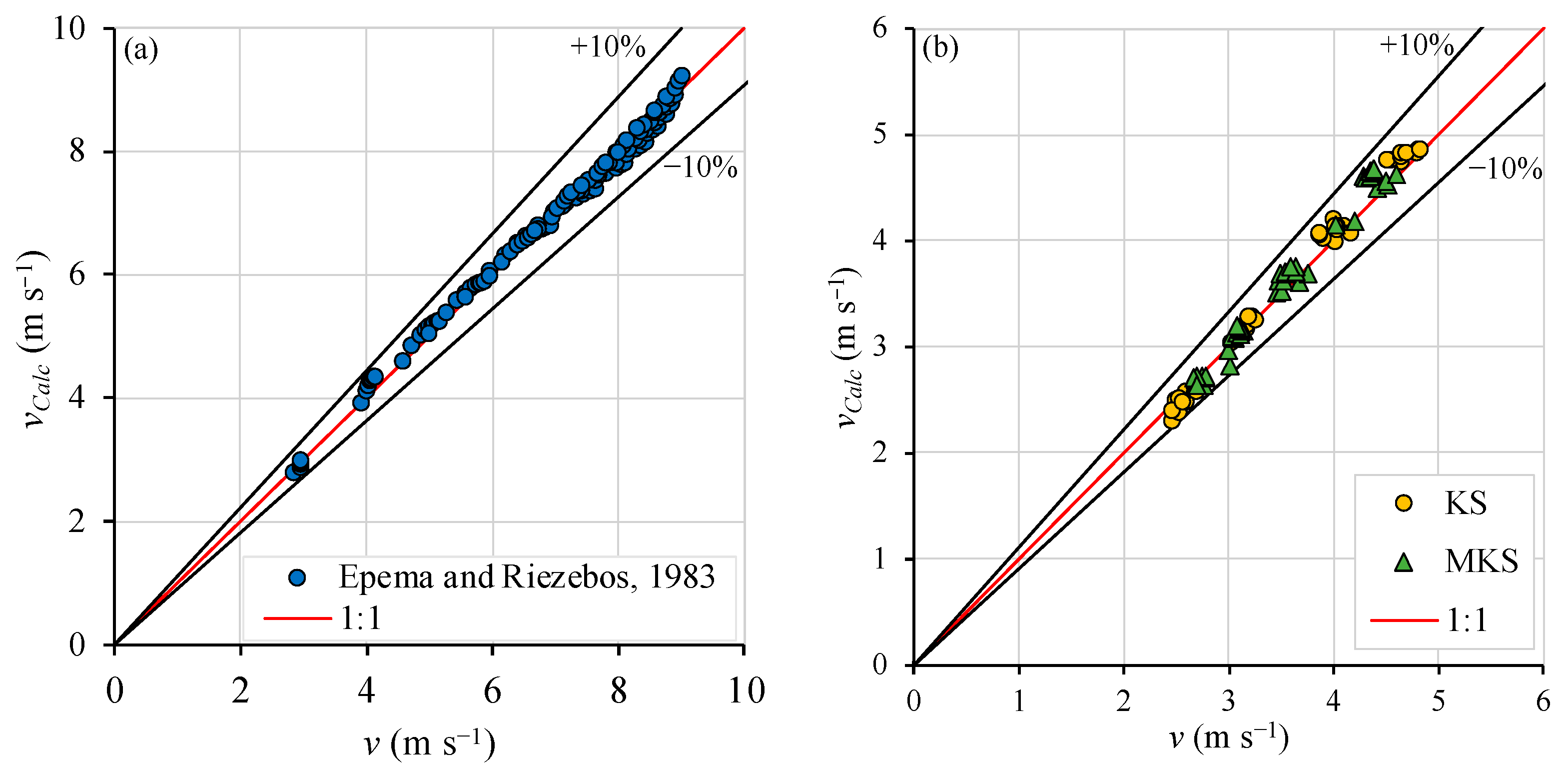
| Laws [30] | Epema and Riezebos [33] | KS | MKS | |
|---|---|---|---|---|
| Mean relative error [%] | 0.21 | −0.32 | −0.58 | −1.73 |
| Mean absolute error [%] | 2.10 | 1.78 | 2.43 | 3.02 |
| Measurements with absolute error ≤ 10% [%] | 98.04 | 100.00 | 100.00 | 100.00 |
| Coefficient of determination [R2] | 0.9994 | 0.9997 | 0.9993 | 0.9990 |
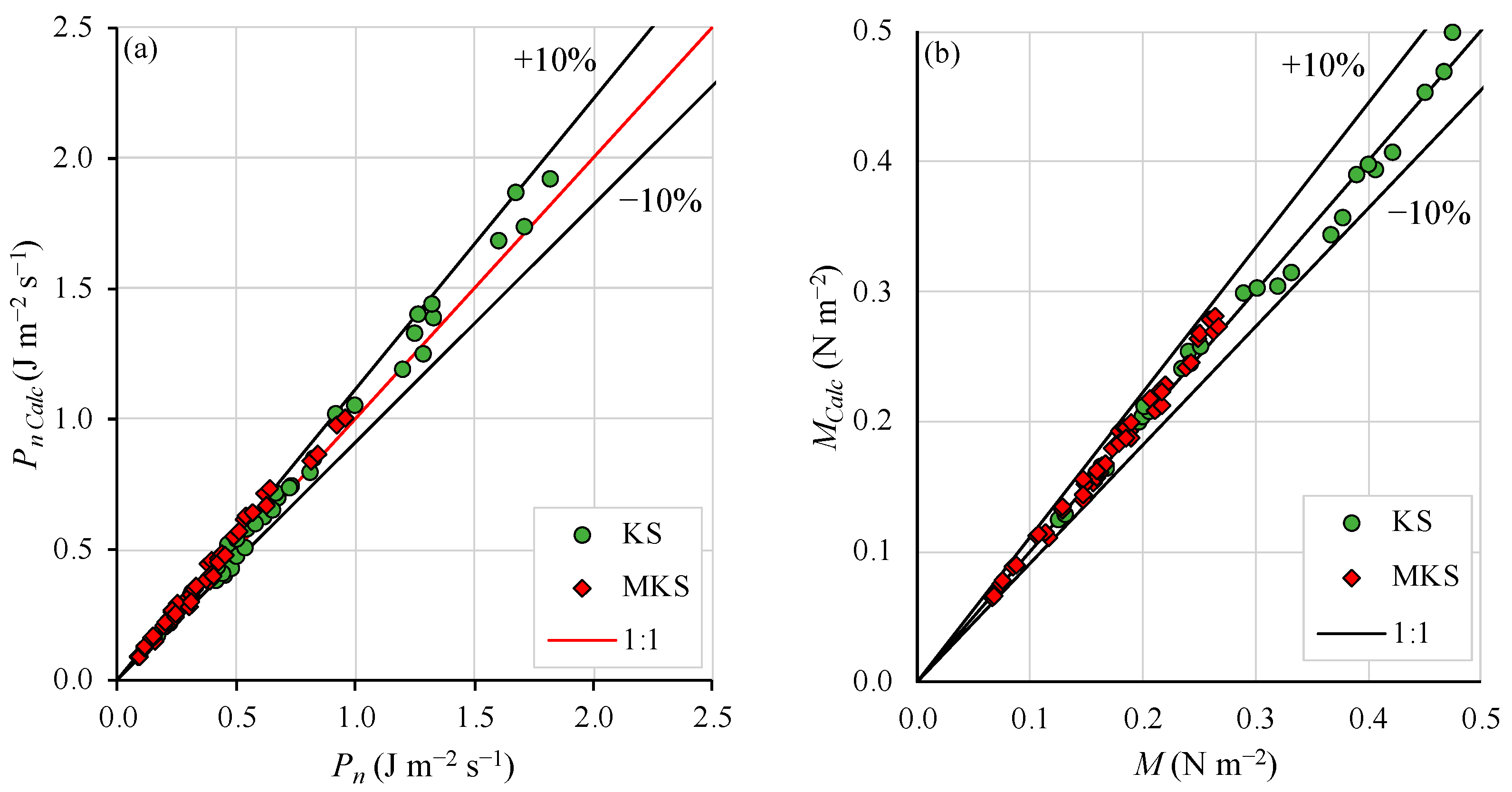
| KS | MKS | |||
|---|---|---|---|---|
| Pn [J m−2 s−1] | M [N m−2] | Pn [J m−2 s−1] | M [N m−2] | |
| Mean relative error [%] | 1.21 | 0.56 | 3.59 | 1.73 |
| Mean absolute error [%] | 4.95 | 2.47 | 6.13 | 3.02 |
| Measurements with absolute errors ≤ 10% [%] | 82.50 | 100.00 | 80.00 | 100.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Serio, M.A.; Carollo, F.G.; Caruso, R.; Ferro, V. Guidelines for the Energetic Characterization of a Portable Drip-Type Rainfall Simulator for Soil Erosion Research. Water 2024, 16, 2100. https://doi.org/10.3390/w16152100
Serio MA, Carollo FG, Caruso R, Ferro V. Guidelines for the Energetic Characterization of a Portable Drip-Type Rainfall Simulator for Soil Erosion Research. Water. 2024; 16(15):2100. https://doi.org/10.3390/w16152100
Chicago/Turabian StyleSerio, Maria Angela, Francesco Giuseppe Carollo, Roberto Caruso, and Vito Ferro. 2024. "Guidelines for the Energetic Characterization of a Portable Drip-Type Rainfall Simulator for Soil Erosion Research" Water 16, no. 15: 2100. https://doi.org/10.3390/w16152100
APA StyleSerio, M. A., Carollo, F. G., Caruso, R., & Ferro, V. (2024). Guidelines for the Energetic Characterization of a Portable Drip-Type Rainfall Simulator for Soil Erosion Research. Water, 16(15), 2100. https://doi.org/10.3390/w16152100








