An Improved Index-Velocity Method for Calculating Discharge in Meandering Rivers
Abstract
:1. Introduction
2. Method
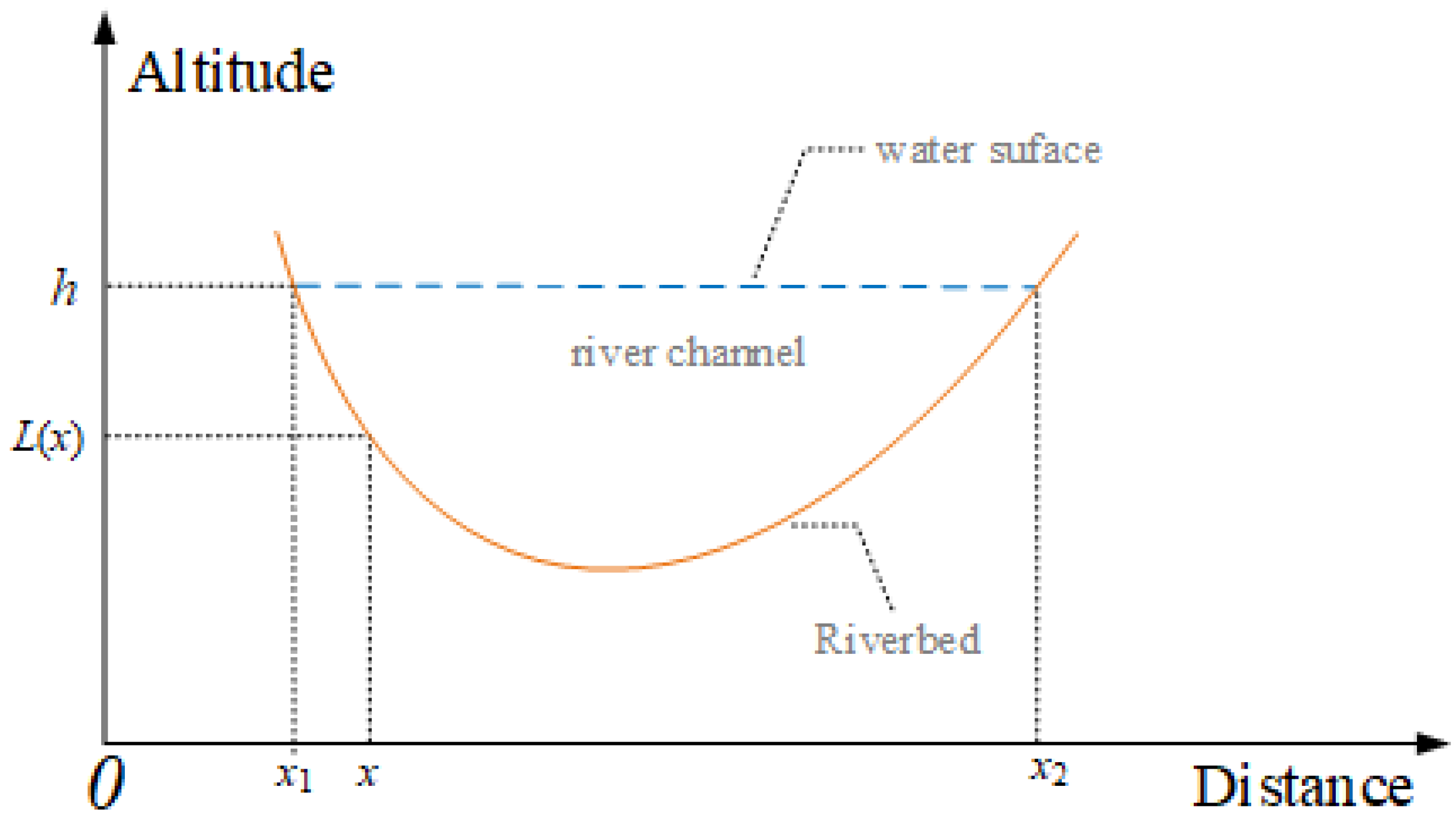
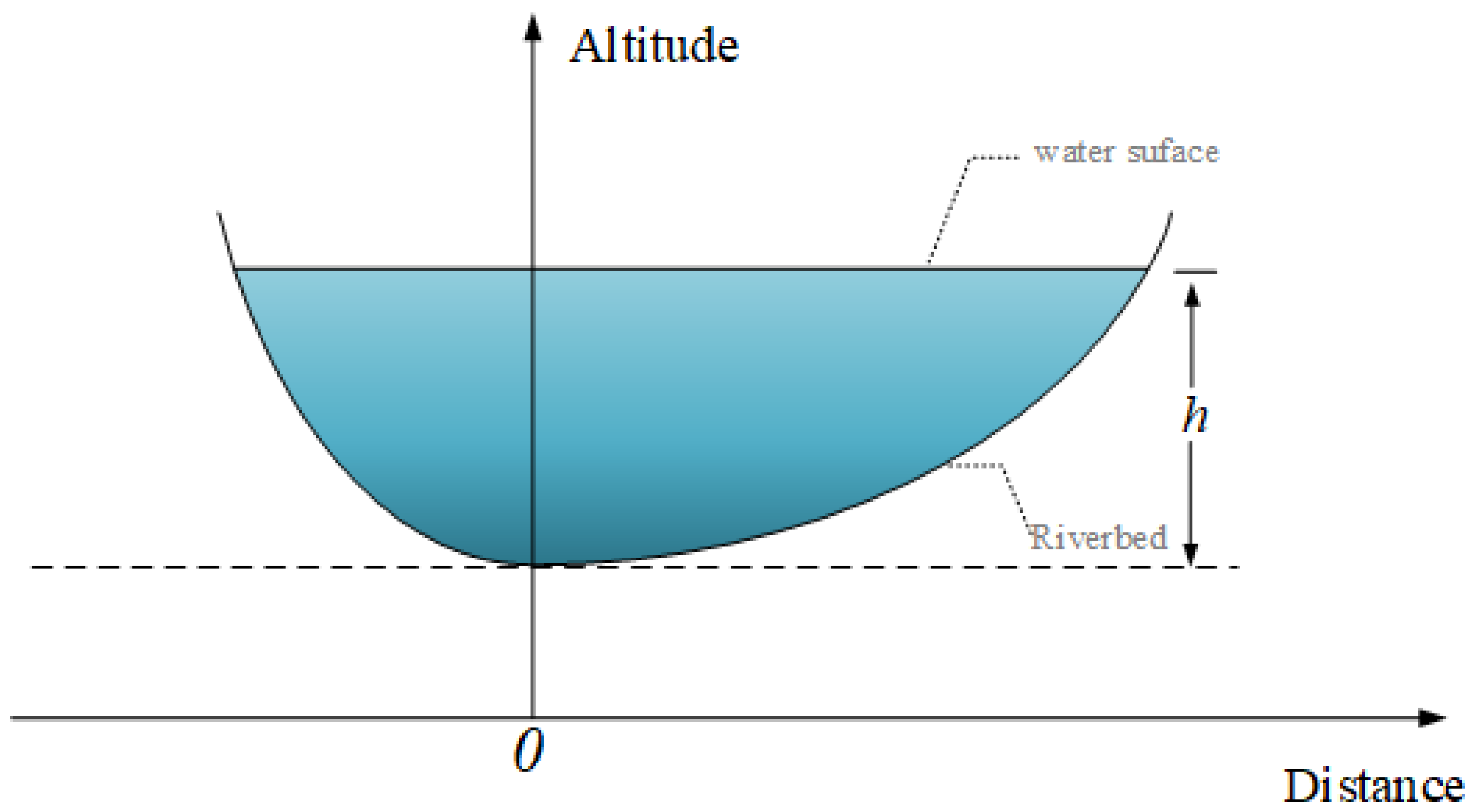
2.1. Previous Index-Velocity Method
2.2. Improved Index-Velocity Method
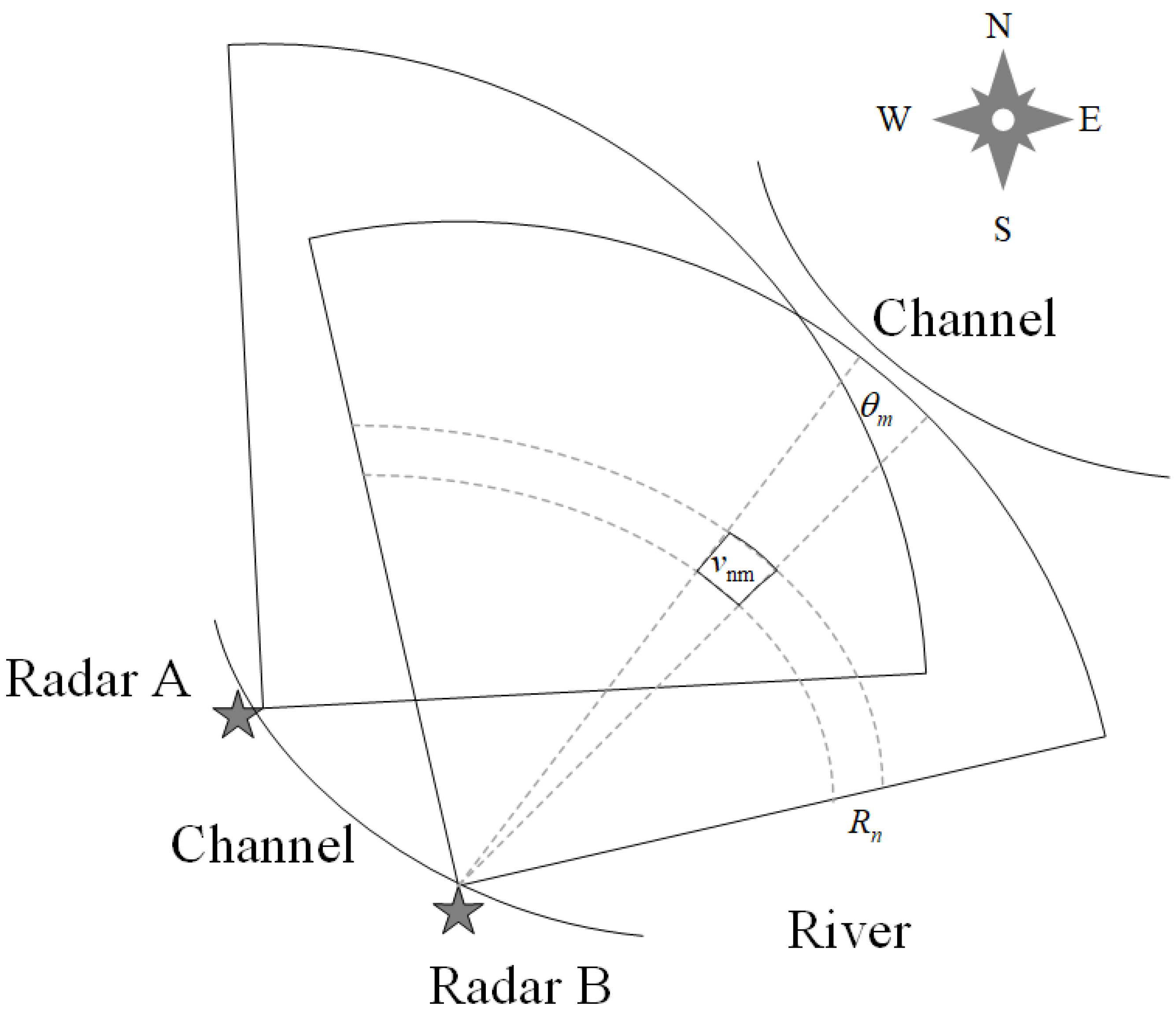
2.3. Selection of Index Velocity
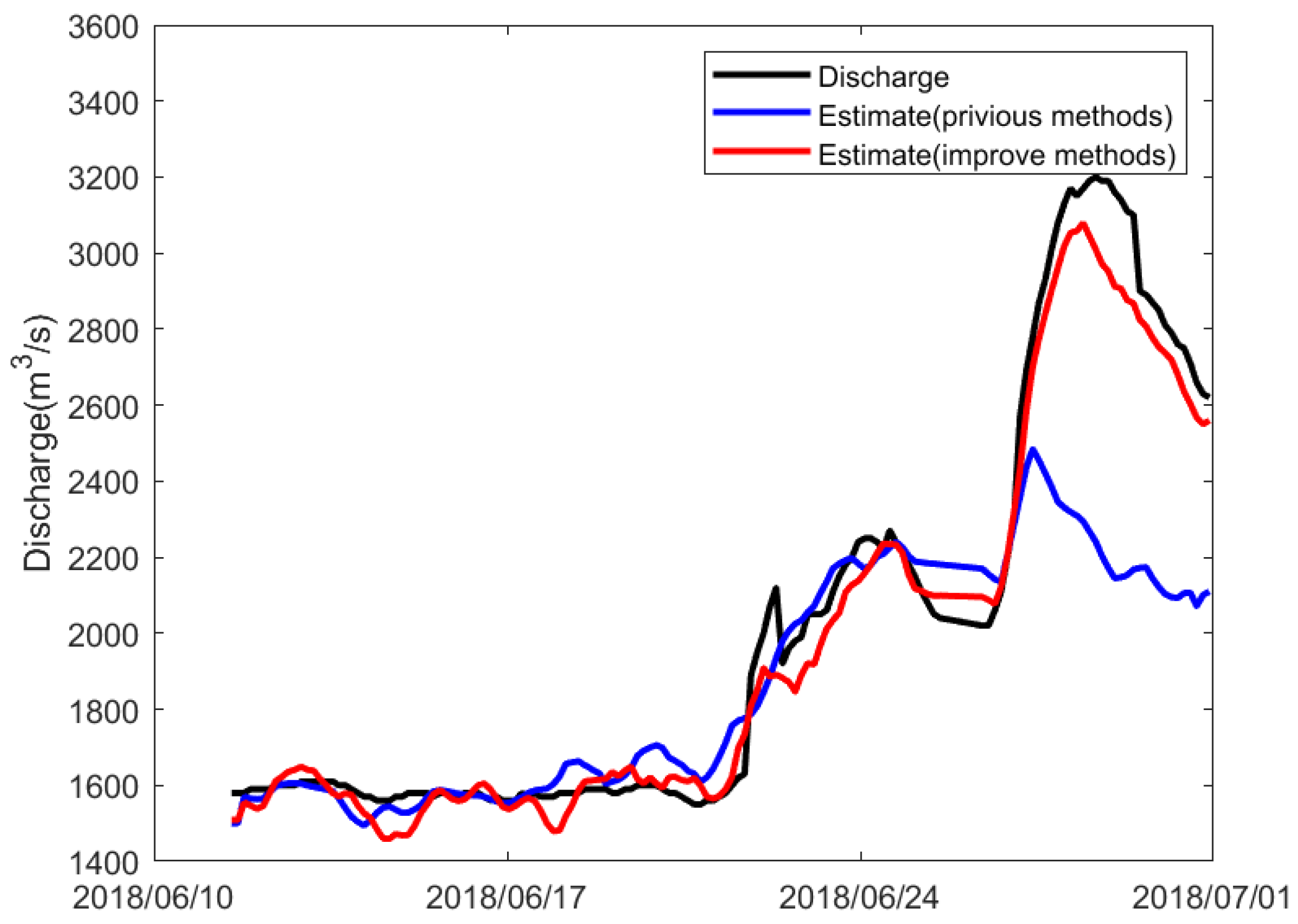
3. Experiment Analysis
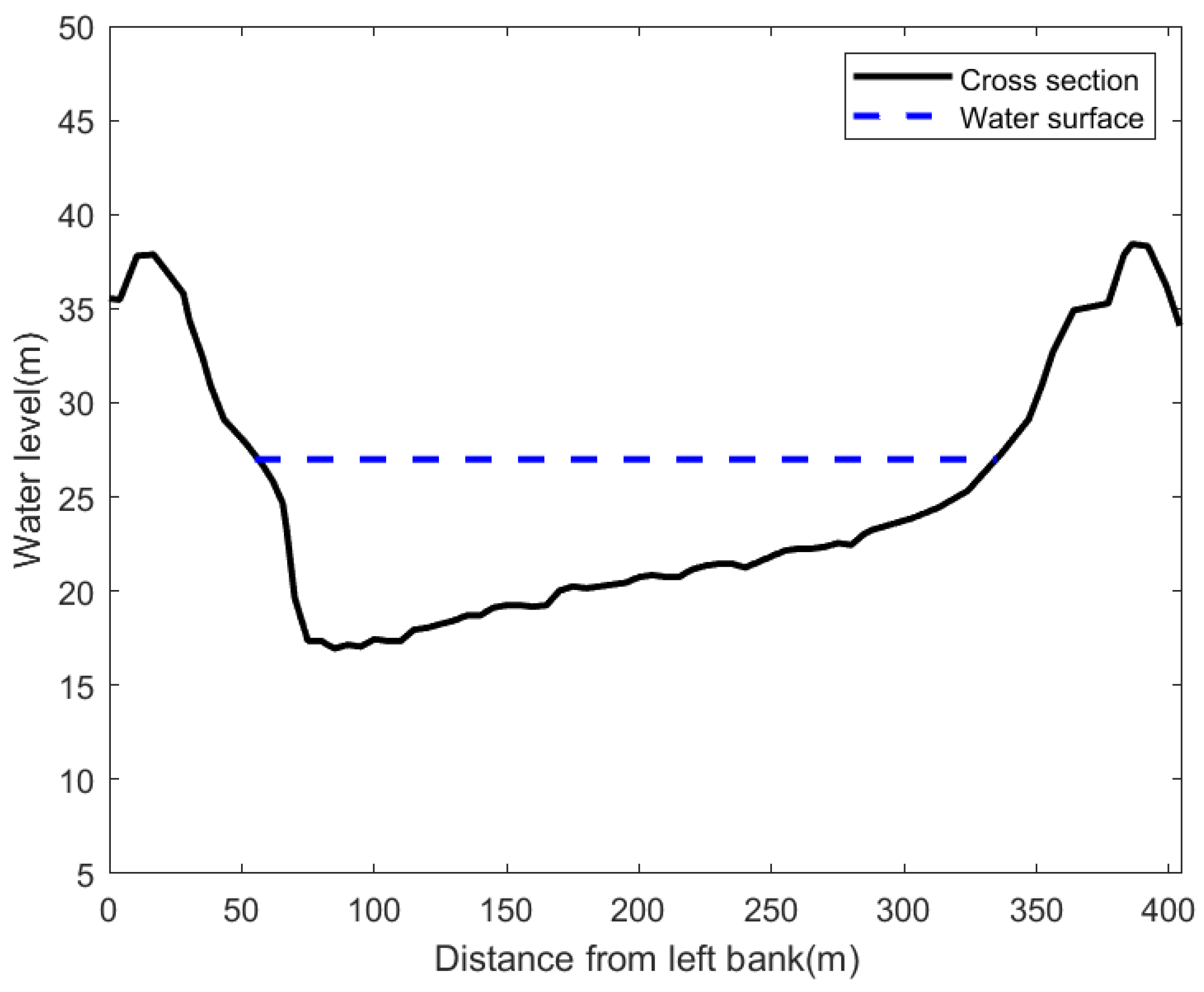
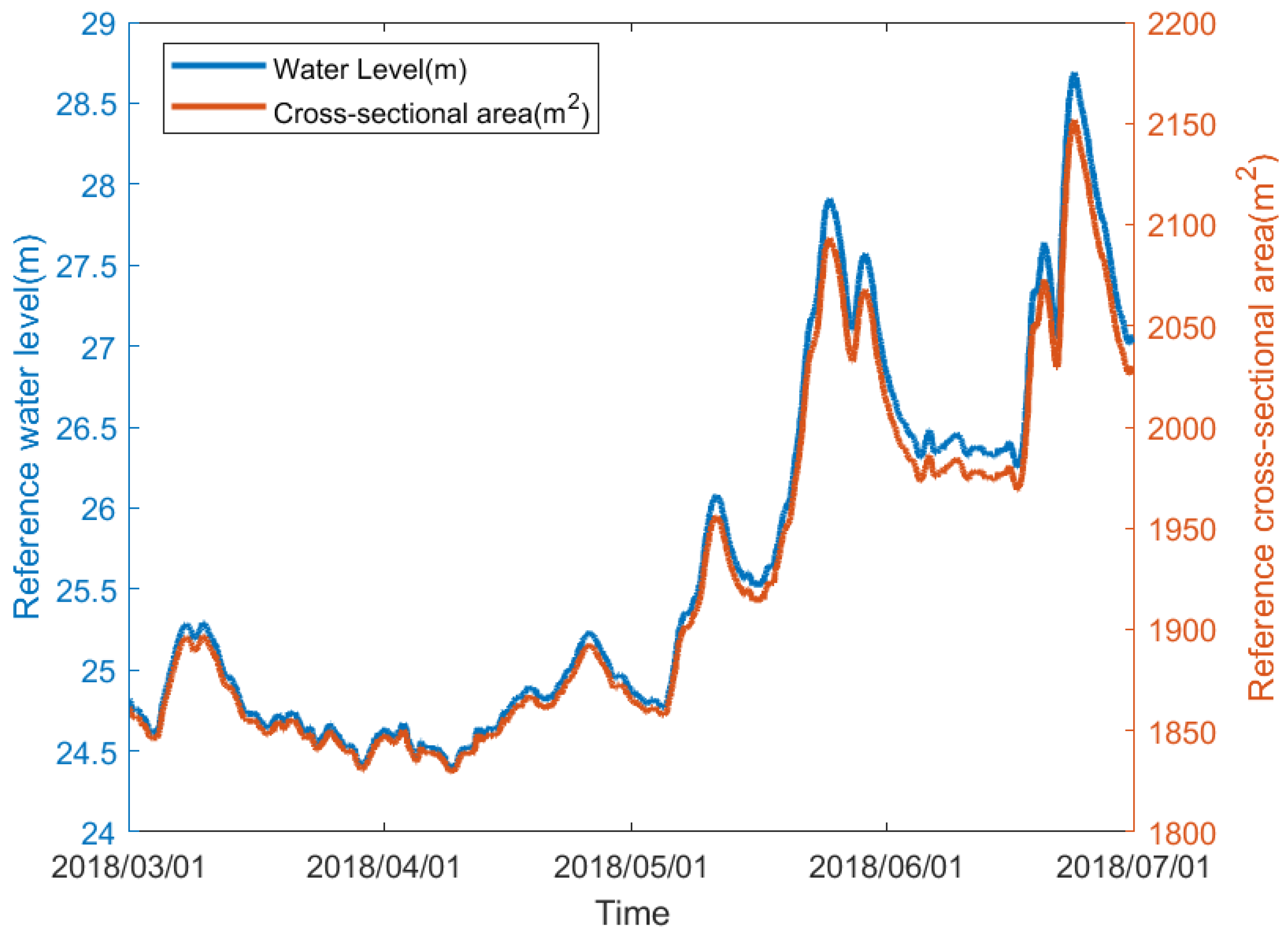
3.1. Experiment Description
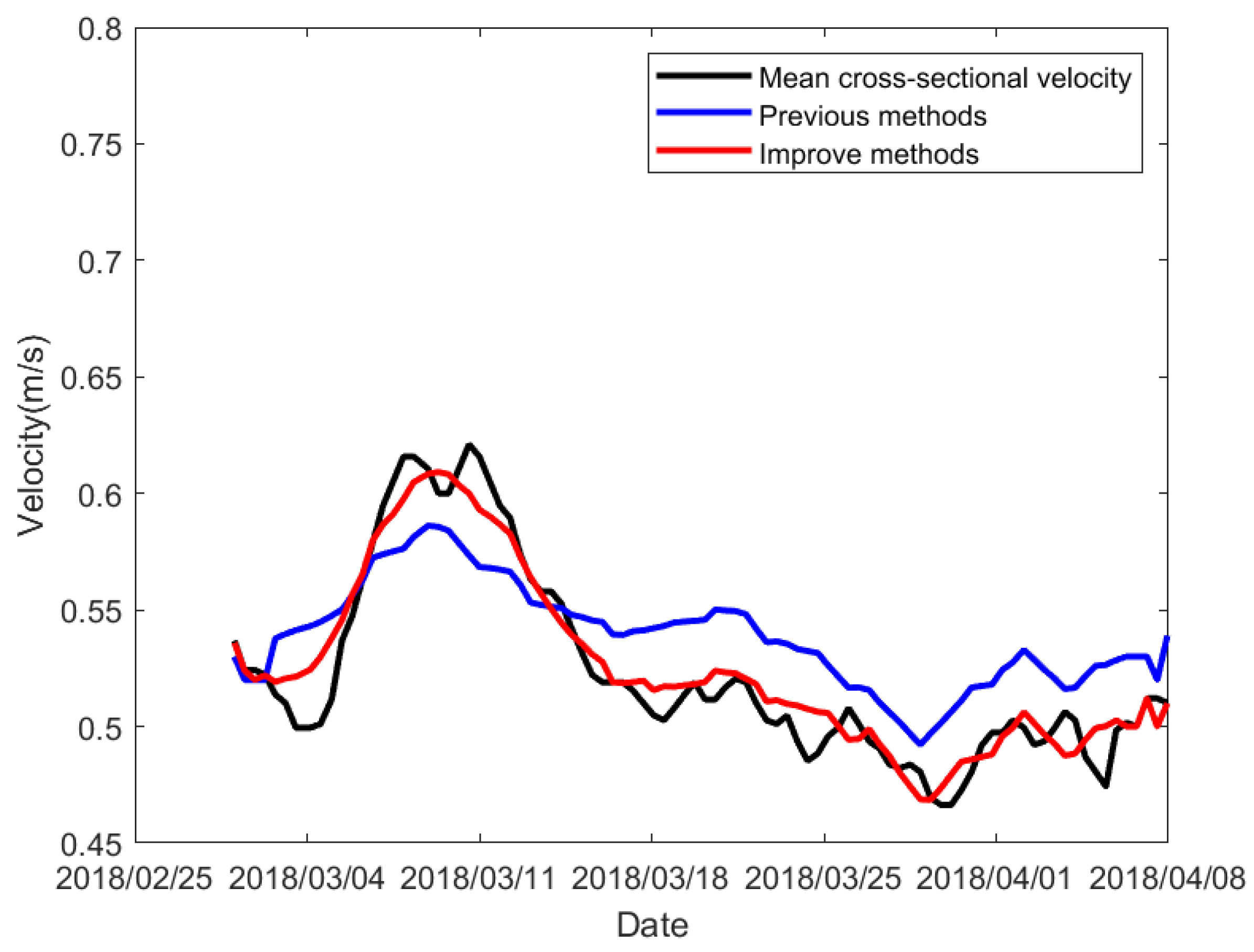
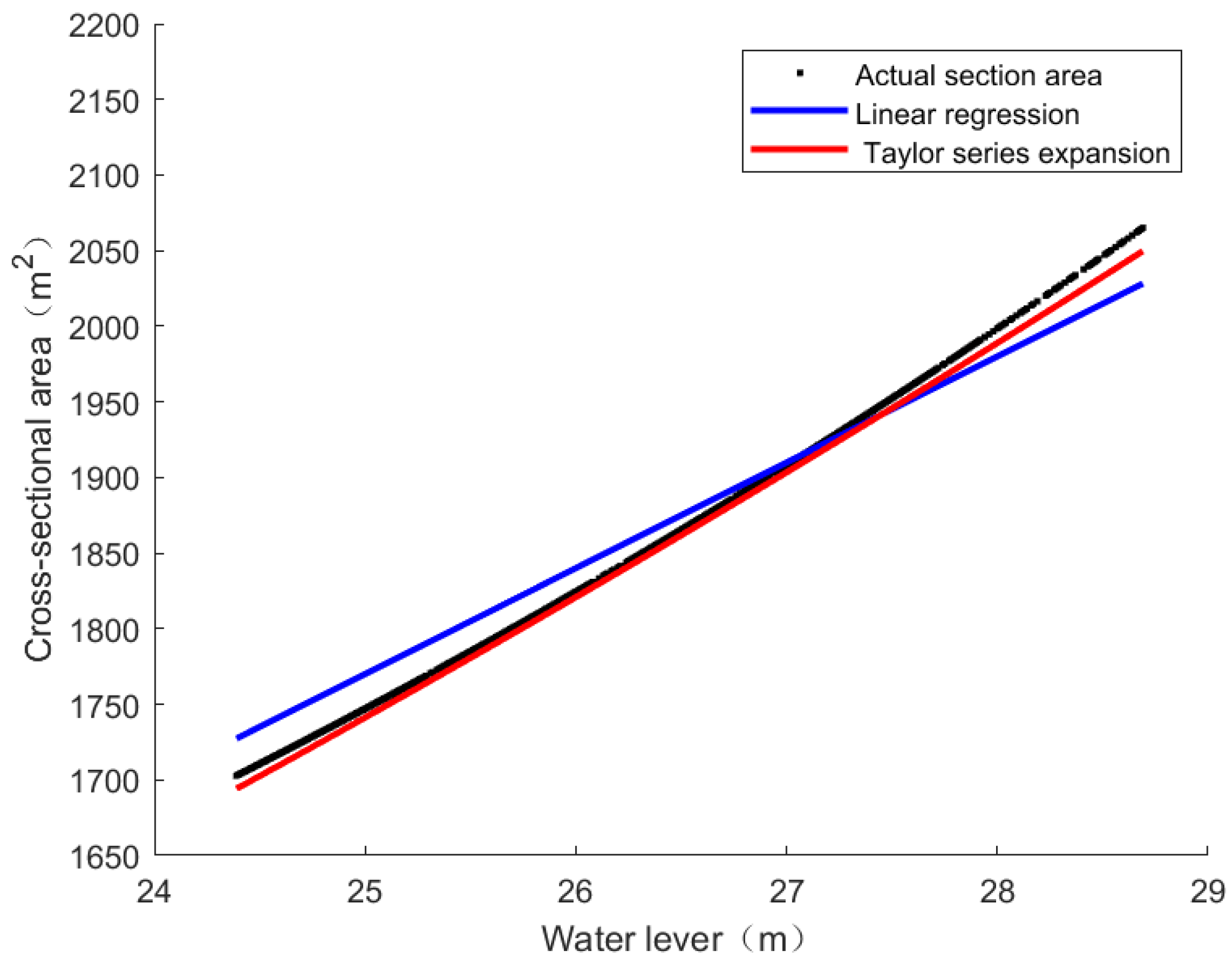
3.2. Cross-Sectional Velocity Model Fitting
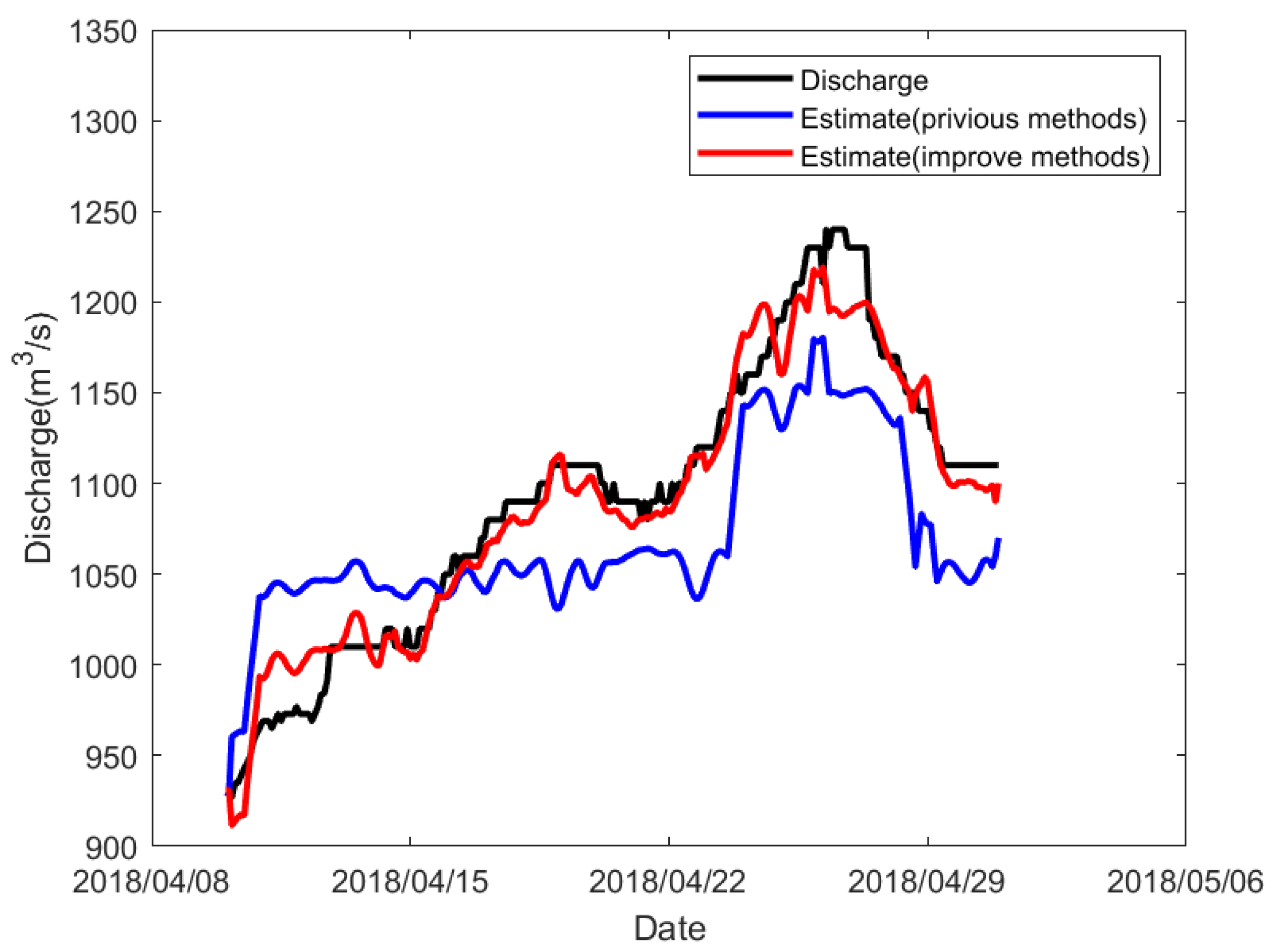
3.3. River Discharge Forecasting
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aguilera, R.; Melack, J.M. Relationships among nutrient and sediment fluxes, hydrological variability, fire, and land cover in coastal California catchments. J. Geophys. Res. Biogeosci. 2018, 123, 2568–2589. [Google Scholar] [CrossRef]
- Allen, G.H.; Pavelsky, T.M. Global extent of rivers and streams. Science 2018, 361, 585–588. [Google Scholar] [CrossRef]
- Haddel, I.; Clark, D.B.; Franssen, W.; Ludwig, F.; Voß, F.; Arnell, N.W.; Bertr, N.; Best, M.; Folwell, S.; Gerten, D.; et al. Multimodel estimate of the global terrestrial water balance: Setup and first results. J. Hydrometeorol. 2011, 12, 869–884. [Google Scholar] [CrossRef]
- Vyas, J.K.; Perumal, M.; Moramarco, T. Non-contact discharge estimation at a river site by using only the maximum surface flow velocity. J. Hydrol. 2024, 638, 131505. [Google Scholar] [CrossRef]
- Fulford, J.M.; Thibodeaux, K.G.; Kaehrle, W.R. Comparison of current meters used for stream gaging. In Proceedings of the Symposium on Fundamentals and Advancements in Hydraulic Measurements and Experimentation, Buffalo, NY, USA, 1–5 August 1994; pp. 376–385. [Google Scholar]
- Vermeulen, B.; Sassi, M.G.; Hoitink, A.J.F. Improved flow velocity estimates from moving-boat ADCP measurements. Water Resour. Res. 2014, 50, 4186–4196. [Google Scholar] [CrossRef]
- Lin, H.; Cheng, X.; Liu, J.; Shi, Q.; Li, T.; Zheng, L.; Hou, X.; Du, J. Estimating river discharge across scales with a novel regional gauging method driven by Sentinel satellite data. Remote Sens. Environ. 2024, 311, 114266. [Google Scholar] [CrossRef]
- Xu, J.; Wang, L.; Yao, T.; Chen, D.; Wang, G.; Jing, Z.; Zhang, F.; Wang, Y.; Li, X.; Zhang, Y.; et al. Totaling river discharge of the third pole from satellite imagery. Remote Sens. Environ. 2024, 308, 114181. [Google Scholar] [CrossRef]
- Sichangi, A.W.; Wang, L.; Yang, K.; Chen, D.; Wang, Z.; Li, X.; Zhou, J.; Liu, W.; Kuria, D. Estimating continental river basin discharges using multiple remote sensing data sets. Remote Sens. Environ. 2016, 179, 36–53. [Google Scholar] [CrossRef]
- Keulegan, G.H. Laws of Turbulent Flow in Open Channels. J. Res. Natl. Bur. Stand. 1938, 21, 707–741. [Google Scholar] [CrossRef]
- Cheng, N.S. Power-Law Index for Velocity Profiles in Open Channel Flows. Adv. Water Resour. 2007, 30, 1775–1784. [Google Scholar] [CrossRef]
- Bonakdari, H.; Larrarte, F.; Lassabatere, L.; Joannis, C. Turbulent Velocity Profile in Fully-Developed Open Channel Flows. Environ. Fluid Mech. 2008, 8, 1–17. [Google Scholar] [CrossRef]
- Coles, D. The Law of the Wake in the Turbulent Boundary Layer. J. Fluid Mech. 1956, 1, 191–226. [Google Scholar] [CrossRef]
- Wang, S.; Wen, B.; Wang, C.; Zhou, Y. UHF Surface Dynamics Parameters Radar Design and Experiment. IEEE Microw. Wirel. Compon. Lett. 2014, 24, 65–67. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Y. Automatic Flow Detection System for Rectangular Channels Based on the Five-Point Method. Chin. Rural Water Hydropower 2014, 5, 115–117. [Google Scholar]
- Sarma, K.V.N.; Lakshminarayana, P.; Rao, N.S.L. Velocity Distribution in Smooth Rectangular Open Channels. J. Hydraul. Eng. 1983, 109, 270–289. [Google Scholar] [CrossRef]
- Levesque, V.A.; Oberg, K.A. Computing Discharge Using the Index Velocity Method; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2012.
- Teague, C.C.; Barrick, D.E.; Lilleboe, P.M.; Cheng, R.T.; Ruhl, C.A. UHF RiverSonde observations of water surface velocity at Threemile Slough, California. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Seoul, Republic of Korea, 29 July 2005; Volume 50, pp. 4186–4196. [Google Scholar]
- Fulton, J.W.; Mason, C.A.; Eggleston, J.R.; Nicotra, M.J.; Chiu, C.L.; Henneberg, M.F.; Best, H.R.; Cederberg, J.R.; Holnbeck, S.R.; Lotspeich, R.R.; et al. Near-field remote sensing of surface velocity and river discharge using radars and the probability concept at 10 US geological survey streamgages. Remote Sens. 2022, 12, 1296. [Google Scholar] [CrossRef]
- Alimenti, F.; Bonafoni, S.; Gallo, E.; Palazzi, V.; Gatti, R.V.; Mezzanotte, P.; Roselli, L.; Zito, D.; Barbetta, S.; Corradini, C.; et al. Noncontact Measurement of River Surface Velocity and Discharge Estimation With a Low-Cost Doppler Radar Sensor. IEEE Trans. Geosci. Remote Sens. 2022, 58, 5195–5207. [Google Scholar] [CrossRef]
- Qiu, J.; Long, K.; Du, Y.; Xie, H.; Wei, Z.; Shangguan, W.; Dai, Y. A hybrid deep learning algorithm and its application to streamflow prediction. J. Hydrol. 2021, 601, 126636. [Google Scholar]
- Alizadeh, F.; Gharamaleki, A.F.; Jalilzadeh, R. A two-stage multiple-point conceptual model to predict river stage-discharge process using machine learning approaches. J. Water Clim. Chang. 2021, 12, 278–295. [Google Scholar] [CrossRef]
- Difi, S.; Elmeddahi, Y.; Hebal, A.; Singh, V.P.; Heddam, S.; Kim, S.; Kisi, O. Monthly streamflow prediction using hybrid extreme learning machine optimized by bat algorithm: A case study of Cheliff watershed, Algeria. Hydrol. Sci. J. 2022, 68, 189–208. [Google Scholar] [CrossRef]
- Shabbir, M.; Chand, S.; Iqbal, F. A novel hybrid method for river discharge prediction. Water Resour. Manag. 2022, 36, 253–272. [Google Scholar] [CrossRef]
- Mutschler, M.A.; Scharf, P.A.; Rippl, P.; Gessler, T.; Walter, T.; Waldschmidt, C. River Surface Analysis and Characterization Using FMCW Radar. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 2493–2502. [Google Scholar] [CrossRef]
- Le Coz, J.; Camenen, B.; Peyrard, X.; Dramais, G. Uncertainty in open-channel discharges measured with the velocity–area method. Flow Meas. Instrum. 2012, 26, 18–29. [Google Scholar] [CrossRef]
- Ruhl, C.A.; Simpson, M.R. Computation of Discharge Using the Index-Velocity Method in Tidally Affected Areas; US Department of the Interior, US Geological Survey: Denver, CO, USA, 2005.
- Morse, B.; Hamai, K.; Choquette, Y. River discharge measurement using the velocity index method. In Proceedings of the 13th CRIPE Workshop on the Hydraulics of Ice Covered Rivers, Hanover, NH, USA, 15–16 June 2005. [Google Scholar]
- Yang, Y.; Wen, B.; Wang, C.; Hou, Y. Real-Time and Automatic River Discharge Measurement With UHF Radar. IEEE Geosci. Remote Sens. Lett. 2022, 17, 1851–1855. [Google Scholar] [CrossRef]
- Liu, C.; Wen, B.; Duan, Z.; Tian, Y. Measurement of Mountain River Discharge Based on UHF Radar. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Ma, M.; Li, G.; Ning, J. Large-Eddy Simulation of Hydrodynamic Structure in a Strongly Curved Bank. Appl. Sci. 2022, 12, 11883. [Google Scholar] [CrossRef]
- Sy, E. River Water Surface Velocity Measurement Using Large-Scale Particle Image Velocimetry. 2024. Available online: https://mspace.lib.umanitoba.ca/items/3aea13aa-8be1-487f-bf28-e9c67f457b69 (accessed on 21 July 2024).
- Zhang, E.; Li, L.; Huang, W.; Jia, Y.; Zhang, M.; Kang, F.; Da, H. Measuring Velocity and Discharge of High Turbidity Rivers Using an Improved Near-Field Remote-Sensing Measurement System. Water 2024, 16, 135. [Google Scholar] [CrossRef]



| Operating Frequency | Value |
|---|---|
| Operating frequency f (MHz) | 340 |
| Sweep bandwidth B (MHz) | 15 |
| Sweep width (ms) | 41 |
| Sweep period T (ms) | 40 |
| Maximum detection range (m) | 500 |
| Range resolution (m) | 10 |
| Maximum detection speed (m/s) | 5.489 |
| Speed resolution (m/s) | 0.0214 |
| Time | Dry Season | Wet Season | ||
|---|---|---|---|---|
| Method | Previous | Improve | Previous | Improve |
| MAE | 0.0331 | 0.0094 | 0.0546 | 0.0355 |
| RMSE | 0.0251 | 0.0124 | 0.0762 | 0.0359 |
| NSE | 0.5902 | 0.9228 | 0.8578 | 0.9555 |
| Time | Dry Season | Wet Season | ||
|---|---|---|---|---|
| Method | Previous | Improve | Previous | Improve |
| CC | 0.8280 | 0.9523 | 0.9333 | 0.9908 |
| RMSE | 48.1057 | 23.0383 | 140.62 | 65.4929 |
| MAPE | 0.0473 | 0.0232 | 0.0729 | 0.0391 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, K.; Li, Z. An Improved Index-Velocity Method for Calculating Discharge in Meandering Rivers. Water 2024, 16, 2361. https://doi.org/10.3390/w16172361
Liang K, Li Z. An Improved Index-Velocity Method for Calculating Discharge in Meandering Rivers. Water. 2024; 16(17):2361. https://doi.org/10.3390/w16172361
Chicago/Turabian StyleLiang, Kaiyan, and Zili Li. 2024. "An Improved Index-Velocity Method for Calculating Discharge in Meandering Rivers" Water 16, no. 17: 2361. https://doi.org/10.3390/w16172361
APA StyleLiang, K., & Li, Z. (2024). An Improved Index-Velocity Method for Calculating Discharge in Meandering Rivers. Water, 16(17), 2361. https://doi.org/10.3390/w16172361







