Characteristics of Transient Flow in Rapidly Filled Closed Pipeline
Abstract
:1. Introduction
2. Materials Methods
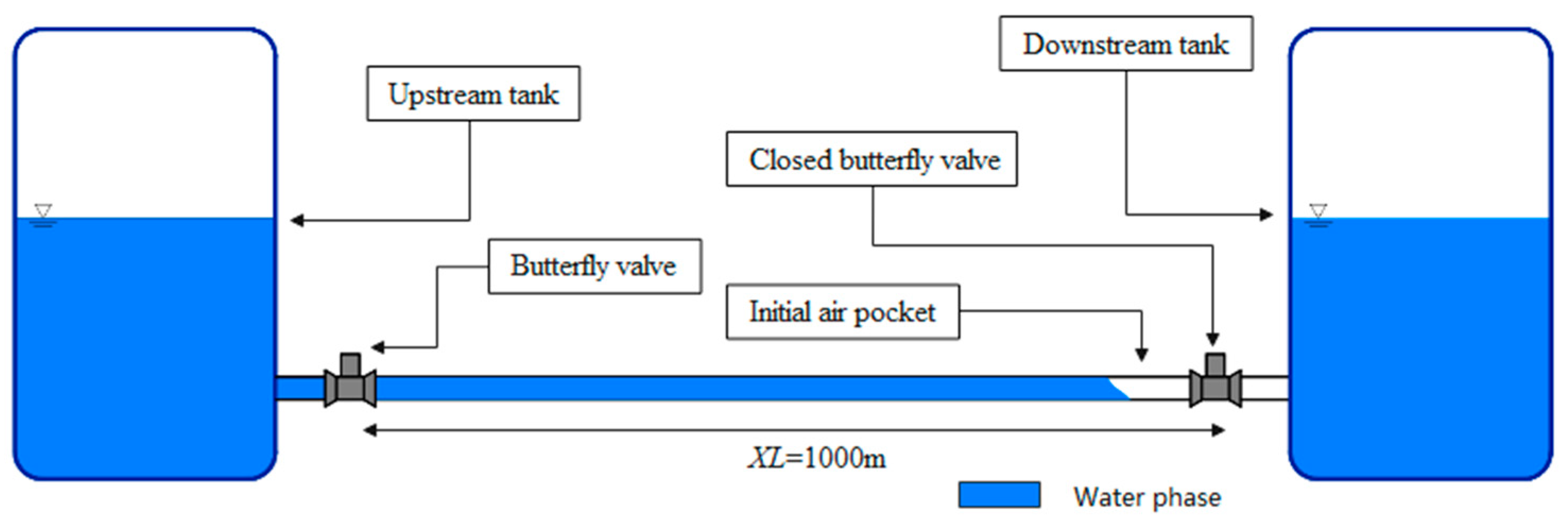
2.1. Rigid Model
2.2. Polynomial Fitting Principle
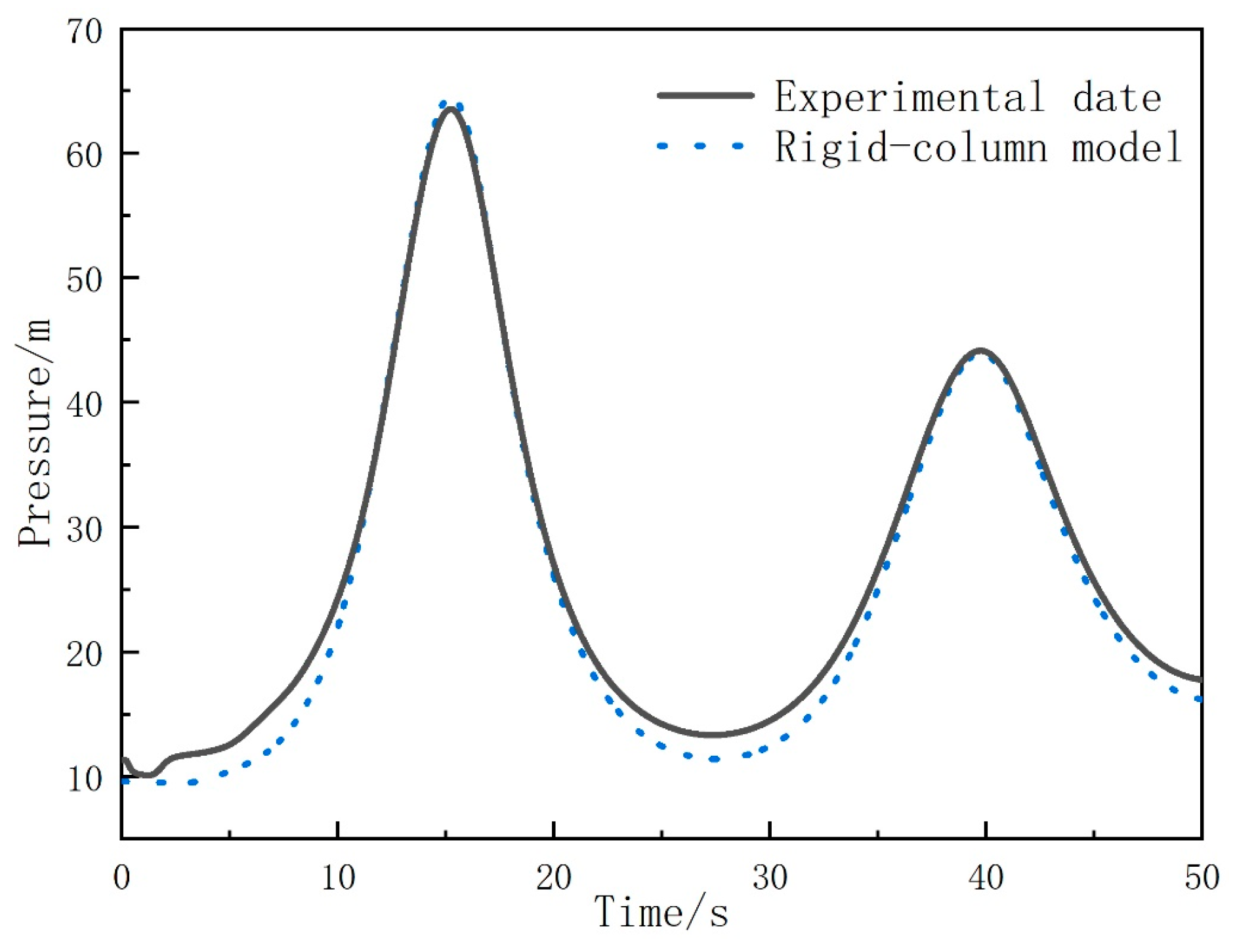
2.3. Mathematical Model Validation
3. Results and Discussion
3.1. Multivariable Analysis of Closed Pipeline Filling
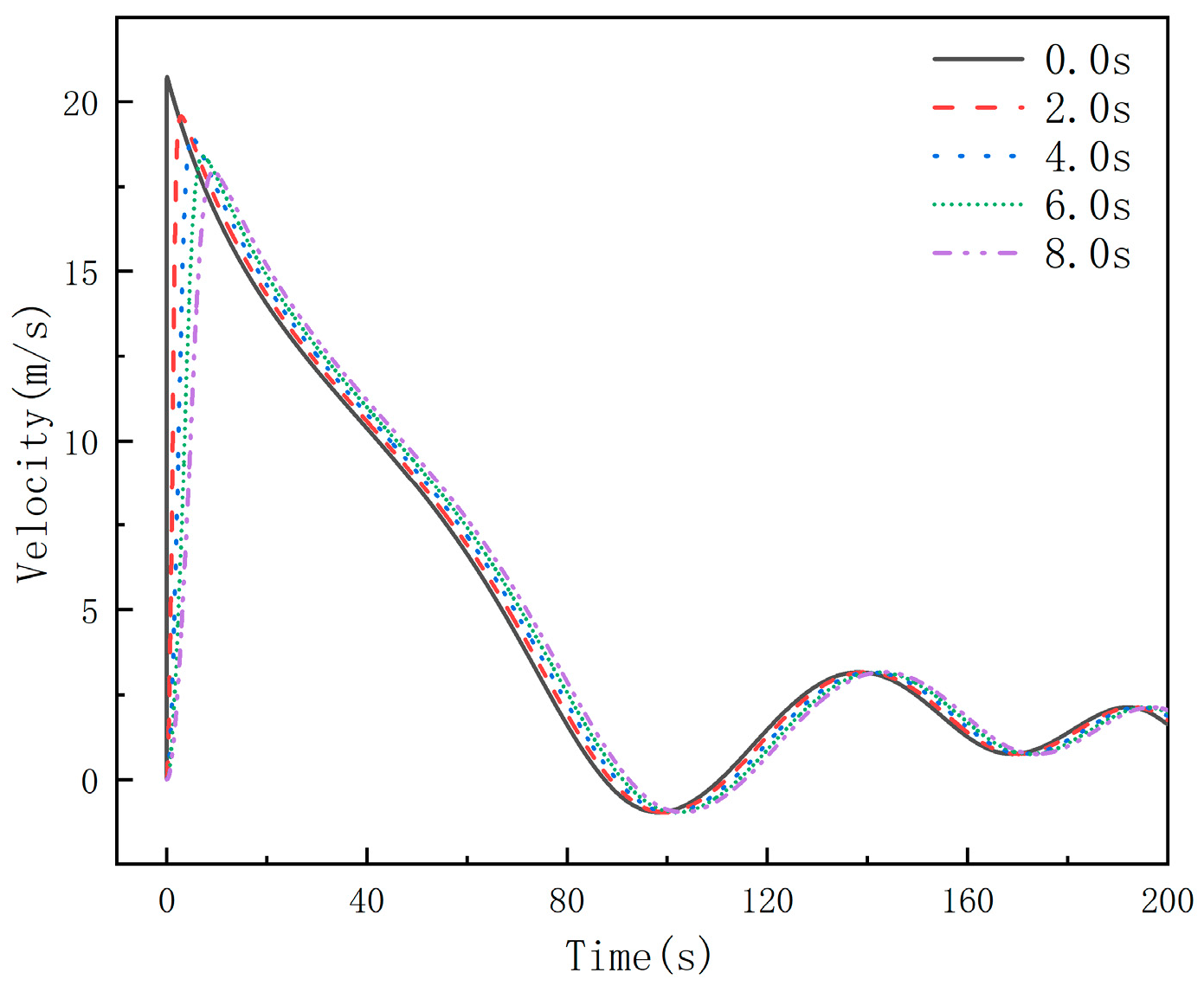
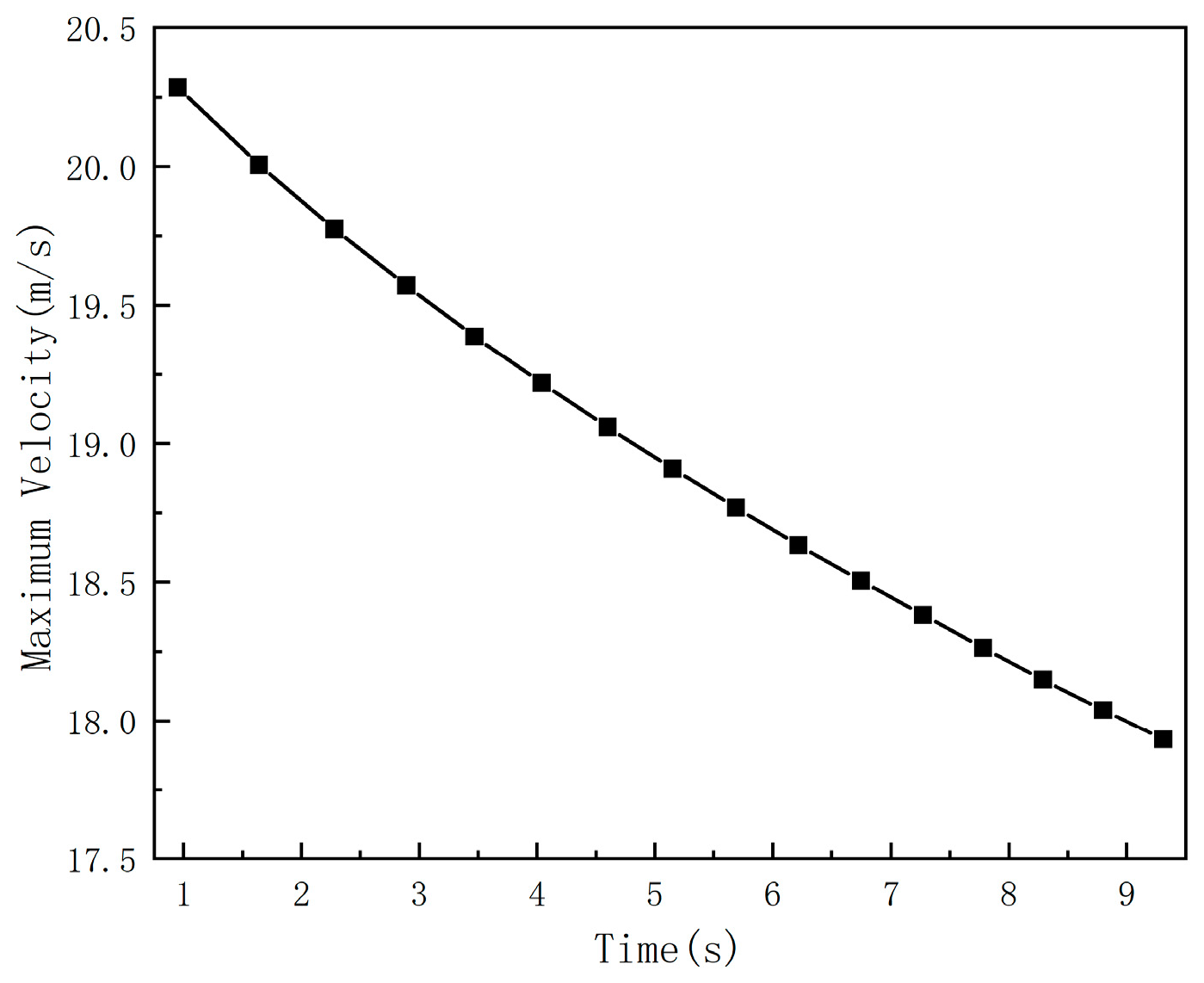
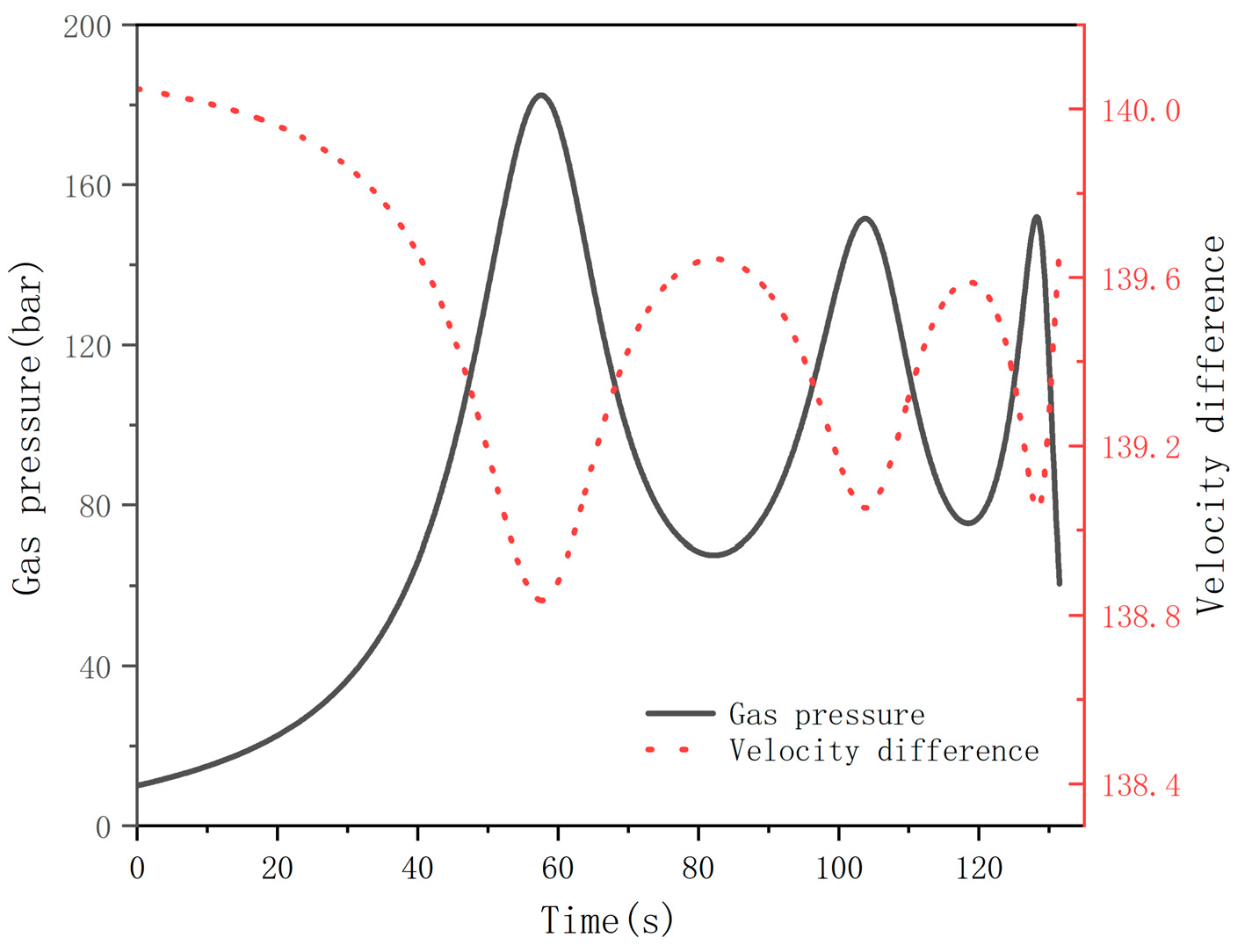
3.2. Analysis of the Impact of Valve-Opening Time
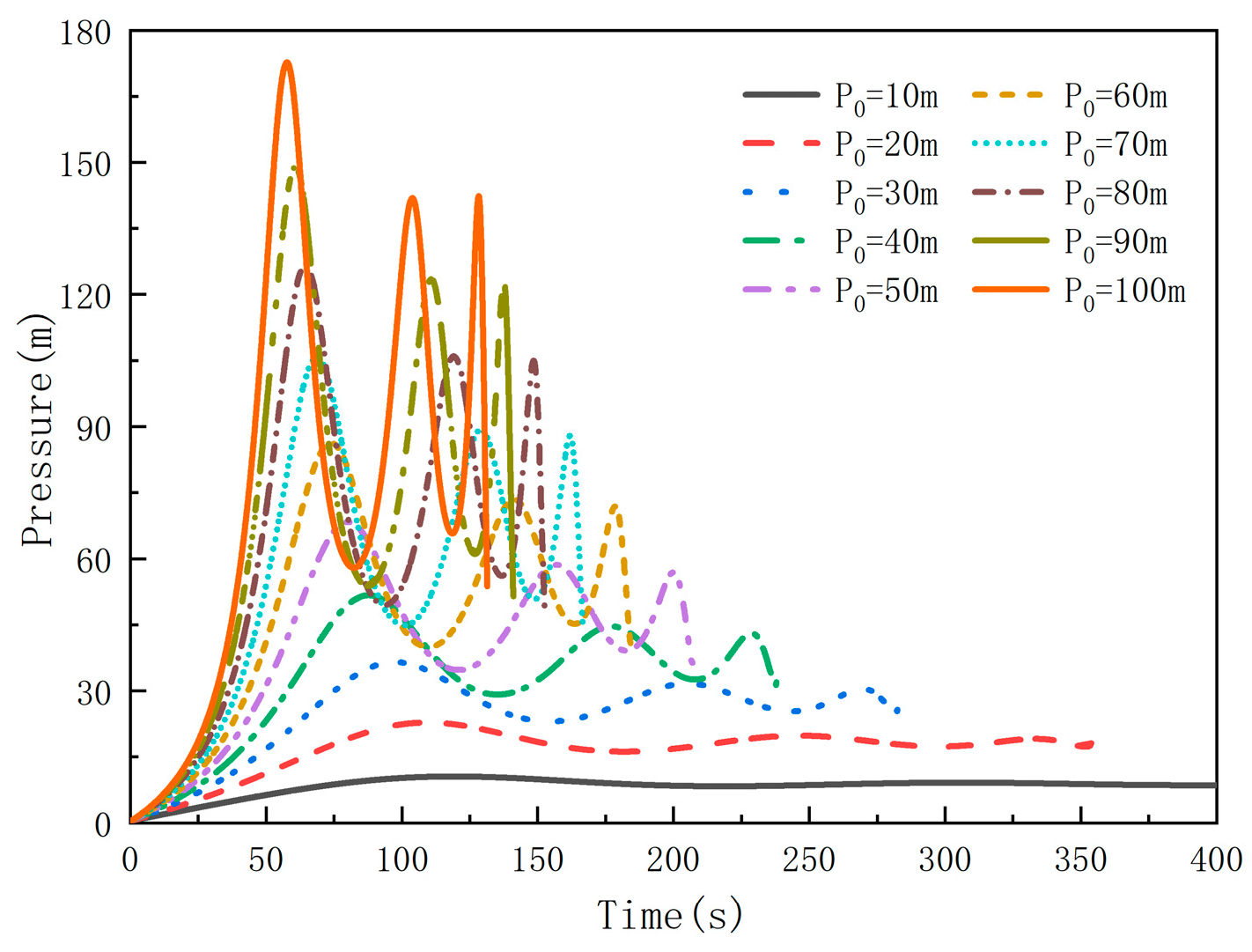
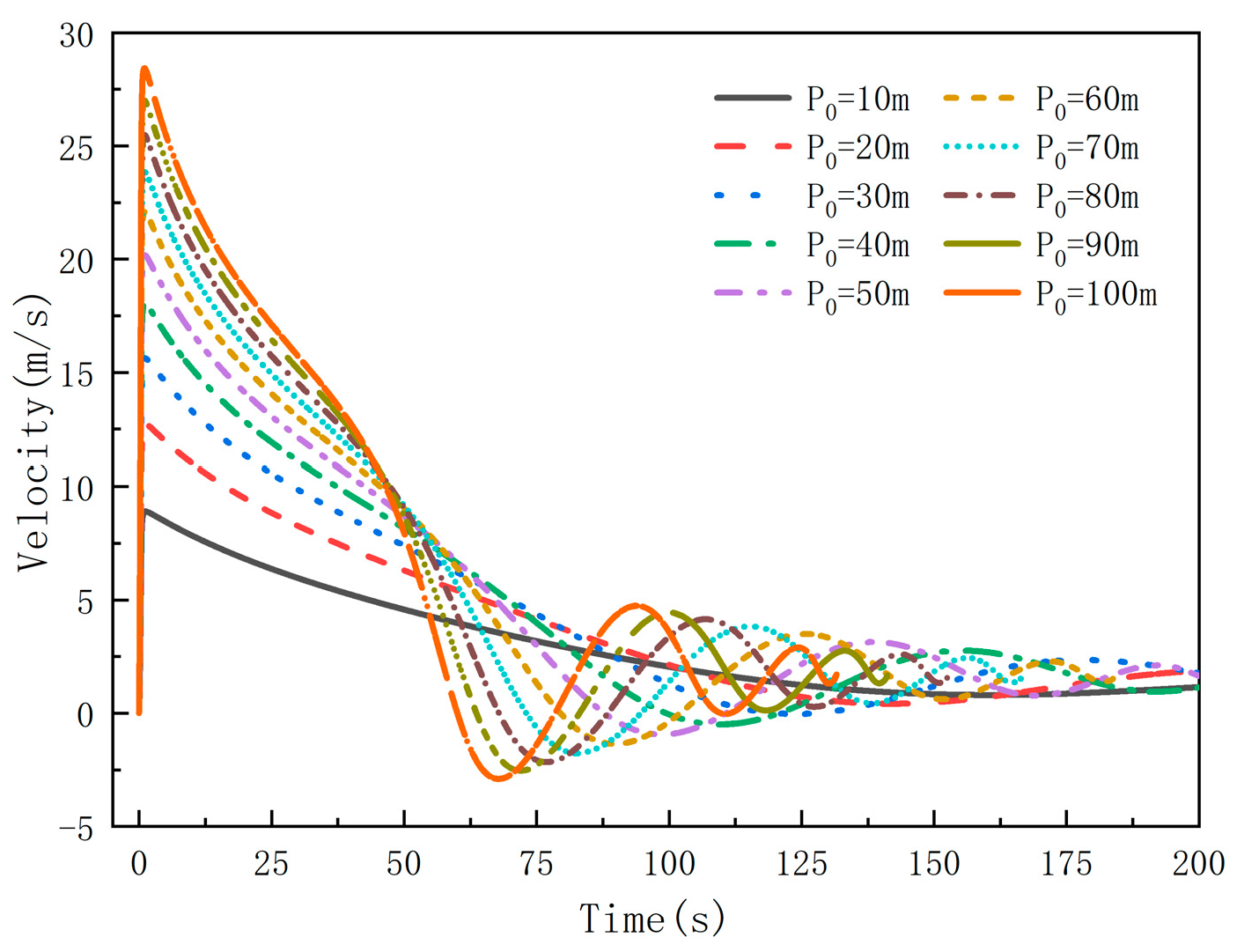
3.3. Analysis of the Influence of Water Head on Performance
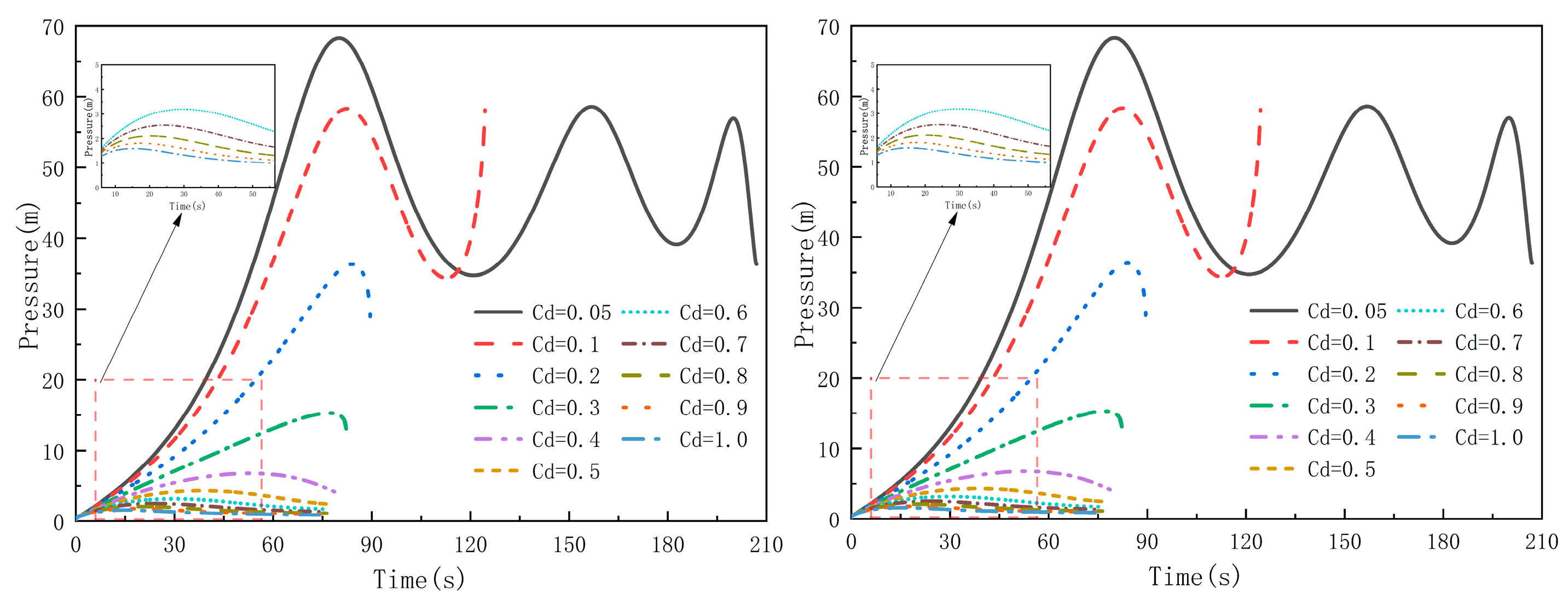
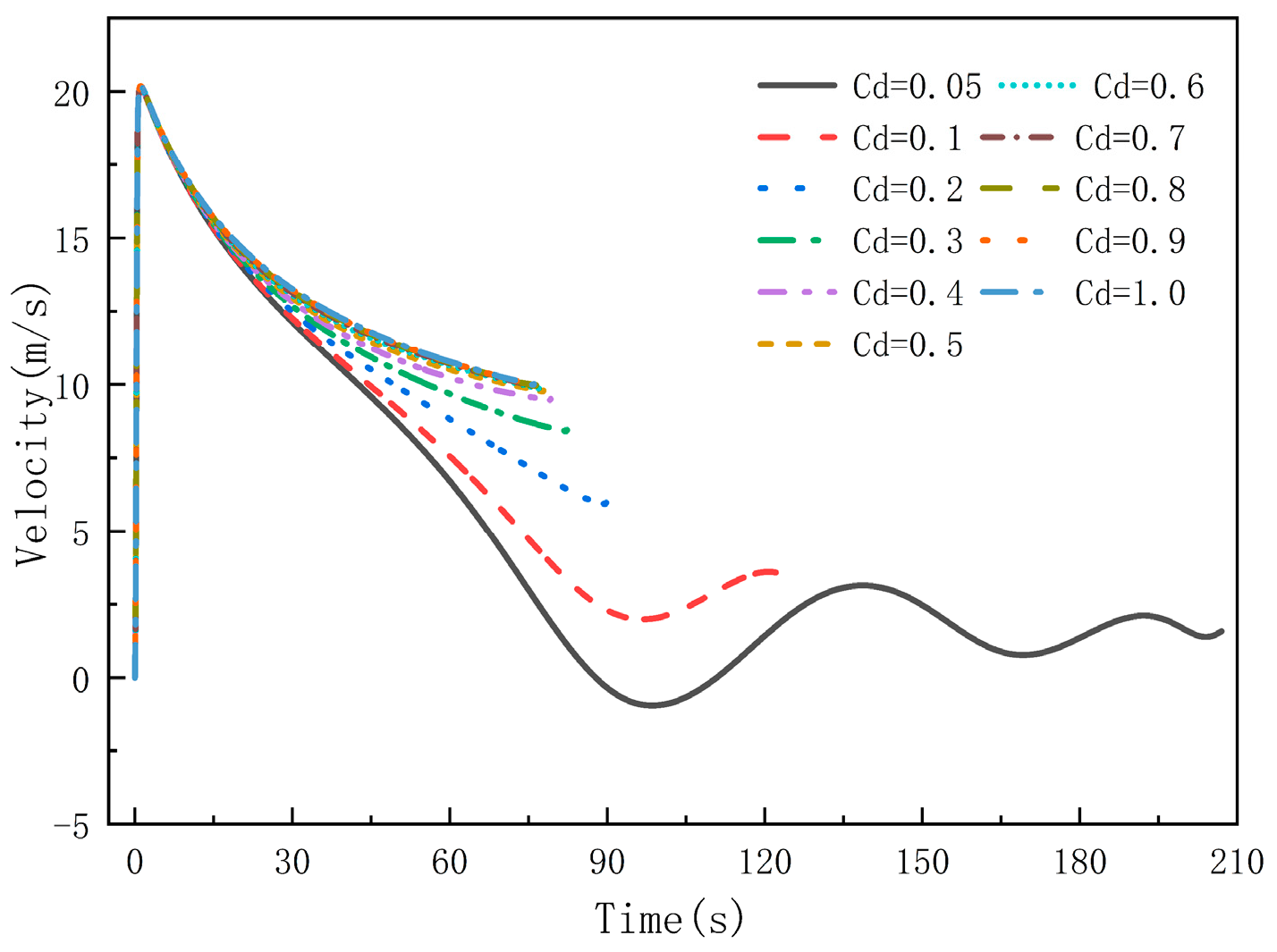
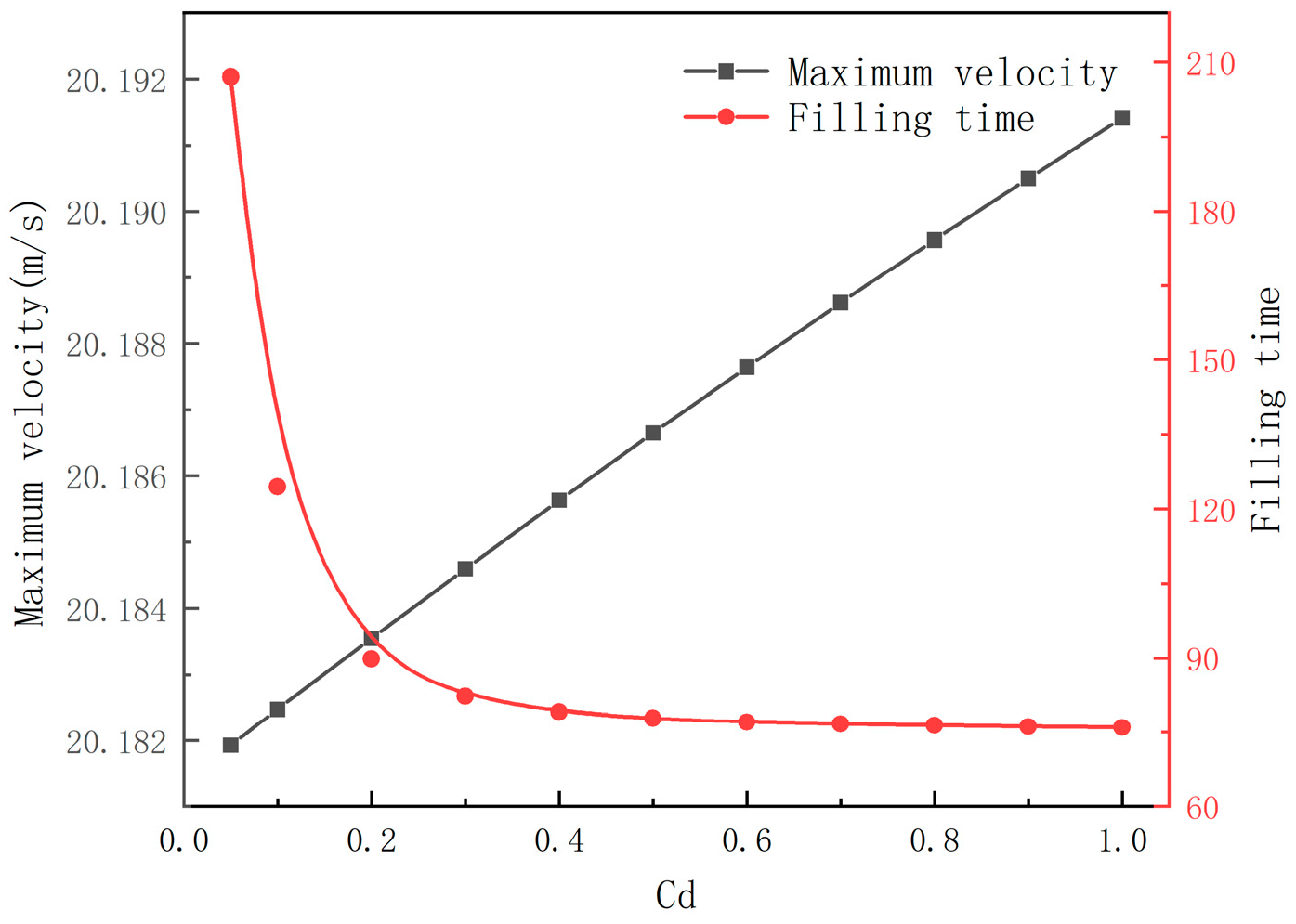
3.4. Analysis of the Impact of Cd
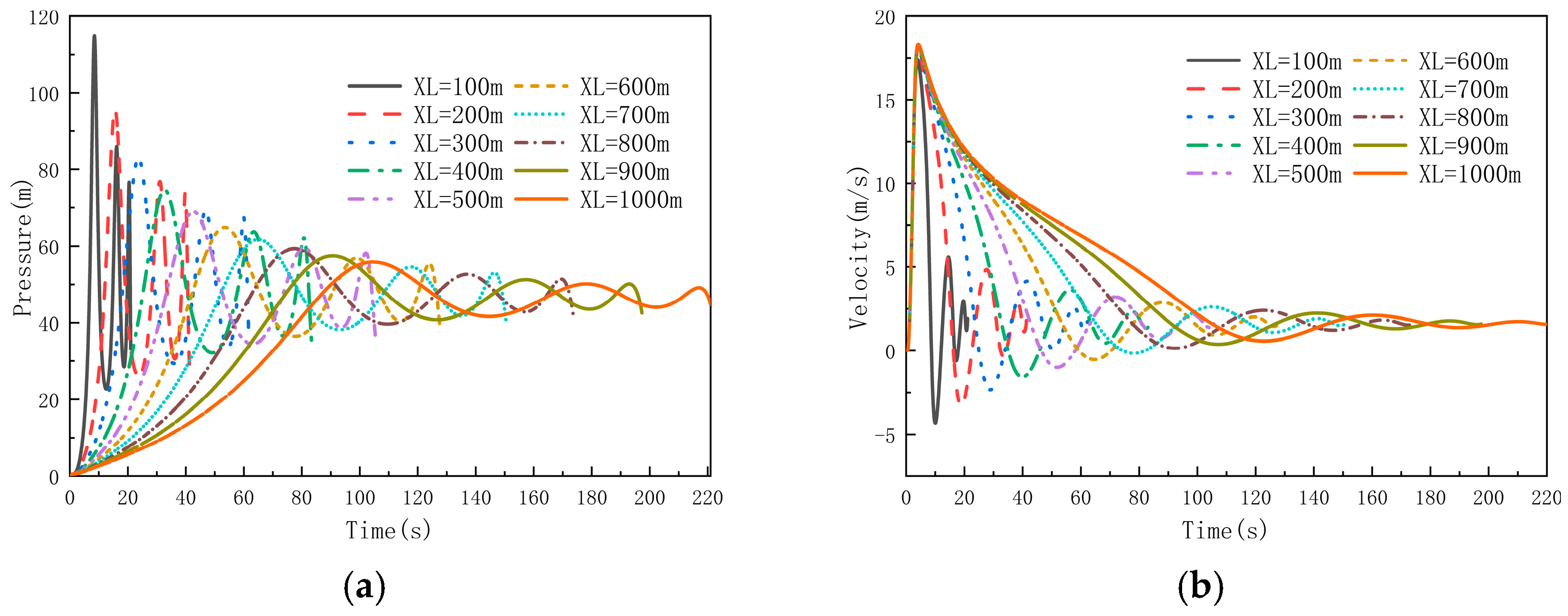
3.5. The Influence of Sectional Water Filling on Rapid Pipeline Filling
4. Conclusions
- (1)
- During the rapid-filling process, the liquid column, acting as a rigid column, moves within the system. Rapid changes only occur in the initial phase of filling, reaching maximum values with very high acceleration. As the length of the liquid column increases (thus increasing inertia and surface friction), the velocity and flow rate gradually decrease. Among these, the initial boundary pressure significantly affects the maximum water inflow velocity, while the filling time is most influenced by the gas discharge coefficient.
- (2)
- When the valve-opening time varies, the maximum water inflow velocity changes accordingly, affecting the pipeline filling time. However, the relative change in water inflow velocity is small, and there is no change in the pressure values within the water delivery system. This is because the pressure fluctuations in the gas–liquid two-phase flow inside the pipeline cause the distribution of velocity difference to be exactly opposite in periodic fluctuations to the change in gas pressure.
- (3)
- When Cd is approximately ≥0.3, the pressure variation within the water delivery system is small, and the filling time and water inflow velocity are no longer affected by the discharge coefficient. In practical engineering applications, sectional water filling can be adopted to fill the pipeline in cases where the pipeline is not completely filled.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, K.; Guo, Y.; Fu, H.; Guo, X. Similarity law for hydraulic transient modelling of pipeline filling. J. Water Resour. 2012, 43, 1188–1193. [Google Scholar]
- Lu, K.; Zhou, L.; Liu, J. Three-dimensional numerical simulation of transient pipe flow with multiple entrapped air pockets. J. Drain. Irrig. Mach. Eng. Pract. 2021, 39, 264–269. [Google Scholar]
- Martin, C.S. Entrapped air in pipelines. In Proceedings of the Second International Conference on Pressure Surges, London, UK, 22–24 September 1976; British Hydromechanics Research Association: London, UK, 1976; pp. F2-15–F2-28. [Google Scholar]
- Cabrera, E.; Abreu, A.; Perez, R.; Vela, A. Influence of liquid length variation in hydraulic transients. J. Hydraul. Eng. 1992, 118, 1639–1650. [Google Scholar] [CrossRef]
- Liou, C.P.; Hunt, W.A. Filling of pipelines with undulating elevation profiles. J. Hydraul. Eng. 1996, 122, 534–539. [Google Scholar] [CrossRef]
- Zhou, F.; Hicks, F.E.; Steffler, P.M. Transient flow in a rapidly filling horizontal pipe containing trapped air. J. Hydraul. Eng. 2002, 128, 625–634. [Google Scholar] [CrossRef]
- Wang, L. Numerical Investigation on Rapid Filling Transients in Pipelines. Ph.D. Thesis, China Agricultural University, Beijing, China, 2017. [Google Scholar]
- Zhou, L.; Li, W.; Liu, D.; Ou, W. A Second Order Godunov Model of Transient Flow with Trapped Air. Water Resour. Power 2021, 39, 95–99. [Google Scholar]
- Zhao, Y.; Zhou, L.; Liu, D.; Zhang, Y.; Wang, J.; Cao, Y.; Pan, T. Water hammer model based on finite volume method and Godunov-type scheme. Adv. Sci. Technol. Water Resour. 2019, 39, 76–81. [Google Scholar]
- Zhou, L.; Wang, N.; Zhao, Y.; Wang, H.; Huang, K.; Lu, K. Godunov model for water column separation and rejoining water hammer considering unsteady friction. J. Harbin Inst. Technol. 2023, 55, 138–144. [Google Scholar]
- Zhou, L.; Cao, Y.; Karney, B.; Bergant, A.; Tijsseling, A.S.; Liu, D.; Wang, P. Expulsion of Entrapped Air in a Rapidly Filling Horizontal Pipe. J. Hydraul. Eng. 2020, 146, 04020047. [Google Scholar] [CrossRef]
- Zhou, L.; Lu, Y.; Karney, B.; Wu, G.; Elong, A.; Huang, K. Energy dissipation in a rapid filling vertical pipe with trapped air. J. Hydraul. Res. 2023, 61, 120–132. [Google Scholar] [CrossRef]
- Malekpour, A.; Karney, B.W. Rapid filling analysis of pipelines with undulating profiles by the method of characteristics. Int. Sch. Res. Not. 2011, 2011, 930460. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, J.; Yu, X. Analytical and numerical investigation on the dynamic characteristics of entrapped air in a rapid filling pipe. J. Water Supply Res. Technol. AQUA 2018, 67, 137–146. [Google Scholar] [CrossRef]
- Coronado-Hernández, Ó.E.; Besharat, M.; Fuertes-Miquel, V.S.; Ramos, H.M. Effect of a commercial air valve on the rapid filling of a single pipeline: A numerical and experimental analysis. Water 2019, 11, 1814. [Google Scholar] [CrossRef]
- Hou, Q.; Tijsseling, A.S.; Laanearu, J.; Annus, I.; Koppel, T.; Bergant, A.; Vučković, S.; Anderson, A.; van’t Westende, J.M. Experimental investigation on rapid filling of a large-scale pipeline. J. Hydraul. Eng. 2014, 140, 04014053. [Google Scholar] [CrossRef]
- Apollonio, C.; Balacco, G.; Fontana, N.; Giugni, M.; Marini, G.; Piccinni, A.F. Hydraulic transients caused by air expulsion during rapid filling of undulating pipelines. Water 2016, 8, 25. [Google Scholar] [CrossRef]
- Paternina-Verona, D.A.; Coronado-Hernández, O.E.; Espinoza-Román, H.G.; Fuertes-Miquel, V.S.; Ramos, H.M. Rapid Filling Analysis with an Entrapped Air Pocket in Water Pipelines Using a 3D CFD Model. Water 2023, 15, 834. [Google Scholar] [CrossRef]
- Tijsseling, A.S.; Hou, Q.; Bozkuş, Z. Rapid liquid filling of a pipe with venting entrapped gas: Analytical and numerical solutions. J. Press. Vessel Technol. 2019, 141, 041301. [Google Scholar] [CrossRef]
- Axworthy, D.H.; Karney, B.W.; Cabrera, E.; Izquierdo, J.; Abreu, J.; Iglesias, P.L. Filling of pipelines with undulating elevation profiles discussions and closure. J. Hydraul. Eng. 1997, 123, 1170–1174. [Google Scholar] [CrossRef]


| Factor | A | C | P | L | Maximum Velocity (m/s2) | Filling Time (s) |
|---|---|---|---|---|---|---|
| Opening the Valve (s) | Cd | Boundary Pressure (m) | Pipeline Length (m) | |||
| 1 | 0 | 0.01 | 10 | 100 | 9.05 | 227.3 |
| 2 | 0 | 0.2 | 30 | 300 | 16.00 | 28.33 |
| 3 | 0 | 0.5 | 50 | 500 | 20.73 | 32.43 |
| 4 | 0 | 0.7 | 70 | 700 | 24.56 | 40.47 |
| 5 | 0 | 1 | 100 | 1000 | 29.39 | 52.77 |
| 6 | 2 | 0.01 | 30 | 500 | 15.13 | 631.9 |
| 7 | 2 | 0.2 | 50 | 700 | 19.55 | 58.52 |
| 8 | 2 | 0.5 | 70 | 1000 | 23.08 | 66.31 |
| 9 | 2 | 0.7 | 100 | 500 | 27.40 | 23.47 |
| 10 | 2 | 1 | 10 | 700 | 8.74 | 113.34 |
| 11 | 4 | 0.01 | 50 | 1000 | 18.91 | 905.8 |
| 12 | 4 | 0.2 | 70 | 100 | 21.07 | 7.43 |
| 13 | 4 | 0.5 | 100 | 300 | 26.18 | 14.87 |
| 14 | 4 | 0.7 | 10 | 500 | 8.50 | 76.67 |
| 15 | 4 | 1 | 30 | 700 | 14.79 | 64.81 |
| 16 | 6 | 0.01 | 70 | 300 | 21.11 | 213 |
| 17 | 6 | 0.2 | 100 | 500 | 25.36 | 28.75 |
| 18 | 6 | 0.5 | 10 | 700 | 8.33 | 118.8 |
| 19 | 6 | 0.7 | 30 | 1000 | 14.44 | 103.6 |
| 20 | 6 | 1 | 50 | 100 | 18.29 | 8.8 |
| 21 | 8 | 0.01 | 100 | 700 | 24.67 | 383.7 |
| 22 | 8 | 0.2 | 10 | 1000 | 8.17 | 213.2 |
| 23 | 8 | 0.5 | 30 | 100 | 13.55 | 11.75 |
| 24 | 8 | 0.7 | 50 | 300 | 17.86 | 22.27 |
| 25 | 8 | 1 | 70 | 500 | 21.04 | 31.28 |
| Ki | Maximum Velocity (m/s2) | Filling Time (s) | ||||||
|---|---|---|---|---|---|---|---|---|
| A | C | P | L | A | C | P | L | |
| K1 | 19.9 | 17.8 | 8.6 | 17.9 | 76.3 | 472.3 | 149.9 | 55.8 |
| K2 | 18.8 | 18.0 | 14.8 | 18.0 | 178.7 | 67.2 | 168.1 | 78.4 |
| K3 | 17.9 | 18.4 | 19.1 | 18.2 | 213.9 | 48.8 | 205.6 | 160.2 |
| K4 | 17.5 | 18.6 | 22.2 | 18.4 | 94.6 | 53.3 | 71.7 | 133.3 |
| K5 | 17.1 | 18.4 | 26.6 | 18.8 | 132.4 | 54.2 | 100.7 | 268.3 |
| R | 2.9 | 0.8 | 18.0 | 0.5 | 137.7 | 423.5 | 133.9 | 212.6 |
| Factor priority | P > A > C > L | C > L > A > P | ||||||
| Optimal group | P5A1C4L5 | C3L1A1P4 | ||||||
| Performance Indicator | Variance Source | Sum of Squares of Deviations | Degrees of Freedom | F Ratio | Critical F Value |
|---|---|---|---|---|---|
| Maximum velocity | A | 26.260 | 4 | 0.106 | 2.33 |
| C | 2.095 | 4 | 0.008 | 2.33 | |
| P | 958.534 | 4 | 3.874 | 2.33 | |
| L | 2.717 | 4 | 0.011 | 2.33 | |
| Error | 989.610 | 16 | - | - | |
| Filling time | A | 65,702.773 | 4 | 0.275 | 2.33 |
| C | 694,652.544 | 4 | 2.905 | 2.33 | |
| P | 56,948.211 | 4 | 0.238 | 2.33 | |
| L | 139,089.027 | 4 | 0.582 | 2.33 | |
| Error | 956,392.560 | 16 | - | - |
| Opening the Valve | Time | Maximum Velocity (m/s) | Time/Opening the Valve | Filling Time |
|---|---|---|---|---|
| 0 | 0.06 | 20.730 | 0.00 | 206.9 |
| 4 | 5.15 | 18.909 | 0.78 | 209.3 |
| 6 | 7.27 | 18.382 | 0.83 | 210.5 |
| 8 | 9.31 | 17.932 | 0.86 | 211.7 |
| Boundary Pressure (m) | Peak Pressure (m) | Pmax/P0 | Relative Change | Maximum Velocity |
|---|---|---|---|---|
| 10 | 10.52 | 1.05 | 8.91 | |
| 20 | 22.78 | 1.14 | 0.087 | 12.73 |
| 30 | 36.52 | 1.22 | 0.078 | 15.63 |
| 40 | 51.70 | 1.29 | 0.075 | 18.06 |
| 50 | 68.30 | 1.37 | 0.074 | 20.18 |
| 60 | 86.33 | 1.44 | 0.073 | 22.10 |
| 70 | 105.77 | 1.51 | 0.072 | 23.85 |
| 80 | 126.65 | 1.58 | 0.072 | 25.49 |
| 90 | 148.96 | 1.66 | 0.072 | 27.02 |
| 100 | 172.76 | 1.73 | 0.072 | 28.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Fu, Y.; Jiang, J. Characteristics of Transient Flow in Rapidly Filled Closed Pipeline. Water 2024, 16, 2377. https://doi.org/10.3390/w16172377
Wang K, Fu Y, Jiang J. Characteristics of Transient Flow in Rapidly Filled Closed Pipeline. Water. 2024; 16(17):2377. https://doi.org/10.3390/w16172377
Chicago/Turabian StyleWang, Kan, You Fu, and Jin Jiang. 2024. "Characteristics of Transient Flow in Rapidly Filled Closed Pipeline" Water 16, no. 17: 2377. https://doi.org/10.3390/w16172377





