Forecasting of Standardized Precipitation Index Using Hybrid Models: A Case Study of Cape Town, South Africa
Abstract
:1. Introduction
2. Materials and Methods
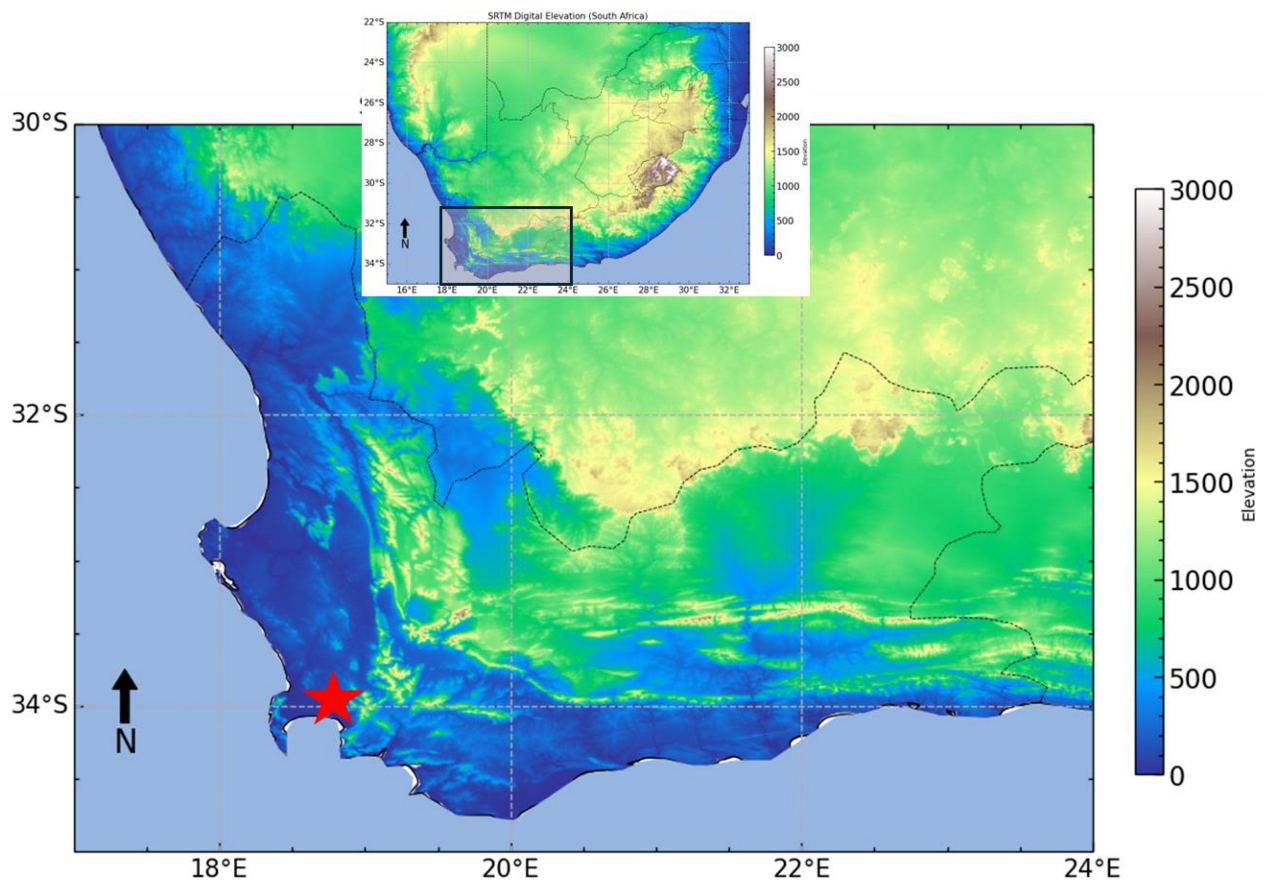
2.1. Study Area
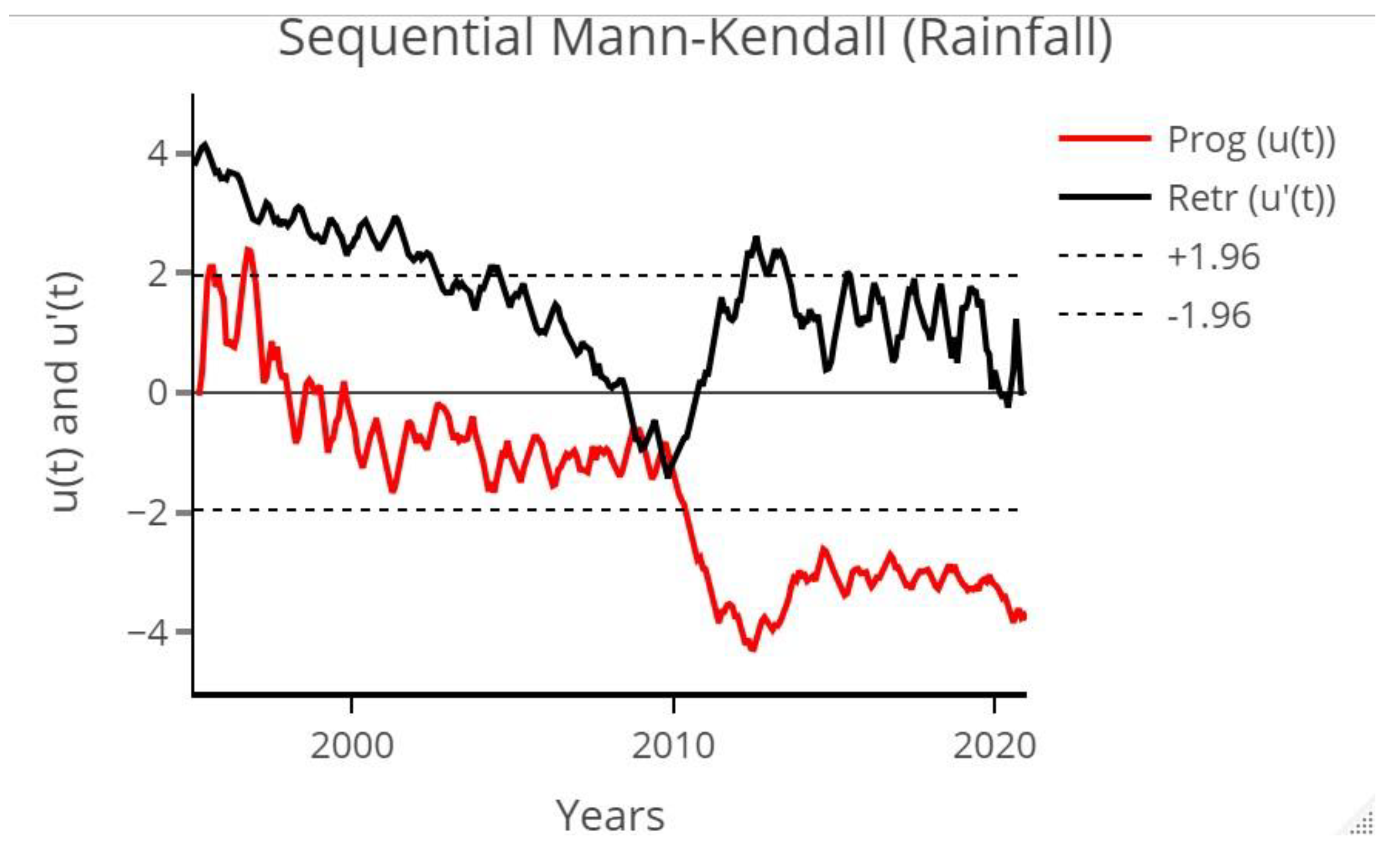
2.2. Mann–Kendall Test Statistics
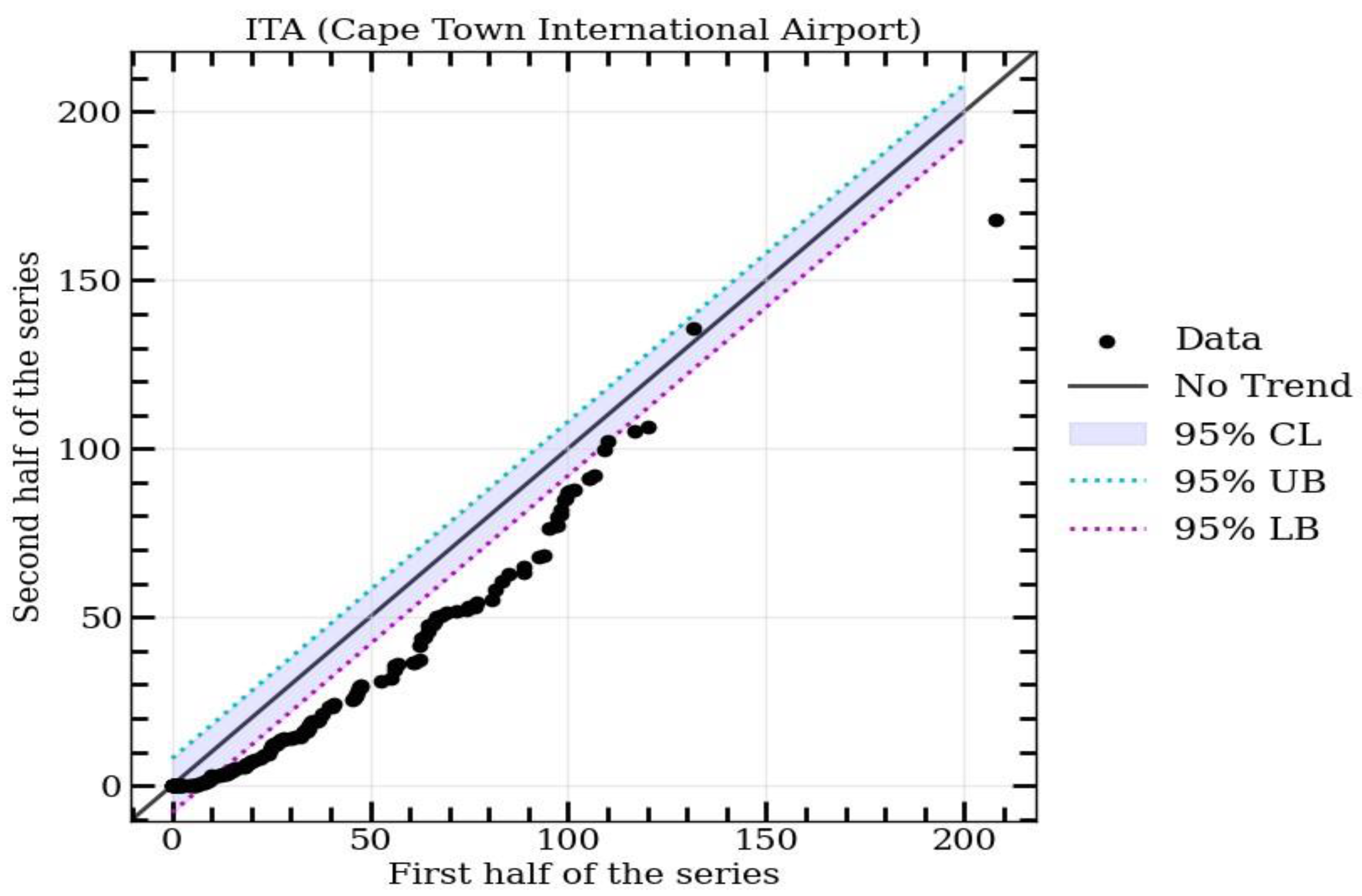
2.3. Innovative Trend Analysis
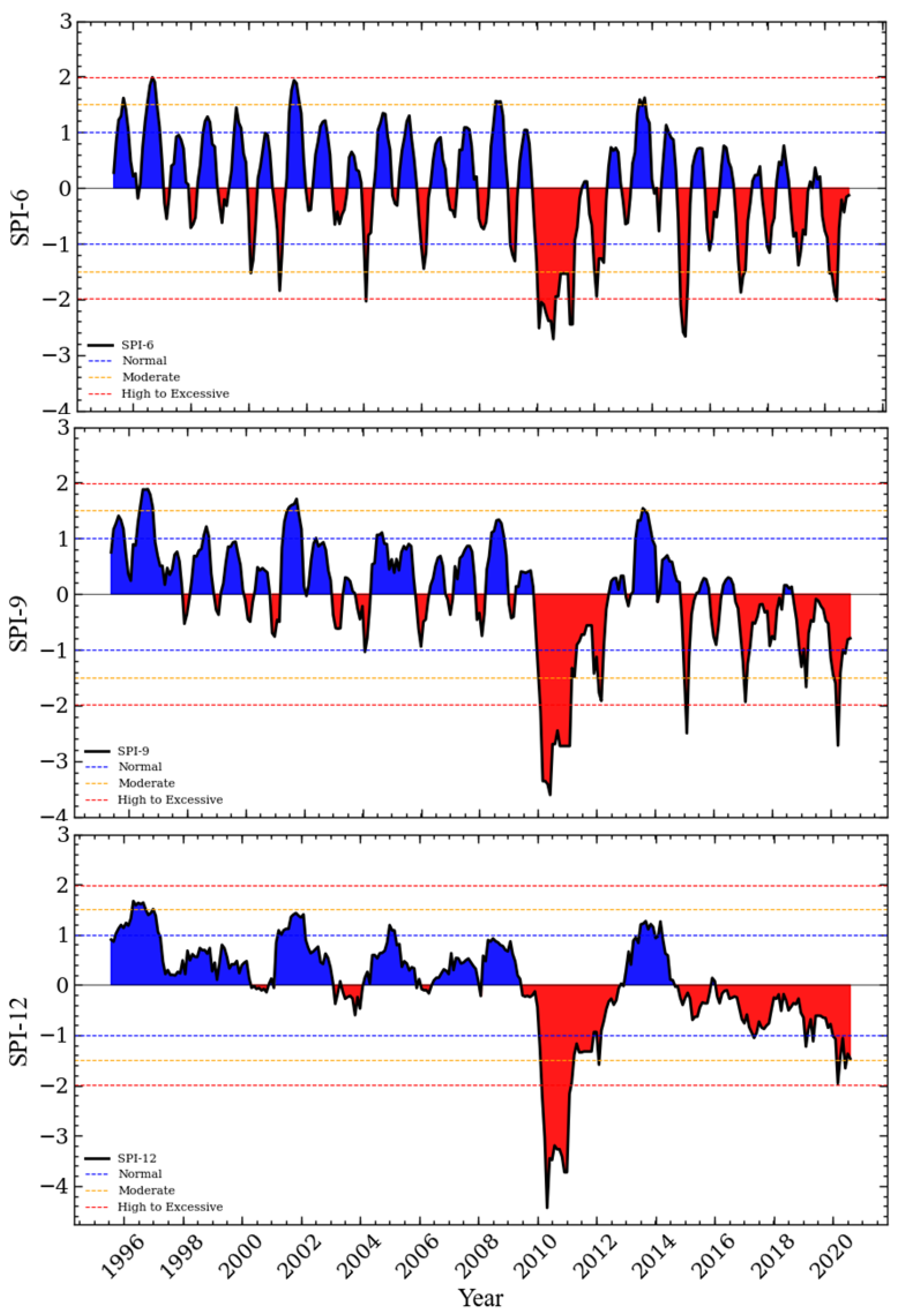
2.4. Standardized Precipitation Index Calculation
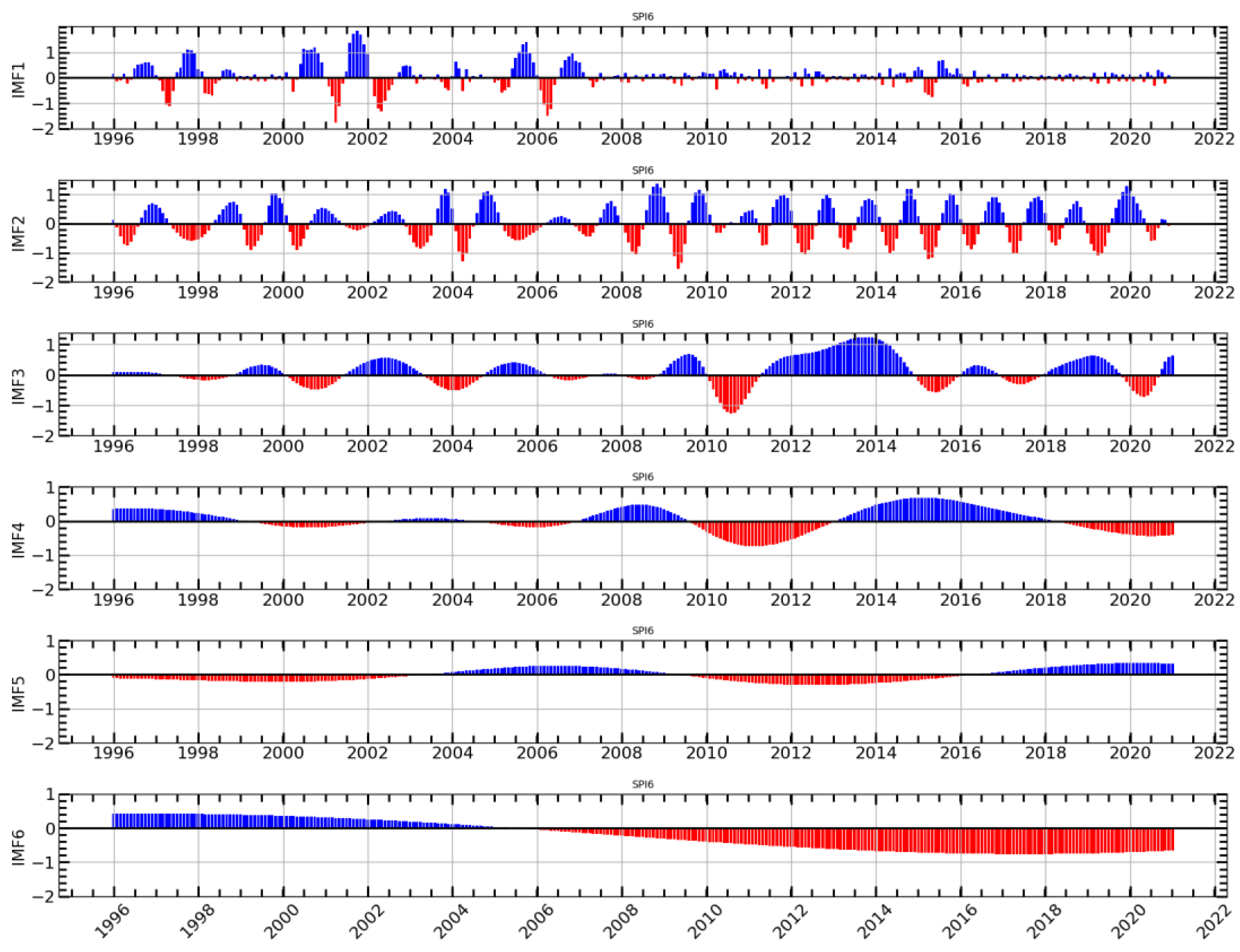
2.5. Complete Ensemble Empirical Mode with Adaptive Noise (CEEMDAN)
- The EMD decomposition is performed for to obtain N new sequences and calculate the mean worth to be the first model component IMF1. The first remaining component will be calculated aswhere E is the EMD decomposition operator, and denotes the residual signal after the first decomposition.
- Specific noise is added to the new signal, and EMD decomposition is continued to obtain the second IMF2 of the original signal and corresponding residual .
- In the following stage, for , the k-th mode component and the corresponding residual signal can be computed in the following equation.
- Step 3 is repeated until the residual satisfies the stoppage criterion.
- Finally, the decomposition consequence of the original signal can be described as
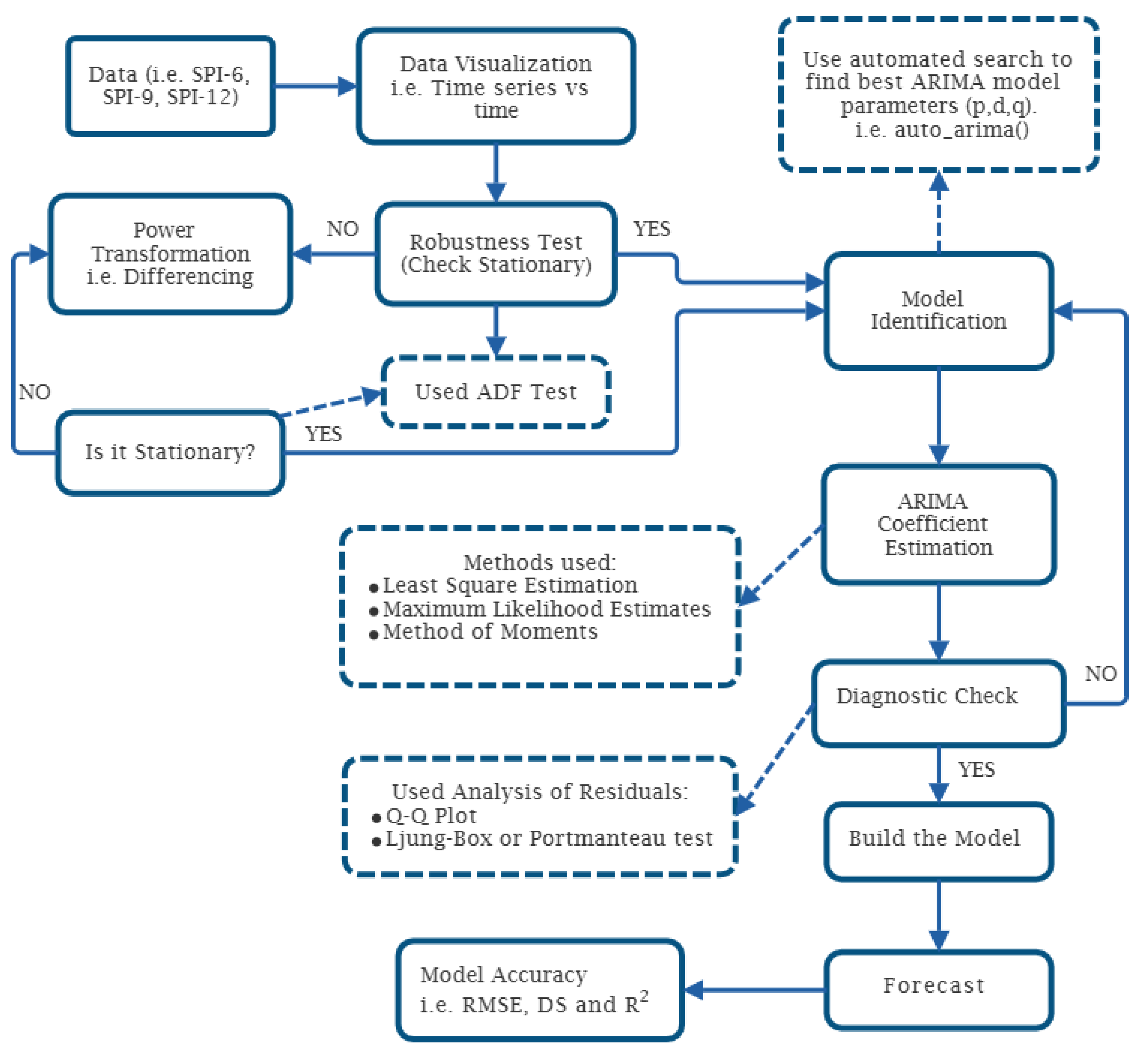
2.6. Autoregressive Integrated Moving Average
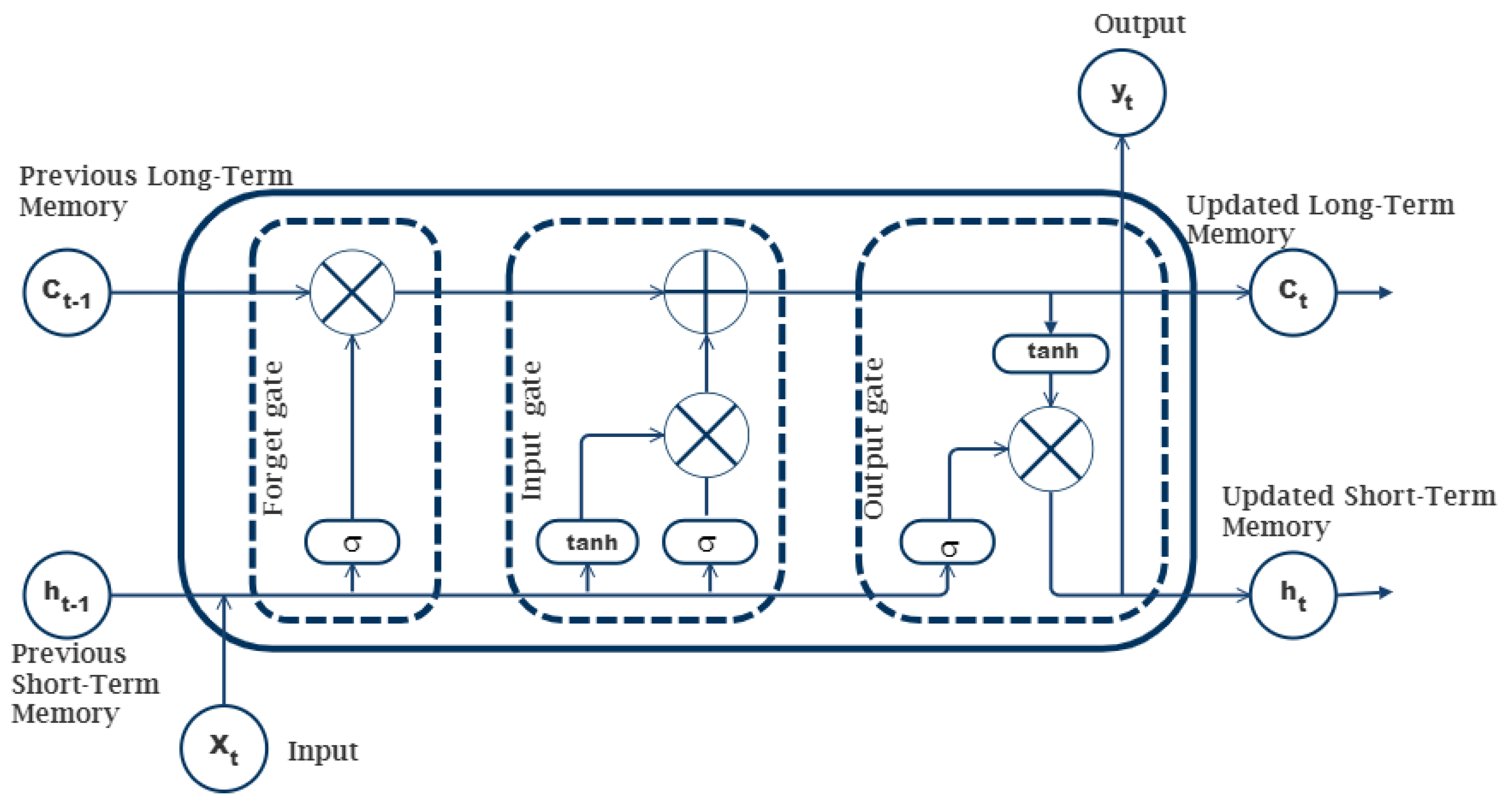
2.7. Long Short-Term Memory Neural Network
2.8. The Development of the Hybrid CEEMDAN-ARIMA-LSTM Model
- The original data are decomposed into Intrinsic Mode Functions (IMFs) and a residual component using the CEEMDAN technique. CEEMDAN decomposes the time series into numerous oscillatory mode components with varying frequencies, capturing both high-frequency and low-frequency components, thereby making it easier for subsequent models to capture distinct patterns.
- The ARIMA models are used to capture temporal dependencies and trends, as well as to analyze individually each of the retrieved IMFs and the residual component derived from CEEMDAN. The ARIMA models is applied for each IMFs and residual components. The residual component is then combined with the forecasts from the ARIMA models of each IMF to reconstruct the predicted series.
- From the ARIMA fitted results, the calculated residuals serve as inputs of the LSTM model. The LSTM model is trained using the training set to generate 1 step ahead forecasts.
- The prediction result is derived by adding the predicted values of the high-frequency components using LSTM and the predicted value of the low-frequency components using ARIMA.
- Steps (1) to (4) are repeated to obtain the final prediction.
2.9. Model Performance Criteria
3. Results
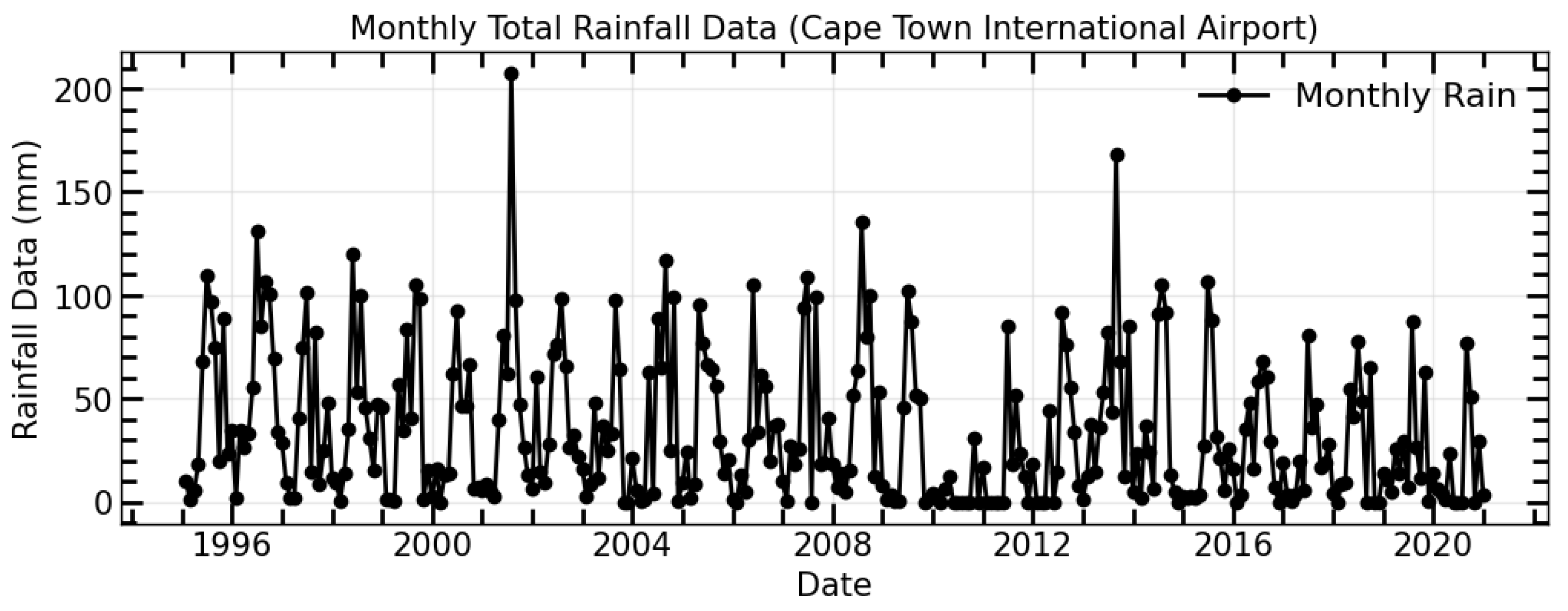
3.1. Rainfall Data Series and Trend Analysis
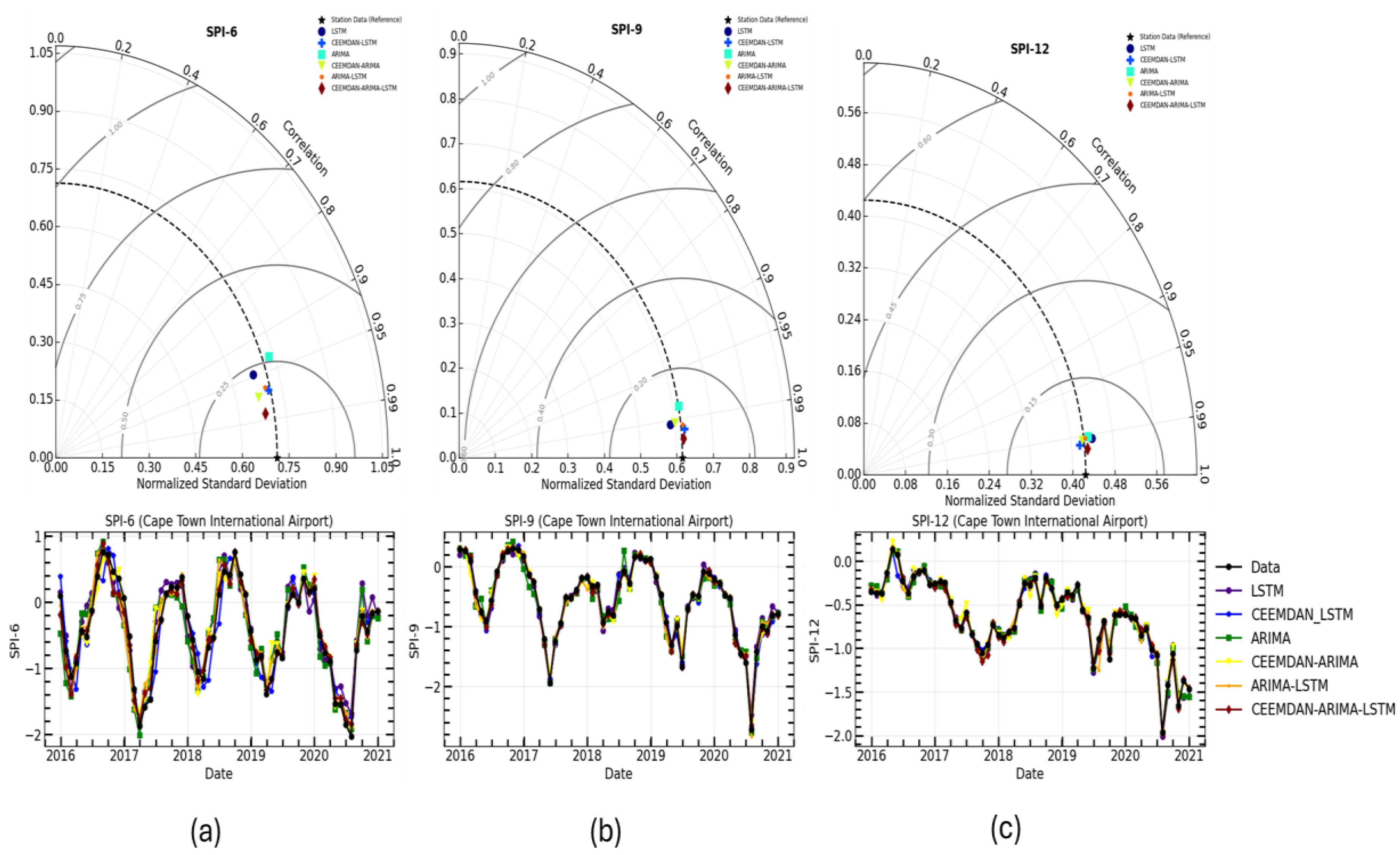
3.2. SPI Time Series and Forecusting Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fang, O.; Zhang, Q.-B.; Vitasse, Y.; Zweifel, R.; Cherubini, P. The frequency and severity of past droughts shape the drought sensitivity of juniper trees on the Tibetan plateau. For. Ecol. Manag. 2021, 486, 118968. [Google Scholar] [CrossRef]
- Murgatroyd, A.; Gavin, H.; Becher, O.; Coxon, G.; Hunt, D.; Fallon, E.; Wilson, J.; Cuceloglu, G.; Hall, J.W. Strategic analysis of the drought resilience of water supply systems. Philos. Trans. R. Soc. A 2022, 380, 20210292. [Google Scholar] [CrossRef]
- Garrick, D.; De Stefano, L.; Yu, W.; Jorgensen, I.; O’Donnell, E.; Turley, L.; Aguilar-Barajas, I.; Dai, X.; de Souza Leão, R.; Punjabi, B.; et al. Rural water for thirsty cities: A systematic review of water reallocation from rural to urban regions. Environ. Res. Lett. 2019, 14, 043003. [Google Scholar] [CrossRef]
- Vorosmarty, C.J.; Green, P.; Salisbury, J.; Lammers, R.B. Global water resources: Vulnerability from climate change and population growth. Science 2000, 289, 284–288. [Google Scholar] [CrossRef]
- Hall, J.W.; Grey, D.; Garrick, D.; Fung, F.; Brown, C.; Dadson, S.J.; Sadoff, C.W. Coping with the curse of freshwater variability. Science 2014, 346, 429–430. [Google Scholar] [CrossRef] [PubMed]
- Murgatroyd, A.; Hall, J.W. Regulation of freshwater use to restore ecosystems resilience. Clim. Risk Manag. 2021, 32, 100303. [Google Scholar] [CrossRef]
- Jin, L.; Whitehead, P.G.; Bussi, G.; Hirpa, F.; Taye, M.T.; Abebe, Y.; Charles, K. Natural and anthropogenic sources of salinity in the Awash River and Lake Beseka (Ethiopia): Modelling impacts of climate change and lake-river interactions. J. Hydrol. Reg. Stud. 2021, 36, 100865. [Google Scholar] [CrossRef]
- Hall, J.W.; Borgomeo, E.; Bruce, A.; Di Mauro, M.; Mortazavi-Naeini, M. Resilience of water resource systems: Lessons from England. Water Secur. 2019, 8, 100052. [Google Scholar] [CrossRef]
- Ding, Y.; Xu, J.; Wang, X.; Cai, H.; Zhou, Z.; Sun, Y.; Shi, H. Propagation of meteorological to hydrological drought for different climate regions in China. J. Environ. Manag. 2021, 283, 111980. [Google Scholar] [CrossRef]
- Esfahanian, E.; Nejadhashemi, A.P.; Abouali, M.; Adhikari, U.; Zhang, Z.; Daneshvar, F.; Herman, M.R. Development and evaluation of a comprehensive drought index. J. Environ. Manag. 2017, 185, 31–43. [Google Scholar] [CrossRef]
- Alley, W.M. The Palmer drought severity index: Limitations and assumptions. J. Clim. Appl. Meteorol. 1984, 23, 1100–1109. [Google Scholar] [CrossRef]
- Byun, H.R.; Wilhite, D.A. Objective quantification of drought severity and duration. J. Clim. 1999, 12, 2747–2756. [Google Scholar] [CrossRef]
- Tsakiris, G.; Pangalou, D.; Vangelis, H. Regional drought assessment based on the Reconnaissance Drought Index (RDI). Water Resour. Manag. 2007, 21, 821–833. [Google Scholar] [CrossRef]
- Beguería, S.; Vicente-Serrano, S.M.; Reig, F.; Latorre, B. Vicente-Serrano, Fergus Reig, and Borja Latorre. Standardized precipitation evapotranspiration index (SPEI) revisited: Parameter fitting, evapotranspiration models, tools, datasets and drought monitoring. Int. J. Climatol. 2014, 34, 3001–3023. [Google Scholar] [CrossRef]
- Lyon, B.; Barnston, A.G. ENSO and the spatial extent of interannual precipitation extremes in tropical land areas. J. Clim. 2005, 18, 5095–5109. [Google Scholar] [CrossRef]
- Erhardt, T.M.; Czado, C. Standardized drought indices: A novel univariate and multivariate approach. J. R. Stat. Soc. Ser. C Appl. Stat. 2018, 67, 643–664. [Google Scholar] [CrossRef]
- Zargar, A.; Sadiq, R.; Naser, B.; Khan, F.I. A review of drought indices. Environ. Rev. 2011, 19, 333–349. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; Volume 17, pp. 179–183. [Google Scholar]
- Hayes, M.; Svoboda, M.; Wall, N.; Widhalm, M. The Lincoln declaration on drought indices: Universal meteorological drought index recommended. Bull. Am. Meteorol. Soc. 2011, 92, 485–488. [Google Scholar] [CrossRef]
- Svoboda, M.D.; Fuchs, B.A. Handbook of Drought Indicators and Indices; World Meteorological Organization: Geneva, Switzerland, 2016; Volume 2. [Google Scholar]
- Latifoğlu, L.; Özger, M. A novel approach for high-performance estimation of SPI data in drought prediction. Sustainability 2023, 15, 14046. [Google Scholar] [CrossRef]
- Wu, H.; Hayes, M.J.; Weiss, A.; Hu, Q.I. An evaluation of the Standardized Precipitation Index, the China-Z Index and the statistical Z-Score. Int. J. Climatol. 2001, 21, 745–758. [Google Scholar] [CrossRef]
- Choubin, B.; Malekian, A.; Gloshan, M. Application of several data-driven techniques to predict a standardized precipitation index. Atmósfera 2016, 29, 121–128. [Google Scholar] [CrossRef]
- Hosseini-Moghari, S.M.; Araghinejad, S.; Azarnivand, A. Drought forecasting using data-driven methods and an evolutionary algorithm. Model. Earth Syst. Environ. 2017, 3, 1675–1689. [Google Scholar] [CrossRef]
- Aghelpour, P.; Kisi, O.; Varshavian, V. Multivariate drought forecasting in short-and long-term horizons using MSPI and data-driven approaches. J. Hydrol. Eng. 2021, 26, 04021006. [Google Scholar] [CrossRef]
- Elbeltagi, A.; AlThobiani, F.; Kamruzzaman, M.; Shaid, S.; Roy, D.K.; Deb, L.; Islam, M.M.; Kundu, P.K.; Rahman, M.M. Estimating the standardized precipitation evapotranspiration index using data-driven techniques: A regional study of Bangladesh. Water 2022, 14, 1764. [Google Scholar] [CrossRef]
- Pande, C.B.; Costache, R.; Sammen, S.S.; Noor, R.; Elbeltagi, A. Combination of data-driven models and best subset regression for predicting the standardized precipitation index (SPI) at the Upper Godavari Basin in India. Theor. Appl. Climatol. 2023, 152, 535–558. [Google Scholar] [CrossRef]
- Noh, S.; Lee, S. Forecasting Meteorological Drought Conditions in South Korea Using a Data-Driven Model with Lagged Global Climate Variability. Sustainability 2024, 16, 6485. [Google Scholar] [CrossRef]
- Khan, M.M.H.; Muhammad, N.S.; El-Shafie, A. Wavelet based hybrid ANN-ARIMA models for meteorological drought forecasting. J. Hydrol. 2020, 590, 125380. [Google Scholar] [CrossRef]
- Han, P.; Wang, P.; Tian, M.; Zhang, S.; Liu, J.; Zhu, D. Application of the ARIMA models in drought forecasting using the standardized precipitation index. In Computer and Computing Technologies in Agriculture VI, Proceedings of the 6th IFIP WG 5.14 International Conference, CCTA 2012, Zhangjiajie, China, 19–21 October 2012; Revised Selected Papers, Part I 6; Springer: Berlin/Heidelberg, Germany, 2013; pp. 352–358. [Google Scholar]
- Tan, Y.X.; Ng, J.L.; Huang, Y.F. A review on drought index forecasting and their modelling approaches. Arch. Comput. Methods Eng. 2023, 30, 1111–1129. [Google Scholar] [CrossRef]
- Achite, M.; Elshaboury, N.; Jehanzaib, M.; Vishwakarma, D.K.; Pham, Q.B.; Anh, D.T.; Abdelkader, E.M.; Elbeltagi, A. Performance of machine learning techniques for meteorological drought forecasting in the Wadi Mina Basin, Algeria. Water 2023, 15, 765. [Google Scholar] [CrossRef]
- Liu, M.-D.; Ding, L.; Bai, Y.-L. Application of hybrid model based on empirical mode decomposition, novel recurrent neural networks and the ARIMA to wind speed prediction. Energy Convers. Manag. 2021, 233, 113917. [Google Scholar] [CrossRef]
- Poornima, S.; Pushpalatha, M. Drought prediction based on SPI and SPEI with varying timescales using LSTM recurrent neural network. Soft Comput. 2019, 23, 8399–8412. [Google Scholar] [CrossRef]
- Dikshit, A.; Pradhan, B.; Alamri, A.M. Long lead time drought forecasting using lagged climate variables and a stacked long short-term memory model. Sci. Total Environ. 2021, 755, 142638. [Google Scholar] [CrossRef] [PubMed]
- Balti, H.; Abbes, A.B.; Mellouli, N.; Sang, Y.; Farah, I.R.; Lamolle, M.; Zhu, Y. Big data based architecture for drought forecasting using LSTM, ARIMA, and Prophet: Case study of the Jiangsu Province, China. In Proceedings of the 2021 International Congress of Advanced Technology and Engineering (ICOTEN), Virtual Conference, 4–5 July 2021; IEEE: New York, NY, USA, 2021; pp. 1–8. [Google Scholar]
- Ding, Y.; Yu, G.; Tian, R.; Sun, Y. Application of a hybrid CEEMD-LSTM model based on the standardized precipitation index for Drought forecasting: The case of the Xinjiang Uygur Autonomous Region, China. Atmosphere 2022, 13, 1504. [Google Scholar] [CrossRef]
- Wang, Z.-Y.; Qiu, J.; Li, F.-F. Hybrid models combining EMD/EEMD and ARIMA for Long-term streamflow forecasting. Water 2018, 10, 853. [Google Scholar] [CrossRef]
- Mathivha, F.; Sigauke, C.; Chikoore, H.; Odiyo, J. Short-term and medium-term drought forecasting using generalized additive models. Sustainability 2020, 12, 4006. [Google Scholar] [CrossRef]
- Guoyang, Z.; Xinjun, T.; Tian, W.; Yuting, X.I.E.; Xiaomei, M.O. Drought Prediction Based on Artificial Neural Network and Support Vector Machine. Pearl River 2021, 42, 1. [Google Scholar]
- Wu, G.; Zhang, J.; Xue, H. Long-Term Prediction of Hydrometeorological Time Series Using a PSO-Based Combined Model Composed of EEMD and LSTM. Sustainability 2023, 15, 13209. [Google Scholar] [CrossRef]
- Rezaiy, R.; Shabri, A. An innovative hybrid W-EEMD-ARIMA model for drought forecasting using the standardized precipitation index. In Natural Hazards; Springer: Berlin/Heidelberg, Germany, 2024; pp. 1–30. [Google Scholar]
- Belayneh, A.; Adamowski, J.; Khalil, B.; Quilty, J. Coupling machine learning methods with wavelet transforms and the bootstrap and boosting ensemble approaches for drought prediction. Atmos. Res. 2016, 172, 37–47. [Google Scholar] [CrossRef]
- Rezaiy, R.; Shabri, A. Drought forecasting using W-ARIMA model with standardized precipitation index. J. Water Clim. Chang. 2023, 14, 3345–3367. [Google Scholar] [CrossRef]
- Coşkun, Ö.; Citakoglu, H. Prediction of the standardized precipitation index based on the long short-term memory and empirical mode decomposition-extreme learning machine models: The Case of Sakarya, Türkiye. Phys. Chem. Earth Parts A/B/C 2023, 131, 103418. [Google Scholar] [CrossRef]
- Libanda, B.; Nkolola, N.B. An ensemble empirical mode decomposition of consecutive dry days in the Zambezi Riparian Region: Implications for water management. Phys. Chem. Earth Parts A/B/C 2022, 126, 103147. [Google Scholar] [CrossRef]
- Xu, D.; Ding, Y.; Liu, H.; Zhang, Q.; Zhang, D. Applicability of a CEEMD–ARIMA Combined Model for Drought Forecasting: A Case Study in the Ningxia Hui Autonomous Region. Atmosphere 2022, 13, 1109. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P.; Xia, Y. Seasonal drought prediction: Advances, challenges, and future prospects. Rev. Geophys. 2018, 56, 108–141. [Google Scholar] [CrossRef]
- Adnan, R.M.; Mostafa, R.R.; Islam AR, M.T.; Gorgij, A.D.; Kuriqi, A.; Kisi, O. Improving drought modeling using hybrid random vector functional link methods. Water 2021, 13, 3379. [Google Scholar] [CrossRef]
- Wu, X.; Zhou, J.; Yu, H.; Liu, D.; Xie, K.; Chen, Y.; Hu, J.; Sun, H.; Xing, F. The development of a hybrid wavelet-ARIMA-LSTM model for precipitation amounts and drought analysis. Atmosphere 2021, 12, 74. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1975. [Google Scholar]
- Seenu, P.Z.; Jayakumar, K.V. Comparative study of innovative trend analysis technique with Mann-Kendall tests for extreme rainfall. Arab. J. Geosci. 2021, 14, 536. [Google Scholar]
- Körük, A.E.; Kankal, M.; Yıldız, M.B.; Akçay, F.; Şan, M.; Nacar, S. Trend analysis of precipitation using innovative approaches in northwestern Turkey. Phys. Chem. Earth Parts A/B/C 2023, 131, 103416. [Google Scholar] [CrossRef]
- Mbatha, N.; Xulu, S. Time series analysis of MODIS-Derived NDVI for the Hluhluwe-Imfolozi Park, South Africa: Impact of recent intense drought. Climate 2018, 6, 95. [Google Scholar] [CrossRef]
- Onoz, B.; Bayazit, M. The power of statistical tests for trend detection. Turk. J. Eng. Environ. Sci. 2003, 27, 247–251. [Google Scholar]
- Othman, M.A.; Zakaria, N.A.; Ghani, A.A.; Chang, C.K.; Chan, N.W. Analysis of trends of extreme rainfall events using Mann Kendall test: A case study in Pahang and Kelantan river basins. J. Teknol. 2016, 78. [Google Scholar] [CrossRef]
- Hamed, K.H.; Rao, A.R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Kumar, S.; Machiwal, D.; Dayal, D. Spatial modelling of rainfall trends using satellite datasets and geographic information system. Hydrol. Sci. J. 2017, 62, 1636–1653. [Google Scholar] [CrossRef]
- Singh, R.N.; Sah, S.; Das, B.; Potekar, S.; Chaudhary, A.; Pathak, H. Innovative trend analysis of spatio-temporal variations of rainfall in India during 1901–2019. Theor. Appl. Climatol. 2021, 145, 821–838. [Google Scholar] [CrossRef]
- Sneyers, R. On the Statistical Analysis of Series of Observations; Technical Note No. 143, WMO No. 415; World Meteorological Organization: Geneva, Switzerland, 1991; p. 192. [Google Scholar]
- Bisai, D.; Chatterjee, S.; Khan, A. Detection of recognizing events in lower atmospheric temperature time series (1941–2010) of Midnapore Weather Observatory, West Bengal, India. J. Environ. Earth Sci. 2014, 4, 61–66. [Google Scholar]
- Şen, Z. Innovative trend analysis methodology. J. Hydrol. Eng. 2012, 17, 1042–1046. [Google Scholar] [CrossRef]
- Paulo, A.A.; Pereira, L.S. Prediction of SPI drought class transitions using Markov chains. Water Resour. Manag. 2007, 21, 1813–1827. [Google Scholar] [CrossRef]
- World Meteorological Organization. WMO Statement on the Status of the Global Climate in 2015; World Meteorological Organization (WMO): Geneva, Switzerland, 2016. [Google Scholar]
- Wilhite, D.A.; Hayes, M.J.; Knutson, C.; Smith, K.H. Planning for drought: Moving from crisis to risk management1. JAWRA J. Am. Water Resour. Assoc. 2000, 36, 697–710. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, Y. SPI based meteorological drought assessment over a humid basin: Effects of processing schemes. Water 2016, 8, 373. [Google Scholar] [CrossRef]
- Zhang, X.; Peng, Y.; Zhang, C.; Wang, B. Are hybrid models integrated with data preprocessing techniques suitable for monthly streamflow forecasting? Some experiment evidences. J. Hydrol. 2015, 530, 137–152. [Google Scholar] [CrossRef]
- Koudahe, K.; Kayode, A.J.; Samson, A.O.; Adebola, A.A.; Djaman, K. Trend analysis in standardized precipitation index and standardized anomaly index in the context of climate change in Southern Togo. Atmos. Clim. Sci. 2017, 7, 401. [Google Scholar] [CrossRef]
- Nourani, V.; Alami, M.T.; Vousoughi, F.D. Wavelet-entropy data pre-processing approach for ANN-based groundwater level modeling. J. Hydrol. 2015, 524, 255–269. [Google Scholar] [CrossRef]
- Lloyd-Hughes, B.; Saunders, M.A. A drought climatology for Europe. Int. J. Climatol. 2002, 22, 1571–1592. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; IEEE: New York, NY, USA, 2011; pp. 4144–4147. [Google Scholar]
- Box, G.E.; Jenkin, G.M.; Wisconsin University Madison Department of Statistics. Time Series Analysis Forecasting and Control; Wiley: Hoboken, NJ, USA, 1970. [Google Scholar]
- Sharma, R.R.; Kumar, M.; Maheshwari, S.; Ray, K.P. EVDHM-ARIMA-based time series forecasting model and its application for COVID-19 cases. IEEE Trans. Instrum. Meas. 2020, 70, 6502210. [Google Scholar] [CrossRef]
- El-Dakak, A.M.; Saleh, O.K.; Mosad, K.; Elnikhely, E.A. Drought forecast using ARIMA model for the standardized precipitation index (SPI) and precipitation data. Int. J. Civ. Eng. Technol. 2021, 12, 63–79. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Calverley, C.M.; Walther, S.C. Drought, water management, and social equity: Analyzing Cape Town, South Africa’s water crisis. Front. Water 2022, 4, 910149. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, J. Aqi prediction based on ceemdan-arma-lstm. Sustainability 2022, 14, 12182. [Google Scholar] [CrossRef]
- Makridakis, S. Accuracy measures: Theoretical and practical concerns. Int. J. Forecast. 1993, 9, 527–529. [Google Scholar] [CrossRef]
- Sameen, M.I.; Pradhan, B.; Lee, S. Application of convolutional neural networks featuring Bayesian optimization for landslide susceptibility assessment. Catena 2020, 186, 104249. [Google Scholar] [CrossRef]
- Sameen, M.I.; Pradhan, B.; Lee, S. Self-learning random forests model for mapping groundwater yield in data-scarce areas. Nat. Resour. Res. 2019, 28, 757–775. [Google Scholar] [CrossRef]
- Ndebele, N.E.; Grab, S.; Turasie, A. Characterizing rainfall in the south-western Cape, South Africa: 1841–2016. Int. J. Climatol. 2020, 40, 1992–2014. [Google Scholar] [CrossRef]
- Jury, M.R. Climate trends in the Cape Town area, South Africa. Water SA 2020, 46, 438–447. [Google Scholar]
- Wolski, P.; Conradie, S.; Jack, C.; Tadross, M. Spatio-temporal patterns of rainfall trends and the 2015–2017 drought over the winter rainfall region of South Africa. Int. J. Climatol. 2021, 41, E1303–E1319. [Google Scholar] [CrossRef]
- Nxumalo, G.; Bashir, B.; Alsafadi, K.; Bachir, H.; Harsányi, E.; Arshad, S.; Mohammed, S. Meteorological drought variability and its impact on wheat yields across South Africa. Int. J. Environ. Res. Public Health 2022, 19, 16469. [Google Scholar] [CrossRef] [PubMed]
- Muse, N.M.; Tayfur, G.; Safari, M.J.S. Meteorological drought assessment and trend analysis in Puntland region of Somalia. Sustainability 2023, 15, 10652. [Google Scholar] [CrossRef]
- Tladi, T.M.; Ndambuki, J.M.; Olwal, T.O.; Rwanga, S.S. Groundwater Level Trend Analysis and Prediction in the Upper Crocodile Sub-Basin, South Africa. Water 2023, 15, 3025. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, X.; He, S.; Zhao, D. Precipitation forecast based on CEEMD–LSTM coupled model. Water Supply 2021, 21, 4641–4657. [Google Scholar] [CrossRef]
- Salisu, A.M.; Shabri, A. A hybrid wavelet-ARIMA model for standardized precipitation index drought forecasting. Matematika 2020, 36, 141–156. [Google Scholar] [CrossRef]
- Rezaiy, R.; Shabri, A. Improving drought prediction accuracy: A hybrid EEMD and support vector machine approach with standardized precipitation index. Water Resour. Manag. 2024, 1–23. [Google Scholar] [CrossRef]
- Alquraish, M.; Ali Abuhasel, K.; Alqahtani, A.S.; Khadr, M. SPI-based hybrid hidden Markov–GA, ARIMA–GA, and ARIMA–GA–ANN models for meteorological drought forecasting. Sustainability 2021, 13, 12576. [Google Scholar] [CrossRef]

| SPI Value | Class | Probability (%) |
|---|---|---|
| SPI ≥ 2.00 | Extremely wet | 2.3 |
| 1.5 ≤ SPI < 2.00 | Severely wet | 4.4 |
| SPI < 1.50 | Moderately wet | 9.2 |
| SPI < 1.00 | Mildly wet | 34.1 |
| −1.00 ≤ SPI < 0.00 | Mild drought | 34.1 |
| −1.50 ≤ SPI < −1.00 | Moderate drought | 9.2 |
| −2.00 ≤ SPI < −1.50 | Severe drought | 4.4 |
| SPI < −2.00 | Extreme drought | 2.3 |
| ITA Variables | Values |
|---|---|
| Trend slope | −0.083083 |
| Trend indicator | −3.214672 |
| Correlation | 0.985378 |
| Slope standard deviation | 0.002202 |
| Confidence Limit () | 0.003415 |
| Variables | Mann–Kendall | Modified Mann–Kendall |
|---|---|---|
| slope | ||
| S | ||
| Var(s) | ||
| z-value | ||
| p-value | ||
| Decision (Trend) | Decreasing | Decreasing |
| SPI-6 | SPI-9 | SPI-12 | |||
|---|---|---|---|---|---|
| Model | AIC | Model | AIC | Model | AIC |
| ARIMA (0,1,1) | 378.558 | ARIMA (2,1,0) | 278.225 | ARIMA (0,1,0) | 77.828 |
| ARIMA (1,0,1) | 364.877 | ARIMA (3,1,1) | 253.817 | ARIMA (1,1,0) | 79.810 |
| ARIMA (1,1,1) | 366.480 | ARIMA (4,0,1) | 250.291 | ARIMA (0,1,1) | 79.813 |
| ARIMA (2,1,0) | 366.163 | ARIMA (4,1,2) | 252.270 | ARIMA (1,1,1) | 80.713 |
| ARIMA (2,1,1) | 367.573 | ARIMA (5,1,2) | 251.784 | ARIMA (0,2,0) | 80.810 |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Number of LSTM units | [32, 256] | Activation function | ReLU |
| Number of LSTM hidden units | [32, 25] | Optimizer | Adam |
| Batch size | [16, 128] | Loss function | Mean square error |
| Epoch | [50, 300] | Dropout | [0.05, 0.1] |
| LSTM learning rate | [0.0001, 0.001] | Regularization | Early stopping |
| Model | SPI-6 | SPI-9 | SPI-12 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | DS | RMSE | DS | RMSE | DS | ||||
| ARIMA | 0.262 | 0.872 | 0.867 | 0.118 | 0.964 | 0.850 | 0.059 | 0.981 | 0.867 |
| LSTM | 0.234 | 0.897 | 0.883 | 0.081 | 0.984 | 0.883 | 0.058 | 0.984 | 0.883 |
| ARIMA-LSTM | 0.186 | 0.931 | 0.883 | 0.077 | 0.983 | 0.867 | 0.057 | 0.985 | 0.900 |
| CEEMDAN-ARIMA | 0.169 | 0.945 | 0.850 | 0.083 | 0.983 | 0.833 | 0.054 | 0.984 | 0.933 |
| CEEMDAN-LSTM | 0.178 | 0.938 | 0.800 | 0.066 | 0.987 | 0.917 | 0.047 | 0.989 | 0.950 |
| CEEMDAN-ARIMA-LSTM | 0.121 | 0.972 | 0.950 | 0.044 | 0.991 | 0.917 | 0.042 | 0.995 | 0.950 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sibiya, S.; Mbatha, N.; Ramroop, S.; Melesse, S.; Silwimba, F. Forecasting of Standardized Precipitation Index Using Hybrid Models: A Case Study of Cape Town, South Africa. Water 2024, 16, 2469. https://doi.org/10.3390/w16172469
Sibiya S, Mbatha N, Ramroop S, Melesse S, Silwimba F. Forecasting of Standardized Precipitation Index Using Hybrid Models: A Case Study of Cape Town, South Africa. Water. 2024; 16(17):2469. https://doi.org/10.3390/w16172469
Chicago/Turabian StyleSibiya, Siphamandla, Nkanyiso Mbatha, Shaun Ramroop, Sileshi Melesse, and Felix Silwimba. 2024. "Forecasting of Standardized Precipitation Index Using Hybrid Models: A Case Study of Cape Town, South Africa" Water 16, no. 17: 2469. https://doi.org/10.3390/w16172469
APA StyleSibiya, S., Mbatha, N., Ramroop, S., Melesse, S., & Silwimba, F. (2024). Forecasting of Standardized Precipitation Index Using Hybrid Models: A Case Study of Cape Town, South Africa. Water, 16(17), 2469. https://doi.org/10.3390/w16172469







