Transboundary Water Allocation under Water Scarcity Based on an Asymmetric Power Index Approach with Bankruptcy Theory
Abstract
:1. Introduction
2. Methods
2.1. Step 1: Collect Basic Data and Information on Transboundary Water Allocation System
2.2. Step 2: Aggregate Multiple Characteristic Factors That Affect the Decision-Making Agent’s External Power into Their Negotiation Weight Coefficients
2.3. Step 3: Calculate the Disagreement Utility Value of the Decision-Making Agents
2.4. Step 4: Propose the Water Allocation Framework Using the Asymmetric Power Index Approach
3. Study Area and Data
3.1. Study Area
3.2. Data Collection and Analysis
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Tian, J.; Yu, Y.; Li, T.; Zhou, Y.; Li, J.; Wang, X.; Han, Y. A cooperative game model with bankruptcy theory for water allocation: A case study in China Tarim River Basin. Environ. Sci. Pollut. Res. 2022, 29, 2353–2364. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Pan, Z.; Li, H.; Wang, D.; Wang, J.; Wu, C.; Wu, X. Study on the Spatiotemporal Evolution and Driving Factors of Water Resource Carrying Capacity in Typical Arid Regions. Water 2024, 16, 2142. [Google Scholar] [CrossRef]
- Ssekyanzi, G.; Ahmad, M.J.; Choi, K.S. Sustainable Solutions for Mitigating Water Scarcity in Developing Countries: A Comprehensive Review of Innovative Rainwater Storage Systems. Water 2024, 16, 2394. [Google Scholar] [CrossRef]
- Eliasson, J. The rising pressure of global water shortages. Nature 2015, 517, 6. [Google Scholar] [CrossRef]
- UN. The Sustainable Development Goals Report 2022; UN: New York, NY, USA, 2022. [Google Scholar]
- Qin, J.; Fu, X.; Peng, S.; Xu, Y.; Huang, J.; Huang, S. Asymmetric Bargaining Model for Water Resource Allocation over Transboundary Rivers. Int. J. Environ. Res. Public Health 2019, 16, 1733. [Google Scholar] [CrossRef]
- Zeng, Y.; Li, J.; Cai, Y.; Tan, Q. Equitable and reasonable freshwater allocation based on a multi-criteria decision making approach with hydrologically constrained bankruptcy rules. Ecol. Indic. 2017, 73, 203–213. [Google Scholar] [CrossRef]
- Giuliani, M.; Castelletti, A.; Amigoni, F.; Cai, X. Multiagent systems and distributed constraint reasoning for regulatory mechanism design in water management. J. Water Resour. Plan. Manag. 2015, 141, 04014068. [Google Scholar] [CrossRef]
- Read, L.; Madani, K.; Inanloo, B. Optimality versus stability in water resource allocation. J. Manag. Eng. 2014, 133, 343–354. [Google Scholar] [CrossRef]
- Housh, M. Optimizing bilinear multi-source water supply systems using mixed-integer linear programming approximations: An analysis of the Israeli seawater desalination array. Adv. Water Resour. 2023, 178, 104498. [Google Scholar] [CrossRef]
- Nematollahi, B.; Nikoo, M.R.; Gandomi, A.H.; Talebbeydokhti, N.; Rakhshandehroo, G.R. A Multi-criteria Decision-making Optimization Model for Flood Management in Reservoirs. Water Resour. Manag. 2022, 36, 4933–4949. [Google Scholar] [CrossRef]
- Ayele, W.T.; Tenagashaw, D.Y.; Belew, A.Z.; Andualem, T.G. Optimal Water Allocation Under Climate Change, Based on Stochastic Dynamic Programming Model Approach in Ribb Reservoir, Amhara, Ethiopia. Water Conserv. Sci. Eng. 2022, 7, 33–44. [Google Scholar] [CrossRef]
- Tabari, M.M.R.; Safari, R. Development of water re-allocation policy under uncertainty conditions in the inflow to reservoir and demands parameters: A case study of Karaj AmirKabir dam. Soft. Comput. 2023, 27, 6521–6547. [Google Scholar] [CrossRef]
- Li, S.; He, Y.; Chen, X.; Zheng, Y. The improved bankruptcy method and its application in regional water resource allocation. J. Hydro-Environ. Res. 2020, 28, 48–56. [Google Scholar] [CrossRef]
- Degefu, D.M.; He, W.; Yuan, L.; Zhao, J. Water Allocation in Transboundary River Basins under Water Scarcity: A Cooperative Bargaining Approach. Water Resour Manag. 2016, 30, 4451–4466. [Google Scholar] [CrossRef]
- Madani, K.; Zarezadeh, M.; Morid, S. A new framework for resolving conflicts over transboundary rivers using bankruptcy methods. Hydrol. Earth Syst. Sci. 2014, 18, 3055–3068. [Google Scholar] [CrossRef]
- Darvishi Boloorani, A.; Najafi Marghmaleki, S.; Soleimani, M.; Papi, R.; Kardan Moghaddam, H.; Samany, N.N. Development of a scenario-based approach using game theory for the restoration of Hawizeh Marsh and dust mitigation. Hydrol. Sci. J. 2022, 68, 131–147. [Google Scholar] [CrossRef]
- Eleftheriadou, E.; Mylopoulos, Y. Game Theoretical Approach to Conflict Resolution in Transboundary Water Resources Management. J. Water Resour. Plan. Manag. 2008, 134, 466–473. [Google Scholar] [CrossRef]
- Kucukmehmetoglu, M. An integrative case study approach between game theory and Pareto frontier concepts for the transboundary water resources allocations. J. Hydrol. 2012, 450–451, 308–319. [Google Scholar] [CrossRef]
- Mehrparvar, M.; Ahmadi, A.; Safavi, H.R. Resolving water allocation conflicts using WEAP simulation model and non-cooperative game theory. Simulation 2020, 96, 17–30. [Google Scholar] [CrossRef]
- Madani, K.; Hipel, K.W. Non-Cooperative Stability Definitions for Strategic Analysis of Generic Water Resources Conflicts. Water Resour. Manag. 2011, 25, 1949–1977. [Google Scholar] [CrossRef]
- Sedghamiz, A.; Nikoo, M.R.; Heidarpour, M.; Sadegh, M. Developing a non-cooperative optimization model for water and crop area allocation based on leader-follower game. J. Hydrol. 2018, 567, 51–59. [Google Scholar] [CrossRef]
- Houba, H.; Do, K.H.P.; Zhu, X. Saving a river: A joint management approach to the Mekong River Basin. Environ. Dev. Econ. 2012, 18, 93–109. [Google Scholar] [CrossRef]
- Madani, K.; Hooshyar, M. A game theory-reinforcement learning (GT-RL) method to develop optimal operation policies for multi-operator reservoir systems. J. Hydrol. 2014, 519, 732–742. [Google Scholar] [CrossRef]
- Noori, M.; Emadi, A.; Fazloula, R. An agent-based model for water allocation optimization and comparison with the game theory approach. Water Supply 2021, 21, 3584–3601. [Google Scholar] [CrossRef]
- Gómez, R.; Weikard, H.P. Cooperative water-sharing agreements between highlands and drylands: The Tambo-Santiago-Ica river basin in Peru. Int. J. Water Resour. Dev. 2023, 39, 796–818. [Google Scholar] [CrossRef]
- Far, S.M.; Ashofteh, P.S. Optimization Operation of Water Resources Using Game Theory and Marine Predator Algorithm. Water Resour. Manag. 2024, 38, 665–699. [Google Scholar] [CrossRef]
- Janjua, S.; Hassan, I. Use of bankruptcy methods for resolving interprovincial water conflicts over transboundary river: Case study of Indus River in Pakistan. River Res. Appl. 2020, 36, 1334–1344. [Google Scholar] [CrossRef]
- Mianabadi, H.; Mostert, E.; Zarghami, M.; van de Giesen, N. A new bankruptcy method for conflict resolution in water resources allocation. J. Manag. Eng. 2014, 144, 152–159. [Google Scholar] [CrossRef]
- Fletcher, S.; Hadjimichael, A.; Quinn, J.; Osman, K.; Giuliani, M.; Gold, D.; Figueroa, A.J.; Gordon, B. Equity in water resources planning: A path forward for decision support modelers. J. Water Resour. Plan. Manag. 2022, 148, 02522005. [Google Scholar] [CrossRef]
- Gullotta, A.; Campisano, A.; Creaco, E.; Modica, C. A Simplified Methodology for Optimal Location and Setting of Valves to Improve Equity in Intermittent Water Distribution Systems. Water Resour. Manag. 2021, 35, 4477–4494. [Google Scholar] [CrossRef]
- Nyahora, P.P.; Babel, M.S.; Ferras, D.; Emen, A. Multi-objective optimization for improving equity and reliability in intermittent water supply systems. Water Supply 2020, 20, 1592–1603. [Google Scholar] [CrossRef]
- Yang, G.; Giuliani, M.; Castelletti, A. Operationalizing equity in multipurpose water systems. Hydrol. Earth Syst. Sci. 2023, 27, 69–81. [Google Scholar] [CrossRef]
- Koh, H. Why do nations obey International Law? Yale Law J. 1997, 106, 2599–2659. [Google Scholar] [CrossRef]
- Konow, J. Which is the fairest one of all? A positive analysis of justice theories. J. Econ. Lit. 2003, 41, 1188–1239. [Google Scholar] [CrossRef]
- Rahaman, M.M. Principles of transboundary water resources management and water-related agreements in Central Asia: An analysis. Int. J. Water Resour. Dev. 2012, 28, 475–491. [Google Scholar] [CrossRef]
- Shapley, L.S.; Shubik, S.M. A method for evaluating the distribution of power in a committee. Am. Polit. Sci. Rev. 1954, 48, 787–792. [Google Scholar] [CrossRef]
- Loehman, E.; Orlando, J.; Tschirhart, J.; Whinston, A. Cost allocation for a regional wastewater treatment system. Water Resour. Res. 1979, 15, 193–202. [Google Scholar] [CrossRef]
- Dinar, A.; Howitt, R.E. Mechanisms for Allocation of Environmental Control Cost: Empirical Tests of Acceptability and Stability. J. Manag. Eng. 1997, 49, 183–203. [Google Scholar] [CrossRef]
- Masood, M.; Ahmad, I.; Sarwar, M.K.; Khan, N.M.; Waseem, M.; Nabi, G.; Saleem, M. A Bilevel Multiobjective Model for Optimal Allocation of Water Resources in the Punjab Province of Pakistan. Arab. J. Sci. Eng. 2021, 46, 10597–10612. [Google Scholar] [CrossRef]
- Wu, W.; Zhao, X.; Zhang, X.; Wu, X.; Zhao, Y.; Guo, Q.; Yao, L.; Liu, X. An ordered multi-objective fuzzy stochastic approach to sustainable water resources management: A case study from Taiyuan City, China. Water Supply 2024, 24, 10–11. [Google Scholar] [CrossRef]
- Hussein, H.; Grandi, M. Dynamic political contexts and power asymmetries: The cases of the Blue Nile and the Yarmouk Rivers. Int. Environ. Agreem. 2017, 17, 795–814. [Google Scholar] [CrossRef]
- Zeitoun, M.; Mirumachi, N.; Warner, J.F. Transboundary water interaction II. Int. Environ. Agreem. 2011, 11, 159–178. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The critic method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Rostamzadeh, R.; Ghorabaee, M.K.; Govindan, K.; Esmaeili, A.; Nobar, H.B.K. Evaluation of sustainable supply chain risk management using an integrated fuzzy TOPSIS-CRITIC approach. J. Clean. Prod. 2018, 175, 651–669. [Google Scholar] [CrossRef]
- Curiel, I.J.; Maschler, M.; Tijs, S.H. Bankruptcy games. Math. Methods Oper. Res. 1987, 31, 143–159. [Google Scholar] [CrossRef]
- Wu, Q.; Xu, N. Improved interactive methods of multi-objective decision-making based on target satisfaction degree. J. Manag. Eng. 1996, 4, 217–222. [Google Scholar]
- Janjua, S.; Ali, M.U.; Kallu, K.D.; Zafar, A.; Hussain, S.J.; Gardezi, H.; Lee, S.W. An Asymmetric Bargaining Model for Natural-Gas Distribution. Appl. Sci. 2022, 12, 5677. [Google Scholar] [CrossRef]
- Gao, R.; Chen, H.; Wei, C.; Jiang, Y.; Zeng, S.; Zhang, C.; Jin, Y.; Zhang, W. Research Hotspots and Trends in the Environment Condition of the Yellow River Basin (2014–2024): A Bibliometric and Visualization. Water 2024, 16, 2359. [Google Scholar] [CrossRef]
- Omer, A.; Ma, Z.; Xing, Y.; Zheng, Z.; Saleem, F. A hydrological perspective on drought risk-assessment in the Yellow River Basin under future anthropogenic activities. J. Manag. Eng. 2021, 289, 112429. [Google Scholar] [CrossRef]
- Zhao, F.; Ma, S.; Wu, Y. Changes in Dry-Season Water Availability and Attributions in the Yellow River Basin, China. Front. Environ. Sci. 2021, 9, 762137. [Google Scholar] [CrossRef]
- Sun, X.; Zhou, Z.; Wang, Y. Water resource carrying capacity and obstacle factors in the Yellow River basin based on the RBF neural network model. Environ. Sci. Pollut. Res. 2023, 30, 22743–22759. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, J.; Cai, X. Decentralized Optimization Method for Water Allocation Management in the Yellow River Basin. J. Water Resour. Plan. Manag. 2012, 138, 313–325. [Google Scholar] [CrossRef]
- Zhou, K.; Wang, Y.; Chang, J.; Zhou, S.; Guo, A. Spatial and Temporal Evolution of Drought Characteristics Across the Yellow River basin. Ecol. Indic. 2021, 131, 108207. [Google Scholar] [CrossRef]
- Herrero, C.; Villar, A. The three musketeers: Four classical solutions to bankruptcy problems. Math. Soc. Sci. 2001, 42, 307–328. [Google Scholar] [CrossRef]
- Thomson, W. Axiomatic and game-theoretic analysis of bankruptcy and taxation problems: An update. Math. Soc. Sci. 2015, 74, 41–59. [Google Scholar] [CrossRef]
- UN Watercourses Convention. Convention on the Law of the Non-navigational Uses of International Watercourses. Adopted by the General Assembly of the United Nations on 21 May 1997. Available online: https://unece.org/environment-policy/water/un-watercourses-convention (accessed on 1 September 2024).


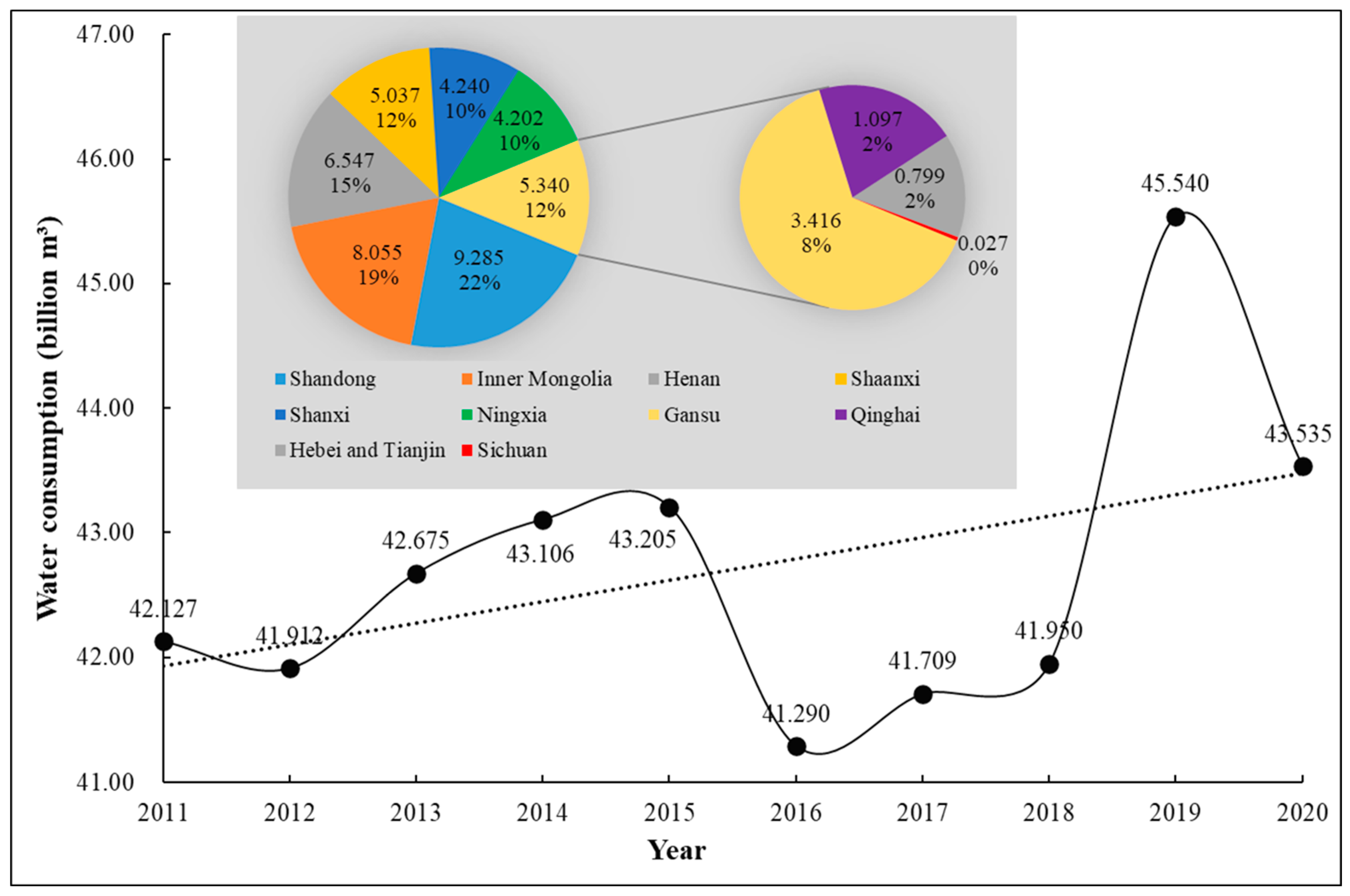
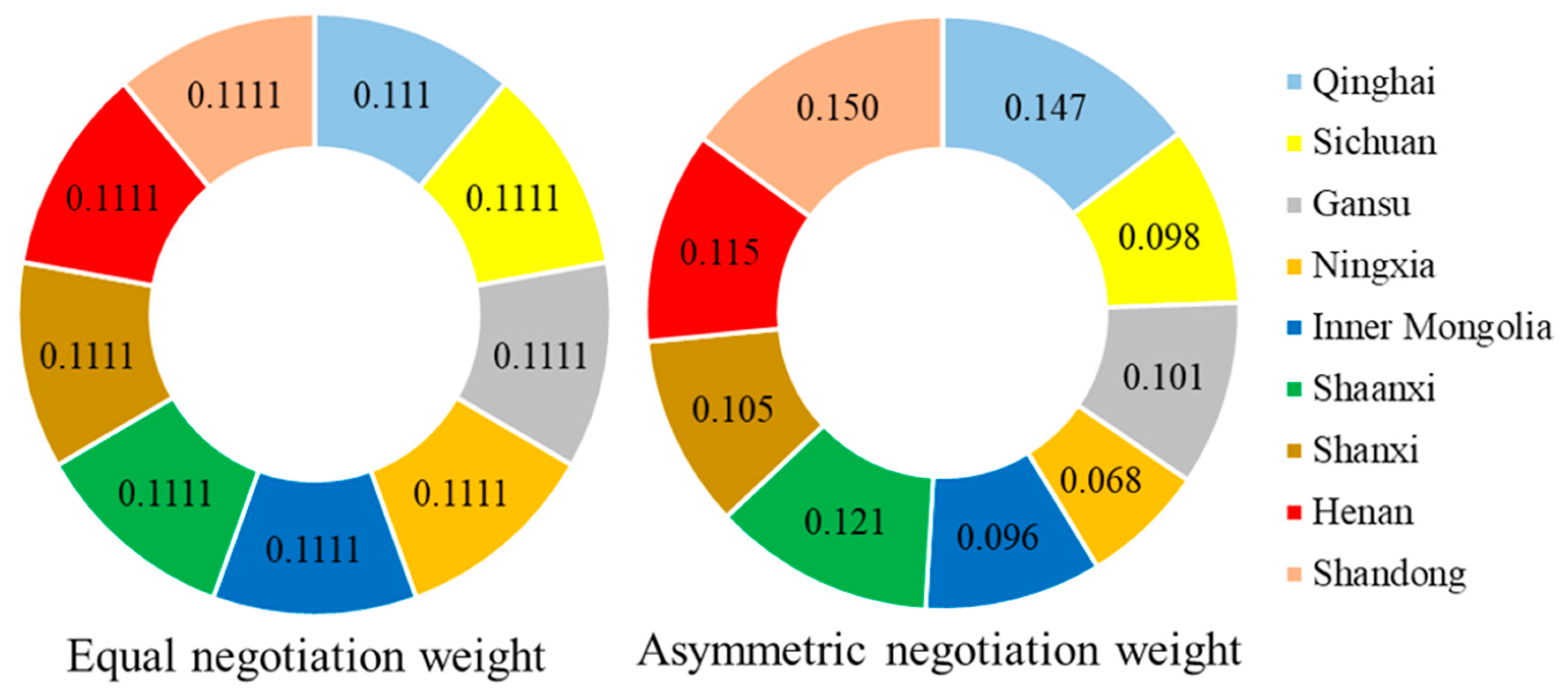


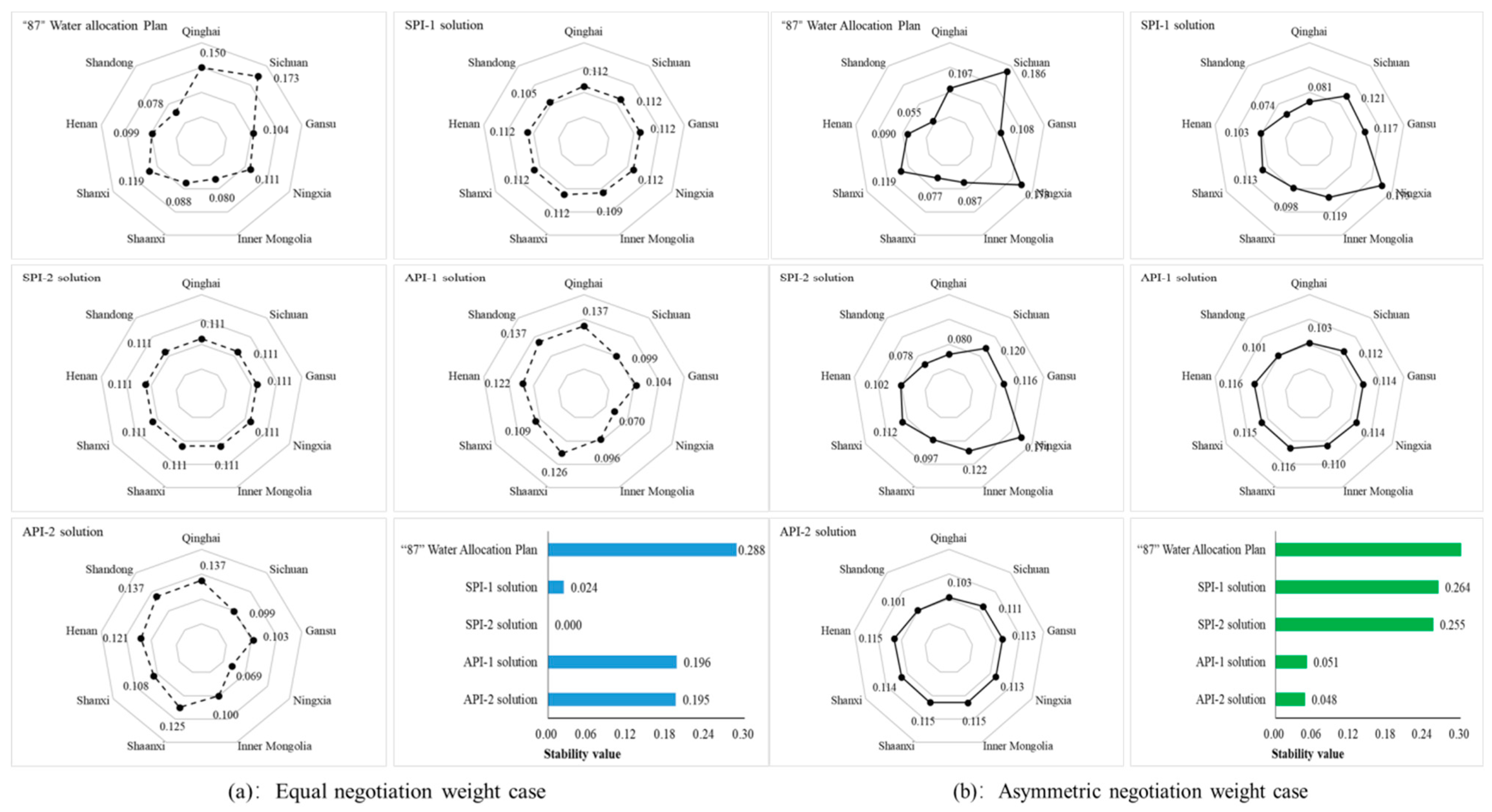
| Objective Layer | Criterion Layer | Indicator Layer | Unit | Attribute |
|---|---|---|---|---|
| Solving the transboundary water allocation conflicts under scarcity | Water contribution | Proportion of annual average runoff to the total runoff of the entire watershed | % | Positive |
| Respecting the current situation | Current water consumption | 108 m3 | Positive | |
| Economic efficiency | Economic output per cubic meter of water consumption | Yuan/m3 | Positive | |
| Eco-environmental sustainability | Reserved water for inner-river eco-environment | 108 m3 | Positive | |
| Sewage discharged | 108 ton | Negative |
| Existing Planning | Decision-Making Agents | Off-Stream Water Allocation | Inner-river Water Allocation | Total | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Qinghai | Sichuan | Gansu | Ningxia | Inner Mongolia | Shaanxi | Shanxi | Henan | Shandong | Hebei and Tianjin | ||||
| “87” Water Allocation Plan | 1.410 | 0.040 | 3.040 | 4.000 | 5.860 | 3.800 | 4.310 | 5.540 | 7.000 | 2.000 | 37.000 | 21.000 | 58.000 |
| Yellow River Basin Plan | 1.316 | 0.037 | 2.837 | 3.732 | 5.468 | 3.546 | 4.022 | 5.169 | 6.532 | 0.620 | 33.279 | 18.700 | 51.979 |
| Indicator | Unit | Decision-Making Agents | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Qinghai | Sichuan | Gansu | Ningxia | Inner Mongolia | Shaanxi | Shanxi | Henan | Shandong | ||
| Proportion of annual average runoff to the total runoff of the entire watershed | % | 34.05 | 7.82 | 20.11 | 1.56 | 3.44 | 14.94 | 8.15 | 7.18 | 2.75 |
| Current water consumption | 108 m3 | 10.64 | 0.20 | 30.30 | 44.19 | 84.52 | 50.09 | 43.03 | 65.18 | 88.87 |
| Economic output per cubic meter of water consumption | Yuan/m3 | 123.80 | 205.18 | 82.05 | 55.85 | 89.30 | 288.98 | 242.47 | 231.96 | 328.67 |
| Reserved water for riverine eco-environment | 108 m3 | 71.51 | 16.43 | 42.22 | 3.29 | 7.23 | 31.36 | 17.12 | 15.08 | 5.78 |
| Sewage discharged | 108 ton | 1.41 | 0.03 | 4.72 | 3.12 | 5.72 | 9.89 | 6.64 | 6.94 | 5.54 |
| Existing Planning | Decision-Making Agents | Total | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Qinghai | Sichuan | Gansu | Ningxia | Inner Mongolia | Shaanxi | Shanxi | Henan | Shandong | ||
| Water demand | 1.097 | 0.027 | 3.416 | 4.202 | 8.055 | 5.037 | 4.240 | 6.547 | 9.285 | 41.906 |
| “87” Water Allocation Plan | 0 | 0 | 0 | 0 | 1.149 | 0 | 0 | 0 | 2.379 | 3.528 |
| Yellow River Basin Plan | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.038 | 0.038 |
| Allocation Scenarios | Decision-Making Agents | PRO | SPI-1 | SPI-2 | API-1 | API-2 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Available water quantity under the “87” Water Allocation Plan | Qinghai | 9.17 | 1.81 | 9.17 | 1.81 | 9.00 | 1.97 | 10.97 | 0.00 | 10.97 | 0.00 |
| Sichuan | 0.23 | 0.04 | 0.23 | 0.04 | 0.22 | 0.05 | 0.20 | 0.07 | 0.19 | 0.08 | |
| Gansu | 28.53 | 5.63 | 28.53 | 5.63 | 28.01 | 6.15 | 26.04 | 8.12 | 25.76 | 8.40 | |
| Ningxia | 35.09 | 6.92 | 35.09 | 6.92 | 34.46 | 7.56 | 21.40 | 20.62 | 21.17 | 20.85 | |
| Inner Mongolia | 67.28 | 13.27 | 67.28 | 13.27 | 68.12 | 12.43 | 59.96 | 20.59 | 62.04 | 18.52 | |
| Shaanxi | 42.07 | 8.30 | 42.07 | 8.30 | 41.30 | 9.06 | 46.50 | 3.87 | 45.97 | 4.39 | |
| Shanxi | 35.41 | 6.99 | 35.41 | 6.99 | 34.77 | 7.63 | 33.80 | 8.60 | 33.43 | 8.97 | |
| Henan | 54.68 | 10.79 | 54.68 | 10.79 | 53.69 | 11.78 | 58.28 | 7.19 | 57.60 | 7.87 | |
| Shandong | 77.55 | 15.30 | 77.55 | 15.30 | 80.42 | 12.43 | 92.85 | 0.00 | 92.85 | 0.00 | |
| Total | 350.00 | 69.06 | 350.00 | 69.06 | 350.00 | 69.06 | 350.00 | 69.06 | 350.00 | 69.06 | |
| Qinghai | 8.55 | 2.42 | 8.55 | 2.42 | 8.55 | 2.42 | 10.97 | 0.00 | 10.97 | 0.00 | |
| Available water quantity under the Yellow River Basin Plan | Sichuan | 0.21 | 0.06 | 0.21 | 0.06 | 0.21 | 0.06 | 0.18 | 0.09 | 0.18 | 0.09 |
| Gansu | 26.62 | 7.54 | 26.62 | 7.54 | 26.62 | 7.54 | 23.79 | 10.37 | 23.79 | 10.37 | |
| Ningxia | 32.74 | 9.27 | 32.74 | 9.27 | 32.74 | 9.28 | 19.60 | 22.42 | 19.60 | 22.42 | |
| Inner Mongolia | 62.78 | 17.77 | 62.78 | 17.77 | 62.76 | 17.79 | 53.91 | 26.64 | 53.91 | 26.64 | |
| Shaanxi | 39.25 | 11.11 | 39.25 | 11.11 | 39.24 | 11.12 | 42.07 | 8.29 | 42.07 | 8.29 | |
| Shanxi | 33.04 | 9.36 | 33.04 | 9.36 | 33.04 | 9.36 | 30.77 | 11.63 | 30.77 | 11.63 | |
| Henan | 51.02 | 14.45 | 51.02 | 14.45 | 51.01 | 14.46 | 52.44 | 13.03 | 52.44 | 13.03 | |
| Shandong | 72.36 | 20.49 | 72.36 | 20.49 | 72.43 | 20.42 | 92.85 | 0.00 | 92.85 | 0.00 | |
| Total | 326.59 | 92.47 | 326.59 | 92.47 | 326.59 | 92.47 | 326.59 | 92.47 | 326.59 | 92.47 | |
| Agents | “87” Water Allocation Plan | Yellow River Basin Plan | ||
|---|---|---|---|---|
| SPI-2~SPI-1 | API-2~API-1 | SPI-2~SPI-1 | API-2~API-1 | |
| Qinghai | −1.52 | 0.00 | −0.02 | 0.00 |
| Sichuan | −1.52 | −0.71 | −0.02 | 0.00 |
| Gansu | −1.52 | −0.81 | −0.02 | 0.00 |
| Ningxia | −1.52 | −0.53 | −0.02 | 0.00 |
| Inner Mongolia | 1.05 | 2.58 | −0.02 | 0.00 |
| Shaanxi | −1.52 | −1.04 | −0.02 | 0.00 |
| Shanxi | −1.51 | −0.87 | −0.02 | 0.00 |
| Henan | −1.52 | −1.04 | −0.02 | 0.00 |
| Shandong | 3.10 | 0.00 | 0.07 | 0.00 |
| Agents | Water Allocation Satisfaction | Relative Changes in Water Allocation Satisfaction | ||
|---|---|---|---|---|
| “87” Water Allocation Plan | Yellow River Basin Plan | “87” Water Allocation Plan | Yellow River Basin Plan | |
| Qinghai | 128.49 | 119.92 | −28.49 | −19.92 |
| Sichuan | 148.15 | 137.04 | −76.25 | −69.82 |
| Gansu | 88.99 | 83.05 | −13.58 | −13.40 |
| Ningxia | 95.20 | 88.82 | −44.81 | −42.19 |
| Inner Mongolia | 72.75 | 67.88 | 4.26 | −0.96 |
| Shaanxi | 75.45 | 70.41 | 15.83 | 13.13 |
| Shanxi | 101.65 | 94.86 | −22.80 | −22.29 |
| Henan | 84.62 | 78.95 | 3.37 | 1.15 |
| Shandong | 75.39 | 70.35 | 24.61 | 29.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, J.; Fu, X.; Wu, X.; Wang, J.; Huang, J.; Chen, X.; Liu, J.; Zhang, J. Transboundary Water Allocation under Water Scarcity Based on an Asymmetric Power Index Approach with Bankruptcy Theory. Water 2024, 16, 2828. https://doi.org/10.3390/w16192828
Qin J, Fu X, Wu X, Wang J, Huang J, Chen X, Liu J, Zhang J. Transboundary Water Allocation under Water Scarcity Based on an Asymmetric Power Index Approach with Bankruptcy Theory. Water. 2024; 16(19):2828. https://doi.org/10.3390/w16192828
Chicago/Turabian StyleQin, Jianan, Xiang Fu, Xia Wu, Jing Wang, Jie Huang, Xuxun Chen, Junwu Liu, and Jiantao Zhang. 2024. "Transboundary Water Allocation under Water Scarcity Based on an Asymmetric Power Index Approach with Bankruptcy Theory" Water 16, no. 19: 2828. https://doi.org/10.3390/w16192828
APA StyleQin, J., Fu, X., Wu, X., Wang, J., Huang, J., Chen, X., Liu, J., & Zhang, J. (2024). Transboundary Water Allocation under Water Scarcity Based on an Asymmetric Power Index Approach with Bankruptcy Theory. Water, 16(19), 2828. https://doi.org/10.3390/w16192828






