Analysis of Local Scour around Double Piers in Tandem Arrangement in an S-Shaped Channel under Ice-Jammed Flow Conditions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dimensional Analysis
2.2. Experimental Setup
2.3. Experiment Procedure
- (1)
- At the beginning of each experiment, the sand bed in the flume was leveled using a sand scraper to maintain an even surface. Flow stability was achieved by controlling the weir head at the upstream rectangular weir through precise adjustments to the pipe valve.
- (2)
- The flow depth in the flume was gradually increased by slow rotation of the pipe valve to avoid rapid rises that could result in riverbed scour. Once the flow depth stabilized, the valve was adjusted to reach desired experimental conditions, as monitored in the upstream CS-3 piezometer tube. The experiment proceeded only when the flow depth remained constant for 10 min.
- (3)
- A simulated ice cover was installed between CS-25 and CS-26, and the piers were placed in designated positions in the flume. The ice hopper was simultaneously opened to initiate ice flow around the pier. The mass of model ice corresponding to the experiment condition Qi was added to the ice hopper every 10 min.
- (4)
- Upon commencement of the experiment, the local scour depths around the tandem double piers were recorded by a point gauge accurate to 0.1 mm initially every 5 min for 30 min, then every 10 min for the next 30 min, and subsequently every 30 min. Similar time intervals were used for recording the leading-edge development of the initial ice jams and their thickness at each cross-section.
- (5)
- An Acoustic Doppler Velocimeter (ADV) was positioned 2 cm in front of the tandem piers to measure velocity fields. The vertical distribution of flow velocity in front of the piers was measured by moving the probe up and down, with flow velocity data recorded at each location. Chiew [33] showed that the maximum local scour depth around a pier is related to the flow intensity. Under the ice-jammed flow condition, the flow intensity is enhanced because the ice jam of the cross-section where the pier is located narrows the flow section area, so the upstream flow velocity of the pier is measured. It is observed that the effect of the probe at this location on the scour hole is negligible. Subsequently, the point gauge was utilized to measure scour hole data near the pier, which included information on the local scour depth and range as well as the height and range of accumulation.
3. Results
3.1. Variation in Scour Depth and Average Ice Jam Thickness with Time
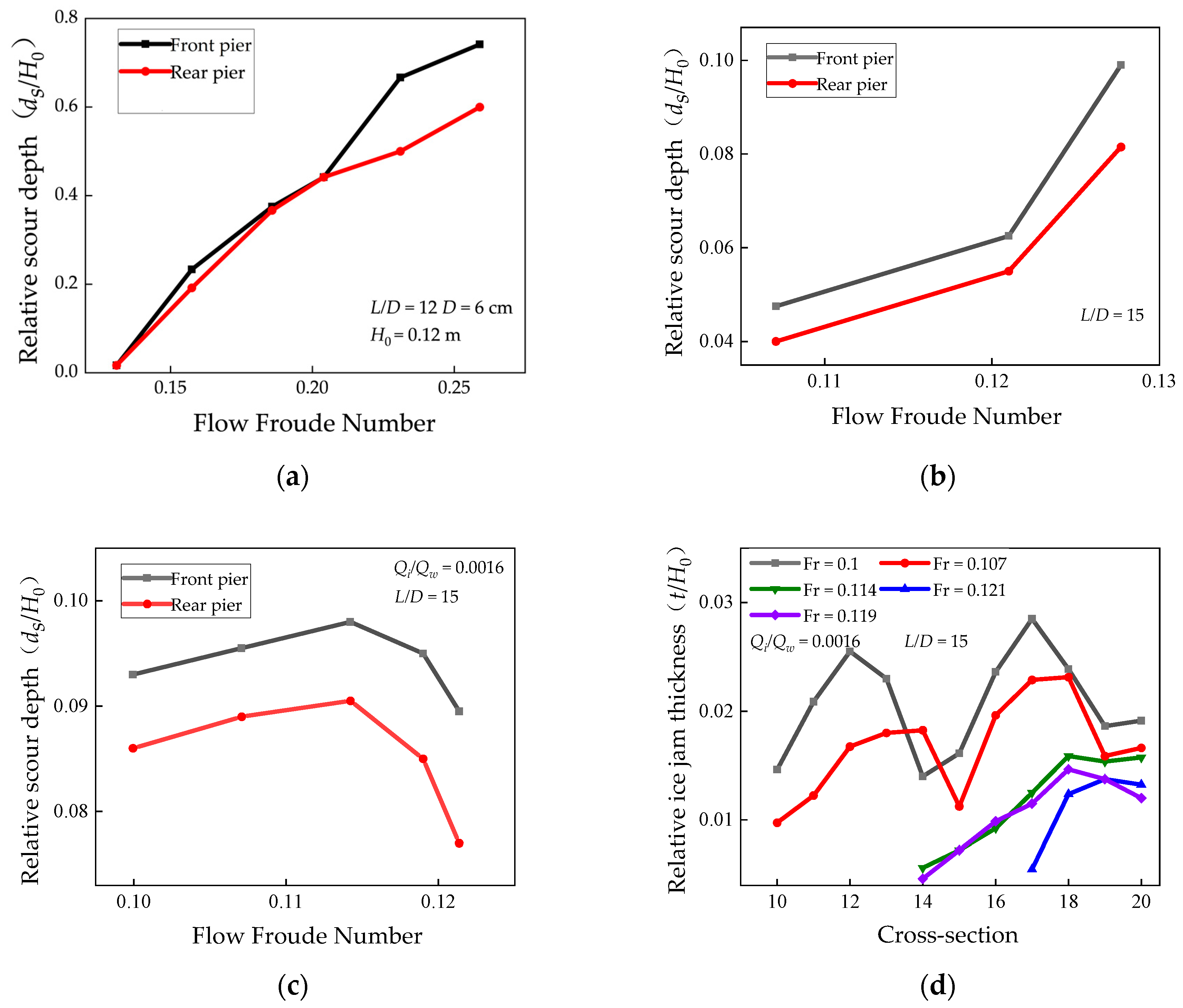
3.2. Influence of Flow Froude Number on Maximum Local Scour Depth and Ice Jam Thickness Distribution
3.3. Influence of Ice–Water Discharge Rate on Maximum Local Scour Depth and Ice Jam Thickness Distribution
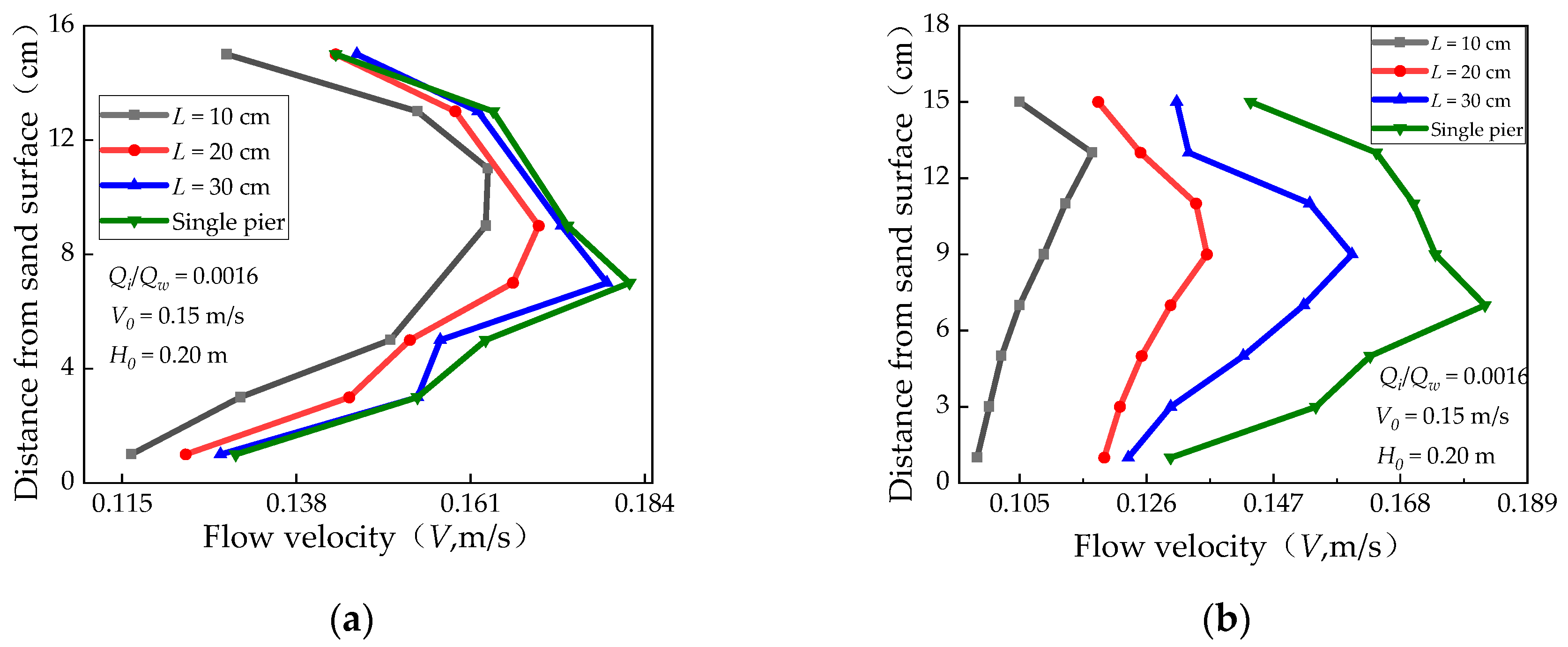
3.4. Influence of Pier Spacing and Pier Diameter on Maximum Local Scour Depth and Ice Jam Thickness Distribution
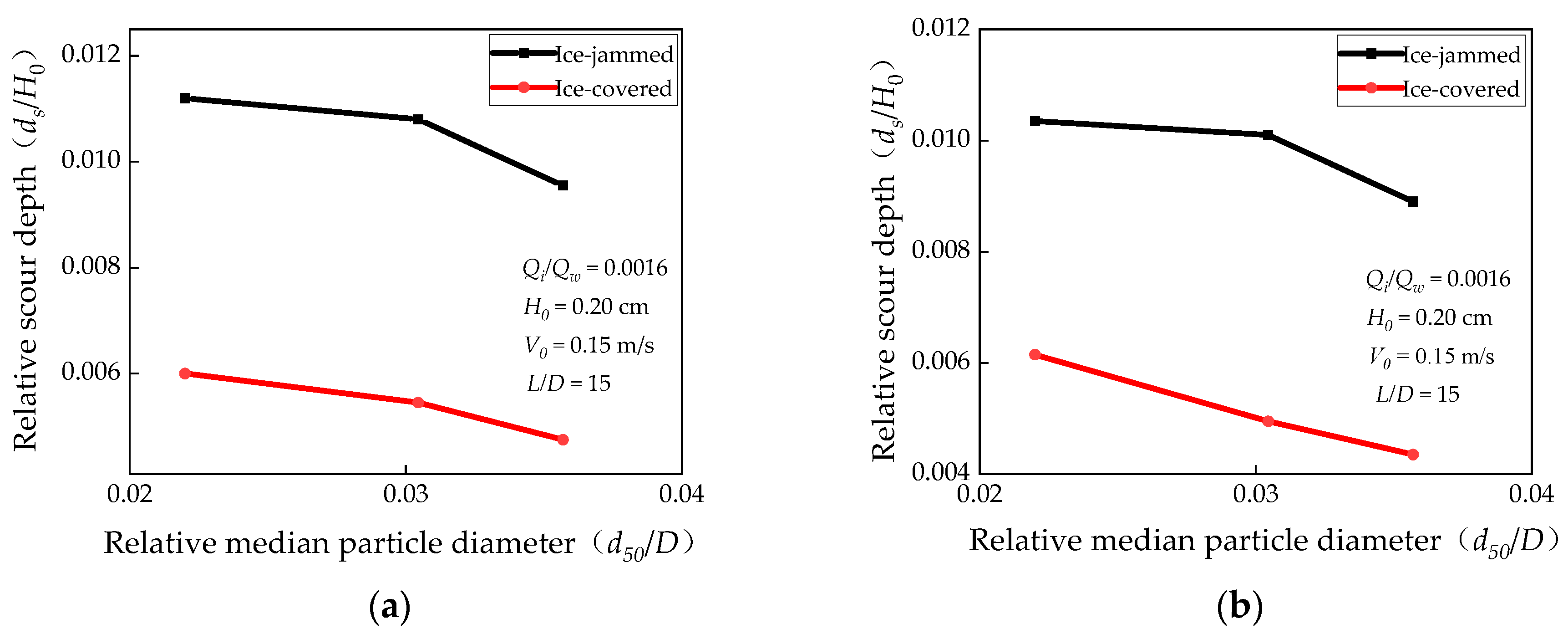
3.5. Influence of Median Particle Diameter on Maximum Local Scour Depth
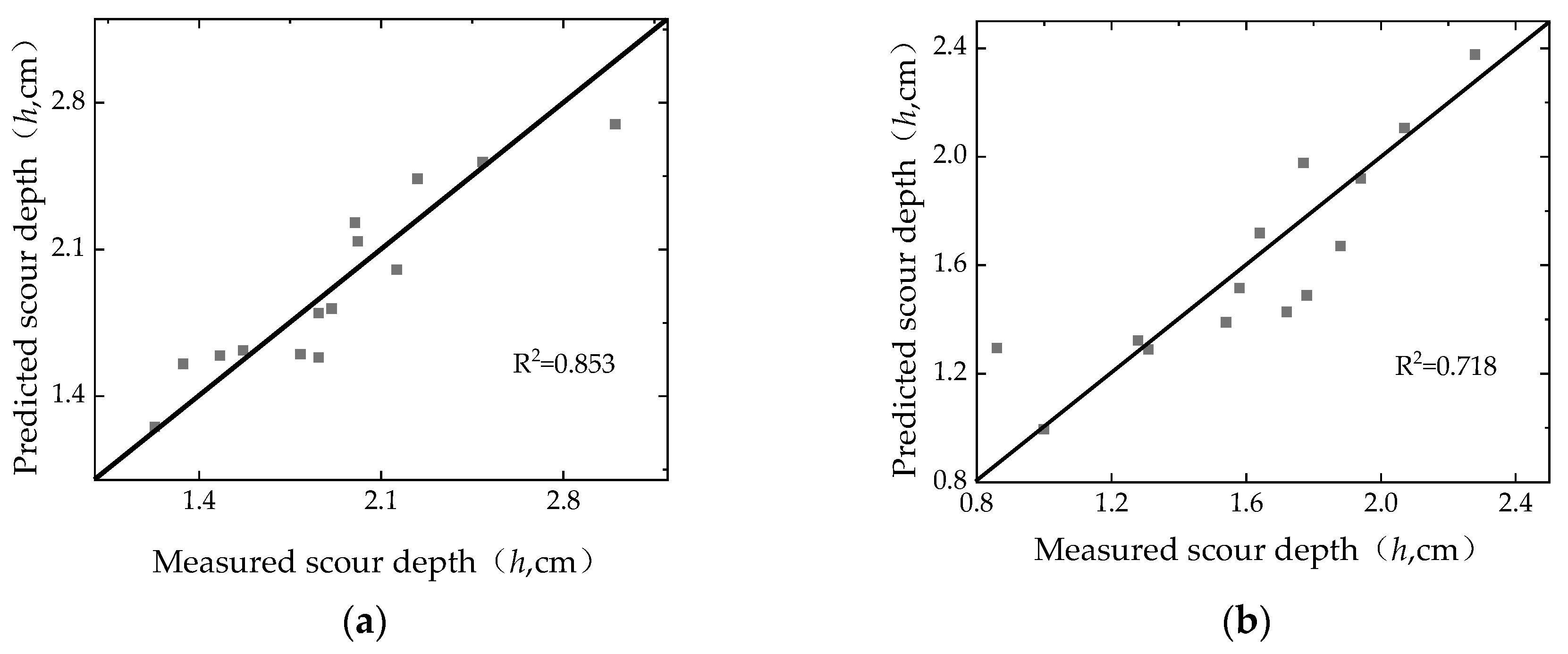
3.6. Regression Analysis of Maximum Local Scour Depth under Ice-Jammed Flow Condition
4. Discussions
- (1)
- Natural rivers vary significantly, each with its unique flow depth and velocity. Changes in these factors impact the local scour depth around piers and the distribution of ice jam thickness. This paper aims to study these mechanisms and explore their patterns. Therefore, it does not determine the flow depth and velocity for any specific river.
- (2)
- The bending coefficients of natural rivers vary greatly. The S-shaped bend used in this experiment has a relatively small bending coefficient, which is common in natural rivers [44]. Keshavarzi et al. [45] researched the effect of vegetation on bed topography. They also used the flume with a mildly curved meander bend. Different bending coefficients impact the local scour around piers and ice jam thickness distribution. Additionally, the shape and size of ice particles affect the local scour and ice jam thickness distribution, warranting further study.
- (3)
- A 1.8 cm thick Styrofoam panel simulated the ice cover between CS-25 and CS-26, where ice particles accumulated to form an ice jam. Under natural conditions, the thickness of the ice cover is not fixed. Different thicknesses of the ice cover will have a certain impact on the formation and accumulation of the upstream ice jam. When the thickness of the ice cover is relatively small, it may be difficult for the upstream ice jam to accumulate and thicken, leading to a relatively low-thickness ice jam. But the difference in the thickness of the ice cover is not within the scope of this study, and further research is needed.
- (4)
- Experimental measurements inherently contain errors. When using a piezometer to measure flow depth, water levels fluctuate slightly (about 0–1 mm), and the average flow depth is recorded. An ADV measures flow velocity, and water level fluctuations affect these readings, so the average value is used. Data collected from the ADV were filtered, analyzed, and processed using WinADV software (2.0.0024) [46]. The local scour depth around piers was measured with a point gauge accurate to 0.1 mm, while the ice jam thickness was measured with a ruler accurate to 0.1 cm. During the experiment, each measuring point was measured three times, and the value with the largest difference was removed. Finally, the average value was taken to reduce error. Measurement errors may arise from manual readings. In the experiment, the change range of the local scour depth and ice jam thickness under different conditions was much greater than the instrument accuracy, so these did not impact the study of general patterns of local scour around piers and ice jam thickness distribution under ice-covered and ice-jammed conditions at the mechanistic level.
- (5)
- It was observed that the maximum local scour depth and the distribution of ice jam thickness are affected by different pier spacings and arrangements. In the future, the influence of more pier arrangement forms (parallel arrangement), pier shapes, and different pier inclination angles on the maximum local scour depth around piers and ice jam thickness can be studied. It was observed in the experiment that the increase in the local scour depth around the pier will increase the thickness of the ice jam, which will further aggravate the local scour depth around the pier. Adding collar plates at the bottom of the pier can reduce the local scour depth around the pier [47,48]. This will reduce the flow section area, which may facilitate the ice transport of the river and reduce the thickness of the ice jam. Under the ice-jammed flow condition, the influence of the increase in the collar plates on the scour around the pier and the ice jam needs further study.
- (6)
- It was observed in the experiment that the local scour depth under the ice-jammed flow condition is greater than that under the open flow condition and ice-covered flow condition under the same approach flow depth and approach flow velocity. This needs to be properly considered in the planning and design of bridges affected by river ice in cold regions. It is necessary to consider not only the ice-induced abutment and pier local scour, but also the ice forces on piers and the ice passage [49]. However, the experiment only considered the impact of ice on pier local scour, and further experimental studies are needed for other factors.
5. Conclusions
- (1)
- Under ice-jammed conditions, temporal changes in scour depth around piers are more complex than under ice-covered conditions. The local scour rate increases as the ice wave crest passes a pier and decreases as the trough passes.
- (2)
- Under the condition of open flow and ice-covered flow, the flow Froude number is positively correlated with the maximum local scour depth around the piers. Under the condition of ice-jammed flow, if the ice–water discharge ratio is kept constant, the relationship between the flow Froude number and the maximum local scour depth around the pier is no longer single. A critical Froude number exists where the relationship changes: below this value, the correlation is positive; above it, the correlation turns negative, affecting ice jam thickness. At the critical value, the maximum local scour depth peaks. Increased ice–water discharge rates under ice-jammed conditions result in thicker ice jams and greater maximum local scour depths.
- (3)
- With constant flow conditions and ice–water discharge rates, wider pier spacing and larger pier diameters lead to thicker ice accumulation and increased ice jam thickness and local scour depths. For single piers, ice jam thickness and near-bottom velocity are greater than for tandem piers, resulting in deeper local scour depths for single piers. When designing bridge piers in cold regions, reducing pier spacing may be beneficial to the stability of bridge piers and ice transport in rivers. However, the experiment only considered the relationship between the pier spacing and the maximum local scour depth around piers under a specific flow condition. Due to the complex and various flow conditions in a natural river, the experimental results have some limitations in practical applications.
- (4)
- The multiple regression analysis produced Equations (4) and (5) for the relative equilibrium scouring depth (dS/H0), aligning closely with empirical data.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Beltaos, S. River Ice Jams; Water Resources Publications: Highlands Ranch, CO, USA, 1995; ISBN 978-0-918334-87-9. [Google Scholar]
- Beltaos, S.; Burrell, B.C. Hydraulic Interaction Between Ice and Bridges. In Proceedings of the 12th Workshop on the Hydraulics of Ice Covered Rivers, Edmonton, AB, Canada, 19–20 June 2003. [Google Scholar]
- Shahriar, A.R.; Ortiz, A.C.; Montoya, B.M.; Gabr, M.A. Bridge Pier Scour: An Overview of Factors Affecting the Phenomenon and Comparative Evaluation of Selected Models. Transp. Geotech. 2021, 28, 100549. [Google Scholar] [CrossRef]
- Ozgenc Aksoy, A.; Bombar, G.; Arkis, T.; Guney, M.S. Study of the Time-Dependent Clear Water Scour around Circular Bridge Piers. J. Hydrol. Hydromech. 2017, 65, 26–34. [Google Scholar] [CrossRef]
- Dey, S.; Raikar, R.V.; Roy, A. Scour at Submerged Cylindrical Obstacles under Steady Flow. J. Hydraul. Eng. 2008, 134, 105–109. [Google Scholar] [CrossRef]
- Dey, S.; Bose, S.K.; Sastry, G.L.N. Clear Water Scour at Circular Piers: A Model. J. Hydraul. Eng. 1995, 121, 869–876. [Google Scholar] [CrossRef]
- Jain, S.C. Maximum Clear-Water Scour around Circular Piers. J. Hydraul. Div. 1981, 107, 611–626. [Google Scholar] [CrossRef]
- Raudkivi, A.J.; Ettema, R. Clear-Water Scour at Cylindrical Piers. J. Hydraul. Eng. 1983, 109, 338–350. [Google Scholar] [CrossRef]
- Melville, B.W.; Chiew, Y.-M. Time Scale for Local Scour at Bridge Piers. J. Hydraul. Eng. 1999, 125, 59–65. [Google Scholar] [CrossRef]
- Oliveto, G.; Hager, W.H. Temporal Evolution of Clear-Water Pier and Abutment Scour. J. Hydraul. Eng. 2002, 128, 811–820. [Google Scholar] [CrossRef]
- Kim, H.S.; Nabi, M.; Kimura, I.; Shimizu, Y. Numerical Investigation of Local Scour at Two Adjacent Cylinders. Adv. Water Resour. 2014, 70, 131–147. [Google Scholar] [CrossRef]
- Amini, A.; Melville, B.W.; Ali, T.M.; Ghazali, A.H. Clear-Water Local Scour around Pile Groups in Shallow-Water Flow. J. Hydraul. Eng. 2012, 138, 177–185. [Google Scholar] [CrossRef]
- Bozkuş, Z.; Özalp, M.C.; Dinçer, A.E. Effect of Pier Inclination Angle on Local Scour Depth around Bridge Pier Groups. Arab. J. Sci. Eng. 2018, 43, 5413–5421. [Google Scholar] [CrossRef]
- Wang, H.; Tang, H.; Xiao, J.; Wang, Y.; Jiang, S. Clear-Water Local Scouring around Three Piers in a Tandem Arrangement. Sci. China Technol. Sci. 2016, 59, 888–896. [Google Scholar] [CrossRef]
- Liu, Q.-S.; Tang, H.-W.; Wang, H.; Xiao, J.-F. Critical Velocities for Local Scour around Twin Piers in Tandem. J. Hydrodyn. 2018, 30, 1165–1173. [Google Scholar] [CrossRef]
- Melville, B.W.; Dongol, D.M. Bridge pier scour with debris accumulation. J. Hydraul. Eng. 1992, 118, 1306–1310. [Google Scholar] [CrossRef]
- Pagliara, S.; Carnacina, I. Influence of large woody debris on sediment scour at bridge piers. Int. J. Sediment Res. 2011, 26, 121–136. [Google Scholar] [CrossRef]
- Lyn, D.A.; Cooper, T.J.; Yi, Y.-K.; Sinha, R.N.; Rao, A.R. Debris Accumulation at Bridge Crossings: Laboratory and Field Studies; Federal Highway Administration: Washington, DC, USA, 2003. [Google Scholar] [CrossRef]
- Hamidifar, H.; Shahabi-Haghighi, S.M.B.; Chiew, Y.M. Collar performance in bridge pier scour with debris accumulation. Int. J. Sediment Res. 2022, 37, 328–334. [Google Scholar] [CrossRef]
- Zhang, W.; Nistor, I.; Rennie, C.D. Influence of Debris Jam Formed by Trees on Bridge Pier Scour. J. Hydraul. Eng. 2024, 150, 04024035. [Google Scholar] [CrossRef]
- Ackermann, N.L.; Shen, H.T.; Olsson, P. Local Scour around Circular Piers under Ice Covers. In Proceedings of the 16th IAHR International Symposium on Ice, Dunedin, New Zealand, 2–6 December 2002; IAHR: Madrid, Spain, 2002. [Google Scholar]
- Wu, P.; Balachandar, R.; Sui, J. Local Scour around Bridge Piers under Ice-Covered Conditions. J. Hydraul. Eng. 2016, 142, 04015038. [Google Scholar] [CrossRef]
- Namaee, M.R.; Sui, J. Local Scour around Two Side-by-Side Cylindrical Bridge Piers under Ice-Covered Conditions. Int. J. Sediment Res. 2019, 34, 355–367. [Google Scholar] [CrossRef]
- Wang, J.; Li, Z.; Cheng, T. Time-dependent local scour around bridge piers under ice cover—An experimental study. J. Hydraul. Eng. 2021, 52, 1174–1182. [Google Scholar]
- Sirianni, D.A.B.; Valela, C.; Rennie, C.D.; Nistor, I.; Almansour, H. Effects of developing ice covers on bridge pier scour. J. Hydraul. Res. 2022, 60, 645–655. [Google Scholar] [CrossRef]
- Sang, L.; Wang, J.; Cheng, T.; Hou, Z.; Sui, J. Local Scour around Tandem Double Piers under an Ice Cover. Water 2022, 14, 1168. [Google Scholar] [CrossRef]
- Li, Z.; Wang, J.; Sui, J.; Cheng, T.; Liu, P.; Li, G. Channel Bed Deformation around Double Piers in Tandem Arrangement in an S-Shaped Channel under Ice Cover. Water 2023, 15, 2568. [Google Scholar] [CrossRef]
- Hu, H.; Wang, J.; Cheng, T.; Hou, Z.; Sui, J. Channel Bed Deformation and Ice Jam Evolution around Bridge Piers. Water 2022, 14, 1766. [Google Scholar] [CrossRef]
- Wang, T.; Chen, P.; Li, S.; Wang, J. Experimental Study of Critical Condition of Ice Jam Formation in a Curved Channel. South North Water Transf. Water Sci. Technol. 2016, 14, 87–90. [Google Scholar]
- Wang, J.; Wang, T.; Li, S.; Chen, P. Impacts of Bridge Pier on Ice Jam Initiation and Ice Thickness in a Curved Channel-an Experimental Study. J. Hydraul. Eng. 2017, 48, 588–593. [Google Scholar] [CrossRef]
- Leppäranta, M. Structure and Properties of Lake Ice. In Freezing of Lakes and the Evolution of their Ice Cover; Springer Praxis Books; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Gazette of the Ministry of Water Resources of the People’s Republic of China. Specification for Observation of Ice Regime in Rivers; China Water Resources and Hydropower Press: Beijing, China, 2015; Volume 3, p. 36. [Google Scholar]
- Chiew, Y.M. Local Scour at Bridge Piers. Ph.D. Thesis, ResearchSpace, Auckland, New Zealand, 1984. [Google Scholar]
- Zufelt, J.; Sun, Z. A laboratory study of transverse velocities and ice jamming in a river bend. In Proceedings of the IAHR Symposium on Ice Problems, Sapporo, Japan, 23–27 August 1988; pp. 23–27. [Google Scholar]
- APeters, M.; Dow, K.; Clark, S.P.; Malenchak, J.; Danielson, D. Experimental investigation of the flow characteristics beneath partial ice covers. Cold Reg. Sci. Technol. 2017, 142, 69–78. [Google Scholar] [CrossRef]
- Calkins, D.J.; Ashton, G.D. Arching of Fragmented Ice Covers. Can. J. Civ. Eng. 1975, 2, 392–399. [Google Scholar] [CrossRef]
- Lucie, C.; Nowroozpour, A.; Ettema, R. Ice jams in straight and sinuous channels: Insights from small flumes. J. Cold Reg. Eng. 2017, 31, 04017006. [Google Scholar] [CrossRef]
- Urroz, G.E.; Ettema, R. Bend ice jams: Laboratory observations. Can. J. Civ. Eng. 1992, 19, 855–864. [Google Scholar] [CrossRef]
- Tatinclaux, J.C.; Lee, C. Initiation of ice jams—A laboratory study. Can. J. Civ. Eng. 1978, 5, 202–212. [Google Scholar] [CrossRef]
- Wang, J. A study on the relationship about initial ice jam thickness with its stream conditions and ice discharge. Hydro-Sci. Eng. 1999, 4, 383–388. [Google Scholar]
- Namaee, M.R.; Sui, J. Effects of ice cover on the incipient motion of bed material and shear stress around side-by-side bridge piers. Cold Reg. Sci. Technol. 2019, 165, 102811. [Google Scholar] [CrossRef]
- Hains, D.; Zabilansky, L. Laboratory Test of Scour under Ice: Data and Preliminary Results; U.S. Army Engineer Research and Development Center, Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 2004; p. 182. [Google Scholar]
- Wang, H.; Tang, H.; Liu, Q.; Wang, Y. Local scouring around twin bridge piers in open-channel flows. J. Hydraul. Eng. 2016, 142, 06016008. [Google Scholar] [CrossRef]
- Begin, Z.B. Stream curvature and bank erosion: A model based on the momentum equation. J. Geol. 1981, 89, 497–504. [Google Scholar] [CrossRef]
- Keshavarzi, A.; Hamidifar, H.; Ball, J. Bed morphology in vegetated estuarine river with mild-curved meander bend. Hydrol. Sci. J. 2016, 61, 2033–2049. [Google Scholar] [CrossRef]
- Wahl, T.L. Analyzing ADV data using WinADV. Building Partnerships; ASCE: Reston, VA, USA, 2000. [Google Scholar] [CrossRef]
- Tanaka, S.; Yano, M. Local scour around a circular cylinder. In Proceedings of the 12th IAHR Congress, Delft, The Netherlands, 11–14 September 1967. [Google Scholar]
- Zarrati, A.R.; Nazariha, M.; Mashahir, M.B. Reduction of local scour in the vicinity of bridge pier groups using collars and riprap. J. Hydraul. Eng. 2006, 132, 154–162. [Google Scholar] [CrossRef]
- Burrell, B.C.; Comfort, G.; Beltaos, S. Considerations in the planning and design of bridges in ice affected rivers: A review. Can. J. Civ. Eng. 2024, 51, 109–124. [Google Scholar] [CrossRef]
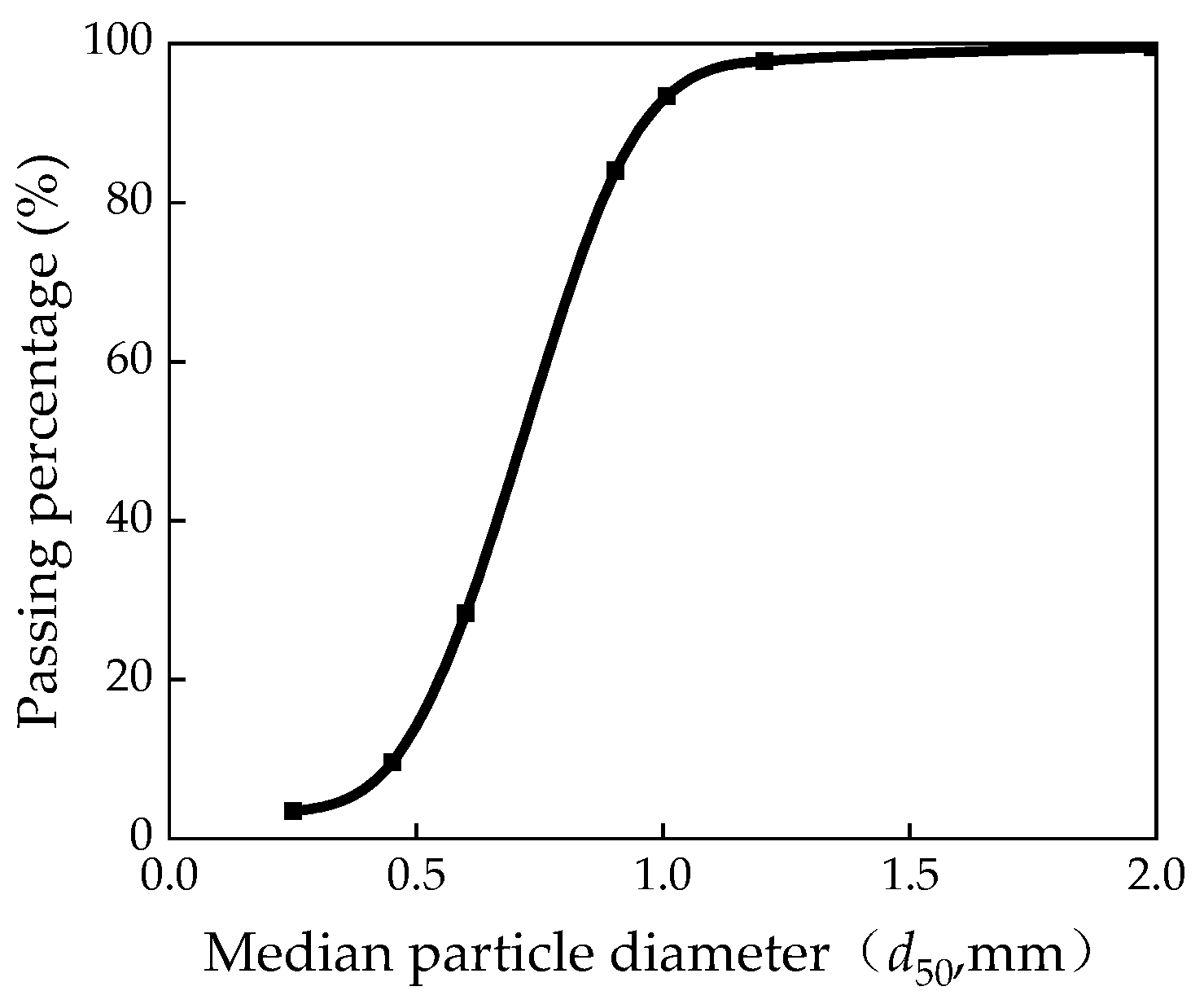

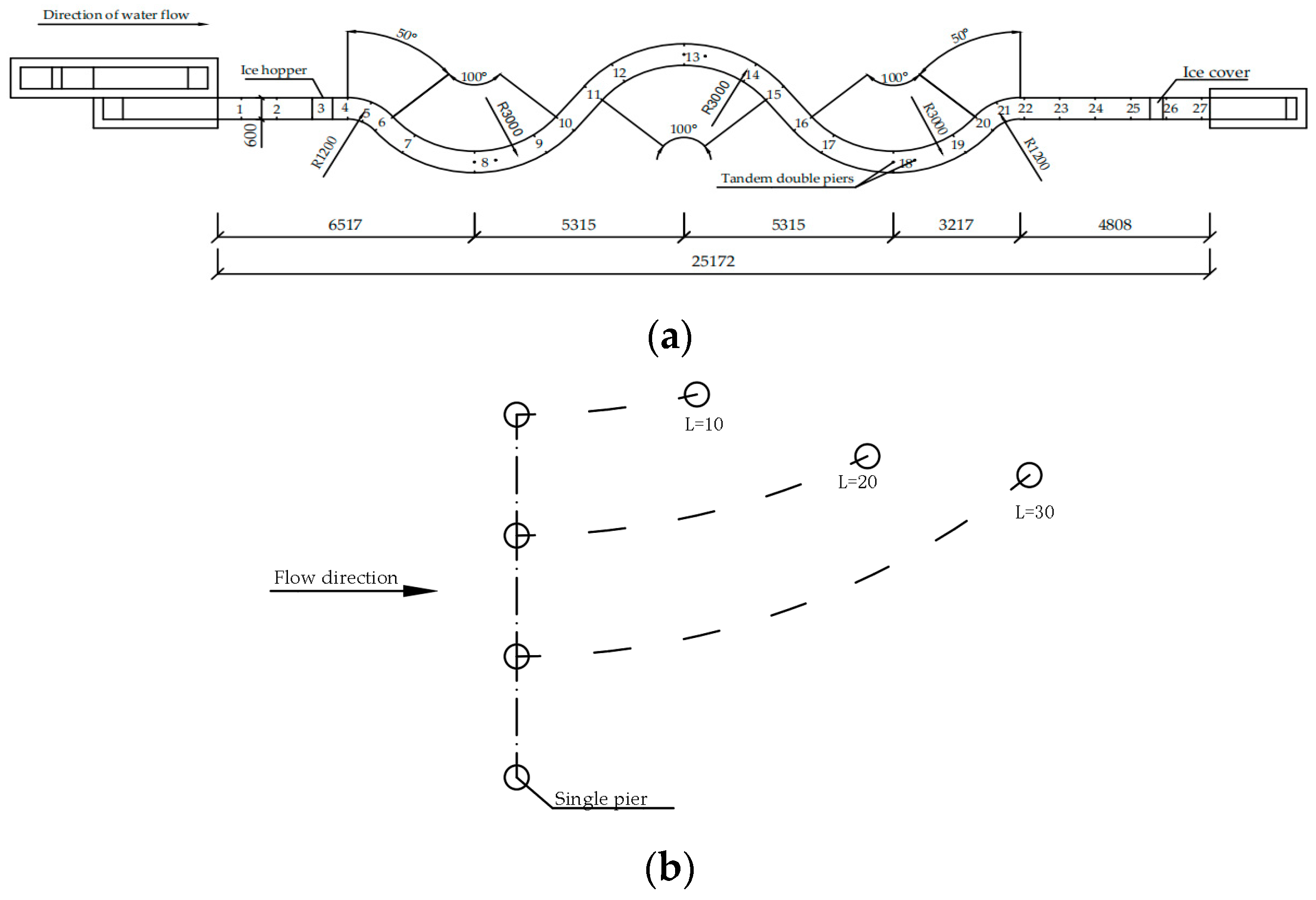

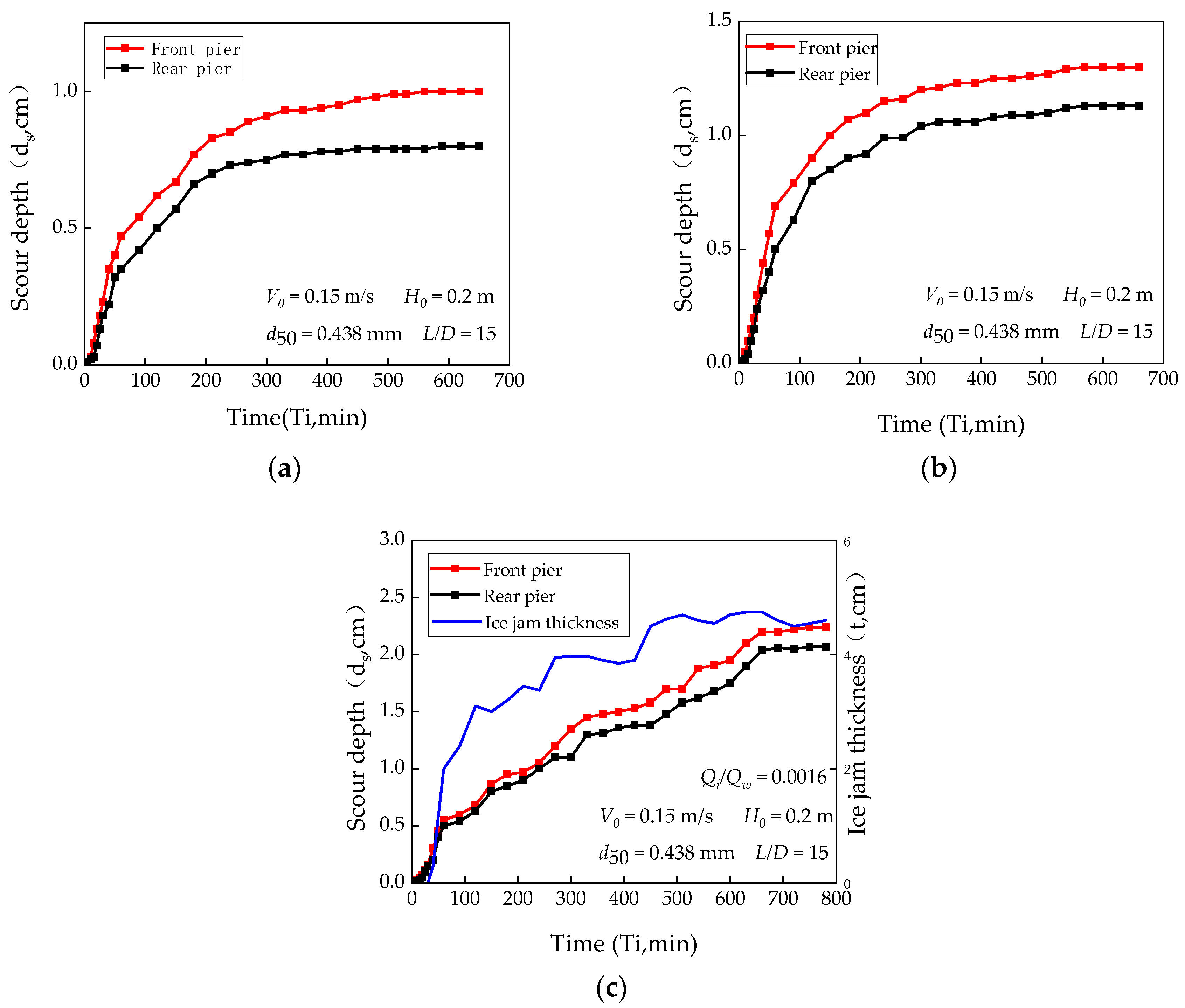
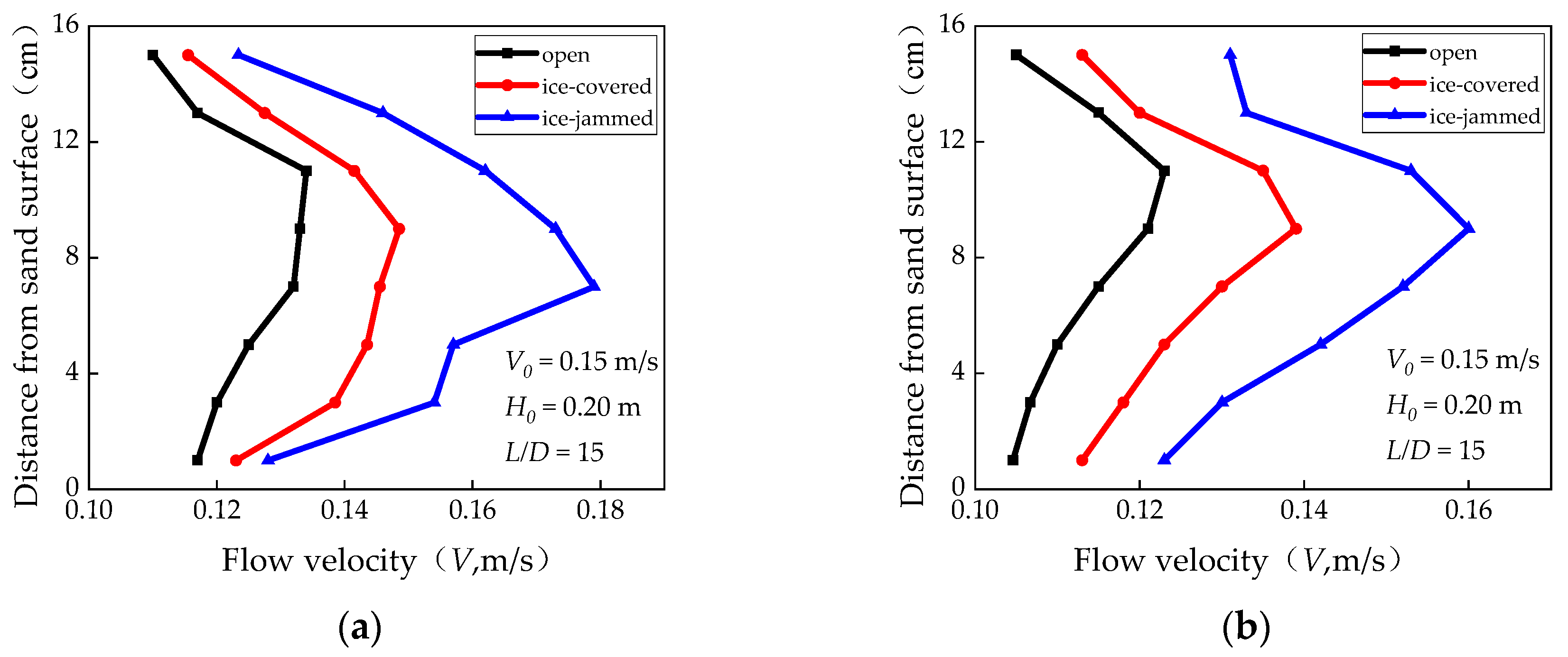



| Serial Number | Ice Discharge Rate Qi (L/s) | Approach Flow Depth H0 (m) | Approach Flow Velocity V0 (m/s) | Pier Spacing L (m) | Pier Diameter D (m) | Median Particle Diameter d50 (mm) | Flow Condition |
|---|---|---|---|---|---|---|---|
| 1 | 2.9 × 10−5 | 0.20 | 0.15 | 0.30 | 0.02 | 0.609 | Ice-jammed |
| 2 | 2.9 × 10−5 | 0.20 | 0.15 | 0.30 | 0.02 | 0.438 | Ice-jammed |
| 3 | 2.9 × 10−5 | 0.20 | 0.15 | 0.30 | 0.03 | 0.714 | Ice-jammed |
| 4 | 2.9 × 10−5 | 0.20 | 0.15 | 0.30 | 0.04 | 0.714 | Ice-jammed |
| 5 | 2.9 × 10−5 | 0.20 | 0.15 | 0.30 | 0.02 | 0.714 | Ice-jammed |
| 6 | 4.1 × 10−5 | 0.20 | 0.15 | 0.30 | 0.02 | 0.714 | Ice-jammed |
| 7 | 3.6 × 10−5 | 0.20 | 0.15 | 0.30 | 0.02 | 0.714 | Ice-jammed |
| 8 | 2.6 × 10−5 | 0.20 | 0.15 | 0.30 | 0.02 | 0.714 | Ice-jammed |
| 9 | 2.9 × 10−5 | 0.20 | 0.15 | 0.10 | 0.02 | 0.714 | Ice-jammed |
| 10 | 2.9 × 10−5 | 0.20 | 0.15 | 0.20 | 0.02 | 0.714 | Ice-jammed |
| 11 | 2.9 × 10−5 | 0.20 | 0.15 | 0.25 | 0.02 | 0.714 | Ice-jammed |
| 12 | 2.7 × 10−5 | 0.20 | 0.14 | 0.30 | 0.02 | 0.714 | Ice-jammed |
| 13 | 2.9 × 10−5 | 0.20 | 0.15 | 0.30 | 0.02 | 0.714 | Ice-jammed |
| 14 | 3.0 ×10−5 | 0.20 | 0.16 | 0.30 | 0.02 | 0.714 | Ice-jammed |
| 15 | 3.2 × 10−5 | 0.20 | 0.167 | 0.30 | 0.02 | 0.714 | Ice-jammed |
| 16 | 3.3 × 10−5 | 0.20 | 0.17 | 0.30 | 0.02 | 0.714 | Ice-jammed |
| 17 | 2.9 × 10−5 | 0.20 | 0.20 | - | 0.02 | 0.714 | Ice-jammed |
| 18 | - | 0.20 | 0.15 | 0.30 | 0.02 | 0.438 | Ice-covered |
| 19 | - | 0.20 | 0.15 | 0.30 | 0.02 | 0.609 | Ice-covered |
| 20 | - | 0.20 | 0.15 | 0.30 | 0.02 | 0.714 | Ice-covered |
| 21 | - | 0.20 | 0.17 | 0.30 | 0.02 | 0.714 | Ice-covered |
| 22 | - | 0.25 | 0.20 | 0.30 | 0.02 | 0.714 | Ice-covered |
| 23 | - | 0.20 | 0.15 | 0.30 | 0.02 | 0.438 | Open |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, S.; Zhang, Z.; Li, Z.; Chen, P.; Wang, J.; Li, G. Analysis of Local Scour around Double Piers in Tandem Arrangement in an S-Shaped Channel under Ice-Jammed Flow Conditions. Water 2024, 16, 2831. https://doi.org/10.3390/w16192831
Dong S, Zhang Z, Li Z, Chen P, Wang J, Li G. Analysis of Local Scour around Double Piers in Tandem Arrangement in an S-Shaped Channel under Ice-Jammed Flow Conditions. Water. 2024; 16(19):2831. https://doi.org/10.3390/w16192831
Chicago/Turabian StyleDong, Shihao, Zhenhua Zhang, Zhicong Li, Pangpang Chen, Jun Wang, and Guowei Li. 2024. "Analysis of Local Scour around Double Piers in Tandem Arrangement in an S-Shaped Channel under Ice-Jammed Flow Conditions" Water 16, no. 19: 2831. https://doi.org/10.3390/w16192831
APA StyleDong, S., Zhang, Z., Li, Z., Chen, P., Wang, J., & Li, G. (2024). Analysis of Local Scour around Double Piers in Tandem Arrangement in an S-Shaped Channel under Ice-Jammed Flow Conditions. Water, 16(19), 2831. https://doi.org/10.3390/w16192831








