Assessment of the Impacts of Rainfall Characteristics and Land Use Pattern on Runoff Accumulation in the Hulu River Basin, China
Abstract
:1. Introduction
2. Materials and Methods
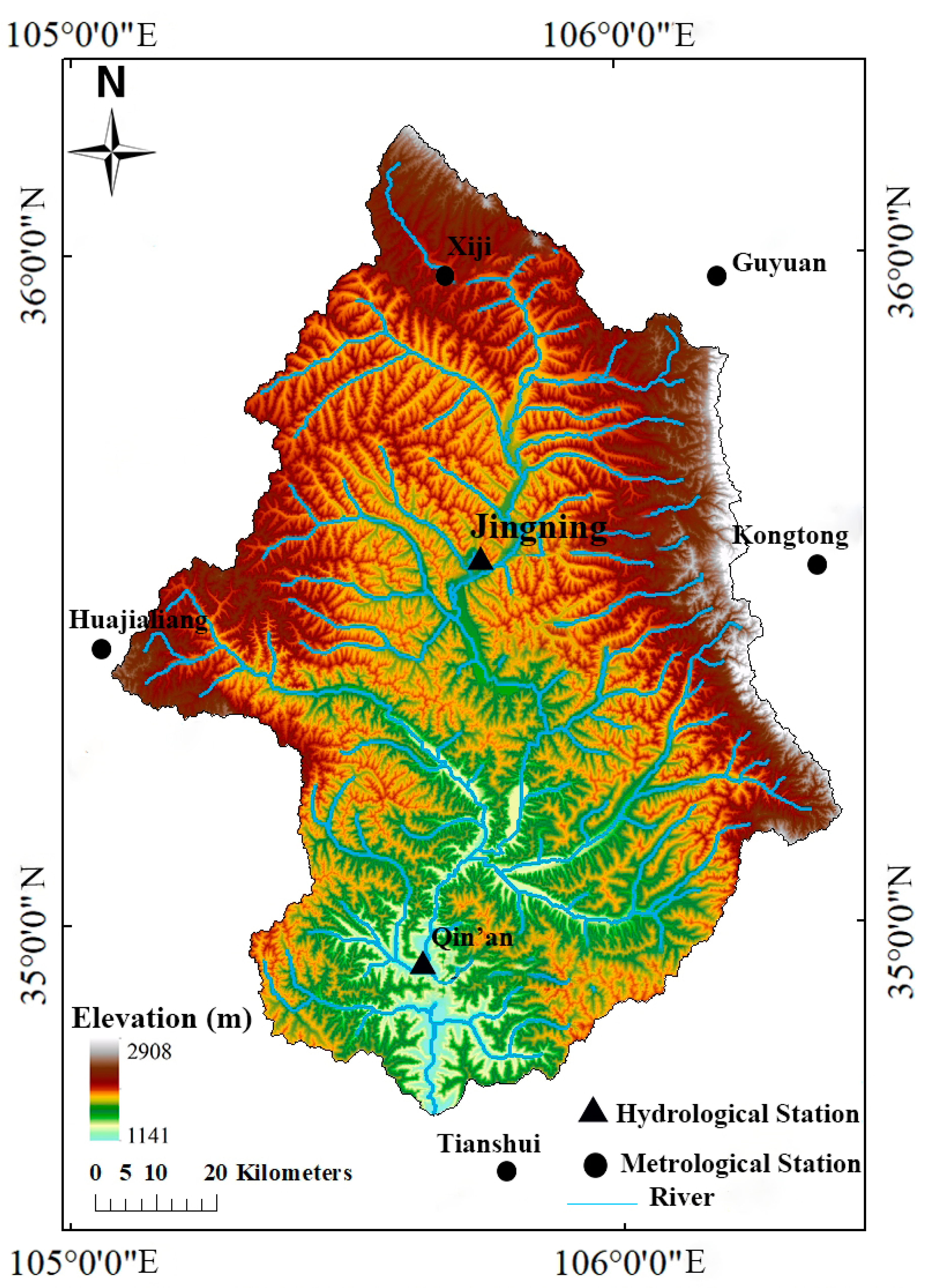
2.1. Study Area
2.2. GAST Model
2.2.1. Model Governing Equations
2.2.2. Numerical Methods of the Model
2.3. Model Setup and Validation
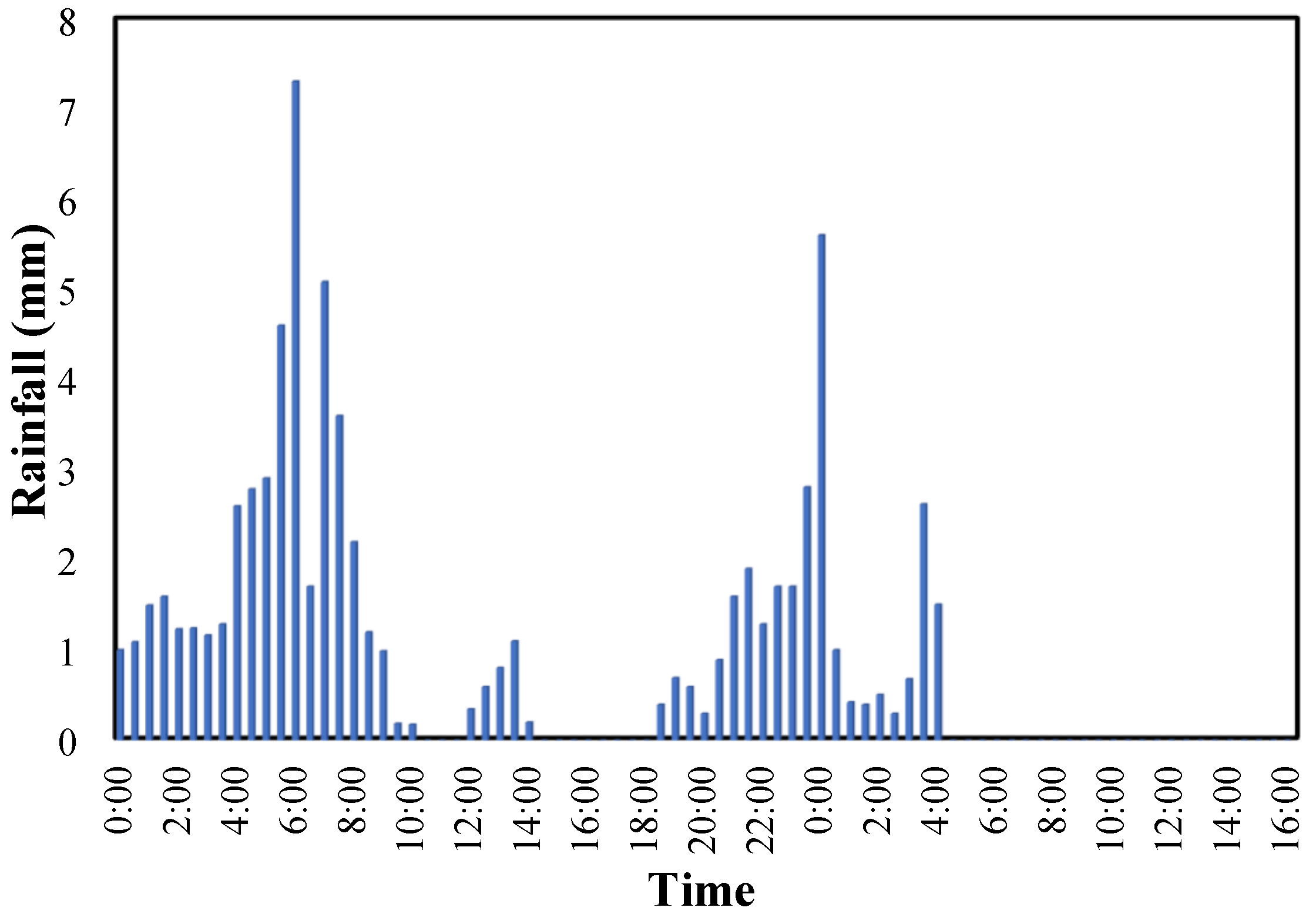
2.3.1. Input Data
2.3.2. Model Validation
2.3.3. Root Mean Square Error (RMSE)
2.3.4. Relative Error
2.4. Simulation of River Flooding under Different Rainfall Characteristics Scenarios
Scenario Setup
2.5. Simulation of River Floods Occurance under Different Land Use Scenarios
Scenario Setup
2.6. Simulation of River Floods under the Combined Influence of Rainfall Characteristics and Land Use
Scenario Setup
3. Results
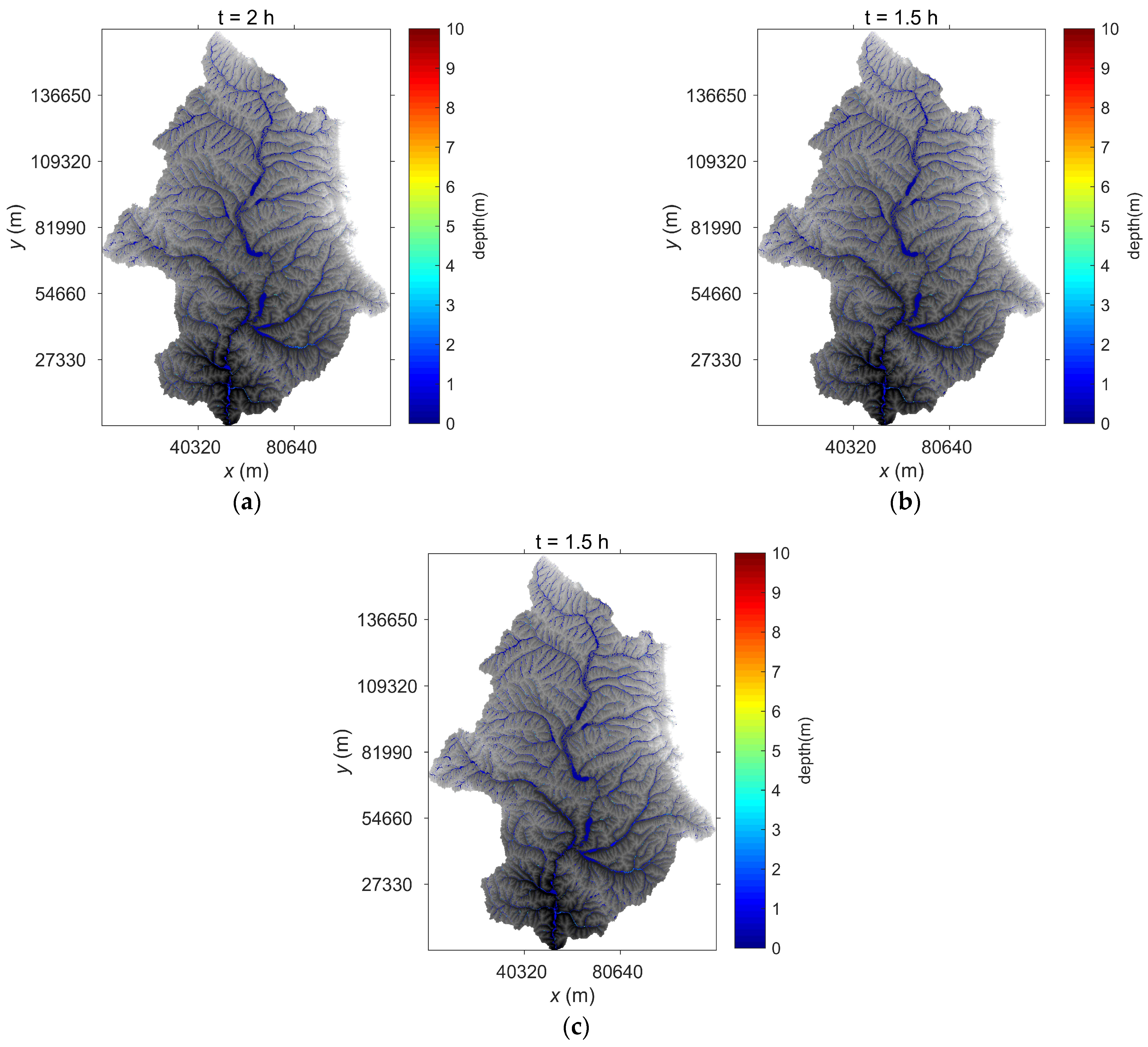
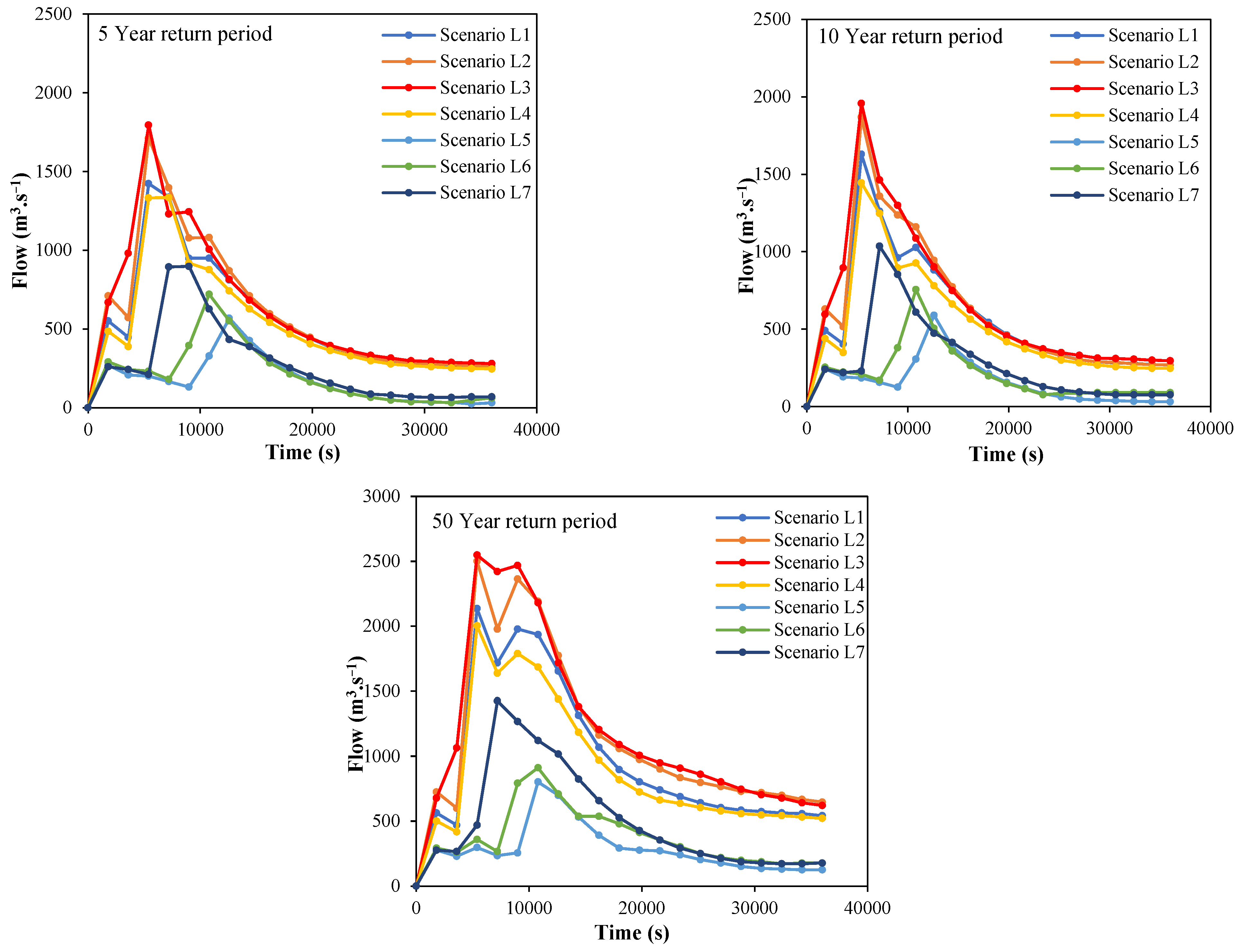
3.1. Simulation of River Flooding under Different Rainfall Characteristics Scenarios
3.2. Simulation of River Flooding under Different Land Use Scenarios
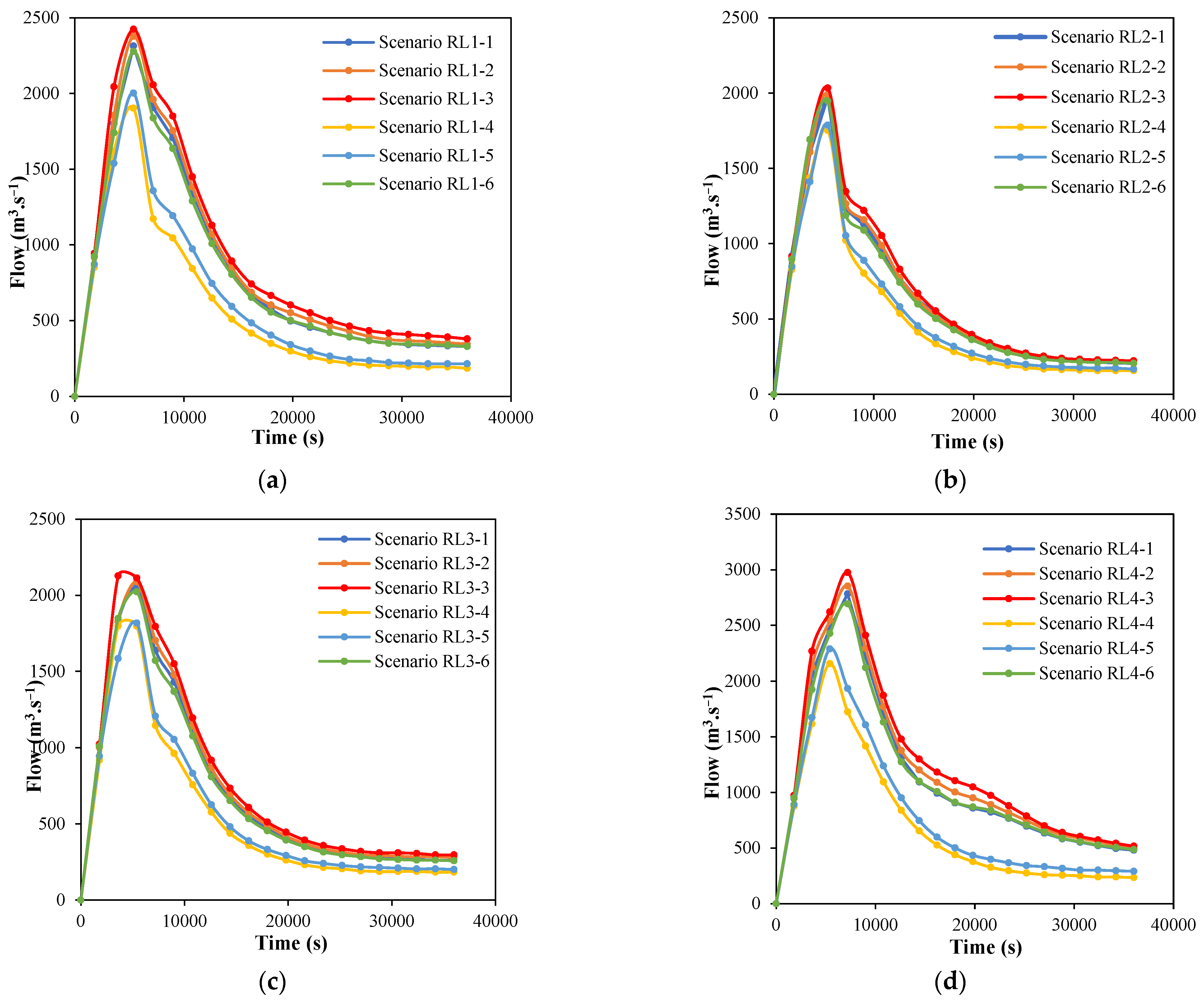
3.3. Simulating the Interacting Effects of Rainfall and Land Use Characteristics on River Flooding
4. Discussion
4.1. Flood Evolution under Different Rainfall Characteristics Scenarios
4.2. Flood Evolution Process under Different Land Use Scenarios
4.3. Flood Evolution under the Combined Influence of Different Rainfall Characteristics and Land Use
5. Conclusions
6. Policy Implications
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, X.; Zhang, P.; Liu, L.; Li, D.; Wang, Y. Effects of human activities on hydrological components in the Yiluo River basin in middle Yellow River. Water 2019, 11, 689. [Google Scholar] [CrossRef]
- Zhan, C.; Jiang, S.; Sun, F.; Jia, Y.; Niu, C.; Yue, W. Quantitative contribution of climate change and human activities to runoff changes in the Wei River basin, China. Hydrol. Earth Syst. Sci. 2014, 18, 3069–3077. [Google Scholar] [CrossRef]
- Allen, M.R.; Ingram, W.J. Constraints on future changes in climate and the hydrologic cycle. Nature 2002, 419, 224–232. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Xia, J.; Chen, J. Quantification of effects of climate variations and human activities on runoff by a monthly water balance model: A case study of the Chaobai River basin in northern China. Water Resour. Res. 2009, 45, W00A11. [Google Scholar] [CrossRef]
- Wang, S.; Yan, M.; Yan, Y.; Shi, C.; He, L. Contributions of climate change and human activities to the changes in runoff increment in different sections of the Yellow River. Quat. Int. 2012, 282, 66–77. [Google Scholar] [CrossRef]
- Xu, C.-Y. Climate change and hydrologic models: A review of existing gaps and recent research developments. Water Resour. Manag. 1999, 13, 369–382. [Google Scholar] [CrossRef]
- Sharma, C.S.; Behera, M.D.; Mishra, A.; Panda, S.N. Assessing flood induced land-cover changes using remote sensing and fuzzy approach in Eastern Gujarat (India). Water Resour. Manag. 2011, 25, 3219–3246. [Google Scholar] [CrossRef]
- Suwanwerakamtorn, R. Register | Login. ITC J. 1994, 4, 343–348. [Google Scholar]
- Brooks, K.N.; Ffolliott, P.F.; Gregersen, H.M.; Thames, J. Hydrology and the Management of Watersheds; Iowa State University Press: Ames, IA, USA, 1991. [Google Scholar]
- Fohrer, N.; Haverkamp, S.; Eckhardt, K.; Frede, H.-G. Hydrologic response to land use changes on the catchment scale. Phys. Chem. Earth Part B Hydrol. Ocean. Atmos. 2001, 26, 577–582. [Google Scholar] [CrossRef]
- Liu, J.; Wang, S.-Y.; Li, D.-M. The analysis of the impact of land-use changes on flood exposure of Wuhan in Yangtze River Basin, China. Water Resour. Manag. 2014, 28, 2507–2522. [Google Scholar] [CrossRef]
- Chen, D.; Lu, X.; Hu, W.; Zhang, C.; Lin, Y. How urban sprawl influences eco-environmental quality: Empirical research in China by using the Spatial Durbin model. Ecol. Indic. 2021, 131, 108113. [Google Scholar] [CrossRef]
- Ahmadi, A.; Aghakhani Afshar, A.; Nourani, V.; Pourreza-Bilondi, M.; Besalatpour, A. Assessment of MC&MCMC uncertainty analysis frameworks on SWAT model by focusing on future runoff prediction in a mountainous watershed via CMIP5 models. J. Water Clim. Chang. 2020, 11, 1811–1828. [Google Scholar]
- Tan, M.L.; Yusop, Z.; Chua, V.P.; Chan, N.W. Climate change impacts under CMIP5 RCP scenarios on water resources of the Kelantan River Basin, Malaysia. Atmos. Res. 2017, 189, 1–10. [Google Scholar] [CrossRef]
- O’Neill, B.C.; Tebaldi, C.; Van Vuuren, D.P.; Eyring, V.; Friedlingstein, P.; Hurtt, G.; Knutti, R.; Kriegler, E.; Lamarque, J.-F.; Lowe, J. The scenario model intercomparison project (ScenarioMIP) for CMIP6. Geosci. Model Dev. 2016, 9, 3461–3482. [Google Scholar] [CrossRef]
- Song, M.; Tao, W. Coupling and coordination analysis of China’s regional urban-rural integration and land-use efficiency. Growth Chang. 2022, 53, 1384–1413. [Google Scholar] [CrossRef]
- Li, C.; Li, Y.; Wang, P.; Shen, J. Natural runoff prediction of the Yellow River in the future under climate change. In Proceedings of the International Conference on Advanced Education and Management Engineering, Bangkok, Thailand, 29–30 October 2016. [Google Scholar]
- Zhu, X.; Zhang, C.; Qi, W.; Cai, W.; Zhao, X.; Wang, X. Multiple climate change scenarios and runoff response in Biliu River. Water 2018, 10, 126. [Google Scholar] [CrossRef]
- Yang, W.; Long, D.; Bai, P. Impacts of future land cover and climate changes on runoff in the mostly afforested river basin in North China. J. Hydrol. 2019, 570, 201–219. [Google Scholar] [CrossRef]
- Asselman, N.E.; Middelkoop, H.; Van Dijk, P.M. The impact of changes in climate and land use on soil erosion, transport and deposition of suspended sediment in the River Rhine. Hydrol. Process. 2003, 17, 3225–3244. [Google Scholar] [CrossRef]
- Ouyang, L.; Liu, S.; Ye, J.; Liu, Z.; Sheng, F.; Wang, R.; Lu, Z. Quantitative assessment of surface runoff and base flow response to multiple factors in Pengchongjian small watershed. Forests 2018, 9, 553. [Google Scholar] [CrossRef]
- Liu, J.; Luo, M.; Liu, T.; Bao, A.; De Maeyer, P.; Feng, X.; Chen, X. Local climate change and the impacts on hydrological processes in an arid alpine catchment in Karakoram. Water 2017, 9, 344. [Google Scholar] [CrossRef]
- Zuo, D.; Xu, Z.; Yao, W.; Jin, S.; Xiao, P.; Ran, D. Assessing the effects of changes in land use and climate on runoff and sediment yields from a watershed in the Loess Plateau of China. Sci. Total Environ. 2016, 544, 238–250. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Hu, W.; Li, Y.; Zhang, C.; Lu, X.; Cheng, H. Exploring the temporal and spatial effects of city size on regional economic integration: Evidence from the Yangtze River Economic Belt in China. Land Use Policy 2023, 132, 106770. [Google Scholar] [CrossRef]
- Houghton, R.A. The worldwide extent of land-use change. BioScience 1994, 44, 305–313. [Google Scholar] [CrossRef]
- Hathout, S. The use of GIS for monitoring and predicting urban growth in East and West St Paul, Winnipeg, Manitoba, Canada. J. Environ. Manag. 2002, 66, 229–238. [Google Scholar] [CrossRef]
- Li, F.; Zhang, S.; Yang, J.; Chang, L.; Yang, H.; Bu, K. Effects of land use change on ecosystem services value in West Jilin since the reform and opening of China. Ecosyst. Serv. 2018, 31, 12–20. [Google Scholar]
- Song, M.; Xie, Q.; Chen, J. Effects of government competition on land prices under opening up conditions: A case study of the Huaihe River ecological economic belt. Land Use Policy 2022, 113, 105875. [Google Scholar] [CrossRef]
- Shi, C.; Zhou, Y.; Fan, X.; Shao, W. A study on the annual runoff change and its relationship with water and soil conservation practices and climate change in the middle Yellow River basin. Catena 2013, 100, 31–41. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, S. Effects of restoration practices on controlling soil and water losses in the Wei River Catchment, China: An estimation based on longitudinal field observations. For. Policy Econ. 2019, 100, 120–128. [Google Scholar] [CrossRef]
- Wang, T.; Li, P.; Li, Z.; Hou, J.; Xiao, L.; Ren, Z.; Xu, G.; Yu, K.; Su, Y. The effects of freeze–thaw process on soil water migration in dam and slope farmland on the Loess Plateau, China. Sci. Total Environ. 2019, 666, 721–730. [Google Scholar] [CrossRef]
- Chen, J.; Li, Q.; Wang, H.; Deng, M. A machine learning ensemble approach based on random forest and radial basis function neural network for risk evaluation of regional flood disaster: A case study of the Yangtze River Delta, China. Int. J. Environ. Res. Public Health 2020, 17, 49. [Google Scholar] [CrossRef]
- Dewan, T.H. Societal impacts and vulnerability to floods in Bangladesh and Nepal. Weather Clim. Extrem. 2015, 7, 36–42. [Google Scholar] [CrossRef]
- Wang, S.; Fu, B.; Piao, S.; Lü, Y.; Ciais, P.; Feng, X.; Wang, Y. Reduced sediment transport in the Yellow River due to anthropogenic changes. Nat. Geosci. 2016, 9, 38–41. [Google Scholar] [CrossRef]
- Yin, J.; He, F.; Xiong, Y.J.; Qiu, G.Y. Effects of land use/land cover and climate changes on surface runoff in a semi-humid and semi-arid transition zone in northwest China. Hydrol. Earth Syst. Sci. 2017, 21, 183–196. [Google Scholar] [CrossRef]
- Feng, X.; Sun, G.; Fu, B.; Su, C.; Liu, Y.; Lamparski, H. Regional effects of vegetation restoration on water yield across the Loess Plateau, China. Hydrol. Earth Syst. Sci. 2012, 16, 2617–2628. [Google Scholar] [CrossRef]
- Zhao, G.; Mu, X.; Tian, P.; Wang, F.; Gao, P. Climate changes and their impacts on water resources in semiarid regions: A case study of the Wei River basin, China. Hydrol. Process. 2013, 27, 3852–3863. [Google Scholar] [CrossRef]
- Hu, C.; Ran, G.; Li, G.; Yu, Y.; Wu, Q.; Yan, D.; Jian, S. The effects of rainfall characteristics and land use and cover change on runoff in the Yellow River basin, China. J. Hydrol. Hydromech. 2021, 69, 29–40. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, R.; Yao, W.; Li, Z. Relationship Between Watershed Landscape Pattern Change and Runoff-Sediment in Wind-Water Erosion Crisscross Region. J. Landsc. Res. 2017, 9, 53–58. [Google Scholar]
- Zhan, F.; Zeng, W.; Li, B.; Li, Z.; Chen, J.; He, Y.; Li, Y. Inhibition of native arbuscular mycorrhizal fungi induced increases in cadmium loss via surface runoff and interflow from farmland. Int. Soil Water Conserv. Res. 2023, 11, 213–223. [Google Scholar] [CrossRef]
- Delgado, M.I.; Carol, E.; Casco, M.A. Land-use changes in the periurban interface: Hydrologic consequences on a flatland-watershed scale. Sci. Total Environ. 2020, 722, 137836. [Google Scholar] [CrossRef]
- Lin, B.; Chen, X.; Yao, H.; Chen, Y.; Liu, M.; Gao, L.; James, A. Analyses of landuse change impacts on catchment runoff using different time indicators based on SWAT model. Ecol. Indic. 2015, 58, 55–63. [Google Scholar] [CrossRef]
- Hernández-Bedolla, J.; García-Romero, L.; Franco-Navarro, C.D.; Sánchez-Quispe, S.T.; Domínguez-Sánchez, C. Extreme Runoff Estimation for Ungauged Watersheds Using a New Multisite Multivariate Stochastic Model MASVC. Water 2023, 15, 2994. [Google Scholar] [CrossRef]
- Liu, R. Remote Sensing Estimation and Spatiotemporal Evolution Analysis of Urban Surface Runoff in Xuzhou Based on Impervious Surface; China University of Mining and Technology: Beijing, China, 2022. [Google Scholar]
- Fang, G.; Li, H.; Dong, J.; Teng, H.; Pablo, R.D.A.; Zhu, Y. Extraction and Spatiotemporal Evolution Analysis of Impervious Surface and Surface Runoff in Main Urban Region of Hefei City, China. Sustainability 2023, 15, 10537. [Google Scholar] [CrossRef]
- Yonaba, R.; Biaou, A.C.; Koïta, M.; Tazen, F.; Mounirou, L.A.; Zouré, C.O.; Queloz, P.; Karambiri, H.; Yacouba, H. A dynamic land use/land cover input helps in picturing the Sahelian paradox: Assessing variability and attribution of changes in surface runoff in a Sahelian watershed. Sci. Total Environ. 2021, 757, 143792. [Google Scholar] [CrossRef] [PubMed]
- Sheng, F.; Liu, S.-Y.; Zhang, T.; Yu, M.-Q. Runoff effect of precipitation variation and landscape pattern evolution in Lianshui watershed, Jiangxi, China. Ying Yong Sheng Tai Xue Bao J. Appl. Ecol. 2023, 34, 196–202. [Google Scholar]
- Prokešová, R.; Horáčková, Š.; Snopková, Z. Surface runoff response to long-term land use changes: Spatial rearrangement of runoff-generating areas reveals a shift in flash flood drivers. Sci. Total Environ. 2022, 815, 151591. [Google Scholar] [CrossRef] [PubMed]
- Han, H.; Hou, J.; Huang, M.; Li, Z.; Xu, K.; Zhang, D.; Bai, G.; Wang, C. Impact of soil and water conservation measures and precipitation on streamflow in the middle and lower reaches of the Hulu River Basin, China. Catena 2020, 195, 104792. [Google Scholar] [CrossRef]
- Hou, J.; Li, G.; Li, G.; Liang, Q.; Zhi, Z. Research on the application of efficient and high-precision hydrodynamic model in flood evolution. J. Hydropower 2018, 37, 96–107. [Google Scholar]
- Hou, J.; Liang, Q.; Simons, F.; Hinkelmann, R. A stable 2D unstructured shallow flow model for simulations of wetting and drying over rough terrains. Comput. Fluids 2013, 82, 132–147. [Google Scholar] [CrossRef]
- Liu, F.; Hou, J.; Guo, K.; Li, D.; Xu, S.; Zhang, X. Numerical simulation of rainwater and flood processes in watersheds based on full hydrodynamic model. Hydrodyn. Res. Prog. 2018, 33, 778–785. [Google Scholar]
- Sivakumar, P.; Hyams, D.; Taylor, L.K.; Briley, W.R. A primitive-variable Riemann method for solution of the shallow water equations with wetting and drying. J. Comput. Phys. 2009, 228, 7452–7472. [Google Scholar] [CrossRef]
- Hou, J.; Liang, Q.; Simons, F.; Hinkelmann, R. A 2D well-balanced shallow flow model for unstructured grids with novel slope source term treatment. Adv. Water Resour. 2013, 52, 107–131. [Google Scholar] [CrossRef]
- Simons, F.; Busse, T.; Hou, J.; Özgen, I.; Hinkelmann, R. A model for overland flow and associated processes within the Hydroinformatics Modelling System. J. Hydroinform. 2014, 16, 375–391. [Google Scholar] [CrossRef]
- Hubbard, M. Multidimensional slope limiters for MUSCL-type finite volume schemes on unstructured grids. J. Comput. Phys. 1999, 155, 54–74. [Google Scholar] [CrossRef]
- Bai, G.; Hou, J.; Han, H.; Shi, Y.; Guo, K.; Li, B.; Fu, D. Analysis of the Contribution Rates of Factors to Runoff in Hulu River Based on Support vector Machine Regression. Res. Soil Water Conserv. 2020, 27, 112–117. [Google Scholar] [CrossRef]
- Yang, P.; Li, R.; Pan, E.; Wang, Y.; Huang, M.; Zhang, L. Effects of surface roughness and vegetation coverage on the Manning resistance coefficient of slope flow. Trans. Chin. Soc. Agric. Eng. 2020, 36, 106–114. [Google Scholar]
- Wang, J.; Zhang, K.; Gong, J.; Yang, F.; Dong, X. Laws of water flow resistance on slopes under different coverage conditions. J. Soil Water Conserv. 2015, 29, 1–6. [Google Scholar] [CrossRef]
- Wang, J.; Wu, F.; Meng, Q.; Zhang, Q. Experimental study on soil water infiltration characteristics under different utilization types. Agric. Res. Arid Areas 2006, 24, 159–162. [Google Scholar]
- Gao, P.; Mu, X. Comparative experiment on soil moisture infiltration under different land use patterns in loess hilly areas. China Soil Water Conserv. Sci. 2005, 3, 27–31. [Google Scholar]
- Horton, R.E. An approach toward a physical interpretation of infiltration capacity. Soil Sci. Soc. Am. Proc. 1940, 5, 24. [Google Scholar] [CrossRef]
- Qin, J.; Su, B.; Tao, H.; Wang, Y.; Huang, J.; Jiang, T. Projection of temperature and precipitation under SSPs-RCPs Scenarios over northwest China. Front. Earth Sci. 2021, 15, 23–37. [Google Scholar] [CrossRef]
- Tian, J.; Zhang, Z.; Ahmed, Z.; Zhang, L.; Su, B.; Tao, H.; Jiang, T. Projections of precipitation over China based on CMIP6 models. Stoch. Environ. Res. Risk Assess. 2021, 35, 831–848. [Google Scholar] [CrossRef]
- Li, E.; Mu, X.; Zhao, G.; Gao, P.; Shao, H. Variation of runoff and precipitation in the hekou-longmen region of the yellow river based on elasticity analysis. Sci. World J. 2014, 2014, 929858. [Google Scholar] [CrossRef] [PubMed]
- Ran, D.; Zuo, Z.; Wu, Y.; Li, X.; Li, Z. Variation of Streamflow and Sediment in Response to Human Activities in the Middle Reaches of the Yellow River; Science Press: Beijing, China, 2012. [Google Scholar]
- Hou, J.; Li, X.; Pan, Z.; Wang, J.; Wang, R. Effect of digital elevation model spatial resolution on depression storage. Hydrol. Process. 2021, 35, e14381. [Google Scholar] [CrossRef]


| Time | Measured Flow/(m3·s−1) | Time | Simulated Flow/(m3·s−1) | Relative Error |
|---|---|---|---|---|
| 13 September 6:03:00 | 38.9 | 13 September 6:00:00 | 39.15 | 0.64% |
| 13 September 8:00:00 | 35.5 | 13 September 8:00:00 | 38.23 | 7.68% |
| 13 September 14:39:00 | 85.8 | 13 September 14:30:00 | 78.39 | 8.64% |
| 14 September 5:54:00 | 131 | 14 September 6:00:00 | 135.68 | 3.57% |
| 14 September 6:18:00 | 133 | 14 September 6:30:00 | 133.99 | 0.75% |
| 14 September 8:00:00 | 92.5 | 14 September 8:00:00 | 95.58 | 3.33% |
| Scenario | Scenario Description |
|---|---|
| Scenario R1 | Uniform spatial distribution of 5-year return period rainfall |
| Scenario R2 | Uniform spatial distribution of 10-year return period rainfall |
| Scenario R3 | Uniform spatial distribution of 50-year return period rainfall |
| Scenario R4 | Rainfall gradually decreasing from southeast to northwest |
| Scenario R5 | Relatively high rainfall in southeast and northwest regions, while relatively low rainfall in northeast and southwest regions |
| Scenario R6 | Set upstream rainfall center |
| Scenario R7 | Set middle reaches rainfall center |
| Scenario R8 | Set downstream rainfall center |
| Scenarios | Scenario Description |
|---|---|
| Scenario L1 | 1985 Annual land use data |
| Scenario L2 | 2000 Annual land use data |
| Scenario L3 | 2010 Annual land use data |
| Scenario L4 | 2020 Annual land use data |
| Scenario L5 | 2020 Conversion of farmland to forest |
| Scenario L6 | 2020 Conversion of farmland to grassland |
| Scenario L7 | Generalize various water conservation measures such as check dams |
| Scenario | Scenario Description | |
|---|---|---|
| Rainfall Variation | Land Use Change | |
| Scenario RL1-1 | 50-year return period rainfall gradually decreases from southeast to northwest | 1985 |
| Scenario RL1-2 | 50-year return period rainfall gradually decreases from southeast to northwest | 2000 |
| Scenario RL1-3 | 50-year return period rainfall gradually decreases from southeast to northwest | 2010 |
| Scenario RL1-4 | 50-year return period rainfall gradually decreases from southeast to northwest | farmland to forest |
| Scenario RL1-5 | 50-year return period rainfall gradually decreases from southeast to northwest | farmland to grassland |
| Scenario RL1-6 | 50-year return period rainfall gradually decreases from southeast to northwest | soil and water conservation measures |
| Scenario RL2-1 | 50-year return period rainfall: The southeast and northwest regions have higher rainfall, while the northeast and southwest regions have smaller rainfall | 1985 |
| Scenario RL2-2 | 50-year return period rainfall: The southeast and northwest regions have higher rainfall, while the northeast and southwest regions have smaller rainfall | 2000 |
| Scenario RL2-3 | 50-year return period rainfall: The southeast and northwest regions have higher rainfall, while the northeast and southwest regions have smaller rainfall | 2010 |
| Scenario RL2-4 | 50-year return period rainfall: The southeast and northwest regions have higher rainfall, while the northeast and southwest regions have smaller rainfall | farmland to forest |
| Scenario RL2-5 | 50-year return period rainfall: The southeast and northwest regions have higher rainfall, while the northeast and southwest regions have smaller rainfall | Resume farmland to grassland |
| Scenario RL2-6 | 50-year return period rainfall: The southeast and northwest regions have higher rainfall, while the northeast and southwest regions have smaller rainfall | Soil and water conservation measures |
| Scenario RL3-1 | 50-year return period rainfall center is upstream | 1985 |
| Scenario RL3-2 | Set upstream 50-year rainfall center | 2000 |
| Scenario RL3-3 | Set upstream 50-year rainfall center | 2010 |
| Scenario RL3-4 | Set upstream 50-year rainfall center | farmland to forest |
| Scenario RL3-5 | Set upstream 50-year rainfall center | farmland to grassland |
| Scenario RL3-6 | Set upstream 50-year rainfall center | soil and water conservation measures |
| Scenario RL4-1 | Set downstream 50-year rainfall center | 1985 |
| Scenario RL4-2 | Set downstream 50-year rainfall center | 2000 |
| Scenario RL4-3 | Set downstream 50-year rainfall center | 2010 |
| Scenario RL4-4 | Set downstream 50-year rainfall center | farmland to forest |
| Scenario RL4-5 | Set downstream 50-year rainfall center | farmland to grassland |
| Scenario RL4-6 | Set downstream 50-year rainfall center | soil and water conservation measures |
| Peak Flow Rate/(m3·s−1) | Time of Peak Flow/(s) | Peak Water Depth/(m) | Time of Peak Water Depth Occurrence/(s) | |
|---|---|---|---|---|
| Scenario R1 | 1332.90 | 7200 | 5.42 | 9000 |
| Scenario R2 | 1445.33 | 5400 | 5.44 | 9000 |
| Scenario R3 | 2003.04 | 5400 | 8.57 | 9000 |
| Return Period/ Scenario | Scenario R4 | Scenario R5 | Scenario R6 | Scenario R7 | Scenario R8 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Flow (m3·s1) | Water Depth (m) | Flow (m3·s1) | Water Depth (m) | Flow (m3·s1) | Water Depth (m) | Flow (m3·s1) | Water Depth (m) | Flow (m3·s1) | Water Depth (m) | |
| 5 years return period | 1836.19 | 5.38 | 1825.59 | 5.61 | 1813.82 | 5.60 | 1813.73 | 5.60 | 1883.34 | 5.39 |
| 10 years return period | 1954.21 | 5.41 | 1894.72 | 5.39 | 1883.36 | 5.39 | 1883.31 | 5.39 | 2023.48 | 5.71 |
| 50 years return period | 2277.76 | 7.39 | 1947.12 | 5.40 | 2023.07 | 5.86 | 2023.22 | 5.86 | 2694.34 | 8.82 |
| Return Period/ Scenario | Scenario L1 | Scenario L2 | Scenario L3 | Scenario L4 | ||||
|---|---|---|---|---|---|---|---|---|
| Flow (m3·s−1) | Water Depth (m) | Flow (m3·s−1) | Water Depth (m) | Flow (m3·s−1) | Water Depth (m) | Flow (m3·s−1) | Water Depth (m) | |
| 5 years return period | 1422.8 | 5.39 | 1711.02 | 5.41 | 1795.2 | 5.50 | 1332.9 | 5.42 |
| 10 years return period | 1630.3 | 5.40 | 1869.7 | 5.89 | 1958.04 | 6.28 | 1445.33 | 5.44 |
| 50 years return period | 2135.57 | 8.43 | 2501.61 | 8.75 | 2548.2 | 8.98 | 2003.04 | 8.57 |
| Return Period/ Scenario | Scenario L5 | Scenario L6 | Scenario L7 | |||
|---|---|---|---|---|---|---|
| Flow (m3·s−1) | Water Depth (m) | Flow (m3·s−1) | Water Depth (m) | Flow (m3·s−1) | Water Depth (m) | |
| 5-year return period | 568.63 | 4.79 | 720.86 | 4.93 | 897.96 | 5.26 |
| 10-year return period | 589.79 | 4.80 | 755.52 | 4.97 | 1035.85 | 5.30 |
| 50-year return period | 803.09 | 4.98 | 912.13 | 5.10 | 1426.29 | 5.53 |
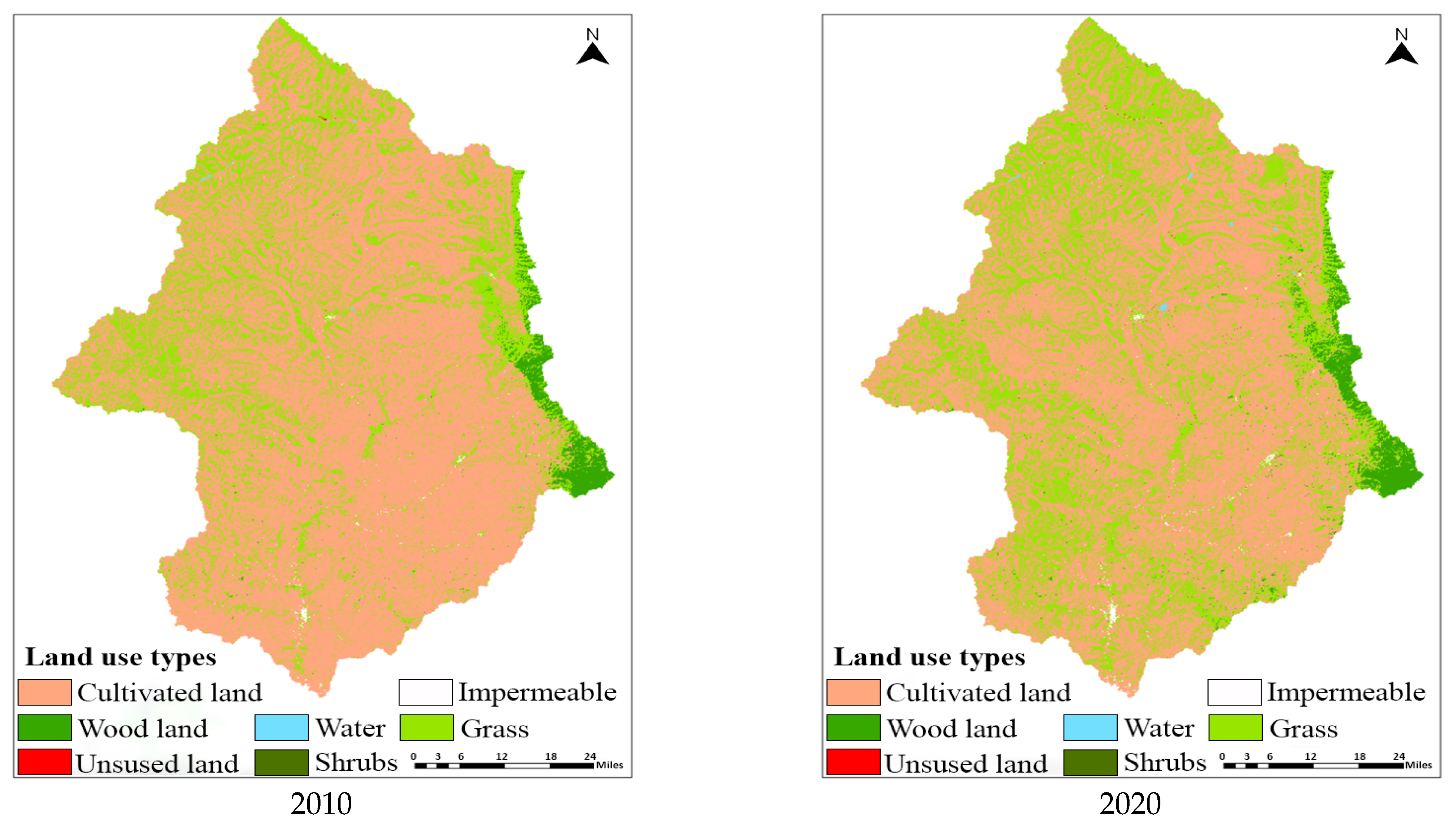
| Type/Area | 1985 | 2000 | 2010 | 2020 | ||||
|---|---|---|---|---|---|---|---|---|
| Area/km2 | Proportion/% | Area/km2 | Proportion/% | Area/km2 | Proportion/% | Area/km2 | Proportion% | |
| Cultivated land | 6415.3 | 60.09 | 8073.5 | 75.62 | 7787.25 | 72.94 | 6689.71 | 62.66 |
| Woodland | 182.3 | 1.71 | 201.3 | 1.89 | 217.64 | 2.04 | 299.99 | 2.81 |
| shrubs | 0.9 | 0.009 | 0.7 | 0.01 | 0.55 | 0.01 | 1.81 | 0.02 |
| Grassland | 4058.9 | 38.02 | 2380.8 | 22.30 | 2645.55 | 24.78 | 3640.56 | 34.10 |
| Water | 7.9 | 0.07 | 5.6 | 0.050 | 6.96 | 0.07 | 13.04 | 0.12 |
| Unused land | 1.5 | 0.014 | 0.5 | 0.005 | 0.63 | 0.01 | 2.13 | 0.02 |
| Impermeable | 9.04 | 0.08 | 13.33 | 0.13 | 17.1 | 0.16 | 28.44 | 0.27 |
| Scenario | Peak Flow Rate/(m3·s−1) | Peak Water Depth/(m) |
|---|---|---|
| Base period | 2003.04 | 8.57 |
| RL1-1 | 2313.54 | 7.47 |
| RL1-2 | 2377.32 | 8.17 |
| RL1-3 | 2424.66 | 8.36 |
| RL1-4 | 1902.56 | 5.39 |
| RL1-5 | 2002.31 | 5.42 |
| RL1-6 | 2277.76 | 7.39 |
| Scenario | Peak Flow Rate/(m3·s−1) | Peak Water Depth/(m) |
|---|---|---|
| Base period | 2003.04 | 8.57 |
| RL2-1 | 1989.97 | 5.42 |
| RL2-2 | 1990.56 | 5.41 |
| RL2-3 | 2033.76 | 5.55 |
| RL2-4 | 1751.75 | 5.34 |
| RL2-5 | 1786.75 | 5.34 |
| RL2-6 | 1947.12 | 5.40 |
| Scenario | Peak Flow Rate/(m3·s−1) | Peak Water Depth/(m) |
|---|---|---|
| Base period | 2003.04 | 8.57 |
| RL3-1 | 2052.46 | 5.90 |
| RL3-2 | 2088.33 | 6.21 |
| RL3-3 | 2127.37 | 6.49 |
| RL3-4 | 1796.61 | 5.34 |
| RL3-5 | 1817.12 | 5.36 |
| RL3-6 | 2023.07 | 5.71 |
| Scenario | Peak Flow Rate/(m3·s−1) | Peak Water Depth/(m) |
|---|---|---|
| Base period | 2003.04 | 8.57 |
| RL4-1 | 2783.00 | 8.81 |
| RL4-2 | 2853.87 | 8.82 |
| RL4-3 | 2974.82 | 9.00 |
| RL4-4 | 2156.24 | 5.91 |
| RL4-5 | 2289.18 | 6.87 |
| RL4-6 | 2694.34 | 8.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Imran, M.; Hou, J.; Wang, T.; Li, D.; Gao, X.; Noor, R.S.; Jing, J.; Ameen, M. Assessment of the Impacts of Rainfall Characteristics and Land Use Pattern on Runoff Accumulation in the Hulu River Basin, China. Water 2024, 16, 239. https://doi.org/10.3390/w16020239
Imran M, Hou J, Wang T, Li D, Gao X, Noor RS, Jing J, Ameen M. Assessment of the Impacts of Rainfall Characteristics and Land Use Pattern on Runoff Accumulation in the Hulu River Basin, China. Water. 2024; 16(2):239. https://doi.org/10.3390/w16020239
Chicago/Turabian StyleImran, Muhammad, Jingming Hou, Tian Wang, Donglai Li, Xujun Gao, Rana Shahzad Noor, Jing Jing, and Muhammad Ameen. 2024. "Assessment of the Impacts of Rainfall Characteristics and Land Use Pattern on Runoff Accumulation in the Hulu River Basin, China" Water 16, no. 2: 239. https://doi.org/10.3390/w16020239
APA StyleImran, M., Hou, J., Wang, T., Li, D., Gao, X., Noor, R. S., Jing, J., & Ameen, M. (2024). Assessment of the Impacts of Rainfall Characteristics and Land Use Pattern on Runoff Accumulation in the Hulu River Basin, China. Water, 16(2), 239. https://doi.org/10.3390/w16020239







