Investigation of Hydraulic Performance and Arrangement Optimization of Non-Prismatic Water Conveyance Tunnel—A Case Study of Project X

Abstract

The water conveyance tunnel is an important hydraulic structure in water conservancy projects. Typically, it manifests as a non-prismatic tunnel due to variations in the cross-sectional geometry, which give rise to an unpredictable flow pattern that significantly impacts the secure and stable operation of the tunnel. This study takes water conservancy project X as a case and investigates the hydraulic performances of a non-prismatic water conveyance tunnel using a scale model test and numerical simulation; the hydraulic performance, such as flow pattern, discharge, flow velocity, and water depth profile are analyzed for both free flow and submerged flow conditions. The results show that the simulation data fit well with the experimental value observed in the scale model test for free flow; however, a substantial discrepancy emerges under submerged flow conditions. This discrepancy is attributable to the presence of a vacuum in the distortional plan section. Notably, the effect of water entrainment phenomena on flow rate and velocity is diminished in the scale model test, emphasizing the advantage of numerical simulation in predicting hydraulic parameters for the prototype. On this basis, the optimization of the gate shaft arrangement is executed through numerical simulation; the results indicate that the vacuum issues in the contraction section were partially resolved through structure optimization. The simulation values are close to the experimental results, and the modified design of the tunnel can be used in a water conveyance project.

1. Introduction

Water conservancy projects play an important role in flood control, water supply, and agriculture irrigation; as integral elements of hydraulic infrastructures, water conveyance tunnels are extensively employed in various water conservancy projects [1]. In order to regulate flow rates, gate shafts are strategically positioned within the tunnels, leading to abrupt changes in the cross-sectional profile. Additionally, variations in lining thickness occur due to shifts in the surrounding geological conditions; consequently, these tunnels are commonly classified as non-prismatic water conveyance tunnels [2,3]. Because the tunnel is divided by different hydraulic sections, an unpredictable flow pattern, discharge, and vacuum can occur that are harmful to the project [4,5,6,7]. Consequently, it is very important to predict the characteristics of hydraulic performance in the tunnel and to propose corresponding protective measures.

Water delivery capacity is an important hydraulic parameter for the water delivery tunnel, and it is necessary to calculate the maximum flow rate accurately. Currently, the methods employed for assessing the water conveyance capacity of tunnels include theoretical calculation, scale model testing, and numerical simulation [8,9,10]. Nevertheless, due to the influence of transition side walls, variations in wall roughness, and operating conditions, the discharge obtained through theoretical calculation methods often results in significant errors [11,12]. Considering that the theoretical model applied for the structure of the tunnel cannot be described mathematically with sufficient details, the implementation of scale hydraulic model experiments proves to be an effective method for predicting hydraulic performances [13,14]. In order to verify the rationality of the original layout scheme of the spillway tunnel, Zhao et al. [15] analyzed the discharge capacity, pressure distribution, water surface, energy dissipation, and scour prevention using a 1:40 monomer normal model according to Froude’s law. Wu and Ai [16] analyzed the factors affecting the critical thickness using dimensional analysis and proposed a formula to calculate the critical thickness in tunnels with sudden lateral enlargement. In view of the considerable length of the tunnel, the ratio of axial length to cross-profile height is substantial. When employing scale model tests to investigate the hydraulic performance of water delivery tunnels, the resulting small cross-sectional area due to the extensive length ratio proves inadequate to meet the requirements of gravity similarity [17]. While reducing the length ratio enhances prediction accuracy, it concurrently necessitates an increase in the model’s length, thereby leading to elevated costs. Primarily, the transformation of pressure is susceptible to the induction of cavitation on the lateral walls by sudden reductions and enlargements within the tunnel [18]. Heller [19] analyzed the scale effects between a model and a prototype, discussed the compensating or correcting methods of avoiding scale effects, and suggested possible future research directions. Owing to the scale effects in model testing, accurately predicting the corresponding pressure distribution in the prototype has proven to be unattainable.

The pressure distribution within the tunnel significantly impacts air aspiration; insufficient air intake into the tunnel leads to considerable variations in hydraulic performance, including flow rate and water surface profile. This variation complicates the prediction of cavitation and free-surface-pressurized flow occurrences, thereby affecting the operational safety of the water conveyance tunnel. Consequently, the application of numerical simulation becomes imperative to explore the disparities in hydraulic performance between the prototype and the scale model. Olsen NR et al. [20] simulated the scour hole around a circular cylinder in a flume in three dimensions; the simulation results compared well with the empirical formulas. Guha et al. [21] simulated high-speed turbulent water jets using the RNG k-ε turbulence model and the Eulerian–Eulerian multiphase model; the simulated pressure distribution at the impinging surface matched closely with the experimental results. Lu et al. [22] provided a practical numerical method for precisely evaluating the hydraulic transient process for the water delivery system. Calomino F et al. [23] proposed a discharge computational model based on the integration of the velocity profile in an internally corrugated tunnel; the numerical solutions of the velocity profiles and water depths were accurate compared with the experimental value. Prior research [24,25] has substantiated the suitability of computational fluid dynamics (CFD) in predicting the hydraulic performance of water conservancy projects. Consequently, the numerical simulation method proves to be a precise and efficient alternative for estimating flow patterns and designing the structure of water conveyance tunnels.

Given the limited literature addressing the distortion of pressure distribution at the lateral sudden reduction and sudden enlargement of walls in tunnels through scale model testing, this study, which takes a water conservancy project as a case, aims to assess disparities between numerical simulation and model testing in the manifestation of cavitation in the contraction section; on this basis, the optimization of a gate shaft arrangement is performed through numerical simulation.

2. Experimental Method

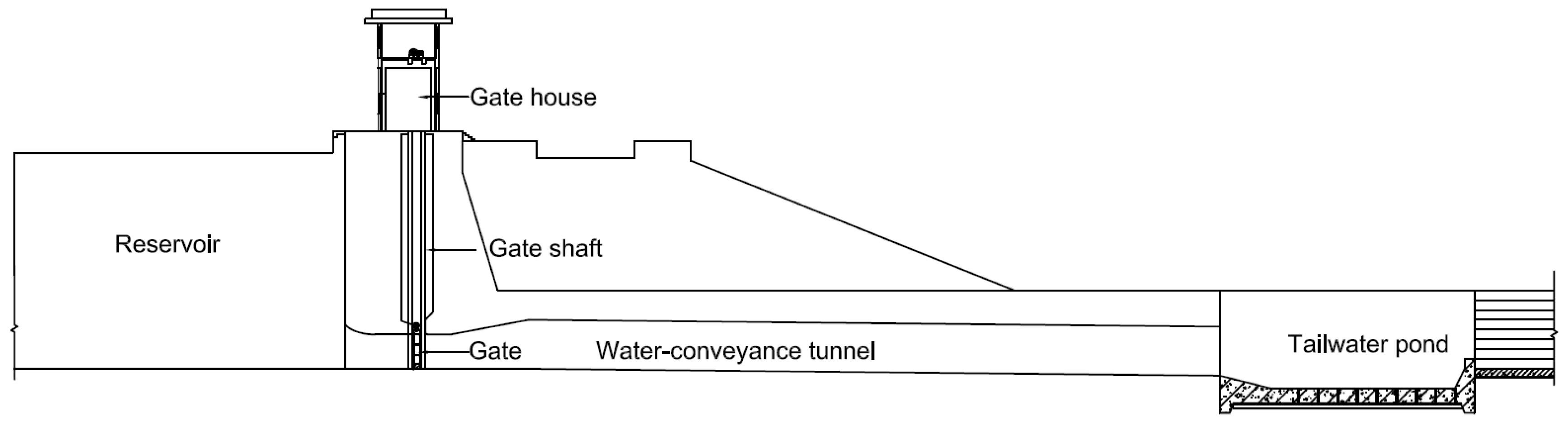
2.1. Project Profile

The water conservancy project, which is located in the upper reaches of Zhaohe River, a tributary of Tangbai River in the Yangtze River basin, is depicted in Figure 1. The primary objectives of the project include flood control, water supply, and irrigation. The reservoir features a normal pool level of 175 m and a dead storage level of 166 m, with a total storage volume of 1.15 × 10⁸ m³ and an effective storage volume of 4.84 × 10⁷ m³. The design flood stages for events occurring once in 100 years and once in 2000 years are specified as 177.20 m and 179.65 m, respectively.

This study focuses on a non-prismatic water conveyance tunnel, which is depicted in Figure 1. The tunnel spans a length of 89.5 m and comprises distinct sections, namely the tunnel inlet, distortional plan section, throat, transitional section, draft tube, and tunnel outlet. The cross-section of the inlet and throat sections is rectangular, while the draft tube features arched conduits. The longitudinal slope of the draft tube is 0.025; the specific dimensions for the other sections are detailed in Figure 2.

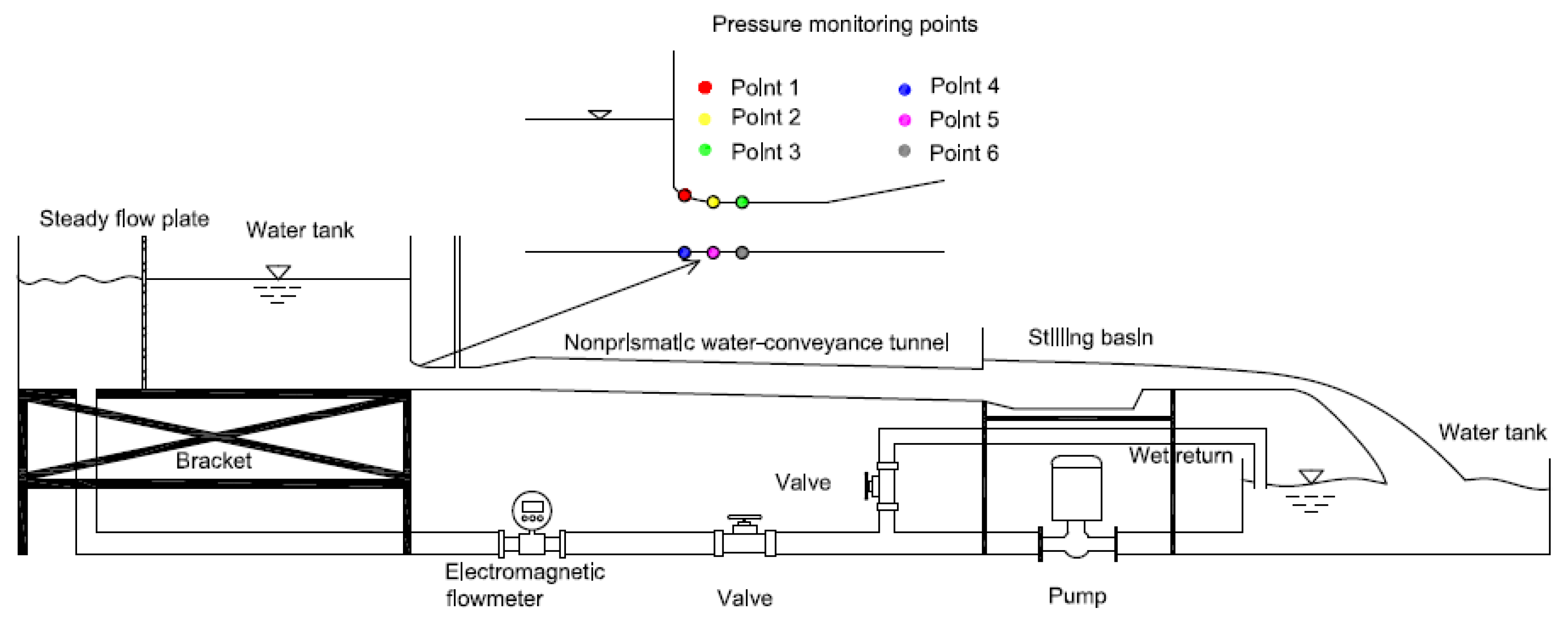
2.2. Experimental Setup

To analyze the hydraulics of the non-prismatic water conveyance tunnel, a reduced-scale model was employed at a 1:50 ratio. The model experiments were conducted in a recirculating water tank within the hydraulic laboratory of the Water Conservancy Research Institute in Henan Province. The equipment setup included a water tank, bracket, water conveyance tunnel, stilling basin, pump, valves, electromagnetic flowmeter, pump electronic control terminal, and PVC pipes, as illustrated in Figure 2. A steady flow pore plate was installed at the outlet of the return pipe to mitigate the turbulence and surface wave formation at the upstream water tank inlet. The water conveyance tunnel was constructed from plexiglass. The pressure and flow velocity were measured using a piezometric tube and flow velocity meter, respectively, with each measurement being repeated three times in each group. The pressure monitoring points are depicted in Figure 3, where the horizontal distances of points 1, 2, and 3 are 1 m, 3 m, and 5 m from the tunnel entrance’s top, respectively. Correspondingly, the measurement points at the bottom are designated as points 4 to 6.

2.3. Similarity Theory

The model test is commonly used to investigate the performances of the hydraulic structure through a scaled model. To ensure congruence in the flow patterns between the scaled and prototype models, the similarity theory is employed to achieve both geometric and mechanical similarity.

The similar characteristics of the two flow systems can be described by geometric similarity, motion similarity, and dynamic similarity. When the physical quantities, such as velocity, pressure, and the various forces on the corresponding points of the model flow and the prototype flow, have a fixed proportional relationship, the two flows are similar. When the flow is driven by the effect of gravity, the gravity similarity criterion is more applicable.

In adherence to the similitude principle, the scale selection of the hydraulic model should satisfy the gravity similitude criterion. The model geometric scale is 1:50, i.e., the geometric scale is ${\lambda }_L={\lambda }_H=50$, and ${\lambda }_L$ and ${\lambda }_H$ are the horizontal scale and vertical scale, respectively.

• Discharge scale: ${\lambda }_Q={\lambda }_L{}^{2.5}$
• Velocity scale: ${\lambda }_v={\lambda }_L{}^{0.5}$
• Time scale: ${\lambda }_t={\lambda }_L{}^{0.5}$

2.4. Design of Experiment

In accordance with the design requirements, the designed flood standard of the reservoir is once in 100 years, and the verified flood standard is once in 2000 years; the characteristic water depth of the verified flood standard is 11.0 m above the bottom of the tunnel. Consequently, the experimental upstream flow depth in the prototype model is set within the range of 1.0 to 11.0 m. Adhering to similarity theory, the upstream flow depth in the scaled model is set at one-fiftieth of the prototype model. The water intake height is 4.5 m, and free flow is proposed with forebay water depths ranging from 0.5 m to 4.0 m; the submerged flows are in the range of 5.0 to 11.0 m. The specific experimental upstream flow depths are detailed in

Table 1. Experimental upstream flow depth.

Flow Regime	Operating Conditions
	Upstream Flow Depth in Scaled Model for Experiment (Model Scale Is 1:50)	Upstream Flow Depth in Prototype Model for Simulation
Free flow	0.01 m	0.5 m
	0.02 m	1.0 m
	0.03 m	1.5 m
	0.04 m	2.0 m
	0.05 m	2.5 m
	0.06 m	3.0 m
	0.07 m	3.5 m
	0.08 m	4.0 m
Submerged flow	0. 10 m	5.0 m
	0.12 m	6.0 m
	0.14 m	7.0 m
	0.16 m	8.0 m
	0.18 m	9.0 m
	0. 20 m	10.0 m
	0.22 m	11.0 m

.

3. Numerical Simulation

3.1. Geometric Model

A prototype model was built based on the physical dimensions of the water conveyance tunnel using the software Solidworks (Version 2017); then, it was imported to Ansys ICEM (2021 R1); ANSYS ICEM software (2021 R1) is used for grid partition. Figure 4 illustrates the use of a hexahedral mesh for the forebay and stilling pool. The cell grid size was set to 0.35 m; the number of nodes and total grid cells were 353,321 and 1,216,866, respectively. Given the complexity and extensive length range of the water conveyance tunnel, a tetrahedral mesh was employed for the tunnel. The model boundaries were defined as water inlet, air outlet, water outlet, and walls (Figure 4). Pressure inlet conditions were applied to the water inlet, while pressure outlet conditions were applied to the air outlets and water outlet. The walls were subjected to a no-slip condition.

3.2. Governing Equation

The numerical simulations were conducted utilizing ANSYS FLUENT 2021, which is based on FVM. The mass conservation equation and Navier–Stokes equations were used for the incompressibility; the standard k-ε turbulence model was chosen to solve the unsteady calculation.

The continuity and Navier–Stokes equations for fluid flow are given by Equations (1) and (2) [26]

$$\frac{\partial \rho }{\partial \mathrm{t}}+\frac{\partial \left(\rho \mathrm{u}\right)}{\partial \mathrm{x}}+\frac{\partial \left(\rho \mathrm{v}\right)}{\partial \mathrm{y}}+\frac{\partial \left(\rho \mathrm{w}\right)}{\partial \mathrm{z}}=0$$

(1)

$$\frac{\partial \left(\rho \mathrm{u}\right)}{\partial \mathrm{t}}+\mathrm{d}\mathrm{i}\mathrm{v}\left(\rho \mathrm{u}\mathrm{u}\right)=-\frac{\partial \mathrm{p}}{\partial \mathrm{x}}+\mathrm{d}\mathrm{i}\mathrm{v}\left(\mathsf{\mu }\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{u}\right)+{\mathrm{F}}_{\mathrm{x}}$$

(2)

In these equations, t is time (s); $\rho$ is the density of the fluid (kg/m³); $\mathrm{u}$ is the flow velocity (m/s); u, v, and w are the averaged flow velocity components in the Cartesian coordinates x, y, and z, respectively (m/s); $\mathsf{\mu }$ is the dynamic viscosity of the fluid (N·s/m²); ${\mathrm{F}}_{\mathrm{x}}$, ${\mathrm{F}}_{\mathrm{y}}$, and ${\mathrm{F}}_{\mathrm{z}}$ are body forces (N); and p is pressure (pa).

The turbulent kinetic energy and dissipation rate of the standard k-epsilon model were chosen to solve the unsteady calculation. The standard k-ε three-dimensional turbulence models are shown as follows:

$$\frac{\partial }{\partial \mathrm{t}}(\rho \mathrm{k})+\frac{\partial }{\partial {\mathrm{x}}_{\mathrm{i}}}(\rho \mathrm{k}{\mathrm{u}}_{\mathrm{i}})={\mathsf{\mu }}_{\mathrm{t}}(\frac{\partial {\mathrm{u}}_{\mathrm{i}}}{\partial {\mathrm{x}}_{\mathrm{i}}}+\frac{\partial {\mathrm{u}}_{\mathrm{j}}}{\partial {\mathrm{x}}_{\mathrm{j}}})\frac{\partial {\mathrm{u}}_{\mathrm{i}}}{\partial {\mathrm{x}}_{\mathrm{j}}}+\frac{\partial }{\partial {\mathrm{x}}_{\mathrm{j}}}\left[(\mathsf{\mu }+{\mathsf{\mu }}_{\mathrm{t}})\frac{\partial \mathrm{k}}{\partial {\mathrm{x}}_{\mathrm{j}}}\right]-\rho \mathsf{\epsilon }$$

(3)

$$\begin{array}{l}\frac{\partial }{\partial \mathrm{t}}(\rho \mathsf{\epsilon })+\frac{\partial }{\partial {\mathrm{x}}_{\mathrm{i}}}(\rho \mathsf{\epsilon }{\mathrm{u}}_{\mathrm{i}})\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\frac{1}{2}\rho {\mathrm{C}}_{\mathsf{\epsilon }1}\mathsf{\epsilon }((\frac{\partial {\mathrm{u}}_{\mathrm{i}}}{\partial {\mathrm{x}}_{\mathrm{j}}}+\frac{\partial {\mathrm{u}}_{\mathrm{j}}}{\partial {\mathrm{x}}_{\mathrm{i}}})+\frac{\partial }{\partial {\mathrm{x}}_{\mathrm{j}}}\left[(\mathsf{\mu }+{\mathsf{\mu }}_{\mathrm{t}}/{\mathsf{\sigma }}_{\mathsf{\epsilon }})\frac{\partial \mathsf{\epsilon }}{\partial {\mathrm{x}}_{\mathrm{j}}}\right]\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\rho {\mathrm{C}}_{\mathsf{\epsilon }2}\frac{{\mathsf{\epsilon }}^2}{\mathrm{k}+\sqrt{\mathrm{v}\mathsf{\epsilon }}}\end{array}$$

(4)

where k is turbulence kinetic energy (m²/s²); ε is turbulence dissipation (kg m²/s³); i and j are vectors; and C_ε1, C_ε1, and σ_ε are correcting coefficients.

The multiphase VOF (volume of fluid) model, which is accurate in tracking the free surface of complex flows, is adopted for this study; open channel flow is applied in VOF sub-models. The flow specification method is set as the free surface level and total height. Standard wall functions are used for the near-wall treatment. The SIMPLE algorithm is chosen to solve the mass conservation and Navier–Stokes equations [27]. A pressure-based solver is used in the numerical scheme; the gravity and operating pressure are set to 9.81 m/s² and 101,325 Pa, respectively. The time step size (t) is set to 0.001 s, and the convergence precision is set to 0.0001 for all the equations.

4. Results

4.1. Validation of Free Flow

In order to verify the accuracy of the numerical simulation, the proposed structural model was tested in the laboratory under a free flow condition with eight upstream flow depths; the experimental values for the flow pattern, flow rate, and water surface profile were collected to compare with the simulation data.

(1)

Flow pattern

As the upstream water from the stabilization pond enters the water conveyance tunnel, the flow regime undergoes a transition from subcritical to supercritical, leading to a reduction in water depth over increasing flow distances. In the event of elevated water levels within the stilling basin, backwater may develop in the tunnel as water advances to a certain point, resulting in a transition from a supercritical to a subcritical flow. The flow patterns observed in the water conveyance tunnel under free flow conditions, with upstream flow depths of 1.5 and 3.5 m, are depicted in Figure 5. Notably, both the experimental and the simulation data indicate backwater occurrences at approximately 67 m and 88 m for the upstream flow depths of 1.5 and 3.5 m, respectively; this indicated a good agreement between the experimental results and the simulation predictions.

(2)

Flow rate

Table 2. Flow rate of free flow.

Upstream Flow Depth (m)	Discharge (m3/s)		Relative Deviation
	Experimental Value	Simulation Value
0.5	1.79	1.71	−4.46%
1	4.78	4.99	4.39%
1.5	9.15	8.92	−2.51%
2	12.82	13.73	7.10%
2.5	18.21	18.67	2.52%
3	23.32	25.15	7.85%
3.5	30.92	31.68	2.49%
4	36.80	38.67	5.08%

presents a comparison of the flow rates between the experimental and simulated data under free flow conditions. Both the experimental and the simulated discharges exhibited an increase in conjunction with elevated elevation heads. The relative deviation (calculated by Equation (5)), which falls within the range of −4.46% to 7.85%, demonstrates a substantial alignment between the simulation results and the measured data. This signifies the high level of accuracy achievable through the numerical method.

$$Rd=\frac{Sv-Ev}{Ev}\times 100\%$$

(5)

where $Rd$ is relative deviation; $Sv$ is the simulation value; and $Ev$ is the experimental value.

(3)

Water surface profile

Water depth along the centerline of the channel was measured, and the comparison of the water surface profiles, as shown in Figure 6, reveals the congruence between the experimental results and the simulated values with different upstream flow depths. As shown, the changes in the water profile using the simulation method were similar to the experimental data. Notably, the water depth diminished as water from the basin flowed into the tunnel, with a more pronounced decrease observed under higher elevation head conditions. For sections with a positive slope, the water depth continued to decrease with increasing flow distance in the tunnel and then increased sharply in a particular position; this indicates that hydraulic jumps were generated in this section. This transition from subcritical to supercritical flow occurred further downstream under higher elevation head conditions. These results collectively underscore the strong agreement between the simulated and experimental water profiles.

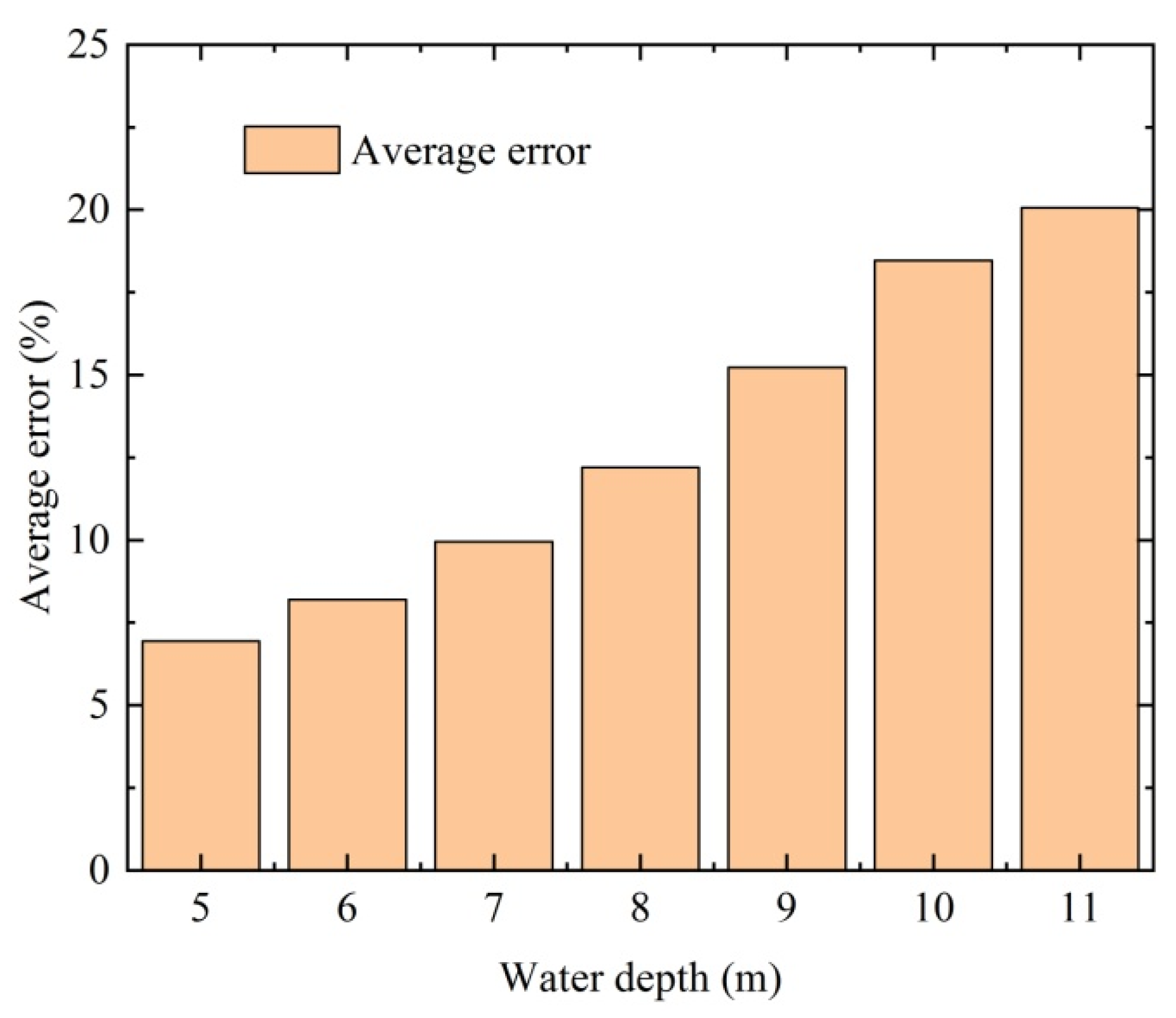
4.2. Hydraulic Discrepancy of Submerged Flow

(1)

Flow rate

Table 2 depicts the comparison of flow rates between the simulation values and the experimental data under the submerged flow conditions. As with the free flow, the discharges exhibited an increase with the rising upstream flow depth. However, it is worth noting that the simulation discharge consistently exceeded the corresponding experimental values under the same elevation head. Furthermore, as the elevation head increased, the relative deviations showed an upward trend. The minimum error of 7.19% was observed at an upstream flow depth of 5 m, but when the upstream flow depth exceeded 6 m, the relative deviations surpassed 10%. The highest relative deviation reached 17.94%, signifying notable disparities between the computed values and the experimental measurements.

(2)

Velocity along the centerline

The disparities of the velocities were evaluated between the simulated and experimental results, as depicted in Figure 7, which shows the velocities at varying upstream flow depths. The reported measured velocity represents the mean value derived from three measurements. It is noteworthy that the simulated velocities consistently exceeded the measured values, and these differences increased with the higher upstream flow depths, as illustrated in Figure 8. The red shade is the average error ranged from 6.94% to 20.05% as the elevation head increased from 5 m to 11 m, mirroring a similar trend observed in the case of the flow rates.

The disparities in flow rate and velocity under submerged flow conditions suggest that either the scale model test or numerical simulation may not be suitable for forecasting the flow state in non-prismatic tunnels. To address this issue, a more comprehensive analysis of hydraulic performance is required.

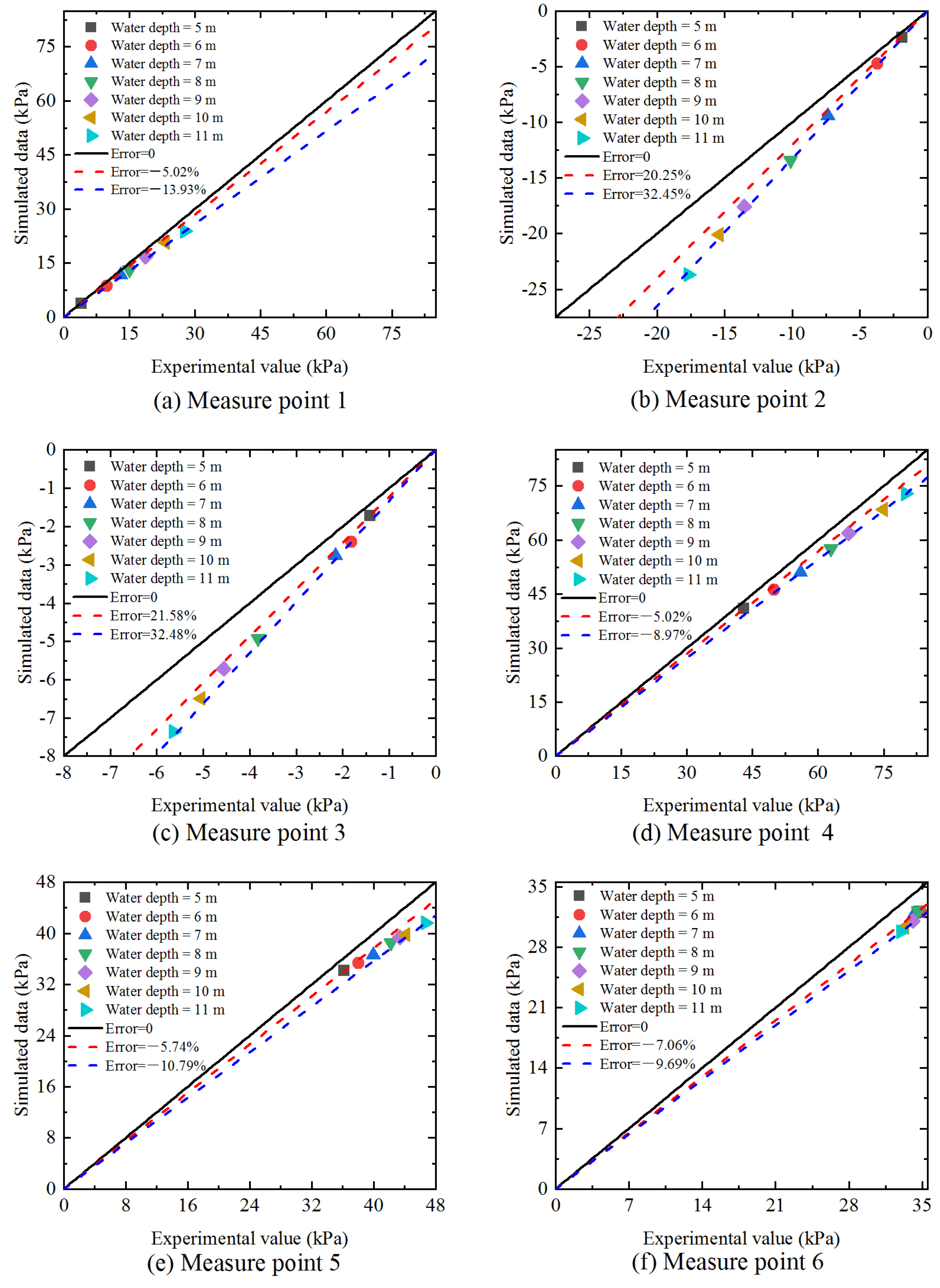
4.3. Hydraulic Performance in Contraction Section of Submerged Flow

When the upstream flow depth exceeds the height of the tunnel entrance, it leads to a submerged flow, with the emergence of a vacuum in the distorted cross-sectional area, which is primarily attributable to the presence of a contraction section. In general, when vacuum phenomena manifest in scale model tests, the application of the similarity theory becomes impractical for predicting hydraulic performance, and the error will increase with the increasing of the vacuum. In order to investigate the vacuum value and distribution, the pressure in the contraction section and the wind velocity in the gate shaft are analyzed.

(1)

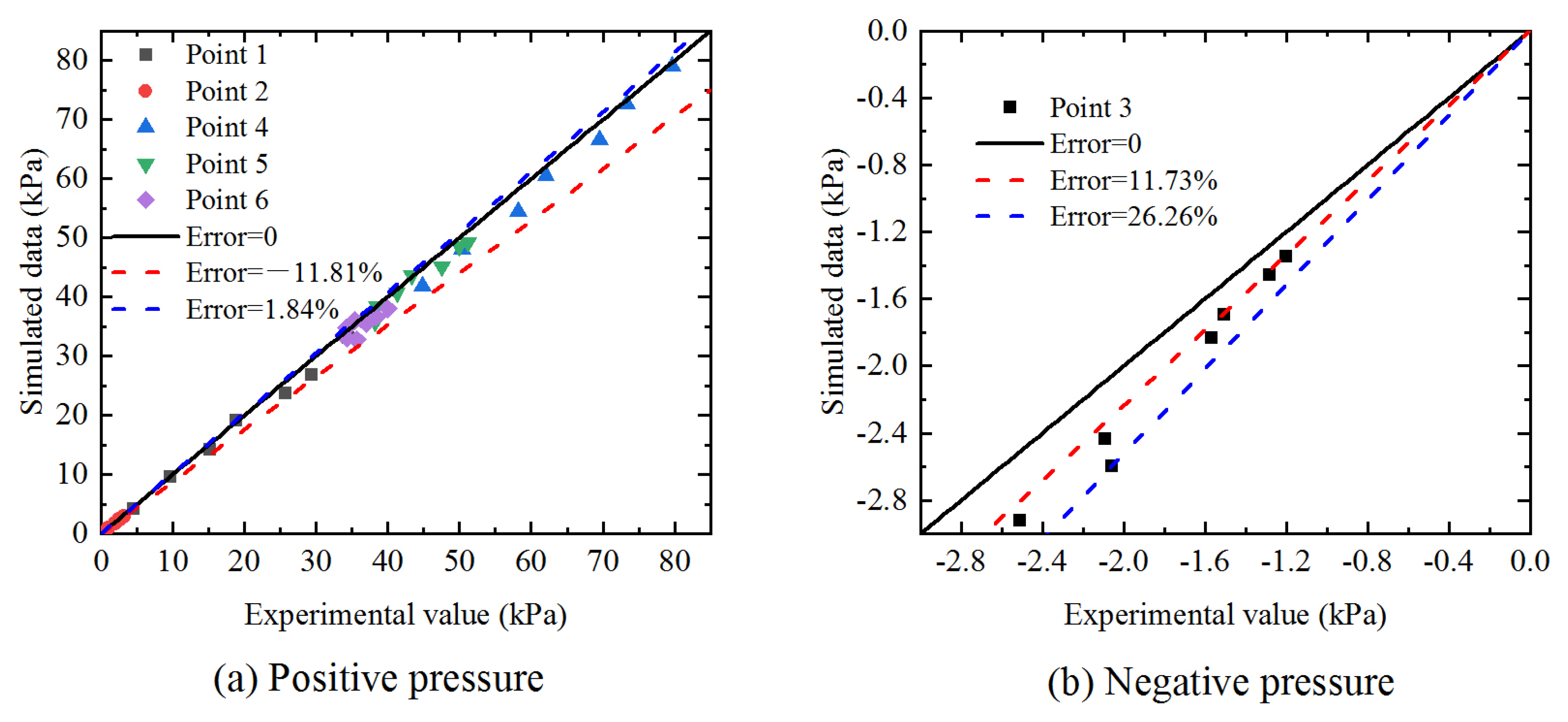
Pressure in the contraction section

Figure 9 presents a comparative analysis of the experimental and simulated data at six measurement points under varying elevation heads. Notably, the pressure at the bottom of the tunnel within the contraction section remains positive (Figure 9d–f), and initially, positive pressure is observed at the top of the tunnel (Figure 9a). However, with the progression of flow, vacuum conditions emerge at measurement points 2 and 3 (Figure 9b,c). Moreover, it is worth mentioning that the simulated values of the positive pressure consistently register as lower than those obtained through the scale model testing, with errors spanning from −5.02% to −13.93% for point 1, point 4, point 5, and point 6; these errors vary with the elevation head. Conversely, the simulated vacuums are always much larger than the experimental value, resulting in errors ranging from 20.25% to 32.45% at measurement point 2 and from 21.58% to 32.48% at measurement point 3; the results verified the inadequacy of the similarity theory; meanwhile, they indicate the reliability of the simulation method. Figure 9 also shows that the error presents an increasing tendency as the upstream flow depth increases. Additionally, Figure 9 highlights that the errors exhibit an upward trend as the upstream flow depth increases.

Due to the proximity of the contraction section to the reservoir, the upstream propagation of the vacuum induces water entrainment phenomena in the reservoir, consequently leading to an augmentation in flow rate. As a consequence of the inapplicability of similarity theory in the scale model test, the experimental vacuum values prove to be smaller than those obtained in the prototype test. The significance of the entrainment phenomena in the scale model test is diminished, thereby resulting in a reduction in both flow rate and velocity, as evidenced by the data presented in

Table 3. Flow rate of submerged flow.

Upstream Flow Depth (m)	Discharge (m3/s)		Relative Deviation
	Experimental Value	Simulation Value
5	52.3	56.06	7.19%
6	71.19	78.28	9.96%
7	78.58	85.56	11.43%
8	85.35	97.84	14.63%
9	95.12	109.69	15.32%
10	101.77	118.98	16.91%
11	108.43	127.89	17.94%

and Figure 7.

(2)

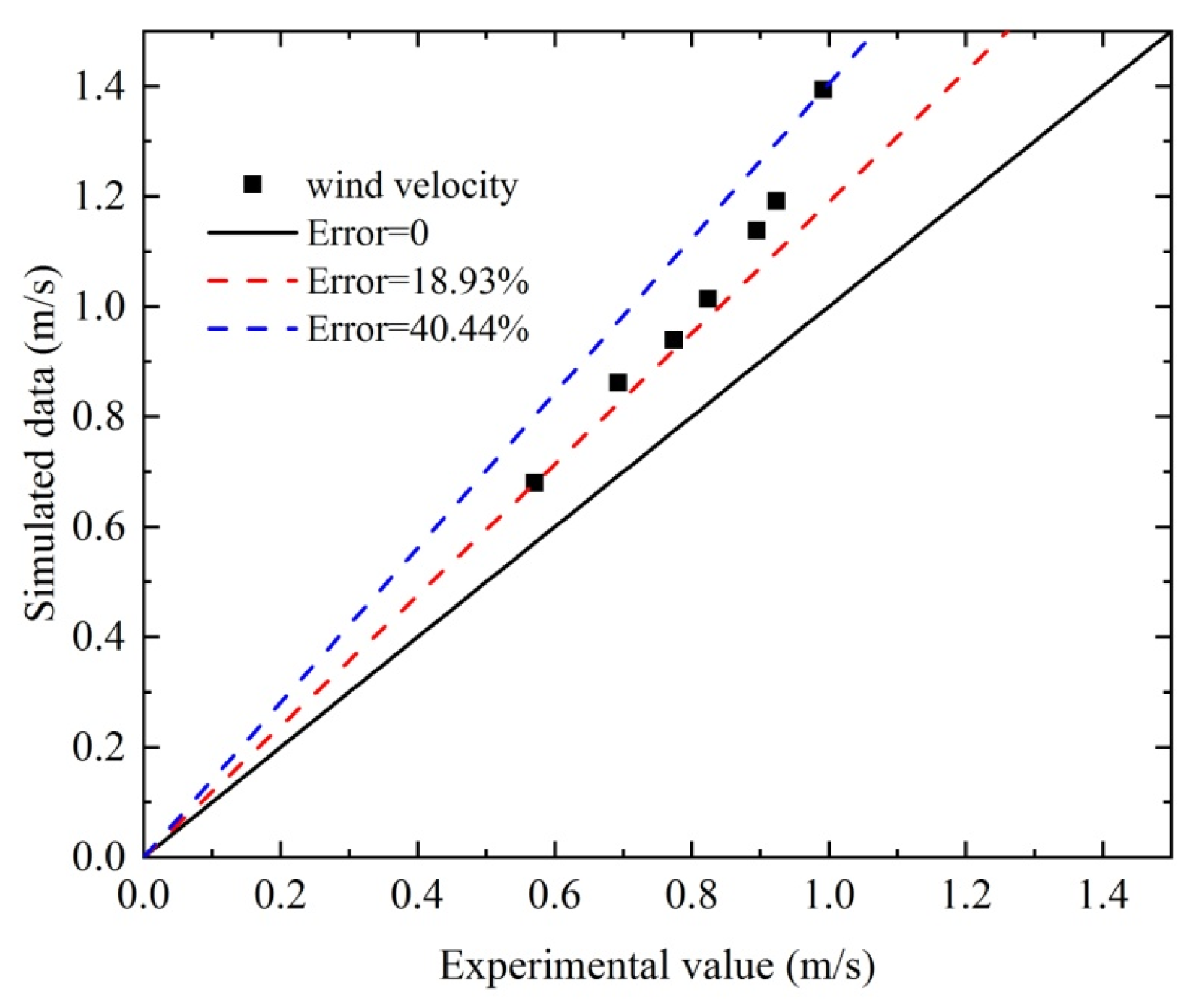
Wind velocity

As the gate shaft is positioned within the center of the contraction section, the vacuum propagates downstream towards the gate, causing an inflow of external air into the tunnel. Figure 10 displays the relative deviation of wind velocity between the simulation and scale model tests under various elevation heads. The data reveal that the simulated values consistently exceed the experimental values, with errors ranging from 18.93% to 40.44%. A huge difference between the simulation and experimental data is obtained; the results gave a further verification of the failure in the scale model test.

4.4. Prevention Measures

(1)

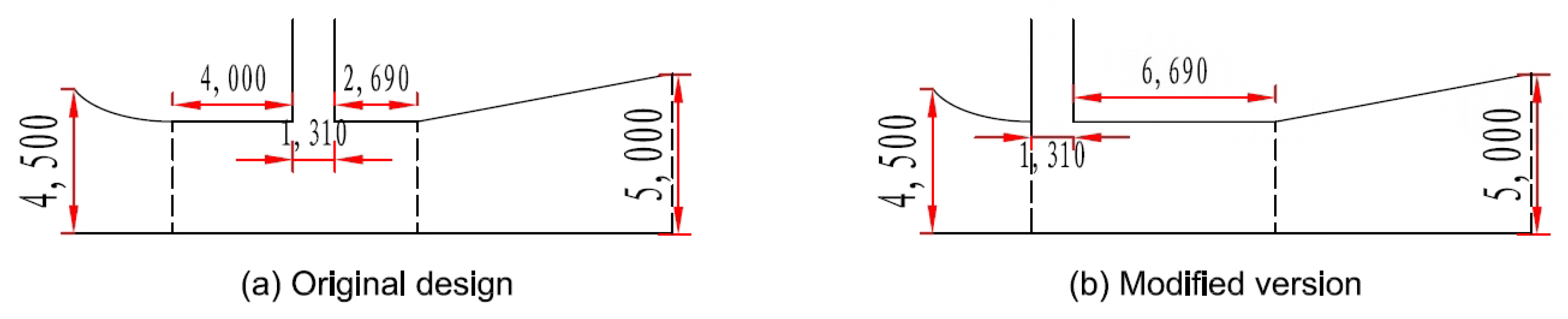
Scheme design

As indicated in the preceding analysis, a vacuum emerges as the predominant factor contributing to the inadequacy of the similarity theory in the scale models. To rectify the hydraulic disparities associated with submerged flow and to mitigate the detrimental effects of cavitation damage, engineering interventions are proposed. Figure 11 illustrates the modified gate shaft design. In contrast to the original design, the gate shaft has been relocated forward by 4 m and is adjacent to the distorted cross-sectional area.

(2)

Flow rate

The hydraulic performance of the modified design was assessed through a combination of scale model testing and simulation. In

Table 4. Flow rate of non-prismatic water conveyance tunnel.

Flow Regime	Elevation Head	Discharge (m3/s)		Relative Deviation
		Experimental Value	Simulation Data
Free flow	0.5	1.68	1.70	1.41%
	1.0	4.77	4.93	3.42%
	1.5	8.76	8.93	1.94%
	2.0	13.52	13.08	−3.24%
	2.5	18.57	18.73	0.88%
	3.0	24.93	25.25	1.27%
	3.5	31.42	30.31	−3.53%
	4.0	38.29	37.31	−2.56%
Submerged flow	5.0	51.52	52.31	1.53%
	6.0	65.53	65.95	0.63%
	7.0	76.32	77.67	1.77%
	8.0	82.21	87.88	6.90%
	9.0	89.07	97.17	9.10%
	10.0	95.63	106.24	11.09%
	11.0	101.98	114.28	12.06%

, the flow rates for the tunnel are presented at various elevation heads. The relative deviations range from −3.52% to 9.10% when the upstream flow depth is less than 9 m. However, these deviations increase to 11.09% and 12.06% when the elevation head exceeds 10 m. This indicates that, to some extent, the vacuum continues to influence hydraulic performance in the modified design as the upstream flow depth increases. Nevertheless, there is strong concordance between the simulation data and the experimental values.

(3)

Pressure in contraction section

In Figure 12, a comparison is presented between the experimental pressure values and the simulation data. The relative deviations for positive pressure and negative pressure range from −11.81% to 1.84% and from 11.73% to 26.26%, respectively, highlighting the continued limitations of the similarity theory. However, when compared with the original design, a notable change is observed at measurement point 2, as it transitions from negative pressure to positive pressure. Although the pressure at this point remains below 3.23 kPa, this alteration has contributed to a partial alleviation of the water entrainment phenomena. In the context of the modified design, measurement point 3 has been repositioned downstream of the gate shaft, effectively reducing the impact of the vacuum at this location on the flow state within the tunnel.

The results indicate that structural optimization partially mitigated the vacuum issues in the contraction section. There is a close alignment between the simulation results and the experimental data, supporting the viability of the modified tunnel design for application in water conveyance projects.

5. Conclusions

In this study, the hydraulic performances of the non-prismatic water conveyance tunnel were investigated using a scale model test and CFD analyses; the main results can be summarized as follows:

(1)

For free flow, the flow characteristics, such as flow pattern, flowrate, and water surface profile, showed good agreement between the experimental results and the simulation predictions; this indicated that the numerical simulation effectively aligned with the experimental scale model test data when assessing the hydraulic performance of a water conveyance tunnel with a contraction section under free flow conditions.

(2)

For submerged flow, notable deviations of the flow rate and velocity in non-prismatic tunnels emerged. The primary factor behind this divergence was the development of a vacuum within the distorted cross-sectional area caused by the presence of the contraction section, and the similarity theory proved inadequate for predicting the hydraulic performance during scale model tests.

(3)

In order to figure out the applicability of the scale model test and numerical simulation for forecasting the flow state, the hydraulic performances in the contraction section of the submerged flow were analyzed; the results of the pressure and wind velocity verified the inadequacy of the similarity theory in non-prismatic tunnels and indicated the reliability of the simulation method.

(4)

The reason for the failure of the scale model test in non-prismatic tunnels is that the vacuum created within the distorted cross-sectional area and the contraction section can be promptly released through the gate shaft. As the vacuum propagates upstream, it gives rise to water entrainment phenomena within the reservoir, which consequently leads to an increase in the flow rate.

(5)

To mitigate the adverse effects of negative pressure on both cavitation damage and the hydraulic performance within the tunnel, the placement of the gate shaft was optimized. The vacuum issue was settled in the distorted plan section, and the numerical simulations agreed well with the scale model test. These findings not only validated the accuracy of the CFD analyses, but also substantiated the applicability of the modified design for implementation in water conservancy projects.