Abstract
Under the impact of global climate change and human activities, the occurrence of compound disasters such as cascading landslides and flash floods caused by heavy rainfall is increasing. In response to these compound disaster events, it is important to simultaneously transport emergency resources from multiple emergency rescue points to the disaster sites to promptly control the cascading development of disasters and reduce the areas affected by the disasters and associated adverse impacts. This study proposes a dynamic game model for emergency resources dispatch to comprehensively consider the evolution of the compound disaster states and the timely dispatch of emergency resources from the rescue points to the disaster site. The dynamic game model is exemplarily applied to the emergency resource dispatch for a rainstorm-induced compound disaster that occurs in the Guangdong–Hong Kong–Macao Greater Bay Area (GBA). Starting with the analysis of the characteristics of emergency resource management and the attributes of a cascading of heavy rainstorms, landslides, and flash floods, the game model simulates the dynamic game process between the “disaster state” and the “emergency resource manager” in the rescue operations. A two-stage dynamic game model can support decision-making with the objectives of minimal time cost and sufficient resource dispatch for the disaster sites. Game results show that the united emergency resource dispatch in the three GBA metropolitan areas can efficiently respond to compound disasters that occur within the GBA metropolitan area. The dynamic game model could be extended for compound disaster emergency responses with more complicated compound effects and resource constraints.
1. Introduction
Impacts of climate warming and human activities have increased the amount of water vapor content in the atmosphere and induced changes in atmospheric circulations at various spatiotemporal scales [1,2,3]. These changes have continuously intensified the water cycle and resulted in an increasing frequency [4], severity [5], and spatial extent [6] of extreme precipitation events and thus rainstorm-related disasters [7,8]. Therefore, it is of great importance to have preparedness for reducing rainstorm-related disaster risks for climate change adaptation [9].
When a rainstorm occurs, the prior decision, often made by emergency resource managers, is to involve resources stored in the nearest rescue points for emergency relief to reduce the area affected by the rainstorm-related disaster. A smooth and successful rescue requires that the rescue point should provide sufficient emergency resources to meet the needs of the neighboring disaster site. However, under a changing climate and increasing occurrences of compound climate extreme events [10,11], rainstorm-related disasters often occur with successive, concurrent, and compound multi-hazards, instead of a single hazard [7]. Intense rainstorms trigger disasters such as flash floods, urban waterlogging, and landslides. If emergency rescue is not timely and effective, it could further increase casualties and property losses, due to escape panic [12] and infrastructure failures. According to the Ministry of Emergency Management of the People’s Republic of China, flooding disasters in 2023 affected more than 50 million people with varying hazard degrees, including 309 people dead or missing and 130,000 houses collapsing. The direct economic losses of flood-related hazards in China during 2023 amounted to CNY 244.57 billion. In addition, intense rainstorms caused 3666 geological disasters such as landslides, mudslides, and the collapse of the roadbeds and the slopes. Therefore, to minimize the losses caused by a heavy rainstorm, emergency rescue plans should be made to respond to successive hydrological and geological disasters [13].
For complex and rapidly changing compound disasters, individual rescue points typically cannot provide sufficient emergency resources needed at multiple disaster sites [14], so emergency resources collected from multiple rescue points should be allocated and transported to multiple disaster sites [15]. Therefore, with the objectives of minimizing the cost and rescue time, and maximizing the equity, the allocation of emergency resources involves multi-disaster sites, multi-rescue points, and multi-stage dynamic dispatching activities [15,16,17]. To simplify the resources dispatch processes, most models proposed for the allocation of emergency resources often only consider a specific objective [18,19], although the time and financial cost and the uncertainties of compound hazard development are of great importance for emergency responses to compound nature hazards [20,21]. Considering the hazard uncertainty based on the multi-objective cellular genetic algorithm (MOCGA), Wang et al. (2022) [22] proposed an emergency resource allocation model under the conditions of natural disaster chains. However, MOCGA focuses on scenarios that emergency resources are centrally distributed, but MOCGA does not adequately consider the dynamic game between the emergency resource managers and the compound disaster occurrences. To rapidly and efficiently mitigate hazard impacts and cut off the possible hazard chains, during disaster rescue operations, emergency resource managers need to continuously adjust their implementation strategies during the development of specific compound disaster situations [17,22].
Game theory has been widely used in various stages of disaster management [17,19,21,23], including mitigation [24], preparedness [25], responses [26], and recovery [27]. Some game theory-based allocation models were proposed to dispatch resources to multiple emergencies with objectives to minimize the time from rescue points to disaster sites while maximize the impact of emergency help [26]. However, previous game theory-based allocation models for emergency resources more-so focus on a single disaster alleviation, so this paper proposes a mathematical model for decision-making in emergency responses to compound disasters resulting from a heavy rainstorm using the incomplete information dynamic game theory. Specifically, the proposed model is used to a time-minimizing emergency resources for successive hazards, including landslides and torrential floods caused by heavy rainfall.
2. Materials and Methods
2.1. Problem Description
The management of significant compound disaster events often requires the allocation of a vast array of emergency materials across different regions. A single material support agency cannot accomplish the logistics tasks associated with compound disaster events; typically, numerous logistics and production companies work together to fulfill these tasks. Therefore, there is a need for an agency to assign tasks and coordinate among various enterprises, and this coordinating agency is often formed temporarily by the government drawing personnel from various units according to emergency plans. The government operates through the exercise of administrative authority to bring relevant functional departments together to manage the allocation of emergency materials. In this text, we refer to this coordinating body as the emergency resource manager. Its operation is guaranteed by strong governmental authority.
In the process of emergency avoidance management for compound disasters, a single disaster within the compound disaster continuously engages in a game with the development of time and changes in the surrounding environment. The result of this game is the transformation of the state of the compound disaster event. A compound disaster event represents the leap from quantitative to qualitative change in the inherent contradictions of things, triggered by certain opportunities. When the affirmative aspects of factors in a single disaster event are dominant, the event maintains its original nature and existence, remaining in a relatively stable state of quantitative change. When other aspects gain dominance, the situation will transform or evolve into other disaster events. Often, it is the interaction and influence among compound disaster events that lead to an expansion of impact, thereby increasing the extent and scope of the impact of compound disaster events. This transformation, derivation, or coupling between compound disaster events can, in fact, be regarded as a game process between single events of compound disasters, and between compound disaster events and the external environment.
After the occurrence of a compound disaster, the emergency resource manager analyzes and organizes the various impacts generated by the event based on its development, predicts the future trends in development, and makes corresponding decisions on various response measures according to the analysis results. At the same time, since compound disaster events will continue to change during the management process, the emergency resource manager needs to adjust strategies based on phase results and changes in available information during the event development. Therefore, the decision-making process in emergency management is a dynamic game process under incomplete information between the “Emergency Management Subject” and the “Emergency Management Object”. In this context, the “Emergency Management Subject” is the emergency resource manager of the compound disaster event, while the “Emergency Management Object” refers to the specific compound disaster event.
Ultimately, changes in disaster developments will cause changes in the rescue process and emergency resource management. Therefore, the structure of the decision network will also change subsequently. Strategic adjustments are often adopted in response to changes in the state of the environment, so rescue planning is a game process. This dynamic game of emergency resource management is characterized by the dynamical development of a compound disaster event, the gradual increases in the environmental information of that compound disaster event, and the adjustability of the decision made on the condition of incomplete information for the condition of incomplete information. Therefore, the core of the game of emergency resource dispatch is the dynamic adjustment of strategies.
We propose an emergency rescue planning model to facilitate rescue decisions in response to a potential compound disaster for the multi-stage allocation of emergency resources from rescue points to disaster sites. Based on the state changes in the disaster development process and the corresponding information supplement, the dynamic game network model uses the incomplete information dynamic game theory to adjust the planning network structure for rapid rescue that responds to a possible compound disaster to minimize the negative utility losses of material shortage and the time cost of resource allocation. The decision processes for the dynamic rescue of a compound disaster consist of the evaluation and grading of the stage status of the dynamic decision networks, the management of critical chains, and the optimal allocation and scheduling of resources.
The schematic diagram of the dynamic game network model is shown in Figure 1. A guarantee rate function is the benefit function of emergency resource managers and plays an important role in the entire game process. The ultimate goal of the emergency resource allocation game is to maximize the guarantee rate function, which is composed of factors such as process time, the objectives of emergency resource managers involved in a compound disaster event, possible states and their transformation trends in that compound disaster event, the specific attributes of that compound disaster event, and the potential schemes of reasonable emergency resource allocation.
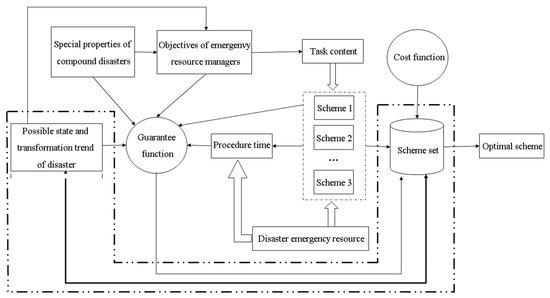
Figure 1.
Decision-making diagram of emergency resources dispatch for compound disaster events in the dynamic game framework. The dotted lines in the diagram are the “optimal schemes” evaluated by emergency resource managers in different disaster states.
Given the differences in the dynamic development of a compound hazard, the limited emergency resources available at each rescue point, and the distance and road conditions from each rescue point to the disaster site, there usually are several emergency resource allocation schemes for disaster response. Different schemes have different costs and process times, which are exactly associated with the effectiveness and efficiency of emergency resource allocation. The proposed dynamic game model searches for the optimal schemes for emergency resource dispatches.
2.2. General Model for Multi-Stage Emergency Resources Dispatch
An n discrete variable is used to describe the available emergency resources for a compound disaster rescue in the stage , where is the emergency resource quantity of the state in the stage i and is constrained to the total storage of emergency resources at the rescue points in that stage. Given that is the emergency resource dispatched in the stage i and the state j under the implementation of scheme , the preliminarily estimated average emergency resource dispatched in the stage i is Equation (1), in which is the emergency resource dispatch function used to describe the detailed scheme r for dispatching emergency resources from rescue points to disaster sites, and is constrained by Equation (2).
Assuming that the quantity of emergency resources stored in all rescue sites before the occurrence of a compound disaster is A, the optimal emergency resource dispatch scheme can be obtained by optimization of the problem involving the multivariable extreme value equation , with the objective of dispatching emergency resources (, D is the resource demand and is the guarantee rate) for each disaster site with a minimal time cost (c). Taking the partial derivatives of with respect to a and c can obtain the emergency resource dispatch model of dynamic game processes (Equation (3)).
2.3. Simplified Model Definitions
In the emergency management process of compound disaster events, the main basic concepts involved in the dynamic game problem with incomplete information include players, strategy spaces, and payoff functions.
- Players
The two parties involved in the dynamic game during the emergency management process of sudden compound disasters are defined as the decision-maker and the compound disaster event. The “Emergency Resource Manager” generally refers to the decision-maker or organization that must quickly make corresponding decisions in response to sudden compound disaster events, while the compound disaster refers to a specific type of sudden compound disaster event, such as various compound disasters like rainstorms–flooding–waterlogging, depending on the specific situation.
- 2.
- Strategy Spaces
The strategy space of a compound disaster is its state space, while the strategy space of the emergency resource manager is their plan space.
- 3.
- Payoff Functions
In the emergency management process of compound disaster events, we assume that there is a dynamic zero-sum game between the compound disaster and the emergency resource manager, meaning that one party’s loss is the other party’s gain. Therefore, we only need to provide the payoff function of one party to determine the payoff situation of both parties under different game outcomes. The emergency resource manager engages in a game with the compound disaster with a clear objective, which is to control the compound disaster in a timely manner and minimize losses. As the compound disaster evolves dynamically, the duty of the emergency resource manager may remain the same or may change accordingly, but in any case, the strategy of the emergency resource manager is to choose a plan from the plan space to achieve their specific goals. Since the implementation of the plan depends on the degree of resource support, to characterize the extent to which a specific plan achieves its goals, a concept of “guarantee rate” is defined. It is a function of resource conditions, the start time of processes, process time, the state of the compound disaster event, the plan selected by the emergency resource manager, the specific objectives of the emergency resource manager, and the relevant attributes of the compound disaster event that needs special attention (such as the specific time, place, and specific targets of the event, etc.). On the other hand, different plans obviously result in different costs. For the emergency resource manager, in addition to considering how to improve the guarantee rate, efforts should also be made to minimize costs. That is to say, the standard for the emergency resource manager to judge whether a plan is the best plan should be that the plan minimizes costs while meeting a certain guarantee rate constraint.
To simplify the description and illustrate the game processes for decision-making in a compound disaster rescue, we have made the following definitions to illustrate the dynamic game model for dispatching the emergency resources responding to a typical compound disaster. The exemplary compound disaster is a cascade of heavy rainstorms, landslides, and flash floods. The players in the game processes are the emergency resource managers and the compound disaster events.
Definition 1.
Assuming that there are three possible disaster stages when a compound disaster occurs. For example, represents an independent rainstorm disaster, represents a compound occurrence of torrential rain disaster accompanied by landslides or flash floods, and shows that the three disasters are of a high degree of compound. The stage space of the disaster is defined as , with the degrees of the compound . The stage transition probabilities between them are denoted as . Because heavy rainstorms are often accompanied by unstable atmosphere that increases the aviation disaster risk and the time costs of aviation transport along the riverine regions. Therefore, it is assumed that during the rescue process, emergency resource managers only use land-based transportation to dispatch emergency resources stored in the rescue point.
Definition 2.

The time radius required from the rescue point to the disaster sites is r. The time cost of the emergency resource dispatch is related to the distance from the rescue point to the disaster site of the compound disaster. The guarantee rate, defined as , represents the degree of control over the disaster, ranging from 0 to 100%. When , the disaster accident is completely controlled. In certain disaster states , the disaster can be completely controlled by transporting a sufficient quantity of emergency resources to the disaster sites within the assumed time radius. For example, the relationship between the quantity of emergency resources and the guarantee rate is shown in Table 1.

Table 1.
The relationship between the quantity of emergence resources and guarantee rate .
Definition 3.
The payment vector of the emergency resource manager is a two-dimensional vector , where the first component is the guarantee rate and the second one is the time cost.
Definition 4.
In the first stage of the game, the compound disaster event occurred with the stage of the compound disaster with a probability of . Note that here we mainly focus on the generation process of schemes in dynamic games for rescue resource management, but the real probability of the stage transition, which is highly dependent on the hydrological and geological processes, is not discussed. The stage transition probability function in the second stage is . Here, is the guarantee rate expected by the emergency resource manager after adopting a rescue scheme for a compound disaster in the first stage of the game; is the state of the compound disaster event in the first stage of the game; is the evolution state of the compound disaster event in the second stage of the game. The larger is, the more effective the rescue scheme adopted by the emergency resource manager in the first stage for controlling the disaster, so the probability of the compound disaster transiting to a less-severe disaster in the second stage of the game is higher, and the probability of transiting into a more-severe disaster is lower, and vice versa.
2.4. Simplified Dynamic Game Processes
The compound disaster events and emergency resource managers engage in the dynamic game processes according to the following steps (Figure 2).
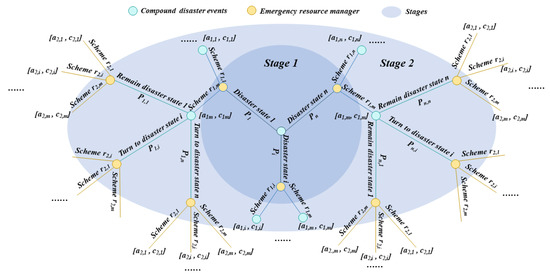
Figure 2.
A diagram of the two-stage dynamic game process for compound disaster events.
Stage 1: A compound disaster occurs and stays in a state. The emergency resource manager makes rescue schemes based on the observed disaster state. Each rescue scheme corresponds to a two-dimensional payment vector. The emergency resource manager adopts the optimal scheme for the state of the disaster by then based on the minimum of the payment vector.
Stage 2: For the results generated after implementing the optimal scheme in the previous stage, the compound disaster event transitions from the state to a new state . Specifically, shows that the original disaster state remains. The emergency resource manager could adopt a new rescue scheme set based on the observed disaster state transition. The new rescue scheme set includes the preceding rescue scheme adopted for the previous disaster state by the emergency resource manager in the previous stage of the game. Then, the emergency resource manager adopts the optimal rescue scheme for this stage based on the minimal payment vectors of each scheme.
Stage t: For the results generated after implementing the rescue scheme in stage , the compound disaster event comes across a transition from the preceding disaster state to a new disaster state . Specifically, shows that the original disaster state remains unchanged. Based on the observed disaster state transition, emergency resource managers could adopt a new rescue scheme set. Again, this scheme set includes the scheme adopted by the emergency resource manager in stage in the game process. The emergency resource managers adopt the optimal scheme of this stage for implementation based on the minimal payment vectors of each scheme.
In practical applications, the emergency resource managers and associated stakeholders should classify and grade the states of compound disaster events in advance. For example, the specific classification criteria should be set up for heavy rainstorms, landslides, and flash floods, respectively. It is can be classified with a least-severe disaster state (State 1) and a most-severe disaster state (State n), and with several middle states between State 1 and State n (such as State 2, State 3, …, State n-1, etc.).
Since the probability of the compound disaster state and the probability of the transition from the state to the state affect the completeness of the emergency rescue schemes made by the emergency resource manager, it is necessary to define prior probability distributions for them based on the current theoretic understanding of the regional compound disaster. The emergency resource manager should estimate the probability distribution of the various disaster states and the transition probability matrix between the various disaster states . Furthermore, these prior probability distributions should be dynamically corrected using Bayes’ theorem as the game advances.
For the emergency resource manager, the rescue scheme set in the same game stage is the same, while the rescue scheme set in different game stages is different. Theoretically, the dynamic game process can continue infinitely, given that the compound disaster evolves continuously. To generate an effective rescue scheme efficiently for practical problems, the emergency resource managers can predefine the number of rounds in the game process based on the specific features of the compound disaster event in order.
2.5. Processes of Using the Dynamic Model
For a typical regional emergency rescue resources dispatch for a dynamic compound disaster, the following seven steps are suggested to apply the proposed dynamic game model.
- (1)
- Determine the transition probabilities of compound disasters based on the previous understanding of the characteristics of the compound disaster development, the resource storage capacity, and transportation capabilities of each rescue point.
- (2)
- Set the model parameters based on actual conditions, including the probabilities of disaster development, and constraints on resource allocation, such as transportation time for emergency materials.
- (3)
- Define the strategy space, showing the different rescue plans that emergency resource managers might adopt.
- (4)
- Estimate the expected results of payoff functions according to the disaster development state and resource allocation plan, and conduct dynamic games to simulate the interaction between emergency resource managers and disaster events.
- (5)
- Evaluate the effectiveness of different rescue plans based on model outputs, and choose the optimal plan to minimize time costs.
- (6)
- Implement rescue plan, i.e., dispatch the emergency resources according to the optimal plan recommended by the dynamic game results.
- (7)
- Monitor the development of disasters and the status of resource allocation in real-time during the rescue process, and adjust the rescue plans dynamically using the model based on changes in actual conditions.
2.6. Case Study
The Guangdong–Hong Kong–Macao Greater Bay Area (GBA) is located in the southeast of China, and it often suffers from various meteorological disasters such as typhoons and local heavy rains [28,29], resulting in frequent floods and geological disasters [30]. With global climate warming, the threat of torrential rain and floods in the entire GBA continues to rise [2,31]. Rainstorm-induced disaster events such as landslides and embankment collapses could increase subsequently [30]. A total of 1459 geological disasters have occurred in GBA, and 98.97% of which are landslides and embankment collapses.
To provide strong safety guarantees for high-quality socioeconomic development in the GBA metropolitan area, the nine cities in the GBA are divided into three major areas. They are the “GFZ” metropolitan area, including the cities of Guangzhou, Foshan, and Zhaoqing, the “SDH” metropolitan area, including the cities of Shenzhen, Dongguan, and Huizhou, and the “ZZJ” metropolitan area, including the cities of Zhuhai, Zhongshan, and Jiangmen. Figure 3 shows the specific distribution of the three major metropolitan area. The GBA’s emergency rescue planning is made to construct large rescue points to promote the comprehensive emergency rescue management system, which aims to be regionally coordinated and cover the entire GBA for various disasters.
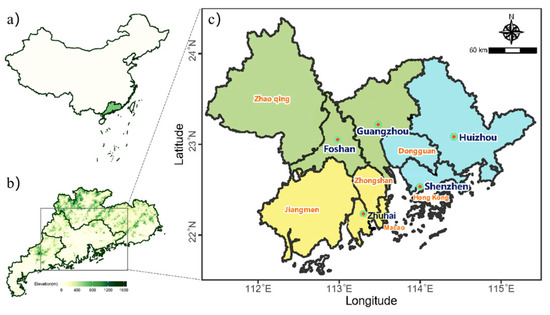
Figure 3.
Overview of Guangdong–Hong Kong–Macao Greater Bay Area (GBA). (a), Regional overview map of China. (b), Regional overview map of Guangdong Province. (c), Three major metropolitan area of the GBA, with green representing “GFZ” metropolitan areas, blue representing “SDH” metropolitan areas and yellow representing “ZZJ” metropolitan areas.
It is assumed that there will be five large rescue points established in Guangzhou, Shenzhen, Zhuhai, Huizhou, and Foshan. When a disaster occurs within the “GFZ” metropolitan area, the transportation time costs for emergency resources dispatched to the disaster site are shown in Figure 4.
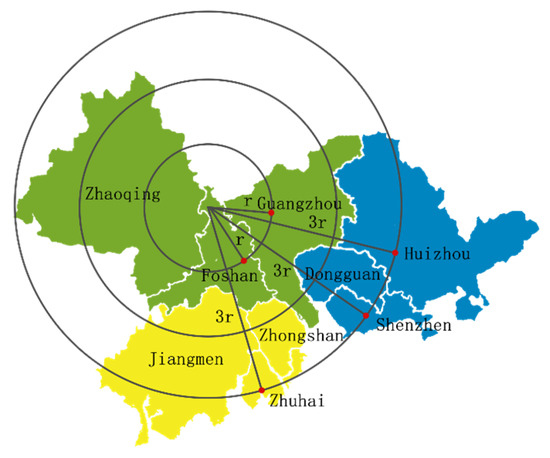
Figure 4.
GBA metropolitan areas and resource transportation time cost for compound disasters in “GFZ” (green), “SDH” (blue), and “ZZJ” (yellow) metropolitan areas.
When the disaster occurs in the “GFZ” metropolitan area, emergency resources dispatched from rescue points in Guangzhou and Foshan to the disaster site is within a one-time radius, r, while those from rescue points in Shenzhen, Huizhou, and Zhuhai to the disaster site require three-time radii, 3 r. Based on the regional plans for emergency infrastructure and the socioeconomic capacities, it is estimated that the total quantity of resources stored at each rescue point and the time cost of transporting a certain quantity of resources to the disaster site are shown in Table 2.

Table 2.
The shipping quantity and the time cost of emergency resources in the first stage of the game.
3. Results
3.1. First Stage of the Game
It is assumed that a rainstorm-induced landslide occurred and only the rescue points in Guangzhou and Foshan can reach the disaster site within a unit time radius due to the occurrence quickness of the landslide. In this stage, there is only one rescue scheme that can be adopted in emergency resource transportation. In this optimal rescue scheme, referred to as optimal Strategy 1, there will be 300 units of emergency resources transported from the rescue points in Guangzhou and Foshan to the disaster points. In the second stage of the game, there are three rescue schemes for emergency resource transportation in which the quantity of emergency resources available is shown in Table 3.

Table 3.
The shipping quantity of emergency resources in the second stage of the game.
3.2. Second Stage of the Game
It is assumed that the flash flood occurred due to the cascading effects of proceeding rainstorms and landslides. The rainstorm’s increase could suddenly increase the flood, and the landslides could block the river to decrease the flood-carrying capacity of the rivers, so the flash flood could be highly devastating. In this stage, there will be several rescue schemes available for rapid disaster response, each consisting of several sub-schemes. For example, in the first type of rescue scheme, which has a cumulative 550 units of emergency resources, there are three sub-schemes (Scheme 2, Scheme 3, and Scheme 4 in Table 2), in which Scheme 4, referred to as optimal Strategy 2, shows the lowest time cost. In the second type of Scheme, which has a cumulative of 600 units of emergency resources, there are three sub-schemes (Scheme 5, Scheme 6, and Scheme 7 in Table 2), in which Scheme 7, referred to as optimal Strategy 3, shows the lowest time cost. In the third type of Scheme, which has a cumulative of 630 units of emergency resources, there are five sub-schemes (Scheme 8, Scheme 9, and Scheme 10 in Table 2), in which Scheme 10, referred to as optimal Strategy 4, shows the lowest time cost.
3.3. Tree Structure of Emergency Resources Dispatch
The strategy space for emergency resource dispatch in the first stage of the game is , and that in the second stage of the game is . Therefore, when a rainstorm-induced compound disaster occurs in the “GFZ” metropolitan area, the game process and their associated payment vectors (guarantee rate and time cost) of emergency resource dispatches can be illustrated in the tree structure shown in Figure 5.
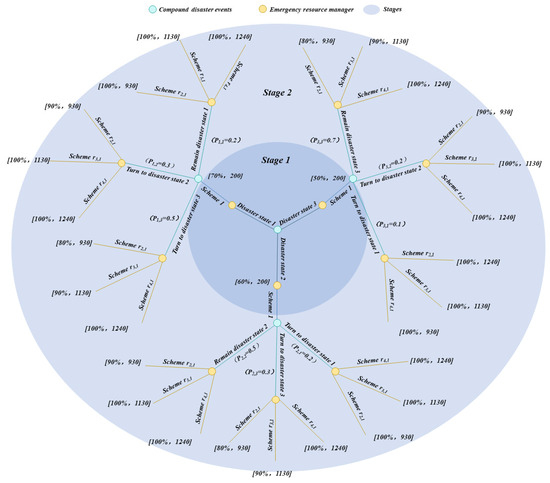
Figure 5.
The two-stage game processes and associated payments for emergency resource dispatch in a rainstorm-induced compound disaster.
3.4. The Time Cost for Different Rescue Schemes
Given the above game procedures and payment vectors, the emergency resource manager can make decisions to ensure that the multi-stage subsequent schemes adopted resulted in full control of the compound disaster. In this cascade of rainstorm–landslide–flash flood disasters, the flash flood disaster can be fully controlled after the second stage of the game, which means the expected guarantee rate in the second stage reaches 100% but with the minimal time cost under the constraints of emergency resources preparedness. If the guarantee rate at the end of the second stage does not reach 100%, a time cost of 25 units is required to compensate for a 1% increase in the guarantee rate. Therefore, the optimization problem becomes the minimization of the expected time cost for emergency resource manager. The time cost for different rescue schemes and their associated sub-schemes in different game stages is estimated and shown in Table 4.

Table 4.
The optimal rescue strategies and associated time cost in different game stages.
3.5. Emergency Rescue Scheme
In this exemplary case, the dynamic game model resulted in the emergency rescue scheme for a rainstorm-induced compound disaster that occurred in the “GFZ” metropolitan area.
- If the compound disaster state is observed as S_1, then emergency resource dispatch Scheme 1 should be implemented immediately with 200 units and 100 units of resources transported from Guangzhou and Foshan rescue points to the disaster site, respectively. At the same time, Scheme 4 should be implemented with 100 units, 30 units, and 120 units of resources, respectively, transported from rescue points in Shenzhen, Zhuhai, and Huizhou to the disaster site. The compound disaster is expected to be completely controlled in the spatial range of 3 r and with an expected total time cost of 1240 units.
- If the state of the rainstorm–landslide–flood disaster event is observed as S_2, then Scheme 1 should be implemented immediately with 200 units and 100 units of resources transported from Guangzhou and Foshan to the disaster site, respectively. At the same time, Scheme 2 should be implemented, with 100, 80, and 120 units of resources transported from Shenzhen, Zhuhai, and Huizhou to the disaster site, respectively. The compound disaster is expected to be completely controlled in the spatial range of 3 r and with an expected total time cost of 1130 units.
- If the state of the compound disaster event is observed as S_3, then Scheme 1 should be implemented immediately with 200 units and 100 units of resources transported from Guangzhou and Foshan to the disaster site, respectively. At the same time, Scheme 2 should be implemented, with 100, 100, and 130 units of resources transported from Shenzhen, Zhuhai, and Huizhou to the disaster site, respectively. The compound disaster is expected to be completely controlled in the spatial range of 3 r and with an expected total time cost of 1055 units.
3.6. Formatting of Mathematical Components
Equation (1):
where is the emergency resource dispatch function used to describe the detailed scheme r for dispatching emergency resources from rescue points to disaster sites, and is constrained by Equation (2):
Equation (3):
4. Discussion
Rainstorm-induced landslide and flood compound disasters could have a significant impact on human safety and socio-economy, but timely emergency resource supply in the post-disaster emergency rescue and recovery stage can substantially reduce the losses and adverse impacts. To comprehensively consider the evolution of the compound disaster states and the timely dispatch of emergency resources from the rescue points to the disaster site that occurred with a rainstorm-induced compound disaster, we propose a dynamic game model for emergency resource dispatches. Based on the constraints of emergency resource transportation under rainstorm-induced compound disasters, we comprehensively illustrate the game processes between emergency resource managers and the evolution of the compound disaster. A two-stage dynamic game model can support decision-making, with the objectives of minimal time cost and sufficient resource supplies for the disaster sites.
The model is then exemplarily applied to the possible rainstorm-landslide-flood compound disasters that occur in the Guangdong–Hong Kong–Macao Greater Bay Area (GBA). A virtual scenario of emergency rescue schemes is simulated by the proposed model for the “GFZ” metropolitan areas in the GBA, focusing on a compound disaster of cascading rainstorms, landslides, and flash floods. The game results indicate that the proposed model can effectively identify optimal emergency resource dispatch schemes for a compound disaster that occurs within a district equipped with emergency resources in several rescue points.
Because a real compound disaster could impact several disaster sites, especially for flood disasters, which often impact the entire riverine regions, the time cost and transportation conditions, including the transportation capacity of rescue points, types of rescue materials, and resources demanded at disaster sites, are much more complicated than the case we analyzed. Also, the disaster evolution is highly uncertain for the compound effects. The proposed model can be adjusted for decision-making using a game with more stages.
Author Contributions
Conceptualization, X.T. and Y.W.; methodology, X.T.; software, Y.W.; validation, X.T., Y.W. and X.L.; formal analysis, X.T. and Y.W.; investigation, X.T. and Y.W.; resources, X.T. and X.C.; supervision, X.T. and X.C.; project administration, F.Y. and X.C.; funding acquisition, X.T., F.Y. and X.C. All authors contribute to data curation, writing—original draft preparation, writing—review and editing, and visualization. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key R&D Program of China (2021YFC3001000, X.T., F.Y. and X.C.), the National Natural Science Foundation of China (42471022, 52179030, X.T.), and the Province Natural Science Foundation of Guangdong (2024B1515020046, 2022A1515240018, X.T.). X.T. is also supported by the Fundamental Research Funds for the Central Universities, Sun Yat-sen University.
Data Availability Statement
All data are available on reasonable request from the corresponding author.
Acknowledgments
We are grateful for the data curation from the emergency department of Guangdong province.
Conflicts of Interest
We declare that we have no conflicts of interest, and no related work is in press or submitted elsewhere.
References
- Chen, S.; Liu, B.; Tan, X.; Huang, Z. Characteristics and circulation background of extreme precipitation over East China. Nat. Hazards 2019, 99, 537–552. [Google Scholar] [CrossRef]
- Huang, Z.; Tan, X.; Gan, T.Y.; Liu, B.; Chen, X. Thermodynamically enhanced precipitation extremes due to counterbalancing influences of anthropogenic greenhouse gases and aerosols. Nat. Water 2023, 1, 614–625. [Google Scholar] [CrossRef]
- Tan, X.; Gan, T.Y.; Chen, S.; Horton, D.E.; Chen, X.; Liu, B.; Lin, K. Trends in persistent seasonal-scale atmospheric circulation patterns responsible for seasonal precipitation totals and occurrences of precipitation extremes over Canada. J. Clim. 2019, 32, 7105–7126. [Google Scholar] [CrossRef]
- Toreti, A.; Naveau, P.; Zampieri, M.; Schindler, A.; Scoccimarro, E.; Xoplaki, E.; Dijkstra, H.A.; Gualdi, S.; Luterbacher, J. Projections of global changes in precipitation extremes from Coupled Model Intercomparison Project Phase 5 models. Geophys. Res. Lett. 2013, 40, 4887–4892. [Google Scholar] [CrossRef]
- Tan, X.; Gan, T.Y.; Horton, D.E. Projected timing of perceivable changes in climate extremes for terrestrial and marine ecosystems. Glob. Chang. Biol. 2018, 24, 4696–4708. [Google Scholar] [CrossRef]
- Tan, X.; Wu, X.; Liu, B. Global changes in the spatial extents of precipitation extremes. Environ. Res. Lett. 2021, 16, 054017. [Google Scholar] [CrossRef]
- De Angeli, S.; Malamud, B.D.; Rossi, L.; Taylor, F.E.; Trasforini, E.; Rudari, R. A multi-hazard framework for spatial-temporal impact analysis. Int. J. Disaster Risk Reduct. 2022, 73, 102829. [Google Scholar] [CrossRef]
- Owolabi, T.A.; Sajjad, M. A global outlook on multi-hazard risk analysis: A systematic and scientometric review. Int. J. Disaster Risk Reduct. 2023, 92, 103727. [Google Scholar] [CrossRef]
- Smit, B.; Wandel, J. Adaptation, adaptive capacity and vulnerability. Glob. Environ. Chang. 2006, 16, 282–292. [Google Scholar] [CrossRef]
- Matthews, T.; Wilby, R.L.; Murphy, C. An emerging tropical cyclone–deadly heat compound hazard. Nat. Clim. Chang. 2019, 9, 602–606. [Google Scholar] [CrossRef]
- Zscheischler, J.; Westra, S.; Van Den Hurk, B.J.; Seneviratne, S.I.; Ward, P.J.; Pitman, A.; AghaKouchak, A.; Bresch, D.N.; Leonard, M.; Wahl, T.; et al. Future climate risk from compound events. Nat. Clim. Chang. 2018, 8, 469–477. [Google Scholar] [CrossRef]
- Helbing, D.; Farkas, I.; Vicsek, T. Simulating dynamical features of escape panic. Nature 2000, 407, 487–490. [Google Scholar] [CrossRef]
- Wang, L.; Liao, Y.; Yang, L.; Li, H.; Ye, B.; Wang, W. Emergency response to and preparedness for extreme weather events and environmental changes in China. Asia Pac. J. Public Health 2014, 28, 59S–66S. [Google Scholar] [CrossRef]
- Rawls, C.G.; Turnquist, M.A. Pre-positioning of emergency supplies for disaster response. Transp. Res. Part B Methodol. 2010, 44, 521–534. [Google Scholar] [CrossRef]
- Wang, Y.; Bier, V.M.; Sun, B. Measuring and achieving equity in multiperiod emergency material allocation. Risk Anal. 2019, 39, 2408–2426. [Google Scholar] [CrossRef]
- Liu, J.; Guo, Y.; An, S.; Lian, C. A study on the mechanism and strategy of cross-regional emergency cooperation for natural disasters in China-based on the perspective of evolutionary game theory. Int. J. Environ. Res. Public Health 2021, 18, 11624. [Google Scholar] [CrossRef]
- Seaberg, D.; Devine, L.; Zhuang, J. A review of game theory applications in natural disaster management research. Nat. Hazards 2017, 89, 1461–1483. [Google Scholar] [CrossRef]
- Nagurney, A. Supply chain game theory network modeling under labor constraints: Applications to the COVID-19 pandemic. Eur. J. Oper. Res. 2021, 293, 880–891. [Google Scholar] [CrossRef]
- Zhang, M.; Kong, Z. A tripartite evolutionary game model of emergency supplies joint reserve among the government, enterprise and society. Comput. Ind. Eng. 2022, 169, 108132. [Google Scholar] [CrossRef]
- Chen, D.; Fang, X.; Li, Y.; Ni, S.; Zhang, Q.; Sang, C.K. Three-level multimodal transportation network for cross-regional emergency resources dispatch under demand and route reliability. Reliab. Eng. Syst. Saf. 2022, 222, 108461. [Google Scholar] [CrossRef]
- Fleming, K.; Abad, J.; Booth, L.; Schueller, L.; Baills, A.; Scolobig, A.; Petrovic, B.; Zuccaro, G.; Leone, M.F. The use of serious games in engaging stakeholders for disaster risk reduction, management and climate change adaption information elicitation. Int. J. Disaster Risk Reduct. 2020, 49, 101669. [Google Scholar] [CrossRef]
- Wang, F.; Xie, Z.; Liu, H.; Pei, Z.; Liu, D. Multiobjective emergency resource allocation under the natural disaster chain with path planning. Int. J. Environ. Res. Public Health 2022, 19, 7876. [Google Scholar] [CrossRef]
- Moosakhaani, M.; Salimi, L.; Sadatipour, M.T.; Niksokhan, M.H.; Rabbani, M. Game theoretic approach for flood risk management considering a financial model. Environ. Eng. Res. 2021, 27, 210368. [Google Scholar] [CrossRef]
- Bier, V.M.; Zhou, Y.; Du, H. Game-theoretic modeling of pre-disaster relocation. Eng. Econ. 2019, 65, 89–113. [Google Scholar] [CrossRef]
- Álvarez, X.; Gómez-Rúa, M.; Vidal-Puga, J. River flooding risk prevention: A cooperative game theory approach. J. Environ. Manag. 2019, 248, 109284. [Google Scholar] [CrossRef]
- Vasquez, í.C.; Sepulveda, J.M.; Alfaro, M.D.; Osorio-Valenzuela, L. Disaster response project scheduling problem: A resolution method based on a game-theoretical model. Int. J. Comput. Commun. Control 2013, 8, 334–345. [Google Scholar] [CrossRef][Green Version]
- Jeong, H.; Ha, S.; Kim, H. Flood protection cost allocation using cooperative game theory for adapting infrastructure to climate change. J. Water Resour. Plan. Manag. 2018, 144. [Google Scholar] [CrossRef]
- Tan, X.; Mai, Q.; Chen, G.; Liu, B.; Wang, Z.; Lai, C.; Chen, X. Intensity-duration-frequency curves in the Guangdong-Hong Kong-Macao Greater Bay Area inferred from the Bayesian hierarchical model. J. Hydrol. Reg. Stud. 2023, 46, 101327. [Google Scholar] [CrossRef]
- Yang, F.; Wang, X.; Zhou, X.; Wang, Q.; Tan, X. Effects of Urbanization on Changes in Precipitation Extremes in Guangdong-Hong Kong-Macao Greater Bay Area, China. Water 2023, 15, 3438. [Google Scholar] [CrossRef]
- Tan, X.; Li, Y.; Wu, X.X.; Dai, C.; Zhang, X.L.; Cai, Y.P. Identification of the key driving factors of flash flood based on different feature selection techniques coupled with random forest method. J. Hydrol. Reg. Stud. 2024, 51, 101624. [Google Scholar] [CrossRef]
- Tan, X.; Wu, X.; Huang, Z.; Fu, J.; Tan, X.; Deng, S.; Liu, Y.; Gan, T.Y.; Liu, B. Increasing global precipitation whiplash due to anthropogenic greenhouse gas emissions. Nat. Commun. 2023, 14, 2796. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).