Numerical Estimation of Potable Water Production for Single-Slope Solar Stills in the Caspian Region
Abstract
:1. Introduction
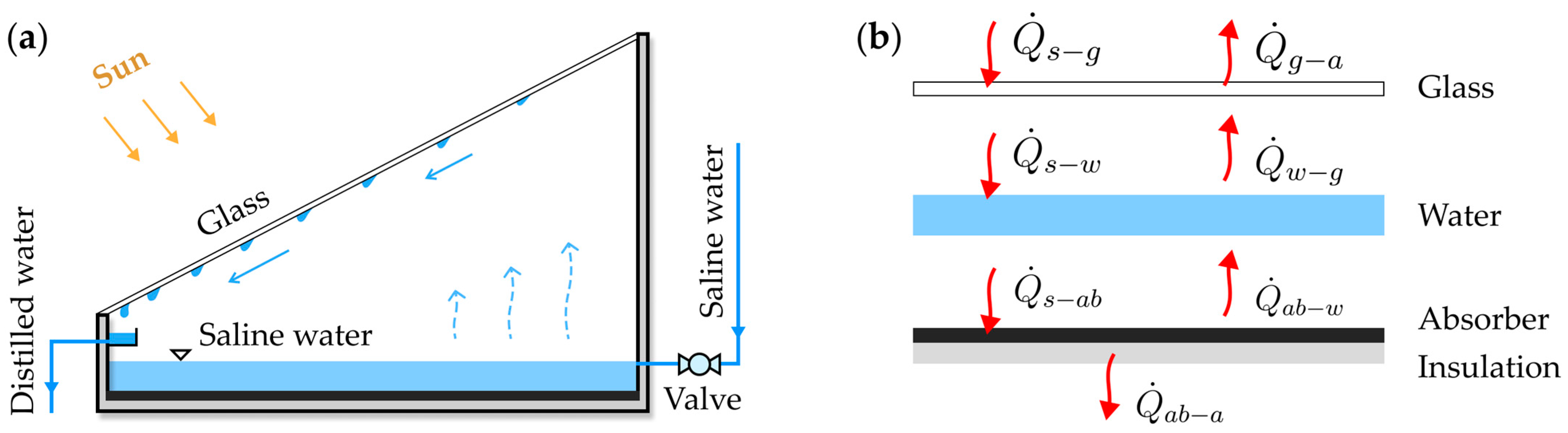
2. System Description
3. Mathematical Model
3.1. Heat Balance Model
- Water vapor losses through leakages are considered negligible.
- Effects related to potential, kinetic, and chemical energy changes are disregarded.
- The temperature distribution of the saline water within the basin is assumed to be uniform throughout.
- The effect of seawater freezing is not taken into account.
3.2. Economic Analysis Model
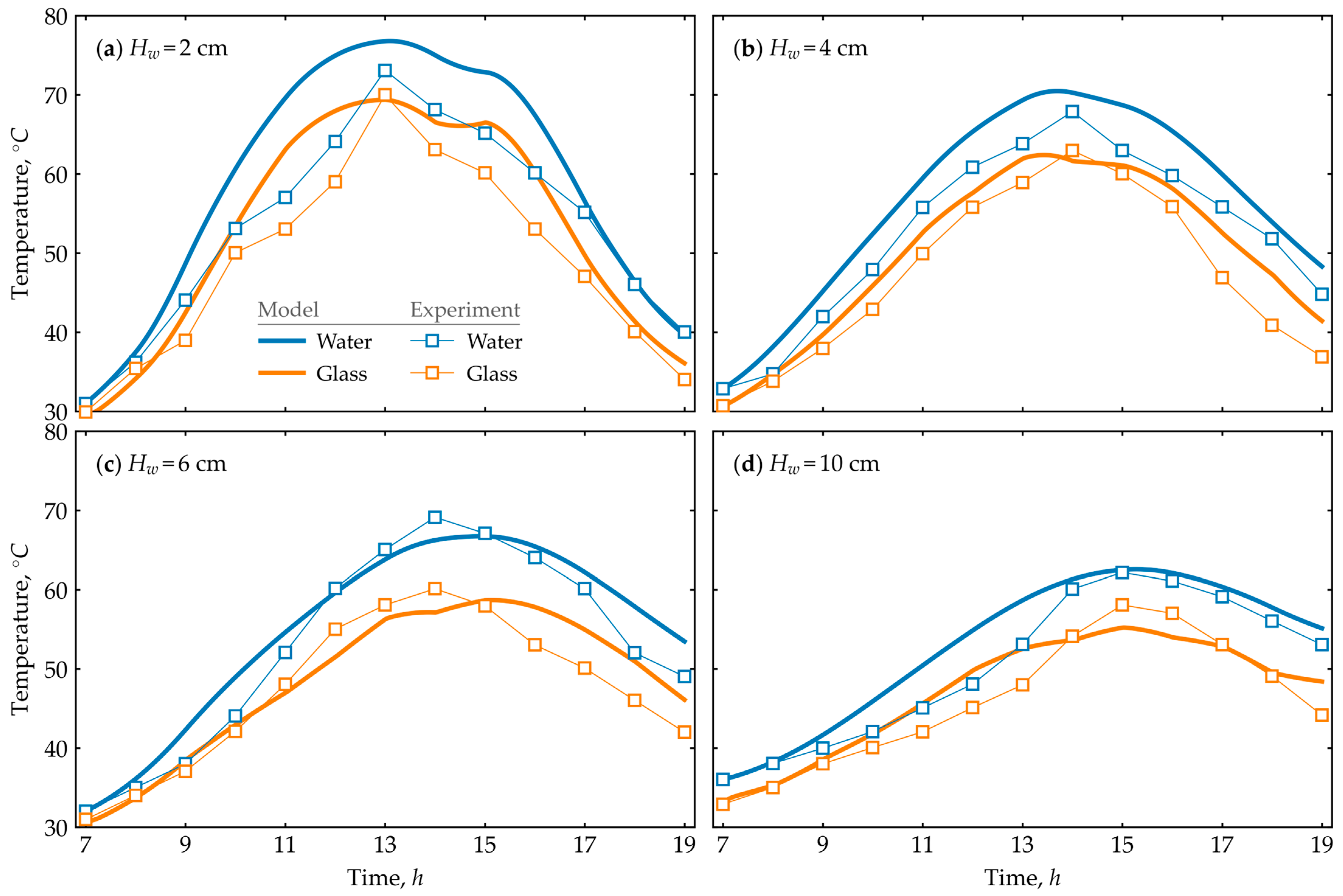
4. Model Validation
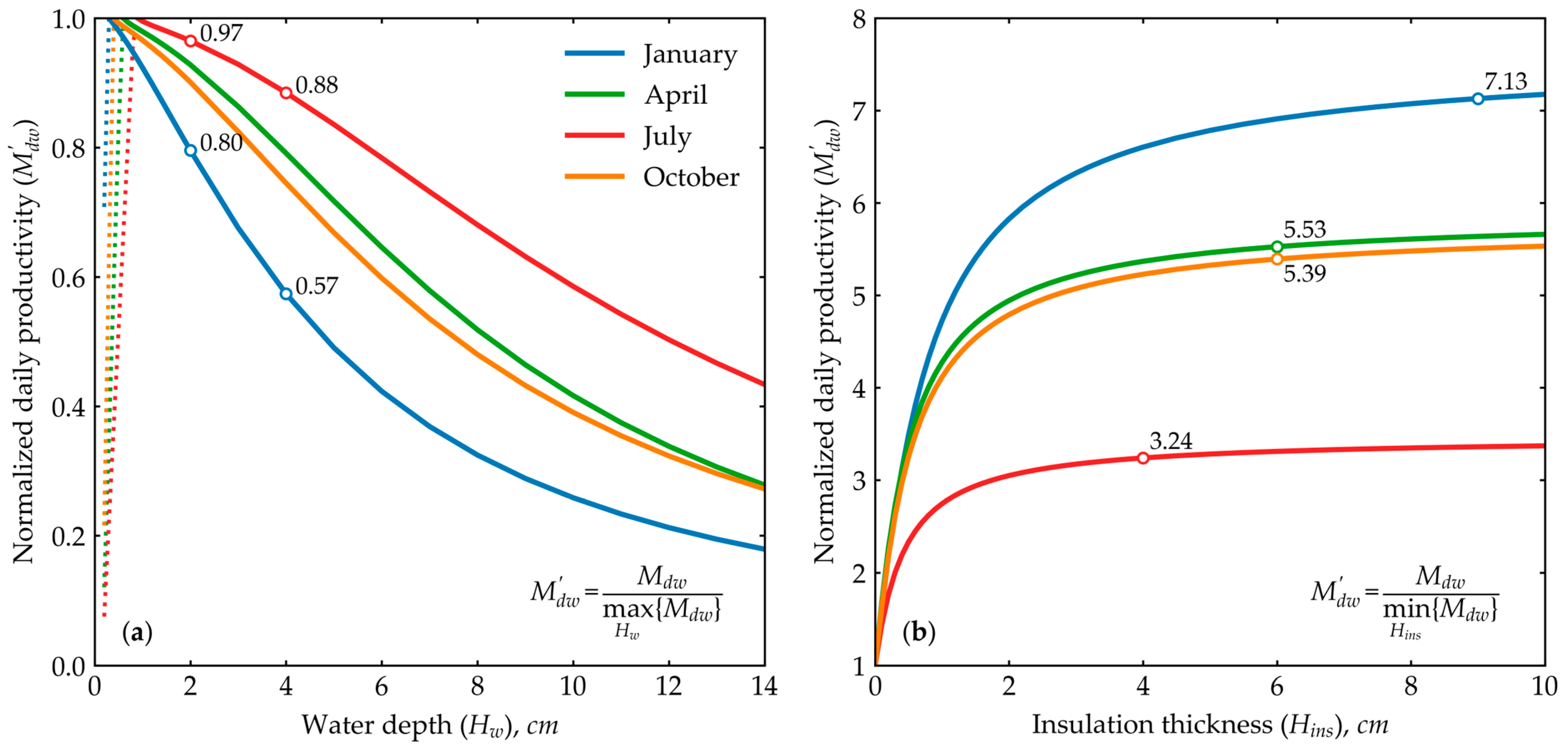
5. Heat Balance Results
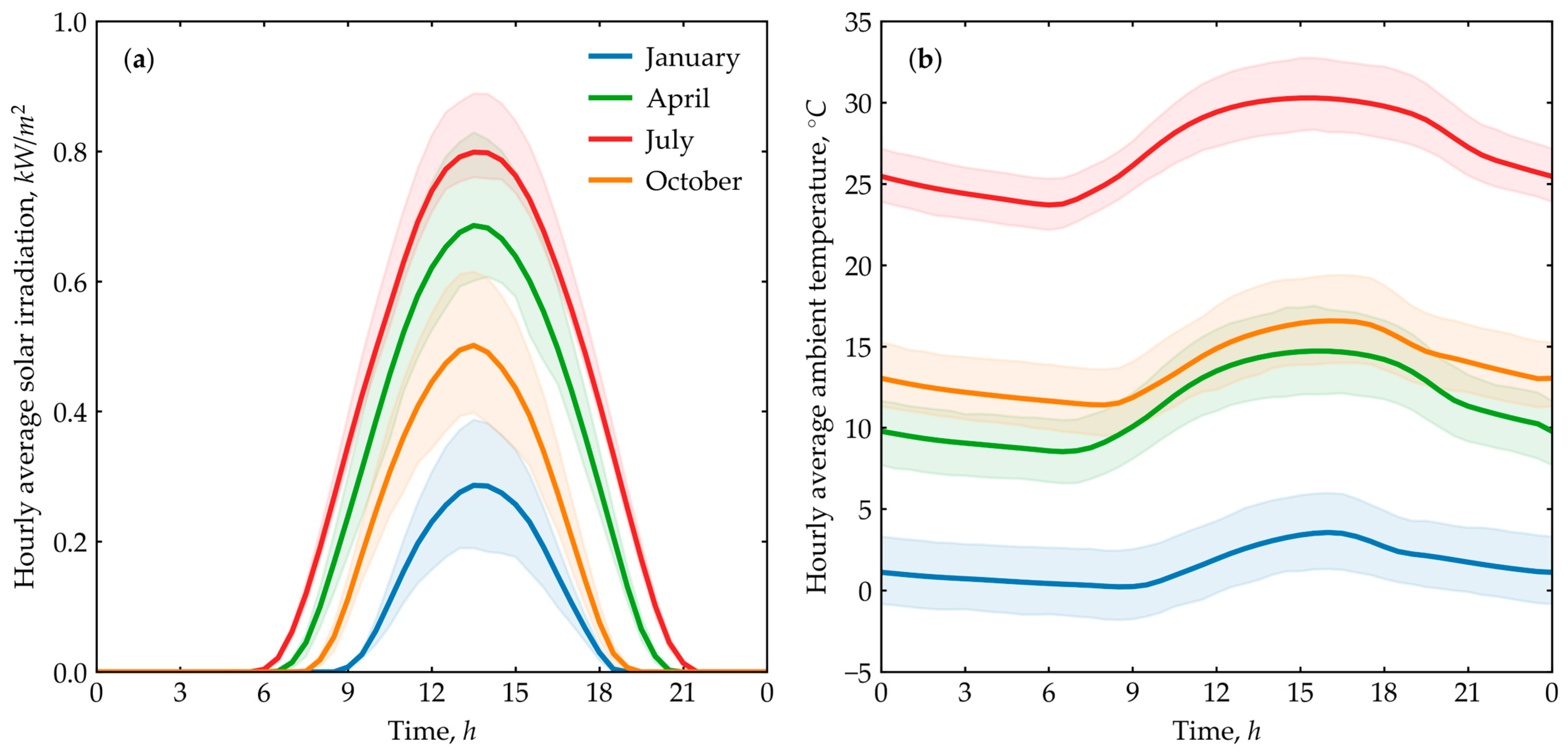
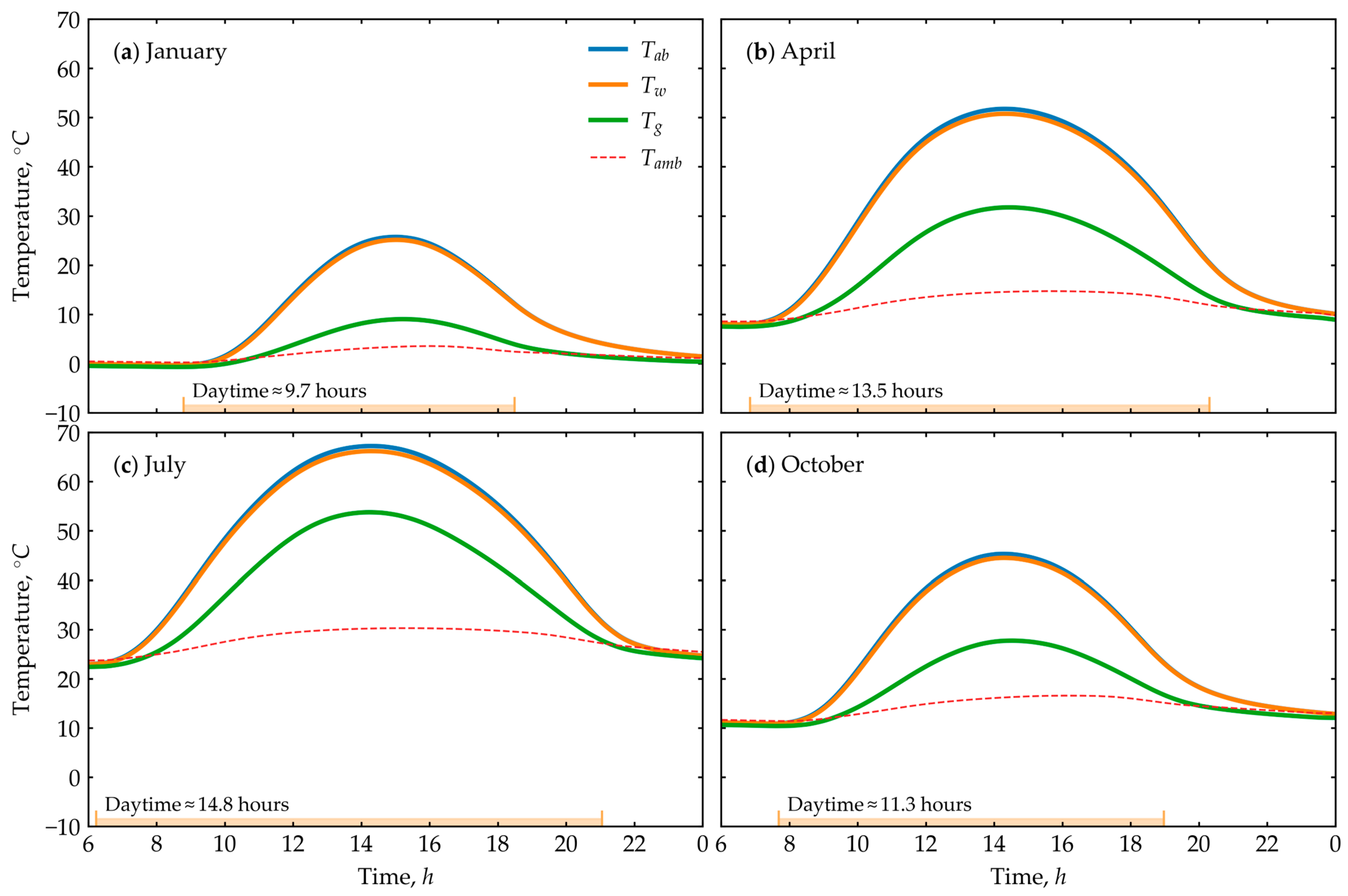
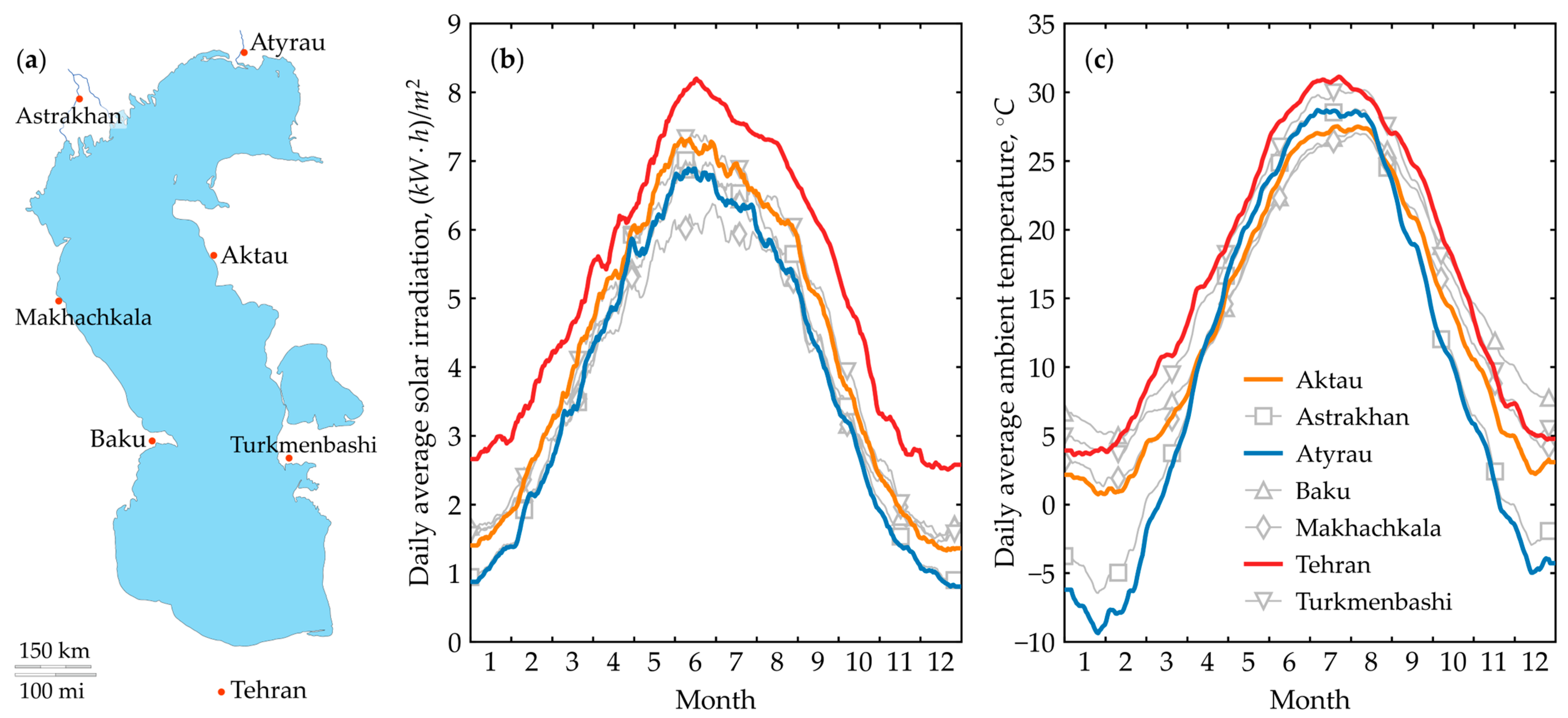
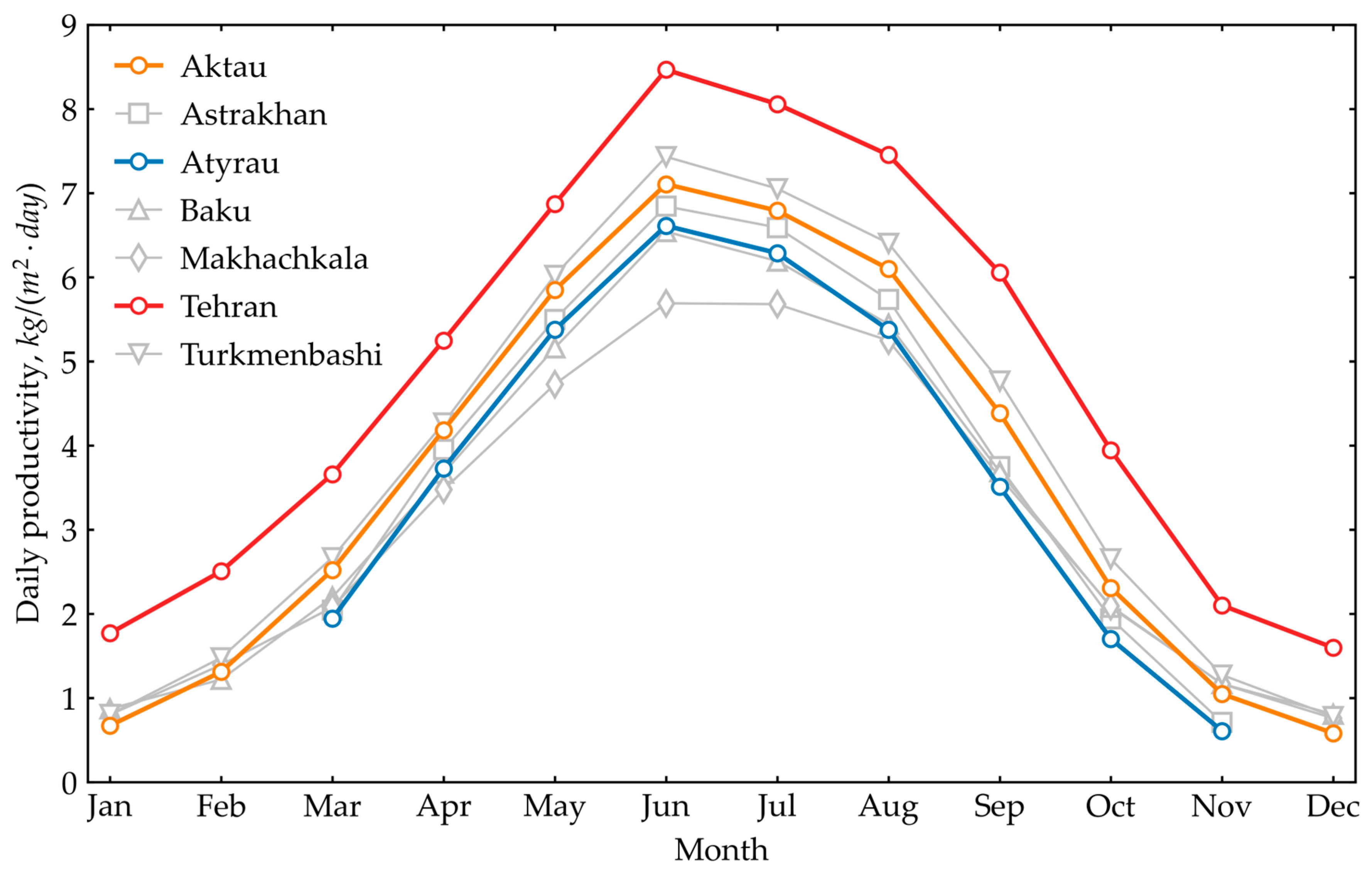
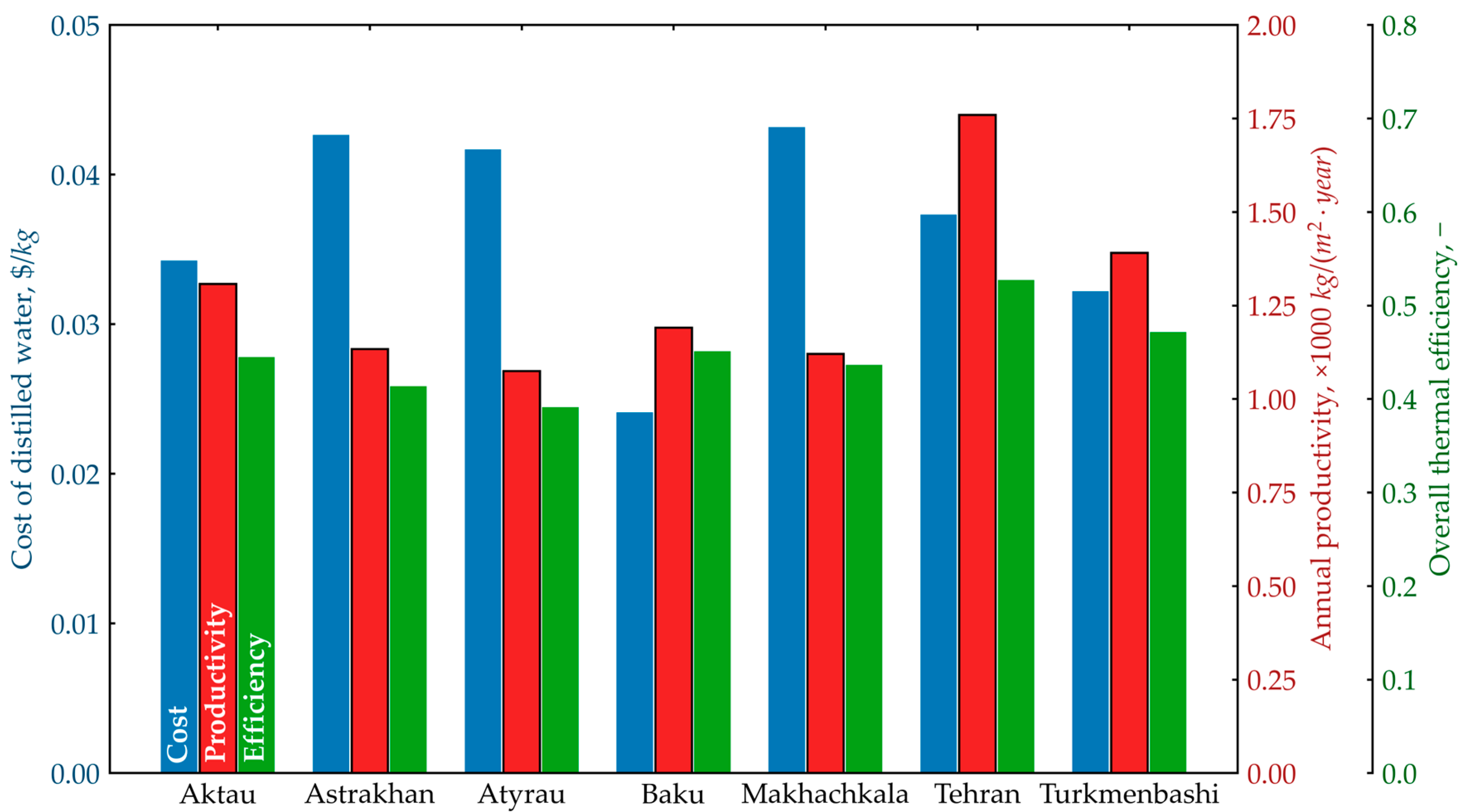
6. Caspian Region Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Surface area (m2) |
| AMC | Annual maintenance cost (USD) |
| AOC | Annual operating cost (USD) |
| ASV | Annual salvage value |
| C | Specific heat capacity (J/kg°C) |
| Cost of distilled water (USD) | |
| CC | Capital cost of solar still (USD) |
| CRF | Capital recovery factor |
| FAC | Fixed annual cost (USD) |
| H | Thickness/ depth (m) |
| h | Heat transfer coefficient (W/(m2°C)) |
| Latent heat (J/kg) | |
| I | Solar irradiation (W/m2) |
| i | Interest rate per year |
| k | Thermal conductivity coefficient (W/m°C) |
| L | Length (m) |
| L′ | Characteristic length |
| m | Mass (kg) |
| Instantaneous productivity (kg/m2s) | |
| Daily productivity (kg/m2day) | |
| M | Annual productivity (kg/m2year) |
| n | Lifetime of the system (year) |
| P | Pressure (Pa) |
| Pr | Prandtl number |
| R | Reflectivity |
| Ra | Rayleigh number |
| S | Salinity (g/kg) |
| SFF | Sinking Fund Factor |
| SV | Salvage value |
| t | Time (s) |
| T | Temperature (°C) |
| TAC | Total annualized cost (USD) |
| U | Overall heat transfer coefficient (W/(m2°C)) |
| V | Wind speed (m/s) |
| W | Width (m) |
| Greek symbol | |
| α | Absorptivity |
| ε | Emissivity |
| η | efficiency |
| σ | Stefan–Boltzmann constant (W/(m2K4)) |
| Subscripts | |
| ab | absorber |
| amb | ambient |
| c | convective |
| dw | distilled water |
| e | evaporative |
| eff | effective |
| g | glass |
| ins | insulation |
| r | radiative |
| sky | sky |
| t | total |
| w | water |
Appendix A
- is the thermal conductivity of distilled water in critical point,
- is the critical temperature of distilled water.
References
- Elsheikh, A.; Hammoodi, K.A.; Ibrahim, A.M.M.; Mourad, A.-H.I.; Fujii, M.; Abd-Elaziem, W. Augmentation and evaluation of solar still performance: A comprehensive review. Desalination 2024, 574, 117239. [Google Scholar] [CrossRef]
- Younis, O.; Hussein, A.K.; Attia, M.E.H.; Aljibori, H.S.S.; Kolsi, L.; Togun, H.; Ali, B.; Abderrahmane, A.; Subkrajang, K.; Jirawattanapanit, A. Comprehensive review on solar stills—Latest developments and overview. Sustainability 2022, 14, 10136. [Google Scholar] [CrossRef]
- Abdullah, A.S.; Essa, F.A.; Panchal, H.; Alawee, W.H.; Elsheikh, A.H. Enhancing the performance of tubular solar stills for water purification: A comprehensive review and comparative analysis of methodologies and materials. Results Eng. 2024, 21, 101722. [Google Scholar] [CrossRef]
- Hussein, A.K.; Rashid, F.L.; Abed, A.M.; Al-Khaleel, M.; Togun, H.; Ali, B.; Akkurt, N.; Malekshah, E.H.; Biswal, U.; Al-Obaidi, M.A.; et al. Inverted solar stills: A comprehensive review of designs, mathematical models, performance, and modern combinations. Sustainability 2022, 14, 13766. [Google Scholar] [CrossRef]
- Rashid, F.L.; Kaood, A.; Al-Obaidi, M.A.; Mohammed, H.I.; Alsarayreh, A.A.; Al-Muhsen, N.F.O.; Abbas, A.S.; Zubo, R.H.A.; Mohammad, A.T.; Alsadaie, S.; et al. A review of configurations, capabilities, and cutting-edge options for multistage solar stills in water desalination. Designs 2023, 7, 67. [Google Scholar] [CrossRef]
- Alawad, S.M.; Mansour, R.B.; Al-Sulaiman, F.A.; Rehman, S. Renewable energy systems for water desalination applications: A comprehensive review. Energy Convers. Manag. 2023, 286, 117035. [Google Scholar] [CrossRef]
- Sayed, E.T.; Olabi, A.G.; Elsaid, K.; Al Radi, M.; Alqadi, R.; Abdelkareem, M.A. Recent progress in renewable energy based-desalination in the Middle East and North Africa MENA region. J. Adv. Res. 2023, 48, 125–156. [Google Scholar] [CrossRef]
- Belyayev, Y.; Mohanraj, M.; Jayaraj, S.; Kaltayev, A. Thermal performance simulation of a heat pump assisted solar desalination system for Kazakhstan climatic conditions. Heat Transf. Eng. 2019, 40, 1060–1072. [Google Scholar] [CrossRef]
- Shakir, Y.; Saparova, B.; Belyayev, Y.; Kaltayev, A.; Mohanraj, M.; Jayaraj, S. Numerical simulation of a heat pump assisted regenerative solar still with PCM heat storage for cold climates of Kazakhstan. Therm. Sci. 2017, 21, 411–418. [Google Scholar] [CrossRef]
- Yousef, M.S.; Hassan, H.; Ahmed, M.; Ookawara, S. Energy and exergy analysis of single slope passive solar still under Egyptian climate conditions. Energy Procedia 2017, 141, 18–23. [Google Scholar] [CrossRef]
- Abujazar, M.S.S.; Fatihah, S.; Lotfy, E.R.; Kabeel, A.E.; Sharil, S. Performance evaluation of inclined copper-stepped solar still in a wet tropical climate. Desalination 2018, 425, 94–103. [Google Scholar] [CrossRef]
- Esfe, M.H.; Toghraie, D. Numerical investigation of wind velocity effects on evaporation rate of passive single-slope solar stills in Khuzestan province in Iran. Alex. Eng. J. 2023, 62, 145–156. [Google Scholar] [CrossRef]
- Gupta, A.; Gupta, A.; Yadav, A.C.; Kumar, A. Performance analysis of single slope solar still under composite climate in India: Numerical simulation and thermal modeling approach. Mater. Today Proc. 2022, 63, 699–705. [Google Scholar] [CrossRef]
- Nomor, E.; Islam, R.; Alim, M.A.; Rahman, A. Production of fresh water by a solar still: An experimental case study in Australia. Water 2021, 13, 3373. [Google Scholar] [CrossRef]
- Al-Helal, I.M.; Alsadon, A.; Marey, S.; Ibrahim, A.; Shady, M.R. Optimizing a single-slope solar still for fresh-water production in the deserts of arid regions: An experimental and numerical approach. Sustainability 2024, 16, 800. [Google Scholar] [CrossRef]
- Modi, K.V.; Patel, S.K.; Patel, A.M. Impact of modification in the geometry of absorber plate on the productivity of solar still—A review. Sol. Energy 2023, 264, 112009. [Google Scholar] [CrossRef]
- Serradj, D.E.B.; Anderson, T.; Nates, R. The effect of geometry on the yield of fresh water from single slope solar stills. Energies 2022, 15, 7244. [Google Scholar] [CrossRef]
- Tei, E.A.; Hameed, R.M.S.; Illyas, M.; Athikesavan, M.M. Experimental investigation of inclined solar still with and without sand as energy storage materials. J. Energy Storage 2024, 77, 109809. [Google Scholar] [CrossRef]
- Katekar, V.P.; Deshmukh, S.S. A review of the use of phase change materials on performance of solar stills. J. Energy Storage 2020, 30, 101398. [Google Scholar] [CrossRef]
- Kabeel, A.E.; El-Samadonya, Y.A.F.; El-Maghlany, W.M. Comparative study on the solar still performance utilizing different PCM. Desalination 2018, 432, 89–96. [Google Scholar] [CrossRef]
- Dunkle, R.V. Solar water distillation: The roof type still and multiple effect diffusion still. International Developments in Heat Transfer. In Proceedings of the International Heat Transfer, Boulder, Colorado, 28 August–1 September 1961; ASME: New York, NY, USA, 1961; Volume 5, pp. 895–902. [Google Scholar]
- Shukla, S.K.; Sorayan, V.P.S. Thermal modeling of solar stills an experimental validation. Renew. Energy 2005, 30, 683–699. [Google Scholar] [CrossRef]
- Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar]
- Halima, H.B.; Frikha, N.; Slama, R.B. Numerical investigation of a simple solar still coupled to a compression heat pump. Desalination 2014, 337, 60–66. [Google Scholar] [CrossRef]
- Rajaseenivasan, T.; Shanmugam, R.K.; Hareesh, V.M.; Srithar, K. Combined probation of bubble column humidification dehumidification desalination system using solar collectors. Energy 2016, 116, 459–469. [Google Scholar] [CrossRef]
- Sivakumar, S.; Siva, K.; Mohanraj, M. Energy performance and economic assessments of a solar air collector and compression heat pump-integrated solar humidifier desalination system. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2023, 237, 2045–2059. [Google Scholar] [CrossRef]
- Agrawal, A.; Rana, R.S.; Srivastava, P.K. Heat transfer coefficients and productivity of a single slope single basin solar still in Indian climatic condition: Experimental and theoretical comparison. Resour.-Effic. Technol. 2017, 3, 466–482. [Google Scholar] [CrossRef]
- The National Aeronautics and Space Administration (NASA) Langley Research Center (LaRC) Prediction of Worldwide Energy Resource (POWER) Project’s Hourly 2.3.6 Version. Available online: https://power.larc.nasa.gov/ (accessed on 1 October 2024).
- Belessiotis, V.; Kalogirou, S.; Delyannis, E. Thermal Solar Desalination: Methods and Systems; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Shahrim, N.A.; Abounahia, N.M.; Ahmed El-Sayed, A.M.; Saleem, H.; Zaidi, S.J. An overview on the progress in produced water desalination by membrane-based technology. J. Water Process Eng. 2023, 51, 103479. [Google Scholar] [CrossRef]
- Sharqawy, M.H.; Lienhard, J.H.V.; Zubair, S.M. Thermophysical properties of seawater: A review of existing correlations and data. Desalin. Water Treat. 2010, 16, 354–380. [Google Scholar] [CrossRef]

| Relevant Parameters | Symbol | Value | Unit |
|---|---|---|---|
| Absorptivity | αg [24] | 0.0475 | |
| αw | 0.3 | ||
| αab | 0.95 | ||
| Reflectivity | Rg [8,9] | 0.0735 | |
| Rw | 0.025 | ||
| Emissivity | εg [24] | 0.95 | |
| εw | 0.94 | ||
| Size of absorber/water | Lab = Lw | 1 | m |
| Wab = Ww | 1 | m | |
| Hab | 0.002 | m | |
| Thickness of insulation | Hins | 0.05 | m |
| Saline water depth | Hw | 0.01 | m |
| Slope of glass cover | 30 | degree | |
| Thermal conductivity | kab | 16.3 | W/m°C |
| kins | 0.039 | W/m°C | |
| Specific heat capacity | Cg | 800 | J/kg°C |
| Cab | 480 | J/kg°C | |
| Mass of glass/absorber | mg | 10.12 | kg/m2 |
| mab | 15.6 | kg/m2 | |
| Salinity | S | 13 | g/kg |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baimbetov, D.; Yerdesh, Y.; Karlina, Y.; Syrlybekkyzy, S.; Radu, T.; Mohanraj, M.; Belyayev, Y. Numerical Estimation of Potable Water Production for Single-Slope Solar Stills in the Caspian Region. Water 2024, 16, 2980. https://doi.org/10.3390/w16202980
Baimbetov D, Yerdesh Y, Karlina Y, Syrlybekkyzy S, Radu T, Mohanraj M, Belyayev Y. Numerical Estimation of Potable Water Production for Single-Slope Solar Stills in the Caspian Region. Water. 2024; 16(20):2980. https://doi.org/10.3390/w16202980
Chicago/Turabian StyleBaimbetov, Dinmukhambet, Yelnar Yerdesh, Yelizaveta Karlina, Samal Syrlybekkyzy, Tanja Radu, Murugesan Mohanraj, and Yerzhan Belyayev. 2024. "Numerical Estimation of Potable Water Production for Single-Slope Solar Stills in the Caspian Region" Water 16, no. 20: 2980. https://doi.org/10.3390/w16202980
APA StyleBaimbetov, D., Yerdesh, Y., Karlina, Y., Syrlybekkyzy, S., Radu, T., Mohanraj, M., & Belyayev, Y. (2024). Numerical Estimation of Potable Water Production for Single-Slope Solar Stills in the Caspian Region. Water, 16(20), 2980. https://doi.org/10.3390/w16202980








