Efficient Productivity-Aware Control Parameter Optimization in Cutter Suction Dredger Construction Using Machine Learning with Parallel Global Search
Abstract
:1. Introduction
2. Theoretical Foundations and Framework
2.1. Preliminaries
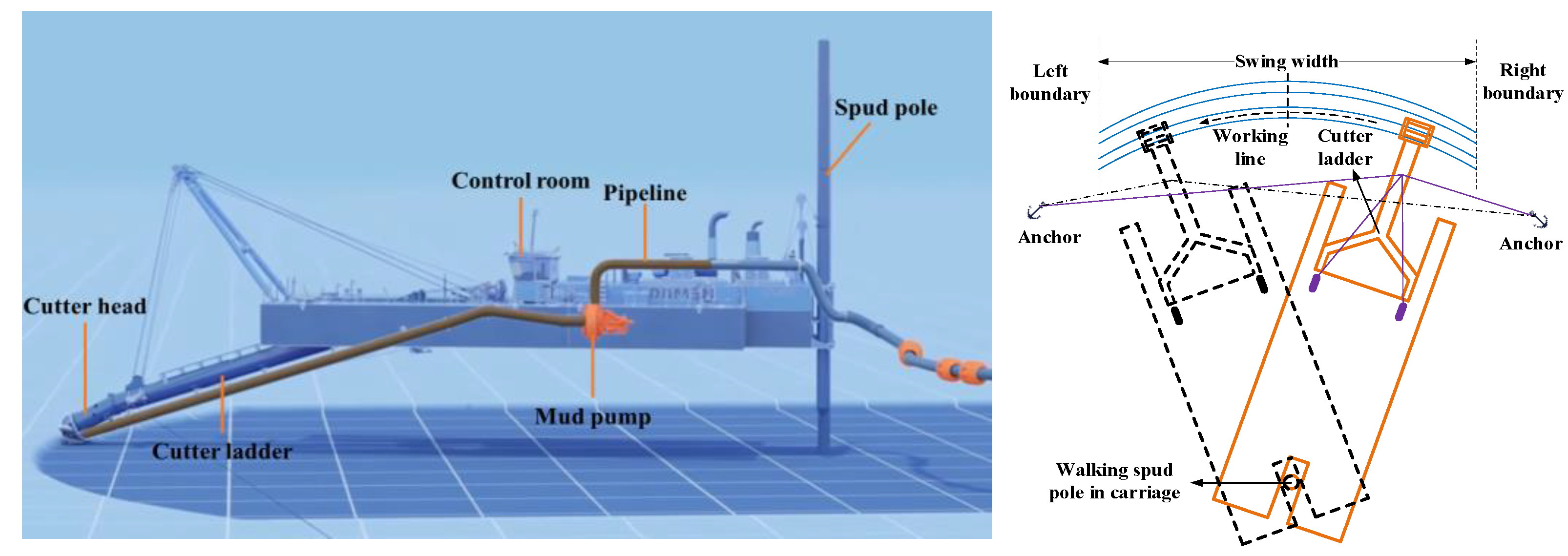
2.1.1. Dredging Construction of CSD
2.1.2. Theory of Control Parameter Optimization
2.2. Proposed Optimization Framework
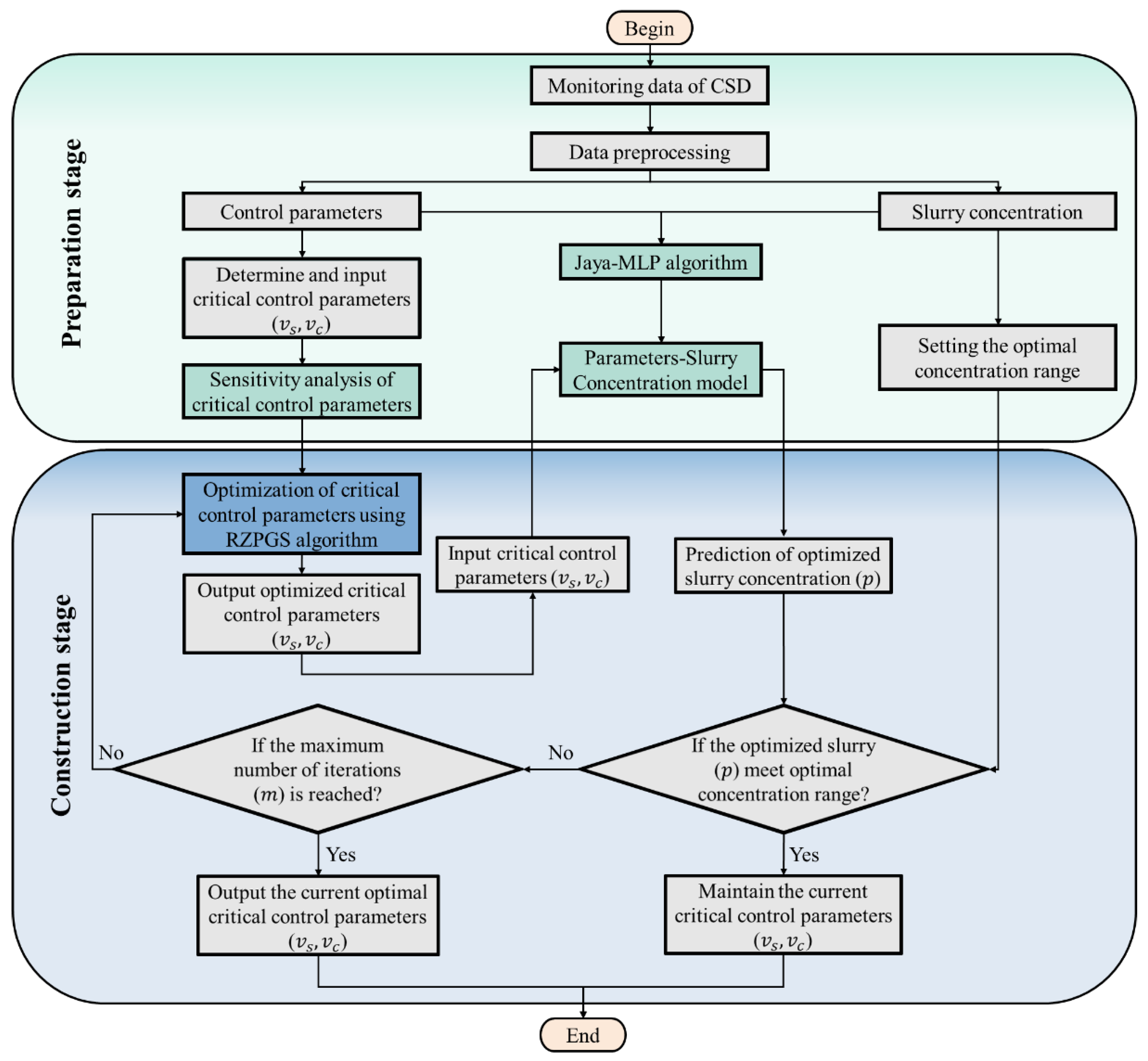
2.2.1. Overall Workflow
2.2.2. Construction Parameters–SC Interaction Relationship Model
2.2.3. Multi-Parameter Sensitivity Analysis of CCPs
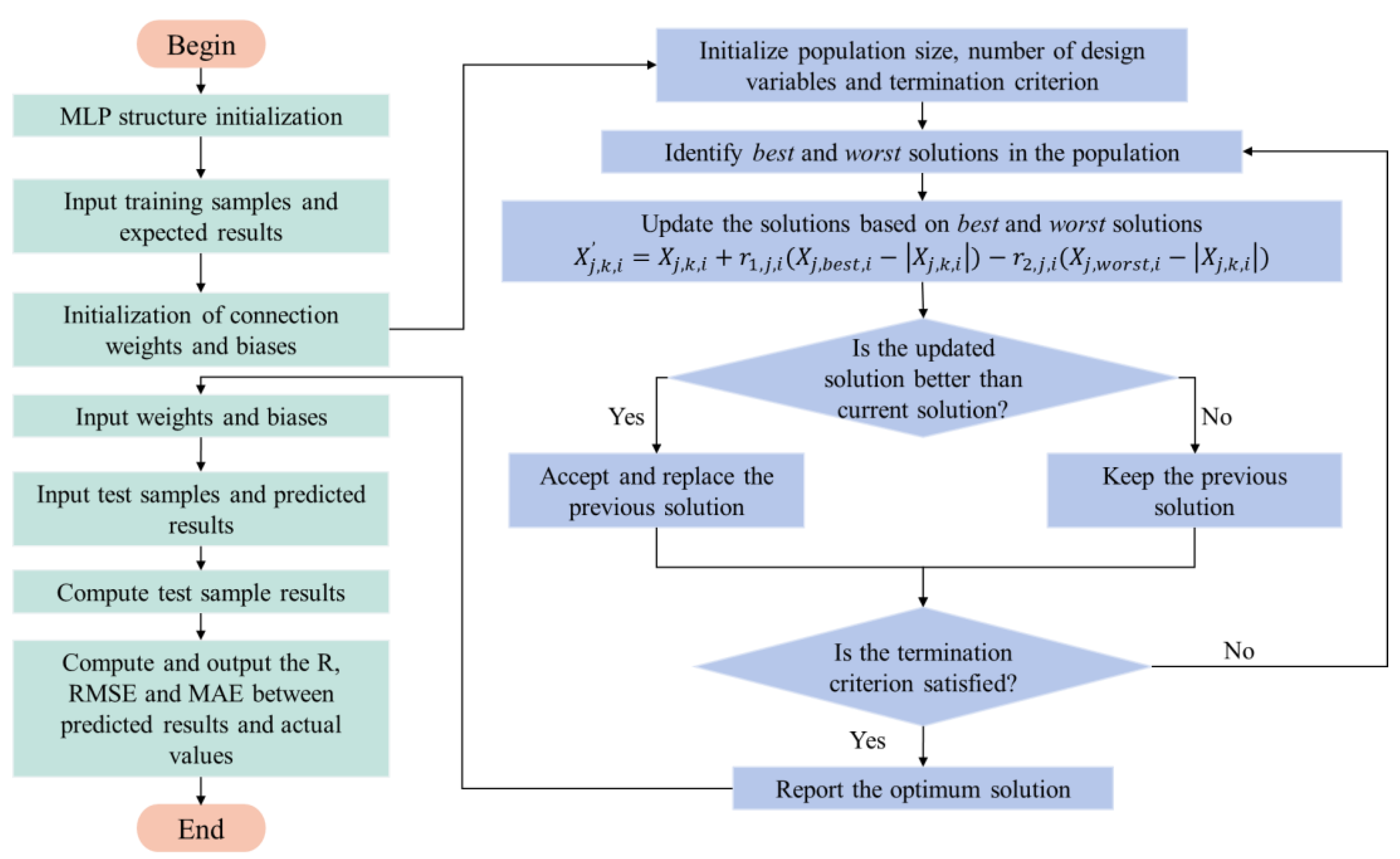
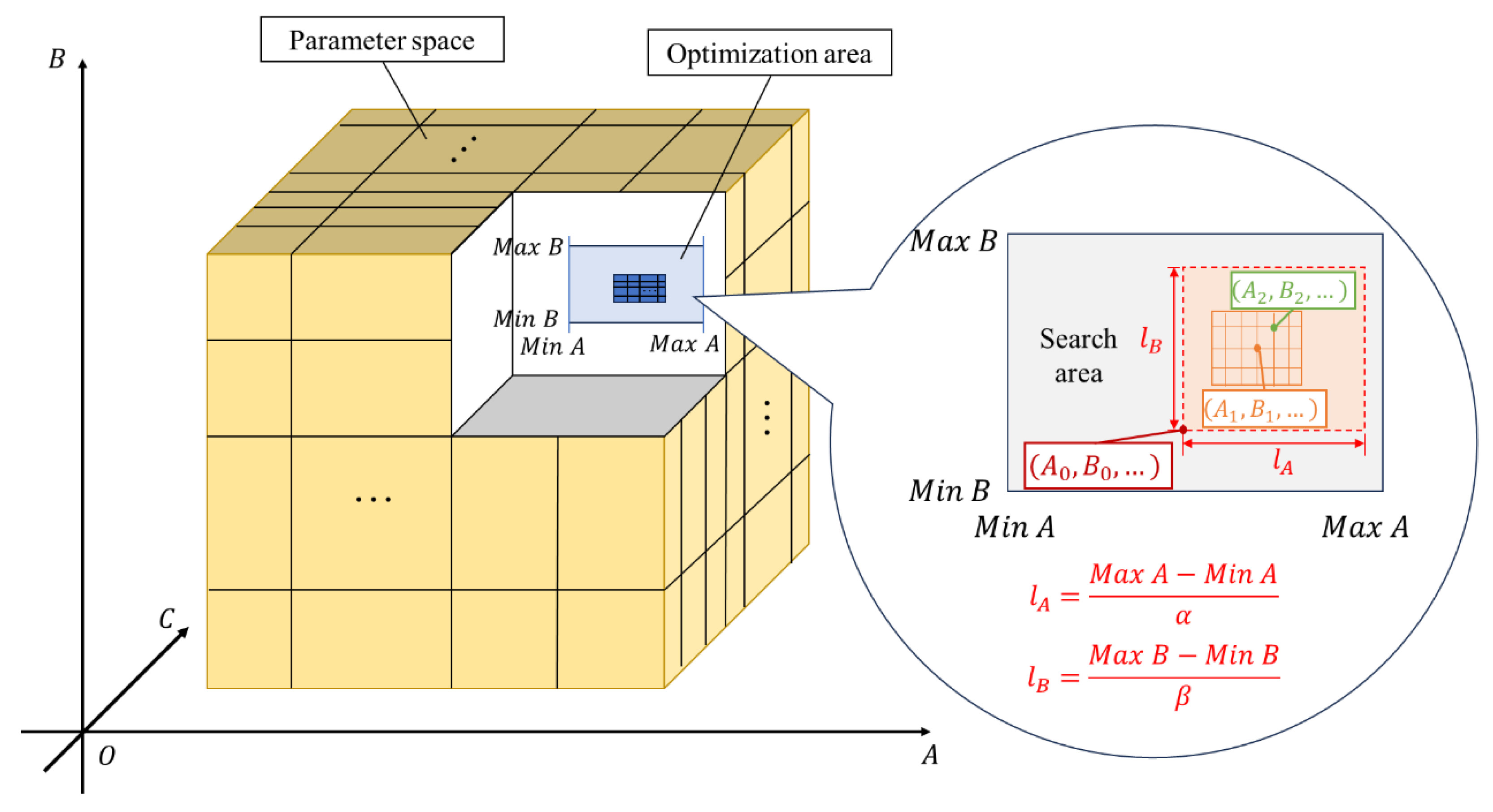
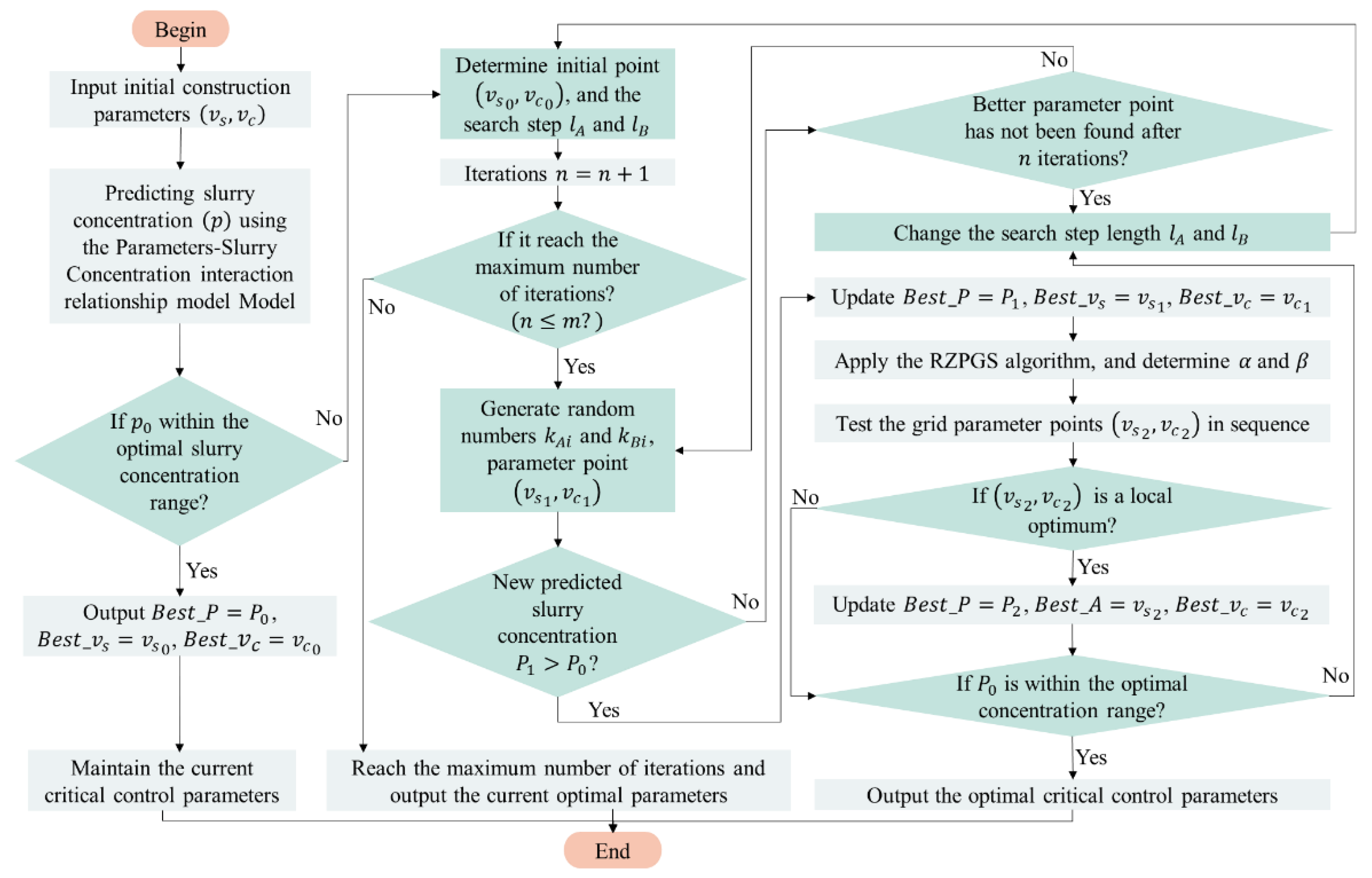
2.2.4. RZPGS-Based Optimal Control Strategy
3. Case Study and Results
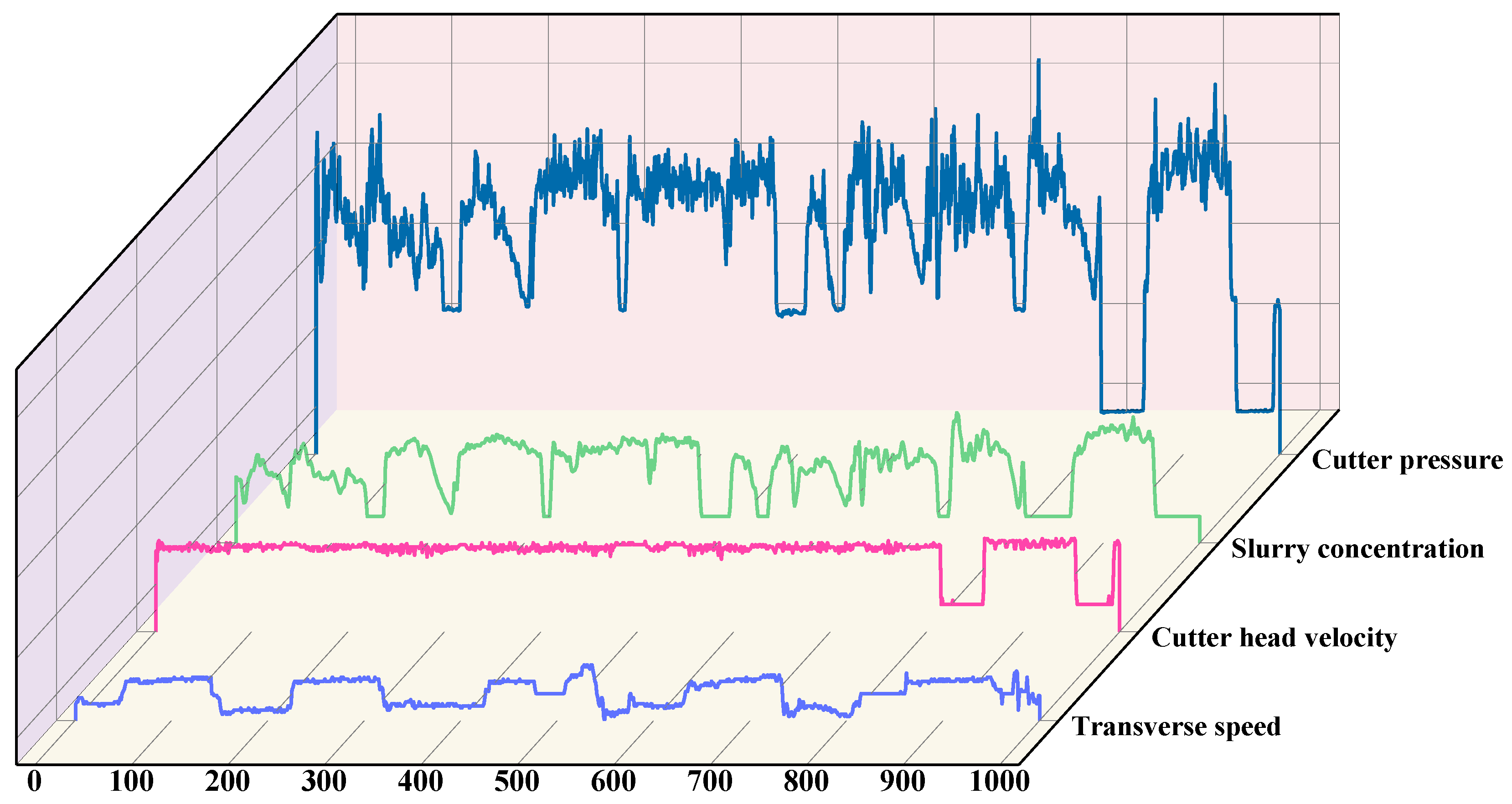
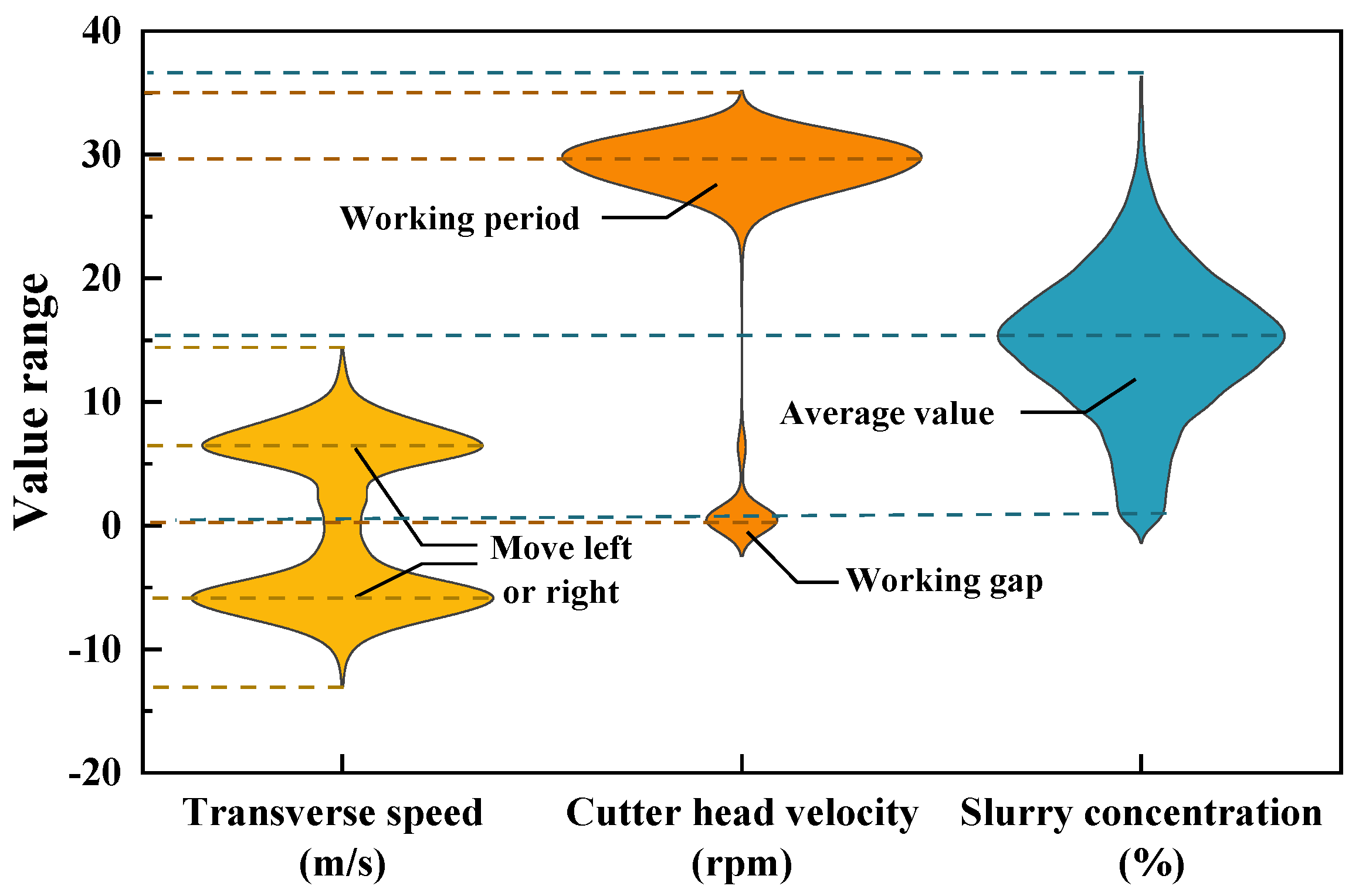
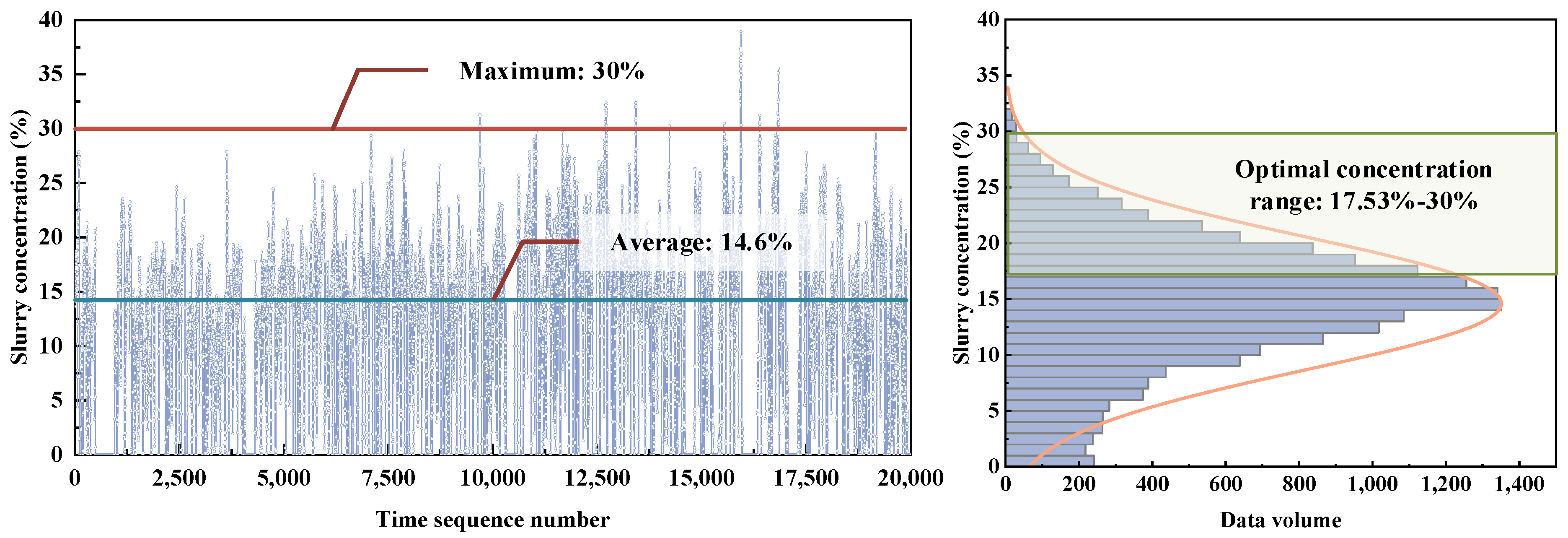
3.1. Project Profile and Construction Data
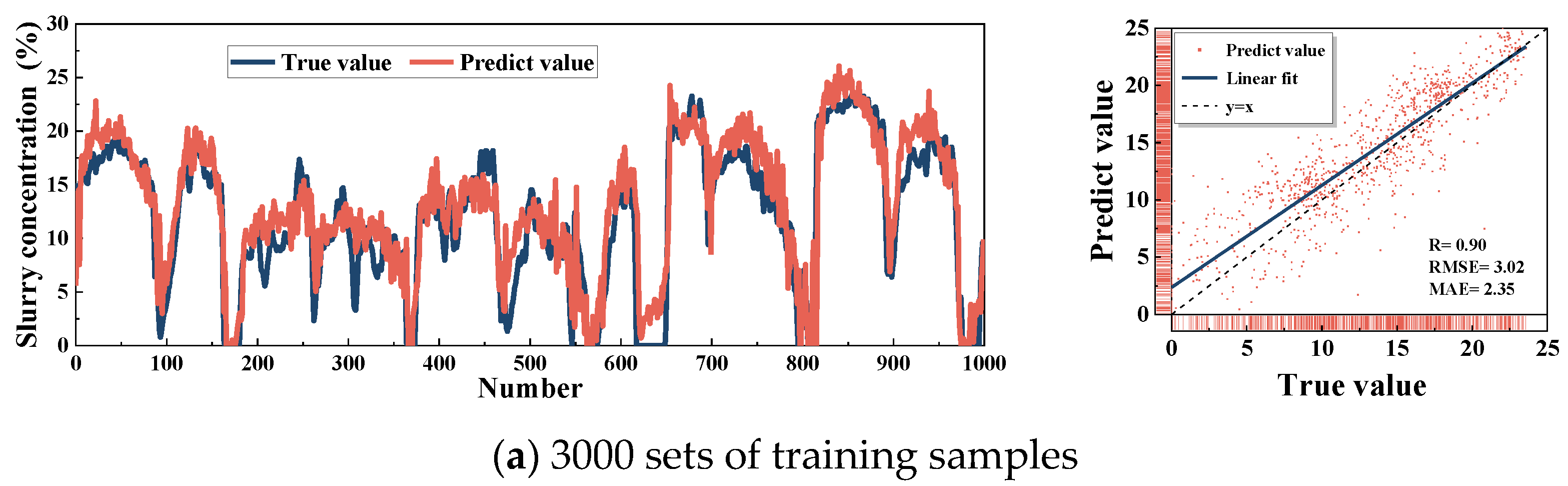
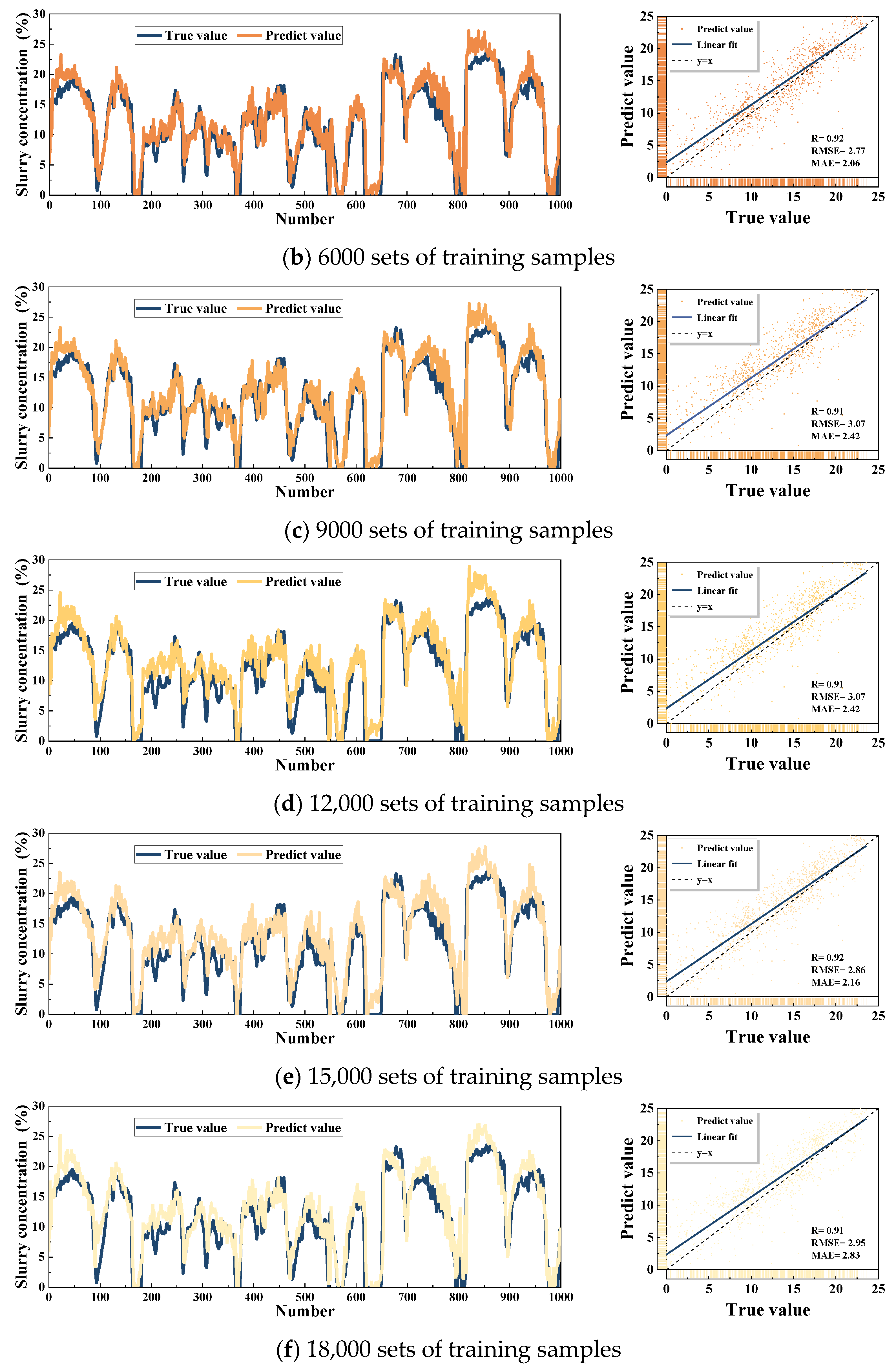
3.2. Model Performance Verification
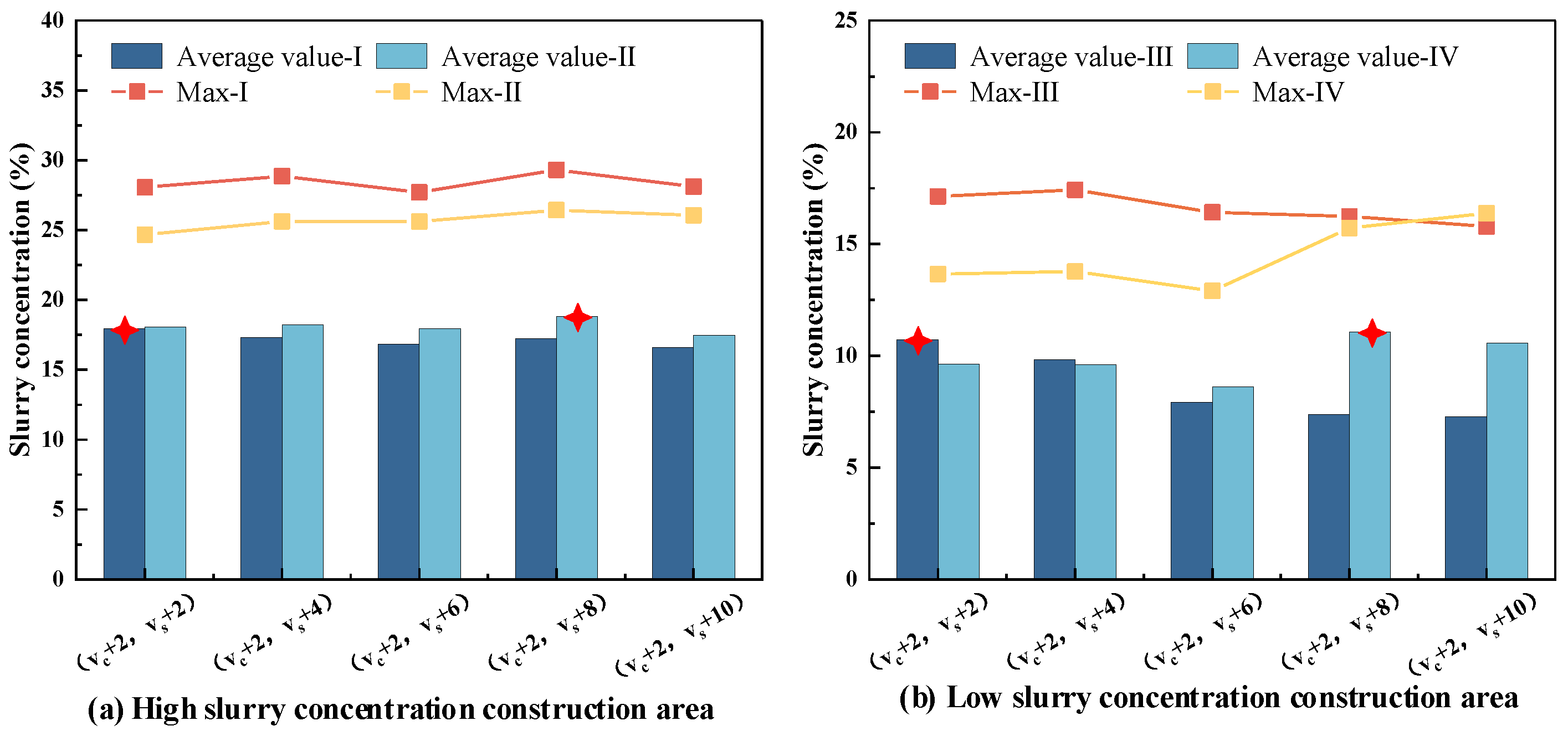
3.3. Multi-Parameter Sensitivity Analysis
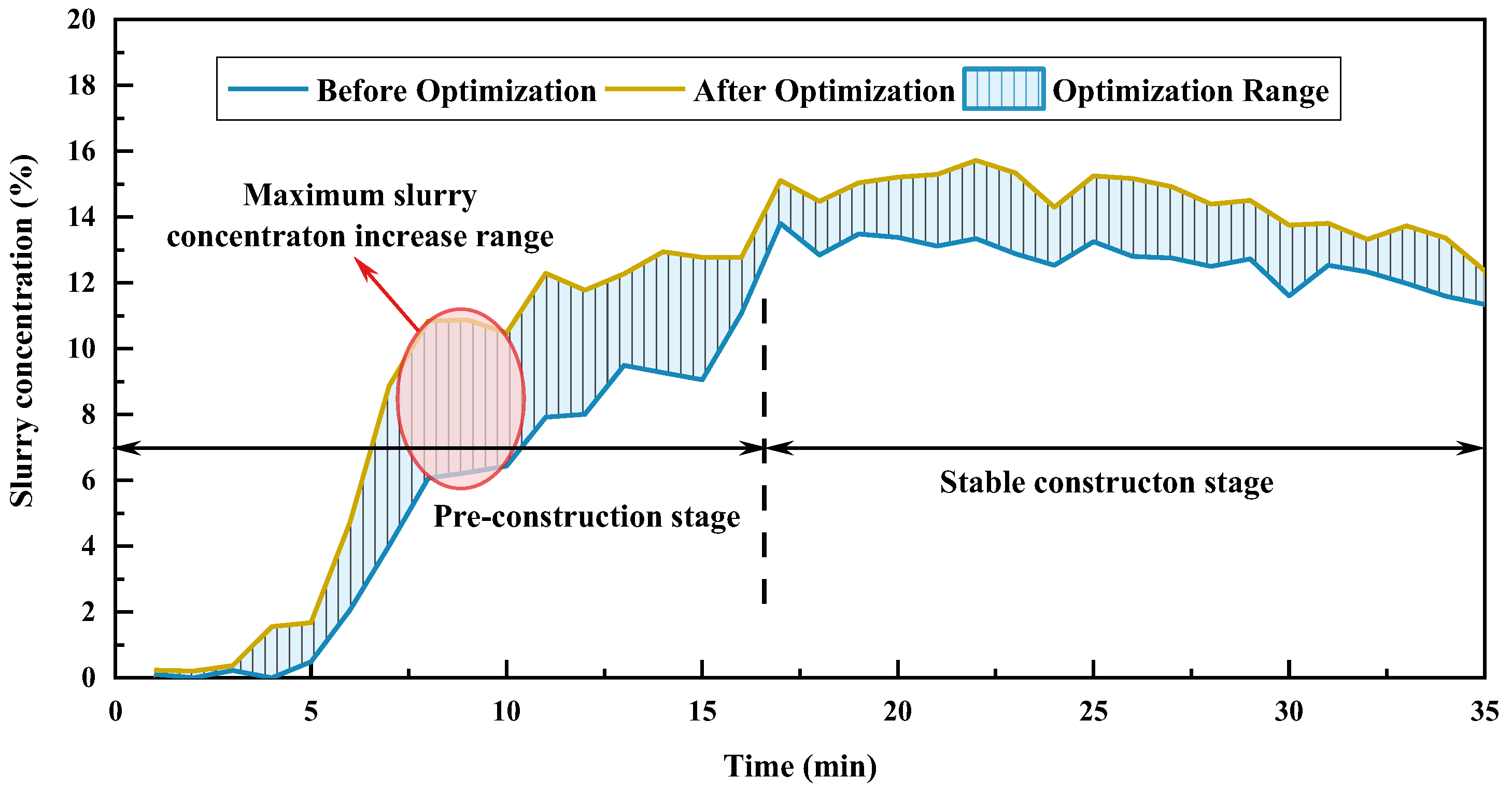
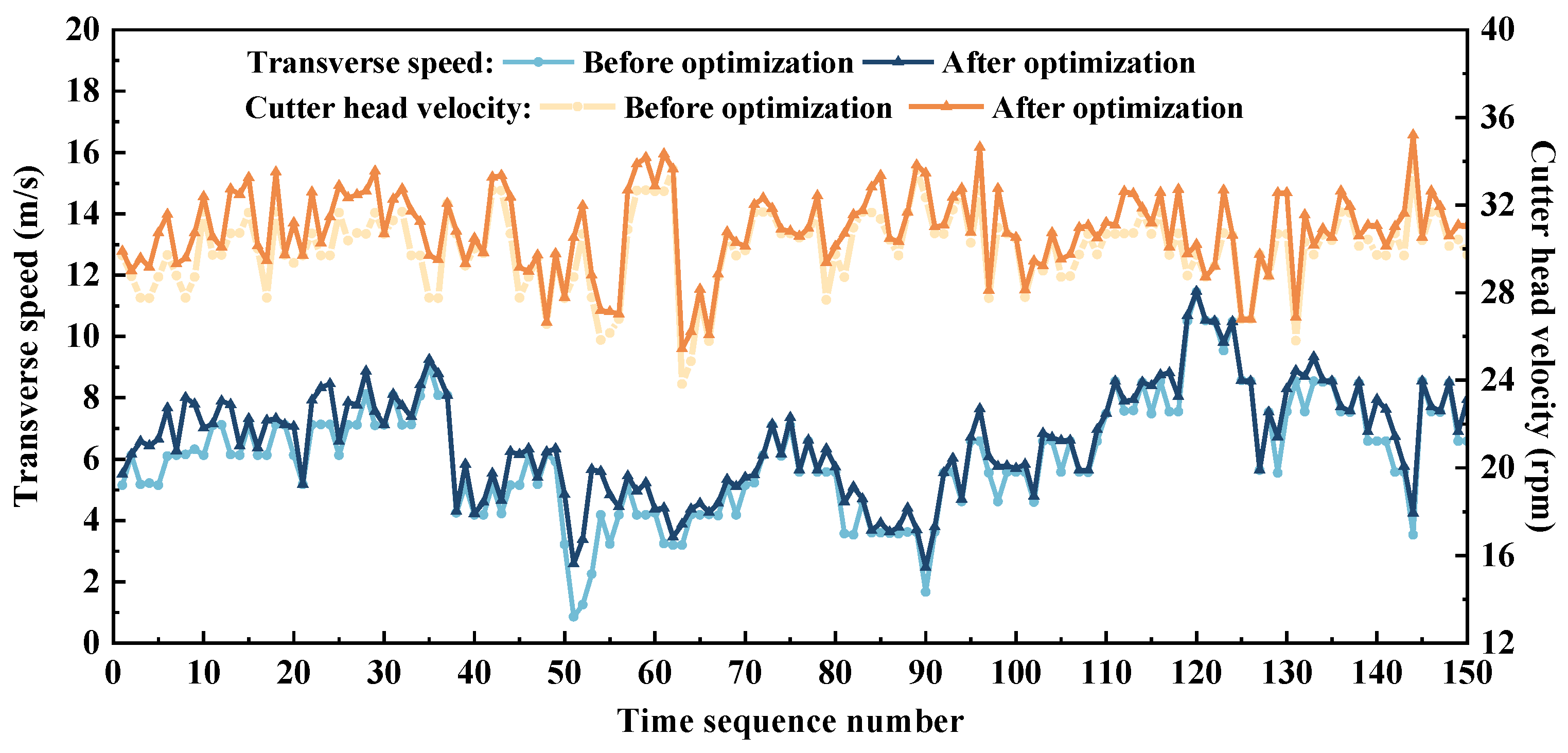
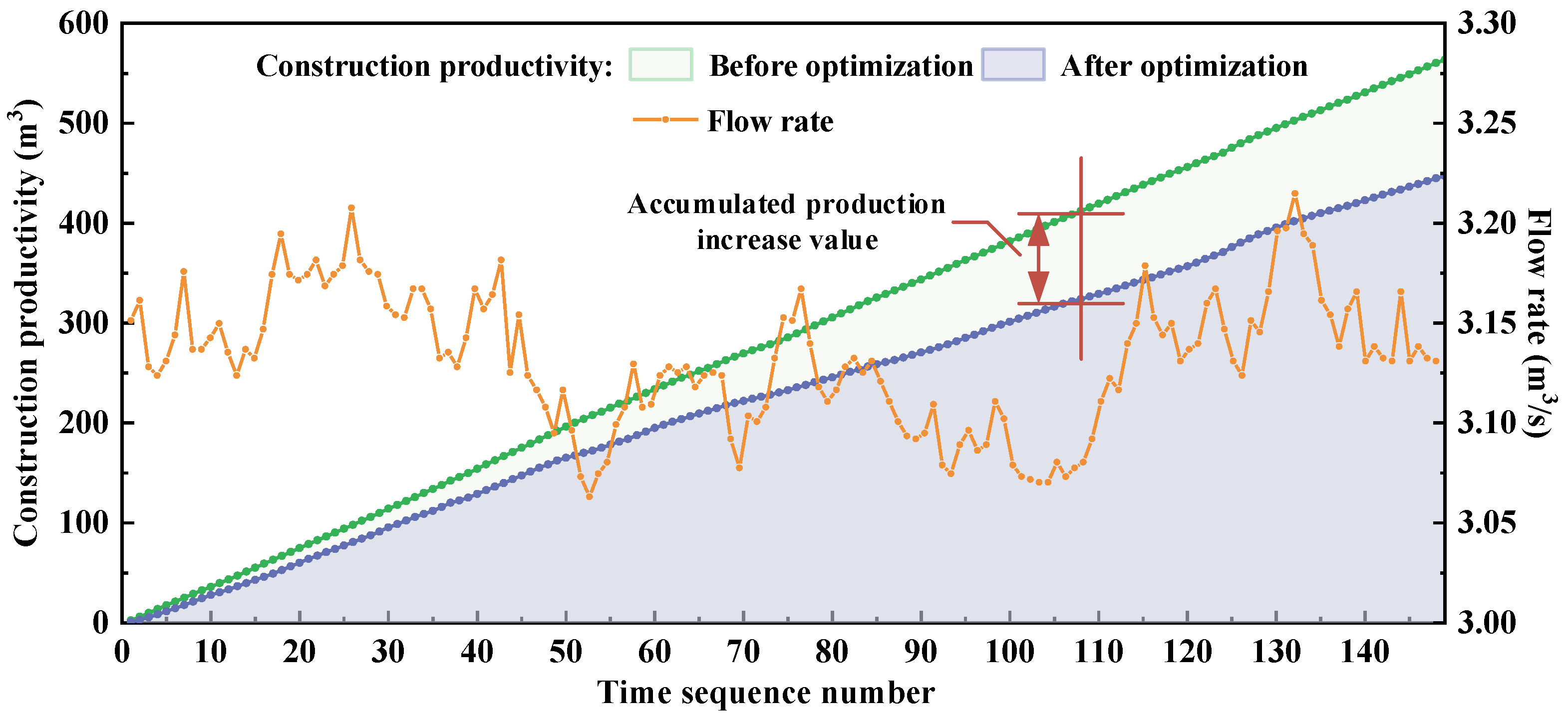
3.4. Optimization of Critical Control Parameters
3.5. Practical Application Considerations
4. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Erftemeijer, P.L.A.; Lewis, R.R.R. Environmental impacts of dredging on seagrasses: A review. Mar. Pollut. Bull. 2006, 52, 1553–1572. [Google Scholar] [CrossRef] [PubMed]
- Bai, S.; Li, M.C.; Kong, R.; Han, S.; Li, H.; Qin, L. Data mining approach to construction productivity prediction for cutter suction dredgers. Autom. Constr. 2019, 105, 102833. [Google Scholar] [CrossRef]
- Wei, C.Y.; Bai, H.N.; Wei, Y.; Ji, Z.; Liu, Z.H. Learning manipulation skills with demonstrations for the swing process control of dredgers. Ocean Eng. 2022, 246, 110545. [Google Scholar] [CrossRef]
- Wei, Y.; Wei, C.Y.; Yuan, B. Flow velocity stability control of slurry pipeline transportation of cutter suction dredgers. J. Nanjing Univ. Sci. Technol. 2021, 45, 332–337, 351. [Google Scholar] [CrossRef]
- Zhang, M.; Fan, S.D.; Zhua, H.H.; Han, S. Numerical simulation of solid-fluid 2-phase-flow of cutting system for cutter suction dredgers. Pol. Marit. Res. 2018, 25, 117–124. [Google Scholar] [CrossRef]
- Bai, Y.M.; Wang, D.S.; Wang, W. The swing control system design of cutter suction dredger based on predictive control. Navig. Chin. 2021, 44, 28–32, 38. [Google Scholar]
- Shang, G.; Xu, L.Y.; Tian, J.Z.; Cai, D.W. Productivity regression analysis of cutter suction dredger considering operating characteristics and equipment status. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2023, 237, 406–419. [Google Scholar] [CrossRef]
- Vancauwenbergh, L.; Vandepitte, D.; Moens, D.; Vanneste, G.; Vercruijsse, P. Reconstruction and analysis of the torsional excitation force component of a cutter suction dredger in hard rock conditions. In Proceedings of the International Conference on Noise and Vibration Engineering (ISMA)/International Conference on Uncertainty in Structural Dynamics (USD), Leuven, Belgium, 7–9 September 2020; pp. 2699–2713. [Google Scholar]
- Vijayan, K.; Barik, C.R.; Sha, O.P. Shock transmission through universal joint of cutter suction dredger. Ocean Eng. 2021, 233, 109185. [Google Scholar] [CrossRef]
- Wei, C.Y.; Wei, Y.; Ji, Z. Model predictive control for slurry pipeline transportation of a cutter suction dredger. Ocean Eng. 2021, 227, 108893. [Google Scholar] [CrossRef]
- Xiong, T.; Wang, J.X.; Wei, W.; Jiang, P.; Zhang, Y.J. Numerical simulation of rock cutting process with cutter-suction dredger. Navig. Chin. 2022, 45, 69–75. [Google Scholar]
- Shang, G.; Xu, L.Y.; Tian, J.Z.; Cai, D.W.; Xu, Z.; Zhou, Z. A real-time green construction optimization strategy for engineering vessels considering fuel consumption and productivity: A case study on a cutter suction dredger. Energy 2023, 274, 127326. [Google Scholar] [CrossRef]
- Fu, J.K.; Tian, H.J.; Song, L.G.; Li, M.C.; Bai, S.; Ren, Q.B. Productivity estimation of cutter suction dredger operation through data mining and learning from real-time big data. Eng. Constr. Archit. Manag. 2021, 28, 2023–2041. [Google Scholar] [CrossRef]
- Jena, D.P.; Panigrahi, S.N. Estimating acoustic transmission loss of perforated filters using finite element method. Measurement 2015, 73, 1–14. [Google Scholar] [CrossRef]
- Martins, R.S.; de Aquino, G.S.; Martins, M.F.; Ramos, R. Sensitivity analysis for numerical simulations of disturbed flows aiming ultrasonic flow measurement. Measurement 2021, 185, 110015. [Google Scholar] [CrossRef]
- Üstünyagiz, E.; Nielsen, C.V.; Tiedje, N.S.; Bay, N. Combined numerical and experimental determination of the convective heat transfer coefficient between an AlCrN-coated Vanadis 4E tool and Rhenus oil. Measurement 2018, 127, 565–570. [Google Scholar] [CrossRef]
- Wang, B.; Fan, S.D.; Chen, Y.; Zheng, L.Y.; Zhu, H.H.; Fang, Z.L.; Zhang, M. The replacement of dysfunctional sensors based on the digital twin method during the cutter suction dredger construction process. Measurement 2022, 189, 110523. [Google Scholar] [CrossRef]
- Wang, B.; Fan, S.D.; Jiang, P.; Zhu, H.H.; Xiong, T.; Wei, W.; Fang, Z.L. A novel method with stacking learning of data-driven soft sensors for mud concentration in a cutter suction dredger. Sensors 2020, 20, 6075. [Google Scholar] [CrossRef]
- Yao, M.H.; Wang, Y.L.; Shang, J.; Zhang, J.Y. Study on the cutter suction dredgers productivity model and its optimal control. In Proceedings of the International Conference on Modeling, Simulation and Optimization Technologies and Applications (MSOTA), Xiamen, China, 18–19 December 2016; pp. 81–85. [Google Scholar] [CrossRef]
- Han, S.; Li, H.; Li, M.C.; Tian, H.J.; Qin, L.; Yu, Y.; Ma, J. Intelligent short-term forecasting for mud concentration in CSD dredging construction. Ocean Eng. 2022, 266, 113151. [Google Scholar] [CrossRef]
- Yang, K.; Yuan, J.L.; Xiong, T.; Wang, B.; Fan, S.D. A novel principal component analysis integrating long short-term memory network and its application in productivity prediction of cutter suction dredgers. Appl. Sci. 2021, 11, 8159. [Google Scholar] [CrossRef]
- Lang, X.; Wu, D.; Mao, W.A. Physics-informed machine learning models for ship speed prediction. Expert Syst. Appl. 2024, 238, 121877. [Google Scholar] [CrossRef]
- Parkes, A.I.; Savasta, T.D.; Sobey, A.J.; Hudson, D.A. Power prediction for a vessel without recorded data using data fusion from a fleet of vessels. Expert Syst. Appl. 2022, 187, 115971. [Google Scholar] [CrossRef]
- Elhaki, O.; Shojaei, K.; Mehrmohammadi, P. Reinforcement learning-based saturated adaptive robust neural-network control of underactuated autonomous underwater vehicles. Expert Syst. Appl. 2022, 197, 116714. [Google Scholar] [CrossRef]
- Bai, S.; Li, M.C.; Lu, Q.R.; Fu, J.K.; Li, J.F.; Qin, L. A new measuring method of dredging concentration based on hybrid ensemble deep learning technique. Measurement 2022, 188, 110423. [Google Scholar] [CrossRef]
- Li, M.C.; Lu, Q.R.; Bai, S.; Zhang, M.X.; Tian, H.J.; Qin, L. Digital twin-driven virtual sensor approach for safe construction operations of trailing suction hopper dredger. Autom. Constr. 2021, 132, 103961. [Google Scholar] [CrossRef]
- Li, M.C.; Kong, R.; Han, S.; Tian, G.P.; Qin, L. Novel method of construction-efficiency evaluation of cutter suction dredger based on real-time monitoring data. J. Waterw. Port Coast. Ocean Eng. 2018, 144, 05018007. [Google Scholar] [CrossRef]
- Bai, S.; Li, M.C.; Lu, Q.R.; Tian, H.J.; Qin, L. Global time optimization method for dredging construction cycles of trailing suction hopper dredger based on Grey System Model. J. Constr. Eng. Manag. 2022, 148, 04021198. [Google Scholar] [CrossRef]
- Wang, W.; Shen, Y.C.; Wang, L.Y.; Wang, D.S.; Bai, Y.M. Design of dredging process control system for cutter suction dredger. In Proceedings of the 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021; pp. 5932–5937. [Google Scholar] [CrossRef]
- Li, J.Y.; Shi, Y.Y.; Rao, K.P.; Zhao, K.Y.; Xiao, J.F.; Xiong, T.; Huang, Y.Z.; Huang, Q.B. The design and analysis of double cutter device for hinge and suction dredger based on feedback control method. Appl. Sci. 2022, 12, 3793. [Google Scholar] [CrossRef]
- Lan, Y.; Hu, J.W.; Huang, J.H.; Niu, L.K.; Zeng, X.H.; Xiong, X.Y.; Wu, B. Fault diagnosis on slipper abrasion of axial piston pump based on Extreme Learning Machine. Measurement 2018, 124, 378–385. [Google Scholar] [CrossRef]
- Wei, C.Y.; Wang, H.; Bai, H.A.; Ji, Z.; Liu, Z.H. PPLC: Data-driven offline learning approach for excavating control of cutter suction dredgers. Eng. Appl. Artif. Intell. 2023, 125, 106708. [Google Scholar] [CrossRef]
- Wang, B.; Fan, S.D.; Jiang, P.; Xing, T.; Fang, Z.L.; Wen, Q. Research on predicting the productivity of cutter suction dredgers based on data mining with model stacked generalization. Ocean Eng. 2020, 217, 108001. [Google Scholar] [CrossRef]
- Gondia, A.; Siam, A.; El-Dakhakhni, W.; Nassar, A.H. Machine learning algorithms for construction projects delay risk prediction. J. Constr. Eng. Manag. 2020, 146, 04019085. [Google Scholar] [CrossRef]
- Bai, S.; Li, M.C.; Song, L.G.; Ren, Q.B.; Qin, L.; Fu, J.K. Productivity analysis of trailing suction hopper dredgers using stacking strategy. Autom. Constr. 2021, 122, 103470. [Google Scholar] [CrossRef]
- Lai, H.H.; Chang, K.H.; Lin, C.L. A novel method for evaluating dredging productivity using a data envelopment analysis-based technique. Math. Probl. Eng. 2019, 2019, 5130835. [Google Scholar] [CrossRef]
- Wei, C.Y.; Ni, F.S.; Chen, X.J. Obtaining human experience for intelligent dredger control: A reinforcement learning approach. Appl. Sci. 2019, 9, 1769. [Google Scholar] [CrossRef]
- Yang, J.B.; Ni, F.S.; Wei, C.Y. A BP neural network model for predicting the production of a cutter suction dredger. In Proceedings of the 3rd International Conference on Material, Mechanical and Manufacturing Engineering (IC3ME), Guangzhou, China, 27–28 June 2015; pp. 1221–1226. [Google Scholar] [CrossRef]
- JTJ 319-1999; The Technical Code of Dredging Engineering. China Communications Press: Beijing, China, 1999.
- Wang, B.; Fan, S.D.; Jiang, P.; Chen, Y.; Zhu, H.H.; Xiong, T. Cutting state estimation and time series prediction using deep learning for cutter suction dredger. Appl. Ocean Res. 2023, 134, 103515. [Google Scholar] [CrossRef]
- Li, W.; Wang, F.X.; Jiang, J.A. Parameter identification, verification and simulation of the CSD transport process. In Proceedings of the 11th International Conference on Advanced Computational Intelligence (ICACI), Guilin, China, 7–9 June 2019; pp. 118–123. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.T.; Cao, Y.; Hu, H.; Wei, Y.X.; Zhang, Z.; Lin, S.; Guo, B.N. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the 18th IEEE/CVF International Conference on Computer Vision (ICCV), Electr Network, Montreal, QC, Canada, 11–17 October 2021; pp. 9992–10002. [Google Scholar] [CrossRef]
- Kim, T.; Adali, T. Approximation by fully complex multilayer Perceptrons. Neural Comput. 2003, 15, 1641–1666. [Google Scholar] [CrossRef]
- Castro, J.L.; Mantes, C.J.; Benítez, J.M. Neural networks with a continuous squashing function in the output are universal approximators. Neural Netw. 2000, 13, 561–563. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Uzlu, E. Application of Jaya algorithm-trained artificial neural networks for prediction of energy use in the nation of Turkey. Energy Sources Part B 2019, 14, 183–200. [Google Scholar] [CrossRef]
- Jothi, G.; Inbarani, H.H.; Azar, A.T.; Devi, K.R. Rough set theory with Jaya optimization for acute lymphoblastic leukemia classification. Neural Comput. Appl. 2019, 31, 5175–5194. [Google Scholar] [CrossRef]
- Yu, K.J.; Liang, J.J.; Qu, B.Y.; Chen, X.; Wang, H.S. Parameters identification of photovoltaic models using an improved JAYA optimization algorithm. Energy Conv. Manag. 2017, 150, 742–753. [Google Scholar] [CrossRef]
- Lujan-Moreno, G.A.; Howard, P.R.; Rojas, O.G.; Montgomery, D.C. Design of experiments and response surface methodology to tune machine learning hyperparameters, with a random forest case-study. Expert Syst. Appl. 2018, 109, 195–205. [Google Scholar] [CrossRef]



| Parameters | Classification | Index | |
|---|---|---|---|
| Construction parameters | Controllable parameters | Real-time control parameters | Cutter head velocity, transverse speed, … |
| Preset parameters | Step length, cutting depth, … | ||
| Uncontrollable parameters | Angle of cutter head, pump suction vacuum, hull draft, … | ||
| Orthogonal Experiments | Are Set. | |||
|---|---|---|---|---|
| On the parameter , gradients of size are set. | … | |||
| … | ||||
| … | … | … | … | |
| … | ||||
| Time | 1 | 2 | 3 | 4 | 5 | … | 255 | 256 |
|---|---|---|---|---|---|---|---|---|
| Density (t/m3) | Cutter Head Velocity (rpm) | Cutter Pressure (bar) | Flow Rate (m/s) | Transverse Speed (m/s) | … | Pump Vacuum (bar) | Power (kW) | |
| 0:00:01 | 1.17 | 31.68 | 124.07 | 5.88 | −6.59 | … | −0.64 | 625.28 |
| 0:00:09 | 1.16 | 27.77 | 130.16 | 5.91 | −7.5 | … | −0.63 | 624.4 |
| 0:00:17 | 1.17 | 26.79 | 130.97 | 5.91 | −5.6 | … | −0.61 | 631.69 |
| 0:00:25 | 1.18 | 29.74 | 111.99 | 5.88 | −6.59 | … | −0.59 | 616.4 |
| 0:00:33 | 1.19 | 29.76 | 111.99 | 5.84 | −6.59 | … | −0.58 | 635.53 |
| 0:00:41 | 1.18 | 30.66 | 109.92 | 5.84 | −6.59 | … | −0.59 | 618.03 |
| 0:00:49 | 1.17 | 29.7 | 109.11 | 5.81 | −6.59 | … | −0.59 | 643.14 |
| 0:00:57 | 1.16 | 30.7 | 112.91 | 5.78 | −6.6 | … | −0.58 | 637.44 |
| 0:01:05 | 1.16 | 27.78 | 123.15 | 5.83 | −6.59 | … | −0.59 | 647.82 |
| 0:01:13 | 1.17 | 28.76 | 109.57 | 5.83 | −5.58 | … | −0.59 | 630.67 |
| 0:01:21 | 1.17 | 29.69 | 111.87 | 5.80 | −6.59 | … | −0.6 | 609.73 |
| 0:01:29 | 1.17 | 29.69 | 113.37 | 5.76 | −5.52 | … | −0.61 | 619.71 |
| 0:01:37 | 1.17 | 29.69 | 107.39 | 5.77 | −4.62 | … | −0.61 | 625.3 |
| 0:01:45 | 1.17 | 31.66 | 107.16 | 5.75 | −6.6 | … | −0.61 | 610.05 |
| … | … | … | … | … | … | … | … | … |
| 0:28:49 | 1.17 | 27.75 | 158.23 | 6.17 | 10.03 | … | −0.68 | 636.71 |
| 0:28:57 | 1.17 | 27.75 | 150.87 | 6.19 | 9.03 | … | −0.73 | 609.03 |
| … | … | … | … | … | … | … | … | … |
| 5:48:41 | 1.21 | 29.72 | 113.6 | 5.58 | 11.56 | … | −0.64 | 615.17 |
| 5:48:49 | 1.2 | 31.69 | 115.78 | 5.53 | 11.55 | … | −0.64 | 642.44 |
| Max. | 1.21 | 31.69 | 158.23 | 6.19 | 11.71 | … | −0.58 | 647.82 |
| Min. | 1.16 | 26.79 | 107.16 | 5.53 | −12.21 | … | −0.73 | 626.23 |
| Avg. | 1.17 | 29.30 | 120.47 | 5.82 | −1.17 | … | −0.61 | 626.23 |
| Parameters | Value |
|---|---|
| The number of neurons in the input layer | 255 |
| The number of neurons in the two hidden layers | 100, 40 |
| The number of neurons in the output layer | 1 |
| Activation function | ReLU |
| Iteration number | 50 |
| SC (%) | + 2 | + 4 | + 6 | + 8 | + 10 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Avg. | Max. | Avg. | Max. | Avg. | Max. | Avg. | Max. | Avg. | Max. | ||
| I | + 2 | 17.93 | 28.06 | 17.32 | 28.86 | 16.82 | 27.70 | 17.23 | 29.31 | 16.58 | 28.11 |
| + 4 | 17.47 | 28.22 | 17.65 | 29.47 | 15.49 | 26.49 | 15.39 | 26.77 | 15.92 | 28.27 | |
| + 6 | 17.39 | 28.22 | 16.94 | 27.98 | 15.91 | 27.65 | 15.86 | 27.34 | 15.87 | 28.74 | |
| + 8 | 17.80 | 29.66 | 16.65 | 28.65 | 16.43 | 28.07 | 14.93 | 26.51 | 14.57 | 25.07 | |
| + 10 | 17.51 | 29.49 | 16.89 | 29.29 | 15.39 | 27.11 | 13.39 | 27.23 | 14.11 | 25.40 | |
| II | + 2 | 18.08 | 24.67 | 18.23 | 25.62 | 17.96 | 25.61 | 18.82 | 26.42 | 17.45 | 26.02 |
| + 4 | 17.19 | 24.51 | 17.71 | 25.35 | 16.11 | 23.94 | 17.05 | 24.82 | 17.05 | 25.98 | |
| + 6 | 17.13 | 24.59 | 16.59 | 24.03 | 16.84 | 23.21 | 17.03 | 24.52 | 16.73 | 25.16 | |
| + 8 | 17.26 | 24.45 | 16.73 | 25.04 | 17.29 | 23.59 | 16.67 | 23.27 | 16.69 | 24.52 | |
| + 10 | 17.22 | 24.45 | 16.83 | 25.42 | 17.27 | 25.25 | 13.92 | 23.24 | 15.09 | 22.89 | |
| III | + 2 | 10.73 | 17.13 | 9.83 | 17.43 | 7.93 | 16.42 | 7.37 | 16.24 | 7.28 | 15.79 |
| + 4 | 10.24 | 18.49 | 9.99 | 17.86 | 8.96 | 17.59 | 7.19 | 17.24 | 7.34 | 15.65 | |
| + 6 | 9.94 | 17.66 | 8.46 | 17.86 | 9.43 | 17.07 | 7.75 | 17.29 | 7.28 | 17.18 | |
| + 8 | 9.59 | 17.49 | 8.62 | 17.62 | 7.85 | 17.42 | 6.86 | 16.31 | 6.61 | 18.27 | |
| + 10 | 8.41 | 16.17 | 8.75 | 17.39 | 5.83 | 14.24 | 6.63 | 16.69 | 7.25 | 18.36 | |
| IV | + 2 | 9.62 | 13.66 | 9.60 | 13.77 | 8.62 | 12.90 | 11.05 | 15.72 | 10.57 | 16.38 |
| + 4 | 8.57 | 12.38 | 9.05 | 12.76 | 8.95 | 13.40 | 9.39 | 14.30 | 11.03 | 16.61 | |
| + 6 | 6.55 | 9.52 | 8.62 | 12.38 | 10.00 | 14.17 | 9.33 | 14.13 | 10.48 | 15.81 | |
| + 8 | 7.16 | 10.44 | 7.81 | 12.27 | 8.07 | 12.96 | 8.90 | 12.89 | 8.31 | 12.71 | |
| + 10 | 5.78 | 9.78 | 6.77 | 9.63 | 4.24 | 7.91 | 7.48 | 11.56 | 9.94 | 13.80 | |
| ) | I | II | III | IV | Average |
|---|---|---|---|---|---|
| RZPGS algorithm | 6.8 | 6.3 | 6.9 | 6.7 | 6.7 |
| Grid search algorithm | 64.2 | 62.7 | 62.8 | 62.7 | 63.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Liu, R.; Bai, S.; Chen, Y.; Liu, L. Efficient Productivity-Aware Control Parameter Optimization in Cutter Suction Dredger Construction Using Machine Learning with Parallel Global Search. Water 2024, 16, 3067. https://doi.org/10.3390/w16213067
Liu H, Liu R, Bai S, Chen Y, Liu L. Efficient Productivity-Aware Control Parameter Optimization in Cutter Suction Dredger Construction Using Machine Learning with Parallel Global Search. Water. 2024; 16(21):3067. https://doi.org/10.3390/w16213067
Chicago/Turabian StyleLiu, Hao, Ruizhe Liu, Shuo Bai, Yong Chen, and Leping Liu. 2024. "Efficient Productivity-Aware Control Parameter Optimization in Cutter Suction Dredger Construction Using Machine Learning with Parallel Global Search" Water 16, no. 21: 3067. https://doi.org/10.3390/w16213067
APA StyleLiu, H., Liu, R., Bai, S., Chen, Y., & Liu, L. (2024). Efficient Productivity-Aware Control Parameter Optimization in Cutter Suction Dredger Construction Using Machine Learning with Parallel Global Search. Water, 16(21), 3067. https://doi.org/10.3390/w16213067






