Water Temperature Model to Assess Impact of Riparian Vegetation on Jucar River and Spain
Abstract
:1. Introduction
2. Study Case and Methodology
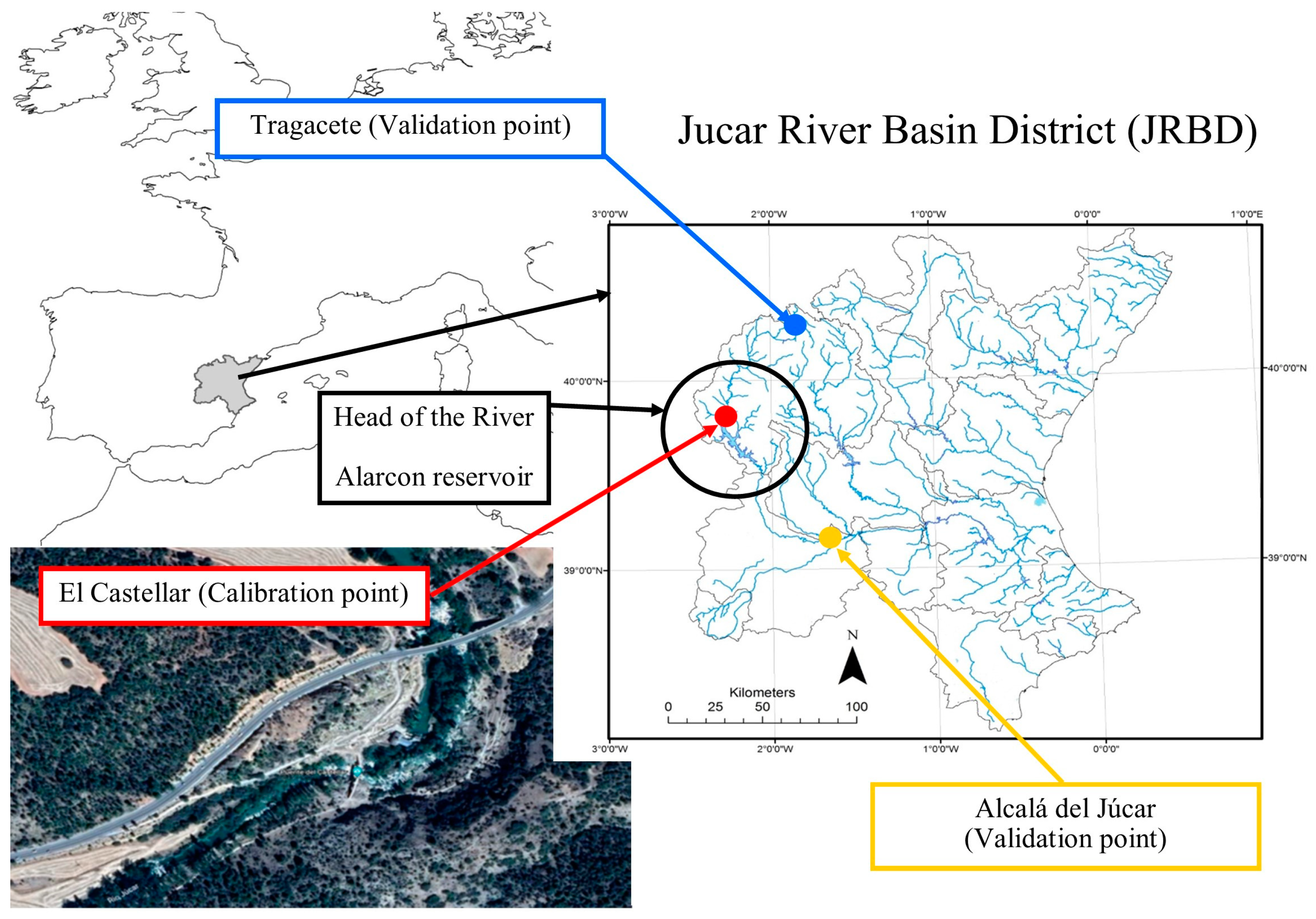
2.1. Jucar River
2.2. Methodology and Thermal Model
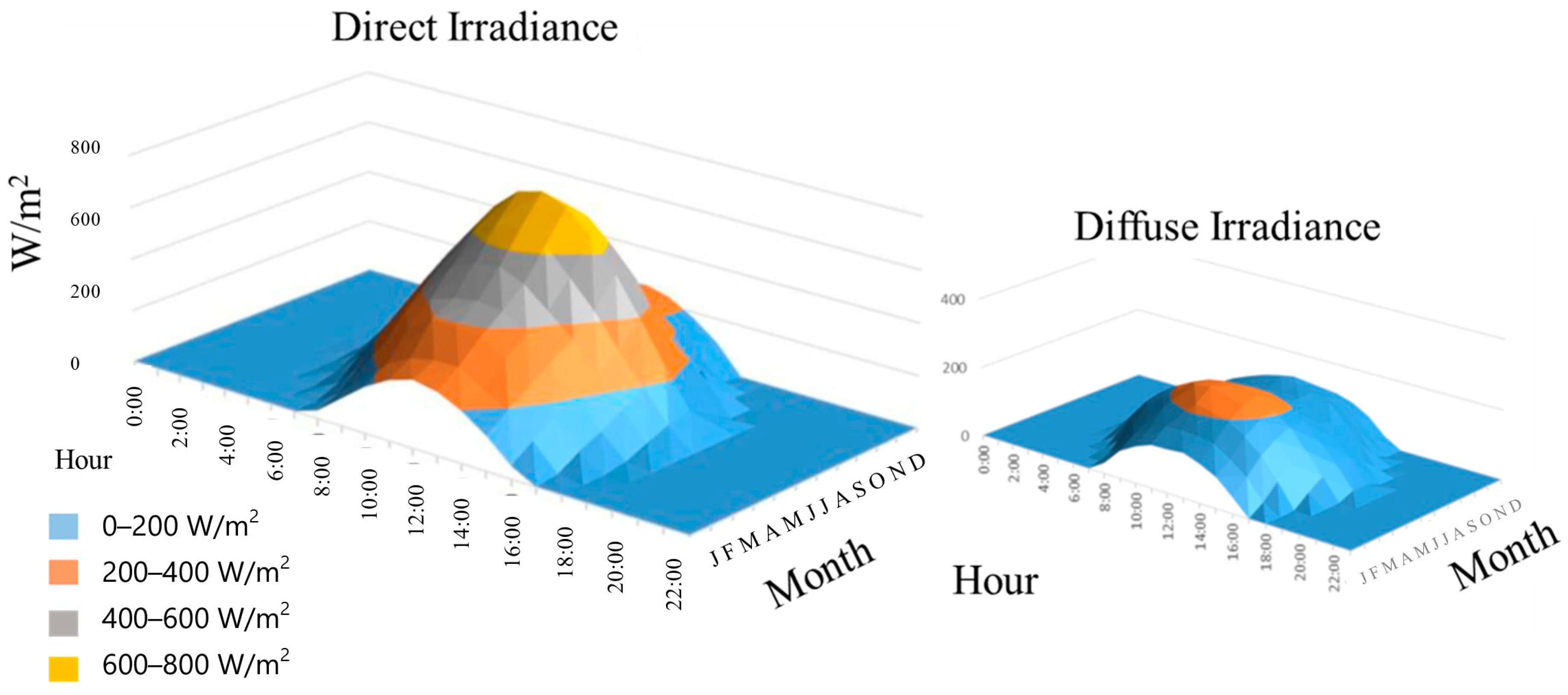
2.2.1. Net Short-Wave Radiation (Ks)
2.2.2. Air to Water Net Long-Wave Radiation (Law)
2.2.3. Water to Air Long-Wave Radiation (Lwa)
2.2.4. Latent Heat (Qevap)
2.2.5. Sensible Heat (Qcon)
3. Results and Discussion
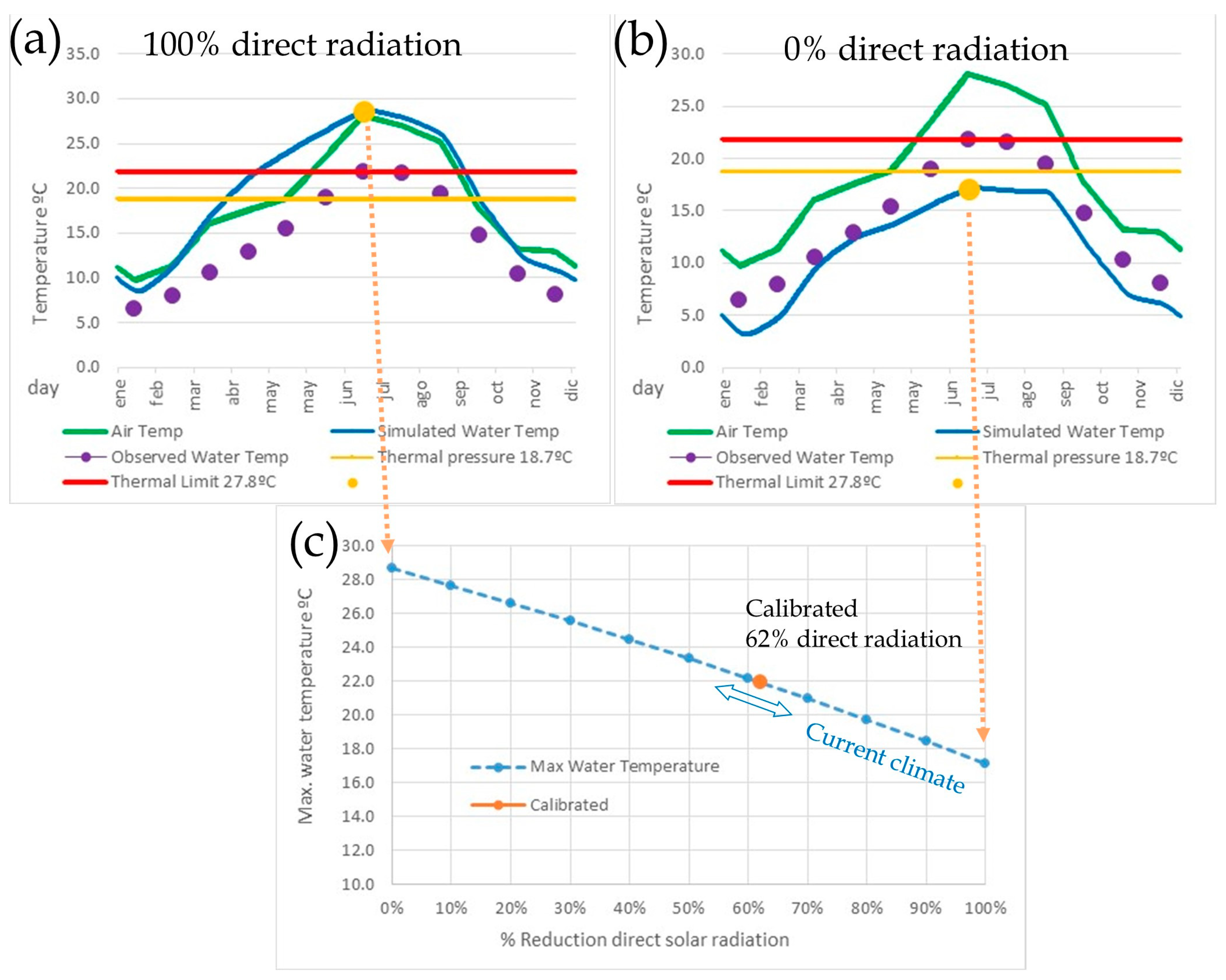
3.1. Model Calibration and Water Energy Balance
3.2. Vegetation Coverage and Water Temperature
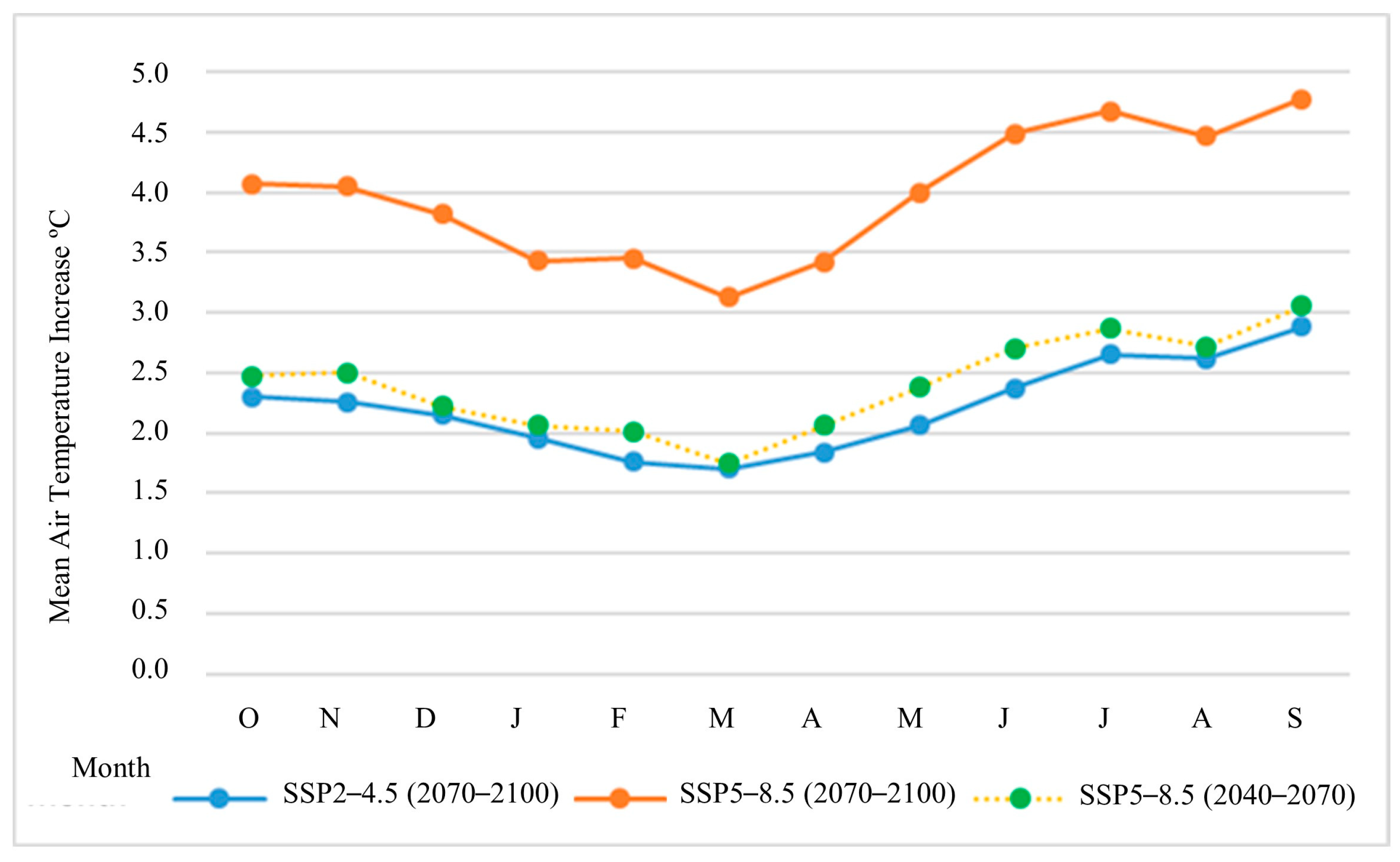
3.3. Water Temperature Under Climate Change Scenarios
3.4. Nature-Based Measures to Reduce Water Temperature

4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kelleher, C.A.; E Golden, H.; Archfield, S.A. Monthly river temperature trends across the US confound annual changes. Environ. Res. Lett. 2021, 16, 104006–104010. [Google Scholar] [CrossRef] [PubMed]
- Jastram, J.D.; Rice, K.C. Air- and Stream-Water-Temperature Trends in the Chesapeake Bay Region, 1960–2014. U.S. Geological Survey Open-File Report 2015-1207. 2015. Available online: https://pubs.er.usgs.gov/publication/ofr20151207 (accessed on 30 October 2024).
- Liu, S.; Xie, Z.; Liu, B.; Wang, Y.; Gao, J.; Zeng, Y.; Xie, J.; Xie, Z.; Jia, B.; Qin, P.; et al. Global river water warming due to climate change and anthropogenic heat emission. Glob. Planet. Chang. 2020, 193, 103289, ISSN 0921-8181. [Google Scholar] [CrossRef]
- Zhu, S.; Luo, Y.; Graf, R.; Wrzesinski, D.; Sojka, M.; Sun, B.; Kong, L.; Ji, Q.; Luo, W. Reconstruction of long-term water temperature indicates significant warming in Polish rivers during 1966–2020. J. Hydrol. Reg. Stud. 2022, 44, 101281, ISSN 2214-5818. [Google Scholar] [CrossRef]
- Isaak, D.J.; Wollrab, S.; Horan, D.; Chandler, G. Climate change effects on stream and river temperatures across the northwest U.S. from 1980–2009 and implications for salmonid fishes. Clim. Chang. 2011, 113, 499–524. [Google Scholar] [CrossRef]
- Basarin, B.; Lukić, T.; Pavić, D.; Wilby, R.L. Trends and Multi-Annual Variability of Water Temperatures in the River Danube, Serbia. Hydrol. Process. 2016, 30, 3315–3329. [Google Scholar] [CrossRef]
- Arora, R.; Tockner, K.; Venohr, M. Changing river temperatures in northern Germany: Trends and drivers of change. Hydrol. Process. 2016, 30, 3084–3096. [Google Scholar] [CrossRef]
- O’Reilly, C.M.; Sharma, S.; Gray, D.K.; Hampton, S.E.; Read, J.S.; Rowley, R.J.; Schneider, P.; Lenters, J.D.; McIntyre, P.B.; Kraemer, B.M.; et al. Rapid and highly variable warming of lake surface waters around the globe. Geophys. Res. Lett. 2015, 42, 10773–10781. [Google Scholar] [CrossRef]
- Sharma, S.; Gray, D.K.; Read, J.S.; O’Reilly, C.M.; Schneider, P.; Qudrat, A.; Gries, C.; Stefanoff, S.; Hampton, S.E.; Hook, S.; et al. A global database of lake surface temperatures collected by in situ and satellite methods from 1985–2009. Sci. Data 2015, 2, 150008. [Google Scholar] [CrossRef]
- NOAA. Great Lakes water level observations. National Oceanic and Atmospheric Administration; NOAA: Washington, DC, USA, 2021. [Google Scholar]
- Graf, R.A. Multifaceted analysis of the relationship between daily temperature of river water and air. Acta Geophys. 2019, 67, 1–16. [Google Scholar] [CrossRef]
- Graf, R.; Wrzesiński, D. Relationship Between Water Temperature of Polish Rivers and Large-Scale Atmospheric Circulation. Water 2019, 11, 1690. [Google Scholar] [CrossRef]
- Benyahya, L.; Caissie, D.; St-Hilaire, A.; Ouarda, T.B.; Bobée, B. A Review of Statistical Water Temperature Models. Can. Water Resour. J. Rev. Can. Ressour. Hydriques 2007, 32, 179–192. [Google Scholar] [CrossRef]
- Watts, G.; Battarbee, R.W.; Bloomfield, J.P.; Crossman, J.; Daccache, A.; Durance, I.; Elliott, J.A.; Garner, G.; Hannaford, J.; Hannah, D.M.; et al. Climate change and water in the UK—past changes and future prospects. Prog. Phys. Geogr. 2015, 39, 6–28. [Google Scholar] [CrossRef]
- Wagner, T.; Midway, S.R.; Whittier, J.B.; DeWeber, J.T.; Paukert, C.P. Annual Changes in Seasonal River Water Temperatures in the Eastern and Western United States. Water 2017, 9, 90. [Google Scholar] [CrossRef]
- Rajesh, M.; Rehana, S. Impact of climate change on river water temperature and dissolved oxygen: Indian riverine thermal regimes. Sci. Rep. 2022, 12, 9222. [Google Scholar] [CrossRef] [PubMed]
- van Vliet, M.T.; Franssen, W.H.; Yearsley, J.R.; Ludwig, F.; Haddeland, I.; Lettenmaier, D.P.; Kabat, P. Global river discharge and water temperature under climate change. Glob. Environ. Chang. 2013, 23, 450–464, ISSN 0959-3780. [Google Scholar] [CrossRef]
- Hardenbicker, P.; Viergutz, C.; Becker, A.; Kirchesch, V.; Nilson, E.; Fischer, H. Water temperature increases in the river Rhine in response to climate change. Reg. Environ. Chang. 2017, 17, 299–308. [Google Scholar] [CrossRef]
- Estrela-Segrelles, C.; Mocholi-Paredes, C.; Pérez-Martín, M.A. Impact of Climate Change on Cold-Water Fish Species: Application in the Jucar River Basin District. In Proceedings of the 39th IAHR World Congress—From Snow to Sea, Granada, Spain, 19–24 June 2022. [Google Scholar] [CrossRef]
- Michel, A.; Schaefli, B.; Wever, N.; Zekollari, H.; Lehning, M.; Huwald, H. Future water temperature of rivers in Switzerland under climate change investigated with physics-based models. Hydrol. Earth Syst. Sci. 2022, 26, 1063–1087. [Google Scholar] [CrossRef]
- Caissie, D The thermal regime of rivers: A review. Freshw. Biol. 2006, 51, 1389–1406. [CrossRef]
- Carraro, L.; Mari, L.; Hartikainen, H.; Strepparava, N.; Wahli, T.; Jokela, J.; Gatto, M.; Rinaldo, A.; Bertuzzo, E. An epidemiological model for proliferative kidney disease in salmonid populations. Parasit. Vect. 2016, 9, 487. [Google Scholar] [CrossRef]
- Rahel Frank, J.; Keleher Christopher, J.; Anderson Jeffry, L. Potential habitat loss and population fragmentation for cold water fish in the North Platte River drainage of the Rocky Mountains: Response to climate warming. Limnol. Oceanogr. 1996, 41, 1116–1123. [Google Scholar] [CrossRef]
- Eaton John, G.; Scheller Robert, M. Effects of climate warming on fish thermal habitat in streams of the United States. Limnol. Oceanogr. 1996, 41, 1109–1115. [Google Scholar] [CrossRef]
- Estrela-Segrelles, C.; Pérez-Martín, M.A. Hazard, Exposure, Vulnerability and Risk Maps Associated with the Impact of Climate Change: Application in Júcar River Basin District. In Proceedings of the 39th IAHR World Congress—From Snow to Sea, Granada, Spain, 19–24 June 2022. [Google Scholar] [CrossRef]
- Paillex, A.; Schuwirth, N.; Lorenz, A.W.; Januschke, K.; Peter, A.; Reichert, P. Integrating and extending ecological river assessment: Concept and test with two restoration projects. Ecol. Indic. 2017, 72, 131–141. [Google Scholar] [CrossRef]
- Niedrist, G.H.; Füreder, L. Real-time warming of Alpine streams: (Re)defining invertebrates’ temperature preferences. River Res. Appl. 2021, 7, 283–293. [Google Scholar] [CrossRef]
- Eaton, J.G.; McCormick, J.H.; Goodno, B.E.; O’Brien, D.G.; Stefany, H.G.; Hondzo, M.; Scheller, R.M. A Field Information-based System for Estimating Fish Temperature Tolerances. Fisheries 1995, 20, 10–18. [Google Scholar] [CrossRef]
- Wehrly, K.E.; Wang, L.; Mitro, M. Field-Based Estimates of Thermal Tolerance Limits for Trout: Incorporating Exposure Time and Temperature Fluctuation. Trans. Am. Fish. Soc. 2007, 136, 365–374. [Google Scholar] [CrossRef]
- Heddam, S.; Kim, S.; Mehr, A.D.; Zounemat-Kermani, M.; Ptak, M.; Elbeltagi, A.; Malik, A.; Tikhamarine, Y. Bat algorithm optimised extreme learning machine (Bat-ELM): A novel approach for daily river water temperature modelling. Geogr. J. 2023, 189, 78–89. [Google Scholar] [CrossRef]
- Heddam, S.; Merabet, K.; Difi, S.; Kim, S.; Ptak, M.; Sojka, M.; Zounemat-Kermani, M.; Kisi, O. River water temperature prediction using hybrid machine learning coupled signal decomposition: EWT versus MODWT. Ecol. Inform. 2023, 78, 102376. [Google Scholar] [CrossRef]
- Piccolroaz, S.; Zhu, S.; Ladwig, R.; Carrea, L.; Oliver, S.; Piotrowski, A.P.; Ptak, M.; Shinohara, R.; Sojka, M.; Woolway, R.I.; et al. Lake Water Temperature Modeling in an Era of Climate Change: Data Sources, Models, and Future Prospects. Rev. Geophys. 2024, 62, e2023RG000816. [Google Scholar] [CrossRef]
- Sun, J.; Di Nunno, F.; Sojka, M.; Ptak, M.; Zhou, Q.; Luo, Y.; Granata, F. Long-Term Daily Water Temperatures Unveil Escalating Water Warming and Intensifying Heatwaves in the Odra River Basin, Central Europe. Geosci. Front. 2024, 15, 101916. [Google Scholar] [CrossRef]
- Ahmadi-Nedushan, B.; St-Hilaire, A.; Ouarda, T.B.; Bilodeau, L.; Robichaud, E.; Thiémonge, N.; Bobée, B. Predicting River Water Temperatures Using Stochastic Models: Case Study of the Moisie River (Québec, Canada). Hydrol. Process. 2007, 21, 21–34. [Google Scholar] [CrossRef]
- Zhu, S.; Piotrowski, A.P. River/Stream Water Temperature Forecasting Using Artificial Intelligence Models: A Systematic Review. Acta Geophys. 2020, 68, 1433–1442. [Google Scholar] [CrossRef]
- Zhu, S.; Nyarko, E.K.; Hadzima-Nyarko, M. Modelling Daily Water Temperature from Air Temperature for the Missouri River. PeerJ 2018, 6, e4894. [Google Scholar] [CrossRef] [PubMed]
- Rabi, A.; Hadzima-Nyarko, M.; Šperac, M. Modelling River Temperature from Air Temperature: Case of the River Drava (Croatia). Hydrol. Sci. J. 2015, 60, 1490–1507. [Google Scholar] [CrossRef]
- Morrill, J.C.; Bales, R.C.; Conklin, M.H. Estimating Stream Temperature from Air Temperature: Implications for Future Water Quality. J. Environ. Eng. 2005, 131, 139–146. [Google Scholar] [CrossRef]
- Moore, R.D. Stream Temperature Patterns in British Columbia, Canada, Based on Routine Spot Measurements. Can. Water Resour. J. 2006, 31, 41–56. [Google Scholar] [CrossRef]
- Smith, K. The Prediction of River Water Temperatures/Prédiction des Températures des Eaux de Rivière. Hydrol. Sci. J. 1981, 26, 19–32. [Google Scholar] [CrossRef]
- Wanders, N.; van Vliet, M.T.H.; Wada, Y.; Bierkens, M.F.P.; van Beek, L.P.H. High-Resolution Global Water Temperature Modeling. Water Resour. Res. 2019, 55, 2760–2778. [Google Scholar] [CrossRef]
- DeWeber, J.T.; Wagner, T. A Regional Neural Network Ensemble for Predicting Mean Daily River Water Temperature. J. Hydrol. 2014, 517, 187–200. [Google Scholar] [CrossRef]
- Punzet, M.; Voß, F.; Voß, A.; Kynast, E.; Bärlund, I. A Global Approach to Assess the Potential Impact of Climate Change on Stream Water Temperatures and Related In-Stream First-Order Decay Rates. J. Hydrometeorol. 2012, 13, 1052–1065. [Google Scholar] [CrossRef]
- van Vliet, M.T.H.; Ludwig, F.; Zwolsman, J.J.G.; Weedon, G.P.; Kabat, P. Global river temperatures and sensitivity to atmospheric warming and changes in river flow. Water Resour. Res. 2011, 47, W02544. [Google Scholar] [CrossRef]
- St-Hilaire, A.; Morin, G.; El-Jabi, N.; Caissie, D. Water temperature modelling in a small forested stream: Implication of forest canopy and soil temperature. Can. J. Civ. Eng. 2000, 27, 1095–1108. [Google Scholar] [CrossRef]
- Edinger, J.E.; Duttweiler, D.W.; Geyer, J.C. The Response of Water Temperatures to Meteorological Conditions. Water Resour. Res. 1968, 4, 1137–1143. [Google Scholar] [CrossRef]
- Caissie, D.; Satish, M.G.; El-Jabi, N. Predicting Water Temperatures Using a Deterministic Model: Application on Miramichi River Catchments (New Brunswick, Canada). J. Hydrol. 2007, 336, 303–315. [Google Scholar] [CrossRef]
- Kalinowska, M.B. Effect of water–air heat transfer on the spread of thermal pollution in rivers. Acta Geophys. 2019, 67, 597–619. [Google Scholar] [CrossRef]
- Dugdale, S.J.; Malcolm, I.A.; Kantola, K.; Hannah, D.M. Stream Temperature Under Contrasting Riparian Forest Cover: Understanding Thermal Dynamics and Heat Exchange Processes. Sci. Total Environ. 2018, 610, 1375–1389. [Google Scholar] [CrossRef]
- Karrasch, P.; Hunger, S. Simulation of Vegetation and Relief Induced Shadows on Rivers with Remote Sensing Data; SPIE: Bellingham, WA, USA, 2017; Volume 10428, pp. 293–305. [Google Scholar]
- Del Tánago, M.G.; Martínez-Fernández, V.; Aguiar, F.C.; Bertoldi, W.; Dufour, S.; de Jalón, D.G.; Garófano-Gómez, V.; Mandzukovski, D.; Rodríguez-González, P.M. Improving River Hydromorphological Assessment Through Better Integration of Riparian Vegetation: Scientific Evidence and Guidelines. J. Environ. Manag. 2021, 292, 112730. [Google Scholar] [CrossRef]
- Martínez-Fernández, V.; Van Oorschot, M.; De Smit, J.; González del Tánago, M.; Buijse, A.D. Modelling Feedbacks Between Geomorphological and Riparian Vegetation Responses Under Climate Change in a Mediterranean Context. Earth Surf. Process. Landf. 2018, 43, 1825–1835. [Google Scholar] [CrossRef]
- De Jalón, D.G.; Bussettini, M.; Rinaldi, M.; Grant, G.; Friberg, N.; Cowx, I.G.; Magdaleno, F.; Buijse, T. Linking Environmental Flows to Sediment Dynamics. Water Policy 2017, 19, 358–375. [Google Scholar] [CrossRef]
- Dala-Corte, R.B.; Melo, A.S.; Siqueira, T.; Bini, L.M.; Martins, R.T.; Cunico, A.M.; Pes, A.M.; Magalhães, A.L.B.; Godoy, B.S.; Leal, C.G.; et al. Thresholds of freshwater biodiversity in response to riparian vegetation loss in the Neotropical region. J. Appl. Ecol. 2020, 57, 1391–1402. [Google Scholar] [CrossRef]
- Casas-Mulet, R.; Pander, J.; Ryu, D.; Stewardson, M.J.; Geist, J. Unmanned Aerial Vehicle (UAV)-Based Thermal Infra-Red (TIR) and Optical Imagery Reveals Multi-Spatial Scale Controls of Cold-Water Areas Over a Groundwater-Dominated Riverscape. Front. Environ. Sci. 2020, 8, 64. [Google Scholar] [CrossRef]
- Keefer, M.L.; Clabough, T.S.; Jepson, M.A.; Johnson, E.L.; Peery, C.A.; Caudill, C.C. Thermal exposure of adult Chinook salmon and steelhead: Diverse behavioral strategies in a large and warming river system. PLoS ONE 2018, 13, e0204274. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Kędra, M.; Wiejaczka, Ł. Climatic and Dam-Induced Impacts on River Water Temperature: Assessment and Management Implications. Sci. Total Environ. 2018, 626, 1474–1483. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Martínez, G.; Pérez-Martín, M.A.; Estrela-Monreal, T.; Del-Amo, P. North Atlantic Oscillation as a Cause of the Hydrological Changes in the Mediterranean (Jucar River, Spain). Water Resour. Manag. 2018, 32, 2717–2734. [Google Scholar] [CrossRef]
- Henley, B.J.; Peel, M.C.; Nathan, R.; King, A.D.; Ukkola, A.M.; Karoly, D.J.; Tan, K.S. Amplification of Risks to Water Supply at 1.5 °C and 2 °C in Drying Climates: A Case Study for Melbourne, Australia. Environ. Res. Lett. 2019, 14, 084028. [Google Scholar] [CrossRef]
- MedECC. Current Situation and Risks for the Future First Mediterranean Assessment Report by Medecc (Mediterranean Experts on Climate and Environmental Change); MedECC: Marseille, France, 2020. [Google Scholar]
- Estrela-Segrelles, C.; Gómez-Martinez, G.; Pérez-Martín, M. Risk assessment of climate change impacts on Mediterranean coastal wetlands. Application in Júcar River Basin District (Spain). Sci. Total Environ. 2021, 790, 148032. [Google Scholar] [CrossRef]
- Theodoropoulos, C.; Karaouzas, I. Climate Change and the Future of Mediterranean Freshwater Macroinvertebrates: A Model-Based Assessment. Hydrobiologia 2021, 848, 5033–5050. [Google Scholar] [CrossRef]
- Pérez-Martín, M.A.; Vicent-Pastor, P.; Miñana-Albanell, C.; Estrela-Segrelles, C. Climate Change Adaptation Plan in the Júcar River Basin District, Spain. In Proceedings of the 39th IAHR World Congress—From Snow to Sea, Granada, Spain, 19–24 June 2022. [Google Scholar] [CrossRef]
- Huld, T.; Müller, R.; Gambardella, A. A New Solar Radiation Database for Estimating PV Performance in Europe and Africa. Sol. Energy 2012, 86, 1803–1815. [Google Scholar] [CrossRef]
- Pérez-Martín, M.A.; Estrela-Segrelles, C.; Miñana-Albanell, C.; Mulet-Rojas, C. Water Temperature Model for Mediterranean Rivers and Climate Change: The Júcar River Case. In Proceedings of the 39th IAHR World Congress—From Snow to Sea, Granada, Spain, 19–24 June 2022. [Google Scholar] [CrossRef]
- Webb, B.W.; Zhang, Y. Spatial and Seasonal Variability in the Components of the River Heat Budget. Hydrol. Process. 1997, 11, 79–101. [Google Scholar] [CrossRef]
- Kim, K.S.; Chapra, S.C. Temperature Model for Highly Transient Shallow Streams. J. Hydraul. Eng. 1997, 123, 30–40. [Google Scholar] [CrossRef]
- Brunt, D. Notes on Radiation in the Atmosphere. Q. J. R. Meteorol. Soc. 1932, 58, 389–420. [Google Scholar] [CrossRef]
- Swinbank, W.C. Long-Wave Radiation from Clear Skies. Q. J. R. Meteorol. Soc. 1963, 89, 339–348. [Google Scholar] [CrossRef]
- Idso, S.B.; Jackson, R.D. Thermal Radiation from the Atmosphere. J. Geophys. Res. 1969, 74, 5397–5403. [Google Scholar] [CrossRef]
- Brutsaert, W. On a Derivable Formula for Long-Wave Radiation from Clear Skies. Water Resour. Res. 1975, 11, 742–744. [Google Scholar] [CrossRef]
- Idso, S.B. A Set of Equations for Full Spectrum and 8-to 14-μm and 10.5-to 12.5-μm Thermal Radiation from Cloudless Skies. Water Resour. Res. 1981, 17, 295–304. [Google Scholar] [CrossRef]
- Bignami, F.; Marullo, S.; Santoleri, R.; Schiano, M.E. Longwave radiation budget in the Mediterranean Sea. J. Geophys. Res. Oceans 1995, 100, 2501–2514. [Google Scholar] [CrossRef]
- Munné, A.; Prat, N.; Solà, C.; Bonada, N.; Rieradevall, M. A simple field method for assessing the ecological quality of riparian habitat in rivers and streams: QBR index. Aquat. Conserv. Mar. Freshw. Ecosyst. 2003, 13, 147–163. [Google Scholar] [CrossRef]
- McCuen, R.H.; Knight, Z.; Cutter, A.G. Evaluation of the Nash–Sutcliffe Efficiency Index. J. Hydrol. Eng. 2005, 11, 597–602. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Noa-Yarasca, E.; Babbar-Sebens, M.; Jordan, C. An improved model of shade-affected stream temperature in Soil & Water Assessment Tool. Hydrol. Earth Syst. Sci. 2023, 27, 739–759. [Google Scholar] [CrossRef]
- Riahi, K.; Van Vuuren, D.P.; Kriegler, E.; Edmonds, J.; O’Neill, B.C.; Fujimori, S.; Bauer, N.; Calvin, K.; Dellink, R.; Fricko, O.; et al. The Shared Socioeconomic Pathways and Their Energy, Land Use, and Greenhouse Gas Emissions Implications: An Overview. Glob. Environ. Chang. 2017, 42, 153–168. [Google Scholar] [CrossRef]
- Masson-Delmotte, V.; Zhai, P.; Pirani, A.; Connors, S.L.; Péan, C.; Berger, S.; Caud, N.; Chen, Y.; Goldfarb, L.; Gomis, M.I.; et al. (Eds.) Climate Change 2021: The Physical Science Basis; Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Summary for Policymakers; IPCC: Geneva, Switzerland, 2021. [Google Scholar]
- Rogelj, J.; Popp, A.; Calvin, K.V.; Luderer, G.; Emmerling, J.; Gernaat, D.; Fujimori, S.; Strefler, J.; Hasegawa, T.; Marangoni, G.; et al. Scenarios Towards Limiting Global Mean Temperature Increase Below 1.5 °C. Nat. Clim. Chang. 2018, 8, 325–332. [Google Scholar] [CrossRef]
- Sedighkia, M.; Abdoli, A.; Ayyoubzadeh, S.A.; Ahmadi, A. Modelling of Thermal Habitat Loss of Brown Trout (Salmo trutta) Due to the Impact of Climate Warming. Ecohydrol. Hydrobiol. 2019, 19, 167–177. [Google Scholar] [CrossRef]
- Kalny, G.; Laaha, G.; Melcher, A.; Trimmel, H.; Weihs, P.; Rauch, H.P. The Influence of Riparian Vegetation Shading on Water Temperature During Low Flow Conditions in a Medium-Sized River. Knowl. Manag. Aquat. Ecosyst. 2017, 418, 5. [Google Scholar] [CrossRef]
- Kristensen, P.B.; Kristensen, E.A.; Riis, T.; Alnoee, A.B.; Larsen, S.E.; Verdonschot, P.F.M.; Baattrup-Pedersen, A. Riparian Forest can help mitigate climate warming effects in lowland temperate streams. Inland Waters 2014, 5, 27–38. [Google Scholar] [CrossRef]
- Bowler, D.E.; Mant, R.; Orr, H.; Hannah, D.M.; Pullin, A.S. What are the effects of wooded riparian zones on stream temperature? Environ. Evid. 2012, 1, 3. [Google Scholar] [CrossRef]
- Qiu, H.; Hamilton, S.K.; Phanikumar, M.S. Modeling the effects of vegetation on stream temperature dynamics in a large, mixed land cover watershed in the Great Lakes region. J. Hydrol. 2020, 581, 124283, ISSN 0022-1694. [Google Scholar] [CrossRef]
- Dugdale, S.J.; Malcolm, I.A.; Hannah, D.M. Understanding the effects of spatially variable riparian tree planting strategies to target water temperature reductions in rivers. J. Hydrol. 2024, 635, 131163, ISSN 0022-1694. [Google Scholar] [CrossRef]
- Yan, H.; Sun, N.; Fullerton, A.; Baerwalde, M. Greater vulnerability of snowmelt-fed river thermal regimes to a warming climate. Environ. Res. Lett. 2021, 16, 054006. [Google Scholar] [CrossRef]
- Lisi, P.J.; Schindler, D.E.; Cline, T.J.; Scheuerell, M.D.; Walsh, P.B. Watershed geomorphology and snowmelt control stream thermal sensitivity to air temperature. Geophys. Res. Lett. 2015, 42, 3380–3388. [Google Scholar] [CrossRef]





| Month | Water Temperature (°C) | Air Temperature (°C) | Wind Speed (m/s) | Relative Humidity (%) | Air Pressure (Hpa) |
|---|---|---|---|---|---|
| January | 6.4 | 9.7 | 1.35 | 73 | 914.9 |
| February | 7.8 | 11.3 | 1.24 | 67 | 916.3 |
| March | 10.5 | 16.0 | 2.04 | 60 | 907.8 |
| April | 12.8 | 17.5 | 1.92 | 60 | 906.8 |
| May | 15.4 | 18.8 | 1.91 | 56 | 909.5 |
| June | 18.9 | 23.4 | 2.15 | 48 | 908 |
| July | 21.7 | 28.1 | 2.04 | 41 | 910.4 |
| August | 21.5 | 27.0 | 1.81 | 45 | 909.0 |
| September | 19.3 | 25.2 | 1.70 | 55 | 910.8 |
| October | 14.7 | 17.8 | 1.62 | 67 | 909.9 |
| November | 10.3 | 13.2 | 1.42 | 73 | 912.7 |
| December | 8.0 | 12.9 | 1.64 | 76 | 906.2 |
| Shadow 62% | COMPONENT | GLOBAL | ||
|---|---|---|---|---|
| Short-wave Radiation | 2.82 | |||
| Rs albedo | −0.14 | |||
| Ks | 2.68 | |||
| Qcon Convective heat (air-water) | 0.47 | |||
| TOTAL INPUT | 3.15 | |||
| Lwa Long-wave Water to Air Emission | −9.04 | |||
| Law Long-wave Air to Water Emission | 7.82 | |||
| Law albedo | −0.23 | |||
| LW Balance (Ls + Lb) | −1.45 | |||
| Qevap evaporation heat | −1.69 | |||
| TOTAL OUTPUT | −3.14 |
| Scheme 62. | COMPONENT | GLOBAL | ||
|---|---|---|---|---|
| Short-wave radiation | 2.82 | |||
| Rs albedo | −0.14 | |||
| Ks | 2.68 (+0.00) | |||
| Qcon convective heat (air–water) | 0.58 (+0.11) | |||
| TOTAL INPUT | 3.26 (+0.11) | |||
| Lwa Long-wave water to air emission | −9.43 | |||
| Law long-wave air to water emission | 8.46 | |||
| Law albedo | −0.25 | |||
| LW balance (Ls + Lb) | −1.23 (+0.22) | |||
| Qevap evaporation heat | −2.04 (−0.35) | |||
| TOTAL OUTPUT | −3.26 (−0.11) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miñana-Albanell, C.; Ryu, D.; Pérez-Martín, M.Á. Water Temperature Model to Assess Impact of Riparian Vegetation on Jucar River and Spain. Water 2024, 16, 3121. https://doi.org/10.3390/w16213121
Miñana-Albanell C, Ryu D, Pérez-Martín MÁ. Water Temperature Model to Assess Impact of Riparian Vegetation on Jucar River and Spain. Water. 2024; 16(21):3121. https://doi.org/10.3390/w16213121
Chicago/Turabian StyleMiñana-Albanell, Carlos, Dongryeol Ryu, and Miguel Ángel Pérez-Martín. 2024. "Water Temperature Model to Assess Impact of Riparian Vegetation on Jucar River and Spain" Water 16, no. 21: 3121. https://doi.org/10.3390/w16213121
APA StyleMiñana-Albanell, C., Ryu, D., & Pérez-Martín, M. Á. (2024). Water Temperature Model to Assess Impact of Riparian Vegetation on Jucar River and Spain. Water, 16(21), 3121. https://doi.org/10.3390/w16213121








