Utilizing a Transparent Model of a Semi-Direct Acting Water Solenoid Valve to Visualize Diaphragm Displacement and Apply Resulting Data for CFD Analysis
Abstract
:1. Introduction
2. Working Principle of the Valve and Problem Statement
3. Experimental Setup and Procedure
4. Numerical Simulation
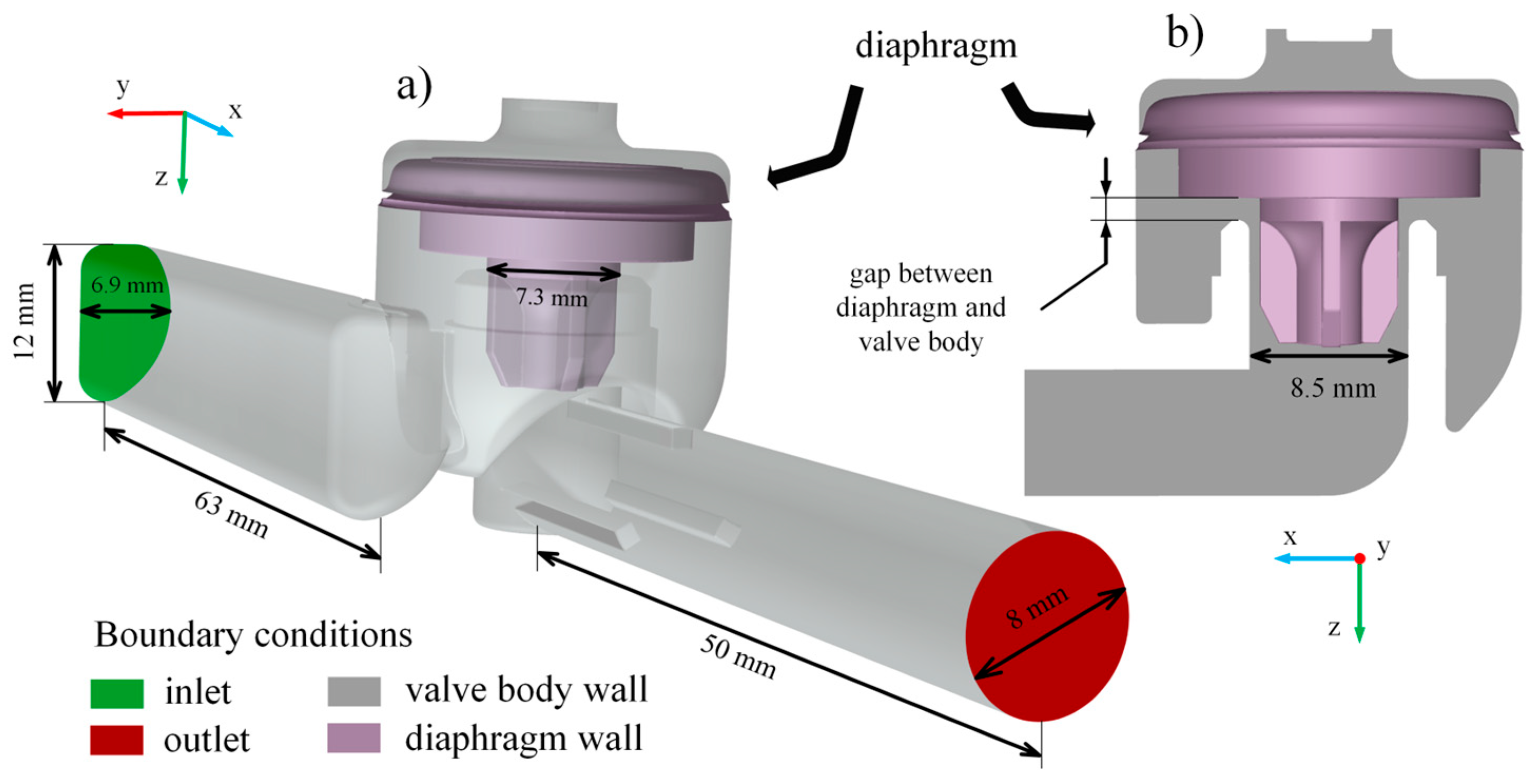
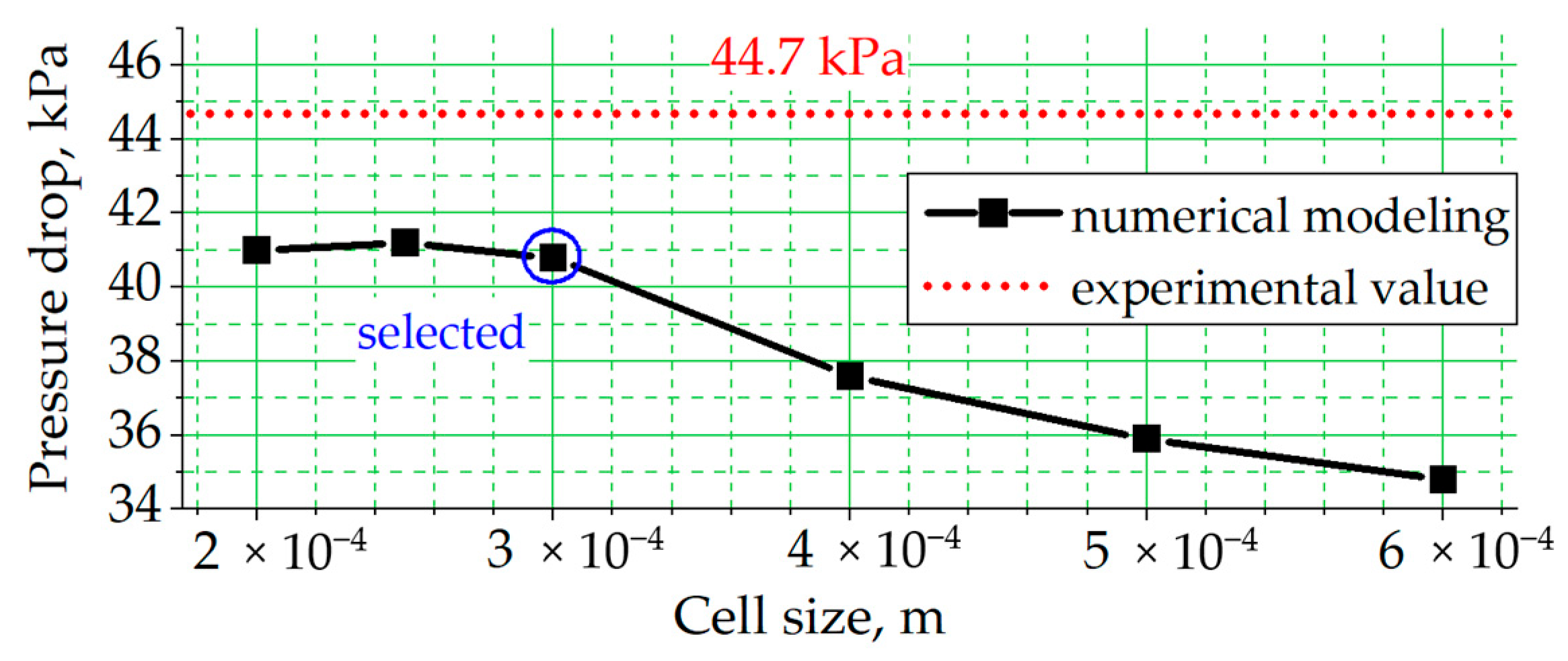
4.1. Computation Domain Boundary Conditions and Mesh
4.2. CFD Governing Equations
4.3. Numerical Methods
5. Results and Discussions
5.1. Experimental Results of Diaphragm Displacement
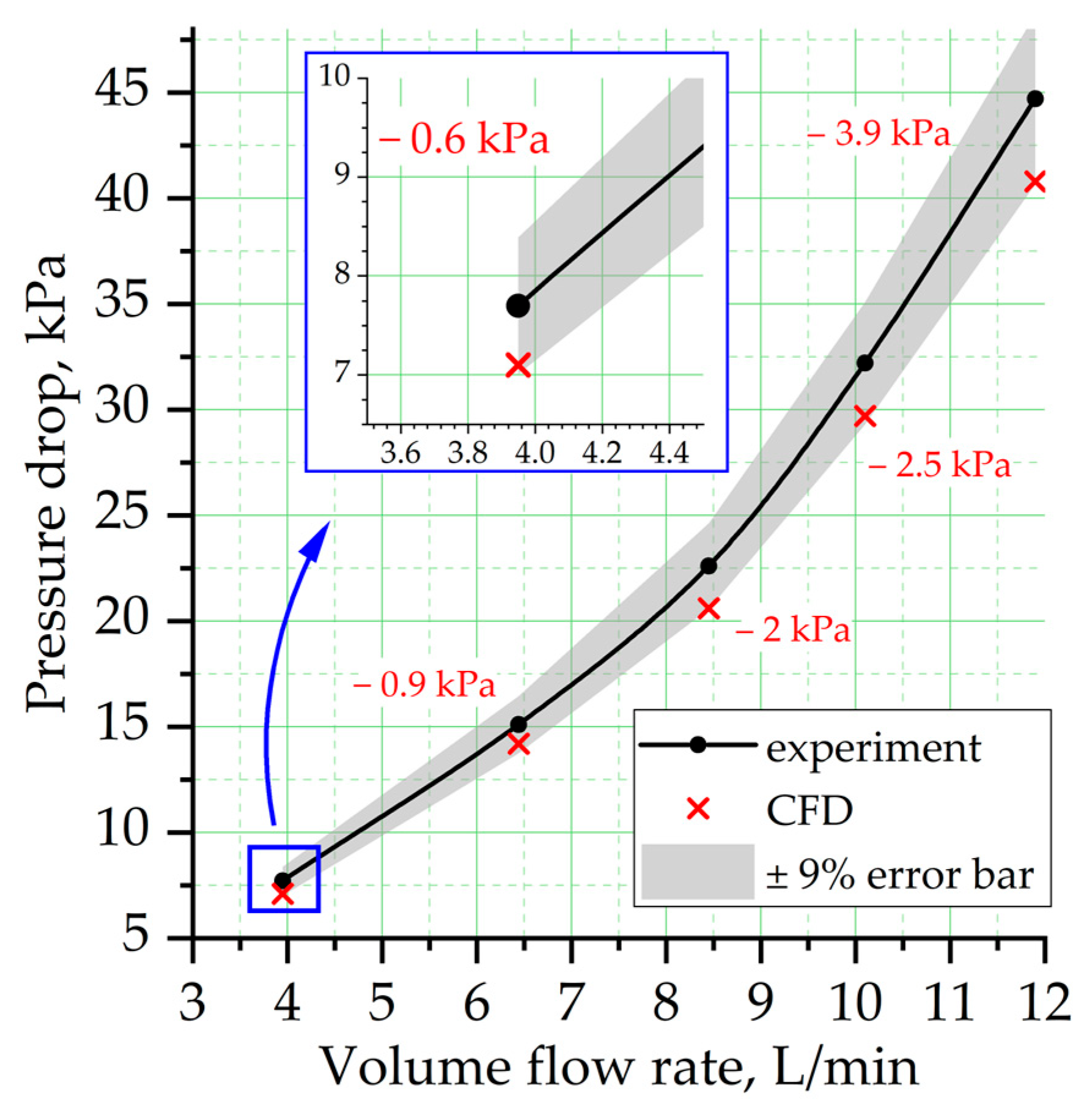
5.2. Pressure Drop Comparison and CFD Model Validation
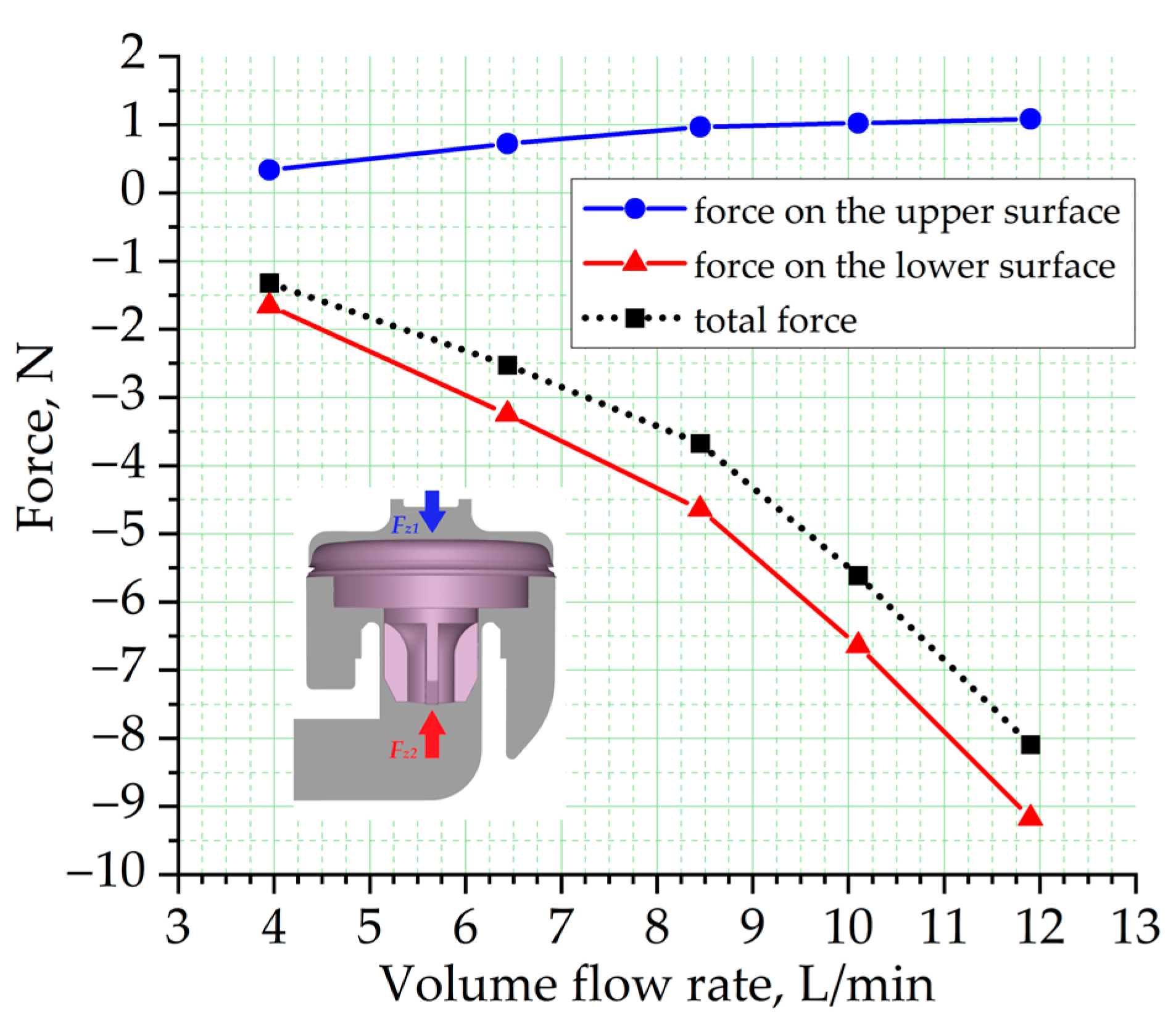
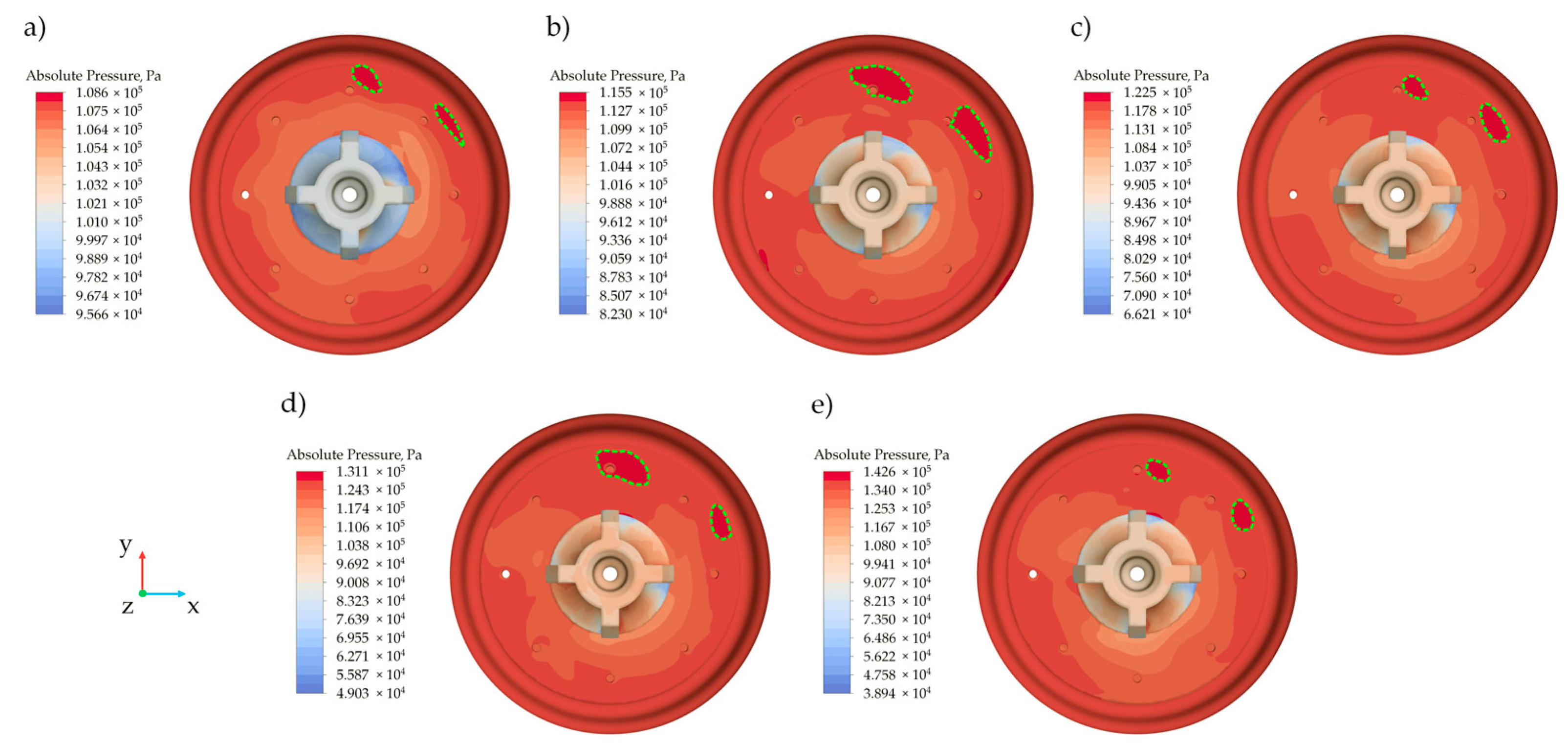
5.3. Force Action and Pressure Distribution on the Diaphragm
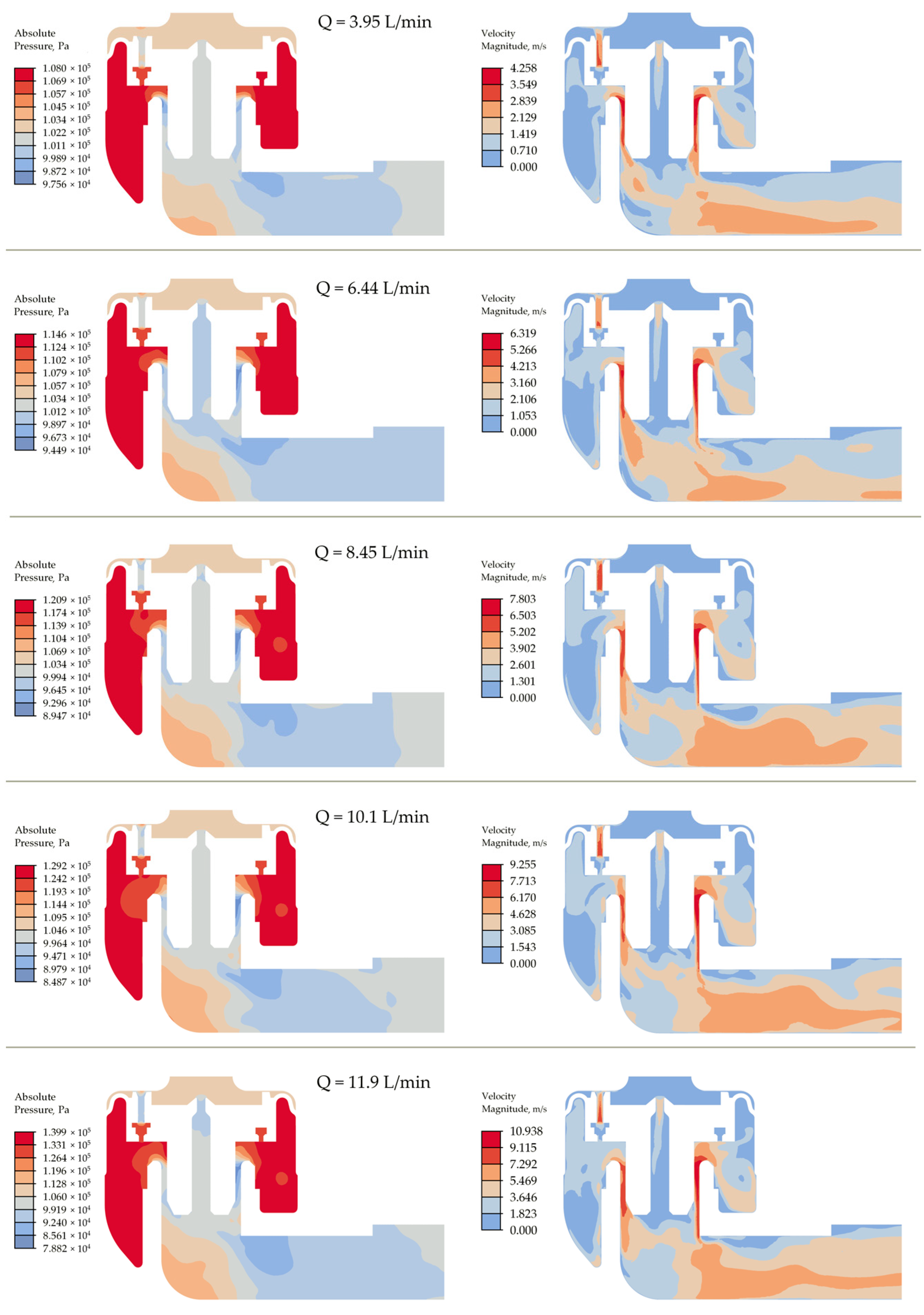
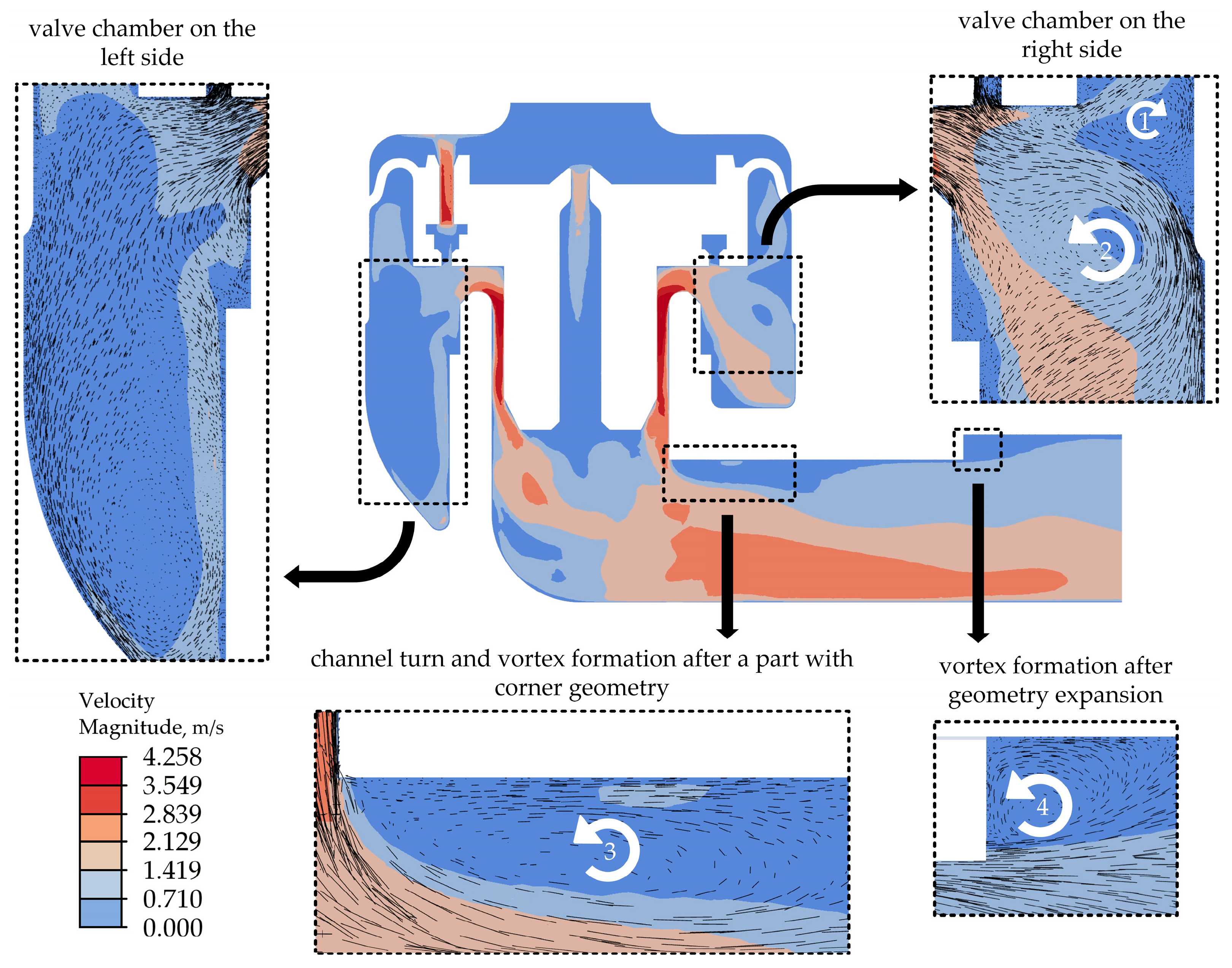
5.4. Pressure and Velocity Distribution Inside the Valve
6. Conclusions
- The analysis of diaphragm displacement as a function of volumetric flow rate in the range of 3.95–10.1 L/min showed linear behavior, confirmed by the regression equation with a high coefficient of determination.
- At a flow rate of 10.1 L/min or higher, the diaphragm reaches its maximum displacement and loses flow control accuracy, nearly touching the valve body due to a design limitation (with a maximum gap of 2.2 mm between the diaphragm surface and the valve body).
- The experiment with the transparent model enabled accurate measurement of the diaphragm displacement, forming the basis for CFD analysis. Validation showed good agreement between the calculated and experimental pressure drop data.
- For all considered cases, the force acting on the upper surface of the diaphragm is insignificant (compared to the force on the lower surface) and changes little with increasing flow rate, reaching a maximum of 1.082 N at 11.9 L/min. At 8.45 L/min, a critical point is observed, beyond which the force on the upper surface of the diaphragm does not significantly increase with further flow rate increases due to the diaphragm reaching its maximum displacement, limited by design constraints.
- The pressure analysis on the lower surface of the diaphragm shows an uneven distribution caused by the water flow from the inlet pipe, with clearly localized areas of increased pressure. Although these zones do not affect the diaphragm’s operational stability, they indicate the need for inlet pipe optimization.
- The pressure and velocity distribution analysis in the sectional view through the diaphragm and outlet channel axes shows the higher flow capacity on the right side of the diaphragm, indicating a flow imbalance. Vortex flows are also observed in the chamber on the right side of the diaphragm. To resolve this issue, designing the valve chamber symmetrically on either side of the diaphragm is recommended.
- The analysis of the outlet channel geometry reveals that the corner protrusions on the inner wall at the channel bend and the abrupt expansion in the channel cause vortex formation and pressure losses, negatively affecting the valve efficiency. To resolve these issues, refining the channel geometry by incorporating smooth transitions and curved forms is recommended.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dickenson, T.C. Valves, Piping and Pipelines Handbook, 3rd ed.; Elsevier Science Ltd.: New York, NY, USA, 1999; ISBN 978-1-85617-252-3. [Google Scholar]
- Nesbitt, B. Handbook of Valves and Actuators: Valves Manual International; Elsevier: Amsterdam, The Netherlands, 2011; ISBN 978-0-08-054928-6. [Google Scholar]
- Berladir, K.; Hatala, M.; Hovorun, T.; Pavlenko, I.; Ivanov, V.; Botko, F.; Gusak, O. Impact of Nitrocarburizing on Hardening of Reciprocating Compressor’s Valves. Coatings 2022, 12, 574. [Google Scholar] [CrossRef]
- Rabie, M.G. Fluid Power Engineering, 2nd ed.; McGraw Hill: New York, NY, USA, 2023; ISBN 978-1-265-51547-8. [Google Scholar]
- Hlubek, N.; Baumann, M.; Heinze, S.; Ostermaier, F. Using Machine Learning for Diaphragm Prediction in Solenoid Valves. In Proceedings of the 2022 IEEE 27th International Conference on Emerging Technologies and Factory Automation (ETFA), Stuttgart, Germany, 6–9 September 2022; pp. 1–4. [Google Scholar]
- Więcławski, K.; Figlus, T.; Mączak, J.; Szczurowski, K. Method of Fuel Injector Diagnosis Based on Analysis of Current Quantities. Sensors 2022, 22, 6735. [Google Scholar] [CrossRef] [PubMed]
- Duan, Z.; Jia, Y.; Ren, X.; Jiang, H.; Lv, Y.; Song, H.; Chen, H.; Zhai, H. Analysis of Fluid-Structure Interaction in Diaphragm Plug Valves for Filling Electrolyte in Lithium-Ion Battery Cells. Flow Meas. Instrum. 2024, 98, 102632. [Google Scholar] [CrossRef]
- Ye, P.; Zhang, C. Flow Field Analysis and Flow Prediction of Pressure Reducing Valves in Power-Law Media. Flow Meas. Instrum. 2024, 99, 102657. [Google Scholar] [CrossRef]
- Demir, U.; Coskun, G.; Soyhan, H.S.; Turkcan, A.; Alptekin, E.; Canakci, M. Effects of Variable Valve Timing on the Air Flow Parameters in an Electromechanical Valve Mechanism—A Cfd Study. Fuel 2022, 308, 121956. [Google Scholar] [CrossRef]
- Han, J.; Xie, Y.; Wang, Y.; Wang, Q.; Zhang, Y.; Ju, J. Research on Dynamicflow Rate Self-Sensing in Control Valves. Prog. Nucl. Energy 2024, 176, 105377. [Google Scholar] [CrossRef]
- Cao, L.; Liu, S.; Hu, P.; Si, H. The Influence of Governing Valve Opening on the Erosion Characteristics of Solid Particle in Steam Turbine. Eng. Fail. Anal. 2020, 118, 104929. [Google Scholar] [CrossRef]
- Wen, Q.; Liu, Y.; Chen, Z.; Wang, W. Numerical Simulation and Experimental Validation of Flow Characteristics for a Butterfly Check Valve in Small Modular Reactor. Nucl. Eng. Des. 2022, 391, 111732. [Google Scholar] [CrossRef]
- Xie, C.; Su, H.; Yang, J.; He, Z. Design and Analysis of Combined Valve Spool with Linear Flow Coefficient. J. Eng. 2022, 2022, 6006810. [Google Scholar] [CrossRef]
- Qu, Q.; Wang, L.; Chen, H.; Dai, N.; Jia, P.; Xu, D.; Li, L. Study on Flow Characteristics of the Cryogenic Throttle Valve for Superfluid Helium System. Cryogenics 2024, 138, 103797. [Google Scholar] [CrossRef]
- Ledvoň, M.; Hružík, L.; Bureček, A.; Polášek, T.; Dýrr, F.; Kolář, D. Experimental and Numerical Analysis of Flow Force Acting on the Spool of Proportional Directional Valve. Processes 2023, 11, 3415. [Google Scholar] [CrossRef]
- Li, Q.; Zong, C.; Liu, F.; Zhang, A.; Xue, T.; Yu, X.; Song, X. Numerical and Experimental Analysis of Fluid Force for Nuclear Valve. Int. J. Mech. Sci. 2023, 241, 107939. [Google Scholar] [CrossRef]
- Filo, G.; Lisowski, E.; Rajda, J. Pressure Loss Reduction in an Innovative Directional Poppet Control Valve. Energies 2020, 13, 3149. [Google Scholar] [CrossRef]
- Filo, G.; Lisowski, E.; Rajda, J. Design and Flow Analysis of an Adjustable Check Valve by Means of CFD Method. Energies 2021, 14, 2237. [Google Scholar] [CrossRef]
- Shu, Z.; Liang, W.; Qin, B.; Lei, G.; Wang, T.; Huang, L.; Che, B.; Zheng, X.; Qian, H. Transient Flow Dynamics Behaviors during Quick Shut-off of Ball Valves in Liquid Hydrogen Pipelines and Storage Systems. J. Energy Storage 2023, 73, 109049. [Google Scholar] [CrossRef]
- Gao, H.; Mo, Y.; Wu, F.; Wang, J.; Gong, S. Impact of Elastic Diaphragm Hardness and Structural Parameters on the Hydraulic Performance of Automatic Flushing Valve. Water 2023, 15, 287. [Google Scholar] [CrossRef]
- Shamsi, A.; Mazloum, J. Numerical Study of a Membrane-Type Micro Check-Valve for Microfluidic Applications. Microsyst. Technol. 2020, 26, 367–376. [Google Scholar] [CrossRef]
- Lin, Z.; Li, X.; Jin, Z.; Qian, J. Fluid-Structure Interaction Analysis on Membrane Behavior of a Microfluidic Passive Valve. Membranes 2020, 10, 300. [Google Scholar] [CrossRef]
- Wu, W.; Guo, T.; Peng, C.; Li, X.; Li, X.; Zhang, Z.; Xu, L.; He, Z. FSI Simulation of the Suction Valve on the Piston for Reciprocating Compressors. Int. J. Refrig. 2022, 137, 14–21. [Google Scholar] [CrossRef]
- Domagala, M.; Fabis-Domagala, J. A Review of the CFD Method in the Modeling of Flow Forces. Energies 2023, 16, 6059. [Google Scholar] [CrossRef]
- Lin, Z.; Hou, C.; Zhang, L.; Guan, A.; Jin, Z.; Qian, J. Fluid-Structure Interaction Analysis on Vibration Characteristics of Sleeve Control Valve. Ann. Nucl. Energy 2023, 181, 109579. [Google Scholar] [CrossRef]
- Xie, J.; Zeng, W.; Pan, X.; Chen, J.; Ye, J. FSI Investigation on the Discharge Valve Lift in a R32 Rotary Compressor and Its Verification. Case Stud. Therm. Eng. 2024, 61, 105108. [Google Scholar] [CrossRef]
- Olivetti, M.; Monterosso, F.G.; Marinaro, G.; Frosina, E.; Mazzei, P. Valve Geometry and Flow Optimization through an Automated DOE Approach. Fluids 2020, 5, 17. [Google Scholar] [CrossRef]
- Rulli, F.; Barbato, A.; Fontanesi, S.; d’Adamo, A. Large Eddy Simulation Analysis of the Turbulent Flow in an Optically Accessible Internal Combustion Engine Using the Overset Mesh Technique. Int. J. Engine Res. 2021, 22, 1440–1456. [Google Scholar] [CrossRef]
- Bornoff, J.; Gill, H.S.; Najar, A.; Perkins, I.L.; Cookson, A.N.; Fraser, K.H. Overset Meshing in Combination with Novel Blended Weak-Strong Fluid-Structure Interactions for Simulations of a Translating Valve in Series with a Second Valve. Comput. Methods Biomech. Biomed. Eng. 2024, 27, 736–750. [Google Scholar] [CrossRef]
- Kim, N.-S.; Jeong, Y.-H. An Investigation of Pressure Build-up Effects Due to Check Valve’s Closing Characteristics Using Dynamic Mesh Techniques of CFD. Ann. Nucl. Energy 2021, 152, 107996. [Google Scholar] [CrossRef]
- Neyestanaki, M.K.; Dunca, G.; Jonsson, P.; Cervantes, M.J. A Comparison of Different Methods for Modelling Water Hammer Valve Closure with CFD. Water 2023, 15, 1510. [Google Scholar] [CrossRef]
- Yao, H.; Ye, Q.; Wang, C.; Yuan, P. CFD Dynamic Mesh-Based Simulation and Performance Investigation of Combined Guided Float Valve Tray. Chem. Eng. Process. -Process Intensif. 2023, 193, 109523. [Google Scholar] [CrossRef]
- Rogovyi, A.; Korohodskyi, V.; Medvediev, Y. Influence of Bingham Fluid Viscosity on Energy Performances of a Vortex Chamber Pump. Energy 2021, 218, 119432. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, H.; Liu, H.; Ding, X.; Zhang, W. Geotechnical Properties of 3D-Printed Transparent Granular Soil. Acta Geotech. 2021, 16, 1789–1800. [Google Scholar] [CrossRef]
- Nilsson, D.P.G.; Holmgren, M.; Holmlund, P.; Wåhlin, A.; Eklund, A.; Dahlberg, T.; Wiklund, K.; Andersson, M. Patient-Specific Brain Arteries Molded as a Flexible Phantom Model Using 3D Printed Water-Soluble Resin. Sci. Rep. 2022, 12, 10172. [Google Scholar] [CrossRef] [PubMed]
- Ju, Y.; Gong, W.; Zheng, J. Effects of Pore Topology on Immiscible Fluid Displacement: Pore-Scale Lattice Boltzmann Modelling and Experiments Using Transparent 3D Printed Models. Int. J. Multiph. Flow 2022, 152, 104085. [Google Scholar] [CrossRef]
- 60335-1:2010; Household and similar electrical appliances-Safety-Part 1: General requirements. International Electrotechnical Commission: Geneva, Switzerland, 2010.
- GB 14536.9-2008; Automatic electrical controls for household and similar use - Particular requirements for electrically operated water valves, including mechanical requirements. China Standard Publishing House: Beijing, China, 2008.
- QB/T 4274-2011; Technical conditions for inlet valve of washing machine. China Standard Publishing House: Beijing, China, 2011.
- QB/T 1291-1991; Water inletting electromagnetic valves intended to be used in automatic washing machines. China Standard Publishing House: Beijing, China, 1991.
- Zhu, G.; Dong, S.M. Analysis on the Performance Improvement of Reciprocating Pump with Variable Stiffness Valve Using CFD. J. Appl. Fluid Mech. 2020, 13, 387–400. [Google Scholar] [CrossRef]
- Wu, W.; Qiu, B.; Tian, G.; Liao, X.; Wang, T. CFD-Based Cavitation Research and Structure Optimization of Relief Valve for Noise Reduction. IEEE Access 2022, 10, 66356–66373. [Google Scholar] [CrossRef]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 2018; ISBN 978-1-315-27513-0. [Google Scholar]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2002; ISBN 978-3-642-56026-2. [Google Scholar]
- LeVeque, R.J. Finite Volume Methods for Hyperbolic Problems; Cambridge Texts in Applied Mathematics; Cambridge University Press: Cambridge, UK, 2002; ISBN 978-0-521-00924-9. [Google Scholar]
- Smith, G.D. Numerical Solution of Partial Differential Equations: Finite Difference Methods, 3rd ed.; Clarendon Press: Oxford, UK, 1986; ISBN 978-0-19-859650-9. [Google Scholar]


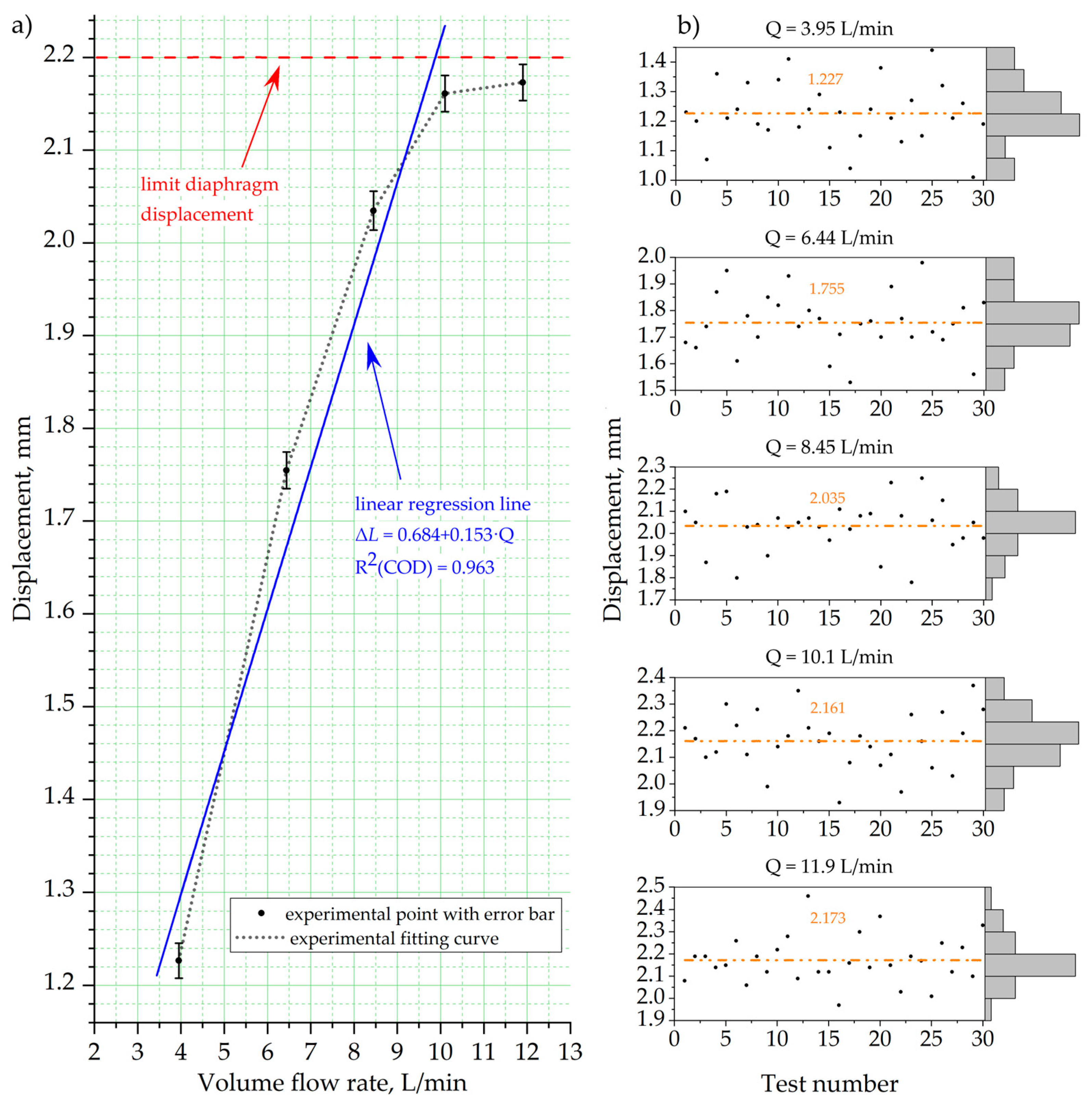
| Flow Rate Q, L/min | Pressure Drop ΔP (exp), kPa | Diaphragm Displacement ΔL, mm | SEM of Diaphragm Displacement |
|---|---|---|---|
| 3.95 | 7.7 | 1.227 | 0.0189 |
| 6.44 | 15.1 | 1.755 | 0.0199 |
| 8.45 | 22.6 | 2.035 | 0.0209 |
| 10.1 | 32.2 | 2.161 | 0.0195 |
| 11.9 | 44.7 | 2.173 | 0.0196 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brazhenko, V.; Cai, J.-C.; Fang, Y. Utilizing a Transparent Model of a Semi-Direct Acting Water Solenoid Valve to Visualize Diaphragm Displacement and Apply Resulting Data for CFD Analysis. Water 2024, 16, 3385. https://doi.org/10.3390/w16233385
Brazhenko V, Cai J-C, Fang Y. Utilizing a Transparent Model of a Semi-Direct Acting Water Solenoid Valve to Visualize Diaphragm Displacement and Apply Resulting Data for CFD Analysis. Water. 2024; 16(23):3385. https://doi.org/10.3390/w16233385
Chicago/Turabian StyleBrazhenko, Volodymyr, Jian-Cheng Cai, and Yuping Fang. 2024. "Utilizing a Transparent Model of a Semi-Direct Acting Water Solenoid Valve to Visualize Diaphragm Displacement and Apply Resulting Data for CFD Analysis" Water 16, no. 23: 3385. https://doi.org/10.3390/w16233385
APA StyleBrazhenko, V., Cai, J.-C., & Fang, Y. (2024). Utilizing a Transparent Model of a Semi-Direct Acting Water Solenoid Valve to Visualize Diaphragm Displacement and Apply Resulting Data for CFD Analysis. Water, 16(23), 3385. https://doi.org/10.3390/w16233385






