Space-Time Variability of Maximum Daily Rainfall in Piura River Basin in Peru Related to El Niño Occurrence
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.2.1. Climatic Indices
2.2.2. Hydrometeorological Data
2.2.3. High-Resolution Gridded Rainfall Dataset—PISCO
2.2.4. CMIP6 GCM
2.3. El Niño Events Determination and Qualification
2.4. Spatial Variability of Maximum Daily Rainfall
2.5. Temporal Variability of Maximum Daily Rainfall
2.6. GCMs Downscaling and Performance Metrics
3. Results
3.1. El Niño Events in Piura Region
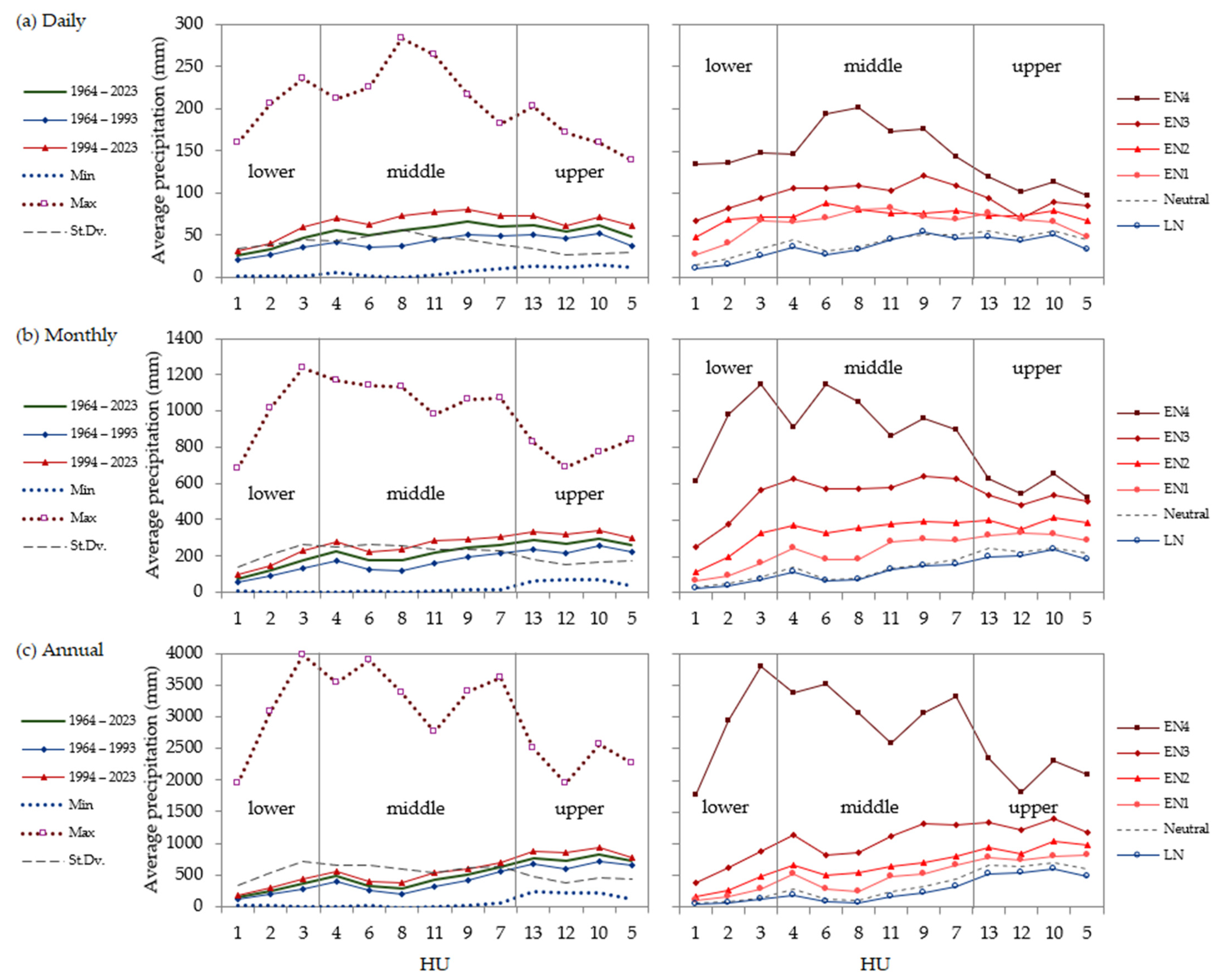
3.2. Temporal Variability
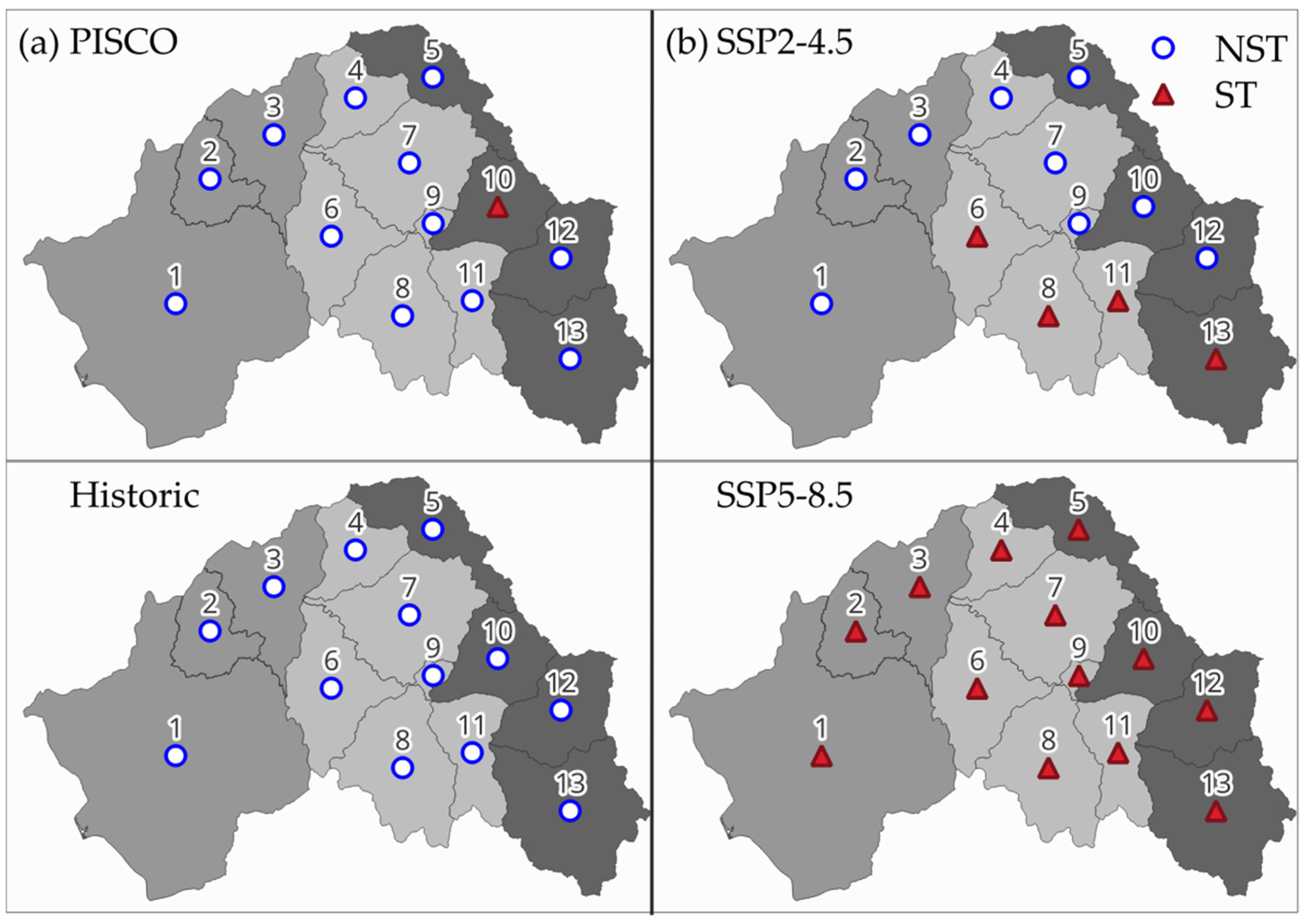
3.3. Spatial Variability
4. Discussion
4.1. Impact of the Recurrence of El Niño
4.2. Change in Spatial Distribution Patterns of Rainfall in the Region
4.3. Projections of General Circulation Models (GCMs)
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- McPhaden, M.J.; Zebiak, S.E.; Glantz, M.H. ENSO as an Integrating Concept in Earth Science. Science 2006, 314, 1740–1745. [Google Scholar] [CrossRef]
- Cai, W.; Santoso, A.; Collins, M.; Dewitte, B.; Karamperidou, C.; Kug, J.-S.; Lengaigne, M.; McPhaden, M.J.; Stuecker, M.F.; Taschetto, A.S.; et al. Changing El Niño–Southern Oscillation in a Warming Climate. Nat. Rev. Earth Environ. 2021, 2, 628–644. [Google Scholar] [CrossRef]
- McPhaden, M.J.; Santoso, A.; Cai, W. (Eds.) El Niño Southern Oscillation in a Changing Climate, 1st ed.; Geophysical Monograph Series; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Takahashi, K. Fenómeno El Niño: “Global” vs “Costero”. In Boletín Técnico: Generación de Información y Monitoreo del Fenómeno El Niño, Instituto Geofísico del Perú; Instituto Geofísico del Perú: Lima, Peru, 2017; Volume 4, pp. 4–7. [Google Scholar]
- Capotondi, A.; Wittenberg, A.T.; Kug, J.-S.; Takahashi, K.; McPhaden, M.J. ENSO Diversity. In El Niño Southern Oscillation in a Changing Climate; Geophysical Monograph Series; Wiley: Hoboken, NJ, USA, 2020; pp. 65–86. [Google Scholar] [CrossRef]
- Capotondi, A.; Sardeshmukh, P.D. Is El Niño Really Changing? Geophys. Res. Lett. 2017, 44, 8548–8556. [Google Scholar] [CrossRef]
- Quinn, W.H.; Neal, V.T.; Antunez De Mayolo, S.E. El Niño Occurrences over the Past Four and a Half Centuries. J. Geophys. Res. 1987, 92, 14449. [Google Scholar] [CrossRef]
- Deser, C.; Wallace, J.M. El Niño Events and Their Relation to the Southern Oscillation: 1925–1986. J. Geophys. Res. Ocean. 1987, 92, 14189–14196. [Google Scholar] [CrossRef]
- Takahashi, K. Física Del Fenómeno El Niño “Costero”. In Generación de Información y Monitoreo del Fenómeno El Niño; Instituto Geofísico del Perú: Lima, Peru, 2017; p. 16. [Google Scholar]
- Sanabria, J.; Bourrel, L.; Dewitte, B.; Frappart, F.; Rau, P.; Solis, O.; Labat, D. Rainfall along the Coast of Peru during Strong El Niño Events. Int. J. Climatol. 2018, 38, 1737–1747. [Google Scholar] [CrossRef]
- Almazroui, M.; Islam, M.N.; Saeed, F.; Saeed, S.; Ismail, M.; Ehsan, M.A.; Diallo, I.; O’Brien, E.; Ashfaq, M.; Martínez-Castro, D.; et al. Projected Changes in Temperature and Precipitation Over the United States, Central America, and the Caribbean in CMIP6 GCMs. Earth Syst. Environ. 2021, 5, 1–24. [Google Scholar] [CrossRef]
- Ashfaq, M.; Ghosh, S.; Kao, S.; Bowling, L.C.; Mote, P.; Touma, D.; Rauscher, S.A.; Diffenbaugh, N.S. Near-term Acceleration of Hydroclimatic Change in the Western U.S. JGR Atmos. 2013, 118, 10676–10693. [Google Scholar] [CrossRef]
- Batibeniz, F.; Ashfaq, M.; Diffenbaugh, N.S.; Key, K.; Evans, K.J.; Turuncoglu, U.U.; Önol, B. Doubling of U.S. Population Exposure to Climate Extremes by 2050. Earth’s Future 2020, 8, e2019EF001421. [Google Scholar] [CrossRef]
- Rastogi, D.; Touma, D.; Evans, K.J.; Ashfaq, M. Shift Toward Intense and Widespread Precipitation Events Over the United States by Mid-21st Century. Geophys. Res. Lett. 2020, 47, e2020GL089899. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An Overview of CMIP5 and the Experiment Design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) Experimental Design and Organization. Geosci. Model. Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- WCRP. CMIP Phase 6 (CMIP6)-Coupled Model Intercomparison Project. Available online: https://wcrp-cmip.org/cmip6/ (accessed on 21 June 2024).
- De Reparaz, G. Los Ríos de la Zona Árida Peruana; Universidad de Piura: Piura, Peru; ICC: Barcelona, Spain, 2013. [Google Scholar]
- Autoridad Nacional del Agua. Delimitación y Codificación de Unidades Hidrográficas del Perú; Memoria descriptiva; Autoridad Nacional del Agua: Lima, Perú, 2012; p. 104.
- Autoridad Nacional del Agua. Plan de Gestión de los Recursos Hídricos de la cuenca Chira-Piura; Autoridad Nacional del Agua: Lima, Perú, 2015.
- Woodman, R.; Takahashi, K. ¿Por qué no llueve en la costa del Perú (salvo durante El Niño)? Boletín Técnico 2014, 1, 4–7. [Google Scholar]
- Gobierno Regional de Piura. La. Zonificación Ecológica Económica de La. Región Piura; Gobierno Regional de Piura: Lima, Perú, 2012.
- Batjes, N.H.; Calisto, L.; De Sousa, L.M. Providing Quality-Assessed and Standardised Soil Data to Support Global Mapping and Modelling (WoSIS Snapshot 2023). Earth Syst. Sci. Data 2024, 16, 4735–4765. [Google Scholar] [CrossRef]
- Trenberth, K.E. Signal versus Noise in the Southern Oscillation. Mon. Weather Rev. 1984, 112, 326–332. [Google Scholar] [CrossRef]
- CPC NOAA. Climate Prediction Center-Monitoring & Data: Current Monthly Atmospheric and Sea Surface Temperatures Index Values. Available online: https://www.cpc.ncep.noaa.gov/data/indices/ (accessed on 25 March 2023).
- Trenberth, K.E. The Definition of El Niño. Bull. Am. Meteorol. Soc. 1997, 78, 2771–2778. [Google Scholar] [CrossRef]
- Huang, B.; Thorne, P.W.; Banzon, V.F.; Boyer, T.; Chepurin, G.; Lawrimore, J.H.; Menne, M.J.; Smith, T.M.; Vose, R.S.; Zhang, H.-M. Extended Reconstructed Sea Surface Temperature, Version 5 (ERSSTv5): Upgrades, Validations, and Intercomparisons. J. Clim. 2017, 30, 8179–8205. [Google Scholar] [CrossRef]
- IGP. Datos ICEN. Available online: http://met.igp.gob.pe/datos/icen.txt (accessed on 15 April 2023).
- ENFEN. Definición Operacional de los Eventos El Niño y La Niña y sus Magnitudes en la Costa del Perú. Available online: https://enfen.imarpe.gob.pe/download/nota-tecnica-enfen-abril-2012-definicion-operacional-de-los-eventos-el-nino-y-la-nina-y-sus-magnitudes-en-la-costa-del-peru/?wpdmdl=770&refresh=628d2f51895cb1653419857 (accessed on 24 May 2022).
- Quispe, J.; Vásquez, L. Índice “LABCOS” para la caracterización de eventos El Niño y La Niña frente a la costa del Perú, 1975–2015. Boletín Trimest. Ocean. 2015, 1, 6. [Google Scholar]
- Quispe, C.; Tam, J.; Demarcq, H.; Romero, C.; Espinoza-Morriberon, D.; Chamorro, A.; Ramos, J.; Oliveros-Ramos, R. El Índice Térmico Costero Peruano (ITCP). Boletín Trimest. Ocean. 2016, 2, 7–11. [Google Scholar] [CrossRef]
- Senamhi. Datos Hidrometeorológicos a Nivel Nacional. Senamhi.gob.pe. Available online: https://www.senamhi.gob.pe/?p=estaciones (accessed on 16 April 2023).
- Aybar, C.; Fernández, C.; Huerta, A.; Lavado, W.; Vega, F.; Felipe-Obando, O. Construction of a High-Resolution Gridded Rainfall Dataset for Peru from 1981 to the Present Day. Hydrol. Sci. J. 2020, 65, 770–785. [Google Scholar] [CrossRef]
- ANA. ANDREA. Available online: https://snirh.ana.gob.pe/ANDREA/Inicio.aspx (accessed on 7 December 2023).
- Shrestha, M. Linear Scaling Bias Correction (V.1.0) Microsoft Excel File. 2015. Available online: https://www.researchgate.net/publication/289290337_Linear_Scaling_bias_correction_V10_Microsoft_Excel_file (accessed on 7 December 2023).
- Bağçaci, S.Ç.; Yucel, I.; Duzenli, E.; Yilmaz, M.T. Intercomparison of the Expected Change in the Temperature and the Precipitation Retrieved from CMIP6 and CMIP5 Climate Projections: A Mediterranean Hot Spot Case, Turkey. Atmos. Res. 2021, 256, 105576. [Google Scholar] [CrossRef]
- Yao, N.; Li, L.; Feng, P.; Feng, H.; Li Liu, D.; Liu, Y.; Jiang, K.; Hu, X.; Li, Y. Projections of Drought Characteristics in China Based on a Standardized Precipitation and Evapotranspiration Index and Multiple GCMs. Sci. Total Environ. 2020, 704, 135245. [Google Scholar] [CrossRef]
- Almeida, M.P.; Perpiñán, O.; Narvarte, L. PV Power Forecast Using a Nonparametric PV Model. Sol. Energy 2015, 115, 354–368. [Google Scholar] [CrossRef]
- Farias de Reyes, M.; Montero, K. Increased Recurrence of Global and Coastal El Niño Events on the South American Coasts. In Proceedings of the 40th IAHR World Congress, Vienna, Austria, 21–25 August 2023; IAHR: Viena, Austria, 2023. [Google Scholar]
- QGIS Project. Bienvenido al Proyecto QGIS! Available online: https://www.qgis.org/es/site/ (accessed on 22 June 2024).
- GRASS Development Team; Landa, M.; Neteler, M.; Metz, M.; Petrášová, A.; Petráš, V.; Clements, G.; Zigo, T.; Larsson, N.; Kladivová, L.; et al. GRASS GIS, Version 8.4.0; Zenodo: Genève, Switzerland, 2024. [CrossRef]
- Hofierka, J.; Parajka, J.; Mitasova, H.; Mitas, L. Multivariate Interpolation of Precipitation Using Regularized Spline with Tension. Trans. GIS 2002, 6, 135–150. [Google Scholar] [CrossRef]
- Li, H.; Mu, H.; Jian, S.; Li, X. Assessment of Rainfall and Temperature Trends in the Yellow River Basin, China from 2023 to 2100. Water 2024, 16, 1441. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods, 4th ed.; 2d Impression; Griffin London: London, UK, 1975. [Google Scholar]
- Li, Y.; Horton, R.; Ren, T.; Chen, C. Prediction of Annual Reference Evapotranspiration Using Climatic Data. Agric. Water Manag. 2010, 97, 300–308. [Google Scholar] [CrossRef]
- Xavier Júnior, S.F.A.; Jale, J.d.S.; Stosic, T.; dos Santos, C.A.C.; Singh, V.P. Precipitation Trends Analysis by Mann-Kendall Test: A Case Study of Paraíba, Brazil. Rev. Bras. Meteorol. 2020, 35, 187–196. [Google Scholar] [CrossRef]
- Koudahe, K.; Kayode, A.J.; Samson, A.O.; Adebola, A.A.; Djaman, K. Trend Analysis in Standardized Precipitation Index and Standardized Anomaly Index in the Context of Climate Change in Southern Togo. ACS 2017, 7, 401–423. [Google Scholar] [CrossRef]
- Júnior, I.B.d.S.; Araújo, L.d.S.; Stosic, T.; Menezes, R.S.C.; da Silva, A.S.A. Space-Time Variability of Drought Characteristics in Pernambuco, Brazil. Water 2024, 16, 1490. [Google Scholar] [CrossRef]
- Chiew, F.; Siriwardena, L.; Arene, S.; Rahman, J. TREND. 2005. Available online: https://toolkit.ewater.org.au/Tools/TREND (accessed on 11 July 2023).
- Sen, P. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Lettenmaier, D.P.; Wood, E.F.; Wallis, J.R. Hydro-Climatological Trends in the Continental United States, 1948–1988. J. Clim. 1994, 7, 586–607. [Google Scholar] [CrossRef]
- Douglas, E.M.; Vogel, R.M.; Kroll, C.N. Trends in Floods and Low Flows in the United States: Impact of Spatial Correlation. J. Hydrol. 2000, 240, 90–105. [Google Scholar] [CrossRef]
- Ahmed, K.; Shahid, S.; Nawaz, N. Impacts of Climate Variability and Change on Seasonal Drought Characteristics of Pakistan. Atmos. Res. 2018, 214, 364–374. [Google Scholar] [CrossRef]
- Ali, R.; Kuriqi, A.; Abubaker, S.; Kisi, O. Long-Term Trends and Seasonality Detection of the Observed Flow in Yangtze River Using Mann-Kendall and Sen’s Innovative Trend Method. Water 2019, 11, 1855. [Google Scholar] [CrossRef]
- Lee, S.; Ha, J.; Na, O.; Na, S. The Cusum Test for Parameter Change in Time Series Models. Scand. J. Stat. 2003, 30, 781–796. [Google Scholar] [CrossRef]
- Hallouz, F.; Meddi, M.; Ali Rahmani, S.E.; Abdi, I. Innovative versus Traditional Statistical Methods in Hydropluviometric: A Detailed Analysis of Trends in the Wadi Mina Basin (Northwest of Algeria). Theor. Appl. Climatol. 2024, 155, 8263–8286. [Google Scholar] [CrossRef]
- Sam, M.G.; Nwaogazie, I.L.; Ikebude, C.; Dimgba, C.; El-Hourani, D.W. Detecting Climate Change Trend, Size, and Change Point Date on Annual Maximum Time Series Rainfall Data for Warri, Nigeria. Open J. Mod. Hydrol. 2023, 13, 165–179. [Google Scholar] [CrossRef]
- Afzal, M.; Gagnon, A.S.; Mansell, M.G. The Impact of the Variability and Periodicity of Rainfall on Surface Water Supply Systems in Scotland. J. Water Clim. Chang. 2016, 7, 321–339. [Google Scholar] [CrossRef]
- Autoridad Nacional del Agua. Evaluación Del Régimen Hidrológico En Las Cuencas de Los Ríos Chillón, Rímac, Mala y Cañete Para Escenarios de Cambio Climático; Autoridad Nacional del Agua: Lima, Peru, 2012.
- Teutschbein, C.; Seibert, J. Bias Correction of Regional Climate Model Simulations for Hydrological Climate-Change Impact Studies: Review and Evaluation of Different Methods. J. Hydrol. 2012, 456–457, 12–29. [Google Scholar] [CrossRef]
- Wang, L.; Li, Y.; Li, M.; Li, L.; Liu, F.; Liu, D.L.; Pulatov, B. Projection of Precipitation Extremes in China’s Mainland Based on the Statistical Downscaled Data from 27 GCMs in CMIP6. Atmos. Res. 2022, 280, 106462. [Google Scholar] [CrossRef]
- Lenderink, G.; Buishand, A.; van Deursen, W. Estimates of Future Discharges of the River Rhine Using Two Scenario Methodologies: Direct versus Delta Approach. Hydrol. Earth Syst. Sci. 2007, 11, 1145–1159. [Google Scholar] [CrossRef]
- Ahmed, K.; Sachindra, D.A.; Shahid, S.; Demirel, M.C.; Chung, E.-S. Selection of Multi-Model Ensemble of General Circulation Models for the Simulation of Precipitation and Maximum and Minimum Temperature Based on Spatial Assessment Metrics. Hydrol. Earth Syst. Sci. 2019, 23, 4803–4824. [Google Scholar] [CrossRef]
- Jiang, Z.; Li, W.; Xu, J.; Li, L. Extreme Precipitation Indices over China in CMIP5 Models. Part I Model Eval. 2015, 28, 8603–8619. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the Use of “Goodness-of-fit” Measures in Hydrologic and Hydroclimatic Model Validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Willmott, C.J. On the Validation of Models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]

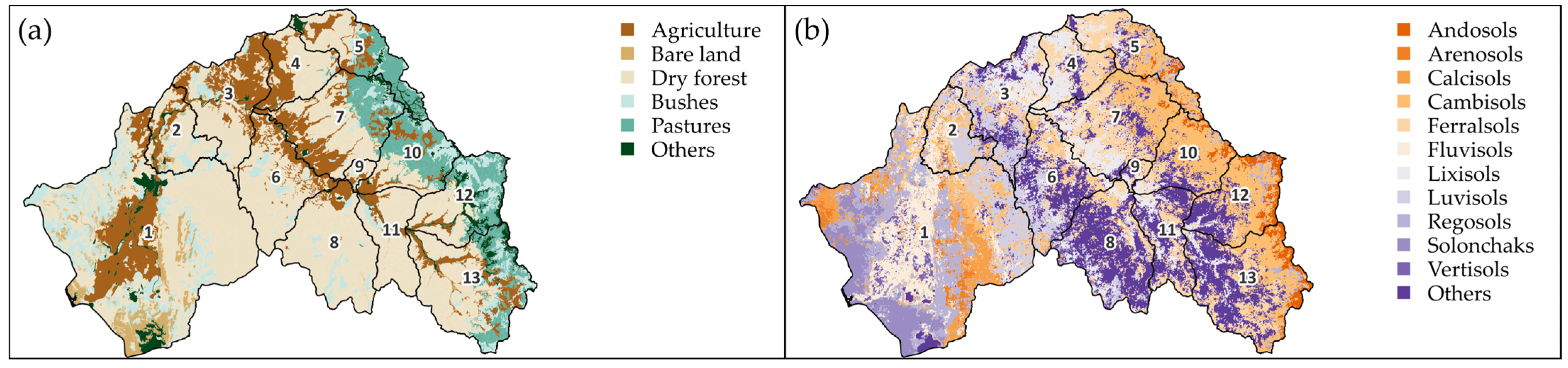
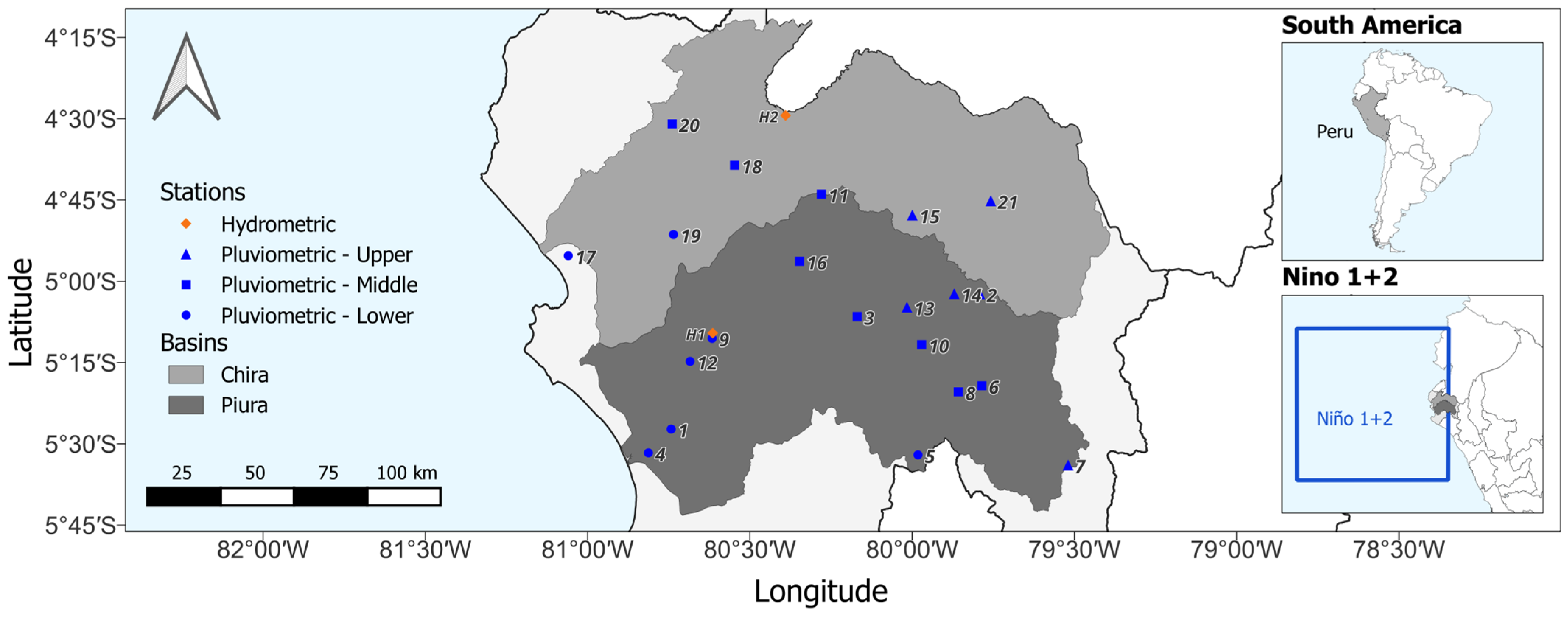

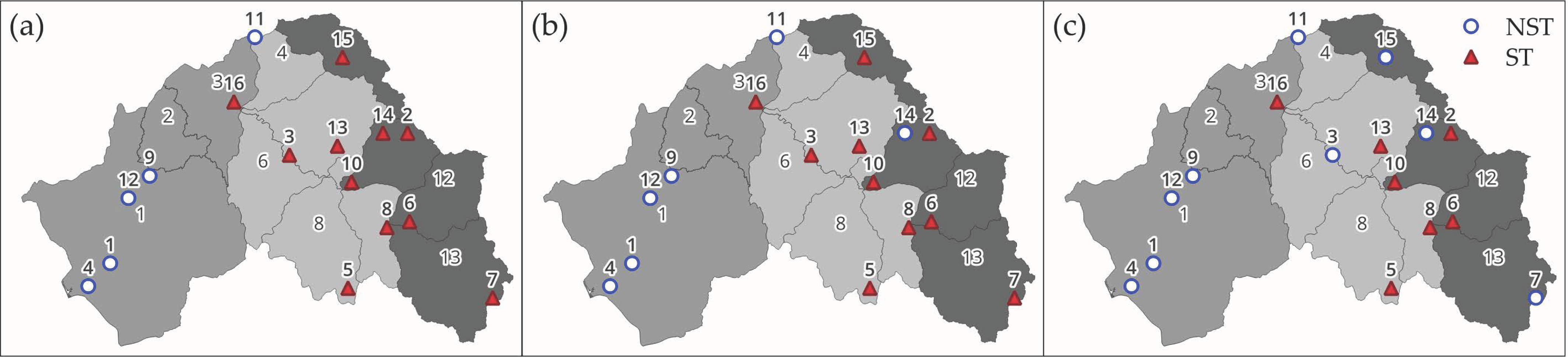
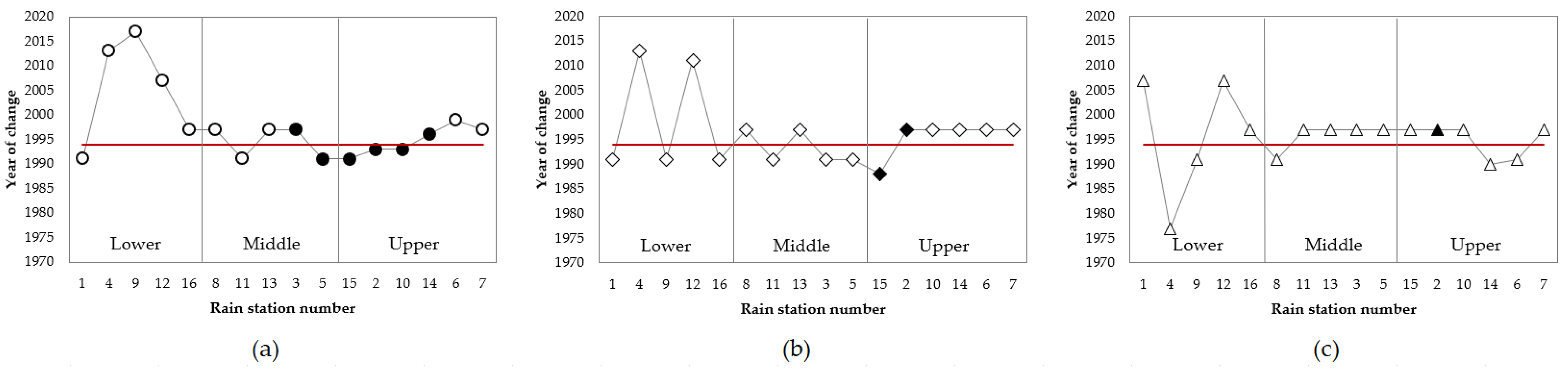



| Subbasin | HU | Name | Subbasin | HU | Name |
|---|---|---|---|---|---|
| Lower | 1 | Bajo Piura | Middle | 4 | San Francisco |
| 2 | Los Ejidos | 6 | Margen Izquierda | ||
| 3 | La Penita | 7 | Margen Derecha | ||
| Upper | 5 | Chipillico | 8 | La Matanza | |
| 12 | Bigote | 9 | Medio Piura | ||
| 13 | Alto Piura | 11 | Medio Alto Piura | ||
| 10 | Corrales |
| N° | Meteorological | Subbasin | River | Altitude | N° | Meteorological | Subbasin | River | Altitude |
|---|---|---|---|---|---|---|---|---|---|
| Station | Basin | (m a.s.l.) | Station | Basin | (m a.s.l.) | ||||
| 1 | Bernal | Lower | Piura | 11 | 11 | Partidor | Middle | Piura | 254 |
| 2 | Chalaco | Upper | Piura | 2290 | 12 | San Miguel | Lower | Piura | 24 |
| 3 | Chulucanas | Middle | Piura | 89 | 13 | San Pedro | Upper | Piura | 240 |
| 4 | Chusís | Lower | Piura | 8 | 14 | Santo Domingo | Upper | Piura | 1490 |
| 5 | El Virrey | Lower | Piura | 211 | 15 | Sapillica | Upper | Chira | 1406 |
| 6 ** | Hacienda Bigote | Middle | Piura | 198 | 16 | Tambogrande | Middle | Piura | 60 |
| 7 | Huarmaca | Upper | Piura | 2171 | 17 * | La Esperanza | Lower | Chira | 12 |
| 8 | Malacasí | Middle | Piura | 153 | 18 * | Lancones | Middle | Chira | 133 |
| 9 | Miraflores | Lower | Piura | 34 | 19 * | Mallares | Lower | Chira | 45 |
| 10 ** | Morropón | Middle | Piura | 128 | 20 * | Pananga | Middle | Chira | 360 |
| 21 * | Sausal de Culucán | Upper | Chira | 980 |
| N° | GCM Name | Institution | Country | Spatial Resolution lat° × lon° |
|---|---|---|---|---|
| 1 | ACCESS-CM2 * | CSIROARCCSS | Australia | 1.875° × 1.25° |
| 2 | CanESM5 | CCCma | Canada | 2.8125° × 2.79° |
| 3 | CESM2 * | NCAR | USA | 1.25° × 0.9424° |
| 4 | CESM2-WACCM * | |||
| 5 | CMCC-ESM2 | CMCC | Italy | |
| 6 | CNRM-CM6-1 | Centre National de Recherches Météorologiques | France | 1.25° × 1.25° |
| 7 | CNRM-ESM2-1 | 1.25° × 1.25° | ||
| 8 | EC-Earth3 * | International Centre for Earth Simulation | Norway | 1.0° × 1.0° |
| 9 | EC-Earth3-Veg-LR * | EC—Earth Consortium | Europe | 1.125° × 1.121° |
| 10 | HadGEM3-GC31-LL * | Met Office Hadley Centre | United Kingdom | 1.25° × 1.25° |
| 11 | INM-CM4-8 | INM | Rusia | 2° × 1.5° |
| 12 | INM-CM5-0 * | |||
| 13 | MIROC6 * | MIROC | Japan | 1.4° × 1.4° |
| 14 | MIROC-ES2L | 1.406° × 1.406° | ||
| 15 | MPI-ESM1-2-HR | Max Planck Institute for Meteorology | Germany | 0.6° × 0.6° |
| 16 | MPI-ESM1-2-LR | 1.875° × 1.875° | ||
| 17 | MRI-ESM2-0 | Meteorological Research Institute | Japan | 1.125° × 1.125° |
| 18 | NESM3 | University of Bergen and Norwegian Climate Centre | Norway | 1.0° × 1.0° |
| 19 | NorESM2-LM * | Norwegian Climate Centre | 2.5° × 1.89° | |
| 20 | NorESM2-MM * | 1.25° × 0.94° |
| EN/LN Category | P_Index | Lower Zone | Middle Zone | Upper Zone |
|---|---|---|---|---|
| Very strong: EN4 | +4 | 6.26–31.44 | 4.32–19.07 | 2.19–5.22 |
| Strong: EN3 | +3 | 3.88–6.26 | 2.87–4.32 | 2.00–2.19 |
| Moderate: EN2 | +2 | 2.80–3.88 | 2.25–2.87 | 1.83–2.00 |
| Weak: EN1 | +1 | 2.13–2.80 | 2.00–2.25 | 1.71–1.83 |
| Neutral | 0 | 0.30–2.13 | 0.50–2.00 | 0.90–1.71 |
| Weak: LN1 | −1 | 0.15–0.30 | 0.27–0.50 | 0.75–0.90 |
| Moderate: LN2 | −2 | 0.08–0.15 | 0.13–0.27 | 0.62–0.75 |
| Strong: LN3 | −3 | 0.02–0.08 | 0.05–0.13 | 0.49–0.62 |
| Very strong: LN4 | −4 | <0.02 | <0.05 | 0.09–0.49 |
| Categories | Index | CNI Ext (°C) | Streamflow Piura (m3/s) | Streamflow Chira (m3/s) | Volume Piura (hm3) | Volume Chira (hm3) |
|---|---|---|---|---|---|---|
| EN4 | 4 | > 3.0 | 2652–3900 | 3255–8000 | 3510–14,049 | 7081–18,164 |
| EN3 | 3 | 1.7–3.0 | 1747–2652 | 2577–3255 | 2066–3510 | 6291–7081 |
| EN2 | 2 | 1.0–1.7 | 1513–1747 | 2207–2577 | 1659–2066 | 4983–6291 |
| EN1 | 1 | 0.4–1.0 | 1000–1513 | 1654–2207 | 1240–1659 | 3743–4983 |
| Neutral | 0 | −1.0–0.4 | 350–1000 | 798–1654 | 624–1240 | 3615–3743 |
| LN1 | −1 | −1.2–−1.0 | 122–350 | 578–798 | 420–624 | 2148–3615 |
| LN2 | −2 | −1.4–−1.2 | 74–122 | 405–578 | 204–420 | 1737–2148 |
| LN3 | −3 | −2.0–−1.4 | 34–74 | 307–405 | 83–204 | 1358–1737 |
| LN4 | −4 | <−2.0 | 0–34 | 150–307 | 0–83 | 767–1358 |
| Category | Hydrological Years | Total and Incidence | Total by Intensity | Return Period (Years) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EN1/LN1 | EN2/LN2 | EN3/LN3 | EN4/LN4 | 1 to 4 | 2 to 4 | 3 to 4 | 4 | EN1/LN1 | EN2/LN2 | EN3/LN3 | EN4/LN4 | ||
| Global El Niño | 1957–58 | 2015–16 | 1952–53 | 1982–83 | 10; 13% | 19 | 10 | 8 | 3 | 4.0 | 7.6 | 9.5 | 25.3 |
| 1986–87 | 1991–92 | 1997–98 | |||||||||||
| 1992–93 | |||||||||||||
| 2018–19 | |||||||||||||
| 2023–24 | |||||||||||||
| Coastal El Niño | 1956–57 | 1971–72 | 2001–02 | 2016–17 | 9; 12% | ||||||||
| 1964–65 | 2007–08 | ||||||||||||
| 1996–97 | 2022–23 | ||||||||||||
| 2011–12 | |||||||||||||
| Global La Niña | 1954–55 | 1970–71 | 1973–74 | 1949–50 | 12; 16% | 18 | 15 | 10 | 4 | 4.2 | 5.1 | 7.6 | 19.0 |
| 1955–56 | 2010–11 | 1984–85 | 1967–68 | ||||||||||
| 2020–21 | 2021–22 | 1995–96 | |||||||||||
| 2017–18 | |||||||||||||
| Coastal La Niña | 1961–62 | 1953–54 | 1963–64 | 6; 8% | |||||||||
| 1980–81 | 2012–13 | 1965–66 | |||||||||||
| Neutral * | 1950–51 | 1974–75 | 1988–89 | 2004–05 | 38; 51% | 38 | 2.0 | ||||||
| 1951–52 | 1975–76 | 1989–90 | 2005–06 | ||||||||||
| 1958–59 | 1976–77 | 1990–91 | 2006–07 | ||||||||||
| 1959–60 | 1977–78 | 1993–94 | 2008–09 | ||||||||||
| 1960–61 | 1978–79 | 1994–95 | 2009–10 | ||||||||||
| 1962–63 | 1979–80 | 1998–99 | 2013–14 | ||||||||||
| 1966–67 | 1981–82 | 1999–00 | 2014–15 | ||||||||||
| 1968–69 | 1983–84 | 2000–01 | 2019–20 | ||||||||||
| 1969–70 | 1985–86 | 2002–03 | |||||||||||
| 1972–73 | 1987–88 | 2003–04 | |||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farias de Reyes, M.; Chávarri-Velarde, E.; Cotrina, V.; Aguilar, P.; Vegas, L. Space-Time Variability of Maximum Daily Rainfall in Piura River Basin in Peru Related to El Niño Occurrence. Water 2024, 16, 3452. https://doi.org/10.3390/w16233452
Farias de Reyes M, Chávarri-Velarde E, Cotrina V, Aguilar P, Vegas L. Space-Time Variability of Maximum Daily Rainfall in Piura River Basin in Peru Related to El Niño Occurrence. Water. 2024; 16(23):3452. https://doi.org/10.3390/w16233452
Chicago/Turabian StyleFarias de Reyes, Marina, Eduardo Chávarri-Velarde, Valeria Cotrina, Pierina Aguilar, and Laura Vegas. 2024. "Space-Time Variability of Maximum Daily Rainfall in Piura River Basin in Peru Related to El Niño Occurrence" Water 16, no. 23: 3452. https://doi.org/10.3390/w16233452
APA StyleFarias de Reyes, M., Chávarri-Velarde, E., Cotrina, V., Aguilar, P., & Vegas, L. (2024). Space-Time Variability of Maximum Daily Rainfall in Piura River Basin in Peru Related to El Niño Occurrence. Water, 16(23), 3452. https://doi.org/10.3390/w16233452






